摘要: 合金凝固过程中, 游离枝晶在熔体中的运动行为是研究合金凝固组织形成过程的关键问题之一. 元胞自动机-格子玻尔兹曼耦合模型是近年来进行凝固微观组织数值模拟的主要数值模型. 本文改进了模拟枝晶生长的元胞自动机和格子玻尔兹曼模型, 使其能够模拟过冷熔体中等轴晶的运动行为. 改进的模型采用伽利略不变的动量交换法计算流体力, 通过求解质心运动方程计算枝晶的运动位移, 并通过动网格技术实现枝晶的运动, 运用硬球模型处理枝晶的碰撞. 采用该模型模拟了Al-4.7%Cu合金过冷熔体中单枝晶的沉降、牛顿流体中两圆形粒子的沉降和两枝晶的弹性碰撞. 模拟结果表明, 本模型在计算枝晶生长运动过程时可以很好地维持枝晶的形貌. 采用本模型计算等轴枝晶的碰撞过程表明, 枝晶的运动会扰动其周围的熔体, 造成周围熔体浓度显著变化, 进而影响枝晶的生长, 加剧枝晶生长的不对称性.
关键词: 元胞自动机 /
格子玻尔兹曼 /
枝晶碰撞 /
动网格 English Abstract Simulation of dendrite collision behavior based on cellular automata-lattice Boltzmann model Zhang Shi-Jie Wang Ying-Ming Wang Qi Li Chen-Yu Li Ri School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300401, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 51475138, 51975182).Received Date: 11 July 2021Accepted Date: 03 August 2021Available Online: 20 August 2021Published Online: 05 December 2021Abstract: In the alloy solidification process, the movement behavior of free dendrites in the melt is one of the key issues in studying the formation process of the alloy solidification structure. The cellular automata-lattice Boltzmann coupling model has become a main numerical model for numerical simulation of solidification microstructure in recent years. In this paper, cellular automata and lattice Boltzmann model for simulating dendrite growth are improved to simulate the movement of equiaxed grains in undercooled melt. In the improved model, the Galilean invariant momentum exchange method is used to calculate the fluid force, the motion equation of the center of mass is solved to calculate the motion displacement of the dendrite, the motion of the dendrite is realized through the dynamic mesh technology, and the rigid sphere model is used to deal with the collision of the dendrite. The settlement of a single dendrite in the undercooled melt of Al-4.7% Cu alloy, the settlement of two round particles in the Newtonian fluid, and the elastic collision of two dendrites are all simulated by this model. The simulation results show that this model can maintain the morphology of dendrites well in the process of calculating dendrite growth motion, and this model can calculate the collision process of irregular dendrites. The movement of dendrite disturbs the melt around it, resulting in a significant change in the concentration of melt around it, which affects the growth of dendrite and aggravates the asymmetry of dendrite growth.Keywords: cellular automata /lattice Boltzmann /dendrite collision /dynamic grid 全文HTML --> --> --> 1.引 言 合金凝固过程中, 铸型壁面的表层细晶粒可能会脱落, 已经凝固的枝晶臂(特别是二次枝晶臂)也可能发生熔断现象, 再加上在熔体中随机出现的数量可观的自由等轴晶, 所以在液相区会出现大量游离的等轴晶, 这些游离的等轴晶在重力和对流的推动下在合金熔体中运动(平移和旋转), 且常常会发生碰撞现象[1 ] . 熔体中游离枝晶的运动对铸件的组织形貌和成分分布会有很大的影响[2 ] .[3 -5 ] , 并已发展到了三维(3 dimension, 3D)[6 -8 ] . 而关于枝晶运动的模拟, 由于在计算枝晶运动的同时还要同时计算枝晶生长, 所以有一定难度. 目前该方面的研究比较少, 已发表的枝晶运动的文献中大多采用相场(phase field, PF)方法[9 -13 ] . 采用PF计算出的界面是连续扩散界面, 对运动界面的处理有天然的优势, 但是计算量非常大, 计算效率较低, 计算规模小. 而具有计算简单快速、天然并行等优点的元胞自动机(cellular automata, CA)模型在模拟微观组织方面的应用, 大多数都只模拟了静止枝晶的生长[14 -17 ] , 对于枝晶运动的模拟研究很少, 且不能很好地维持枝晶的形貌[18 ,19 ] . 本文旨在改进CA模型, 使其在模拟枝晶运动时能够较好地维持枝晶的形貌和成分, 在提升效率的同时提高模拟精度; 同时, 在模型中还加入了碰撞处理机制, 使该模型能够处理枝晶运动引起的碰撞现象.2.模拟方法 采用格子玻尔兹曼(lattice Boltzmann, LB)模型计算流场、温度场和浓度场, 采用CA方法模拟微观枝晶生长, 通过求解运动方程来计算枝晶的运动位移(平动和转动), 采用硬球模型计算枝晶碰撞(假设枝晶碰撞为完全弹性碰撞), 耦合上述方法建立起枝晶运动生长的数值模型以研究枝晶在熔体中的运动行为.2.1.LB模型 2.1.LB模型 采用单松弛时间的D2Q9双分布函数模型[20 ] , 流场、温度场和浓度场的玻尔兹曼方程为$ \boldsymbol{x} $ 和$t$ 分别为粒子的位置和时间; $\Delta t$ 为时间步长; $ {\boldsymbol{e}_{\rm{i}}} $ 为离散粒子速度; ${f_{\rm{i}}},{g_{\rm{i}}}, {m_{\rm{i}}} $ 分别为流场、温度场和浓度场的粒子分布函数; $f_{\rm{i}}^{\rm eq}, g_{\rm{i}}^{\rm eq}, m_{\rm{i}}^{\rm eq}$ 分别为流场、温度场和浓度场的平衡分布函数; ${\tau _{\rm{f}}}, {\tau _{\rm{t}}}$ , ${\tau _{\rm{c}}}$ 分别为流场、温度场和浓度场的松弛时间; $ {F_{\rm{i}}} $ , $ {H_{\rm{i}}} $ , $ {G_{\rm{i}}} $ 分别为流场、温度场和浓度场的源项.${\omega _{\rm{i}}}$ 是权重函数; $c$ 是格子速度; $ \boldsymbol{u} $ 是流体宏观速度, 温度场和浓度场的格式和流场一样. 流体的流场、温度场和浓度场的松弛时间${\tau _{\rm{f}}}$ , ${\tau _{\rm{t}}}$ , ${\tau _{\rm{c}}}$ 分别和动力学黏度$\nu $ 、热扩散系数$\alpha $ 、溶质扩散系数$D$ 有关:$\Delta {f_{\rm{s}}}$ 是固相率增量; $ L $ 是潜热; ${C_{\rm{p}}}$ 是比热容; ${C_{\rm{l}}}$ 是液相浓度; $ k $ 是平衡分配系数; $\boldsymbol{F}$ 是粒子受到的合力, 由Boussinesq近似[21 ] 给出:$ \boldsymbol{g} $ 为重力加速度; ${\rho _{\text{0}}}$ , $ {T_0} $ , $ {C_0} $ 分别为初始密度、温度和浓度; ${\beta _{\rm{T}}}$ 和${\beta _{\rm{C}}}$ 分别为温度膨胀系数和溶质膨胀系数.$ \rho $ , 速度$ \boldsymbol{u} $ , 温度$ T $ 和浓度$ C $ 分别为2.2.CA模型 -->2.2.CA模型 溶质扩散模型最早由Rappaz 和Thévoz[22 ] 于1987年提出的, 之后经过多次改进. 2007年, Zhu 和 Stefanescu[23 ] 提出了用于定量化计算合金凝固过程中树枝晶生长的虚拟前沿跟踪模型. 该模型认为合金枝晶生长是由局部液体平衡成分和局部液体实际成分的差异所驱动的. 根据局部平衡的热力学概念, 界面平衡温度$ {T^*} $ 定义为$T_{\rm{l}}^{\rm eq}$ 为初始组分$ {C_0} $ 处的液相线温度; ${m_l}$ 是液相线斜率; $\varGamma$ 是Gibbs-Thomson系数; $ K $ 为固/液界面处的曲率; $ f\left( {\phi , {\theta _0}} \right) $ 是考虑界面张力各向异性的函数, 其中$ {\theta _0} $ 是择优生长方向与x -轴的夹角, $ \phi $ 是界面法向与x -轴之间的生长角. 局部界面曲率可由下式计算:${f_{\rm{s}}}$ 为元胞的固相分数. 根据Gibbs-Thomson公式, 界面能各向异性函数可以表示为$ \delta $ 为各向异性系数. 因此, 界面平衡浓度可以计算为2.3.枝晶运动方程 -->2.3.枝晶运动方程 将运动枝晶看作刚体处理, 枝晶在熔体中运动所受到的流体力采用伽利略不变的动量交换法[24 ] 计算, 流体对$\alpha$ 枝晶的边界点$ \boldsymbol{x} $ 的作用力为$i$ 和$\bar i$ 表示粒子迁移的相反方向; 下标${\rm{f}}$ 和${\rm{b}}$ 表示相邻的流体和边界点, ${\tilde f_i}({\boldsymbol{x}_{\rm{f}}}, t)$ 和${\tilde f_{\bar i}}({\boldsymbol{x}_{\rm{b}}}, t)$ 表示流体和边界节点的碰后分布函数, 采用曲线边界条件[25 ] 计算, $ \boldsymbol{v} $ 为边界速度$ \boldsymbol{R} $ 为枝晶质心的位置矢量; $ {\boldsymbol{v}_\alpha } $ 和${\omega _\alpha }$ 分别为平动和转动速度.$\alpha $ 枝晶受到总的力$ {\boldsymbol{F}_\alpha } $ 和扭矩$ {\boldsymbol{T}_\alpha } $ 为$\varOmega$ 是$\alpha $ 枝晶的边界区域; ${\rho _{\rm{l}}}$ 和${\rho _{\rm{s}}}$ 分别为流体和固体的密度, 固体质量${M_\alpha } = \displaystyle\sum\nolimits_{\boldsymbol{x} \in \alpha } {{\rho _{\rm{s}}}{f_{\rm{s}}}(\boldsymbol{x})}$ .$ {\boldsymbol{I}_\alpha } $ 为惯性张量.2.4.碰撞模型 -->2.4.碰撞模型 游离的枝晶在熔体中碰撞的情况很复杂, 初步假定枝晶间的碰撞为完全弹性碰撞, 因此采用硬球模型来处理碰撞步骤. 将枝晶看做刚性粒子处理. 对枝晶应用动量定理和动量矩定理:$m$ 为枝晶质量; $ {\boldsymbol{v}_0} $ 和$ \boldsymbol{v} $ 是碰撞前、后的速度; ${\omega _0}$ 和$\omega $ 是碰撞前、后的角速度; $ \boldsymbol{S} $ 为内力冲量.${\omega _{10}}$ , ${\omega _{20}}$ 和${\omega _1}$ , ${\omega _2}$ 分别为碰撞前、后枝晶1和枝晶2的角速度; $ {\boldsymbol{v}_{10}} $ , $ {\boldsymbol{v}_{{\text{2}}0}} $ 和$ {\boldsymbol{v}_1} $ , $ {\boldsymbol{v}_{\text{2}}} $ 分别为碰撞前、后枝晶1和枝晶2的速度; $ {\boldsymbol{I}_{\text{1}}} $ , $ {\boldsymbol{I}_{\text{2}}} $ 为枝晶1, 2的转动惯量; $ {\boldsymbol{r}_1} $ 和$ {\boldsymbol{r}_{\text{2}}} $ 分别为碰撞点与枝晶1和枝晶2质心的位置矢量.$ \boldsymbol{e} $ , 并与(26 )式联立写成矩阵$ \boldsymbol{AX} = \boldsymbol{b} $ 形式:2.5.动网格方案 -->2.5.动网格方案 虽然CA方法计算效率高, 但是在处理移动边界问题上存在困难. 由于CA方法的界面是尖锐界面, 所以其界面在空间上的移动是不连续的, 然而浓度在空间上的传输必须保证是连续的, 这导致了在处理枝晶运动时溶质浓度在枝晶周围积聚, 人为地改变了枝晶的环境, 影响了枝晶的生长. 为了解决这个问题, 本文改进了CA-LB模型, 采用局部动网格技术处理枝晶的运动.图1 所示). 在背景网格中求解流场和温度场, 计算枝晶受到的力和转矩. 在每个动网格和背景网格中同时求解浓度场, 将动网格中的溶质浓度覆盖背景网格, 动网格中流体节点的速度是相对速度,图 1 动网格方案示意图Figure1. Schematic diagram of dynamic grid scheme.M θ )是旋转矩阵, v 1 是流体节点在动网格中的速度, v g 是流体节点在背景网格中的速度, v d 是动网格在该点的合速度, 由方程(19 )求出. 旋转矩阵被定义为θ 是枝晶的转动角度. 动网格的边界从全局网格插值得出. 枝晶的生长和捕获在动网格中计算, 将枝晶的固相分数在每一步插值到背景网格中.3 )中的源项为0, 方程退化为简单的对流扩散方程, 因为动网格中的速度是相对速度, 每个动网格中的流动相对于背景网格都是一样的, 所以每个动网格中的浓度值都是相等的; 如果有界面节点和固体节点, 则选定该值为背景网格的值. 本方法的优点是将不连续的枝晶移动转化为连续的熔体流动, 通过局部网格中流体的相对流动体现枝晶的运动, 避免了直接处理枝晶时溶质的积聚现象.2.6.算法 -->2.6.算法 模型的耦合算法流程如图2 所示, 算法如下:图 2 算法流程图Figure2. Algorithm flowchart.1 )计算流场, 根据方程(18 )—方程(21 )计算枝晶受到的力和扭矩;2 )和方程(3 );13 )—方程(17 )计算枝晶的生长和捕获, 更新枝晶的质量、质心和转动惯量;22 )和方程(23 )计算枝晶的位移和转动角, 据此移动局部网格;${f_{\rm{s}}}$ 、温度和浓度插值到背景网格;2 )—(8 )步, 直至程序结束.3.模拟结果与讨论 选取Al-4.7%Cu(质量含量)合金为模拟材料, 其物性参数如表1 所列.Physical parameter Value Melting temperature, T m /K 933.3 Solidification temperature, T 0 /K 920.1 Diffusivity in liquid, D /(10–9 m2 ·s–1 ) 3.0 Partition coefficient, k 0.145 Gibbs-Tomson coefficient, Γ /(10–7 m·K) 2.4 Specific heat capacity, C p /(J·kg–1 ·K–1 ) 1179 Latent heat, L /(103 J·kg–1 ) 397 Density, ρ /(kg·m–3 ) 2606
表1 Al-4.7%Cu(质量含量)合金的热物性参数[26 ] Table1. Physical properties of Al-4.7%Cu (weight percent) alloy[26 ] .3.1.自然对流下单枝晶沉降 3.1.自然对流下单枝晶沉降 将计算区域划分为300 × 600个网格, 网格间距为0.5 $\text{μ} {\rm{m}}$ , 时间步长为${\text{2}}{\text{.5}} \times {\text{1}}{{\text{0}}^{{ - 6}}}{\text{ }}{\rm{s}}$ , 初始过冷度为7 K, 流场边界为非平衡外推边界条件, 温度场和浓度场采用无扩散边界条件, 固液边界为无滑移边界条件. 初始时刻, 在计算域(150, 450)处设置1个择优生长角为45°的晶核. 图3 为自然对流下单枝晶沉降过程中溶质浓度和流体速度演化. 在枝晶运动早期, 由于枝晶运动速度较小, 运动及熔体对流对枝晶生长的影响较小, 枝晶生长比较均衡, 四个一次枝晶臂形貌比较接近, 如图3(a) 所示. 随着枝晶的下落, 枝晶迎流端生长加快, 二次枝晶臂相比于顺流端发达, 枝晶的下游熔体的溶质浓度高于上游的溶质浓度, 如图3(b) 和图3(c) 所示.图 3 自然对流下单枝晶沉降过程中溶质浓度和流体速度的时间演化 (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 sFigure3. Evolution of solute concentration and fluid velocity during precipitation of single dendrite under natural convection: (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 s.图4 为图3(b) 中O 点(150, 250)竖直方向上的溶质浓度变化. 图中横坐标r 为距O 点的距离, O 点水平线下边为枝晶的迎流端上边为顺流端. 从图4 可以看出, 迎流端的峰值比顺流端的高, 这是因为枝晶呈45°生长时, 随着枝晶的下落溶质会积聚在枝晶凹形的枝晶臂间; 在溶质变化平稳后, 顺流端的溶质浓度略高于迎流端, 即如图3(b) 所示, 在枝晶后会形成一段淡淡的拖尾. 图5 为枝晶尖端生长速度随时间的变化. 从图5 中可以看出, 在枝晶凝固初期, 无论是上游尖端还是下游尖端的生长速率基本一致, 都处于快速下降, 这是由于凝固初期枝晶生长所需的过冷以热过冷为主. 随着生长进入稳定阶段, 可以看出上游尖端的生长速度明显高于下游尖端, 上游尖端的稳态生长速度平均约为2.49 mm/s , 下游尖端的稳态生长速度平均约为1.47 mm/s, 上游尖端的生长速度比下游尖端的生长速度快了约1.7倍. 从图3 可以看出, 相比于之前的研究[18 ,19 ] , 采用本文提出的动网格方案计算枝晶移动可以很好地保持枝晶的形貌. 对于单个枝晶而言, 小的计算域便可以展示枝晶的运动情况, 因此设置的计算域较小, 应用本模型在Intel Reon E5-2650 v4 2.20 GHz CPU, 内存64 G的服务器上单线程计算时间为1085 s, 而采用openMP加速后, 12线程计算共用时246 s.图 4 t = 0.015 s时, 模拟域O 点处竖直方向上的溶质浓度变化Figure4. When t = 0.015 s, the solute concentration change in the vertical direction at point O in the simulation domain.图 5 枝晶尖端生长速度随时间的变化Figure5. The change of dendrite tip growth rate with time.3.2.牛顿流体中两圆形粒子的沉降 -->3.2.牛顿流体中两圆形粒子的沉降 为了验证碰撞程序的可行性, 模拟了牛顿流体中两圆形粒子的沉降. 模拟域设置为宽$W = 2{\text{ }}{\rm{cm}}$ , 高$H = 8{\text{ }}{\rm{cm}}$ , 两密度${\rho _{\rm{p}}} = 1.01{\text{ }}{\rm{g}} \cdot {\rm{c{m^{-3}} }}$ , 直径$D = $ $ 0.2{\text{ }}{\rm{cm}}$ 粒子位于模拟域水平方向的中间, 竖直方向两粒子分别在7.2和6.8 cm处. 域中充满密度${\rho _{\rm{f}}} = 1{\text{ }}{\rm{g}} \cdot {\rm{c{m^{-3}}}}$ , 运动黏度${\nu _{\rm{f}}} = 0.01{\text{ }}{\rm{c}}{\rm{{m^2}/s}}$ 的水. 在LB模型中, 将模拟域剖分为200 × 800的网格, 松弛时间$\tau = {\text{0}}{\text{.65}}$ , 上下边界采用非平衡外推格式, 左右边界采用无滑移边界条件. 这里使用的条件与Feng 和Michaelides[27 ] 使用的条件一样. 初始时刻, 两粒子和流体都处于静止状态, 粒子受到重力和浮力的作用开始运动.图6(a) —(d) 分别是t = 1.0 s, t = 1.5 s, t = 2.5 s, t = 4.0 s时两粒子沉降过程的瞬时涡量轮廓. 图7(a) 和图7(b) 分别为粒子质心横、纵坐标随时间变化的图像. 多粒子沉降时会出现漂移-接触-翻滚(drafting-kissing-tumblin, DKT)现象, 由图6 中可以看出, 运动早期粒子1被粒子2沉降产生的尾涡捕获使其沉降速度加快, 到1.5 s时与粒子1接触, 直至2.5 s时两粒子发生翻滚. 运用本文的模型成功模拟再现了Feng的结果. 在图7 中比较了Feng和Michaelides[27 ] 的结果, 可以看出粒子下落的轨迹是一致的, 存在的一些误差是本文对流体力和碰撞的处理与Feng和Michaelides的不同, 本文计算流体力采用的动量交换法满足伽利略不变性, 排除了边界速度的影响, Feng和Michaelides[27 ] 采用的动量交换法不满足伽利略不变性. 由于粒子边界速度的影响造成计算流体力时存在误差.图 6 两个球形粒子沉降过程中, 四个时间的瞬时涡量轮廓 (a) 1 .0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 sFigure6. The instantaneous vorticity profiles of two spherical particles in the process of settling at four times: (a) 1.0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 s.图 7 粒子质心坐标 (a) 横坐标; (b) 纵坐标Figure7. Coordinates of the particles centroid: (a) Transverse coordinates; (b) longitudinal coordinates.3.3.双枝晶弹性碰撞 -->3.3.双枝晶弹性碰撞 计算区域为600 × 400个网格, 初始过冷度为7 K, 温度场边界为绝热边界条件, 溶质场为无扩散边界条件. 为了便于研究枝晶的碰撞行为, 将初始流场设置为静止状态, 在计算域(200, 200)和(400, 230)的位置放置两个晶核, 相对于水平方向的择优生长角分别为0°和45°, 组成为${C_{\rm{s}}} = k{C_{\rm{l}}}$ . 当枝晶生长一定大小时, 枝晶不在生长并直接赋给两个枝晶0.1和–0.1 (lattice unit)的水平速度, 忽略重力的影响.图8(a) , 左边是枝晶1右边是枝晶2, 两个枝晶受到熔体的阻力作减速运动直至发生碰撞如图8(b) , 碰撞前枝晶1, 2的水平速度分别为0.08和–0.082, 碰撞后速度分别为–0.029和0.024, 碰后角速度为0和0.0036 rad. 图8(c) 和图8(d) 显示两枝晶碰撞后的运动情况. 碰撞时, 由于碰撞点和枝晶1的质心在同一高度, 所以碰撞产生的冲量对枝晶1的转矩为0, 枝晶1不发生转动.图 8 枝晶偏心碰撞形貌图 (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s. 箭头表示速度v 的大小和方向, 灰度表示流体溶质浓度C Figure8. The morphology of dendrite eccentric collision: (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s . The arrow indicates the size and direction of velocity v , and the gray scale indicates the concentration of solute C .图9 为0.008和0.009 s时, 枝晶2周围熔体的平均溶质浓度C ave , x- 轴表示距离枝晶2质心的元胞个数. C ave 的计算规则如图10 所示, 图10 中白色格子表示枝晶的质心, x 表示距离质心的元胞数. 当x = 1时, C ave 等于浅灰色格子中所有液相格点的平均浓度; 当x = 2时, C ave 等于浅黑色格子中所有液相格点的平均浓度; 其他与x 值对应的C ave 同理计算. 从图9 中可以看出, 在0.008 s时枝晶处于静止生长状态, 枝晶2周围的溶质浓度在界面处最大随后缓慢的减少直至稳定. 这是因为枝晶生长时在固液界面处向外排出溶质, 排出的溶质向周围均匀的扩散, 所以形成了这样的浓度梯度. 在0.009 s时, 溶质浓度的变化变得不均衡, 在枝晶尖端附近浓度最高. 因为枝晶2在碰撞后发生了转动, 对周围熔体进行了扰动, 使周围的熔体浓度变化混乱, 将溶质甩在了枝晶的尖端附近. 通过对双枝晶弹性碰撞的计算可以证明本文所用碰撞模型可以表达不规则等轴枝晶的碰撞过程.图 9 枝晶2附近熔体平均溶质浓度Figure9. Average solute concentration of melt near dendrite 2图 10 熔体平均溶质浓度计算规则Figure10. Calculation rules of melt average solute concentration.4.结 论 本文建立了一个改进的CA-LB模型, 该模型采用动网格技术实现枝晶的运动, 每个枝晶拥有一个可移动的局部网格, 在局部网格内通过流体的相对流动来体现枝晶的移动; 模型中还加入了处理枝晶的碰撞的机制. 应用该模型模拟了自然对流下单枝晶的沉降过程, 模拟结果表明, 枝晶运动的上游端浓度变化梯度大, 生长速度加快, 二次枝晶臂发达; 同时表明该模型可以很好地模拟枝晶的运动过程, 并维持枝晶的形貌. 对模型的碰撞机制进行了测试, 模拟了牛顿流体中两圆形粒子的沉降, 成功再现了DKT现象, 证明了碰撞算法的可行性. 计算了两枝晶的弹性碰撞, 模拟结果表明该模型可以处理不规则枝晶的偏心碰撞. 























































































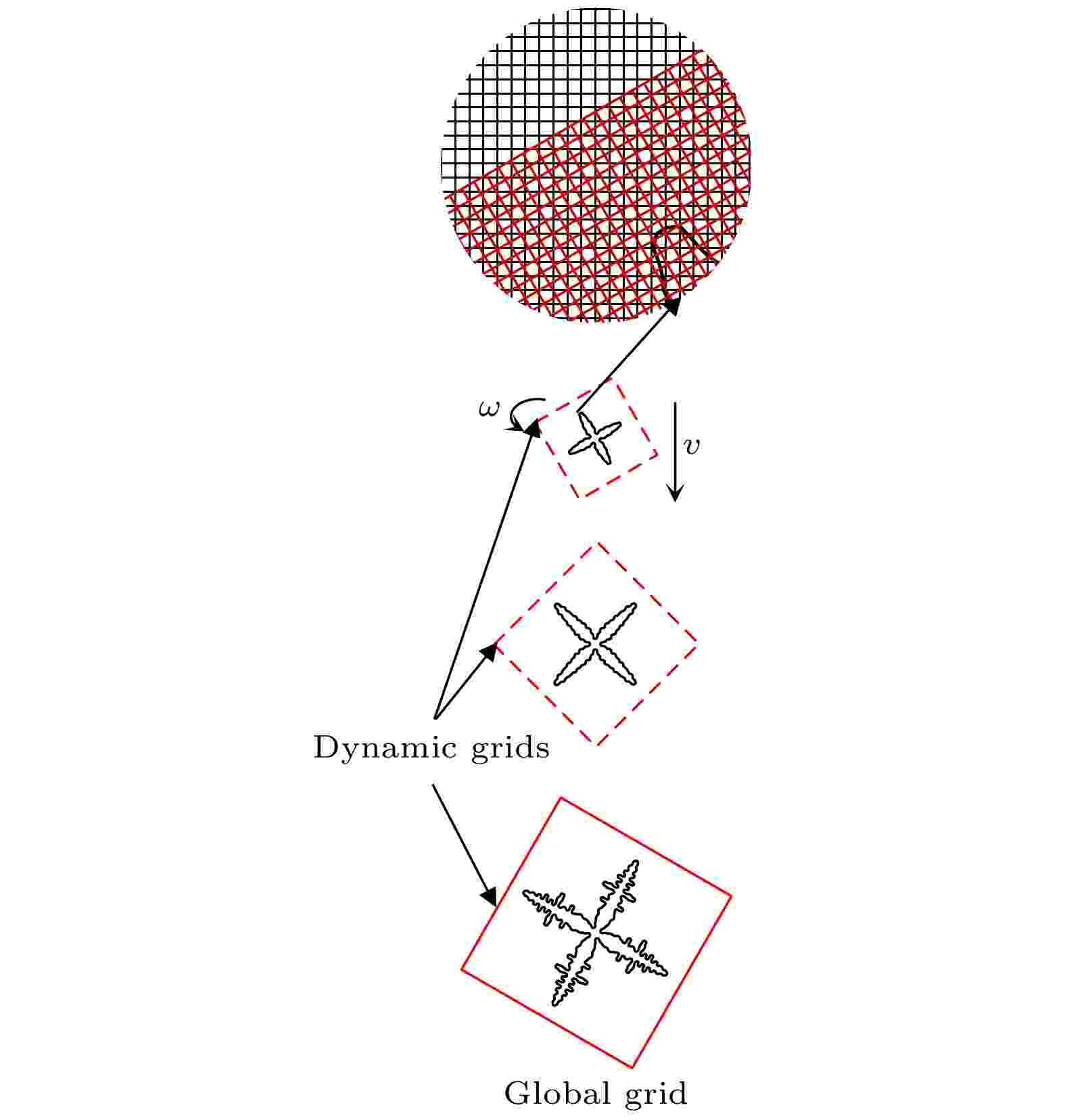 图 1 动网格方案示意图
图 1 动网格方案示意图 图 2 算法流程图
图 2 算法流程图


 图 3 自然对流下单枝晶沉降过程中溶质浓度和流体速度的时间演化 (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 s
图 3 自然对流下单枝晶沉降过程中溶质浓度和流体速度的时间演化 (a) t = 0.005 s; (b) t = 0.015 s; (c) t = 0.025 s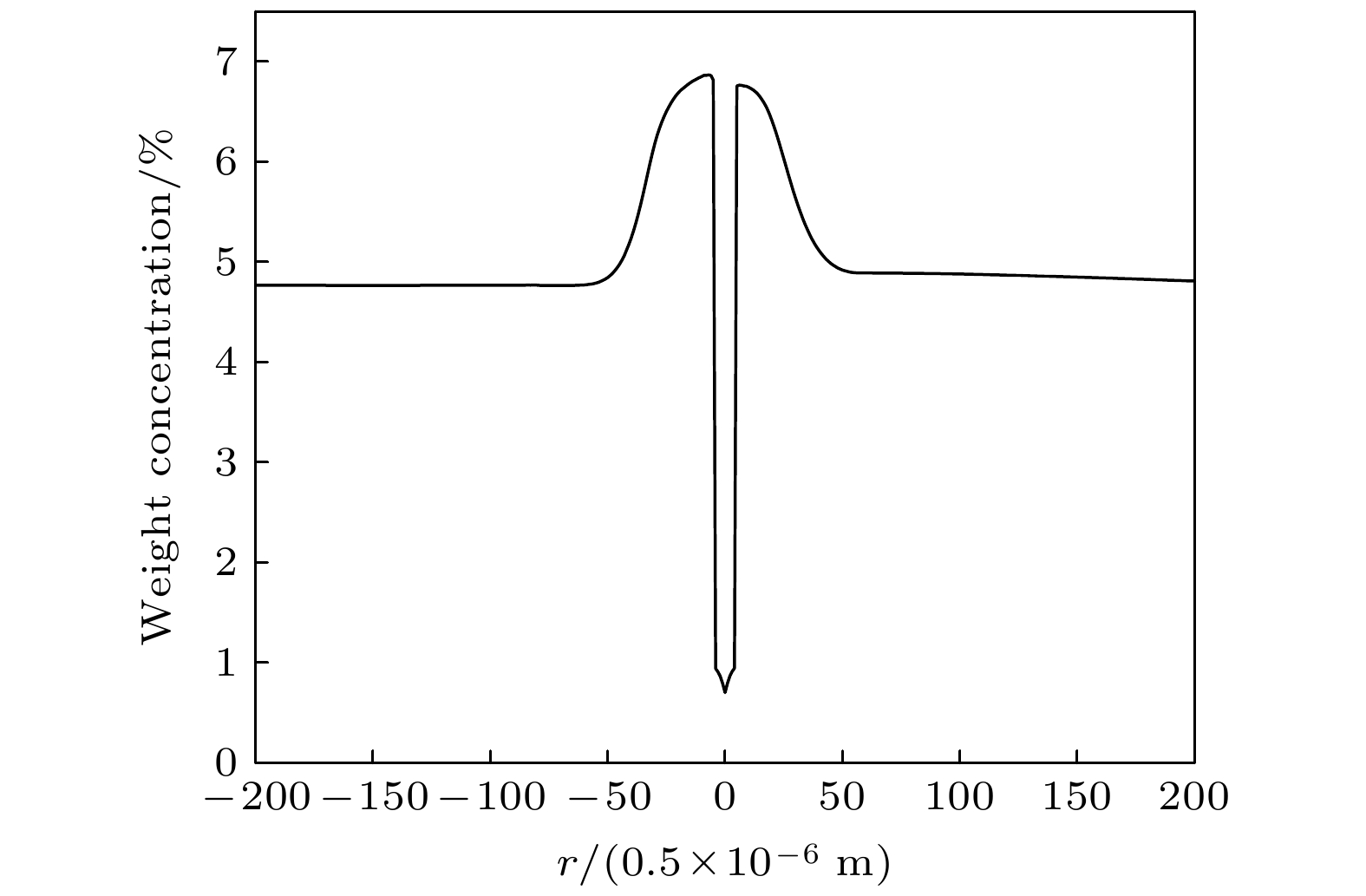 图 4 t = 0.015 s时, 模拟域O点处竖直方向上的溶质浓度变化
图 4 t = 0.015 s时, 模拟域O点处竖直方向上的溶质浓度变化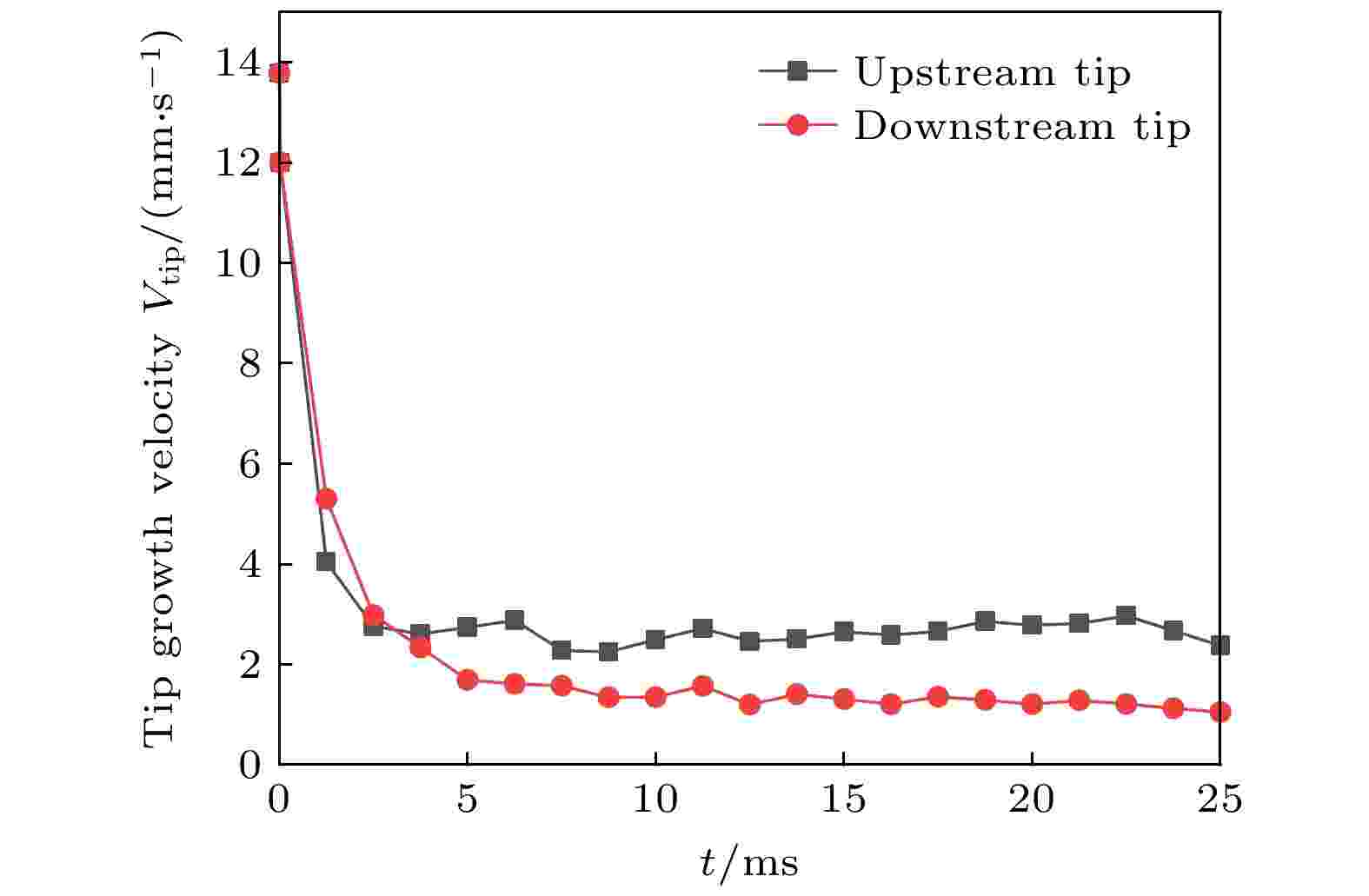 图 5 枝晶尖端生长速度随时间的变化
图 5 枝晶尖端生长速度随时间的变化







 图 6 两个球形粒子沉降过程中, 四个时间的瞬时涡量轮廓 (a) 1 .0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 s
图 6 两个球形粒子沉降过程中, 四个时间的瞬时涡量轮廓 (a) 1 .0 s; (b) 1.5 s; (c) 2.5 s; (d) 4.0 s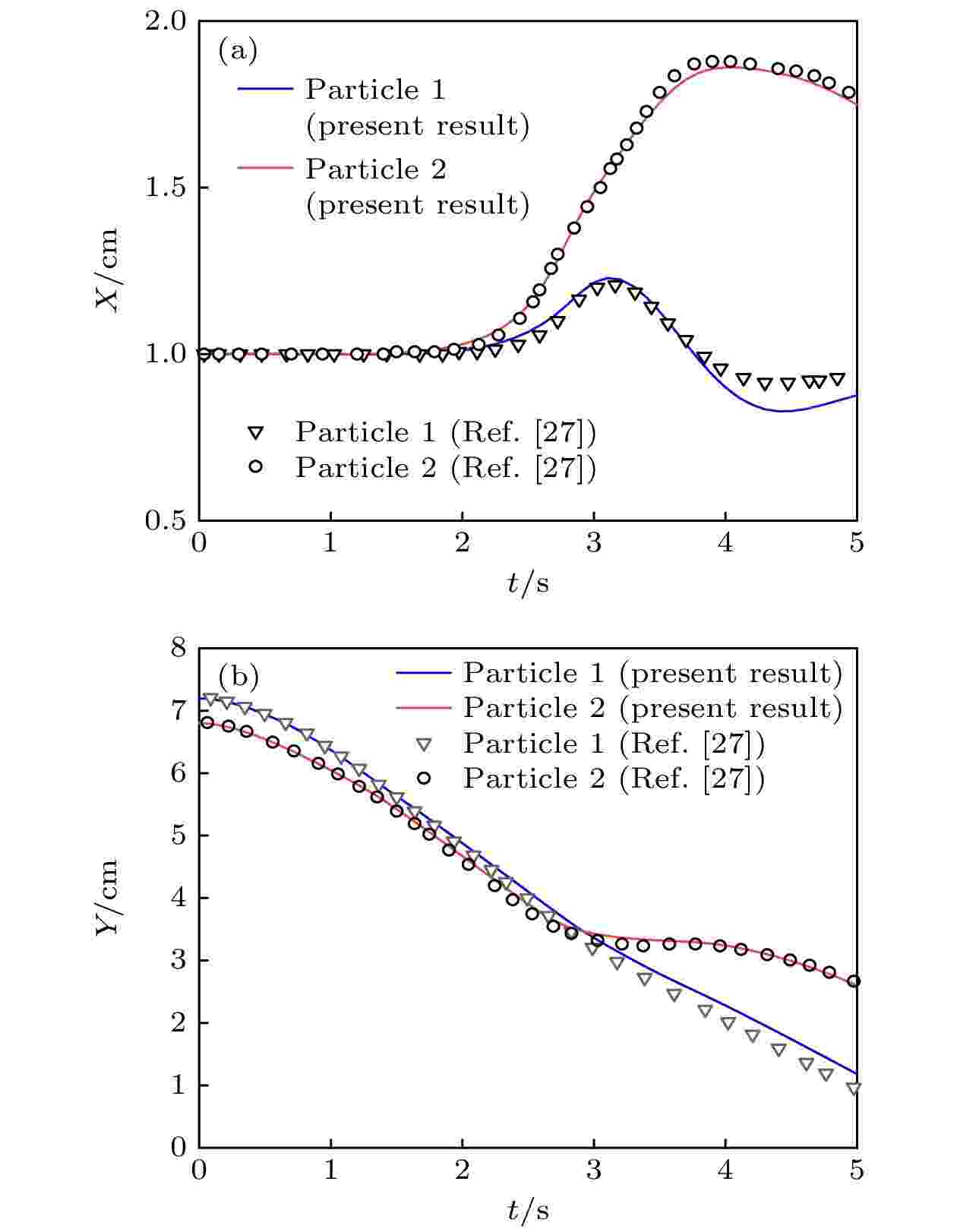 图 7 粒子质心坐标 (a) 横坐标; (b) 纵坐标
图 7 粒子质心坐标 (a) 横坐标; (b) 纵坐标
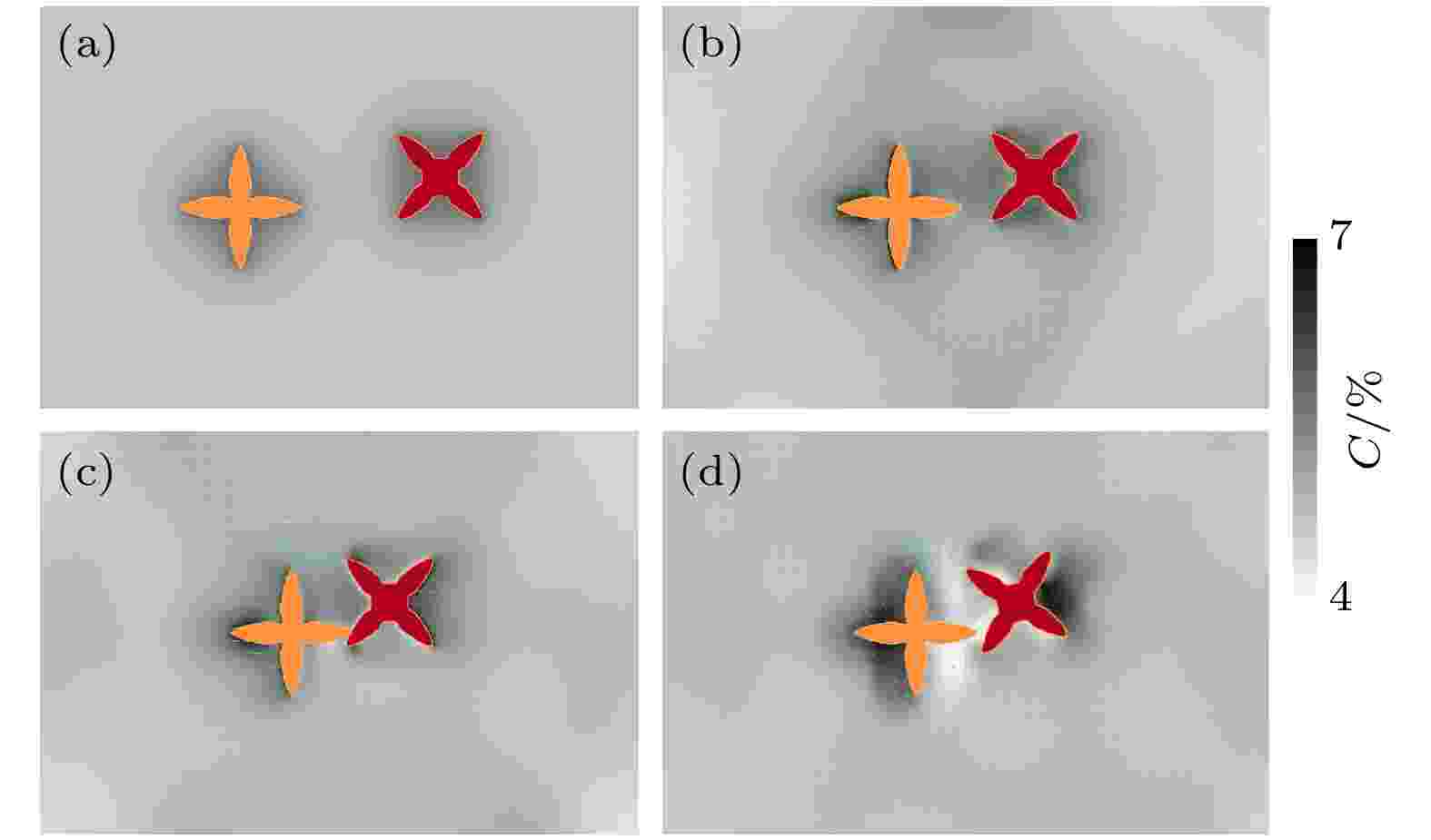 图 8 枝晶偏心碰撞形貌图 (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s. 箭头表示速度v的大小和方向, 灰度表示流体溶质浓度C
图 8 枝晶偏心碰撞形貌图 (a) 0.008 s; (b) 0.0089 s; (c) 0.009 s; (d) 0.00915 s. 箭头表示速度v的大小和方向, 灰度表示流体溶质浓度C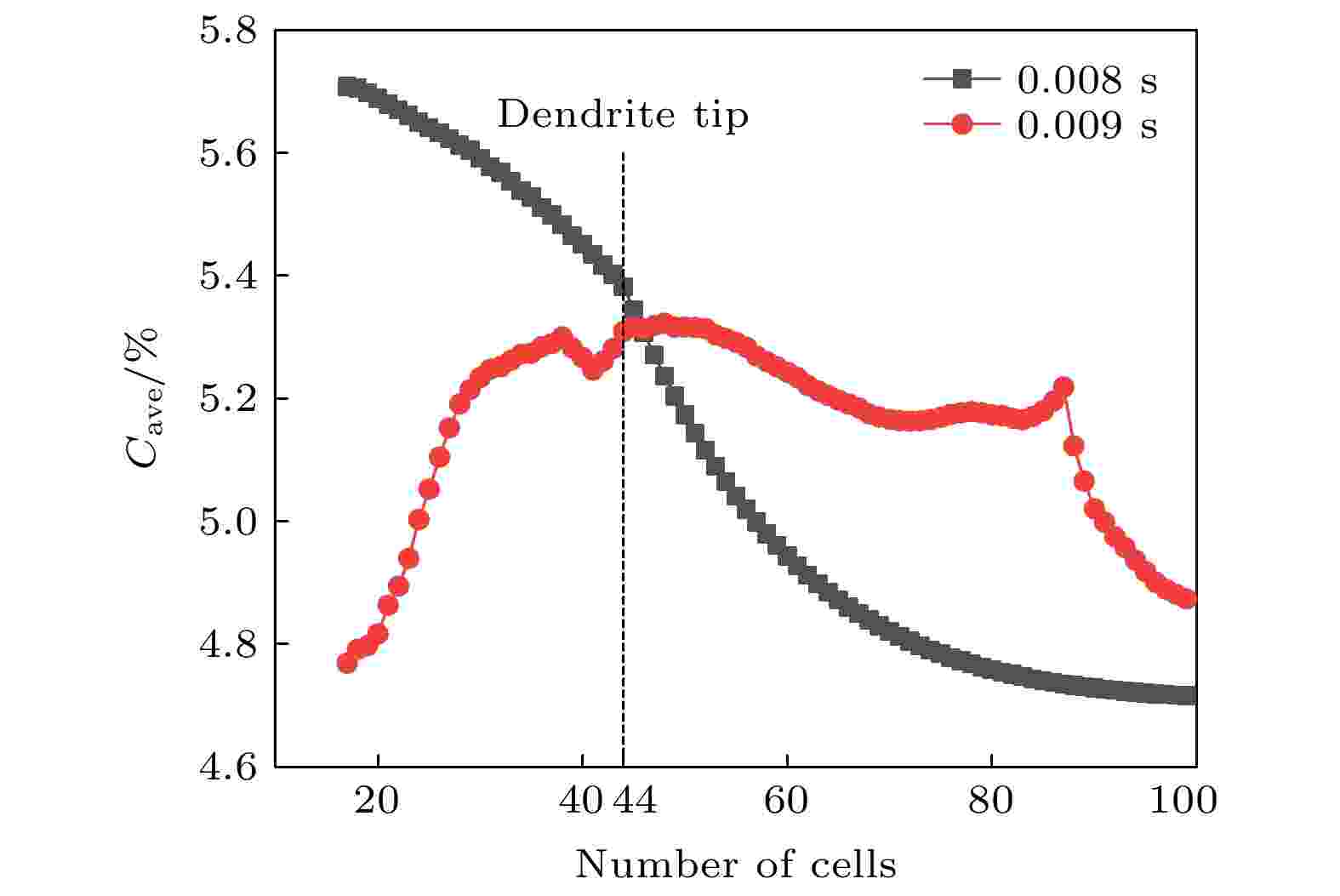 图 9 枝晶2附近熔体平均溶质浓度
图 9 枝晶2附近熔体平均溶质浓度 图 10 熔体平均溶质浓度计算规则
图 10 熔体平均溶质浓度计算规则