删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

非对称银膜多孔硅-氟化钙等离子体波导及其波导灵敏度特性

本站小编 Free考研考试/2021-12-29
摘要:本文研究了一种非对称银膜多孔硅-氟化钙混合等离子体波导, 并对其模式特性和波导灵敏度进行了分析. 利用有限元方法分析了波导中两个不同偏振态基模(PM 1和PM 2)的有效折射率、传输损耗、归一化有效模场面积、品质因数和波导灵敏度, 并对几何参数进行优化. 结果表明, 在中红外波长3.5 μm附近, 非对称银膜多孔硅-氟化钙混合等离子体波导具有良好的模场约束能力和低损耗特性; 此时, PM 1和PM 2的归一化有效模场面积分别为0.30和0.52, 传输损耗分别为0.019 dB/μm和0.016 dB/μm, 品质因数分别为1335.54和1594.99, 波导灵敏度分别为0.080和0.064. 通过制造容差分析可知, 非对称银膜多孔硅-氟化钙混合等离子波导在 ± 10 nm的制造容差范围内保持了良好的模式特性和传感特性. 非对称银膜多孔硅-氟化钙混合等离子体波导结构简单, 损耗小, 易于实现表面等离子体传感, 为无标记生物化学传感提供了一种可行的方案, 另外, 波导的非对称结构也可用于模式偏振态变换.
关键词: 混合等离子波导/
表面等离子体/
传输特性/
波导灵敏度

English Abstract


全文HTML

--> --> -->
1.引　言
随着微纳米技术的高速发展, 纳米光子学取得了许多重大的突破, 尤其是表面等离子体技术, 已经成为纳米光子学领域中最活跃的研究之一. 表面等离子体激元(surface plasmon polaritons, SPP)中最简单的一种形式是电磁激励, 它沿着金属和介质的交界面以波状方式传播, 其振幅从界面进入金属或介质呈指数衰减[1-3]. SPP是由于光子与金属表面自由电子的耦合而在金属与介质界面共振产生的横磁(transverse magnetic, TM)表面模[4]. SPP具有许多优点, 例如: 突破衍射极限, 强光场约束力, 局部场能量增强, 尺寸小以及与周围环境相互作用的敏感度高等[5,6]. 因此, 广泛应用于光子和光电器件, 例如: 耦合器[7]、传感器[8-10]、调制器[11,12]、环形谐振器[12,13]、M-Z干涉仪(Mach-Zehnder interferometer, MZI)[14]、光栅耦合器[15]、偏振转换器[16]、光探测器[17]以及纳米天线[18]. 虽然SPP在很多方面都有广大的应用前景, 但实现前景的最大限制是SPP传输损耗高. 为了减少SPP的传输损耗, 可利用光增益介质、低温冷却、金属薄膜和改进等离子体波导等方法来解决[19]. 与传统的等离子体波导(surface plasmon polaritons waveguides, SPPW)相比, 混合表面等离子体(hybrid plasmonic waveguides, HPW)在损耗和约束之间提供了更好的平衡[20], 并且与绝缘体上的硅(silicon on insulator, SOI)技术兼容.
目前, 传统的光学传感器体积大, 不易携带, 为使传感器小型化, 研究者提出了许多可微型化的传感结构. 由于HPWs与周围环境的强相互作用和局域增强效应, HPWs为实现新型生物化学传感提供了一种可行的方案.
多孔硅(porous silicon, PS)具有良好的光学特性, 例如光致发光效应和反射干涉效应. 由于PS有较大的比表面积, 增强了光与物质的相互作用. 另外, PS的可调孔隙率随制造参数的变化而变化[21], 使其折射率(refractive index, RI)在空气和多孔硅之间可调. 由于PS的这些优势, 它被广泛应用于光电子学领域[22–26]、电力工程[27]和传感领域[28]. 此外, 由于氟化钙穿透性好, 宽带透过率高、环境抗性强和独特光学特性, 致使它在半导体的应用上有着悠久的传统. 并且氟化钙(CaF2)红外透过率高、光谱色散低和更宽的中红外(mid-infrared, MIR)光谱透明窗口, 是一种很有前途的SiO2替代材料.
本文研究了一种非对称银膜PS-CaF2混合等离子体波导(PS-CaF2 HPW), 它是在氮化硅波导的顶面和一侧侧壁沉积覆盖氟化钙层和银薄膜层而形成的一种非对称波导结构. 利用有限元方法(finite element method, FEM)对波导中的等离子体模式进行了数值计算, 研究了波导中存在的两个基模在中红外波长(3.5 μm)处的有效折射率、品质因数、有效模场面积和传输损耗特性, 并采用参数扫描方法对结构的几何尺寸参数进行了优化. 通过改变波导包层的折射率, 研究了利用等离子体模式进行传感时的波导灵敏度. 随后, 分析了非对称银膜PS-CaF2混合等离子体波导的制造容差.
2.波导建模和数值模拟
建立非对称银膜PS-CaF2混合等离子体波导的模型, 其三维示意图和二维截面图如图1(a)和图1(b)所示, PS-CaF2 混合等离子体波导由SiO2衬底上的 PS 条状波导、CaF2层和Ag薄膜层组成. PS条形波导的宽度和高度分别为W1 和H1, CaF2和Ag层的右侧壁宽度分别为W2 和W3, 上覆盖层的厚度分别为H2和H3. PS, CaF2和SiO2的折射率分别为2 [29], 1.44和1.45. 波导上覆盖层为待测溶液, 其折射率为nc. 工作波长为3.5 μm时, Ag的介电常数可近似为–86.64+8.74 i [30].
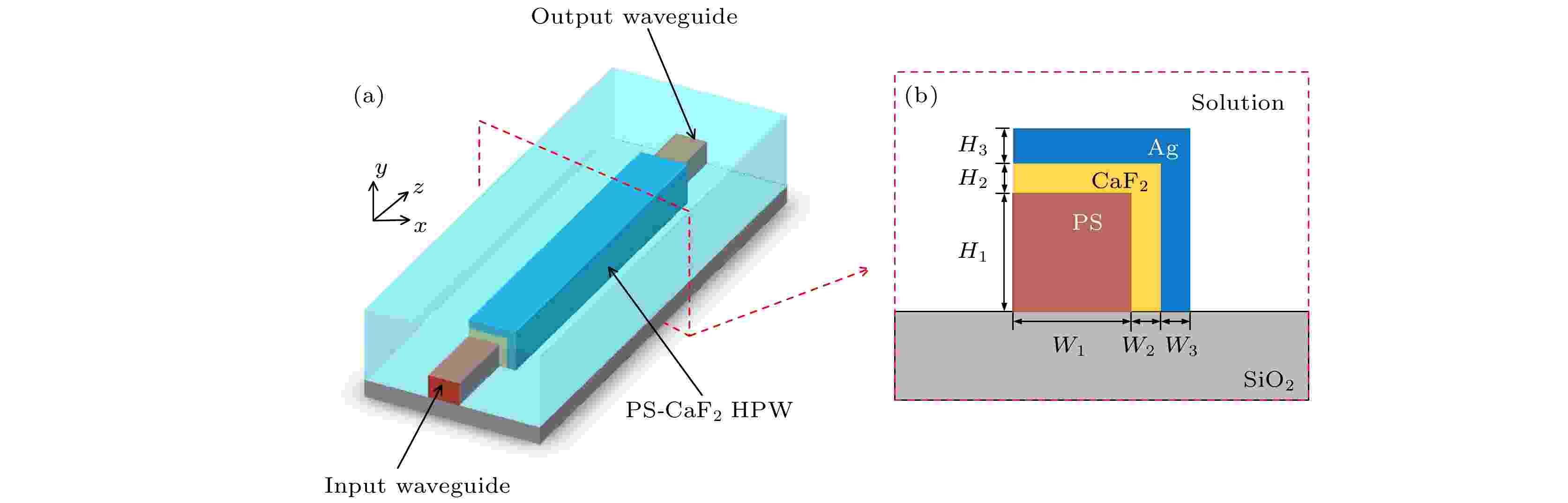图 1 非对称银膜的PS-CaF2混合等离子体波导示意图　(a)三维图; (b)波导截面图
Figure1. Schematic diagram of Ag film coated asymmetric PS-CaF2 hybrid plasma waveguide: (a) 3D diagram; (b) cross-sectional view.

为了衡量非对称银膜PS-CaF2 混合等离子体波导的模式特性、传输特性和传感性能, 通常用有效折射率(neff)、品质因数(FOM)、传输损耗(α)、归一化模场面积(A)以及波导灵敏度(Swg)参数来进行分析.
品质因数(FOM)可综合衡量波导的模式特性, 计算公式如下:
${ {FOM}} = \dfrac{{{\rm{Re}}({n_{{\rm{eff}}}})}}{ {{\rm{Im}}({n_{{\rm{eff}}}})}}, $
其中Re(neff)和 Im(neff)是模式的有效折射率实部和虚部.
模式的有效折射率虚部与其传输损耗(α)成正比:
$\alpha = \frac{{40{\rm{\pi}} }}{{\lambda \ln10}}{\rm{Im}}\left( {{n_{{\rm{eff}}}}} \right)~ \left( {{\rm{dB}}/{{\text{μ}}\rm{m}}} \right).$
有效模场面积Aeff反映了波导对模式的束缚能力, 其定义式为
$\begin{split}{A_{{\rm{eff}}}}\; & = \frac{{{W_{{\rm{eff}}}}}}{{\max\left\{ {W(x,y)} \right\}}}\\ & = \frac{1}{{\max\left\{ {W(x,y)} \right\}}}\iint {W(x,y){\rm{d}}x{\rm{d}}y}.\end{split}$
通常用归一化模场面积A = Aeff/A0来描述, A0 = λ2/4表示自由空间中的衍射限制面积. (3)式中, Weff和W(x, y)分别是模式的总能量和能量密度.
传感性能通常用灵敏度(sensitivity, S)表示, 它描述了待测物质的变化与某种物理量的变化的对应关系. 灵敏度一般分为两部分: 器件灵敏度(device sensitivity, Sdev)和波导灵敏度(waveguide sensitivity, Swg). 器件灵敏度取决于器件的性能, 而波导灵敏度取决于波导结构, 因此, 本文对非对称银膜PS-CaF2 混合等离子体波导的波导灵敏度进行了分析, 其定义为 [31]
${S_{{\rm{wg}}}} = {{\Delta {n_{{\rm{eff}}}}}}/{{\Delta {n_{\rm{c}}}}}, $
其中Δnc和Δneff分别是周围折射率(nc)的变化量和引起的有效模式折射率的变化量.
本文采用FEM对非对称银膜PS-CaF2混合等离子体波导在中红外波段的模式特性、传输特性和波导灵敏度进行了研究. 根据光场的模式分析原理, 将非对称银膜PS-CaF2混合等离子体波导的待计算区域剖分为非均匀三角形网格, CaF2和Ag层的最小网格值为5 nm, 其他计算区域为0.3 μm, 在边界上使用散射边界条件来模拟吸收边界, 并通过收敛性测试确保计算的准确性.
3.模式特性分析及参数优化
为了分析波导的中红外特性, 选取工作波长λ = 3.5 μm, 并对尺寸参数W1 (= H1), W2 (= H2)和W3 (= H3)进行参数化扫描. 利用FEM中的模式分析方法计算了非对称银膜PS-CaF2混合等离子体波导中存在的模式, 结果表明, 波导中存在两个不同偏振态的基模(PM 1和PM 2). 当波导的尺寸参数选取W1 (= H1) = 1500 nm、W2 (= H2) = 300 nm和W3 (= H3) = 70 nm时, PM 1和PM 2的模式分布如图2(a)和图2(b)所示. 图2中红色箭头表示PM 1和PM 2的电场分量的方向, 因此, PM 1和PM 2具有不同的偏振方向. 波导中心沿x方向的电场模如图2(c)和图2(d)所示, PM 1和PM 2中的电场主要集中在PS和CaF2层.
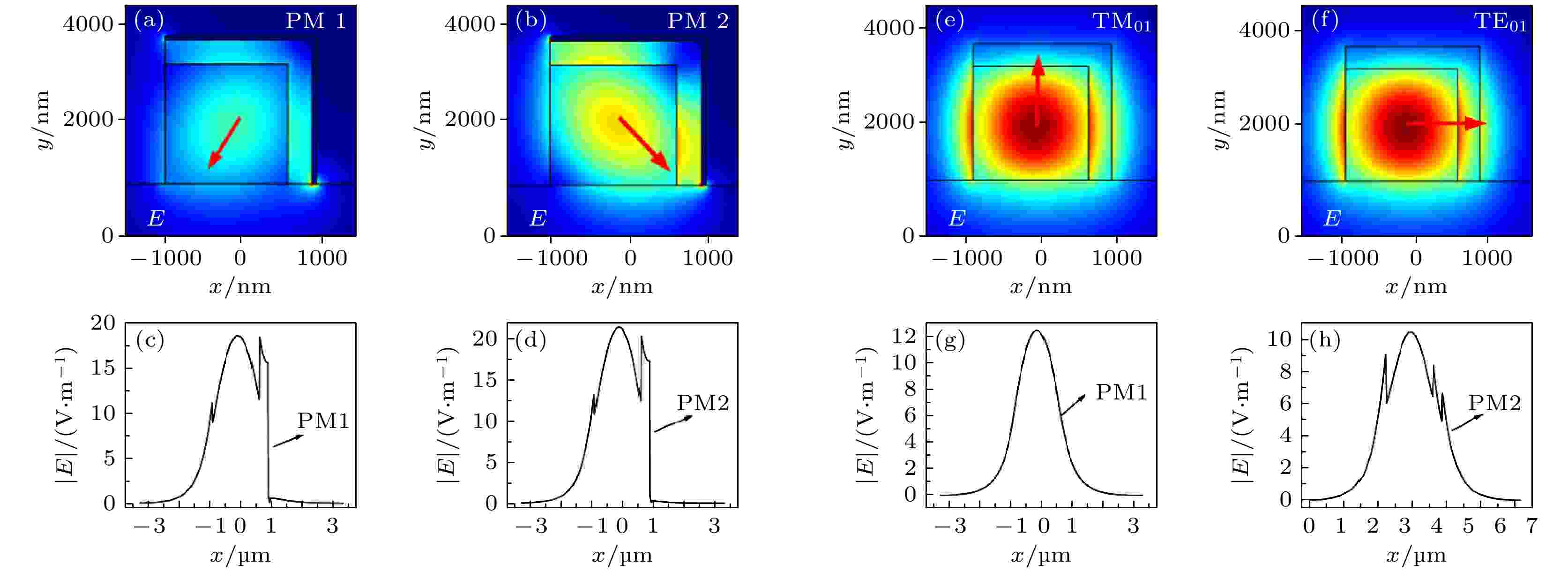图 2 W1 (= H1) = 1500 nm, W2 (= H2) = 300 nm和W3 (= H3) = 70时, 非对称银膜PS-CaF2混合等离子体波导中不同模式的模场分布图　(a) PM 1; (b) PM 2; 波导中心沿x方向的电场分布图 (c) PM 1; (d) PM 2; W1 (= H1) = 1500 nm和W2 (= H2) = 300 nm时, 无银膜普通波导的模场分布图 (e) TM01; (f) TE01; 波导中心沿x方向的电场分布图 (g) TM01, (h) TE01
Figure2. Mode field distributions of (a) PM 1 and (b) PM 2; electric field distribution along the x axis of (c) PM 1 and (d) PM 2; mode field distributions of (e) TM01 and (f) TE01; electric field distribution along the x axis of (g) TM01 and (h) TE01 when W1 (= H1) = 1500 nm, W2 (= H2) = 300 nm and W3 (= H3) = 70.

为了分析非对称银膜对模式偏振方向的影响, 仿真了无Ag膜的普通波导, 其两个基模如图2(g)和图2(f)所示, 图中红色箭头表示电场方向. 对比图2(a)、图2(b)和图2(e)、图2(f)可以看出, 相比无Ag膜的波导, PM 1和PM 2的电场方向偏转了45°角. 对比图2(c)、图2(d)和图2(g)、图2(h)可知, 增加Ag膜的等离子体波导的PS芯层的模式能量比普通波导高.
图3(a)—(c)是PM 1和PM 2的Re和α随W1, W2和W3 的变化曲线图4(a)—(c)是PM 1和PM 2的FOM和A随W1, W2和W3 的变化曲线. 从图4(a)可以看出, 当W2 = 300 nm, W3 = 70 nm时, 随着W1增大, FOM和A都增加. 这是因为W1增大, 更多的模场能量被限制在了PS层, 减小了模式的有效模场面积和损耗(折射率虚部), 从而使FOM和A增大. 如图4(b)所示, 当W1 = 1500 nm, W3 = 70 nm时, 在W2 = 350 nm之前, PM 2的A逐渐减小而PM 1的A则是逐渐增大, 而在W2 = 350 nm之后PM 1和PM 2的A几乎都保持不变. PM 1的FOM在整个过程中是一直增大, 而在W2 = 350 nm之前, PM 2的FOM先减小, 之后缓慢增大. 在图4(c)中, 当W1 = 1500 nm, W2 = 300 nm时, 在W3 = 70 nm之前, PM 1和PM 2的FOM随着增加, 而在W3 = 70 nm之后, 则都几乎保持不变, 这与银膜厚度满足模式指数衰减要求相关. PM 2的A保持一直不变的状态; 在W3 = 150 nm之前, PM 1的A呈现增长趋势, 之后基本保持不变.
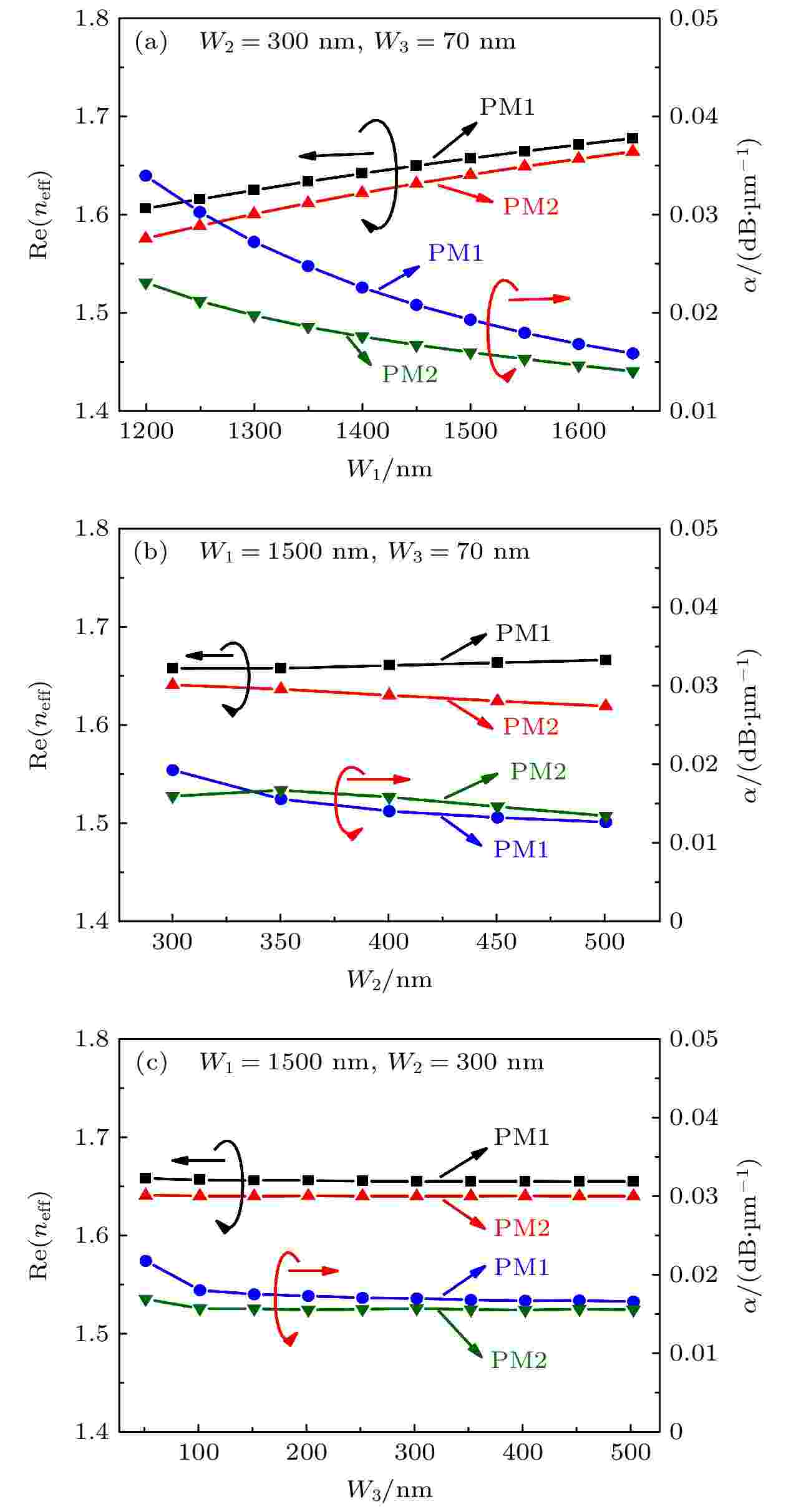图 3 PM 1和PM 2的Re(neff)和α随(a)W1 (= H1), (b) W2 (= H2) 和 (c) W3 (= H3)变化的规律, W1 (= H1), W2 (= H2) 和W3 (= H3)分别取1500 nm, 300 nm和70 nm
Figure3. Re(neff) and α of the PM 1 and PM 2 with different: (a) W1 (= H1) at W2 (= H2) = 300 nm and W3 (= H3) = 70 nm; (b) W2 (= H2) at W1 (= H1) = 1500 nm and W3 (= H3) = 70 nm; (c) W3 (= H3) at W2 (= H2) = 300 nm and W1 (= H1) = 1500 nm.

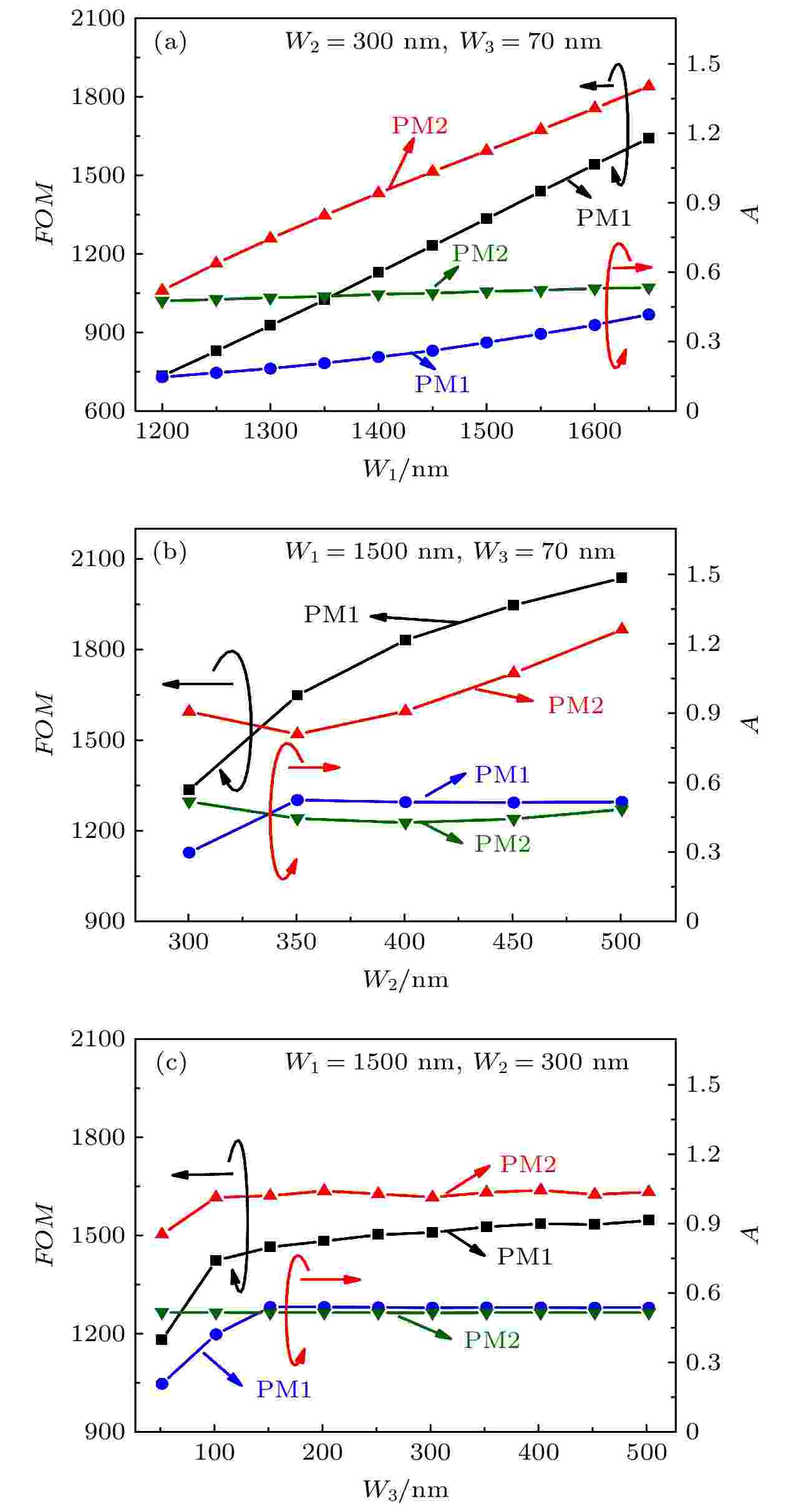图 4 PM 1和PM 2 的FOM 和A随(a)W1 (= H1), (b) W2 (= H2)和(c) W3 (= H3)变化的规律, W1 (= H1), W2 (= H2) 和W3 (= H3)分别取1500 nm, 300 nm和70 nm
Figure4. FOM and A of the PM 1 and PM 2 with different: (a) W1 (= H1) at W2 (= H2) = 300 nm and W3 (= H3) = 70 nm; (b) W2(= H2) at W1 (= H1) = 1500 nm and W3 (= H3) = 70 nm; (c) W3 (= H3) at W2 (= H2) = 300 nm and W1 (= H1) = 1500 nm.

4.波导传感特性分析
图5(a)和图5(b)反映了nc变化对PM 1和PM 2的Re(neff), FOM和A的影响. 当W1 = 1500 nm, W2 = 350 nm和W3 = 70 nm时, 从图5(a)可以看出, 随着nc的增大, PM 1和PM 2的Re(neff)随之增大. 对PM 1和PM 2的Re(neff)做线性拟合, 线性拟合线的斜率为波导灵敏度Swg, PM 1和PM 2的Swg分别为0.080和0.064. 如图5(b)所示, 随着nc的增大, PM 1的FOM逐渐递减, 而 PM 1的A在nc小于1.4之前略微递减, 之后则剧烈下降. PM 2的FOM和A随着nc的增大呈略微上升趋势.
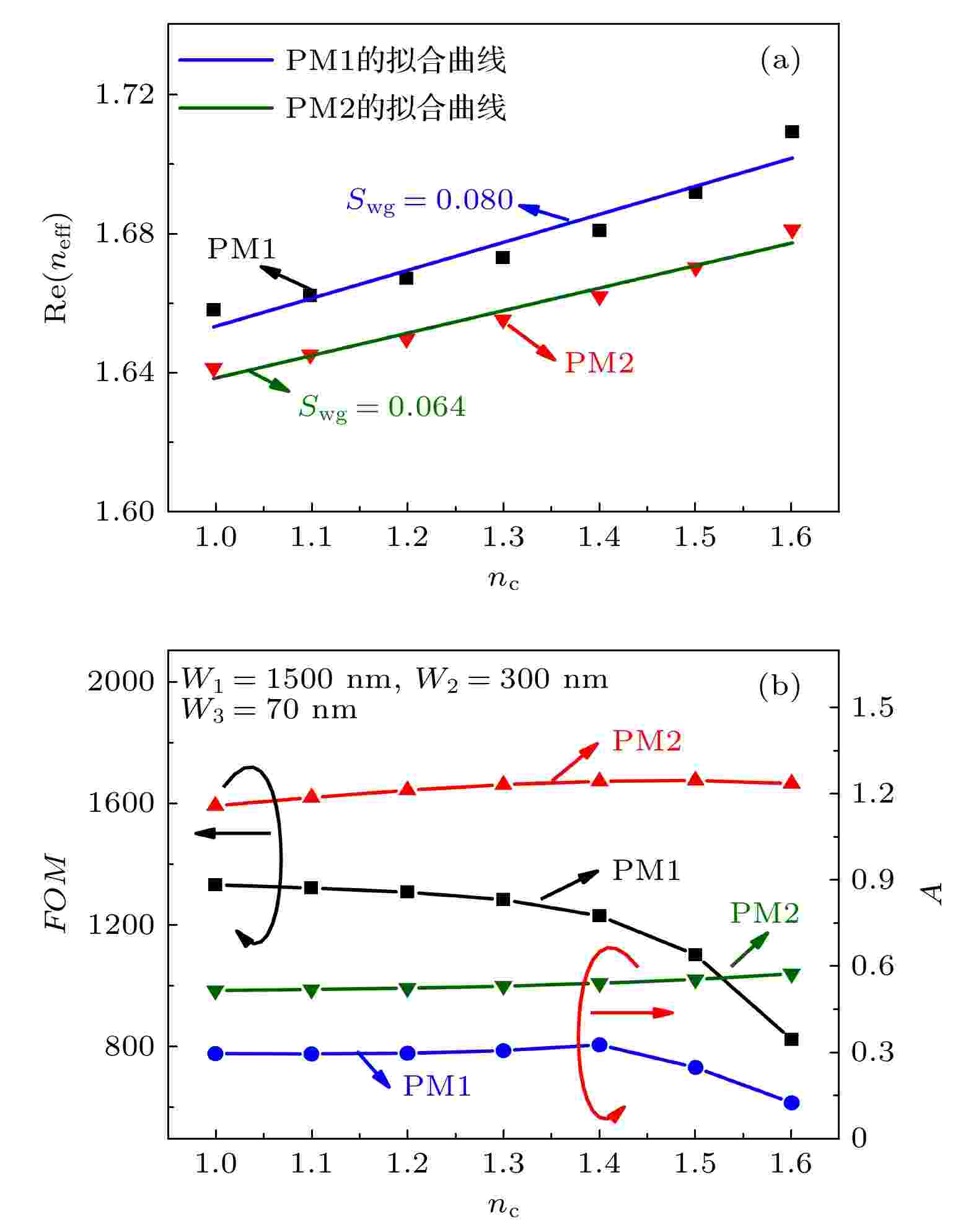图 5 在不同的nc下, PM 1和PM 2的(a) Re(neff), (b) FOM和A的变化规律, W1 (= H1), W2 (= H2) 和W3 (= H3)分别取1500 nm, 300 nm和70 nm
Figure5. (a) Re(neff) and (b) FOM and A of the PM 1 and PM 2 with different nc as W1 (= H1) = 1500 nm, W2 (= H2) = 300 nm and W3 (= H3) = 70 nm.

图6(a)—(c)是非对称Ag膜多孔硅-氟化钙混合等离子体波导的Swg随着W1, W2和W3的变化情况. 从图6(a)中可以看出, 当W2 = 300 nm和W3 = 70 nm时, PM 1和PM 2的Swg随W1的增加而减小. 由于W1的增加有利于更多的模式能量被限制在PS芯层, 从而导致PM 1和PM 2的Swg减小. 如图6(b)所示, 当W1 = 1500 nm和W3 = 70 nm时, PM 1的Swg 随着W2的增加而减小, 然而PM 2的Swg反而增大. 这是因为模式的极化方向不同, 致使PM 1和PM 2的Swg呈现出相反的变化趋势. 图6(c)中, 当W1 = 1500 nm和W2 = 300 nm时, PM 1和PM 2的Swg 随着W3变化而保持不变, 说明W3的变化基本不影响Swg. 因为模式的模场能量几乎都被限制在PS层和CaF2层中(如图2(a)和图2(b)所示). 当W1 = 1500 nm, W2 = 300 nm和W3 = 70 nm时, PM 1和PM 2的波导灵敏度分别为0.080和0.065.
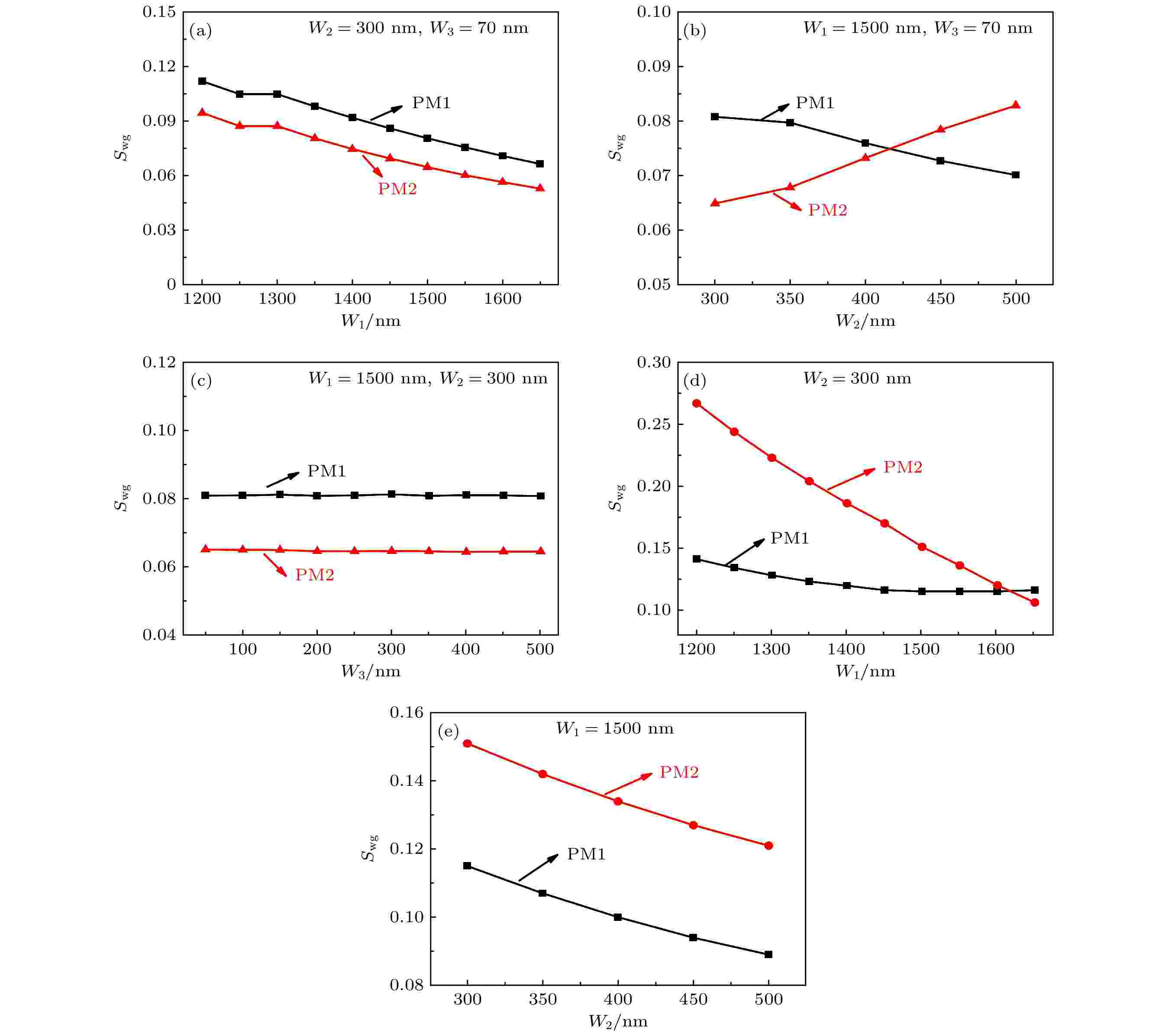图 6 非对称PS-CaF2混合等离子体波导的PM 1 和 PM 2 的Swg 随(a) W1 (= H1), (b) W2 (= H2)和(c) W3 (= H3) 的变化规律, W1 (= H1), W2 (= H2) 和W3 (= H3)分别取1500 nm, 300 nm和70 nm; 无Ag膜波导的PM 1 和 PM 2 的Swg 随(d) W1 (= H1)和 (e) W2 (= H2)的变化规律, W1(= H1)和W2(= H2)分别取1500 nm和300 nm
Figure6. with an asymmetric Ag film of Swg of the PM 1 and PM 2 in the PS-CaF2HPW with an asymmetric Ag films with different: (a) W1 (= H1) at W2 (= H2) = 300 nm and W3 (= H3) = 70 nm; (b) W2 (= H2) at W1 (= H1) = 1500 nm and W3 (= H3) = 70 nm; (c) W3 (= H3) at W2 (= H2) = 300 nm and W1 (= H1) = 1500 nm. Without an asymmetric Ag film of Swg of the PM 1 and PM 2 in the waveguide without an asymmetric Ag film of with different (d) W1 (= H1) at W2 (= H2) = 300 nm; (b) W2 (= H2) at W1 (= H1) = 1500 nm.

为了分析Ag膜对波导灵敏度的影响, 无Ag膜时Swg随着W1和W2的变化情况如图6(d)和图6(e)所示. 从图6(d)中可以看出, 当W2 = 300 nm时, PM 1和PM 2的Swg随W1的增加而减小, 但PM 1的减小幅度远小于PM 2. 因为随着W1的增大, 对于PM 2来说, 模场能量被更多地限制在PS层, 而PM 1的模场能量分布主要集中在在PS层中心位置, 故W1的增大对PM 1的影响并不大. 如图6(f)所示, 当W1 = 1500 nm时, PM 1和PM 2的Swg随着W2的增大而逐渐变小. 因为随着W2的增大, 被限制在PS层和CaF2层模场能量增加. 当W1 = 1500 nm和W2 = 300 nm时, PM 1和PM 2的灵敏度分别为0.115和0.151. 增加非对称Ag膜后, 波导的表面等离子体效应降低了结构的波导灵敏度, 然而, 能量分布更加集中的优势可以提高传感系统的集成度, 有利于提高传感的器件灵敏度. 这里提出的非对称Ag膜结构还可以实现不同偏振模式的复用和多参数传感.
温度变化对波导灵敏度的影响是传感结构必须考虑的因素, 因此, 我们分析了温度变化对波导灵敏度的影响, 如图7(a)所示. 在环境温度为295 K附近时, PS, CaF2, PMMA和Ag的热光系数(thermo-optical coefficient, TOC)分别是2.45 × 10–5/K, 2.8 × 10–5/K, –1.1 × 10–4/K和2.13 × 10–4/K. 当温度变化时, 波导的Swg基本不变化. 由图7(b)和图7(c)可知, 温度变化对α, FOM和A的影响也不大, 几乎不发生变化. 从图7可以看出, 波导的性能受温度影响较小.
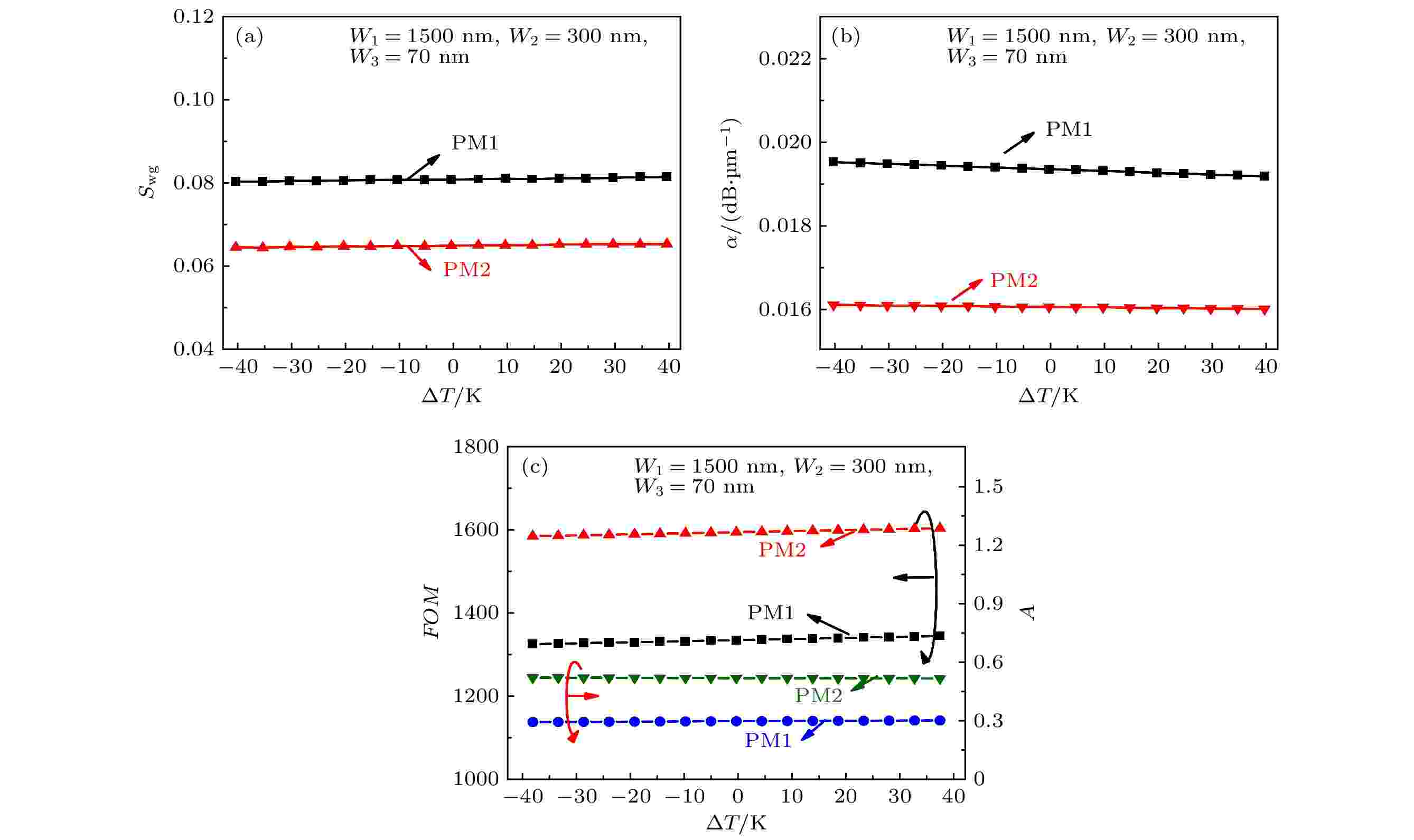图 7 W1 (= H1) = 1500 nm, W2 (= H2) = 300 nm和W3 (= H3) = 70 nm时, 在不同的ΔT下 (a) Re(neff), (b) α, (c) FOM和A的变化规律
Figure7. (a) Re(neff), (b) α, (c) FOM and A with different ΔT as W1 (= H1) = 1500 nm, W2 (= H2) = 300 nm and W3 (= H3) = 70 nm

5.波导制备方法与容差分析
本文提出了制备非对称银膜PS-CaF2混合等离子体波导的可行方案, 流程图如图8所示: 首先, 在SiO2衬底层上使用分子束外延(molecular beam epitaxy, MBE)技术在超高真空下外延生长PS层, 并用传统的深紫外线光刻刻蚀PS层; 其次, 利用分子束外延技术在超高真空条件下外延生长非对称CaF2层; 再利用真空蒸发法沉积不对称Ag膜; 最后, 利用固态水等离子体刻蚀法刻蚀掉多余的PS和CaF2部分.
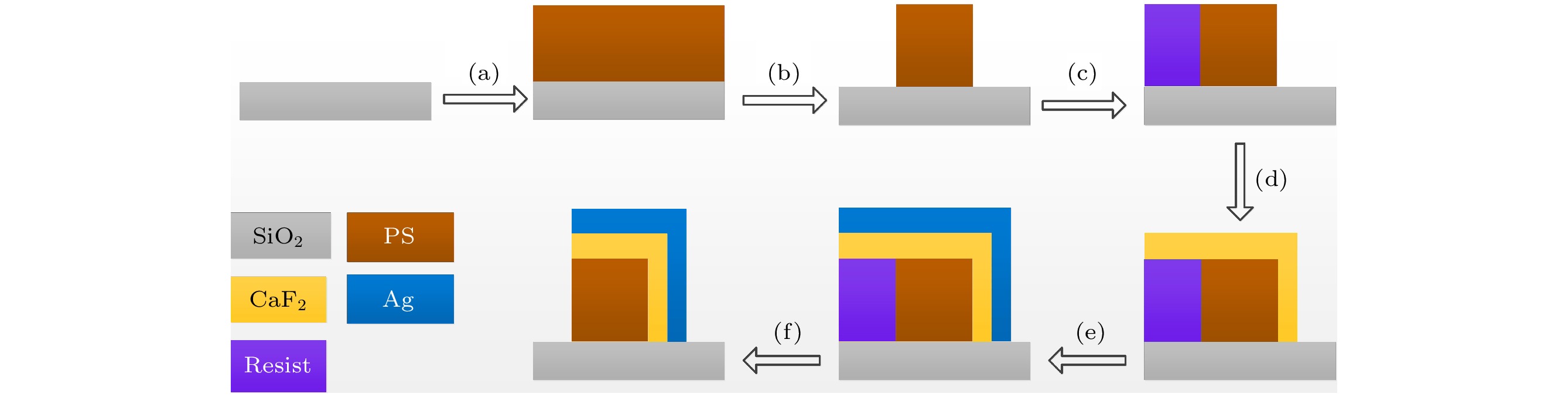图 8 制造流程　(a)在SiO2衬底上外延生长PS层; (b)电子束光刻使其成型; (c)涂上抗蚀剂; (d) 在PS上外延生长CaF2层; (e) 倾斜沉积金属Ag层; (f)电子束光刻使其成型, 并清除抗蚀剂
Figure8. (a) Grow PS on a SiO2 substrate; (b) pattern the resist through E-beam lithography; (c) it is coated with a resist; (d) grow CaF2 layers epitaxially on a PS layer; (e) oblique deposition of metal Ag; (f) electron beam lithography moulds it and removes the resist.

尺寸容差对非对称银膜PS-CaF2 混合等离子体波导的影响是波导实际应用必须考虑的问题, 因此需要讨论尺寸容差对非对称银膜PS-CaF2 混合等离子体波导性能的影响. 本文设计的非对称银膜PS-CaF2 混合等离子体波导部分覆盖CaF2和Ag薄膜, 在制造过程中要求较大的对准容差. 尺寸容差对非对称银膜PS-CaF2 混合等离子体波导性能的影响如图9—图11所示. 根据前文的参数优化, 在下面的仿真过程中, W1(= H1), W2(= H2)和W3(= H3)分别为1500 nm, 300 nm和70 nm. 此时, PM 1和PM 2的FOM分别是1335.45和1594.99; A分别为0.30, 0.52; Swg分别为0.080, 0.064. 在 ± 10 nm的容差范围内, 研究了ΔW1, ΔH1, ΔW2, ΔH2, ΔW3和ΔH3对FOM, A和Swg的影响.
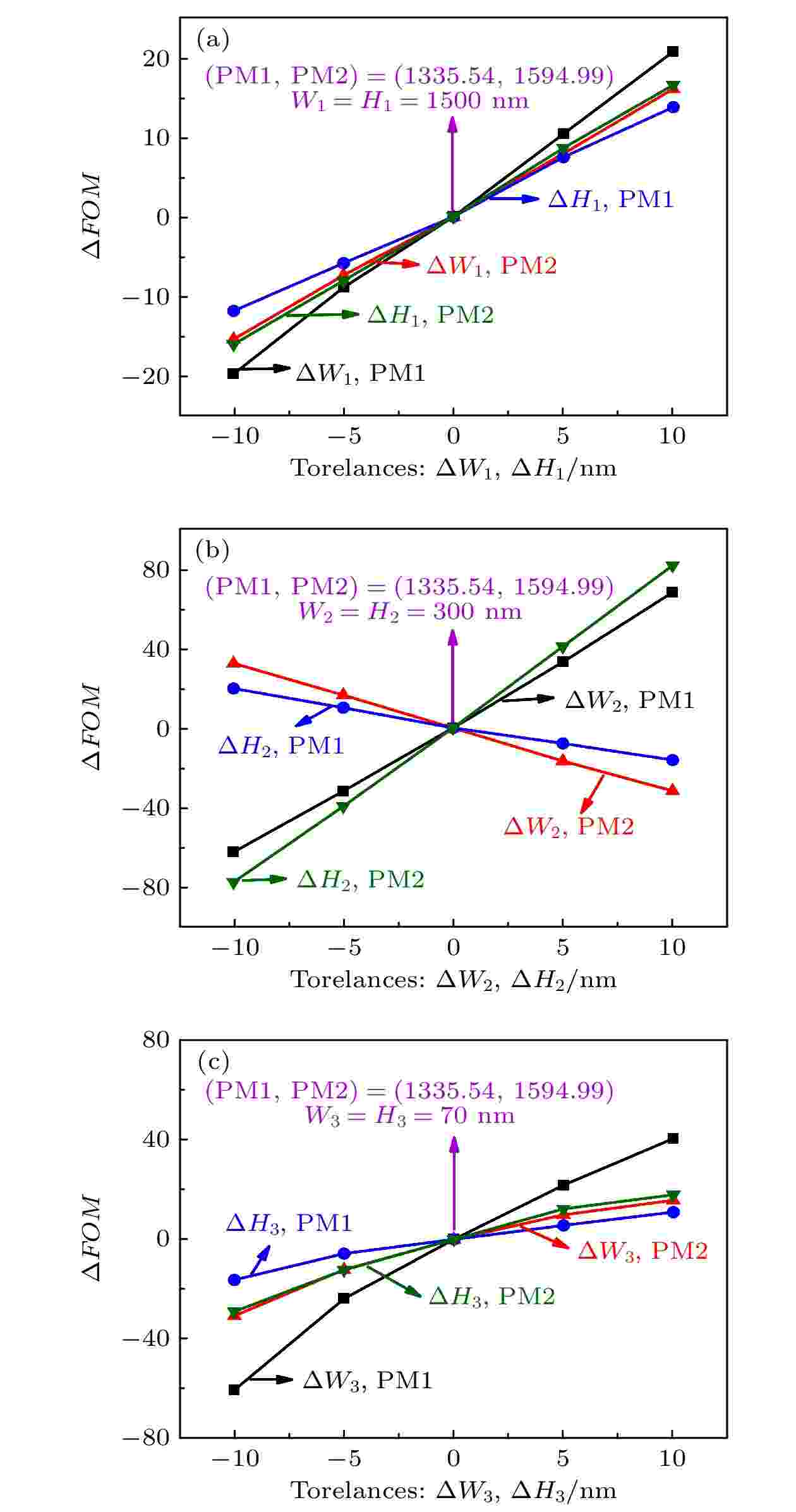图 9 不同的尺寸容差下, PM 1和PM 2 的FOM的变化 (ΔFOM)随(a) ΔW1和ΔH, (b) ΔW2和ΔH2; (c) ΔW3和ΔH3的变化规律, W1 (= H1), W2 (= H2) 和W3 (= H3)分别取1500 nm, 300 nm和70 nm
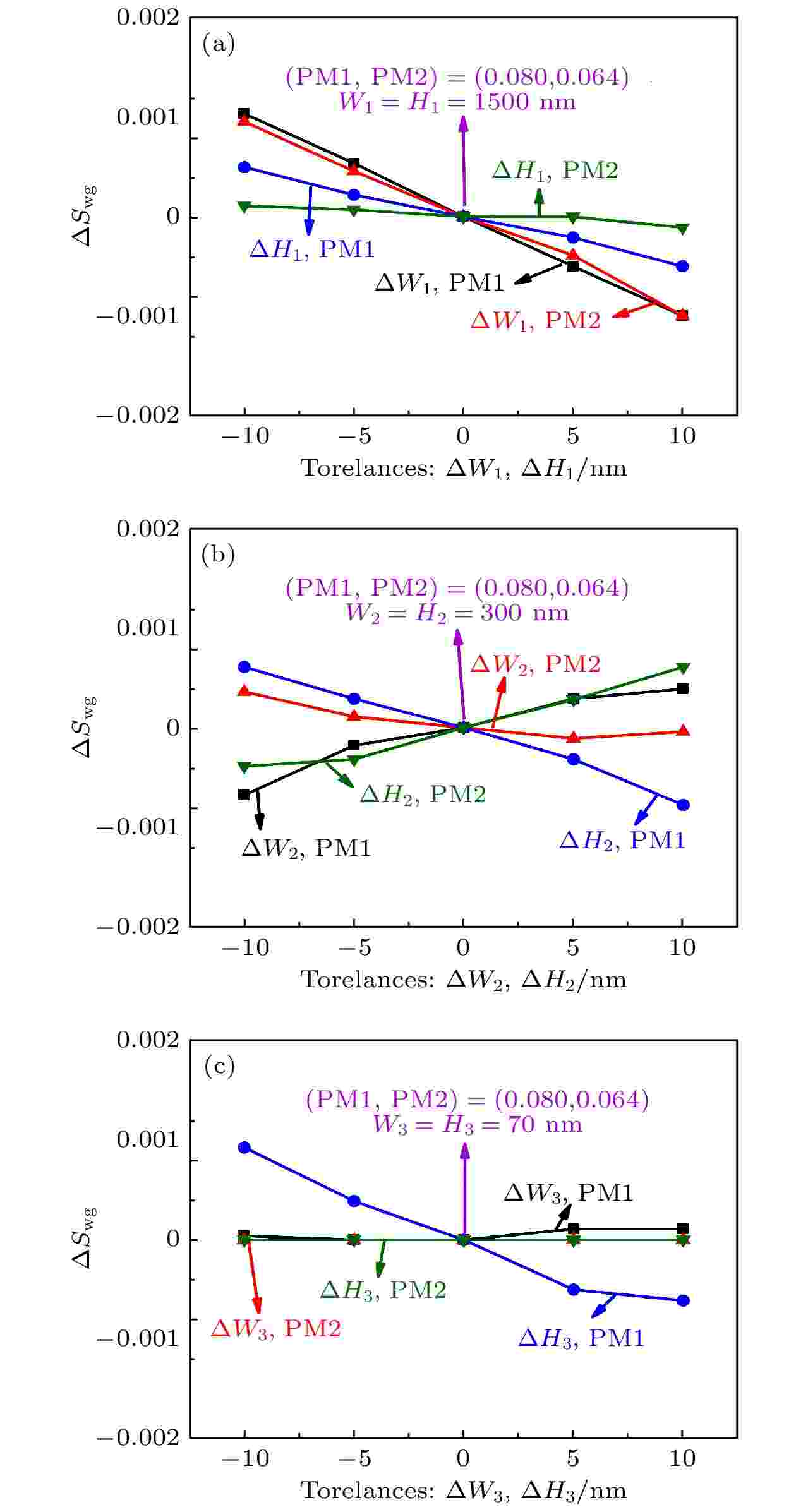Figure9. The changes of FOM (ΔFOM) for the PM 1 and PM 2 with different dimensional tolerances: (a) ΔW1 and ΔH1 at W2 (= H2) = 300 nm and W3 (= H3) = 70 nm; (b) ΔW2 and ΔH2 at W1 (= H1) = 1500 nm and W3 (= H3) = 70 nm; (c) ΔW3 and ΔH3 at W1 (= H1) = 1500 nm and W2 (= H2) = 300 nm.

图 11 不同的尺寸容差, PM 1和PM 2 的Swg (ΔSwg)随(a) ΔW1和ΔH1, (b) ΔW2和ΔH2, (c) ΔW3和ΔH3的变化规律. W1(= H1), W2(= H2) 和W3(= H3)分别取1500 nm, 300 nm和70 nm
Figure11. The changes of Swg (ΔSwg) for the PM 1 and PM 2 with different dimensional tolerances: (a) ΔW1 and ΔH1 at W2(= H2) = 300 nm and W3(= H3) = 70 nm; (b) ΔW2 and ΔH2 at W1(= H1) = 1500 nm and W3(= H3) = 70 nm; (c) ΔW3 and ΔH3 at W1(= H1) = 1500 nm and W2(= H2) = 300 nm.

不同尺寸容差下, FOM的变化(ΔFOM)如图9(a)—(c)所示. 在图9(a)中, ΔW1和ΔH1的变化对ΔFOM的影响较小, 变化幅度小于20.7和16.5. 然而, 因为银膜厚度与欧姆损耗紧密相关, ΔW3和ΔH3的变化对ΔFOM有明显的影响. 对于PM 1来说, ΔW1(ΔW2或ΔW3)的影响比ΔH1(ΔH2或ΔH3)大. 对于PM 2来说, ΔW1(或ΔW3)和ΔH1(或ΔH3)对ΔFOM的影响基本一样. 由于极化方向的不同, ΔW2(或ΔH2)对PM 1和PM 2的ΔFOM有相反的影响, 如图9(b)所示. 由图9可知, 不同尺寸容差对FOM的影响小于80.
不同尺寸容差下, A的变化(ΔA)如图10(a)—(c)所示. 在图10(a)中, ΔW1(或ΔH1)对于PM 2的A几乎没有影响; 而对于PM 1来说, A都随ΔW1(或ΔH1)增大而增加, 但ΔW1的影响更明显. 在图10(b)中, ΔW2(或ΔH2)对PM 2的A没有明显影响; 而对ΔW2和ΔH2对PM 1的A的影响呈现相反的趋势. 如图10(c)所示, ΔW3 (或ΔH3)对PM 2的A几乎没有影响; 然而ΔW3和ΔH3对PM 1的A有不同的影响, A先随ΔW3增大而增大然后几乎不变, ΔH3对A几乎没影响. 总的来说, 不同尺寸容差对A的影响都小于0.06.
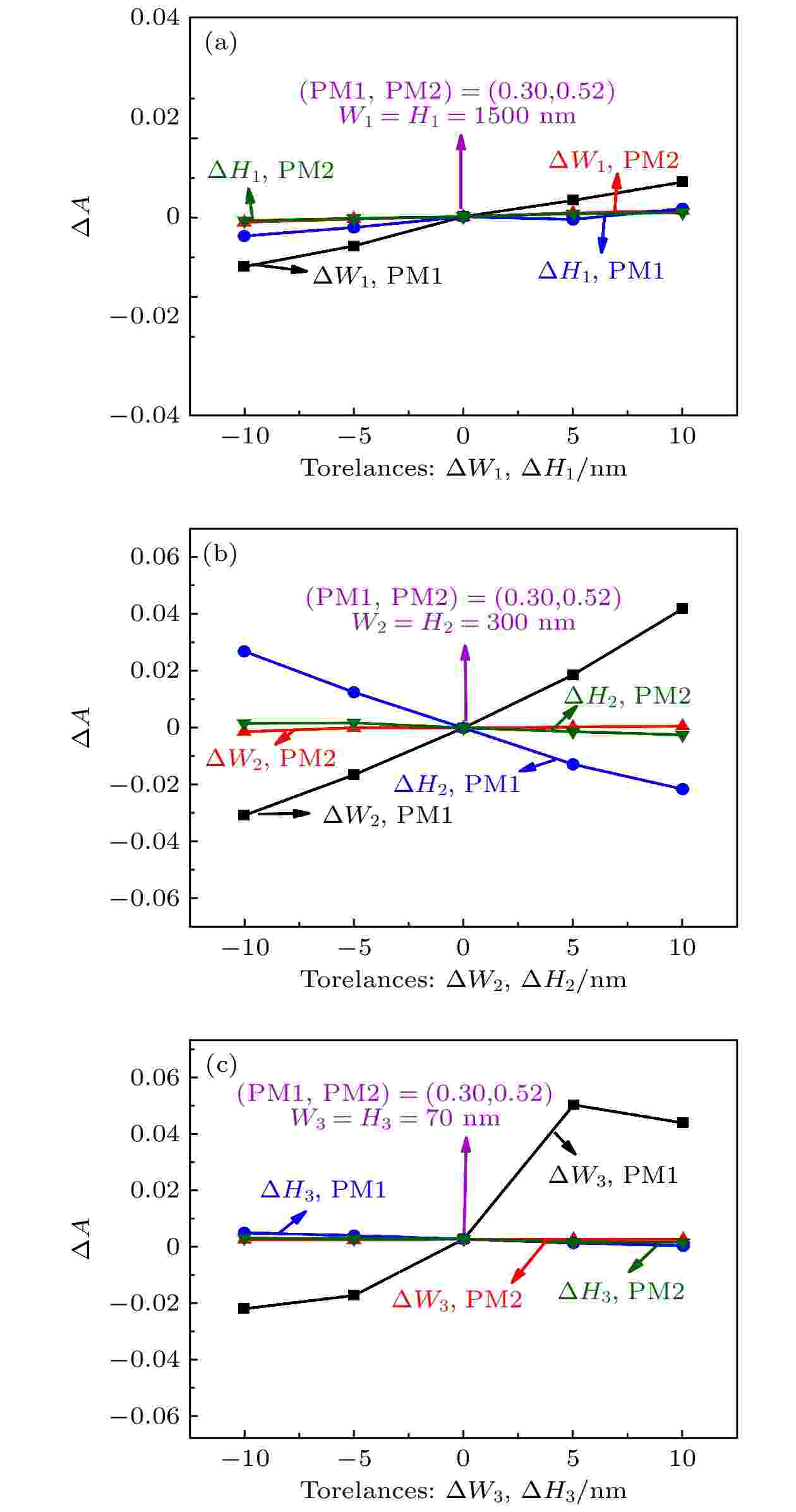图 10 在不同的尺寸容差下, PM 1和PM 2 的A 的变化(ΔA)随(a) ΔW1和ΔH1, (b) ΔW2和ΔH2, (c) ΔW3和ΔH3的变化规律. W1(= H1), W2(= H2) 和W3(= H3)分别取1500 nm, 300 nm和70 nm
Figure10. The changes of A (ΔA) for the PM 1 and PM 2 with different dimensional tolerances: (a) ΔW1 and ΔH1 at W2 (= H2) = 300 nm and W3 (= H3) = 70 nm; (b) ΔW2 and ΔH2 at W1 (= H1) = 1500 nm and W3 (= H3) = 70 nm; and (c) ΔW3 and ΔH3 at W1 (= H1) = 1500 nm and W2 (= H2) = 300 nm.

不同尺寸容差, Swg的变化(ΔSwg)如图11(a)—(c)所示. 在图11(a)中, ΔW1(或ΔH1)对PM 1和PM 2的Swg的影响趋势基本相同. PM 1和PM 2 的Swg随着ΔW1增大逐渐减小. ΔH1对PM 1和PM 2 的Swg的影响比ΔW1小. 从图11(b)可知, 对于PM 1和PM 2, ΔW2对Swg的影响与ΔH2相反. 也就是说, 随ΔW2的增大, PM 1的Swg逐渐增大而PM 2的Swg逐渐减小. 然而随着ΔH2的增大, PM 2的Swg逐渐增大而PM 1的Swg却逐渐减小. 从图11(c)上可以看出, ΔW3对PM 1和PM 2的Swg都几乎没有影响; ΔH3对PM 2的Swg也没有明显影响, 而只对PM 1的Swg有影响. 由以上可知, 不同尺寸容差对Swg的影响都小于0.001.
6.结　论
本文研究了一种能够实现低损耗传输的非对称银膜PS-CaF2混合等离子体波导. 利用有限元分析法(FEM)对波导中存在的两种模式(PM 1和PM 2)的几何参数进行了研究和优化. 在中红外波长3.5 μm附近, 当W1 = 1500 nm, W2 = 300 nm 和W3 = 70 nm时, PM 1和PM 2的归一化有效模场面积分别为0.30和0.52, 传输损耗分别为0.019 dB/μm和0.016 dB/μm, 品质因数分别为1335.54, 1594.99, 以及波导灵敏度分别为0.080和0.064. 制造容差分析表明非对称银膜PS-CaF2混合等离子体波导具有良好的制造误差容忍度. 非对称银膜PS-CaF2混合等离子体波导在传输性能和降低损耗等方面都具有优势, 为实现无标记生物化学传感开辟了新的途径, 并且为实现模式的偏振转换提供了一种新的波导结构.
相关话题/波导 结构 制造 优化 金属
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于太赫兹石墨烯等离激元的多参数相位可调谐结构及其应用
    摘要:太赫兹波的振幅和相位进行主动调控由于在太赫兹功能器件方面的广泛应用,受到了广泛关注.目前采用的金属-介质-金属超表面结构结合石墨烯等二维材料可实现太赫兹振幅/相位的动态调控,但存在调控自由度少(电压或光强)以及超表面结构加工工艺复杂及价格昂贵等缺点.本文提出了一种棱镜耦合石墨烯等离激元结构的相 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三层芯结构在单模大模场面积低弯曲损耗光纤中的应用和分析
    摘要:研究并分析了一种采用三层芯结构的单模大模场面积低弯曲损耗光纤.纤芯由纤芯高折射率层、包层低折射率层和下陷低折射率层三层结构构成.系统地分析了三层芯光纤(three-layer-corefiber,TLF)中不同结构参数对基模模场面积及弯曲损耗的影响.研究表明,通过调整三层芯的结构参数,在不牺牲 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 扭转变形对掺金黑磷烯电子结构和光学性质的影响
    摘要:基于密度泛函理论的第一性原理方法研究了扭转变形对掺金黑磷烯电子结构和光学性质的影响.研究发现,与本征黑磷烯受扭体系相比,掺金黑磷烯体系的电子结构对扭转变形的敏感度提高.能带结构分析发现,本征黑磷烯是直接带隙半导体,金掺杂后,可实现其从半导体到金属的转变.掺金黑磷烯体系扭转1°后,带隙被打开,成 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Nb<sup>5+</sup>掺杂钛酸锶结构与性能的第一性原理研究
    摘要:本文选取SrTiO3材料进行B位Nb5+离子掺杂改性,采用第一性原理计算了不同含量(0%,12.5%和25%)Nb5+掺杂SrTiO3的电子结构、光学、力学和热学性质.结果表明,当Nb5+掺杂浓度上升,材料晶胞参数增大;Nb5+掺杂后SrTiO3由间接带隙化合物转变为直接带隙化合物,Nb5+掺 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 掺杂维度和浓度调控的δ掺杂的La:SrTiO<sub>3</sub>超晶格结构金属-绝缘体转变
    摘要:利用密度泛函理论计算,本文系统研究了δ掺杂的La:SrTiO3超晶格结构的电子性质随掺杂维度和掺杂浓度改变而变化的规律性.该结构通过在SrTiO3等间距的单元层中掺入一定浓度的La来实现.在25%La掺杂浓度下,随着相邻掺杂层间距从1个单层增加到5个单层,掺杂维度从三维过渡到二维,超晶格从金属 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于电荷和热输运的石墨烯热电子器件性能优化
    摘要:科研人员近年来提出了石墨烯热电子能量转换器件(graphenethermionicenergyconverter,GTEC)的模型,对其物理机理与参数优化展开了研究,为高品位热能开发提供了新途径.然而,空间电荷积累和近场热辐射效应对GTEC能量转换性能的影响却鲜有报道.本文结合热电子发射、朗缪 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 三元Hf-C-N体系的空位有序结构及其力学性质和电子性质的第一性原理研究
    摘要:采用第一性原理方法,研究了三元Hf-C-N体系的空位有序结构及其力学性质和电子性质.首先采用第一性原理和进化算法,预测得到8种可能存在的热力学稳定的Hf-C-N空位有序结构;这些结构都具有岩盐结构,与实验发现的无序固溶体的结构类型一致.本文的预测结果证明了Hf-C-N空位化合物能够以有序结构形 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 渔网超结构的等离激元模式及其对薄膜电池的陷光调控
    摘要:渔网超结构具有平面、近光学无损、特定光场中可以激发表面等离激元等特点,在增强光子器件的响应效率方面极具潜力.本文基于时域有限差分方法和严格耦合波分析,系统研究了渔网超结构的等离共振模式及其对晶硅薄膜电池的光波调控性能.研究结果表明,渔网结构对光波的吸收、散射和消光特性强烈依赖金属层的厚度、线宽 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 单缺陷对Sc, Ti, V修饰石墨烯的结构及储氢性能的影响
    摘要:寻找稳定高效的储氢材料是实现氢经济的关键.过渡金属修饰石墨烯储氢材料在理论上被广泛研究,但存在H2解离和金属团聚的问题.本文基于密度泛函理论对Sc,Ti,V修饰单缺陷石墨烯的结构及储氢性能进行计算.结果表明:单缺陷使Sc,Ti,V与石墨烯的结合能提高4—5倍;Sc,Ti,V离子特性增强,可以通 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维共价键子结构Zintl相热电材料研究及进展
    摘要:热电材料可以实现热能和电能间的直接相互转换,在半导体制冷和热能回收方面有着重要应用.Zintl相热电材料由电负性差异较大的阴阳离子组成,其输运特征符合“声子玻璃,电子晶体”的概念,因此受到了广泛的研究,特别是具有二维共价键子结构Zintl相热电材料凭借优异的电性能更是被寄予厚望.本文综述了具有 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.