摘要: 提出并验证了一种基于双偏振调制生成可变对称三角波形的方法. 通过设置合适的调制器的调制指数和移相器的相移, 使得调制器生成信号光的强度近似等于理想三角波形傅里叶级数展开式的前三项, 从而生成不同对称因子的三角波形(三阶近似波形). 之前的三角波形生成方案大多生成对称三角波形或锯齿波形(锯齿波形可认为是非对称三角波形), 且对称因子不可调谐, 而本方案生成的三角波形的对称因子可调谐范围可达0%—100%, 这极大地拓展了三角波形的应用范围. 引入均方根误差(root-mean-square error, RMSE)来衡量生成波形与理论波形的相似度, 计算可发现, 理论上本方案生成的对称因子范围在14%—86%的三角波形与理想波形有良好的相似度(RMSE < 0.044), 仿真中生成波形的RMSE也非常接近理论误差. 在实验中, 通过使用频率为4GHz的射频信号生成了对称因子范围在20%—80%的三角波形.
关键词: 三角波形 /
双偏振调制 /
傅里叶级数展开式 /
均方根误差 English Abstract Triangular-shaped waveform generation with variable symmetry based on dual-polarization modulation Wang Chuang-Ye 1 ,Ning Ti-Gang 1 ,Li Jing 1 ,Pei Li 1 ,Zheng Jing-Jing 1 ,Li Yu-Jian 1 ,Ai Bo 2 1.Key Laboratory of All Optical Network and Advanced Telecommunication Network of EMC, Institute of Lightwave Technology, Beijing Jiaotong University, Beijing 100044, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61827817, 62005012) and the Natural Science foundation of Beijing, China (Grant No. 4192022).Received Date: 20 April 2021Accepted Date: 16 June 2021Available Online: 15 August 2021Published Online: 20 November 2021Abstract: Photonic generation of triangular-shaped waveform with variable symmetry based on dual-polarization modulation is proposed and demonstrated. Based on the external modulation method, a dual-polarization modulator is used to modulate the radio frequency signal to generate the needed optical signal. By setting the modulation index of the modulator and phase shift of phase shifters appropriately, the optical intensity of generated signal can equal approximately the first three terms of the Fourier series expansion of the ideal triangular-shaped waveform, so triangular-shaped waveforms with different symmetry factors can be generated. Most of previous triangular waveform generation schemes generate symmetrical triangular waveform or sawtooth waveform (sawtooth waveform can be regarded as an asymmetrical triangular waveform), and the symmetry factor is not tunable. The tunable range of symmetry factor of triangular-shaped waveform generated by this scheme can reach 0%–100%, which will greatly expand the application range of triangular-shaped waveforms. The root-mean-square error (RMSE) is introduced to measure the similarity between the generated waveform and the theoretical waveform. It can be found that theoretically the triangular-shaped waveform with a symmetry factor in a range from 14% to 86% has a good similarity to the ideal waveform (RMSE < 0.044), and the RMSE of the generated waveform in the simulation is also very close to the theoretical RMSE. Experimentally, the 4GHz triangular-shaped waveforms with different values of symmetry factor (20%–80%) are obtained by using 4GHz radio frequency signal.Keywords: triangular-shaped waveform /dual-polarization modulation /Fourier series expansion /root-mean-square error 全文HTML --> --> --> 1.引 言 近些年, 任意波形的生成是微波光子学的一个研究热点. 常见的任意波形包括对称三角波、方波、锯齿波(锯齿波可认为是非对称三角波)和高斯波. 在这些波形中, 三角波形(对称三角波和非对称三角波)由于光强度具有线性上升和线性下降的性质被广泛地应用于通信、雷达系统、传感和光信号处理等领域[1 -5 ] , 因而被广泛地研究. 传统基于电子学生成任意波形的方法由于具有生成波形的重复率低、带宽小、易受电磁干扰等缺点已不适合未来的发展, 而基于光子学的方法则完美地克服了这些缺点. 过去一些年研究者们基于光子学提出了很多生成对称三角波形的方法. 例如, 基于光谱切割结合频率时间映射的方法生成对称三角波[6 ,7 ] , 利用光纤非线性的方法[8 ] 生成对称三角波和利用外部调制连续波激光器的方法生成对称三角波. 在这些方法中, 外部调制连续波激光器的方法由于简单的结构和原理被研究者们进行了大量的研究, 其主要原理是利用调制器调制射频信号, 生成光信号的光强度近似等于理想对称三角波形傅里叶级数展开式来生成对称三角波. 研究者们基于外部调制的方法提出了很多方案, 例如, 利用调制器结合色散光纤的方式生成对称三角波[9 ,10 ] , 利用调制器结合滤波器的方式生成对称三角波[11 ,12 ] , 基于受激布里渊散射的方式生成对称三角波[13 ] , 基于光电振荡器的方式生成对称三角波[14 ,15 ] , 基于两个级联调制器的方式生成对称三角波[16 ] 等等. 除了研究对称三角波的生成, 研究者们基于外部调制的方法还提出了很多生成锯齿波的方案[17 -20 ] . 但无论是生成对称三角波还是生成锯齿波[6 -20 ] , 其波形的对称是无法调节的. 因此研究可变对称三角波形的生成具有重要意义, 这将极大地拓展三角波形的应用范围. 这里引入对称因子的概念, 对称因子定义为三角波形上升沿经历时间与周期的比值, 这样对称三角波和锯齿波就可被认为是对称因子分别为50%和0%的三角波形. 文献[21 ]中, 作者利用单驱动马赫曾德尔调制器结合平衡探测器实现了不同对称因子三角波形的生成, 是通过控制调制器的偏置电压和移相器的相移来实现的, 然而控制调制器偏置电压的过程会存在偏置电压偏移的问题.2.理论和模型 22.1.可变对称三角波形的傅里叶级数 2.1.可变对称三角波形的傅里叶级数 对称因子δ 定义为三角波形上升沿经历的时间与周期的比值, 从文献[21 ]中可知, 不同对称因子的三角波形的傅里叶级数展开式可表示为(1 )式所示的无数正弦函数的加权和.Ω 为三角波形的角频率. 不同对称因子对应的b 1 , b 2 , b 3 的值如图1 所示. 如图1(b) 所示, 当$0{\text{%}}\leqslant \delta \leqslant100{\text{%}}$ 时, b 1 > 0; 当δ < 50%时, b 2 > 0; δ > 50%时, b 2 < 0; 当$0{\text{%}}\leqslant \delta \lt34{\text{%}}$ 或$66{\text{%}}\lt \delta \leqslant $ $ 100{\text{%}}$ 时, b 3 > 0; 34% < δ < 66%时b 3 < 0.图 1 不同对称因子对应的b 1 , b 2 , b 3 值Figure1. Magnitude of b 1 , b 2 and b 3 versus symmetry factor δ .2.2.模型和原理 -->2.2.模型和原理 可变对称三角波形生成方案的原理示意图如图2 所示. 主要部分为一个双偏振调制器, 这个双偏振调制器是一个集成的调制器, 包括一个光功分器、两个单驱动马赫曾德尔调制器(子调制器1和子调制器2), 一个90°偏振旋转器和一个偏振合束器. 连续波激光器生成的光信号通过一个偏振控制器后输入双偏振调制器, 偏振控制器用来控制入射光的偏振状态从而减少系统的偏振损耗. 射频源生成的射频信号首先通过一个电功分器分为两路信号, 每路信号分别通过一个电放大器和一个电移相器后分别进入子调制器1和子调制器2的射频输入口进行调制, 双偏振调制器输出的调制信号经过一个光电探测器后输入一个电移相器, 电移相器3输出的信号即为需要的信号. 假设射频源输出的电信号的表达式为$ V_{\rm{RF}}\left(\rm{t}\right) = V_{\rm{RF}}\sin(\omega t) $ , 其中$ V_{\rm{RF}} $ 和ω 分别代表电信号的幅度和角频率; 连续波激光器生成的光信号的表达式为$ E_{\rm{in}}\left(\rm{t}\right) = E_{\rm{0}} \exp({\rm{j\omega}}_{\rm{0}}\rm{t}) $ , 其中$ E_{\rm{0}} $ 和$ { \omega }_{\rm{0}} $ 分别代表光信号的幅度和角频率; 三个移相器PS1, PS2, PS3引起的相移分别为${\theta}_{\rm{1}}$ , ${\theta}_{\rm{2}}$ 和${\theta}_{\rm{3}}$ . 子调制1和子调制2分别偏置于正交传输点和最小传输点, 则子调制1和子调制器2输出的光信号可表示为图 2 可变对称三角波形生成方案的原理示意图. CW laser, 连续波激光器; PC, 偏振控制器; RF source, 射频源; EPS, 电功分器; EA, 电放大器; PS, 电移相器; OPS, 光功分器; MZM, 单驱动马赫曾德尔调制器; PBC, 偏振合束器; 90°PR, 90°偏振旋转器; PD, 光电探测器Figure2. Schematic diagram of the proposed scheme. CW laser, continuous wave laser; PC, polarization controller; RF source, radio frequency source; EPS, electrical power splitter; EA, electrical amplifier; PS, phase shifter; OPS, optical power splitter; MZM, single-drive Mach-Zehnder Modulator; PBC, polarization beam combiner; 90° PR, 90° polarization rotator; PD, photodiode.m 1 和m 2 分别代表子调制器1和子调制器2的调制系数. ${m_1} = \dfrac{{\rho _1}{\text{π}}{V_{{\rm{RF}}}}}{ {2{V_{\text{π}}}} }$ , ${m_2} = \dfrac{{\rho _2}{\text{π}}{V_{{\rm{RF}}}}}{ {2{V_{\text{π}}}} }$ , 这里 $ {\rm{ρ}}_{\rm{1}} $ 和$ {\rm{ρ}}_{\rm{2}} $ 分别代表电放大器1和电放大器2的放大系数, $ V_{\rm{π}} $ 代表马赫曾德尔调制器的半波电压.m < 1.5), 光电探测器输出的电信号可表示为$\Re$ 代表光电探测器的灵敏度.5 )式可进一步转化为DC 代表直流项, $DC = \dfrac{1}{4}\Re E_0^2\left[ {2 - {J_0}\left( {2{m_2}} \right)} \right]$ . p , q 为整数.6 )式和(1 )式, 为了生成不同对称因子的三角波形, 需满足k , l 为整数. 即8 )式可解出不同对称因子三角波形生成条件的一组特征解, 如表1 所列.对称因子 相移1 相移2 相移3 调制系数1 调制系数2 δ θ 1 θ 2 θ 3 m 1 m 2 0% 0 π/4 0 1.15 0.83 10% 0 π/4 0 1.1 0.81 20% 0 π/4 0 0.92 0.76 30% 0 π/4 0 0.49 0.53 40% π/2 π/2 3π/2 0.61 0.41 50% π/2 0 3π/2 0.76 0 60% π/2 0 3π/2 0.61 0.41 70% 0 3π/4 0 0.49 0.53 80% 0 3π/4 0 0.92 0.76 90% 0 3π/4 0 1.1 0.81 100% 0 3π/4 0 1.15 0.83
表1 不同对称因子三角波形的生成条件Table1. Generated conditions for triangular-shaped waveforms with different symmetry factor.3.仿真及讨论 在OptiSystem软件中对方案进行了仿真. 连续波激光器的中心波长、功率和线宽分别设置为1550 nm, 20 dBm和1 MHz; 马赫曾德尔调制器的消光比、半波电压和插入损耗分别设置为30 dB, 4 V和5 dB; 光电探测器的灵敏度、暗电流和热噪声密度分别设置为0.8 A/W, 10 nA和10 –21 W/Hz; 射频源的频率设置为10 GHz. 子调制器1和子调制器2分别偏置于正交传输点和最小传输点. 当调制器的调制指数和移相器的相移分别设置为表1 所列的参数时, 得到生成的时域波形如图3 所示.图 3 仿真生成的对称因子为0%—100%的时域波形Figure3. Simulated generated temporal triangular-shaped waveforms with δ = 0%?100%.图4(a) 和图4(b) 分别为仿真生成的对称因子为20%的三角波形的时域波形图和对应的电谱, 从图4(b) 可以看出, 一阶谐波与二阶谐波和三阶谐波的功率比分别为7.77和14.93 dB, 这非常接近理论值7.86和14.91 dB.图 4 仿真生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱Figure4. Simulated generated triangular-shaped waveform with δ = 20%: (a) Temporal waveform; (b) corresponding electrical spectrum.图5 为对称因子为20%的三角波形的合成示意图. I 1 和I 2 分别代表子调制器1和子调制器2的输出光包络, I 4 代表移相器3的输出光包络.图 5 对称因子为20%的三角波形的合成示意图Figure5. Synthesis schematic diagram of triangular-shaped waveform with δ = 20%.y 0 和y 1 分别代表近似波形和理论波形的归一化幅度, z 代表三角波形一个周期内的采样点数. RMSE越小代表近似波形与理论波形越相似.图6(a) 为不同对称因子下三阶近似波形、五阶近似波形和十阶近似波形的理论RMSE, 可以看出, 近似阶数越大, 波形的RMSE越小, 近似波形和理论波形的相似度越高. 图6(b) 中黑线代表三阶近似波形的理论RMSE, 红点代表仿真生成的不同对称因子的三角波形的RMSE, 可以看出, 仿真生成波形的RMSE非常接近理论RMSE, 从黑线(三阶近似波形的理论RMSE)可以看出, 当$\rm{14{\text{%}}\leqslant} \delta \rm{\leqslant86{\text{%}}}$ 时, 波形的理论RMSE均小于0.044, 这表明对称因子在$14{\text{%}}\leqslant \delta \leqslant86{\text{%}}$ 的三角波形非常接近理论波形.图 6 (a) 三阶近似波形、五阶近似波形和十阶近似波形的理论RMSE; (b) 仿真生成波形的RMSEFigure6. (a) Theoretical RMSE for third-order approximate waveform, fifth-order approximate waveform and tenth-order approximate waveform; (b) the RMSE of simulated generated waveforms.4.实验与验证 在实验室对所提出的可变对称三角波形生成方案进行了实验验证, 搭建的实验平台如图7 所示. 实验中, 使用的激光器为双波长激光器, 激光器的波长和功率分别设置为1550.12 nm和10 dBm. 双偏振调制器由一个双偏振BPSK调制器(Fujitsu FTM7980 EDA/301)和两个180°电桥(GHC-180-040180)组成, 其中双偏振BPSK调制器有4个射频输入口且两个子调制器中没有内置180°电桥. 一个偏振控制器连接在连续波激光器和双偏振调制器中间用于调节系统的偏振损耗. 由于只有单一频率的电信号通过电移相器1和电移相器2, 所以实验中可以用两个电延迟线(SHF 2000 DEL)分别代替电移相器1和电移相器2. 从之前的理论分析中可知, 移相器3需要的相移均为特殊角(0°或者270°), 实验中用一个90°电桥(带宽为2-26.5 GHz)和一个180°电桥(带宽为2-26.5 GHz)串联来代替270°的相移. 射频源(AV1431 A)的频率设置为4 GHz. 由于实验室只有一个电放大器, 所以通过同时调整电放大器的放大系数和射频源的功率来调整两个子调制器的调制系数. 通过调节两个子调制器的直流偏置电压使得两个子调制器分别偏置在正交传输点和最小传输点. 实验中用一个宽带的示波器(Agilent 86100 B+86116 A)和一个信号分析仪(Agilent EXA N9010 A)来分别捕获生成的波形和对应的电谱. 如图6(b) 所示, 当δ < 14%或 δ > 86%时, 对应三角波形的RMSE > 0.044, 三角波形与理论波形存在较大的误差, 因此此次实验中只验证了对称因子为20%—80%的三角波形的生成. 实验中生成的波形如图8 所示. 由于实验中电延迟线的延迟量和调制器的调制指数精确控制比较困难, 所以实验结果和仿真结果存在一定的差异.图 7 可变对称三角波形生成方案的实验平台. Dual-wavelength laser, 双波长激光器; Polarization controller, 偏振控制器; Signal generator, 信号发生器; Power splitter, 电功分器; Electrical delay line, 电延迟线; Electrical amplifier, 电放大器; 180° hybrid coupler, 180°电桥; DP-BPSK modulator, 双偏振BPSK调制器; Photodiode, 光电探测器; Oscilloscope, 示波器Figure7. Experimental platform for triangular-shaped waveform with variable symmetry generation scheme.图 8 实验生成的对称因子为20%, 30%, 40%, 50%, 60%, 70%和80%的三角波形Figure8. Generated triangular-shaped waveforms with δ = 20%, 30%, 40%, 50%, 60%, 70% and 80% in the experiment.图9(a) 和图9(b) 分别为实验中生成的对称因子为20%的三角波形的时域图和对应的电谱. 从图9(b) 可以看出, 一阶谐波与二阶谐波和三阶谐波的功率比分别为7.8和15.4 dB, 非常接近理论值.图 9 实验生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱Figure9. Generated triangular-shaped waveform with δ = 20%: (a) Temporal waveform; (b) corresponding electrical spectrum.5.总 结 提出了一种生成对称因子可调谐三角波形的方法. 相比之前大多数三角波形生成方案中生成的三角波形的对称不可调谐, 本方案生成的三角波形的对称因子可调谐范围可达0%—100%, 这极大地拓展了三角波形的可应用范围. 通过计算, 对称因子为$\rm{14{\text{%}}\leqslant}\rm{δ}\rm{\leqslant86{\text{%}}}$ 的三角波形与理论波形显示出很好的相似度(RMSE < 0.044). 本方案是基于三阶近似波形来拟合的不同对称因子的三角波形, 由第3部分的研究可知, 随着拟合阶数的增大, 生成波形与理论波形的相似度会增高, 未来将向更高阶近似波形拟合进行研究, 这样会进一步提升生成波形与理论波形的相似度. 



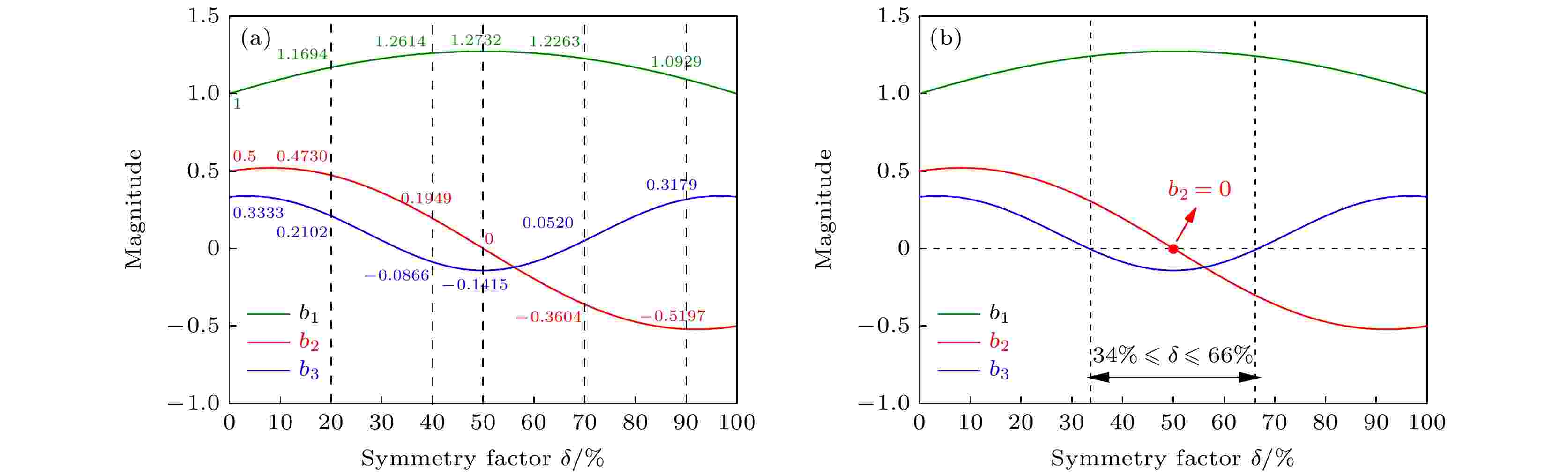 图 1 不同对称因子对应的b1, b2, b3值
图 1 不同对称因子对应的b1, b2, b3值







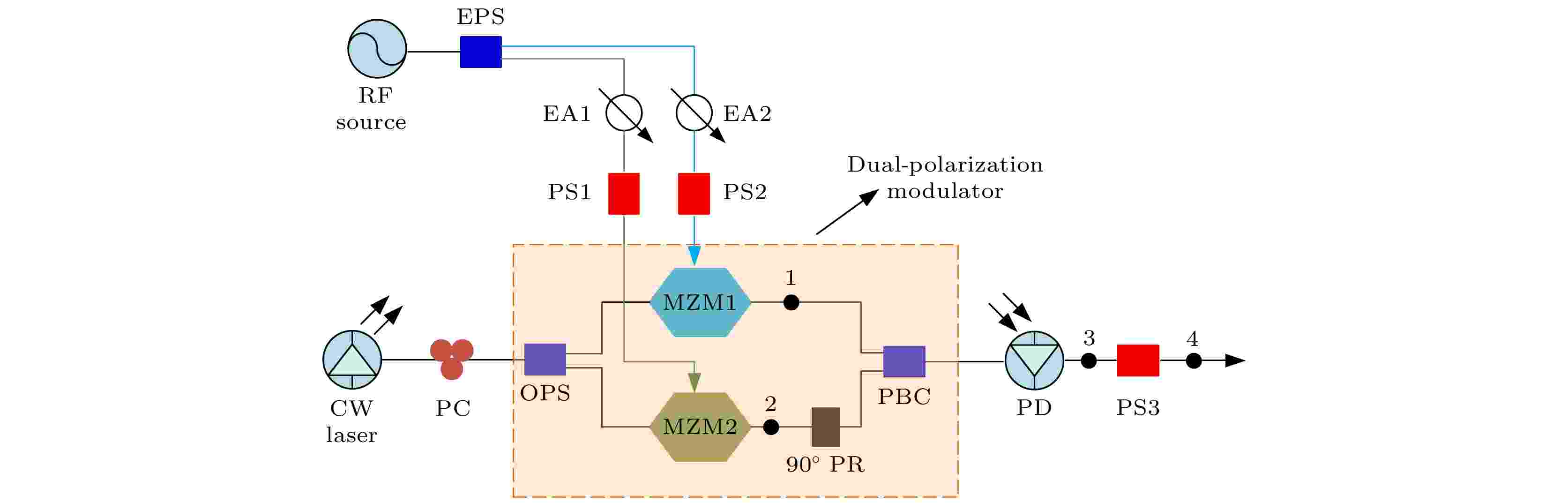 图 2 可变对称三角波形生成方案的原理示意图. CW laser, 连续波激光器; PC, 偏振控制器; RF source, 射频源; EPS, 电功分器; EA, 电放大器; PS, 电移相器; OPS, 光功分器; MZM, 单驱动马赫曾德尔调制器; PBC, 偏振合束器; 90°PR, 90°偏振旋转器; PD, 光电探测器
图 2 可变对称三角波形生成方案的原理示意图. CW laser, 连续波激光器; PC, 偏振控制器; RF source, 射频源; EPS, 电功分器; EA, 电放大器; PS, 电移相器; OPS, 光功分器; MZM, 单驱动马赫曾德尔调制器; PBC, 偏振合束器; 90°PR, 90°偏振旋转器; PD, 光电探测器






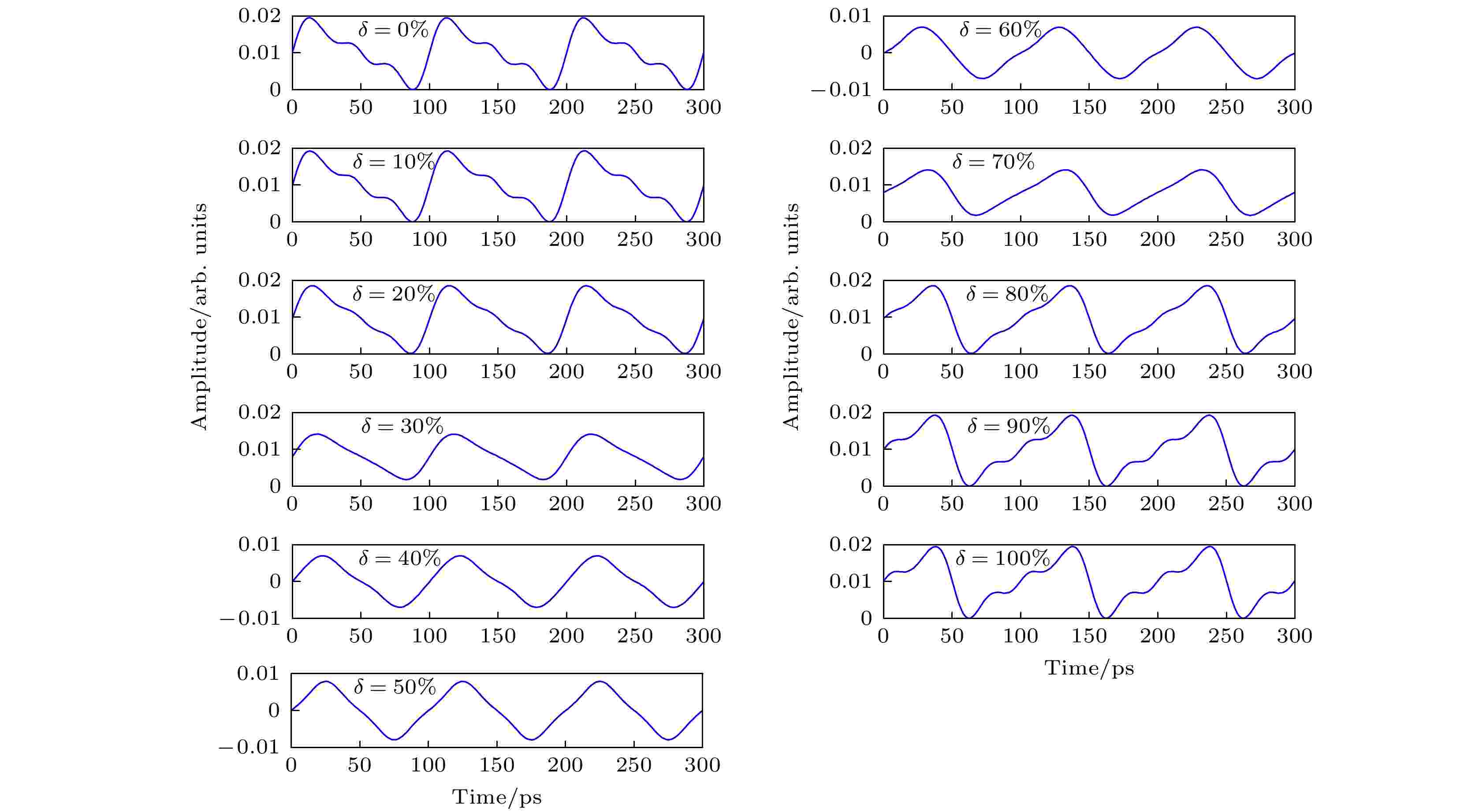 图 3 仿真生成的对称因子为0%—100%的时域波形
图 3 仿真生成的对称因子为0%—100%的时域波形 图 4 仿真生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱
图 4 仿真生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱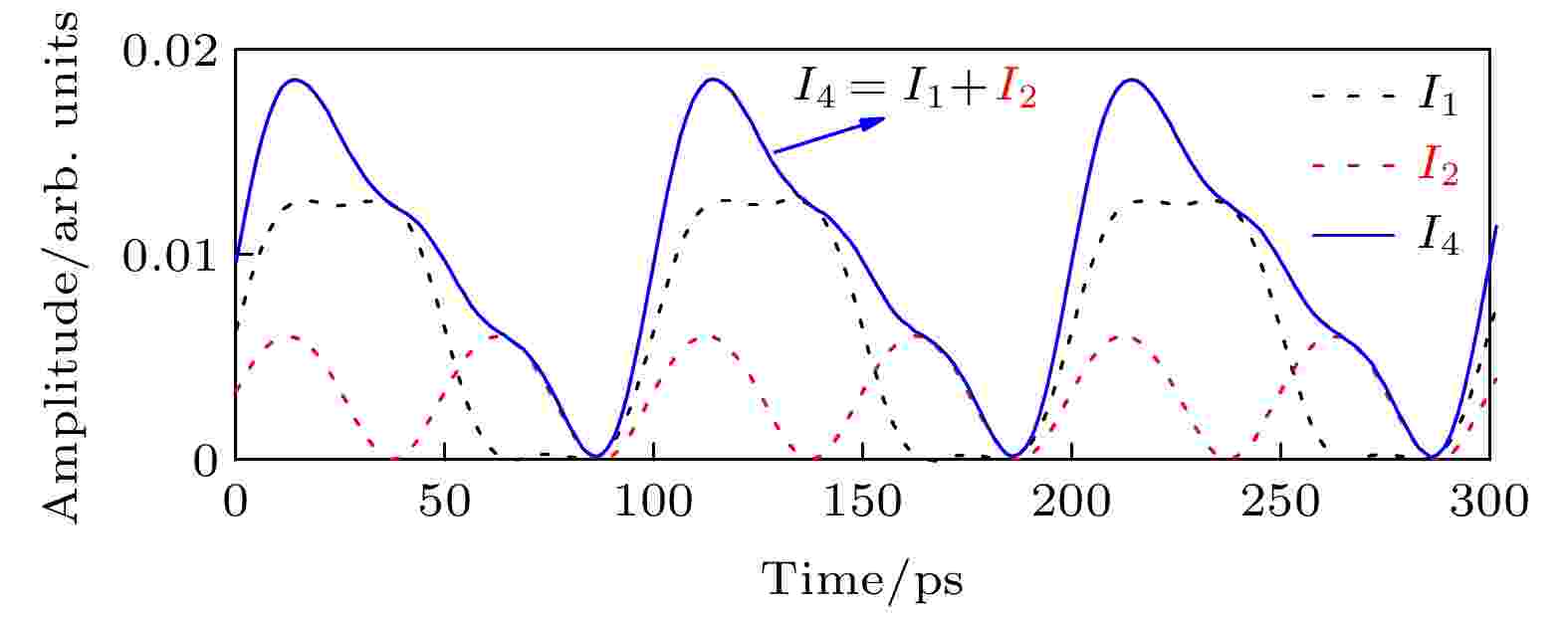 图 5 对称因子为20%的三角波形的合成示意图
图 5 对称因子为20%的三角波形的合成示意图

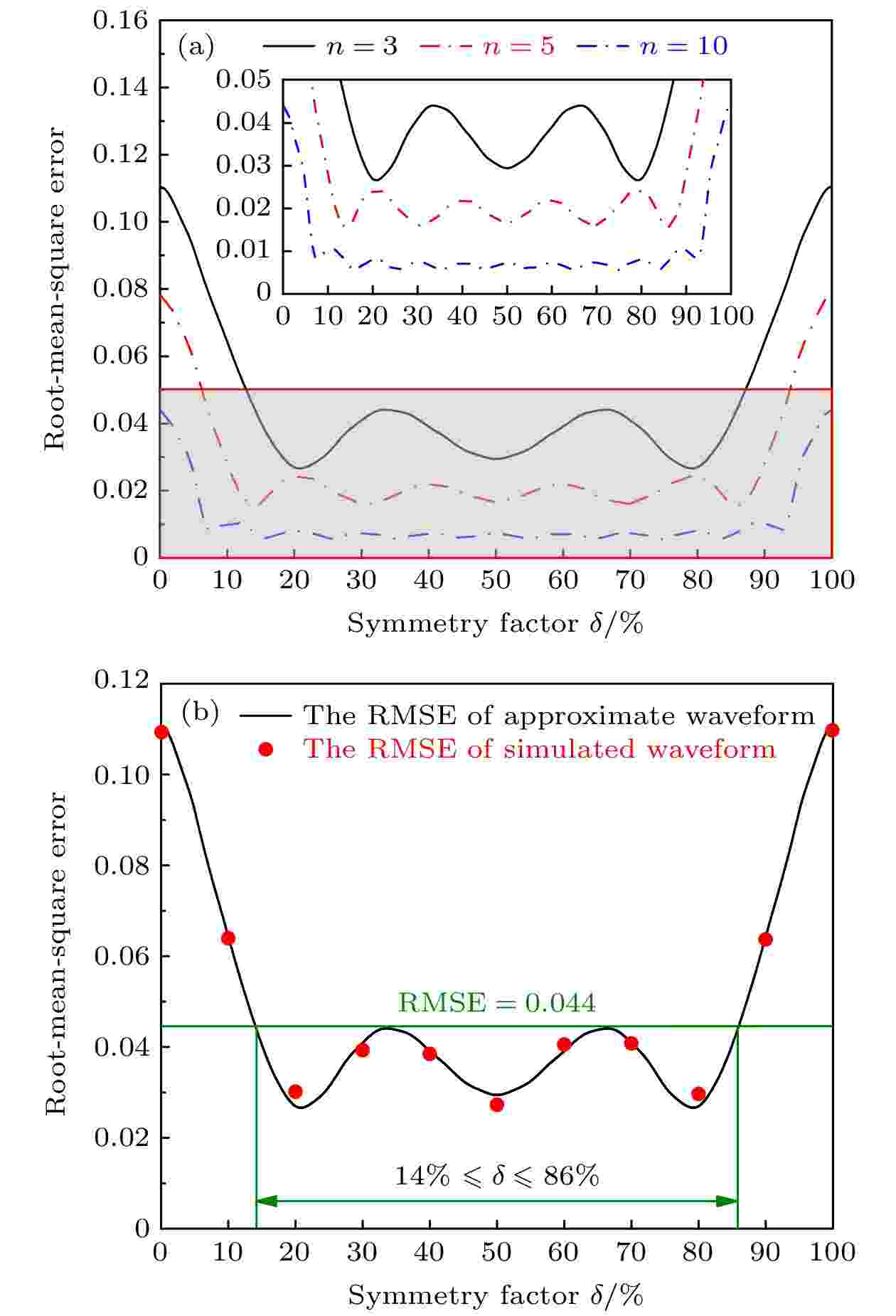 图 6 (a) 三阶近似波形、五阶近似波形和十阶近似波形的理论RMSE; (b) 仿真生成波形的RMSE
图 6 (a) 三阶近似波形、五阶近似波形和十阶近似波形的理论RMSE; (b) 仿真生成波形的RMSE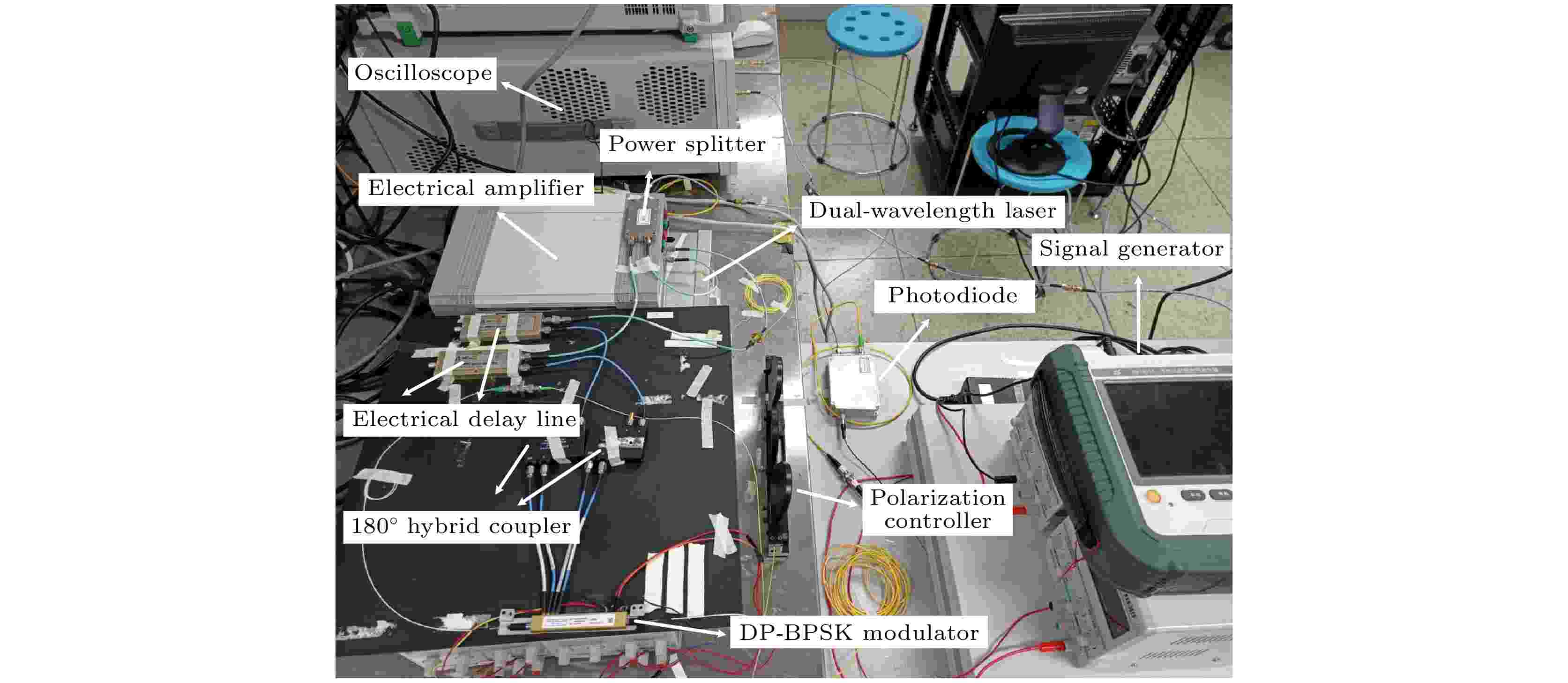 图 7 可变对称三角波形生成方案的实验平台. Dual-wavelength laser, 双波长激光器; Polarization controller, 偏振控制器; Signal generator, 信号发生器; Power splitter, 电功分器; Electrical delay line, 电延迟线; Electrical amplifier, 电放大器; 180° hybrid coupler, 180°电桥; DP-BPSK modulator, 双偏振BPSK调制器; Photodiode, 光电探测器; Oscilloscope, 示波器
图 7 可变对称三角波形生成方案的实验平台. Dual-wavelength laser, 双波长激光器; Polarization controller, 偏振控制器; Signal generator, 信号发生器; Power splitter, 电功分器; Electrical delay line, 电延迟线; Electrical amplifier, 电放大器; 180° hybrid coupler, 180°电桥; DP-BPSK modulator, 双偏振BPSK调制器; Photodiode, 光电探测器; Oscilloscope, 示波器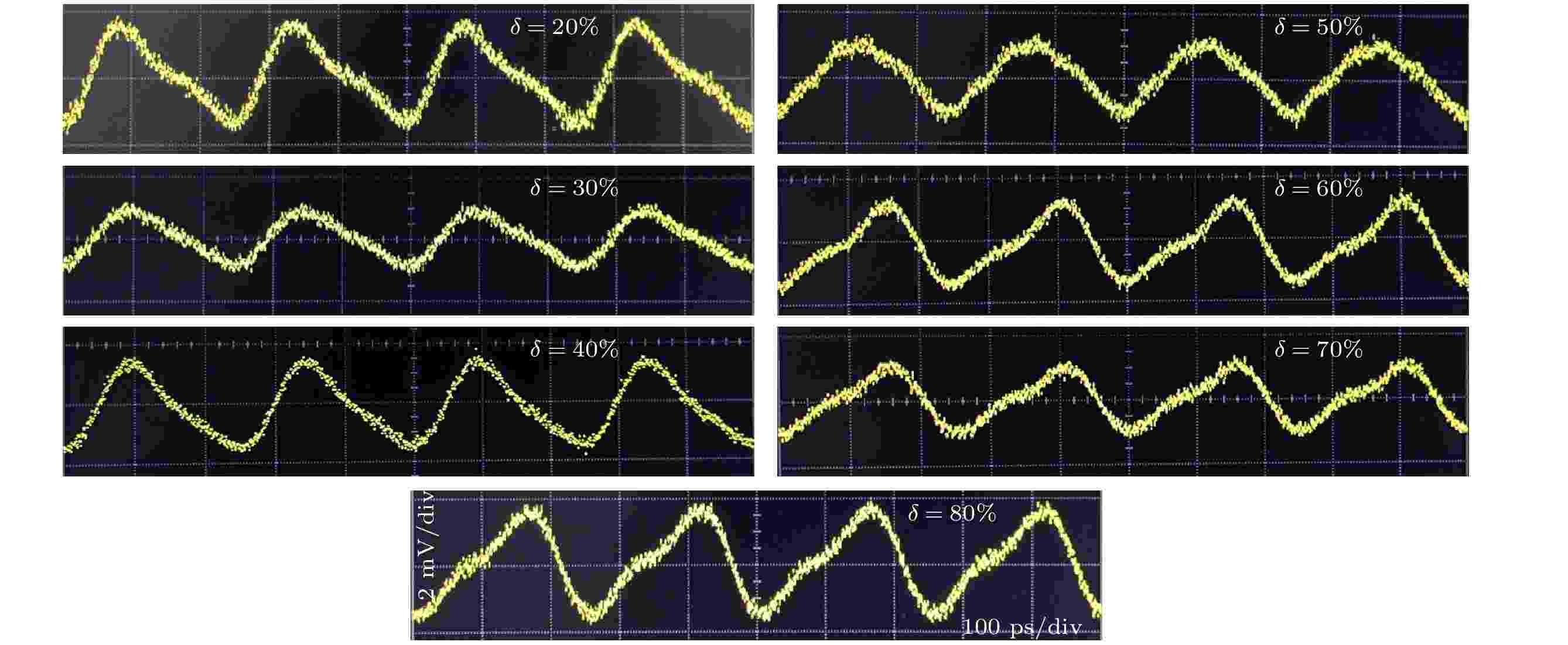 图 8 实验生成的对称因子为20%, 30%, 40%, 50%, 60%, 70%和80%的三角波形
图 8 实验生成的对称因子为20%, 30%, 40%, 50%, 60%, 70%和80%的三角波形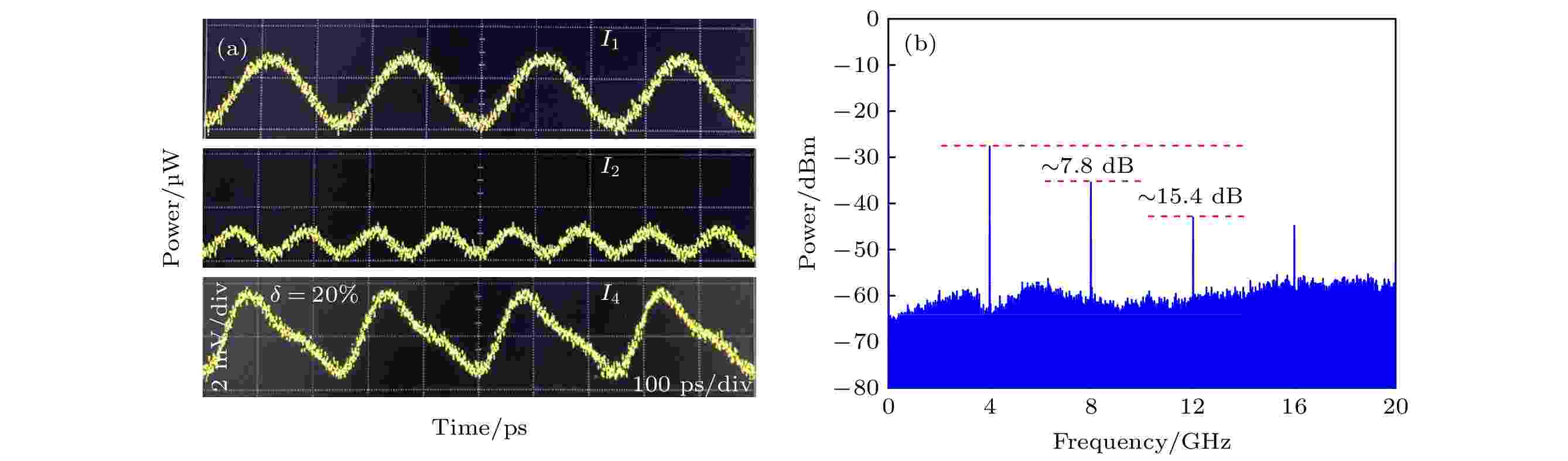 图 9 实验生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱
图 9 实验生成的对称因子为20%的三角波形 (a) 时域波形; (b) 对应的电谱
