摘要:涡流场影响着声场分布, 进而影响着声空化特性, 以机械搅拌产生的涡流场为研究对象, 使用COMSOL软件数值模拟了不同搅拌速度下的声场分布情况. 结果显示, 机械搅拌增加了声场分布的均匀性和声压幅值. 接下来将仿真得到的瞬时声压值用Origin软件拟合, 然后将拟合得到的声压函数代入Keller-Miksis气泡动力学方程中, 得到了不同搅拌速度下空化泡的半径随时间的变化情况, 从计算结果中发现, 未加机械搅拌的条件下, 只有z = 7.3 cm截面上有空化效应产生. 最后根据所得到的空化泡半径, 计算了空化泡内部的温度. 结果显示, 空化泡在有搅拌存在的条件下, 内部温度得到了大幅增加, 当搅拌速度达到1000 r/min后, 空化泡内部温度会随着搅拌速度的增加而降低. 最后设计实验验证了仿真结果. 仿真得到的结果不仅从理论上解释了机械搅拌提高有机溶液超声降解率的原因, 还发现了过高的搅拌速度会降低声空化强度, 从而降低声化学反应速率, 这为通过机械搅拌来进一步提高超声降解率提供了新思路.
关键词: 涡流/
超声降解率/
声场/
温度

English Abstract

全文HTML

--> --> -->

工业化进程的加速推进已经造成了大量有机污染物排放到水中. 这些污染物相互反应, 产生了大量有害人类和水生物健康的物质, 而这些有害物质大多数又是难以降解的. 因此, 寻找一个能有效降解有机物的方法至关重要. 高级氧化技术(AOPs)是20世纪80年代发展起来的一种深度氧化技术, 它的工作机理是在催化剂以及声、光辐射、高温高压等作用下, 产生一种氧化性极强的活性自由基(如·OH等), 由于该自由基的存在, 会使得一些难氧化的有机物在其作用下发生开环、断键、加成、取代以及电子转移, 最终降解为CO₂和H₂O, 从而达到净化污水的目的^[1]. 常见的高级氧化技术主要有光化学氧化、声化学氧化、臭氧氧化、电化学氧化和Fenton氧化等. 不同的技术特点不同, 应用条件有所不同^[2].
超声技术作为一种高级氧化技术已经被证实可以用于处理任何种类的废水, 因此被广泛地用于降解水中有机污染物^[3]. 跟一些传统的降解方法相比, 超声技术更加简单、清洁和高效. 这种方法的工作机理是利用超声空化产生的羟基自由基与水中的有机污染物发生化学反应, 从而实现有机物的降解^[4-7]. 超声空化是指在超声波的驱动下, 空化泡发生缩塌破裂, 在破裂的瞬间, 气泡内部产生了高温高压, 伴随着冲击波的形成. 与此同时, 空化产生的高温会将水分子分解成H原子和羟基自由基^[8-15]. 此外, 空化气泡产生的冲击波和微射流导致氧化剂逃逸到界面和水溶液中, 这将导致氧化剂和溶液中的有机污染物之间的快速氧化^[16].
然而, 由于在产生超声空化时能量转换效率低, 并且难以扩大其规模. 研究人员试图通过使用超声波混合技术来克服这些困难. Lesko等^[17]研究发现, 当臭氧和超声波同时应用时, 可以观察到明显的协同效应, 提高了有机物的降解效率. 此外, 文献[1]中报道过超声波与过氧化氢、芬顿试剂、光催化剂等联合使用可以降低有机污染物的降解成本.
近年来, 一些****开始使用超声辐射协同机械搅拌来提高有机物的降解率. 这种方法因其操作简单, 已经引起了越来越多研究者的重视. Yasuda等^[18]通过实验研究了搅拌器的类型和速度对声化学反应速率的影响. 也有一些研究人员^[19-21]认为, 机械搅拌引起的液体流动可以通过二次 Bjerknes 力来减少空化气泡的聚集, 从而了提高声空化效率, 此外, Nakui等^[22] 在搅拌 (300 r/min) 和超声辐照(200 kHz, 200 W) 条件下对肼进行了降解. 实验结果表明, 在只有机械搅拌的条件下, 有机物没有被降解. 这个研究表明, 声场分布对机械搅拌作用下的超声降解起着非常重要的作用. 因此, Zhang等^[23] 研究了搅拌速度对水溶液中罗丹明B降解率的影响, 并使用声波方程模拟有搅拌和无搅拌时的声场分布. 但仅用气泡来代替涡流对声压的影响会降低结果的准确性, 并且也没有分析模拟得到的声场对空化的影响.
大量的实验研究表明, 超声空化降解有机污染物受多种因素的影响, 主要包括空化泡产生的温度、压力和冲击波等因素. 而对于的给定溶液而言, 这些因素主要受超声场特性的影响. 本文从声场分布和温度这两个方面分析涡流对超声空化强度的影响, 为机械搅拌提高有机物的降解率提供了理论依据.

2

-->

2.1.数学模型

Navier-Stokes方程经常被用于计算流体的流动, 通过求解该方程可以得到流场内的流速和压力随时间的变化情况, 其数学表达式为^[24]:

$\begin{split} &{\rho }_{0}\left({\boldsymbol{V}}_{\boldsymbol{0}}\cdot\nabla \right){\boldsymbol{V}}_{\boldsymbol{0}}\\=\;&\nabla \cdot\left(-{\rho '}+\mu \left(\nabla {\boldsymbol{V}}_{\boldsymbol{0}}+{\left(\nabla {\boldsymbol{V}}_{\boldsymbol{0}}\right)}^{\rm{T}}\right)\right)+{\rho }_{0}g , \end{split}$

其中$ {\rho _0} $是密度, $ {{\boldsymbol{V}}_{\rm{0}}} $是速度, $\rho '$是密度的扰动量, $ \mu $是粘滞系数, $ g $是重力加速度. 在这里可设水为不可压缩流体, 连续性方程则变为:

$ \nabla \cdot{\boldsymbol{V}}_{\boldsymbol{0}}=0 . $

搅拌引起的涡流场会影响水槽内的声场分布, 因此, 通过求解(1)式和(2)式, 就可以得到涡流场中的速度和压力分布. 众所周知, (3)式—(5)式被用来计算声场分布^[25], 该方程组考虑了背景流速和压力对声波传播的影响. 结合上述方程得到的速度和压力, 就可以计算出水槽内的声场分布.

$ \begin{split}&\frac{\partial {\rho '}}{\partial t}+\left({\boldsymbol{V}}_{\rm{0}}\cdot\nabla \right){\rho' }+\left({\boldsymbol{V}}\cdot\nabla \right){\rho }_{0}\\&+{\rho' }\left(\nabla \cdot{\boldsymbol{V}}_{\rm{0}}\right)+{\rho }_{0}\left(\nabla \cdot{\boldsymbol{V}}\right)=0 , \end{split}$

$\begin{split}&\frac{\partial {\boldsymbol{V}}}{\partial t}+\left({\boldsymbol{V}}_{\rm{0}}\cdot\nabla \right){\boldsymbol{V}}+\left({\boldsymbol{V}}\cdot\nabla \right){\boldsymbol{V}}_{\rm{0}}\\&+\frac{1}{{\rho }_{0}}\nabla {p}_{\rm{a}}-\frac{{\rho '}}{{\rho }_{0}{}^{2}}\nabla {p}_{0}=0 ,\end{split} $

$ \rho = {{{p_{\rm{a}}}}}/{{{c_0}^2}} , $

其中, $ {p_0} \;=\; 1 $ atm (1 atm = 1.0 × 10⁵ Pa)是媒质的静态压力, $ \rho $是密度的扰动量, $ p $是声压, $ u $是质点振动速度, $ {c_0} $是声速.
空化泡的运动方程采用修正的可压缩性Keller-Miksis方程^[26]

$ \begin{split}&\left( {1 - \frac{{\dot R}}{c}} \right)R\ddot R + \frac{3}{2}{\dot R^2}\left( {1 - \frac{{\dot R}}{{3c}}} \right) \\=\;& \left(1 + \frac{{\dot R}}{c}\right)\frac{{{p_{\rm{b}}}}}{{{\rho _{\rm{w}}}}} + \frac{R}{{{\rho _{\rm{w}}}c}}\frac{{{\rm{d}}{p_{\rm{b}}}}}{{{\rm{d}}t}} ,\end{split}$

其中, ${p_{\rm{b}}}\big( {R, \dot R, t} \big)$的表达式为:

$\begin{split}{p_{\rm{b}}}( {R,\dot R,t}) =\;& \left( {{p_0} - {p_{\rm{v}}} + \frac{{{\rm{2}}\sigma }}{R}} \right){\left( {\frac{{{R_0}}}{R}} \right)^{3\kappa }} - {{{\rm{2}}\sigma }}/{R} \\&- 4\mu \frac{{\dot R}}{R} - {p_0} + {p_{\rm{v}}} - {p_{\rm{A}}}\sin \left( {2{\rm{\pi }}ft} \right) ,\end{split}$

$ R(t) $是气泡的瞬时半径, $ \dot R(t) $是气泡半径对时间$ t $的一阶导数, $ {\rho _{\rm{w}}} = 1000 \;{\rm{ kg/}}{{\rm{m}}^{\rm{3}}} $是水的密度, $ {p_0} = 1.013 \times {10^5}\; {\rm{ Pa}} $是环境压力, $ \sigma = 0.076\; {\rm{ N/m}} $是液体表面张力$ \mu = 1 \times {10^{ - 3}}\; {\rm{ Pa}} \cdot {\rm{s}} $是液体的粘滞系数, $ \kappa = 1.4 $是绝热过程气泡的多方指数, $ {p_{\rm{v}}} = $$ 2330\; {\rm{ Pa}} $是液体饱和蒸汽压, ${R_0} = 4.5\; {\rm{ μ}} \rm m$是气泡的初始半径, $ c = 1480\; {\rm{ m/s}} $是声速. 首先使用Matlab软件中ode45函数得到了$ R(t) $和$ \dot R(t) $, 然后就能进一步得到了气泡温度随时间演化规律. 气泡温度随时间变化的表达式为

$ {T_{\rm{g}}} = {T_0}{\left( {\frac{{{R_0}^3 - {a^3}}}{{{R^3} - {a^3}}}} \right)^{\kappa - 1}} , $

其中, $ {T_0} $是气泡环境温度, 可以取$ {T_0} = 280\;{\rm{ K}} $, 而$ a = {R_0}/8.54 $为范德瓦尔斯排斥核半径.
2 -->

2.2.数值方法

为了模拟搅拌引起的涡流场对声场分布的影响, 首先利用Comsol软件对模型进行数值研究. 该软件是基于有限元方法, 通过求解偏微分方程实现多物理场的耦合. 整个仿真过程分为两个步骤. 首先, 在两相流模块中模拟搅拌引起的流场; 其次, 将模拟所得到的速度和压力作为声波传播过程中介质的速度和压力代入到对流波动方程模块中的背景速度和压力中, 进而得到了水槽内的声场分布. 接下来, 详细介绍仿真过程中所涉及的计算域和边界条件.
根据超声降解实验所用到的超声清洗系统来设计的仿真模型如图1(a) 所示. 该模型由一个立方体水槽 (30 cm × 24 cm × 15 cm) 和一个月牙形搅拌器组成, 搅拌器位于水槽底部中间. 在这个模型中, 蓝色和白色区域分别代表水和空气, 所用的材料参数见表1. 为了模拟搅拌器在清洗槽中发挥的作用, 采用滑动壁边界条件来设定搅拌器的速度, 如图1(a) 所示, 可以将该速度表示如下:
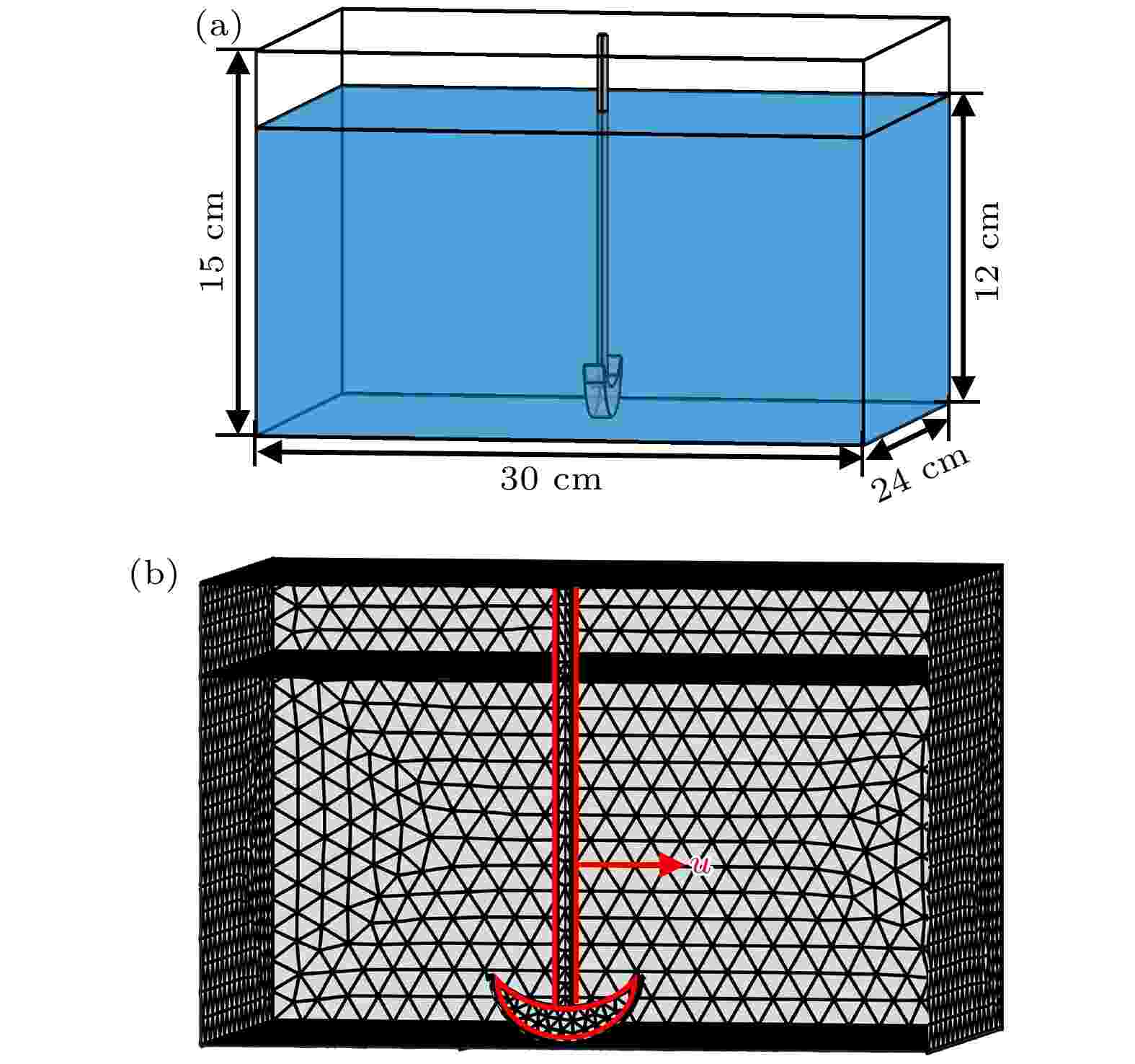图 1 (a) 超声清洗槽模型的结构示意图; (b) 仿真模型的网格图
Figure1. (a) Geometry and configurations of the cleaning tank; (b) the mesh used for simulations.

材料	$ {\rho _0} $/($ {\rm{kg}} \cdot {{\rm{m}}^{{\rm{ - 3}}}} $)	$ {c_0} $/(m s–1)	$ \mu $/(Pa s)
水	1000	1500	1.01 × 10–3
空气	1.29	340	1.79 × 10–5

表1材料参数.
Table1.Material parameters.

$ u = \left( { - 2{\rm{\pi }}ny,2{\rm{\pi }}nx,0} \right) , $

其中, $ n $是转速. 此外, 在流体模块中, 水槽的四壁被设置为$ {u_{\rm{w}}} = 0 $. 在声学模块中, 它们被设置为声学硬边界条件, 该边界条件下的质点振动速度和背景流速满足如下公式:

$ n \cdot v = 0,\;n \cdot {u_0} = 0 , $

其中, $ v $是质点振动速度, $ {u_0} $是背景流速, $ n $是壁面的法向量. 根据实际清洗槽内换能器的位置, 将声源设置在仿真模型的底部, 其声源$ p $的表达式如下:

$ p = 1.2 \times {10^5} \times \sin \left( {2{\rm{\pi }}ft} \right) , $

这里$ f $是超声波频率.

2

-->

3.1.材料和实验装置

亚甲基蓝(分析纯, 纯度≥98.5%, 天津市致远化学试剂有限公司); 配制溶液的水为二次蒸馏水; 数显测速电动搅拌机(型号: JJ-1A, 功率: 100 W, 常州荣华仪器制造有限公司); 超声波清洗机(型号: SB-5200DTD, 30 cm × 24 cm × 15 cm, 超声功率: 300 W, 超声频率: 40 kHz, 宁波新艺超声设备有限公司).
2 -->

3.2.实验方法

室温下将20 mg的亚甲基蓝试剂与6 L的水配制成亚甲基蓝溶液, 然后在搅拌条件下, 将得到的溶液在清洗槽中进行超声辐射处理420 min, 在反应过程中每30 min取一次样. 超声照射后的溶液采用紫外可见分光光度计(UV-2400)测定其吸光度, 紫外分光光度计采用的扫描范围为190?—1100 nm. 并且使用循环水将温度控制在24 ℃. 降解率$ \eta $的计算公式如下:

$ \eta = ({{M{B_0} - MB}})/{{M{B_0}}} , $

这里, $ MB $是超声处理后的溶液吸光度, $ M{B_0} $初始溶液的吸光度.

2

-->

4.1.搅拌速度对声场分布的影响

在这一部分, 分析了不同搅拌速度下的声场分布. 声场分布是影响超声降解的一个重要因素, 这一结论之前已经被多次报道过^[27-29]. 对于超声空化而言, 超声波的声压幅值必须超过空化阈值, 空化效应才能发生^[30,31]. 因此, 通过对声场分布的分析, 就可以得到清洗槽内发生空化效应的区域. 仿真所得到的声场分布如图2所示. 图2(a)为搅拌速度为0 r/min时的声场分布图, 它被用来表示没有机械搅拌时的声场分布图, 这样做的目的是排除搅拌器本身对声场分布的影响. 可以发现, 声波从水槽底部向上传播, 经过不断的反射, 最终形成了驻波声场. 驻波的一个重要特征是, 有些地方(波节)从不振动, 而有些地方(波腹)总是以最大振幅振动, 两个相邻波腹之间的间距为半个波长. 驻波声场降低了声场的均匀性, 使得声化学反应效率大大降低^[32].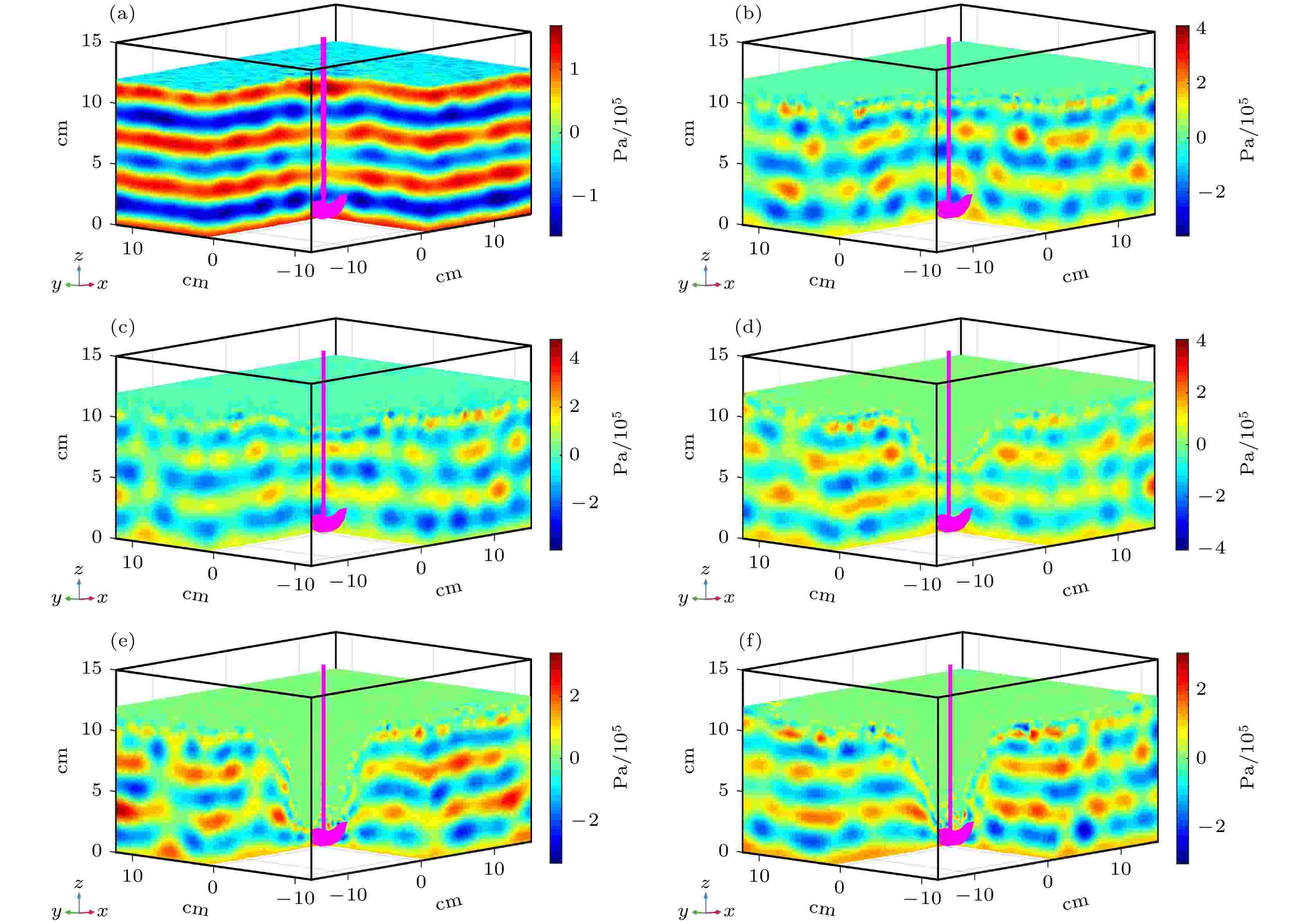
图 2 不同搅拌速度下的声场分布图　(a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min
Figure2. Acoustic pressure distribution at the stirring speed of various value: (a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min.

图2显示了不同搅拌速度下的声场分布特征. 然而, 当搅拌速度达到300 r/min时, 如图2(b)所示, 驻波场已经削弱了, 声场变得更加趋于均匀分布. 除此之外, 发现跟没有搅拌时的声压相比, 转速为300 r/min时的声压幅值增加到了2倍以上. 通过观察其它转速下的声场分布(图2(c)—(f)), 也发现声场分布与没有搅拌时相比变得更加均匀了, 且声压幅值得到了大幅增加. 这主要是由于搅拌引起的涡流. 一方面, 由于空气的声阻抗远低于水的声阻抗, 当声波从水槽底部经过水-气交界面时, 该界面相当于声学软边界, 从而使得声波在此处发生了全反射. 因为涡流是抛物线型的, 并根据斯奈尔声波反射与折射定律^[33], 声波遇到分界面时, 反射角等于入射角. 所以声波通过涡流时会向各个方向发生反射, 反射波和入射波相互叠加, 从而使得声场分布趋于均匀. 另一方面, 当声波通过涡流时, 会出现声散射现象^[34].
我们知道, 在驻波声场中, 只有波腹附近区域的声压幅值超过了环境压力, 才可以发生声空化效应. 而在有搅拌的条件下, 声场分布变得均匀, 这会使得水槽内更多的区域能发生超声空化, 从而进一步提高有机溶液的超声降解率.
由图2可以发现, 机械搅拌能够消除驻波声场, 使得声场分布变得更加均匀. 为了进一步展现水槽内部的声场, 我们选取了波峰, 波谷以及声压为零的三个截面, 其具体位置如图3所示. 众所周知, 驻波场是由波峰和波节组成的. 因此, 通过分析波峰, 波节以及两者之间位置处的声压分布就能大致清楚整个三维容器内的声场分布情况. 如图4(a)所示, 在z = 2.8 cm的截面中, 没有机械搅拌时声压接近于零, 不发生超声空化效应. 从图4(b)— 4(f)中可以看出, 搅拌之后声压明显增加, 而且分布更加均匀. 除此之外, 一方面, 在z = 5.4 cm和z = 7.3 cm的截面上, 我们也发现搅拌提高了声压幅值. 在相同的声场结构前提下, 声压越大, 声空化越强. 另一方面, 注意到搅拌速度超过600 r/min后, z = 5.4 cm截面上的声场分布的均匀性会降低, 声能量主要集中在截面的中心, 四周的声压几乎为零. 因此, 搅拌速度是影响声场分布和声压幅值的一个重要因素. 在一定的条件下, 存在一个最佳的搅拌速度. 因此, 我们可以总结出, 机械搅拌增加了声场分布的均匀性和声压幅值, 这有利于提高空化强度, 从而提高超声降解实验中溶液的降解率.
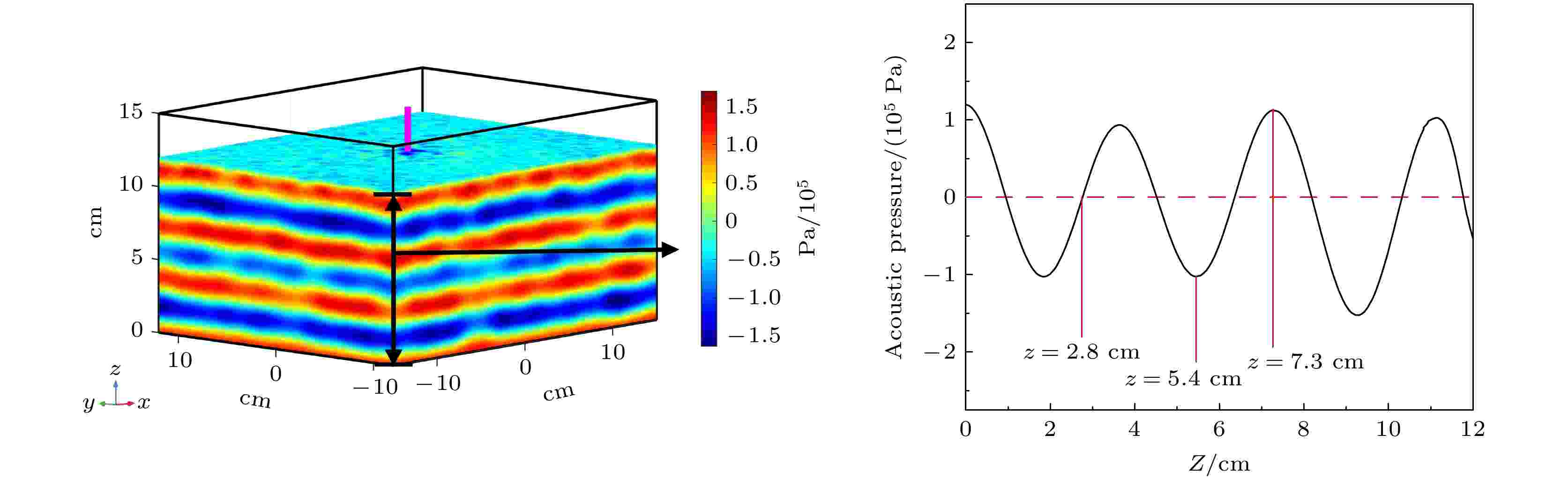图 3 驻波声场中波腹和波节的位置
Figure3. The position of the peaks and troughs in the standing wave acoustic field.

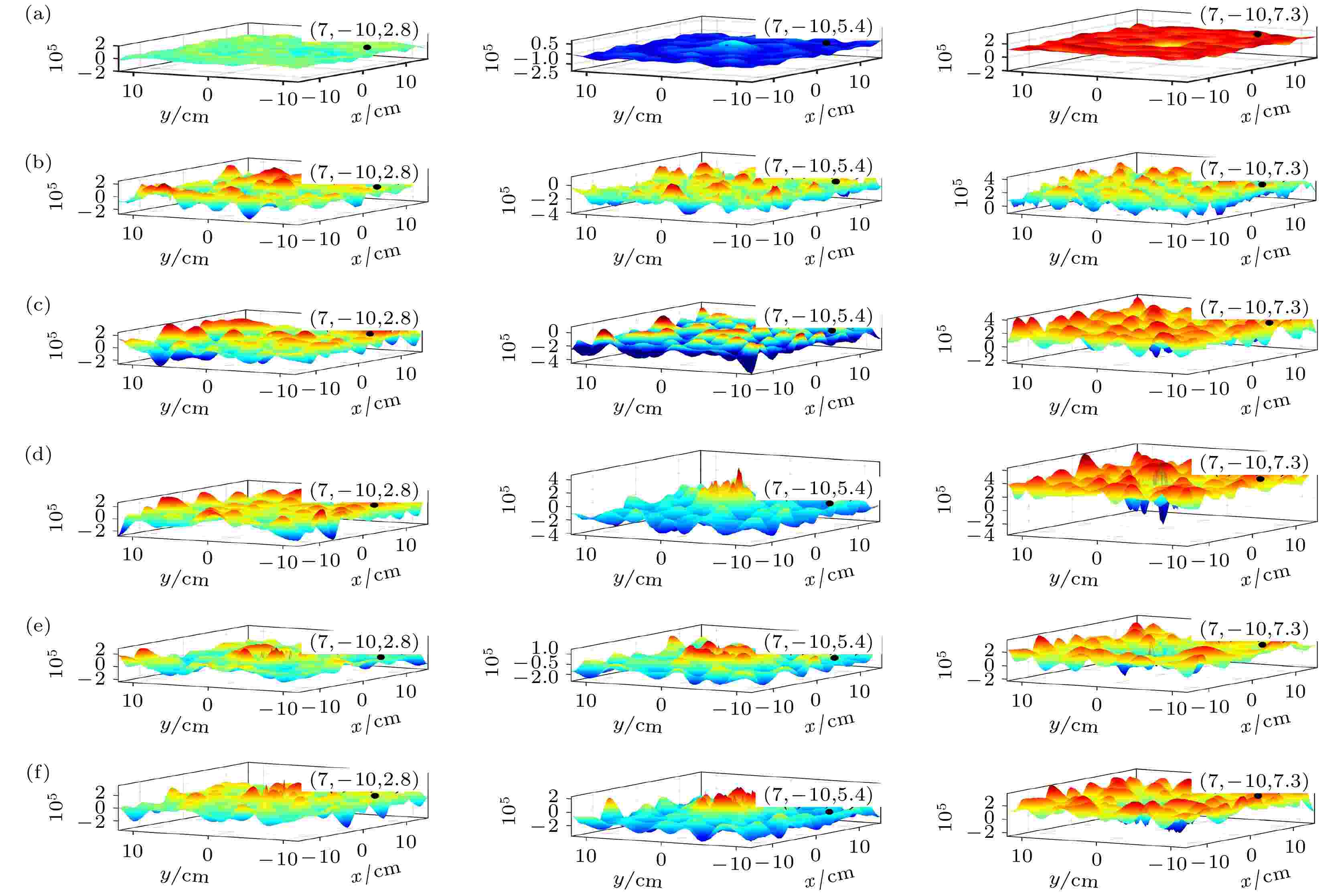图 4 水槽内各个截面上声场分布图　(a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d)1000 r/min; (e) 1500 r/min; (f) 2000 r/min
Figure4. Acoustic pressure distribution at the stirring speed of various value: (a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min.

为了定量计算清洗槽内的空化强度, 首先, 我们在上述三个截面的坐标(7, –10)处选取一个点, 从仿真结果中得到不同时刻下这个点处的声压值. 而超声空化需要在简谐声波驱动下才能发生, 为此, 我们采用文献[35]中提到的方法, 首先用Origin软件拟合了提取点的声压值, 它被显示在图5中. 可以看出, 拟合曲线显示出良好的正弦形态. 此外, 发现搅拌之后, 点(7, –10, 2.8)处的声压幅值得到了大幅提升, 扩大了5倍以上, 而且另外两个点处的声压幅值也有明显提高.
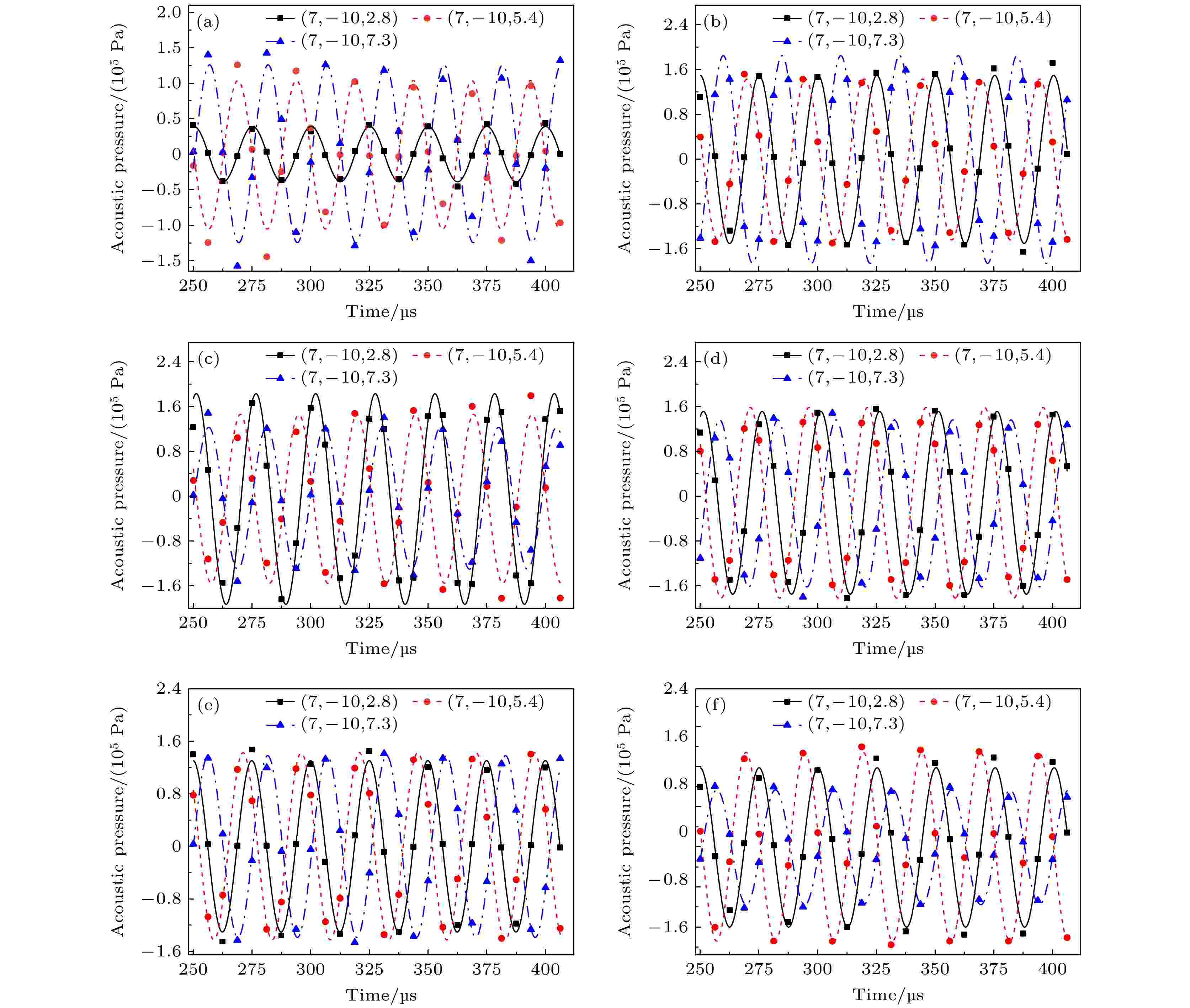图 5 不同搅拌速度下, 提取点处的声压随时间变化图　(a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min
Figure5. Acoustic pressure versus time for extracted point at the stirring speed of various value: (a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min.

2 -->

4.2.搅拌速度对空化泡半径的影响

接下来, 将拟合得到的声压函数用代入(6)式中, 得到了空化泡半径随时间的变化曲线, 如图6中所示. 从图6(a)中可以看出, 未加机械搅拌时z = 2.8 cm和z = 5.4 cm截面上的气泡在声压的驱动下没有发生瞬间崩溃, 这是因为这两个位置处的声压幅值太小, 分别为39051 Pa和104679 Pa. 因此可以得出, 未加机械搅拌的条件下, 只有z = 7.3 cm截面上有空化效应产生. 有机械搅拌时的气泡半径随时间变化图如图6(b)—(f)所示, 根据超声过程中空化泡半径随时间的变化规律可知, 搅拌速度从300 r/min增加到2000 r/min, 水槽内三个截面上均有空化效应产生.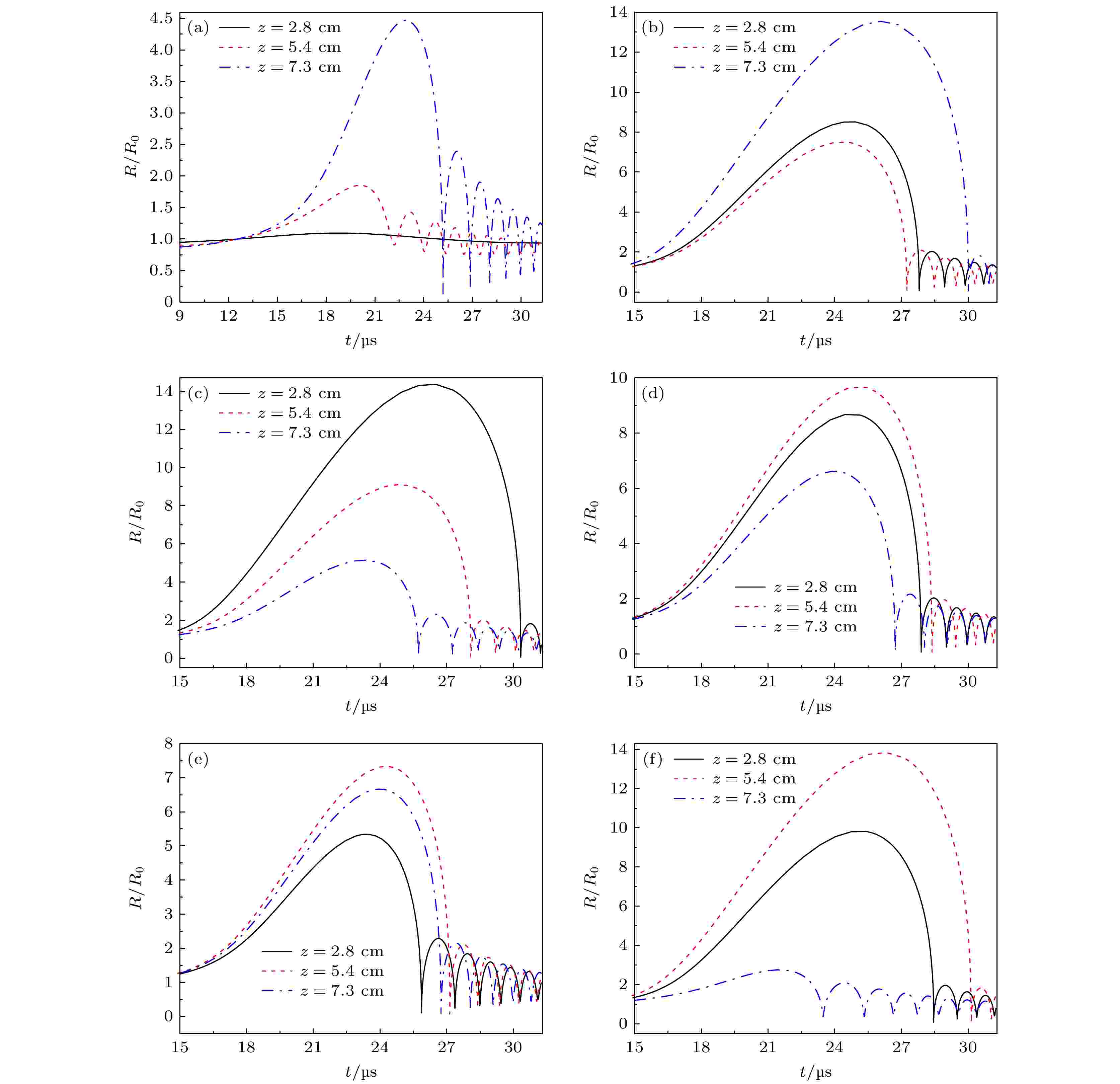
图 6 不同搅拌速度下, 空化泡半径随时间变化图　(a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min
Figure6. The radius of cavitation bubble at the stirring speed of (a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min.

此外, z = 2.8 cm和z = 5.4 cm截面上气泡膨胀的最大幅值与压缩的最小幅值之间的差值随着搅拌速度的增加, 先增大后减小, 它们分别在600 r/min和1000 r/min时达到最大值$ 14.3{R_0} $和$ 9.62{R_0} $, 而当搅拌速度到达2000 r/min时, z = 2.8 cm和z = 5.4 cm截面上气泡从最大半径压缩到最小半径的差值虽然再次变大, 但压缩过程中所用的时间也增加到了$ 3\;{\text{μ}{{\rm{ s}}}} $和$ 3.8\;{\rm{ \text{μ} s}} $, 而转速为1000 r/min时压缩过程中所用的时间只有$ 2.8\;{\rm{ \text{μ} s}} $和$ 3.2\;{\rm{ \text{μ} s}} $, 这是由于随着声压幅值的增大, 气泡膨胀的最大幅值与压缩的最小幅值之间的差值增大, 在压缩过程中所用的时间也在增加, 在同样的条件下, 气泡压缩所用的时间越短, 气泡崩溃越剧烈. z = 7.3 cm截面上的气泡在转速为2000 r/min时气泡膨胀的最大幅值与压缩的最小幅值之间的差值($ 2.39{R_0} $)甚至小于未加搅拌时的差值($ 4.37{R_0} $), 在转速为300 r/min时其压缩的幅值差值虽然大于600 r/min时的差值, 但在压缩过程中所用的时间是$ 3.9\;{\rm{ \text{μ} s}} $, 远大于600 r/min时所用的时间($ 2.3\;{\rm{ \text{μ} s}} $). 因此, 经过综合分析不同截面上的空化泡半径随时间的变化曲线可知, 当搅拌速度太小或太大时都会降低空化强度.
2 -->

4.3.搅拌速度对气泡内部温度的影响

图7为搅拌速度对空化泡崩溃泡内温度的影响. 从图7(a)中可知, 当搅拌速度为0 r/min时, z = 2.8 cm和z = 5.4 cm截面上的气泡的内部温度始终没变, 一直保持为初始温度, 仅仅只有z = 7.3 cm截面上的温度在气泡破裂时升高至5000 K. 这是因为由图6(a)可知, 当搅拌速度为0 r/min时, z = 2.8 cm和z = 5.4 cm截面上的气泡没有发生空化效应. 一旦在超声辐射中加入机械搅拌, 三个截面中的气泡温度均上升10000 K以上 (图7(b)—(f)), 而当搅拌速度为600 r/min时的 z = 2.8 cm和z = 5.4 cm截面上, 1000 r/min时的 z = 2.8 cm和z = 7.3 cm截面上, 其温度高达20000 K以上. 此外, 我们还发现, 当搅拌速度超过1000 r/min后, z = 2.8 cm和z = 7.3 cm截面上气泡的内部温度随着搅拌速度的增加而下降. 虽然当搅拌速度为1500 r/min时z = 5.4 cm截面上气泡的内部温度大于搅拌速度为1000 r/min时其截面上的温度, 但仅仅只提高了4 K, 而z = 2.8 cm和z = 7.3 cm截面上气泡的内部温度却下降了10 K以上, 当搅拌速度为2000 r/min (图7(f)) 时, z = 7.3 cm截面上的空化泡的内部温度几乎没有变化, 这是因为根据图6(f)可知, z = 7.3 cm截面上的气泡在转速为2000 r/min时气泡膨胀的最大幅值与压缩的最小幅值之间的差值非常小. 所以可以总结, 气泡的内部温度随着搅拌速度的增加先增加后下降. 而空化泡内部的温度的高低反映了声空化强度的大小, 其温度越高, 声空化强度越大. 因此可以得出结论, 当搅拌速度过高时声空化强度会降低.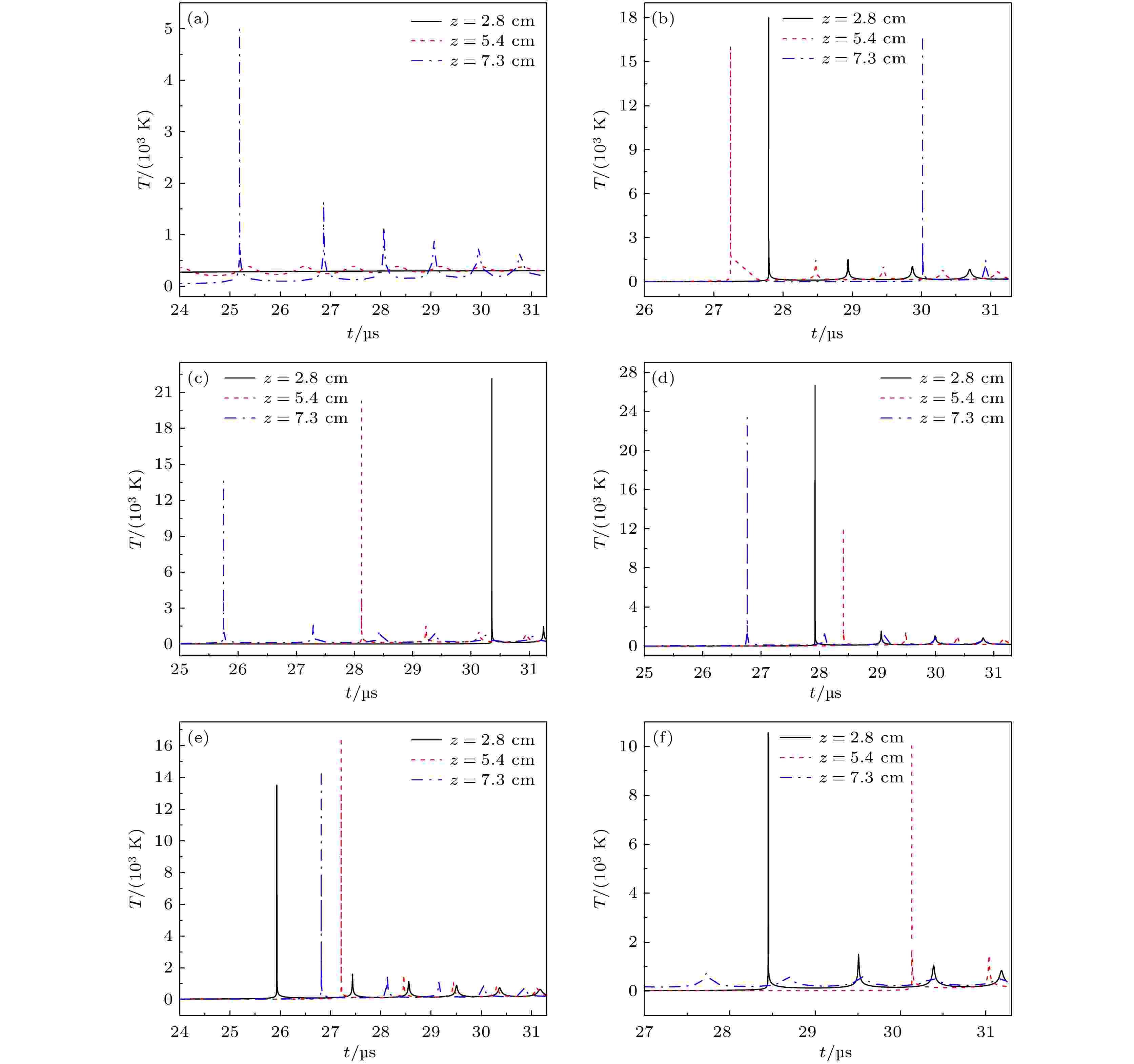
图 7 不同搅拌速度下, 空化泡内部的温度随时间变化图　(a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min
Figure7. Internal temperature of bubble under distinct stirring speeds in the plane of various value: (a) 0 r/min; (b) 300 r/min; (c) 600 r/min; (d) 1000 r/min; (e) 1500 r/min; (f) 2000 r/min.

综上所述, 我们采用数值模拟的方法分析了有无机械搅拌时的声场分布, 空化泡半径和内部温度变化特性. 可以发现, 机械搅拌不仅可以使得声场分布更加均匀, 也极大地提高了溶液中空化泡内部温度. 这些因素都可以增强声空化强度, 从而进一步提高有机溶液的降解率. 因此, 根据仿真结果可以总结出, 第一, 机械搅拌可以增强声空化强度. 第二, 考虑了不同搅拌速度下的气泡内部温度, 可以发现转速为600 r/min和1000 r/min时的声空化强度最大, 当搅拌速度超过1000 r/min后, 声空化强度会下降.
2 -->

4.4.实验验证

为了验证数值计算的正确性, 本文设计了超声协同机械搅拌实验来测量亚甲基蓝溶液的降解率. 图8(a)是进行降解实验的实物图, 实验装置主要由电动搅拌器和超声清洗机组成. 测得的实验结果如图8(b)所示, 可以看出, 未加机械搅拌时的溶液的降解率是最低的, 降解率会随着搅拌速度的增加而增加, 而当搅拌速度增加到1000 r/min时, 溶液的降解率与转速为600 r/min时的降解率相同, 之后随着搅拌速度的继续增加而降低. 这是因为搅拌在物理上一方面改变了清洗槽内的声场分布, 使得声场分布变得均匀(图2(b)—(f)), 从而扩大发生空化效应的区域, 另一方面, 搅拌也提高了水槽内超声波的声压幅值(图5(b)—(f)), 声压越大, 声空化越强. 正是基于这两方面的原因, 搅拌在物理上增强了空化效果. 此外, 由于搅拌速度会影响声波的声压幅值(图5), 从而影响到空化泡崩溃时的内部温度. 由图7(b)—(f)可知, 当搅拌速度为1500 r/min和2000 r/min时, 空化泡崩溃时的内部温度反而下降了, 导致空化效果减弱. 因此, 由图7可知, 在搅拌速度为600 r/min和1000 r/min时的空化效果最强.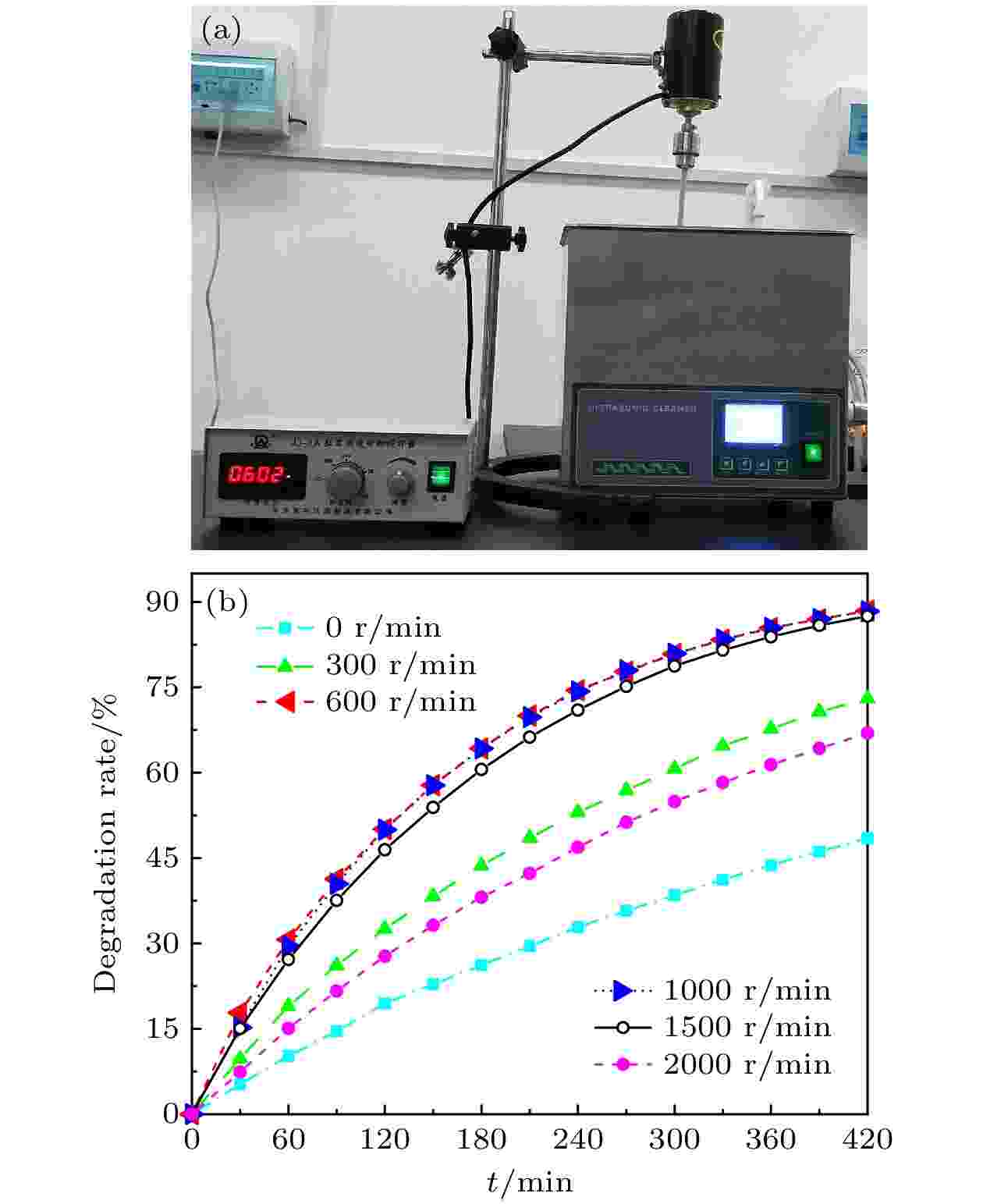
图 8 (a) 实验装置图; (b) 不同搅拌速度下溶液的降解率
Figure8. (a) The experimental apparatus; (b) degradation rate of solution at different stirring speeds.

本文首先采用数值模拟的方法, 分析了有无机械搅拌时的声场分布情况, 然后从计算结果中选取声场内某一点处随时间变化的声压值并拟合出一个正弦函数. 最后将声压函数带入Keller-Miksis方程中, 并结合相关方程得到了空化泡半径和温度随时间的变化情况. 从这些计算结果中发现: 机械搅拌能提高声场分布均匀性, 从而提高空化面积; 机械搅拌提高了气泡温度. 这些结果说明了搅拌能增强声空化强度, 从而提高有机污染物的超声降解率. 此外, 还发现过高的搅拌速度会降低空化泡的温度, 从而减少了声空化强度, 这与实验结果相一致. 本文从声场分布和气泡的空化反应这两方面分析机械搅拌对声空化强度的影响, 从理论上进一步解释了搅拌提高声降解率的原因, 为研究有机溶液的超声降解提供了新方法.