摘要:针对水下前向散射探测中基于敏感核函数的定位方法存在环境失配带来的稳健性问题, 提出了一种基于迁移学习的前向散射定位方法, 利用模型生成?的目标前向散射声场扰动信息训练卷积神经网络, 将目标定位问题转化为分类问题. 在基于先验信息和仿真数据集的预训练模型基础上, 通过少量实验数据集对神经网络参数进行迁移学习, 以提高神经网络模型的稳健性. 仿真结果表明, 该方法在声速剖面失配下可以实现对目标较准确的定位, 且对目标散射函数、海底底质、阵元数和布设深度等参数不甚敏感, 方法具有较好的稳健性.
关键词: 迁移学习/
目标定位/
前向散射/
环境失配

English Abstract

全文HTML

--> --> -->

近年来, 在对水声目标的探测定位问题中, 双/多基地主动声呐由于其特有的收发分置特性而越来越受到关注^[1-3], 但是当目标位于收发连线附近时, 直达波与目标前向散射波在接收端上发生严重混叠^[4], 使用传统时延处理方法在收发连线附近会形成双基地探测盲区. 然而, 相对于没有目标时的接收声场, 目标的前向散射会引起接收声场的幅度、相位发生扰动变化, 已经证明该现象可以作为入侵目标探测的一种思路^[5,6].
为了充分利用目标前向散射引起的声场扰动现象来实现双基地盲区中的目标探测, 国内外****提出了多种方法. 例如, Song等^[7]利用时间反转镜技术构建了水声绊网, 将声能量聚焦于源阵列的探针声源处, 并通过观察焦区周围旁瓣的能量变化来检测目标, 该研究结果引起了对时反目标探测的关注. 由于时反镜处理物理上的需求, 该方法需要有复杂的硬件系统支持^[8], 此后水声工作者又进一步提出了基于虚拟时反的处理方法^[9]. 雷波等^[10]基于多个接收点前向散射声扰动现象的时间差和几何关系, 提出了运动目标定位方法. Folegot等^[11]提出了基于声射线的定位方法, 采用双波束形成来分辨携带主要能量的声线, 利用目标对声线的“遮挡”效应, 对强度衰减的特征声线进行加权求和, 加权系数为声线能量的衰减程度, 将所有处理后的特征声线绘制在一起, 得到的模糊图上的“亮点”即为目标位置. Marandet等^[12]提出了敏感核定位方法, 将目标定位问题转化为线性反演问题, 利用声场模型计算出每条特征声线在不同位置处的敏感核, 然后从实际接收数据中提取出每条特征声线的实际声压幅度变化量, 结合敏感核矩阵构建出以目标位置权值向量为解的线性方程组, 通过求解欠定方程组实现对目标的定位, 并在超声波导条件下完成了验证实验. Yildiz等^[13]进一步研究了多基地配置下敏感核定位方法, 并开展了水池实验验证. 本质上说, 敏感核方法属于基于模型的匹配场处理, 对环境信息敏感, 因而易受到环境失配的影响.
近期, 机器学习已经越来越多地被用于解决水下声源的定位问题. 牛海强等^[14,15]使用机器学习进行声源距离的估计, 获得了比传统匹配场处理更佳的性能, 并使用残差神经网络估计了声源的距离深度^[16]. 徐及等^[17]使用了两种神经网络在没有精确环境信息的复杂水体下对水下目标距离进行估计. 李整林等^[18]提出了一种在深海直达区的卷积神经网络声源测距方法. 杨益新等^[19]使用仿真与实际数据训练卷积神经网络, 对深海目标进行距离和深度估计.
迁移学习作为机器学习的一种典型方法^[20], 可以通过小样本的更新学习, 提高学习方法的适应性. 本文提出一种基于迁移学习的水下目标定位方法, 从目标前向散射引起声场扰动的角度出发, 利用卷积神经网络建立起声场扰动信息与目标位置的映射关系, 从而把目标定位问题转化为分类问题. 进一步考虑环境失配带来的稳健性问题, 利用基于先验信息的仿真数据对卷积神经网络进行训练以构建预训练模型, 而后基于迁移学习思想, 结合少量实际数据对预训练模型进行微调, 有效降低环境失配对定位性能的影响.

在利用目标前向散射进行目标定位的研究中, 通常采用由垂直发射阵和垂直接收阵构成的声屏障^[7]进行入侵目标的探测和定位, 如图1所示, 发射阵和接收阵分别为由M个发射阵元和N个接收阵元构成的垂直阵. 在没有目标的情况下, 接收信号可以表示为
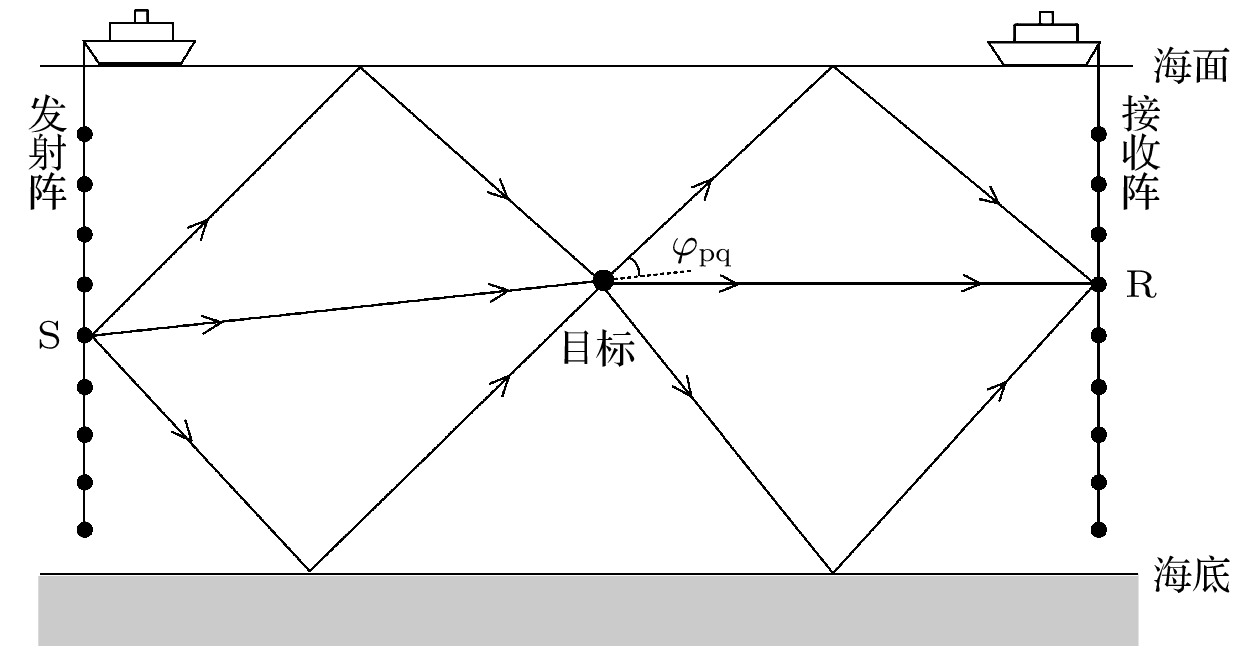图 1 声屏障示意图
Figure1. Schematic diagram of sound barrier with transmitter and receiver arrays.

$ P_{i j}(t) = s(t) \otimes h_{i j}(t)+n(t), $

其中, $ P_{i j}(t) $表示由第i个发射阵元发射信号时在第j个接收阵元上的信号, t为相对于发射时刻的时间, $1 \leqslant i \leqslant M$, $1 \leqslant j \leqslant N$, $ s(t) $为发射信号, $ h_{i j}(t) $表示水声信道的冲激响应函数, $ \otimes $表示卷积运算, $ n(t) $表示海洋环境噪声.
在收发连线之间存在目标的情况下, 散射声场可以近似认为是声源S发射的源信号经多径传播后到达目标处并发生散射, 而后散射波经多径传播后到达接收点R, 如图1所示. 声波在目标上的散射与目标的散射函数$ f_{\infty} $有关, 是频率、目标形态、目标材料、散射角等参数的函数. 简正波理论^[21]和射线声学理论^[22]的信道散射模型表明, 目标的散射函数引起了入射场与散射场之间的耦合, 导致声波能量在声场空间上重新分配^[23].
假设位于$ (r, z) $点的目标处共有X条入射声线, Y条散射声线, 入射声线到达目标处的冲激响应为$ G_{\rm p}(r, z) $, 时延为$ T_{\rm p} $, $1 \leqslant p \leqslant X$, 散射声线到达接收点的冲激响应为$ \tilde{G}_{\rm q}(r, z) $, 时延为$ \tilde{T}_{\rm q} $, $1 \leqslant $$ q \leqslant Y$, 则任意一组入射、出射声线的冲激响应和时延可以分别近似表示为

$ \hat{G}_{\rm p q}(r, z) = G_{\rm p}(r, z) \tilde{G}_{\rm q}(r, z) f_{\infty}\left(\varphi_{\rm p q}(r, z)\right), $

$ \hat{T}_{\rm p q} = T_{\rm p}+\tilde{T}_{\rm q}, $

其中, $ \varphi_{\rm p q} $表示这一组入射、出射声线对应的散射角, 如图1所示. 将$ X \cdot Y $组入射和出射声线形成的冲激响应$ \hat{G}_{\rm p q} $在时域上按时延$ \hat{T}_{\rm p q} $叠加在一起, 得到目标信道响应函数$ \tilde{h}_{i j}(t) $. 实际上由于信道传播路径损失, 部分路径上的能量非常微弱, 可以忽略不计. 假设环境和背景噪声保持不变, 接收信号$ \tilde{P}_{i j}(t) $可以表示为

$ \tilde{P}_{i j}(t) = s(t) \otimes\big(\tilde{h}_{i j}(t)+h_{i j}(t)\big)+n(t), $

其中, $ \tilde{P}_{i j}(t) $表示目标位于$ (r, z) $时由第i个发射阵元发射信号的情况下在第j个接收阵元上的信号. 由(3)式中的时延可以看出, 部分目标散射信号的时延与直达波(即没有目标)基本相同, 直接检测目标散射信号难度大. 根据主动声纳检测一般原理, 对接收信号进行脉冲压缩处理, 脉冲压缩输出信号分别表示为

$ D_{i j}(t) = P_{i j}(t) \otimes s^{*}(-t), $

$ E_{i j}(t) = \tilde{P}_{i j}(t) \otimes s^{*}(-t), $

其中, “*”表示取复共轭. 分别对脉冲压缩输出信号$ D_{i j}(t) $和$ E_{i j}(t) $取模值, 得到脉冲压缩输出包络, 表示为$ \bar{D}_{i j}(t) $和$ \bar{E}_{i j}(t) $. 为了提取目标入侵引起的声场变化, 对目标前向散射引起的声场扰动量进行归一化处理, 即

$ A_{i j}(t) = \left(\bar{E}_{i j}(t)-\bar{D}_{i j}(t)\right) / \bar{D}_{i j}(t), $

式中, 声场扰动量$ A_{i j}(t) $是时间的函数, 在脉冲长度时间内认为目标的位置不会发生变化, 其表征的是信号包络相对变化.
Marandet等^[12]对敏感核定位方法的研究表明, 由入侵目标引起的接收端声场扰动与目标位置存在着映射关系. 而由本文的(2)式—(4)式也可以看出, 收发连线间存在目标时的接收信号$ \tilde{P}_{i j}(t) $与目标位置$ (r, z) $有关, 也就是说经处理得到的声场扰动量$ A_{i j}(t) $隐含了目标位置信息, 如果利用神经网络来建立声场扰动信息与目标位置的映射关系, 可以将目标定位问题转化为分类问题.

不失一般性, 本文提出的定位方法流程由预训练和参数迁移两部分构成, 如图2所示, 其中预训练过程是利用声场模型生成的仿真数据对神经网络模型进行训练, 而参数迁移过程是先冻结预训练模型的卷积池化层参数, 然后利用少量的实际数据对预训练模型的全连接层参数进行微调, 这样的好处是对实际训练数据量的需求大幅度减少. 和匹配场处理类似, 由于对实际环境参数如声速剖面、海底底质声学特性、水深等水文环境信息获取存在失配, 预训练模型的定位能力可能会下降, 需通过少量数据的迁移学习来提高环境失配下定位方法的稳健性.
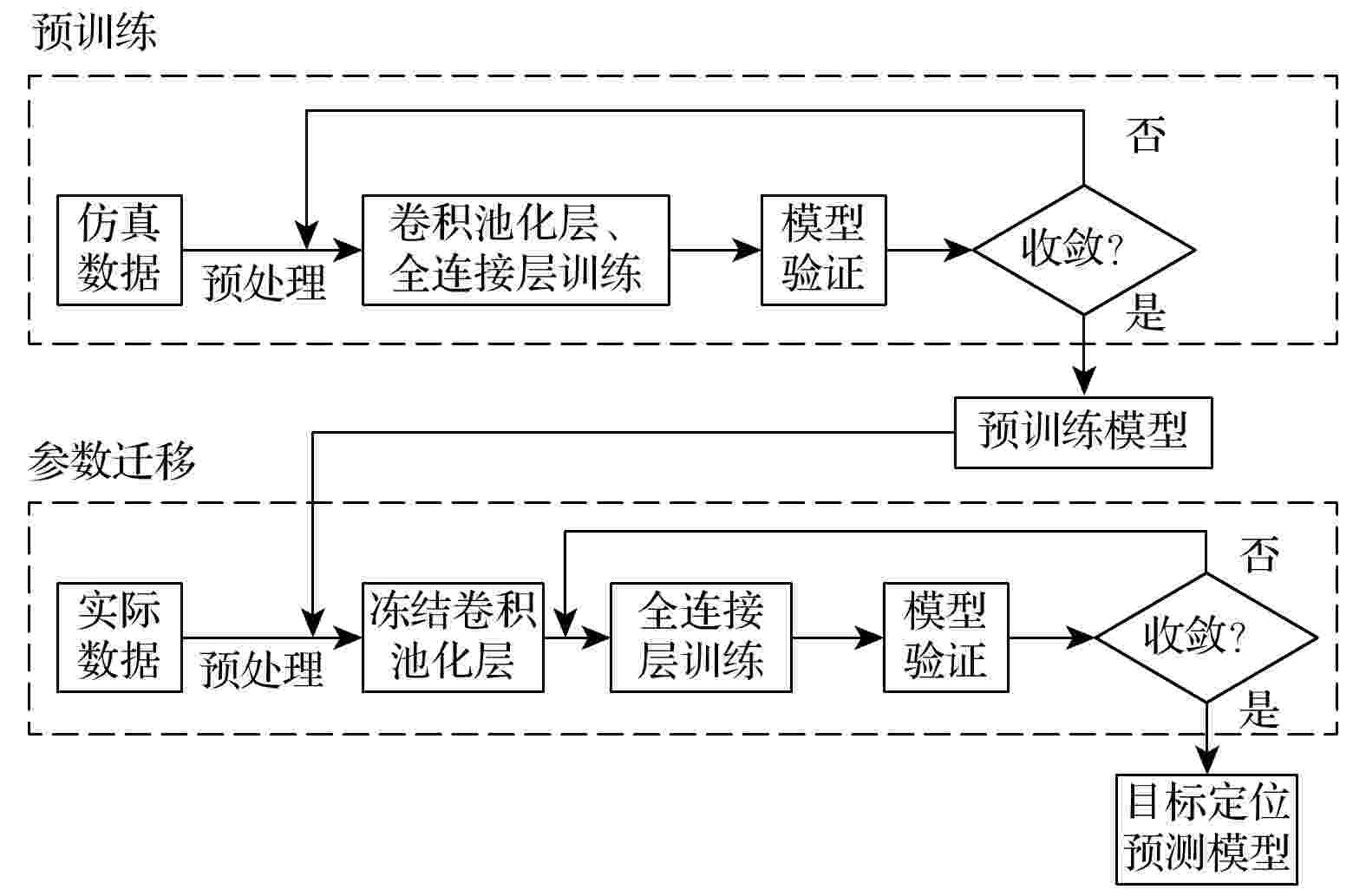图 2 定位方法流程图
Figure2. Flow chart of positioning method.

2

-->

3.1.数据预处理

对数据进行合理的预处理可以降低数据维度, 加快神经网络收敛, 本文提取声场扰动的部分特征信息, 构建与目标位置相关的三维特征数据作为输入数据.
由(1)式—(6)式得到脉冲压缩输出包络$ \bar{D}_{i j}(t) $, $ \bar{E}_{i j}(t) $, 令$ \bar{D}_{i j}(t) $取最大值时对应的时刻记为$ t_{i j} $, 在其附近取一短时时间窗, 于窗内均匀取Z个时域采样点, 得到这Z个时间点对应的声场相对扰动量, 记为Z维向量$ l_{i j} $. 对M个发射阵元和N个接收阵元组成的收发对, 分别计算其对应的声场扰动向量$ l_{i j} $, 从而组合构成$ M \times N \times Z $维的矩阵H, 矩阵H是与目标位置存在映射关系的三维矩阵, 将其作为特征数据输入神经网络.
2 -->

3.2.预训练模型

一般情况下, 为了保证较好的学习性能, 神经网络通常需要大量的训练数据, 但实际水声目标数据获取较为困难. 因此, 先使用基于先验水文环境信息和声场模型的仿真数据对神经网络进行训练, 建立预训练模型. 对距离深度二维平面定位区域进行网格划分, 使用独热编码对划分的网格区域进行标记. 目标位于不同网格内时, 将其对应的数据矩阵H作为神经网络的输入, 对应的独热编码作为神经网络的预期输出.
采用的卷积神经网络的结构主要由2层卷积池化层和2层全连接层构成, 如图3所示, 其他参数见表1. 将预处理后的仿真数据输入卷积神经网络, 通过梯度下降算法调整卷积神经网络各层的参数以极小化损失函数, 本文采用常用的交叉熵损失函数, 表示如下:
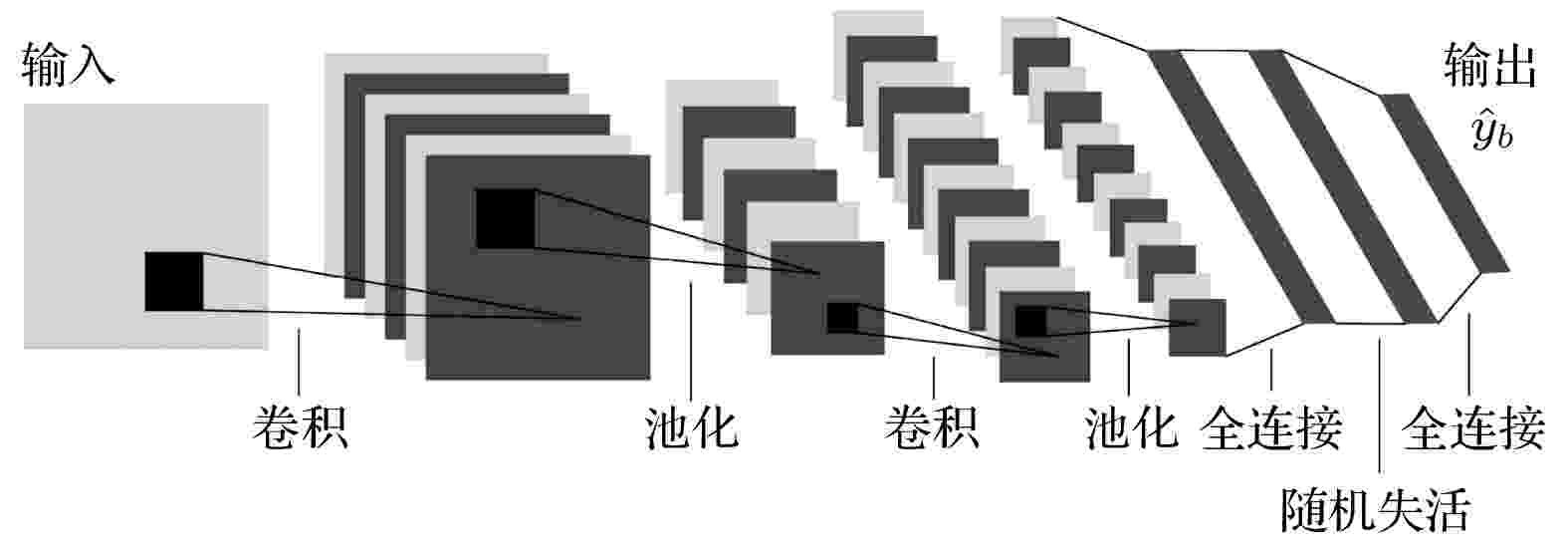图 3 卷积神经网络结构示意图
Figure3. Structure diagram of convolution neural network.

结构参数	具体设置
池化方法	最大池化
优化器	Adam
损失函数	交叉熵
学习率	0.001
b随机失活层丢弃率	0.5

表1卷积神经网络参数设置
Table1.Parameter setting of convolutional neural network

$ L = -\frac{1}{B} \sum\limits_{b = 1}^{B}\left[y_{b} \ln \hat{y}_{b}+\left(1-y_{b}\right) \ln \left(1-\hat{y}_{b}\right)\right], $

其中, B为网格分类数, $ y_{b} $为预期输出, $ \hat{y}_{b} $为神经网络输出.
实际水文环境与仿真环境往往存在环境失配, 这会严重降低预测模型的定位性能, 故而此时的预训练模型并非最终模型, 需要对预训练模型进行参数迁移以降低环境失配对模型的影响.
2 -->

3.3.迁移学习调整

目标位置与信道特征以声场扰动的形式给出, 卷积神经网络的卷积池化层可以提取基础和抽象特征, 而全连接层根据特征建立声场扰动与目标位置的映射关系进行分类, 因此可以认为基于仿真数据的预训练模型和基于实际数据的预测模型共享卷积池化层参数. 参数失配使原有映射在实际环境中产生误差, 通过参数迁移方法冻结预训练模型的卷积池化层参数, 并利用少量实际数据对全连接层参数进行修正, 建立新的映射以实现目标学习任务, 如图2中的处理流程所示. 全连接层可以表示为

$ \hat{y} = f\left(w_{k} x+b_{k}\right), $

其中, $ \hat{y} $为第k层的输出, x为第k层的输入, $ w_{k} $和$ b_{k} $分别为第k层的权值和偏置, f表示Relu激活函数^[24]. 通过梯度下降算法对各层的参数进行更新:

$ w_{k} \leftarrow w_{k}+\Delta w_{k}, $

$ b_{k} \leftarrow b_{k}+\Delta b_{k}, $

其中, $ \Delta w_{k} $和$ \Delta b_{k} $分别表示第k层权值和偏置的变化量. 本文采用基于适应性低阶矩估计的Adam算法作为梯度下降算法.
将实际数据经过预处理后输入预训练模型, 冻结卷积池化层的参数, 仅调整全连接层的参数以极小化损失函数. 这样将基于仿真数据的预训练模型迁移到存在环境失配时的定位问题中, 经过学习后建立基于实测数据修正后的水下目标定位预测模型, 从而根据接收信号数据预测获得目标的位置.

为了对本文提出的方法进行验证, 假设仿真中的水文环境先验信息和布阵方式如图4(a)所示, 海深为100 m, 收发阵列的水平距离为5 km. 垂直发射阵由5个发射阵元构成, 均匀分布于海深20—80 m; 垂直接收阵由21个接收阵元构成, 均匀分布于海深20—80 m处; 海底底质为砂泥, 其声速为1664 m/s, 密度为1.787 ${\rm{g}}/{\rm{ c m}}^{3}$, 衰减系数为0.756 dB/(m·kHz). 考虑到海洋水文环境的随机起伏变化, 先验声速剖面采用图4(a)中5条实线所示的声速剖面(在海面以1510 m/s为中心声速). 各声源依次发射中心频率1 kHz、脉冲宽度50 ms、带宽200 Hz的线性调频信号. 假设环境噪声为带限高斯白噪声(实际处理中会对接收信号进行滤波), 相对于目标散射信号的信噪比为0 dB. 考虑到水下目标的尺度和定位精度要求, 对定位海域进行网格划分, 深度间隔为15 m, 距离间隔为200 m, 从而在深度-距离平面上得到5 × 25个网格区域. 入侵目标为长半轴40 m、短半轴3 m的刚性长旋转椭球体, 这里采用变形圆柱方法^[25]计算其散射函数.
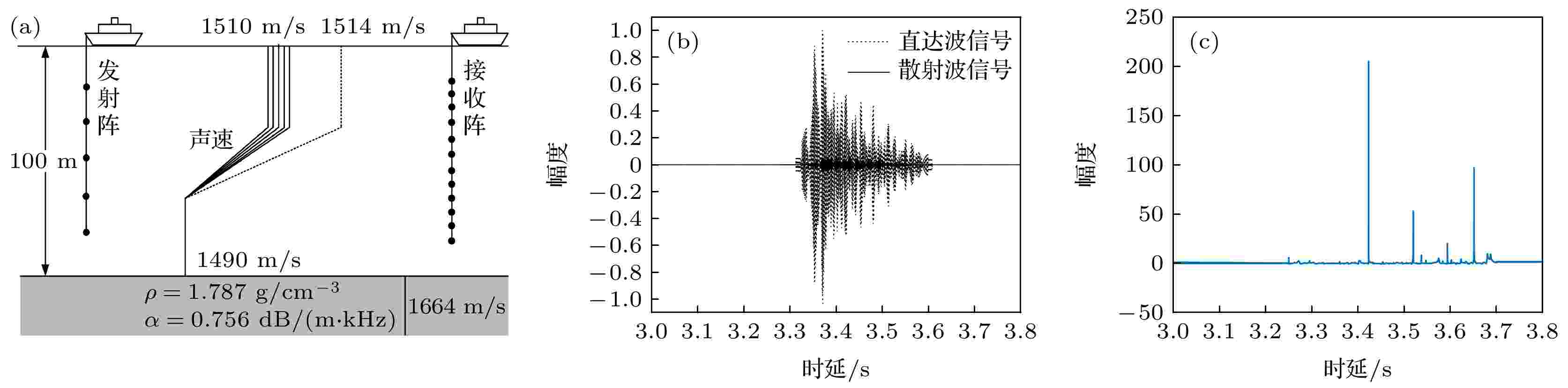图 4 仿真实验环境　(a) 仿真实验示意图; (b) 接收到的信号波形; (c) 声场扰动量$ A(t)$
Figure4. Simulation experiment: (a) Diagram of simulation experiment; (b) received signal waveforms; (c) sound field aberration $ A(t)$

发射阵和接收阵最上方阵元记为1号阵元, 按深度向下依次排序. 令1号发射阵元发射脉冲信号, 在各接收阵元完成信号采集后, 其他发射阵元依次发射同样的脉冲信号并在接收端完成信号采集. 对于1号发射阵元和11号接收阵元组成的收发对, 在没有入侵目标时接收到的直达波信号如图4(b)中点线所示. 若目标位于水平距离1900 m、深度50 m的位置, 则散射波信号波形如图4(b)中实线所示. 可以看出目标的散射信号强度远低于直达波, 在前向散射探测中被严重淹没. 将该接收信号代入(5)式和(7)式中, 可以计算出声场扰动量A随时间t的变化, 波形如图4(c)所示. 可以看出, 散射信号在多个时段对声场的相对扰动量较大, 这种扰动可以作为目标位置的定位依据.
2

-->

4.1.无失配时的仿真结果

使用独热编码对划分的网格区域进行标记, 然后使用BELLHOP声场模型^[26]对目标位于不同网格区域时的接收数据进行仿真, 生成30000组接收信号数据, 并将预处理后的仿真数据按5∶1的比例随机划分为训练集和测试集.
对卷积神经网络进行训练, 训练过程中测试集预测准确率和交叉熵损失函数变化分别如图5(a)和图5(b)所示, 可以看出随着迭代次数的增加, 卷积神经网络对测试集的预测准确率逐渐提高, 当迭代次数为850时基本达到收敛, 此时得到预训练模型参数, 这将作为存在失配时进行迁移学习的基础模型参数.
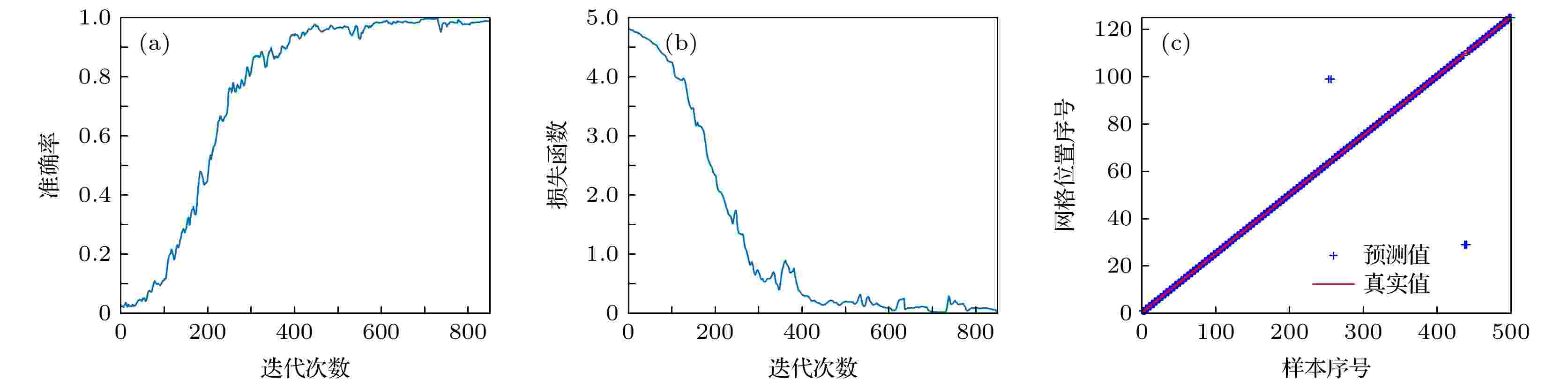图 5 预训练模型的训练过程和预测结果　(a) 准确率变化; (b) 损失函数变化; (c) 无失配时的预训练模型预测结果
Figure5. Training process and prediction results of the pre-training model: (a) Variation of accuracy; (b) variation of loss function; (c) prediction results of the pre-training model without mismatch

在测试集中随机选取500个样本, 预训练模型对这些样本的预测结果如图5(c)所示, 统计准确率达到了98.8%, 可以看出在没有环境失配的情况下预训练模型能够对目标进行准确定位.
2 -->

4.2.声速剖面失配时的仿真结果

假设实际环境与仿真环境间存在声速剖面失配, 实际声速剖面为图4(a)中的虚线声速剖面. 对于存在失配的实际声速剖面, 仿真生成500组接收信号数据并进行预处理, 作为实际数据. 使用预训练模型对这500组数据进行预测, 预测结果如图6(a)所示, 准确率降低为22.4%, 这表明声速剖面失配严重降低了预测模型的定位性能, 但预训练模型和理想预测模型仍具有一定的相关性. 此时需要利用这些实际数据对预训练模型进行迁移学习, 以降低声速剖面失配对定位性能的影响.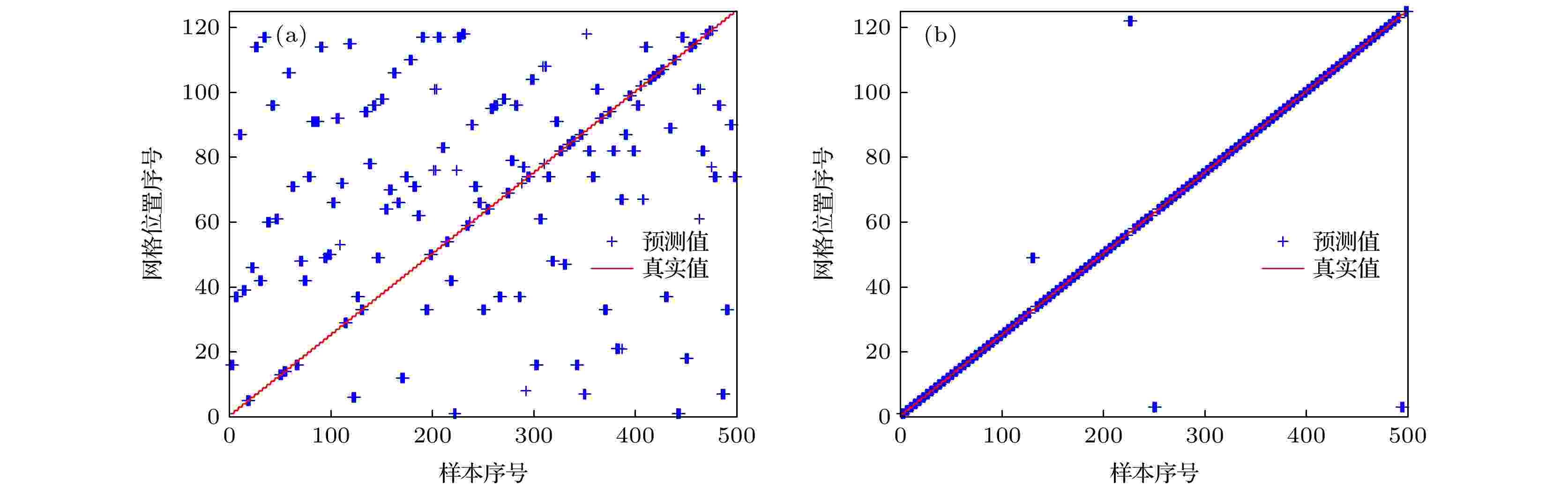
图 6 环境失配时神经网络模型预测结果　(a) 预训练模型预测结果; (b) 迁移学习后预测结果
Figure6. Prediction results of neural network model with environment mismatch: (a) Prediction results of pre-training model; (b) prediction results after transfer learning

将实际数据按3∶1的比例随机划分为训练集和测试集, 按照图2所示参数迁移方法流程, 保持卷积池化层的权值参数不变, 仅调整全连接层的权值参数, 对神经网络模型进行重新训练. 使用经过迁移学习的神经网络预测模型对实际数据集进行预测, 预测结果如图6(b)所示, 统计准确率为96.8%. 通过比较图6(a)和图6(b)的预测结果可以看出, 迁移学习方法在声速剖面存在失配时仍保持着较高的定位精度.
在相同的声速剖面失配的情况下, 使用敏感核函数^[12]定位结果进行对比. 仿真生成同样数量的接收信号数据并进行预处理, 作为实际数据. 使用仿真生成的理论敏感核模型对这500组数据进行预测, 预测结果如图7所示. 当实际声速剖面与仿真声速剖面失配, 导致拷贝场向量的计算产生较大误差, 使敏感核函数方法的定位性能严重降低, 几乎不能准确对目标位置进行预测.
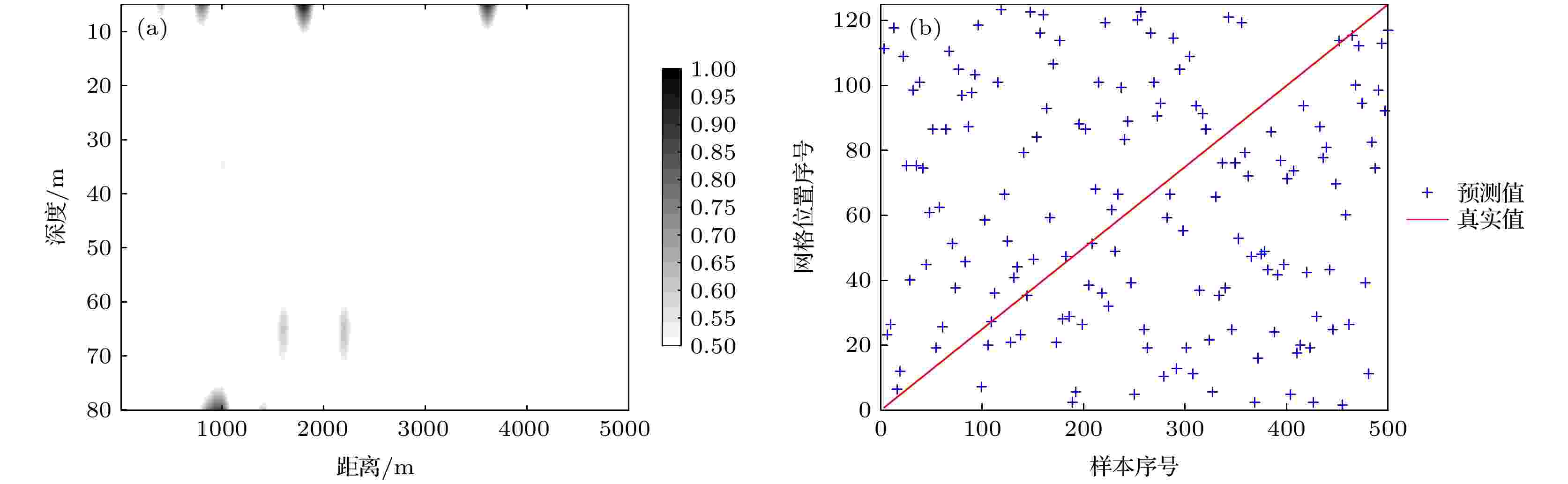图 7 环境失配时敏感核函数预测结果　(a) 单个样本定位结果; (b)多样本预测结果
Figure7. Prediction results of sensitive kernel function with environmental mismatch: (a) Location results of single sample; (b) results of multiple samples

2 -->

4.3.目标散射函数敏感性分析

目标散射函数通过影响入射声场和散射声场的耦合, 改变散射过程中能量的重新分配, 进而影响到接收声场. 实际情况下目标的散射函数是未知的, 预训练过程中所采用的模拟目标只是对实际目标近似, 两者存在目标散射函数失配, 因此有必要分析定位方法对目标散射函数的敏感性.
假设模拟目标为长半轴40 m、短半轴3 m的刚性长旋转椭球体, 实际目标为刚性圆柱体, 长度分别为35, 40和45 m, 圆柱半径分别为2.5, 3.0和3.5 m. 保持其他仿真参数不变, 除目标散射函数失配外无其他失配存在. 此时用仿真数据训练得到的预训练模型并不发生变化, 在预训练模型的基础上通过参数迁移进行微调, 对于不同尺寸的实际目标, 仿真结果如表2所列.

实际目标 长度/m	实际目标圆柱半径/m	目标失配时预测准确率/%	迁移学习后预测准确率/%
35	2.5	77.2	95.2
40	3	79.4	96.0
45	3.5	74.8	93.6

表2目标散射函数失配时的仿真结果
Table2.Simulation results of target scattering function mismatch

可以看出, 当实际目标的长度为40 m、圆柱半径为3 m时, 目标失配的程度较小, 预训练模型对实际数据的预测准确率为79.4%, 经过迁移学习后神经网络模型的预测准确率达到96.0%, 有效降低了目标散射函数失配对定位性能的影响; 当目标失配程度增大时, 预训练模型的预测准确率出现下降, 经过迁移学习后神经网络模型出现了定位性能的略微降低, 但仍可以满足目标定位的精度需求. 以上分析表明定位方法对目标散射函数具有较好的稳健性.
2 -->

4.4.海底底质敏感性分析

仿真环境的海底参数往往与实际海底参数存在失配, 会影响预训练模型的定位性能. 假设水体参数不变, 当实际环境的海底底质分别为泥砂、细砂、粗砂时, 仿真结果如表3所列.

实际海底 底质类型	密度/ (g·cm–3)	声速/ (m·s–1)	海底底质失配时 预测准确率/%	迁移学习后 预测准确率/%
泥砂	1.806	1668	78.4	96.0
细砂	1.957	1753	74.6	93.6
粗砂	2.034	1836	71.0	92.0

表3海底底质失配时的仿真结果
Table3.Simulation results of sediment properties mismatch

可以看出, 当实际海底底质与仿真海底底质存在失配时, 预训练模型的预测准确率下降了20%左右, 定位方法的性能受到较大影响, 且失配程度越大, 预训练模型的预测准确率越低. 经过迁移学习后神经网络模型的预测准确率得到提升, 尽管随着失配程度的增大, 预测准确率会出现小幅下降, 但在实际海底底质为粗砂的情况下仍能达到92%, 这表明定位方法对海底底质具有较好的稳健性.
2 -->

4.5.阵元数量和布设深度敏感性分析

发射和接收点的位置决定了特征声线的传播路径, 只有目标位于声线附近时, 才能对声场产生影响. 假设模拟目标和实际目标均为刚性长旋转椭球体, 模拟目标的长半轴为40 m、短半轴为3 m, 实际目标的长半轴为60 m、短半轴为5.6 m, 无其他失配存在. 令接收阵元数为25, 发射阵元数分别取3—6, 保持其他仿真参数不变, 仿真结果如表4所示; 令发射阵元数为5, 接收阵元数分别取17—23, 保持其他仿真参数不变, 仿真结果如表5所列; 改变发射阵元的布设深度, 令5个发射阵元的布设深度分别为20—32 m, 20—80 m, 68—80 m, 保持其他仿真参数不变, 仿真结果如表6所列.

发射阵元数	无失配时预测准确率/%	目标失配时预测准确率/%	迁移学习后预测准确率/%
3	95.8	77.6	89.4
4	97.3	81.2	92.6
5	98.7	83.4	95.0
6	99.0	85.4	95.8

表4不同发射阵元数时的仿真结果
Table4.Simulation results of different number of transmitting array elements

接收阵元数	无失配时预测准确率/%	目标失配时预测准确率/%	迁移学习后预测准确率/%
17	92.6	71.4	90.8
19	94.6	77.2	92.2
21	98.7	83.4	95.0
23	98.9	86.8	96.6

表5不同接收阵元数时的仿真结果
Table5.Simulation results with different number of receiving array elements

发射阵元布设深度/m	无失配时预测准确率/%	目标失配时预测准确率/%	迁移学习后预测准确率/%
20—32	96.2	81.4	90.8
20—80	98.7	83.4	95.0
68—80	96.8	84.0	91.2

表6不同布设深度时的仿真结果
Table6.Simulation results of different layout depths

由表4和表5可以看出, 当提高发射、接收阵元数量时, 可以得到准确率更高的预训练模型, 且预训练模型的定位性能受目标尺寸失配的影响更小, 经过参数迁移后, 与较少阵元数的情况相比模型的预测准确率更高. 这是因为发射、接收阵元数量的增多会使得收发连线的数量增多, 可以从波导空间结构的维度上得到更多与目标位置相关的信号数据, 故而输入神经网络的数据矩阵隐含着更多的目标位置特征信息, 有助于神经网络训练过程中对特征更加高效的提取, 能够更好地训练和构建神经网络模型, 提高模型的预测准确率.
表6的结果表明, 发射阵元布设深度为20—80 m时, 与布设深度为20—32 m, 68—80 m的情况相比可以得到准确率更高的预测模型. 这是因为当发射阵元布设在较小的深度覆盖范围时, 对于不同的发射阵元, 其对应接收信号数据的信道响应函数差异较小, 包含的目标位置信息有限; 而当发射阵元布设在较宽的深度覆盖范围时, 接收信号数据的信道响应函数差异增大, 此时接收数据中隐含着更多目标位置信息, 有助于神经网络更准确地提取数据的特征, 提高模型的定位性能. 同时也可以看出, 在仿真环境下改变发射阵元数、接收阵元数、发射阵元布设深度的取值, 经过迁移学习后模型的预测准确率仍能达到90%以上, 这表明定位方法对阵元数、布设深度均具有较好的稳健性.
2 -->

4.6.对信道起伏的敏感性分析

海洋环境的起伏会导致声信道的幅度和相位起伏, 从而引起接收信号起伏. 为了便于研究本文方法对信道起伏的稳健性, 这里分别对信道冲激响应的幅度和相位添加扰动, 分析不同扰动强度下的定位效果.
根据信道多途冲激响应, 对信道加入幅度扰动, 可以表示为

$ h_{i j}(t) = \sum\limits_{k = 1}^{K} a_{ij}^k \delta\left(t-\tau_{ij}^k \right) {\rm e}^{{\rm j} \varphi_{ij}^k}, $

$ h_{i j}^{\prime}(t) = \sum\limits_{k = 1}^{K} \left(a_{ij}^k +\xi_{ij}^k \right) \delta\left(t-\tau_{ij}^k \right) {\rm e}^{{\rm j} \varphi_{ij}^k}, $

$ \tilde{h}_{i j}^{\prime}(t) = \sum\limits_{k = 1}^{K} \left(\tilde{a}_{ij}^k+\tilde{\xi}_{ij}^k\right) \delta\left(t-\tilde{\tau}_{ij}^k\right) {\rm e}^{{\rm j} \tilde{\varphi}_{ij}^k}, $

$ {\boldsymbol{P}}_{i j}^{\prime}(f) = {\cal{F}}[s(t)] \cdot {\cal{F}}\left[h_{i j}^{\prime}(t)\right]+{\boldsymbol{N}}(f), $

$ \tilde{{\boldsymbol{P}}}_{i j}^{\prime}(f) = {\cal{F}}[s(t)] \cdot {\cal{F}}\left[\left(\tilde{h}_{i j}^{\prime}(t)+h_{i j}^{\prime}(t)\right)\right]+{\boldsymbol{N}}^{\prime}(f), $

其中, k为信道冲激响应的第k条路径, $ a_{ij}^k $为幅度因子, $ \tau_{ij}^k $为时延因子, ${\rm e}^{{\rm j} \varphi_{ij}^k}$为相位因子, N为频域噪声. $ {h}_{i j}^{\prime}(t) $与$ \tilde{h}_{i j}^{\prime}(t) $分别为添加扰动后的直达波信道冲激响应函数和目标信道冲激响应函数, $ {\boldsymbol{P}}_{i j}^{\prime}(f) $与$ \tilde{{\boldsymbol{P}}}_{i j}^{\prime}(f) $分别为起伏环境下的直达波与有目标时的接收信号.
对时域内各收发对间的幅度最大的前10条声线添加幅度扰动$ \xi_{ij}^k $, 以模拟环境起伏引起的信道幅度扰动, 幅度扰动$ \xi_{ij}^k $相互独立且$ \xi_{ij}^k \sim {\cal{N}} \left(0, \sigma^{2}\right) $. 本方法在不同幅度起伏强度下的接收信号强度起伏和定位准确率如图8(a)所示, 定位准确率随着信道幅度起伏方差与信道冲激响应最大值之比的增大逐渐减小, 接收信号能量起伏随该比值的增大逐渐增大. 当该比值小于0.2时, 信号强度起伏不超过1.7 dB, 定位准确率保持85%以上; 当该比值增大至大于0.3时, 信号强度起伏超过2.7 dB, 定位准确率小于75%.
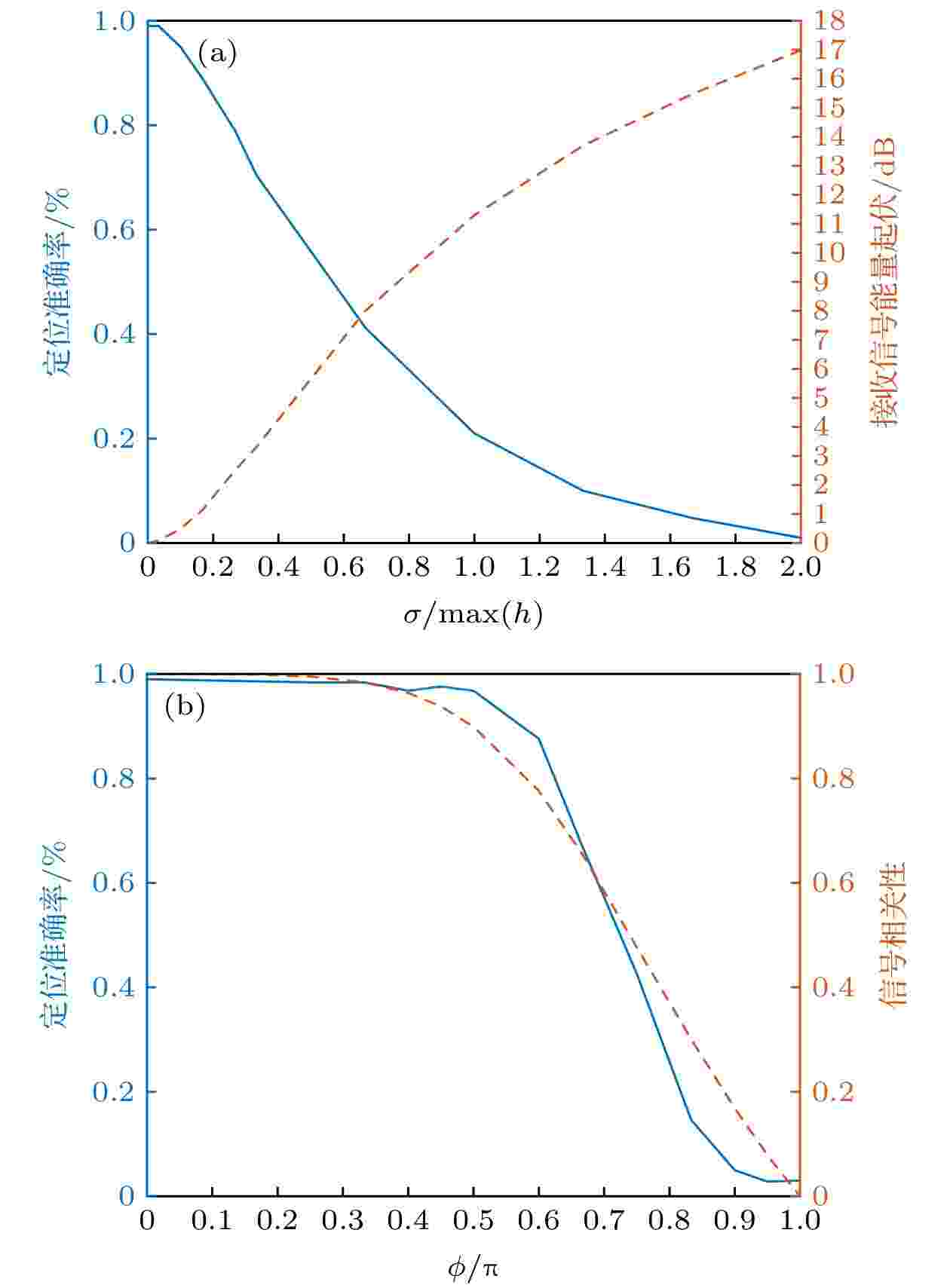图 8 定位准确率随起伏变化　(a) 定位准确率随幅度起伏的变化; (b) 定位准确率随相位起伏的变化
Figure8. Position accuracy with fluctuation variation: (a) Position accuracy with magnitude fluctuation; (b) position accuracy with phase fluctuation

根据信道多途冲激响应, 对信道加入相位扰动, 可以表示为:

$ h_{i j}(t) = \sum\limits_{k = 1}^{K} a_{ij}^k \delta\left(t-\tau_{ij}^k\right) {\rm e}^{{\rm j} \varphi_{ij}^k}, $

$ h_{i j}^{\prime}(t) = \sum\limits_{k = 1}^{K} a_{i j}^k \delta\left(t-\tau_{ij}^k\right) {\rm e}^{{\rm j} \varphi_{ij}^k} \cdot {\rm e}^{{{\rm j} \varphi ^{\prime}_{ij}}^k(t)}, $

$ \tilde{h}_{i j}^{\prime}(t) = \sum\limits_{k = 1}^{K}\tilde{a}_{ij}^k \delta\left(t-\tilde{\tau}_{ij}^k\right) {\rm e}^{{\rm j} \tilde{\varphi}_{ij}^k} \cdot {\rm e}^{{{\rm j} \tilde{\varphi}^{\prime}_{ij}}^k(t)}, $

$ {\boldsymbol{P}}_{i j}^{\prime}(f) = {\cal{F}}[s(t)] \cdot {\cal{F}}\left[h_{i j}^{\prime}(t)\right]+{\boldsymbol{N}}(f), $

$ \tilde{{\boldsymbol{P}}}_{i j}^{\prime}(f) = {\cal{F}}[s(t)] \cdot {\cal{F}}\left[\left(\tilde{h}_{i j}^{\prime}(t)+h_{i j}^{\prime}(t)\right)\right]+{\boldsymbol{N}}^{\prime}(f). $

假设信道相位起伏$ {\varphi^{\prime}_{ij}}^k $相互独立且${\varphi^{\prime}_{ij}}^k \sim $$ {\cal{U}} \left(-\phi, \phi \right)$, 对信道所有路径施加相位起伏. 本方法在不同相位起伏强度下的信号相关性和定位准确率如图8(b)所示, 当相位角起伏范围?小于$ \pi/2 $时, 信号相关性大于0.85, 定位准确率可保持95%以上; 随着起伏范围角的继续增大, 信号相关性及定位准确率随之下降, 在$ \phi = \pi $时接近0.
以上仿真表明, 本文方法对海洋环境起伏导致的信道扰动具有一定的稳健性, 在较为稳定的信道环境下可以保持较好的定位准确率.
在无目标信道中存在起伏时, 分别考虑幅度和相位起伏. 计算起伏环境下的定位预测结果, 如图9所示, 环境随机扰动使得无目标定位结果具有较强的随机性, 无法判定目标的存在与位置. 这是由于无目标时, 由(7)式得到的扰动量变化只由噪声和信道扰动决定, 因此具有较强的随机性.
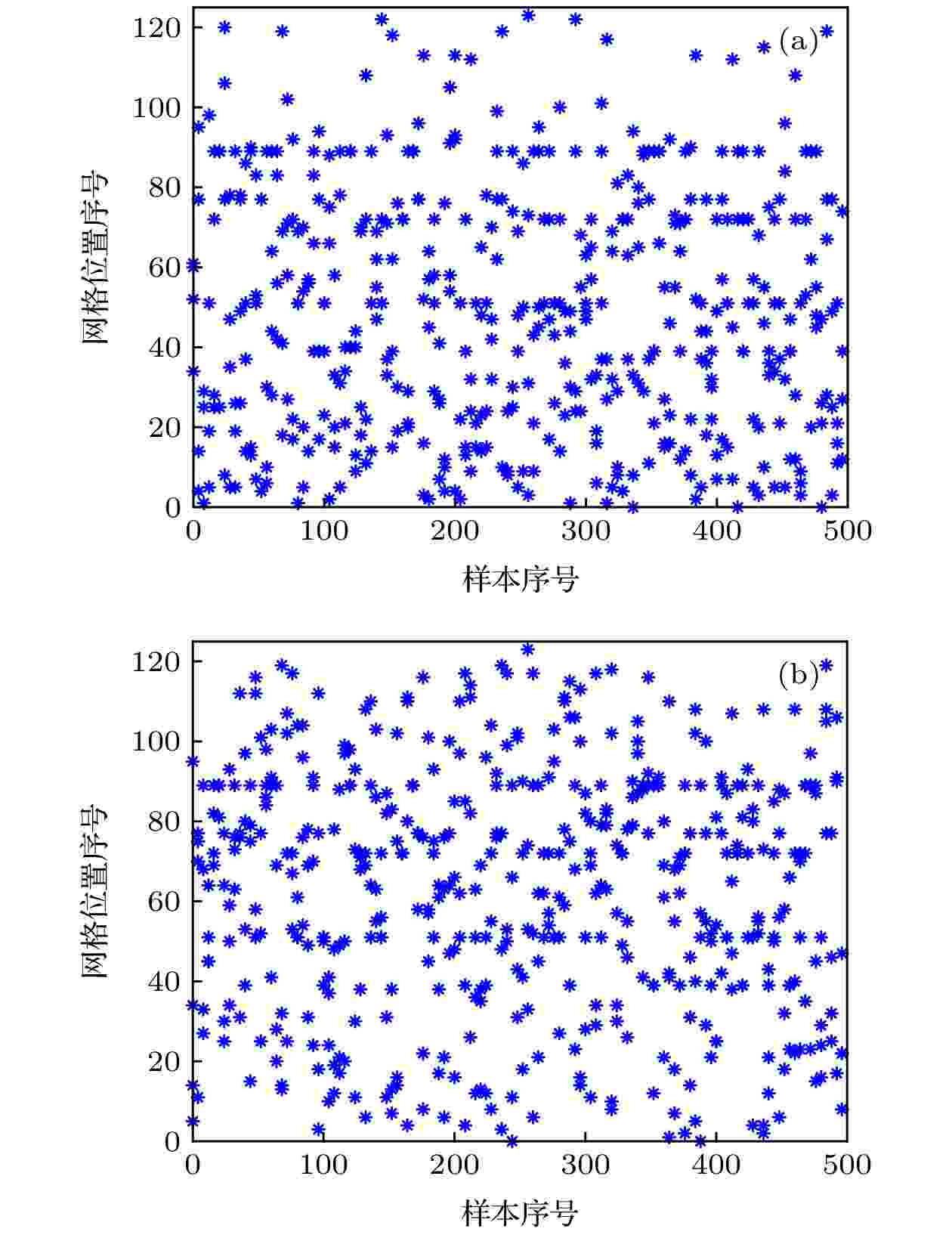图 9 起伏信道下无目标定位预测结果　(a) 无目标幅度起伏$ \sigma/{\rm {max}}(h)=0.6$的定位预测结果; (b) 无目标相位起伏$ \phi=2\pi/3$的定位预测结果
Figure9. Position result without target in fluctuated channel: (a) Position results without target in magnitude fluctuated channel $ \sigma/{\rm {max}}(h)=0.6$; (b) position results without target in phase fluctuated channel $ \phi=2\pi/3$

由仿真结果可以看出, 方法的定位预测结果在起伏信道中有无目标的情况下有显著差别, 相比于有目标情况, 无目标时定位预测结果的分布呈现很强的随机性, 因此不能作为目标定位依据.

本文研究了一种基于迁移学习的水下目标前向散射稳健定位方法, 提取目标前向散射引起的声场幅度扰动作为特征, 利用仿真数据训练神经网络构建预训练模型, 而后使用少量实际数据对预训练模型进行参数迁移. 浅海环境仿真结果表明, 在声速剖面失配时可以获得稳健的定位结果; 对多种失配情况进行了敏感性分析, 仿真结果表明该方法对目标散射函数、海底底质具有较好的稳健性, 虽然在存在失配时预测性能出现小幅下降, 但仍可以满足目标定位的精度需求; 对发射接收阵元数目以及阵元布设深度进行了敏感性分析, 仿真结果表明增大以上参数可以使得接收数据隐含更多的目标位置特征信息, 提高神经网络的特征提取能力和定位性能, 实际中需综合考虑布阵设计与定位性能, 选取合适的发射、接收阵元数与布设深度; 进一步对信道幅度与相位扰动进行了敏感性分析, 结果表明方法在较稳定的环境下可保持较好的定位性能.
该方法由模型和数据共同驱动, 可以较好地解决环境失配问题, 但值得注意的是迁移学习的前提是源域和目标域具有一定相似性, 这意味着预训练模型不能和理想预测模型在结构上相差过大, 选取先验水文环境信息构建预训练模型时应尽可能考虑多种水文情况, 使得预训练模型具有较好的泛化能力, 这也有助于避免迁移学习时出现过拟合的问题.