摘要: 晶硅光伏组件的工作温度严重制约着电池效率及组件寿命的提升, 因此光伏冷却研究具有重要意义. 通过将纳米结构引入主流光伏组件的高分子背板, 从而获得具有增强热传导及热辐射特性的直冷背板, 已成为新一代光伏冷却技术的发展趋势. 本文聚焦于组件背面的散热特性研究, 联合能量平衡方程及光学模拟, 分别计算了三种典型环境温度下标准背板与直冷背板的热学功率及降温效果. 计算中采用主流商用硅电池的结构参数及封装方式, 详细讨论了背板的传热系数与发射率增强对光伏组件热学过程及工作温度的影响. 以期为光伏组件直冷背板的设计与制备提供方向.
关键词: 晶硅太阳电池 /
光电效率 /
光伏热效应 /
光伏组件 English Abstract Analyses of heat dissipation of direct-cooling backsheets of crystalline silicon photovoltaic modules at ambient temperatures Zhu Jing-Yan 1 ,Zou Shuai 1,2 ,Sun Hua 1 ,Su Xiao-Dong 1 1.Jiangsu Key Laboratory of Thin Films, School of Physical Science and Technology, Soochow University, Suzhou 215006, China Fund Project: Project supported by the Key University Science Research Project of Jiangsu Province, China (Grant No. 16KJA140002), the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (Grant No. KYCX19_1967), and the Priority Academic Program Development of Jiangsu Higher Education Institutions (PAPD), ChinaReceived Date: 20 October 2020Accepted Date: 06 December 2020Available Online: 19 April 2021Published Online: 05 May 2021Abstract: The working temperature of the crystalline silicon photovoltaic (PV) module seriously restricts the cell efficiency and the module lifetime. Therefore, it is of great significance to investigate the cooling effects of PV modules. Recently, introducing nanostructures into polymer backsheets to obtain direct-cooling effects due to enhanced heat conduction and radiation characteristics, has become a new trend for PV cooling technology. In this paper, we study the backside thermal properties of the PV module by combining the energy balance equation and optical simulations. The thermal power and cooling effect are calculated and compared between the standard backsheet and three types of direct-cooling backsheets for three typical ambient temperatures. The structure parameters and encapsulating mode of mainstream commercial silicon cells are adopted in the simulations and calculations. The influences of thermal parameters, i.e, the heat transfer coefficient and the emissivity, on the thermal process and the operating temperature are discussed in detail. We hope that this study may provide a certain reference for the future design of PV-direct-cooling backsheets.Keywords: crystalline silicon solar cell /photovoltaic efficiency /photovoltaic thermal effects /photovoltaic module 全文HTML --> --> --> 1.引 言 晶硅太阳电池具有优异的光电性能及相对较低的制备成本, 在当今光伏产业中成为商用主流. 通过不断引入新的物理效应与制备技术, 晶硅电池的产线效率得以逐年提升[1 ,2 ] . 从基本机制上看, 晶硅电池的光电效率是电池的光、电、热等性能的综合体现. 其中, 电池的温度效应对其工作效率及寿命具有着不可忽略的影响. 理想条件下, 每升高1 K温度, 晶硅太阳电池的最大输出功率将下降0.4%; 若计及更多实际因素(例如热斑效应), 则其温衰特性可达到0.65%/K[3 ] . 同时, 温度升高也会加快封装层老化速度, 缩短电池寿命. 因此, 如何实现有效的冷却降温是晶硅太阳电池研究及应用领域中广受关注的问题.[4 ] 在光伏封装用EVA中添加了15%质量分数的石墨烯纳米材料, 制备得到的EVA复合材料热导率提高了22%. Kim等[5 ] 将70%质量分数的AlN/BN导热填料以8∶2比例混合进PVDF背板中, 制备出最大热导率达$5.85 \; {\rm{W}}\cdot {\rm{m}}^{-1}\cdot {\rm{K}}^{-1} $ 的复合背板, 其导热性是原来的31倍. 除了提高导热性, 通过在材料表面制备微结构来实现辐射冷却也是晶硅电池的有效降温手段. Zhu等[6 ] 在Si吸收体表面设计了$ {\rm{Si}}{\rm{O}}_{2} $ 光子晶体结构层, 其温度比硅基降低了13 ℃. Li等[7 ] 设计了$ {\rm{Si}}{\rm{O}}_{2}/{\rm{Al}}_{2}{\rm{O}}_{3} $ 等多层冷却介质膜, 并将其置于晶硅光伏组件的正面. 模拟结果显示组件温度降低了5.7 ℃. Lu等[8 ] 制备了微米尺度的$ {\rm{Si}}{\rm{O}}_{2} $ 绒面作为晶硅太阳电池的封装层, 其在大气窗口(8—13 μm)具有接近1的发射率, 最终使得组件相对效率提升了3.13%. 另外还有其他结构, 如$ {\rm{Si}}{\rm{O}}_{2} $ 绒毛绒面[9 ] 、$ {\rm{Si}}{\rm{O}}_{2} $ 颗粒膜[10 ] 等, 都在维持或提升光学性质的前提下进一步提高了组件的辐射表现.[11 -13 ] , 导致人们对背板冷却的研究兴趣以改善导热性能为主. 在某些研究过程中, 如Li等[7 ] 构建的晶硅组件热学模型, 甚至完全忽略了背面的热辐射交换, 导致计算得到的工作温度明显高于组件的实际工作温度.$20 \; {\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ 时趋于稳定.2.晶硅光伏组件的热学特性分析 如图1 所示, 晶硅光伏组件的基本结构包含玻璃、EVA、硅电池(由金字塔绒面、硅衬底和铝背极构成)以及高分子背板. 组件的封装顺序和各部分的常见厚度已在图中给出. 组件工作时, 一方面从入射阳光和环境中吸收能量, 另一方面通过光伏效应和热交换过程(包括热传导、热对流和热辐射三种方式)释放能量. 根据能量守恒定律, 当组件温度达到稳定时, 其吸收和释放的能量形成平衡, 即图 1 晶硅光伏组件结构和工作时的能量输入与输出Figure1. Structure and energy input and release of crystalline silicon photovoltaic modules at work.$ {P}_{\rm{sun}} $ 、对环境辐射的吸收功率$ {P}_{\rm{atm}} $ 、辐射散热功率$ {P}_{\rm{rad}} $ 、非辐射散热功率$ {P}_{\rm{con}} $ (包括热传导和热对流)以及光电输出功率$ {P}_{\rm{PV}} $ , 并对应如下物理过程.$ {P}_{\rm{sun}} $ , $ {P}_{\rm{PV}} $ —光电转换过程$ {P}_{\rm{sun}} $ 表达式为$ {I}_{\rm{sun}}{(}\lambda {)} $ 为波长$ \lambda $ 对应的太阳光谱强度, $ {\epsilon}_{\rm{sun}}\left(\lambda \right) $ 为光伏组件对太阳光的吸收率. 我们采用AM1.5G太阳光谱[14 ] , 并利用硅太阳电池专业模拟软件SunSolve[15 ] 计算组件吸收率. 计算中采用主流商用硅电池的结构参数: 硅衬底厚度设置为180 μm, 绒面设置为3 μm高度的随机分布的正金字塔绒面, 抗反层为80 nm厚度的$ {\rm{Si}}{\rm{N}}_{{x}} $ . 组件其他部分厚度如图1 所示. 当太阳光垂直入射到组件正面时, 计算得到的组件吸收率$ {\epsilon}_{\rm{sun}}\left(\lambda \right) $ 及吸收功率$ {\rm{d}}{P}_{\rm{sun}}/{\rm{d}}\lambda $ 如图2(a) 所示. 对吸收功率积分, 得到${P}_{\rm{sun}}= $ $ {777}\;{\rm{W}}\cdot {\rm{m}}^{-2}$ , 该结果与文献[16 ]相符合. 在吸收的太阳辐射中, 波长大于1200 nm的辐射被组件封装材料吸收变为热量, 300—1200 nm内的辐射则大部分通过硅的光伏反应转换为电能, 其对应的光电输出功率$ {P}_{\rm{PV}} $ 随组件温度$ {T}_{\rm{PV}} $ 的升高而降低[3 ,17 ] :图 2 (a) 组件吸收谱和吸收功率谱(黄色背景为AM1.5G太阳光谱); (b) 黑体辐射谱Figure2. (a) Absorption spectrum and absorption power spectrum of the module (AM1.5G solar spectrum is marked as yellow background); (b) blackbody radiation spectrum.$\eta _{{300}\;{\rm{K}}}\!=\!{20{\text{%}}, }\;{P}_{\rm{solar}}\!=\!{1000}\;{\rm{W}}\cdot {\rm{m}}^{-2}{, }\;{\beta }\!=\! -{0.45}{{\text{%}}}{ }$ 为组件的温度系数[17 ] . (3 )式中为简便起见将组件温度视为均匀. 实际工作时组件各部分的温差很小, 可近似忽略[18 ] .$ {P}_{\rm{con}} $ —组件和环境的非辐射热交换过程(热传导及热对流)${T}_{\rm{PV}}-{T}_{\rm{a}}{)}$ 及组件表面处的风速大小最为关键[19 ,20 ] . 考虑到正面玻璃及背面高分子背板的热学性质差异及风速的不同, 可令$ {h}_{1} $ 和$ {h}_{2} $ 定义为正面及背面传热系数, 其取值综合考虑了热传导与热对流过程. 在标准组件中, 根据玻璃及高分子背板的典型热学性质及风速条件[21 ] , 可取$ {h}_{1}{=10}\;{\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ , ${h}_{2}= $ $ {5}\;{\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1}$ [7 ] .[3 ,17 ] . 在(4a )式和(4b )式中取T a = 10 ℃, 25 ℃和50 ℃, 分别代表组件在低温、常温和高温下的三种工作环境. 需要注意的是, 环境温度的高低不仅影响非辐射热交换过程, 同时也是下节讨论的辐射性热交换中的重要因素. 从图2(b) 可看出, 在理想黑体近似下, T a = 10 ℃, 25 ℃和50 ℃时环境的辐射强度集中分布于2.5 μm以上的红外区. 下节将详细讨论这3个环境温度下组件正面与背面的热辐射吸收与发射效率.$ {P}_{\rm{atm}}{, }{\;{P}}_{\rm{rad}} $ —组件和环境的辐射热交换过程$ {\epsilon} $ 和发射率$ \varepsilon $ 衡量. 根据基尔霍夫热辐射定律[22 ] , 热平衡物体的发射率$ \varepsilon $ 与吸收率$ {\epsilon} $ 在数值上相等. 这里采用文献[23 ]中的玻璃红外折射率参数计算组件正面封装玻璃的吸收率W 为玻璃厚度, $ \theta $ 为入射角, k 为玻璃折射率虚部, R 为由菲涅尔定律计算得到的玻璃反射率. 从计算结果可以观察到玻璃红外吸收谱的典型特征[8 ] . 图3 所示为垂直入射时组件正面的玻璃吸收谱, 在8—13 μm以及20—25 μm处出现明显的低谷, 反映出$ {\rm{Si}}{\rm{O}}_{2} $ 在此波段具有强烈的声子极化激元响应. 组件正面所在环境大气的发射率可表示为${\varepsilon }_{\rm{atm}}\left(\lambda , \theta \right)=1-{{t}_{\rm{atm}}{\left(\lambda \right)}^{\tfrac{1}{{\rm{cos}}\theta }}}^{}$ . 其中, $ {t}_{\rm{atm}}(\lambda ) $ 为大气透射率(如图3 粉色背景所示)[24 ,25 ] .图 3 玻璃吸收谱(垂直入射时)及大气透射谱(粉色背景)Figure3. Absorption spectrum and atmospheric transmission spectrum (pink background) of the glass.${\overline{{\epsilon}}}_{\rm{back}}= $ $ {\overline{\varepsilon }}_{\rm{back}}={0.85}$ [26 ] ; 2)理想背板辐射, 以理想辐射冷却体为背板时, 其吸收率(发射率)为与波长和角度均无关的常数[10 ] : ${{\epsilon}}_{\rm{back}}^{*}={\varepsilon }_{\rm{back}}^{*}=\left\{\begin{array}{l}1, ~~\lambda > {2.5}\;{\rm{\text{μ} m}}\\ {0}, ~~\lambda { < }{2.5}\;{\rm{\text{μ} m}}\end{array}\right.$ , 此时可令背板的辐射散热效果达到最佳.$ {I}_{\rm{atm}}\left({T}_{\rm{a}}\right)={I}_{\rm{BB}}({T}_{\rm{a}}, \lambda ){\varepsilon }_{\rm{atm}}(\lambda , \theta ) $ 为大气辐射功率, ${I}_{\rm{BB}}\left({T}_{\rm{a}}, \lambda \right)=\dfrac{{2}{h}{{c}}^{2}}{{\lambda }^{{5}}}\frac{1}{{\rm{e}}^{\tfrac{{hc}}{{\lambda k}{T}_{\rm{a}}}{ -}1}}$ 为单色黑体辐射强度. 组件的辐射散热功率同样分为正面和背面两部分, 其表达式为2 )—(7 )式代入(1 )式中, 即可得到关于组件工作温度$ {T}_{\rm{PV}} $ 的方程.3.标准背板与直冷背板的降温效果对比 我们讨论了四种组件, 其中各自包含了具有不同热传导系数及发射率的背板, 并计算了相应的热学过程及工作温度. 背板的热学参数见表1 . 这里, 标准背板的发射率和传热系数的取值参照组件的测量结果($ {\overline{\varepsilon }}_{\rm{back}}{=0.85} $ , $ {h}_{2}^{\rm{s}}{=5}\;{\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ )[21 ,26 ] . 三种直冷背板分别以三种方式从标准背板改善而来: 1)直冷背板A, 增强非辐射散热($ {h}_{2}^{*} $ ), 保持背板发射率$ {\overline{\varepsilon }}_{\rm{back}} $ 不变; 2)直冷背板B, 增强辐射散热($ {\varepsilon }_{\rm{back}}^{*} $ ), 保持背板传热系数$ {h}_{2}^{\rm{s}} $ 不变; 3)直冷背板C, 同时增强辐射与非辐射散热($ {h}_{2}^{*} $ , $ {\varepsilon }_{\rm{back}}^{*} $ ).名称 发射率$ {\varepsilon }_{\rm{back}} $ 传热系数$ {h}_{2}{/({\rm{W}}\cdot {\rm{m}}}^{-2}\cdot {\rm{K}}^{-1}) $ 标准背板O $ {\overline{\varepsilon }}_{\rm{back}} $ $ {h}_{2}^{\rm{s}} $ 直冷背板A $ {\overline{\varepsilon }}_{\rm{back}} $ $ {h}_{2}^{*} $ 直冷背板B $ {\varepsilon }_{\rm{back}}^{*} $ $ {h}_{2}^{\rm{s}} $ 直冷背板C $ {\varepsilon }_{\rm{back}}^{*} $ $ {h}_{2}^{*} $
表1 标准背板与直冷背板的热学参数Table1. Thermal parameters of the standard backsheet and direct-cooling backsheets.T a = 10 ℃(低温), 25 ℃(常温)和50 ℃(高温). 图4 —6 给出了计算得到的在不同环境温度下各组件的吸收、散热及光电输出功率, 并分别列出组件正面/背面与环境的各项热交换功率. 为方便对比, 在不同的环境温度下采用了同一太阳光谱. 故图4 —6 中组件从太阳辐射中吸收的功率统一为$777\; {\rm{W}}\cdot {\rm{m}}^{-2} $ . 从计算结果可以明显看出, 相对于标准组件, 采用了直冷背板后光电输出功率都有所提升, 说明相应的工作温度都有所下降. 然而, 仅通过增强背板的热辐射特性所导致的降温效果及光电输出增强十分有限. 即使当背板具有理想热发射率$ {\varepsilon }_{\rm{back}}^{*} $ 时, 其光电输出功率相对于标准发射率$ {\overline{\varepsilon }}_{\rm{back}} $ 的结果仅增加了$1\; {\rm{W}}\cdot {\rm{m}}^{-2} $ . 此效果不随环境温度变化(参见图4 —6 中标准背板O与直冷背板B的光电输出功率对比, 以及直冷背板A和直冷背板C的光电输出功率对比). 相对地, 组件光电输出功率的提升在背板非辐射热学特性增强时更明显, 且与环境温度密切相关. 当T a = 10 ℃(低温), 25 ℃(常温)和50 ℃(高温)时, 由$ {h}_{2} $ 的提升导致的光电输出功率增加分别为$4 \; {\rm{W}}\cdot {\rm{m}}^{-2} $ , $3 \; {\rm{W}}\cdot {\rm{m}}^{-2} $ , $2 \; {\rm{W}}\cdot {\rm{m}}^{-2} $ (参见图4 —6 中标准背板O与直冷背板A的光电输出功率对比).图 4 T a = 10 ℃时各组件的吸收、散热及光电输出功率(单位为$ {\rm{W}}\cdot {\rm{m}}^{-2} $ )Figure4. Absorption power, heat dissipation power and PV output power for each module at T a = 10 ℃ (unit: $ {\rm{W}}\cdot {\rm{m}}^{-2} $ ).图 5 T a = 25 ℃时各组件的吸收、散热及光电输出功率(单位为$ {\rm{W}}\cdot {\rm{m}}^{-2} $ )Figure5. Absorption power, heat dissipation power and PV output power for each module at $ {T}_{\rm{a}} $ = 25 ℃ (unit: $ {\rm{W}}\cdot {\rm{m}}^{-2} $ ).图 6 T a = 50 ℃时各组件的吸收、散热及光电输出功率(单位为$ {\rm{W}}\cdot {\rm{m}}^{-2} $ )Figure6. Absorption power, heat dissipation power and PV output power for each module at T a = 50 ℃ (unit: $ {\rm{W}}\cdot {\rm{m}}^{-2} $ ).表2 所列. 计算结果表明, 标准组件的工作温度比环境温度高约20 ℃, 其光电效率受环境温度影响明显: 由低温(T a = 10 ℃)时的19.62%迅速下降到高温(T a = 50 ℃)时的16.39%. 组件的最高效率出现在低温时的直冷背板C中: $ \eta = $ 20.01%. 图7 给出了不同环境温度下各直冷背板的降温效果及对应的相对效率提升. 相对于标准组件, 以非辐射增强为单一改良方式的直冷背板A在不同环境温度下降温效果分别为3.7 ℃ (T a = 10 ℃), 3.3 ℃ (T a = 25 ℃), 2.7 ℃ (T a = 50 ℃); 以辐射增强为单一改良方式的直冷背板B降温效果仅为0.8 ℃ (T a = 10 ℃), 0.7 ℃ (T a = 25 ℃), 0.7 ℃ (T a = 50 ℃). 可以看到, 直冷背板A的降温效果明显高于直冷背板B, 这与图4 —6 所示的光电输出功率结果一致. 而非辐射联合辐射增强时, 温度分别降低了4.3 ℃ (T a = 10 ℃), 3.8 ℃ (T a = 25 ℃), 3.2 ℃ (T a = 50 ℃), 相对效率则分别提升了1.99% (T a = 10 ℃), 1.85% (T a = 25 ℃), 1.77% (T a = 50 ℃).背板类型 T a = 10 ℃T a = 25 ℃T a = 50 ℃$ {T}_{\rm{PV}}/ $℃ $ \eta / $% $ {T}_{\rm{PV}}/ $℃ $ \eta / $% $ {T}_{\rm{PV}}/ $℃ $ \eta / $% 标准背板O 31.2 19.62 44.7 18.41 67.1 16.39 直冷背板A 27.5 19.96 41.4 18.71 64.4 16.63 直冷背板B 30.4 19.63 43.9 18.48 66.4 16.45 直冷背板C 26.9 20.01 40.9 18.75 63.9 16.68
表2 不同环境温度下组件的工作温度及光电转换效率Table2. Module temperatures and PV conversion efficiencies under different ambient temperatures.图 7 不同环境温度下各直冷背板的降温效果及相对效率提升Figure7. Temperature decrease and the relative efficiency improvement for each direct-cooling backsheet under different ambient temperatures.图8 给出了背板发射率分别为$ {\overline{\varepsilon }}_{\rm{back}} $ 和$ {\varepsilon }_{\rm{back}}^{*} $ 时组件的工作温度随背板传热系数$ {h}_{2}^{*} $ 的变化. $ {h}_{2}^{*} =5\; {\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ 时对应的工作温度即为标准组件的工作温度. 随着$ {h}_{2}^{*} $ 的增加, 组件的工作温度单调下降. 当$ {h}_{2}^{*} =30 \; {\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ , T a = 10 ℃, 25 ℃和50 ℃时的工作温度分别降低至20.2 ℃, 34.7 ℃和58.9 ℃, 与环境温度的温差约为10 ℃. 背板的辐射增强带来的额外降温效果在$ {h}_{2}^{*} $ 增大时则进一步减弱, 这与文献[7 ]中组件正面的降温趋势一致. 当$ {h}_{2}^{*} > 20 \;{\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ 时, 直冷背板A与直冷背板C的工作温度几乎重合, 并近似以$\Delta {T}_{\rm{PV}}/\Delta {h}_{2}^{*} = -0.27$ (T a = 10 ℃), –0.25 (T a = 25 ℃), –0.21 (T a = 50 ℃)的速度随$ {h}_{2}^{*} $ 线性下降.图 8 背板发射率为$ {\overline{\varepsilon }}_{\rm{back}} $ 和$ {\varepsilon }_{\rm{back}}^{*} $ 时组件工作温度随背板传热系数$ {h}_{2}^{*} $ 的变化Figure8. Relationship between the module temperature and $ {h}_{2}^{*} $ when the backsheet emissivity is $ {\overline{\varepsilon }}_{\rm{back}} $ and $ {\varepsilon }_{\rm{back}}^{*} $ .图8 所示, 工作温度随背板传热系数$ {h}_{2}^{*} $ 的变化曲线特征与实验结果定性一致. 文献[27 ]测试了电池工作温度随风速的下降曲线, 室温及标准光照下, 当风速从零增加到2 m/s时, 强制对流引起的传热系数从零增加到约$ 5 \;{\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ (总对流传热系数大约从$5 \; {\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ 增加到$10 \; {\rm{W}}\cdot {\rm{m}}^{-2}\cdot {\rm{K}}^{-1} $ ), 对应的工作温度则下降了5 ℃左右, 与我们的计算结果基本一致. 随着风速进一步增大, 实验测试数据的误差开始扩大, 但曲线趋势明显: 在强制对流传热系数保持稳定持续增长的同时, 温度下降速度变缓, 温度曲线渐趋平坦. 类似的温度变化趋势在以热传导为背板主要散热方式的光伏组件中亦有报道. 如文献[11 ]中对比了热导性质显著不同的三种背板(高分子材料TPT、玻璃、Al合金)厚度对多晶硅光伏组件工作温度的影响. 虽然背板热阻总是与其厚度成正比, 但当背板采用Al合金这类良热导材料时, 背板厚度增加导致的工作温度上升曲线亦呈现出明显的平坦化, 反映出高传热条件下背板降温效果的稳定性.4.讨论与结论 综上, 本文基于能量平衡方程对晶硅光伏组件的热学特性进行了计算与分析, 并着重讨论了在不同的背板散热条件下组件的各项热学功率、光电输出及工作温度的变化. 通过对比标准背板与三种直冷背板的降温效果, 分析背板与环境发生热交换的两种方式(辐射热交换与非辐射热交换)在降温过程中的作用, 得到如下结论.[17 ,18 ,28 ] . 这一结果可与文献[7 ]的计算结果对比. 文献[7 ]中未考虑背板的热辐射效果, 导致计算得到的组件温度远高于环境温度: 在正面未做特殊冷却处理时, 工作温度比环境温度高40 ℃左右; 即使当正面玻璃具有理想辐射特性时, 组件温度仍比环境温度高30 ℃左右. 可见, 背板的热辐射交换过程对光伏组件工作温度的影响不可忽略.图4 —6 ), 导致背板的冷却功率未得到有效提升. 这意味着在背板的热学特性改良设计中, 应集中于背板的非辐射热学特性(如热导率)的增强.$ {h}_{2}^{*} $ 描述. 计算表明, 当$ {h}_{2}^{*} $ 温和增加时($ {h}_{2}^{*} =2{h}_{2}^{\rm{s}} $ ), 环境温度对非辐射增强的降温效果产生较为明显的影响, 低温环境更利于背板的非辐射降温. 而对于具有高传热系数的背板($ {h}_{2}^{*} > 20\;{\rm{W}}\cdot {\rm{m}}^{-{2}}\cdot {\rm{K}}^{-1} $ ), 同一背板在不同环境温度下的降温程度十分接近, 且由辐射改良引起的额外降温效果几乎可以忽略, 即高传热系数背板的降温效果趋于稳定. 
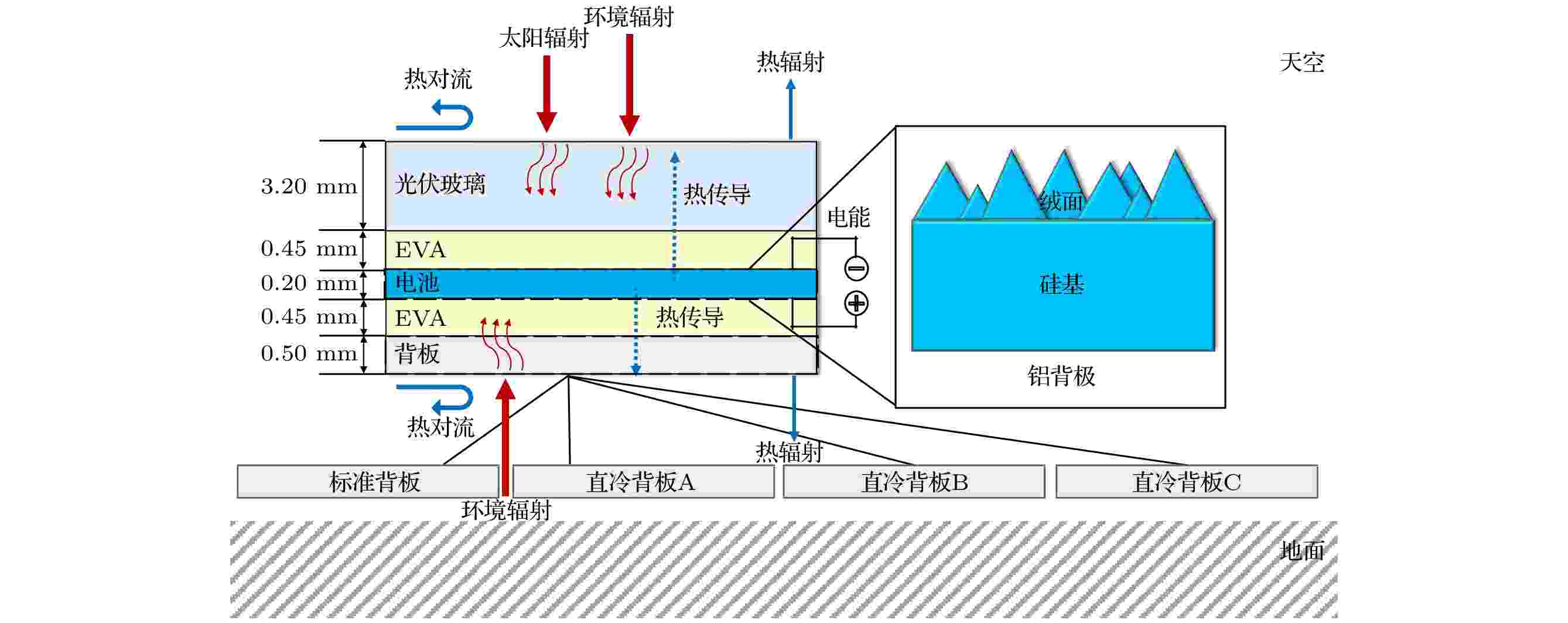图 1 晶硅光伏组件结构和工作时的能量输入与输出
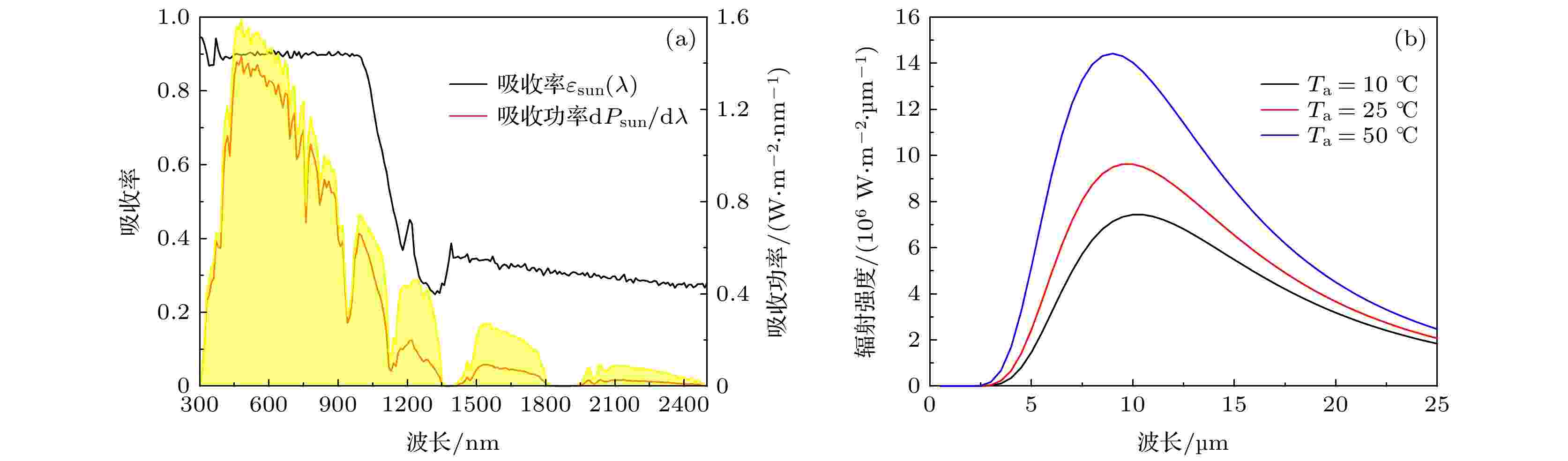图 2 (a) 组件吸收谱和吸收功率谱(黄色背景为AM1.5G太阳光谱); (b) 黑体辐射谱
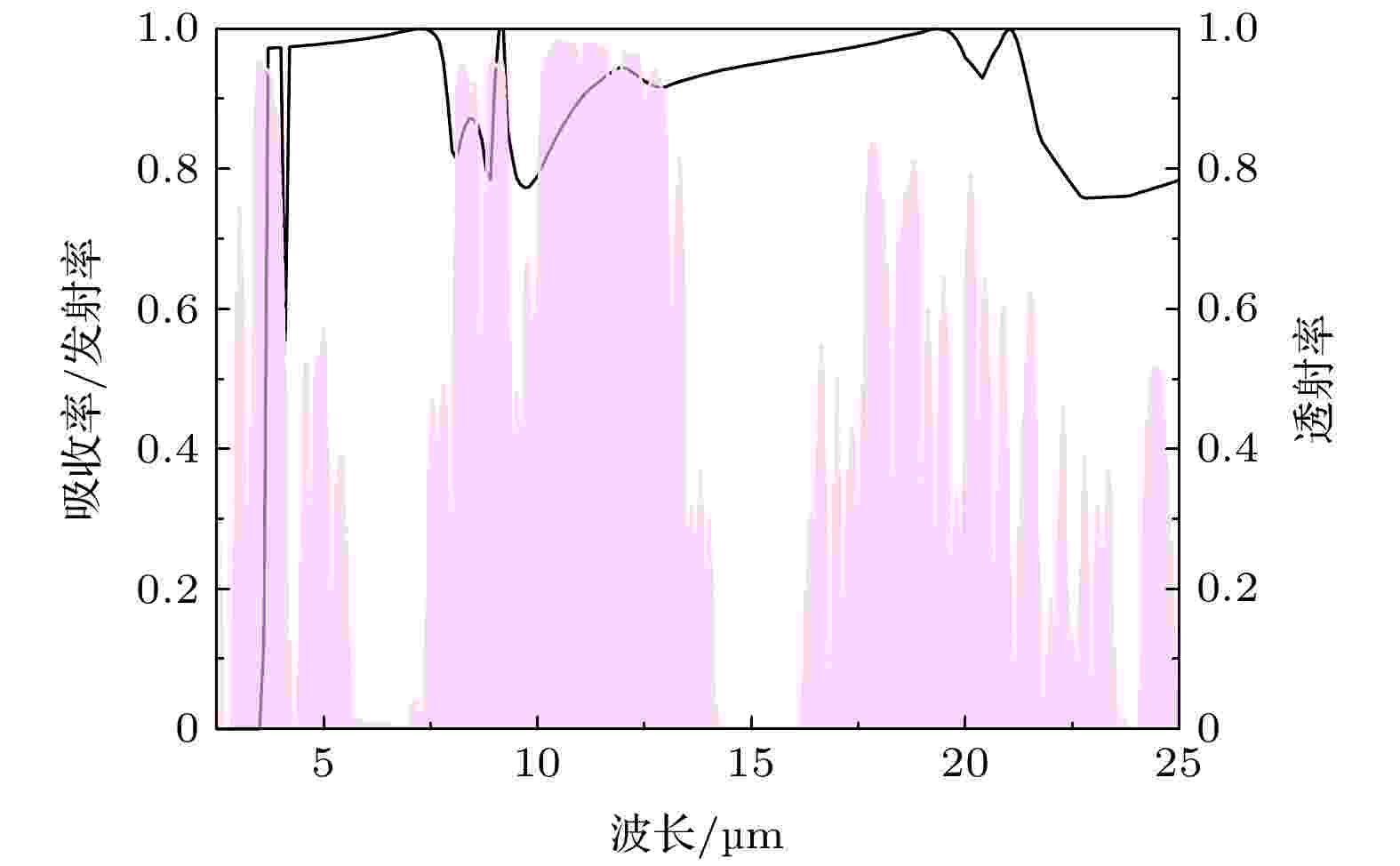图 3 玻璃吸收谱(垂直入射时)及大气透射谱(粉色背景)
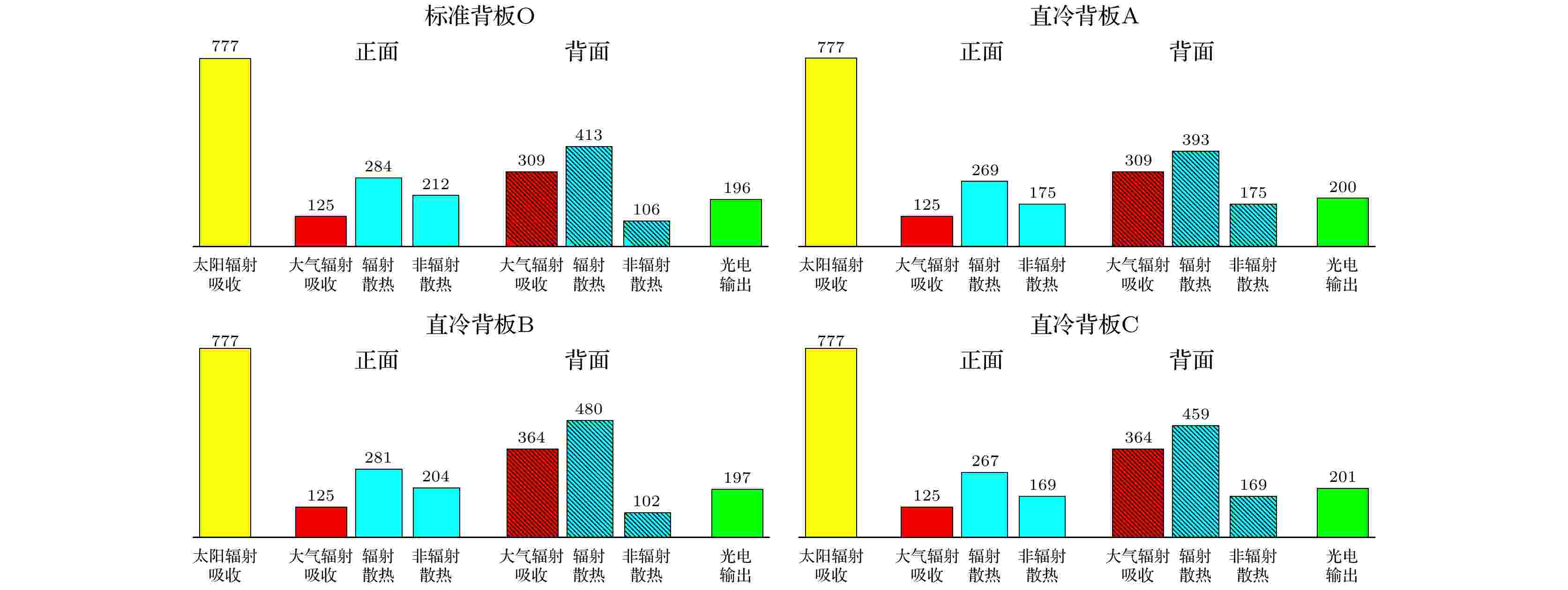图 4 Ta = 10 ℃时各组件的吸收、散热及光电输出功率(单位为
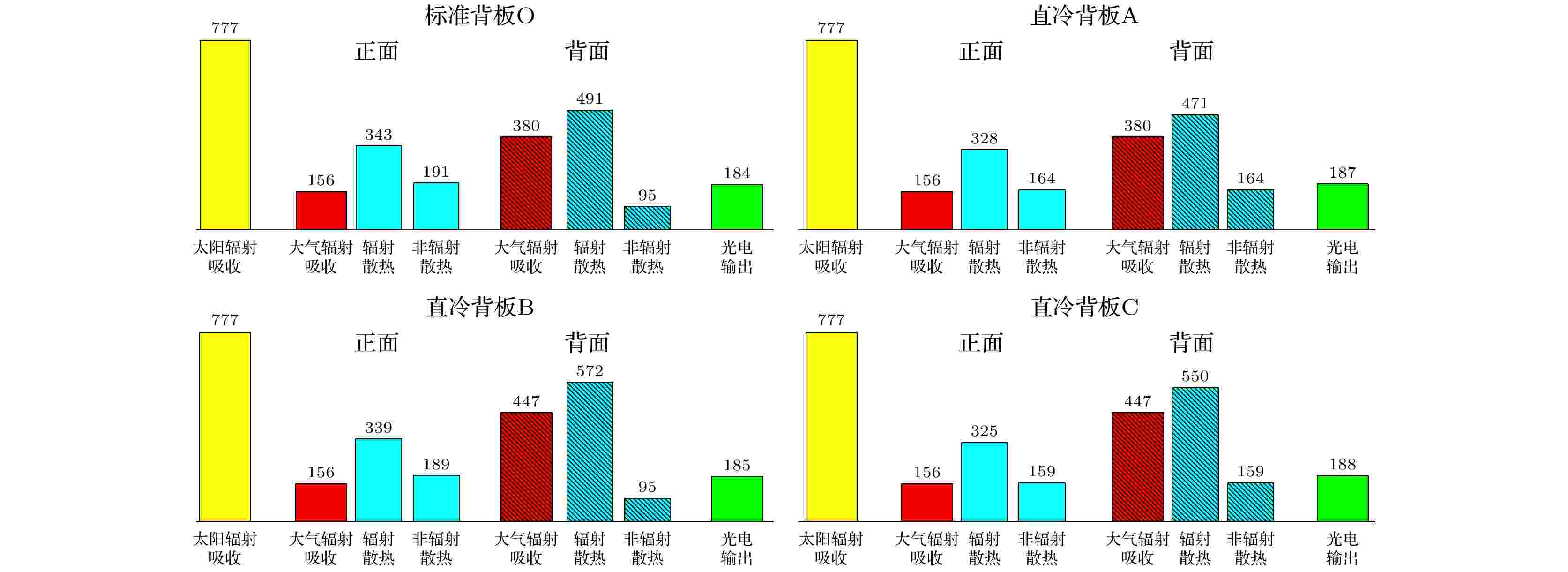图 5 Ta = 25 ℃时各组件的吸收、散热及光电输出功率(单位为
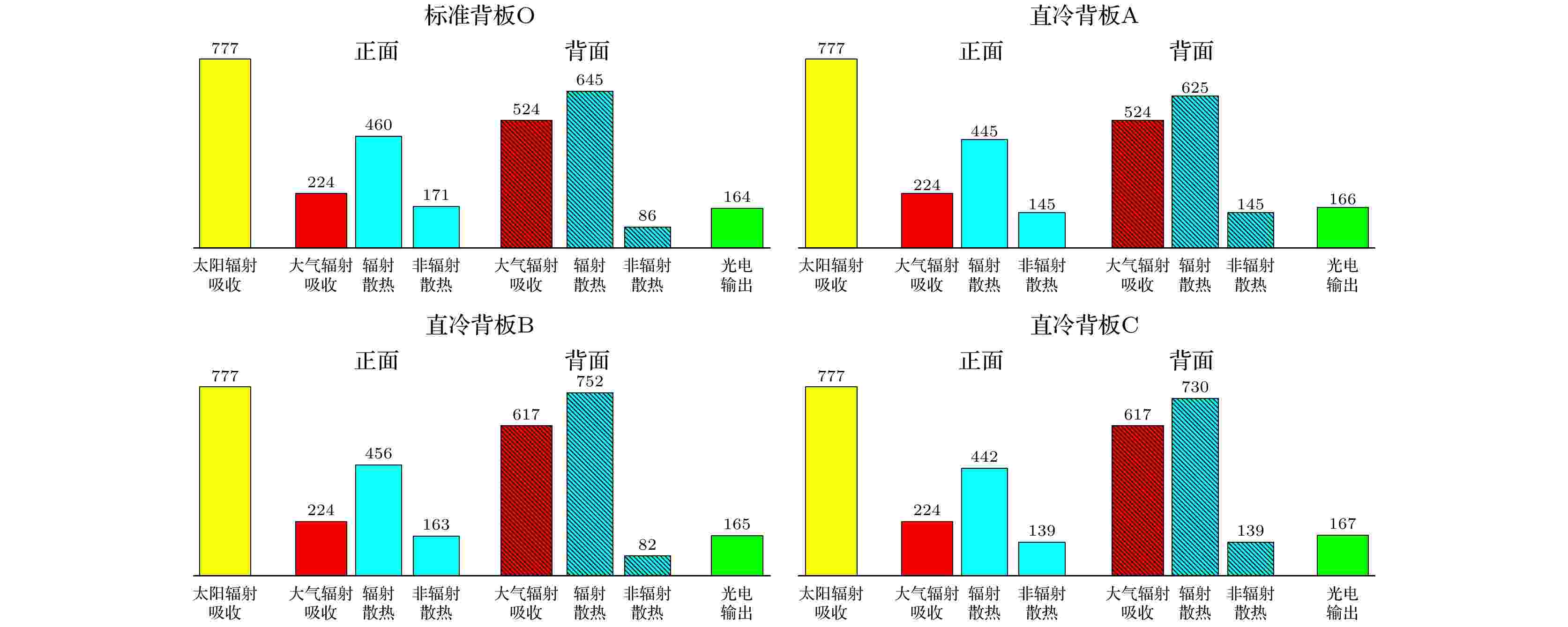图 6 Ta = 50 ℃时各组件的吸收、散热及光电输出功率(单位为
图 7 不同环境温度下各直冷背板的降温效果及相对效率提升
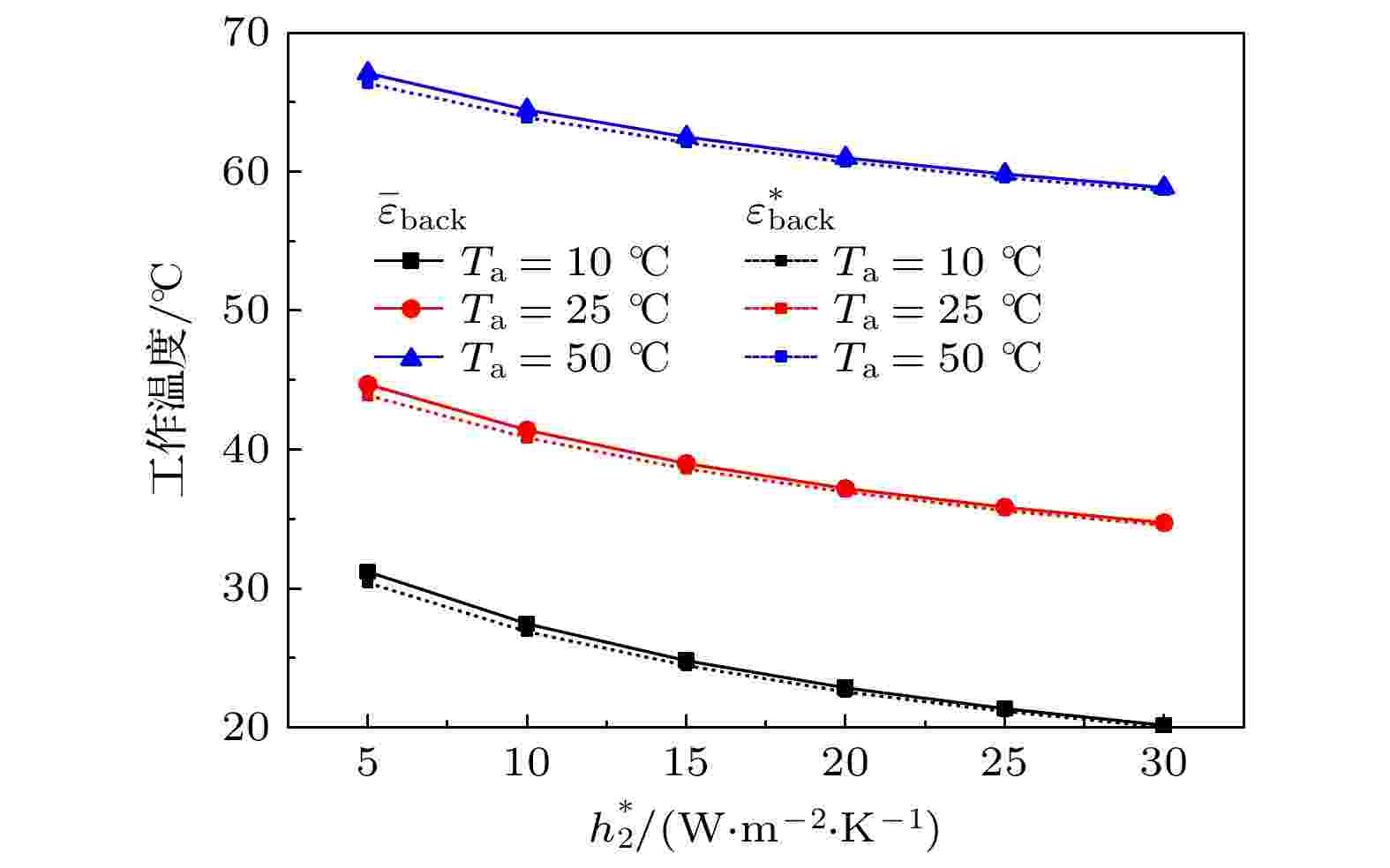图 8 背板发射率为
