摘要:研究复杂海洋环境中海底地震波激发及其传播特性, 对海底物理力学特性研究、资源勘探等具有重要的意义. 目前针对时域海底地震波的研究大都局限于水平分层的情况, 而实际的海底地质条件比较复杂, 基于理想环境假设得出的数值解与实际差别较大. 本文在考虑倾斜、隆起等非水平海底模型的情形下, 采用时间2阶精度、空间10阶精度的交错网格有限差分方法, 同时结合多轴完全匹配层边界条件, 对复杂海洋环境下的海底地震波进行时域数值模拟与分析. 利用计算得到的声场时域波形, 分析了复杂海洋环境下海底地震波的传播特性. 结果表明, 采用空间高阶精度的交错网格有限差分方法, 可改善数值计算中的频散问题; 同时采用多轴完全匹配层替代传统的完全匹配层, 解决了液-固介质中远距离声场数值模拟不稳定的问题. 在含倾斜与隆起构造的复杂海底模型中, 海底基岩隆起改变了Scholte波的传播方向, 更有利于在较浅深度处接收到Scholte波.
关键词: 海底地震波/
复杂海底/
高阶交错网格时域有限差分/
多轴完全匹配层

English Abstract

全文HTML

--> --> -->

海深、海底和海水声速剖面等海洋声学环境的复杂性, 对声传播影响很大, 导致海洋中的声传播过程非常复杂^[1,2]. 特别是低频/甚低频声波, 由于其具有很强的穿透性, 能量可透射到海底介质中, 因此声波的传播会受到海底弹性基岩层特性的影响. 建立符合实际海底环境的声传播模型, 对于复杂的海洋环境中的声传播特性研究、海底地质反演、海底石油与天然气的勘探等方面有重要的意义.
近几十年来, 压缩波和剪切波在液-固界面处干涉形成的Scholte界面波为检测和反演介质属性提供了新的思路^[3]. Scholte 波是一种沿液-固耦合界面传播的面波^[4], 与体波相比, Scholte界面波具有能量强、易识别、衰减慢、传播距离远、损耗小、抗干扰能力强等特点. 液-固界面Scholte波的频散特征与海底介质特性之间存在密切联系, 利用界面波的频散特性可有效反演海底沉积物参数以及海底浅层地质结构, 因此, 研究Scholte界面波的激发、传播、检测与应用对海洋声学与海洋地球物理等领域具有重要的理论意义和应用价值^[5]. 卢再华等^[6]将Scholte界面波简化为液-固多层半无限空间低频点声源引起的地震波动问题, 基于波数积分方法, 通过FFP数值积分得到了海底表面声压、位移和加速度的频率特性曲线, 分析了不同浅海环境对点声源海底地震波的波动特征的影响. 卢再华等^[7]采用大型有限元软件ANSYS中的液-固耦合计算模块, 结合黏弹性人工边界条件, 对水平分层海洋环境下低频点声源海底地震波进行了数值计算. 韩庆邦等^[8]分析了Scholte波在两相流体与多孔介质固体界面处的传播特性, 以及Scholte波速与两相流体积含量、粒径等介质属性的关系. 左雷等^[9]研究了不同海底介质下浅海海底地震波的传播机理, 分析了硬质/软质海底条件下这种波的存在条件及其波动成分, 给出了质点的位移分布和运动轨迹.
以上研究主要在频域内进行, 通过计算地震波场的传播损失和频率特性曲线获取海底地震波的传播特性, 但频域内的计算不能直观地区分海底地震波中纵波、横波和表面波等波动成分. 时域的场量波场快照能比较直观地显示海底地震波的传播及波动成分组成, 而且时域波形也能为计算波场中各成分的传播速度提供有效途径^[10]. 因此, 有必要在时域对低频点声源激发的海底地震波进行波形的数值计算, 以便更直观地掌握在复杂海洋环境中海底地震波的波动特征和传播规律.
卢再华等^[11]基于有限元数值计算模型, 对二维半无限空间层状海洋环境极低频点声源作用下的海底地震波进行了数值模拟, 得到了远场海底表面处加速度和水压的时域信号. 卢再华等^[12]基于多孔介质波动理论建立了海底地震波的三维交错网格有限差分算法, 计算了浅海厚沉积层环境下多孔介质低频声源激励的海底地震波. 任波等^[13]采用有限元软件ANSYS/LS-DYNA, 对简单水平分层海洋环境下的海底地震波进行了数值模拟, 并分析了基岩介质下海底地震波在液-固界面产生的Scholte波的特性和传播规律. 但是这些时域海底地震波的研究都仅限于水平分层的情况, 而实际的海底地质条件比较复杂^[14], 多数为不均匀厚度分层的楔形或倾斜海底环境, 有时海底还存在不规则洼地或台地^[15,16], 上述研究尚未考虑这些比较复杂的实际海底环境.
本文在考虑倾斜、隆起等非水平海底模型的情形下, 对复杂海洋环境下的低频地震波进行时域数值模拟与分析, 重点研究Scholte波在该海洋环境下的传播. 计算过程中采用时间2阶精度、空间10阶精度的交错网格有限差分方法^[17,18], 同时结合在液-固介质长时间模拟中具有独特稳定性优势的多轴完全匹配层(MPML)边界条件^[19,20], 并对计算得到的声场时域合成波形进行分析, 以进一步明确复杂海洋环境下海底地震波的传播特性, 评价海洋环境对Scholte界面波信号的影响.

以波动理论为基础, 建立平面直角坐标系, 采用一阶速度-应力形式的弹性波方程描述二维液-固多层半无限空间海洋环境模型. 在交错网格中, 利用空间10阶、时间2阶精度的有限差分算子对该弹性波方程进行求解. 同时, 由于计算区域是有限的, 在波场模拟中采用MPML作为吸收边界条件^[21], 以压制截断边界造成的人工反射, 同时能够保证长时间数值模拟的稳定性^[22].
2

-->

2.1.波动方程及其有限差分

在直角坐标系中, 设海水层表面位于x轴, H为海水深度, $0 \leqslant z \leqslant {{H}}$的区域为海水介质, $z > {{H}}$的半无限区域为弹性海底介质. 对于二维液-固多层半无限空间海洋环境模型, 其场量满足如下所示的一阶速度-应力形式的二维弹性波方程(假定体力为零):

$ \left\{ {\begin{aligned}& {\frac{{\partial {\tau _{xx}}}}{{\partial t}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {v_x}}}{{\partial x}} + \lambda \frac{{\partial {v_z}}}{{\partial z}}} \\ &{\frac{{\partial {\tau _{zz}}}}{{\partial t}} = \lambda \frac{{\partial {v_x}}}{{\partial x}} + \left( {\lambda + 2\mu } \right)\frac{{\partial {v_z}}}{{\partial z}}} \\ &{\frac{{\partial {\tau _{xz}}}}{{\partial t}} = \mu \left( {\frac{{\partial {v_z}}}{{\partial x}} + \frac{{\partial {v_x}}}{{\partial z}}} \right)} \\ &{\frac{{\partial {v_x}}}{{\partial t}} = {b_x}\left( {\frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right)} \\ & {\frac{{\partial {v_z}}}{{\partial t}} = {b_z}\left( {\frac{{\partial {\tau _{xz}}}}{{\partial x}} + \frac{{\partial {\tau _{zz}}}}{{\partial z}}} \right)} ,\end{aligned}} \right. $

其中, x和z分别为水平方向和垂直深度方向, ${v_x}$和${v_z}$为x和z方向的速度, ${\tau _{xx}}$和${\tau _{zz}}$为正应力, ${\tau _{xz}}$为剪应力, $\lambda $和$\mu $为拉梅系数, ${b_x}$和${b_z}$表示密度的倒数.
震源采用雷克子波, 波形函数为 $f(t) = \big[ 1 - $$ 2{{( {{\text{π }}{f_{\text{p}}}t})}^2} \big]\exp \big[ { - {{\left( {{\text{π }}{f_{\text{p}}}t} \right)}^2}} \big]$, 其中${f_p}$为峰值频率. 数值计算时仅考虑单频简谐声源, 对于海底地震波包含的多个频率成分, 可由不同频率的简谐声源结果叠加而成.
研究采用董良国提出的交错网格高阶差分格式进行网格的离散剖分, 采用空间2L阶、时间二阶精度差分格式时, 方程(1)对应的离散格式为

$ \left\{ \begin{aligned} &\tau _{xx,i,j}^{k + \tfrac{1}{2}} = \tau _{xx,i,j}^{k - \tfrac{1}{2}} + \Delta t\left[ {{{\left( {\lambda + 2\mu } \right)}_{i,j}}D_{x,i,j}^{{L_x}}v_x^k + {\lambda _{i,j}}D_{z,i,j}^{{L_z}}v_z^k} \right], \\ &\tau _{zz,i,j}^{k + \tfrac{1}{2}} = \tau _{zz,i,j}^{k - \tfrac{1}{2}} + \Delta t\left[ {{\lambda _{i,j}}D_{x,i,j}^{{L_x}}v_x^k + {{\left( {\lambda + 2\mu } \right)}_{i,j}}D_{z,i,j}^{{L_z}}v_z^k} \right], \\& \tau _{xz,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k + \tfrac{1}{2}} = \tau _{xz,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k - \tfrac{1}{2}} + \Delta t\mu _{i + \tfrac{1}{2},j + \tfrac{1}{2}}^ * \left[ {D_{x,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{{L_x}}v_z^k + D_{z,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{{L_z}}v_x^k} \right], \\ &v_{x,i + \tfrac{1}{2},j}^{k + 1} = v_{x,i + \tfrac{1}{2},j}^k + {b_{x,i + \tfrac{1}{2},j}}\Delta t\left( {D_{x,i + \tfrac{1}{2},j}^{{L_x}}\tau _{xx}^{k + \tfrac{1}{2}} + D_{z,i + \tfrac{1}{2},j}^{{L_z}}\tau _{xz}^{k + \tfrac{1}{2}}} \right), \\ &v_{z,i,j + \tfrac{1}{2}}^{k + 1} = v_{z,i,j + \tfrac{1}{2}}^k + {b_{z,i,j + \tfrac{1}{2}}}\Delta t\left( {D_{x,i,j + \tfrac{1}{2}}^{{L_x}}\tau _{xz}^{k + \tfrac{1}{2}} + D_{z,i,j + \tfrac{1}{2}}^{{L_z}}\tau _{zz}^{k + \tfrac{1}{2}}} \right) ,\end{aligned} \right. $

其中, $i$和$j$分别为x和z方向的空间网格位置, $k$为时间层位置, $\Delta t$为时间步长. $D_{x, i + \tfrac{1}{2}, j}^{{L_x}}\tau _{xx}^{k + \tfrac{1}{2}} = $$ { {\dfrac{{\partial \tau _{xx}^{k + \tfrac{1}{2}}}}{{\partial x}}} \Bigg|_{i + \tfrac{1}{2}, j}}$和$D_{z, i, j}^{{L_z}}v_z^k = {\left. {\dfrac{{\partial v_z^k}}{{\partial z}}} \right|_{i, j}}$分别表示变量$ \tau _{xx}^{k + \tfrac{1}{2}} $和$ v_z^k $在x和z方向上空间一阶偏导数的$2{L_x}$和$2{L_z}$阶精度交错网格有限差分格式, ${L_x}$和${L_z}$为差分算子长度, 差分格式满足:

$D_{x,i + \tfrac{1}{2},j}^{{L_x}}\tau _{xx}^{k + \tfrac{1}{2}} \approx \dfrac1{{{\Delta x}}}{{\displaystyle \sum\limits_{m = 1}^{{L_x}} {{a_m}\left[ {\tau _{xx}^{k + \tfrac{1}{2}}\left( {i + m,j} \right) - \tau _{xx}^{k + \tfrac{1}{2}}\left( {i - \left( {m - 1} \right),j} \right)} \right]} }} \text{, } $

$ D_{z,i,j}^{{L_z}}v_z^k \approx \frac1{{\Delta z}} {{\displaystyle \sum\limits_{m = 1}^{{L_z}} {{a_m}\left[ {v_z^k\left( {i,j + \dfrac{{2m - 1}}{2}} \right) - v_z^k\left( {i,j - \dfrac{{2m - 1}}{2}} \right)} \right]} }} \text{, } $

其中, ${a_m}$为$2 L$阶空间差分精度的差分系数, 且

$ {a_m} = \dfrac{{{{\left( { - 1} \right)}^{m + 1}}}}{{2 m - 1}} \displaystyle\prod\limits_{i = 1, i \ne m}^L \Bigg| {\dfrac{{{{\left( {2 i - 1} \right)}^2}}}{{{{\left( {2 m - 1} \right)}^2} - {{\left( {2 i - 1} \right)}^2}}}}\Bigg|. $

当使用时间二阶、空间十阶差分格式时, 在最短波长达到6个网格以上时可以保证在地震波采集时间内不会发生频散^[18].
2 -->

2.2.自由边界条件

在自由表面上, 应力必须满足自由表面边界条件, 即所有应力分量为0. 本文采用Zeng等^[23]改进的真空法, 即对$\mu $, ${b_x}$, ${b_z}$等参数作如下设置:

$\begin{split} & \mu _{i + \tfrac{1}{2},j + \tfrac{1}{2}}^ * = \\& \left\{ \begin{aligned} &{\left[ {\dfrac{1}{4}\left( {\dfrac{1}{{{\mu _{i,j}}}} + \dfrac{1}{{{\mu _{i + 1,j}}}} + \dfrac{1}{{{\mu _{i,j + 1}}}} + \dfrac{1}{{{\mu _{i + 1,j + 1}}}}} \right)} \right]^{ - 1}}, \\ &\qquad {{\mu _{i,j}}{\mu _{i + 1,j}}{\mu _{i,j + 1}}{\mu _{i + 1,j + 1}} \ne 0} ,\\ & 0 , \quad {\text{otherwise}},\;\;\;\quad \qquad\qquad\qquad\qquad\end{aligned} \right. \end{split}$

$ {b_{x,i + \tfrac{1}{2},j}} = \left\{ \begin{aligned}& \frac{2}{{{\rho _{i + 1,j}} + {\rho _{i,j}}}} , & {{\rho _{i + 1,j}} \ne 0{\text{ or }}{\rho _{i,j}} \ne 0} ,\\ &0 , & {{\rho _{i + 1,j}} = 0{\text{ , }}{\rho _{i,j}} = 0} , \;\;\end{aligned} \right. $

$ {b_{z,i,j + \tfrac{1}{2}}} = \left\{ \begin{aligned} &\frac{2}{{{\rho _{i,j}} + {\rho _{i,j + 1}}}} ,& {{\rho _{i,j + 1}} \ne 0{\text{ or }}{\rho _{i,j}} \ne 0} ,\\ & 0 , & {{\rho _{i,j + 1}} = 0{\text{ , }}{\rho _{i,j}} = 0} .\end{aligned} \right. $

通过(5)式—(7)式保证了模型上边界处自由边界条件的实现. 而且通过该方法, 在海水与海底交界处, 对应的液-固界面处剪应力为零的边界条件也能自动实现.
2 -->

2.3.吸收边界条件

在波场模拟中由于计算区域是有限的, 为了压制截断边界造成的人工边界反射, 本文采用MPML作为吸收边界条件. 该边界条件作为传统PML边界条件的扩展, 在多个正交方向同时引入衰减因子, 通过调整不同方向衰减因子的比例系数达到改善MPML稳定性的目的. 以x方向为例, 传统的PML方程中, 只有一个衰减因子是空间变量x的函数, 即

$ {d_x} = {d_x}\left( x \right), \;\; {d_y} = 0,\;\; {d_z} = 0 $

而在MPML中, 3个正交方向上的衰减因子同为坐标x的函数, 即

$ {d_x} = d_x^{\left( x \right)}\left( x \right),\;\;{d_y} = d_y^{\left( x \right)}\left( x \right),\;\;{d_z} = d_z^{\left( x \right)}\left( x \right) $

其中, $d_y^{( x )}( x ) = {p^{( {y/x} )}}d_x^{( x )}( x)$, $d_z^{( x )}( x ) = {p^{( {z/x} )}}d_x^{( x )}( x)$, $ {\kern 1 pt} {p^{\left( {y/x} \right)}} $和$ {p^{\left( {z/x} \right)}} $分别为y, z方向衰减因子的比例系数, 通过调整该系数可达到改善计算结果稳定性的目的^[19].
时间域的分裂式MPML方程表达式如下:

$ \left\{ \begin{aligned} &{\partial _t} + {d_x}{\tau _{xxx}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {v_x}}}{{\partial x}}, \hfill \\& {\partial _t} + {d_z}{\tau _{xxz}} = \lambda \frac{{\partial {v_z}}}{{\partial z}} ,\end{aligned} \right. $

$ \left\{ \begin{aligned} &{\partial _t} + {d_x}{\tau _{zzx}} = \lambda \frac{{\partial {v_x}}}{{\partial x}}, \hfill \\ &{\partial _t} + {d_z}{\tau _{zzz}} = \left( {\lambda + 2\mu } \right)\frac{{\partial {v_z}}}{{\partial z}} , \end{aligned} \right. $

$ \left\{ \begin{aligned} &{\partial _t} + {d_x}{\tau _{xzx}} = \mu \frac{{\partial {v_z}}}{{\partial x}}, \qquad\quad \hfill \\& {\partial _t} + {d_z}{\tau _{xzz}} = \mu \frac{{\partial {v_x}}}{{\partial z}}, \qquad\quad\end{aligned} \right. $

$ \left\{ \begin{aligned} &{\partial _t} + {d_x}{v_{xx}} = {b_x}\frac{{\partial {\tau _{xx}}}}{{\partial x}}, \hfill \\ &{\partial _t} + {d_z}{v_{xz}} = {b_x}\frac{{\partial {\tau _{xz}}}}{{\partial z}}, \end{aligned} \right. $

$ \left\{ \begin{aligned} &{\partial _t} + {d_x}{v_{zx}} = {b_z}\frac{{\partial {\tau _{xz}}}}{{\partial x}}, \\& {\partial _t} + {d_z}{v_{zz}} = {b_z}\frac{{\partial {\tau _{zz}}}}{{\partial z}},\end{aligned} \right. $

其中:

$ {\kern 1pt} {\kern 1pt} {d_x} = d_x^{\left( x \right)}\left( x \right) + d_x^{\left( z \right)}\left( z \right) , $

$ {\kern 1pt} {\kern 1pt} {d_z} = d_z^{\left( x \right)}\left( x \right) + d_z^{\left( z \right)}\left( z \right) . $

当比例系数均为零时, MPML方程(10)—(14)退化为传统的PML形式. 在高泊松比介质中, MPML能保证数值模拟的稳定性.
同样地, 采用空间2L阶精度、时间2阶精度的有限差分方法对上述二维分裂式MPML方程求解, 表达式如下:

$ \left\{ \begin{aligned} &\tau _{xxx,i,j}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_x}}}\left[ {\left( {1 - 0.5dt{d_x}} \right)\tau _{xxx,i,j}^{k - \tfrac{1}{2}} + dt{{\left( {\lambda + 2\mu } \right)}_{i,j}}D_{x,i,j}^{}v_x^k} \right],\qquad\qquad~~ \hfill \\ &\tau _{xxz,i,j}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_z}}}\left[ {\left( {1 - 0.5dt{d_z}} \right)\tau _{xxz,i,j}^{k - \tfrac{1}{2}} + dt{\lambda _{i,j}}D_{z,i,j}^{}v_z^k} \right], ~~ \qquad\qquad\end{aligned} \right. $

$ \left\{ \begin{aligned} &\tau _{zzx,i,j}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_x}}}\left[ {\left( {1 - 0.5dt{d_x}} \right)\tau _{zzx,i,j}^{k - \tfrac{1}{2}} + dt{\lambda _{i,j}}D_{x,i,j}^{}v_x^k} \right],\qquad\qquad ~~\hfill \\& \tau _{zzz,i,j}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_z}}}\left[ {\left( {1 - 0.5dt{d_z}} \right)\tau _{zzz,i,j}^{k - \tfrac{1}{2}} + dt{{\left( {\lambda + 2\mu } \right)}_{i,j}}D_{z,i,j}^{}v_z^k} \right] ,\qquad\qquad~~\end{aligned} \right. $

$ \left\{ \begin{aligned}& \tau _{xzx,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_x}}}\left[ {\left( {1 - 0.5dt{d_x}} \right)\tau _{xzx,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k + \tfrac{1}{2}} + dt\mu _{i + \tfrac{1}{2},j + \tfrac{1}{2}}^ * D_{x,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{}v_z^k} \right],\hfill \\ &\tau _{xzz,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k + \tfrac{1}{2}} = \frac{1}{{1 + 0.5dt{d_z}}}\left[ {\left( {1 - 0.5dt{d_z}} \right)\tau _{xzz,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{k + \tfrac{1}{2}} + dt\mu _{i + \tfrac{1}{2},j + \tfrac{1}{2}}^ * D_{z,i + \tfrac{1}{2},j + \tfrac{1}{2}}^{}v_x^k} \right] , \end{aligned} \right. $

$ \left\{ \begin{aligned}& v_{xx,i + \tfrac{1}{2},j}^{k + 1} = \frac{1}{{1 + 0.5dt{d_x}}}\left[ {\left( {1 - 0.5dt{d_x}} \right)v_{xx,i + \tfrac{1}{2},j}^{k + 1} + dt{b_{x,i + \tfrac{1}{2},j}}D_{x,i + \tfrac{1}{2},j}^{}\tau _{xx}^{k + \tfrac{1}{2}}} \right],\qquad\quad \hfill \\& v_{xz,i + \tfrac{1}{2},j}^{k + 1} = \frac{1}{{1 + 0.5dt{d_z}}}\left[ {\left( {1 - 0.5dt{d_z}} \right)v_{xz,i + \tfrac{1}{2},j}^{k + 1} + dt{b_{x,i + \tfrac{1}{2},j}}D_{z,i + \tfrac{1}{2},j}^{}\tau _{xz}^{k + \tfrac{1}{2}}} \right] ,\qquad\quad\end{aligned} \right. $

$ \left\{ \begin{aligned} &v_{zx,i,j + \tfrac{1}{2}}^{k + 1} = \frac{1}{{1 + 0.5dt{d_x}}}\left[ {\left( {1 - 0.5dt{d_x}} \right)v_{zx,i,j + \tfrac{1}{2}}^{k + 1} + dt{b_{z,i,j + \tfrac{1}{2}}}D_{x,i,j + \tfrac{1}{2}}^{}\tau _{xz}^{k + \tfrac{1}{2}}} \right],\qquad\quad \hfill \\ &v_{zz,i,j + \tfrac{1}{2}}^{k + 1} = \frac{1}{{1 + 0.5dt{d_z}}}\left[ {\left( {1 - 0.5dt{d_z}} \right)v_{zz,i,j + \tfrac{1}{2}}^{k + 1} + dt{b_{z,i,j + \tfrac{1}{2}}}D_{z,i,j + \tfrac{1}{2}}^{}\tau _{zz}^{k + \tfrac{1}{2}}} \right], \qquad\quad\end{aligned} \right. $

设计了横向距离较大的两层介质模型, 分别采用不同的空间差分精度(4阶和10阶)以及PML和MPML边界条件进行该模型中声场传播计算, 对比验证空间高阶精度方法抑制频散的能力以及MPML边界条件在稳定性方面的优势.
2

-->

3.1.模型介绍

计算采用的模型为横向狭长结构, 横向距离为10 km, 纵向深度为150 m. 为了更加清楚地展示该模型结构, 仅显示了横向距离为500 m的情形, 如图1所示, 模型上层为海水介质, 纵横波速度分别为v_p1 = 1500 m/s, v_s1 = 0, 海水深度为50 m; 下层为半无限空间, 纵横波速度分别为v_p2 = 3200 m/s, v_s2 = 1800 m/s, 厚度100 m. 计算时所用的网格大小为d_x = 2 m, d_z = 1 m, 时间步长为0.2 ms, 时间长度为10 s. 震源子波主频为50.0 Hz, 其位置坐标为(10 m, 45 m) (图1中红色星形), 分别在10 m, 30 m, 45 m, 50 m(海水与海底分界面), 55 m, 70 m等深度处布置接收点(图1中红色倒三角).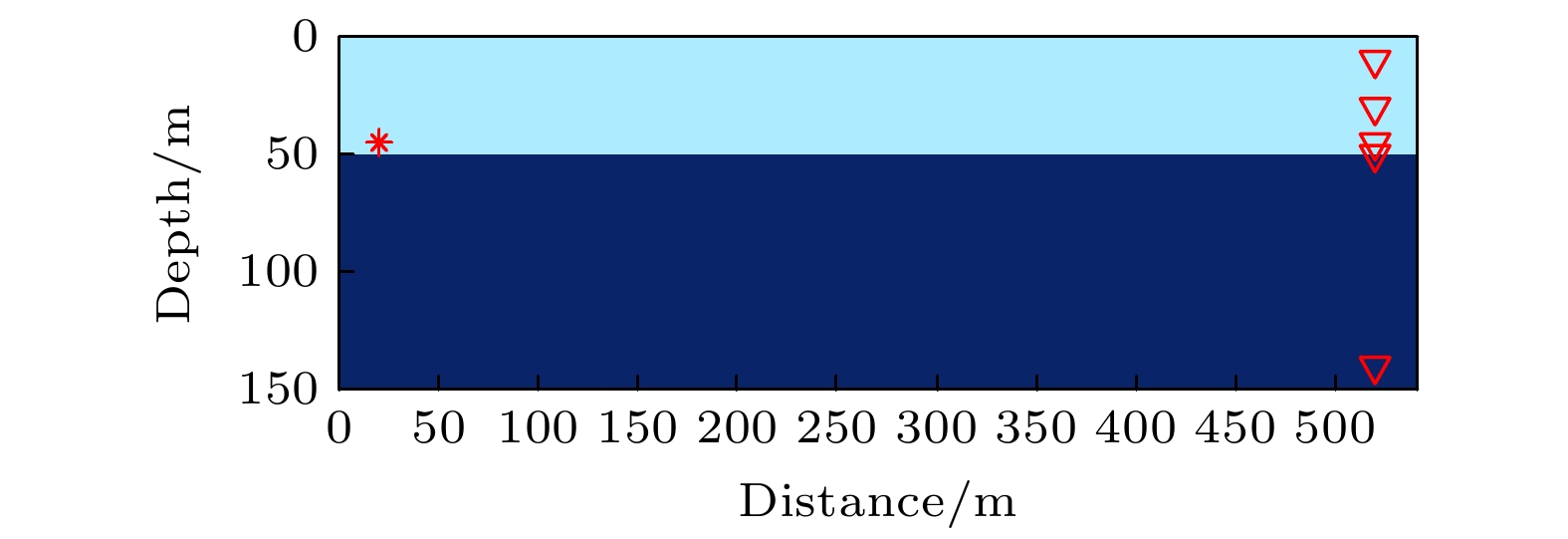
图 1 半无限空间海洋环境模型
Figure1. Ocean enviroment model with infinite half-space.

2 -->

3.2.空间4阶和10阶差分精度数值计算对比

首先, 采用空间4阶精度的有限差分方法对该半无限空间模型进行计算, 横向5000 m、深度50 m处接收到的波形记录及时频分析结果如图2所示. 从时域波形记录可以看出, 在记录的结尾出现了波形抖动, 而且时频分析结果中, Scholte波所在的能量集中区域也有频散现象, 这与Scholte波在高频段非频散的特性是相悖的.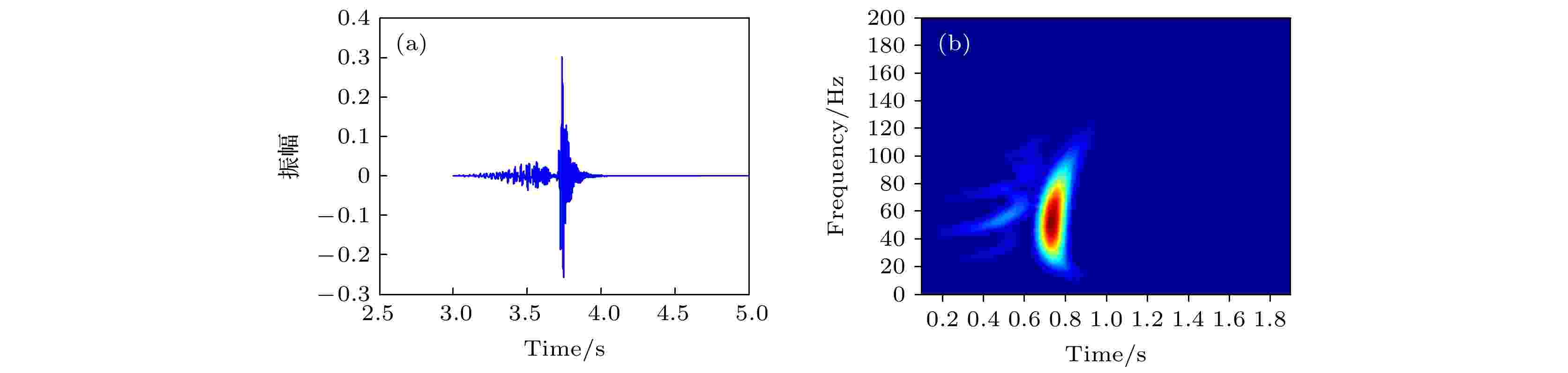
图 2 空间4阶精度的波形记录和时频分析结果　(a)时域波形; (b)时频分析
Figure2. Seismogram and frequency domain result by method with 4 th order spatial accuracy: (a) Time domain waveform; (b) Time-frequency analysis.

保持空间网格大小不变, 将时间步长改变为dt = 0.1 ms或0.05 ms, 对模型重新计算, 图3给出了计算的结果, 从图中可以看出, 频散的现象仍然存在.
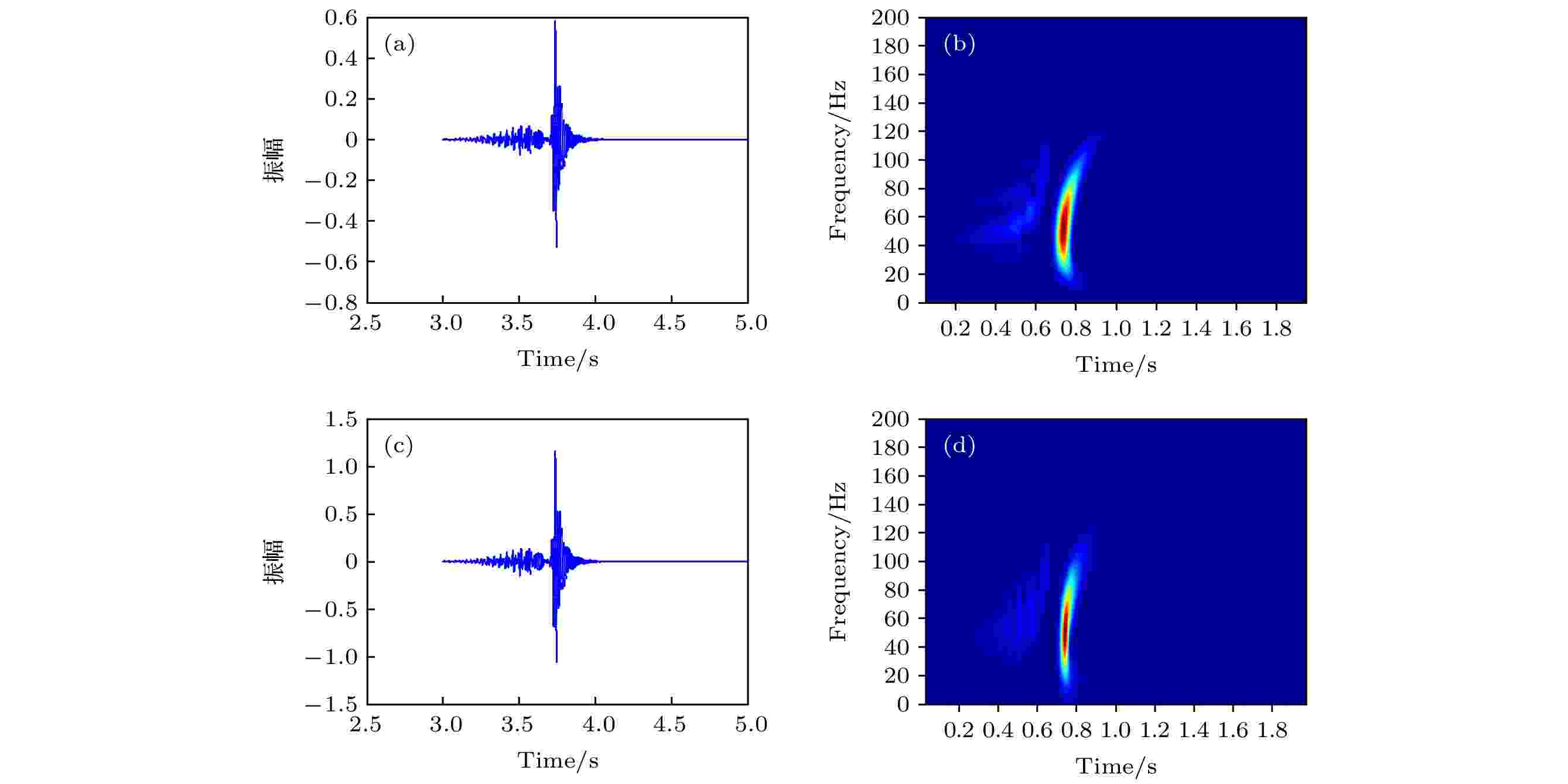图 3 源距5 km深度为50 m的波形记录和频域结果　(a)时域波形, 时间步长为0.1 ms; (b)时频分析, 时间步长为0.1 ms; (c)时域波形, 时间步长为0.05 ms; (d)时频分析, 时间步长为0.05 ms
Figure3. Seismogram and frequency domain result of offset 5 km and depth 50 m: (a) Time domain waveform, time step is 0.1 ms; (b) Time-frequency analysis, time step is 0.1 ms; (c) Time Domain waveform, time step is 0.05 ms; (d) Time-frequency analysis, time step is 0.05 ms.

尝试改变空间网格大小之后, 设置d_x = 1.0 m, d_z = 1.0 m, 图4展示了重新计算后的模拟结果, 从图中可以看出, 时域波形末端干净清晰, 之前波形中的“尾巴”消失, 而频域分析中高频段的频散现象也得到了很好地控制, 模拟结果更加符合Scholte波的频散特性. 总结以上不同参数的计算结果可以发现, 空间网格的减小而非时间步长的减小对高频频散的改善起到了关键的作用, 因此, 该频散现象主要归根于空间网格离散, 可定性为空间离散造成的数值频散, 而该频散问题可通过提高空间差分精度来解决.
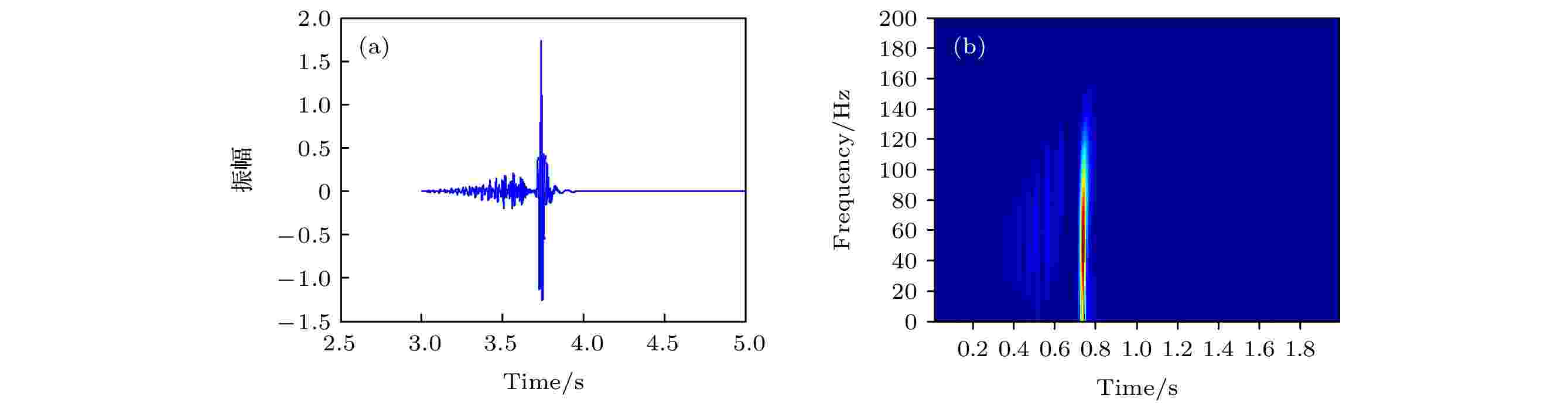图 4 源距5 km深度为50 m的波形记录和频域结果, 空间网格大小为1 m　(a)时域波形; (b)时频分析
Figure4. Seismogram and frequency domain result of offset 5 km and depth 50 m, with spatial interval 1 m: (a) Time domain waveform; (b) Time-frequency analysis.

采用空间高阶(取2L = 10)精度差分算法对半无限空间模型重新计算, 其余参数保持不变, 图5给出了空间10阶精度计算结果, 从图中可以看出, 空间10阶精度计算的时域波形更加干净清晰, 无数值频散造成的“尾巴”, 时频分析的结果也表明采用空间高阶差分, Scholte波的高频频散现象也得到了较好的控制.
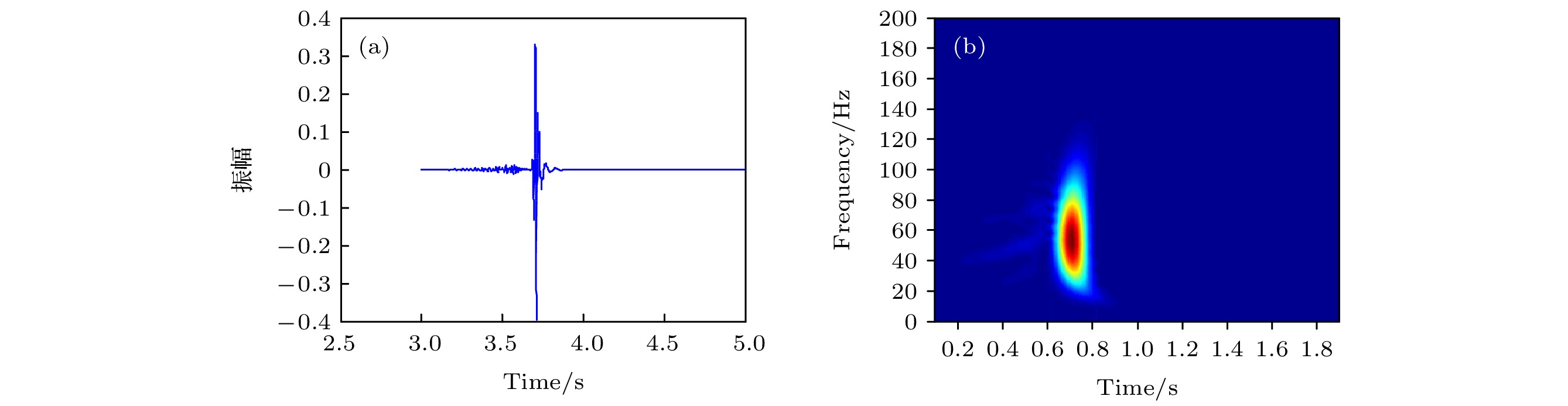图 5 空间10阶精度的波形记录和频域结果　(a)时域波形; (b)时频分析
Figure5. Seismogram and frequency domain result by method with 10 th order spatial accuracy: (a) Time domain waveform; (b) Time-frequency analysis.

2 -->

3.3.PML与MPML边界条件

当交错网格差分方法的精度和参数设置不变, 只改变边界条件, 图6给出了分别采用PML和MPML边界条件时, 在50 m深度处接收到的不同横向位置的时域波形. 从图6可以看出, 在模拟时间较长时(时间长度40 s), 采用PML作为边界条件, 数值模拟出现了不稳定现象, 表现为波形幅值特别大, 掩盖了真实的波形信号, 导致数值计算失败. 采用MPML替代传统的PML, 不稳定现象得到控制, 因此MPML有助于改善长时间数值模拟的稳定性.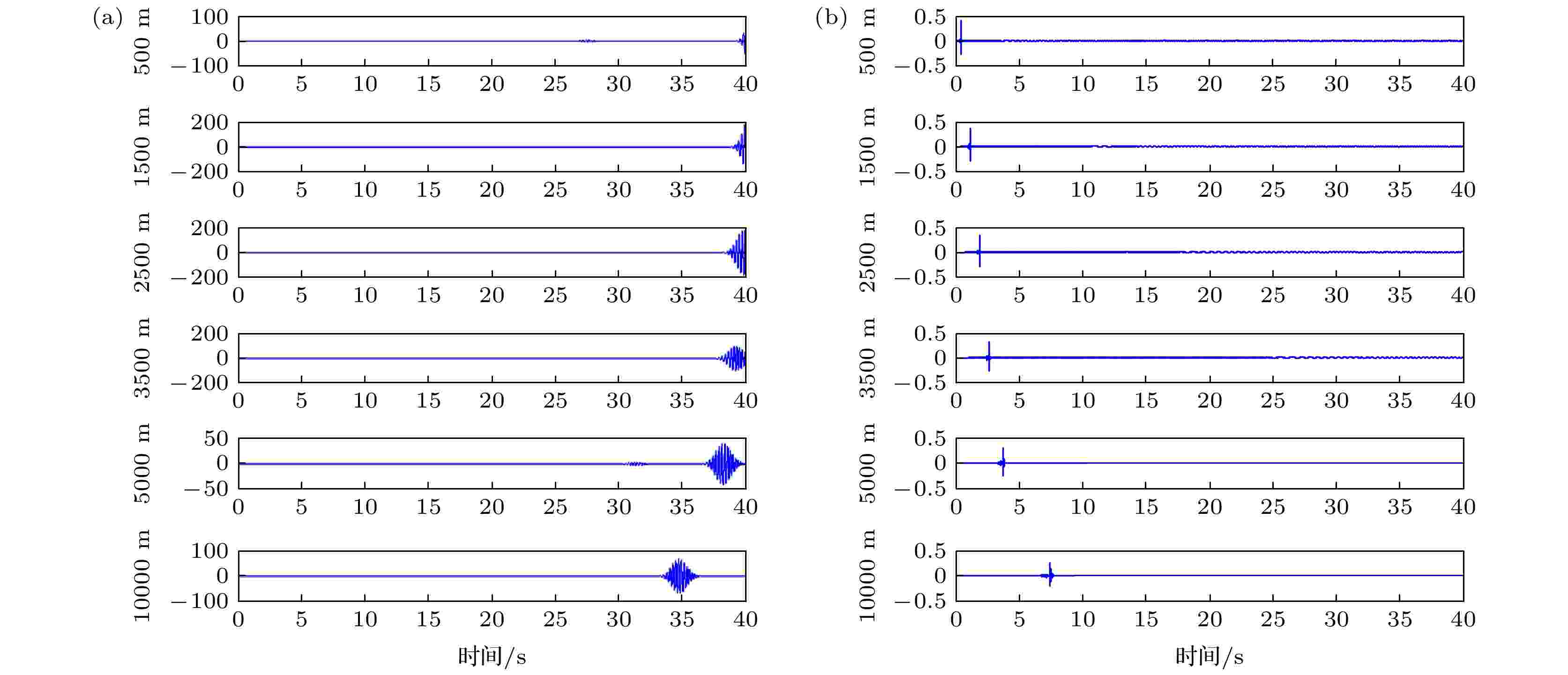
图 6 深度50 m处的接收记录　(a) PML; (b) MPML
Figure6. Record at depth 50 m: (a) PML; (b) MPML.

2

-->

4.1.模型介绍

设计了含倾斜构造与隆起的复杂海底模型, 以考察倾斜构造及隆起对Scholte波产生及接收的影响, 尤其是海底隆起是否更有利于Scholte波的接收. 模型最大横向距离为50 km, 整体速度模型如图7(a)所示, 其中, 在横向5—35 km处有倾角3°左右的倾斜构造, 在41—44 km处有海底隆起穿透软泥层一直向上延伸到海水层底界面(隆起构造放大显示见图7(a)). 模型自上而下有四层介质组成, 各层介质的弹性参数见表1, 其中由于非水平界面的存在, 各层介质的厚度仅给出了对应的范围. 海水层声速随深度呈分段线性变化, 在水面处声速为1540 m/s然后线性减小, 到1000 m深度处达到最低值1480 m/s, 然后海水声速线性增大, 到2000 m深度处达到1490 m/s, 对应的声速曲线见图7(b).
图 7 复杂海底模型　(a) 模型及隆起构造放大显示; (b)海水层声速曲线
Figure7. Model with complex seafloor topography: (a) Whole model and zoomed display of uplift structure; (b) Sound speed profile of sea water.

层	纵波速度 Vp/(${\text{m} }/{ {\text{s} }}$)	横波速度 Vs/(${\text{m} }/{ {\text{s} }^{} }$)	密度 ρ/(${\text{kg} }/{ {\text{m} }^{3} }$)	厚度 d/m
海水	1480—1540	0	1000	100—1600
软泥	1600	0	1750	0—10
海底 基岩1	3200	1800	1850	100—110
海底 基岩2	4000	2000	2000	∞

表1含倾斜与隆起的模型参数
Table1.Parameters of model including slope and uplift

仿真计算时, 接收点沿3个非水平界面(如图7(a)中白色虚线所示)布置, 分别是海水与软泥层分界面(简记为界面1)、软泥层与海底基岩1分界面(隆起处稍有不同, 简记为界面2)、海底两层基岩之间分界面(简记为界面3), 模型整个横向范围每隔1 km间距设置接收点, 如图7(a)中白色倒三角所示. 由于该模型横向距离远大于深度, 为了提高计算效率, 在横向和纵向设置不同的网格间距, 计算时采用的网格大小为d_x = 5.0 m, d_z = 1.0 m, 所用Ricker子波的主频为15.0 Hz.
2 -->

4.2.数值结果与分析

(1)倾斜构造下两种激发-接收模式对比
在倾斜构造存在的情况下, 首先测试震源位置不同对Scholte波接收的影响, 以确定有利的震源激发位置. 设计了两种激发模式: 1)在模型最左侧界面1上方50 m深度处激发, 即激发-接收沿倾斜界面下倾方向; 2)在模型最右侧界面1上方50 m深度处激发, 即激发-接收沿倾斜界面上倾方向. 接收记录总长度为40 s.
图8展示了两种激发模式下不同界面处接收到的波形记录, 其中图8左栏(图8(a), 图8(c), 图8(e))、右栏(图8(b), 图8(d), 图8(f))分别对应震源在模型左、右侧的情形. 对比相同界面处, 左栏中的波场幅值均小于右栏中波场幅值, 说明震源设置在模型右侧更有利于接收到幅值较强的声场信号, 有助于更好地观察与分析Scholte波的传播.
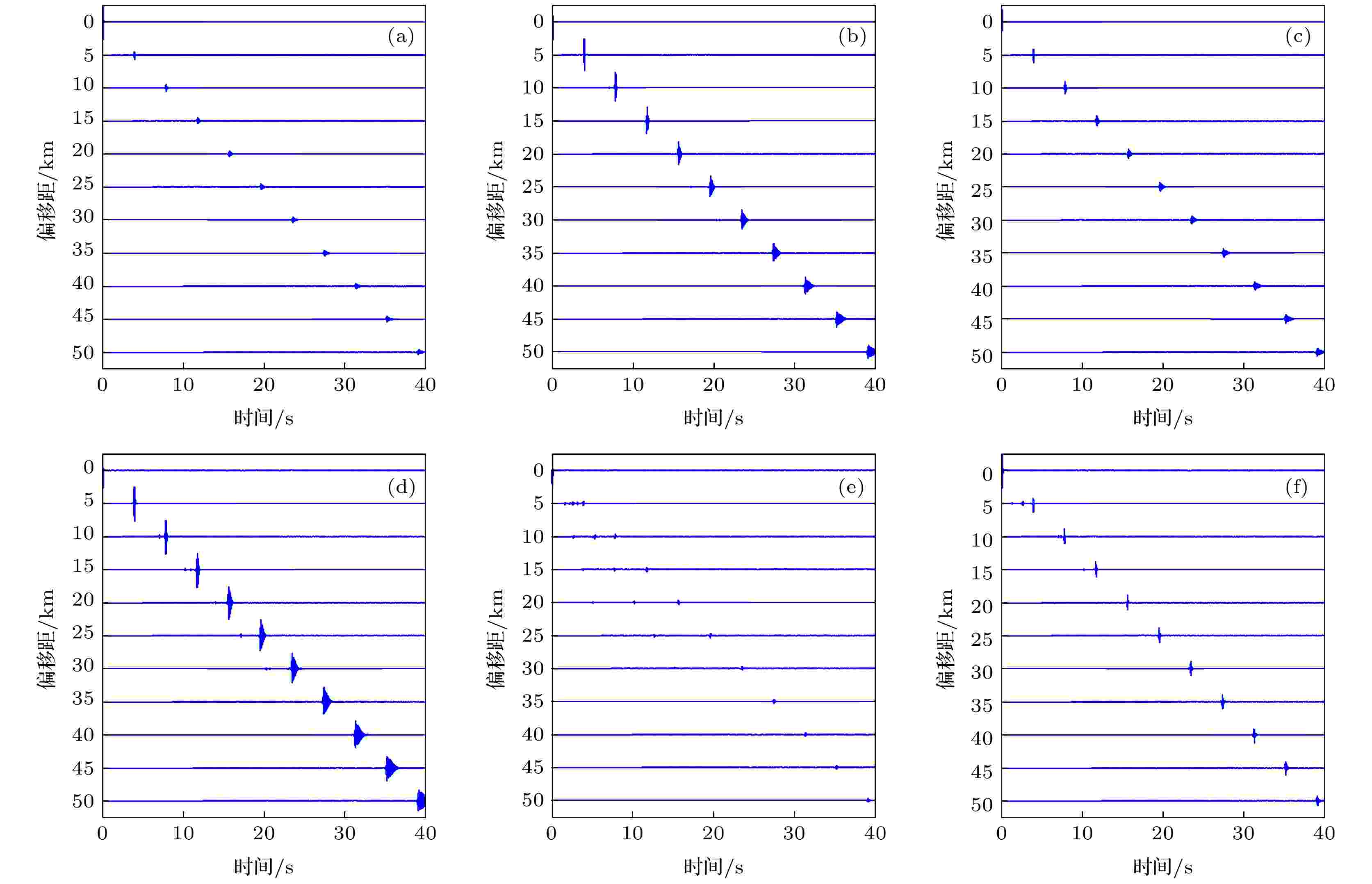图 8 不同界面处的接收记录　(a) 界面1, 震源在左; (b) 界面1, 震源在右; (c) 界面2, 震源在左; (d) 界面2, 震源在右; (e) 界面3, 震源在左; (f) 界面3, 震源在右
Figure8. Records at different interfaces: (a) Interface 1, the source is on the left; (b) Interface 1, the source is on the right; (c) Interface 2, the source is on the left; (d) Interface 2, the source is on the right; (e) Interface 3, the source is on the left; (f) Interface 3, the source is on the right.

另外, 观察每种激发方式中不同界面处接收到的波形记录, 可以看出, 每个深度处都可以接收到横波、纵波等到时较早的波形, 而Scholte波在界面2处接收到的波形幅值最大, 界面1、界面3两个深度的信号幅值略小. 可见, Scholte波在界面2(液-固界面)产生, 即海底基岩上表面处, 向上和向下传播10 m离开界面后Scholte波的幅值迅速减小; 而且, 观察同一深度不同源距的Scholte波, 可以看到沿横向距离传播, Scholte波幅值没有明显变化, 而体波传播较近的距离之后幅值就衰减较严重, 这与Scholte界面波具有衰减慢、传播距离远等特点是吻合的. 在近源距处, 由于水声反射强度较大, 与此处的Scholte波反射强度差异相对较小, 导致Scholte波在时间或幅值上都不易识别. 而传播较远距离后, 体波衰减大, 此时Scholte波能量相对更高, 更容易与地层中的纵横波反射区分开来. 因此, 远距离接收更有利于Scholte波的检测与识别.
(2)隆起构造对Scholte波传播影响
通过上述仿真与分析得知, 相比声源放置在模型最左侧的情形, 当声源放置在模型右侧界面1上方时, 更有利于声信号接收. 在此基础上, 采用同样的震源位置设置方式, 仿真分析隆起对Scholte波传播的影响. 隆起构造放大显示见图7(a), 其横向范围为41—44 km, 在42—43 km处隆起顶部与软泥沉积层上表面平齐.
仿真时, 震源位置设置在模型最右侧界面1上方20 m深度处, 沿3个非水平界面分别布置接收点, 接收水平间距为1 km, 如图7中白色倒三角所示, 接收排列总水平长度为50 km, 接收记录时间长度为45 s. 由于界面3处接收到的波形幅值较弱, 且该界面是两层海底基岩间的分界面, 对于观察Scholte波传播规律影响较小, 因此, 仅展示了界面1和界面2处各接收点采集的波形记录, 如图9(a)和(b)所示. 由于隆起构造所处横向距离对应偏移距6—9 km, 单独展示了偏移距为0—10 km时界面1和界面2接收到的波形记录, 见图9(c)和9(d), 以便更清晰地观察隆起构造对Scholte波传播的影响.
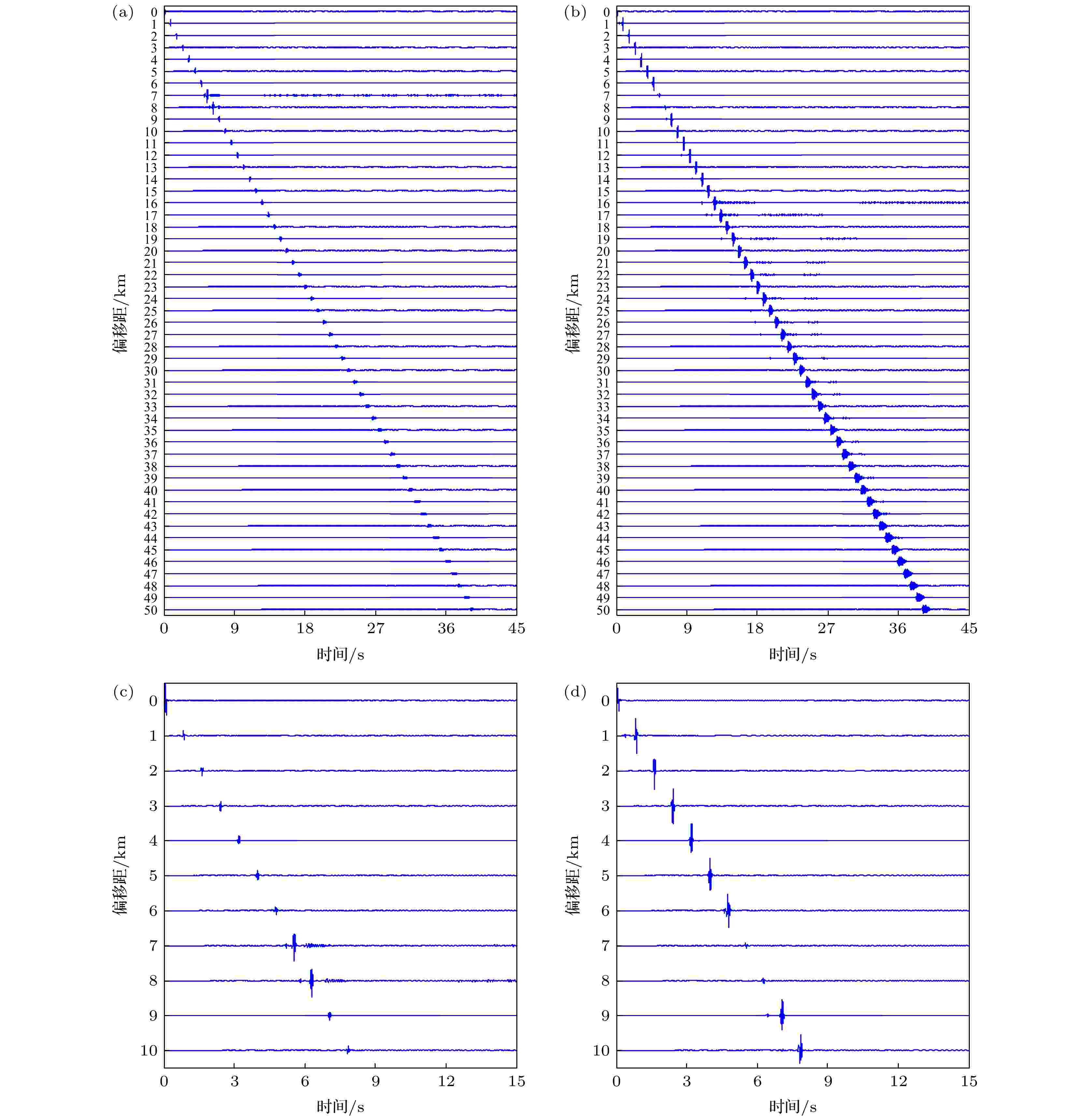图 9 不同界面处的接收记录　(a) 界面1, 偏移距 ≤ 50 km; (b) 界面2, 偏移距 ≤ 50 km; (c) 界面1, 偏移距 ≤ 10 km; (d) 界面2, 偏移距 ≤ 10 km
Figure9. Records at different interfaces: (a) Interface 1, offset ≤ 50 km; (b) Interface 2, offset ≤ 50 km; (c) Interface 1, offset ≤ 10 km; (d) Interface 2, offset ≤ 10 km.

从图9可以看出, 在界面1的接收记录中, 相比其他源距, 源距7 km(对应模型横向距离43 km)和8 km (对应模型横向距离42 km)处的波形幅值显著增大, 而界面2的接收记录中, 以上两个源距处的波形幅值则显著减小.
对模型横向41 km, 42 km, 43 km, 44 km四个位置处(分别对应源距为9 km, 8 km, 7 km, 6 km)接收到的波形局部放大进行分析, 波形图如图10所示.
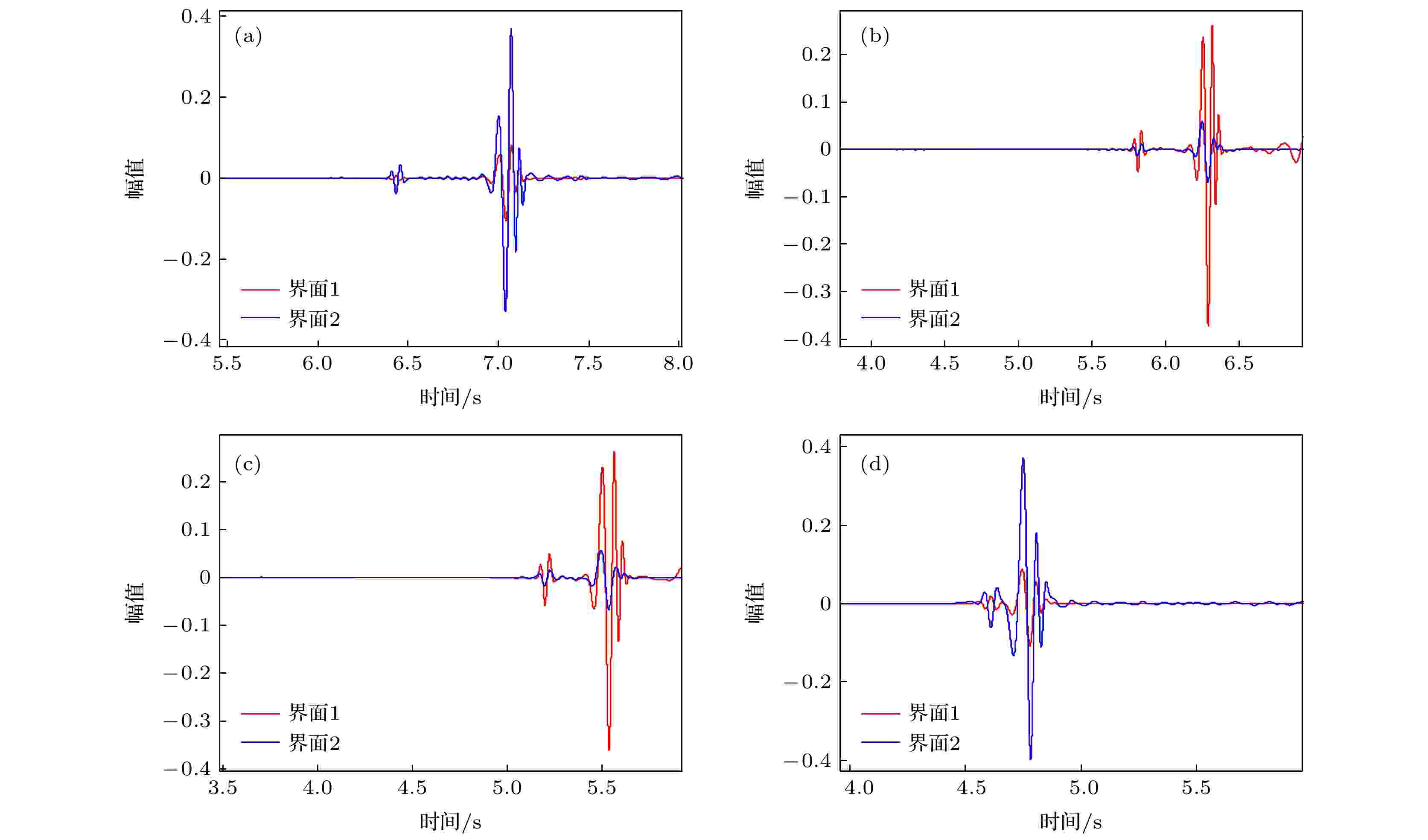图 10 隆起处的波形记录　(a) 偏移距9 km; (b) 偏移距8 km; (c) 偏移距7 km; (d) 偏移距6 km
Figure10. Seismograms at uplit structure: (a) Offset 9 km; (b) Offset 8 km; (c) Offset 7 km; (d) Offset 6 km.

对于不同界面处接收到的记录, 沿着横向传播, 大体上都有两组波形, 第一组到时较早, 该组波形对应海底基岩1中的纵横波、软泥沉积层中的纵波以及海水中的纵波, 随着传播距离增大, 该组波的能量衰减比较迅速; 第二组波形到时较晚, 但能量较为集中. 从图10中可以看出, 横向41 km, 42 km, 43 km, 44 km四个位置处(对应偏移距分别为9 km, 8 km, 7 km, 6 km)能量最强的波形到时分别为6.9 s、6.2 s、5.4 s、4.6 s, 计算出该波形对应的速度大致为1300 m/s, 与Scholte波速度基本一致, 从而可以确定图10中接收到的波形大部分能量为Scholte波.
而且, 41 km和44 km处界面2接收到的信号幅度较大, 42 km和43 km处由于海底沉积层的隆起, 界面1在该横向范围上成为海水与海底基岩的分界面, 取代了界面2成为Scholte波产生的有利位置, 因此在界面1处接收到的Scholte波能量比界面2处更强; 而界面2在此处相当于已离开Scholte波产生的界面一段距离, 因而Scholte波能量迅速衰减, 检测到的信号幅值减小. 在纵向上, Scholte波在海底基岩上表面产生后, 离开界面向上传播后幅值迅速减小; 而沿横向距离传播, 不同源距处的Scholte波幅值变化较小. 这与Scholte波水平和垂直方向衰减特性是相符的.
形象地说, Scholte波到了横向41 km处开始沿着隆起构造传播, 改变了之前的水平传播方向, 到了44 km处, 隆起消失, 波的传播又回到了隆起右侧界面2的水平方向上. 总结来说, 海底基岩隆起有利于在较浅深度接收到Scholte波.

本文借助有限差分方法, 对倾斜与隆起等复杂构造存在时的低频海底地震波进行时域数值模拟与分析, 主要实现了以下的方法:
1)在对远距离海洋模型计算的过程中, 发现当计算时间较长时, 数值模拟容易陷入不稳定的问题. 采用多轴完全匹配层替代传统的PML, 将其应用于低频点源激发的海洋声场模型的数值计算, 解决了远距离低频声场数值模拟不稳定的问题.
2)在低频声场计算过程中采用时间2阶精度、空间高阶精度的交错网格有限差分方法, 改善数值计算中的频散问题.
针对含倾斜与隆起构造的复杂海底模型, 根据仿真计算结果与分析, 可以得出结论:
1)相对于沿倾斜界面下倾方向的激发-接收模式, 沿倾斜界面上倾方向激发-接收更有利于声波的检测;
2)海底基岩的隆起可改变Scholte波的传播方向, 更有利于在较浅深度处接收到Scholte波.