摘要:五边形石墨烯是近年来提出的一种完全由碳五元环组成的新型二维纳米材料. 本文采用分子动力学方法研究了氢基、环氧基和羟基等官能团表面修饰及官能化率对五边形石墨烯力学性能和变形破坏机制的影响以及官能化对升温时五边形石墨烯结构转变的影响规律. 研究发现, 分别引入3种官能基团均可以有效地调控五边形石墨烯的力学性能和变形破坏机制. 五边形石墨烯的杨氏模量和弹性极限均随官能化率的增大先剧烈减小再缓慢增大, 而极限弹性应变单调递增. 低官能化率五边形石墨烯在拉伸载荷下仍然表现出类似于完美五边形石墨烯的塑性变形破坏特征, 不受约束升温时出现碳环结构转变, 临界转变温度高于五边形石墨烯, 而完全官能化可使五边形石墨烯由塑性向脆性变形破坏机制的转变, 升温时五边形石墨烯并未出现碳环结构的转变. 研究结果可为有效调控五边形石墨烯等二维纳米尺度材料的力学性能提供理论基础和结构设计依据.
关键词: 五边形石墨烯/
力学性能/
官能化/
分子动力学

English Abstract

全文HTML

--> --> -->

碳是自然界中最广泛存在的重要元素, 碳原子由于其独特的电子构型和较小的原子半径, 成键与杂化方式灵活多样, 可以形成多种结构和性能迥异的同素异形体. 从古老的石墨、金刚石到新近发现的富勒烯、碳纳米管和石墨烯乃至石墨炔, 探索发现新的碳结构是碳材料研究的热点问题之一. 2014年, 一种新的碳的同素异形体—五边形石墨烯被提出^[1]. 五边形石墨烯完全由碳五元环作为结构基元, 形似于开罗五边形瓷砖, 可以从实验已经合成的三维的T12碳中剥离出来. 不同于仅由sp²杂化碳原子组成的石墨烯, 五边形石墨烯结构的每个单胞中含有2个sp³杂化的碳原子和4个sp²杂化的碳原子, 且碳碳单键和双键并存, 是一种准二维的亚稳态碳结构, 如图1所示. 五边形石墨烯由于其独特的几何构型, 具有与石墨烯非常不同的物理化学特性. 研究表明^[1-3], 与零带隙的石墨烯不同, 五边形石墨烯的带隙为 3.25 eV, 可视为准直接带隙半导体, 五边形石墨烯也表现出优异的热稳定性和力学稳定性, 并且可以承受1000 K的高温. 五边形石墨烯具有罕见的负泊松比特性和与石墨烯媲美的超高力学性能, 表现出良好的可延展性和塑性力学行为. 基于以上特性, 五边形石墨烯有望在光电光伏、纳米力学器件、微机电系统等领域有广阔的应用前景. 然而, 五边形石墨烯的实验合成仍然具有挑战, 其难点不仅在于从其同素异形体中剥离五边形石墨烯比较困难, 而且由于其亚稳态结构, 微量的催化杂质即可使五边形石墨烯重组为六边形石墨烯. 研究表明^[4-7], 五边形石墨烯的电学和物理化学性质具有可调性, 近年来研究人员采用多种方法如吸附、掺杂、缺陷、化学修饰、应变等调控五边形石墨烯的性质^[8-12]. 此外, 适当的化学功能化可以通过部分释放应变来稳定五边形石墨烯的结构, 这为以五边形石墨烯的功能化状态为前驱体的成功合成铺平了道路.
图 1 五边形石墨烯及其官能化几何模型示意图　(a) 五边形石墨烯薄膜的拉伸模型; (b) 完美五边形石墨烯的2×2超晶胞; (c)完全氢化五边形石墨烯的2×2超晶胞; (d)完全环氧基化五边形石墨烯的2×2超晶胞; (e)完全羟基化五边形石墨烯的2×2超晶胞
Figure1. Schematics of simulation models and atomic structures for pristine and functionalized penta-graphene. Side view and top view of (a) tensile model of pristine penta-graphene sheet, 2×2 supercell of (b) pristine penta-graphene, (c) fully hydrogenated penta-graphene, (d) fully epoxylated penta-graphene, (f) fully hydroxylated graphene.

研究表明, 化学功能化可以调控石墨烯的带隙和电子性质, 控制石墨烯的变形和形态, 并广泛用于改善石墨烯/聚合物纳米复合材料的界面力学性能, 但化学功能化往往伴随着其内在力学性能的显著恶化. 模拟和实验均表明, 氧化石墨烯的杨氏模量和拉伸强度远低于原始石墨烯^[13,14]. 分子动力学模拟结果显示, 随着氢化率的增大, 石墨烯的杨氏模量、破坏强度和应变急剧降低^[15]. 与原始石墨烯相比, 完全氢化石墨烯的杨氏模量降低了30%, 而破坏强度降低了65%^[15]. 毋容置疑, 化学功能化也可以拓展五边形石墨烯的潜在应用领域, 但化学功能化对这种完全由碳五元环组成五边形石墨烯的力学性能是否也有与石墨烯相类似的影响呢? 密度泛函理论计算和分子动力学模拟均表明, 施加应变和升高温度均可诱发五边形石墨烯结构中不可逆的碳五元环到多元环的结构转变, 化学功能化对五边形石墨烯的变形破坏机制有何影响仍有待进一步深入研究. 本文采用分子动力学方法系统研究了氢基、环氧基和羟基等官能团表面修饰及官能化率对五边形石墨烯力学性能和变形破坏机制的影响, 以及官能化对升温时五边形石墨烯结构转化的影响规律, 研究结果可为有效调控五边形石墨烯等二维纳米尺度材料的力学性能提供理论基础和结构设计依据.

2

-->

2.1.五边形石墨烯及其官能化几何模型

五边形石墨烯的晶格结构具有P-42₁m(空间群号113)对称性的正方形晶格, 晶格常数a = b = 3.64 ? (1 ? = 0.1 nm), c = 4.65 ?. 每个晶格内共有6个碳原子, 其中sp³杂化的C1原子2个, sp²杂化的C2原子4个. 两种键的长度分别为C1—C2键长1.55 ?、C2—C2键长1.34 ?. 图1为五边形石墨烯及其官能化几何模型示意图, 模型尺寸约为200 ?×100 ?, 红色虚线表示一个晶胞结构. 在官能化时, 只有三配位碳原子C2可以吸附氢原子或其他原子. 五边形石墨烯的屈曲结构为C2位置原子吸附其他原子提供了更大的空间, 并且五边形石墨烯中的三配位C2原子比四配位C1原子具有更高的化学活性, 而C1原子由于π电子的离域性而表现出相对惰性. 在氢化时, 氢原子全部枝接在C2原子上, 环氧基化时, 氧原子枝接在相邻的两个C2原子上, 羟基化时, 氧原子枝接在C2原子上, 氢原子枝接在氧原子上. sp³杂化的C原子标记为C1, 呈黄色, sp²杂化的C原子标记为C2, 呈棕色或蓝色, 氧原子呈红色, 氢原子呈粉色. 本文主要研究双面官能化, 官能化率定义为官能化的C2碳原子数与C2碳原子总数的比率. 官能化时, 五边形石墨烯的上下两层的C2碳原子随机吸附官能团且保持两层中C2碳原子的官能化比例相同. 为便于与双面官能化比较, 单面官能化时的官能化率定义为官能化的C2碳原子数与该层C2碳原子总数的比率. 本文中所研究的完美五边形石墨烯, 氢化、环氧基化和羟基化五边形石墨烯模型均采用相同的尺寸, 约为200 ?×100 ?, 其中完全氢化、环氧基化和羟基化五边形石墨烯模型的原子个数分别为9324个, 15484个(其中H原子为6160个), 12487个(其中O原子3163个), 21644个(其中氧原子6160个, 氢原子6160个).
为了验证完全官能化后的五边形石墨烯的稳定性, 计算了以上3种完全官能化后的五边形石墨烯的总势能随时间的变化曲线. 结果表明完全氢化、完全羟基化或完全环氧基化并没有改变五石墨烯的晶体对称性. 在300 K和1000 K时, 完全氢化、完全羟基化或完全环氧基化的五边形石墨烯的总势能的平均值随时间的增大几乎保持不变, 可以达到能量最小化状态. 原子构型图显示二维薄膜保持其完整的结构, 这表明完全官能化的五边形石墨烯不仅在室温下表现出良好的热稳定性, 而且能承受1000 K的高温.
2 -->

2.2.模拟方法及过程

本文采用经典全原子分子动力学方法, 该方法基于经验力场或势函数求解牛顿运动方程, 以获得模拟体系中所有原子的运动轨迹和速度分布, 并根据统计物理学原理求得模拟体系的宏观物理量. 分子动力学模拟的准确性主要取决于原子间相互作用势的选择. Winczewski等^[16]比较了适合描述碳原子相互作用的14种势函数, 研究发现由Erhart和Albe参数化的Tersoff势函数^[17]最适合描述五边形石墨烯碳原子之间的相互作用, 并可以获得与第一性原理计算相一致的结构、力学和能量等参数. 但是, Tersoff势函数并不能捕捉五边形石墨烯在施加应变和升温过程中的碳环转变过程, 而密度泛函理论计算^[18]和分子动力学模拟^[19-21]均已发现五边形石墨烯在变形过程中出现了碳环结构转变现象. ReaxFF^[22,23]是一种基于键级的描述原子间成键相互作用的反应力场, 可模拟化学键的生成与断裂. 相较于密度泛函理论计算结果, 该反应力场虽然在计算弹性力学常数时不如Tersoff势函数精确, 但该力场也可以得到比较一致的弹性力学常数, 并可以准确捕捉五边形石墨烯在施加应变和升温过程中的相变现象. 该力场已被成功应用于五边形石墨烯^{[12,19-21,24]}, 五边形石墨烯纳米管^[25]和石墨烯^[26]等材料的力学行为研究. 因此, 本文中选取由Chenoweth等^[23]开发的ReaxFF反应力场参数来模拟完美和官能化的五边形石墨烯在拉伸载荷作用下的大变形力学行为.
和其他基于键级的反应力场相比, ReaxFF反应力场中所有与成键相关的能量项均基于键级计算, 使得键断裂时能量能平滑过渡. ReaxFF 反应力场的势能函数如下^[22]:

$\begin{aligned} {E}_{\mathrm{system}}=&{E}_{\mathrm{bond}}+{E}_{\mathrm{lp}}+{E}_{\mathrm{over}}+{E}_{\mathrm{under}}+{E}_{\mathrm{val}}+{E}_{\mathrm{pen}}\\&+{E}_{\mathrm{coa}}+{{E}_{\mathrm{C}2}+{E}_{\mathrm{triple}}+E}_{\mathrm{tors}}+{E}_{\mathrm{conj}}\\&+{{E}_{\mathrm{H}-\mathrm{bond}}+E}_{\mathrm{vdWaal}\mathrm{s}}+{E}_{\mathrm{Coulomb}} \text{, } \\[-10pt] \end{aligned}$

其中, $ {E}_{\mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m}} $为体系的总势能, 由共价相互作用和非键相互作用势加和而成, 其中共价相互作用包括键能$ {E}_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}} $、孤对电子能$ {E}_{\mathrm{l}\mathrm{p}} $、配位能校正$ {E}_{\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}} $和$ {E}_{\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{r}} $、惩罚能$ {E}_{\mathrm{p}\mathrm{e}\mathrm{n}} $、共价键角作用能$ {E}_{\mathrm{v}\mathrm{a}\mathrm{l}} $、三体共轭作用能$ {E}_{\mathrm{c}\mathrm{o}\mathrm{a}} $、C2修正项$ {E}_{\mathrm{C}2} $、三键修正项$ {E}_{\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{p}\mathrm{l}\mathrm{e}} $、二面角作用能$ {E}_{\mathrm{t}\mathrm{o}\mathrm{r}\mathrm{s}} $、四体共轭作用能$ {E}_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{j}} $和氢键能$ {E}_{\mathrm{H}-\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}} $, 非键相互作用包括范德瓦尔斯相互作用$ {E}_{\mathrm{v}\mathrm{d}\mathrm{W}\mathrm{a}\mathrm{a}\mathrm{l}\mathrm{s}} $和库仑相互作用$ {E}_{\mathrm{C}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{o}\mathrm{m}\mathrm{b}} $. 每一项的具体表达式见文献[22].
分子动力学模拟中C原子、O原子和H原子的质量分别取12.01, 16.0, 1.008. 模拟五边形石墨烯的拉伸破坏过程如下: 首先采用共轭梯度算法优化初始构型, 使系统处于能量最低的平衡状态, 再在NVT 系综下对初始构型进行无约束弛豫, 然后对驰豫后的五边形石墨烯沿x方向进行拉伸, 拉伸时固定五边形石墨烯两端形成夹头, 宽度约为1 nm, 然后对夹头施加恒定的速度, 应变率控制在1.0×10⁹ s^–1, 直至五边形石墨烯被拉伸破坏. 模拟时, 五边形石墨烯在x, y方向均未施加周期性边界条件, 采用Nose-Hoover方法^[27,28]进行等温调节控制在300 K, 时间步长取0.25 fs, 系统运动方程求解均采用velocity-Verlet算法^[29].
本文在计算原子应力时, 采用位力应力(virial stress), 其定义如下^[30]:

$ S_{\alpha \beta }^i = \frac{1}{V}\sum\limits_{i \in V} {\left[ { - {m^{(i)}}v_\alpha ^{(i)}v_\beta ^{(i)} + \frac{1}{2}\sum\limits_{j \in V} {(r_\alpha ^{(j)} - r_\alpha ^{(i)})f_\beta ^{(ij)}} } \right]} , $

其中$ \alpha $和$ \beta $代表笛卡尔坐标系下各矢量在不同方向($ x, y, z $)的分量, $ {S^i} $代表$ i $原子的原子应力, $ V $为系统的总体积, $ {m^{(i)}} $为$ i $原子的质量, $ {v^{(i)}} $为$ i $原子的速度, $ j $为$ i $原子的邻接原子, $ {r^{(i)}} $和$ {r^{(j)}} $分别表示$ i $原子和$ j $原子的位置矢量, $ {f^{(ij)}} $为邻接原子$ j $作用于$ i $原子的力矢量. 具体详见相关文献[31].

2

-->

3.1.官能化五边形石墨烯的拉伸应力应变响应规律

图2分别绘出了部分和完全官能化五边形石墨烯的拉伸应力应变曲线. 需要指出的是, 本文在计算应力时忽略了五边形石墨烯的厚度, 因此, 本文中的所有应力均为二维应力, 其单位为N/m, 该方法已被广泛用于表示石墨烯等原子厚度二维纳米材料的力学性能参数, 如杨氏模量和强度等. 通过拟合完美五边形石墨烯的应力应变曲线的线性阶段可以得到五边形石墨烯的杨氏模量约为275.0 N/m, 与通过密度泛函理论计算得到的263.8 N/m^[1]和267.7 N/m^[32], 以及其他分子动力学模拟的结果282 N/m^[24]非常接近, 得到的弹性极限应力为15.63 N/m, 极限弹性应变为0.06, 也与相关文献报道的结果一致^[20], 从而验证了本文分子动力学模拟的准确性.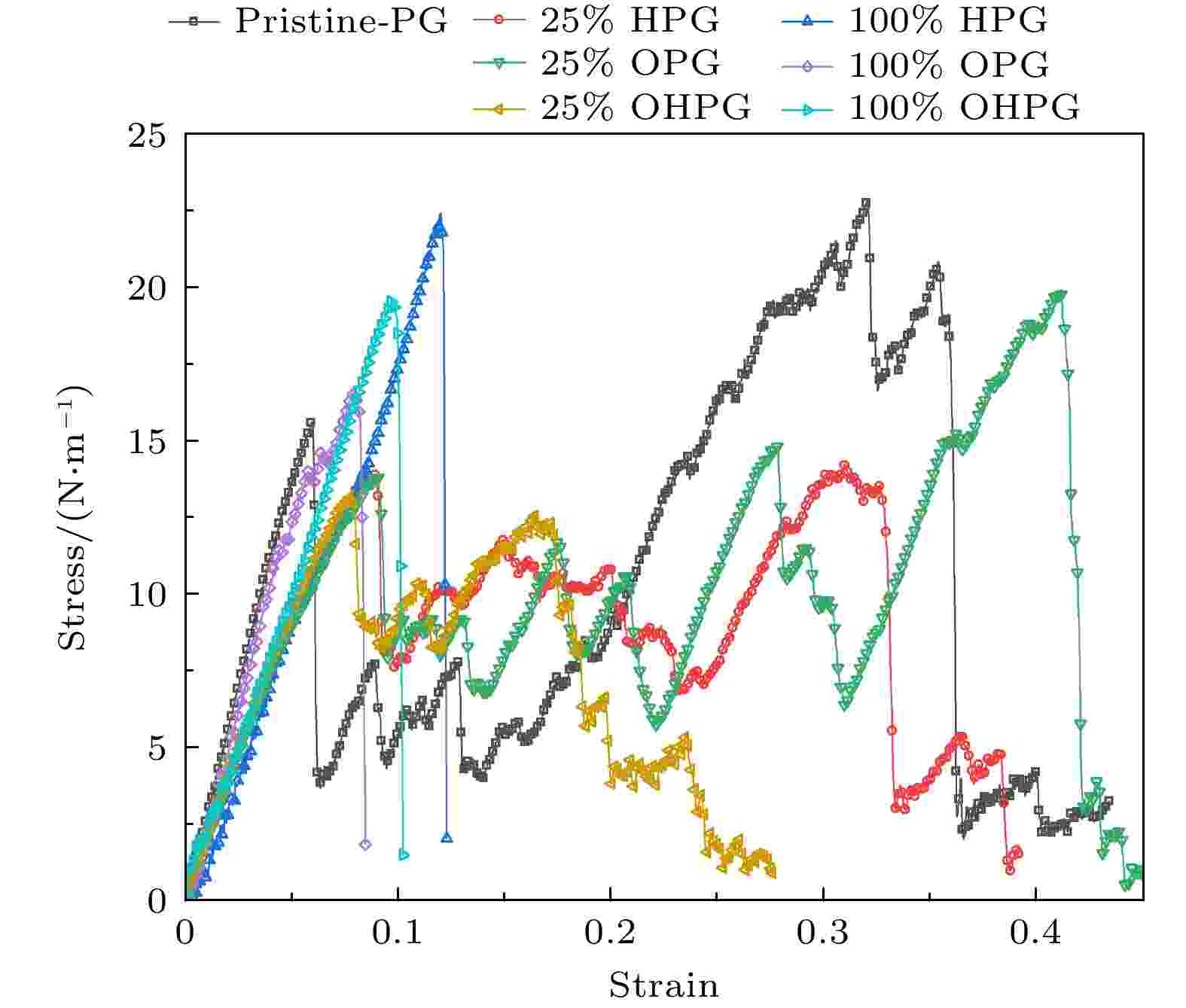
图 2 部分和完全官能化五边形石墨烯的拉伸应力应变曲线
Figure2. Stress-strain curves of partially and fully functionalized penta-graphene.

由图2可以看出, 25%氢化、环氧基化和羟基化的五边形石墨烯的拉伸应力应变响应与完美五边形石墨烯相似, 均表现出明显的大变形力学行为, 具有塑性变形特征. 变形过程大概分为4个阶段, 首先是弹性变形阶段, 应力随应变呈近直线增大, 发现部分官能化五边形石墨烯的极限弹性应力和应变均小于完美五边形石墨烯; 然后随着应变的增大, 应力急剧下降, 部分官能化使下降的幅度减小, 该阶段应力随应变的增大表现出锯齿状波动; 随后应力随应变的增大再次增大, 与25%氢化和环氧基化相比, 25%羟基化的五边形石墨烯在该阶段应力增大幅度较小; 最后五边形石墨烯断裂破坏. 由图2也可看出, 完全氢化、环氧基化和羟基化的五边形石墨烯的拉伸应力应变曲线特征完全不同于完美和部分官能化的五边形石墨烯, 表现出明显的脆性破坏特征. 更值得注意的是, 完全氢化、环氧基化和羟基化均能提高五边形石墨烯的极限弹性应力和应变, 氢化最明显, 羟基化次之. 而无论部分还是完全官能化的五边形石墨烯, 其应力应变曲线的线性阶段的斜率均小于完美五边形石墨烯, 说明官能化会降低五边形石墨烯的杨氏模量.
2 -->

3.2.官能化对五边形石墨烯拉伸破坏变形机制的影响

密度泛函理论计算和分子动力学模拟均表明^[18-21], 完美的五边形石墨烯在施加应变时表现出塑性变形特性, 这是由于加载过程中发生的不可逆的五元环到多元环结构的结构转变. 为了深入研究表面化学修饰对五边形石墨烯的变形破坏机制的影响, 可以分析官能化后五边形石墨烯拉伸变形过程的原子构型演变. 以环氧化为例, 图3和图4分别为25%环氧基化和完全环氧基化五边形石墨烯在不同变形阶段的原子构型图.
图 3 25%环氧基化五边形石墨烯在不同变形阶段的原子构型图　(a) ε = 0; (b) ε = 0.091; (c) ε = 0.331; (d) ε = 416
Figure3. Snapshots of the atom configurations of 25% epoxylated penta-graphene at different stain: (a) ε = 0; (b) ε = 0.091; (c) ε = 0.331; (d) ε = 416.

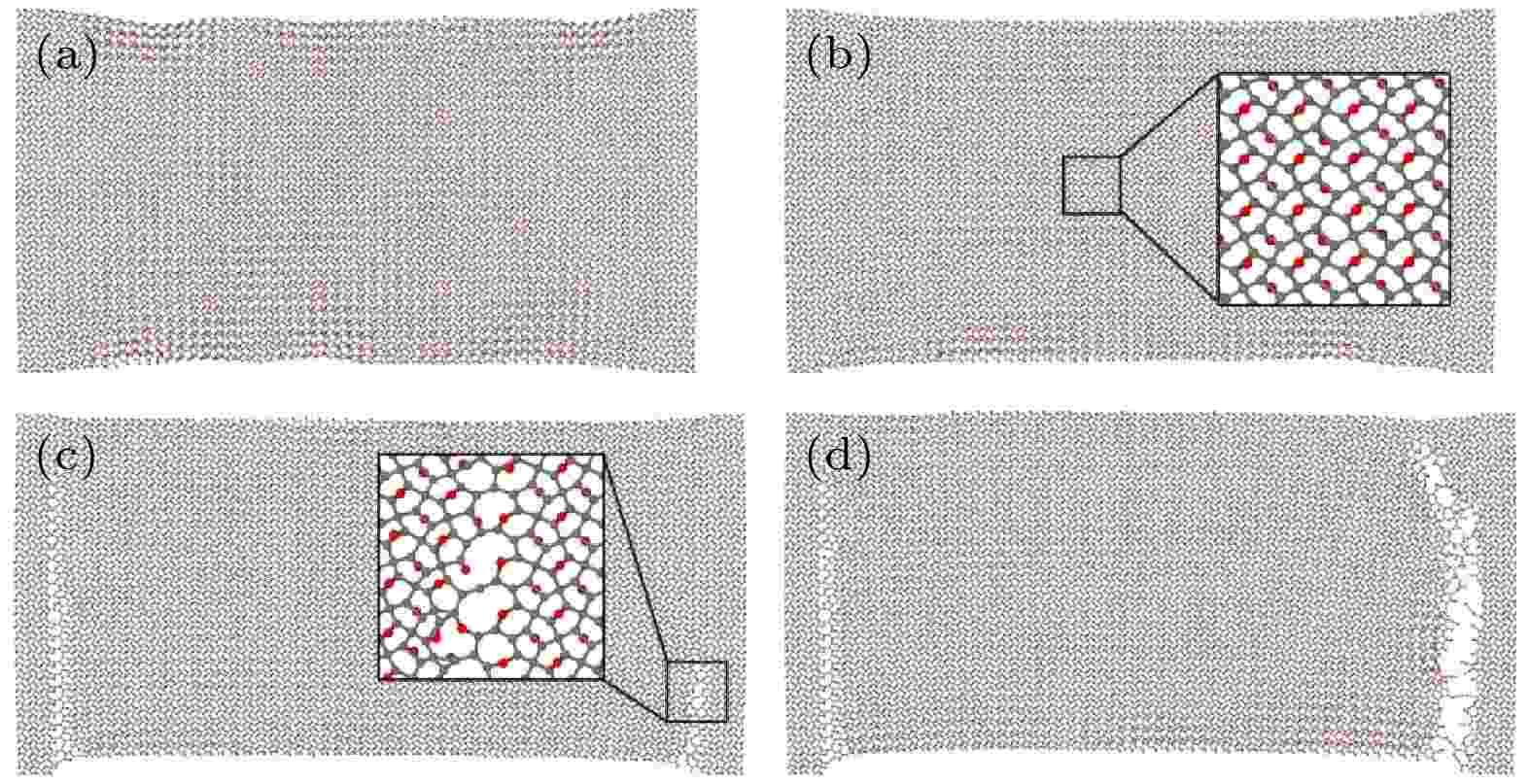图 4 完全环氧基化五边形石墨烯在不同变形阶段的原子构型图　(a) ε = 0; (b) ε = 0.043; (c) ε = 0.080; (d) ε = 0.083
Figure4. Snapshots of the atom configurations of fully epoxylated penta-graphene at different stain: (a) ε = 0; (b) ε = 0.043; (c) ε = 0.080; (d) ε = 0.083.

由图3可以看出, 对于25%环氧基化的五边形石墨烯, 当应变较小时, 五边形石墨烯中的碳环仍然保持为五边形, 碳碳键发生弹性变形. 但当应变增大到0.091时, 碳碳键开始断裂, 碳五元环开始转变为6, 7, 8等多元环结构, 这即是导致图2应力应变曲线中应变为0.091时应力急剧下降的原因. 随着应变的增大, 五边形石墨烯中的碳五元环逐渐转变为多元环混合结构, 如图3(c)所示, 该阶段对应应力应变曲线中的屈服阶段. 当应变增大到约0.31时, 转变过程结束, 此时五边形石墨烯薄膜变成了一个多元环组合的结构. 随着应变的继续增大, 碳多元环混合结构中的碳碳键继续伸长, 在应力应变曲线中表现为应力随着应变的增大而增大, 当应变增大到0.416时, 五边形石墨烯出现局部断裂, 最后断裂失效. 以上变形破坏过程与完美的五边形石墨烯基本一致. 通过分析其他低环氧基官能化率的五边形石墨烯的原子构型, 也发现类似的变形破坏过程.
对于完全环氧基化五边形石墨烯, 变形破坏机制与25%环氧基化的五边形石墨烯完全不同. 如图4所示, 完全环氧基化后, 五边形石墨烯表现出明显的脆性断裂特征, 这与图2中的应力应变曲线特征一致. 在拉伸变形过程中, 并没有发现类似于25%环氧基化五边形石墨烯的碳环转变过程. 随着应变增大, 五边形石墨烯在夹头附近出现断裂, 如图4(c)和图4(d)所示. 在断裂前, 五边形石墨烯中的碳五元环虽然也转变为多元环, 但该过程很短, 碳碳键迅速断裂导致薄膜断裂失效. 由此表明, 完全环氧基化可以使五边形石墨烯由塑形变形转变为脆性断裂.
不同官能化率导致五边形石墨烯表现出不同的力学性能和变形破坏机制的根本原因在于相关结构的不同的稳定性. 官能化可以将sp²杂化的C2碳原子转变为sp³杂化. 原始的和部分官能化的五边形石墨烯中碳原子为sp²和sp³混合杂化方式, 这种具有较高势能的屈曲结构很容易转化为平面的低势能结构, 因此, 碳五元环在外载荷作用下很容易转变为平面碳多元环结构, 变形过程中表现出明显的塑形变形特征. 而完全官能化的五边形石墨烯中, 所有sp²杂化的碳原子全部转变为sp³杂化, 大大提高了结构稳定性, 从而可以有效阻碍结构中碳环的转变, 只有较高的应力才能使结构失效, 因此破坏时表现出明显的脆性断裂特征.
需要说明的是, 对于由其他官能团氢基或羟基部分和完全官能化的五边形石墨烯, 研究发现其变形破坏过程和变形机制分别与部分和完全环氧基化的五边形石墨烯的规律基本一致. 基于以上分析, 低官能化率五边形石墨烯在拉伸载荷下仍然表现出类似于完美五边形石墨烯的塑性变形破坏特征, 而完全官能化均可导致五边形石墨烯由塑性变形向脆性变形破坏机制的转变.
2 -->

3.3.官能化率对五边形石墨烯力学性能参数的影响

图5为官能化五边形石墨烯的杨氏模量, 弹性极限和极限弹性应变随官能化率的变化趋势图. 官能化对五边形石墨烯的力学性能有较大的影响. 由图5(a)和图5(b)可以看出, 对于氢化、环氧基化和羟基化3种官能化方式, 五边形石墨烯的杨氏模量和弹性极限均随官能化率的增大呈先剧烈减小再缓慢增大的趋势. 当五边形石墨烯官能化至10%—15％时, 其具有最低的杨氏模量和弹性极限. 氢化、环氧基化和羟基化使杨氏模量从275 N/m分别降低了132.4 N/m, 121.1 N/m和127.3 N/m, 降低幅度分别约48.2%, 44.1%和46.3%. 随后, 五边形石墨烯杨氏模量和弹性极限随着官能化率的增大呈单调缓慢增大趋势. 将杨氏模量与官能化率的变化规律进行非线性多项式拟合可得到以下经验公式: $ Y=(A{x}^{3}+B{x}^{2}+Cx+D)/({x}^{2}+Ex+F) $. 以氢化为例, 拟合结果为: A = –0.1525, B = 223.2009, C = –3129.371, D = 22161.42, E = 8.7517, F = 80.18425. 对于其他官能化的情况, 也可以采用该经验公式进行拟合.
图 5 官能化五边形石墨烯的杨氏模量, 弹性极限和极限弹性应变随官能化率的关系
Figure5. Young’s modulus, elastic stress and strain of penta-graphene functionalized with different functional groups as a function of functionalization percentage.

值得注意的是, 与完美的五边形石墨烯相比, 完全氢化、环氧基化和羟基化均使五边形石墨烯的杨氏模量降低, 幅度分别为29.9%, 20.1%和29.6%, 完全官能化均使五边形石墨烯的弹性极限提高, 幅度分别为43.6%, 16.5%和25.9%. 这一规律与六边形石墨烯不完全相同. 对于六边形石墨烯, 氧化石墨烯的杨氏模量和拉伸强度均远低于原始的六边形石墨烯. 与原始石墨烯相比, 完全氢化石墨烯的杨氏模量降低了30%, 而破坏强度降低了65%. 由图5(c)可以看出, 随着官能化率的增大, 五边形石墨烯的极限弹性应变单调递增. 完全氢化、环氧基化和羟基化分别使极限弹性应变增大为101.9%, 54.5%和87.9％. 由以上结果可以看出, 3种官能团对五边形石墨烯力学性能参数的影响, 氢化最显著, 羟基化次之.
2 -->

3.4.单面官能化对五边形石墨烯结构和力学性能的影响

以上的研究均讨论的是双面官能化对五边形石墨烯力学性能和变形破坏机制的影响. 本文还研究了单面官能化对五边形石墨烯的力学性能参数和变形破坏的影响, 并和双面官能化进行了对比. 以单面氢化为例进行说明, 其他类型的官能化有类似的规律. 通过分析单面氢化和双面氢化五边形石墨烯的杨氏模量, 弹性极限和应变随氢化率的关系发现, 虽然单面氢化时的绝对氢化率(官能化的C2碳原子数与C2碳原子总数的比率)是双面氢化的一半, 但单面氢化和双面氢化对五边形石墨烯的力学性能参数的影响的区别并不大. 但是, 单面氢化对五边形石墨烯薄膜的形貌有重要影响. 当单面氢化率较低时, 单面氢化后的五边形石墨烯经过充分弛豫后, 表面呈平整二维结构, 在拉伸载荷作用下, 随着应变的增大, 类似于双面氢化的五边形石墨烯, 出现了五元环向多元环结构的转变, 具有明显的塑形变形特征. 而当单面氢化率较高时, 单面氢化五边形石墨烯经过充分弛豫后, 表面不再呈平整二维结构, 发生了卷曲现象, 氢化率越大, 这种卷曲现象越明显, 而双面氢化时并没有发生类似的卷曲现象. 这是由于单面氢化致使五边形石墨烯一侧产生很多C—H悬键, 为保持结构稳定和能量最低从而发生卷曲. 另外, 值得注意的是, 虽然单面完全氢化时的绝对氢化率是50%, 但单面完全氢化仍然可以提高五边形石墨烯的整体稳定性, 在拉伸载荷下并没有出现五元环向多元环结构的转变现象, 而类似于双面完全氢化的五边形石墨烯, 表现出明显的脆性断裂特征.
由以上分析, 可以得出结论, 当单面氢化率较高时, 单面氢化会使五边形石墨烯发生卷曲现象, 但单面氢化和双面氢化对五边形石墨烯的力学性能参数和变形破坏机制的影响规律基本一致. 对于其他两种官能化类型也有类似的结论.
2 -->

3.5.温度诱发官能化五边形石墨烯结构的转变

低官能化率的五边形石墨烯在拉伸荷载作用下发生类似于完美五边形石墨烯的由五元环向多元环结构的转变. 研究表明, 五边形石墨烯还可以通过升高温度转变为能量较低的六元环占主导的类似于石墨烯的结构^[19,20]. 升高温度会导致五边形石墨烯的势能上升, 越过结构间的能量壁垒发生相变. 升高温度会如何影响官能化后五边形石墨烯的结构转变, 对它们的临界转变温度和熔点有何影响? 为了探究这个问题, 通过对不同官能化率的未受载荷的五边形石墨烯逐渐升高温度, 研究了官能化对五边形石墨烯在升温时结构转变和临界转变温度和熔点的影响. 选取同样尺寸(约为200 ?×100 ?)的五边形石墨烯, 25％和100%的氢化、环氧基化和羟基化的五边形石墨烯, 对初始结构在100 K的NVT系综中进行弛豫, 然后以0.25 K/fs的速率均匀升温, 直至升温至7000 K, 模型中的原子不受任何约束可以不受限制地自由移动.
图6为完美石墨烯和官能化后的五边形石墨烯的势能随温度的变化曲线. 通过观察能量温度曲线, 会发现25%氢化、环氧基化和羟基化的五边形石墨烯均存在一个类似于五边形石墨烯的随温度升高能量降低的区域, 由图6的虚线框标出, 区间分别为1550—2350 K, 1500—2600 K, 1800—2300 K. 通过观察原子构型发现, 25%官能化的五边形石墨烯在该温度区间均发生了从碳五元环到碳六元环的结构转变. 其临界转变温度(1500—1800 K)明显高于完美的五边形石墨烯(600 K), 说明部分官能化可以提高五边形石墨烯的临界转变温度, 即可以延迟五边形石墨烯的结构转变. 利用Los等^[33]提出准二维材料熔点的确定方法可以确定25%氢化、环氧基化和羟基化的五边形石墨烯的熔点分别为4400 K, 4750 K, 4700 K, 与完美的五边形石墨烯的熔点4700 K相近, 说明官能化对五边形石墨烯的熔点影响不大. 对于其他官能化率(低于或高于25%)的五边形石墨烯, 也发现了相似的碳环转变以及临界转变温度提高的现象.
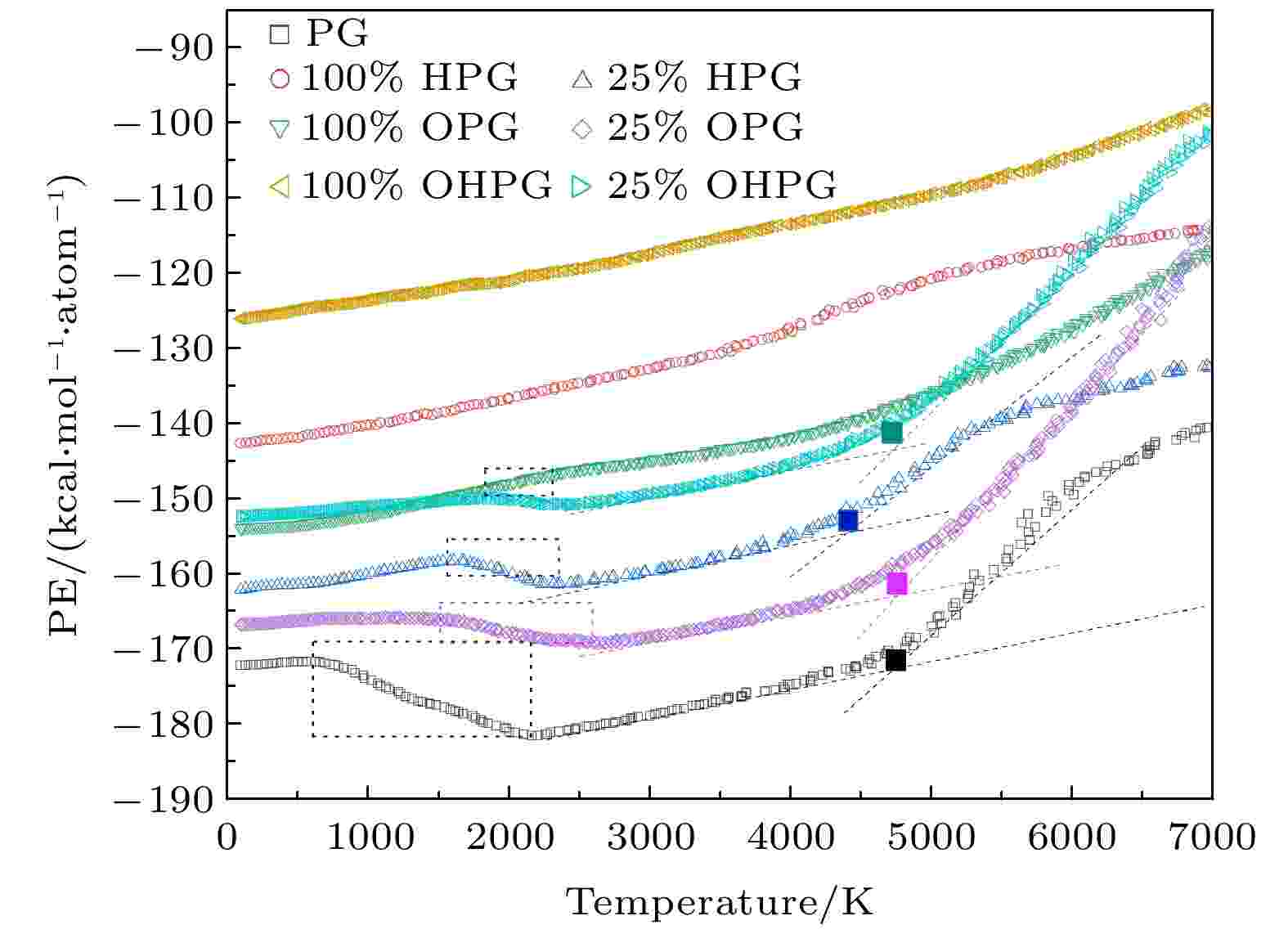图 6 完美的和官能化的五边形石墨烯的势能与温度的关系曲线
Figure6. Potential energy versus temperature for pristine and functionalized penta-graphene

而对于完全氢化、环氧基化和羟基化的五边形石墨烯, 势能温度曲线中并不存在随温度升高能量降低的区域, 通过观察原子构型并未发现碳环转变现象. 由此说明类似于施加应变, 完全官能化后的五边形石墨烯在升温时并不存在碳环结构转变现象, 这是由于完全官能化改变了五边形石墨烯中碳原子的sp²和sp³混合杂化方式, 使所有sp²杂化转变为sp³杂化, 从而提高了结构的稳定性.
基于以上分析, 低官能化率的五边形石墨烯在升温时出现碳环结构转变现象, 部分官能化可以提高五边形石墨烯的临界转变温度, 延迟碳环结构的转变, 但对熔点影响不大, 而完全官能化五边形石墨烯在升温时并未出现碳环结构的转变.

本文采用分子动力学方法研究了氢基、环氧基和羟基等官能团表面修饰及官能化率对五边形石墨烯力学性能和变形破坏机制的影响以及官能化对升温时五边形石墨烯结构转变的影响规律. 本文得到如下结论:
(1)氢基、环氧基和羟基3种官能基团均可以有效地调控五边形石墨烯的力学性能和变形破坏机制, 低官能化率五边形石墨烯在拉伸载荷下仍然表现出类似于完美五边形石墨烯的塑性变形破坏特征, 而完全官能化均可提高结构稳定性, 导致五边形石墨烯由塑性变形向脆性变形破坏机制的转变.
(2)五边形石墨烯的杨氏模量和弹性极限均随官能化率的增大先剧烈减小再缓慢增大, 而极限弹性应变单调递增. 当官能化至10%—15％时, 五边形石墨烯具有最低的杨氏模量和弹性极限, 而完全官能化均使五边形石墨烯的杨氏模量降低, 使弹性极限和应变提高.
(3)单面官能化和双面官能化对五边形石墨烯的力学性能参数和变形破坏机制的影响规律基本一致. 当单面官能化率较高时, 单面官能化会使五边形石墨烯发生卷曲现象, 官能化率越大, 卷曲现象越明显.
(4)低官能化率的五边形石墨烯不受约束在升温时出现碳环结构转变现象, 部分官能化可以提高五边形石墨烯的临界转变温度, 延迟碳环结构的转变, 但对熔点影响不大, 而完全官能化五边形石墨烯在升温时并未出现碳环结构的转变.