全文HTML
--> --> -->二维铁电异质结因其独特的物性吸引了关注. 如在MoTe2/CuInP2S6异质结中, CuInP2S6的极化反转会改变异质结的开态及关态电压[9]. 最近, 由二维铁电材料α-In2Se3(简称In2Se3)组成的异质结也吸引了大量研究. Ayadi等[10]的研究表明在In2Se3/石墨烯异质结中In2Se3的极化反转会引起肖特基势垒的改变. Li等[11]制备了基于In2Se3/MoS2异质结制成的场效应管, 结果表明In2Se3/MoS2异质结场效应管可使用垂直方向电场控制开关, 开关比高达200%. 这些研究表明In2Se3异质结在多个领域的应用潜能, 因此开发新型二维In2Se3异质结值得进一步研究.
目前, In2Se3异质结已成为学界的研究热点, 但当前的研究主要集中于分析其光学性质[12]、电学性质[13]及极化反转对其物理性质的影响[14], 对能带调控方面的研究还不多. 在诸多调控手段中, 应力是目前实验较为容易施加的一种调控手段[15-17], 而且许多计算研究也表明应力是一种调控材料能带性质的有效手段[18,19]. 本工作使用与单层In2Se3晶格常数接近的单层InSe组成二维垂直范德瓦尔斯异质结, 使用第一性原理计算, 计算该异质结的能带结构及应力调控. 结果表明, 改变单层In2Se3的极化方向可调控异质结带隙大小及能带匹配性质, 此外施加合适的面内力学应变可有效调控异质结的带隙类型, 并产生半导体到金属的转变.
本文讨论了异质结的多种可能结构, 根据结合能来选取能量最低构型. 结合能Ef定义为
平面平均微分电荷密度
3.1.二维铁电In2Se3/InSe垂直异质结的能带结构
单层In2Se3与单层InSe均为六角晶胞, 其中InSe的晶格常数a = b = 4.094 ?, 单层In2Se3的晶格常数为a = b = 4.106 ?, 均与相关文献的计算结果吻合[21,22]. 二者的晶格失配比为0.2%, 晶格高度匹配. 将单层In2Se3置于单层InSe上方以构建In2Se3/InSe垂直异质结. 根据两层之间In原子的相对位置关系, 构建了AA, AB, AC三种结构, 如图1(a)所示. 图1(b)为3种结构的结合能与层间距的关系, 可看出AA结构的结合能明显小于AB结构的结合能. 因此在本文中只研究AA-In2Se3/InSe异质结的能带性质及调控方式. 根据In2Se3的极化特点[23], 构建了极化方向相反的两种AA构型, 当In2Se3的极化方向垂直异质结所在平面(x-y面)且指向面外时(+z), 称为In2Se3/InSe (I), 当极化方向垂直指向面内(–z)时, 称之为In2Se3/InSe(II), 两种结构如图2(a)所示. 它们的结合能对比如图2(b)所示, 可看出In2Se3/InSe(I)的结合能比In2Se3/InSe(II)的结合能小0.019 eV, 表明In2Se3/InSe(I)较In2Se3/InSe(II)更为稳定. 这是因为在In2Se3/InSe (I)中In2Se3的自发极化方向与整体的电荷转移方向相同, 使得异质结中产生了更强的范德瓦尔斯相互作用[24].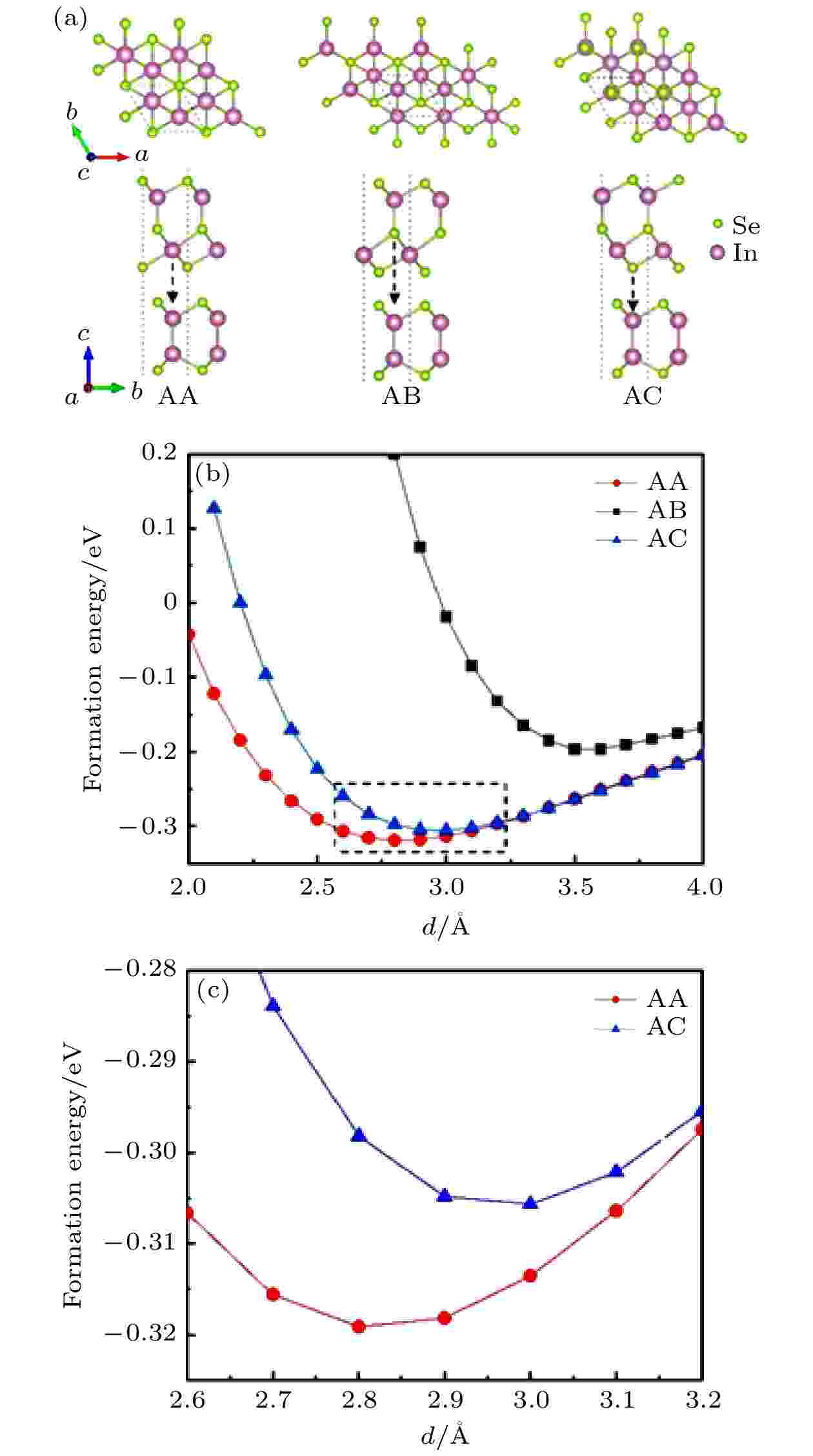
图 1 (a) InSe/In2Se3异质结的3种堆叠方式, 黑色虚线箭头标注了异质结不同层的In原子的位置关系; (b) 3种结构在不同层间距下的能量; (c)图1(b)中黑色虚框部分的局部放大图Figure1. (a) Three stacking methods of InSe/In2Se3heterojunctions, where black dashed arrows mark the positional relationship of In atoms in different layers of the heterojunction; (b) formation energy of the three structures at different layer spacings; (c) a partial enlarged view of the black dashed part in Fig.1 b).
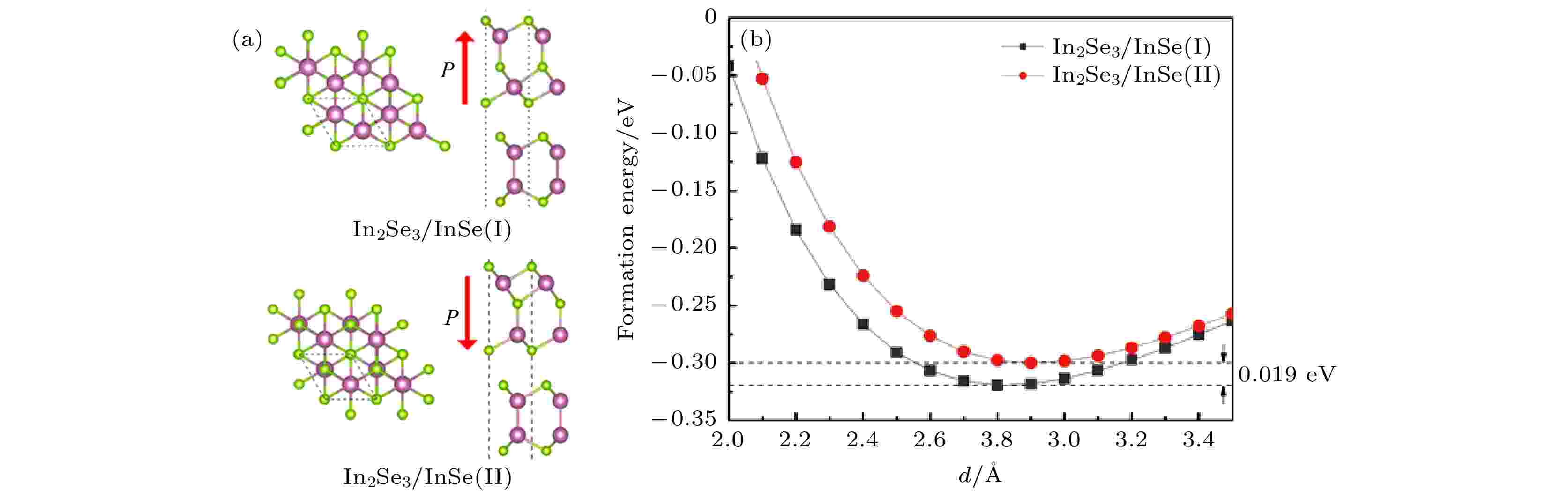图 2 (a) In2Se3/InSe (I)和In2Se3/InSe (II)的晶格结构, 黑色虚框表示晶格, 红色箭头表示异质结中In2Se3的自发极化方向; (b) In2Se3/InSe (I)和In2Se3/InSe (II)的结合能对比Figure2. (a) Lattice structure of In2Se3/InSe (I) and In2Se3/InSe (II), where the black dashed frame represents the crystal lattice, and the red arrow represents the spontaneous polarization direction of In2Se3; (b) binding energy comparison of In2Se3/InSe (I) and In2Se3/InSe (II).
图3给出了In2Se3/InSe (I) 和In2Se3/InSe (II)的投影能带结构, 其中红色表示InSe对能带的贡献, 蓝色部分表示In2Se3对能带的贡献. 可看出, In2Se3/InSe (I) 是间接带隙半导体, 带隙为0.50 eV; In2Se3/InSe (II) 也是间接带隙半导体, 带隙为0.46 eV. In2Se3/InSe (I) 的带隙较In2Se3/InSe (II) 增大了0.04 eV, 可见极化反转减小了带隙. 在In2Se3/InSe (I) 中, 价带顶 (valence band maximum, VBM)主要来自InSe的贡献, 而导带底(conduction band minimum, CBM)几乎全部来自于In2Se3. 与之相反, 在In2Se3/InSe (II)中, VBM几乎全部分布于In2Se3, CBM主要分布于InSe. 图3(c)给出了两种异质结VBM及CBM的电荷空间分布, 可以明显看到上述特点. 这表明In2Se3/InSe异质结具有II型能带匹配, 且极化反转会使CBM和VBM的空间分布对调.
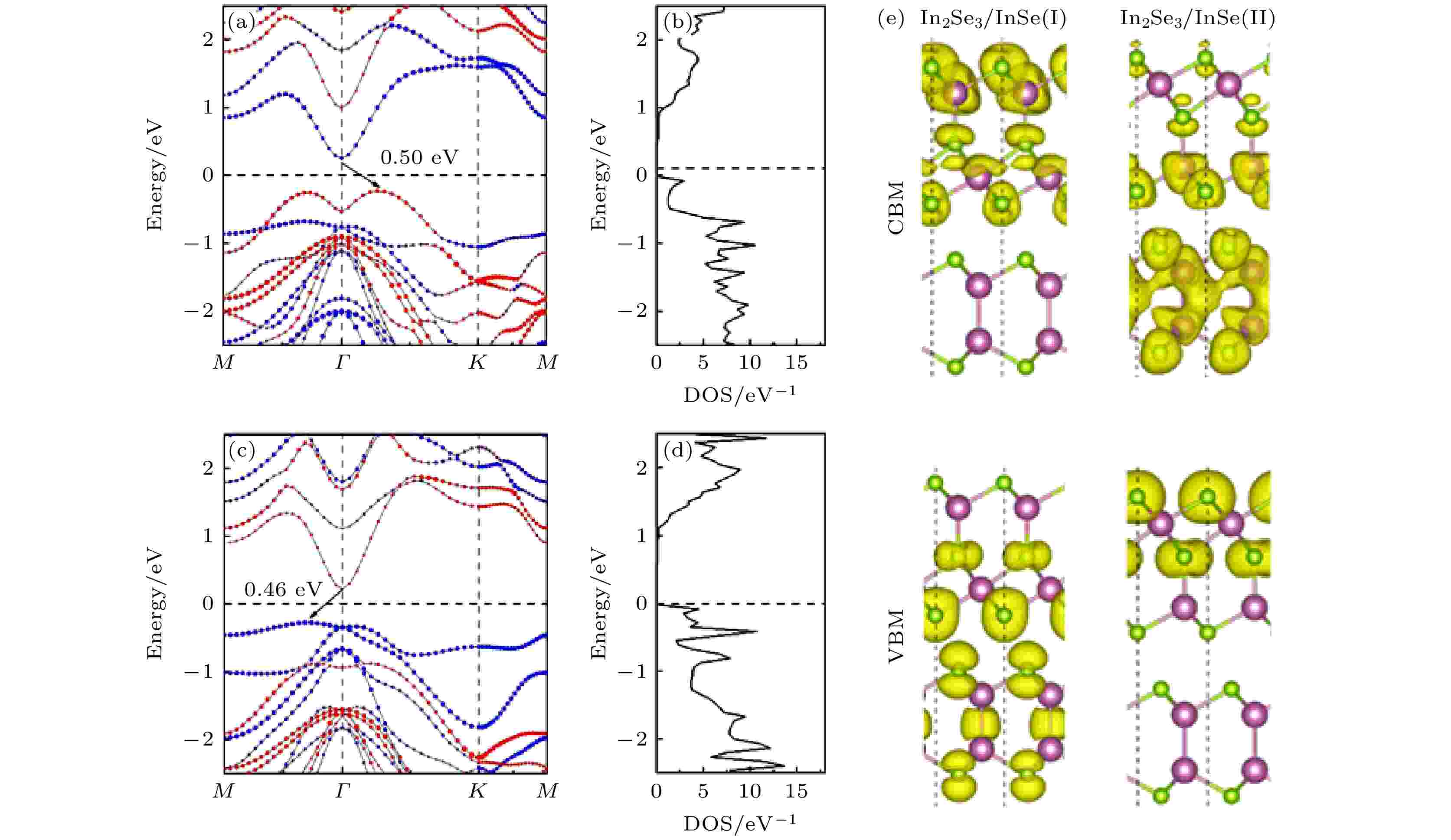图 3 (a) In2Se3/InSe (I)的能带结构及(b)态密度; (c) In2Se3/InSe (II)的能带结构及(d)态密度. 能带图中红色和蓝色表示InSe及In2Se3对能带的贡献, 黑色箭头表示带隙, 由CBM指向VBM;(e)In2Se3/InSe (I)和In2Se3/InSe (II) CBM和VBM所在能带的电荷空间分布Figure3. (a) Band structure of In2Se3/InSe (I) and (b) density of states; (c) band structure of In2Se3/InSe (II) and (d) density of states, where the red and blue in the energy band diagram indicate the contribution of InSe and In2Se3 to the energy band, and the black arrow indicates the band gap, pointing from CBM to VBM; (e) decomposed charge densities of CBM and VBM for In2Se3/InSe (I) and In2Se3/InSe (II).
计算In2Se3/InSe (I)和In2Se3/InSe (II)的差分电荷密度, 分别如图4(a)和4(b)所示, 其中黄色和青色区域分别表示电荷的聚集区和耗尽区. 从图4可看出, 界面上的电荷分布主要存在于层间相邻的Se原子之间, 电子主要在In2Se3一侧聚集, 在InSe一侧耗尽. 使用Hirshfeld-I方法[25]求出In2Se3/InSe (I)和In2Se3/InSe (II)的层间电荷转移分别为0.033 e和0.031 e. 这一计算结果表明In2Se3/InSe (I)较In2Se3/InSe (II)发生了更多的层间电荷转移, 说明In2Se3/InSe (I)的层间相互作用要强于In2Se3/InSe (II), 这也是In2Se3/InSe (I)的结合能比In2Se3/InSe(II)更低的原因.
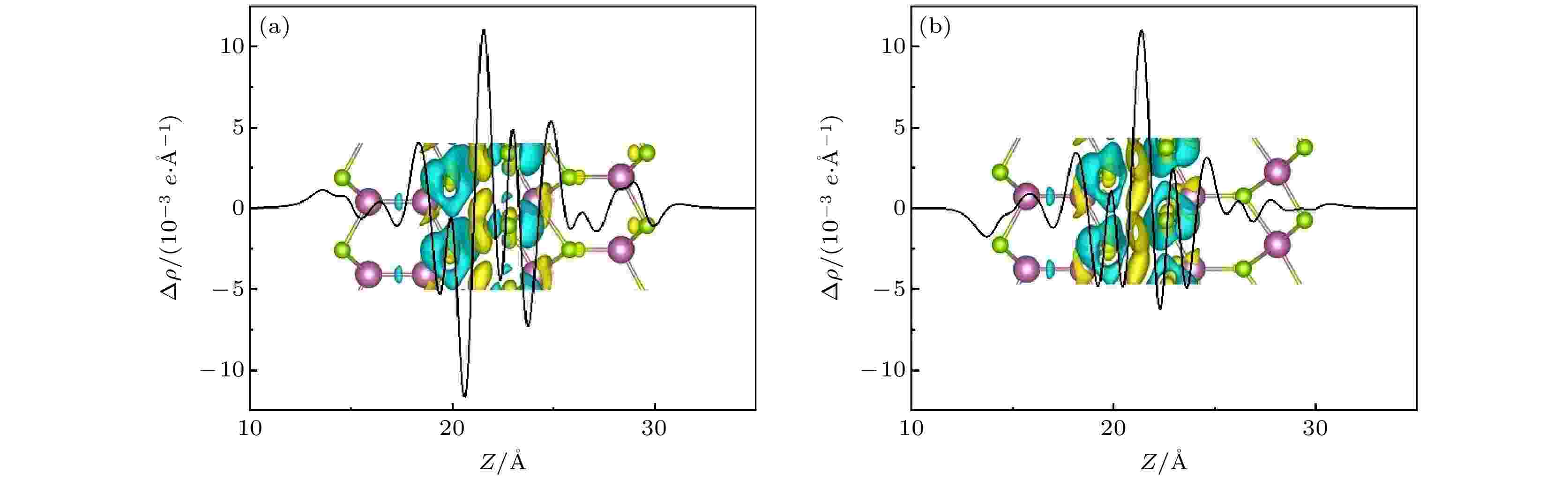图 4 (a) In2Se3/InSe (I) 和 (b) In2Se3/InSe (II)沿Z方向的平面平均差分电荷密度. 图中黄色和青色包络面分别表示电子的聚集和耗尽区Figure4. (a) Plane-averaged charge density difference forIn2Se3/InSe (I) and (b) In2Se3/InSe (II) at equilibrium distance along the Z direction, where the yellow and cyan envelope areas representelectron accumulation and depletion, respectively.
2
3.2.In2Se3/InSe异质结能带结构的应力调控
分别研究了水平单轴和双轴应变对In2Se3/InSe异质结能带结构的影响. 应变的施加方式如图5所示, 其中双轴应变沿原胞的两个基矢方向施加; 施加单轴应变时, 先将原胞转换成矩形晶胞, 再沿两个晶向施加应变. 本工作中应变量μ表示为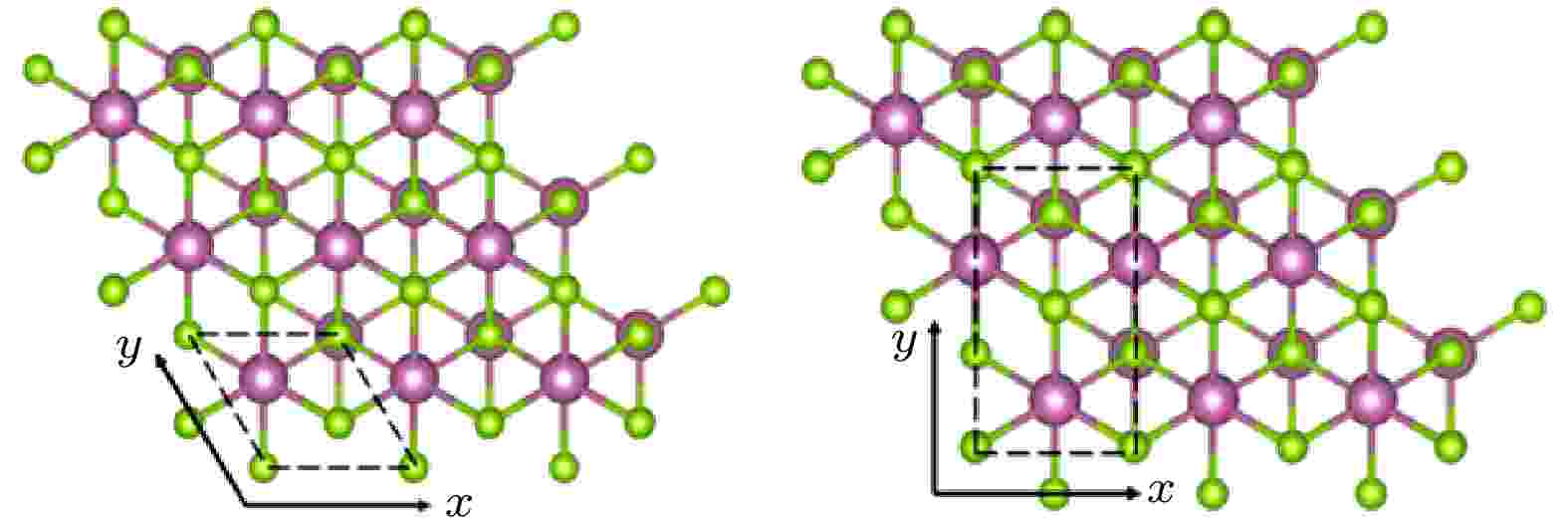
图 5 双轴应变(左)和单轴应变(右)的晶胞选取以及应变施加方向.Figure5. Unit cell selection and strain application direction of biaxial strain (left) and uniaxial strain (right).
图6给出了双轴应变下In2Se3/InSe (I)和In2Se3/InSe (II)的带隙变化. 如图6(a)所示, 对于In2Se3/InSe (I) 异质结双轴拉伸会减小异质结的带隙, 当拉伸应变大于6%时, 异质结带隙减小为0, 即发生半导体-金属转变. 压缩应变对异质结能带的影响则较为复杂, 较小的单轴应变会使异质结的带隙增大, 但当压缩应变大于6%时异质结的带隙会减小, 同时还从间接带隙变为直接带隙. 不同应变下带隙的大小和类型见表1. 综合比较In2Se3/InSe (I)和In2Se3/InSe (II)在不同应变下的带隙大小, 可发现在施加相同大小拉伸应变时, In2Se3/InSe (I)的带隙均小于In2Se3/InSe (II)的带隙; 施加相同大小压缩应变时, In2Se3/InSe (I)的带隙均大于In2Se3/InSe (II)的带隙, 这说明In2Se3的极化方向反转对处于拉伸和压缩应变下的异质结能带的影响相反.
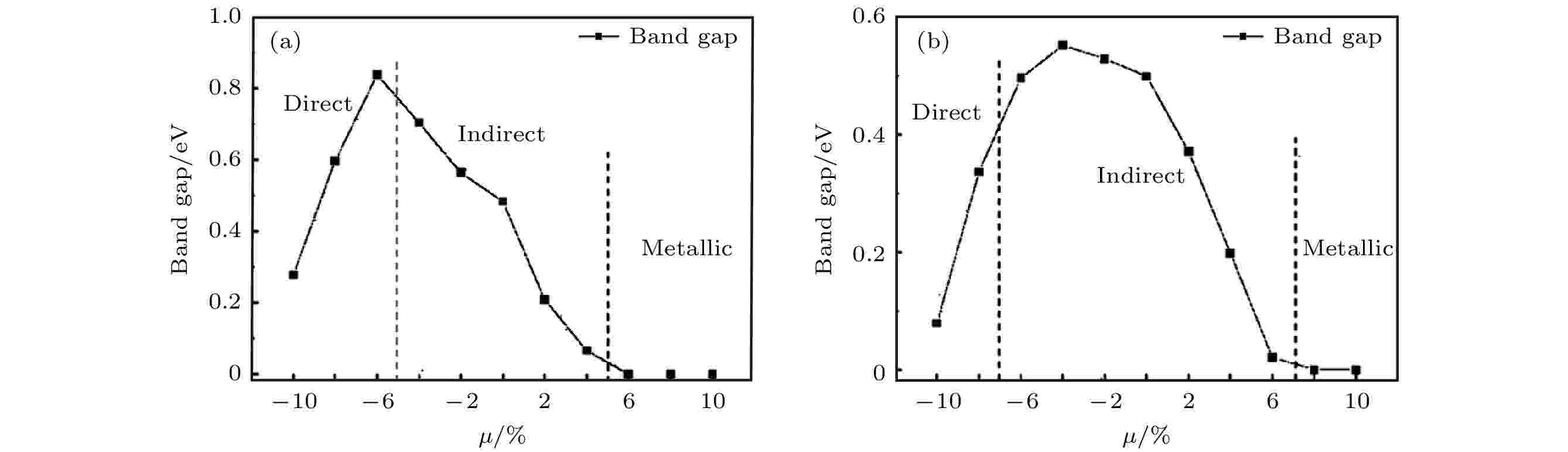图 6 (a) 不同双轴应变下In2Se3/InSe (I)的带隙; (b)不同双轴应变下In2Se3/InSe (II)的带隙Figure6. (a) Band gap of In2Se3/InSe (I) under biaxial strain; (b) band gap of In2Se3/InSe (II) under biaxial strain.
| μ/% | In2Se3/InSe (I) | In2Se3/InSe (II) | |||
| Gap/eV | Character | Gap/eV | Character | ||
| –10 | 0.28 | direct | 0.08 | direct | |
| –8 | 0.60 | direct | 0.34 | direct | |
| –6 | 0.84 | direct | 0.50 | indirect | |
| –4 | 0.70 | indirect | 0.55 | indirect | |
| –2 | 0.56 | indirect | 0.53 | indirect | |
| 0 | 0.50 | indirect | 0.46 | indirect | |
| 2 | 0.21 | indirect | 0.37 | indirect | |
| 4 | 0.07 | indirect | 0.20 | indirect | |
| 6 | — | metallic | 0.02 | indirect | |
| 8 | — | metallic | — | metallic | |
| 10 | — | metallic | — | metallic | |
表1双轴应变下In2Se3/InSe (II)及In2Se3/InSe (I)的带隙.
Table1.Band gap of In2Se3/InSe (I) and In2Se3/ InSe(II) under biaxial strain.
图7给出了In2Se3/InSe (I)和In2Se3/InSe (II)异质结能带随应变的变化规律. 图中标出了不同部分对能带的贡献. 计算结果表明, 施加–8%双轴压缩应变时, In2Se3/InSe (I)的CBM和VBM所在能带均主要由In2Se3贡献. 图8为施加–4%和–8%双轴压缩应变时In2Se3/InSe (I)的CBM和VBM所在能带的空间电荷分布. 可看出, 在–8%双轴压缩应变下, CBM和VBM所在能带均主要分布于In2Se3. 以上计算结果表明施加压缩应变还会使In2Se3/InSe (I)的能带匹配类型由II型变为I型.
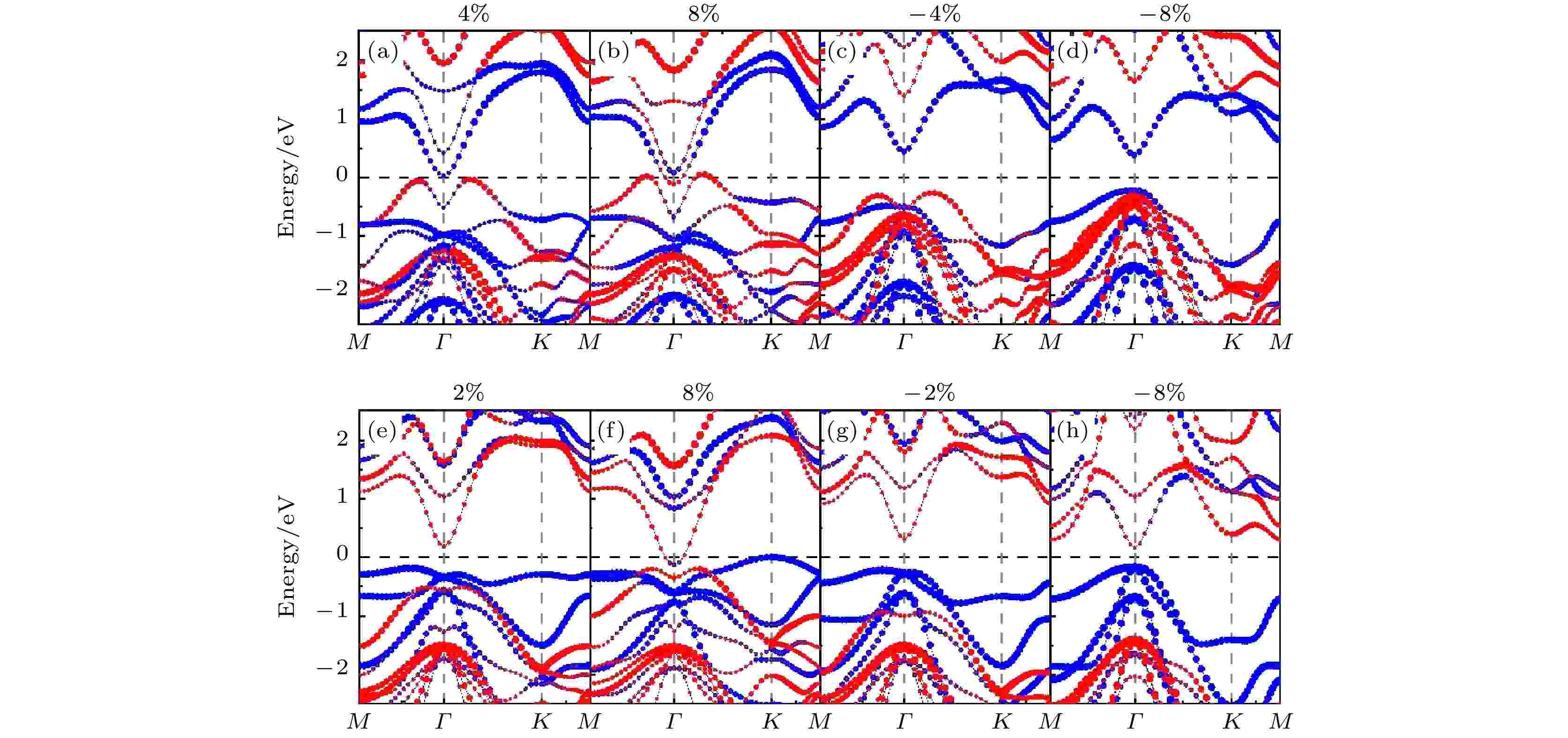图 7 (a)?(d)4%、8%、–4%和–8%双轴应变下In2Se3/InSe (I)的投影能带结构; (e)?(h) 2%、8%、–2%和–8%双轴应变下In2Se3/InSe (II)的投影能带结构. 能带图中红色部分表示InSe对能带的贡献, 蓝色部分表示In2Se3对能带的贡献Figure7. (a)?(d) The projected band structure of In2Se3/InSe (I) under 4%, 8%, –4% and –8% biaxial strain; (e)?(h) Projected band structure of In2Se3/InSe (II) under 2%, 8%, –2% and –8% biaxial strain. The red part of the energy band indicates the contribution of InSe, the blue part indicates the contribution of In2Se3.
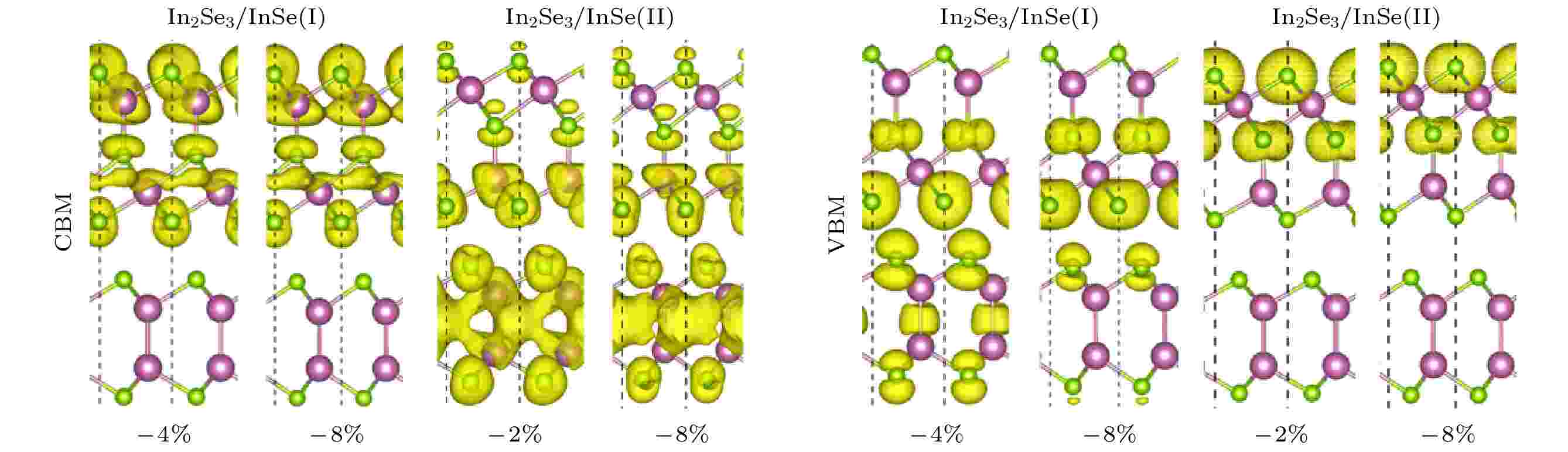图 8 –4%和–8%双轴应变下In2Se3/InSe(I)CBM和VBM所在能带的电荷空间分布以及–2%及–8%双轴应变下In2Se3/InSe (II)CBM和VBM所在能带的电荷空间分布Figure8. Decomposed charge densities of CBM and VBM for In2Se3/InSe (I) under –4% and –8% biaxial strain and thedecomposed charge densities of CBM and VBM for In2Se3/InSe (II) under –2% and –8% biaxial strain.
图9为In2Se3/InSe (I)和In2Se3/InSe (II) 在单轴应变下的带隙变化. 异质结在单轴应变下的带隙变化趋势与双轴应变类似: 拉伸应变会减小带隙, 较小的压缩应变会使带隙增大, 但较大的压缩应变则会使带隙减小, 同时也会使带隙类型由间接带隙变为直接带隙. 图10为两种结构在单轴应变下的能带结构, 可看出在等量的拉伸应变下双轴应变对带隙的影响较单轴应变更大, x方向和y方向应变对带隙的影响近似. 在较小的等量压缩应变下双轴应变使带隙增加的更多, 但较小的单轴压缩应变便可使带隙由间接带隙变为直接带隙, 这可由图7与图10的对比中看出.
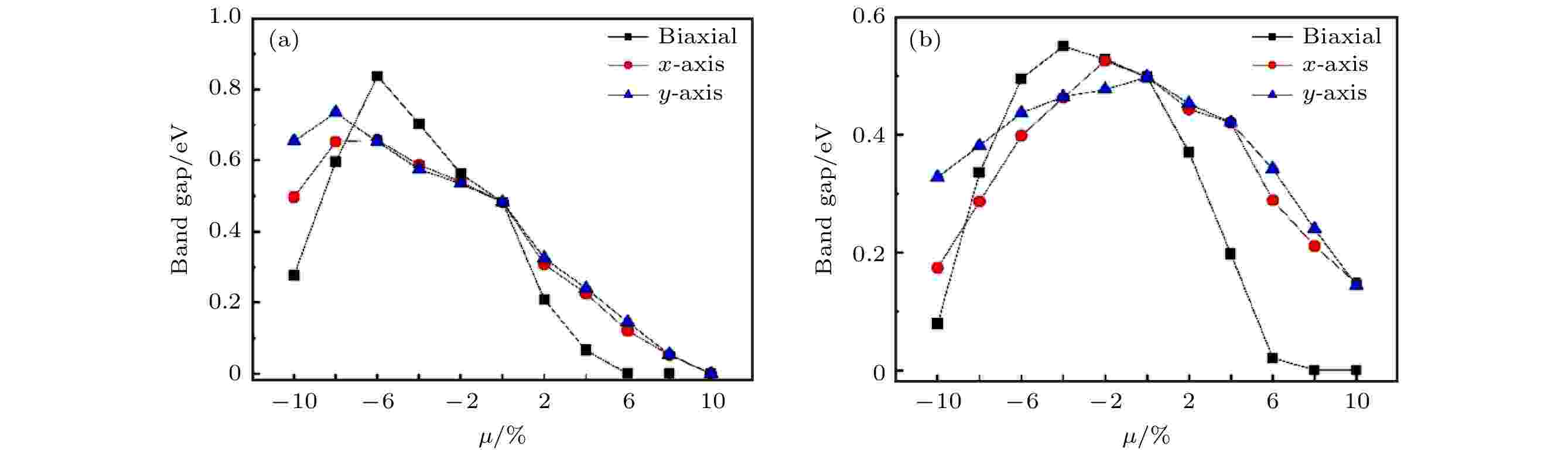图 9 (a) x方向与y方向单轴应变和双轴应变下In2Se3/InSe (I)的带隙; (b) x方向与y方向单轴应变和双轴应变下In2Se3/InSe (II)的带隙Figure9. (a) Band gap of In2Se3/InSe (I) under x-axis strain, y-axis strain and biaxial strain; (b) band gap of In2Se3/InSe (II) under x-axis strain, y-axis strain and biaxial strain.
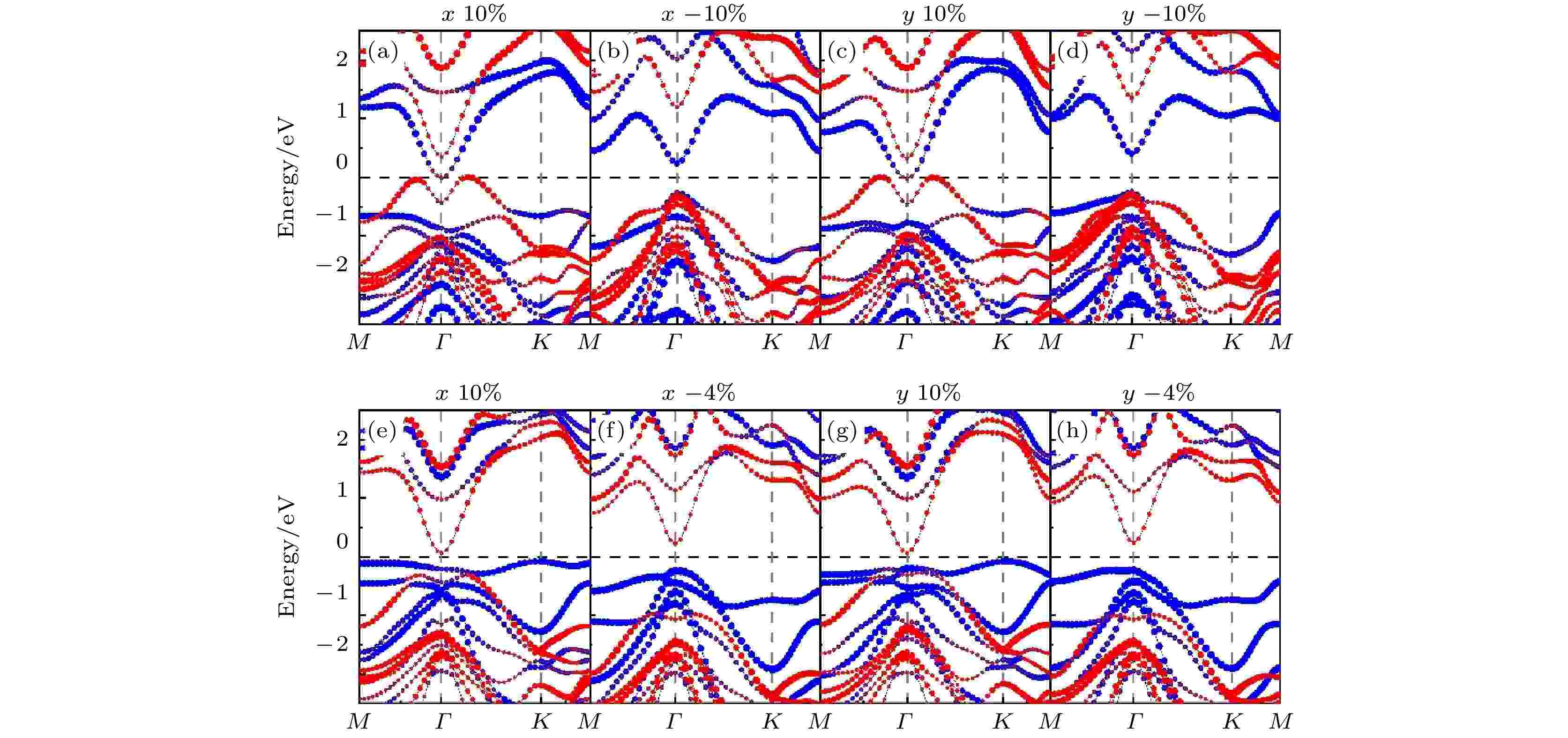图 10 (a)?(d)x和y方向10%、–10%应变下In2Se3/InSe (I)的投影能带结构; (e)?(h)x和y方向10%、–4%应变下In2Se3/InSe (II)的投影能带结构. 能带图中红色部分表示InSe对能带的贡献, 蓝色部分表示In2Se3对能带的贡献Figure10. (a)?(d) Projected band structure of In2Se3/InSe (I) under 10%, –10% x-axis strain and 10%, –10% y-axis strain; (e)?(h) projected band structure of In2Se3/InSe (II) under 10%, –4% x-axis strain and 10%, –4% y-axis strain. The red part of the energy band indicates the contribution of InSe, the blue part indicates the contribution of In2Se3.
值得注意的是, 通常应力会改变铁电材料的极化矢量的取向及大小, 也即挠曲效应[26,27]. 本文虽然没有直接计算不同应力下单层In2Se3极化矢量的变化, 但应力对极化矢量的影响在自洽计算中自然包含在内, 故本文不对极化矢量做具体的计算, 而是主要聚焦于能带在应力下的演化规律.
