摘要: 置信传播(BP)算法作为推断概率图模型的主流算法是求解随机块模型中联合概率分布的重要方法之一. 但现有的方法要么在处理核边结构问题上存在精度不足问题, 要么在理论的推导上存在近似太多, 导致求解过程复杂且难以理解问题, 或两个问题均存在. 当然, 精度不足也是由近似多造成的. 导致理论近似多且推导复杂的主要原因, 是随机块模型推断过程中求解联合概率分布并不是直接套用BP算法, 即处理的图(网络)与概率图模型的图不统一. 因此, 本文利用平均场近似修正联合概率分布, 使其完全匹配BP算法的迭代公式, 这样使得在理论推导上简单易懂. 最后通过实验验证, 该方法是有效的.
关键词: 随机块模型 /
置信传播算法 /
联合概率分布 /
平均场近似 English Abstract A mean-field approximation based BP algorithm for solving the stochastic block model Ma Chuang 1 ,Yang Xiao-Long 1 ,Chen Han-Shuang 2 ,Zhang Hai-Feng 3 1.School of Internet, Anhui University, Hefei 230039, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 12005001, 61973001, 11875069),the University Synergy Innovation Program of Anhui Province, China (Grant No. GXXT-2021-032), and the Natural Science Foundation of Anhui Province, China (Grant No. 2008085QF299)Received Date: 16 March 2021Accepted Date: 29 July 2021Available Online: 16 August 2021Published Online: 20 November 2021Abstract: As a mainstream algorithm for inferring probabilistic graphical models, belief propagation (BP) algorithm is one of the most important methods to solve the joint probability distribution in the stochastic block model. However, existing methods either lead to low accuracy in dealing with the core-periphery structure problem, or the theoretical derivation is difficult to understand due to a large number of approximation, or both exist. Of course, the reason for low accuracy comes from too many approximations. The main reason for many approximations and complex theoretical derivation is that the joint probability distribution in the inference process of the stochastic block model is not directly solved by the BP algorithm, that is, the graph (network) being processed is not consistent with the graph considered in the probabilistic graph model. Therefore, in this paper, a mean-field approximation is developed to modify the joint probability distribution to make the BP algorithm match perfectly, which makes the theoretical derivation easy to understand. Finally, the effectiveness of the proposed method is validated by the experimental results.Keywords: stochastic block model /belief propagation algorithm /joint probability distribution /mean-field approximation 全文HTML --> --> --> 1.引 言 复杂系统可以用复杂网络进行建模, 而复杂网络主要由点与边组成. 在现实中, 点与边的信息是可以直接或间接[1 ] 获取的, 如在航空网络系统中[2 ] , 节点为机场, 如果机场之间具有航班, 就存在一条边; 科学家合作网络[3 ] , 节点表示科学家, 如果两个科学家有合作就存在一条边等. 这些简单的点与连边关系可以帮助我们揭示复杂系统的隐藏信息, 如节点的属性, 可以对应着节点在系统中属于哪个功能块或组织[4 ] . 如航空网络中的核心与外围(边缘)机场[5 ] , 科学家合作网络中的特定研究领域的小组[6 ] 等. 因此, 如何通过节点的连边信息去探测这些中尺度结构, 如社团结构、核边结构(核心-边缘), 是一个重要的科学问题, 这些问题得到了来自各个领域****的研究.[6 ] . 社团结构的探测方法已经有很多, 主要有基于模块度的方法[7 -9 ] 、谱划分的方法[4 ,10 ] 、矩阵分解的方法[11 ,12 ] 、基于动力学的方法[13 ,14 ] 、随机块模型的方法[15 ,16 ] 以及其他方法[17 ,18 ] ; 核边结构的描述为核与核紧密相连, 核与边紧密相连, 边与边连接稀疏[19 ,20 ] . 相较于社团结构, 对核边结构探测方法的研究相对较少. 主要有给定某种中心性指标, 然后通过截断选取最重要的一部分节点作为核心节点[21 ,22 ] ; 定义核边结构的指标, 然后利用最优化方法求解[23 ,24 ] ; 通过随机块模型探测核边结构[25 ,26 ] 以及其他方法[5 ,27 -29 ] .[25 ] . 随机块模型是一种生成模型, 可以生成具有模块结构的网络[15 ] . 即首先给定n 个节点, 随机分配到k 个模块中. 假设向量$ {\boldsymbol {\gamma}} $ 表示每个模块的规模, 即$ \gamma_r $ 表示第r 个模块的大小占总节点个数的比例, 则每个节点就以$ \gamma_r $ 的概率分配到第r 模块中. 然后给定一个$ k\times k $ 的关联矩阵p s , 一个节点属于模块r )以$ p_{rs} $ 的概率相连. 这样就可以得到一个以参数$ {\boldsymbol {\gamma}} $ 与p $ k = 2 $ 时, 如果$ p_{11} > p_{12}, \;p_{22} > $ $ p_{12} $ , 生成的网络具有社团结构; 如果$p_{11}\geqslant p_{12} \geqslant p_{22}$ , 生成的网络具有核边结构.$ {\boldsymbol {\gamma}} $ 与p [16 ,25 ,26 ,30 ,31 ] , 而通过联合概率公式, 确定边际概率又是EM算法的关键部分与难点. 基于马尔科夫链的蒙特卡罗方法(MCMC)是解决该难点的一种较好的方法[30 ] , 但是由于采样空间非常大, 会造成时间复杂度过高、精度低的问题. 置信传播(BP)算法[32 ] 可以很好地解决上述问题[16 ,25 ,26 ,31 ] , 因此被广泛用来解决社团或核边结构的探测问题. BP算法用来推断马尔科夫随机场中的边际概率, 当马尔可夫网络是树状图时, 具有精确解; 当马尔可夫网络是稀疏的, 会得到近似精确解[33 ] .[16 ,31 ] , 但是处理核边结构探测问题时, 这种近似却是致命的, 因为核节点具有天然的大度性质. 因此, 在另外一篇文章中, 我们对BP算法进行了稍微的改进(IBP), 就可以很好地解决此问题[25 ] . 但是伴随而来的就是IBP算法的推导过程中, 需要进行大量的近似处理, 以及各种模糊的推导, 并不是可以套用BP算法公式[34 ] 直接得到的. 同样的道理, BP算法解决社团结构的探测问题时, 即使其中各种近似是合理的, 也会存在上述不能套用BP算法公式直接得到的情况. 这使得即使BP或IBP算法在社团划分或核边结构探测中能得到很好的结果, 但是推导过程却是复杂且难于理解, 或者说是不那么精确的. 因此, 本文从平均场近似[35 ] 的角度出发, 先应用平均场近似对联合概率进行处理, 得到可以完全匹配BP算法的形式, 然后再套用BP算法公式(而不是以往的先套用公式, 然后在公式里近似处理), 在不需要任何修改、近似以及假设的情况下直接得到求解边际概率的迭代公式. 使得随机块模型解决社团结构或核边结构探测问题时, 既可以保证结果的精度, 又可以保证理论的简单明了、有理有据.2.知识回顾 随机块模型最直接的用处就是按照某种需求生成具有某种模块结构的人工网络. 例如在社团探测中, 就可以用随机块模型生成具有社团结构的人工网络, 以此来评估社团挖掘算法的好坏. 但是本文将用到它的另外一个重要应用, 就是通过学习随机块模型中的参数使其最好地匹配给定网络, 从而揭示给定网络的结构. 显然, 这是一个参数估计问题, 可以采用最大似然估计的方法进行解决[16 ,25 ,26 ] .2.1.最大似然估计 2.1.最大似然估计 最大似然估计研究的是给定什么样的参数可以使得似然函数的值最大, 也就是使得已经发生的事件概率最大. 假设给定一个无权无向网络的邻接矩阵A $ A_{ij} = 1 $ 表示第i 个节点与第j 个节点相连, $ A_{ij} = 0 $ 表示不相连. 在随机块模型中, 当给定参数p $\boldsymbol {\gamma}$ , 则似然函数就可以用$ P({\boldsymbol{A}}|{\boldsymbol{p}}, {\boldsymbol{\gamma}}) $ 来表示. 因此, 需要最大化$ P({\boldsymbol{A}}|{\boldsymbol{p}}, {\boldsymbol{\gamma}}) $ , 以此求解p $ {\boldsymbol{\gamma}} $ , 从而来揭示网络的结构. 但是, 通过观察可以发现, 似然函数里包含一个隐形变量g $ g_i $ 表示节点i 所属的模块. 因此有1 )是一个含有隐变量的最大似然估计问题, 因此可以应用EM算法进行求解[36 ] .2.2.EM算法求解随机块模型 -->2.2.EM算法求解随机块模型 EM算法在理论推导上是根据詹森不等式不断求解对数似然函数的下界函数最优值, 以此逐渐收敛到原始函数的最优值. 因此, 对(1 )式取对数, 然后根据詹森不等式有[25 ,26 ] :$ q({\boldsymbol{g}}) = P({\boldsymbol{g}}|{\boldsymbol{A}}, {\boldsymbol{p}}, {\boldsymbol{\gamma}}) $ , 表示给定一个网络, 在参数p $ {\boldsymbol{\gamma}} $ 给定的条件下, 该网络每个节点分配为g 3 )式成立的情况下, (2 )式等号成立, 所以最大化公式(1 )问题可以转化为最大化$L\left( {\boldsymbol{p}}, {\boldsymbol{\gamma}} \right)$ 问题. 对$ L\left( {{\boldsymbol{p}}, {\boldsymbol{\gamma}} } \right) $ 进一步推导有:$ q({\boldsymbol{g}}) $ 的边际概率$ q^i_{\boldsymbol{r}} $ 表示节点i 属于群组r $ q({\boldsymbol{g}}) $ 的边际概率$ q^{ij}_{{\boldsymbol{rs}}} $ 表示节点i 属于群组r j 属于群组s $ g_i = {\boldsymbol{r}} $ , 则$ \delta _{{g_i}, {\boldsymbol{r}}} = 1 $ , 否则$ \delta _{{g_i}, {\boldsymbol{r}}} = 0 $ .4 )式求解最大值(满足约束条件$\displaystyle\sum\nolimits_{\boldsymbol{r}} {{\gamma _{\boldsymbol{r}}}} = $ $ 1$ ), 应用拉格朗日乘子法可以得到:p $ {\boldsymbol{\gamma}} $ , 根据(3 )式计算边际概率$ q^i_{\boldsymbol{r}} $ 与$ q^{ij}_{{\boldsymbol{rs}}} $ , 然后根据(7 )式与(8 )式计算新的p $ {\boldsymbol{\gamma}} $ , 重复上述过程直到收敛为止. 最后可以通过收敛的边际概率$ q^i_{\boldsymbol{r}} $ 的值对每个节点进行划分. 其中, 当需要探测社团结构时, 只需初始化p p 7 )式求解$ p_{{\boldsymbol{rs}}} $ 时, 需要计算任意节点对之间的$ q^{ij}_{{\boldsymbol{rs}}} $ 值, 这将花费大量的计算时间. 因此可以化简为$n_{\boldsymbol{r}} = \displaystyle\sum\nolimits_i {{\delta _{{g_i}, {\boldsymbol{r}}}}}$ , $ \left\langle \cdots \right\rangle $ 表示期望. 于是有7 )式可以写成:11 )式代替(7 )式只需要计算有边的节点对的两节点边际概率, 这将很大程度上减少计算量, 特别是在稀疏网络. 而且在BP算法中这种处理更显得尤为必要, 后面将进一步介绍.$ k^n $ 种构型)的方法根据(3 )式求解全概率$ q({\boldsymbol{g}}) $ 以此求解边际概率$ q^i_{\boldsymbol{r}} $ 与$ q^{ij}_{{\boldsymbol{rs}}} $ 是显然不可行的. 因此如何根据(3 )式求解边际概率$ q^i_{\boldsymbol{r}} $ 与$ q^{ij}_{{\boldsymbol{rs}}} $ 是EM算法的难点, 也是关键部分. 下面将介绍两种求解方法: MC采样和BP算法, 并分析他们在处理社团与核边结构探测中存在的不足之处.2.3.马尔科夫链蒙特卡罗方法(MCMC) -->2.3.马尔科夫链蒙特卡罗方法(MCMC) 这里应用MCMC模拟的方法按照联合概率公式(3 )对网络的划分构型(即$g = [g_1, g_2, \cdots, g_n]^{\rm T}$ )进行采样. 本文将采用单分量 Metropolis-Hastings (M-H) 方法[37 ] . 设$g^t = [g_1^t,\; g_2^t, \;\cdots, \;g_n^t]^{\rm T}$ 表示在马尔科夫链中第t 轮迭代后的状态, 其中每一轮迭代都需要对每个分量的状态进行一次迭代更新.$ t+1 $ 轮迭代中, 已经迭代好的分量(第i 个分量)的状态记为$ g_i^{t+1} $ . 假设要对第j 个分量进行采样, 首先设$ g_{-j}^{t+1} $ 表示在$ t+1 $ 轮迭代中在对第j 个分量进行处理时, 其他分量的状态. 特别地, 当对每一轮的各个分量进行迭代是按照顺序处理时, 有:j 个分量的状态$ g_j^{t} $ 随机变为一种状态$ \hat{g}_j^{t+1} $ , 因为有k 个模块, 所以建议转移概率$ q(g_j^{t}, \hat{g}_j^{t+1}) = $ $ q(\hat{g}_j^{t+1}, g_j^{t}) = 1/k $ . 根据(3 )式, 按照 M-H 规则接收这种状态(从状态$ g_j^{t} $ 变为状态$ \hat{g}_j^{t+1} $ )的概率:$ g_i(i\neq j) $ 为$ g_{-j}^{t+1} $ 中分别对应的量. 在区间$ (0, 1) $ 内按均匀分布取出一个数记为$ \mu $ , 如果$\mu\leqslant $ $ \alpha(g_j^{t}, \hat{g}_j^{t+1})$ , 则$ {g}_j^{t+1} = \hat{g}_j^{t+1} $ , 否则$ {g}_j^{t+1} = {g}_j^{t} $ . 当每一轮所有结点的状态更新完以后(也可以不按顺序更新), 再进行下一轮的更新. 在更新的轮数足够大的情况下, 采样的分布收敛到(3 )式的概率分布, 因此可以通过统计估计出边际概率$ q^i_{\boldsymbol{r}} $ 与$ q^{ij}_{{\boldsymbol{rs}}} $ .$ k^n $ 种可能, 在网络较大的情况下, 采样空间巨大, 很难收敛到(3 )式的概率分布, 从而造成计算结果产生误差, 并且不稳定. 下面介绍一种快速求解边际概率的方法, 即BP算法.2.4.BP算法 -->2.4.BP算法 32.4.1.BP算法简介 -->2.4.1.BP算法简介 BP算法可以用来推断马尔科夫随机场(又称为概率图模型)中的边际概率[33 ] . 在本文中, 考虑一种特殊的概率图模型—成对图模型. 成对图模型定义在一个无向图$G({\boldsymbol{V}}, {\boldsymbol{E}})$ 上, 每一个顶点$v_i\in {\boldsymbol{V }}$ 表示X $ x_i $ , 每一条边$(v_i, v_j)\in {\boldsymbol{E}}$ 表示随机变量$ x_i $ 与$ x_j $ 之间的某种依赖关系. 给定每个节点$ v_i $ 一个点位势$ \phi_i(x_i) $ , 以及每一条边$(v_i, v_j)\in {\boldsymbol{E}}$ 一个边位势$ \psi_{ij}(x_i, x_j) $ , 则在该成对马尔科夫网上的分布为Z 为归一化常数, 通常称为配分函数.14 )式这个联合概率的边际概率可以通过BP算法迭代公式求得, 迭代过程如下[34 ] :$ N(i) $ 表示节点$ v_i $ 的邻居, $ v_{i \to j}\left( {{x_i}} \right) $ 为概率图修改后(即删除节点$ v_j $ ) $ x_i $ 的边际概率, $ b_i(x_i) $ 为$ x_i $ 的边际概率. 另外还可以得到一条边上两个节点的联合概率:2.4.2.BP算法求解随机块模型 -->2.4.2.BP算法求解随机块模型 对于联合概率公式(3 ), 可以看成是一个马尔科夫网上的概率分布. 在这里, 马尔科夫网是一个全连通图, 且随机变量为$g = [g_1,\; g_2, \;\cdots, \;g_n]^{\rm T}$ . 对于一对节点$ (v_i, v_j) $ , 如果$ A_{ij} = 1 $ , 其边位势为$ \psi_{ij}(g_i, g_j) = $ $ P_{g_ig_j} $ , 如果$ A_{ij} = 0 $ , 其边位势为$ \psi_{ij}(g_i, g_j) = 1- $ $ P_{g_ig_j} $ , 节点$ v_i $ 的点位势为$ \phi_i(g_i) = \gamma_{g_i} $ . 所以根据BP 算法的迭代公式(15 ), 当j 节点是i 节点的邻居时, 可以得到[26 ,31 ] :$ \eta _{\boldsymbol{r}}^{i \to j} $ 对应于(15 )式中的$ v_{i \to j}( {{x_i}} ) $ , 在这里可以理解为移除节点$ v_j $ , $ v_i $ 属于模块r $ Z_{i \to j} $ 表示配分函数, $ N(i) $ 表示节点$ v_i $ 的邻居, $ N^*(i) = N(i)\bigcup \{i\} $ . 为了更方便更快捷地计算, 需要做两个假设, 会得到两个近似.假设1 如果第j 个节点不是第i 节点的邻居, 移除节点$ v_j $ 对节点$ v_i $ 属于模块r $ \eta _{\boldsymbol{s}}^{k \to i} \approx q^k_{\boldsymbol{s}} $ ;假设2 当网络规模很大且很稀疏的时候, 对集合$ {\boldsymbol{V}}/{N^ * } $ 中所有元素做运算近似于对集合V $ f({\boldsymbol{V}}/{N^ * } )\approx f({\boldsymbol{V}}) $ , 其中$ f(*) $ 代表某种运算.18 )式可以写成:16 )式可以得到边际分布$ q^i_{\boldsymbol{r}} $ :17 )式可以得到一条边上两个点的联合概率:20 )式和(22 )式, 直到收敛, 然后通过(22 )式与(24 )式即可计算出$ q^i_{\boldsymbol{r}} $ 与$ q^{ij}_{{\boldsymbol{rs}}} $ .$ {\boldsymbol{V}}/{N^ * } $ 中所有元素做运算近似于对集合V [25 ] , 可以很好地解决这个问题.2.4.3.修正后的BP算法(IBP) -->2.4.3.修正后的BP算法(IBP) 首先对联合概率分布公式(3 )稍作处理, 可得:[25 ,38 ] 假设3 当网络很大且很稀疏的时候, 对集合$ {\boldsymbol{V}}/\{i, j\} $ 中所有元素做运算近似于对集合V 19 )式一样的外场量, 但是这里的近似与(19 )式的近似相比, 也就是假设3与假设2相比不会依赖节点度的大小, 所以更适用于具有核边结构的网络. (26 )式可以写成:$q^i_{\boldsymbol{r}}$ 为[25 ,38 ] 17 )式可以得到一条边上两个点的联合概率:28 )式, (30 )式, (32 )式与(20 )式, (22 )式, (24 )相比, 可以发现算法改进后, 最终的结果仅仅是$ \dfrac{{{p_{{\boldsymbol{rs}}}}}}{{1 - {p_{{\boldsymbol{rs}}}}}} $ 代替了$ p_{{\boldsymbol{rs}}} $ , 没有增加任何多余的计算复杂度, 但是修改后的方法已经验证了更适用于含有大度节点的网络[25 ] , 如核边结构网络.15 ), 从联合概率公式(25 )并不能直接推导得到的信使迭代公式(26 )(这种直接写法是参考文献[35 ]). 这是因为概率分布公式(25 )相比(3 )式虽然做了变形处理, 但是两个公式在数值上依然相等, 即在把一个全连通图当做一个马尔科夫网的情况下, 对于一对节点$ (v_i, v_j) $ , 如果$ A_{ij} = 1 $ , 其边位势还是$ \psi_{ij}(g_i, g_j) = P_{g_ig_j} $ , 如果$ A_{ij} = 0 $ , 其边位势也还是$\psi_{ij}(g_i, g_j) = 1- P_{g_ig_j}$ . 所以说这里得到的信使迭代公式应该还是(18 )式而不是(26 )式.25 )得到相比信使迭代公式(18 )更好的(26 )式, 换句话说, 如果想得到比BP算法更好的IBP 算法, 可以按照下面的思路去理解. 这里的马尔科夫网不仅仅是一个全连通图, 还需要在全连通图上再加上M (原网络上边的个数)条额外边. 对于一对节点$ (v_i, v_j) $ , 如果$ A_{ij} = 1 $ , 马尔科夫网上的边就要看成两条边, 其边位势就分解成$ \psi_{ij}(g_i, g_j) = 1-P_{g_ig_j} $ 与$\psi_{ij}(g_i, g_j) = \dfrac{P_{g_ig_j}}{1-P_{g_ig_j}}$ , 如果$ A_{ij} = 0 $ , 其边位势还是$ \psi_{ij}(g_i, g_j) = 1-P_{g_ig_j} $ . 这样理解以后, 就可以按照BP算法公式(15 )得到信使迭代公式(26 ). 即使这样, 根据假设3与假设2还是得不到最终的信使迭代公式(28 ), 在这里还应满足相比假设2更严格的假设, 即: 在马尔科夫网中所有边位势为$ \psi_{ij}(g_i, g_j) = {1-P_{g_ig_j}} $ 的节点对$ {(v_i, v_j)} $ (包括原网络中不存在边以及额外增加的存在边), 有$ q^i_{\boldsymbol{r}} \approx \eta _{\boldsymbol{r}}^{i \to j} $ . 意思就是存在一些少部分节点对$ {(v_i, v_j)} $ , 即使$ v_j $ 是$ v_i $ 的邻居也要近似处理, 即移除节点$ v_j $ 对节点$ v_i $ 属于模块r 2.4.4.小 结 -->2.4.4.小 结 BP算法可以对联合概率公式(3 )与(25 )进行求解, 以此得到两种迭代公式(前者用BP算法表示, 后者用IBP算法表示)求解边际概率. 但是都存在一些问题: 1)在BP 算法中, 要满足假设1与假设2, 因此不适用核边结构的探测; 2)在IBP算法中, 虽然在实验中已经验证了比BP算法有着更好的性能, 但是在理论上处理得太过复杂, 还存在一些在理论上不易理解的假设.3 )与(25 )进行近似处理(而不是在BP算法的推理中近似处理), 得到一个新的概率公式, 这个概率公式要满足两个条件: 1)由这个公式导出的马尔科夫随机网与原始网络一致; 2)这个公式在形式上与(14 )式完全一致. 前者可以保证马尔科夫网的稀疏性, 后者可以保证在应用BP算法的时候简洁明了且便于理解.3.基于平均场近似的BP算法 首先对联合概率公式(3 )进行平均场近似处理. 概率分布(3 )式可以表示为${h_i} = \displaystyle\sum\nolimits_{j \ne i} {\left( {1 - {A_{ij}}} \right)\ln \left( {1 - {p_{{g_i}{g_j}}}} \right)}$ , 通过平均场近似有${d_i} = \displaystyle\sum\nolimits_j {{A_{ij}}}$ , 表示节点$ v_i $ 的度. 则(34 )式可以写成:3 )经过两次平均场近似可以写成:$ (v_i, v_j) $ , 其边位势为$ \psi_{ij}(g_i, $ $ g_j) = P_{g_ig_j} $ , 对于一个节点$ v_i $ , 其点位势为$\phi_i(g_i) = $ $ {\exp \left[ {\displaystyle\sum\nolimits_{\boldsymbol{s}} {\ln \left( {1 - {p_{{g_i}{\boldsymbol{s}}}}} \right)\left( {1 - \dfrac{{{d_i}}}{n}} \right)\displaystyle\sum\nolimits_j {q_{\boldsymbol{s}}^j} } } \right]{\gamma _{{g_i}}}}$ . 所以直接根据BP算法的公式(15 )—(17 )式, 可以不经过任何近似地得到:$ Z_{i\rightarrow j} $ 与$ Z_i $ 可以分别表示为3 )先进行变形、再平均场近似处理. 即概率分布(3 )式可以表示为${\hat h_i} = \displaystyle\sum\nolimits_{j \ne i} {\ln \left( {1 - {p_{{g_i}{g_j}}}} \right)}$ , 通过平均场近似有3 )经过一次平均场近似可以写成$ (v_i, v_j) $ , 其边位势为$\psi_{ij}(g_i, g_j) = $ $ {\dfrac{{{p_{{g_i}{g_j}}}}}{{1 - {p_{{g_i}{g_j}}}}}}$ , 对于一个节点$ v_i $ , 其点位势为$\phi_i(g_i) = $ $ \exp \left[ {\displaystyle\sum\nolimits_{\boldsymbol{s}} {\ln \left( {1 - {p_{{g_i}{\boldsymbol{s}}}}} \right)\displaystyle\sum\nolimits_j {q_{\boldsymbol{s}}^j} } } \right]{\gamma _{{g_i}}}$ . 所以直接根据BP 算法的公式(15 )—(17 )式, 可以得到:$ Z_{i\rightarrow j} $ 与$ Z_i $ 可以分别表示为$ {{{d_i}}}/{n} \to 0 $ 且$\ln \left( {1 - {p_{{\boldsymbol{rs}}}}} \right) \to $ $ {p_{{\boldsymbol{rs}}}}$ , 则MFBP算法的外场量可以近似为4.中尺度结构的探测 下面将在社团结构及核边结构探测上进行实验验证. 在社团结构探测中, 为了验证不同算法探测结果的好坏, 将采用NMI指标进行衡量, 即[39 ] :X 与Y 分别为算法探测的结果以及真实的结果; $ I(X, Y) $ 表示X 与Y 之间的互信息; $ H(X) $ 与$ H(Y) $ 分别表示X 与Y 的信息熵.$ F1 $ 指标进行衡量, 即[40 ] :P 表示预测结果中, 预测为正(本文中为核)的样本中预测正确的概率, R 表示数据样本中, 正样本中预测正确的概率.4.1.社团结构探测 4.1.社团结构探测 首先采用随机块模型生成具有社团结构的基准网络, 以此来验证MFBP算法和MFIBP算法分别与BP算法和IBP算法的区别. 假设有k 个模块, 则每个节点就以$ \gamma_{\boldsymbol{r}} $ 的概率分配到第r $ p_{{\boldsymbol{rs}}} = c_{\rm in}/n ({\boldsymbol{r}} = {\boldsymbol{s}}) $ 和$p_{{\boldsymbol{rs}}} = c_{\rm out}/n ({\boldsymbol{r}} \ne {\boldsymbol{s}})$ , 因此网络的平均度为$c = $ $ \displaystyle\sum\nolimits_{{\boldsymbol{r}} < {\boldsymbol{s}}} {2{\gamma _{\boldsymbol{r}}}{\gamma _{\boldsymbol{s}}}{c_{\rm out}}} + \displaystyle\sum\nolimits_{\boldsymbol{r}} {\gamma _{\boldsymbol{r}}^2{c_{\rm in}}}$ .$ \gamma_{\boldsymbol{r}} = 1/k $ , 则网络的平均度为$ c = \left[ {{c_{\rm in}} + q\left( {{c_{\rm out}} - 1} \right)} \right]/q $ . 定义模块外部与社团内部的连接概率比为$ \varepsilon = {c_{\rm out}}/{c_{\rm in}} $ . 所以, 当$ \varepsilon < 1 $ 时生成网络具有社团结构, 且越小社团结构越明显; 当$ \varepsilon = 1 $ 时生成网络为ER随机图. 当$ n \to \infty $ 时, 网络检测社团结构会存在一个阈值[38 ] :$ \varepsilon > \varepsilon ^ * $ 时, 各种社团算法都无法检测出社团结构; 当$ \varepsilon < \varepsilon ^ * $ 时, BP算法可以探测出社团结构.图1(a) 可以验证, 所有结果为10 次结果的平均值(下同). 通过图1(b) —图1(d) 可以发现, 当网络连接稀疏且规模较小时, BP算法、MFBP算法、IBP算法以及MFIBP算法的结果也是一致的. 但是, 在网络连接稠密的情况下(如图2 ), 可以发现MFBP算法要优于BP算法, 且与MFIBP算法、IBP算法一致.图 1 稀疏基准网络社团结构探测 (a) $n = 10000$ , $c = 3$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.27$ ; (b) $n = 200$ , $c = 10$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.520$ ; (c) $n = 200$ , $c = 10$ , $\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (d) $n = 200$ , $c = 10$ , $\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ , $\varepsilon^* = 0.419$ Figure1. Community structure detection in sparse benchmark networks: (a) $n = 10000$ , $c = 3$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.27$ ; (b) $n = 200$ , $c = 10$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.520$ ; (c) $n = 200$ , $c = 10$ , $\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (d) $n = 200$ , $c = 10$ , $\gamma = {[1/3,\; 1/3, \;1/3]^{\rm T}},$ $\varepsilon^* = 0.419$ 图 2 稠密基准网络社团结构探测 (a) $n = 200$ , $c = 50$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.75$ ; (b) $n = 200$ , $c = 50$ , $\gamma = {[0.3, \;0.7]^{\rm T}}$ , (c) $n = 200$ , $c = 30$ , $\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ , $\varepsilon^* = 0.599$ Figure2. Community structure detection in dense benchmark networks: (a) $n = 200$ , $c = 50$ , $\gamma = {[0.5,\; 0.5]^{\rm T}}$ , $\varepsilon^* = 0.75$ ; (b) $n = 200$ , $c = 50$ , $\gamma = {[0.3,\; 0.7]^{\rm T}}$ ; (c) $n = 200$ , $c = 30$ , $\gamma = {[1/3,\; 1/3,\; 1/3]^{\rm T}}$ , $\varepsilon^* = 0.599$ 4.2.核边结构探测 -->4.2.核边结构探测 生成具有核边结构特性的基准网络来验证MFBP算法和MFIBP算法分别与BP算法和IBP算法的区别. 给定3个参数: 核与核的连边概率$ P_{\rm CC} $ , 核与边的连边概率$ P_{\rm CP} $ , 以及边与边的连边概率$ P_{\rm PP} $ , 当设置$ {P_{\rm CC}} > {P_{\rm CP}} > {P_{\rm PP}} $ 时, 可以生成一个具有核边结构的网络[28 ] . 在本文中, 设$ P_{\rm PP} = $ $ 0.05 $ , $ P_{\rm CC} = \theta $ , $ P_{\rm CP} = 0.6\theta $ . 网络的大小$ n = 200 $ , 其中核节点的个数为50, 边节点的个数为150. 图3 所示为4种算法在不同参数基准网络的核边结构的探测情况, 其中实验结果为10次结果的平均值. 同样可以发现, MFBP算法要优于BP算法, 且与MFIBP算法、IBP算法一致. 在BP 算法中, 当核边结构足够明显时, 却表现出了较差的结果, 这是因为核边结构明显, 意味着网络结构稠密, 特别是核节点的度很大, 这会导致(19 )式关于用所有节点集合近似邻居的补集变得极其不合理, 而MFBP算法、IBP算法以及MFIBP算法没有这方面的缺陷.图 3 基准网络的核边结构探测Figure3. CP structure detection in benchmark networks.[5 ] . 应用BP 算法, 求解结果有27 个核; 应用MFBP算法, 求解结果有34个核; 应用IBP算法, 求解结果有47 个核; 应用MFIBP算法, 求解结果有47个核. 其中对应的参数结果见(54 )式—(57 )式. 为了验证上述4个算法求得结果的精确性, 采用MCMC采样求解EM算法, 共采样1000 轮(每轮n 次), 得到的结果共有47 核, 具体参数如(58 )式. 如果把MCMC结果作为真实结果, 则BP算法、MFBP算法、IBP算法以及MFIBP算法结果的$ F1 $ 值分别为0.730, 0.840, 1.000以及1.000. 从上述结果可以看出, 在美国航空网络的核边结构实验中, MFBP算法结果要优于BP算法, MFIBP算法结果与IBP算法一致, 且接近精确解. 而且MFIBP算法要优于MFBP算法, 这是因为MFBP算法比MFIBP算法多一次平均场近似.5.结 论 本文详细描述了随机块模型探测社团结构、核边结构的理论, 以及MCMC和BP算法求解该理论的方法, 并分析其优缺点. 通过理论分析以得到: 1)原始的BP算法不适用于核边结构的探测; 2)修正后得到的IBP算法, 虽然适用于核边结构, 但在理论上推导近似多且不明朗; 3)无论是BP算法还是IBP算法, 所处理的马尔科夫网(联合概率分布), 既不是原始网络, 也不满足网络稀疏条件. 最后一条是造成随机块模型中BP算法和IBP算法理论难以理解的主要原因. 针对于此, 本文首先对联合概率分布进行平均场近似, 得到一个好的联合分布函数, 然后可以直接套用BP 算法理论, 且在这一步不需要任何近似, 使得BP算法求解随机块模型这一套方法, 不仅在结果上效果显著, 而且在理论上通俗易懂. 这种先通过平均场近似再套用BP 算法还适用于利用最小化哈密顿量(关于模块度的函数)探测社团结构的方法中[38 ] , 和本文一样, 将使得理该论推导部分变得简单易懂. 




















































































































































































































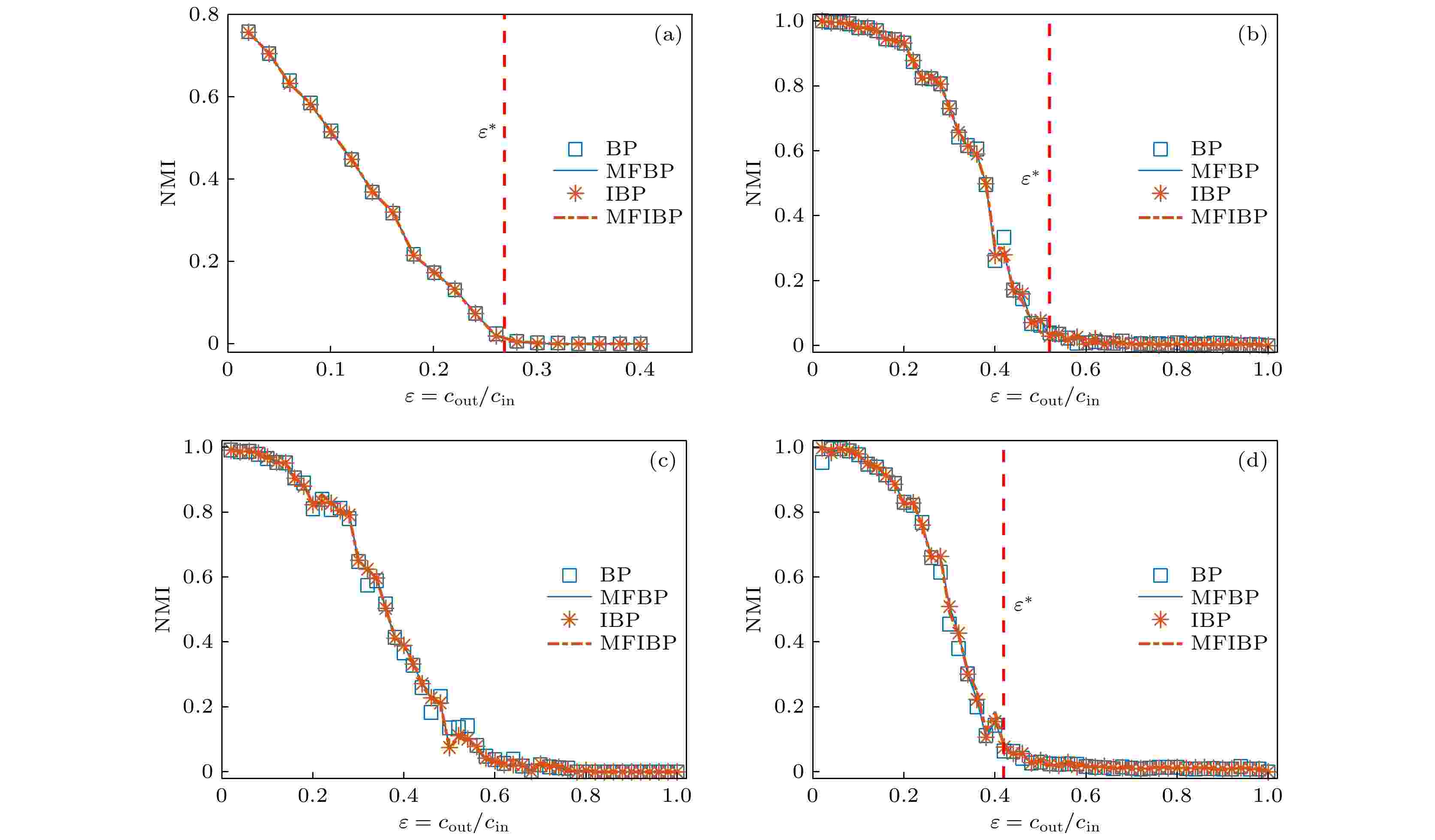 图 1 稀疏基准网络社团结构探测 (a)
图 1 稀疏基准网络社团结构探测 (a) 

























































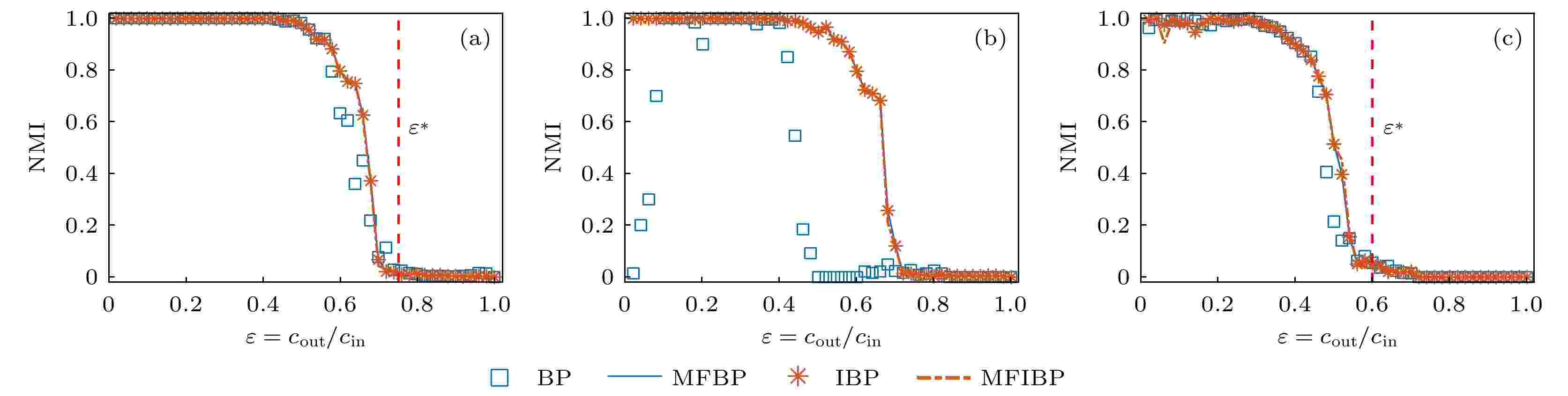 图 2 稠密基准网络社团结构探测 (a)
图 2 稠密基准网络社团结构探测 (a) 














































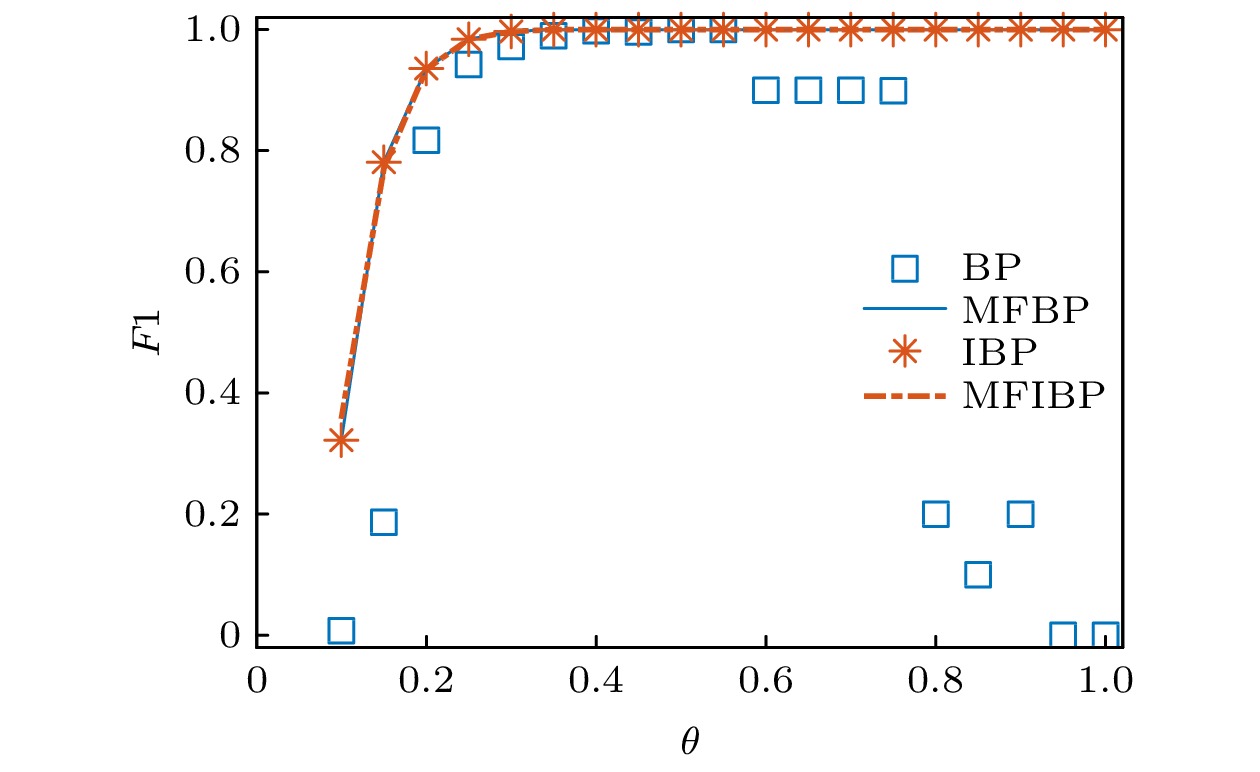 图 3 基准网络的核边结构探测
图 3 基准网络的核边结构探测
