摘要:高铬铸铁中M₇C₃碳化物大小适中、弥散均匀分布, 有利于提高合金的耐磨性. 为分析凝固过程中M₇C₃碳化物晶粒在基体中的形貌及分布、M₇C₃碳化物与奥氏体晶粒生长的相互作用、引起的溶质偏聚对最终M₇C₃碳化物粒径分布的影响, 本文开发了Fe-C-Cr三元合金小面晶M₇C₃碳化物与奥氏体晶粒共生长的二维微观元胞自动机模型, 模型中加入潜热释放对凝固过程温度场的影响, 由C, Cr两溶质界面扩散共同确定晶体生长速度, 由凝固路径数据表插值获取液相元胞的溶质平衡浓度, 设定M₇C₃碳化物邻胞结构并优化形状因子来保持M₇C₃碳化物小面晶形貌, 模拟了Fe-4%C-17%Cr三元合金(C和Cr的质量分数分别为4%和17%)初生M₇C₃碳化物和共晶奥氏体晶粒的生长演变过程. 研究表明, M₇C₃碳化物和奥氏体晶粒各自的生长速度随着界面液相中C, Cr溶质的超饱和度和贝克列数的增大而增大; 随着奥氏体的析出和晶粒生长, M₇C₃碳化物晶粒的生长速度明显增快; 当奥氏体晶粒逐渐接触并包围M₇C₃碳化物晶粒时, 两相晶粒生长速度逐渐降低. 凝固过程中, 奥氏体晶粒生长向外排出C, Cr溶质, 与吸收C, Cr溶质生长的M₇C₃碳化物晶粒互补, 致使二者生长互相促进, 最终奥氏体晶粒包围M₇C₃碳化物晶粒生长. 预测的冷却曲线与实验冷却曲线变化趋势相符; 最终凝固组织形貌和M₇C₃碳化物体积分数与实验相符; 剩余液相、奥氏体中C, Cr溶质浓度演变也与Gulliver-Scheil, Partial Equilibrium, Lever Rule模型预测结果相符.
关键词: Fe-C-Cr三元合金/
M₇C₃小面晶/
二相共生长/
元胞自动机

English Abstract

全文HTML

--> --> -->

高铬铸铁被广泛应用于发电厂、矿山、炼钢厂的高耐磨零部件中^[1], 其优异的耐磨性主要来自增强相M₇C₃碳化物的高硬度^[2-5]. M₇C₃碳化物大小适中, 弥散均匀分布于基体中, 有利于提高基体的韧性与合金的耐磨性. ****们^[6-8]针对高铬铸铁凝固过程中Cr/C比、冷却速率等对M₇C₃碳化物、奥氏体的数量、尺寸、分布等展开了大量实验研究, 本文作者^[9]也预测了高铬铸铁的凝固路径, 以期改进材料的耐磨性. 对于凝固过程中M₇C₃小面晶碳化物在基体中的形貌分布受何影响, M₇C₃碳化物与奥氏体枝晶生长的相互作用, 引起的溶质偏聚对最终M₇C₃碳化物粒径分布作用规律的相关数值模拟未见他人报道.
晶粒生长及形貌演变的数值模拟方法中, 微观元胞自动机 (microscopic-scale cellular automata, MCA)方法能够耦合温度场、溶质场、流场等各物理场演变过程, 有效描述凝固过程中枝晶内部形貌的演化特征, 相比于相场法, MCA法能够模拟较大尺寸材料的组织演变, 计算耗时较短, 因而被广泛应用于模铸、连铸、定向凝固、增材制造及焊接等过程的组织模拟中^[10,11].
目前, 采用微观元胞自动机方法进行单相枝晶生长的模拟已发展至三元以上合金^[12-18], 为确定多元合金中枝晶的生长速度, 一种做法是采用界面动力学系数与过冷度的乘积来计算, 其界面平衡固相成分、平衡液相线温度通过热力学计算引擎(如PanEngine、Thermo-Calc等)来获得. 基于此, Zhu等^[12]预测了Al-Cu-Mg合金中单一枝晶相的微观结构; 戴挺^[13]等进行了Al-Cu-Mg-Si四元合金枝晶生长模拟. 此法未体现多元合金溶质间扩散对生长速度的相互作用关系. 再一种做法是, 生长速度采用局部溶质平衡浓度与实际浓度的差值求得. 如Zhu等^[19]针对Al-Si二元合金共晶组织演变的模型, 以及张蕾等^[20]针对球墨铸铁(Fe-C二元合金)中石墨与奥氏体离异共晶生长的模型. 此方法多针对二元合金. 第三种做法是基于界面生长速度与多溶质生长贝克列(Pe)数对应关系, 通过耦合各溶质的超饱和度方程和界面溶质守恒方程求得界面生长速度, 可明确给出多元合金各溶质间扩散对生长速度的相互作用. 其中界面溶质浓度对应的液相线温度及液相线斜率等热力学参数由热力学平衡计算获得. 基于此, 本文作者模拟了Fe-C-Cr三元合金凝固过程中奥氏体^[14]及铁素体+奥氏体包晶相^[15]的生长速度, 石玉峰等^[16]模拟了Al-Si-Mg三元合金枝晶生长形貌. 另外, Michelic等^[17]等基于元胞自动机法改进的VFT (virtual front-tracking)模型, 引入外插函数求解界面两侧溶质平衡浓度, 再利用界面溶质守恒方程求得生长速度, 模拟了Fe-C-Si-Mn-P五元合金枝晶的生长过程. 在枝晶和第二相晶粒共生长的模拟中, Zhu等^[19]模拟了Al-Si二元合金共晶组织演变; 张蕾等^[20]模拟了球墨铸铁(Fe-C二元合金)中石墨与奥氏体依循离异共晶模式的协同竞争生长, 并将石墨晶粒处理成球状. 本课题组张晛韦等^[18]模拟了亚共晶球墨铸铁(Fe-C-Si三元合金)中石墨与奥氏体的离异共晶生长, 其石墨和奥氏体的生长速度采用上述第三种做法.
本研究中, M₇C₃碳化物为密排六方(HCP)小面晶结构^[21,22], 在二维截面中呈现六边形形状. 对于小面晶生长过程中形状的保持, Stefan-Kharicha等^[23]采用的前沿跟踪模型, 分别计算生长面法向和切向速度, 并通过保持晶角位置随邻面生长移动来保持晶面形状, 模拟了热浸镀锌过程中六边形面晶(Fe₂Al₅)的生长. 付振南等^[24]通过特别规定元胞邻居关系及界面单元捕获规则, 模拟了AZ91D镁合金中密排六方结构枝晶的生长. 董祥雷等^[25]在相场模型中引入小面晶各向异性修正方程, 模拟了各向异性稳态六方GaN螺旋结构形貌. 综上, 目前仅有****针对其他体系中相近的六方小面晶形貌进行了模拟, 未见针对Fe基三元合金中M₇C₃碳化物生长, 尤其是M₇C₃碳化物与奥氏体共生长模拟的报道.
本课题组前期工作^[26]中, 采用微观元胞自动机模型结合传热传质过程, 引入界面溶质贝克列数和超饱和度方程来求解界面多溶质平衡浓度, 模拟了高Cr铸铁(Fe-C-Cr合金)凝固过程中M₇C₃碳化物和奥氏体晶粒的协同生长过程. 本文进一步加入了潜热释放影响. 将液相元胞溶质平衡浓度更新, 由原采用的Fe-C二元合金液相溶质平衡浓度公式, 替换为通过Gulliver-Scheil (GS)模型结合热力学平衡计算预测的Fe-C-Cr三元合金凝固路径获得; 将相变界面溶质扩散系数由线性插值改为调和插值, 更合理反映相变界面扩散特性; 并优化了M₇C₃碳化物形状修正因子. 模拟了Fe-4%C-17%Cr合金(C和Cr的质量分数分别为4%和17%, 下同)凝固过程中M₇C₃碳化物和奥氏体晶粒形貌演变及浓度迁移, 深入分析了M₇C₃碳化物和奥氏体共生长过程中溶质贝克列数、超饱和度与界面溶质平衡浓度、生长速度之间关系, 预测的冷却曲线和最终凝固组织形貌分别与实验进行了对照, 并将剩余液相和奥氏体中C, Cr溶质浓度演变规律与凝固路径预测结果进行了对比.

建立Fe-4%C-17%Cr三元合金M₇C₃碳化物和奥氏体共生长演变过程二维微观元胞自动机模型.
2

-->

2.1.基本假设

1)不考虑熔体的流动;
2)忽略动力学过冷;
3)忽略溶质间互扩散;
4)固/液界面始终处于平衡状态;
5)忽略M₇C₃碳化物在奥氏体中的生长;
6)热扩散的尺度比溶质扩散高3—4个数量级, 全场温度均匀变化.
2 -->

2.2.温度场

由于热量传递速率远大于溶质扩散速率, 认为温度场均匀变化. 考虑凝固过程中潜热释放的影响, 温度场控制方程如下:

$ \frac{{\partial T}}{{\partial t}} = \dot T + \frac{{\mathop L\nolimits_{{\gamma }} }}{{\mathop c\nolimits_{\rm p} }} \frac{{\partial \mathop f\nolimits_{{\gamma }} }}{{\partial t}} + \frac{{\mathop L\nolimits_{\text{M}} }}{{\mathop c\nolimits_{\rm p} }} \frac{{\partial \mathop f\nolimits_{\text{M}} }}{{\partial t}} \text{, } $

式中, $ \dot{T} $为冷却速率, 冷却速率的选取参照实验^[22]冷却曲线; $ \mathop L\nolimits_{{\gamma }} $为奥氏体凝固潜热; $ \mathop L\nolimits_{\text{M}} $为M₇C₃碳化物凝固潜热; ${c}_{\rm p}$为液相比热容; $ \mathop f\nolimits_{{\gamma }} $为奥氏体质量分数; $ \mathop f\nolimits_{\text{M}} $为M₇C₃碳化物质量分数.
2 -->

2.3.溶质扩散方程

在计算区域内引入势函数P (等效液相成分), 把整个计算区域处理为单相. 统一的溶质扩散方程为

$ \frac{{\mathop {\partial \overline C }\nolimits_i }}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\mathop D\nolimits_i \frac{{\mathop {\partial P}\nolimits_i }}{{\partial {x^{}}}}} \right) + \frac{\partial }{{\partial y}}\left( {\mathop D\nolimits_i \frac{{\mathop {\partial P}\nolimits_i }}{{\partial {y^{}}}}} \right) \text{, } $

式中D_i为溶质扩散系数; 下标i代表溶质C, Cr, 下同. 在液相L, M₇C₃碳化物M, 奥氏体γ和界面胞中, $ {P_i} $分别为$ C_{{\text{L}}, i}^{} $, $\displaystyle \sum\nolimits_n \Delta f_{\text{M}}^nC_{{\text{L}}, i}^n$, $C_{{{\gamma }}, i}^{}/{k_{{\text{p}}, {{\gamma/{\rm L} }}, i}}$及$C_{{\text{L}}, i}(1 - f_{{\gamma }} - f_{\text{M}}^{}) + \displaystyle \sum\nolimits_n \Delta f_{\text{M}}^nC_{{\text{L}}, i}^n + f_{{\gamma }}^{}C_{{{\gamma }}, i}/{k_{{{{\rm p}, \gamma/{\rm L} }}, i}}$. 这里$ {C}_{\mathrm{\gamma }, i} $和$ {C}_{\mathrm{L}, i} $为对应的奥氏体和液相的溶质浓度; $ \Delta f_{\text{M}}^n $为M₇C₃碳化物质量分数增量; ${k_{{{{\rm p}, \gamma/{\rm L} }}, i}}$为奥氏体/液相界面平衡溶质分配系数.
方程(2)离散时, 当两个相邻元胞有1个为M₇C₃碳化物或奥氏体时界面扩散系数$ \mathop D\nolimits_{i/{\text{e}}} $相应取$ {D}_{\mathrm{M}, i} $或$ {D}_{\mathrm{\gamma }, i} $, 否则通过调和插值计算界面扩散系数:

$ \mathop D\nolimits_{i/{\text{e}}} = \left( {\mathop D\nolimits_{i/{\text{E}}} \cdot \mathop D\nolimits_{i/{\text{P}}} } \right)/\left[ {(1 - \mathop f\nolimits_{\text{e}} )\mathop D\nolimits_{i/{\text{E}}} + \mathop f\nolimits_{\text{e}} \mathop D\nolimits_{i/{\text{P}}} } \right], $

式中, 下标e为两元胞界面位置, 下标P和E为中心元胞和其邻居元胞; 每个元胞中的溶质扩散系数为其中各相的加权平均值, 即${D}_{i}={f}_{\mathrm{\gamma }}{D}_{\mathrm{\gamma }, i}+{f}_{\mathrm{M}}{D}_{\mathrm{M}, i}+ $$ {f}_{\mathrm{L}}{D}_{\mathrm{L}, i}$; $ {f}_{\mathrm{e}} $为界面e距E元胞中心距离与P和E元胞中心间距之比, 这里网格均匀, $ {f}_{\mathrm{e}} $=1/2.
$ \mathop {\bar C}\nolimits_i $为平均溶质浓度:

$ \bar {\mathop C\nolimits_i } = \mathop {\mathop f\nolimits_{\text{M}} \mathop C\nolimits_{{\text{M}},i} + f}\nolimits_{{\gamma }} \mathop C\nolimits_{{{\gamma }},i} + \mathop f\nolimits_{\text{L}} \mathop C\nolimits_{{\text{L}},i} \text{, } $

式中, $ \mathop f\nolimits_{\text{L}} $为液相质量分数, $ {C}_{\mathrm{M}, i} $为对应的M₇C₃碳化物溶质浓度. 浓度场采用无扩散的边界条件:$\dfrac{{\partial C}}{{\partial x}} = \dfrac{{\partial C}}{{\partial y}} = 0$.
2 -->

2.4.形　核

模型中, 为与实验^[22]结果对照, M₇C₃碳化物、奥氏体晶粒的形核位置和形核数量参照实验形貌设定. 实际形核数量为形核密度、形核过冷度等的函数关系^[27], 还受铸锭尺寸影响, 同时由形核Gaussian分布可知, 增大形核过冷度会减小形核数量. 实验分析表明^[28], 增大冷却速率, 一次、二次枝晶臂尺寸减小, 说明形核数量随冷却速率增大而增大. 由GS模型凝固路径预测, Fe-4%C-17%Cr合金中M₇C₃碳化物和奥氏体晶粒的析出温度分别是1304 ℃和1266 ℃, 形核过冷度随机设定. 当元胞局部过冷度大于形核过冷时, 该元胞形核, 单元状态即刻由液态转变为界面元胞, 并被赋予1个随机的晶体学取向θ. 基于奥氏体为四重对称的枝晶状, 奥氏体晶粒的取向范围设为[–π/4, π/4]; 而M₇C₃碳化物晶粒在二维截面具有六重对称性, 其晶粒取向范围设为[–π/6+2, π/6+2], 此处+2是为了区分M₇C₃碳化物与奥氏体晶粒而设置.
2 -->

2.5.生长动力学

3 -->

2.5.1.界面热力学平衡

界面元胞满足局部热力学平衡条件, 局部温度与液相线温度之间满足(5)式:

$ T = \mathop T\nolimits_{{\text{L}},k} - \mathop {\Delta T}\nolimits_{\text{R}} - \mathop {\Delta T}\nolimits_{\text{C}} \text{, } $

式中, T是界面胞温度; $ {T}_{{\rm L},k} $是液相线温度(下标k指析出M或γ相); $ {\Delta T}_{\mathrm{R}} $和$ {\Delta T}_{\mathrm{C}} $分别是曲率过冷和成分过冷.
3 -->

2.5.2.曲率过冷

曲率过冷表达式为

$ \Delta {T_{\text{R}}} = \varGamma Kf(\varphi ,\theta ) \text{, } $

式中, $ \varGamma $为固液界面Gibbs-Thomson系数, M₇C₃碳化物和奥氏体分别对应${\varGamma _{\text{M}}}$, ${\varGamma _{{\gamma }}}$; $ K $为界面曲率, 采用计数法计算^[29]; $ f(\varphi , {\theta _{}}) $为界面各向异性函数. 根据Gibbs-Thomson方程, 界面各向异性函数如下:

$ f(\varphi ,\theta ) = 1 + (1 - {k^2})\varepsilon \cos [k(\varphi - \theta )] \text{, } $

式中, $ k $为晶体对称相关数, 对于面心立方晶体, 如奥氏体取$ k $ = 4, 对于密排六方晶体, 如M₇C₃碳化物, 取$ k $ = 6; $ \varepsilon $为界面能各向异性系数, 界面各向异性大于临界值后会在固液界面上出现晶向缺失现象, 因此界面能各向异性系数$ \varepsilon $须满足$ \varepsilon \leqslant \left| {1/(1 - \mathop k\nolimits^2 )} \right| $, 否则会出现晶向缺失现象^[30], 导致凝固组织处于热力学不稳定状态, 对于奥氏体, $ \varepsilon $ = 0.04, 对于M₇C₃碳化物, $ \varepsilon $ = 0.025. $ \theta $为晶体取向; $ \varphi $为晶体界面法线方向与参考坐标轴(x轴)的夹角, 由法向定义计算^[26].
3 -->

2.5.3.成分过冷

界面前沿的成分过冷与界面实际溶质浓度及平衡溶质浓度有关, Fe-C-Cr三元合金需考虑C和Cr两种溶质浓度对于成分过冷的影响:

$ \Delta {T_{\text{C}}} = {m_{{\text{L}/k,{\rm C}}}}({C_{0,{\text{C}}}} - C_{{\text{L,C}}}^*) + {m_{{\text{L}/k,{\rm Cr}}}}({C_{{\text{0,Cr}}}} - C_{{\text{L,Cr}}}^*),$

式中, ${m_{{\text{L}/k}, i}}$为液相线斜率(下标中k指M, γ相),$ C_{{\text{L, C}}}^{\text{*}} $为溶质C的界面平衡液相浓度, $ C_{{\text{L, Cr}}}^{\text{*}} $为溶质Cr的界面平衡液相浓度.
3 -->

2.5.4.界面前沿溶质超饱和度

对于溶质C和Cr而言, 不考虑溶质之间的互扩散^[31], 界面前沿溶质超饱和度满足

$ \mathop \varOmega \nolimits_i = \frac{{C_{{\text{L}},i}^* - {C_{0,i}}}}{{C_{{\text{L}},i}^*(1 - {k_{\text{p,S/L},i}})}} = Iv(P{e_i}), $

设奥氏体/液相界面溶质分配系数为常数, 则

$ C_{{\text{L}},i}^* = \frac{{{C_{0,i}}}}{{1 - (1 - {k_{{{{\rm p},\gamma/{\rm L} }},i}}){\varOmega _i}}},$

M₇C₃碳化物晶粒中溶质浓度$ \mathop C\nolimits_{{\text{S}}, i} $设为常数, 则M₇C₃碳化物/液相界面的液相平衡浓度:

$ C_{{\text{L}},i}^* = \frac{{{C_{0,i}} - {\varOmega _i} \cdot \mathop C\nolimits_{{\text{S}},i} }}{{1 - {\varOmega _i}}} \text{, } $

式中, $ {C}_{\mathrm{L}, i}^{\mathrm{*}} $为界面处溶质的液相平衡浓度; $ {C}_{0, i} $为初始液相浓度, 对于(10)式, 对应GS凝固路径数据表中奥氏体初始析出时的液相溶质浓度. 对于(11)式, 分别对应GS凝固路径数据表中M₇C₃碳化物和奥氏体初始析出时的液相溶质浓度.
$ Iv\left({Pe}_{i}\right) $为溶质i的Ivantsov函数, $Iv\left({Pe}_{i}\right)= $$ \left({Pe}_{i}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left({Pe}_{i}\right)\displaystyle\int _{{Pe}_{i}}^{{\infty }}\dfrac{\mathrm{e}\mathrm{x}\mathrm{p}(-x)}{x}\mathrm{d}x$;
$ {Pe}_{i} $为溶质i贝克列(Peclet)数, 表达为

$ P{e_i} = \frac{{{V_n}R}}{{2{D_{{\text{L}},i}}}} \text{, } $

式中, $ {V_n} $为晶粒生长速度, $ R $为晶粒生长半径.
在相界面处, 生长速度唯一, $ {Pe}_{\mathrm{C}} $和$ {Pe}_{\mathrm{C}\mathrm{r}} $存在如下关系:

$ P{e_{\text{C}}} = \dfrac{{P{e_{{\text{Cr}}}} {D_{{\text{L,Cr}}}}}}{{{D_{{\text{L,C}}}}}} . $

通过(8)—(13)式, 可确定成分过冷$ {\Delta T}_{\mathrm{C}} $与Cr溶质贝克列数$ {Pe}_{\mathrm{C}\mathrm{r}} $间单一函数关系.
2 -->

2.6.界面法向速度

M₇C₃碳化物和奥氏体晶粒生长过程中, 由固液界面处溶质质量守恒, 得到界面元胞的法向生长速度:

$ \begin{split}\;& \boldsymbol {V_n}(C_{{\text{L}},i}^* - C_{{\text{S}},i}^*) = \left[ - {D_{{\text{L}},i}}\left( {\frac{{\partial {C_{{\text{L}},i}}}}{{\partial x}} + \frac{{\partial {C_{{\text{L}},i}}}}{{\partial y}}} \right) \right.\\ & ~~~~~~~~~~~ \left.~~~~~~~~~~~~ + {D_{{\text{S}},i}}\left( {\frac{{\partial {C_{{\text{S}},i}}}}{{\partial x}} + \frac{{\partial {C_{{\text{S}},i}}}}{{\partial y}}} \right) \right] \cdot {\boldsymbol{n}} . \end{split} $

界面速度分量为

$ {V_x} = \frac{1}{{(C_{{\text{L}},i}^ * - C_{{\rm{S}},i}^ * )}}\left( - D_{{\text{L}},i}^{}\frac{{\partial C_{{\text{L}},i}^{}}}{{\partial x}} + D_{{\text{S}},i}^{}\frac{{\partial C_{{\rm{S}},i}^{}}}{{\partial x}}\right) \mathop \mu \nolimits_k \text{, } $

$ {V_y} = \frac{1}{{(C_{{\text{L}},i}^ * - C_{{\rm{S}},i}^ * )}}\left( - D_{{\text{L}},i}^{}\frac{{\partial C_{{\text{L}},i}^{}}}{{\partial y}} + D_{{\text{S}},i}^{}\frac{{\partial C_{{\rm{S}},i}^{}}}{{\partial y}}\right) \mathop \mu \nolimits_k . $

式中μ_k为动力学系数(下标k表示M/L, γ/L界面). Burbelko等^[32]采用动力学系数进行生长速度的计算, $ {\mu }_{\mathrm{\gamma }/\mathrm{L}} $ = 10^–3, $ {\mu }_{\mathrm{g}\mathrm{r}/\mathrm{L}} $ = 10^–8. Zhu等^[12]通过比较其模拟与GS模型模拟的固相分数随温度变化差异确定界面动力学系数$ {\mu }_{\mathrm{\gamma }/\mathrm{L}} $ = 3 $ \times $ 10^–4. 孙玉成^[33]引入 $[1- $$ ({f}_{\mathrm{S}}- {\mathrm{\pi }}/{6}\left)\right]^{n}$(n为经验常数)对共晶团晶粒生长速度进行修正, 以解决在模拟计算过程中晶粒长大后其晶粒度预测失准的问题. 本研究通过与实验观测到M₇C₃碳化物晶粒的大小进行对比, 对M₇C₃碳化物和奥氏体晶粒的生长速度进行动力学修正, 动力学系数分别为$ {\mu }_{\mathrm{M/L}} $ = 4.8 $ \times $ 10^–4, $ {\mu }_{\mathrm{\gamma/L }} $ = 2.6 $ \times $10^–4 .
2 -->

2.7.更新固相分数

晶体的固相分数增量与固-液界面推进速度有关, 可用(17)式表示:

$ \Delta {f_{\rm S}} = \frac{{\Delta t}}{{\Delta s}}\left( {{V_{x,{\rm S}}} + {V_{y,{\rm S}}} - {V_{x,{\rm S}}}{V_{y,{\rm S}}}\frac{{\Delta t}}{{\Delta s}}} \right) \text{, } $

式中$ \Delta s $为元胞单元尺寸(单位m), $\Delta x = \Delta y = \Delta s$.
对于奥氏体晶粒, 为体现界面扰动的因素, 将固相分数增量乘上1个扰动函数, 即$1+ A\;\times\; $$ [1 - 2\mathrm{Rand}(\cdot)]$, 其中A代表随机扰动振幅, 取值0.1, Rand(·)为[0, 1]之间的随机数.
对于M₇C₃碳化物晶粒, 为了减小网格各向异性对M₇C₃碳化物晶粒形貌的影响, 以及减少M₇C₃碳化物晶粒内不完全凝固点的问题, 将M₇C₃碳化物晶粒的固相分数增量乘G, G是与邻位网格状态有关的形状因子, 其表达式如下:

$ \begin{split}&G = \max \left[ 1,a\left( \sum\limits_{m = 1}^4 \mathop s\nolimits_m^{\text{I}} + \frac{1}{{\sqrt 2 }}\sum\limits_{m = 1}^4 \mathop s\nolimits_m^{{\text{II}}} \right.\right. \\&\qquad\left.\left.+ \frac{1}{2}\sum\limits_{m = 1}^4 {\mathop s\nolimits_m^{{\text{III}}} } + \frac{1}{{\sqrt 5 }}\sum\limits_{m = 1}^4 {\mathop s\nolimits_m^{{\text{IV}}} } \right) \right] \text{, }\\&\mathop s\nolimits^{\text{I}} ,\mathop s\nolimits^{{\text{II}}} ,\mathop s\nolimits^{{\text{III}}} ,\mathop s\nolimits^{{\text{IV}}} = \left\{ \begin{gathered} 0,~~~~ f _{\text{s}} < 1, \hfill \\ 1,~~~~ f _{\text{s}} = 1, \hfill \end{gathered} \right. \end{split}$

式中: $ \mathop s\nolimits_m^{\text{I}} $为近邻的4个网格的状态参数, $ \mathop s\nolimits_m^{{\text{II}}} $为次近邻的4个网格的状态参数, $ \mathop s\nolimits_m^{{\text{III}}} $为距中心网格为2$ \Delta s $的4个网格的状态参数, $ \mathop s\nolimits_m^{{\text{IV}}} $为距中心网格为$ \sqrt 5 $$ \Delta s $的4个网格的状态参数.
图1是不同系数a所对应的同一时刻同一位置下碳化物晶粒质量分数图. 可以看出随着系数a的不断增加, M₇C₃碳化物晶粒内不完全凝固点的数量逐渐减小, 当a = 0.50时, M₇C₃碳化物晶粒内完全凝固; 然而当a $ \geqslant $ 0.50, 随着系数a的不断增加, M₇C₃碳化物晶粒的六边形外轮廓偏向弧度化. 因此本模拟最终选取a = 0.40.
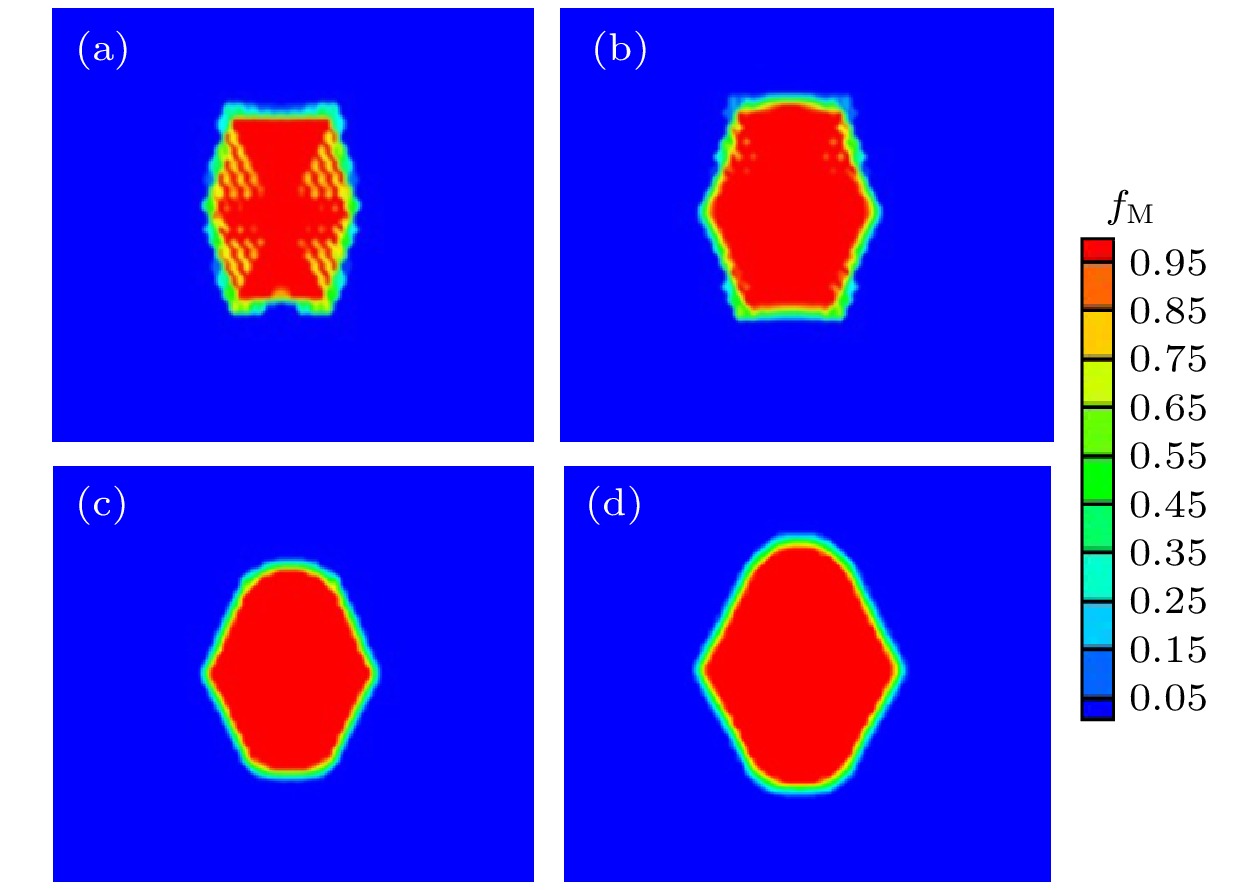图 1 t = 99.99 s时, 不同系数a条件下模拟的M₇C₃质量分数图　(a) a = 0.25; (b) a = 0.40; (c) a = 0.50; (d) a = 0.60
Figure1. M₇C₃ morphology in form of mass fraction with several values of coefficient a at t = 99.99 s: (a) a = 0.25; (b) a = 0.40; (c) a = 0.50; (d) a = 0.60.

在用(17)式求出元胞内的固相分数增量后, 更新元胞新时刻的固相分数:

$ {f_{\text{S}}}^{n + 1} = f_{\text{S}}^n + \Delta {f_{\text{S}}} . $

2 -->

2.8.更新固相浓度

对于奥氏体晶粒内溶质固相浓度, 用(20)式更新:

$ {C_{{\text{S}},i}} = {{(C_{{\text{S}},i}^nf_{\text{S}}^n + {k_{{{{\rm{p}},\gamma/{\rm L}}},i}}C_{{\text{L}},i}^n\Delta {f_{\text{S}}})} \mathord/ {(f_{\text{S}}^n + \Delta {f_{\text{S}}})}} . $

由GS凝固路径预测模型计算, 凝固过程中C, Cr溶质在M₇C₃碳化物中浓度变化较小, 因此, 本研究将M₇C₃碳化物晶粒内溶质固相浓度设为常数.
2 -->

2.9.M₇C₃碳化物与奥氏体元胞邻居关系

通过实验观测分析, Fe-4%C-17%Cr合金中的M₇C₃碳化物晶粒在二维平面上理想状态具有六重对称的特征, 但实际合金凝固过程中受到一些凝固缺陷等因素的影响, 二维平面观测的结果有的为规则六边形, 有的为近似六边形等状态^[34-36]. 据其形貌特征^[24], 本研究定义了CA方法中M₇C₃碳化物晶粒的二维邻居单元如图2所示, 其中黑色方框为某一CA单元, 周围紧邻的16个单元为其邻居. 奥氏体晶粒采用Moore型邻居单元, 包括最近邻的8个元胞, 如图3所示.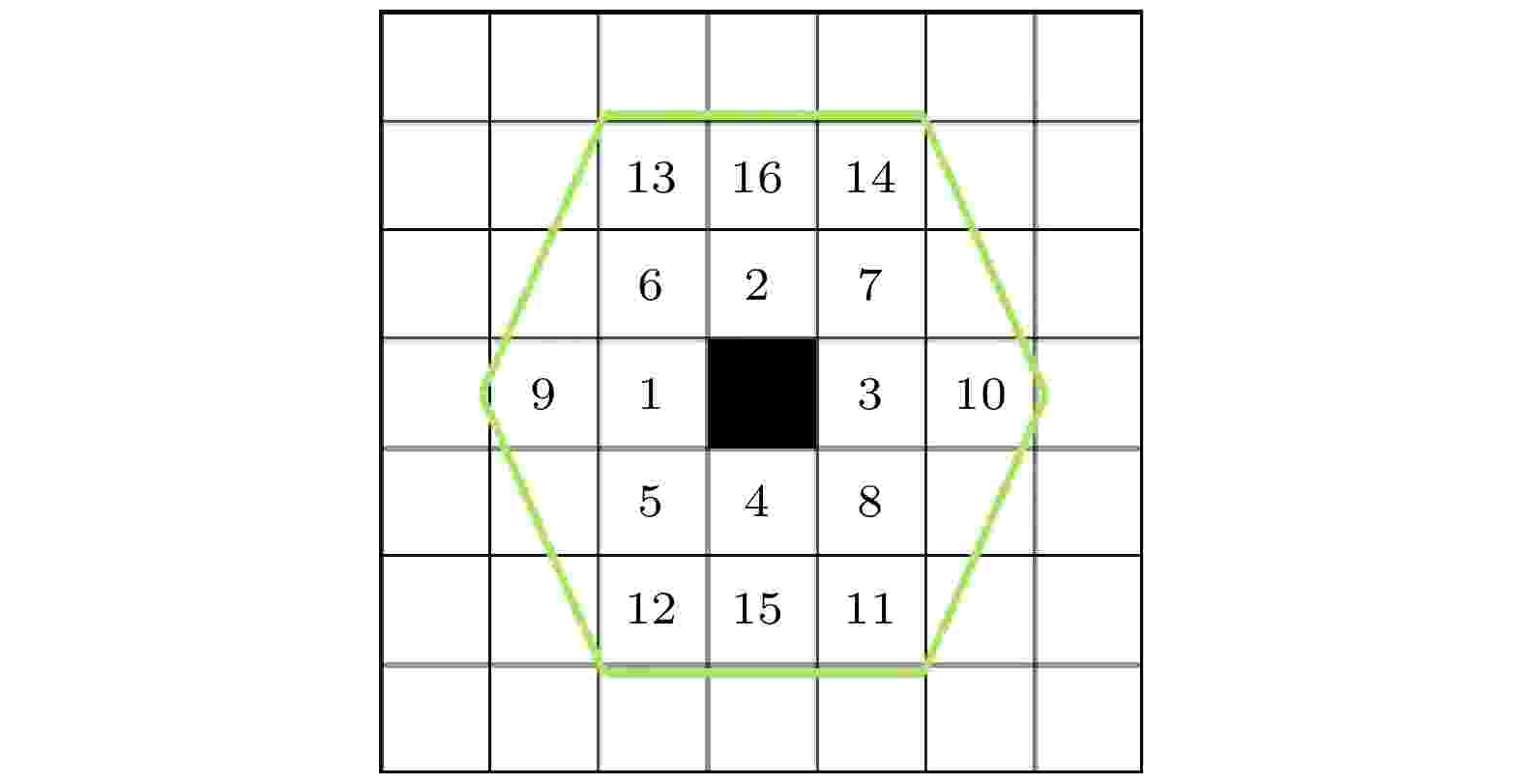
图 2 M₇C₃元胞邻居单元
Figure2. Neighborhood relations for M₇C₃ grain.

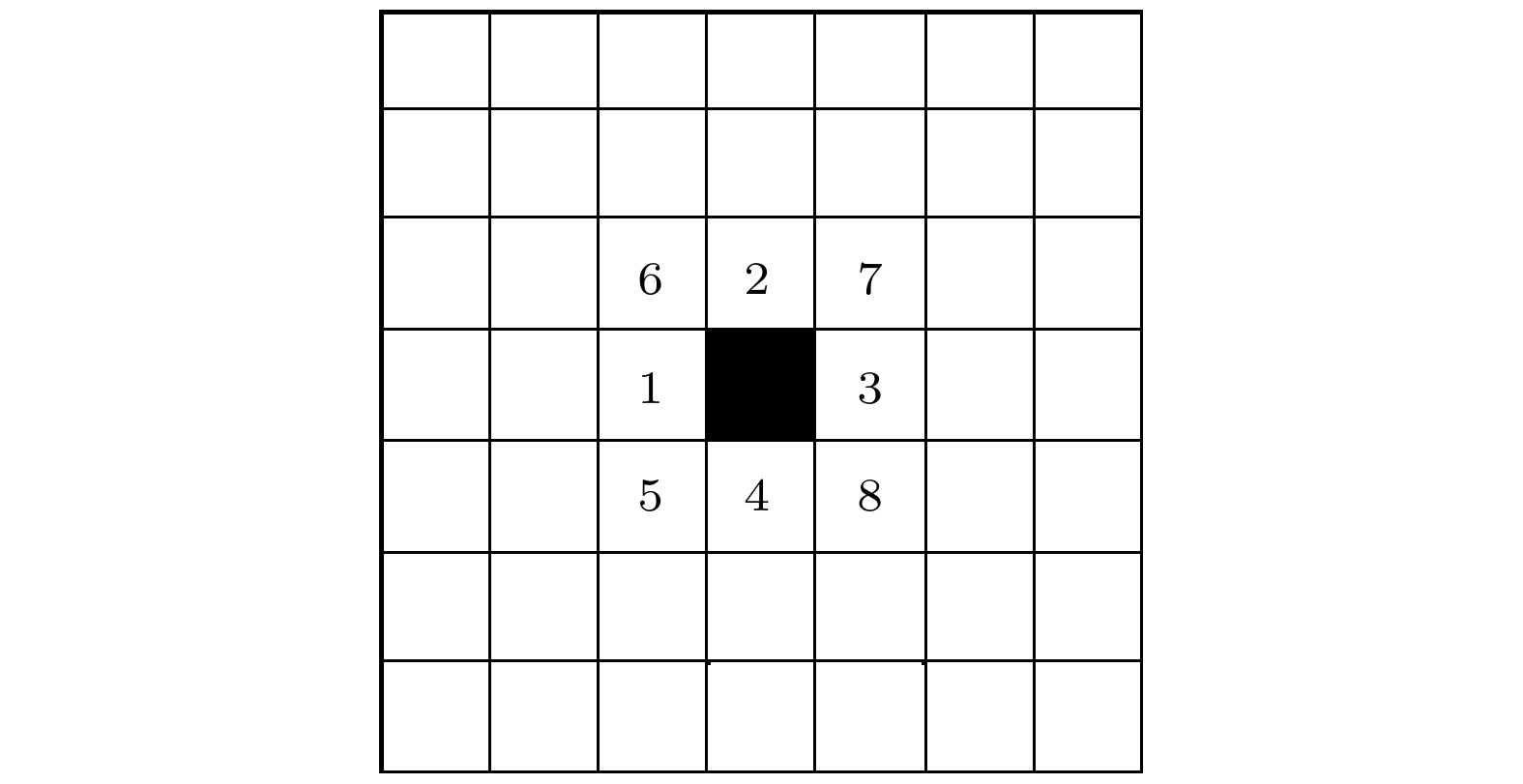图 3 γ元胞Moore型邻居单元
Figure3. Moore neighborhood relations for austenite grain.

2 -->

2.10.晶粒捕获规则

模拟区域中每个元胞共有3种状态: 液相、固相及界面(固液相区)状态. 捕获规则定义如下: 液相元胞形核后, 此元胞为界面状态; 当该元胞生长至固相分数为1时, 此元胞为固相状态, 周围邻居元胞即时转变为界面元胞. 当某一元胞同时被奥氏体和M₇C₃碳化物元胞捕获时, 该元胞变为两相共存的界面胞, 且变为固相元胞后只能各自捕获周围8个邻居元胞; 其余界面元胞成长为固相元胞后, 按奥氏体或M₇C₃碳化物各自的邻居关系捕获周围邻居元胞, 逐渐生长.
2 -->

2.11.溶质再分配

在生长界面, M₇C₃碳化物晶粒从界面液相中吸收C, Cr溶质(M/L界面分配系数均大于1); 奥氏体晶粒生长向界面液相中排出C, Cr溶质(γ/L界面分配系数小于1), 进而引起界面前沿液相溶质重新进行分配.
假设上一时刻界面胞固相溶质浓度为$ C_{{\text{S}}, s, i}^n $, 固相分数为$ f_s^n $; 液相溶质浓度为$ C_{{\rm{L}}, s, i}^n $, 液相分数为$ (1 - f_{\rm{M}}^n - f_\gamma ^n) $. 新时刻界面胞固相分数增量为$ \Delta {f_s} $(下标s为M, γ).
1)当$ \Delta {f_s} < 1 - f_{\text{M}}^n - f_{{\gamma }}^n $, 上一时刻界面胞剩余液相可以满足新时刻固相分数的转变. 新时刻M₇C₃碳化物界面胞液相溶质浓度为

$ C_{{\text{L,M}},i}^{n + 1} = \frac{{C_{{\text{L,M}},i}^n(1 - f_{\text{M}}^n - f_{{\gamma }}^n) - \Delta {f_{\text{M}}}C_{{\rm{S}},{\text{M}},i}^n}}{{1 - f_{\text{M}}^n - f_{{\gamma }}^n - \Delta {f_{\text{M}}}}} . $

奥氏体界面胞液相的溶质浓度为

$ C_{{{{\rm{L}},\gamma }},i}^{n + 1} = \frac{{C_{{{{\rm{L}},\gamma }},i}^n(1 - f_{{\gamma }}^n - f_{\text{M}}^n) - {k_{{{{\rm{p}},\gamma /{\rm{L}}}},i}}\Delta {f_{{\gamma }}}C_{{{{\rm{L}},\gamma }},i}^n}}{{1 - f_{{\gamma }}^n - f_{\text{M}}^n - \Delta {f_{{\gamma }}}}} . $

若新时刻界面胞液相溶质浓度低于溶质平衡浓度$ C_{{\text{L}}, s, i}^* $, 且不小于0, 则无需进行溶质再分配. 若新时刻界面胞液相溶质浓度高于溶质平衡浓度$ C_{{\text{L}}, s, i}^* $, 则多出部分溶质$\Delta {C_i} = (C_{{\text{L}}, s, i}^{n + 1} - C_{{\text{L}}, s, i}^*)(1 - $$ f_{\text{M}}^n - f_{{\gamma }}^n - \Delta {f_s})$均匀分配给界面胞周围有液相的邻胞, 界面胞液相溶质浓度修正为 $ C_{{\text{L}}, s, i}^{n + 1} = C_{{\text{L}}, s, i}^* $. 若新时刻界面胞液相溶质浓度低于0, 则需要从邻胞吸收溶质$\Delta {C_i} = (0 - C_{{\text{L}}, s, i}^{n + 1})(1 - $$ f_{\text{M}}^n - f_{{\gamma }}^n - \Delta {f_s})$, 界面胞液相溶质浓度修正为$ C_{{\text{L}}, s, i}^{n + 1} = 0 $.
2)当$ \Delta {f_s} \geqslant 1 - f_{\text{M}}^n - f_{{\gamma }}^n $, 界面胞剩余液相需完全转变为固相, 并将其修正为$ \Delta {f_s} = 1 - f_{\text{M}}^n - f_{{\gamma }}^n $. 新时刻界面胞已完全转变为固相, 对于M₇C₃碳化物需要从邻胞吸收溶质$\mathop {\Delta C}\nolimits_i = (C_{{\text{S, M}}, i}^n - $$ C_{{\text{L, M}}, i}^n) \mathop {\Delta f}\nolimits_{\text{M}}$; 奥氏体则排出溶质$\Delta {C_i} = C_{{{{\rm{L}}, \gamma , }}i}^{\text{n}}(1 - {k_{{{{\rm{p}}, \gamma /L}}, i}})\Delta {f_\gamma }$.
2 -->

2.12.时间步长

$ \Delta t \leqslant 0.2\min ({{\Delta {s^2}}/ {{D_{{\text{L,C}}}}}},{{{\text{ }}\Delta {s^2}}/{{D_{{\text{L,Cr}}}}}},{{{\text{ }}\Delta s}/ {{V_{\max }}}}, \Delta {t_0}). $

式中$ \mathop {\Delta t}\nolimits_0 $是初始时间步长.
2 -->

2.13.计算步骤

1)所有元胞均赋予相同的初始温度和初始浓度, 计算时间步长;
2)温度场考虑潜热释放, 温度缓慢下降((1)式);
3)当达到M₇C₃碳化物或奥氏体的形核过冷度, 该元胞转变为界面元胞;
4)计算M₇C₃碳化物和奥氏体界面各向异性函数$ \mathop f\nolimits_{(\varphi , \theta )} $((7)式), 求得曲率过冷$ {\Delta T}_{\mathrm{R}} $((6)式);
5)通过(5)式, 计算界面元胞成分过冷$ {\Delta T}_{\mathrm{C}} $;
6)通过(8)—(13) 式, 求解界面元胞$ {Pe}_{\mathrm{C}\mathrm{r}} $, 再求得$ {Pe}_{\mathrm{C}} $和界面平衡浓度$ \mathop C\nolimits_{{\text{L, C}}}^ * $, $ \mathop C\nolimits_{{\text{L, Cr}}}^ * $;
7)液相元胞的平衡浓度按对应温度, 通过GS凝固路径预测模型计算的数据表插值获得;
8)求解界面法向生长速度((1)—(16) 式)并更新固相分数((17)—(19) 式);
9) M₇C₃碳化物和奥氏体界面胞进行局部溶质再分配((21)—(22)式);
10)计算扩散引起的浓度场变化((2)—(4)式);
11)再重复步骤2)—10)进行时间层循环, 直到全场凝固结束, 计算中止.
表1列出了?Fe-4%C-17%Cr 三元合金模拟所用的物性参数^[22,37,38].

Parameters	Symbol	Unit	Value	Note
Initial composition C	$ {C_{{\text{C0}}}} $	%	4.00	文献[22]
Initial composition Cr	$ {C_{{\text{Cr0}}}} $	%	17.00	文献[22]
Austenite nucleation temperature	$ \mathop T\nolimits_{{\gamma }} $	℃	1266.00	GS model
M7C3 nucleation temperature	$ \mathop T\nolimits_{\text{M}} $	℃	1304.00	GS model
C partition coefficient at austenite/liquid interface	${k_{ { {{\rm p}, {\mathrm{\gamma }/\mathrm{L} } , {\rm C} } } } }$	—	0.407	GS model
Cr partition coefficient at austenite/liquid interface	${k_{ { {{\rm p}, {\mathrm{\gamma }/\mathrm{L} } , {\rm Cr} } } } }$	—	0.576	GS model
Liquidus slope of C at austenite/liquid interface	${m_{ { { {\mathrm{L}/\mathrm{\gamma } }, {\rm C} } } } }$	℃/%	–95.49	GS model
Liquidus slope of Cr at austenite/liquid interface	${m_{ { { {\mathrm{L}/\mathrm{\gamma } }, {\rm Cr} } } } }$	℃/%	6.14	GS model
Liquidus slope of C at M7C3/liquid interface	${m_{ {{\rm L/M}, \text{C} } } }$	℃/%	90.37	GS model
Liquidus slope of Cr at M7C3/liquid interface	${m_{ {{\rm L/M},\text{Cr} } } }$	℃/%	15.29	GS model
Diffusion coefficient of C in austenite	${D_{ { \mathrm{\gamma }, {\rm C} } } }$	m2/s	2.57×10–10	GS model
Diffusion coefficient of Cr in austenite	${D_{ { {\mathrm{\gamma } , \rm Cr} } } }$	m2/s	3.67×10–14	GS model
Diffusion coefficient of C in liquid phase	${D_{ {\text{L,C} } } }$	m2/s	9.60×10–10	GS model
Diffusion coefficient of Cr in liquid phase	${D_{ {\text{L,Cr} } } }$	m2/s	8.23×10–10	GS model
Diffusion coefficient of C in M7C3	${D_{ {\text{M,C} } } }$	m2/s	0.0
Diffusion coefficient of Cr in M7C3	${D_{ {\text{M,Cr} } } }$	m2/s	0.0
Gibbs-Thomson coefficient at austenite/liquid interface	${\varGamma _{ {\gamma } } }$	$ {\text{m}} \cdot {\text{K}} $	1.9×10–7	文献[37]
Gibbs-Thomson coefficient at M7C3/liquid interface	${\varGamma _{\text{M} } }$	$ {\text{m}} \cdot {\text{K}} $	6.213×10–7	文献[38]
Latent heat of fusion for austenite	$ \mathop L\nolimits_{{\gamma }} $	J/kg	1.86×105	GS model
Latent heat of fusion for M7C3	$ \mathop L\nolimits_{\text{M}} $	J/kg	2.38×105	GS model
Specific heat capacity	$\mathop c\nolimits_{\rm p}$	J/(kg$ \cdot $℃)	839	GS model

表1Fe-4%C-17%Cr三元合金模拟所用的物性参数(单位%是指质量分数)
Table1.Physical properties used for Fe-4%C-17%Cr ternary alloy. Unit of % represents mass fraction (wt%).

本研究利用微观元胞自动机方法研究二维空间Fe-4%C-17%Cr三元合金中初生相M₇C₃碳化物和奥氏体晶粒共生长过程. 选取的计算域参照实验^[22]显微组织图片尺寸, 确定为700 μm × 520 μm, 划分为350 × 260个均匀正方形网格, 网格尺寸为2 μm × 2 μm. 形核位置和形核数量参照实验^[22]结果进行设置. 熔体初始温度参照实验冷却曲线的起始温度设定为1334.32 ℃, 冷却速率参照石墨铸型^[22]实验冷却曲线选取, 分为4个阶段: M₇C₃碳化物析出且独立生长阶段(T > 1266 ℃), 冷却速率为4.6 K/s; 奥氏体析出初始阶段(1220 ℃ < T $ \leqslant $1266 ℃), 冷却速率为1.4 K/s; 奥氏体和M₇C₃碳化物潜热释放引起模拟区域温度上升阶段(1194 ℃ < T $\leqslant$1220 ℃), 冷却速率为2.4 K/s; 接近凝固结束潜热作用较小阶段(T $ \leqslant $ 1194℃), 冷却速率为2.0 K/s. 随着温度的不断下降, M₇C₃碳化物和奥氏体晶粒依次形核生长, 直至模拟区域达到最终凝固状态.
本文模拟的Fe-4%C-17%Cr合金凝固冷却曲线, 将与文献[22]中同成分添加1.5%Ti (质量分数)合金及文献[39]中Fe-3.23%C-23.8%Cr合金(C和Cr的质量分数分别为3.23%和23.8%)添加4%Ti与否的凝固冷却曲线进行对比.
2

-->

3.1.合金凝固路径

表2列出了上述二种成分合金由GS模型预测和在Fe-C伪二元相图中的析出相(M₇C₃碳化物、奥氏体、渗碳体)及对应析出温度. 可以看出, 同一成分GS模型预测和Fe-C伪二元相图给出的各相析出趋势一致: Fe-4%C-17%Cr合金中, 添加Ti元素后, M₇C₃碳化物析出温度均变低、奥氏体析出温度变高; 二者给出的各相析出温度差较小. 由表2可知, 添加Ti元素后, 至固相线或Cementite (CEM)相析出, Fe-4%C-17%Cr-1.5%Ti体系, TiC体积分数为3.00%, 奥氏体体积分数为63.04%, M₇C₃体积分数为26.38%; Fe-3.23%C-23.8%Cr-4%Ti体系, TiC体积分数为7.92%, 奥氏体体积分数为74.28%, M₇C₃体积分数为17.80%. 因而冷却曲线的拐点和温度回复主要反映奥氏体和M₇C₃相的析出及共生长演变.

Model	Alloy composition	M7C3 precipitation temperature/℃	γ precipitation temperature/℃	CEM precipitation temperature or solidus /℃	Phase volume fraction at CEM precipitation temperature or solidus
GS model	Fe-4%C-17%Cr	1304	1266	1194(CEM)	29.91%(M7C3) 57.22%(γ)
GS model	Fe-4%C-17%Cr-1.5%Ti	1288	1271	1193(CEM)	26.38%(M7C3) 63.20%(γ)
Fe-C phase diagram	Fe-4%C-17%Cr	1305	1266	1239(solidus)	—
Fe-C phase diagram	Fe-4%C-17%Cr-1.5%Ti	1285	1271	1248(solidus)	—
GS model	Fe-3.23%C-23.8%Cr	1305	1297	1193(CEM)	28.18%(M7C3) 71.62%(γ)
GS model	Fe-3.23%C-23.8%Cr-4%Ti	1296	1324	1296(solidus)	17.80%(M7C3) 74.28%(γ)
Fe-C phase diagram	Fe-3.23%C-23.8%Cr	1305	1296	1292(solidus)	—
Fe-C phase diagram	Fe-3.23%C-23.8%Cr-4%Ti	1295	1328	1295(solidus)	—

表2GS模型和Fe-C伪二元相图中二种成分Fe-C-Cr合金析出相及析出温度
Table2.Phase type and precipitation temperature in two Fe-C-Cr alloys by GS prediction and in Fe-C pseudo binary phase diagram.

由图4中Fe-C伪二元合金相图可知, 添加Ti元素后, 共晶点右移, 导致Fe-4%C-17%Cr合金(图4(c)—(d))中M₇C₃碳化物析出温度降低、奥氏体析出温度升高. 但从凝固路径来看, 未改变M₇C₃→γ析出顺序, 即由无Ti添加的L→M₇C₃→γ→CEM, 至添加Ti的L→TiC→M₇C₃→γ→CEM. 但是, 对于文献[39]实验合金成分Fe-3.23%C-23.8%Cr, 由于离共晶点较近, 添加Ti后, 相变路径已移至共晶点左侧, 析出顺序由无Ti添加的L→M₇C₃→γ→CEM, 变为添加Ti后, 奥氏体先于M₇C₃相析出的L→TiC→γ→M₇C₃→Solidus. 但合金内主要析出相仍为M₇C₃和γ. 对比分析图4(a)与图4(b)可知, Fe-4%C-17%Cr合金与Fe-3.23%C-23.8%Cr均为过共晶三元合金, 析出相M₇C₃与奥氏体及顺序均相同, 冷却曲线拐点和温度回复应相近.
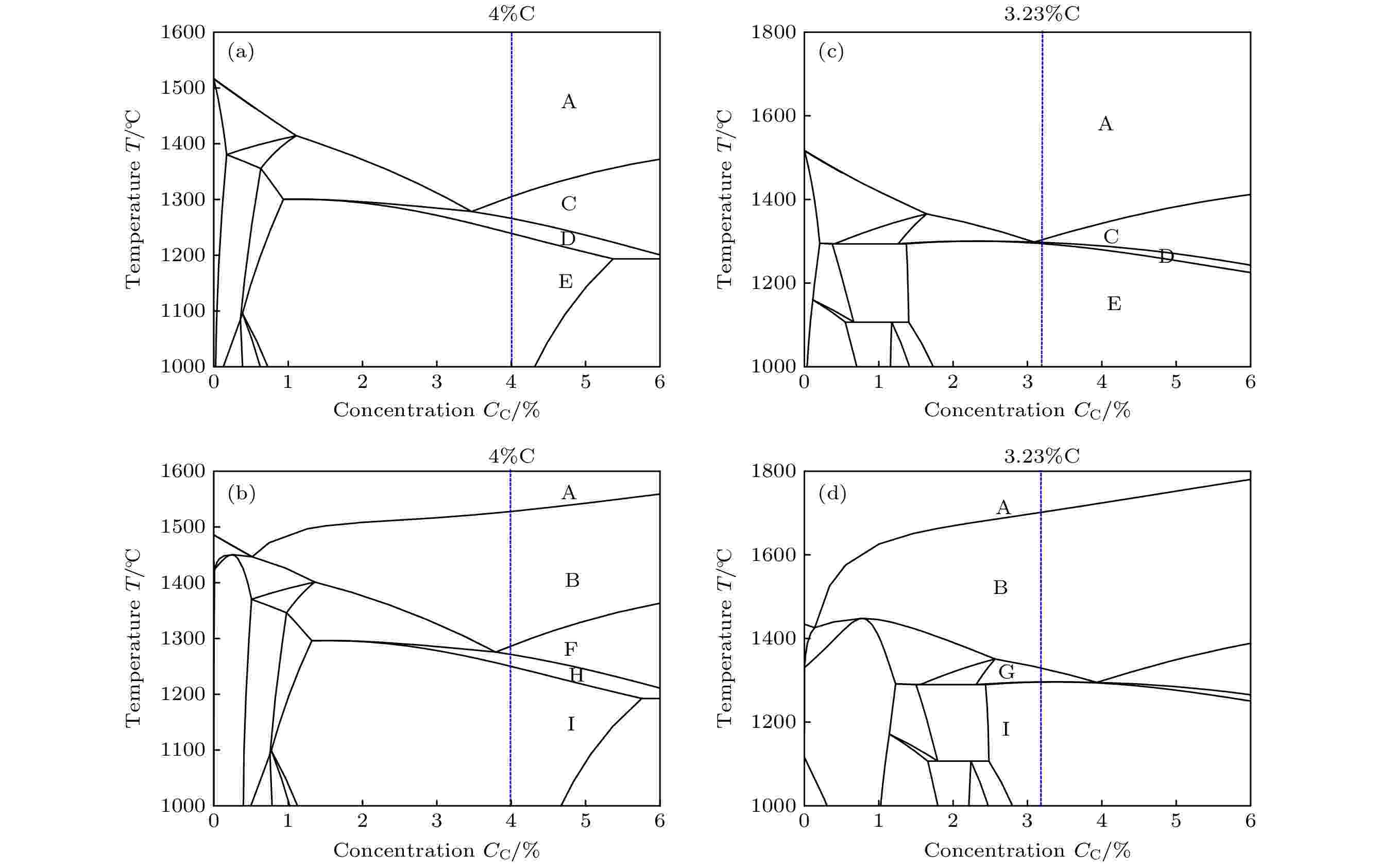图 4 Fe-C伪二元合金相图(A 区, 液相; B区, 液相 + TiC; C 区, 液相 + M₇C₃; D区, 液相+ M₇C₃ + γ; E 区, M₇C₃ + γ; F区, 液相 + TiC + M₇C₃; G区, 液相+ TiC + γ; H区, 液相+ TiC + M₇C₃ + γ; I 区, TiC + γ + M₇C₃)　(a) Fe-C-17%Cr; (b) Fe-C-23.8%Cr; (c) Fe-C-17%Cr-1.5%Ti; (d) Fe-C-23.8%Cr-4%Ti
Figure4. Fe-C pseudo binary phase diagram: (a) Fe-C-17%Cr; (b) Fe-C-23.8%Cr; (c) Fe-C-17%Cr-1.5%Ti; (d) Fe-C-23.8%Cr-4%Ti. A zone, Liquid; B zone, Liquid + TiC; C zone, Liquid + M₇C₃; D zone, Liquid + M₇C₃ + γ; E zone, M₇C₃ + γ; F zone, Liquid + TiC + M₇C₃; G zone, Liquid + TiC + γ; H zone, Liquid + TiC + M₇C₃ + γ; I zone, TiC + γ + M₇C₃.

2 -->

3.2.冷却曲线和相分数演变

图5给出了本模拟得到的Fe-4%C-17%Cr合金冷却曲线(黑色). 可以看出, 在温度高于1266 ℃阶段, 仅有M₇C₃碳化物析出, 相分数较少, 潜热释放未对冷却曲线产生明显影响, 冷却曲线基本以恒定冷却速率下降; 至1266 ℃奥氏体析出, 温度场受到M₇C₃碳化物与奥氏体凝固释放潜热的共同作用, 冷却曲线斜率产生改变. 直到82.51 s时(见图7), 大部分M₇C₃碳化物与奥氏体晶粒相互接触, 生长相互促进, 使得凝固过程潜热释放量高于散热量, 模拟域冷却曲线温度回复明显. 82.51—120.19 s, 冷却曲线产生明显温度回复, 温度从1200.39 ℃升高到1210.03 ℃, 此时间段M₇C₃与奥氏体晶粒两相体积分数之和从24.72%升高到68.62%. 随后, M₇C₃碳化物与奥氏体晶粒生长速度逐渐减小, 随之潜热作用减小, 冷却曲线恢复下降趋势, 直至最终凝固.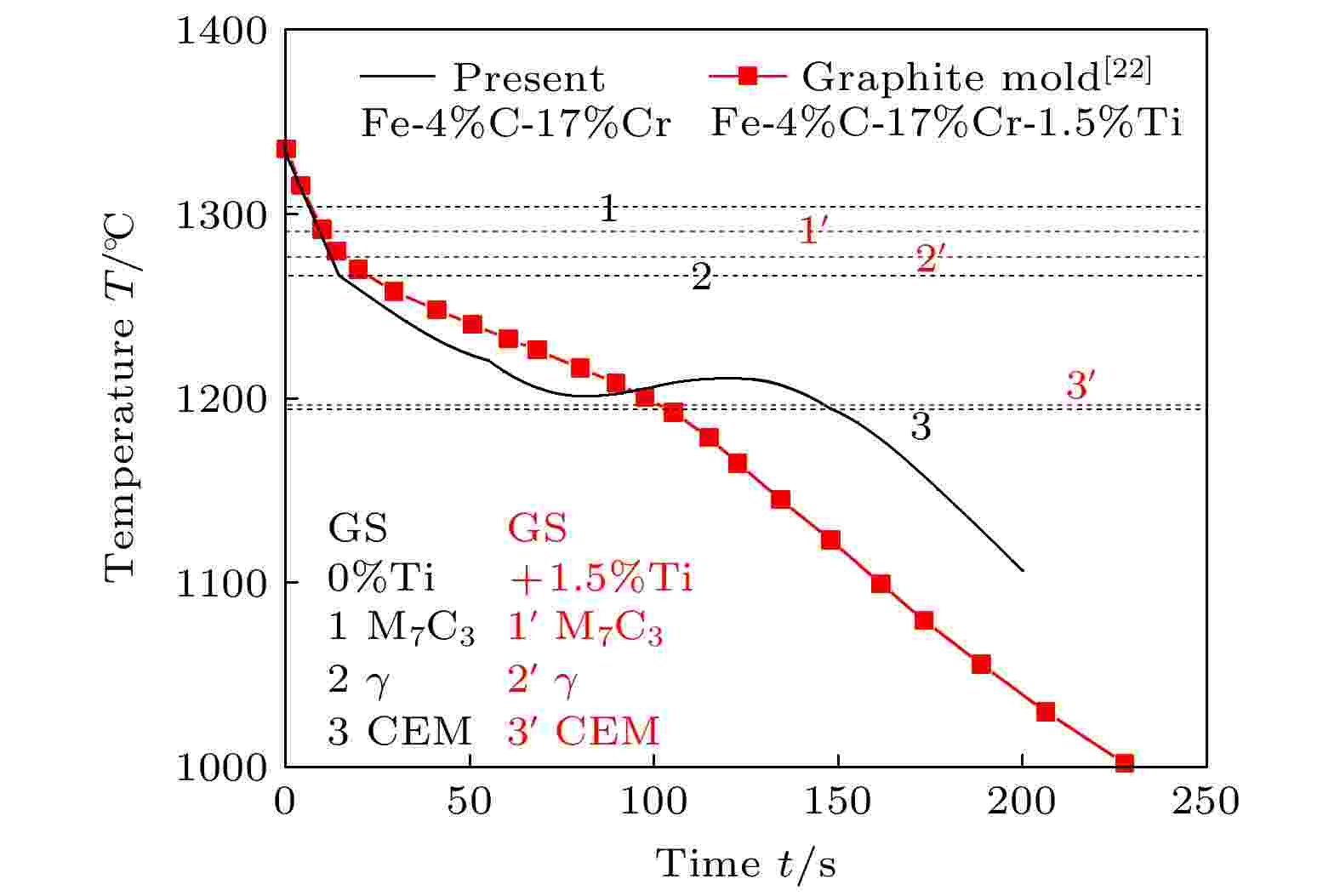
图 5 预测的Fe-4%C-17%Cr合金冷却曲线及添加1.5%Ti合金石墨型实验冷却曲线^[22]对比
Figure5. Comparison of predicted cooling curve for Fe-4%C-17%Cr alloy and experimental cooling curve with 1.5%Ti addition in graphite mold ^[22].

本文模拟的Fe-4%C-17%Cr合金的实验冷却曲线^[40]仅监测到1200 ℃温度以下的相变行为, 未能反映奥氏体和M₇C₃相的析出. 为此, 采用文献[39]中同为过共晶成分的相近体系(即Fe-3.23%C-23.8%Cr合金添加4%Ti与否)的凝固路径及文献砂型实验冷却曲线(如图6所示)进行对照分析, 间接验证本模拟冷却曲线的正确性.
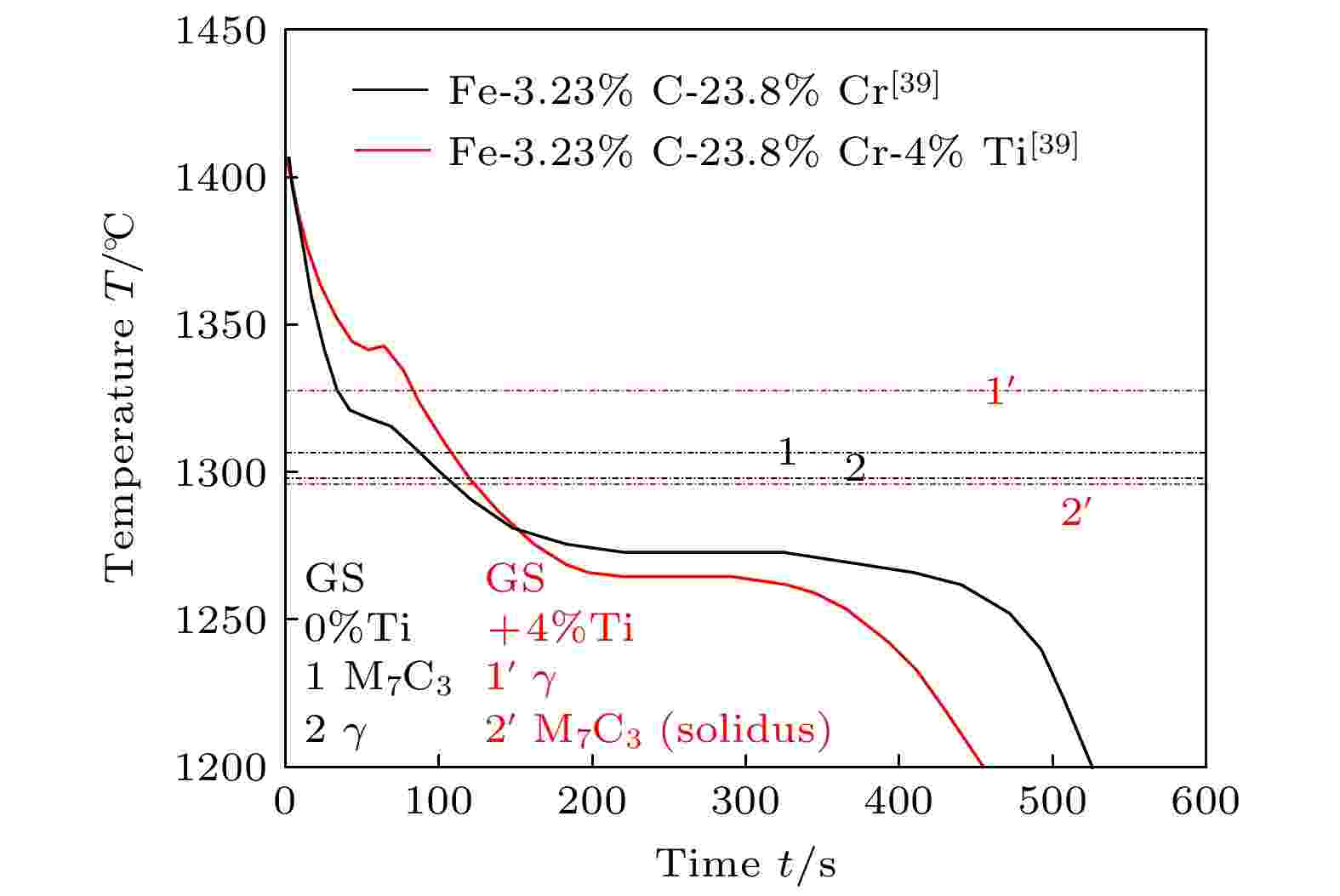图 6 Fe-3.23%C-23.8%Cr合金添加4%Ti与否砂型实验冷却曲线^[39]
Figure6. Experimental cooling curves in sand mold for Fe-3.23%C-23.8%Cr alloy with or without 4%Ti addition^[39].

将图5中模拟得到的Fe-4%C-17%Cr合金冷却曲线(黑色)与添加1.5%Ti后实验冷却曲线(红色+实心方框)和图6添加Ti与否的实验^[39]冷却曲线进行对比. 本模拟合金添加Ti前后冷却曲线变化趋势与文献合金添加Ti前后实验冷却曲线变化趋势相同, 从而验证了本模拟得到的冷却曲线的正确性. 另外, 图5、图6还分别给出GS凝固路径计算的两成分合金添加Ti与否的析出相顺序, 可以看出, Fe-4%C-17%Cr合金添加1.5%Ti后, 合金的析出相顺序不变; Fe-3.23%C-23.8%Cr合金添加4%Ti后M₇C₃与奥氏体析出顺序发生了交换, 但仍以M₇C₃和奥氏体为主要相. 图5和图6中黑色曲线的趋势相近, 拐点和温度回复都发生在GS凝固路径预测的相析出温度以下较低温度处, 温度滞后明显, 砂型冷却凝固时间比本模拟石墨型冷却时间更长.
图7给出了本模拟过程中奥氏体、M₇C₃碳化物和液相体积分数的演变过程. 开始时, 熔体处于完全液相, 初始温度高于M₇C₃碳化物形核温度. 在t = 7.03 s时, 熔体冷却至M₇C₃碳化物形核过冷度, M₇C₃碳化物形核, 生长初始阶段M₇C₃碳化物相分数增长缓慢, 冷却曲线斜率未发生改变. 在t = 15.22 s时, 熔体冷却至奥氏体形核过冷度, 温降曲线出现第一个拐点, 表明奥氏体晶粒形核并开始生长. 在15.22—82.51 s时大部分M₇C₃碳化物与奥氏体晶粒独自生长、未接触. 当时间t > 82.51 s时, M₇C₃碳化物与奥氏体晶粒相互接触共同生长, 各相分数增长较快. 冷却曲线发生温度回复阶段, 与模拟过程中M₇C₃碳化物、奥氏体相体积分数快速增长阶段相对应; 冷却曲线温度回复结束之后, M₇C₃碳化物、奥氏体相体积分数增长缓慢, 接近最终凝固状态, 冷却曲线又恢复下降趋势. 通过比较M₇C₃碳化物晶粒独自生长阶段(t < 15.22 s)与M₇C₃碳化物和奥氏体晶粒共同生长阶段(t $ \geqslant $15.22 s), 可以看出合金凝固过程中M₇C₃碳化物与奥氏体晶粒的生长主要集中在二者相互接触、共生长阶段. 当t = 200.00 s时, 模拟区域中合金几乎完全凝固, M₇C₃碳化物、奥氏体体积分数之和为97.744%, 剩余液相分数为2.256%. 此后, 模拟区域内M₇C₃碳化物、奥氏体相分数及液相分数随着时间的推移几乎没有改变, 本文以此刻状态为最终凝固状态. 此时已达到Cementite相形核温度, 本模拟仅考虑M₇C₃碳化物和奥氏体晶粒的生长, 因此, 模拟结束状态时奥氏体枝晶臂间仍存在少量液相.
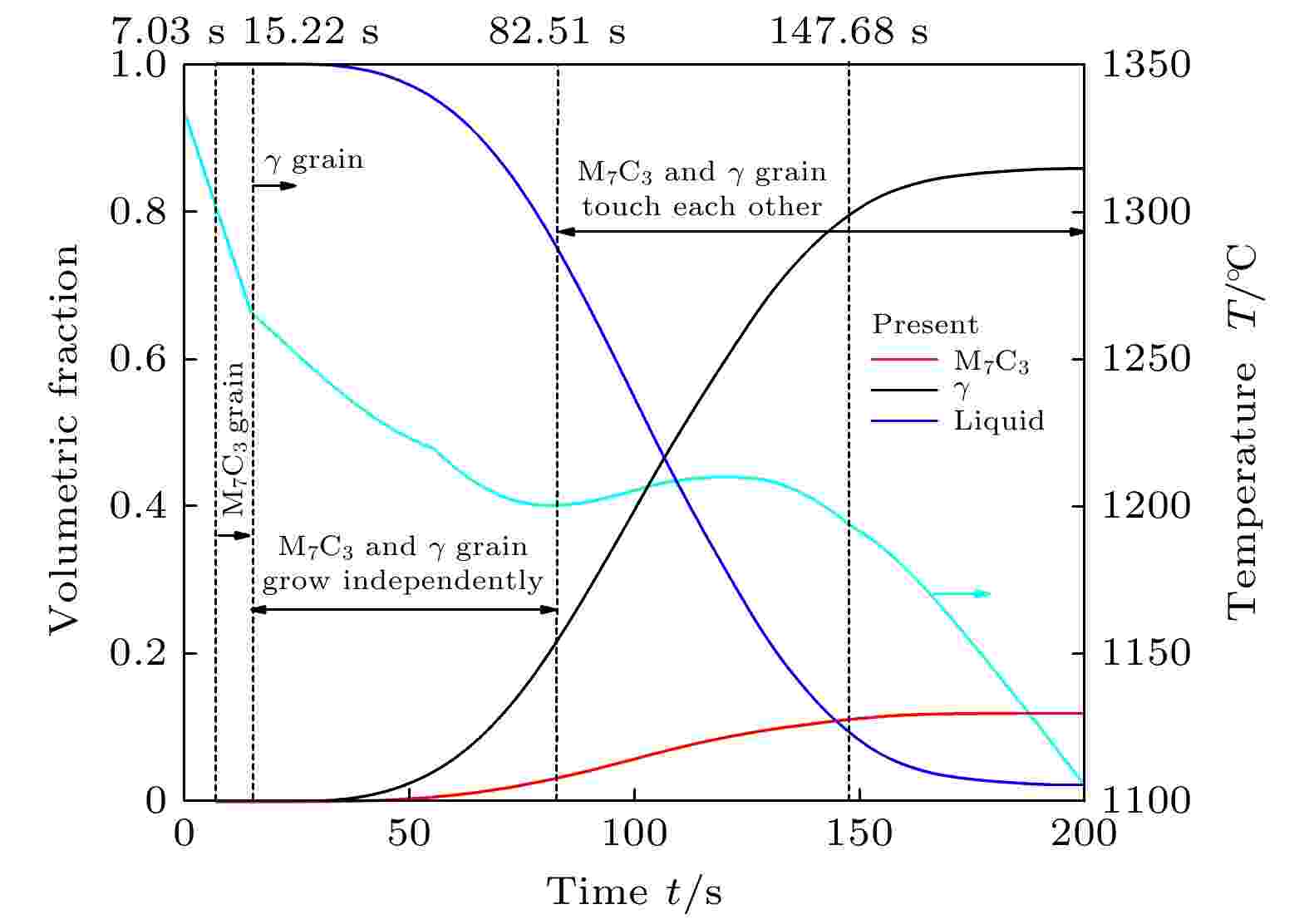图 7 本模拟冷却曲线及各相质量分数演变
Figure7. Predicted cooling curves and evolution of phase mass fraction.

图8给出了本模拟与GS模型预测的凝固路径中各相分数随温度的变化曲线, 其中1304 ℃对应图7中7.03 s; 1266 ℃对应15.22 s; 1194 ℃对应147.68 s; 1200.39 ℃为模拟冷却曲线温度回复起点; 1151 ℃为模拟结束温度. 为与实验晶粒尺寸进行比对分析, 本模拟中晶粒生长速度乘了动力学系数(10^–4数量级). 因此, 图8中1266 ℃时模拟的M₇C₃碳化物晶粒所占的模拟区域体积分数为0.0025%, 比GS模型预测值小; 1200.39 ℃时, M₇C₃碳化物晶粒所占的模拟区域体积分数为3.15%, 奥氏体晶粒所占的模拟区域体积分数为21.57%. 此后, M₇C₃碳化物和奥氏体晶粒相互接触共生长, 快速生长阶段与GS凝固路径快速生长阶段相同, 各相分数的整体变化趋势相同, 说明模拟过程各相生长的合理性. 在1200.39—1210.03 ℃区间, 各相分数曲线非单调增加, 这是由于相分数大幅增加致使潜热释放未及时散出导致温度回复所引起的, 该阶段M₇C₃碳化物、奥氏体相分数增长较快, 潜热释放作用持续增强, 冷却曲线呈现上升趋势. 相比较而言, 图7中各相分数随时间的变化曲线呈单调变化, 冷却曲线温度回复与图8中潜热释放各相体积分数在温度回复阶段继续增长相对应.
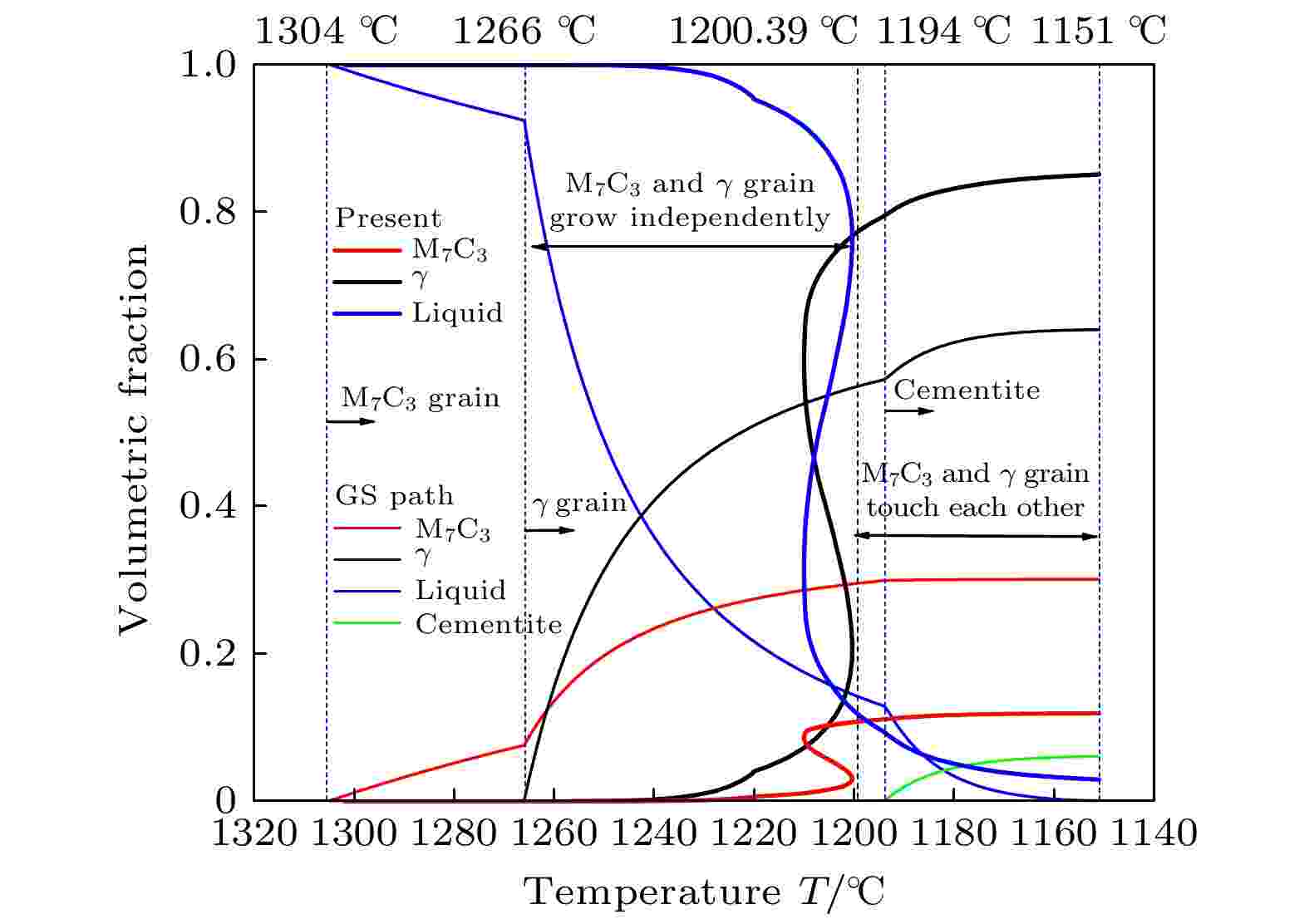图 8 本模拟与GS模型中各相质量分数随温度变化
Figure8. Evolution of phase mass fraction with temperature by present model and GS model.

2 -->

3.3.界面平衡浓度、晶粒生长速度随溶质贝克列数演变

随着凝固进行, 界面前沿的成分过冷不断增大, 溶质超饱和度将不断增大. 图9给出了M₇C₃碳化物/液相和奥氏体/液相界面液相中溶质C, Cr的贝克列数以及溶质界面平衡浓度随溶质Cr超饱和度的变化, 均取模拟区域中所有界面胞数据的平均值作图. 可以看出, 随Cr超饱和度增大, M₇C₃碳化物/液相和奥氏体/液相界面液相中溶质贝克列数均增大; 在相同超饱和度下, Cr溶质贝克列数大于C溶质贝克列数, 这与界面液相中溶质贝克列数与溶质的扩散系数成反比((12)式)、而液相中溶质Cr扩散系数小于C扩散系数(见表1)的规律相一致.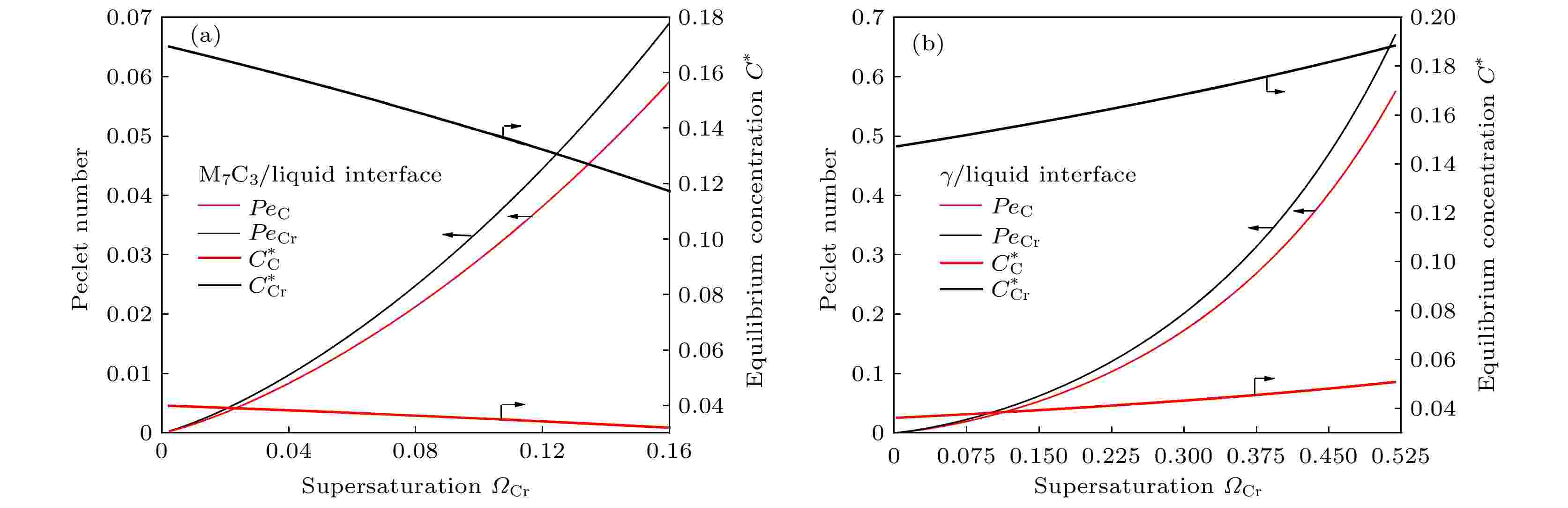
图 9 M₇C₃碳化物和奥氏体界面液相溶质贝克列数、平衡浓度演变　(a) M₇C₃界面; (b)奥氏体界面
Figure9. Evolution of solute Peclet number and equilibrium concentration in liquid at M₇C₃ and austenite interface cell: (a) M₇C₃/liquid interface; (b) austenite/liquid interface.

M₇C₃碳化物/液相界面C, Cr溶质液相平衡浓度随Cr超饱和度呈下降趋势(图9(a)), 与之相反, 奥氏体/液相界面C, Cr溶质液相平衡浓度随Cr超饱和度呈上升趋势(图9(b)). 这是由于M₇C₃碳化物/液相界面溶质C, Cr的分配系数均大于1, 而奥氏体/液相界面C, Cr溶质的分配系数均小于1, 由(10)式, 碳化物/液相界面溶质液相平衡浓度与超饱和度成反比, 奥氏体界/液相界面溶质液相平衡浓度与超饱和度成正比, 导致随着Cr超饱和度增大, 奥氏体/液相界面溶质液相平衡浓度不断增大, M₇C₃碳化物/液相界面溶质液相平衡浓度不断减小. 这与奥氏体生长向外排出C, Cr溶质, M₇C₃碳化物生长吸收C, Cr溶质的特性相符.
图10进一步给出M₇C₃碳化物/液相和奥氏体/液相界面生长速度随Cr溶质贝克列数的变化曲线, 界面生长速度分别为M₇C₃/液相或奥氏体/液相界面各元胞生长速度的平均值. 在M₇C₃/液相界面(图10(a)), Pe_Cr = 0.0116时, 奥氏体析出, 此后M₇C₃碳化物晶粒的生长速度明显增快, 说明二相晶粒相互促进生长. 在Pe_Cr < 0.0413 (交点1)区间, 晶粒生长速度整体随Cr溶质贝克列数的增加逐渐增大, 此处(交点1)对应冷却曲线上温度回复起始位置; Pe_Cr = 0.0366 (交点2)为冷却曲线温度回复达到最大值位置. 同样, 在奥氏体/液相界面处(图10(b)), 在Pe_Cr < 0.2688 (交点3)区间内, 晶粒生长速度随Cr溶质贝克列数的增加逐渐增大, 并在Pe_Cr = 0.2688 (交点3)时, 生长速度达最大, 此处对应冷却曲线上温度回复起始位置; Pe_Cr下降至0.2114 (交点4)为冷却曲线回复温度达到最大值位置. 在冷却曲线温度开始回复后, 两相晶粒生长速度逐渐降低, 这是由于该时刻已有部分奥氏体晶粒与M₇C₃碳化物晶粒相接触, 其后奥氏体晶粒不断包围M₇C₃碳化物晶粒, 接触部位越来越多, 晶粒没有继续生长空间, 导致M₇C₃碳化物、奥氏体晶粒的平均生长速度降低. 若冷却速率增大, 会加快模拟区域温度的下降, 由(5)式可知, 会增加成分过冷和曲率过冷; 通过图9和图10可知, 随着成分过冷度的不断增大, 贝克列数逐渐增大, 进而会增大M₇C₃碳化物和奥氏体独立生长阶段界面的生长速度, 缩短彼此独立生长时间, 相对来说奥氏体晶粒生长速度较快, 会快速包围M₇C₃碳化物晶粒, 从而减小M₇C₃碳化物尺寸.
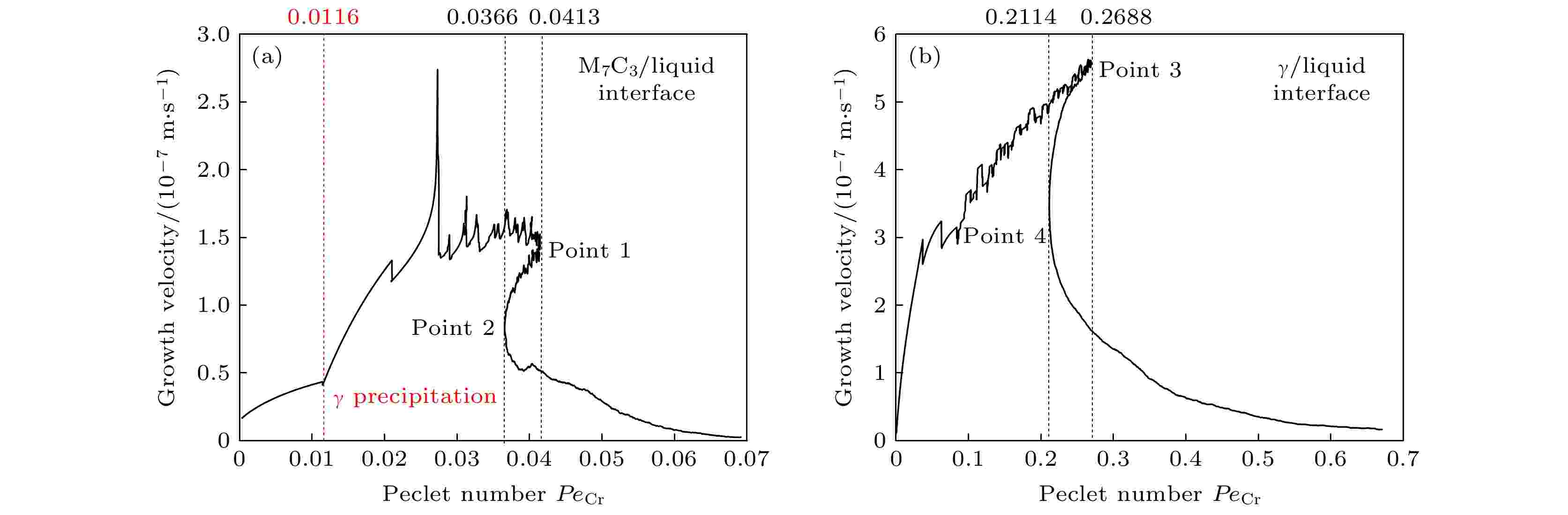图 10 M₇C₃碳化物/液相和奥氏体/液相界面生长速度演变:　(a) M₇C₃界面; (b)奥氏体界面
Figure10. Evolution of growth velocity with Pe_Cr at M₇C₃/liquid and austenite/liquid interface: (a) M₇C₃/liquid interface; (b) austenite/liquid interface.

2 -->

3.4.奥氏体、M₇C₃碳化物晶粒共生长

图11为凝固过程中不同时刻奥氏体晶粒的形貌演变, 以奥氏体相质量分数显示; 图12为相应时刻晶粒取向图, 显示出奥氏体晶粒(绿-蓝颜色晶粒)与M₇C₃碳化物晶粒(粉-红颜色晶粒)共同生长过程. t = 70.83 s时刻(图11(a)和图12(a)), 奥氏体晶粒A, B, C与M₇C₃碳化物晶粒彼此独立生长; t = 95.83 s时刻(图11(b)和图12(b)), 奥氏体晶粒A的右侧与M₇C₃碳化物晶粒左侧接触, 奥氏体晶粒A外轮廓右侧形貌发生改变; t = 120.83 s时刻(图11(c)和图12(c)), 奥氏体晶粒B, C接触到M₇C₃碳化物晶粒, 此时奥氏体晶粒A, B, C围绕M₇C₃碳化物晶粒生长, 呈现出包围趋势; t = 145.83 s时刻(图11(d)和图12(d)), M₇C₃碳化物晶粒被奥氏体晶粒完全包围.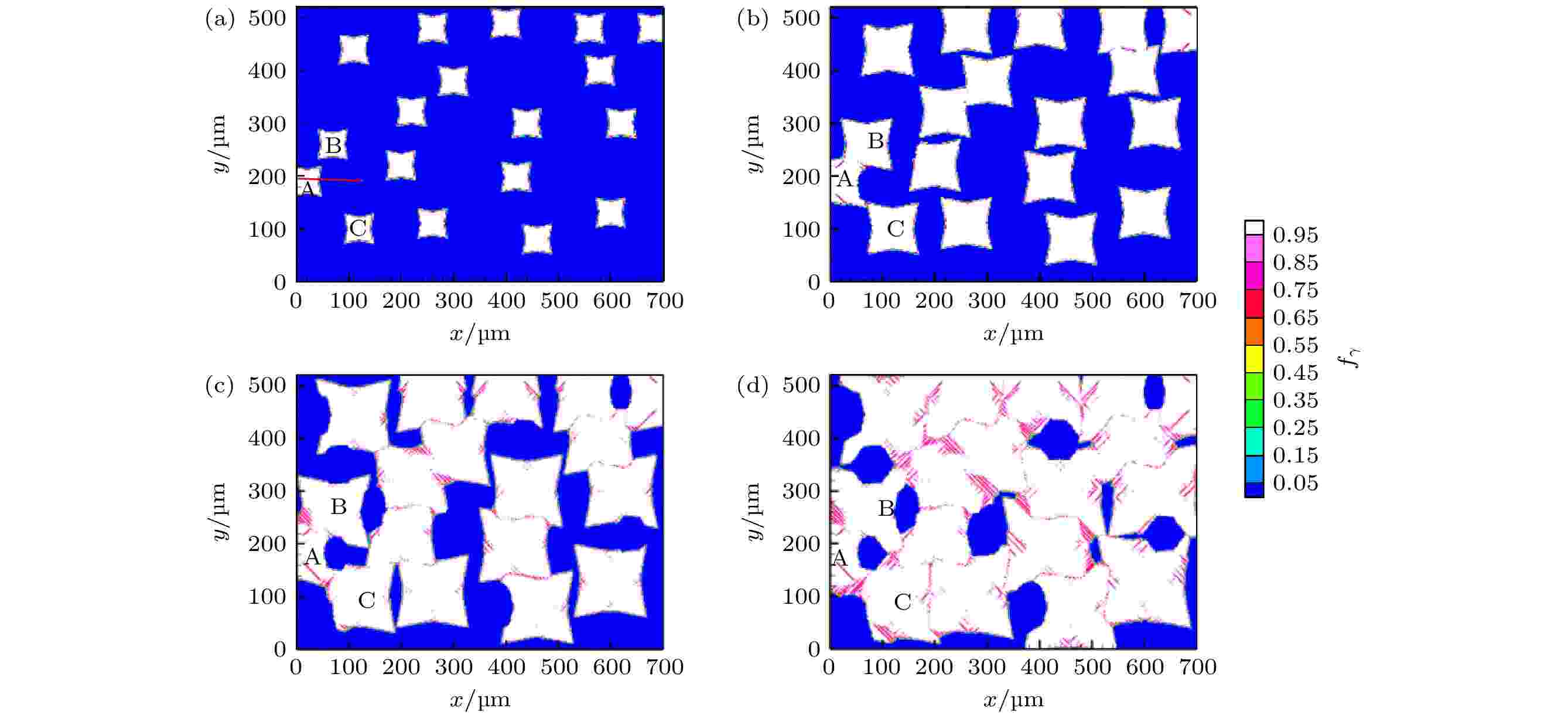
图 11 不同时刻奥氏体晶粒形貌　(a) t = 70.83 s; (b) t = 95.83 s; (c) t = 120.83 s; (d) t = 145.83 s
Figure11. Morphologies of austenite grains at different moment: (a) t = 70.83 s; (b) t = 95.83 s; (c) t = 120.83 s; (d) t = 145.83 s.

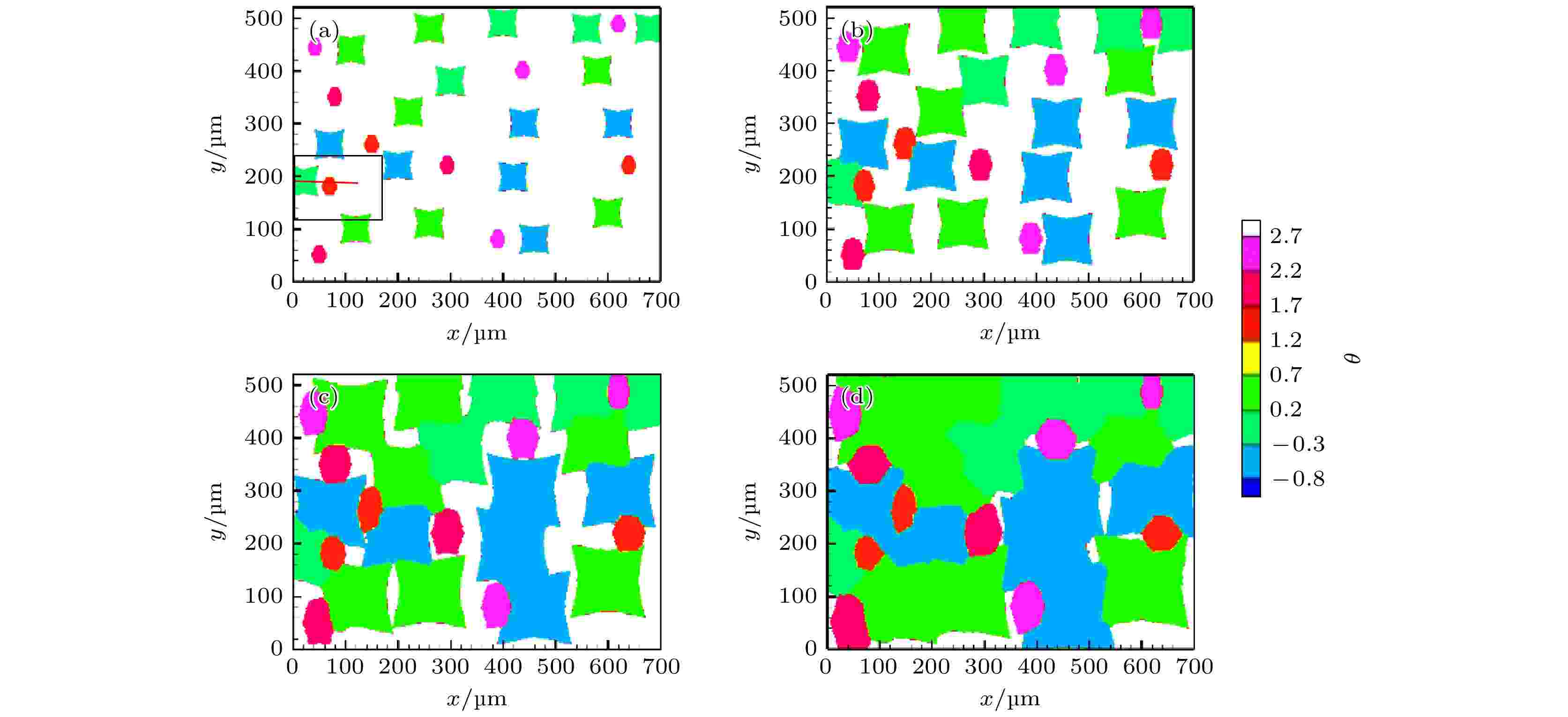图 12 不同时刻晶粒取向　(a) t = 70.83 s; (b) t = 95.83 s; (c) t = 120.83 s; (d) t = 145.83 s
Figure12. Crystallographic orientations of M₇C₃ and austenite grains at different moment: (a) t = 70.83 s; (b) t = 95.83 s; (c) t = 120.83 s; (d) t = 145.83 s.

图13为图11、图12中y = 180 μm处红色线位置奥氏体晶粒A和M₇C₃碳化物晶粒中C, Cr溶质浓度的变化曲线. 当t = 70.83 s时, 奥氏体晶粒A与M₇C₃碳化物晶粒未接触, 此时奥氏体晶粒和M₇C₃碳化物晶粒中间尚有液相区域(图13(a)对应1—2段; 图13(b)对应$1' $—$2' $段)与图12(a)黑色框内奥氏体晶粒和M₇C₃碳化物晶粒之间的液相区域相对应; 当t = 95.83 s时, 奥氏体晶粒和M₇C₃碳化物晶粒接触; 当t = 120.83, 145.83 s时M₇C₃碳化物晶粒左侧边界几乎未发生改变, 仅M₇C₃碳化物晶粒的右侧向外生长. 随着时间的推移, M₇C₃碳化物晶粒逐渐长大, 并最终被奥氏体晶粒完全包围. 由图13还可知, M₇C₃碳化物晶粒内C, Cr溶质的浓度高于界面液相浓度, 奥氏体晶粒内的C, Cr溶质溶度低于界面液相溶质浓度, 这与M₇C₃/液相及奥氏体/液相界面溶质分配规律相符.
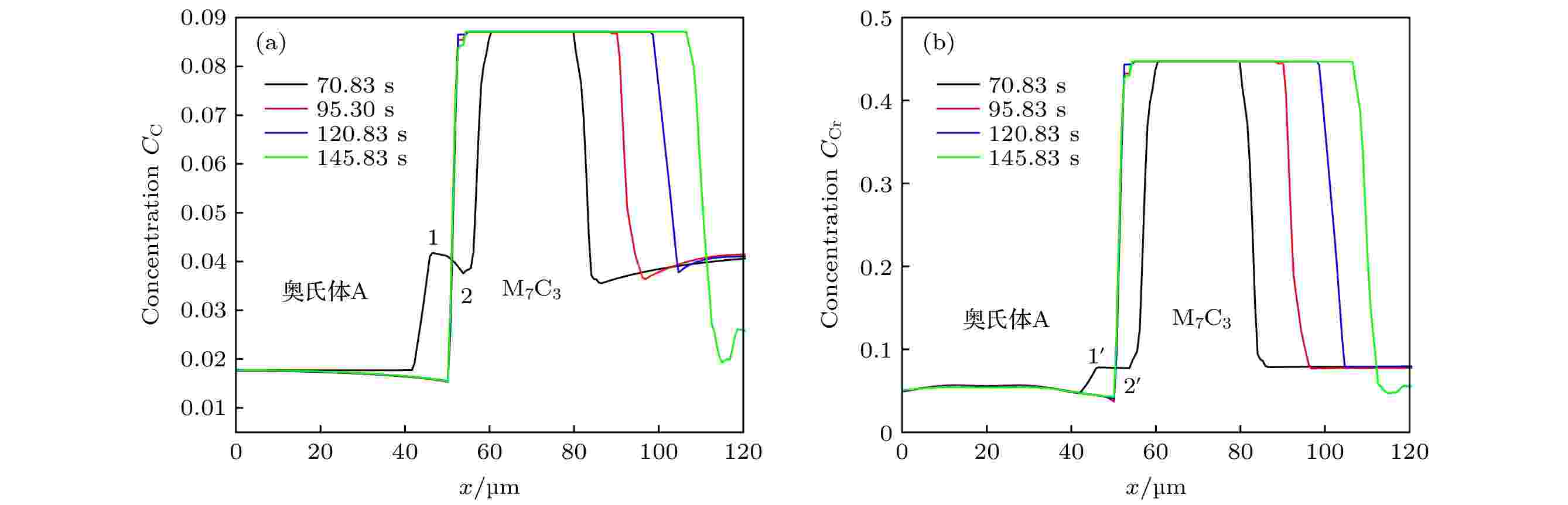图 13 奥氏体晶粒A和邻近M₇C₃碳化物晶粒周围溶质浓度的演变:　(a) C浓度; (b) Cr浓度
Figure13. Evolution of solute concentration around austenite grain A and adjacent M₇C₃ carbide grain: (a) C concentration; (b) Cr concentration.

2 -->

3.5.最终凝固组织形貌及体积分数与实验对比

图14给出Fe-4%C-17%Cr合金在石墨型冷却条件下显微组织^[22](图14(a))与相同条件下本模拟的最终凝固结果(图14(b)—(d)). 其中, 图14(b)为以奥氏体质量分数显示的晶粒形貌, 图中蓝色区域为M₇C₃碳化物晶粒, 白色区域为奥氏体晶粒, 红色区域为奥氏体晶臂处剩余液相区; 图14(c)和图14(d)为模拟的最终凝固时的C, Cr溶质浓度分布. 通过Image-Pro Plus 6.0软件测得实验显微组织图中M₇C₃碳化物体积分数为12.00%, 本模拟的M₇C₃碳化物体积分数为11.94%, 模拟结果与实验结果中M₇C₃碳化物晶粒大小形貌均相近.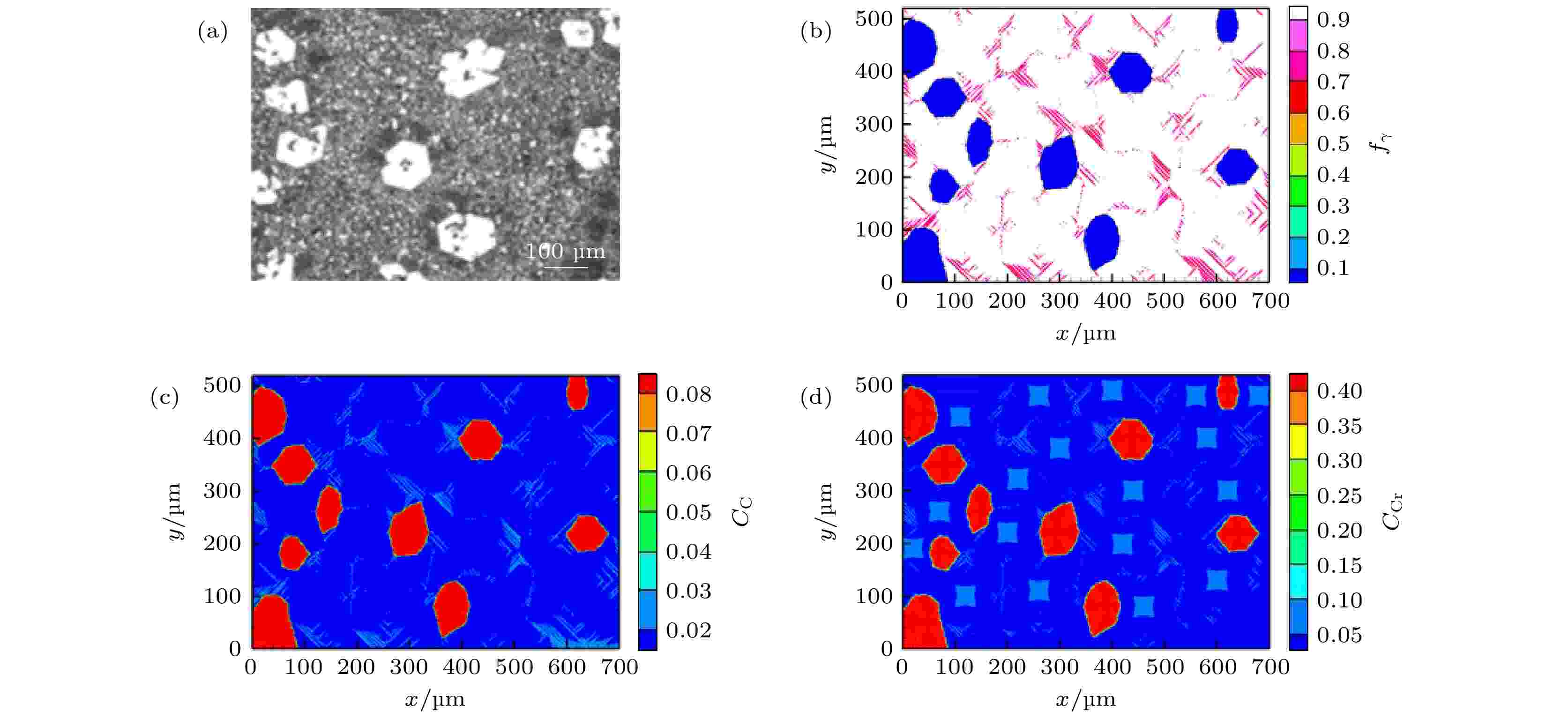
图 14 Fe-4%C-17%Cr合金实验^[22]和预测的凝固组织　(a)实验凝固形貌; (b)本模拟奥氏体质量分数; (c)本模拟C浓度场; (d)本模拟Cr浓度场
Figure14. Experimental^[22] and predicted solidification microstructure for Fe-4%C-17%Cr alloy: (a) experimental microstructure; (b) predicted austenite mass fraction; (c) predicted C concentration field; (d) predicted Cr concentration field.

2 -->

3.6.剩余液相与奥氏体中溶质浓度

3 -->

3.6.1.剩余液相中C, Cr溶质浓度演变

图15为本模拟(黑色曲线)与GS (各溶质在固相无扩散, 红色曲线)、PE (C溶质在固相充分扩散、Cr无扩散, 绿色曲线)、LR (各溶质在固相充分扩散, 蓝色曲线)模型预测的剩余液相中溶质C, Cr浓度的变化趋势对比. 本模拟的剩余液相溶质浓度由所有元胞中剩余液相溶质总和除以剩余总液相分数得到. 凝固初期, M₇C₃碳化物先行析出, 其生长过程中会吸收液相中的C, Cr溶质, 所以C, Cr溶质都为下降趋势; γ相析出后, γ生长过程中向液相中排出C, Cr溶质($ {k_{{{{\rm{p}}, \gamma/{\rm{L , C}}}}}} < {k_{{{{\rm{p}}, \gamma/{\rm{L , Cr}}}}}} < 1 $), 但由于M₇C₃碳化物生长所需的Cr溶质量较多($ \mathop C\nolimits_{{\text{M,Cr}}} $ = 44.7%, $ \mathop C\nolimits_{{\text{M,C}}} $ = 8.71%), 所以M₇C₃与γ共生长阶段, 液相中C浓度逐渐增加而Cr浓度持续减小. 可以看出, 从初始浓度点到与相图中$ \mathrm{\gamma } $/M₇C₃相界线相交阶段为M₇C₃碳化物形核析出、独自生长阶段; 奥氏体析出对应曲线与相界线交点, 此时模拟区域变为液相、M₇C₃碳化物和奥氏体三相区, 曲线沿着相图中$ \mathrm{\gamma } $/M₇C₃相界线行走, 直至CEM相析出结束(对应右下三相交界点), 这与GS, PE, LR模型预测曲线符合很好, 验证了本模拟的合理性.
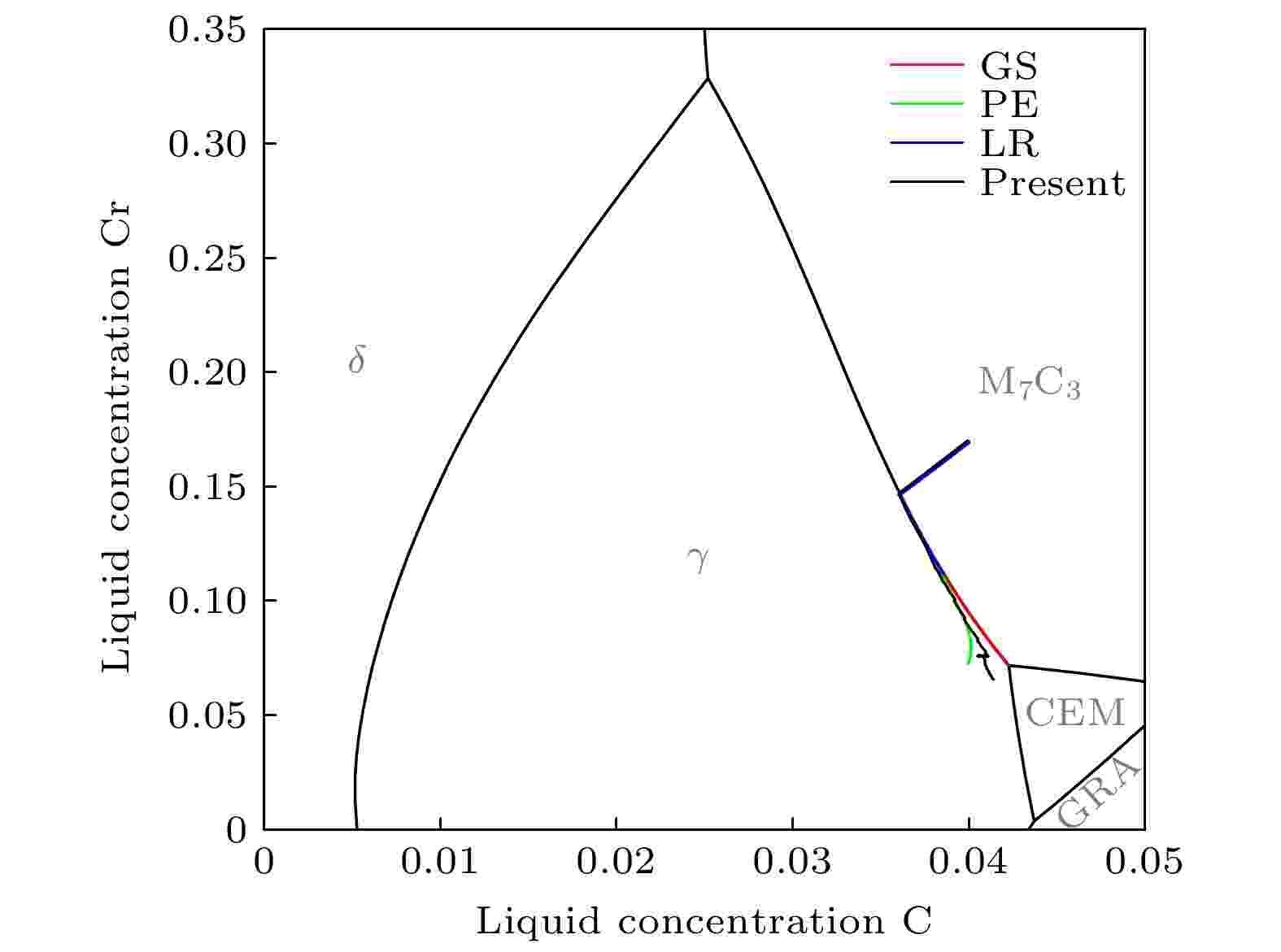图 15 剩余液相中C, Cr溶质浓度演变
Figure15. Evolution of C and Cr concentration in residual liquid.

3 -->

3.6.2.奥氏体中C, Cr溶质浓度演变

图16给出了本模拟的奥氏体中C, Cr溶质浓度随奥氏体体积分数的变化曲线及与GS, PE, LR模型曲线的对比. 本模拟中C, Cr溶质在奥氏体中有限扩散, 为对比GS结果, 亦给出C, Cr溶质在奥氏体中$ {D}_{\mathrm{\gamma }} $ = 0结果. 图16(a)中初期C溶质有扩散曲线在无扩散曲线上方, 在奥氏体相分数约为0.42时交叉, 之后变为无扩散曲线在有扩散曲线上方. 这种趋势是由于, 交叉点处为奥氏体和M₇C₃碳化物快速生长阶段, 奥氏体中溶质C的扩散系数比Cr大4个数量级, 奥氏体晶粒和M₇C₃碳化物晶粒接触、包围M₇C₃晶粒后, 缓慢的凝固过程为奥氏体晶粒中C溶质扩散提供了更长的时间, 进而导致C浓度低于无扩散结果. 图16(b)中Cr溶质无扩散曲线在有扩散曲线上方, 二者浓度值几乎重合, 这是因为Cr溶质扩散系数较小(3.67$ \times $10^–14 m²/s), 接近0的缘故. 总体来看, 奥氏体中C溶质浓度随凝固的进行呈逐渐增大趋势, Cr溶质浓度呈持续下降趋势, C, Cr溶质浓度值虽与GS, PE, LR凝固路径曲线存在一定差异, 但C, Cr整体变化趋势与GS, PE, LR模型曲线演变趋势相同, C, Cr溶质有无扩散曲线的上下位置与GS模型、LR模型曲线位置对应吻合.
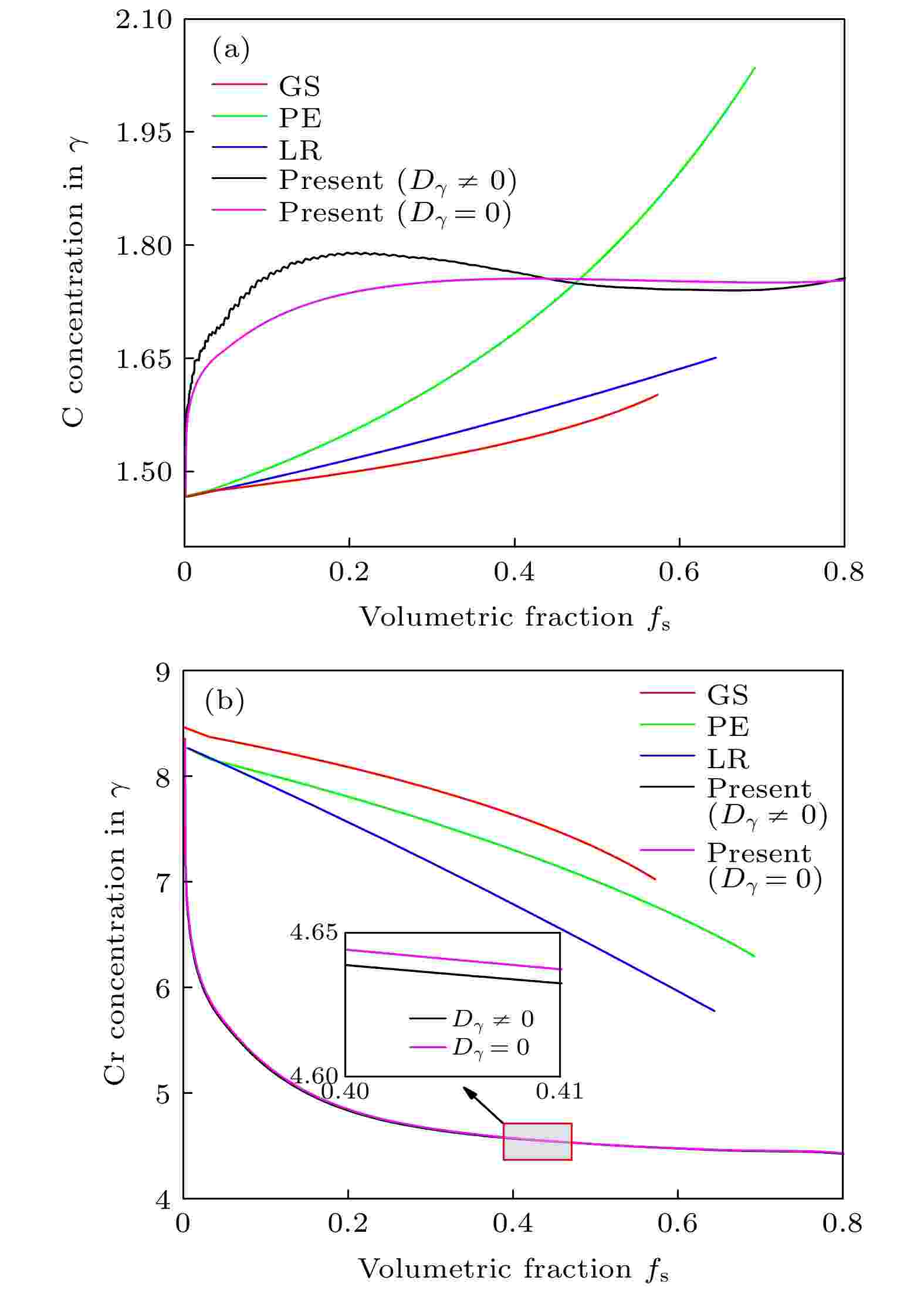图 16 奥氏体中C, Cr溶质浓度演变与凝固路径模型对比　(a) C 浓度; (b) Cr浓度
Figure16. Comparison of C and Cr solute concentration evolution in austenite with GS, PE and LR solidification path prediction: (a) C concentration; (b) Cr concentration.

1)开发了Fe-C-Cr三元合金小面晶M₇C₃碳化物与枝晶共生长的二维微观元胞自动机模型. 模型中加入潜热释放对凝固过程温度场的影响, 由C, Cr两溶质界面扩散共同确定晶体生长速度, 由凝固路径数据表插值获取液相元胞的溶质平衡浓度, 通过设定M₇C₃碳化物邻胞结构并优化形状因子来保持M₇C₃小面晶形貌, 模拟了Fe-4%C-17%Cr三元合金初生M₇C₃碳化物和共晶奥氏体晶粒的生长演变过程.
2) M₇C₃碳化物和奥氏体晶粒在液相中各自的生长速度随界面液相中C, Cr溶质的超饱和度和贝克列数的增大而不断增大. 随着奥氏体的析出和晶粒生长, M₇C₃碳化物晶粒的生长速度明显增快, 二者生长相互促进. 当奥氏体晶粒逐渐接触并包围M₇C₃碳化物晶粒, 对应于冷却曲线温度回复开始后, 晶粒没有继续生长空间, 两相晶粒生长速度遂逐渐降低.
3) Fe-4%C-17%Cr合金凝固过程中, 奥氏体晶粒生长向外排出C, Cr溶质, 与吸收C, Cr溶质生长的M₇C₃碳化物晶粒互补, 致使二者生长互相促进, 最终奥氏体晶粒包围M₇C₃碳化物晶粒生长, 奥氏体枝晶形貌趋近M₇C₃碳化物晶粒外轮廓.
4) 预测的Fe-4%C-17%Cr合金冷却曲线及添加1.5%Ti后石墨铸型实验冷却曲线^[22]和Fe-3.23%C-23.8%Cr合金添加4%Ti与否的砂型实验冷却曲线^[39]的变化趋势相符, 最终凝固组织形貌和M₇C₃碳化物体积分数与实验^[22]相符, 剩余液相、奥氏体中C, Cr溶质浓度演变与GS, PE, LR模型均相符.
5)实际工程应用中, 通过增大M₇C₃形核过冷度(如进行熔体洁净化处理), 增加形核密度(如采取合金化手段, 添加Ti, V等合金元素增加M₇C₃形核质点)或增大冷却速率, 可实现减小M₇C₃碳化物尺寸和均匀分布.