全文HTML
--> --> -->通常, 人们用无量纲的ZT值来衡量热电材料性能的优劣, 可以表示为[8]
近些年来, 在众多热电材料体系中, 类金刚石结构化合物热电材料由于其稳定的四面体结构及优良的热电性能受到了广泛的关注. 它们是由II-VI二元闪锌矿(ZnSe)结构衍生而来, 逐渐发展出复杂的I-III-VI2, II-IV-V2, II-III2-VI4, I2-IV-VI3, I3-V-VI4三元化合物以及I2-II-IV-VI4四元化合物[9]. 先前的大部分研究表明, 性能优异的热电材料通常具有较小的带隙[10,11], 然而大多数类金刚石化合物的带隙都比较大(通常大于1 eV), 因此早年关于该热电材料体系的研究很少. 直到2009年, Shi等[12]报道了掺杂In元素的Cu2ZnSnSe4类金刚石结构化合物在850 K时的ZT值为0.95. 这一令人兴奋的发现再次引起了人们对类金刚石结构热电材料的兴趣, 它为在宽带隙半导体中寻找高性能的热电材料提供了新的方向. 从那时起, 相关研究人员对各种三元和四元类金刚石化合物进行了系统的探索, 并报道出很多具有优异热电性能(较高ZT值)的系列材料[12-22].
例如, Parker和Singh [23]以及Wu等[24]以理论计算形式预测了AgGaTe2材料的热电性能, 由于其在900 K 附近较高的热电势而使得其 ZT 值可达到 1.19, 甚至更高; Kosuga团队[25]也研究了CuInTe2 体系的热电性能, 合成了 ZT = 0.54 (710 K)的样品; Yusufu等[26]实验研究发现, Ag0.95GaTe2材料的 ZT 值在 850 K 时达到 0.77. 至于CuGaTe2材料, 早在1997年, Kuhn等[27]就研究了CuGaTe2材料在低温区的热电性质, 其在研究温区内表现出较高的热导率, CuInTe2, CuGaTe2和CuIn0.64Ga0.36Te2的单晶样品热导率在360 K左右分别为3.11, 3.22和5.09 W?m–1?K–1, 在80 K左右时更是高达6.03, 6.90, 8.73 W?m–1?K–1, 因而获得的ZT值仅为0.08, 0.04, 0.06, 由于其较低的ZT 值该材料体系没有引起人们广泛的关注, 也没有更多的后续研究. 直到 2012 年, Plirdpring等[20]研究发现, CuGaTe2 材料在中高温区域有着优异的热电性能, 其ZT值在950 K时达到1.4左右, 这才使得该体系热电材料备受关注.
CuGaTe2是带隙宽度约为 1.2 eV的p型半导体, 属于 I-42d空间群. 近几年, 对于该体系热电材料有很多相关报道, 比如有研究报道了300—610 K温度范围内少量Ag掺杂对CuGaTe2热电性能的影响, 发现在590 K时其ZT值达到0.31, 比相应的基体CuGaTe2提升约82％[28]; 另外, Cui 等[29]研究了Cu1–xGaSbxTe2化合物, 结果发现掺杂原子Sb主要占据晶胞中Te原子的位置, 而不是Cu原子的位置; Shen等[30]在CuGaTe2材料中引入In2Te3和Ga2Te3, 以设计空位的方式降低材料的晶格热导率, 最终材料的平均ZT值约提升了75%; Ahmed等[31]在报道中指出, 在Ga位引入磁性元素Mn掺杂后载流子浓度增加, 最终CuGa0.99Mn0.01Te2样品在870 K下的最大ZT值为0.83.
然而, 当前还鲜有关于在CuGaTe2中Cu位掺杂磁性元素的研究. 本文探索了磁性元素Ni替代Cu位对其热电性能的影响. 用真空熔炼法合成了一系列Ni掺杂的Cu1–xNixGaTe2(x = 0, 0.25%, 0.50%, 0.75%)样品, 结果表明, Ni原子可以有效地替代晶格中的Cu原子并引起材料载流子浓度的略微下降. 同时, 掺杂Ni后样品的Seebeck系数显著提高, 并且Ni掺杂引起的点缺陷散射有效地降低了材料的热导率. 最终, 在873 K下, Cu0.095Ni0.005GaTe2的最大ZT值为1.26, 比基体CuGaTe2的ZT值增大了约56％. 本文的工作表明, 在Cu位掺杂磁性元素Ni是提升CuGaTe2体系材料热电性能的有效手段之一.
在室温下, 利用X射线衍射仪(XRD, 型号为Philips X’Pert PRO)对热压烧结后的样品进行物相分析, 选用的是Cu靶 Kα射线(λ = 1.54056 ?), 测试电压40 kV, 电流400 mA, 测试角度为15°≤2θ≤90°, 步长2θ为0.008°, 样品的结构精修是利用GSAS II软件对XRD的结果进行全谱拟合得到的. 样品的密度采用阿基米德原理测得, 比热系数Cp采用Dulong-Petit 公式计算得到. 电学性能(电导率、Seebeck系数)由商用热电性能测试系统(ZEM-3(M10), ULVAC-RIKO)测得, 测试原理为四探针法, 测试需要氦气作为保护气且保持负压状态. 室温载流子浓度和迁移率使用CVM-200 霍尔效应测量系统测得, 扫描磁场为±3.0 T. 紫外吸收光电子能谱(UPS)仪器型号为PHI 5000 Versa Probe II, 测试时的光源为单色He I光源(21.2 eV). 热扩散系数使用NETZSCH LFA-457激光热导仪测得.
文中所有密度泛函理论(DFT)[32,33]的计算均使用Vienna ab-initio simulation package(VASP)5.4代码[34]. 对于Ni元素掺杂的模型, 先建立2 × 2 × 2的超胞, 然后将其中的一个Cu原子被Ni原子取代. 在模拟过程中, Cu, Ni, Ga 和 Te 的价电子数分别为 11, 10, 13 和 6. 以上两个体系的布里渊区均使用Monkhorst-Pack网格采样, 5 × 5 × 3和2 × 2 × 1的k点设置分别用于单胞和超胞的结构优化. 为了更好地描述电子结构, 在自洽场 (SCF) 计算中引入了 MBJ 校正, 以获得更准确的带隙和态密度 (DOS). 对于单胞, 力和能量收敛标准设置为 0.0001 eV/?和10–7 eV, 而对于超胞则设置为 0.01 eV/?和 10–5 eV. 文中采用 DFT-D3 (BJ)[35,36]方法来考虑范德瓦耳斯修正.
3.1.物相分析
图1(a)给出了室温下Cu1–xNixGaTe2(x = 0, 0.25%, 0.50%, 0.75%)样品的XRD衍射图, 可以看出, 几乎所有样品的衍射峰均与CuGaTe2四面体的标准卡片(PDF#065-2746)对应, 这表明本文合成的样品中几乎没有产生杂质相. 另外, 图1(a)的右上角插图中放大了所有样品的最强衍射峰(112), 可以看出, 随着Ni元素含量x的增加, 所有衍射峰都逐渐向低角度偏移, 这意味着Ni掺杂后导致晶胞逐渐膨胀.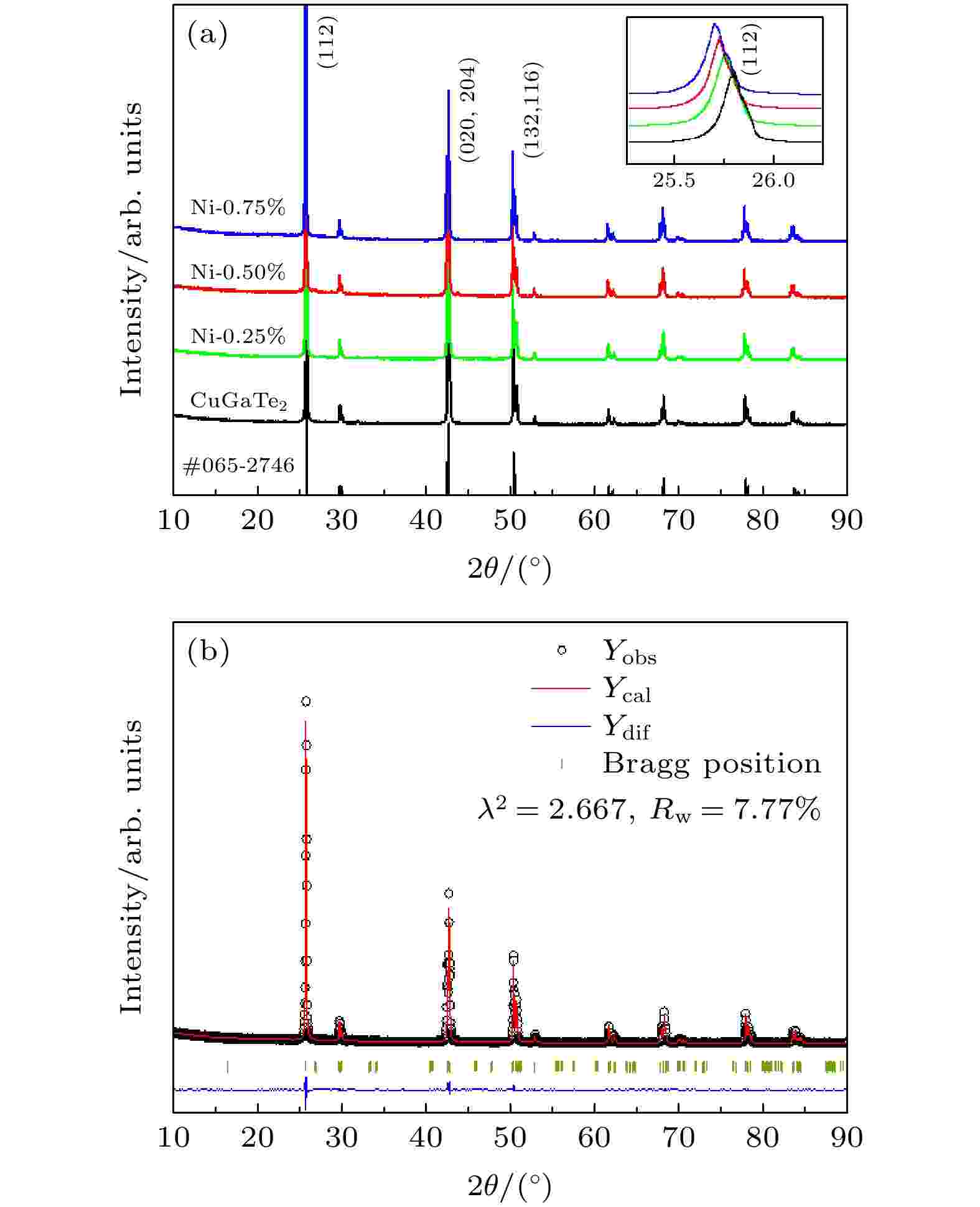
图 1 (a) Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%)样品室温下的XRD图谱, 其中, 在右上角附注(112)衍射峰的放大图; (b) Cu0.995Ni0.005GaTe2样品的XRD数据结构精修图, λ2和Rw为精修的误差参数Figure1. (a) XRD results of Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%) samples at room temperature, and the enlarged view of (112) diffraction peak is attached in the upper right corner; (b) results of refined XRD for Cu0.995Ni0.005GaTe2 sample, λ2 and Rw are the refined error parameters.
为了详细确定Cu1–xNixGaTe2样品晶格参数的变化, 利用GSAS II的Rietveld精修法对所有样品的XRD的结果进行全谱拟合, 图1(b)所示的是x = 0.5%样品的精修结果. 其中, XRD的实验数据标记为黑圈(Yobs), 根据晶体结构计算出的XRD图谱标记为红线(Ycal), 实验数据和计算值之间的差异标记为蓝线(Ydif), 另外, 垂直的绿色短线表示纯相CuGaTe2的衍射峰位. 可以看出, 差值蓝线几乎在整个衍射角度范围内保持水平, 并且样品的精修误差Rw在10%以下, 这些都意味着本文精修的结果是合理的.
精修出的样品晶胞参数如图2所示, 发现掺杂Ni元素后主相的晶胞是逐渐膨胀的, 当Ni元素掺杂量x = 0, 0.25%, 0.50%和0.75%时晶胞参数a分别为6.024(3), 6.024(8), 6.025(3)和6.027(3) ?; 晶胞参数c分别为11.941(3), 11.941(6), 11.941(9)和11.946(5) ?. 晶胞的膨胀是由Ni2+的离子半径(rNi = 0.069 nm)大于Cu+的离子半径(rCu = 0.060 nm)导致的, 这也从一定程度上说明了我们成功地将Ni掺进了Cu的位置.
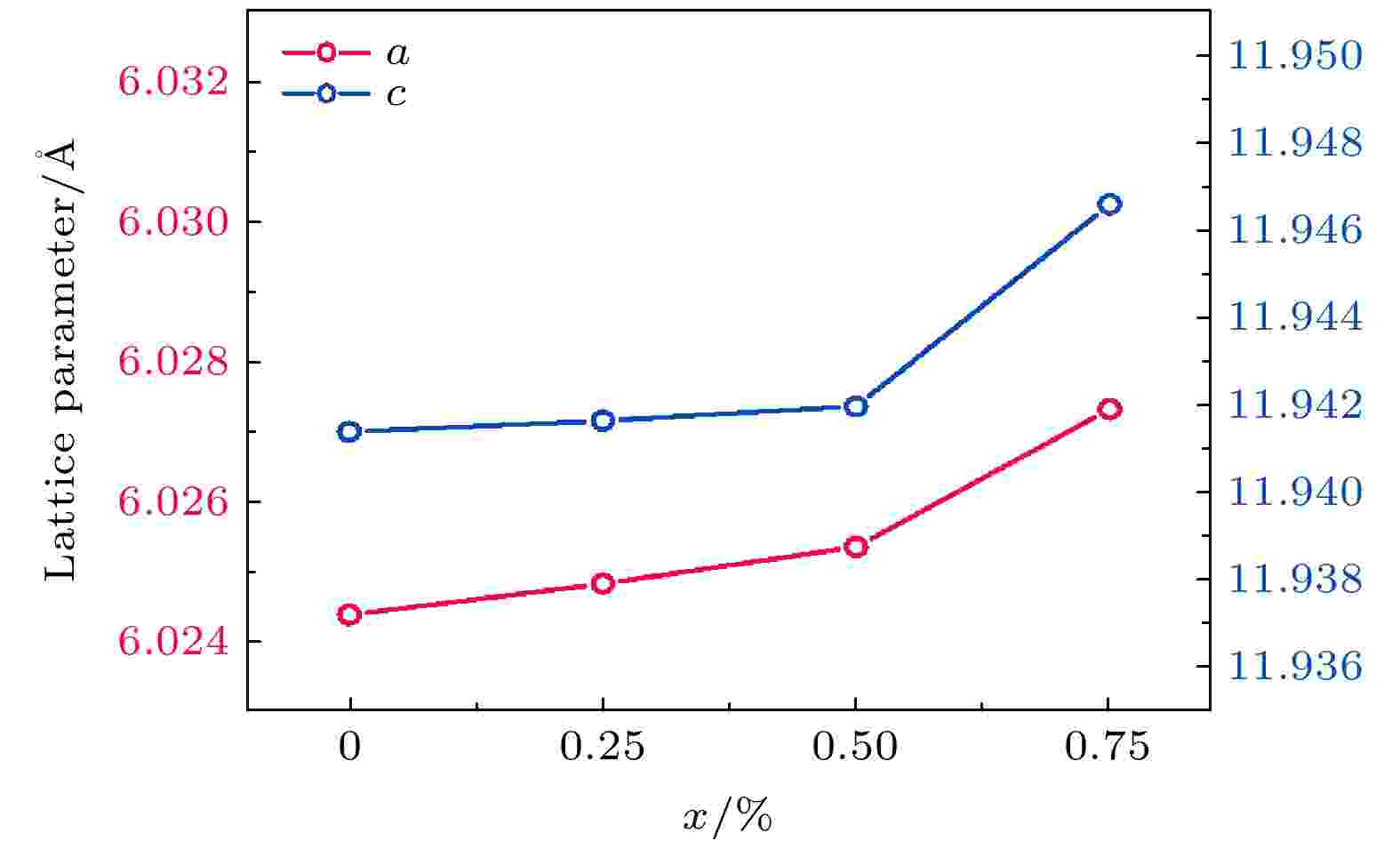图 2 Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%)样品晶格参数随Ni含量x的变化Figure2. Lattice parameters of Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%) samples.
2
3.2.电学性能分析
图3(a)给出所有样品的电导率随温度的变化关系. 对于基体而言, 其电导率先随温度升高而增加, 然后在较高温度时出现了下降的趋势, 在特定温度(Ts)处出现一个最高峰值. 这种异常的电荷传输行为在其他类金刚石结构化合物中也有被观察到(如CuInTe2和AgGaTe2)[37], 是由于材料中存在受主能级的缘故. 通常, 在低温下受主能级为空, 其电子输运性质表现为简并半导体的性质; 但由于受主能级与价带之间的能量差较小, 随着温度的升高, 会有一部分电子受到激发被受主能级激俘获, 进而使材料中的空穴浓度急速增加; 当受主能级所有可占据位置都被激发的电子占满后, 随着温度升高, 样品的载流子浓度几乎不再上升, 此时载流子的迁移率在电输运性质中占主导地位, 即电导率随着温度的升高而降低是因为被激发的电子在受主能级中相互散射造成迁移率的损失. 但值得注意的是, 随着Ni含量的增加, Ts并没有发生很明显的变化, 这可能是由Ni掺杂前后样品受主能级的位置没有发生明显变化导致的.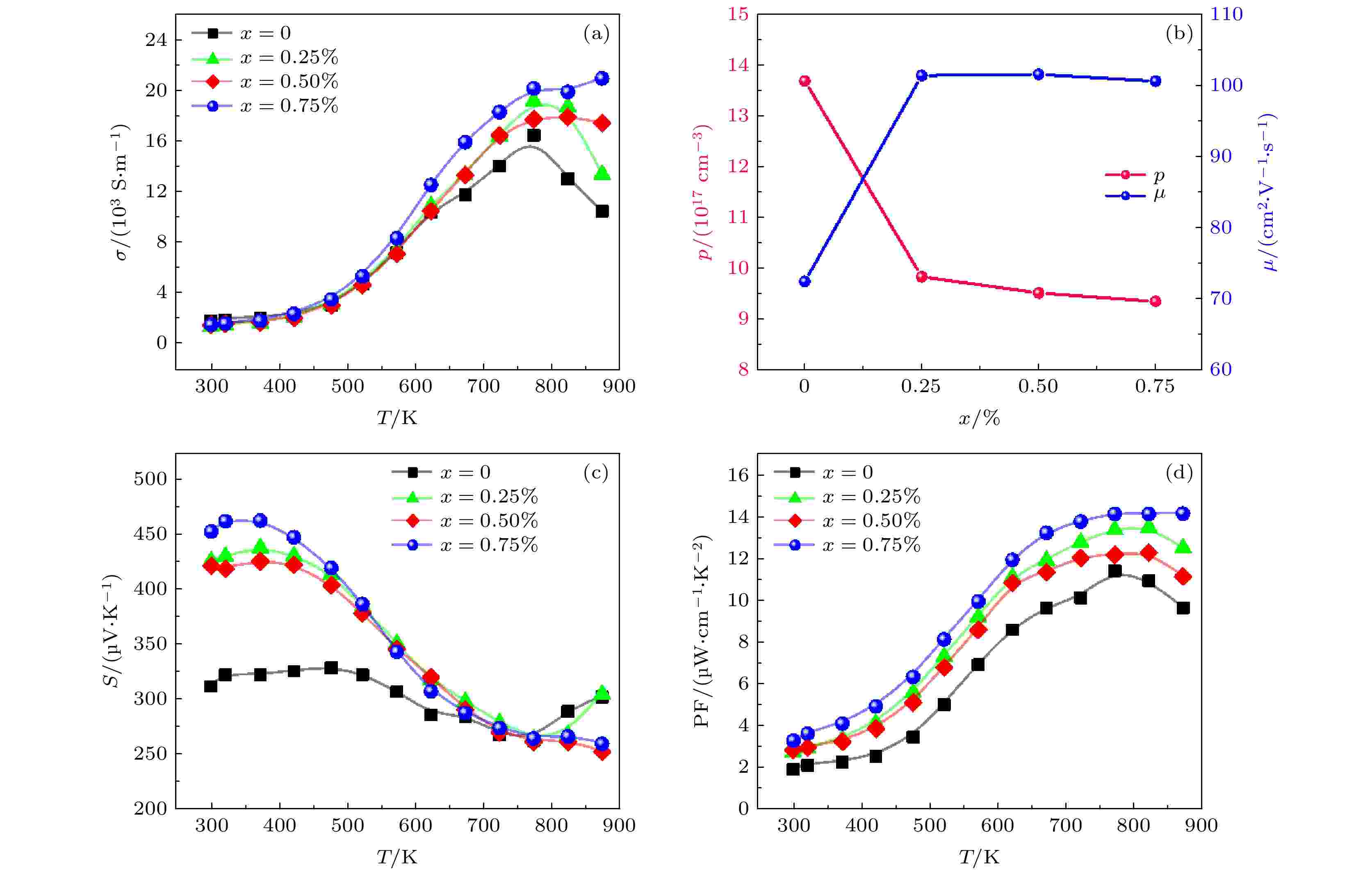
图 3 Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%)样品的 (a)电导率随温度的变化, (b)室温下载流子浓度和迁移率, (c) Seebeck系数和(d)功率因子随温度的变化Figure3. Electrical properties of Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%) samples: (a) Dependence of electrical conductivity with temperature; (b) carrier concentration and carrier mobility at room temperature; dependence of (c) Seebeck coefficient and (d) power factor with temperature.
同时, 根据图3(a)可以发现, 掺杂Ni前后样品的电导率并没有很大的变化, 尤其是约623 K之前数值几乎没有差别. 图3(b)是所有样品室温下的载流子浓度p和迁移率μ随Ni含量x的变化, 可以看出, 掺杂Ni后样品的载流子浓度有所下降, 但迁移率却出现了上升的现象. 根据电导率的公式
图3(c)是样品的Seebeck系数随温度的变化关系, 数据表明, 所有样品的Seebeck系数都是先随温度升高而降低, 然后在高温范围(T > Ts)随温度的增加略微上升, 这与前文中电导率对温度的依赖性几乎一致. 但值得注意的是, 掺杂Ni元素后, 样品的Seebeck系数出现了明显上升. 例如, 室温下基体样品CuGaTe2的Seebeck系数为311 μV/K, 而当x = 0.25%, 0.50%和0.75%时, 其Seebeck系数分别为426, 421和453 μV/K. 通常, 对于简并半导体或金属材料, 根据Mott公式可以将Seebeck系数定义为[38]
但Seebeck系数的大幅上升引起了我们的注意, 根据(2)式, 可以发现Seebeck系数和态密度也是成正比的, 可以用下列公式表示:
为了验证上一结论, 对Ni元素掺杂前后样品的电子结构进行DFT理论计算. 对于掺杂样品, 建立了一个2 × 2 × 2的CuGaTe2超胞, 并将其中一个Cu+替换为Ni2+, Ni元素的掺杂率为3.125%. 选择这个掺杂比例主要有两方面的原因: 一是因为n×n×n超胞可以最好地保留单晶的对称结构; 二是由于计算内存的限制, 2 × 2 × 2超胞几乎是使用 MBJ 校正方法的最大晶胞. 因此, 下文中将它表示为 Cu0.96875Ni0.03125GaTe2. 掺杂Ni前后晶体结构示意图如图4(a)和图4(b)所示.
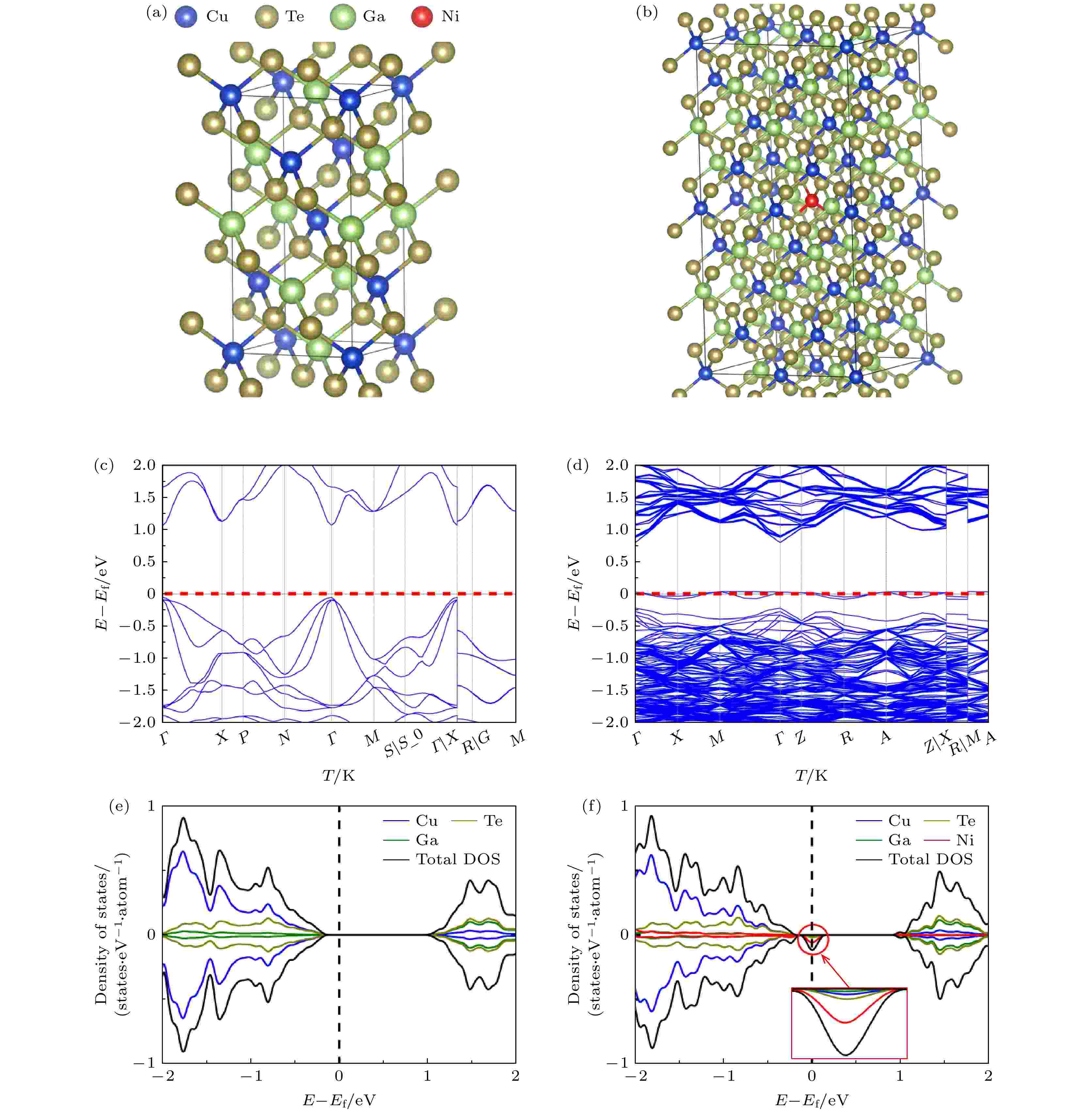图 4 CuGaTe2和Cu0.96875Ni0.03125GaTe2 样品 (a), (b)晶体结构示意图; (c), (d)能带结构图; (e), (f)总态密度和分态密度图Figure4. (a), (b) Visual patterns of structures, (c), (d) band structures, (e), (f) total density of states and partial density of states for CuGaTe2 and Cu0.96875Ni0.03125GaTe2, respectively.
图4(c) 和图4(d) 则给出了基体和掺杂样品的能带图, 从图4(c)可以看出, 未掺杂的CuGaTe2体系所有高对称点的价带都低于费米能级. 价带顶和导带底均位于Γ 点, 属于直接带隙半导体, 带隙约为1.12 eV. 同时还发现, 形成价带最大值 (VBM) 的带是不均匀的. 这些结果表明, 该体系材料的电子输运性质将受到 VBM 中较大带隙和较小带有效质量(约 0.08me)的限制. 同时, 在图4(d) 中, Ni掺杂后出现了极为平坦的混合带, 这直接导致掺杂样品Cu0.96875Ni0.03125GaTe2的带隙明显变小, 约为0.77 eV; 频带的有效质量也锐化增加到 3.24me. 根据(2)式, 掺杂后有效质量的增加对提升样品Seebeck系数是十分有利的.
为了更直观地分析掺杂Ni前后样品态密度的变化, 基体样品CuGaTe2和 Cu0.96875Ni0.03125GaTe2的总态密度(TDOS)和分态密度(PDOS)分别如图4(e)和图4(f) 所示. 通过对比可以发现, 掺杂Ni后样品的态密度在费米能级附近出现了明显的提升, 并且其混合带主要由 Ni 原子轨道组成, 同时 Te 原子是该带的第二贡献者. 因此可以认为, 掺杂后引起的Ni-Te带相互作用是增强电子传输的主要原因.
此外, 根据Xu等[39]的报道, 费米能级附近的态密度和其价电子态(DOVS)曲线的斜率成正比. 因此, 本文也测试了掺杂前后样品的紫外光电子能谱, 如图5所示. 图5(a)是样品的全谱信息, 图5(b)是图5(a)中绿色区域的放大图. 通过图5(b)可以发现: 掺杂Ni后样品费米能级附近DOVS的斜率明显大于基体样品的斜率, 这也充分说明了在Cu位置掺杂Ni元素能有效地增强样品费米能级附近的态密度. 这一实验结果和上文理论计算部分的结论完全一致, 充分说明了掺杂Ni元素后不但能引起载流子浓度的下降, 同时也能引起态密度的有效提升, 这两方面的原因导致掺杂后样品Seebeck系数的有效提升, 这对提升样品电学性质是十分有利的.
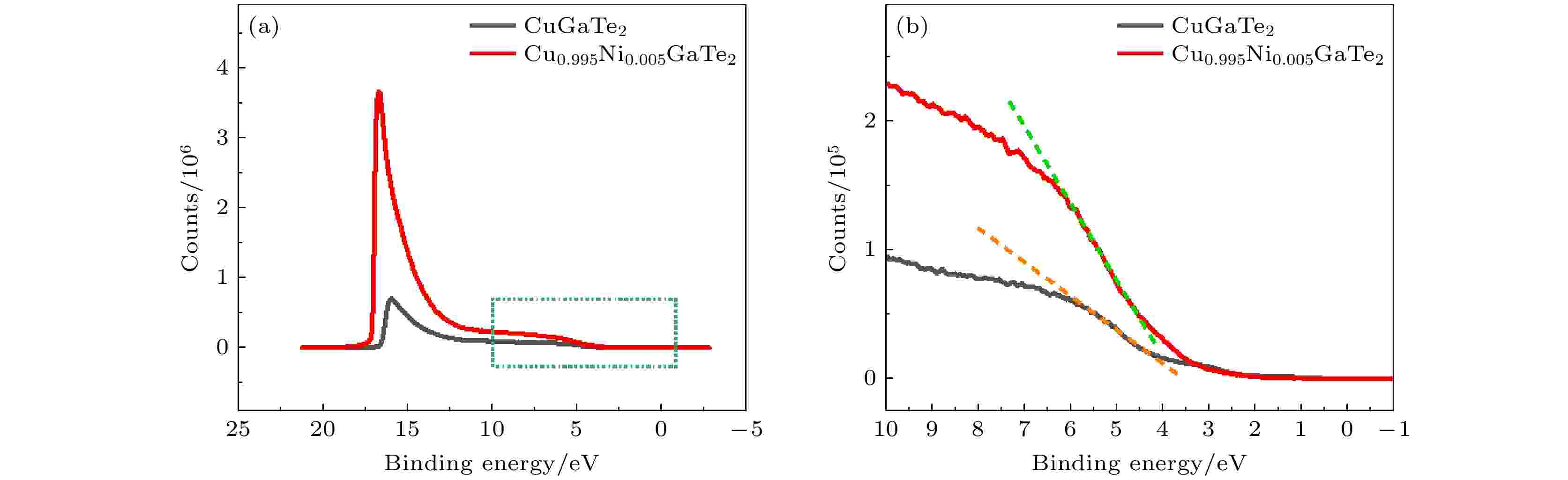图 5 CuGaTe2和 Cu0.995Ni0.005GaTe2 样品的紫外光电子能谱图 (a)全谱图; (b)图(a)中绿色虚线框内的放大图Figure5. UV photoelectron spectra of CuGaTe2 and Cu0.995Ni0.005GaTe2 samples: (a) Full spectrum; (b) enlarged view in the green dashed box in panel (a).
图3(d)是掺杂前后样品的功率因子随温度的变化, 由于掺杂Ni后Seebeck系数明显上升, 相对基体而言, 通过Ni元素掺杂获得了增大的功率因子. 如873 K时, x = 0, 0.25%, 0.50%, 0.75%样品功率因子为9.74, 12.54, 11.10和14.08 μW·cm–1·K–1. 引入Ni元素掺杂后, 最高能将样品的电学性能提升约45%, 能获得如此优异的电学性能完全归根于载流子浓度下降和态密度提高引起的Seebeck系数的显著增强.
2
3.3.热学性能和热电优值
图6(a)是Cu1–xNixGaTe2(x = 0, 0.25%, 0.50%, 0.75%)样品的总热导率对温度的依赖关系图, 结果表明, 样品的热导率先随着掺杂元素Ni含量的增加而略微降低, 当x = 0.50%时获得最低热导率, 在873 K时其热导率为0.95 W·m–1·K–1, 而基体的热导率在该温度下为1.10 W·m–1·K–1. 此外计算了Ni元素掺杂前后样品的晶格热导率, 如图6(b)所示, 其中洛伦兹常数L = 1.5 × 10–8 V2·K–2. 可以看出, 晶格热导率随温度的变化几乎和总热导率的变化一致, 在873 K时x = 0, 0.25%, 0.50%和0.75%样品的晶格热导率分别为0.945, 0.880, 0.726和0.750 W·m–1·K–1, 掺杂Ni元素后其最低晶格热导率在873 K时比基体下降了约30%. 晶格热导率的降低是由于Ni掺杂后引起点缺陷散射增强导致的.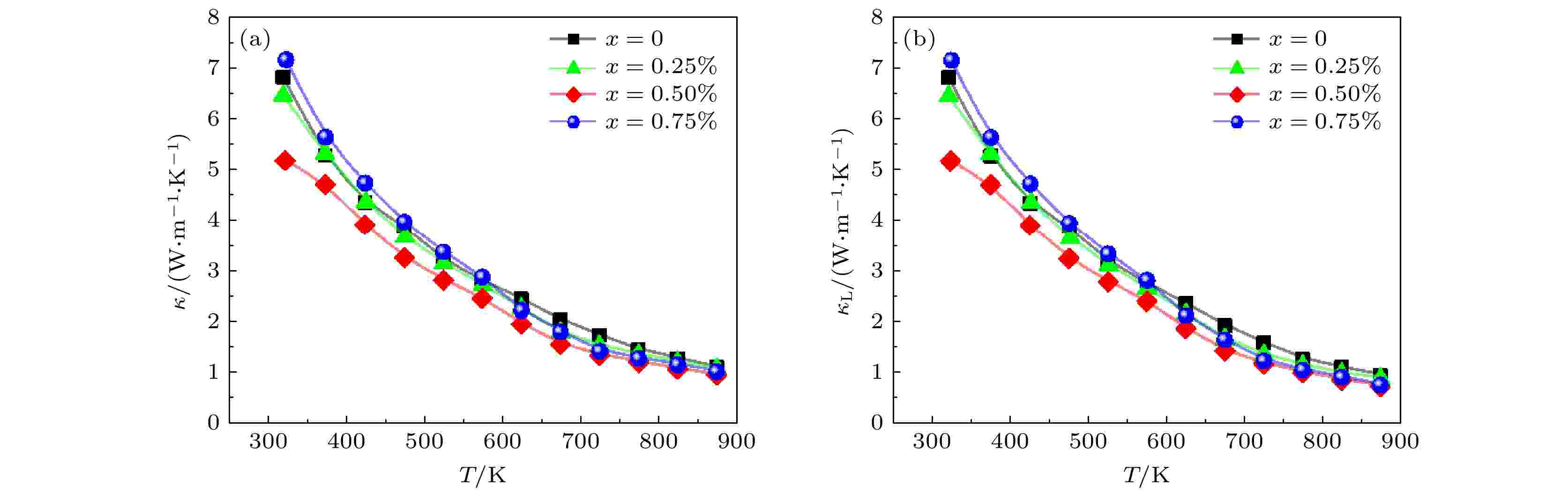
图 6 Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%)样品的(a)总热导率和(b)晶格热导率随温度的变化Figure6. Temperature dependence of (a) total thermal conductivity and (b) lattice thermal conductivity for Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%) samples.
图7是掺杂前后所有样品的ZT值随温度的变化关系, 可以看出, 掺杂Ni元素后样品的ZT值在整个测试温区内都有明显的提升, 当x = 0.50%时获得了最高ZT值1.26 (873 K), 相较于基体提升了56%. ZT值的提升是由掺杂Ni元素后功率因子和热导率的同步优化导致的. 因此, 在Cu位掺杂Ni元素也是提升CuGaTe2体系材料热电性能的有效手段.
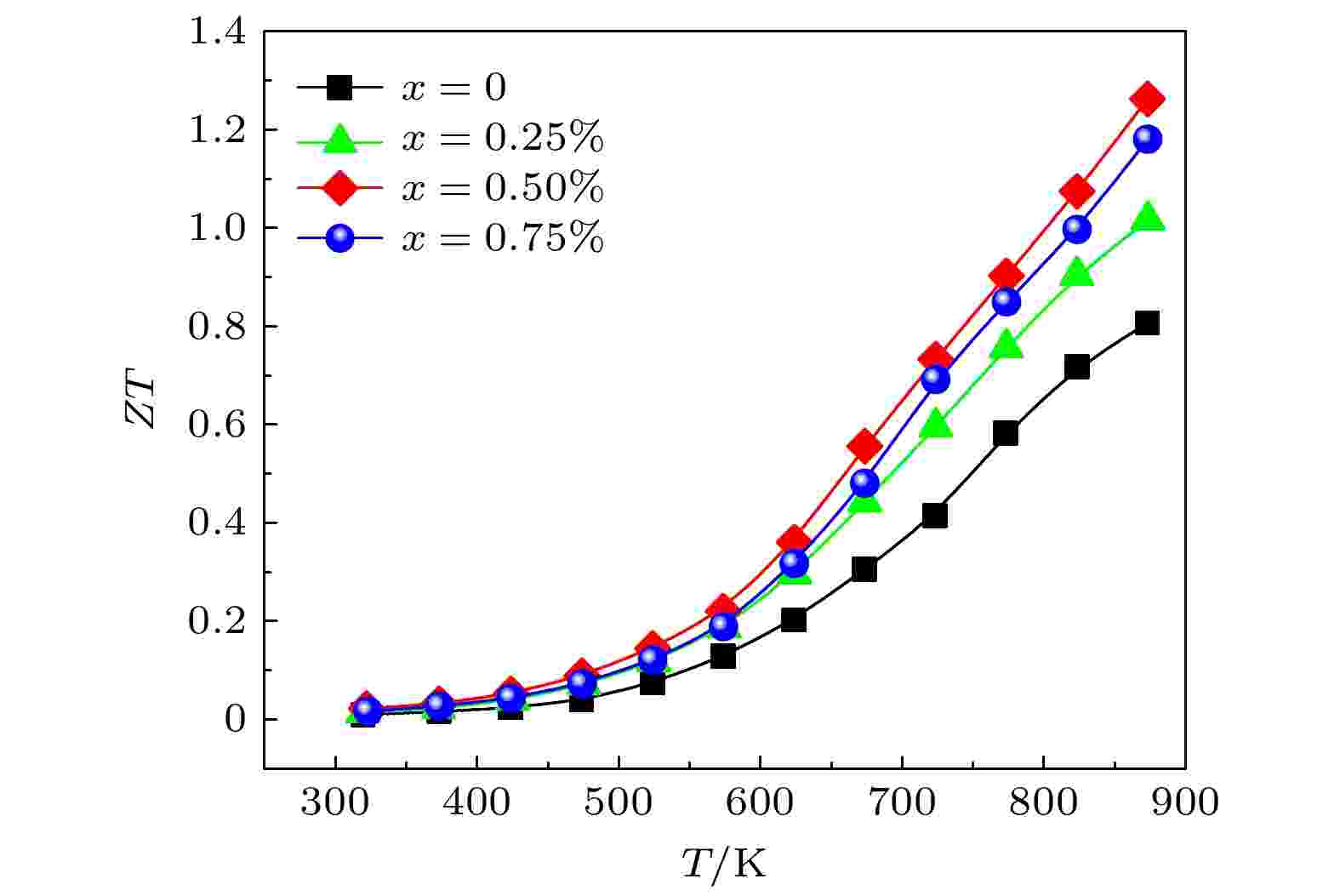图 7 Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%)样品的ZT值随温度的变化Figure7. Temperature dependence of ZT value for Cu1–xNixGaTe2 (x = 0, 0.25%, 0.50%, 0.75%) samples.
感谢中国科学技术大学微尺度中心孔源博士对论文中理论计算部分提供的帮助.
