全文HTML
--> --> -->Feenstra等[8-12]所发展的TIBB模型是目前被较多采用的诠释半导体STS结果的物理模型. 本质上该模型系唯像模型, 当具体被应用于半导体的STS测量结果分析时, 还涉及半导体功函数、表面态等物理参量的影响, 这些参数对STS谱线形、表观带隙大小和带边位置等参量具体影响规律如何, 迄今尚未见到有文献系统阐述. 结合具体实验数据澄清对上述问题的认知, 对于更好地发挥STS这一重要分析手段在半导体表面界面研究上的应用, 无疑是一个非常值得探讨的重要课题.
本文采用XSTM测量技术对分子束外延(MBE)生长的晶格匹配InP/In0.53Ga0.47As异质结构进行了表征. 该结构是构建0.9—1.7 μm近红外波段光电探测器的基础. 不仅应用于制作短波红外焦平面器件[13], 而且基于此结构所发展的雪崩光电二极管(APD)属于应用于长距离和高比特率光纤通信的最重要的器件方案[14]. 目前通过MBE进行的该材料结构生长中, 异质结界面的优化生长一直都是备受重视的研究课题[15]. 与此紧密相关的是需要借助对界面生长质量和界面特性有效表征的技术手段, 而XSTM方法则具备独特优势[5].
本工作所研究的沿InP(001)衬底外延生长的InP/In0.53Ga0.47As异质结构, 其截面为非极化(110)面. I-V谱测量显示, InP的零电流平台宽度略小于材料带隙, 这可基于平带模型予以解释, 说明InP(110)面存在较高DOSS能够引起费米能级钉扎; 较小的表观带隙则与能带的带边态引起的带隙窄化有关. 但与InP缓冲层的STS实验明显不同的是, InGaAs(110)面STS测量显示, 其表观带隙则比材料带隙约大50%, 意味着InGaAs的STM实验中存在明显的TIBB效应. 对此应用Feentra的三维能带弯曲模型进行了分析计算[9,10], 发现仅计入TIBB效应尚不足以准确解释I-V谱的零电流平台的能量起、止位置等特征参数. 对此需纳入参量DOSS, 后者对线形特征有着敏感影响. 通过对DOSS数值的恰当选取能够计算出与实验高度吻合的I-V测量谱线.
图1所示为进行XSTM实验的样品构型图. 薄片样品通过样品托上的夹具垂直于样品托表面固定, 为了获得平整解理面, 先在样品表面沿着夹具上端缘形成轻微划痕, 以便于轻微撞击样品后就获得垂直样品面沿划痕解理的端面. 为避免空气影响, 样品解理操作在氮气手套箱中完成. 另外手套箱与STM预腔密封对接, 使得样品到STM真空进样室的传输也在氮气保护下完成[16]. 样品先在进样室里由分子泵抽真空3 h左右再传入超高真空腔进行STM测量. STM设备为Omicron低温超高真空扫描隧道显微镜, 基准压强小于3.0 × 10–10 mbar (1 mbar = 100 Pa). 采用恒流成像模式, 成像参数设置为: 偏压1.30 V(加在样品上), 参考电流25 pA. STS数据基于I-V数据采集获得. 进行XSTM测量时, 需要在(110)解理面以每次约800 nm的步长向样品表层侧逐步横向移动STM针尖, 每次移动针尖后进行成像扫描, 并通过观察扫描轮廓线有无高度突变来判断是否到达样品表层边缘[17]. 当解理面边缘位置确定后, 再结合样品生长时已确定的外延层厚度参数, 自表层向内移动相应针尖坐标位置找到需要测试的界面区域进行测量.
图 1 处于样品托中用于XSTM实验的样品照片Figure1. Photography of sample in the sample holder for the XSTM experiment.
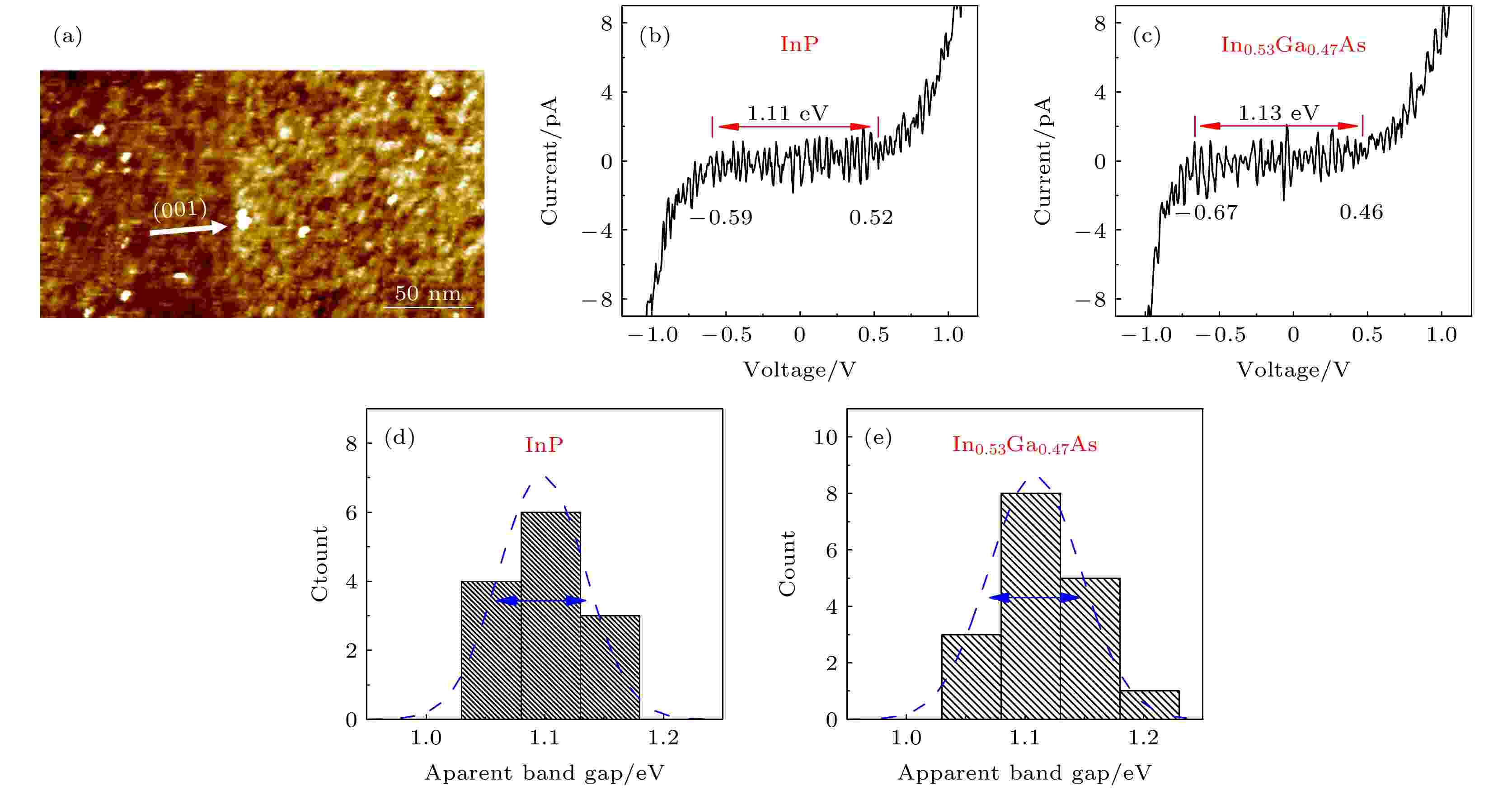图 2 (a) InGaAs/InP异质结(110)解理面的STM形貌; (b)和(c)为InP和InGaAs(110)面的典型的I-V隧道谱给出的表观带隙测量结果; (d)和(e)分别为在InP和InGaAs(110)表面分别随机采样13和17条I-V谱线给出的表观带隙直方图统计结果Figure2. (a) STM topography of the cleaved (110) surface of InGaAs/InP hetero-structure; (b) and (c) are the typical I-V tunneling spectra of InP and InGaAs (110) surface, respectively; (d) and (e) are the statistical histograms of the apparent tunneling gaps with the sampling of 13 and 17 spectra on the (110) surfaces, respectively.
图2(b)为InP表面给出的一典型I-V谱线, 其零电流平台宽度(隧道谱表观带隙)约为1.11 eV, 还注意到I-V曲线零电流平台正负电压侧对应的拐点位置分别为–0.59和0.52 eV(从平带模型来说它们分别对应价带顶和导带底能量位置, 见图3). InP隧道谱表观带隙略小于其材料带隙1.35 eV. 实验中在InP表面随机采集了13条谱线, 总体上其谱线特征和图2(b)所示均非常类似. 根据这些谱线计算出的零电流平台宽度均值为1.098 eV, 均方差为0.035 eV, 进而可利用正态分布函数更直观地反映带隙能量的统计分布, 如图2(d)中与直方图叠加的蓝色虚线所示.
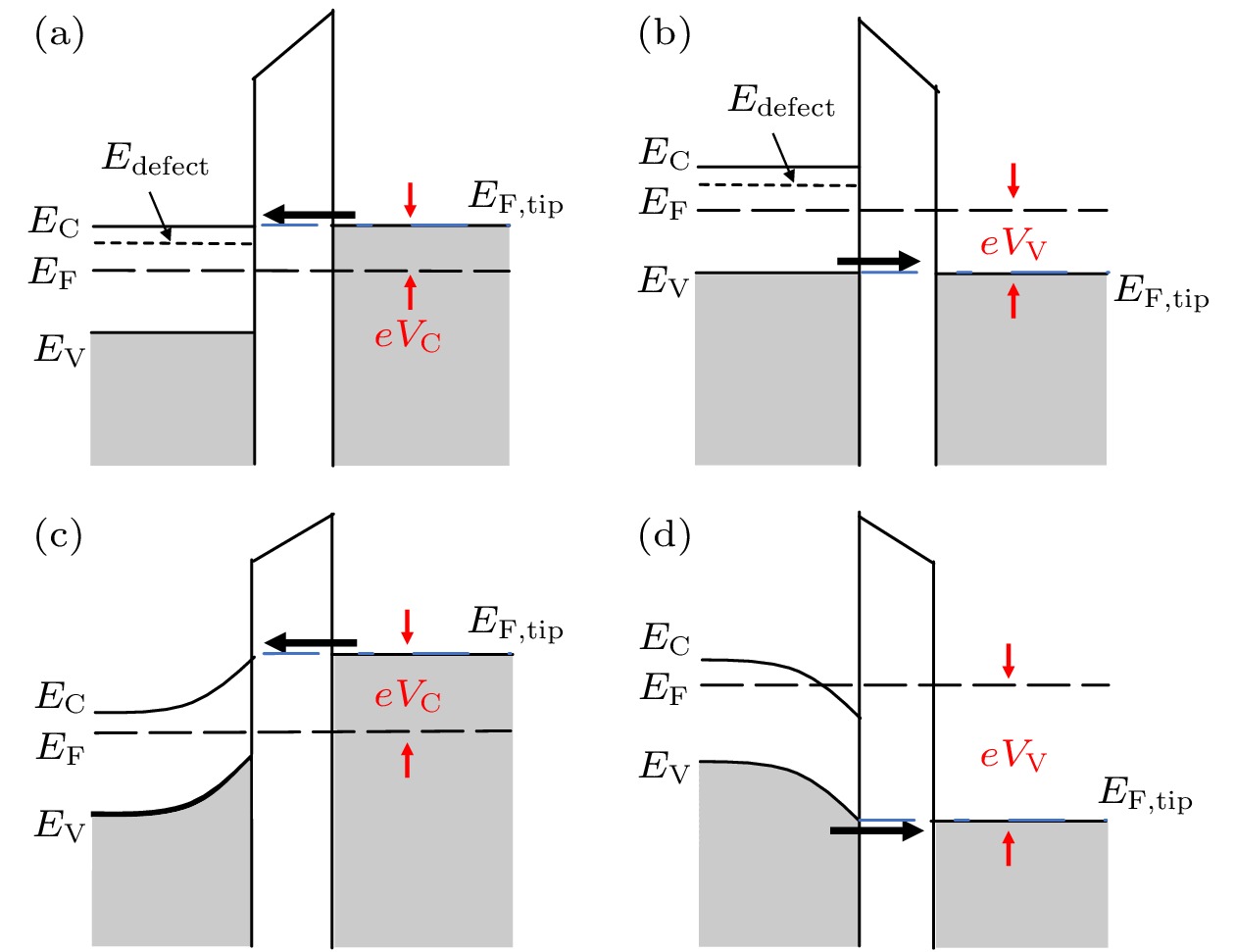图 3 平带模型的STM隧道结能带示意图 (a)正偏压; (b)负偏压; TIBB模型下的隧穿能带图 (c)正偏压; (d)负偏压.EC, EV和EF分别是样品的导带、价带和费米能级, EF, tip是针尖的费米能级, Edefect表示缺陷态能级.Figure3. Schematic energy band diagram of STM tunneling junction with flat band model: (a) Positive sample bias; (b) negative sample bias; schematic energy band diagram of tunneling junction with the TIBB model: (c) positive sample bias; (d) negative sample bias. EC, EV and EF are the conduction band, valence band and Fermi level of the sample respectively, EF, tip is the Fermi level of the tip, and Edefect is the defect level.
图2(c)是测量给出的InGaAs(110)面的典型I-V谱线. 隧道谱表观带隙为1.13 eV, 价带顶和导带底能量分别为–0.67和0.46 eV. 图2(e)为用直方图展示的基于17条测量谱线所绘出的表观带隙直方图的统计分布结果. 其均值为1.108 eV, 均方差为0.038 eV. 值得注意的是, 前面InP的隧道谱表观带隙较接近其材料带隙1.35 eV, 但In0.53Ga0.47As表观带隙明显大于材料带隙0.74 eV; 测量值超过材料带隙的50%. 这一不同特征, 意味着这两种外延层的隧穿模型机制是不同的.
对InP的测量结果, 可基于图3(a)和3(b)所示的平带模型能带图进行解释. 平带模型一般适用于材料高掺杂或有高的DOSS引起的费米能级钉扎情形. 平带模型条件下, 样品正偏压下针尖费米能级高于导带底能量EC (如图3(a)所示eV ≥ EC, e为单位电荷), 电子由针尖隧穿至样品. 如定义eVC = EC, 则平带模型下VC对应图3(a)中零电流平台的右侧拐点. 当偏压如图3(b)所示偏压为负时, 针尖费米能级对准价带顶, 发生电子由样品到针尖的隧穿, VV对应I-V谱零电流平台的左拐点. 这样有e(VC + |VV|) = Eg, 即隧道谱的表观带隙应等于材料的带隙Eg.
不过图2(b)和图2(d)的实验测量结果显示, 平均表观带隙约1.10 eV比InP的带隙1.35 eV (室温)要小一些. 这一现象可解释为: 已有关于InP表面态的实验研究发现[20,21], InP(110)表面很容易因氧吸附而产生在距离导带底0.1—0.3 eV的能量区间产生大量深能级, 而本文I-V隧道谱所测量的InP(110)面的表观带隙比实际带隙数值上小约0.2—0.3 eV, 和上述氧吸附产生的深能级态恰在基本相同的数值范围. 由此看来InP表观带隙的窄化或源自上述深能级表面态对隧穿电流的贡献. 对此还要补充说明的是, 虽然前面提到本样品解理是在氮气手套箱保护氛围下进行的, 包括样品到STM真空腔的传递也是通过氮气手套箱与STM进样室对接来避免样品在空气中的暴露, 但是该制备条件尚不能达到对环境分子吸附充分抑制的超高真空条件原位解理所能提供的效果. 对于洁净半导体表面来说, 表面敏感的气体分子的吸附会是迅速的过程, 所以在我们的样品制备条件下InP表面仍存在产生氧吸附表面态的机制. 不过对同一气体分子的吸附敏感性也会因材料而异. 同一样品中InGaAs(110)解理面的STS结果则展示出不同于InP的特点. 如图2(c)的隧道谱显示, 其零电流平台宽度(表观带隙)比材料带隙大出很多, 意味着平带模型对应的物理图像是不适用的. 故对InGaAs隧道谱的解释必须应用TIBB模型而非平带模型机制[8-12].
先从图3(c)和图3(d)的隧穿能带图就TIBB效应对带隙测量的影响给予定性说明. 当针尖和半导体表面施加电压时, 电场会感应表面处原来电中性的电荷载体(电子、空穴、电离的施主和受主)形成空间电荷的重新分布而对外加电场产生屏蔽作用, 导致外加电势部分偏压降落在半导体上产生所谓TIBB效应: 正偏压下如图3(c)能带向上弯曲; 负偏压下如图3(d)所示能带向下弯曲. 它必然导致大于材料带隙的隧道谱表观带隙, 即e(VC + |VV|) > Eg.
TIBB效应下的I-V谱能量宽度可基于电势微分方程的求解给出定量结果[22,23]. 图3是基于隧穿的一维能带图的说明. 2003年Feenstra[8]进一步考虑STM针尖形状的影响, 发展了更符合STM隧穿情形的三维能带弯曲模型. 对于InGaAs计算所用到的参数选取如下: 针尖曲率半径R = 30 nm, 张角θ = 90°, 针尖-样品间距s = 0.75 nm, 针尖(钨)功函数采用
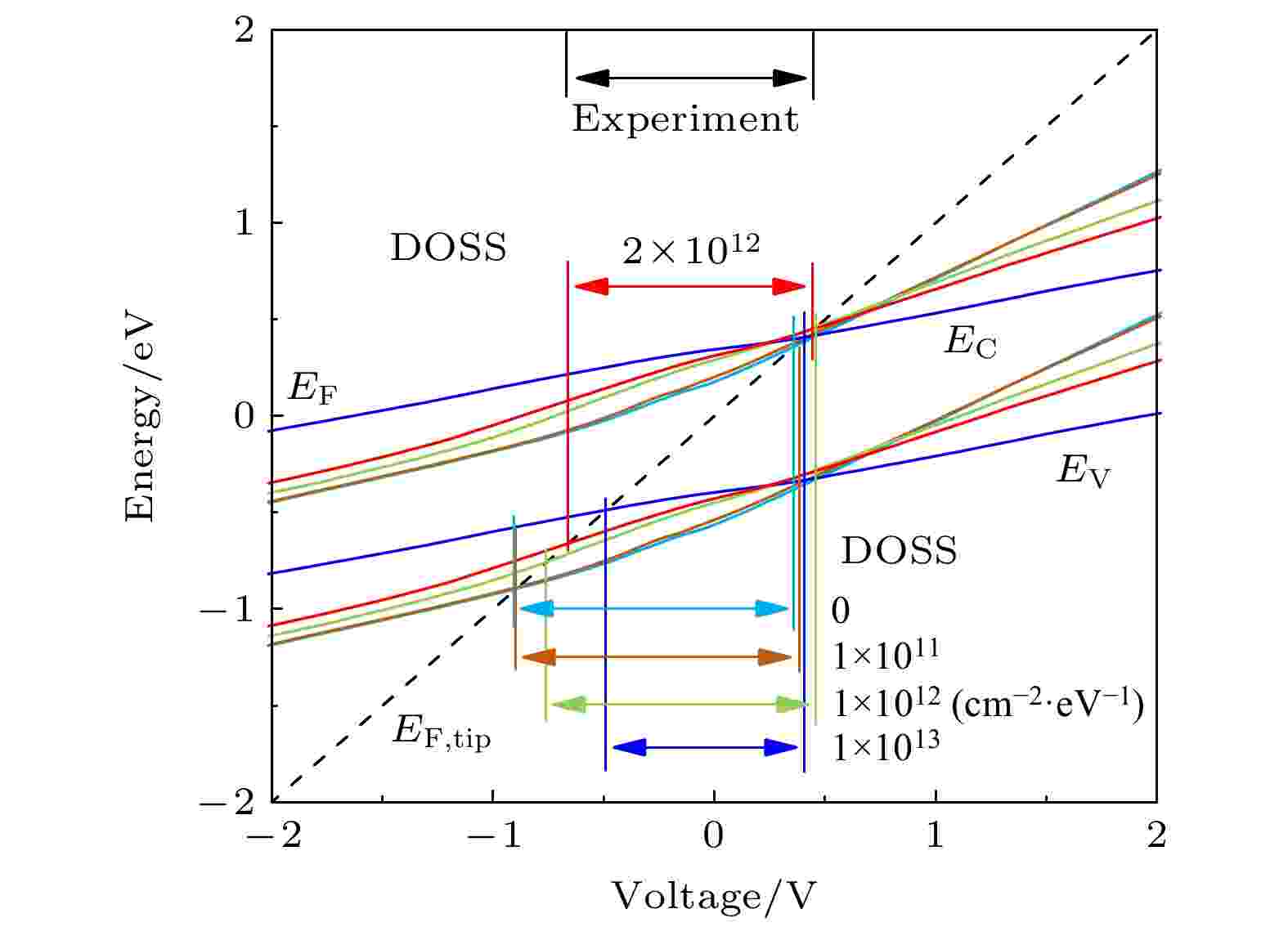图 4 三维TIBB模型给出的InGaAs表面处带边电势能随所加样品偏压的变化关系, 不同颜色的实线对应于不同DOSS, 对应箭头所指为该态密度下计算得到的表观带隙, 优化的DOSS对应计算结果如红色实线所示Figure4. Variation of surface potential of InGaAs with the sample voltage calculated by the 3D TIBB model. The solid lines of different colors correspond to different DOSS, and the corresponding arrows indicate the calculated apparent tunneling gaps at the DOSS. The optimized calculation result is shown by the red line.
表1给出了隧道谱实验测量结果以及不同DOSS情况下(包括不考虑表面态贡献)的TIBB模型对I-V谱特征参数的计算结果. 可看到表面态参数的选取对于表观带隙大小, 尤其是I-V谱零电流平台对应的电压起、止位置(即针尖费米能级对准价带顶和导带底的隧穿的能量位置)有着灵敏的影响. 当不计入表面态贡献时上述参数分别为–0.89 V和0.36 V, 与实验测量明显不一致.
| The parameters of I-V spectra | Apparent band gap/eV | V–onset/V | V+onset/V |
| Experimental | 1.13 | –0.67 | 0.46 |
| Calculations with the density of surface states/(cm2·eV)–1 | |||
| 0 | 1.25 | –0.89 | 0.36 |
| 1.0 × 1011 | 1.29 | –0.89 | 0.40 |
| 1.0 × 1012 | 1.21 | –0.75 | 0.46 |
| 2.0 × 1012 | 1.11 | –0.66 | 0.45 |
| 1.0 × 1013 | 0.90 | –0.49 | 0.41 |
表1InGaAs隧道谱特征参量的实验数据与TIBB模型计算的对比
Table1.Comparison of experimental data and TIBB model calculations on the characteristic parameters of InGaAs tunneling spectra.
注意到Feenstra[11,12]在TIBB模型中引入过DOSS这一唯像参量修正. 模型中该修正对于能量位于禁带中的表面态分布采取如下简化处理, 即中性能级位于禁带中央, 禁带中的施主和受主能态分别在中性能级上下均匀分布. 而DOSS大小的取值目前文献中一般在1011—1013 (cm2·eV)–1量级[25]. 为了考察DOSS取值对I-V谱的影响, 选取1.0 × 1011—1.0 × 1013 (cm2·eV)–1态密度范围内几组典型取值进行计算. 各组取值下的电势能变化如图4所示. 如前所述, 每组的价带和导带带边与针尖费米能量(黑色虚线)交点间的电压间隔预言了相应DOSS下I-V谱的零电流平台宽度(STS表观带隙), 如图4中不同颜色水平箭号线所指示, 具体数值见表1. 为了与实验比较, 图中实验测量给出的表观带隙用黑色水平箭头标明.
如图4上方所标示, 当DOSS取为2.0 × 1012 (cm2·eV)–1时所给出的计算结果(红色线)与实验最为一致: 此时不仅表观带隙值最接近实验结果, 而且对零电流平台起、止能量位置的预测也与实验吻合最好. 另外, 通过比较不同DOSS下的计算结果, 观察到DOSS增大时表观带隙展宽效应变小并趋近材料带隙. 例如当取较高DOSS (1.0 × 1013 (cm2·eV)–1)时, 表观带隙值为0.90 eV已经很接近材料带隙值(室温0.74 eV).
事实上, 对上述模型结果的更充分的验证还可以通过与InGaAs的I-V谱的理论计算结果比较来获得[11,12]. 图2(c)的实验测量谱线与计算谱线放到一起的比对如图5(a)所示. 其中, 红色虚线为计算结果. 图5(b)则是测量谱线(黑线)与计算谱线在更宽测量范围即(–1.6 V, 1.6 V)区间的比对. 可以看到, 无论从图5(a)所展示的细节特征还是图5(b)对整条谱线的线形趋势特征的预言, 计算结果均与实验吻合得很好.
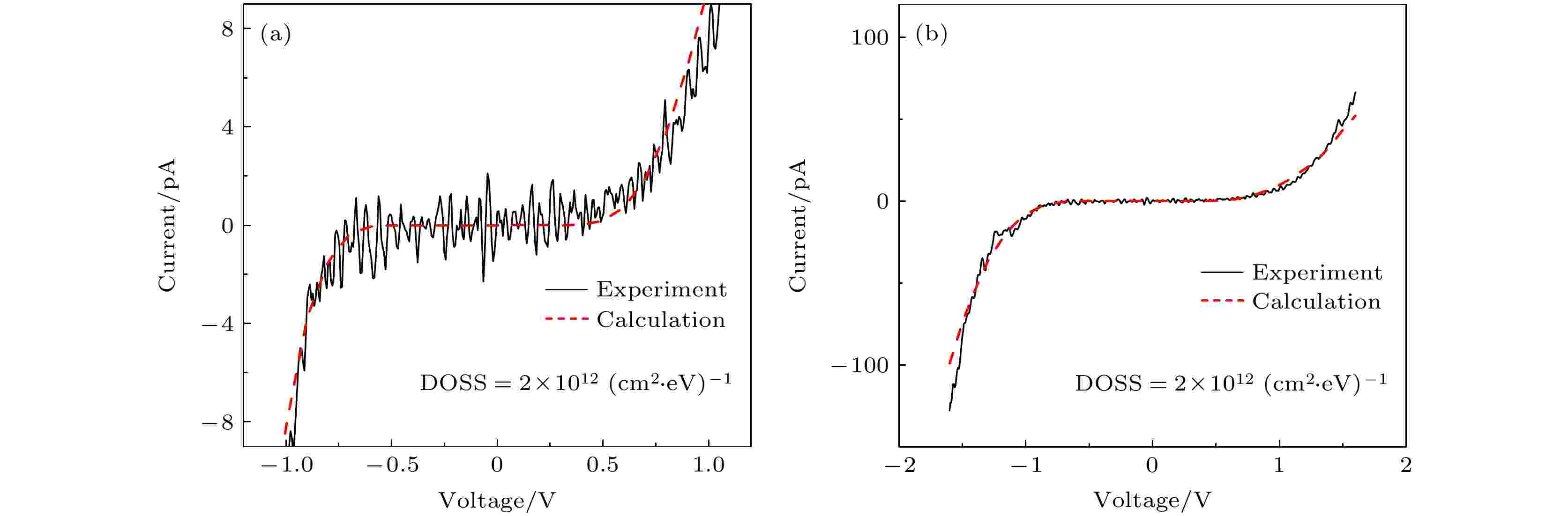图 5 (a) InGaAs的I-V谱的计算(红色虚线)结果与实验谱线(黑色实线)的对比; (b) 图(a)谱线在整个(–1.6 V, 1.6 V)电压范围对计算/实验对比结果的呈现Figure5. (a) Comparison of the I-V spectra between the calculated (red dashed line) and experimental (black solid line); (b) comparison of the spectra within the whole voltage range of (–1.6 V, 1.6 V).
分析认为, 以图5中特定的I-V谱线进行的讨论说明是代表性的. 结合图2(e)的测量统计结果, I-V谱线的零电流平台宽度及其电压起止位置等参数对于来自表面不同位置的测量谱线会略有差异, 但是采用同样方法对其他谱线进行测试计算, 发现只要适当调节DOSS取值, 可以获得对相应实验谱线较满意的拟合结果. 其道理也不难解释, 因为STS给出的是局域电子态信息, 不同位置的I-V线形难免也存在局域性的表面态的调控, I-V谱线形特征自然也携带着具有空间局域特征的表面态信息. 作为进一步的说明, 在图6(a)—(d)中又给出了InGaAs解理面上另外4组测量谱线(黑色)与计算(红色虚线)放到一起比对的结果, 可以看到二者的吻合均令人满意.
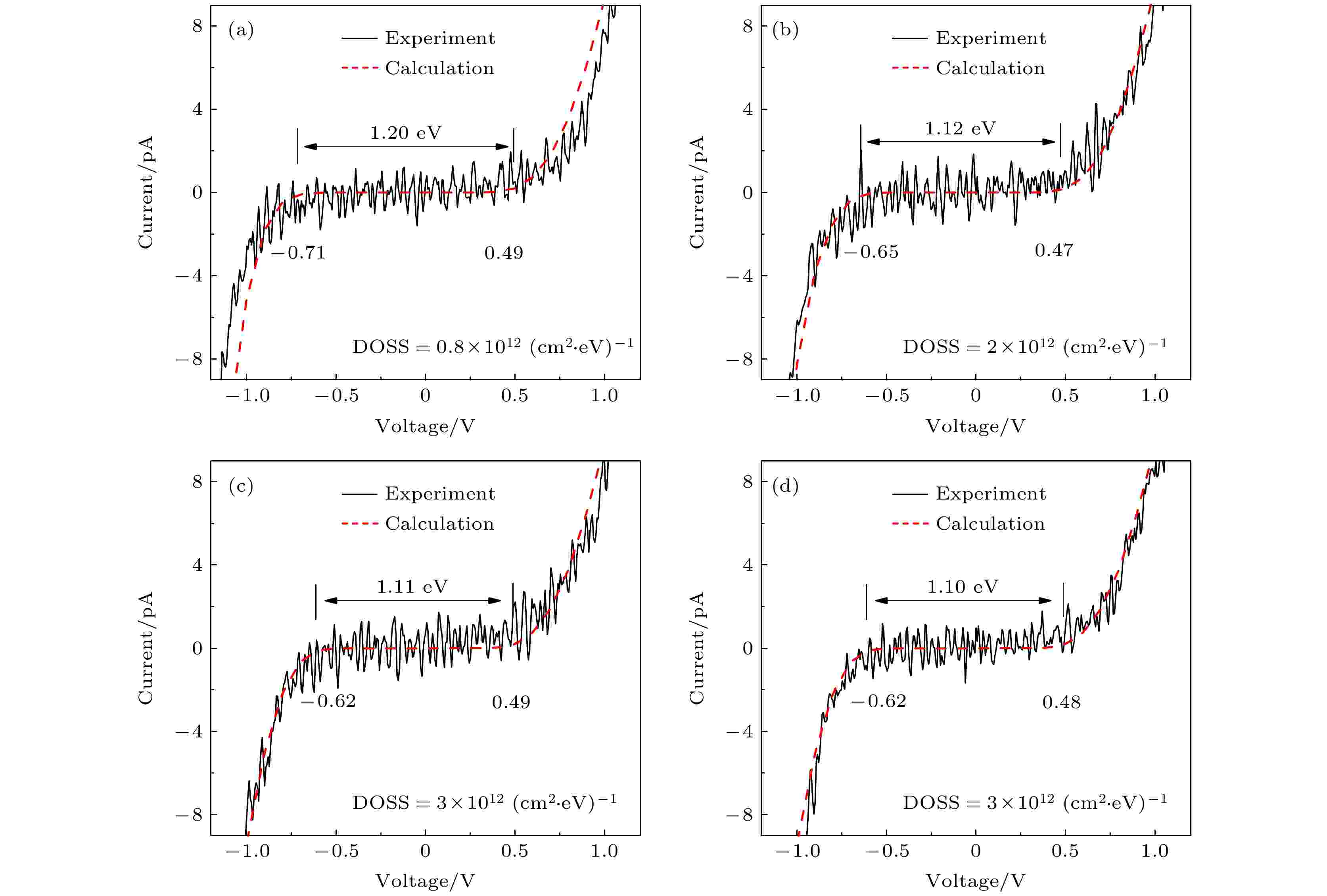图 6 (a)—(d) InGaAs的四组I-V谱实验谱线(黑色实线)与模型计算(红色虚线)的比对, 各图中分别注明了计算时采用的表面态密度(DOSS)数值Figure6. (a)–(d) Comparison of four groups of experimental I-V spectra (black solid lines) with the corresponding calculated I-V spectra (red dashed line). The DOSS for each curve is indicated, respectively.
