摘要: 热自旋电子学结合了热电子学和自旋电子学二者的优势, 在构建高速、低能耗器件技术上具有广泛的应用前景. 本文基于密度泛函理论和非平衡格林函数相结合的方法, 研究了在铁磁态石墨烯纳米带中沿带宽方向引入连续反量子点(六元环缺陷)以获得纯自旋流的模型. 计算发现, 在纳米带的单边引入反量子点会破坏纳米带结构的完整性, 导致器件的透射谱在费米能级附近呈现“X”形交叉. 在温度场下, 不同自旋的电子朝相反方向流动, 形成了自旋流和电荷流, 并且通过微调器件的化学势可以获得电荷流为0, 自旋流不为0的纯自旋流. 结果表明, 对于具有
W 条链宽的锯齿型石墨烯纳米带, 当沿纳米带带宽方向连续引入反量子点数满足(
W /2–1)时, 即可获得最大的纯自旋流, 这一研究结果为设计基于石墨烯纳米带的纯自旋流器件提供了有力的理论依据.
关键词: 热自旋电子学 /
反量子点 /
纯自旋流 /
密度泛函理论 English Abstract Generation of pure spin current in graphene nanoribbons with continous antidots Chen Xing Zhao Han Zhang Yan Liu Lu Yang Zhi-Hong Song Ling-Ling School of Electronic Science and Applied Physics, Hefei University of Technology, Hefei 230601, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 21503061, 11974355)Received Date: 01 February 2021Accepted Date: 17 May 2021Available Online: 19 September 2021Published Online: 05 October 2021Abstract: Spin caloritronics, which combines the characteristics of thermoelectronics with the characteristics of spintronics, has a wide range of promising applications in high-speed and low-dissipation devices. In this paper, according to the density functional theory combined with nonequilibrium Green’s function method, we propose a scheme for generating pure spin current with spin dependent Seebeck effect in the zigzag-edged graphene nanoribbons by introducing continuous antidots (hexagonal defects). Specifically, by creating an antidot at one edge of the nanoribbon, an X-shape transmission spectrum around the Fermi level is formed, which results from the disrupted edge of the nanoribbon. The mechanism is well explained by the cooperation between the varying localization features of the eigenstates around the Fermi level for the unit cell and the scattering states at the Fermi level for the device. Therefore, the electrons of the two spin channels flow in the opposite directions under a temperature gradient, generating the spin current and charge current. By slightly tuning the chemical potential of the device, the charge current can be zero, while the spin current is not equal to zero. With the increase of adjacent antidot number along the width of the nanoribbons, the structures are more disrupted, thus promoting the pure spin current due to the increase of the spin Seebeck coefficient. However, for zigzag graphene nanoribbons with W zigzag carbon chains, the pure spin current decreases when the number of the antidots are more than (W /2–1), which results from the decrease of the spin conductance. So, the maximum pure spin current can be obtained when the number of the continuous antidots introduced along the width of nanoribbons reaches (W /2–1). These findings indicate a novel strategy for thermally generating the spin current by introducing continuous antidots along the nanoribbon bandwidth in zigzag graphene nanoribbons and will be greatly instructive in designing the graphene spintronic devices.Keywords: spin caloritronics /antidot /pure spin current /density functional theory 全文HTML --> --> --> 1.引 言 自旋电子学, 旨在利用电子的固有自旋特性进行信息处理. 与传统电子器件相比, 自旋电子器件具有更快的处理速度, 更低的功耗和更高的集成度等多方面优异的特性[1 ,2 ] . 在自旋电子学的探索历程中, 人们已深入研究了自旋极化输运, 自旋过滤和自旋流等多项自旋相关输运性质[3 -5 ] . 其中, 自旋流已通过许多方法实现, 如自旋霍尔效应、绝热量子泵、电压控制的纯自旋流器件、施加温度场下纯自旋流器件等[6 -10 ] . 其中, 电压驱动实现自旋流的原理为: 在电压驱动下, 体系中的不同自旋电子具有相反的费米分布函数, 两种自旋电子的流动方向相反, 进而产生自旋流. 该方法主要用于集成电路产业中, 利用自旋流传递信息, 大大降低由热电流产生的热功耗; 热电势驱动实现自旋流的原理为: 使用热电势替代电压, 使得处于导带能量范围内的一种自旋电子会与价带能量范围内的另一种自旋电子具有相反的输运方向, 进而实现了自旋流, 主要用于热电循环、集成电路等领域. 热电势驱动的自旋流可以对当下集成电路产生的大量废热进行二次利用, 进一步降低能耗, 符合当今社会绿色发展的主题.[11 ] , 因具有出色的电学和磁学特性受到了广泛的关注[12 -14 ] . 由于锯齿型石墨烯纳米带 (zigzag graphene nanoribbons, ZGNRs)具有边缘局域态和边缘磁性[15 ] , 被认为是构建自旋电子器件的理想材料之一. 因此, 通过诸多调控手段可使ZGNRs实现半金属性[16 -18 ] 、巨磁阻效应[19 ,20 ] 等性质. 前人研究表明, 本征的ZGNRs无论处于无磁态、反铁磁基态还是铁磁态, 都无法直接利用自旋塞贝克效应调控出纯自旋流[21 ] . 因此, 到目前为止在ZGNRs中实现纯自旋流的研究还比较少, 已有的工作是通过在ZGNRs两个边缘分别掺杂硼氮原子实现纯自旋流[22 ] . 然而石墨烯具有强的惰性表面[23 ] , 在实验中不易实现替位掺杂, 且需在石墨烯纳米带边缘上进行规律掺杂, 这无疑提高了实验难度. 相较之下, 在石墨烯纳米带中引入反量子点(缺陷), 在实验中要容易得多, 并且已有诸多成熟方法, 如光刻法[24 ] 、催化刻蚀法[25 ] 、化学气相沉积法[26 ] 等, 可以实现从单个原子尺度大小到数百纳米大小的反量子点制造. 理论上, Yan等[27 ] 研究了在纳米带中心沿周期性方向引入反量子点对其热输运性质的影响. 不过, 相比于在纳米带周期性方向引入反量子点, 沿纳米带带宽方向引入反量子点在实验上更具操作简单和对纳米带结构破坏小等优点. 因此本文提出在ZGNRs中沿带宽方向连续引入反量子点, 通过连续反量子点的数量来调控纳米带的两种自旋电子的输运行为, 并在ZGNRs中获得了纯自旋流.2.计算模型和方法 本文以6条带宽的铁磁态ZGNR(6-ZGNR)为研究对象, 构建了一个双端器件模型, 分为三个部分: 左电极, 右电极和中心散射区, 结构如图1(a) 所示, 研究了在中心区引入反量子点对器件热输运性质的影响. 单个反量子点的定义为一个碳六元环产生的六边形缺陷(如图1(b) 所示), 记为N1模型; 在N1模型的基础上沿着带宽方向去除四个邻近的碳原子, 记为N2模型(如图1(a) 和图1(c) 所示); N3模型为3个相邻的反量子点(如图1(d) 所示). 左电极为红色表示左侧为高温区, 温度为${T_{\text{L}}}$ ; 右电极为蓝色表示右侧为低温区, 温度为${T_{\text{R}}}$ ($ = $ $ {T_{\text{L}}} - \Delta T$ ). 温度从左向右递减, 形成了差值为$\Delta T$ 的温度场. 为了让结构更加稳定, 纳米带边缘和反量子点边缘的碳原子由氢原子饱和[28 ,29 ] .图 1 (a) 引入反量子点的器件模型; (b) N1模型; (c) N2模型; (d) N3模型Figure1. (a) Device model with antidots; (b) model N1; (c) model N2; (d) model N3.[30 ] 进行结构弛豫, 力收敛到0.05 eV/?, 并且结合非平衡格林函数(non-equilibrium Green’s function, NEGF), 采用Nanodcal软件包[31 ] 来进行量子输运计算. 计算过程中, 选用模守恒赝势和双ζ极化的局域原子轨道作为基组, 等效平面波截断能设为160 Ry (1 Ry = 13.6 eV), 交换关联势采用Perdew-Burke-Ernzerhof (PBE)形式的广义梯度近似(generalized gradient approximation, GGA)[32 ] . 为避免相邻超单胞的相互影响, 选取20 ?的真空层, 电极的第一布里渊区采用1 × 1 × 100的k 点. 自旋相关透射谱的计算公式为${G^{\text{r}}}$ (${G^{\text{a}}}$ )是散射区的延迟(超前)格林函数, ${\varGamma _{{\text{L}}\left( {\text{R}} \right)}}$ 是描述左(右)电极与中心区耦合的线宽函数. 在温度场下, 自旋相关电流的计算公式为e 是电子电荷, h 是普朗克常量, ${f_{\text{L}}}\left( {E, {T_{\text{L}}}} \right)$ 和${f_{\text{R}}}\left( {E, {T_{\text{R}}}} \right)$ 分别指左右电极在${T_{\text{L}}}$ 和${T_{\text{R}}}$ 两个不同温度下平衡态的费米狄拉克分布. 在后续的计算中统一将左电极的温度${T_{\text{L}}}$ 定义为T , 右电极的温度${T_{\text{R}}}$ 统一为($T - \Delta T$ ). 自旋流的计算公式被定义为${I_{\text{s}}} = $ $ {I_ \uparrow } - {I_ \downarrow }$ , 电荷流为${I_{\text{c}}} = {I_ \uparrow } + {I_ \downarrow }$ . 在特定条件下, 可以使${I_{\text{c}}} = 0$ 且${I_{\text{s}}} \ne 0$ , 即电荷流为0但是自旋流仍然存在, 实现了纯自旋流. 在线性响应区, 自旋相关电导${G_{ \uparrow \left( \downarrow \right)}}$ 和塞贝克系数${S_{ \uparrow \left( \downarrow \right)}}$ 的计算公式如下[10 ,33 ] :[34 ] ${E_{\text{F}}}$ 是费米能级, ${k_{\text{B}}}$ 是玻尔兹曼常数. 可以看出, 塞贝克系数${S_{ \uparrow \left( \downarrow \right)}}$ 与透射系数${\tau _{ \uparrow \left( \downarrow \right)}}$ 成反比, 与透射谱的斜率${k^{ \uparrow ( \downarrow )}}\left( E \right) = \dfrac{{\partial {\tau _{ \uparrow ( \downarrow )}}\left( E \right)}}{{\partial E}}$ 成正比. 因此, 需要调控器件透射系数和透射谱的斜率来改善器件的塞贝克系数.3.研究结果与讨论 23.1.输运性质 3.1.输运性质 为了研究六边形反量子点数量对ZGNR输运性质的影响, 分别计算了N1(1个反量子点)、N2(2个相邻反量子点)、N3(3个相邻反量子点)双端器件模型的透射谱, 如图2(a) —图2(c) 所示. 与本征体系(图2(d) )相比, 器件的透射谱发生了显著的变化. 本征6-ZGNR的自旋向上电子透射系数${\tau _ \uparrow }$ 和自旋向下电子透射系数${\tau _ \downarrow }$ 分别在(–0.52, –0.4) eV和(0.32, 0.37) eV区间内为3, 将这两个峰值记为${\tau _{ \uparrow {\text{P}}}}$ 和$ {\tau _{ \downarrow {\text{P}}}} $ , ${\tau _ \uparrow }$ 和${\tau _ \downarrow }$ 在(–0.30, 0.30) eV区间内均为1 ($k_{{\text{pristine}}}^{ \uparrow ( \downarrow )} = 0$ ). 而在N1模型中, 单个反量子点的引入破坏了ZGNR单个边缘结构的完整性, 降低了边缘电子的渡越能力, ${\tau _{ \uparrow {\text{P}}}}$ 和${\tau _{ \downarrow {\text{P}}}}$ 均由3降低到2以下, 在(–0.38, 1.45) eV和(–1.50, 0.30) eV区间内的${\tau _ \uparrow }$ 和${\tau _ \downarrow }$ 也由1降低到1以下, 并且${\tau _ \uparrow }$ 和${\tau _ \downarrow }$ 分别在能量点约1.08和–0.95 eV处降至约0.42和0.58, ${\tau _ \uparrow }$ 在(–0.35, 1.08) eV区间内随着能量的增加而减小($k_{{\text{N1}}}^ \uparrow < 0$ ), ${\tau _ \downarrow }$ 在(–0.95, 0.25) eV区间内随着能量的增加而增加($k_{{\text{N1}}}^ \downarrow > 0$ ), 在逼近费米能级处形成“X”形交叉的透射谱. 引入两个反量子点(N2模型)进一步降低了电子的渡越能力, ${\tau _{ \uparrow {\text{P}}}}$ 和${\tau _{ \downarrow {\text{P}}}}$ 均降至1.4以下, ${\tau _ \uparrow }$ 和${\tau _ \downarrow }$ 分别在(0.90, 1.13) eV和(–1.32, –1.25) eV区间内形成了透射率为0的透射谷, 费米能级附近的“X”形交叉更加明显$\left( {\big| {k_{{\rm{N2}}}^{ \uparrow ( \downarrow )}} \big| > \big| {k_{{\rm{N1}}}^{ \uparrow ( \downarrow )}} \big|} \right)$ . 在N3模型中, ${\tau _{ \uparrow {\text{P}}}}$ 和${\tau _{ \downarrow {\text{P}}}}$ 均降低到1以下, ${\tau _ \uparrow }$ 和${\tau _ \downarrow }$ 透射谷的区间分别扩大为(0.40, 1.30) eV和(–1.37, –0.62) eV, 但“X”形交叉依然存在. 由(4 )式和(6 )式可知, 电子透射谱在费米能级处所形成的这一“X”形交叉是实现纯自旋流的关键[34 ] .图 2 自旋相关透射谱 (a) N1模型; (b) N2模型; (c) N3模型. 本征铁磁态锯齿型石墨烯纳米带的(d) 透射谱, (e) 能带图和 (f) 自旋向上电子的本征态Figure2. Spin-dependent transmission spectra: (a) N1 model; (b) N2 model; (c) N3 model. (d) Transmission spectrum, (e) band structure and (f) eigenstates of the spin up band of the pristine FM-ZGNR.图2(a) —图2(c) 所示, N1, N2, N3器件模型的透射系数受反量子点调控的能量区间主要是在(–1.50, 1.45)eV. 无缺陷的器件在此区间内的电子透射系数主要源于石墨烯纳米带中能带1—能带4的贡献, 如图2(e) 所示. 其中能带2和能带3在实空间的电子波函数分布变化是相似的[22 ] , 不妨以能带3为例, 按照能量递增依次选择A, B, C, D四个特征能量点来研究电子波函数在实空间的分布及其变化规律, 如图2(f) 所示. 自旋向上电子的波函数随着能量增加, 逐渐从边缘态(区间为(–0.52, –0.4)eV)过渡到体态(区间为(–0.35, 1.08)eV). 缺陷的引入破坏了单边结构的完整性, 不仅降低了边缘态的导电能力, 也抑制了体态的导电能力. 随着反量子点数沿着纳米带宽度方向的增加, 进一步抑制了纳米带体态电子的渡越能力, 对于N3来说, 体态能量区间电子的渡越能力大部分降为0. 图3 是本征石墨烯纳米带和N1, N2, N3器件模型中自旋向上电子在费米能级处($E = {E_{\text{F}}}$ )的散射态. 如图3(a) 所示, 在本征纳米带器件中, 该散射态均匀分布在整个纳米带上, 这种体态分布与图2(f) 中${E_{\text{C}}} = 0.00$ eV处单胞波函数相对应, 电子从左电极经过中心区渡越到右电极的透射系数为1. 在N1模型中, 反量子点的引入破坏了纳米带单边结构的完整性, 抑制了电子在边缘上的渡越能力, 导致反量子点右侧的散射态比左侧稀疏, 并且主要分布在纳米带中心和无缺陷边缘(如图3(b) 所示). 在N2模型中, 反量子点右侧的散射态相比于N1变得更加稀疏, 并且主要分布在纳米带的无缺陷边缘, 同时存在少量散射态分布在纳米带中心(如图3(c) 所示). 在N3模型中, 反量子点右侧仅有少量散射态分布, 并且主要分布在纳米带无缺陷边缘(如图3(d) 所示), 器件的电子透射系数几乎为0. 自旋向下电子的透射系数受反量子点调控而产生的变化与自旋向上电子的透射系数变化类似.图 3 (a) 本征, (b) N1, (c) N2, (d) N3模型在费米能级处的散射态Figure3. Scattering states of (a) pristine, (b) N1, (c) N2 and (d) N3 model at the Fermi level.3.2.热电性质 -->3.2.热电性质 由(6 )式可知, 器件中${S_{ \uparrow ( \downarrow )}}$ 的调控, 关键在于改变${E_{\text{F}}}$ 处的${\tau _{ \uparrow \left( \downarrow \right)}}$ 和${k^{ \uparrow ( \downarrow )}}$ . ${S_{ \uparrow ( \downarrow )}}$ 的符号与图2(a) —图2(c) 中对应的透射曲线斜率一致, ${E_{\text{F}}}$ 附近透射曲线呈“X”形交叉, 导致${E_{\text{F}}}$ 处的${S_ \uparrow }$ 和${S_ \downarrow }$ 的符号相反(如图4(a) —图4(c) 所示), 表示不同自旋的电子在热温度场$\Delta T$ 的驱动下将沿相反的方向流动, 这是获得纯自旋流的必要条件. ${S_{ \uparrow ( \downarrow )}}$ 的大小与${\tau _{ \uparrow \left( \downarrow \right)}}$ 成反比, 与${k^{ \uparrow ( \downarrow )}}$ 成正比, 当反量子点的数量由1增加到2, 3时, ${\tau _{ \uparrow \left( \downarrow \right)}}$ 的减小和${k^{ \uparrow ( \downarrow )}}$ 的增大导致器件的${S_{ \uparrow ( \downarrow )}}$ 增大(如图4(a) —图4(c) 所示). 另一方面, 对于同一模型, ${S_{ \uparrow ( \downarrow )}}$ 与温度成正比, 当温度从100 K增加到200和300 K时, 温度增加也会导致${S_{ \uparrow ( \downarrow )}}$ 增大 (如图4 所示). 此外, 随着反量子点数量的增加, ${S_{ \uparrow ( \downarrow )}}$ 随着温度变化的幅度愈发明显. 因此可以推测: 增加反量子点会使这一模型的${S_{ \uparrow ( \downarrow )}}$ 对于温度的变化更敏感.图 4 (a) N1, (b) N2, (c) N3模型在100 K下的自旋塞贝克系数; (d) N1, (e) N2, (f) N3模型在200 K下的自旋塞贝克系数; (g) N1, (h) N2, (i) N3模型在300 K下的自旋塞贝克系数Figure4. Spin-dependent Seebeck coefficient of (a) N1, (b) N2 and (c) N3 model at 100 K. Spin-dependent Seebeck coefficient of (d) N1, (e) N2 and (f) N3 model at 200 K. Spin-dependent Seebeck coefficient of (g) N1, (h) N2 and (i) N3 model at 300 K.图4 所示, ${E_{\text{F}}}$ 附近的${S_ \uparrow }$ 和${S_ \downarrow }$ 的符号相反, 表示具有不同自旋的电子在温度场$\Delta T$ 下会向相反的方向移动, 产生自旋流${I_{\text{s}}}$ 和电荷流${I_{\text{c}}}$ , 其中${I_{\text{s}}} = ({S_ \uparrow }{G_ \uparrow } - {S_ \downarrow }{G_ \downarrow })\Delta T$ , ${I_{\text{c}}} = ({S_ \uparrow }{G_ \uparrow } + {S_ \downarrow }{G_ \downarrow })\Delta T$ , 如(3 )式所述, ${G_{ \uparrow ( \downarrow )}}$ 为自旋相关电导. 令${F_{\text{s}}} = ({S_ \uparrow }{G_ \uparrow } - $ $ {S_ \downarrow }{G_ \downarrow })$ 为自旋流因子, 令${F_{\text{c}}} = ({S_ \uparrow }{G_ \uparrow } + {S_ \downarrow }{G_ \downarrow })$ 为电荷流因子. 当${F_{\text{c}}} = 0$ 时, 表示两种自旋状态的电子流向相反, 数量相同, 总电荷流为0, 但${F_{\text{s}}} \ne 0$ , 表示自旋流依然存在, 即纯自旋流. N1, N2, N3器件模型在不同温度下的${F_{\text{s}}}$ 和${F_{\text{c}}}$ 如图5 所示, 在三种模型中均存在一个能量点${E_0}$ 使之满足纯自旋流的条件. 因此可以通过外加门电压的方法将器件的化学势微调至${E_0}$ (分别约为0.065, 0.023和0.038 eV)来获得纯自旋流. 如图4(b) 和图4(c) 所示, 虽然N3的${S_{ \uparrow ( \downarrow )}}$ 比N2大, 但是由于反量子点数量的增加, 结构破坏程度加深, 导致${G_{ \uparrow ( \downarrow )}}$ 减少, 因此N3的纯自旋流比N2小(如图5(e) 和图5(f) 所示). 为了探索自旋流随着带宽、连续反量子点数目的变化, 进一步计算了在8条链宽的纳米带中分别引入2, 3, 4个连续反量子点, 器件(标记为8-N2, 8-N3, 8-N4模型)的透射谱, 如图6(a) —图6(c) 所示; 在10条链宽的情况下, 计算了在纳米带中分别引入3, 4, 5个连续反量子点(标记为10-N3, 10-N4, 10-N5模型)的透射谱, 如图6(d) —图6(f) 所示. 与6条链宽纳米带的情形类似, 以自旋向上电子的透射谱为例, 可以看出8-N2和10-N3模型分别在能量点约为0.95和0.80处出现了一个透射谷, 并且随着反量子点数量的增加, 透射谷的区间会增大, 但“X”形交叉始终保留. 由图7 可知, 在8-ZGNR和10-ZGNR中分别连续引入3个和4个反量子点即可获得最大纯自旋流. 由此可以预测, 对具有W 条链宽的锯齿型石墨烯纳米带, 在连续引入(W /2–1)个反量子点时, 获得最大纯自旋流.图 5 (a) N1, (b) N2, (c) N3模型在不同温度下的电荷流因子${F_{\text{c}}}$ ; (d) N1, (e) N2, (f) N3模型在不同温度下的自旋流因子${F_{\text{s}}}$ Figure5. Charge current factor ${F_{\text{c}}}$ of (a) N1, (b) N2 and (c) N3 model at different temperature. Spin current factor ${F_{\text{s}}}$ of (d) N1, (e) N2 and (f) N3 model at different temperature.图 6 不同模型的自旋相关透射谱 (a) 8-N2; (b) 8-N3; (c) 8-N4;(d) 10-N3; (e) 10-N4; (f) 10-N5Figure6. Spin-dependent transmission spectra of different models: (a) 8-N2; (b) 8-N3; (c) 8-N4; (d) 10-N3; (e) 10-N4; (f) 10-N5.图 7 8-ZGNR和10-ZGNR在200 K下的纯自旋流因子与反量子点数量的关系Figure7. Pure spin current factor of 8-ZGNR and 10-ZGNR at 200 K.4.结 论 本文提出了一种在铁磁态ZGNR的单边沿带宽方向引入连续反量子点来调控器件的输运性质以获得纯自旋流的方案. 计算结果表明, 反量子点的引入破坏了纳米带单个边缘结构的完整性, 导致器件的透射谱在费米能级附近呈现“X”形交叉, 在温度场下, 不同自旋电子的塞贝克系数具有相反的符号, 产生自旋流和电荷流, 通过微调器件的化学势可以获得纯自旋流; 沿纳米带宽度方向增加相邻的反量子点会导致纳米带的受破坏程度加深, 纯自旋流随之增大, 这主要是因为自旋塞贝克系数的增大; 然而, 对于具有W 条链宽的锯齿型石墨烯纳米带, 当增加的反量子点数超过(W /2–1)时, 纯自旋流减少, 这主要是由于自旋电导的减少. 因此, 沿纳米带宽度方向连续引入(W /2–1)个反量子点, 即可获得最大的纯自旋流. 该研究为设计基于石墨烯纳米带的纯自旋流器件提供了有力的理论依据. 




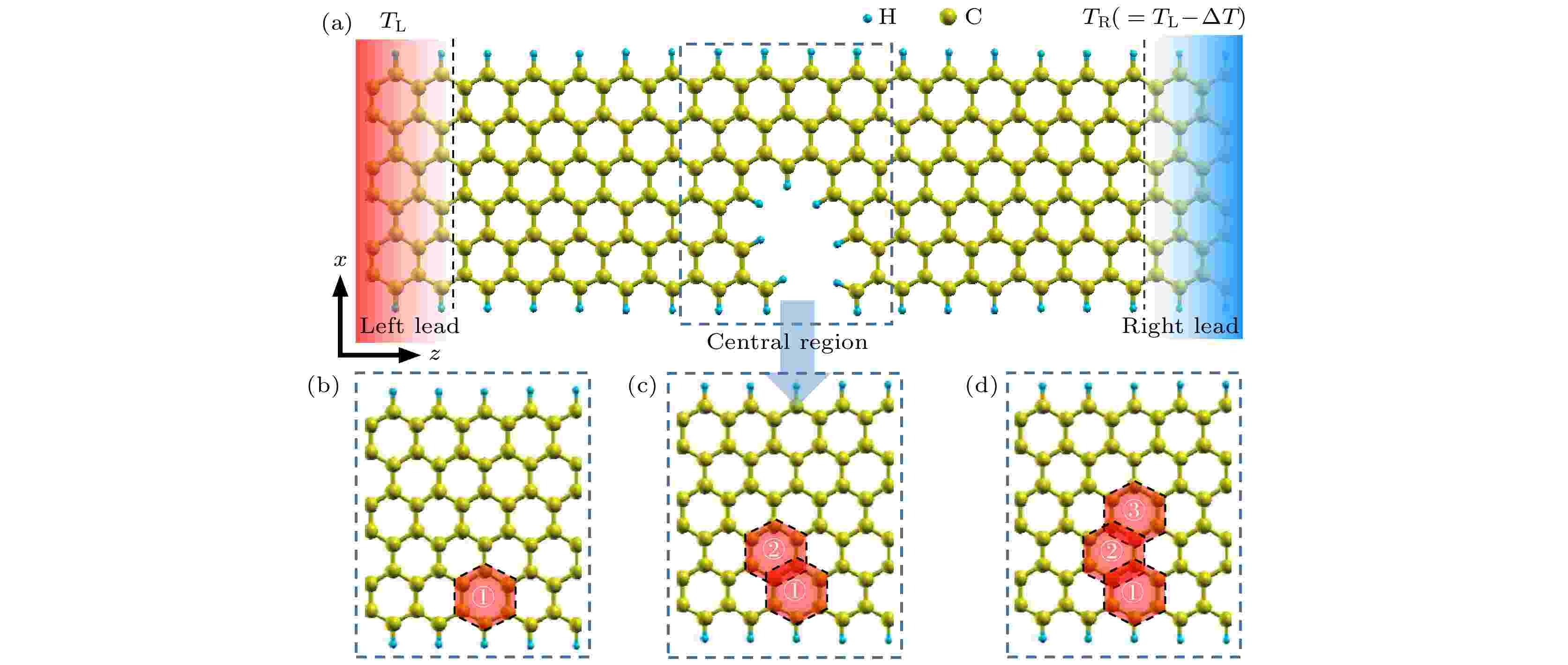 图 1 (a) 引入反量子点的器件模型; (b) N1模型; (c) N2模型; (d) N3模型
图 1 (a) 引入反量子点的器件模型; (b) N1模型; (c) N2模型; (d) N3模型

























































































































































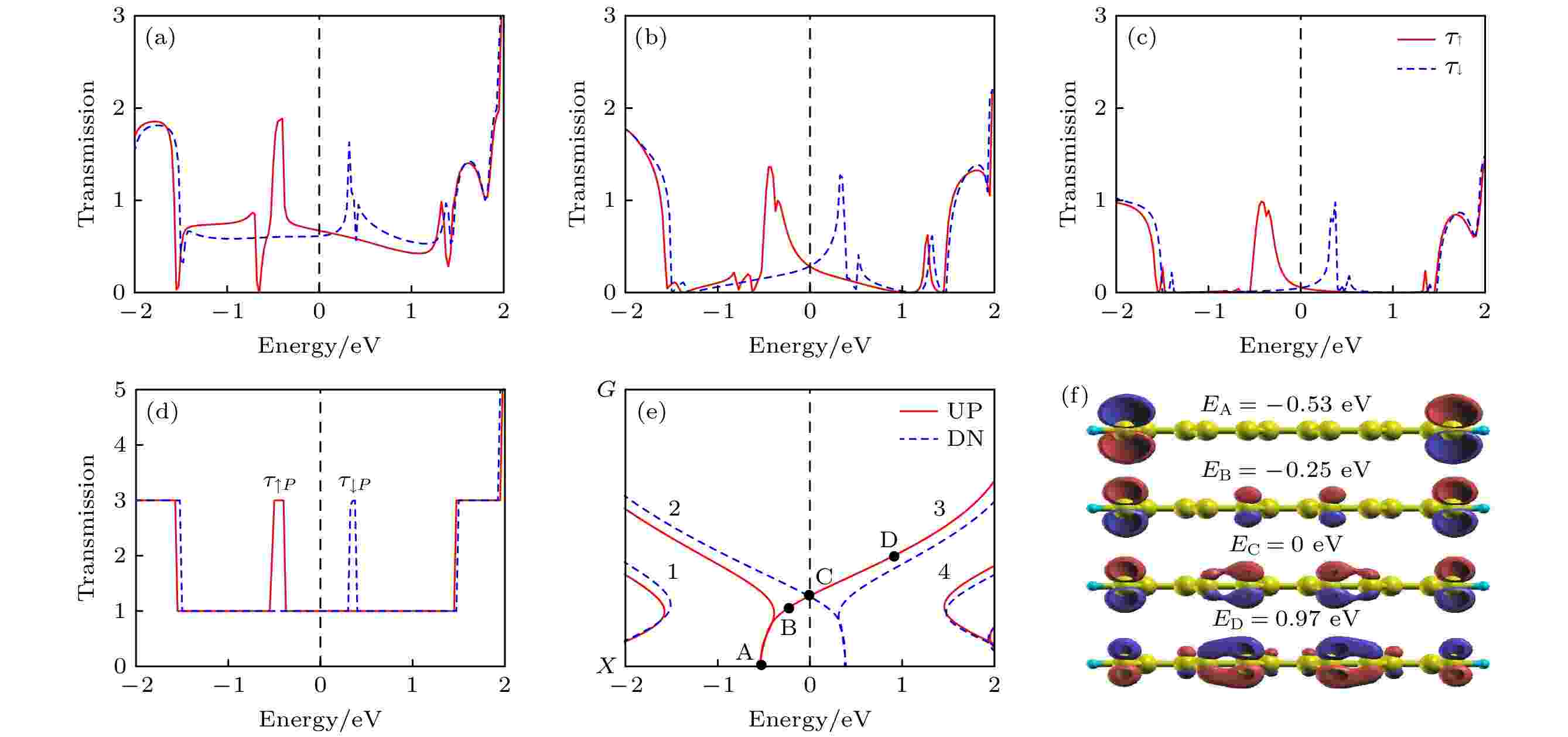 图 2 自旋相关透射谱 (a) N1模型; (b) N2模型; (c) N3模型. 本征铁磁态锯齿型石墨烯纳米带的(d) 透射谱, (e) 能带图和 (f) 自旋向上电子的本征态
图 2 自旋相关透射谱 (a) N1模型; (b) N2模型; (c) N3模型. 本征铁磁态锯齿型石墨烯纳米带的(d) 透射谱, (e) 能带图和 (f) 自旋向上电子的本征态

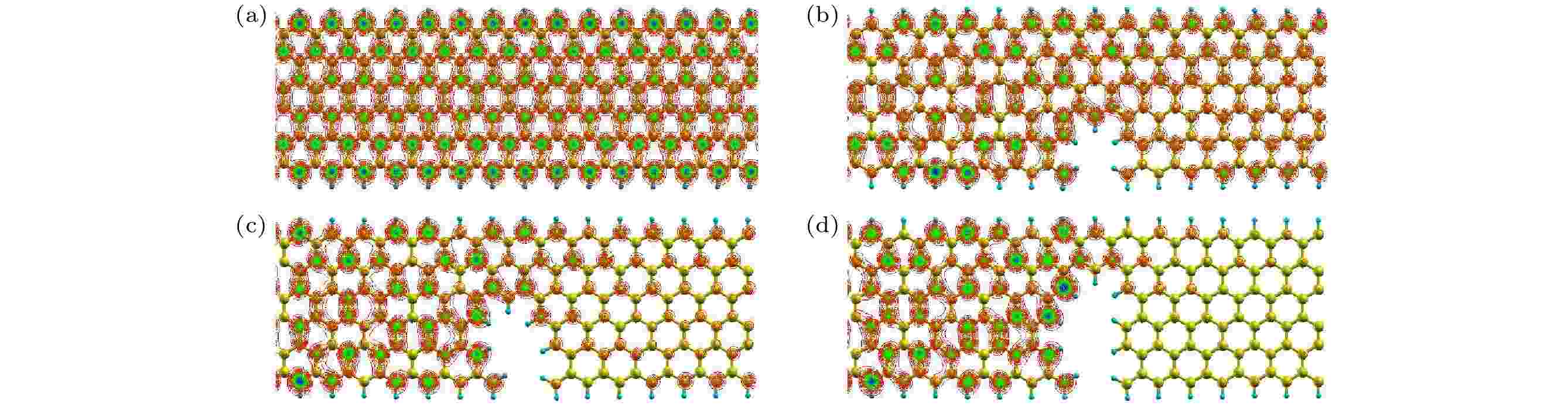 图 3 (a) 本征, (b) N1, (c) N2, (d) N3模型在费米能级处的散射态
图 3 (a) 本征, (b) N1, (c) N2, (d) N3模型在费米能级处的散射态





























































































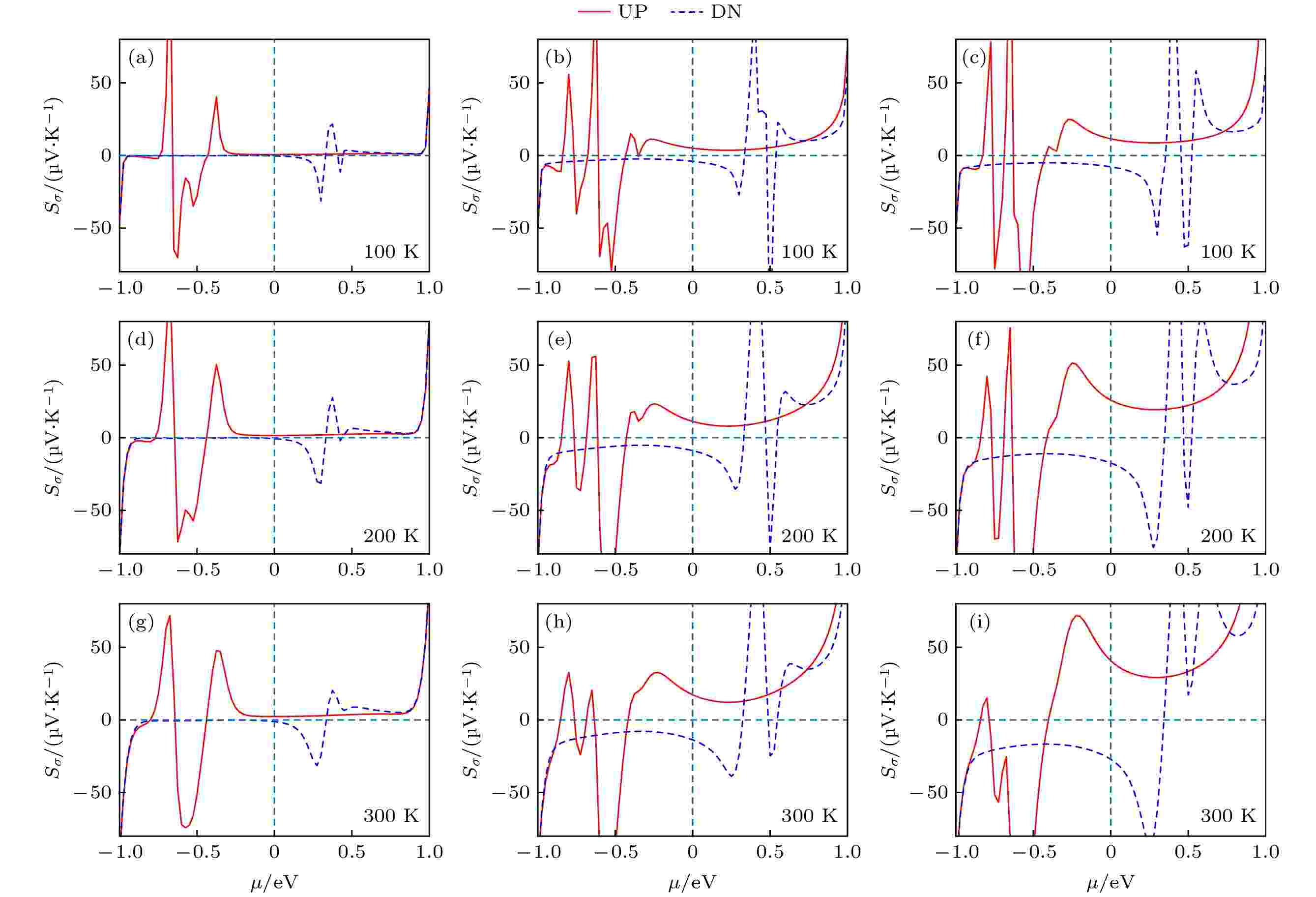 图 4 (a) N1, (b) N2, (c) N3模型在100 K下的自旋塞贝克系数; (d) N1, (e) N2, (f) N3模型在200 K下的自旋塞贝克系数; (g) N1, (h) N2, (i) N3模型在300 K下的自旋塞贝克系数
图 4 (a) N1, (b) N2, (c) N3模型在100 K下的自旋塞贝克系数; (d) N1, (e) N2, (f) N3模型在200 K下的自旋塞贝克系数; (g) N1, (h) N2, (i) N3模型在300 K下的自旋塞贝克系数























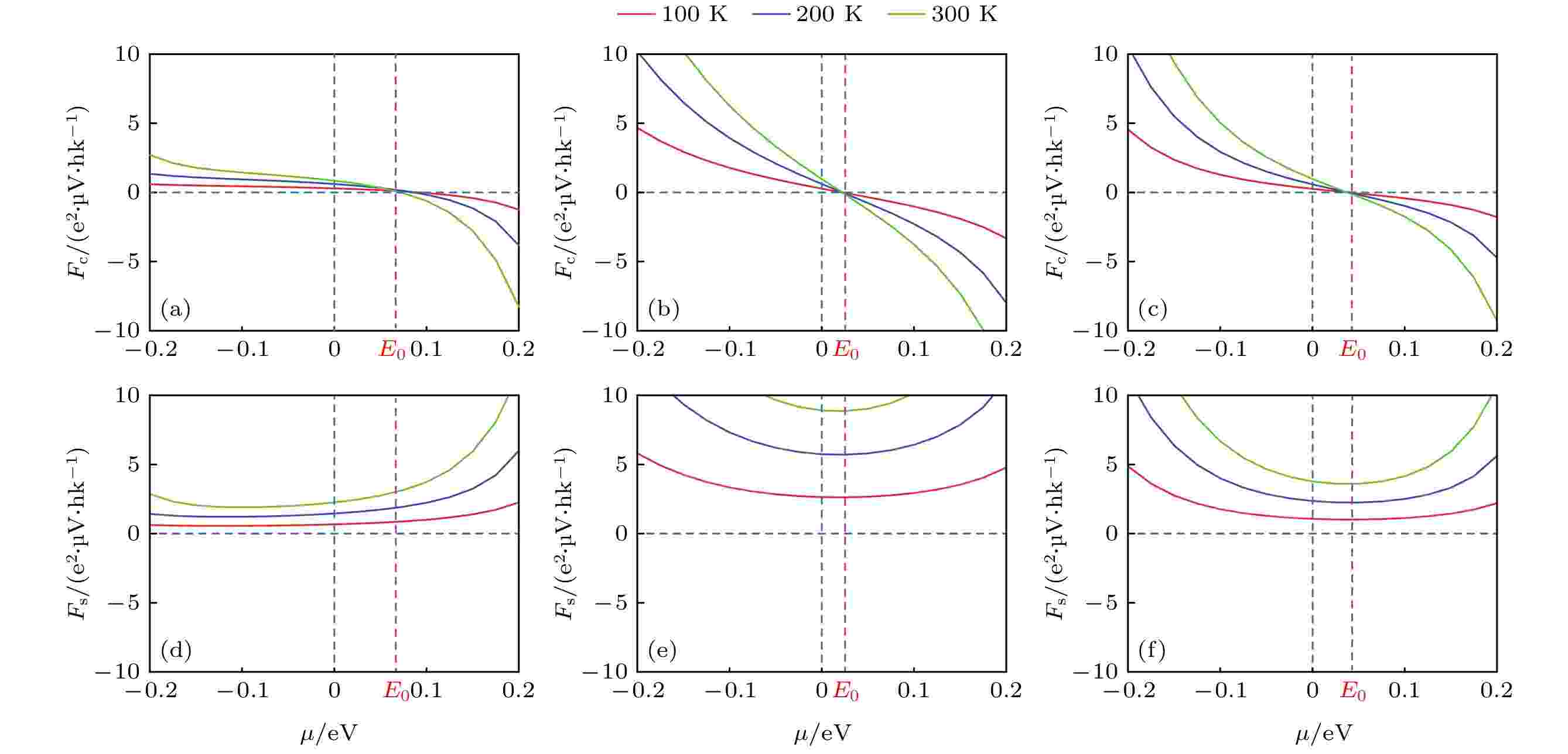 图 5 (a) N1, (b) N2, (c) N3模型在不同温度下的电荷流因子
图 5 (a) N1, (b) N2, (c) N3模型在不同温度下的电荷流因子



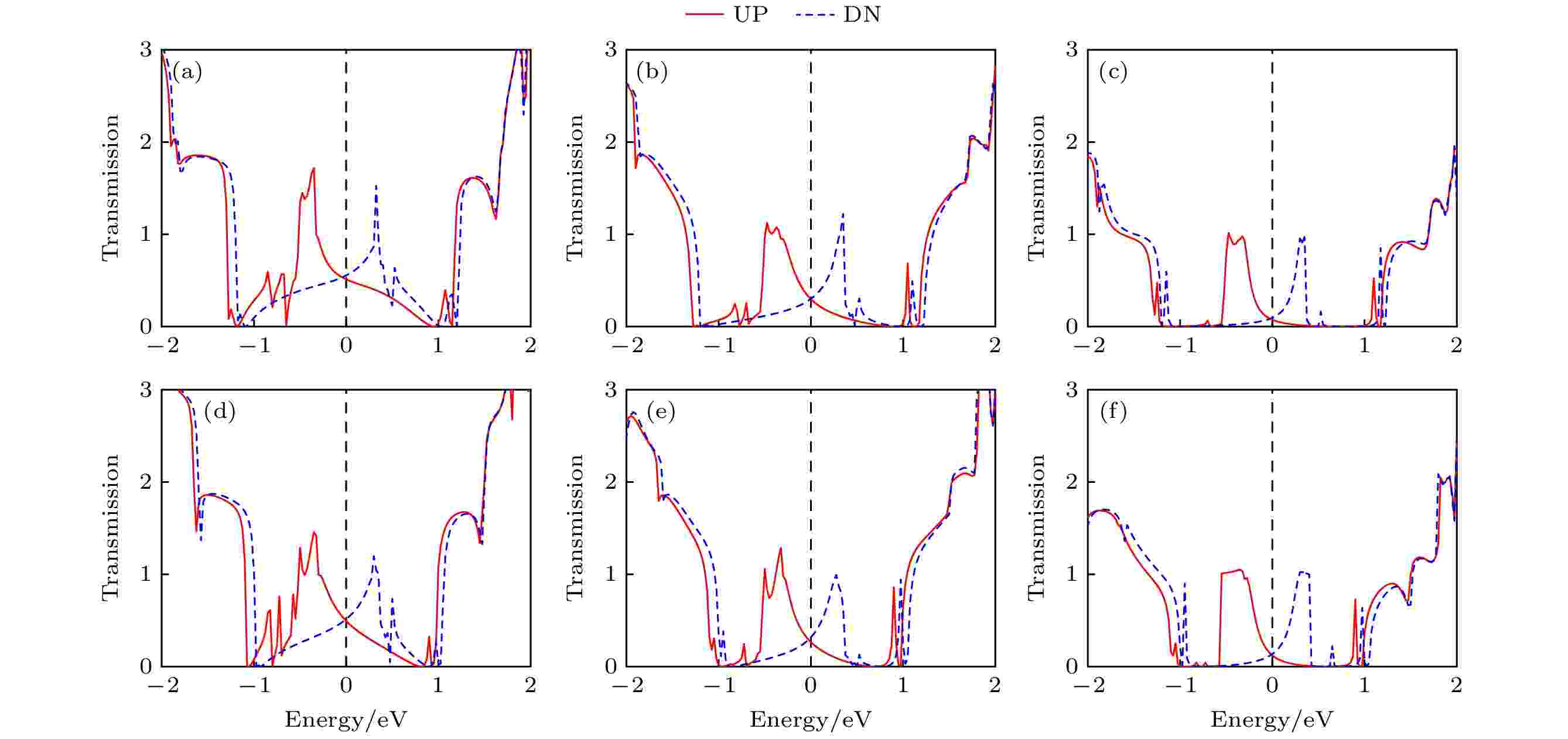 图 6 不同模型的自旋相关透射谱 (a) 8-N2; (b) 8-N3; (c) 8-N4;(d) 10-N3; (e) 10-N4; (f) 10-N5
图 6 不同模型的自旋相关透射谱 (a) 8-N2; (b) 8-N3; (c) 8-N4;(d) 10-N3; (e) 10-N4; (f) 10-N5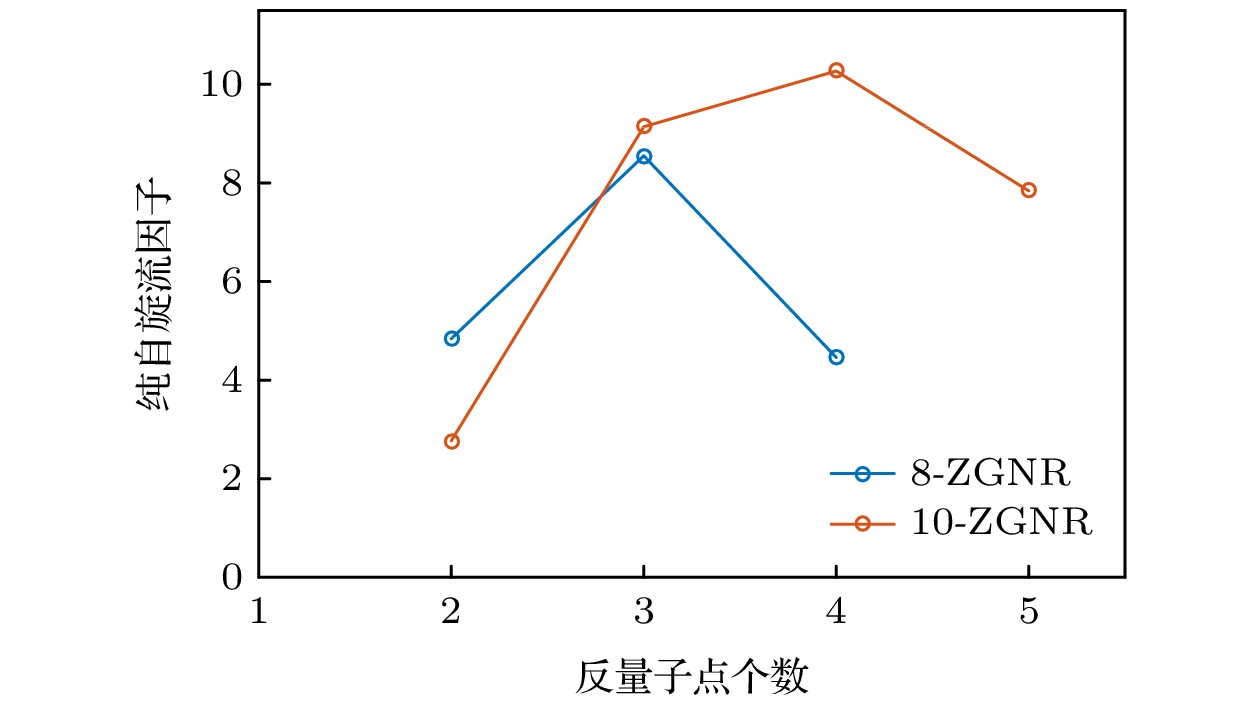 图 7 8-ZGNR和10-ZGNR在200 K下的纯自旋流因子与反量子点数量的关系
图 7 8-ZGNR和10-ZGNR在200 K下的纯自旋流因子与反量子点数量的关系