摘要:提出一种基于小波变换思想的水下测距方法. 根据信号的能量一致性以及小波的带通滤波特性, 并以二元样条插值为架构, 实现信号的时频结合. 该方法先将时域信号进行小波时域分解滤波, 获得较为完整的时域有效信息, 然后对初步处理的时域信号进行小波频域分解, 通过找寻信号时频域对应的能量最值位置锁定目标, 实现精确测距目的. 进行不同衰减长度水体的连续光水下测距实验, 分析该方法对连续光水下探测的影响. 经实验验证, 该测距方法在输出功率2.3 W内, 成功实现对8个衰减长度内目标的准确测量, 其测距精度小于1 cm.
关键词: 小波变换/
水下测距/
带通滤波/
时频结合

English Abstract

全文HTML

--> --> -->

20世纪中后期以来, 水下激光探测领域发展了多种测距方法: 基于时域信号特性的距离选通方法^[1]、相位式测距^[2]以及基于非时域测距的干涉测量、三角测量^[3]、光子计数^[4-6]等方法. 距离选通法和相位式测距等测距方法都是通过设计具有不同控制精度的时域门控宽度以及不同长度的测量标尺等时域信号幅值、强度特性, 来确保其测距精度^[7,8], 实现对物体距离、速度和加速度等信息的检测^[9-12]. 如, 距离选通法具有固定的时域门控宽度, 在此时域范围内的目标具有极高的测距精度, 若目标超过此范围, 便会产生各时域门控之间的响应差异等测距误差; 相位式测距需要时域信号具有一定的周期和相位分立; 距离选通法需要信号在门控范围内的最值唯一. 故可知基于时域信号特性的测距方法, 其测距范围和相应精度均十分有限.
基于非时域信号特性的测距方法中, 干涉法测距最具代表性. 该方法运用光强的周期性变化^[13]实现测距. 理论上, 其纵向测距精度高达微米量级. 该方法适用于检测同一水平位置上多个物体之间的距离, 但不能表示目标的完整空间位置. 调频连续波检测为其改进方法, 通过相干检测扫频后向散射光, 获得物体的距离信息, 但此类方法精度由散斑噪声确定^[14], 而散斑噪声多数与频率无关. 故对于弱信号而言, 其测距精度有较大的不确定性. 如, 浙江大学海洋学院将光学成像原理与激光三角测距法有机结合, 提出水下三点式测距方法^[3]. 该方法在8 m探测范围内, 平均测量误差小于15 cm. 该测距方式采用3个探测器同时探测目标位置, 实现对目标的三维探测, 此方式探测目标存在因同步性和俯仰角度变化等因素带来的测量误差. 基于光子计数的测距方式, 可用于检测微弱信号. 通过检测探测带宽内信号的光子数目, 来确定距离信息. 对于微弱信号而言, 其光子数目可能小于散射光子数目, 而导致无法准确探测. 若想运用该方式测距, 则可通过减少单次光子数和减小频带宽度方法^[15], 提高探测精度.
上述测距方法虽然可以通过时频域相互转化等方式, 实现较为准确的目标探测. 但其时频信号本身具有的分布状态和数目等差异性, 导致无论何种测距方法均无法实现时频信号的准确对应关系. 针对时频信号的对应性问题, 本文提出一种基于小波变换与数学理念相结合, 实现时频信号对应性的探测方法. 根据时域与频域信号的能量一致性和频域带通滤波特性, 通过二元样条插值表现其时频对应关系. 通过时域信号的多点近似逼近以及频谱分解, 提高信号时频分辨率, 进而提高对目标精准探测的能力. 通过记录时域信号幅值区间以及区间内对应的频域能量最大值的方式, 获得目标距离信息. 该方法可对各时域信号进行频域的有效提取和细致分解, 大幅度提升时域信号的可分辨性和有效信息时频对应关系. 通过在水中加入不同含量的Mg(OH)₂来模拟不同浑浊程度的海水, 探究不同浑浊程度水体和调制信号周期对小波时频融合测距方式的影响. 经实验验证, 小波时频融合测距在8个衰减长度内, 测距精度为1 cm以内.

2

-->

2.1.小波变换原理

小波变换(wavelet transform)技术为: 将被观测的信号所包含的频率特性分成多个独立的信号元素, 然后使用带通滤波(bandpass filter)算法将各个独立信号进行分离. 如, 针对信号中不规则的突变部分往往带有十分重要的信息, 可运用其良好的时频局部性特征, 对信号进行多尺度细化分析^[16-18], 确定信号的奇异位置.
水下探测的回波信号大致可以分成后向散射、目标反射和前向散射, 由以下公式表示:

$ E(t) = A\cos (\Delta \omega (t) + \varphi ) , $

这里, $ E(t) $为目标回波光时域信号强度, $ \Delta \omega (t) $涵盖目标回波光的有效频域和散射带宽范围, A为回波信号的振幅平均值.
探测器测量不同时刻回波的响应为: 不同时刻探测器的测量信号对应于海水及目标对不同频率特性的时域信号的响应, 相当于进行回波信号的全体频谱信息采样, 采样后的响应表现为时域强度形式, 对应的极值点即为探测到的目标对应的延时, 而没有利用基于小波变换的时频分析方法, 此极值点对应的很可能是后向散射最强的散射中心位置. 如果利用极值法确定目标位置, 就有可能产生假目标而忽视了真正的被测目标. 使用基于小波变换的时频分析方法, 利用后向散射与目标回波频谱成分的差异性, 将有效信号全部提取出来, 然后再进行有效信息的时频对应关系变换求取极值, 确定目标位置.
基于小波变换的时频分析方法包含时域和频域两种表现形式, 其时域表现为根据时域信号随时间变化的趋势, 将原始信号进行多层近似与还原. 根据时域信号的幅值随时间变化特性, 建立高度近似的小波基函数. 这些小波基函数可将回波时域信号分为近似时域信号和细节时域信号两部分, 也可称此两部分为回波时域信号的近似系数与细节系数^[19,20], 如下式所示:

$ \left\{ \begin{aligned} & x(t) = A'\cos (\Delta \omega (t) + \varphi ), \\& x'(t) = b\cos (\Delta \omega '(t) + \varphi '), \\ &x''(t) = c\cos (\Delta \omega ''(t) + \varphi ''), \end{aligned} \right. $

式中, $ x(t) $为探测器接收的时域信号, $ A' $为探测器接收信号的振幅平均值, $ \Delta \omega (t) $为探测器接收信号的全体频域信息, $ x'(t) $为近似时域信号, b为该信号振幅平均值的近似值, $ \Delta \omega '(t) $为探测器接收的回波信号的有效频域信息, $ x''(t) $为时域信号$ x(t) $与近似信号$ x'(t) $的差值的小波近似, $ \Delta \omega ''(t) $为包括后向散射、前向散射、背景光等噪声的频域信息.
小波变换基于时域信号的幅值随时间变化, 其分离和提取信号能力取决于采样点数和最小时间间隔. 以第1层小波时域分解为例, 假定采样点数为n, 最小时间间隔为T, 则其频率上限为$ 1/T $, 小波时域分解的频率分辨力为$ 1/(2 nT) $. 第1层小波时域分解表示为

$ \left\{ \begin{aligned} &E'(t) = B\cos (2{\rm{\pi }}\Delta {f_1}t + {\varphi _1}), \\ &q(t) = e\cos (2{\rm{\pi }}\Delta {f_2}t + {\varphi _2}), \\& \Delta {f_1} = 1/{T_1},{\text{ }}\Delta {f_2} = 1/T - 1/{T_1}, \end{aligned} \right. $

式中, $ E'(t) $为第1层小波时域分解的近似时域信号, $ \Delta {f_1} = 1/{T_1} $为其时域分解近似信号对应的频域信息, $ q(t) $为第1层小波时域分解的细节时域信号; $[0—1/T]$为信号包含的全体频域信息, $\Delta {f_2} = 1/T - $$ 1/{T_1}$为时域信号包含的散射等杂波信息. 已知采样点数n, 故可得第1层小波时域分解的有效频率分辨力为$ 1/(n{T_1}) $. 由上述可知, 提升频率分辨力的方法为增加采样时间间隔或增加采样点数. 虽然增加采样时间间隔可降低其频率上限和频谱范围, 但是会遗漏许多有效时域信息, 大大降低其时间分辨力和距离分辨力; 增加采样点数虽然可获得更多的有效时频域信息, 但是采集时间与冗余数据量也会显著增加, 大大降低探测信息的时效性. 故拟采用信号时间分辨力不变, 频域分辨力显著提升的多层小波时域分解方法. 以第2层小波时域分解为例:

$ \left\{ \begin{aligned} &E''(t) = B'\cos (2\pi \Delta {f_1'}t + {\varphi _1'}), \\ &q'(t) = e'\cos (2{\rm{\pi }}\Delta {f_2'}t + {\varphi _2'}), \\ &aE'(t) = c\cos (2{\rm{\pi }}\Delta {f_1''}t + {\varphi _1''}), \\ &eq(t) = d\cos (2p\Delta {f_2''}t + {\varphi _2''}), \\ &\Delta {f_1' }+ \Delta {f_2'} = 1/{T_2},{\text{ }}\Delta {f_1''} + \Delta {f_2'' }= \dfrac1T - \dfrac1{T_2}, \end{aligned} \right. $

式中, $\Delta {f_1'} + \Delta {f_2' }= 1/{T_2}$为其时域分解近似信号对应的频域信息; $[0—1/T]$为信号包含的全体频域信息; $\Delta {f_1'' }+ \Delta {f_2''} = 1/T - 1/{T_2}$为时域信号包含的杂波频域信息; $ E''(t) $为近似时域信号$ E'(t) $的再次有效频域近似; $ aE'(t) $为其再次近似信号$ E''(t) $与$ E'(t) $的差值, 即$E''(t) + aE'(t) = E'(t)$; $ q'(t) $和$ eq(t) $分别为细节信号$ q(t) $有效频域的近似时域信号和两者之差. 故可得第2层小波时域分解的近似时域信号$ E''(t) + q'(t) $与细节时域信号$aE'(t) + eq(t)$.
由上述可得, 第2层小波时域分解为第1层小波时域分解的再次分解, 相比于第1层小波时域分解而言, 其频率上限未变而频域采样间隔缩小1倍. 由此可以得出, 多层小波时域分解可以解决因采样点数与最小时间间隔的矛盾性等因素, 引起的小波时域分解的有效频域信息的缺失和其他杂波的影响.
2 -->

2.2.基于小波变换的时频分析方法

多层小波时域分解能够不受采样点数的限制而有效提取时域信号的频域信息, 但小波时域分解的实质为频域信息的提取在时域的叠加表示. 故可知, 分解的层数越多, 必然会加重有效频域变宽和趋于平滑分布趋势, 将严重影响时域信号的有效提取. 因此小波时域分解的分解层数主要取决于时域信号的主要频率范围, 当分解层数i对应的有效频率范围$[ \sim 1/({2^i}T)]\;(i=1,\;2,\;3,\;\cdots)$与其主要频率范围$ \Delta f $相当时, 小波时域分解为最优. 但此方法获得的时频对应关系为时域与频域叠加的形式, 缺乏时频空间的一一对应关系, 即任意时刻的时域信号对应该时刻所有频域信号的分布状态.
针对这一问题, 本文通过小波变换将信号的时频特性相关联, 实现测距目的. 此方法运用小波变换的频域表现形式以时域信号为基础, 通过时频域信号的能量一致性原则, 将时域信号进行频域分解, 进而获得信号时频域的对应关系, 从而找到信号频域能量的幅值信息, 得到目标物距离信息. 具体方法如下:
1) 建立高度近似的小波基函数, 进行时域信号的近似提取. 根据时域信号的周期/带宽特性确定分解的层数, 并重构提取出有效时域信号.
2) 根据信号时频空间的能量一致性, 运用二元样条插值等数学方法建立以能量-时间-频率对应关系的m × n阶矩阵, 分别为时间与能量、时间与频率和频率与能量的矩阵形式. 以第2层小波时域分解提取的时域信号为例, 假定采样点数为n, 频率上限为$ 1/T $, 则经过两层小波时域分解后的频率上限不高于$ 1/\left( {4 T} \right) $, 对应的频率分辨力至少为$ 1/\left( {4 nT} \right) $. 对该信号进行以能量相关的频谱分解, 可得到时域信号的频域能量分布如下式所示:

$ \left\{ \begin{aligned} &P({t_1}) = P({f_1}) + \cdots + P({f_m}), \\ &P({t_2}) = P'({f_1}) + \cdots + P'({f_m}), \\ &~~~~~~\vdots \\& P({t_n}) = {P^n}({f_1}) + \cdots + {P^n}({f_m}), \end{aligned} \right. $

式中, $ P({t_1}), \;\cdots, \;P({t_n}) $为每一时刻信号的时域能量与频域能量的对应关系; $ {f_m} $为频率上限, $ {f_1}, \;\cdots, $$ {f_m} $为经过两层小波时域分解后的全部频域信息, 与第2层小波时域分解的频率分辨力$ {f_m}/n $相比, 该频域信息的分辨能力不受采样点数n的制约, 故可知经过基于小波变换的时域与频域双重分解后, 理论上可以得到完整的频域信号, 其矩阵表现形式如下:

$ \begin{split}&{P_{mn}}(W{T_{\rm{f}}},W{f_{\rm{T}}}) = (W{T_{{\rm{f1}}}},\cdots,W{T_{{\rm{f}}n}}) \\ \;& ~~~~\times \left[ \begin{array}{ccc} {A_{11}} & \cdots & {A_{1m}} \\ \cdots & \cdots & \cdots \\ {A_{n1}} &\cdots &{A_{nm}} \end{array} \right]\left( \begin{array}{c} W{f_{{\rm{T1}}}} \\ \cdots \\ W{f_{{\rm{T}}n}} \end{array} \right) .\end{split} $

上述矩阵中, $ {P_{mn}}(W{T_{\rm{f}}}, W{f_{\rm{T}}}) $为信号的整体能量的时频域分布, 包括关于时间和频率的能量算子$ W{T_{\rm{f}}} $和$ W{f_{\rm{T}}} $, 以及联系两类算子m × n阶矩阵形式的能量分量. 该矩阵的整体形式可以分列为与时间和能量相关的n维矩阵、与频率和能量相关的m维矩阵以及时频对应关系的m × n阶矩阵. 上述矩阵为3个分列的整合形式, 可以得到有关能量对应的时频域幅值信息, 从而找到时频空间的能量极值点, 便可获得目标物距离信息.

实验系统如图1所示, 通过将1.06 μm种子源倍频获得532 nm输出激光, 将输出连续激光进行调制并经过准直后入射到3 m长的水箱中, 准直光斑直径约1 mm, 发散角约0.5 mrad. 水中目标为反射率约0.8的玻璃板, 反射信号被直径2 inch (1 inch = 2.54 cm)、焦距75 mm的透镜接收后聚焦到雪崩光电二极管(APD)探测器上. APD探测器接收的回波信号与信号发生器发出的同一调制频率的参考信号, 输入到锁相放大器或数据采集卡.
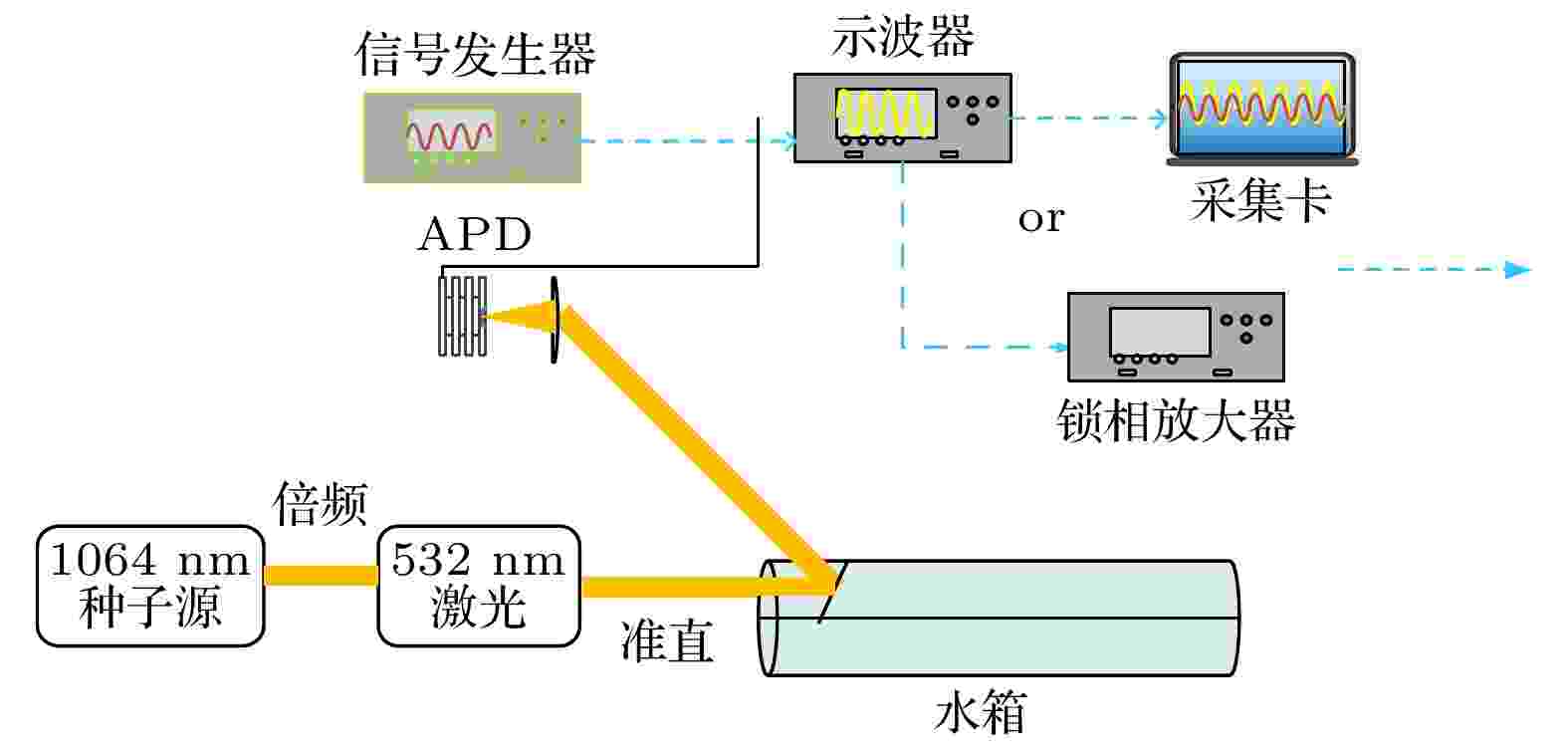图 1 激光水下探测光学系统
Figure1. Laser underwater detection optical system.

通过改变调制频率区间, 锁相放大器输出目标回波信号对应相位. 运用傅里叶逆变换得到时域信号, 使用基于小波变换的时频分析法, 对时域信号包含的有效频域信息进行提取以及频谱分解, 得到时频域的能量极值位置, 进而得到目标距离信息(图2).
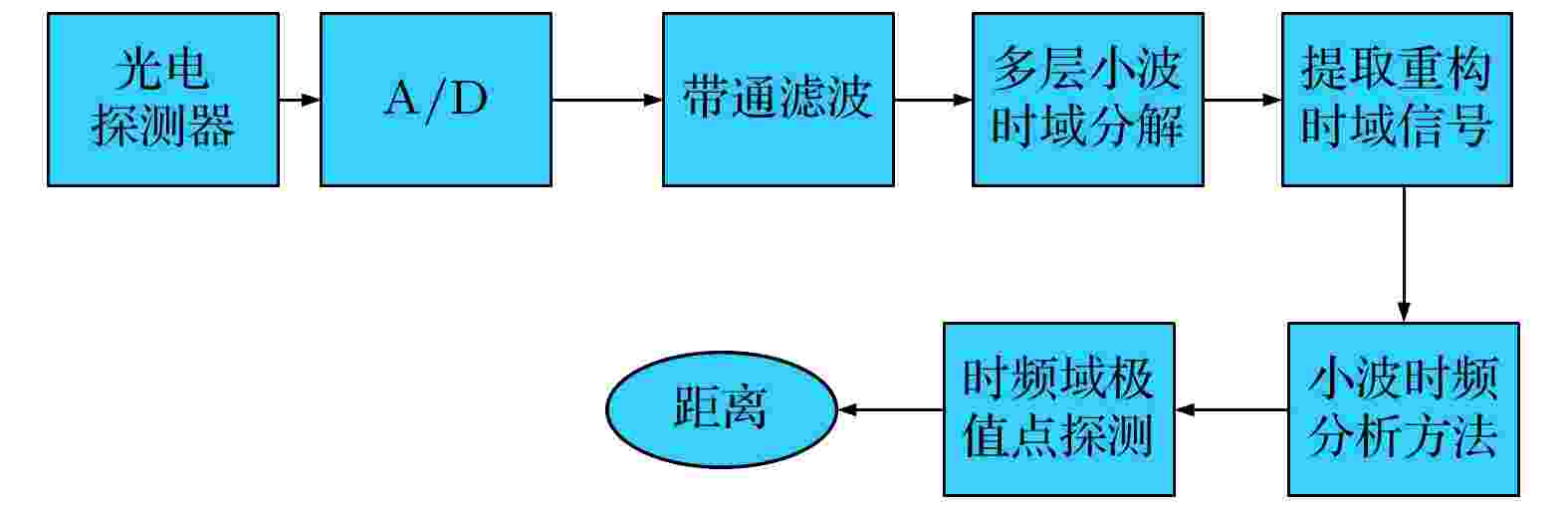图 2 基于小波变换的时频分析方法对水下目标的探测过程
Figure2. Detection process of underwater targets based on wavelet transform time-frequency analysis method.

2

-->

4.1.水的衰减系数测量

光在水中的衰减遵循比尔-朗伯定律, 则其衰减系数k为

$ k = \ln ({P_{{\rm{out}}}}/{P_{{\rm{re}}}})/\left[ {2({x_2} - {x_1})} \right] , $

式中, $ {P_{{\text{out}}}} $为基准位置反射功率, $ {P_{{\text{re}}}} $为目标反射功率, $ {x_2} - {x_1} $为目标与初始位置距离.
Mg(OH)₂粉末难溶于水, 通过在水中添加Mg(OH)₂粉末可以改变水的衰减系数, 从而可以在不同的水体中测量目标的距离. 将水箱入射窗口的内表面作为距离零点并通过记录不同距离目标的回波信号强度, 可推算出以下6个样本水体的衰减系数为0.99, 2, 3, 3.5, 4.5和5.5 m^–1, 测量结果如表1所列. 探测实验中, 所用功率计量程上限为5 W, 所处环境功率计漂移量约为0.01—0.07 mW, 水池采用水循环系统保证水体浑浊程度均匀, 将观测回波反射功率保留至0.1 mW, 相应的衰减系数精度为0.01 m^–1. 目标反射功率随衰减系数的增加而迅速减小, 且测量衰减系数的准确率与标定目标之间距离成反比. 即为了保证测定衰减系数的有效性, 标定距离间距应随衰减系数的增加而减小.

样本	目标距离/m	回波信号 强度/mW	衰减 系数/m–1	平均衰减 系数/m–1
1	0	26.5	—	0.99
	0.25	18.5	0.99
	0.5	9.8	0.99
	1	3.6	0.99
2	0	50	—	2.00
	0.25	18.4	1.99
	0.5	6.5	1.99
	0.6	4.5	2.01
3	0	150	—	3.00
	0.2	45	3.00
	0.4	13.5	3.01
	0.6	4.1	2.99
4	0	150	—	3.50
	0.3	18.4	3.50
	0.5	4.5	3.51
	0.6	2.2	3.49
5	0	200	—	4.50
	0.1	81.5	4.50
	0.2	33	4.51
	0.3	13.5	4.49
6	0	200	—	5.50
	0.1	66	5.54
	0.15	39	5.45
	0.25	12.7	5.51

表1不同衰减系数与距离功率的关系
Table1.Relationship between different attenuation coefficients and distance power.

2 -->

4.2.基于小波变换的时频分析法水下目标测量

采用PIN探测器接收的不同位置回波信号和同频调制的参考信号波形, 锁相放大器输出相应信号波形包含的相位信息和调制频率关系, 也可直接使用数据采集卡采集与输出此类信息. 衰减系数为0.99 m^–1的水体, 调制频率50 MHz为起始频率, 记录50—200 MHz锁相放大器求解出的相位关系, 如图3(a)所示. 图3(b)为图3(a)的频率相位关系进行逆傅里叶变换. 通过图3(b)可知时域幅度曲线的半高宽范围, 可得出有效信息的频域范围约为130—180 MHz, 对该时间幅度信号进行小波频域分解, 获得信号时频空间的能量极值位置. 根据图3(c)可得基准位置能量极值对应时间为0.19646 μs, 1 m目标位置能量基准对应时间为0.20545 μs. 室温下, 海水折射率约为1.339^[21], 则对应基准与目标距离为1.0071 m, 测量误差为0.71 cm, 该测量误差为精度0.1 cm的皮尺标定距离与测量距离之差.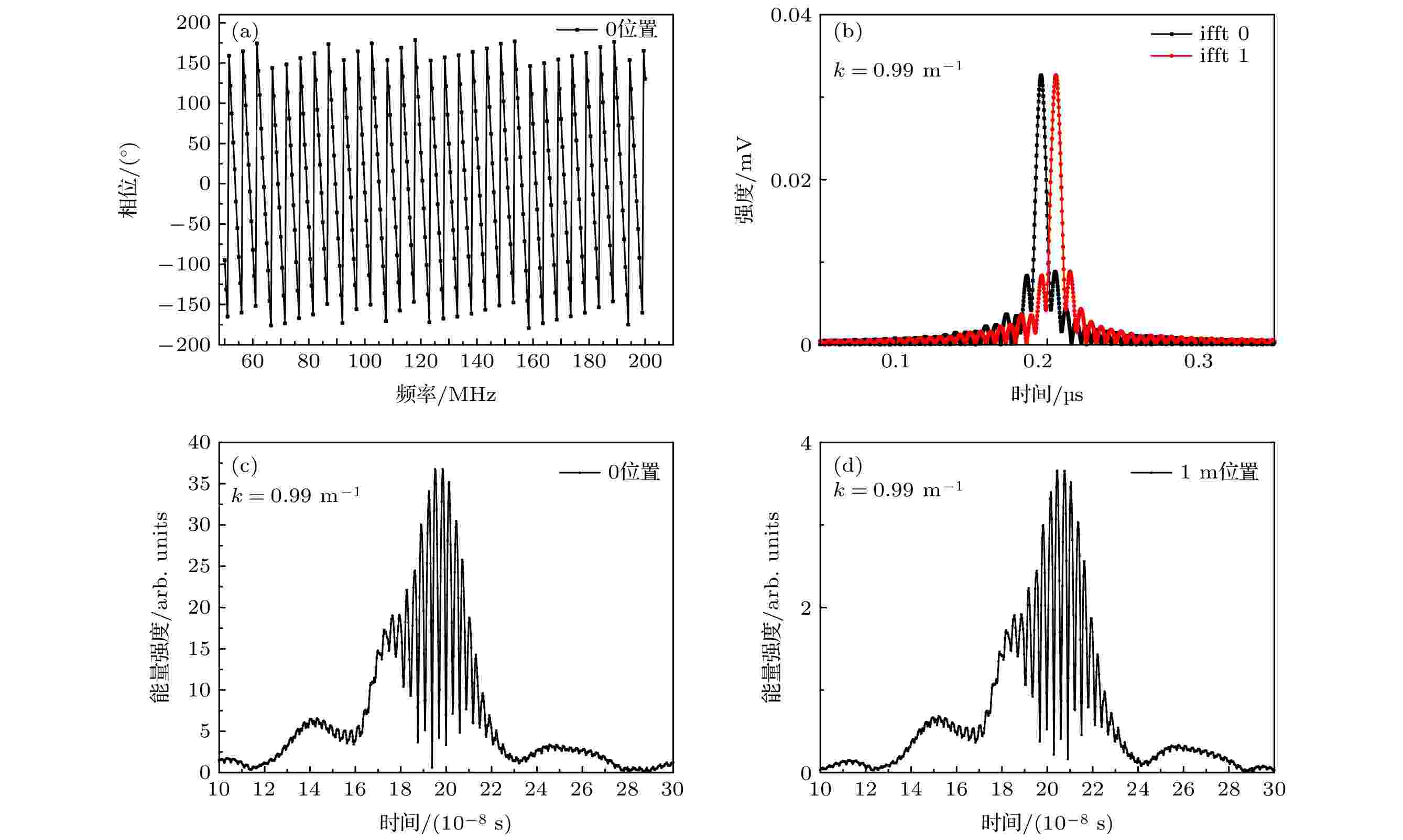
图 3 回波信号与参考信号波形及相应运算结果　(a) 频率-相位差波形图; (b) 图(a)的傅里叶逆运算结果; (c), (d) 基准位置和1 m目标位置的时频能量极值的时域表示
Figure3. Echo signal and reference signal waveforms and corresponding calculation results: (a) Frequency vs. phase difference waveform diagram; (b) the Fourier inverse calculation result of panel (a); (c) and (d) time-frequency energy extreme value positions of the reference position and 1 m position of the target in the time-domain.

水体衰减系数为0.99 m^–1, 分别把目标放置在1.5和2.5 m的位置, 将锁相放大器输出的数据进行记录或直接用数据采集卡采集相位关系, 将变换后的时域信号的幅值进行频域谱分解, 最小频率间隔分别为0.1, 0.075, 0.05和0.025 MHz. 图4(a)和图4(b)为同一水体和目标条件下, 不同频率间隔的测距结果. 图4(c)和图4(d)为不同衰减程度的水体和目标条件下, 不同频率间隔的测距结果. 由图4(a)—(d)的测距结果可以得到, 随着频域分解间隔的减小, 目标测量误差减小.
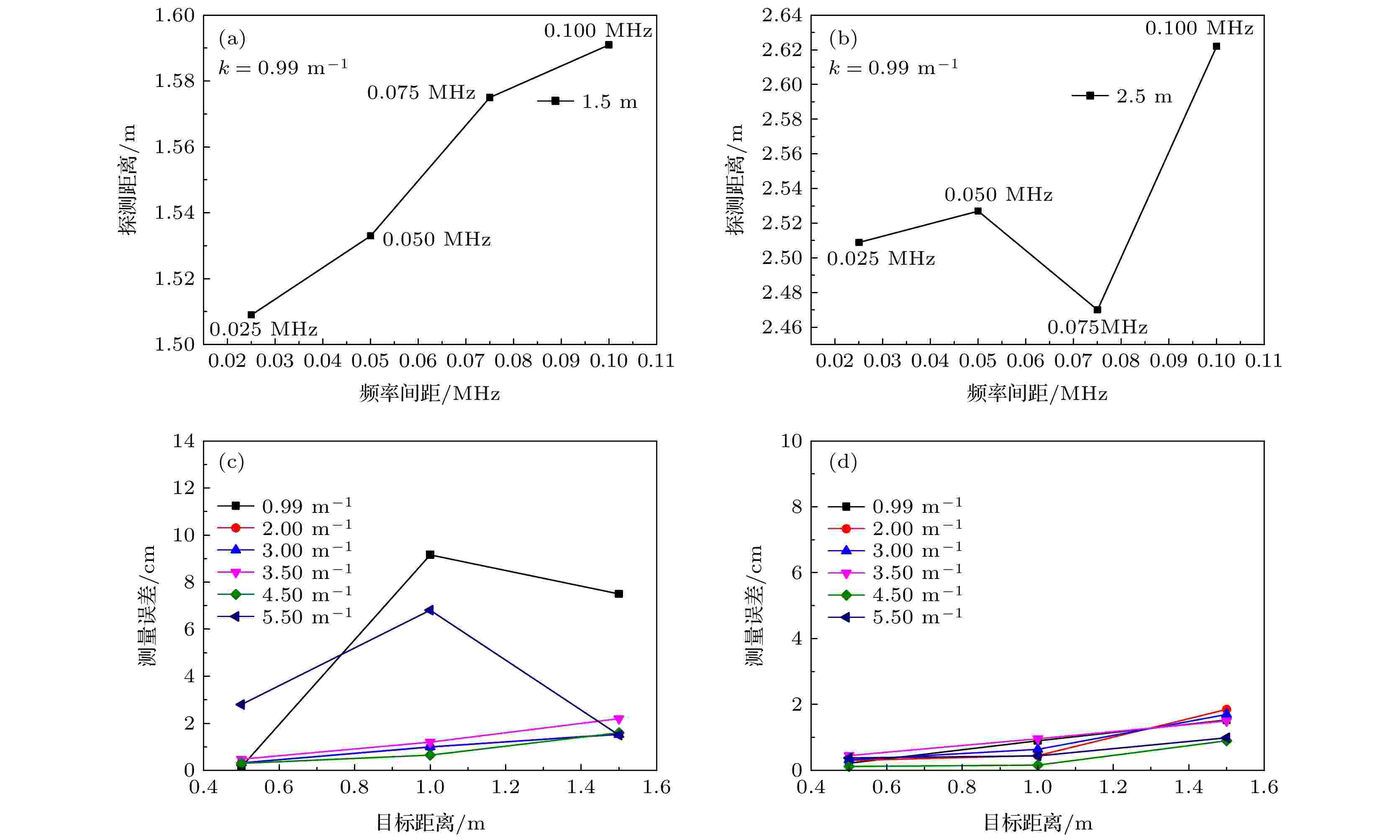图 4 不同频率分解间隔对探测目标的影响　(a), (b) 同一水体条件下, 不同频率分解间隔时1.5和2.5 m目标的测量误差; (c), (d) 不同衰减系数的水体条件下, 频域分解间隔为0.1和0.025 MHz时不同目标距离的测量误差
Figure4. Influences of different frequency decomposition intervals on detection targets: (a), (b) Measurement error at differently frequency decomposition intervals for 1.5 and 2.5 m under the same water body condition; (c), (d) under the water bodies with different attenuation coefficient conditions, the measurement error different distance targets at frequency domain decomposition interval of 0.1 and 0.025 MHz, .

探究不同衰减长度水体下, 不同调制频率区间对该测距方法测量结果的影响. 如图5所示, 将发射源调制频率区间调节至50—200 MHz和700—850 MHz, 采用小波变换时频融合测距法对不同衰减长度水体的目标进行测量. 图5(e)和图5(f)是衰减长度为1—8的水体、调制频率区间为50—200 MHz和700—850 MHz时, 小波时频融合测距方法对目标的测量误差, 以衰减长度起伏表示测量误差波动范围, 得到两调制频率区间内实际探测距离与标定的目标距离的差值绝对值. 通过对图5(e)和图5(f)两组数据的测量误差进行比较, 可以发现低频调制频率范围的测量误差明显小于高频调制频率范围. 图5(a)—(d)给出衰减长度为4.5和6的水体下, 调制频率区间为50—200 MHz和700—850 MHz时通过小波时频变换得到的目标频域极值的时域能量表示, 可以明显地看出低频调制的时域能量极值位置波动范围小于高频调制时域能量极值位置波动范围. 下面从两方面分析低频调制与高频调制对该测距方法的影响: 1) 高频调制对后向散射的抑制作用优于低频调制, 经过高频调制后整体有效信号强度明显提升; 消除大量散射信号的影响, 有效信号波动范围明显降低. 2) 信号源为连续单模激光器时, 回波信号的有效频域波动范围极小. 基于小波变换的时频融合测距依赖于时频域的带通滤波特性, 即信号应包含丰富的频域信息. 低频调制的回波信号包含较多的杂散光频域信息. 这些杂波信号频域分布范围广阔, 有效信号频域分布集中, 能量强度较大, 易于分析提取; 高频调制频率的回波信号中, 杂散光明显减少, 可以获得较为完整的有效信号频域信息. 同时, 由于采样点数与时间间隔限制其频域分解能力, 可知其在固定频域间隔下的小波时频能量分解的频域分布较为分散, 易出现极值位置不明显或多极值现象, 导致高频调制作用的小波时频融合测距的测量误差以及各组测量误差波动范围明显增加.
图 5 调制频率(50—200 MHz和700—850 MHz)对小波时频融合测距方法的影响　(a)—(d)在4.5和6个衰减长度下, 探测目标在极值频率位置的时域能量表示; (e), (f) 两频率范围下不同衰减长度对应的测量误差
Figure5. Influences of modulation frequency on wavelet time-frequency fusion ranging method, where the modulation frequency is a range of 50 to 200 MHz and 700 to 850 MHz: (a)–(d) Time-frequency domain energy extreme frequency position of measurement target under the two attenuation lengths of 4.5 and 6; (e), (f) measurement errors for different attenuation length at the two frequency ranges.

基于小波变换的时频融合测距方法的整体测距结果如图6(a)—(f)所示. 可以看出, 在输出功率为2.3 W以及采用APD探测器探测, 调制频率区间为50—200 MHz时, 结合锁相放大器和示波器的最小可分辨强度与相位, 可知其最远探测距离为8.2个衰减长度. 实际探测距离使用均方根(RMS)运算, 可得该测距方法在8个衰减长度内测距精度小于1 cm. 故可知8个衰减长度内的实际测量误差小于0.1个衰减长度.
图 6 基于小波变换的时频融合测距结果　(a)—(f)对于衰减长度为1—8.2的水体, 该测距方法测量的测量误差以及均方根
Figure6. Time-frequency fusion ranging results based on wavelet transform: (a)–(f) Ranging error and root mean square detected by this ranging method for water bodies with attenuation lengths of 1 to 8.2.

连续光输出功率维持在2.3 W以内, 调制频率控制在50—200 MHz, 该测距方法最远可探测8.2个衰减长度. 在8个衰减长度内, 小波时频融合测距的测距精度保持在1 cm以内(RMS). 上述测距结果表明: 该测距方法实质为时频空间的能量极值探测. 在连续激光作用下, 高频调制的频域能量区分度不明显, 低频调制包含其他频谱信息而易于进行极值检测. 若想提高该方法的测距精度, 可在允许的运行时间和采集频率范围内, 适当提升采集频率和减小频率间距. 在低频调制频率和有效探测距离范围内, 目标信号强度随传播距离的增加而明显减弱, 散射光等干扰信号的频域逐渐丰富, 有效信号的频域变得更加集中. 因此使用小波时频融合测距可以通过频域能量分解能力的提升, 在一定程度上弥补因有效信号大幅衰减造成的测量误差.