摘要:采用大涡模拟方法对横向磁场作用下导电流体Taylor-Couette湍流流动进行数值模拟, 以研究其运动规律. 计算模型为无限长度, 半径比为1/2. 雷诺数分别选取为3000和5000, 磁场加载方式为全局磁场, 哈特曼数取值0—50. 对磁场作用下泰勒涡的演化过程、速度分布和湍动能分布进行分析, 并与轴向磁场作用下泰勒涡演化过程进行对比. 结果表明: 磁场对流场有显著的抑制作用, 扭曲的泰勒涡在横向磁场的作用下破裂成小尺度涡结构, 并沿磁场方向排列; 在外圆筒和垂直于磁场方向的区域, 磁场抑制效果较强; 随着雷诺数的增加, 磁场抑制效果减弱, 在流场不同区域, 流动呈现出不同的特点. 与轴向磁场相比, 横向磁场对流场的抑制效果较弱, 流场分布呈现出明显的各向异性.
关键词: 横向磁场/
Taylor-Couette流动/
湍流/
大涡模拟

English Abstract

全文HTML

--> --> -->

Taylor^[1]首次对同轴旋转圆筒内黏性流体的流动特性进行了研究, 当内圆筒转速较低时, 环形间隙内的流动为Couette流动, 当内圆筒转速达到某一临界值时, 环形间隙内出现轴对称的泰勒涡, 这一流动状态称为Taylor-Couette流动. 随着转速升高, 环形间隙内的流态会依次呈现波状泰勒涡流、调制波状泰勒涡流、湍流泰勒涡流、无特征湍流等^[2].
Taylor-Couette流动具有丰富的运动特性, 因此泰勒涡反应器被广泛应用到工业生产中, 例如颗粒制备^[3]、污水净化^[4]、晶体生长^[5,6]等; 作为生物反应器, 增强流体混合和相间传质, 提高藻类生长速率^[7]; 作为细胞培养平台, 获得高体积浓度的基质细胞用于医学治疗^[8]; 作为化学反应容器, 利用泰勒涡强烈扰动和均匀混合的特点, 生产黑色颜料、合成氧化石墨^[9]; 在可再生能源领域中, 增强热发生器的产热性能, 提高风能转化为热能的效率^[10]. 如果泰勒涡反应器内工质具有导电性, 就可以通过控制外部磁场对流场进行调节, 从而提高反应效率, 改善生产工艺.
磁流体Taylor-Couette 流动通过外部磁场实现对泰勒涡的有效控制, 从而呈现出更加丰富多彩的运动状态, 这引起了众多****的研究兴趣. Donnelly和Ozima^[11]通过实验对汞在同心圆筒间流动的稳定性进行研究, 发现轴向磁场可以延缓泰勒涡的出现, 使泰勒涡产生的临界雷诺数增加. 采用有限差分方法, Tagawa和Kaneda^[12]对磁场作用下液态金属Taylor-Couette流动进行研究, 发现轴向和环形磁场对泰勒涡的影响不同, 轴向磁场对泰勒涡的抑制作用更强. 冷学远等^[13,14]采用直接数值模拟方法对轴向磁场作用下层流和湍流Taylor-Couette流动进行计算, 分析了磁场作用下泰勒涡的演化过程, 对流场变化机理进行研究, 结果表明径向感应电流是引起流场变化和湍流结构改变的主要因素. Zhao等^[15]对环形磁场作用下湍流Taylor-Couette流动进行研究, 发现随着哈特曼数的增加, 泰勒涡结构向内圆筒收缩, 流场最终演化为完全二维轴对称的湍流运动. Kikura等^[16]采用超声波速度剖面方法对横向磁场作用下小长宽比模型内Taylor-Couette流动进行研究, 对泰勒涡结构进行分析, 给出了流场内部轴向速度分布.
已有研究结果表明, 在磁场作用下, 垂直于场强方向的速度分量被抑制, 平行于场强方向的速度分量则基本不受影响, 而平行于场强方向的角动量守恒. 综合以上效应, 流场结构沿着场强方向被拉伸, 最终形成准二维结构^[17]. 轴向磁场作用下的Taylor-Couette层流, 随着磁场强度增加, 泰勒涡数目减少, 尺寸变大, 最终形成充满整个间隙的环流; 如果继续增加磁场强度, Taylor-Couette流动演变为更为简单的Couette层流流动^[14]. 轴向磁场作用下的Taylor-Couette湍流演化过程则更为复杂, 由于湍流脉动和壁面法向动量传输受到抑制, 主流流场结构被改变, 泰勒涡尺寸变小, 最终被磁场完全抑制^[13]. 横向磁场作用下泰勒涡如何演化尚不清楚, 湍流特性如何变化也是一个尚未解决的问题. 在工业生产中, 可用轴向、横向或其他形式的磁场控制晶体生长过程, 熔体在磁场作用下的流动过程和磁流体Taylor-Couette流动有很多相似之处. 因此, 对磁场作用下的Taylor-Couette流场演化过程进行分析, 了解其运动规律, 可为相关研究和设备设计提供一定的理论参考.

2

-->

2.1.物理模型

计算模型如图1所示. 内圆筒半径R₁ = 0.5, 外圆筒半径R₂ = 1. 内圆筒旋转, 外圆筒静止. 本文计算所用模型为无限长模型, 上下壁面采用周期性边界. 模型内、外壁面均满足无滑移和电绝缘边界条件. 模型内工质选用液镓, 密度ρ = 6090 kg/m³, 运动黏度系数ν = 3.2 × 10^–7 m²/s, 电导率σ = 3.7 × 10⁶ S/m. 工质受到均匀横向磁场的作用, 如图1所示. 经计算, 液镓流动的磁雷诺数$R{e_{\rm{m}}} = \mu \sigma U\delta \ll 1$($ \mu $为工质磁导率, σ为工质电导率, U为特征速度, δ为特征长度), 满足低磁雷诺数假设, 则感应磁场相对于施加的外部磁场可以忽略不计^[18].
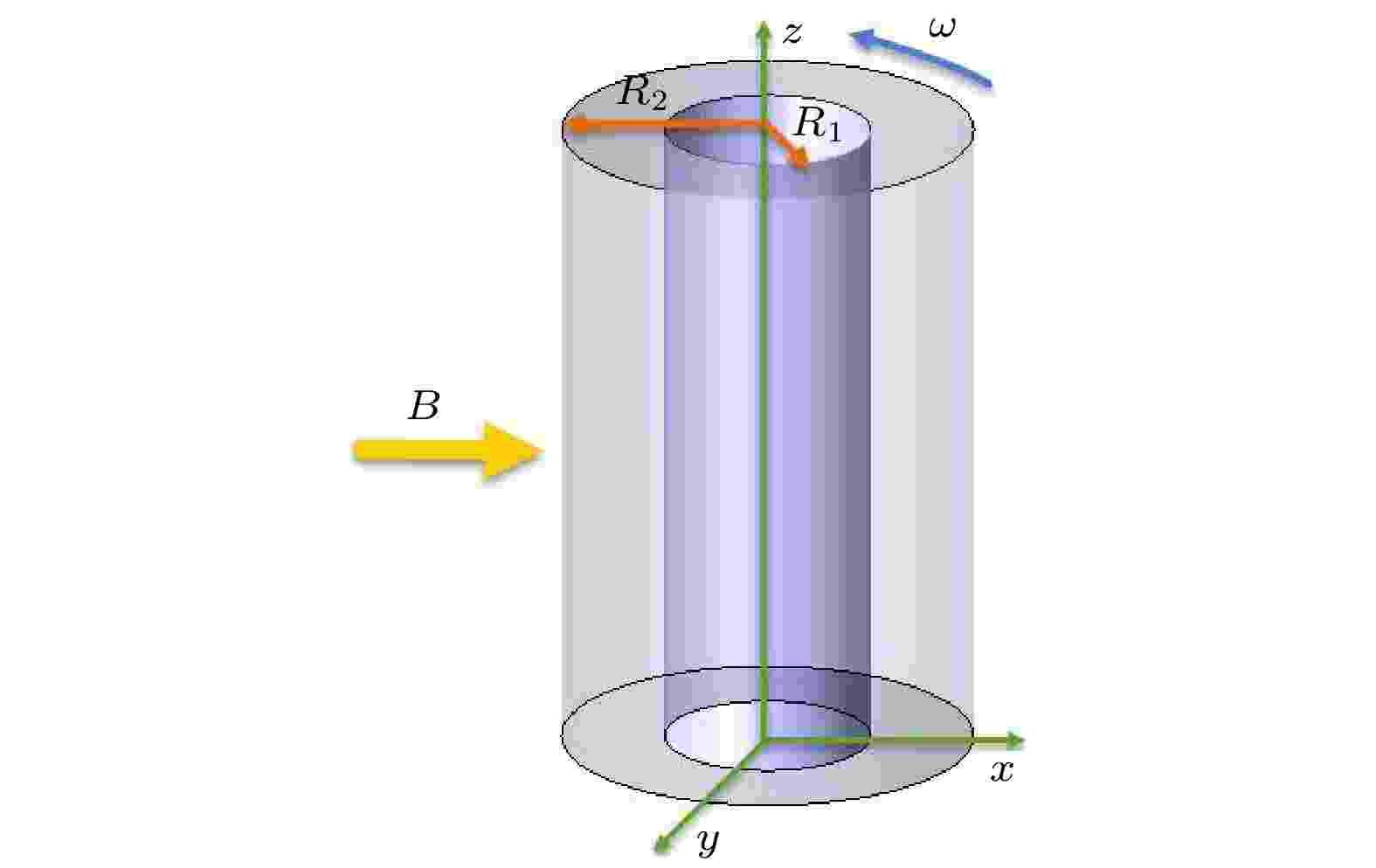图 1 物理模型
Figure1. Physical model.

2 -->

2.2.控制方程

本次计算采用大涡模拟方法, 对大尺度湍流进行直接模拟, 利用亚格子模型模拟小尺度湍流. 连续性方程和动量方程如下所示:

$\nabla \cdot {\boldsymbol{U}} = {\text{0}} ,\qquad\qquad\qquad\quad\quad$

$\begin{split}&\rho \frac{{\partial {\boldsymbol{U}}}}{{\partial t}} + \rho \left( {{\boldsymbol{U}} \cdot \nabla } \right){\boldsymbol{U}} \\=\;& - \nabla p + \rho \nu {\nabla ^{\text{2}}}{\boldsymbol{U}} + \nabla \cdot {\tau ^{{\text{sgs}}}} + {\boldsymbol{F}},\end{split}$

式中, U为速度矢量, ρ为流体密度, p为流体压力, τ^sgs为亚格子应力, F为洛伦兹力.
导电流体在磁场中运动, 产生的感应电流可以根据欧姆定律进行求解^[19]. 电势方程、感应电流密度方程和洛伦兹力方程如下所示:

$\begin{split}{\nabla ^{\text{2}}}\varphi =\;& \nabla \cdot \left( {{\boldsymbol{U}} \times {\boldsymbol{B}}} \right) = {\boldsymbol{U}} \cdot \left( {\nabla \times {\boldsymbol{B}}} \right) \\&+ {\boldsymbol{B}} \cdot \left( {\nabla \times {\boldsymbol{U}}} \right) ,\\[-10pt]\end{split}$

${\boldsymbol{J}} = \sigma \left[ { - \nabla \varphi + \left( {{\boldsymbol{U}} \times {\boldsymbol{B}}} \right)} \right], \;\;\;$

$ {\boldsymbol{F}} = {\boldsymbol{J}} \times {\boldsymbol{B}} ,\qquad\qquad\qquad\;\;\;$

式中, $ \varphi $为电势, B为外部磁场强度, J为感应电流密度.
大涡模拟选用Smagorinsky-Lilly亚格子模型, 其亚格子应力表示为

$ {\tau _{ij}} - \frac{{\text{1}}}{{\text{3}}}{\tau _{kk}}{\delta _{ij}} = - {\text{2}}{\mu _t}{\bar S_{ij}}, $

式中, $ {\mu _t} $为亚格子尺寸的湍流黏度, ${\mu _t} = {\left( {{C_{\rm{s}}}\varDelta } \right)^2}\left| {\overline S } \right|$, 其中$ {{C}}_{\text{s}} $为Smagorinsky常数, $\varDelta = ( \Delta x\Delta y\Delta z )^{1/3}$, $ \left| {\overline S } \right| = \sqrt {2{{\overline S }_{ij}}{{\overline S }_{ij}}} $; $ {\overline S _{ij}} $为亚格子湍流黏性张量旋率, ${\overline S _{ij}} = \dfrac{1}{2}\left( {\dfrac{{\partial {{\overline u }_i}}}{{\partial {x_j}}} + \dfrac{{\partial {{\overline u }_j}}}{{\partial {x_i}}}} \right)$.
计算所用模型为无限长模型, 内外壁面满足的无滑移和电绝缘边界条件为

$\begin{split}&r = {R_1}:\;{u_\theta } = \omega {R_1},{u_r} = {u_z} = 0,\varphi = 0,\\&r = {R_2}:\;{u_\theta } = 0,{u_r} = {u_z} = 0,\varphi = 0.\end{split}$

无量纲参数选取雷诺数$Re = $$ \omega {R_1}d/{\rm{\nu }}$和哈特曼数$Ha = \sqrt {\sigma {B^2}{d^2}/(\rho \nu )} $, 式中ω为内圆筒旋转速度, R₁为内圆筒半径, d为环形间隙宽度.
2 -->

2.3.算例验证

数值计算工作基于ANSYS Fluent 17.0商业软件, 采用大涡模拟(LES)方法进行计算. 基于压力基求解器对模型内的不可压缩导电流体流动进行了求解, 迭代过程采用了压力-速度耦合求解方法, 压力差分选择默认的二阶离散格式, 动量差分选择有限中心差分离散格式, 时间差分选择二阶隐式离散格式.
为验证计算方法的准确性, 对湍流Taylor-Couette流动进行数值模拟. 模型半径比为0.5, 长宽比为2π, 内圆筒旋转, 外圆筒静止, 轴向壁面采用周期性边界条件. 在未加磁场情况下, 对Re = 3000和Re = 5000两种工况进行数值模拟. 对于Re = 3000工况, 径向、轴向和周向网格数量为40 × 251 × 126, 时间步长选择为0.0001 s. 对于Re = 5000工况, 径向、轴向和周向网格数量为50 × 314 × 158, 时间步长选择为0.00005 s. 对$r = \left( {{R_1} + {R_2}} \right)/2$的圆柱面平均周向速度进行监测, 待圆柱面平均周向速度曲线稳定后, 可以判断计算收敛. 将本次模拟中的平均周向速度分布、角动量分布和边界层内湍流结构与Dong^[20]的结果进行对比.
图2为Re = 3000和Re = 5000工况下的平均周向速度分布图, 可以看出本文计算结果和文献[20]中的平均周向速度分布基本一致. 图3为Re = 3000和Re = 5000工况下角动量分布图, 可以看出计算结果和文献[20]相符合. 角动量在内筒和外筒间隙的大部分区域恒为一常数, 且等于内壁和外壁角动量之和的一半, 这和Cheng等^[21]的理论分析结果一致. 图4为Re = 3000和Re = 5000工况下的边界层内湍流结构, 纵坐标为无量纲参数u⁺, 表达式为${u^ + } = \left( {1 - \left\langle {{u_\theta }} \right\rangle } \right)/{u_{{\tau}} }$, 其中$u_{\rm{\tau}} ^2 = $$ - R{e^{ - 1}}r\left( {\partial \langle {u_\theta }/r \rangle /\partial r} \right)$, 横坐标为无量钢参数r ⁺, 表达式为${r^ + } = 2 rR{e_{{\tau}} }$, 其中$R{e_\tau } = 0.5{u_\tau }Re$. 从图4可以看出, LES计算结果符合湍流边界层速度分布规律, 在黏性底层内满足线性规律u⁺ = r⁺, 在对数区域满足u⁺ = 1/k × ln(r⁺) + b. LES计算结果和文献[20]的直接数值模拟(DNS)结果有一定差异, 主要是由于LES只是对大涡进行模拟, 对小涡则进行统计平均, 网格精度也明显低于DNS.
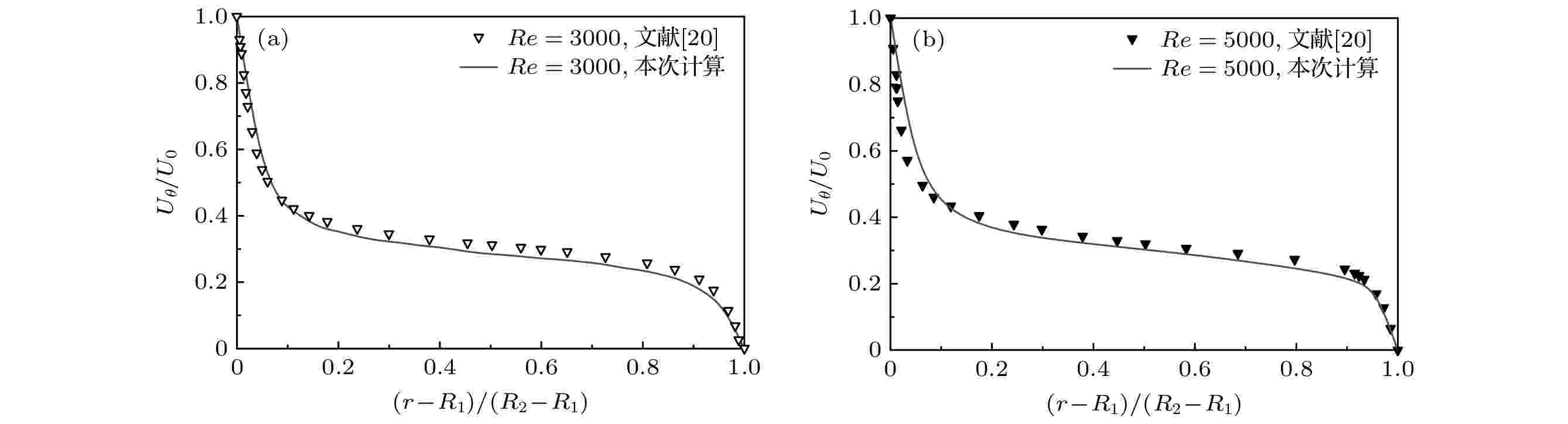图 2 平均周向速度分布曲线　(a) Re = 3000; (b) Re = 5000
Figure2. Distribution of mean azimuthal velocity: (a) Re = 3000; (b) Re = 5000.

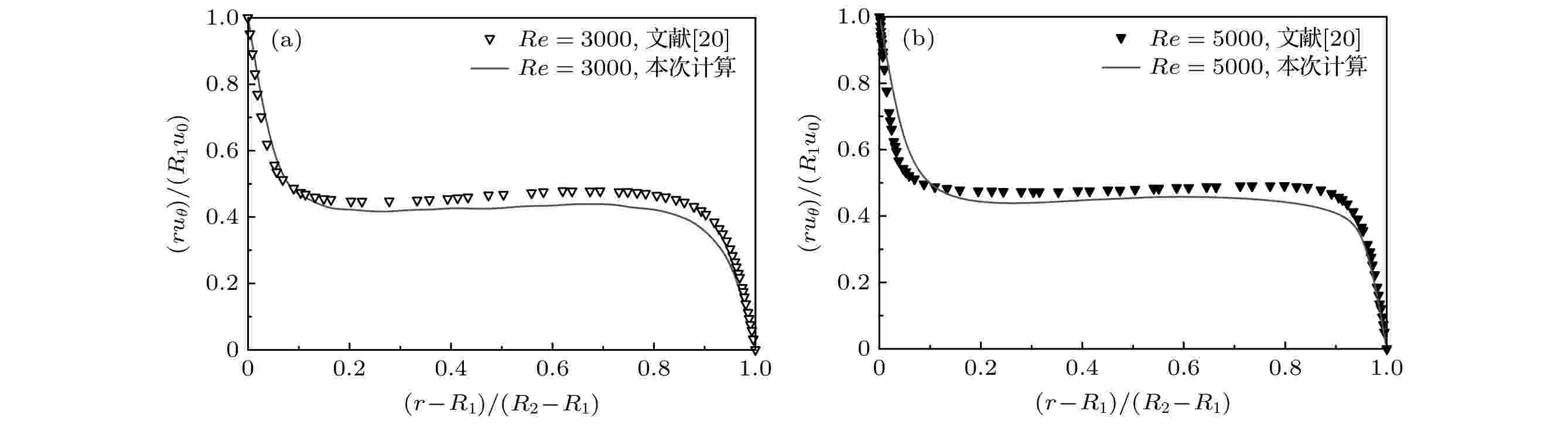图 3 平均角动量分布曲线　(a) Re = 3000; (b) Re = 5000
Figure3. Distribution of mean angular momentum (a) Re = 3000; (b) Re = 5000.

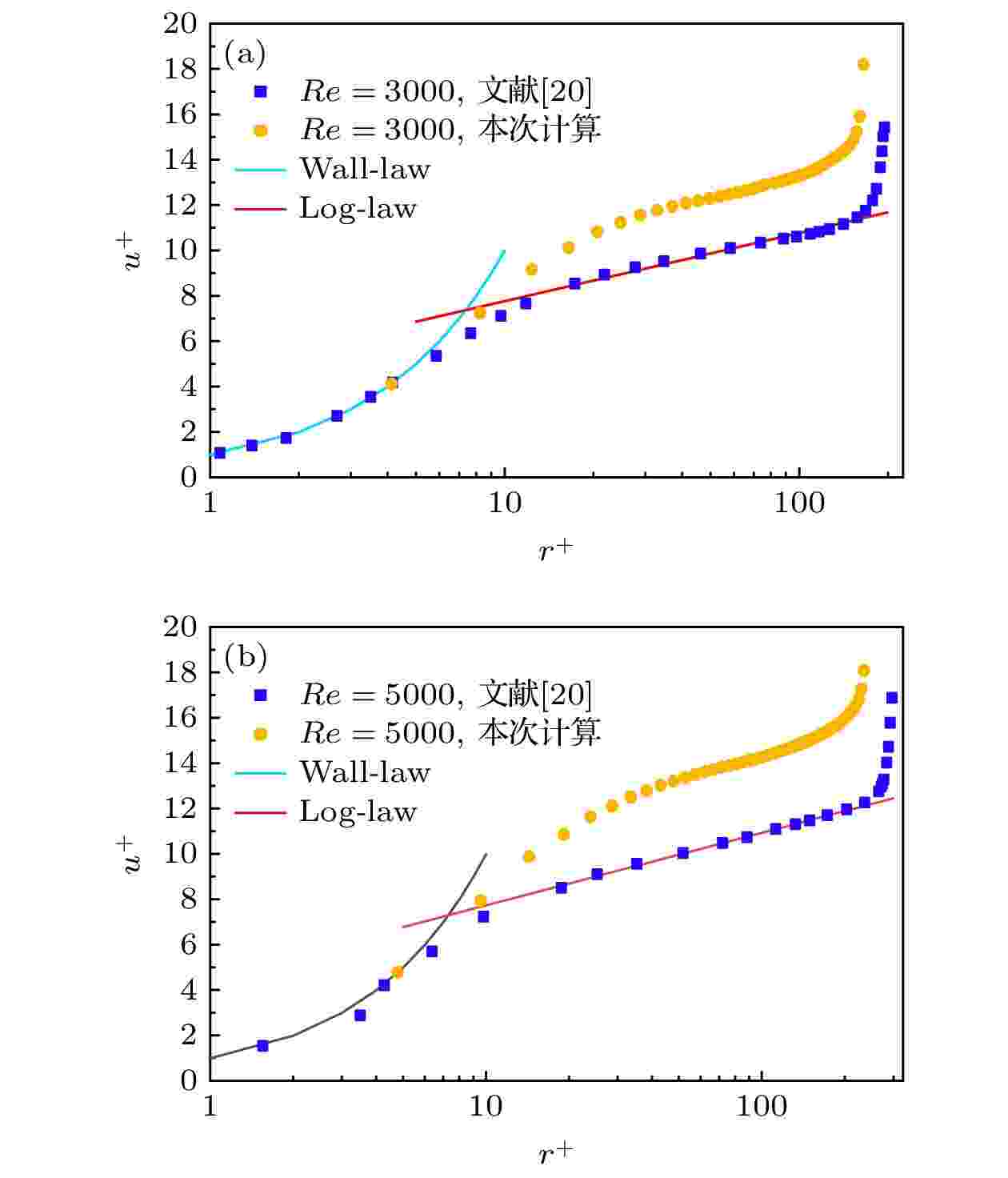图 4 平均速度u⁺分布　(a) Re = 3000; (b) Re = 5000
Figure4. Distribution of mean velocity profile u⁺: (a) Re = 3000; (b) Re = 5000.

综上所述, 对比本文与文献[20]中的平均周向速度分布、角动量分布、边界层内湍流结构等数据, 可以看出本文结果与文献[20]中的结果基本符合, 证明了计算结果的可靠性.

2

-->

3.1.加载横向磁场

3 -->

3.1.1.泰勒涡的演化过程

为了直观地描述泰勒涡在磁场作用下的演化过程, 选用Q准则对泰勒涡的形态和大小进行识别^[22], 其中Q的阈值选取为Q = 2000. 对于Re = 3000, 流场内泰勒涡的演化过程见图5(a). Ha = 0时, 流场内存在3对泰勒涡, 泰勒涡呈现出扭曲状态, 并存在一些小尺度湍流涡结构. Ha = 10时, 泰勒涡被磁场抑制, 流场中小尺度湍流涡结构增多. Ha = 30—50时, 完整的泰勒涡结构消失, 流场内充满小尺度涡结构, 流场内的涡沿着磁场方向呈现出扁平化分布. 对于Re = 5000工况, 流场中泰勒涡的演化过程如图5(b)所示. Ha = 0时, 流场中存在3对泰勒涡, 与Re = 3000工况相比, 泰勒涡的形态更加扭曲. 随着磁场强度增加, 泰勒涡被进一步破坏, 小尺度湍流涡结构逐渐增多. Ha = 50时, 流场中的小尺度涡沿着磁场方向开始出现扁平化分布. 对于Re = 3000工况, 流场中小尺度涡沿磁场方向开始出现扁平化分布对应的哈特曼数为Ha = 30.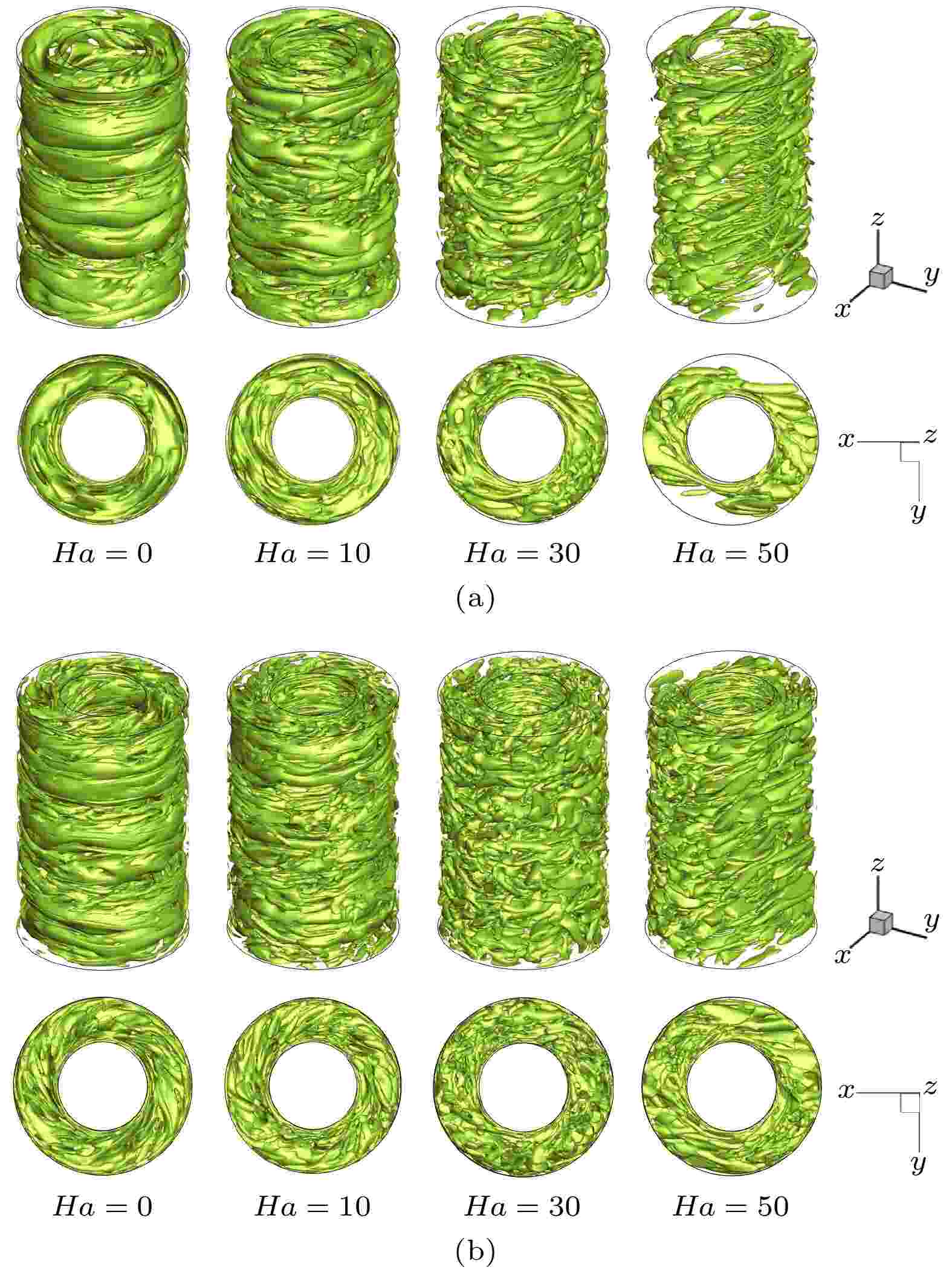
图 5 Q = 2000时泰勒涡的演化过程图　(a) Re = 3000; (b) Re = 5000
Figure5. Diagram of Taylor vortex evolution process with Q = 2000: (a) Re = 3000; (b) Re = 5000.

通过对Re = 3000和Re = 5000工况下泰勒涡在磁场作用下的演化过程进行对比分析, 可以看出相同磁场强度条件下, 随着雷诺数增加, 磁场的抑制作用减弱.
3 -->

3.1.2.子午面平均速度矢量图

对Re = 3000工况, x = 0子午面和y = 0子午面平均速度矢量图进行分析, 结果如图6所示. 左侧为外圆筒壁面, 右侧为内圆筒壁面. Ha = 0时, 流场中存在3对泰勒涡. 随着磁场强度增加, 泰勒涡结构消失, 流场中出现小尺度涡结构. Ha = 50时, 涡结构在靠近外圆筒区域完全消失, 在靠近内圆筒区域少量存在, 说明在外圆筒区域, 磁场作用效果更强.
图 6 Re = 3000工况下子午面平均速度矢量图　(a) x = 0; (b) y = 0
Figure6. Diagram of mean velocity in the meridian plane at Re = 3000: (a) x = 0; (b) y = 0.

对横向磁场作用下x = 0子午面和y = 0子午面速度矢量图进行对比分析, 发现 x = 0子午面和y = 0子午面速度矢量图在磁场作用下的变化过程不同, 磁场对x = 0子午面流场的抑制效果更强. 即在垂直磁场方向的区域, 磁场对流体的抑制作用更强.
Re = 5000工况下x = 0子午面和y = 0子午面平均速度矢量图见图7, 未加载磁场时流场中存在3对泰勒涡, 与杜珩等^[23]的结果一致, 进一步证明了计算结果的可靠性. 加载磁场后, 泰勒涡的演化过程与Re = 3000工况下的演化过程大致相同. 但相同磁场强度条件下, Re = 5000工况子午面存在更多的涡结构.
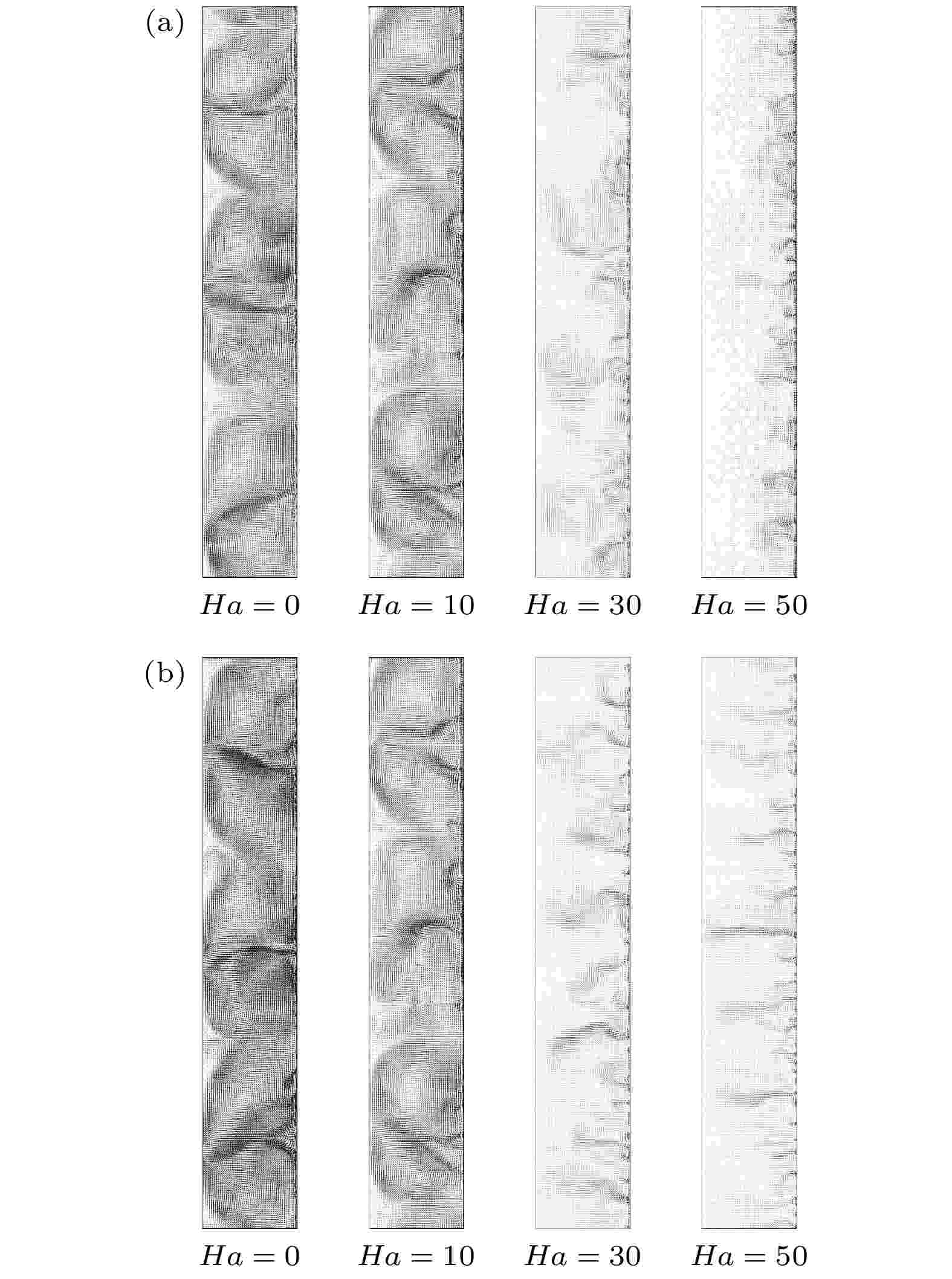图 7 Re = 5000工况下子午面平均速度矢量图　(a) x = 0; (b) y = 0
Figure7. Diagram of mean velocity in the meridian plane at Re = 5000: (a) x = 0; (b) y = 0.

由图6和图7可知, 随着磁场强度增加, 流场平均速度变小(统计平均下), 漩涡尺度减小, 这是由于流场受到了横向磁场的抑制作用, 泰勒涡破碎成小尺度的漩涡, 并主要分布在圆筒内壁. 由分析可知, 内筒旋转产生剪切应力, 在其边界上形成漩涡并进入流场; 在内壁和外壁的间隙内, 由于流体的黏性耗散和焦耳热耗散效应, 漩涡尺寸和强度减小; 在外壁, 漩涡很少, 则是由于外壁静止不动.
3 -->

3.1.3.周向速度

3 -->

3.1.3.1.全流场平均周向速度

在横向磁场的作用下, 沿磁场方向和垂直于磁场方向的流场中, 泰勒涡和速度矢量的演化过程显现出不同特点. 为了进一步研究横向磁场作用下流场的运动规律, 下面对全流场平均周向速度、x = 0子午面和y = 0子午面周向速度进行分析.
图8为全流场平均周向速度分布曲线. 随着磁场强度增加, 平均周向速度逐渐减小. 对于Re = 3000工况, Ha = 30时, 平均周向速度在靠近外圆筒区域出现0值. Ha = 50时, 平均周向速度为0的区域进一步扩大, 由外圆筒一直延伸到圆筒中间区域. 对于Re = 5000工况, Ha = 0—30时, 平均周向速度曲线在0刻度线以上. Ha = 50时, 靠近外圆筒区域出现0值.
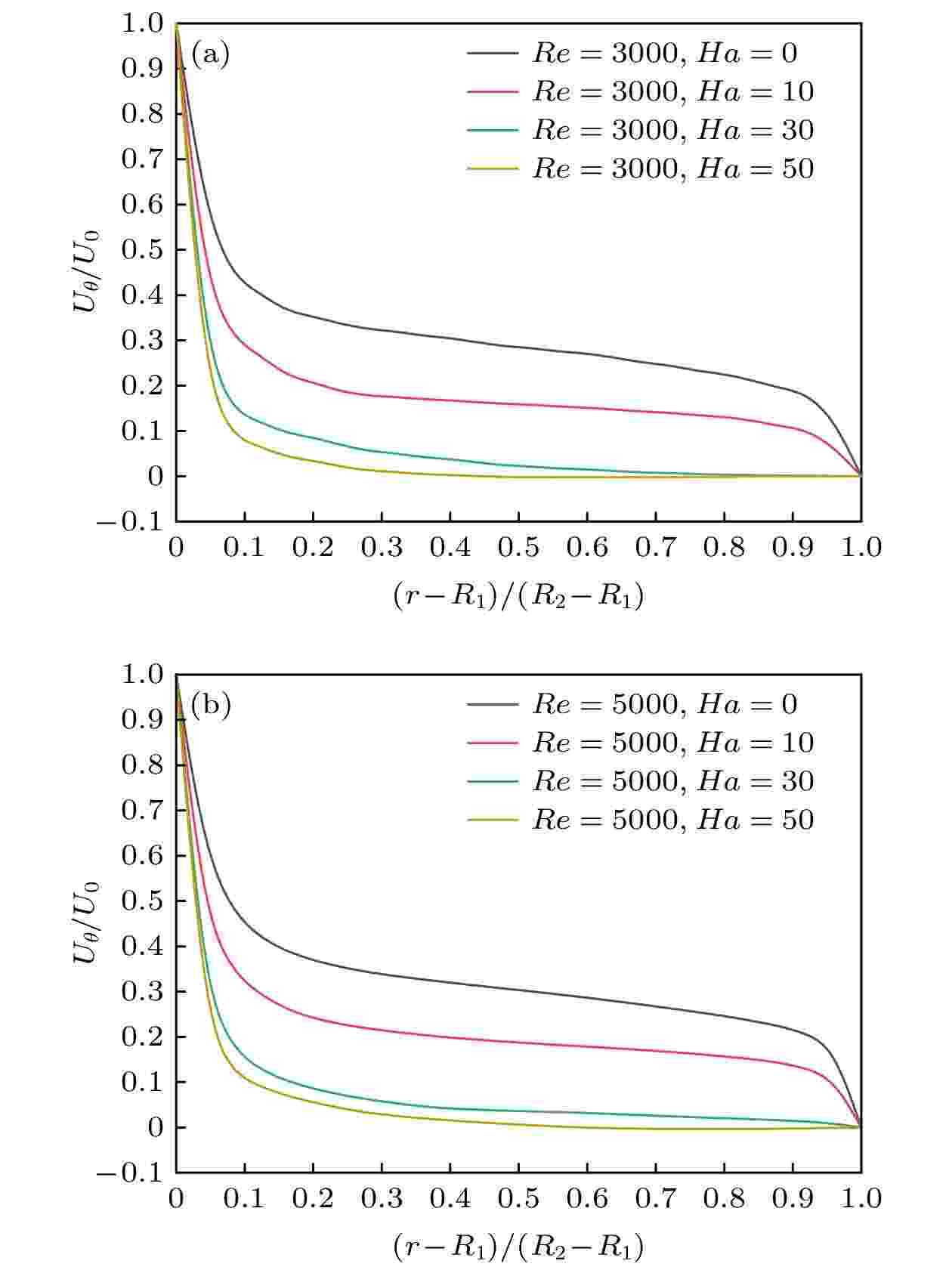图 8 全流场周向速度分布曲线　(a) Re = 3000; (b) Re = 5000
Figure8. Distribution of the azimuthal velocity in the whole flow field: (a) Re = 3000; (b) Re = 5000.

3 -->

3.1.3.2.x = 0子午面周向速度分布曲线

图9给出了x = 0子午面周向速度分布曲线, 可以看出, 周向速度随着磁场强度增加而减小. 在Ha = 30—50时, 周向速度出现负值, 即流体出现顺时针运动. 周向速度为0的位置由圆筒中间向圆筒内侧移动, 与全流场平均周向速度曲线的变化规律一致. 这一现象说明磁场抑制流体正向运动, 当磁场强度达到一定数值后, 流体会出现负向运动, 与冷学远等^[24]的结论相同. 对于Re = 3000工况, Ha = 50时, 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = 0 — 0.2$区域, 周向速度为正值; 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = 0.2 — $$ 0.6$区域, 周向速度为负值; 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = $$ 0.6 — 1$区域, 周向速度为0. 即沿着半径方向, 流场依次为逆时针运动和顺时针运动. 对于Re = 5000, Ha = 50工况, 流场具有相似的流动状态, 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = 0 — 0.4$区域, 周向速度为正值; 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = 0.4 — 0.8$区域, 周向速度为负值; 在$(r - {R_1})/\left( {{R_2} - {R_1}} \right) = 0.8 — 1$区域, 周向速度为0. 由此可知, 对于Re = 3000和Re = 5000工况, 磁场对低雷诺数工况下的导电流体抑制作用更强.
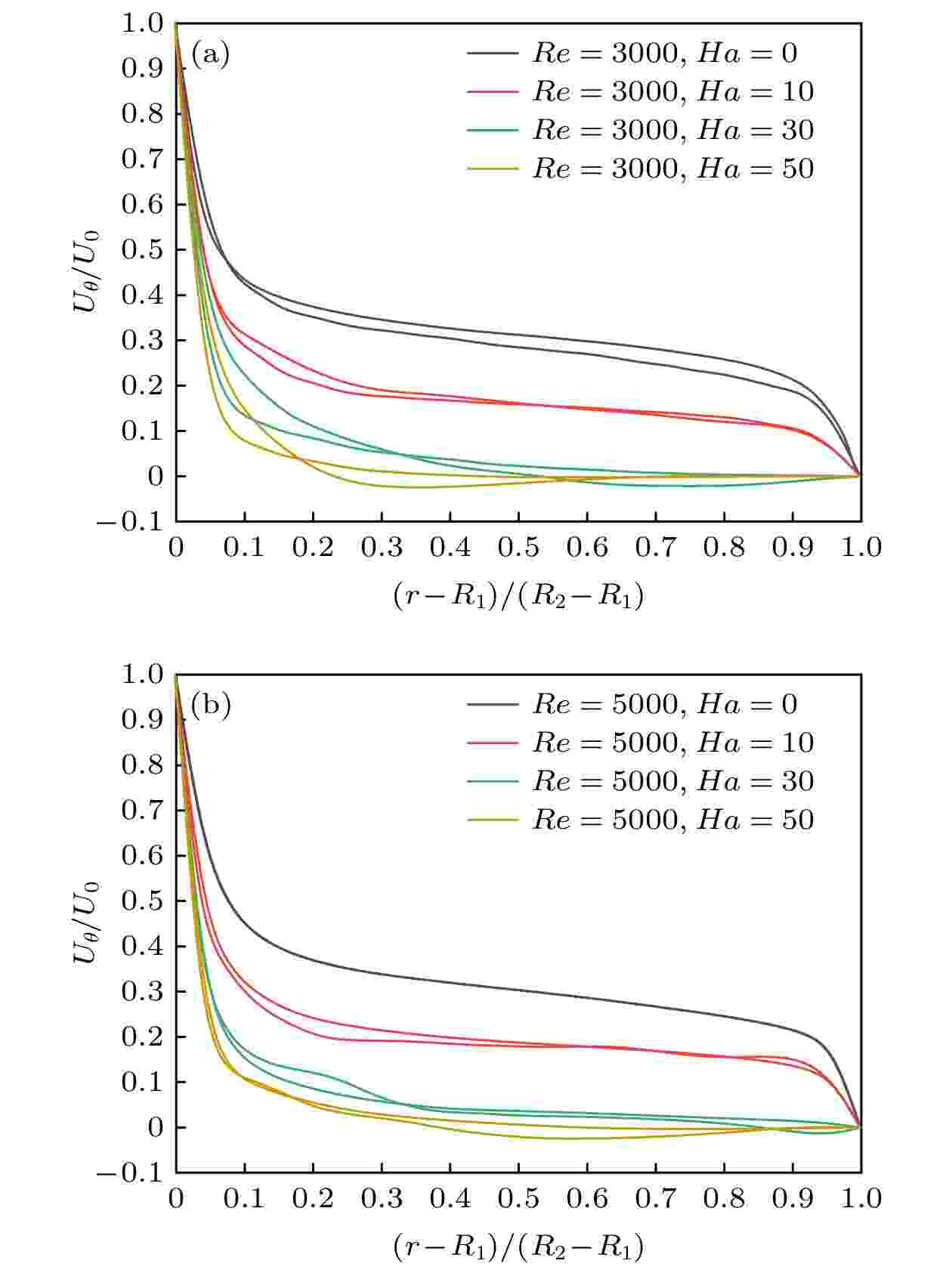图 9 x = 0子午面周向速度分布曲线　(a) Re = 3000; (b) Re = 5000
Figure9. Distribution of the azimuthal velocity in the vertical plane of x = 0: (a) Re = 3000; (b) Re = 5000.

3 -->

3.1.3.3.y = 0子午面周向速度分布曲线

图10为y = 0子午面周向速度分布曲线, 可以看出, 在Ha = 0—50范围内随着磁场强度增加, 流动被逐渐抑制, 但曲线始终位于0刻度线上方, 与x = 0子午面周向速度曲线明显不同. x = 0和y = 0子午面周向速度曲线在横向磁场作用下的差异, 更加直观地反映了沿着磁场方向和垂直于磁场方向不同区域流体运动的区别.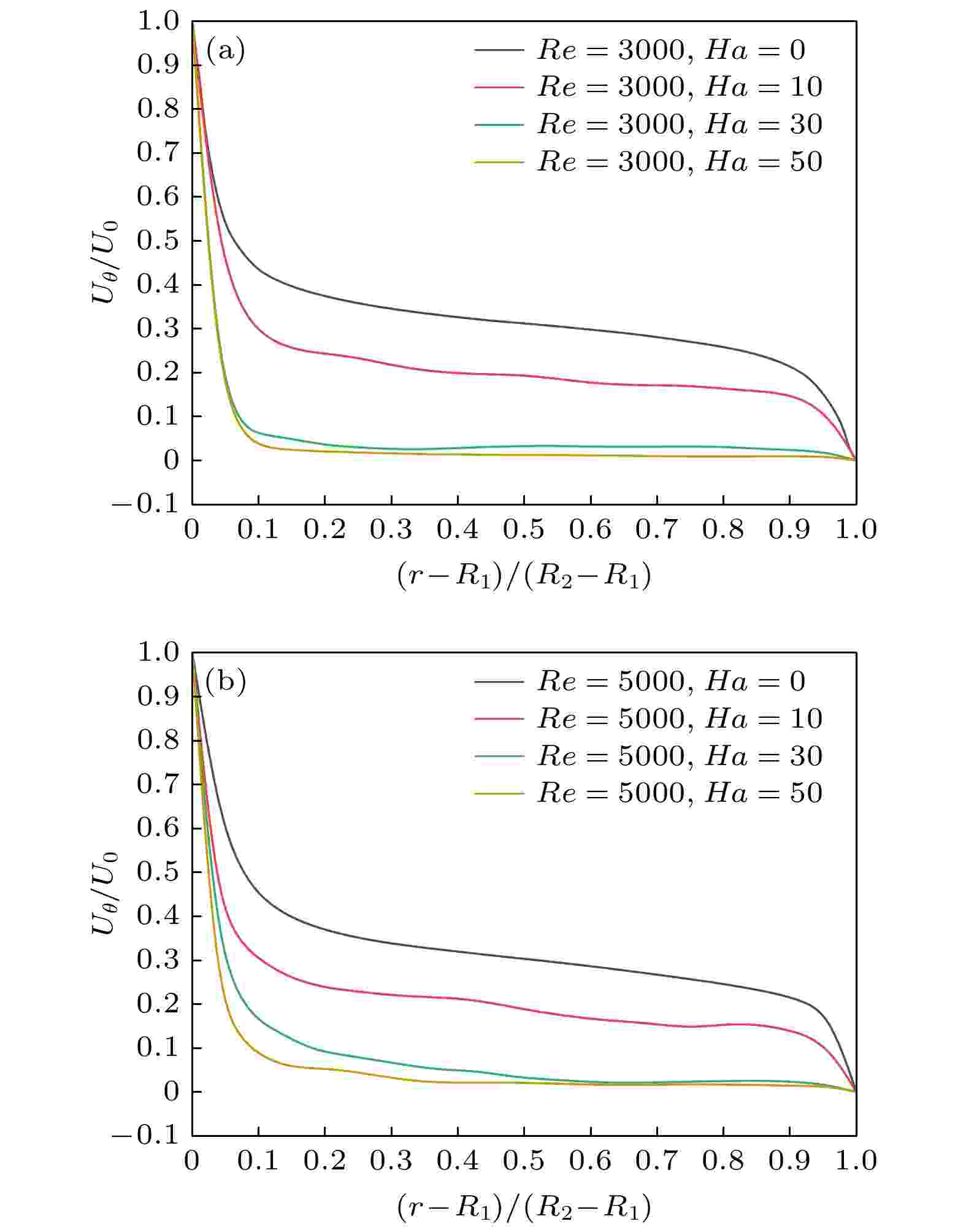
图 10 y = 0子午面周向速度分布曲线　(a) Re = 3000; (b) Re = 5000
Figure10. Distribution of the azimuthal velocity in the vertical plane of y = 0: (a) Re = 3000; (b) Re = 5000.

3 -->

3.1.4.湍动能分布

图11为横向磁场作用下湍动能分布图, 其中湍动能取值k = 1.01 m²/s². 当Ha = 0和Ha = 10时, 湍动能的分布较为规则, 可以反映出泰勒涡的存在. Ha = 30时, 完整的泰勒涡结构消失, 流场内充满小尺度涡结构. 此时, 流场中湍动能的分布较为均匀. 对于Re = 3000工况, Ha = 50时, 垂直于磁场方向湍动能分布出现空白区域, 且空白区域随着磁场强度增加而变大. 对于Re = 5000工况, Ha = 50时, 垂直于磁场方向湍动能分布开始出现空白区域. 这一变化过程与泰勒涡的演化过程一致, 由此可知, 湍动能分布的变化过程可以反映出泰勒涡的演化过程.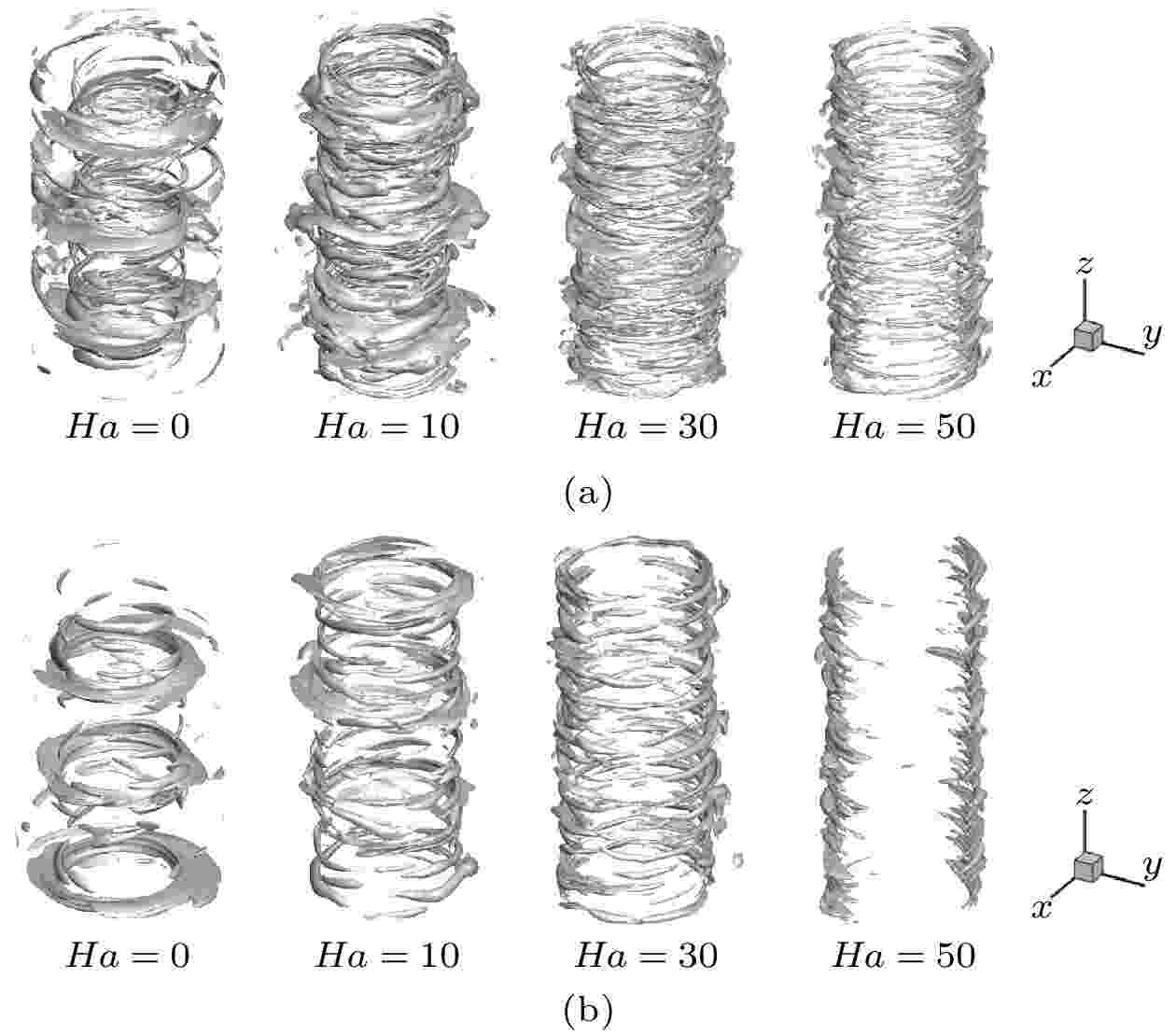
图 11 k = 1.01 m²/s²时湍动能分布图　(a) Re = 3000; (b) Re = 5000
Figure11. Distribution of turbulent kinetic energy with k = 1.01 m²/s²: (a) Re = 3000; (b) Re = 5000.

图12为Re = 3000工况下, Ha = 0和Ha = 30时的湍动能谱, 在流场中设置3个点, 分别位于内、外筒壁面和内外圆筒中间位置, 坐标为 (0, 0.5165, 0.785), (0, 0.75, 0.785), (0, 0.9835, 0.785), 记录一段时间内的周向速度变化, 经由快速傅里叶变换获得湍动能与频率的关系. 由图12可知: Ha = 0时, 在低频下3个点的能谱相差较小, 说明大尺度漩涡(泰勒涡)充满整个间隙; 高频下, 离内壁最近的点的能谱高于其余两点, 说明湍流脉动强烈, 这里是漩涡产生的区域. Ha = 30时, 三条线分离, 意味着在磁场作用下3个点附近的漩涡结构尺度不一样, 和图6平均速度矢量图变化一致.
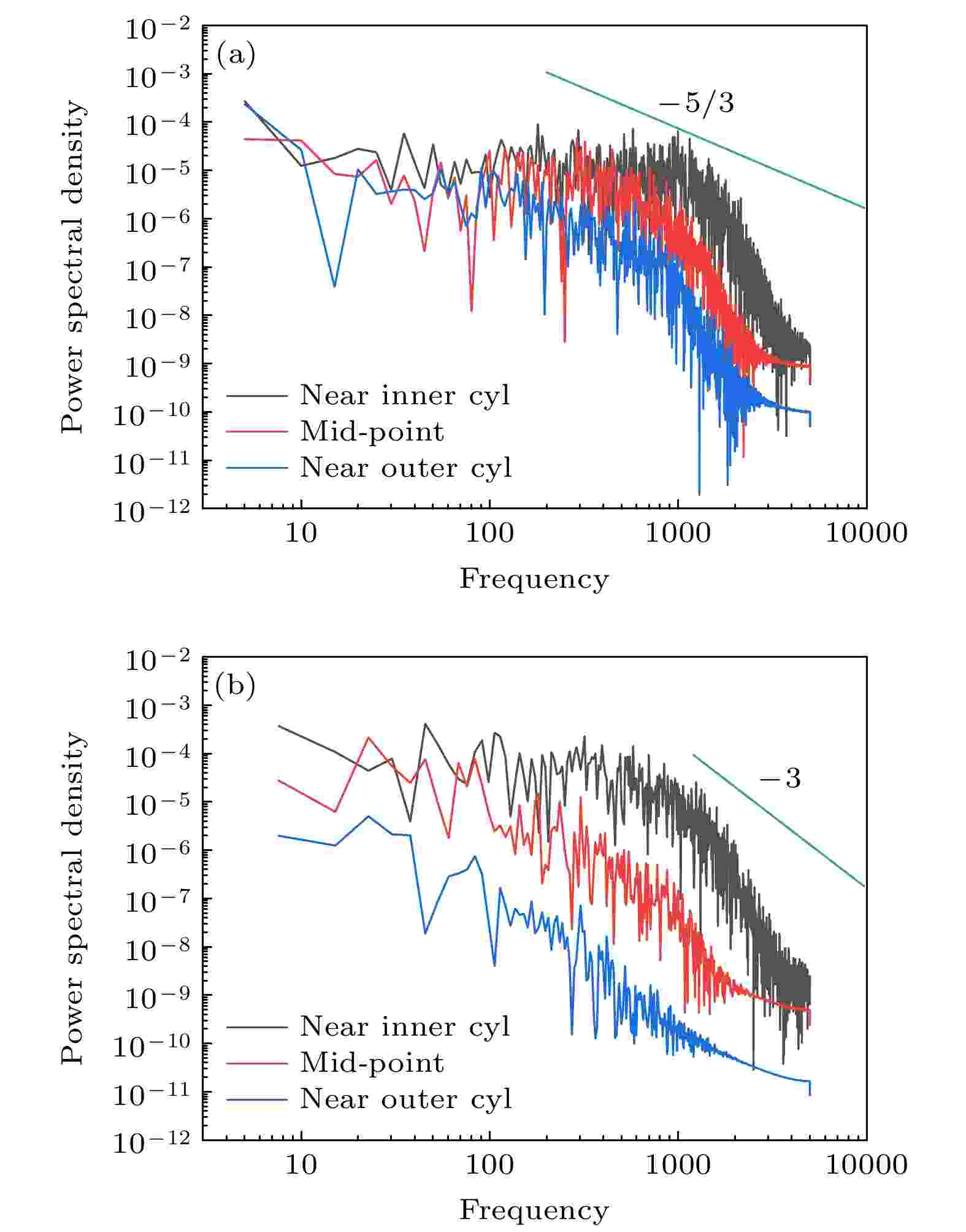图 12 Re = 3000工况下湍动能谱　(a) Ha = 0; (b) Ha = 30
Figure12. Power energy spectra for u_θ at Re = 3000: (a) Ha = 0; (b) Ha = 30.

由图12可知, 湍动能从大尺度涡传递到中尺度涡, 再从中尺度涡传递到小尺度涡, 最后由于黏性耗散和焦耳耗散转化为热能. 图12中标识了两条幂律线, 一条是大家广泛接受的无磁场作用下湍流能谱–5/3指数幂律, 另一条是磁场作用下湍流能谱–3指数幂律, 与文献[15]结果一致.
2 -->

3.2.加载轴向磁场

图13为Re = 3000工况下, 泰勒涡在轴向磁场作用下的演化过程图, Q = 2000. 随着磁场强度增加, 泰勒涡尺寸变小, 并逐渐向内圆筒靠近. Ha = 30时, 完整的泰勒涡结构消失. Ha = 50时, 流场中仅有少量涡结构. 与图5(a)进行对比分析, 发现横向磁场作用下流场结构呈现出各向异性, 磁场抑制垂直于场强方向的流动, 而对平行方向的流动基本没有作用. 轴向磁场作用下流场仍具有轴对称性, 泰勒涡与轴向磁场垂直, 因而沿圆周方向, 物理变量(统计平均值)分布一致. 且轴向磁场对泰勒涡的抑制作用更强.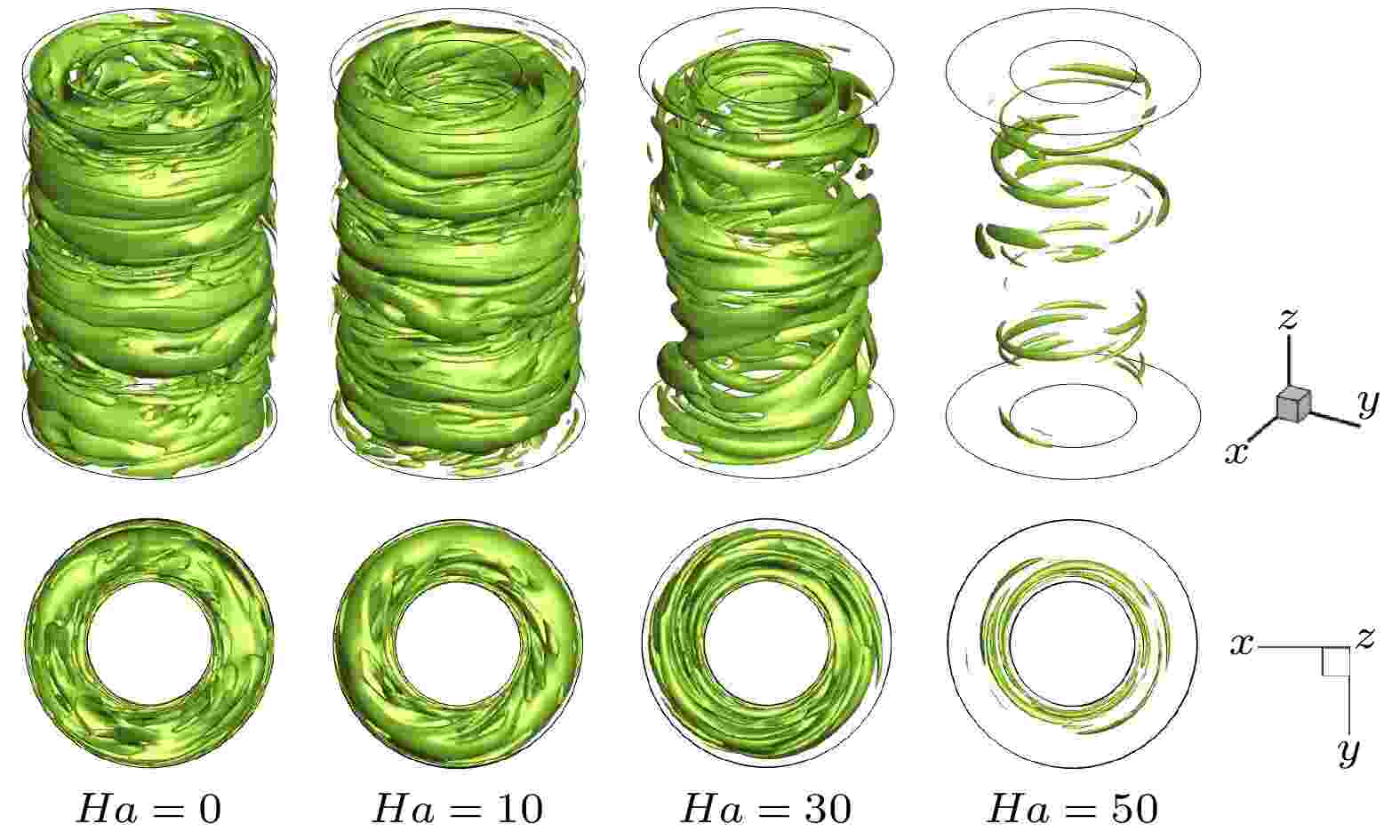
图 13 Re = 3000工况下泰勒涡在轴向磁场作用下的演化过程图(Q = 2000)
Figure13. Diagram of Taylor vortex evolution process under the action of axial magnetic field at Re = 3000, Q = 2000.

本文对横向磁场作用下湍流Taylor-Couette流动进行数值模拟, 对比分析了Re = 3000和Re = 5000工况下, 泰勒涡在磁场作用下的演化过程, 得到以下结论.
1)磁场对流场有显著的抑制作用, 随着磁场强度增加, 扭曲的泰勒涡被抑制, 最终破裂成小尺度涡结构, 小尺度涡结构沿磁场方向呈现扁平化分布.
2)在外圆筒和垂直于磁场方向的区域, 磁场的抑制效果更强, 漩涡尺寸减小, 湍流脉动减弱.
3)加载全局磁场时, 随着雷诺数增加, 磁场对流场的抑制效果减弱. 在流场不同区域, 流动呈现出不同的特点. 垂直于磁场方向的区域, 流体会呈现逆时针运动和顺时针运动. 沿磁场方向区域, 流体均为逆时针运动.
4)与轴向磁场相比, 横向磁场对流场的抑制效果较弱, 流场分布呈现出明显的各向异性.