摘要:高熵合金突破了传统合金的组成框架, 呈现出独特而优越的力学性能. 然而, 作为合金家族近年来出现的新成员, 高熵合金的潜在变形机制亟需进一步揭示. 本文采用分子动力学模拟方法研究了纳米孪晶Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄高熵合金在拉伸载荷下的力学性能, 从原子水平揭示了孪晶界对纳米孪晶Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄高熵合金变形行为的影响. 研究结果表明, 纳米孪晶Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄高熵合金的屈服强度随着孪晶界间距的减小而增大, 呈现Hall-Petch关系. 然而, 孪晶界间距存在一个临界值, 使得高熵合金的屈服强度在该值前后对孪晶界间距的敏感度发生了明显改变. 研究指出, 随着孪晶界间距的减小, 纳米孪晶Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄高熵合金的变形机制发生了从以位错滑移主导到以非晶化相变为主的转变. 本文的研究结果对于设计和制备高性能的高熵合金具有一定的参考价值和指导意义.
关键词: 高熵合金/
分子动力学模拟/
力学行为/
孪晶界

English Abstract

全文HTML

--> --> -->

高熵合金(high-entropy alloys, HEAs)作为一种新型金属材料, 因其优异的性能受到了广泛关注, 如高强度、高硬度、优异的耐磨性、抗氧化性及耐腐蚀性^[1,2], 被认为是许多具有挑战性工业应用的潜在候选材料. 2004年, Cantor等^[3]首次发现了一种新型的单相面心立方(face centered cubic, FCC) CrMnFeCoNi HEA, 引发了激烈的学术探讨浪潮. 随后, 寻求影响HEAs优异性能的内在“基因”成为国内外****关注的焦点. 界面是材料内部力学特性传递的桥梁, 界面结构对纳米多晶金属材料的塑性、强度及变形机制扮演着重要的角色. 孪晶界是一种低能的、稳定的晶界结构, 它可以有效阻碍位错的运动和滑移, 从而提升材料的力学性能^[4,5], 这使得纳米孪晶结构材料具有巨大的发展潜力和广阔的应用前景. 目前, 人们已经做了大量的工作来研究孪晶界对金属材料变形机制和强化机理的影响, 但主要还是聚焦在对传统合金的研究^[6-9], 孪晶界对HEAs力学性能和变形机制的影响仍有待进一步研究. 近年来, Hsieh等^[10]研究了CrMnFeCoNi HEA在室温下高应变速率压缩下的塑性变形和相变行为, 发现塑性变形通过扩展层错和变形孪晶实现, 并诱导了密排六方(hexagonal close packed, HCP)结构相变. Tian等^[11]从原子水平揭示了纳米孪晶FeNiCrCoCu HEA的纳米压痕行为, 其塑性变形主要受第一孪晶层约束的位错滑移、孪晶界的迁移、孪晶界处位错形核和层错四面体的形成控制. Yan等^[12]研究了纳米孪晶CrCoFeNi HEA的力学性能, 研究指出HEA的强度首先随着孪晶界间距的减小而增加, 当到达一临界值时, HEA的强度随着孪晶界间距的减小而减小, 呈现反Hall-Petch关系. 就当前对孪晶结构的HEAs力学性能的研究现状而言, 虽然取得了初步成果, 证明了孪晶界可以有效提升HEAs的力学性能, 但是孪晶界在变形过程中扮演的角色仍不清晰, 为了设计高塑性高强度HEAs, 孪晶界对HEAs变形机制的影响规律仍需进一步揭示.
2014年, Gludovatz等^[13]惊奇地发现CrMnFeCoNi HEA在零下200 ℃展现了比常温更优越的塑性, 其优异的性能归因于变形过程中形成的机械纳米孪晶, 这一奇特现象震惊了学术界, 而CrMnFeCoNi HEA也引起了国内外****的关注. 在实验中, 研究人员发现具有FCC 结构的CrMnFeCoNi HEA中存在大量孪晶^[14,15], 孪晶界对该HEA体系力学性能的提升过程中扮演着重要的角色. 基于以上考虑, 本文以纳米孪晶FCC Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA (nt-Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA, nt-HEA)作为研究对象, 采用分子动力学模拟方法系统地研究了孪晶界间距λ对nt-HEA力学性能和变形行为的影响, 揭示了孪晶界间距对nt-HEA塑性变形模式的影响规律. 本文的研究结果可为设计高性能的HEAs提供一定的理论依据和先期指导.

本文采用分子动力学模拟方法对nt-HEA在拉伸过程中的微观机制演化规律进行了模拟. 采用Atomsk建模软件^[16]构建了nt-HEA模型, 此软件作为一种成熟的建模软件已广泛应用于各种晶体结构的建模研究中^[12,17]. nt-HEA模型如图1(a)所示, nt-HEA中的Cr, Mn, Fe, Co, Ni原子分数分别为26%, 20%, 20%, 20%, 14%, 并且随机分布在FCC晶格中. 为了研究孪晶界间距对nt-HEA力学性能的影响, 在所有nt-HEA模型中嵌入了等间距的孪晶界, 并设计了不同孪晶界间距(λ = 0.62, 1.24, 2.48, 3.72, 4.96, 6.20 nm)的nt-HEA模型, 如图1(b)所示. 值得注意的是, λ = 0.62 nm是由3个原子层组成的理论上最小的孪晶界间距^[12]. 每个模型在X, Y, Z方向的几何尺寸大约为13.0 nm × 2.7 nm × 25.0 nm, 包含约10万个原子, 模型的X, Y, Z轴分别对应晶体的[$ 11\bar{2} $], [$ \bar{1}10 $]和[$ 111 $]晶向. 在对nt-HEA进行拉伸变形前, 采用等温-等压(NPT)系综在300 K下松弛40 ps, 时间步长为1 fs, 使用Nose-Hoover恒温器^[18]控制温度. 在模拟拉伸加载过程中, Y和Z方向施加周期边界条件, X方向施加自由边界条件, 沿Z方向以5 × 10⁸ s^–1的恒定应变率在300 K温度下进行单轴拉伸加载.
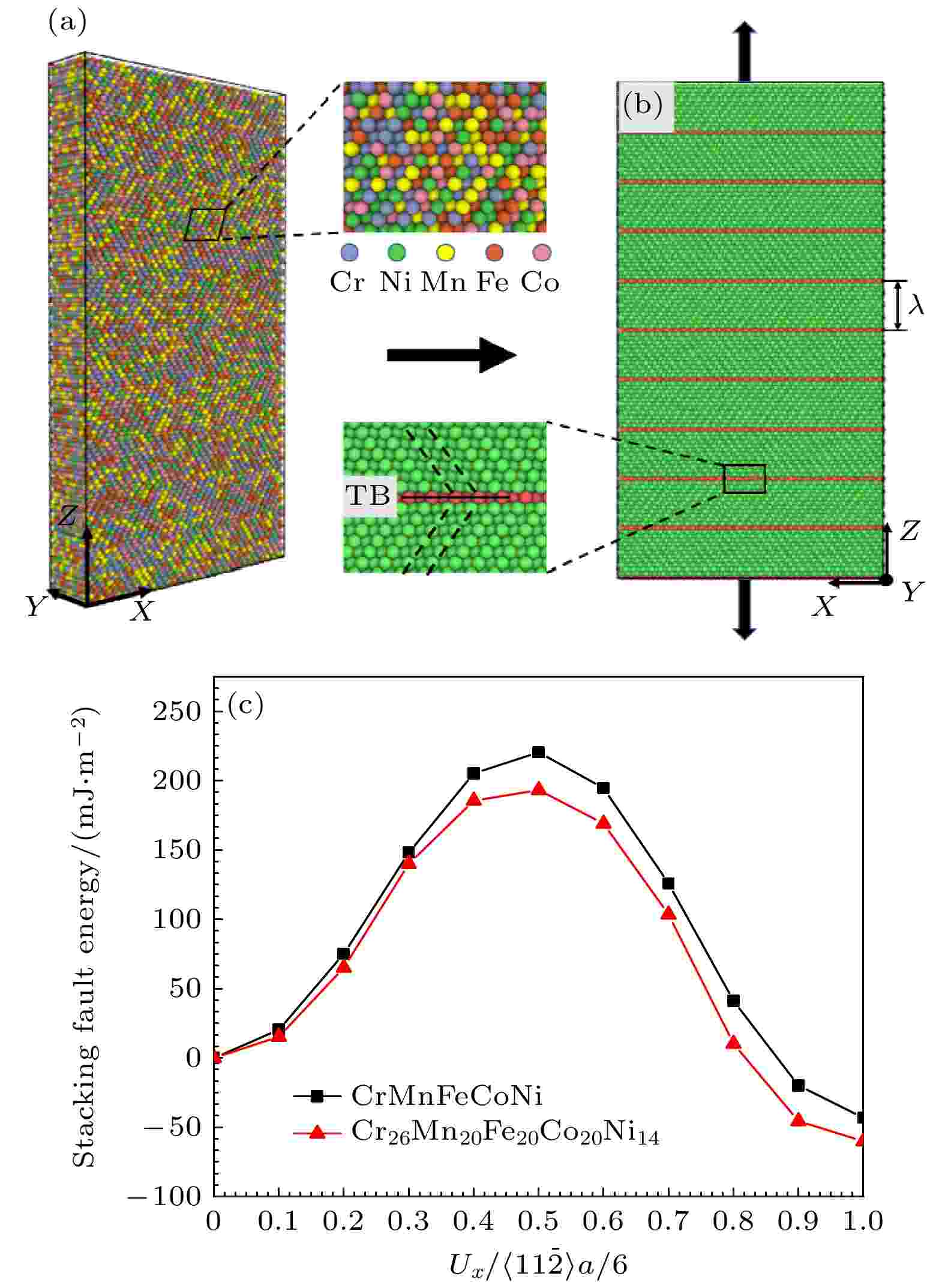图 1 (a) nt-HEA的原子分布图; (b) nt-HEA的模型结构图, 其中绿色区域代表FCC结构, 红色区域代表孪晶界(TB); (c) CrMnFeCoNi HEA与Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA的SFE曲线图
Figure1. (a) Atomic distribution of the nt-HEA; (b) model structure of the nt-HEA, in which the green regions represent the FCC structure and the red regions represent the twin boundary (TB); (c) SFE curves of CrMnFeCoNi HEA and Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA.

势函数的正确选择是保证分子动力学模拟结果准确性和可靠性的关键. 本文采用Choi等^[19]提出的第二近邻修正嵌入式原子方法势模拟原子间的相互作用, 该势函数已成功地应用于CrMnFeCoNi HEA力学性能的模拟研究, 并获得了可靠的研究结果^[20,21]. 本文通过LAMMPS ^[22]软件进行模拟, 采用可视化工具OVITO^[23]分析变形过程中微观结构的演化规律, 利用公共近邻分析法(common neighbor analysis, CNA)^[24]分析晶体的变形行为, 采用位错提取法(dislocation extraction algorithm, DXA)^[25]识别位错的类型. 在使用CNA分析晶体结构时, 用绿色代表FCC结构原子, 红色代表HCP结构原子, 白色代表无序结构原子.
为了计算层错、马氏体和退孪晶形成的能量路径, 构建了一个方向为X = [$ 11\bar{2} $], Y = [$ \bar{1}10 $], Z = [$ 111 $]的矩形单元, 并在X和Y方向施加周期边界条件, 在Z方向施加自由表面边界条件. 然后将单元的下半部分固定, 上半部分沿着X方向在{111}滑移面上刚性剪切. 每次剪切后通过共轭梯度算法进行能量最小化, 计算出当前结构对应的能量, 然后利用剪切前后的能量差来计算滑移面上单位面积的能量.
Gao等^[14]研究了元素浓度对CrMnFeCoNi体系HEA变形机制的影响, 研究结果表明堆垛层错能(stacking fault energy, SFE)决定了CrMnFeCoNi体系HEA中形变孪晶或位错滑移的发生. 因此, 本文首先计算了等原子分数CrMnFeCoNi HEA与非等原子分数Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA的SFE, 如图1(c)所示. 由于层错区附近元素的随机排列, HEA的SFE值会发生波动, 而不是一个单一的值. 因此在模拟中, 通过随机填充元素进行了6次计算获得了CoNiCrFeMn HEA和Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA 的SFE平均值及误差分别为–(41 ± 5) mJ·m^–2和–(60 ± 3) mJ·m^–2. 相比等原子分数的CrMnFeCoNi HEA, 非等原子分数Cr₂₆Mn₂₀Fe₂₀Co₂₀Ni₁₄ HEA具有更低的SFE, 说明在其在变形过程中位错更容易形核与滑移. 并且计算获得的CrMnFeCoNi HEA层错能与Xiao等^[26](相同势函数)的计算结果(–46 mJ·m^–2)和第一性原理计算^[27]得到的结果(–50 mJ·m^–2)相符, 这也证明了本文所选用的势函数是准确且可靠的.

2

-->

3.1.孪晶界间距对nt-HEA力学性能的影响

为了研究孪晶界间距对nt-HEA力学行为的影响, 图2(a)给出了不同孪晶界间距nt-HEA的应力-应变曲线. 从图2(a)可看出, nt-HEA的变形过程分为两个阶段: 弹性阶段和塑性阶段. 在弹性阶段, 随着应变量的不断增大, 所有模型的应力以相同的斜率增加, 说明nt-HEA的杨氏模量几乎不受孪晶界间距的影响. 除此之外, 曲线发生了明显的波动, 这是由于自由表面处一部分原子键的悬空, 温度作用破环了这些原子的平衡, 导致原子发生剧烈热运动引起的^[28]. 当nt-HEA的应力达到峰值后, 随着应变的继续增加, 所有模型的应力都发生了陡然下跌, 这意味着它们进入了塑性变形. 图2(b)给出了nt-HEA的屈服强度、屈服应变随孪晶界间距的变化关系, 结果表明屈服强度与孪晶界间距呈Hall-Petch关系, 并且孪晶界间距对nt-HEA的强化存在一个临界值(2.48 nm). 研究指出, nt-HEA的屈服强度在该临界值前后对孪晶界间距的敏感度发生了变化, 如图2(b)所示. 当孪晶界间距从6.20 nm减小到2.48 nm (即λ > 2.48 nm), 屈服强度从9.85 GPa增加到10.18 GPa, 增加了约3.3%. 而当孪晶界间距从2.48 nm减小到0.62 nm时(即λ ≤ 2.48 nm), 屈服强度从10.18 GPa增加到11.56 GPa, 增加了约13.5%. 这说明, 当孪晶界间距减小到这一临界值之后, 孪晶界对nt-HEA屈服强度的影响会显著增强.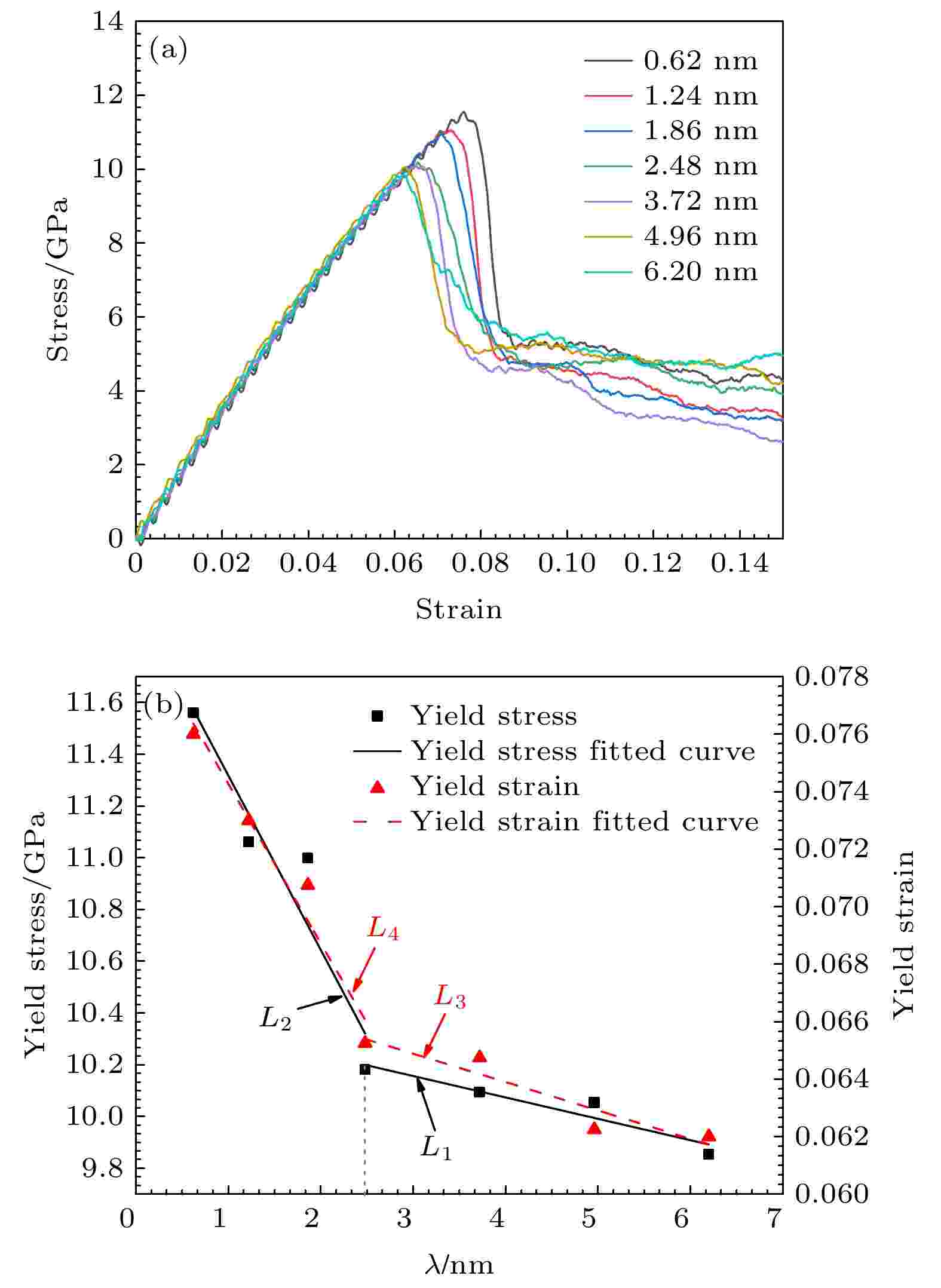
图 2 (a)不同孪晶界间距nt-HEA的应力-应变曲线; (b) nt-HEA的屈服强度、屈服应变随孪晶界间距的变化曲线
Figure2. (a) Stress-Strain curves of the nt-HEA with different twin boundary spacing; (b) curves of the yield stress and yield strain of the nt-HEA with the twin boundary spacing.

众所周知, 纳米孪晶金属的屈服行为取决于位错源数与孪晶界对位错产生的排斥力之间的竞争关系. 在孪晶界间距较大时(即λ > 2.48 nm), 位错源对屈服强度的影响起主导作用, 此时孪晶界间距对材料的屈服强度强化趋势如曲线L₁. 随着孪晶界间距的减小, 位错源对屈服强度的影响越来越弱, 而排斥力的影响会增加^[29], 当孪晶界间距低于一临界值时(即λ ≤ 2.48 nm), 孪晶界引起的排斥力占据了主导因素, 屈服强度强化趋势如曲线L₂. 需要注意的是, 本文的研究结果未发现反Hall-Petch关系, 这与nt-HEA具有负的SFE是密切相关的^[17]. 与屈服强度相似, 屈服应变也随着孪晶界间距的减小而持续增加, 如曲线L₃和L₄所示, 这与Sun等的研究结果^[30]一致. 研究结果指出, 孪晶界间距的减小不但提高了nt-HEA的屈服强度, 也增强了nt-HEA的屈服应变.
从图2(a)可以发现, 在塑性变形过程中, nt-HEA流动应力随着应变的增加而减小, 但是不同孪晶界间距的nt-HEA减小的速度有明显的差异. 为了定量描述孪晶界间距对nt-HEA塑性变形行为的影响, 本文计算了不同孪晶界间距的nt-HEA在10%—15%应变间的平均流动应力, 其变化分布如图3所示. 从图3可以观察到, λ = 0.62 nm和λ ≥ 4.96 nm的nt-HEA拥有更高的平均流动应力, 而0.62 nm < λ < 4.96 nm的nt-HEA的平均流动应力相对较低, 这说明具有不同孪晶间距的nt-HEA存在不同的塑性变形行为, 对于造成这种差异的原因随后将进行讨论.
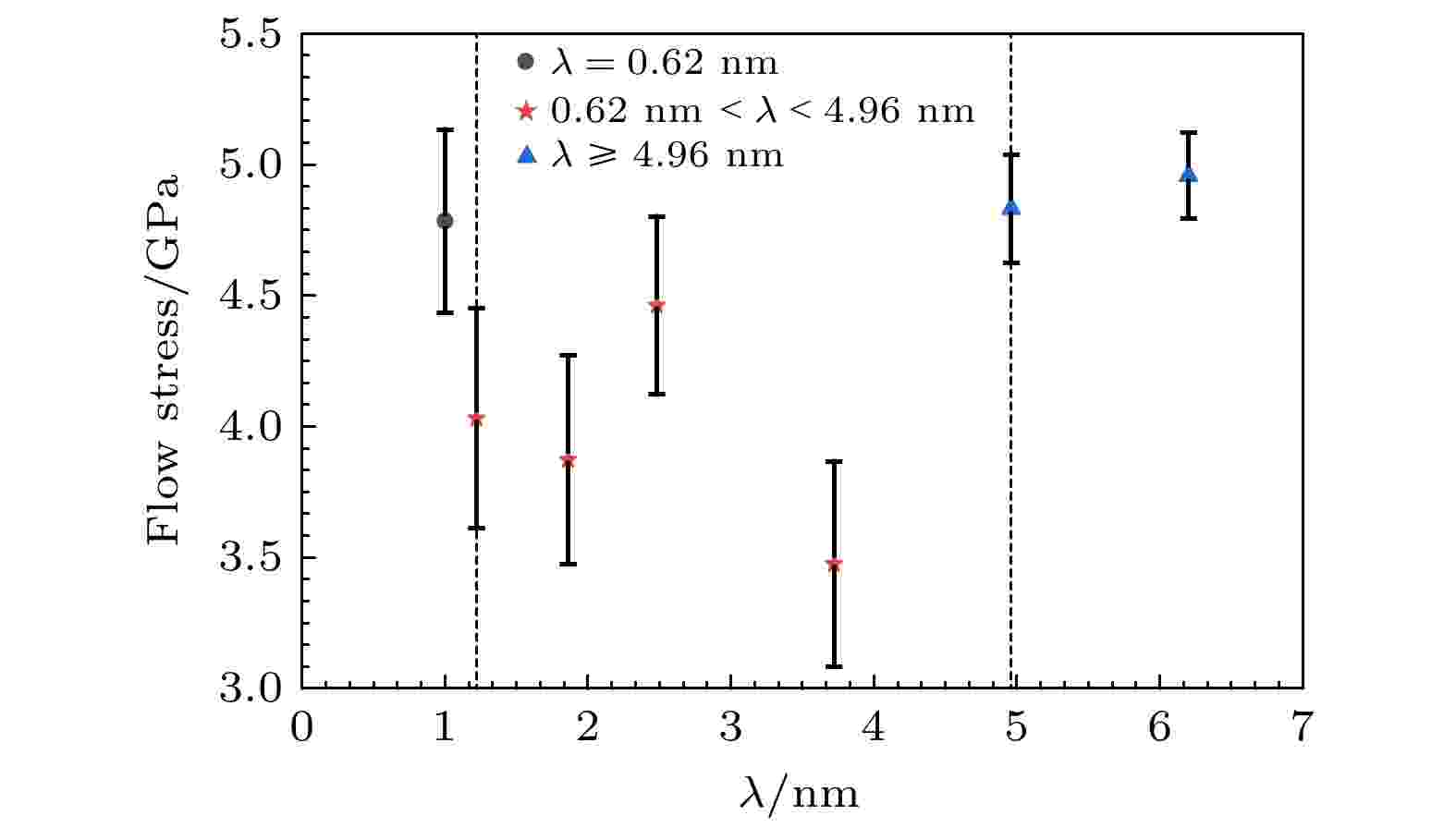图 3 不同孪晶界间距的nt-HEA在10%—15%应变间的平均流动应力分布
Figure3. Average flow stress distribution of the nt-HEA with different twin boundary spacing at 10%–15% strain range.

2 -->

3.2.孪晶界间距对nt-HEA塑性变形行为的影响

为了研究孪晶界间距对nt-HEA塑性变形行为的影响, 根据平均流动应力的分布差异, 本文选取了孪晶界间距为4.96, 3.72, 0.62 nm的代表性模型进行分析. 图4给出了孪晶界间距为4.96 nm的nt-HEA在不同应变下的结构快照图. 从图4(a)可以发现, 在拉伸载荷作用下, 在孪晶界和自由表面的三叉区形成1号位错, 当其滑移至孪晶界表面时被孪晶界所阻挡, 如图4(b)所示. 在1号位错与孪晶界的交叉点处诱发2号位错形核并发射, 此时, 在新的三叉区又激发新的位错成核并发射(如图4(b)中黑色线圈所示), 导致nt-HEA的应力陡然下降. 继续加载的过程中, 当应变为10%甚至15%时, 更多的滑移系统在孪晶界附近被激活, 由于孪晶界对位错运动的阻碍, 这种大量位错的增值在孪晶界处形成塞积导致复杂的位错反应, 形成更多的不可动位错, 导致了较高的流动应力, 如图3所示. 与此同时, 在位错与孪晶交叉点及不同位错交叉区域产生了白色无序原子, 即非晶化现象. 分子动力学模拟^[31]和实验^[32]已经证明, 在这些交叉区位错的积累通常会引起局部应力集中, 导致交叉区的晶格的严重扰动, 并导致晶体结构的最终崩塌, 非晶相形核. 在持续加载过程中, 位错的连续积累所引起的内应力的增加也可以通过在非晶区附近的更多晶体无序化来释放, 从而促进非晶相的进一步扩展, 即形变诱发非晶化^[33]. 当然, 大量的位错塞积也会导致孪晶界逐渐失去共格性, 演化为无序晶界, 从而在孪晶界附近出现非晶化现象.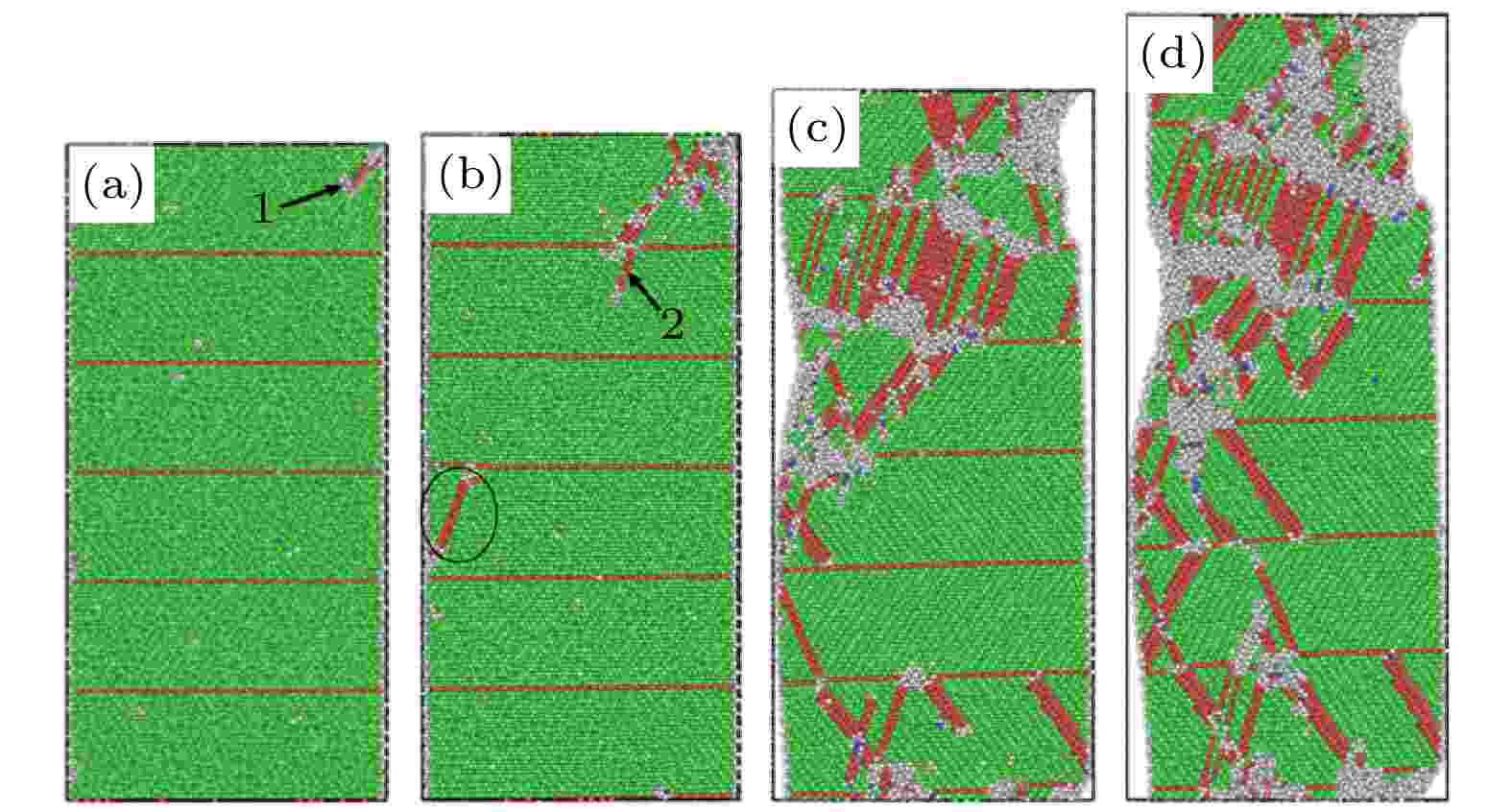
图 4 孪晶界间距为4.96 nm的nt-HEA在应变(a) 6.1%, (b) 6.3%, (c) 10%, (d) 15%下的结构快照图
Figure4. Structural snapshots of the nt-HEA with the twin boundary spacing of 4.96 nm at the strains of (a) 6.1%, (b) 6.3%, (c) 10%, and (d) 15%.

图5给出了孪晶界间距为3.72 nm的nt-HEA在不同拉伸应变下的结构快照图. 在应变达到6.2%时, 初始位错A从nt-HEA的自由表面和孪晶界的交叉点形核并发射, 如图5(a)所示. 位错滑移并受阻于孪晶界, 新的位错B成核并发射(见图5(b)). 随着应变的增加, 只有少量的滑移系被激活, 为了适应连续的塑性变形, 在模型的两端产生了更严重的非晶化. 应当注意, 随着孪晶界间距的减小, 孪晶界阻碍位错滑移的能力增强, 可以有效地阻碍位错的滑移, 因此在模型两端出现了颈缩现象, 如图5(c)所示. 应变增加到15%时颈缩区域进一步扩张, 非晶相的连续形核和相互作用也导致了非晶区的膨胀, 从而在孪晶区形成了大规模的非晶相(见图5(d)). 该nt-HEA严重的非晶化变形行为导致了其在塑性变形阶段具有较低的平均流动应力, 如图3所示. 这表明当孪晶界间距逐渐减小时, 孪晶界对位错形核和传播的阻碍能力会显著提高, 孪晶界对向它靠近的位错施加的排斥力在促使了nt-HEA屈服强度的提高的同时^[34], 也阻碍了塑性变形过程中位错的成核和传播, 从而导致以非晶化区域的扩张来实现nt-HEA的塑性变形.
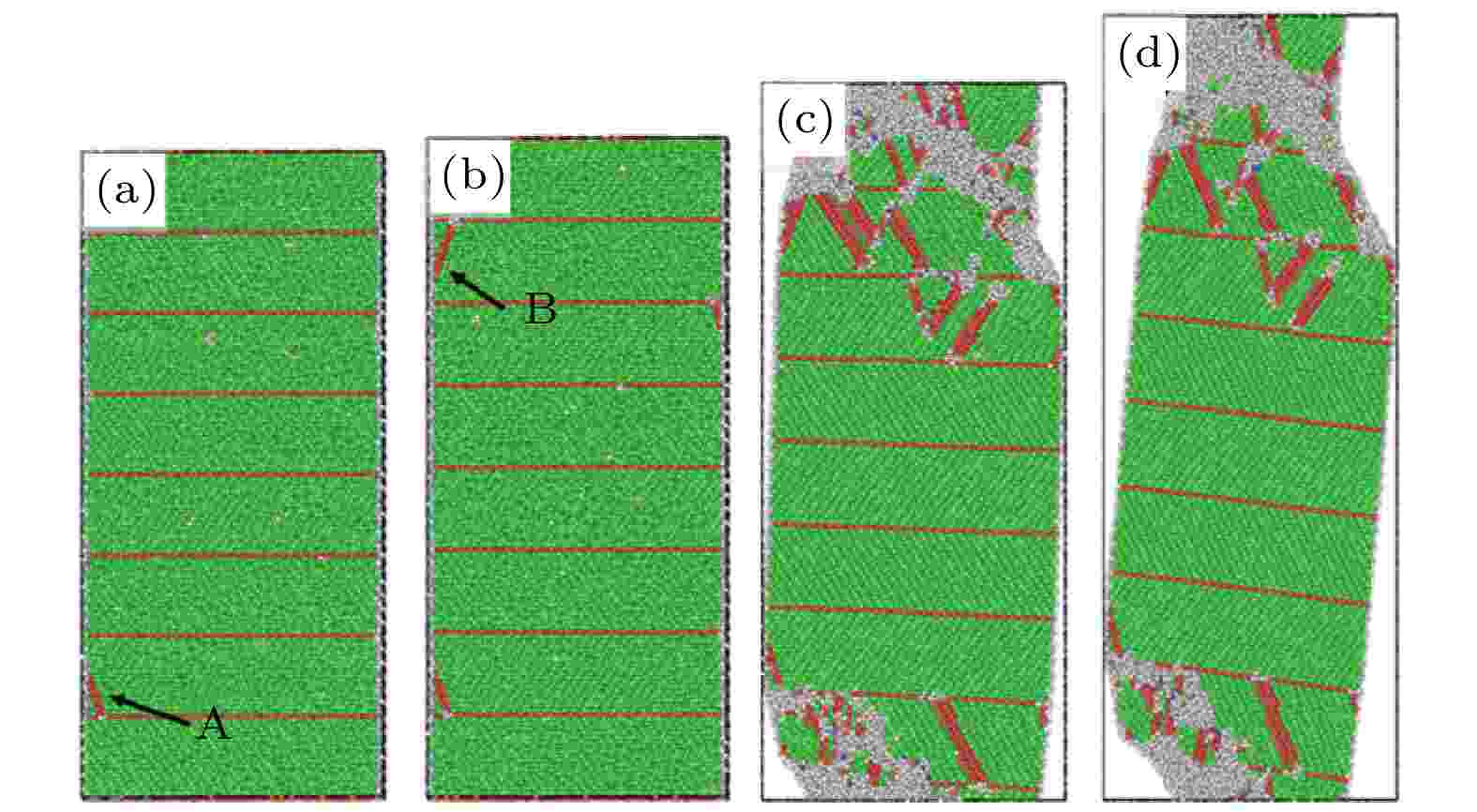图 5 孪晶界间距为3.72 nm 的nt-HEA在应变(a) 6.2%, (b) 6.4%, (c) 10%, (d) 15%下的结构快照图
Figure5. Structural snapshots of the nt-HEA with the twin boundary spacing of 3.72 nm at the strains of (a) 6.2%, (b) 6.4%, (c) 10%, and (d) 15%.

对于理论最小孪晶界间距(3个原子层组成)的nt-HEA, 它拥有最高屈服强度的同时也表现出高的流动应力, 如图2和图3所示, 这与其独特的变形机制相关. 为了阐明该模型的塑性变形行为, 图6给出了孪晶界间距为0.62 nm的nt-HEA在不同应变下的结构快照图. 从图6(a)可以发现, nt-HEA在塑性变形过程中, 并没有像前面两组模型中出现的由于不全位错引导的层错产生, 而是直接出现非晶化现象. 随着拉伸形变的增加, 非晶化区域逐渐扩张. 这表明由最小孪晶界间距构成的nt-HEA的塑性变形的启动是通过晶格畸变来实现的, 造成了非晶化现象的产生. 且晶格畸变优先从自由表面处成核, 导致孪晶界失去共格性. 这主要是因为当孪晶界间距减小到0.62 nm (3个原子层厚度)后, 孪晶界对位错形核以及运动的排斥力已经达到甚至超过晶格畸变形核所需要的力, 因此在塑性变形时nt-HEA只能通过具有高临界应力的晶格畸变产生, 因此该模型呈现了最高的屈服强度, 这与Hao等^[35]研究的具有3个原子层孪晶界间距纳米线的变形机制是相似的. 随着应变的继续增加, 这些晶格畸变区域不断地向周围扩展, 从而导致孪晶界被破坏, 如图6(b)所示. 研究表明, 该nt-HEA除了晶格畸变导致的非晶化外, 发现在非晶区域和孪晶界交叉处位错形核并平行于孪晶界传播, 导致FCC→HCP转变的马氏体(MT)相变的产生, 如图6(c)黑色线圈所示. 当应变从10%增加到15%时, 除了产生更多的MT相变外, 并出现了退孪晶(DT)变形, 如图6(d)和图6(e)黑色线圈区域所示. 根据以往的研究, MT相变和DT变形对材料强度的强化和软化会产生很大影响^[12,26], 因此, 有关MT相变及DT变形在nt-HEA中的演化过程需要进一步分析.
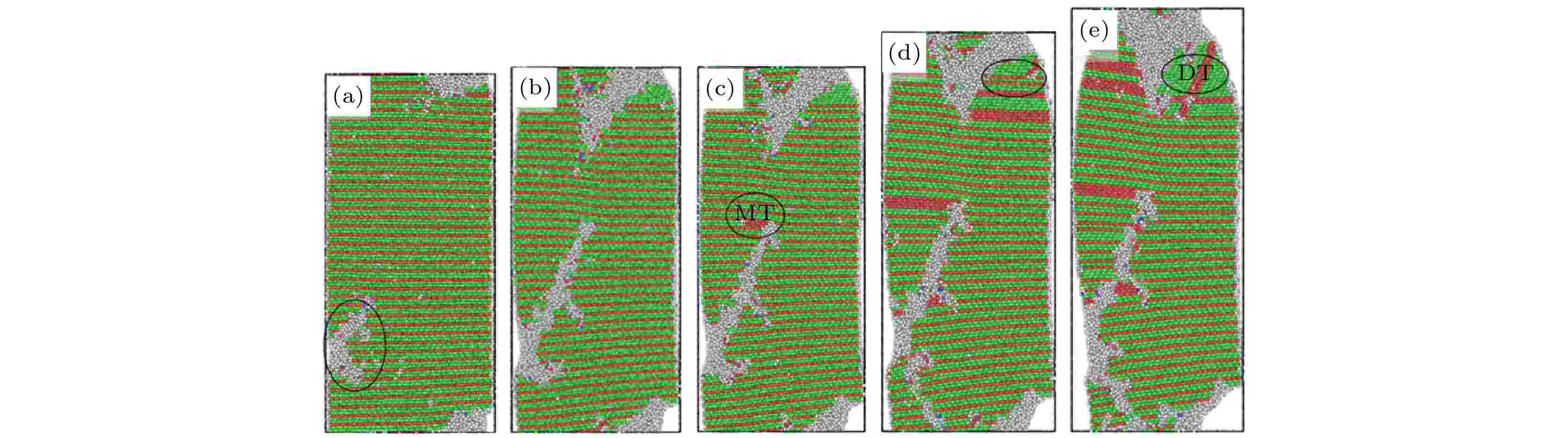图 6 孪晶界间距为0.62 nm的nt-HEA在应变(a) 8.0%, (b) 8.4%, (c) 8.5%, (d) 10%, (e) 15%下的结构快照图
Figure6. Structural snapshots of the nt-HEA with the twin boundary spacing of 0.62 nm at the strains of (a) 8.0%, (b) 8.4%, (c) 8.5%, (d) 10%, and (e) 15%.

2 -->

3.3.马氏体相变诱导nt-HEA强度强化

为了阐明λ = 0.62 nm的nt-HEA在塑性变形过程中的MT相变和DT变形的演化规律, 图7给出了nt-HEA在不同应变下的原子结构图. 为了更清楚地反映位错的运动行为, 在采用DXA对nt-HEA的变形行为进行分析时, 去除了HCP结构以外的原子, 绿色线代表肖克利不全位错, 箭头表示位错传播方向. 从图7(a)和图7(b)可以看出, 在孪晶内部的位错形核后, 逐步扩展为肖克利不全位错, 然后平行于孪晶界滑移(图7(b)黑色线圈所示), 从而导致了FCC→HCP转变的MT相变发生(见图7(a)). 图7(c)—(h)给出了DT变形经历的3个演变过程, 当肖克利不全位错在孪晶界处产生并沿孪晶界滑移(图7(d)黑色线圈所示)时, 会导致孪晶界的迁移, 形成外禀堆垛层错(epitaxy stacking fault, ESF), 如图7(c)所示. 随后, 新的肖克利不全位错产生并沿孪晶界继续滑移(图7(f)黑色线圈所示), 形成内禀堆垛层错(intrinsic stacking fault, ISF)(见图7(e)). 与此同时在孪晶界上部形成了位错并滑移至ISF界面处, 被ISF阻碍(见图7(f)), 这可能造成应力的微小上升. 随着应变的进一步增加, 为了释放存储的应力, 在ISF与非晶界面交界处产生新的位错并沿ISF方向传播(图7(h)黑色线圈所示), ISF消失最终形成了DT现象(见图7(g)).
图 7 孪晶界间距为0.62 nm的nt-HEA的MT相变和DT变形的分析快照图(左侧为CNA分析图, 右侧为DXA分析图), 其中, (a)和(b)的应变为8.6%; (c)和(d)的应变为8.4%; (e)和(f)的应变为12.2%; (g)和(h)的应变为13.5%
Figure7. Analysis snapshot of MT phase transition and DT deformation of the nt-HEA with the twin boundary spacing of 0.62 nm (CNA analysis diagram on the left and DXA analysis diagram on the right), in which the strains of (a) and (b) are 8.6%; (c) and (d) are 8.4%; (e) and (f) are 12.2%; (g) and (h) are 13.5%.

由于位错形核、层错形成、形变孪晶和FCC→HCP转变的MT相变及DT变形都是与材料中SFE有关^[36], 为了阐明最小孪晶界间距(0.62 nm)的nt-HEA的不同变形行为, 本文计算了位于孪晶界和孪晶内部不全位错滑移的能量路径, 如图8所示. 图8中γ_um表示发生MT相变需克服的能垒; γ_mt表示产生MT相变后体系具有的能量; γ_ut表示发生DT变形需先越过的能垒; γ_esf表示形成稳态ESF的能量; γ_us表示孪晶界发生再次迁移时的能垒; γ_isf 表示形成稳态ISF的能量; γ_uf 表示ISF消失时的能垒; γ_dt表示发生DT变形后体系具有的能量、相关结构及过程如图7所示. 从图8可以观察到, nt-HEA中的孪晶内部肖克利不全位错滑移形成MT相变的能垒γ_um约为200 mJ·m^–2, 低于Xiao和Deng^[17]关于nt-CoNiCrFeMn HEA的研究结果(γ_um约为242 mJ·m^–2), 这是由于Ni浓度减小会导致SFE降低^[14,17]. 然而, 对于孪晶界上不全位错滑移形成DT变形需先越过的能垒γ_ut约为229 mJ·m^–2, 明显高于MT相变的能垒γ_um, 即γ_ut/γ_um > 1. 因此, 最小孪晶界间距的nt-HEA更容易发生FCC→HCP转变的MT相变. 并且稳态时的γ_mt = –69 mJ·m^–2, γ_esf = –11 mJ·m^–2, γ_isf = –6 mJ·m^–2, 它们都负值, 而γ_dt = 61 mJ·m^–2为正, 表明具有负层错能的HCP相比FCC相更稳定^[26]. 因此, MT相变强化导致最小孪晶界间距的nt-HEA具有更高的流动应力, 如图3所示.
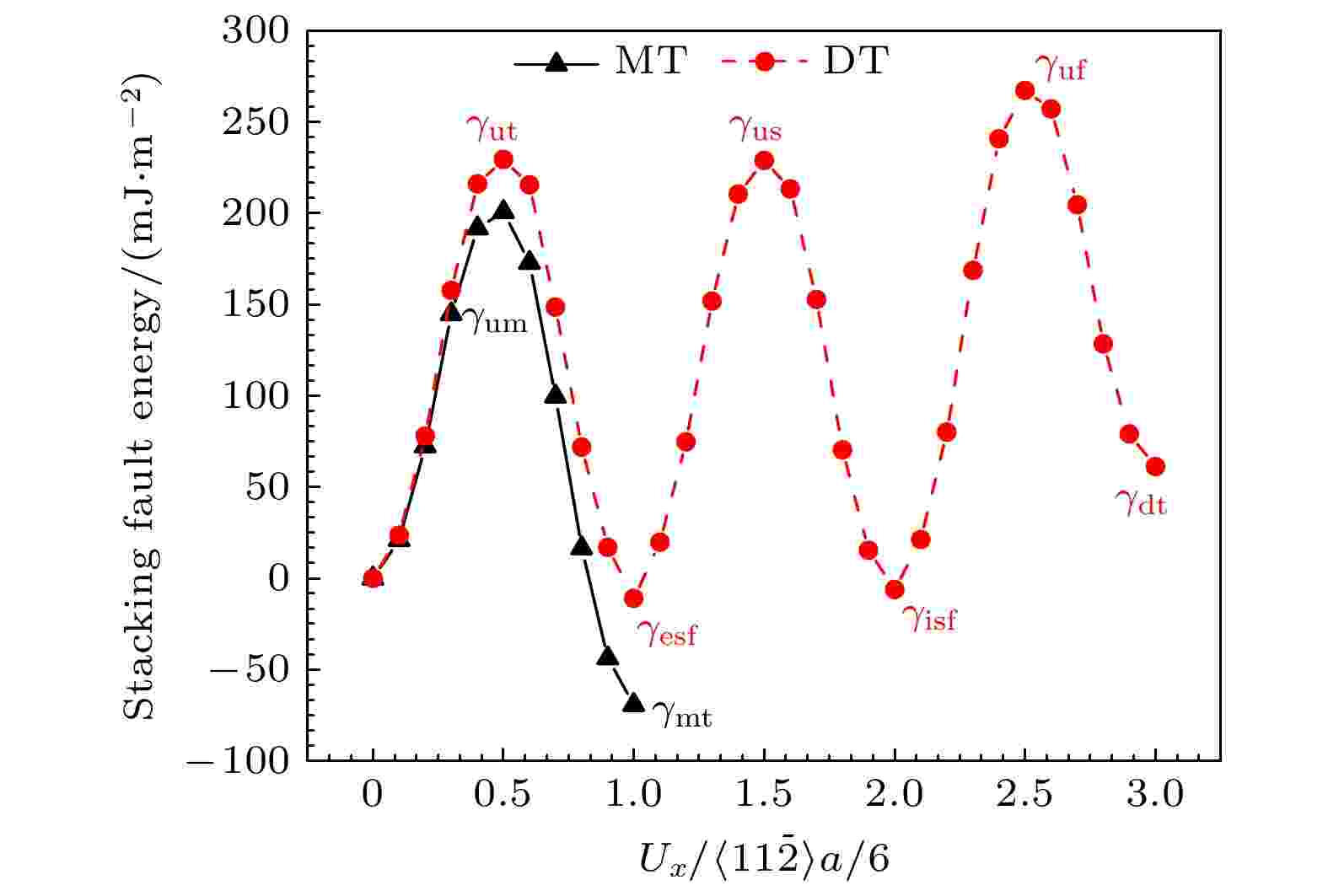图 8 孪晶界间距为0.62 nm的nt-HEA的MT相变和DT变形的能量路径图
Figure8. Energy pathways of MT phase transformation and DT deformation in the nt-HEA with the twin boundary spacing of 0.62 nm.

为了进一步定量描述孪晶界间距对nt-HEA力学性能的影响, 图9给出了nt-HEA在变形过程中的位错密度随应变的变化曲线. 位错密度ρ定义为位错线的总长度D_L与模拟单元的体积V之比, 即$ \rho ={D}_{\mathrm{L}}/V $. 从图9可以看出, 在初始载荷阶段, 随着应变的增加, 所有模型的位错密度均保持为零, 这对应于弹性阶段. 当应变增加到0.06时, λ = 6.20 nm的nt-HEA的位错密度开始增加, 随后其余模型的位错密度随着应变的增加也依次增加, 表明变形过程进入了塑性阶段. 此外, 可以发现, 孪晶界间距对塑性变形阶段位错密度有很大的影响. 对于λ ≥ 4.96 nm的nt-HEA在塑性变形过程中具有较高的位错密度, 特别是λ = 6.20 nm的nt-HEA更为突出, 这主要是由于孪晶界可以有效存储高密度位错, 位错与孪晶界在孪晶界上反应形成可动不全位错, 或不可动位错或位错锁, 造成位错塞积. 这种塑性变形阶段形成的高密度的位错可以增强nt-HEA力学性能, 产生较高的平均流动应力, 如图3所示. 通过对比图9和图3可以发现, 除了λ = 0.62 nm的nt-HEA外, 其余nt-HEA的平均流动应力与塑性阶段的位错密度成正比关系. 然而, 从图9可以看出, λ = 0.62 nm的nt-HEA在其塑性变形过程中位错密度最低, 这从位错塞积强化的角度来说与其拥有最高的平均流动应力不相符. 这种不寻常现象主要是因为λ = 0.62 nm的nt-HEA的塑性变形是以晶格畸变导致的非晶化现象为主, 同时伴随着MT相变和DT变形, 而不是以位错形核和滑移主导的变形模式.
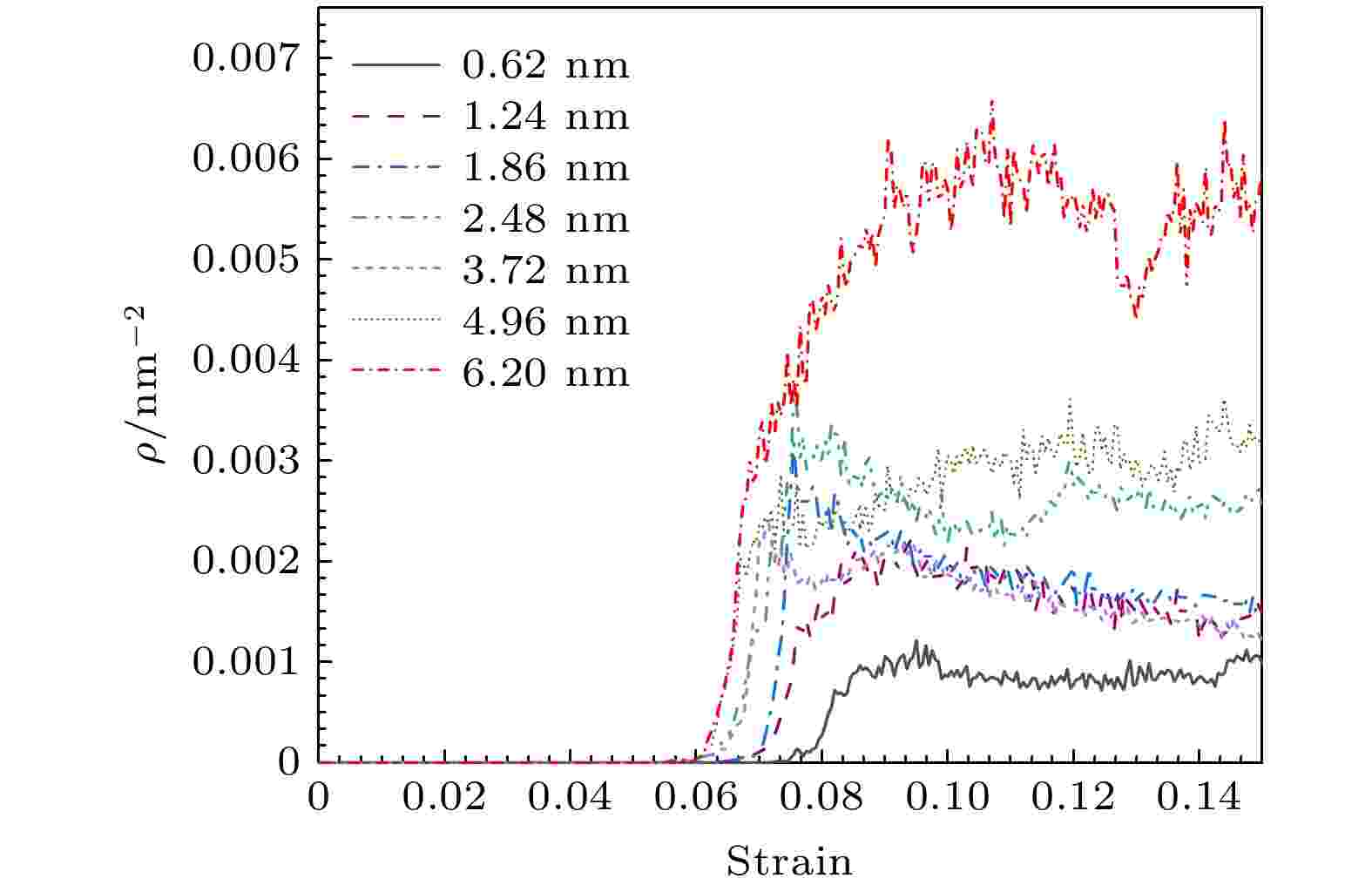图 9 不同孪晶界间距的nt-HEA在变形过程中的位错密度ρ演化曲线
Figure9. Evolution curves of dislocation density ρ during deformation of the nt-HEA with different twin boundary spacing.

本文采用分子动力学模拟方法研究了nt-HEA在拉伸载荷下的力学行为, 系统分析了孪晶界间距λ对nt-HEA力学性能和变形机制的影响. 研究发现, nt-HEA的屈服强度与孪晶界间距呈Hall-Petch关系, 并且孪晶界间距对nt-HEA的强化效果存在一个临界值(2.48 nm), 位错源数与孪晶界对位错的排斥力之间的竞争关系使得屈服强度在该临界值前后对孪晶界间距的敏感度发生了变化. 在塑性变形过程中, λ ≥ 4.96 nm的nt-HEA产生大量位错并在孪晶界处形成塞积, 位错塞积强化导致高的流动应力. 随着孪晶界间距的减小, nt-HEA变形过程中产生的位错数量越来越少, 非晶化现象在其塑性变形过程中的作用逐步显现. 当λ = 0.62 nm时, nt-HEA的塑性变形以晶格畸变导致的非晶化现象为主, 同时伴随着MT相变和DT变形, 而MT相变强化使得nt-HEA具有更高的流动应力. 也就是说, 随着孪晶界间距的减小, nt-HEA的变形机制发生了从以位错滑移主导到以非晶化相变为主的转变. 本文所得结果可为设计高性能的高熵合金提供先期的科学预测和有益借鉴.