摘要:为了调控石墨烯/碳化硅异质界面传热特性, 采用非平衡态分子动力学方法研究温度、尺寸、材料缺陷率对界面热导的影响, 通过声子态密度和声子参与率对界面热导变化的原因进行阐述分析. 研究表明: 两种界面作用力下界面热导均随温度升高而增大, 但共价键的异质界面热导要高于范德瓦耳斯作用力下的界面热导. 异质界面的界面热导随着碳化硅层数的增加而降低, 当层数从10层增加到20层时, 界面热导下降30.5%; 4层时异质结构界面热导最低, 分析认为中低频段更多的声子从局域进入离域模式. 空位缺陷的引入可以有效地提高界面热导, 随着碳化硅和石墨烯缺陷率的增加, 界面热导均先升高再降低. 300 K时当碳化硅和石墨烯缺陷率分别为20%和35%时界面热导达到最大值, 分析认为缺陷的引入会阻碍中频声子的热输运. 研究结果揭示可以通过尺寸效应和空位缺陷来进行异质界面的改性研究, 有利于第三代半导体微纳器件的设计和热管理.
关键词: 异质界面/
尺寸效应/
空位缺陷/
界面热导

English Abstract

全文HTML

--> --> -->

随着微电子器件不断向高密度、微型化、功能化方向发展, 器件内部的结构越来越复杂, 器件界面结构及非连续性结构越来越多. 功率器件在工作过程中经常会受到高温、高压、大电流、静电和强辐射等的冲击, 因此功率器件的可靠性已经成为影响集成电路整体性能的关键问题^[1,2]. 随着集成电路单元中的逻辑器件尺寸达到纳米量级, 功率器件中界面的特性将对器件性能起到关键作用. 异质界面作为功率器件的薄弱环节, 由于两种材料的物理特性的差异, 使得界面处产生一定热应力, 热应力的存在对界面结构及器件的正常工作造成极大的隐患. 因此, 对功率器件异质界面的热力学特性进行分析对于提高功率器件的互联可靠性具有实际价值.
石墨烯的优异性能使其在纳米元器件与复合材料等领域有着广阔的应用前景, 近年来对石墨烯和与之结构类似的二维纳米材料、半导体材料及聚合物等组成的异质界面进行大量的研究. 许多****在制备石墨烯时采用对碳化硅进行热分解, 通过Si原子从单晶碳化硅衬底升华从而形成大面积的石墨烯薄膜, 碳化硅衬底上的表面原子能够促进石墨烯的均匀生成^[3-7]. 不同石墨烯界面制备方法决定界面原子间的相互作用. 制备石墨烯时采用外延生长得到的界面由共价键结合. 而化学气相沉积法则是利用碳源气体与特定衬底发生化学反应, 合成石墨烯薄片, 其界面是由范德瓦耳斯力结合形成. 通过分子动力学的方法可以进一步研究界面的制备. Lai等^[8]用经典分子动力学模拟方法研究石墨烯在6H-SiC(0001)衬底上的外延生长, 在微尺度上对界面热输运的调控能够让器件更加可靠地进行散热. Yue等^[9]采用拉曼测温和焦耳加热相结合的方法, 研究外延石墨烯与4H-SiC之间的接触热阻. 石墨烯和碳化硅之间的温差越大, 界面热膨胀失配越大, 从而导致界面分离分层发生和高热阻的产生, 分析认为局部热膨胀失配引起的界面结构变化引起声子散射效应显著增强. Wang等^[5,6]研究3C-SiC, 4H-SiC和6H-SiC与石墨烯界面不同温度下的界面热阻, 发现6H-SiC与4H-SiC界面热阻的变化趋势接近, 而3C-SiC的界面热阻先增大, 在400 K温度左右达到最大值后开始减小; 此外还采用非平衡分子动力学方法研究Si/3C-SiC/Graphene复合薄膜的界面热阻, 研究发现温度为100—700 K时, Si/3C-SiC和3C-SiC/Graphene界面热阻随温度升高而增大; 与Si相比, 3C-SiC虽然与石墨烯的晶格失配较少, 但晶格失配的缺陷要多. Guo等^[10]用非平衡分子动力学方法研究SiC衬底对外延石墨烯纳米带导热性的影响, 发现石墨烯热导率在范德瓦耳斯作用力下比共价键键合的高, 分析认为共价键破坏石墨烯纳米带的固有导热性, 同时发现边缘缺陷会显著降低. Li和Yue ^[11]采用非平衡分子动力学模拟研究温度、密度以及导热系数与尺寸的关系, 结果表明, 导热系数随着温度的升高而增大直到稳定, 分析认为随温度变化声子平均自由程在纳米薄膜的热输运过程中存在尺寸效应, 特征长度从10 nm增加到50 nm时其导热系数增加约15%, 极小声子平均自由程是由非晶态固体的局域振荡决定, 而不是由整体几何参数决定. 目前有许多关于石墨烯材料热输运相关的研究^[12-17], 相关缺陷的文献也有报道. Nguyen等^[18]研究长宽比、边界条件和缺失原子缺陷对包括石墨烯、氮化硼和碳化硅在内的六方-平面纳米薄片模式行为的影响. 石墨烯的晶格缺陷主要发生在生产过程中, 而一个不可避免的额外无序来源是衬底和环境的相互作用^[19,20]. Lin等^[21]通过对四种表面缺陷(点缺陷、单空穴缺陷、双空穴缺陷、多空穴缺陷)进行研究, 探讨激光产生的石墨烯与4H-SiC之间的界面输运特性. Yang等^[22]采用非平衡态分子动力学方法研究扶手形石墨烯纳米带空位缺陷对热导率的影响, 发现当空位缺陷位置从冷浴向热浴移动过程中热导率先下降后上升, 原因在于结构中声子平均自由程和声子移动速度随着空位缺陷位置的改变发生明显变化.
通过研究发现: 目前对于石墨烯/碳化硅界面的热输运研究还不够充分, 大多数研究仅仅研究单个材料的性能, 而对异质界面特性的研究相对较少. 随着碳化硅制备石墨烯方法的研究, 使得异质界面结构越来越容易得到, 因此有望在未来功率器件中大量使用异质界面结构. 在实际应用中, 功率器件中大多数热量直接通过衬底散失, 这意味着界面间的热输运性能愈加重要. 因此, 本文旨在探讨分析石墨烯/碳化硅异质界面在不同尺寸和缺陷下热学特性.

2

-->

2.1.模型构建

利用商用分子模拟软件Material Studio (MS)建立不同长度和厚度的三明治石墨烯/碳化硅异质界面模型, 其中碳化硅晶格和石墨烯晶格均为ABAB形式堆积的双层结构. 单个石墨烯纳米带的原始结构为11 × 7 × 1个单元; 碳化硅的原始结构为1 × 5 × 3个单元. 模型建立过程中定义石墨烯与碳化硅的晶格匹配程度$S = ( {l_{{\rm{GE}}}} - {l_{{\rm{SiC}}}})/{l_{{\rm{SiC}}}}$, 经过计算异质结构在石墨烯X方向和Y方向晶格的匹配程度S分别为1.53%和1.05%, 界面尺寸分别是2.70 nm与2.98 nm. 建立最小界面结构后, 对其进行Z方向的扩胞, 可以得到不同尺寸的石墨烯/碳化硅异质结构模型. 在界面模型的构建中, 界面作用力为共价键时距离设为2.60 ?, 而范德瓦耳斯力作用下的距离设为3.85 ?. 两者的平衡距离是通过前期一些模拟测试验证得到.
在模型构建过程中石墨烯纳米带位于多层碳化硅的中间, 模型结构为三明治结构. 本文研究不同尺寸下异质结构石墨烯/碳化硅界面热导的变化. 模型构建过程中分别建立2—8层单层石墨烯, 通过在Z方向上施加传热进行特性分析; 接着固定石墨烯层数为3层, 建立不同层数(5—25层)碳化硅, 研究异质结构的界面热导变化; 最后通过在石墨烯模型中间位置添加缺陷, 研究温度(300—800 K)和缺陷率(0%—40%)对界面热导的影响. 通过声子态密度(phonon density of states, PDOS)和声子参与率(phonon participation ratio, PPR)对界面热导的变化进行阐述分析. 本文所构建的3层石墨烯和10层碳化硅异质结构界面模型如图1所示.
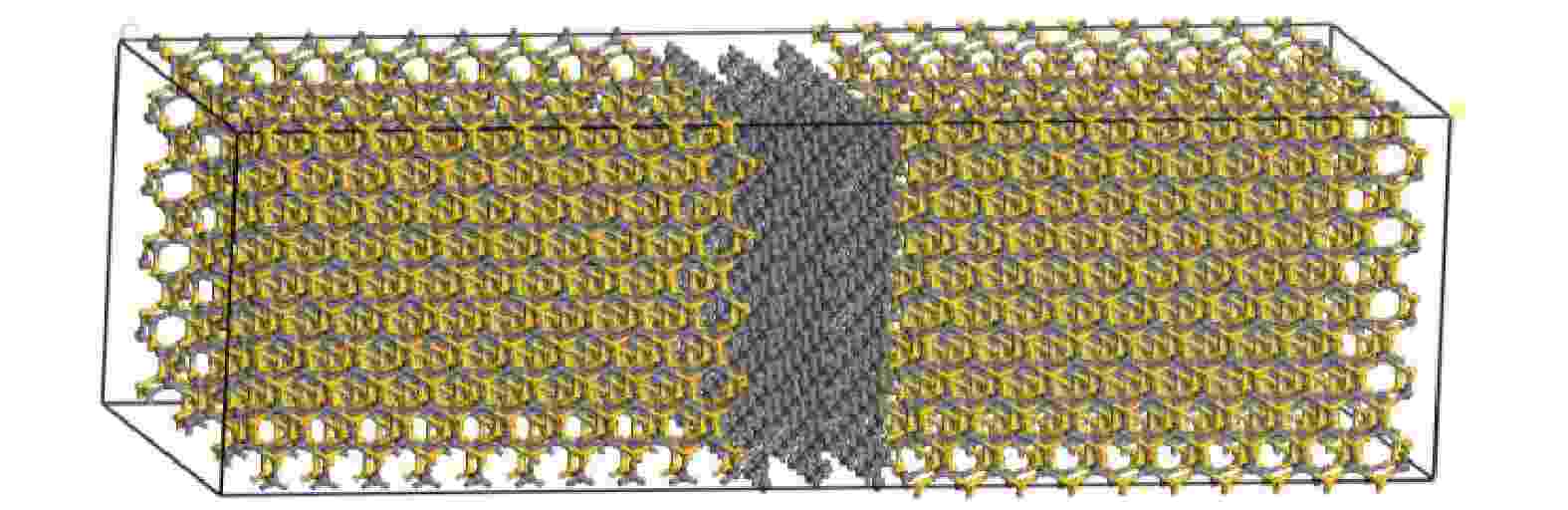图 1 3层石墨烯与10层碳化硅构筑的异质界面模型
Figure1. Heterostructure interface model constructed with 3-layer graphene and 10-layer SiC.

2 -->

2.2.模拟过程

分子动力学研究是在大规模原子/分子并行模拟器(large-scale atomic/molecular massively parallel simulator, LAMMPS)上进行的, 其源代码可以根据用户的需要进行修改. 本文石墨烯原子之间采用AIREBO^[23]势函数, 碳化硅与石墨烯之间以及碳化硅原子采用Tersoff^[24]势函数进行描述. 文献[25, 26]分别对LAMMPS中的存储与后处理和时间积分算法提出优化方法. 本文模拟的3个方向均采用周期性模型, 所以不存在声子-边界散射效应. 在热传导方向的两端固定原子, 设置热源和冷源, 时间步长设置为0.25 fs. 模拟之前首先进行静力学平衡, 采用共轭梯度法对模型进行能量最小化; 接着系统在正则系综下并通过设置好的平衡温度进行动力学优化; 随后切换系统为微正则系综, 采用Langevin热浴进行300万步的弛豫. Langevin热浴对每个粒子引入耗散力和与之相对的随机力, 这两项相互平衡以实现恒温的模拟. Li等^[27]研究发现在非平衡态分子动力学模拟中, Langevin恒温方法比Nosé-Hoover恒温方法更好地控制局部温度. 通过Langevin热浴, 每个粒子与局域的热浴耦合, 避免粒子被限制在一个局域模式里. 弛豫完成后继续在Langevin热浴下运行300万步以收集能量与温度梯度并计算界面热导. 在热传导方向上将模型分为多段来统计温度, 模拟每1000步记录一次原子温度, 采用1000步中每10步取一次值(即100个值)计算平均温度作为1000步时的温度值. 界面热导在同一次模拟中多次测量计算并取平均值. 通过改变模拟中随机数进行多次计算, 以保证模拟结果的准确性. 得到所有温度值后用线性拟合法得到温度梯度, 由下式可以计算热流密度:

$J = \frac{{{\rm{d}}E}}{{A{\rm{d}}T}}, $

其中J代表热流密度, A代表异质界面的面积, dT和dE分别代表体系中原子交换能量的时间和所有原子交换的总能量. 界面热导可由下式计算:

$G =\frac{{J\left( t \right)}}{{\Delta t}}, $

其中G代表界面热导, $\Delta t$为界面温度差. 原子的速度自相关函数(velocity autocorrelation function, VACF)可由下式计算, PDOS通过对VACF进行傅里叶变换计算:

${\rm{VACF}}(t) = \frac{1}{N}\sum\limits_{i = 1}^N {\left\langle {{v_i}(0){v_i}(t)} \right\rangle }, $

$ {\rm{PDOS}}(w)={\int\nolimits _{-\infty }^{\infty }{{\rm{e}}}^{{\rm{i}}wt}{\rm{VACF}}(t){\rm{d}}t}, $

其中${v_i}\left( t \right)$代表粒子i在时间t的速度, N是系统的原子数, w为频率. 由于VACF是归一化和无量纲化, 因此PDOS的单位是THz^–1. 在界面模型中, 撞击界面的所有声子都被弹性散射一次, 然后到相邻的物质中, 概率与各自物质中的声子态密度成正比. PDOS中的重叠可以用来估计以弹性散射方式通过界面的声子传输. 在两个PDOS图中, 重叠面积因子S被定义为

$S = 2\int_0^\infty {{\rm{min}}\left\{ {{P_{{\rm{SiC}}}}\left( w \right),{P_{{\rm{Gr}}}}\left( w \right)} \right\}} {\rm{d}}w, $

其中${P_{{\rm{SiC}}}}$和${P_{{\rm{Gr}}}}$分别为碳化硅和石墨烯的PDOS.
PPR是分析声子运动特别是声子局域化现象的一种有效方法, 原子缺陷、界面、表面和结构变化都会引起声子局域化. 它可以作为研究声子局域化程度及其对界面热导影响的判据. 声子参与率可由晶格动力学和分子动力学计算得到, 在本文中声子参与率由分子动力学方法得到, 可以包含其中非谐波散射的相关信息, 具体由下式计算:

${\rm{PPR}}(w) = \frac{1}{N}\frac{\left(\displaystyle\sum\nolimits_i {\rm PDOS} _i (w)^2 \right)^2}{{\displaystyle\sum\nolimits_i {{\rm{PDO}}{{\rm{S}}_i}{{\left( w \right)}^4}} }}, $

其中${\rm{PDO}}{{\rm{S}}_i}\left( w \right)$为对应频率下原子的PDOS.

2

-->

3.1.温度对石墨烯/碳化硅异质界面热导的影响分析

经典分子动力学模拟中可以根据玻尔兹曼能量均分原理获得温度, 考虑到模拟结构中石墨烯和碳化硅的德拜温度分别为322 K和1200 K. 当系统温度低于碳化硅的拜温度温度时, 大量的声子模式没有被完全的激发出来, 此时的量子效应不可忽略. 因此必须利用量子修正来计算异质结构的界面热导. 量子修正方法同前期研究文献^[23]过程所述. 通过构建石墨烯/碳化硅三明治结构研究不同温度对异质界面热导的影响. 异质结构中石墨烯和碳化硅的层数分别为3层和10层. 界面的作用力考虑范德瓦耳斯力和共价键两种情况, 界面热导的模拟结果如图2所示, 发现界面热导均随着温度的增加而增加.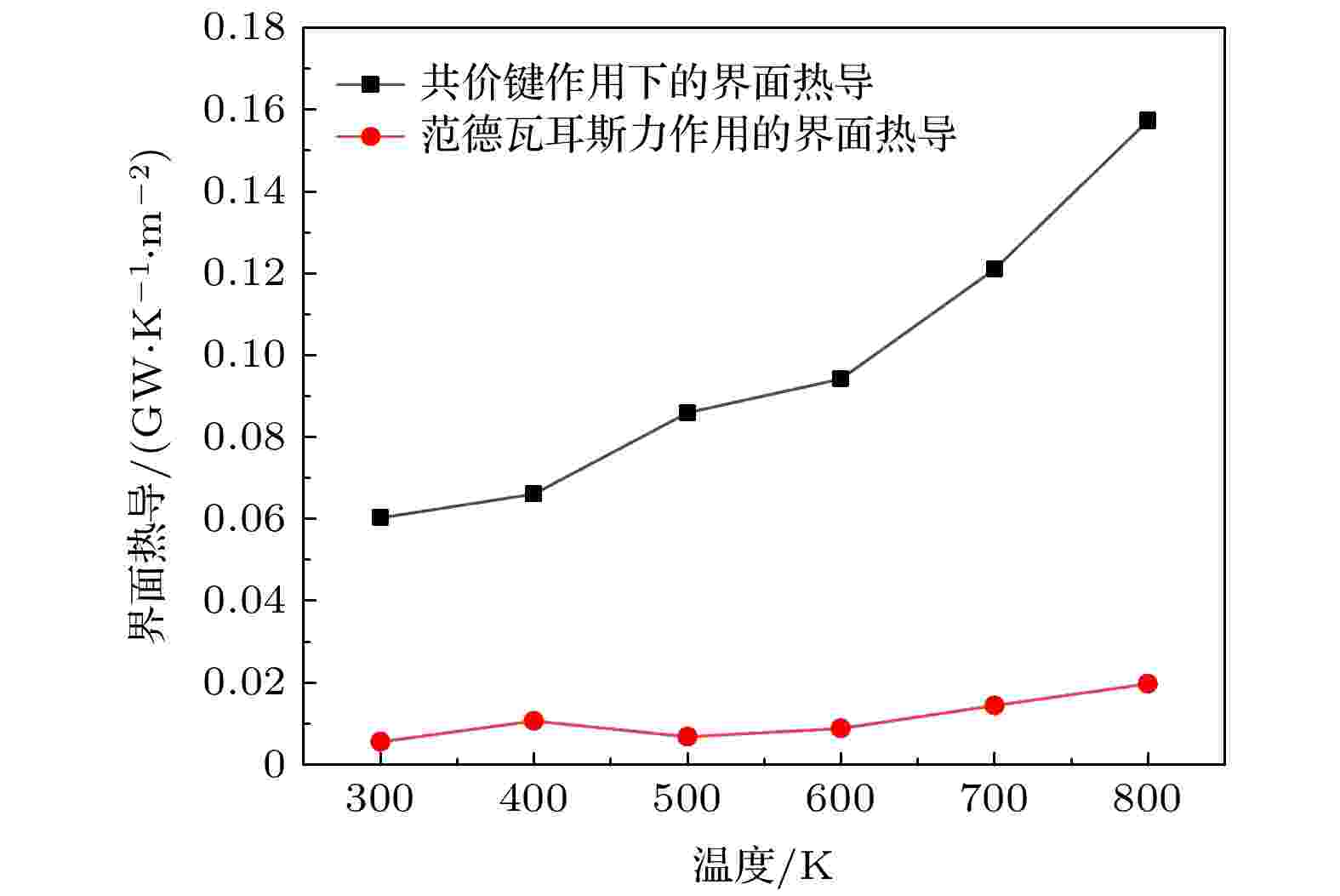
图 2 范德瓦耳斯力与共价键作用下界面热导与温度的关系
Figure2. Temperature dependence of interface thermal conductance under the van der Waals force and the covalent bond.

许多****^[24,28,29]对石墨烯/碳化硅异质结构模型进行了研究. Li等^[24]通过分子动力学计算石墨烯/4H-SiC界面在共价键作用下的界面热导为0.65 GW/(K·m²), 而在范德瓦耳斯力作用下的界面热导为0.017 GW/(K·m²). Mao等^[28]采用第一性原理得到石墨烯/SiC界面热导为0.028 GW/(K·m²), 与本文的结果较为接近. Wang等^[29]采用分子动力学方法计算6H-SiC/石墨烯的界面热导为0.1 GW/(K·m²). 分析认为碳化硅结构的不同造成界面热导的差异, 在结构相同时各种方法得到的界面热导基本在同一数量级. 在本文中当界面作用力为共价键时, 研究发现温度为300 K时界面热导为0.06 GW/(K·m²), 而在700 K时界面热导为0.12 GW/(K·m²). 分析认为随着温度的升高晶格振动加剧, 使得参与热输运的声子增加从而提高界面的热导. 可以看出异质结构在共价键作用下的界面热导约为范德瓦耳斯力作用下界面热导的10倍. 为了阐述解释界面热导的变化, 根据(4)式计算不同温度下石墨烯和碳化硅的PDOS和重叠因子如图3所示, 其中, 计算面内方向声子(XY)和面外(Z)方向的态密度后, 发现界面热导主要受面外(Z)方向声子态密度所影响, 因此在后面研究中主要针对Z方向的声子态密度进行分析.
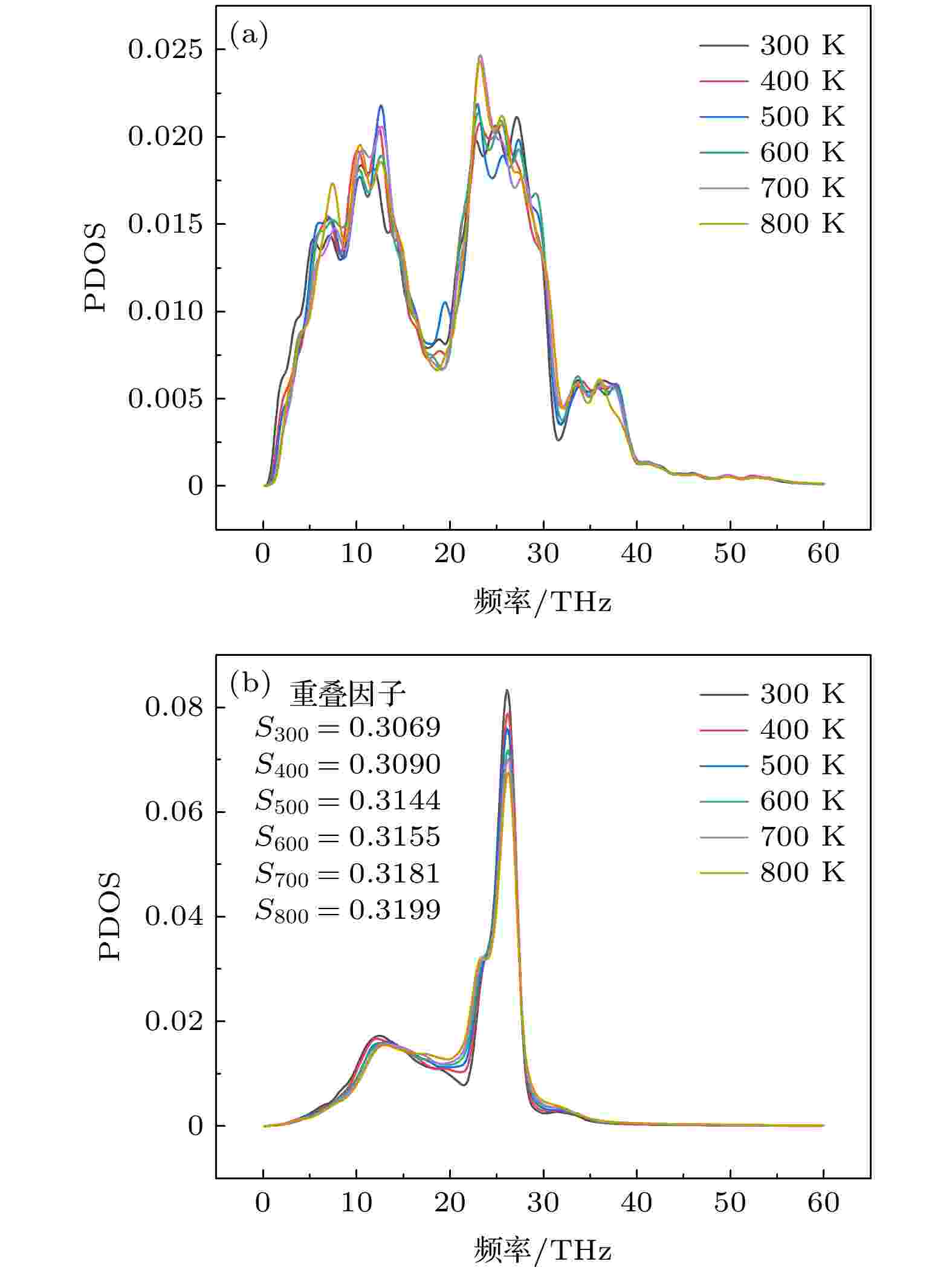图 3 共价键作用下PDOS随温度的变化　(a)石墨烯; (b)碳化硅
Figure3. Temperature dependence of PDOS under covalent bond: (a) Graphene; (b) SiC.

由图3可以看出: 在低频区(0—10 THz)随着温度增加, PDOS变化不明显, 在0—15 THz范围, 随着温度的升高, 态密度反而有小幅降低; 而在中低频(10—30 THz)随着温度的升高石墨烯态密度呈现明显升高; 而碳化硅的态密度在低频区(10—20 THz)随着温度上升有小幅的增大, 而在中频区(20—30 THz)温度的升高使得态密度有所降低. 由于碳化硅中频处态密度相对石墨烯依然很大, 因此温度升高虽然使得碳化硅态密度有所降低, 但界面中频声子态密度重合度升高, 重叠因子增大, 进而使得界面热导升高. 图4给出了当界面作用力为范德瓦耳斯力时PDOS和重叠因子随着温度的变化, 可以发现石墨烯主要由低频声子进行热输运, 而由于10—20 THz范围石墨烯态密度随着温度的升高而增大, 因此界面热导随着温度的升高整体呈现上升的趋势.
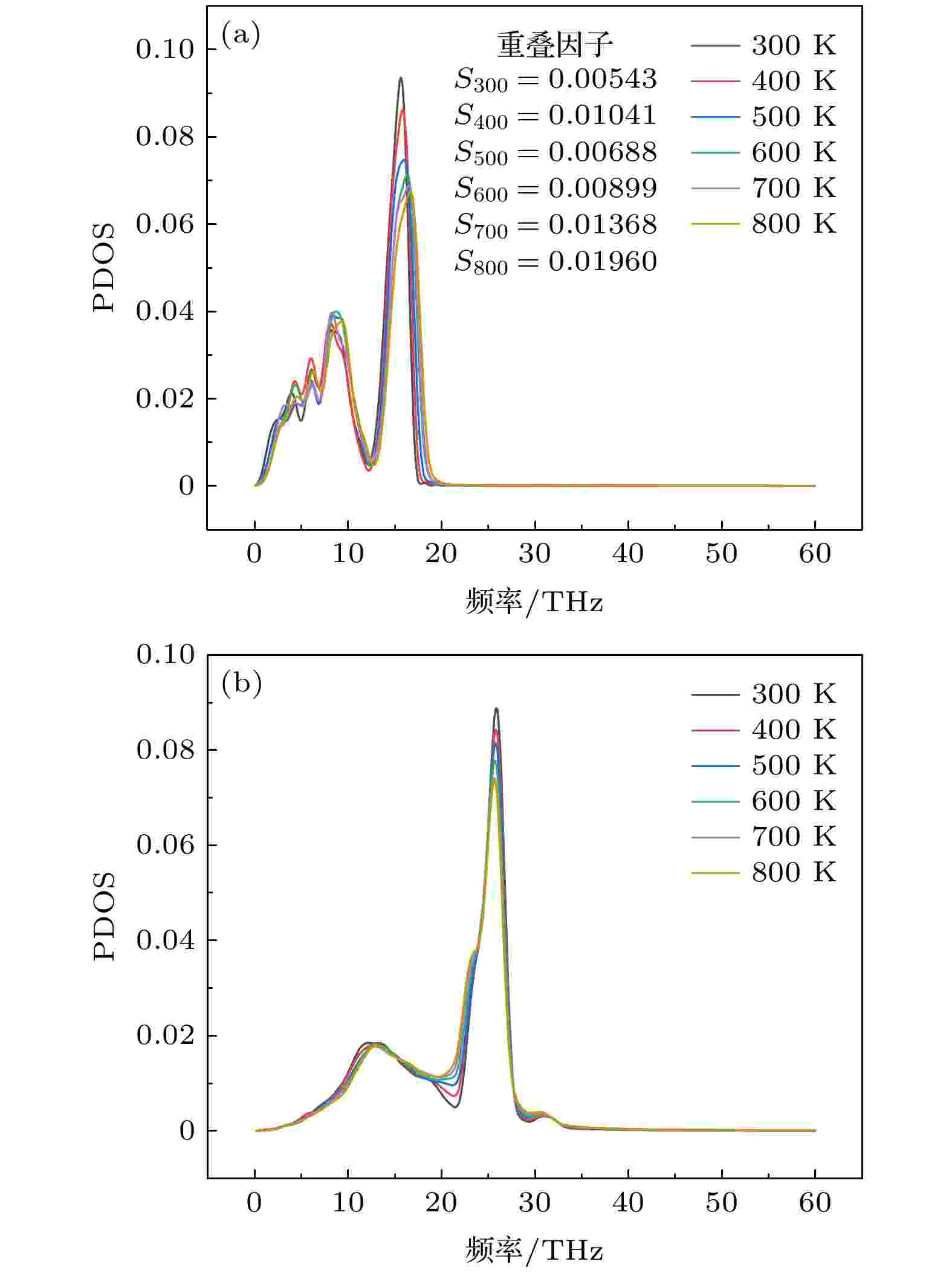图 4 范德瓦耳斯力作用下PDOS随温度的变化　(a)石墨烯; (b)碳化硅
Figure4. Temperature dependence of PDOS under van der Waals force: (a) Graphene; (b) SiC.

2 -->

3.2.尺寸对石墨烯/碳化硅异质界面热导的影响分析

通过建立不同层数的石墨烯/碳化硅三明治结构研究厚度对异质界面热导的影响. 当考虑石墨烯层数为2层时石墨烯的厚度小于原子势的截止距离, 引起两边碳化硅材料之间存在直接声子耦合效应的问题, 与3层及以上石墨烯层数的原子作用不同, 因此仅仅计算2层时界面热导值作为参考. 图5所示为石墨烯和碳化硅异质结构尺寸变化对界面热导的影响. 微纳尺度效应主要由声子波长和声子平均自由程所影响. 当系统的特征尺寸与声子平均自由程接近时, 需要考虑经典的尺寸效应(声子弹道输运), 而当系统的特征尺寸与声子平均自由程进一步接近时, 需要考虑声子的波动性质. 而对于有限模型中的声子散射由本征散射和边界散射组成, 这两个散射可以看作是相互独立的事件. 声子平均自由程随温度的升高而显著降低, 在低温区有明显的尺寸效应, 这是因为声子平均自由程变得更接近计算域的特征长度. 因此当石墨烯层数为3层时, 分析认为声子平均自由程的减少是界面热导降低的原因.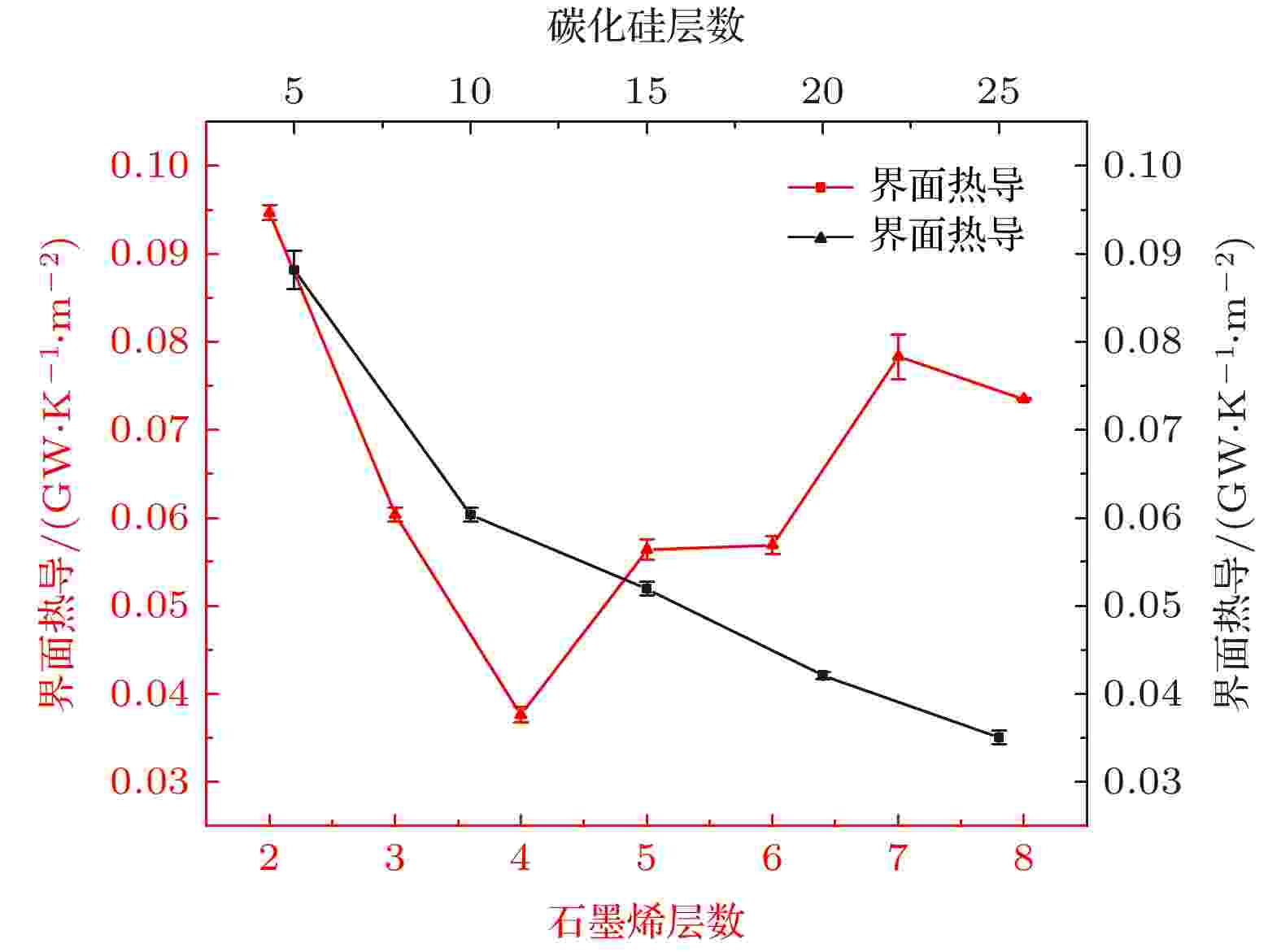
图 5 界面热导随着材料层数(厚度)的变化
Figure5. Relationship between the interfacial thermal conductance and the number of layers (thickness) of the material.

在改变碳化硅层数时, 石墨烯层数固定为3层, 随着碳化硅层数的增加, 异质界面的界面热导降低, 并且降低的速度随着层数增加逐渐平缓. 分析计算得到的石墨烯与碳化硅的PDOS如图6(a)所示, 石墨烯的PDOS在整个频率上变化并不明显, 而随着碳化硅层数的增加, 碳化硅中频段(20—30 THz)的态密度大幅度增加. 在26 THz处, 当碳化硅层数由5层增加至10层时, 碳化硅的态密度由0.05增大到0.082, 但在中频处由于石墨烯的态密度只有0.02左右, 因此碳化硅中频态密度的增加并没有对态密度的重合度造成影响. 除中频段外, 碳化硅其余频率的态密度均随着层数的增加有所降低, 这就造成随着碳化硅层数的增加, 声子重叠率降低, 进而导致界面热导减小.
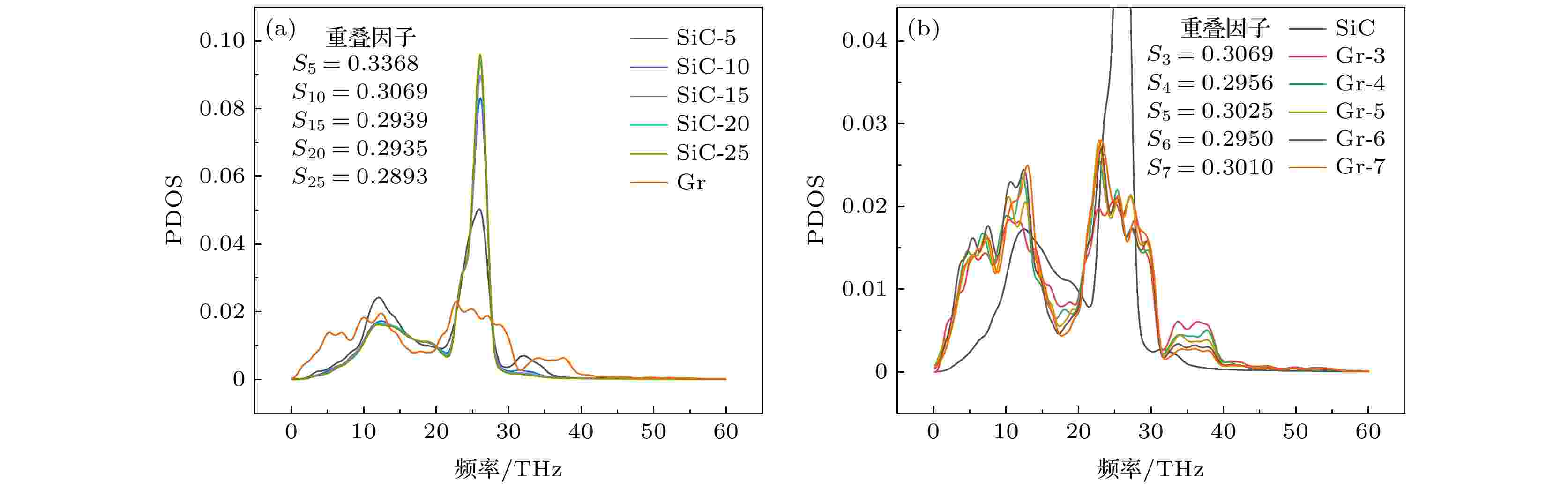图 6 (a)碳化硅层数对PDOS的影响; (b)石墨烯层数对PDOS的影响
Figure6. (a) Effect of SiC layers on PDOS; (b) effect of graphene layers on PDOS.

在研究石墨烯层数对界面热导的影响时, 碳化硅的层数为10层固定值, 发现界面热导随着石墨烯层数的增加先降低再升高, 在石墨烯层数为4层时界面热导最低. 其PDOS和重叠因子如图6(b)所示, 在石墨烯层数变化时, 碳化硅的PDOS是完全一致的, 在整个频率上没有变化. 而在低频段0—10 THz, 由于此时碳化硅的PDOS较低只有0.01左右, 并且碳化硅的态密度总是小于石墨烯的态密度, 因此石墨烯低频声子PDOS的改变并没有影响重合度的大小. 而在中频段10—40 THz, 发现在态密度的波谷, 随着石墨烯层数的增加, 态密度逐渐减小, 而在波峰的情况正好相反. 在计算其重叠因子后, 发现虽然4层石墨烯的重叠因子较小, 但并没有像温度影响下呈现出重叠因子与界面热导清晰的对应关系.
因此, 根据(6)式进一步计算3—5层时石墨烯与碳化硅的PPR如图7所示. 可以看出, 声子有两种模式, 分别是局域和离域, 其中对热传输的贡献主要来自于离域. 以0.3作为大多数声子离域与局域的分界线, 对比不同层数时石墨烯和碳化硅的PPR可以发现, 碳化硅的PPR仅在高频处有所变化, 由于高频时声子态密度很低, 因此对界面热导影响较小. 而相比于3层和5层, 碳化硅层数为4时石墨烯的PPR在中低频段(10—20和30—40 THz)有更多的声子从局域进入离域模式, 声子局部化程度增大, 界面声子热输运受阻, 这就造成界面热导的降低.
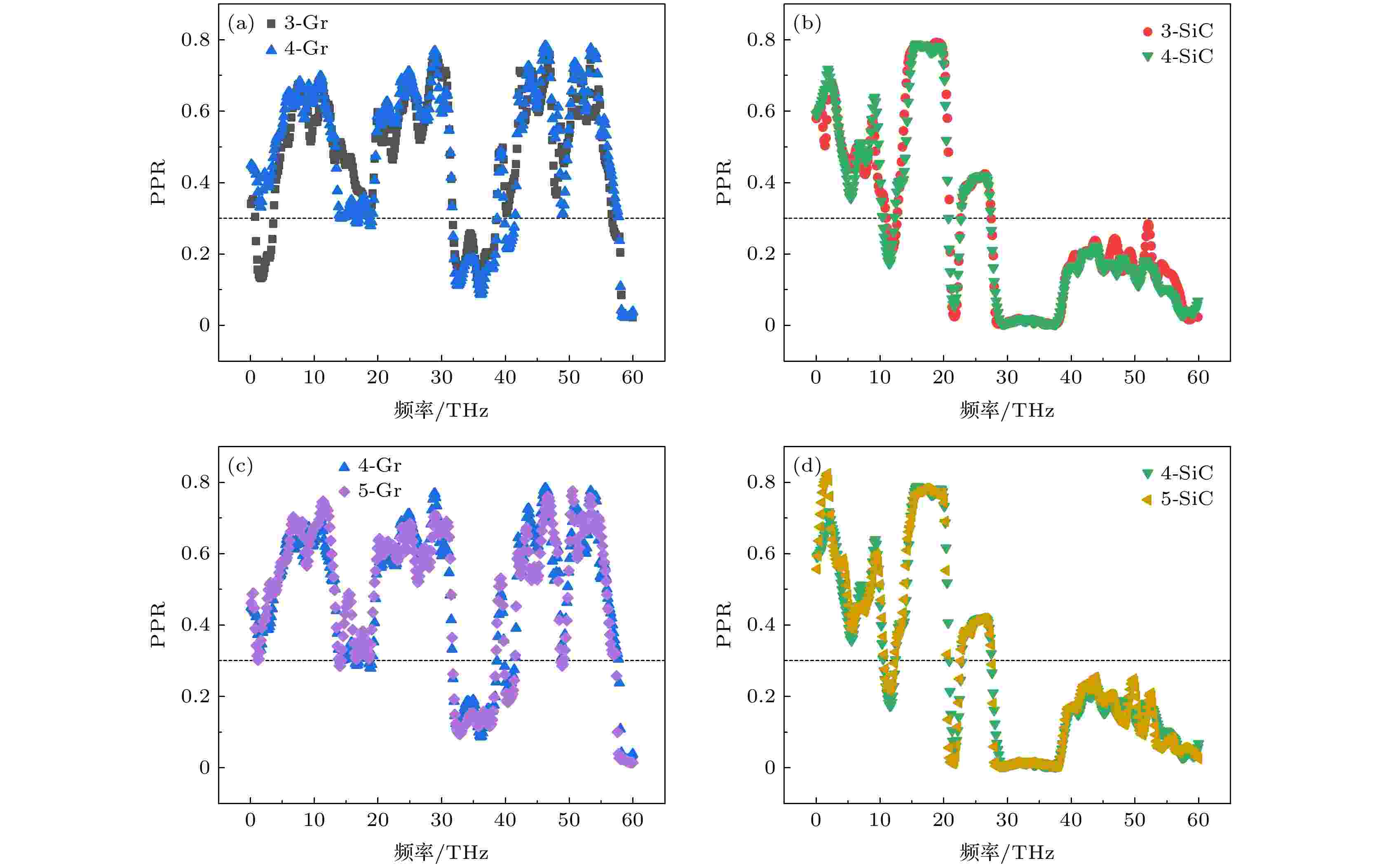图 7 石墨烯层数为3和4层时(a)石墨烯、(b)碳化硅的PPR; 石墨烯层数为4和5层时(c)石墨烯和(d)碳化硅的PPR
Figure7. PPR of (a) graphene and (b) SiC under the condition of 3 and 4 layers of graphene; PPR of (c) graphene and (d) SiC under the condition of 4 and 5 layers of graphene.

2 -->

3.3.缺陷对石墨烯/碳化硅异质界面热导的影响分析

目前SiC材料在制备过程中存在密度缺陷、外延层厚度等问题, 因此研究空位缺陷率对石墨烯/碳化硅异质界面热导的影响. 模拟计算过程中分别对石墨烯和碳化硅材料添加一定百分比的缺陷, 结果表明加入一定量的随机空位缺陷可以有效地提高界面的界面热导. 首先, 单独给碳化硅添加一定的随机空位缺陷, 而石墨烯为理想结构, 碳化硅缺陷率对界面热导的影响和对应的PDOS如图8所示, 当碳化硅添加20%缺陷率时, 界面热导由初始理想结构的0.06116 GW/(K·m²)增加到0.08422 GW/(K·m²). 缺陷的引入使得石墨烯态密度在中频段(0—40 THz)略有减小, 而在低频10 THz处则有所增大, 石墨烯态密度在整个频率上变化幅度不大, 因此在图8中仅给出一条石墨烯的PDOS曲线. 而碳化硅缺陷的引入极大地改变碳化硅的PDOS, 使得碳化硅中低频段(15—30 THz)频率的PDOS急剧减小. 当缺陷率从0增加到10%时, 中频PDOS的最大值已经从0.08减小到0.04, 并且随着缺陷率的增加进一步降低. 而其余部分的PDOS均随着缺陷的引入有小幅增加. 因此, 缺陷的引入会阻碍中频声子的热输运, 并且阻碍效果会随着缺陷率的增加而增加, 当缺陷率从0增加至20%左右, 此时虽然碳化硅中频PDOS降低, 但仍然比石墨烯的PDOS高, 而其余部分PDOS的增加增大了石墨烯/碳化硅的界面热导. 而随着缺陷率的进一步增加, 碳化硅中频部分PDOS的急剧减小使得中频部分的重叠度迅速减小, 从而使得界面热导急剧减小. 当缺陷率达到40%时, 界面热导仅仅为缺陷率10%时的1/3.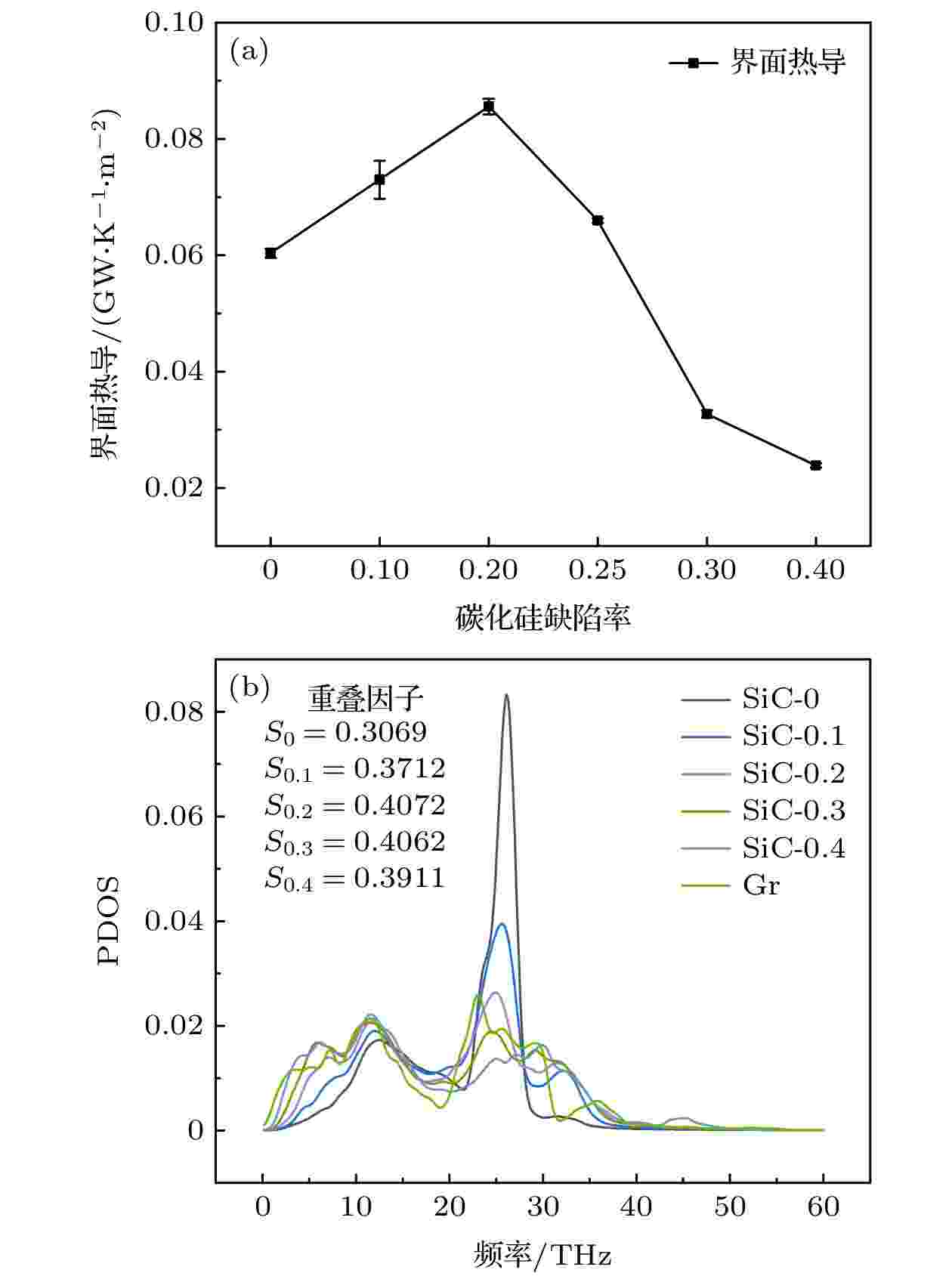
图 8 (a)碳化硅缺陷率对界面热导的影响; (b)不同缺陷率下对应的PDOS的变化情况
Figure8. (a) Effect of defect rate of SiC on interfacial thermal conductance; (b) change of PDOS corresponding to different defect rates.

单独对石墨烯添加随机空位缺陷时界面热导的变化情况和300 K温度时对应的PDOS如图9(a)与图9(b)所示, 考虑到温度可能会影响缺陷石墨烯的界面热导, 因此图中给出300, 600和900 K温度下石墨烯缺陷率对界面热导的影响. 其中, 由于碳化硅的PDOS图在温度不变时不随石墨烯缺陷率的增加发生变化, 因此仅在图中给出一条曲线.
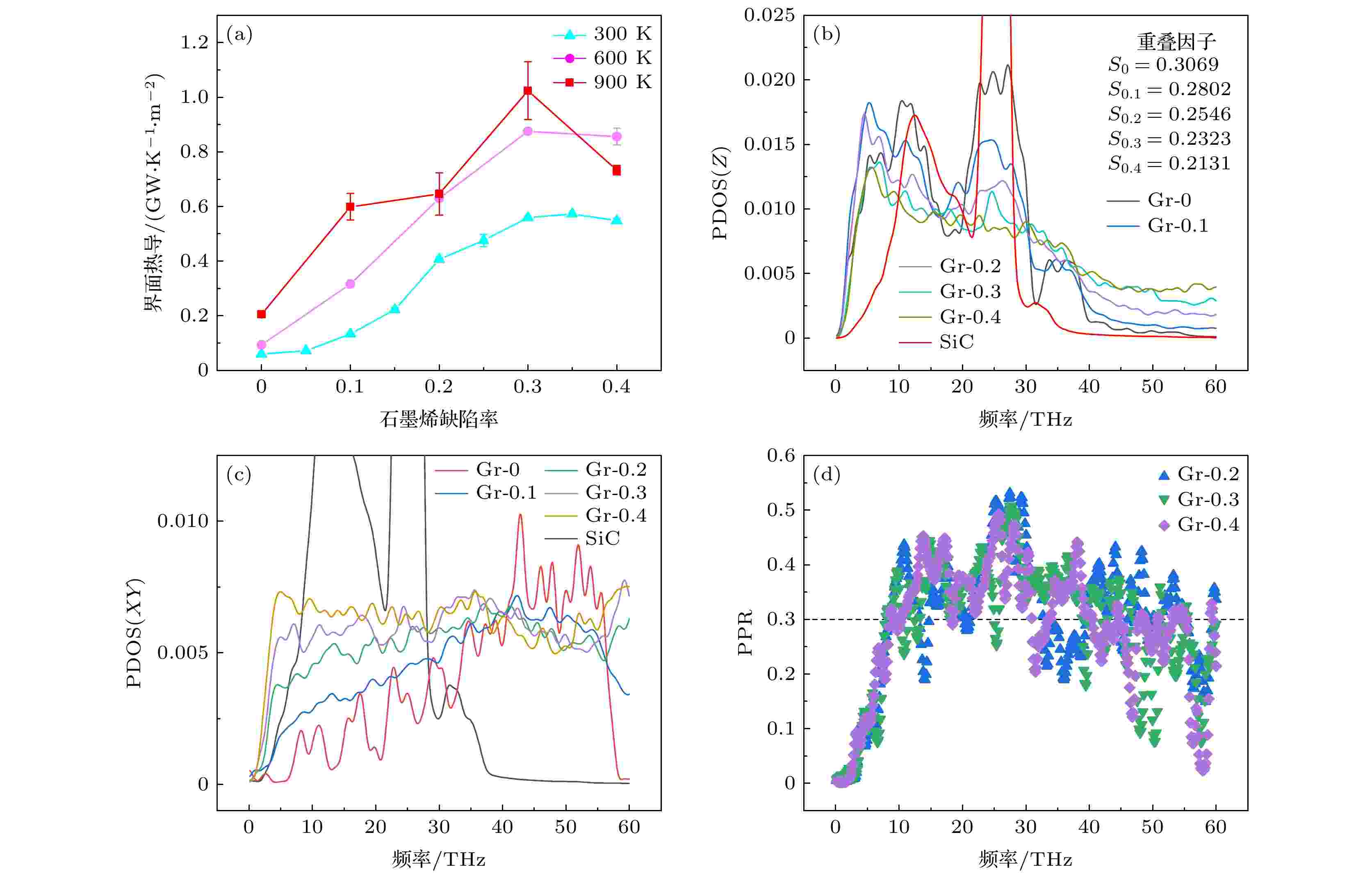图 9 (a)不同温度下石墨烯缺陷对界面热导的影响; (b)不同石墨烯陷率下对应的面外方向(Z) PDOS的变化情况(温度为300 K); (c)不同石墨烯陷率下对应的面内方向(XY) PDOS的变化情况(温度为300 K); (d)缺陷率分别为20%—40%时石墨烯PPR的变化情况
Figure9. (a) Effect of graphene defects on the thermal conductance of the interface at different temperatures; (b) the change of PDOS in the out of plane direction (Z) under different graphene defects rates at the temperature of 300 K; (c) the change of PDOS in the in-plane direction (XY) under different graphene defects rates at the temperature of 300 K; (d) the change of PPR of graphene with defect rate of 20%–40%.

如图9(a)所示, 在三种温度条件下界面热导均随着缺陷率的增加首先急剧增大, 然后慢慢减缓, 在缺陷率达到30%—40%时界面热导会逐渐下降. 石墨烯点缺陷造成部分sp²共价键断裂, 结构刚性下降, 导致其声子态密度的低频分量增加, 增强与碳化硅间的低频声子耦合, 进而提高界面热导. 温度为300 K时, 在缺陷率为35%时界面热导达到最大值0.5732 GW/(K·m²). 而在温度为900 K、缺陷率为30%时界面热导达到最大值1.0242 GW/(K·m²). 温度为900 K时得到的界面热导误差较大, 因此以误差线的形式在图上给出. 比较三种温度下界面热导的变化可看出, 界面热导达到最大值时对应的缺陷率和达到最大值后界面热导减小的程度均与温度有关. 温度越高, 界面热导达到最大值所需的缺陷率越小, 并且界面热导随缺陷率的变化程度越大. 研究300 K时PDOS的变化发现和以往的结果相反, 如图9(b)所示, 界面热导随着缺陷率的增加而增大时, 石墨烯面外(Z)方向的PDOS却在逐渐减小, 这一点在重叠因子上也可以看出, 而600和900 K时石墨烯的PDOS的变化也和300 K时类似. 此时, 面外(Z)方向的PDOS并不能很好地解释界面热导的变化.
因此进一步给出石墨烯面内(XY)方向的PDOS, 如图9(c)所示, 此时温度为300 K. 发现面内PDOS呈现出的变化趋势与界面热导一致, 随着缺陷率增加而增大. 但面内PDOS的值整体较小, 并且在以往的研究中, 已经证明面内PDOS在声子耦合中起次要作用, 因此面内声子并不能很好地解释界面热导的变化情况. 图9(d)给出300 K时石墨烯缺陷率为20%—40%时PPR的变化情况, 可以看出在中低频段, 缺陷率较小时在10—40 THz频率范围内有更多声子从局域进入到离域模式. 考虑到PPR与温度无关, 完全离域声子模的PPR介于O(1)和完全局域声子模的O(1/N)之间, 因此推测界面热导的变化是由石墨烯和碳化硅的本征声子模失配所造成的. 比较石墨烯和碳化硅缺陷率对界面热导影响的结果可以看出, 在石墨烯存在缺陷时, 缺陷会极大地改变石墨烯材料整个频率段的PDOS, 石墨烯中缺陷率的变化对异质界面热导的影响更大.

多层异质结构的热输运特性对纳米器件的应用至关重要. 本文采用非平衡态分子动力学方法研究温度、尺寸、缺陷率对石墨烯/碳化硅异质界面热导的影响, 并通过声子态密度和声子参与率对界面热导变化的原因进行分析. 得到以下三方面的结论:
1) 不论是共价键合还是范德瓦耳斯力作用的界面, 界面热导均随着温度升高而显著提升, 其主要原因是10—30 THz范围石墨烯态密度随温度升高显著增加, 并且在同一温度下, 共价键合的异质界面的界面热导比范德瓦耳斯相互作用时提升一个数量级左右;
2) 界面热导随着碳化硅层数的增加而降低, 当石墨烯层数从2层增加到8层时, 界面热导先减小再逐渐增加; 在4层界面热导最低, 其原因在于在中低频段有更多的声子从局域进入到离域模式;
3) 材料的缺陷对界面热导有着显著的影响, 界面热导随着碳化硅缺陷的增加先增加后减小, 在缺陷率为20%左右时界面热导达到最大值, 碳化硅缺陷的引入会阻碍中频声子的热输运. 不同温度下界面热导均随着石墨烯缺陷的增加先增加后减小, 并且界面热导达到最大值时对应的缺陷率和达到最大值后界面热导减小的程度均与温度有关. 温度为300 K时在缺陷率达到35%时界面热导最大, 而在温度为900 K时缺陷率为30%左右界面热导达到最大值.
研究结果表明通过尺寸效应和空位缺陷可以对异质界面的热学特性进行调控, 有利于以碳化硅为基础的微纳器件热设计.