删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

凝聚态体系中激发态载流子动力学研究

本站小编 Free考研考试/2021-12-29
摘要:激发态动力学是凝聚态物理中至关重要且富有挑战的科学问题, 不仅需要从时间、空间、能量和动量等多个维度来描述, 同时还需要考虑各种准粒子的相互作用以及多体效应. 本文聚焦凝聚态体系激发态动力学的理论和应用研究, 结合含时密度泛函、GW-BSE与面跳跃方法, 发展了激发态动力学第一性原理计算软件Hefei-NAMD, 构建了可以同时从时间、空间、动量、能量、自旋等多个维度研究凝聚态体系激发态动力学的理论和程序框架, 并实现了自旋分辨的GW+ real-time BSE(GW+rtBSE)激子动力学. 利用这套方法, 研究了凝聚态体系激发态动力学的许多问题, 包括界面电荷转移动力学、电子空穴复合动力学以及二维TMD材料的谷激子动力学等. 这些研究从第一性原理计算的角度, 模拟激发态载流子在实空间、能量空间和动量空间的含时演化, 为凝聚态体系的激发态动力学及准粒子耦合过程提供了深刻细致的理解.
关键词: 激发态动力学/
Hefei-NAMD/
非绝热分子动力学/
GW + real-time BSE

English Abstract


全文HTML

--> --> -->
1.引　言
激发态载流子动力学过程广泛地存在于各种光物理和光化学过程中, 对太阳能转化、光电器件等方面的应用有重要的意义, 也是凝聚态物理基础研究中的重要分支. 从实际应用的角度出发, 在光电能量转化的过程中, 激发态载流子的激发、弛豫、迁移等动力学过程对于光电转化效率来说有着至关重要的影响. 例如, 在太阳能电池器件中, 激发态载流子需要在其有限的寿命之内有效地转移到金属电极上[1-6]; 对于光催化过程来说, 激发态电子或空穴则需要被吸附分子捕获, 随后发生进一步的光化学反应[7-12]; 在光电器件的应用中, 不同的器件对于激发态载流子的寿命有着不同的需求, 比如光发射器件需要较长的寿命, 光调制器需要较短寿命, 而光探测器需要中等寿命的激发态载流子[13-17]. 从基础研究的角度出发, 凝聚态物理的核心内容在于研究体系的元激发及其耦合, 激发态载流子在衰减到基态过程中存在不同的弛豫通道, 会与声子、极化子、等离激元等准粒子发生复杂的相互作用, 激发态电子与空穴本身也存在相互作用, 涉及多个超快过程, 理解这些超快过程的物理本质是凝聚态物理研究中的重要内容. 因此, 深入研究各种材料体系中激发态载流子动力学过程无论对实际需求还是基础研究都具有重要的意义.
伴随着计算机科学的发展, 从20世纪80年代到现在是计算物理蓬勃发展的几十年, 其中第一性原理计算在凝聚态物理、材料物理、材料化学等领域取得了巨大的成功, 人们可以摆脱人为确定的参数, 从“第一性原理”的角度出发来研究和预测不同材料的性质. 然而, 凝聚态体系中激发态动力学是一个复杂科学问题, 不仅需要从时间、空间、能量和动量等不同维度对激发态载流子进行描述, 同时还需要理解各种准粒子相互作用产生的多体效应. 这不同层次的复杂度, 让激发态动力学在第一性原理计算领域成为了一个具有严峻挑战的方向.
对于由原子核与电子构成的系统, 由于电子和原子核有三个量级的质量差, 描述其动力学时可以将电子与原子核的自由度分开考虑, 认为电子能够瞬时地适应原子核结构的变化, 电子的量子态由原子核的单一势能面决定, 这就是Bohn-Oppenheimer (BO)近似, 或者称为绝热(adiabatic, AD)近似[18]. 然而, 当体系被激发后, 其弛豫过程会出现电子运动的能量尺度与原子核相近的情况, 这时电子和原子核的耦合大大增强, 分离二者的自由度的绝热近似就会导致很大的误差. 这种无法用绝热近似处理的电子和原子核相互耦合的运动被称为非绝热(nonadiabatic, NA)过程, 包含NA过程的分子动力学被称为非绝热分子动力学(NAMD)[19,20]. 考虑电子自由度和原子核自由度相互耦合的非绝热过程, 问题的复杂度便大大提高了. 人们可以在不同的理论框架下考虑这种非绝热动力学问题, 例如, 将电子与原子核都在量子力学框架下进行考虑的方法被称为全量子方法, 而将原子核作为经典粒子, 将电子作为量子尺度的粒子的方法被称为量子-经典混合(MQC)方法, 在当前的计算条件下, 全量子方法只能适用于原子数较小, 时间较短的体系[21,22], 对于凝聚态体系这类原子数较多的体系, MQC方法则较为实用.
MQC方法的关键问题是量子-经典自洽(QCSCF)问题, 也就是量子子系统与经典子系统如何耦合的问题, 在经典子系统的影响下, 量子子系统需要正常演化, 并且量子态之间沿演化方向存在跃迁的可能性; 同时, 经典子系统必须对量子跃迁做出相应的响应. 其中, 对后者的适当处理尤其具有挑战性. 在这方面, 存在两种被广泛使用的方法, 第一种是Ehrenfest方法, 也被称为平均场方法[23-25]. 在平均场方法中, 经典子系统的粒子运动方程可以写为
$ \begin{array}{c}{M}_{\alpha }{\ddot{\boldsymbol{R}}}_{\alpha }=-{\nabla }_{\alpha }\left\langle {{\widehat{\mathcal{H}}}_{{\rm{e}}{\rm{l}}}(\boldsymbol{r},\boldsymbol{R})} \right\rangle ,\end{array} $
其中$ \langle {{\widehat{\mathcal{H}}}_{{\rm{e}}{\rm{l}}}(\boldsymbol{r},\boldsymbol{R})} \rangle $为平均的势能面. 这里, 可以认为经典子系统所演化的势能面为各个不同量子态确定的势能面的加权平均. 这种方法对量子表象的选择具有不变性, 通常能较好地描述跃迁概率. 当动力学中涉及的不同量子态没有显著差异时, 这种方法是比较有效的. 然而, 在这种方法中量子子系统和经典子系统之间的相关性并没有得到正确的描述. 尤其当各个量子态的差异较大时, 这种方法会得到非物理的结果. 因此, 人们提出了一种通过引入随机跃迁来处理量子-经典关联的面跳跃方法[26-29]. 在面跳跃方法中, 经典子系统的运动方程可以写为
$ {M}_{\alpha }{\ddot{\boldsymbol{R}}}_{\alpha }=-{\nabla }_{\alpha }{E}_{{\rm{k}}}^{{\rm{e}}{\rm{l}}}\left(\boldsymbol{R}\right), $
其中$ {E}_{{\rm{k}}}^{{\rm{e}}{\rm{l}}}\left(\boldsymbol{R}\right) $为电子在k态时的势能面. 可以看出, 这里的经典子系统在某一个量子态的势能面上进行演化, 各个量子态之间的耦合可以用一个非绝热耦合矩阵来描述, 非绝热耦合的大小决定了经典子系统在各个势能面之间跃迁的概率, 再通过对大量的动力学轨线做统计平均, 得到统计学意义上的宏观动力学性质. 在这种方法中, 经典子系统可以在不同势能面之间跳跃, 因而被称为面跳跃方法. 具体而言, 如何由非绝热耦合得到面跳跃概率的算法并不是唯一的, 其中被应用最多的是Tully[28]提出的最少面跳跃算法(FSSH).
这些NAMD方法早期多运用于小分子体系, 随着计算机计算能力的提高, 基于第一性原理计算的非绝热分子动力学在凝聚态体系中的应用慢慢开始发展. 例如, 中国科学院物理研究所孟胜教授与哈佛大学的Kaxirus教授[30]以及Kolesov等[31]基于Erhenfest方法与实时的含时密度泛函理论(real-time TDDFT)发展了TDAP程序. 纽约大学布法罗分校Akimov教授与南加州大学的Prezhdo教授[32,33]以及Craig等[34]将time-dependent Kohn-Sham (TDKS)与surface hopping思想相结合, 发展了Pyxaid程序, 可以在Kohn-Sham (KS) 轨道图像下对凝聚态体系的激发态动力学进行研究. 北京师范大学的崔刚龙教授和Thiel[35]也发展了类似的方法; 加州大学北岭分校的Lu教授课题组[36]发展了针对扩展体系的线性响应含时密度泛函理论(LR-TDDFT)与surface hopping结合的方法; 加州大学伯克利分校的Wang教授等[37]在PWmat程序中实现了基于real time TDDFT的Erhenfest动力学方法, 这些课题组都在这个领域做出了丰富的成果.
与Prezhdo教授思路类似, 我们基于TDKS方程与surface hopping的思想, 发展了第一性原理非绝热分子动力学代码(Hefei-NAMD), 并用该方法研究了不同凝聚态体系的非辐射激发载流子动力学, 包括界面电荷迁移动力学、电子-空穴(e-h)复合动力学、光激发自旋极化动力学. 最近, 我们将单体TDKS方程推广到两体real-time BSE方程, 将GW+BSE方法与NAMD结合, 发展了自旋分辨的GW+rtBSE方法, 可以准确包含激子的多体效应, 是研究激子动力学的有力工具. 本文总结回顾了我们相关的研究工作, 组织如下: 第2节简述了NAMD的计算方法; 第3节到第5节分别介绍利用Hefei-NAMD对界面电荷迁移动力学、半导体e-h复合和磁性材料自旋动力学进行的一系列研究; 第6节介绍最新发展的GW+rtBSE方法, 以及MoS2体系中的自旋谷激子动力学; 第7节进行总结并对未来的研究方向进行展望.
2.计算方法
Hefei-NAMD采用TDKS与surface hopping方法相结合的思想, 将不同势能面之间跃迁的概念类比为载流子在不同KS轨道之间的跃迁, 采用经典路径近似[33,38], 忽略原子核系统对激发态电子的响应, 这样原子核的运动轨迹可以用基态的分子动力学得到. 这个近似对于凝聚态体系, 尤其是固体体系有一定的合理性, 主要有以下几个原因: i) 由于凝聚态体系常常具有大量的电子, 因此单电子的激发对体系的影响有限, 往往会小于一定温度下的热涨落; ii) 密集的能级形成能带, 使得很多能级上的电子寿命非常短, 对于这些寿命较短的激发态载流子, 原子核系统来不及发生响应; iii) 基于surface hopping的思想, 会对很多条轨线进行统计, 经典路径近似带来的误差在这样的统计中被进一步抵消了.
在Hefei-NAMD中, 激发态载流子波函数用一组含时的KS轨道$ \left\{\right|{\psi }_{i}\left(\boldsymbol{r},\boldsymbol{R}\left(t\right)\right)\left. {} \right\rangle \} $展开:
$ |\varPsi \left. {} \right\rangle =\sum\limits_{i}\left|{\psi }_{i}\left. {} \right\rangle \left\langle {} \right.{\psi }_{i}\right|\varPsi \left. {} \right\rangle =\sum\limits_{i}{c}_{i}\left(t\right)|{\psi }_{i}\left(\boldsymbol{r},\boldsymbol{R}\left(t\right)\right)\left. {} \right\rangle , $
其中R, r 分别对应原子核与电子的坐标变量, $ \boldsymbol{R}\left(t\right) $由第一性原理分子动力学得到, ci(t)为展开系数, 也就是载流子的占据数. 将这种形式的载流子波函数代入含时的薛定谔方程:
$ {{\rm{i}}}\hslash \frac{\partial |\varPsi \left(\boldsymbol{r},\boldsymbol{R}\left(t\right)\right)\left. {} \right\rangle }{\partial t}=\widehat{\mathcal{H}}(\boldsymbol{r},\boldsymbol{R}\left(t\right),\sigma )|\varPsi \left(\boldsymbol{r},\boldsymbol{R}\left(t\right)\right)\left. {} \right\rangle , $
即可得到:
$\begin{split}{{\rm{i}}}\hslash \frac{\partial {c}_{i}(t)}{\partial t}=\;&\sum\limits _{j}\left[\left\langle {\psi }_{i}|\widehat{\mathcal{H}}|{\psi }_{j} \right\rangle -{\rm{i}}{\rm{\hslash }}\left\langle {\psi }_{i}|\frac{{\rm{d}}}{{\rm{d}}t}|{\psi }_{j} \right\rangle \right]{c}_{j} (t)\\=\;&\sum\limits_{j}\left[{\varepsilon }_{i}{\delta }_{ij}-{\rm{i}}{\rm{\hslash }}{d}_{ij}\right]{c}_{j}\left(t\right),\\[-18pt]\end{split}$
其中$ {\varepsilon }_{i} $是KS轨道$ |{\psi }_{i}\left(\boldsymbol{r},\boldsymbol{R}\left(t\right)\right)\left. {} \right\rangle $的本征值, $ {d}_{ij} $是i, j两个KS轨道之间的非绝热耦合. 可以证明$ {d}_{ij} $等价于:
$ {d}_{ij}=\left\langle {\psi }_{i}|\frac{{\rm{d}}}{{\rm{d}}t}|{\psi }_{j} \right\rangle =\sum\limits_{I}\frac{\left\langle {} \right.{\psi }_{i}|{\nabla }_{I}\widehat{\mathcal{H}}|{\psi }_{j}\left. {} \right\rangle }{{\varepsilon }_{j}-{\varepsilon }_{i}}{\dot{\boldsymbol{R}}}_{I}, $
这里$ I $是原子核标号. (6)式表明$ {d}_{ij} $与电声耦合$ \left\langle {} \right.{\psi }_{i}|{\nabla }_{I}\widehat{\mathcal{H}}|{\psi }_{j}\left. {} \right\rangle $、原子核速度$ {\dot{\boldsymbol{R}}}_{I} $成正比, 与电子态的能量差$ {(\varepsilon }_{j}-{\varepsilon }_{i}) $成反比. $ {d}_{ij} $决定了载流子在不同KS能级之间跃迁的概率. 在FSSH的框架下, 载流子跃迁的概率可以写为
$\begin{split}& {P}_{ij}\left(t, t+\Delta t\right) \\=& \max\left\{\frac{2\displaystyle\int_{t}^{t+\Delta t}{\rm{R}}{\rm{e}}\left({c}_{i}^{*}{c}_{j}{d}_{ij}\right){\rm{d}}t}{{c}_{j}^{*}{c}_{j}}, 0\right\}.\end{split}$
有了载流子在不同能级间跃迁的概率, 就可以通过统计大量轨线的方法得到载流子的动力学行为. 一般来说, 我们会在分子动力学轨迹的前数皮秒(ps)中取100—200个结构作为初始结构样本, 每个初始结构计算104条载流子轨迹进行统计平均.
在surface hopping方法中, 激发态载流子开始演化时处于一个单一的电子态上, 然而随着演化的过程, 系统会产生相干电子态, 而外界环境的扰动会使得相干态重新塌缩到单一电子态上, 这个过程被称为退相干过程. 当激发态载流子的寿命较长时, 退相干会对研究结果产生较大影响, 此时则需要考虑退相干效应. 考虑退相干的surface hopping的方案也有不止一种, 例如DCSH (decoherence corrected surface hopping), DISH (decoherence induced surface hopping)[39] 等.
在研究电荷空间转移的过程中, 激发态载流子的空间分布可以积分得到:
$ \begin{split} & \int \rho \left(\boldsymbol{r},t\right){\rm{d}}\boldsymbol{r}= \int {\left|\varPsi \left({\boldsymbol{r}},t\right)\right|}^{2}{\rm{d}}r \\=&\; \sum\limits_{i,j}{c}_{i}^{*}\left(t\right){c}_{j}\left(t\right) \int {\psi }_{i}^{*}\left[\boldsymbol{r},\boldsymbol{R}\left(t\right)\right]{\psi }_{j}\left[\boldsymbol{r},\boldsymbol{R}\left(t\right)\right]{\rm{d}}\boldsymbol{r}.\end{split} $
对空间分布做时间微分, 可得:
$ \begin{split} &\frac{{\rm{d}} \displaystyle\int \rho \left(\boldsymbol{r},t\right){\rm{d}}\boldsymbol{r}}{{\rm{d}}t}= \\ \;&\sum\limits_{i,j}\left\{\frac{{\rm{d}}\left({c}_{i}^{*}{c}_{j}\right)}{{\rm{d}}t} \!\int\! {\psi }_{i}^{*}{\psi }_{j}{\rm{d}}\boldsymbol{r} \!+\! {c}_{i}^{*}{c}_{j}\frac{{\rm{d}}\displaystyle\int {\psi }_{i}^{*}{\psi }_{j}{\rm{d}}\boldsymbol{r}}{{\rm{d}}t}\right\}. \end{split} $
由(9)式可以看到, 电荷的空间分布变化由两部分引起, 右边第一项描述了绝热KS轨道占据数$ {c}_{i} $的变化而导致的电荷空间分布的变化, 可以理解为电子在不同能级之间跃迁导致的电荷分布变化, 称为非绝热机制(NA); 右边第二项则是因为绝热KS轨道本身的空间分布发生了变化, 从而导致电荷的空间分布发生变化, 称为绝热机制(AD). 这两项分别对时间积分就能得到电荷转移的绝热和非绝热贡献. 一般而言, AD电荷转移主要是由原子核运动导致的, 如因为能级交叉引起的电荷转移. 而NA的电荷转移则是由于载流子在不同能级之间直接跃迁引起的. 不同能级之间相应的空穴电荷弥散情况以及局域位置不同, 进而跃迁导致了电荷转移. 示意图如图1所示. 由此, 可以分析不同的电荷转移机制.
图 1 激发态载流子动力学中的AD和NA过程示意图(图片经文献[20]允许转载, 版权归2019 Wiley Periodicals, Inc.所有)
Figure1. Schematics of the AD and NA charge transfer process (Reprinted with permission from Ref. [20]. Copyright 2019 Wiley Periodicals, Inc.)

以上讨论中提到的载流子既可以是电子也可以是空穴, 因此这套方法可以用来研究激发态电子或空穴的非绝热分子动力学. Hefei-NAMD程序与第一性原理计算程序VASP或Quantum Espresso接口.
3.界面激发态电荷迁移动力学研究
本节讨论不同界面的激发态电荷转移动力学, 包括分子/固体界面、二维材料异质结界面、氧化物异质结界面等.
2
3.1.分子/固体界面
-->

3.1.分子/固体界面

在光催化过程中, 半导体被光激发后产生电子空穴对, 被激发的载流子转移到表面, 被表面吸附的分子捕获, 并发生进一步的化学反应, 因此, 研究激发态电子或空穴如何被表面吸附分子捕获是理解光催化物理机制的关键之一. 二氧化钛(TiO2)作为典型的光催化材料, 我们研究了其与分子界面CH3OH/TiO2和CO2/TiO2的电荷转移动力学过程.
3
3.1.1.甲醇(CH3OH)在二氧化钛表面光生空穴超快转移过程
-->
3.1.1.甲醇(CH3OH)在二氧化钛表面光生空穴超快转移过程
在TiO2的光催化研究中, CH3OH一直以来都被认为是TiO2表面的“空穴清道夫”, 它可以快速捕获空穴, 从而有效降低电子-空穴复合的概率, 延长激发态电子的寿命, 同时, 被捕获的空穴还可以导致CH3OH进一步被氧化[10,40-44]. 然而, 最近的实验工作对于CH3OH能否捕获空穴却存在一些争议, 一些工作认为只有解离的CH3OH才能够有效地捕获空穴[45,46]. 为了理解这个空穴捕获过程, 我们利用Hefei-NAMD模拟了CH3OH/TiO2 (Rutile 110表面)体系中的激发态空穴动力学[47].
为了研究不同吸附结构的CH3OH对空穴捕获的影响, 我们选择了一个单层三种不同吸附结构的CH3OH进行研究, 如图2(a)所示, M结构代表CH3OH未解离的分子吸附结构, HD代表吸附的CH3OH中有一半的分子发生解离, D代表所有的CH3OH都解离的吸附结构. 研究了激发态空穴从TiO2转移到CH3OH 的空穴捕获过程(图2(b)), 以及从CH3OH到TiO2的空穴释放过程(图2(c)), 同时还研究了具有一定能量的热空穴弛豫到达价带顶(VBM)的过程(图2(d)). 通过模拟, 有三点发现: i) 只有发生解离形成的CH3O (D结构及HD结构)才有捕获空穴的能力, 捕获空穴的时间尺度约为150 fs, 分子吸附的CH3OH(M结构)并不能捕获光激发空穴; ii) 空穴被CH3O捕获之后, 其中一部分会在10 fs的时间尺度内被CH3OH释放重新回到TiO2表面, 剩下的一部分留在分子上的空穴会帮助下一步的光化学反应发生; iii) 相比于没有分子吸附的干净TiO2表面, 分子的振动会加快TiO2内部热空穴向VBM的弛豫.
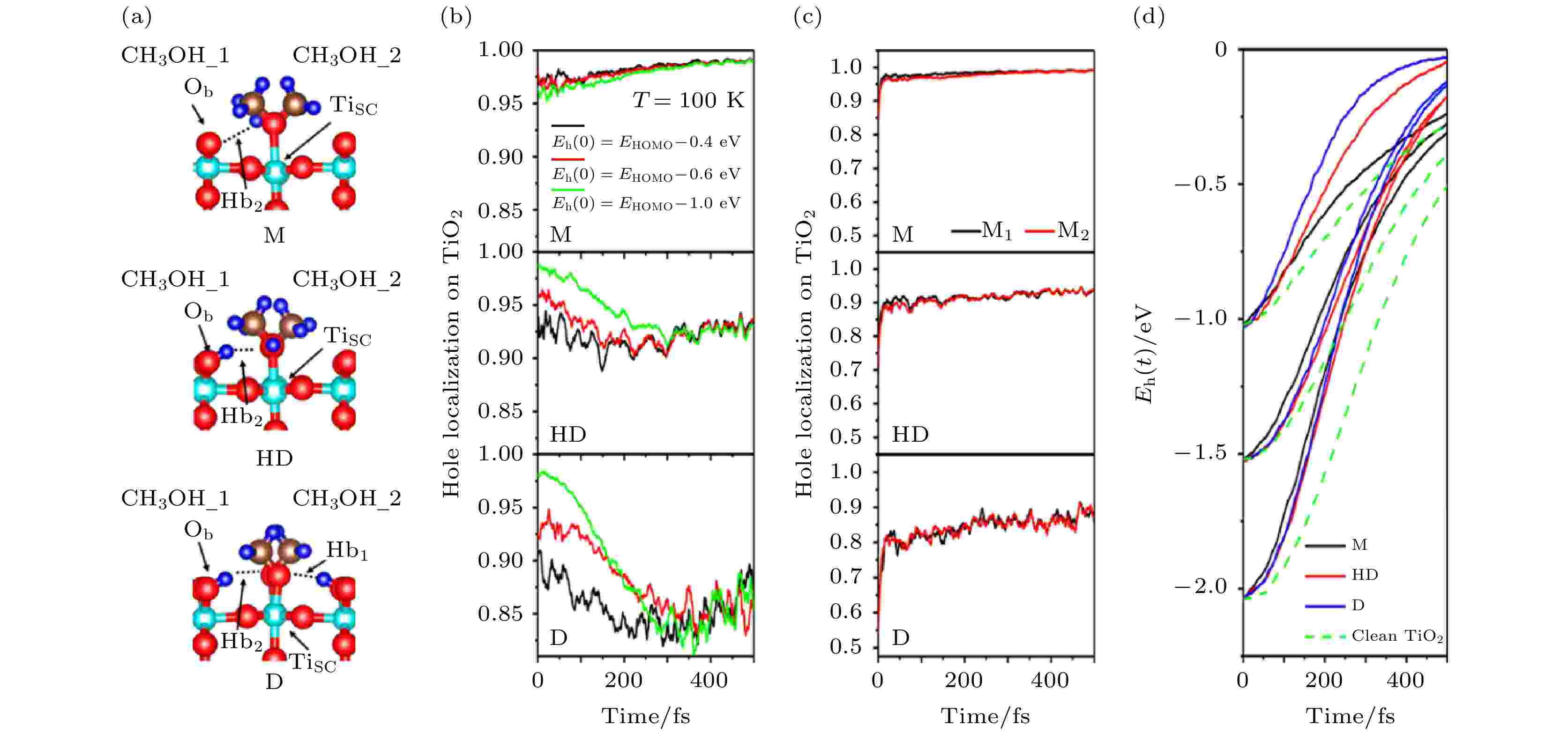图 2 (a) 单层CH3OH在TiO2表面的三种不同吸附结构; (b) 空穴捕获过程; (c) 空穴释放过程; (d) 空穴能量弛豫过程(图片经文献[47]允许转载, 版权归2016 American Chemical Society所有)
Figure2. (a) Three types of adsorption stuctures; (b) averaged forward hole transfer; (c) averaged reverse hole transfer; (d) time dependence of energy relaxation of photogenerated holes (Reprinted with permission from Ref. [47]. Copyright 2016 American Chemical Society)

这里, 只有解离的CH3O能够捕获空穴的原因来自于分子-固体的能级匹配, CH3OH的分子最高占据轨道(HOMO)位于TiO2的VBM之下约1.0 eV, 因为空穴倾向于向更高能量的能级转移, 因此, 分子吸附的CH3OH很难捕获空穴. 在CH3OH解离之后, HOMO会上移至VBM附近, 此时就具有了捕获空穴的能力. 在空穴捕获的过程中, AD与NA机制具有竞争关系, NA机制使得空穴倾向于向CH3OH转移, 而超快的空穴释放过程则由AD机制所主导. 在热空穴弛豫的过程中, 分子的振动导致了分子能级的剧烈振荡, 而这些剧烈振荡的分子能级则大大加速了空穴由高能量向低能量弛豫的过程. 在整个空穴转移动力学过程中, 分子-固体的能级匹配、分子振动及固体声子的激发、以及电声耦合的大小是决定分子捕获空穴的关键因素. 这项研究工作揭示了分子/固体表面电荷转移的时间分辨微观图像与普遍的物理机制, 其主要结论在之后的CH3OH/C3N4的时间分辨超快光谱实验中得到了验证[48].
3
3.1.2.TiO2表面CO2光还原机制
-->
3.1.2.TiO2表面CO2光还原机制
CO2的光还原是清洁能源领域内的重要问题, 其关键在于CO2捕获一个电子并形成阴离子自由基$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $. 这种电子被分子捕获的过程往往需要半导体材料的导带底(CBM)比分子的最低空轨道(LUMO)能量高, 这样在半导体中被激发的电子才能够转移到分子上[49-51]. 然而, 由于CO2的LUMO能量较高, 几乎没有半导体能提供足够高能量的电子被CO2捕获, 这成为CO2光还原的瓶颈问题[52-55].
我们以被广泛研究的Rutile TiO2(110)表面为原型体系研究了这个问题[56]. 结果发现, 如果CO2吸附在Rutile TiO2(110)表面的氧缺陷内, 并将一个电子通过光激发激发到CO2上, 这时会形成一个$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $, 由于CO2的LUMO能量较高, 电子会在一定时间内转移回到TiO2, 随后$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $就重新变回中性的CO2了. 因此, 此时光激发形成的是有一定寿命的“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $(图3(a)). 尽管“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $的寿命有限, 它的形成依然会对CO2的光还原有重要的影响. 计算表明当“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $的寿命达到13 fs时, CO2的弯曲振动模式和反对称拉伸模式会被有效激发, 随后CO2的LUMO能量将会在十几fs的时间尺度内被降低到TiO2的CBM之下, LUMO能量的降低会导致TiO2中被激发的热电子在100 fs之内被CO2捕获, 形成一个稳定的$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $(图3(b)), 并进一步在30—40 fs内将CO2还原成CO(图3(c)).
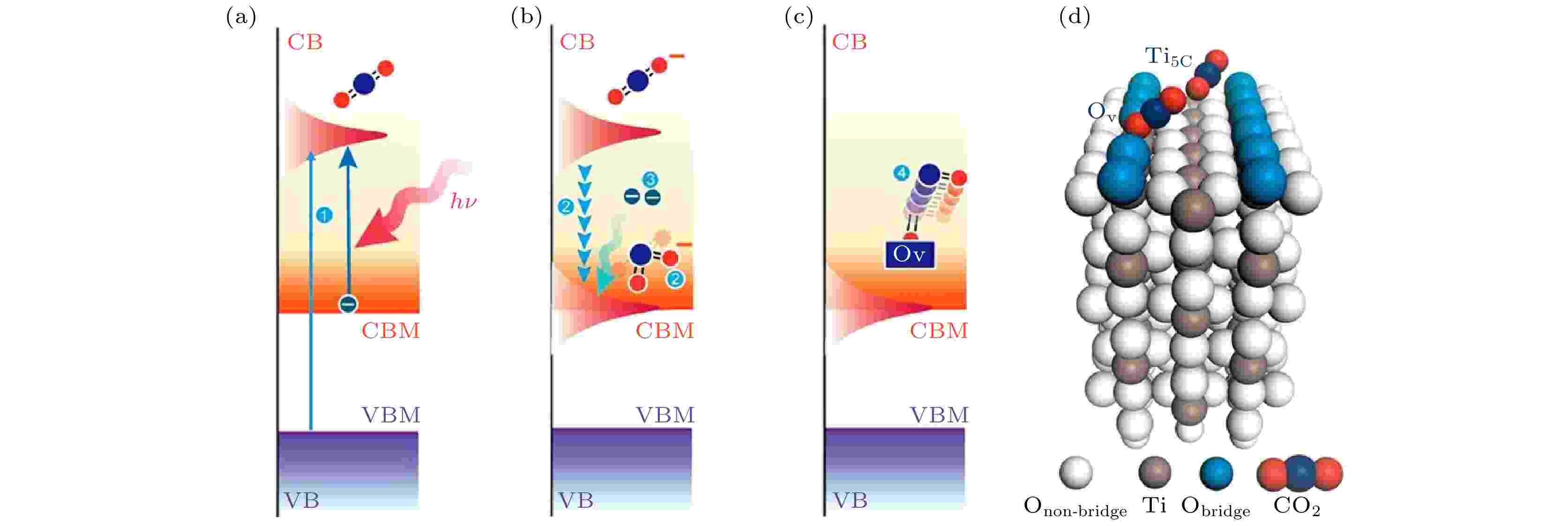图 3 TiO2表面CO2光还原示意图[56]　(a) 吸附在氧空位的CO2被光激发形成“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $; (b) “瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $激发弯曲模式和非对称拉伸模式声子, LUMO能量下降至CBM以下, 并捕获热电子, 形成稳定的 $ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $; (c) 捕获热电子之后的$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $解离形成CO; (d) CO2分子吸附在TiO2(110)表面氧缺陷和Ti5C位置的结构示意图(图片经文献[56]允许转载, 版权归2016 American Chemical Society所有)
Figure3. Photo-reduction diagram of CO2 on TiO2 surface: (a) Photo excitation generates a transient $ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $; (b) transient $ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $ excites the bending and antisymmetric stretching vibrations, which induce LUMO reduce to CBM, hot electron trapped by CO2 and form a new $ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $; (c) $ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $ dissociates in Ov; (d) geometry structure of CO2 trapped on TiO2 (110) surface (Reprinted with permission from Ref. [56]. Copyright 2016 American Chemical Society)

在整个过程中, 发生光还原的关键步骤是CO2 的LUMO的能量降低, 而导致CO2 的LUMO能量降低的原因是分子弯曲模式和非对称拉伸的振动模式的激发, 我们的研究表明, 寿命大于12 fs的“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $可以有效激发这两种振动模式. 然而, 计算表明“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $的寿命在10—15 fs范围内, 恰好是能够有效激发振动模式的阈值, 也就是说这种光化学反应有可能由于“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $的寿命不够长而无法进行, 这也许是TiO2 金红石 (110)表面CO2光还原效率不高的原因.
综上所述, CO2分子弯曲模式和非对称拉伸模式的激发可以有效提高CO2光还原效率, 我们认为这一结论可以推广到许多其他的过渡金属氧化物表面. 实际上, 除了形成“瞬态”$ {{\rm{C}}{\rm{O}}}_{2}^{\cdot -} $的方法, 在不同的表面, 还可以用表面吸附金属原子、太赫兹光激发等方法来有效激发分子特定的振动模式, 提升光还原效率.
3
3.1.3.极化/非极化氧化物异质结界面上湿电子态的超快动力学
-->
3.1.3.极化/非极化氧化物异质结界面上湿电子态的超快动力学
超过6个H2O分子形成的团簇可以有效捕获一个电子, 这种被H2O团簇束缚的电子被称为湿电子. 湿电子广泛地存在于液态物质中, 是许多生物、化学体系中非常重要的电子输运通道. 在H2O分子与固体形成固液界面体系中, 湿电子态是H2O分子贡献的能量最低的电荷输运通道, 非常弥散的波函数分布使它具有良好的输运性质, 在光催化体系中, 湿电子态被认为是激发态电子输运的关键通道[41,44,57-64]. 然而, 与单纯的H2O体系不同的是, 此时的湿电子态的能量往往高于固体的CBM, 因此湿电子会在一定寿命之内转移到固体中[58,59,63], 这使得他们很难在光催化过程中得到应用. 因此, 降低湿电子态能量是提高光催化效率的关键.
从过去的研究中可以知道, 湿电子态对表面的极化非常敏感, 因此, 我们想到可以用极化/非极化(polar-nonpolar)氧化物异质结来实现对湿电子态能量的调控. 我们选择了人们研究最多的LaAlO3/SrTiO3(LAO/STO)来进行模拟[65]. 在这个体系中, STO为非极性氧化物而LAO为极性氧化物, LAO可以为整个体系提供极化电场, 极化产生的电势随着LAO的层厚增加而增大, 而n型与p型两种界面可以提供方向相反的极化电场[66-68]. 其中LAO的层厚用所含原胞(unit cell, uc)的个数表示。如图4所示, 当一单层H2O吸附在具有p型界面的LAO/STO上时, 随着LAO层厚的增加, H2O的湿电子态会随之下降. 在层厚达到8层时降至费米面并被部分占据. 同样的道理, 如果使用n型界面, 湿电子态的能量则可以随着LAO的层厚增加而上升. 这项工作表明, 湿电子态的能量可以通过polar-nonpolar异质结的层厚来有效调制, 对提升光催化效率具有一定的意义[65].
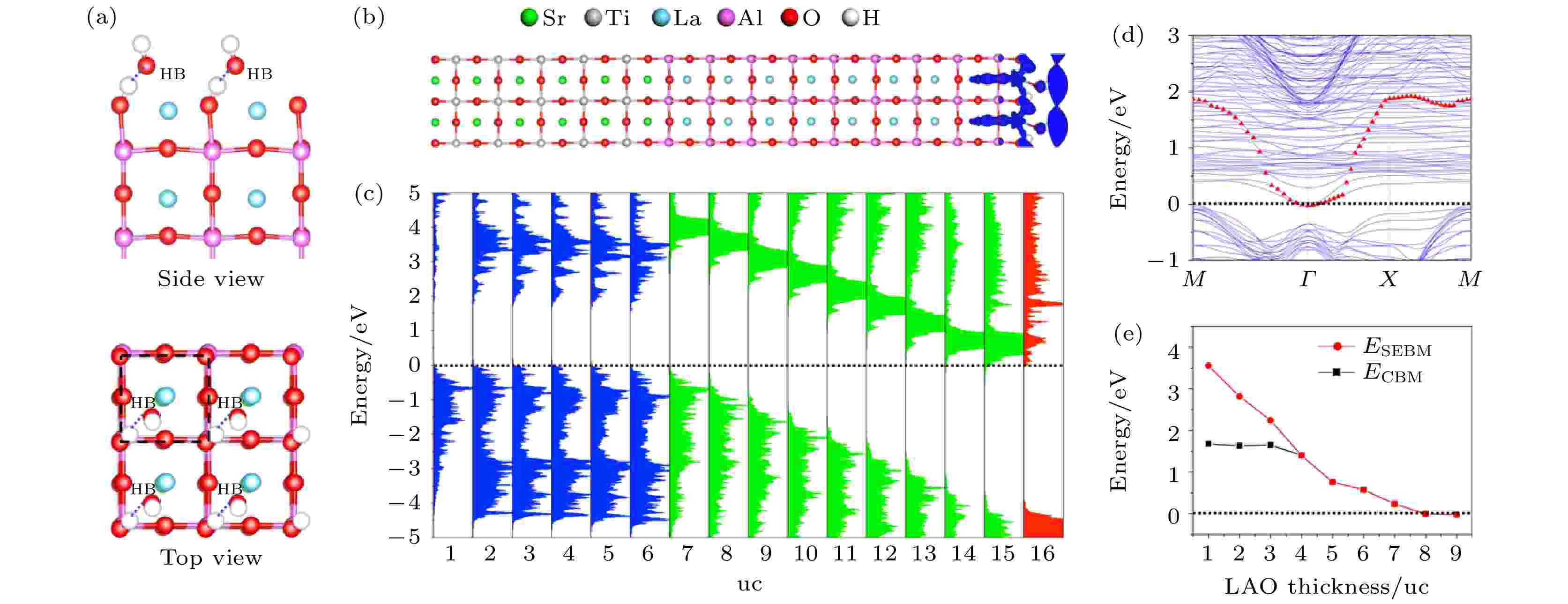图 4 (a) H2O分子吸附在p型LAO/STO异质结表面的结构图; (b) 湿电子态的轨道空间分布图; (c) LAO, STO和H2O的分层电子态密度, 分别用绿色, 蓝色, 和红色表示; (d) H2O/LAO/STO的能带结构, 其中湿电子态的能带用红色三角形标记; (e) 最低湿电子态能量和CBM能量随LAO层厚的变化情况. 在图 (c)—(e) 中, 能量零点为费米能(图片经文献[65]允许转载, 版权归2018 American Chemical Society所有)
Figure4. (a) Geometric structure of H2O adsorbed on p-type LAO/STO heterostructure. (b) Spatial orbital distribution of the solvated state in H2O layer. (c) Layer-resolved DOS for every LAO, STO, and H2O layer, represented by green, blue, and red. (d) Band structure of one ML H2O adsorbed on p-type LAO/STO. The solvated electron band is marked by red triangles. (e) Dependence of solvated electron band minimum and CBM energies on LAO thickness. The energy of VBM is set as the reference in panels (c)–(e) (Reprinted with permission from Reference 65. Copyright 2018 American Chemical Society)

3
3.1.4.C60超原子轨道在界面电荷分离上的应用
-->
3.1.4.C60超原子轨道在界面电荷分离上的应用
在太阳能转换的过程中, 热载流子在向低能级弛豫的过程中常常会将能量通过电声耦合变成热能产生损耗, 这种热能损耗过程是限制太阳能转换效率的重要因素. 想要避免这种热损耗, 需要能够将这些热电子在弛豫之前就通过界面转移到电极上. 因此, 一个能够使热电子弛豫慢、而转移快的电子态对于提高太阳能转换效率是非常重要的. 我们通过对C60/MoS2体系的研究发现, C60的超原子态 (super atom molecular orbital, SAMO) 是可以实现弛豫慢、转移快的电子态[69].
超原子态是以C60为代表的富勒烯分子的一种特殊电子态[70], 这个电子态与其他电子态不同, 它并不局域在某一个C原子上, 而是非常弥散地分布在整个碳笼上. 我们的研究发现, 由于超原子态具有非常弥散的特征, 它表现出非常弱的电声耦合效应, 因此内部热电子弛豫非常缓慢, 如图5所示, 超原子态上的电子弛豫到下面的LUMO+3电子态需要20 ps的时间. 同时, 这样弥散的轨道又非常容易和其他材料的轨道发生杂化, 造成很快的界面电荷转移, 以C60/MoS2为原型体系, 我们发现超原子态上的电子转移到MoS2上的时间尺度为150 fs. 因此, 以C60为代表的富勒烯及碳纳米材料的超原子态和近自由电子态有可能在太阳能转化方面有重要的应用.
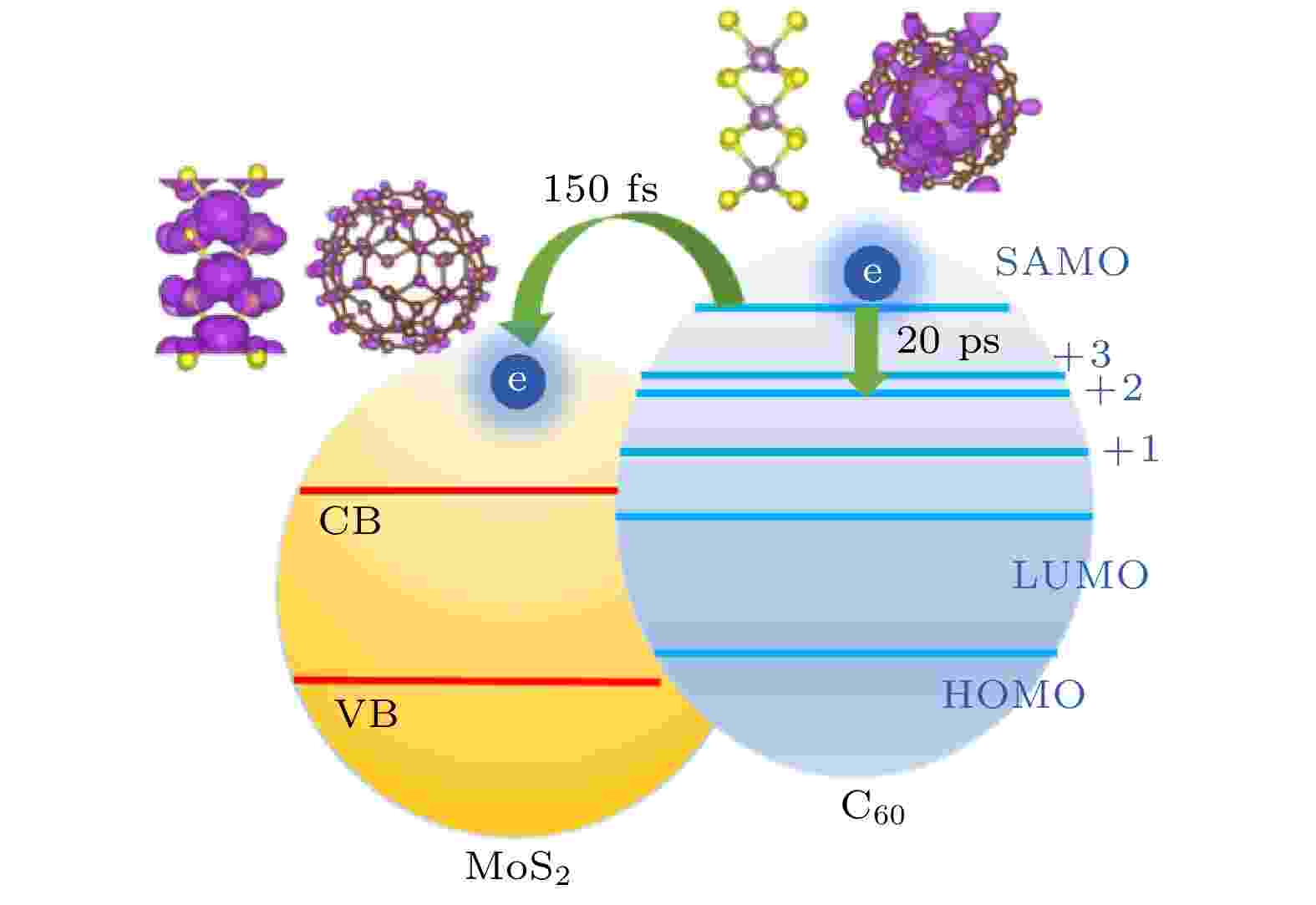图 5 MoS2/C60界面电荷分离示意图(图片经文献[69]允许转载, 版权归2018 American Chemical Society所有)
Figure5. Charge separation diagram of MoS2/C60 interface (Reprinted with permission from Ref. [69]. Copyright 2018 American Chemical Society)

2
3.2.二维材料异质结界面电荷转移动力学
-->

3.2.二维材料异质结界面电荷转移动力学

近二十年来, 二维材料大家族无疑是新材料领域中最重要的发现之一. 由于低维材料的量子限域效应, 二维材料拥有与三维材料迥异的特征. 同时, 不同的二维材料可以自由地像积木一样堆叠在一起, 形成不同的异质结, 通过这种方式可以针对不同应用需求设计新型二维材料. 我们通过Hefei-NAMD的模拟, 研究了二维过渡金属硫族化物(TMD)的界面电荷转移, 发现了声子激发在其中的重要作用, 并给出了可能的调控电荷转移动力学的方案.
3
3.2.1.纵向MoS2/WS2异质结中与声子耦合的超快电荷转移
-->
3.2.1.纵向MoS2/WS2异质结中与声子耦合的超快电荷转移
二维TMD材料是一类非常重要的二维半导体材料, 这类材料的能隙恰好在可见光范围内, 与光的相互作用很强, 电子空穴对非常容易被激发并形成激子[5,71-75]. 同时, 这类体系中还存在非常有趣的谷电子学, 会形成6个能谷并且具有自旋谷耦合效应[76-78]. 因此, 二维TMD材料一直是研究的热点.
MoS2与WS2是两种典型的TMD材料, 当它们沿垂直于表面的方向堆叠形成异质结时, 会形成第二类能带匹配, 如图6(a)所示, 这时整个体系的VBM会位于WS2层, 而CBM则位于MoS2层. 如果在MoS2上激发电子空穴对, 那么电子将从MoS2转移到WS2; 反之, 如果在WS2上激发电子空穴对, 电子则会从WS2转移到MoS2[79,80]. 由此可见, 这样的能带匹配可以使电子空穴分离, 加长电子空穴寿命, 对光电器件的应用有重要的意义.
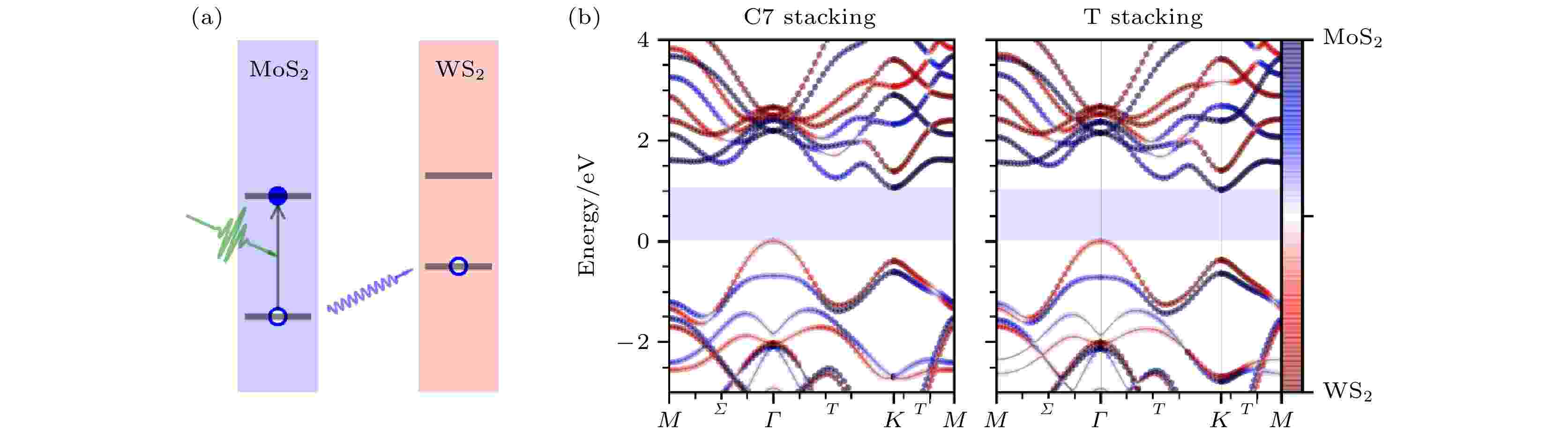图 6 (a) MoS2/WS2形成第二类能带匹配示意图; (b) MoS2/WS2异质结界面能带图(图片经文献[81]允许转载, 版权归2017 American Chemical Society所有)
Figure6. (a) Schematic of the photoexcitation and hole transfer in a MoS2/WS2 heterostructure; (b) band structures of the MoS2/WS2 heterostructure (Reprinted with permission from Ref. [81]. Copyright 2017 American Chemical Society)

虽然MoS2/WS2能够形成第二类能带匹配, 但是MoS2与WS2之间是靠范德瓦耳斯(vdW)相互作用结合在一起的, 因此, 这样的异质结界面是否能够有效发生电荷转移就成了一个问题. 然而, 与人们的直觉相反, 不同课题组的时间分辨超快动力学实验都揭示了界面的超快电荷转移过程, 因此, 理解这种超快电荷转移的物理机制成了一个重要的问题.
首先用Hefei-NAMD研究MoS2/WS2界面的激发态空穴转移动力学过程[81]. 如图6(b)所示, 异质结的VBM位于Γ点, CBM位于K点, 当空穴在MoS2/WS2中被激发之后, 初始位于K点, 但也可能能够通过电子-声子散射转移到Γ点. 选择C7和T两种最稳定的叠加构型, 并考虑了初始空穴位于K点及Γ点的情况. 首先, 当温度为300 K时, 如图7(a)—(d)所示, 无论是C7还是T堆积, 在20 fs左右都可以观察到超快的层间空穴迁移, 随后是时间尺度较长(300 —600 fs)的层内空穴弛豫过程. 在K空间中, 20 fs的超快电荷转移表示的是电子由MoS2的Γ点或K点转移到WS2的Γ与M之间的Σ点, 随后较长的时间尺度对应的是从WS2的Σ点弛豫到Γ点的VBM的过程. 进一步的分析表明, 20 fs的超快层间转移是由AD机制贡献的, 随后较慢的层内电荷弛豫, 则是由NA机制主导的. AD过程与声子的激发直接相关, 因此, 我们推测在层间的电荷转移过程中, 声子的辅助非常重要.
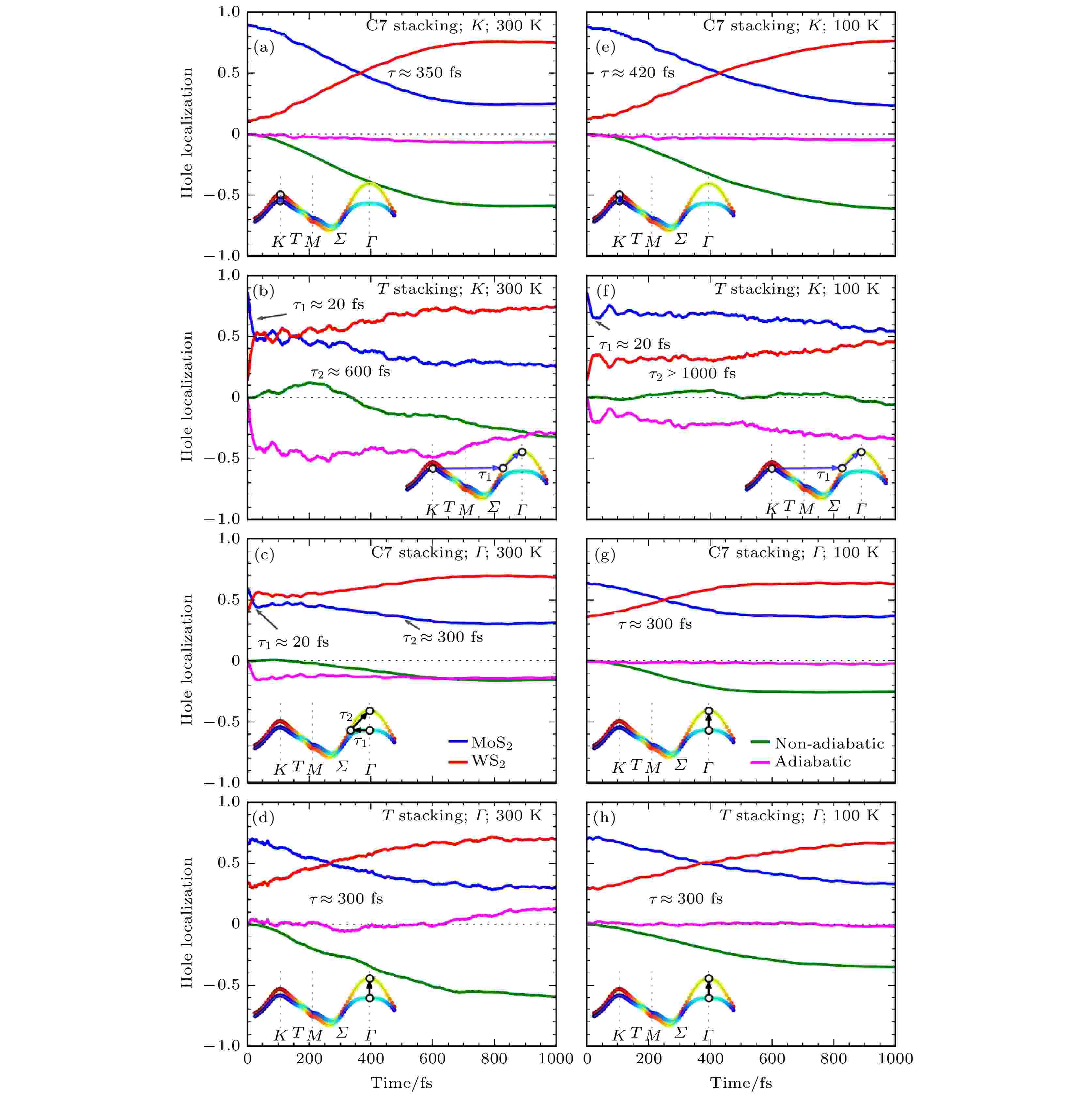图 7 C7堆积或T堆积结构布里渊区Γ点((a), (b), (e), (f))和K点((c), (d), (g), (h))空穴的空间分布随时间变化曲线, 温度分别为300和100 K. 插图给出了空穴在动量空间的演化过程(图片经文献[81]允许转载, 版权归2017 American Chemical Society所有)
Figure7. Time-dependent spatial hole localization at the K and Γ points for the C7 and T stackings at 300 K (K point ((a), (b)), Γ point ((c), (d))] and 100 K (K point ((e), (f)), Γ point ((g), (h))]. The major hole relaxation routes in momentum space are schematically shown in the insets (Reprinted with permission from Ref. [81]. Copyright 2017 American Chemical Society)

为了验证声子激发在这个过程中所起的作用, 将模拟温度由300 K降低到100 K. 如图7(e)—(h)所示, 可以看出, 温度的降低使20 fs的超快过程消失或者减少, 说明降低温度可以有效抑制层间超快电荷转移, 这证实了我们声子激发辅助超快电荷转移的概念. 通过对VBM附近的能级随时间变化的曲线做傅里叶变换(FT), 可以确定辅助超快电荷转移的声子是层内的光学支声子A1模式, 波数为400 cm–1, 周期为83和20 fs左右的层间电荷转移的时间尺度大约是四分之一周期. 值得注意的是, 在模拟中发现了很强的温度效应, 但是这个效应却没有在实验中被观察到[15]. 我们认为原因可能是: i) 模拟中没有考虑核量子效应, 考虑了核量子效应之后, 即使很低的温度下, 零点振动有可能帮助电荷转移; ii) 模拟中没有考虑电子空穴的相互作用, 也就是激子效应. 电子空穴之间的库仑相互作用和交换相互作用也有可能会影响超快电荷转移的过程.
3
3.2.2.纵向MoSe2/WSe2异质结中声子耦合的电荷振荡
-->
3.2.2.纵向MoSe2/WSe2异质结中声子耦合的电荷振荡
在MoS2/WS2异质结的电荷转移研究中, 我们提出了声子辅助超快电荷转移的概念, 基于这个概念, 我们预计将S元素换成Se元素后, 虽然体系的能带结构不会发生变化, 但是声子激发及电声耦合将会发生变化, 由此, 可以进一步理解声子对界面电荷转移动力学的影响. 于是, 针对MoSe2/WSe2异质结的界面电荷转移动力学进行了类似的NAMD模拟, 并与MoS2/WS2异质结的结果进行比较. 结果发现, 将S元素换成Se元素之后, 由于元素质量变大, A1模式频率降低, 由原来的400 cm–1降低到了约230 cm–1. 此时, 相同温度下, MoSe2/WSe2中会激发更多的声子, 能级会随着声子的激发发生剧烈的振荡. 此时, 在300 K的温度下, 如图8所示, 在MoSe2/WSe2中会观察到与声子耦合电荷振荡过程; 在温度降低至100 K时, 由于许多声子被冻结, 与声子耦合电荷振荡也会随之被抑制. 与MoS2/WS2中空穴转移的过程类似, 这个电荷振荡的过程也是AD机制导致的, 因此与声子有非常直接的耦合. 这个工作进一步确认了TMD纵向异质结界面电荷转移动力学与声子激发之间的关系[82].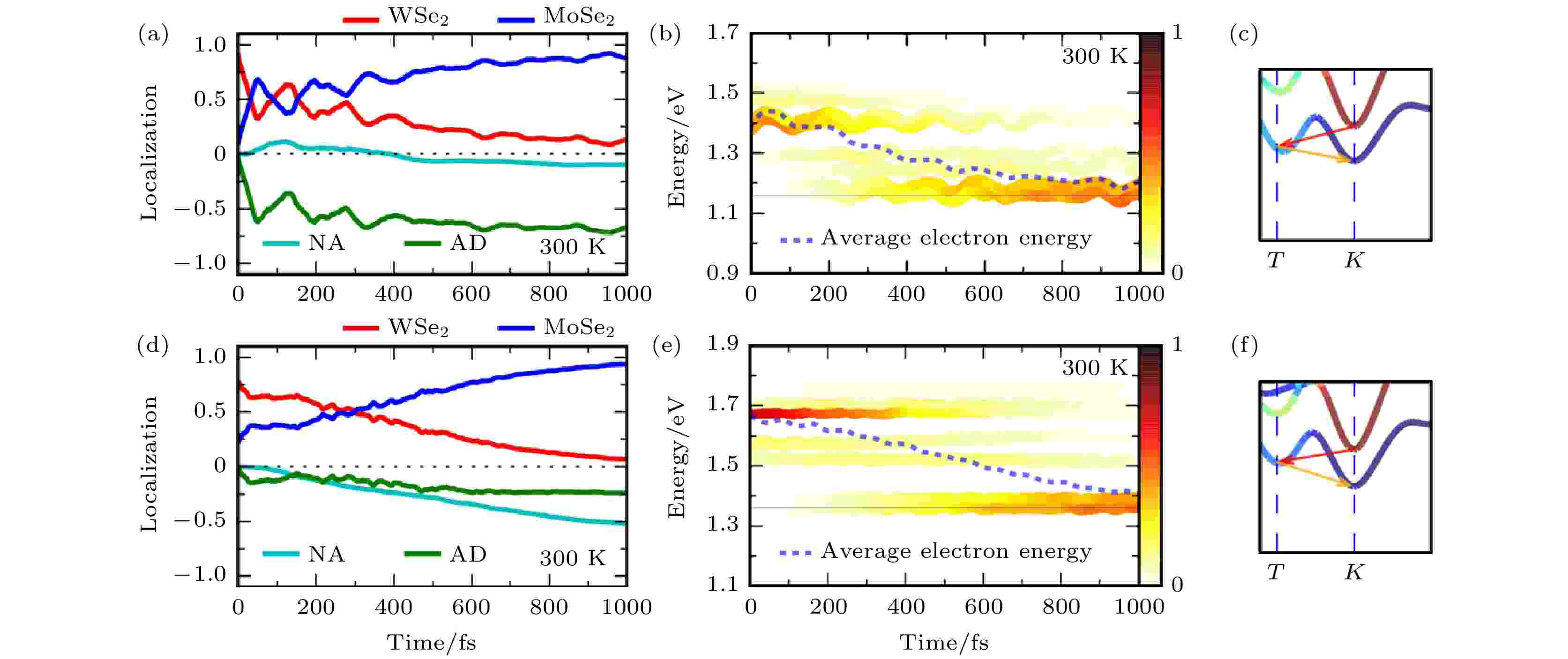
图 8 MoSe2/WSe2和MoS2/WS2异质结光激发电子非绝热分子动力学模拟结果[82]　(a)—(c) MoSe2/WSe2异质结光激发电子的转移过程, 能量变化和动量弛豫路径; (d)—(f) MoS2/WS2异质结光激发电子的转移过程, 能量变化和动量弛豫路径(图片经文献[82]允许转载, 版权归2018 American Physical Society所有)
Figure8. Nonadiabatic molecular dynamics results: (a)–(c) Time-dependent electron spatial localization, energy evolution and relaxation in the momentum space of the MoSe2/WSe2 heterostructure; (d)–(f) time-dependent electron spatial localization, energy evolution and relaxation in the momentum space of the MoS2/WS2 heterostructure (Reprinted with permission from Ref. [82]. Copyright 2018 American Physical Society)

3
3.2.3.应力控制的TMD异质结中的电荷转移
-->
3.2.3.应力控制的TMD异质结中的电荷转移
通过前面讨论的工作, 我们对TMD异质结界面的电荷转移的机制有了一些理解, 在这些理解的基础上, 我们试图提出能够调控TMD异质结电荷转移的方案. 在3.2.1节和3.2.2节中讨论了声子辅助的异质结电荷转移过程, 而声子的激发很有可能被外加应力所影响, 因此我们预计外加应力有可能成为调控异质结载流子动力学的有效手段. 我们的研究发现, 对于MoS2/WS2异质结来说, 拉伸的应力可以抑制电子的界面转移[83]. 如图9所示, 当拉伸应变从0%变到4%时, 空穴转移一直都可以进行, 而电子转移却被严重抑制了. 进一步的分析表明, 当体系没有应变时, 如图9(d)所示, WS2@K (表示倒空间K点上WS2的能级, 以下表述类似)为激发态电子的初始能级, MoS2@K是体系的CBM, 为电子最终到达的受主能级. 这两个能级所对应的轨道分别局域在WS2或MoS2单层, 轨道之间的耦合非常弱, 因此直接从WS2@K到MoS2@K的电子输运是比较困难的, 需要一个很长的时间尺度. 然而, 在这两个能级之间, 还存在一个MoS2@T可以作为电子界面转移的中间态, 它的能量位于WS2@K和MoS2@K之间, 电子的转移路径是从WS2@K到MoS2@T, 再到MoS2@K (3-2-3d). 但是当体系有了拉伸应变之后, K点能级的能量会下降, 应变达到2%的时候, WS2@K的能量就和中间态MoS2@T相当了(如图9(e)所示), 而当应变达到4%的时候, WS2@K的能量甚至低于MoS2@T了, 因此, MoS2@T作为中间态的通道就被抑制了(图9(f)).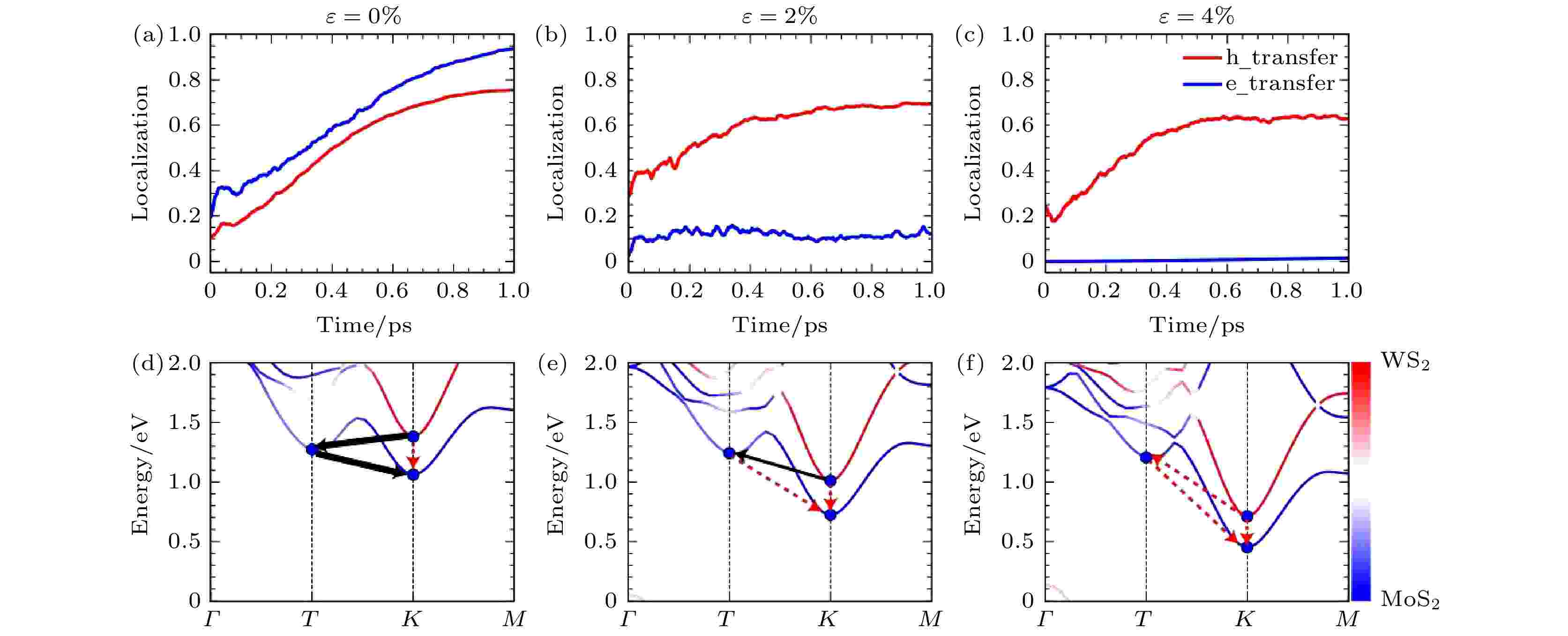
图 9 外加不同应力的情况下MoS2/WS2异质结中的电荷转移　(a)—(c) 电子空穴转移动力学; (d)—(f) 和动量空间转移路径(图片经文献[83]允许转载, 版权归2020 American Chemical Society所有)
Figure9. Charge transfer dynamics in the MoS2/WS2 heterostructure under different tensile strain: (a)–(c) Time-dependent electron and hole spatial localization; (d)–(f) charge transfer in the momentum space (Reprinted with permission from Ref. [83]. Copyright 2020 American Chemical Society)

另一方面, 很容易理解为什么空穴转移难以被外加应力抑制. MoS2/WS2的VBM位于WS2@Γ点, 是一个高度杂化的电子态, 因此这个能级一直与MoS2上的能级有较强的耦合. 即使外加应力改变了能带结构, 如果VBM仍处于强杂化状态, 则层间空穴转移总是很容易发生. 由于K点的电子态一直比较局域, 因此电子的转移需要中间态(MoS2@T)的协助, 这样的电荷转移过程就可以被外加应力所控制. 这个结论可以扩展到许多其他具有杂化VBM和局域CBM的TMD异质结构.
3
3.2.4.横向TMD异质结的超快电荷转移
-->
3.2.4.横向TMD异质结的超快电荷转移
除了沿着垂直表面方向形成的以vdW作用相结合的异质结, TMD材料还可以通过同一平面内的化学键形成横向异质结. 我们想要理解不同的相互作用对界面电荷转移的影响, 于是利用NAMD方法研究了MoS2/WS2横向异质结的激发态载流子动力学. 横向的异质结有两种界面, 分别是Armchair和Zigzag界面, 我们分别模拟了这两种界面在100和300 K下激发态电子转移动力学, 如图10所示. 首先, 研究发现界面电子转移动力学几乎不依赖于界面结构, 对于Armchair和Zigzag界面, 电子转移动力学的行为几乎是一致的. 其次, 研究表明电子转移可以分为一快一慢两个过程, 首先发生的是时间尺度约20 fs的快过程, 由AD机制贡献, 随后发生的是由NA机制贡献的慢过程, 定性上来说这两个过程的发生与垂直方向的vdW TMD异质结是类似的, 尤其是快过程都由A1声子贡献, 因此时间尺度也很类似. 对于慢过程来说横向异质结与纵向vdW异质结的时间尺度稍有不同, 因为横向异质结由化学键相连, 因此轨道之间的相互作用更强, 所以在300 K慢过程的时间尺度大约是100—120 fs, 比纵向异质结的时间尺度要更短. 当温度降低至100 K时, 慢过程被抑制, 时间尺度增大到110—150 fs[84].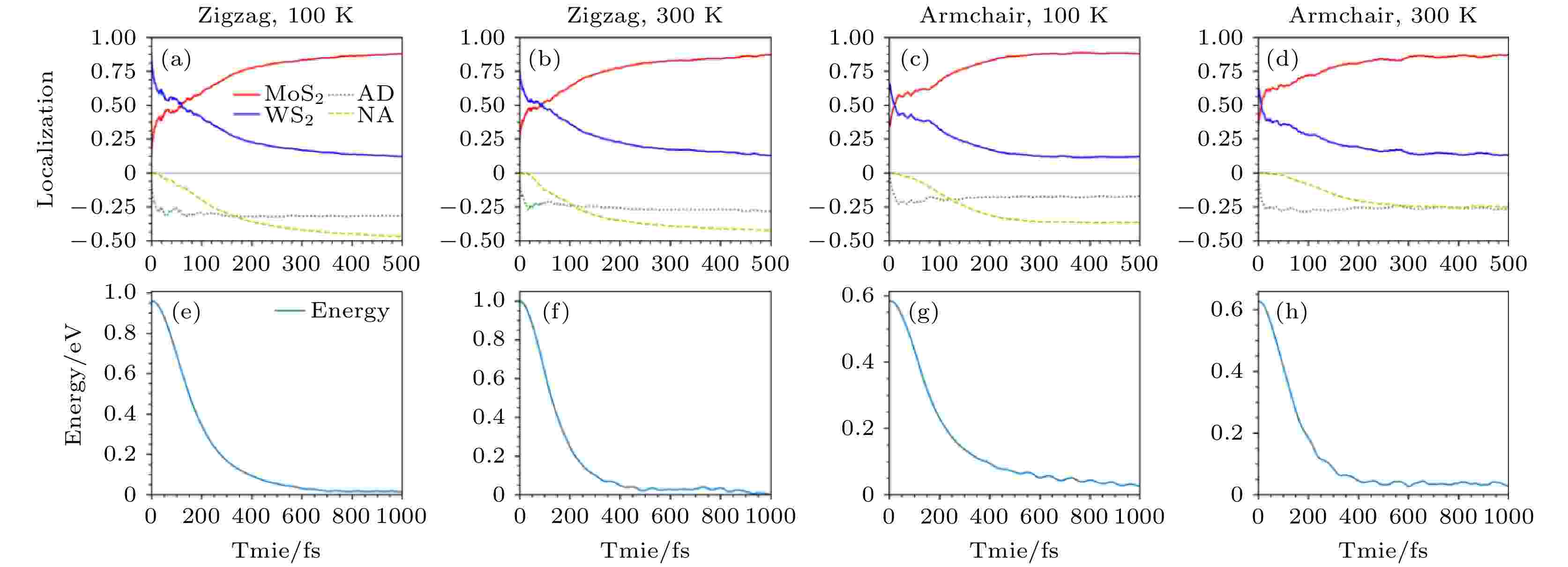
图 10 Zigzag和Armchair横向异质结在100和300 K下(a)—(d)激发态电子空间分布随时间的演化以及(e)—(h)对应的平均能量随时间的演化, 能量零点取平均的VBM值(图片经文献[84]允许转载, 版权归2019 IOP Publishing Ltd所有)
Figure10. Nonadiabatic dynamics of excited elctron in the Zigzag and Armchair MoS2/WS2 at 100 K and 300 K, respectively: (a)–(d) Time-dependent spatial localization; (e)–(h) average energy evolution. The energy of the averaged VBM is set as the reference (Reprinted with permission from Ref. [84]. Copyright 2019 IOP Publishing Ltd)

3
3.2.5.其他课题组对TMD异质结电荷转移的研究
-->
3.2.5.其他课题组对TMD异质结电荷转移的研究
应该指出的是, 除了我们课题组之外, 国内外其他课题组也对TMD异质结界面的电荷转移进行了许多研究. 北京师范大学龙闰和南加州大学Prezhdo[85]利用类似的方法研究了MoS2/MoSe2界面的电子空穴超快转移过程, 除了电声耦合效应, 他们还指出载流子的退相干效应在电荷转移过程中起到重要作用. 美国伦斯勒理工学院的张绳百教授课题组[86]利用基于TDDFT的Erhenfest NAMD方法研究了MoS2/WS2 vdW异质结界面的电荷转移. 在他们的工作中也发现A1振动模式在分子动力学中起到了重要的作用. 他们发现MoS2到WS2之间的空穴转移的时间尺度大约是100 fs, 并且伴随有两层之间的电荷振荡, 他们认为这种电荷振荡与电偶极矩的变化耦合在一起. 中国科学院物理研究所孟胜教授与北京大学刘开辉教授课题组[87]合作的超快光谱实验, 利用同样的方法研究了不同堆叠方式的MoS2/WS2的空穴转移动力学, 他们的工作发现空穴转移与堆叠方式有很强的依赖性, 对于不同的堆叠方式, 空穴转移的时间尺度可以由180 fs变化到1500 fs. 他们认为空穴的转移是通过其中最快的通道来进行的. 通过这些不同的工作可以发现, 基于TDDFT的Erhenfest 和结合了TDKS的surface hopping两种分子动力学方法对TMD界面的电荷转移动力学给出了不同的时间尺度. 作为一个新兴的领域, 两种方案都有各自不同的问题. 例如surface hopping方法的结果说明电荷转移与堆叠方式无关, 与实验符合得不错, 但是其结果中显著的温度效应却与实验有很大的偏差. 同时结合TDKS的surface hopping方法并没有考虑电子空穴的相互作用, 也就是激子效应. 针对这一点, 加州大学北岭分校的吕刚教授课题组[88]用线性响应含时密度泛函(LR-TDDFT)基组代替KS基组, 研究了MoS2/WS2界面的电荷转移动力学, 在这个层次上, 他们发现考虑了激子效应之后, 电子空穴可以以激子的方式发生层间转移, 这为电荷转移带来了更多的通道, 因此考虑了激子效应之后空穴的转移速度比单粒子基组的情况快了很多.
2
3.3.TiO2锐钛矿/金红石界面的电荷转移
-->

3.3.TiO2锐钛矿/金红石界面的电荷转移

除了TMD vdW异质结, 我们还研究了TiO2体系中的锐钛矿/金红石(Anatase/Rutile, A/R)构成的混合相TiO2异质结, 这种结构被认为具有第二类的能带对齐方式, 从而能够实现有效的电荷分离, 因此具有比单相TiO2更高的催化活性[17,89-91].
这个体系的挑战在于其界面结构难以确定, 因此, 我们首先利用自适应基因算法(adaptive genetic algorithm, AGA)[92]分别搜索了没有缺陷和有氧空位缺陷的A/R异质结. 在我们找到的9个能量最低的构型中, 没有缺陷的A/R异质结全部具有第二类的能带对齐方式, 其中VBM和CBM分别位于Rutile和Anatase相中. 然而, 在有氧空位缺陷的情况下, 却有可能形成第一类能带对齐方式, 也可能形成与没有缺陷的A/R异质结相反的第二类能带对齐方式, 也就是说, VBM位于Rutile中, 而CBM位于Anatase中.
对于无缺陷的体系, 选取AGA搜索出来的最稳定的结构进行界面电荷转移动力学模拟. 如图11所示, 当电子被激发到Rutile的CBM上之后, 在约400 fs的时间尺度内从Rutile的CBM(3.7 eV)转移到Anatase的CBM(3.2 eV)上, 空穴的转移时间尺度也很类似. 电子和空穴的转移都存在一快一慢两个过程, 快过程约20 fs, 主要由AD机制贡献, 与TiO2中光学声子密切相关, 400 fs的慢过程中, AD和NA机制都有贡献. 随着时间的增加, NA机制变得越来越重要, 但一直比AD机制的贡献小. 同时研究了电子空穴(e-h)复合的时间尺度, 发现在单相Anatase和Rutile体系中, e-h复合时间尺度分别是7.5和0.5 ns, 与前人的实验结果符合得很好. 形成A/R界面之后, e-h复合时间尺度可以达到150 ns. 与e-h复合时间尺度相比, 界面电荷转移要快得多, 因此, 我们认为对于无缺陷的A/R异质结界面, 界面电荷转移可以有效发生.
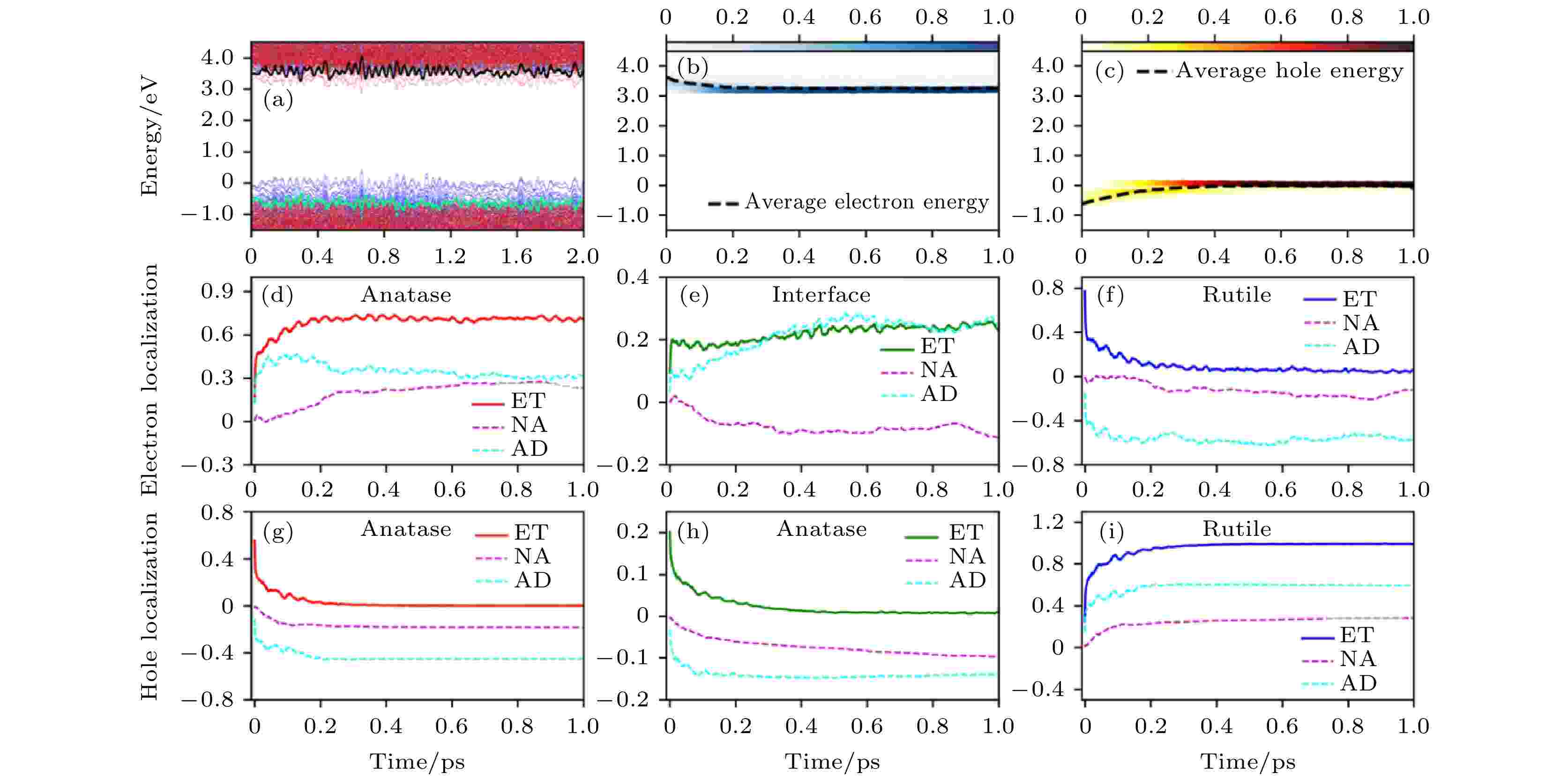图 11 无缺陷A/R异质结中的时间分辨电荷转移动力学过程　(a)电子态的能量随时间演化图, 红色和蓝色线分别代表Anatase和Rutile贡献的电子态; (b), (c) 激发态电子和空穴的能量随着时间的演化图, 颜色条表明电子和空穴在不同态上的分布情况; (d)—(i) 电子和空穴分别投影到Anatase、界面和Rutile区域上的空间分布随时间的演化曲线. 能量零点为VBM的平均能量(图片经文献[93]允许转载, 版权归2018 American Chemical Society所有)
Figure11. Time-dependent charge-transfer dynamics in stoichiometric A/R mixed-phase structure: (a) Time-dependent energy states evolution. The red and blue lines represent the states’ contribution by anatase and rutile, respectively. (b), (c) Time-dependent energy change of excited electron and hole. The color strips indicate the electron/hole distribution on different energy states and the dashed line represents the averaged electron/hole energy. (d)–(i) Time-dependent electron and hole localization projected onto the anatase, interface, and rutile regions, represented by red, olive, and blue, respectively. The energy of the averaged VBM is set as the reference in panels (a)–(c) (Reprinted with permission from Ref. [93]. Copyright 2018 American Chemical Society)

对于有氧空位的A/R异质结, 我们选择具有深缺陷能级的体系作为研究对象, 来研究电荷转移的动力学过程. 这样的深缺陷能级有可能会形成电子–空穴的复合中心. 如图12所示, 可以看到, 激发态的电子能够在初始的150 fs内从Anatase的CBM弛豫到Rutile的CBM上, 随后会在1 ps之内被缺陷态捕获. 而激发态空穴会在400 fs内转移到Anatase的VBM上, 与无缺陷A/R异质结的电子/空穴转移的时间尺度是类似的. 然而, 在1 ps内只有4%的空穴被缺陷态捕获, 这就意味着缺陷态不能有效地捕获空穴. 因此, 有氧空位A/R异质结中, 缺陷态的存在能够捕获电子但是不能捕获空穴, 在这种情况下, e-h复合的时间尺度仍然为ns量级, 界面的电荷转移可以有效发生.
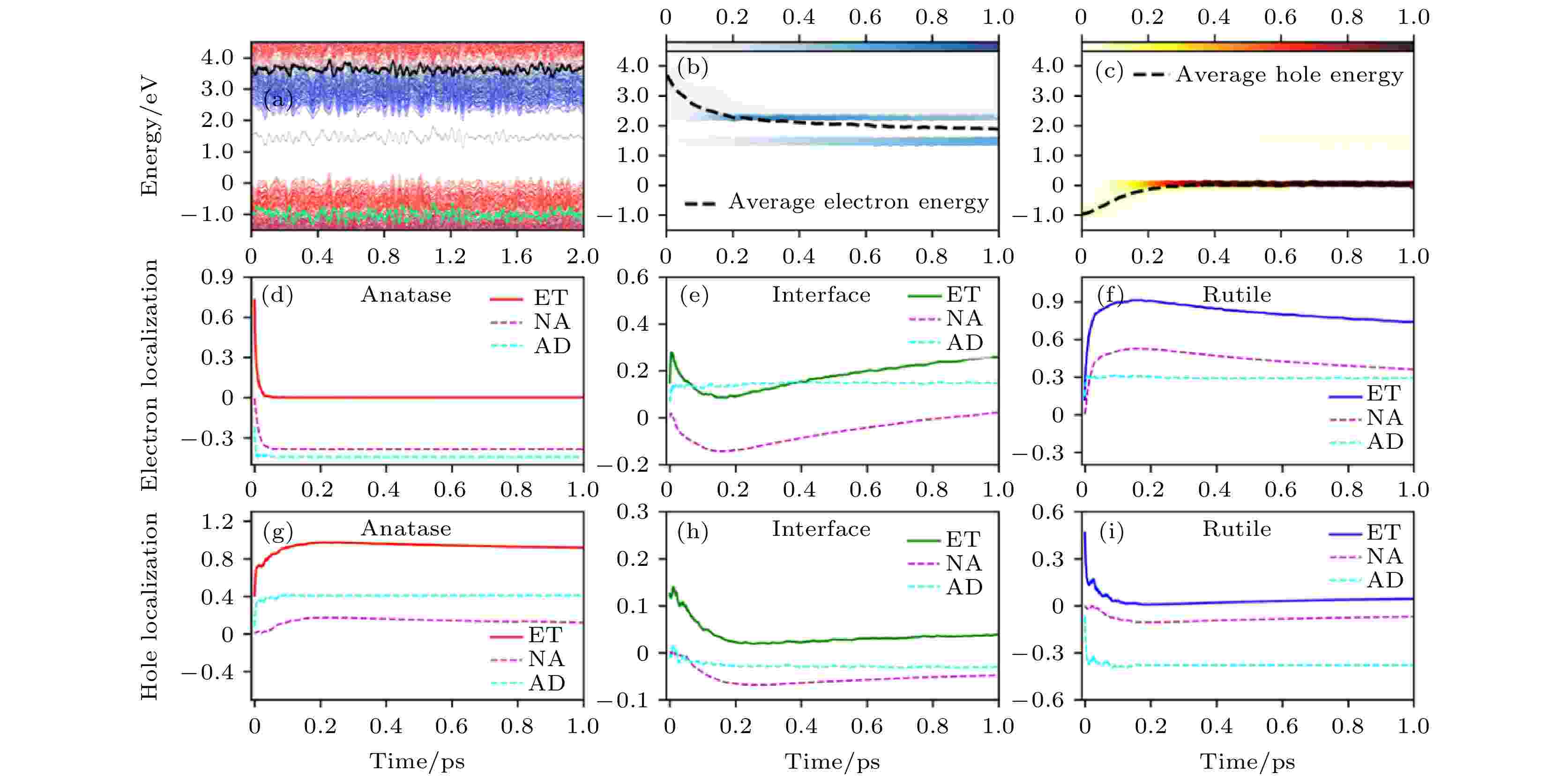图 12 有氧空位A/R异质结的电荷转移动力学过程　(a) 电子态的能量随时间演化图, 红色和蓝色线分别代表Anatase和Rutile贡献的电子态; (b), (c) 激发态电子和空穴的能量随时间的演化图, 颜色条表明电子和空穴在不同态上的分布情况; (d)—(i) 电子和空穴分别投影到Anatase、界面和Rutile区域上的空间分布随时间的演化曲线. 体系VBM的平均能量作为能量零点(图片经文献[93]允许转载, 版权归2018 American Chemical Society所有)
Figure12. Time-dependent charge-transfer dynamics in defective A/R mixed-phase structure: (a) Time-dependent energy states evolution. The red and blue lines represent the states’ contribution by anatase and rutile, respectively. (b), (c) Time-dependent energy change of excited electron and hole. The color strips indicate the electron/hole distribution on different energy states and the dashed line represents the averaged electron/hole energy. (d)–(i) Time-dependent electron and hole localization projected onto the anatase, interface, and rutile regions, represented by red, olive, and blue, respectively. The energy of the averaged VBM is set as the reference in panels (a)–(c) (Reprinted with permission from Ref. [93]. Copyright 2018 American Chemical Society)

这项研究工作表明, A/R界面的能带匹配受具体结构的影响很大, 尤其是当有氧空位存在的时候, 甚至可以形成跟无缺陷异质结相反的能带顺序. 然而, 无论是否有缺陷, 只要界面可以形成第二类半导体能带匹配, 电子/空穴的转移就可以有效地发生, 时间尺度在400 fs左右. 深能级的缺陷态可以有效地捕获电子, 但是捕获空穴的效率较低, e-h复合的时间尺度一直在ns量级. 这项工作为异质结提升太阳能转化效率提供了有力的理论依据[93].
4.激发态e-h复合研究
除了界面间的电荷迁移动力学, Hefei-NAMD还可以用来研究激发态e-h的非辐射复合, 在这个过程中, 激发态载流子通过与声子散射将能量传递给晶格, 转化为热能, 与辐射复合, 也就是发光的过程互为竞争关系. 电子空穴的非辐射复合过程通常被认为是一种能量损耗与浪费的过程, 抑制这个过程对提升材料的太阳能转化效率有非常重要的意义. 在半导体材料中, 大家通常认为缺陷和杂质可以形成电子-空穴复合中心, 早在50年代, Shockley-Read-Hall (SRH) 模型就被提出来解决这个问题[94]. 在SRH模型中, 如果缺陷或杂质可以形成能量位于能隙中间的“深能级”, 那么就会形成电子-空穴复合中心, 相反, 如果缺陷或杂质能级距离CBM及VBM很近, 也就是形成所谓的浅能级, 那么这种缺陷能级就倾向于捕获电子或空穴, 而不会形成e-h复合中心. SRH模型在几十年内被广泛地应用于半导体领域. 然而, 值得注意的是, SRH模型只考虑了缺陷/杂质能级的能量位置, 载流子从CBM/VBM到达缺陷能级的时间尺度都是作为参数来考虑的, 并没有定量地考虑电声耦合在这个过程中的作用. 而在非绝热分子动力学中, 电声耦合被更加准确地考虑了, 因此, 我们决定从不同半导体缺陷的性质出发, 利用Hefei-NAMD研究其e-h复合时间尺度, 并与SRH模型进行比较. 同时, 还提出了一些调控e-h复合时间尺度的方案.
2
4.1.掺杂TiO2中e-h复合
-->

4.1.掺杂TiO2中e-h复合

首先选择双掺杂TiO2体系来研究半导体中杂质能级对e-h复合的影响[95]. TiO2作为宽带隙半导体, 只能吸收太阳能光谱中约占5%的紫外光部分. 为了提高太阳能转换效率, 元素掺杂被认为是一种有效的调控带隙、增大光吸收的手段. 相比于单元素掺杂, 双元素掺杂的半导体材料稳定性更好. 双元素掺杂可以选择采用饱和掺杂和非饱和掺杂的方案, 饱和掺杂中阳离子杂质和阴离子杂质电荷抵消, 不会为体系提供多余的电荷, 而非饱和掺杂中则会引入多余的电荷[11,96]. 然而, 掺杂形成的缺陷态也可能成为e-h的复合中心, 这又导致光转换效率下降. 为了研究e-h复合中心形成的物理机制, 我们使用NAMD方法研究了不同的双元素掺杂对TiO2中e-h复合速率的影响. 如图13所示, 当采用非饱和掺杂, 例如Cr-N掺杂时, 多余的电子会在能隙中间形成一个缺陷能级, 电子空穴会在ps量级内完成复合; 如果采用饱和掺杂的方案, 例如V-N掺杂, 那么只会在CBM引入浅能级, 而浅能级的引入不会导致电子空穴的迅速复合. 由此发现, 在TiO2体系中, 深能级可以形成e-h复合中心, 而浅能级则不能, 这与SRH模型给出的物理图像是一致的.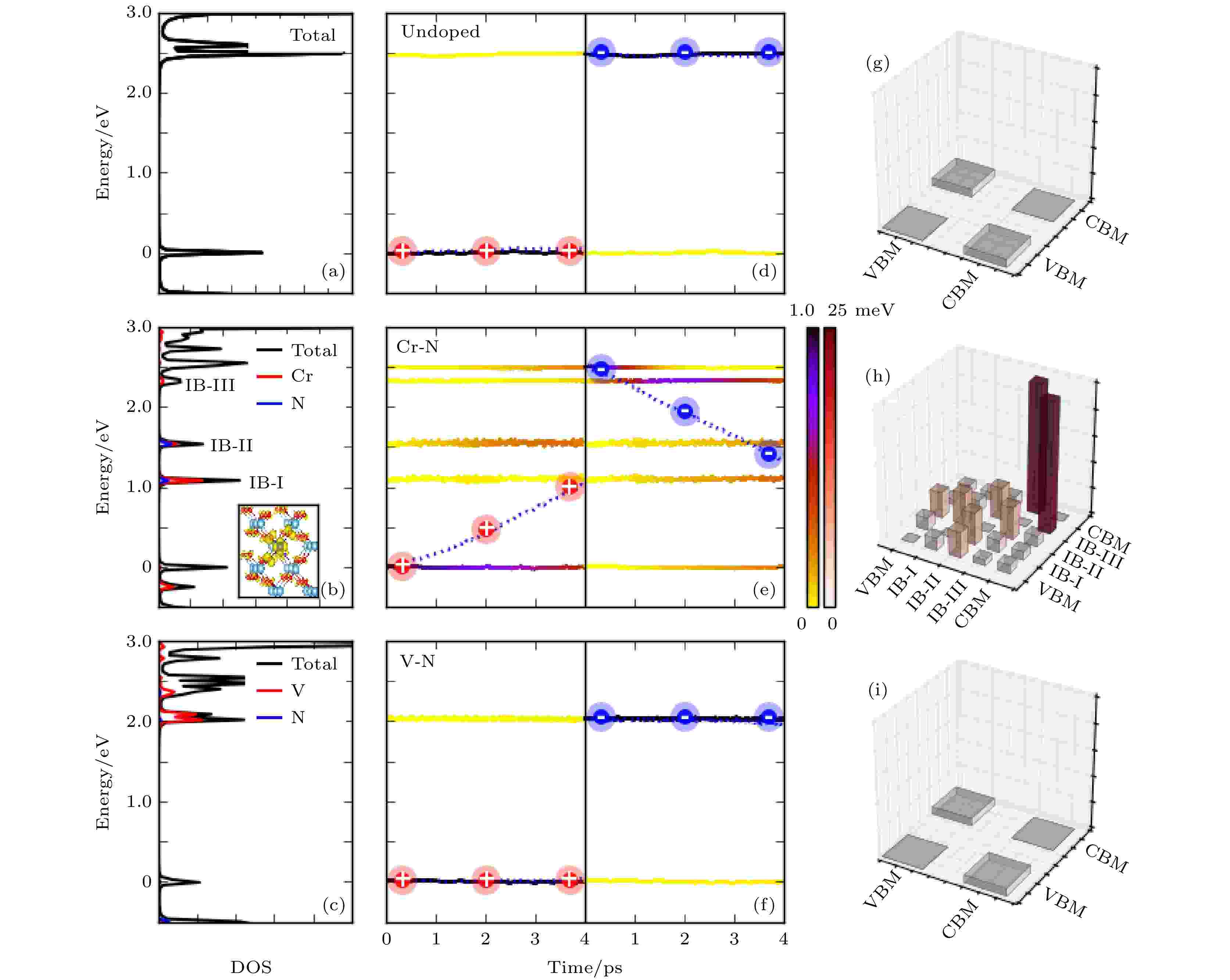
图 13 不同掺杂方案的TiO2体系的电子结构和含时演化的电子/空穴复合动力学过程以及非绝热耦合值, 包括: 干净的TiO2、Cr-N掺杂和V-N掺杂的TiO2体系　(a)—(c) 体系的总态密度及杂质原子的分态密度分布. (d)—(f) 体系在300 和100 K温度下e-h复合的含时演化. 颜色条表示电子/空穴弛豫到不同能态上的分布, 虚线表示电子/空穴的平均能量值. 图中的能级都是以平均的VBM能量为零点. (g)—(i) 相关能级之间的NAC (图片经文献[95]允许转载, 版权归2018 American Chemical Society所有)
Figure13. Electronic structures and the time-dependent electron/hole (e/h) dynamics in undoped, Cr–N- and V–N-doped TiO2: (a)–(c) The total and partial DOS. (d)–(f) The averaged time-dependent e/h energy relaxation at 300 K. The color strip indicates the e/h distribution on different energy states, and the dashed line represents the averaged e/h energy. The energy reference is the average VBM energy. (g)–(i) The averaged NAC elements in undoped and Cr–N- and V–N-doped TiO2 at 300 K. The inset in panel b shows the spatial distribution of the excess charge induced by Cr–N codoping, in which the Ti, O, Cr, and N atoms are marked by large light blue, small red, large deep blue, and small purple balls, respectively (Reprinted with permission from Ref. [95]. Copyright 2018 American Chemical Society)

我们进一步的分析表明, Cr-N掺杂的深能级之所以可以形成e-h复合中心, 主要是由于杂质声子的作用. 当Cr-N掺杂引入一个多余电荷之后, 杂质与周围的TiO2形成了较强的耦合, 因此 Cr-N杂质的声子激发会导致周围的TiO2原子一起发生共振, 如图14所示, 此时激发杂质声子, 会导致电子空穴的快速复合. 相反, 如果激发一个只有TiO2的声子模式, 电子空穴则复合很慢, 这说明e-h复合主要是杂质声子导致的. 而对于饱和型的V-N掺杂, 杂质的振动局域在V-N之间, 周围的TiO2原子不会随之一起振动, 这种局域的杂质声子的影响有限, 不会造成e-h复合中心. 我们进一步通过数据拟合给出了声子局域程度与e-h复合时间的曲线, 如图15所示, 二者几乎呈现指数关系, 局域杂质声子不容易加速电子空穴的复合.
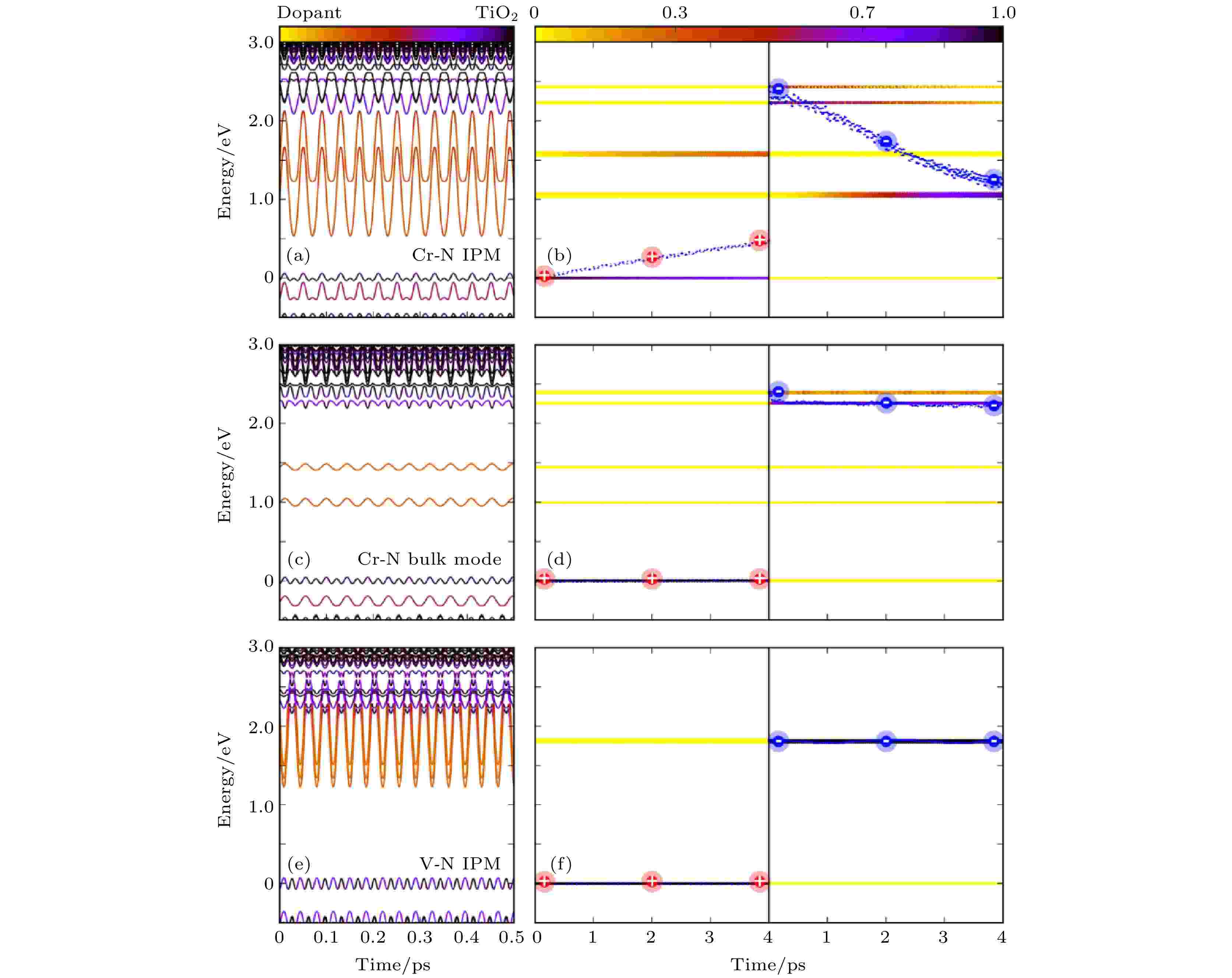图 14 通过激发单一声子模式来研究e-h复合动力学　(a), (b) 激发Cr-N掺杂TiO2中的杂质声子模式; (c), (d) 激发Cr-N掺杂TiO2中的体相声子模式; (e), (f) 激发V-N掺杂TiO2体系中的杂质声子模式. 图中的能量零点为平均的VBM. (a), (c), (e) 中的颜色条表示的是能级轨道分布的投影(黑色代表投影到TiO2上的权重, 黄色代表投影到杂质原子上的权重). (b), (d), (f) 中的颜色条代表含时演化过程中电子/空穴弛豫到不同能级上的分布(图片经文献[95]允许转载, 版权归2018 American Chemical Society所有)
Figure14. Frozen phonon NAMD results for time evolutions of the energy states near VBM and CBM and the averaged time-dependent e/h energy relaxation for Cr–N- and V–N-co-doped TiO2: (a), (b) IPM for Cr–N-doped TiO2; (c), (d) A single bulk mode for Cr–N-doped TiO2; (e), (f) IPM for V–N-doped TiO2. The energy reference is the average VBM energy. The color map in (a) indicates the orbital localization (black on TiO2 and yellow on dopant). The color map in (b) indicates the e/h distribution on different energy states (Reprinted with permission from Ref. [95]. Copyright 2018 American Chemical Society)

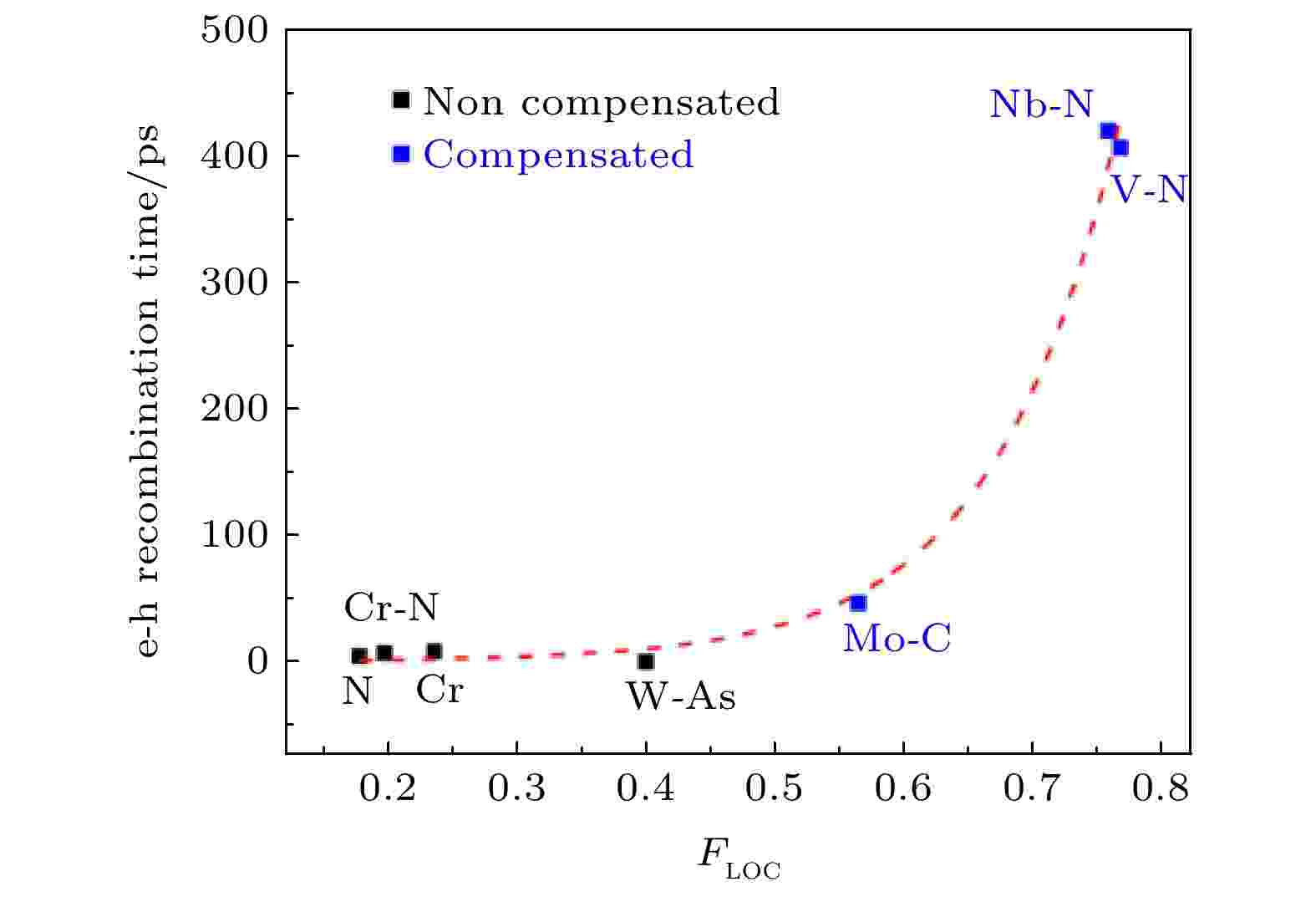图 15 不同掺杂元素的TiO2体系的e-h复合时间与杂质声子局域度的关系[95]. 虚线表示拟合得到的指数曲线(图片经文献[95]允许转载, 版权归2018 American Chemical Society所有)
Figure15. e-h recombination time in different doped TiO2. The fitting exponential correlation is shown with dashed lines (Reprinted with permission from Ref. [95]. Copyright 2018 American Chemical Society)

2
4.2.单层黑磷中的e-h复合研究
-->

4.2.单层黑磷中的e-h复合研究

在传统的半导体材料TiO2中, 我们发现NAMD方法得到的结论和SRH模型是一致的. 随后, 我们选择单层黑磷作为二维半导体的代表来研究缺陷和杂质对e-h复合的影响. 分别研究了黑磷的本征缺陷、氧化物吸附和同族元素掺杂这三种情况. 出乎意料的是, 我们发现SRH模型在黑磷这个体系中完全失效了, 在我们研究的几种情况中, 电子-空穴复合中心都没有形成[97].
首先研究了黑磷中3种不同的本征缺陷对e-h复合动力学的影响, 三种缺陷包括磷空位(Pv)、磷填隙(Pint)和磷吸附(Pad). 这三种缺陷都会在带隙内引入杂质能级, 不同的是, Pv和Pint引入的是靠近VBM较浅的杂质能级; 而Pad引入的是位于带隙中间较深的杂质能级. 出乎意料的是, 如图16所示, NAMD结果表明它们都不会加速e-h复合过程. 无缺陷的黑磷体系e-h复合时间尺度为375 ps, 对于Pv体系, 65%的空穴在80 ps内被缺陷态捕获, 之后需要超过300 ps的时间与CBM的电子复合. 整个体系的e-h复合时间是528 ps, 是无缺陷黑磷的1.5倍. 对于Pint体系, 空穴在VBM和缺陷态之间于5 ps内迅速达到平衡分布, 这是因为两者之间能级几乎简并的缘故. 达到平衡分布之后, 这些在VBM和缺陷态上的空穴与CBM的电子在316 ps内发生复合, 和无缺陷黑磷非常接近. 最有趣的结果是, 对于Pad体系, 尽管缺陷能级位于能隙中间, 但是缺陷捕获空穴的过程发生得很缓慢, 总的e-h的复合时间尺度是473 ps, 是无缺陷黑磷的1.3倍. 因此, 我们发现Pad形成的深能级不仅没有形成e-h复合中心, 而且还使得e-h复合变慢了.
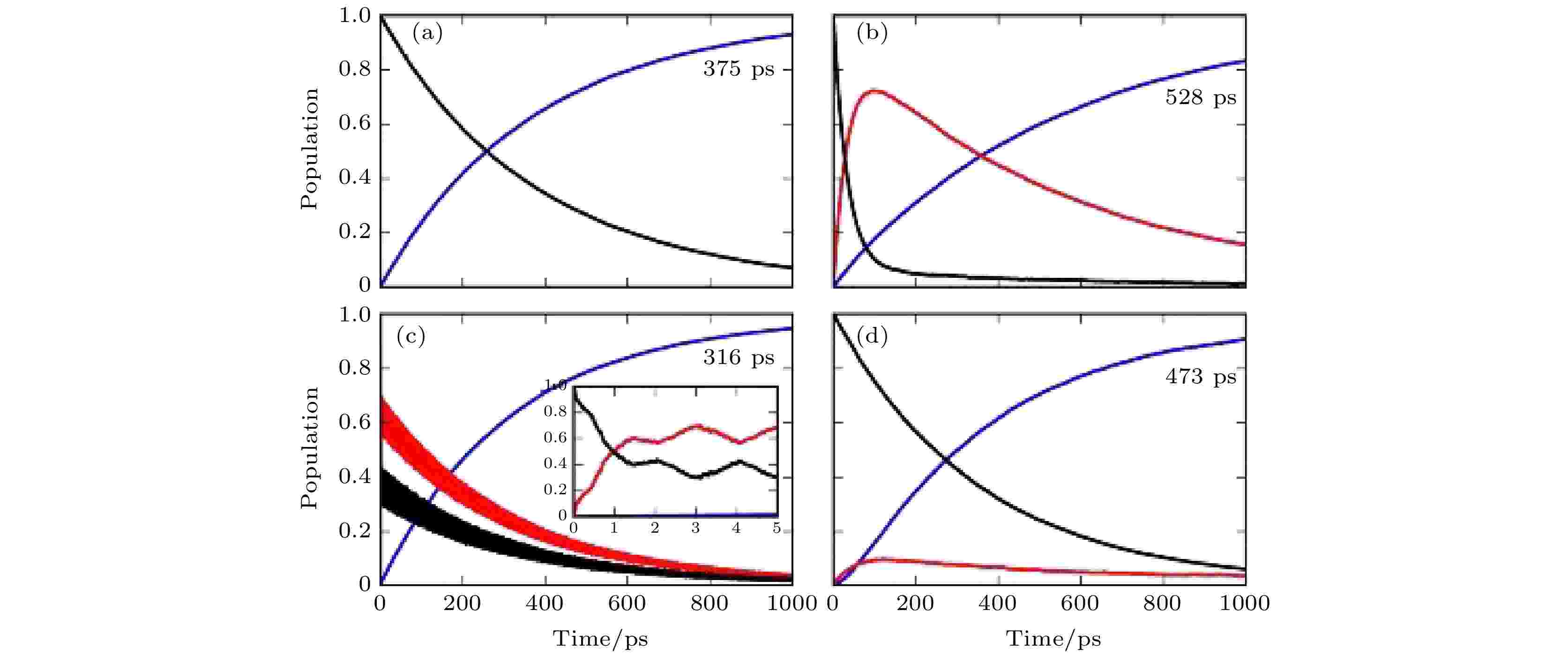图 16 (a) 纯净的BP单层, (b) Pv, (c) Pint和(d) Pad缺陷体系中e-h复合动力学过程. 初始态对应的是VBM上占据一个空穴. VBM, CBM以及缺陷态的空穴占据数分别用黑色、蓝色和红色线条表示. (c) 图中的小插图表示的是在Pini体系中空穴在VBM和缺陷态之间迅速达到一个平衡, 这是由于两个能态之间几乎简并的原因(图片经文献[97]允许转载, 版权归2019 American Chemical Society所有)
Figure16. e–h recombination dynamics in (a) pristine BP monolayer, (b) Pv, (c) Pint, and (d) Pad systems. The initial state corresponds to the electron excitation from the VBM to the CBM. Populations of the excited, ground, and defect states are shown by the black, blue, and red lines, respectively. The inset in panel (c) demonstrates fast hole equilibration between the VBM and the defect state attributed to the near-degeneracy between them (Reprinted with permission from Ref. [97]. Copyright 2019 American Chemical Society)

在NAMD模拟中, e-h复合时间的决定性因素是非绝热耦合矩阵(NAC)和电子态的退相干时间. NAC越大, 相干时间越长, 动力学过程越快. 影响NAC的因素主要有三个: 能级差、电声耦合矩阵元以及原子核的运动速度. 而声子的激发则是导致电子态退相干的重要因素. 图17给出了无缺陷黑磷及三种缺陷黑磷体系的CBM, VBM, 缺陷态之间的能隙随时间变化的FT谱, 可以反映不同能态之间的电声耦合信息. 我们发现, 首先, 与掺杂的TiO2体系不同, 黑磷的缺陷没有引入具有明显特征的缺陷声子, 然而, 缺陷会引入许多频率较低的声子, 这些低频声子对应的原子核运动速度较慢, 导致NAC减小, 同时, 无缺陷的黑磷CBM, VBM以及缺陷态耦合的声子频率比较单一, 而缺陷导致的这些不同频率的声子还会导致电子态的相干寿命缩短. 因此, 在黑磷体系中, 缺陷不但没有引入e-h复合中心, 反而使得e-h复合变得更慢了.
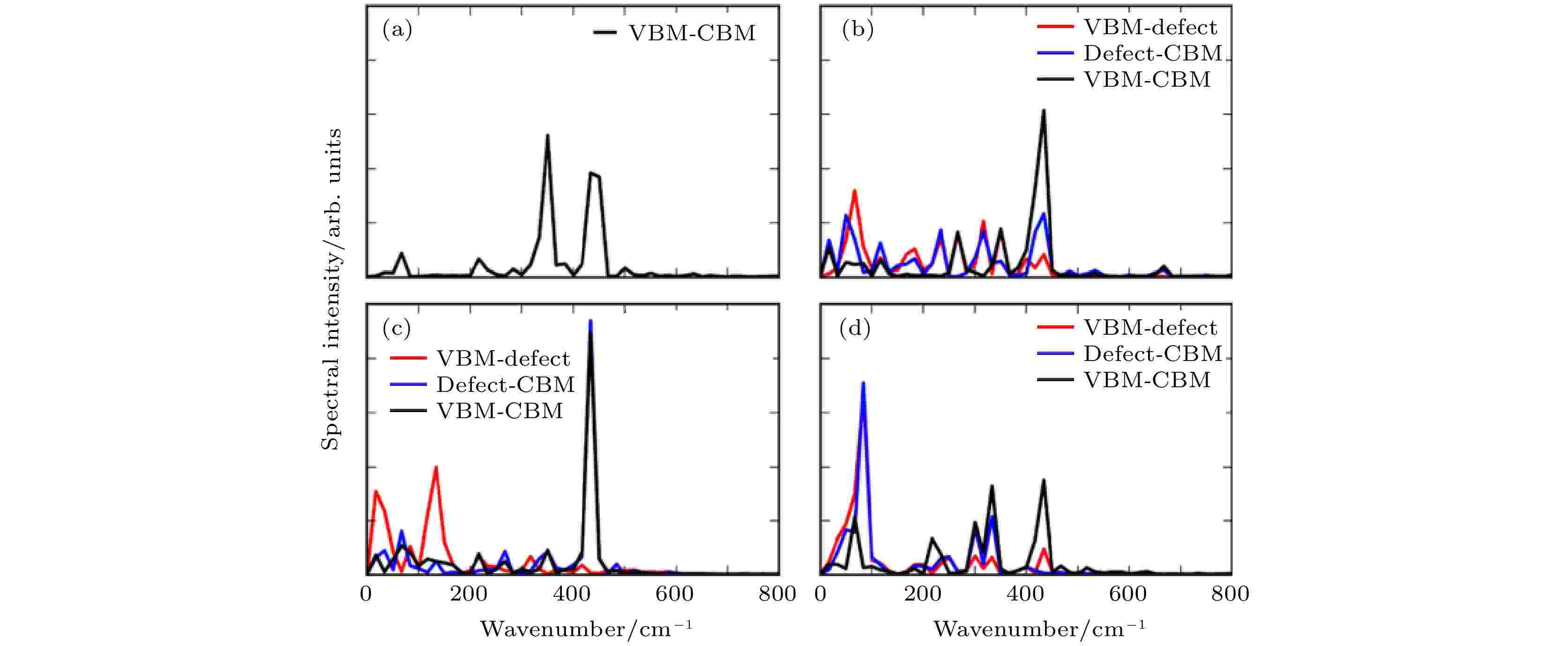图 17 (a) 纯净的BP单层, (b) Pv, (c) Pint和(d) Pad缺陷体系中VBM, CBM及缺陷态之间能级差含时振荡的FT变换(图片经文献[97]允许转载, 版权归2019 American Chemical Society所有)
Figure17. FT phonon-induced fluctuations of the energy gaps between the VBM, the CBM, and the defect states for (a) pristine BP monolayer, (b) Pv, (c) Pint, and (d) Pad systems (Reprinted with permission from Ref. [97]. Copyright 2019 American Chemical Society)

我们用类似的方法研究了O和O2吸附、O掺杂和H2O吸附在黑磷上的情况, 与黑磷本征缺陷的情况类似, 无论是否产生深能级, 都不会产生e-h复合中心[98]. 龙闰教授等[99]用类似的方法研究了黑磷的双空位缺陷, 他们也得到了缺陷使e-h复合时间变长的结论.
由以上的分析可以知道, e-h复合的时间尺度受到NAC的影响, 而NAC正比于原子核的速度, 因此, 我们设想, 如果用不同质量的同族元素对黑磷进行掺杂, 那么应该可以对e-h复合的时间尺度进行调控. 于是, 我们对黑磷进行了N, As, Sb, Be的掺杂, 发现同族元素的掺杂不会在能隙中间带来杂质能级, 同时, 对CBM, VBM轨道分布的影响也非常小, 因此, 我们认为影响e-h穴复合时间的因素基本只有掺杂元素的质量. 通过计算发现, 掺杂黑磷的e-h复合时间与掺杂元素的质量有正相关的关系, 掺杂元素越重, e-h复合时间越长. 由此, 可以利用不同元素的掺杂对黑磷的激发态载流子寿命进行调控[100].
从对黑磷的研究中发现, NAMD给出的结果与SRH模型并不一致, NAMD的结论说明在黑磷中引入缺陷很难形成e-h复合中心. 我们认为这首先与黑磷是一种单质材料有关, 对于单质材料来说, 引入本征缺陷并不容易引入多余的电荷, 因此, 也就不会形成类似TiO2体系中的杂质声子. 其次, 我们发现e-h复合时间的变慢主要源于低频声子的激发, 这与黑磷作为二维材料硬度较低是有关系的, 这一结论解释了黑磷材料在光催化及光电器件领域优异的性质[101-109].
2
4.3.太阳能电池材料MAPbI3中e-h复合的性质
-->

4.3.太阳能电池材料MAPbI3中e-h复合的性质

在黑磷体系中, 我们发现SRH模型失效, 其原因与黑磷材料硬度较低有关. 于是, 我们进一步研究了太阳能电池材料金属卤化物钙钛矿[110], 这也是一种硬度较低的半导体材料. 研究了由甲基胺碘化铅钙钛矿(MAPbI3)中的点缺陷而引起的非辐射复合过程. 研究了5种不同缺陷, 包括一种填隙缺陷: 碘填隙(Ii); 两种空位缺陷: Pbv和Iv; 两种取代缺陷: MA分子被I和Pb取代(MAI和MAPb). 这几种缺陷被认为是这种材料中最稳定的几种缺陷[111]. 如图18所示, 这几种材料中Ii和MAI形成了深能级, 其他三种缺陷形成浅能级. 这些不同的电子给了我们研究e-h复合的很好样本.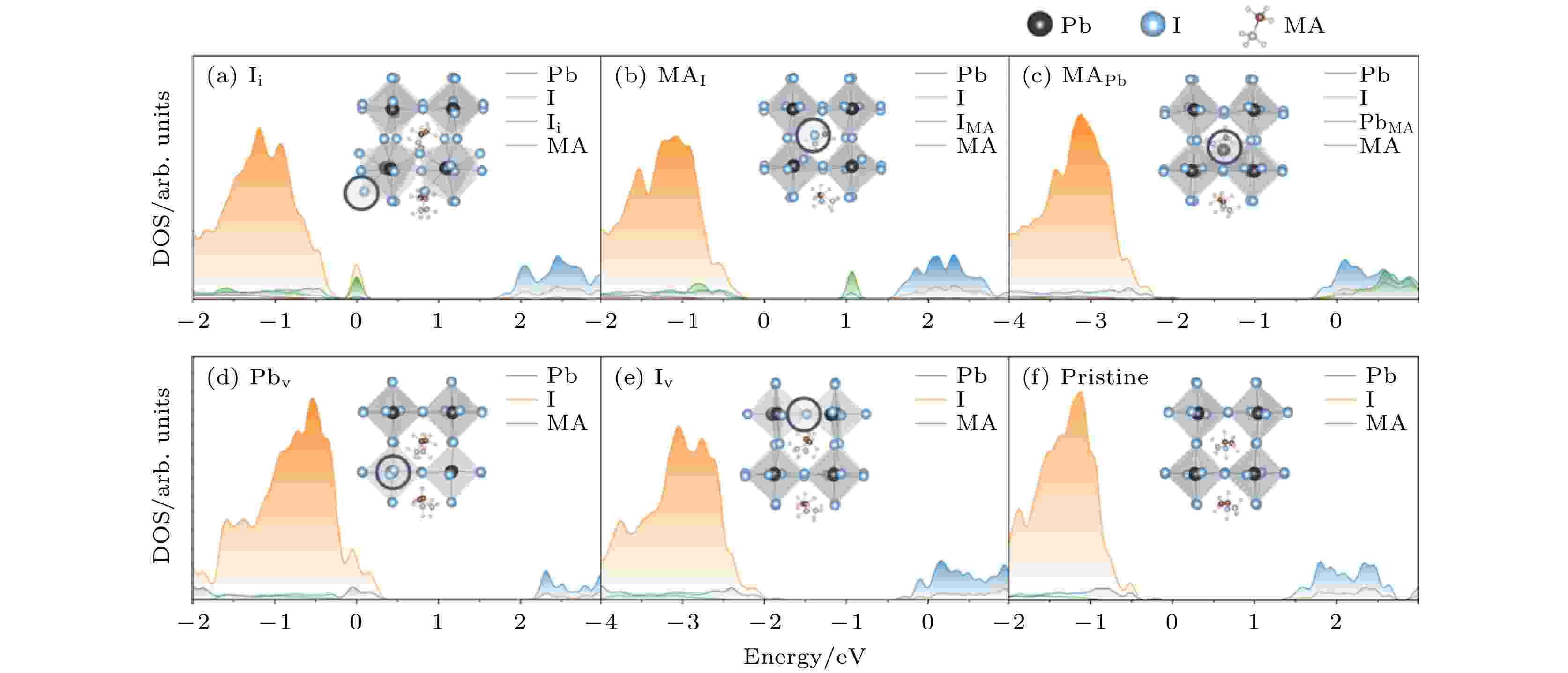
图 18 五种缺陷构型和无缺陷构型的能态态密度以及对应的晶胞结构. 能量零点为费米能, 圆圈表示缺陷的位置(图片经文献[102]允许转载, 版权归2020 American Association for the Advancement of Science所有)
Figure18. Atom-projected DOS for different defective and pristine MAPbI3. ((a)–(f)) Defective and Pristine systems of MAPbI3. The energy reference is located at the Fermi level. Inset shows corresponding atomic structure, with blue circle indicating the defect location (Reprinted with permission from Ref. [102]. Copyright 2020 American Association for the Advancement of Science)

图19给出了不同缺陷体系和无缺陷MAPbI3 e-h复合的动力学信息, 电子可以通过缺陷能级复合(间接复合), 也可以通过CBM和VBM直接复合. 与黑磷体系类似, 在MAPbI3中, 也没有观察到e-h复合中心的形成. 相反, 对于有的缺陷, 例如Ii, 对e-h复合反而有明显的抑制. 对于无缺陷体系, 约19%的e-h在2 ns内发生复合, 估计e-h寿命约为11 ns, Ii缺陷构型e-h复合时间则约为23 ns.
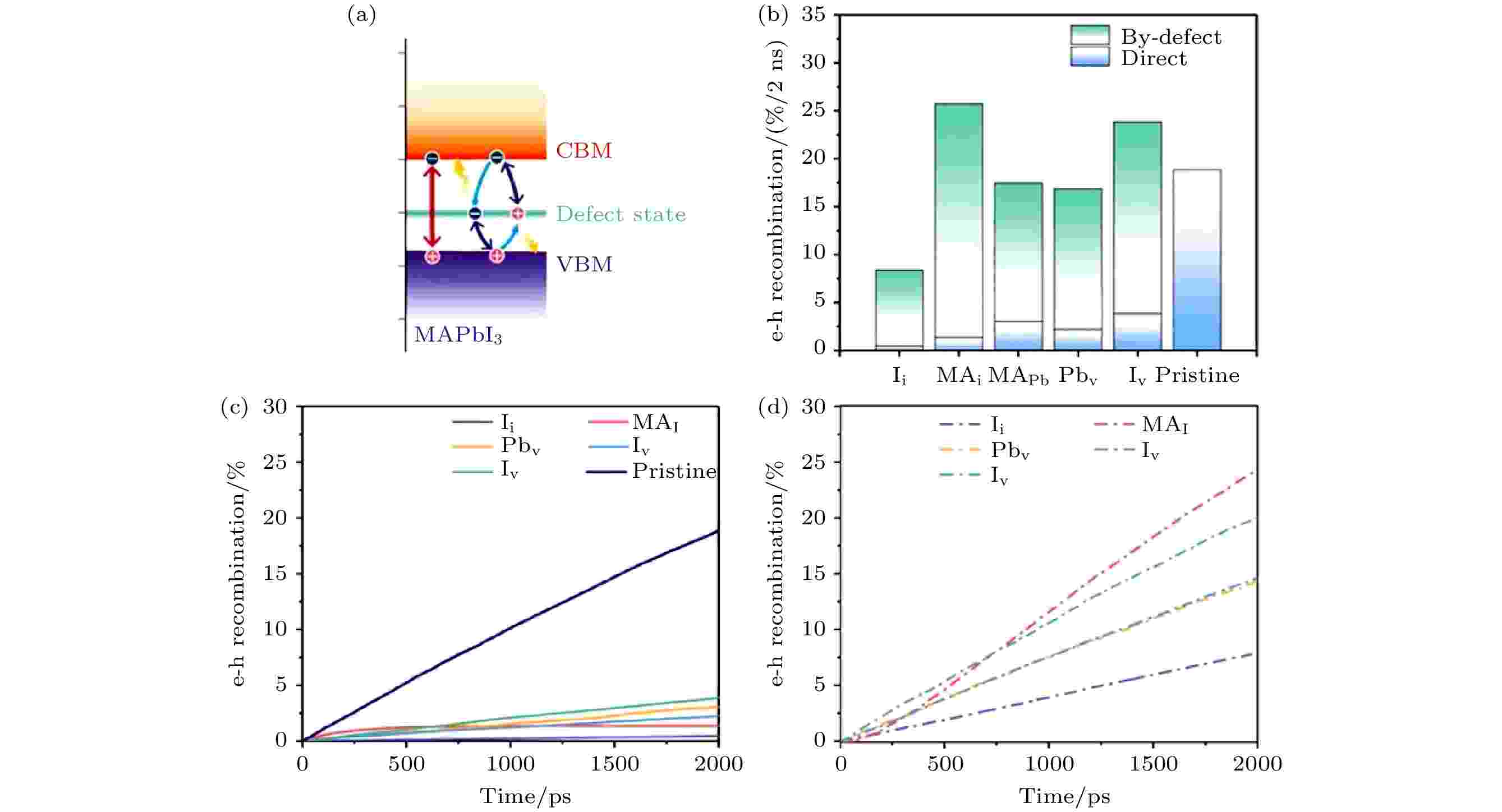图 19 不同构型的MAPbI3中e-h复合过程　(a) e-h直接复合和通过缺陷能级的间接复合过程示意图; (b) 2 ns后不同构型的e-h复合率, 蓝色和绿色彩条分别表示直接和间接复合; (c) 直接复合过程中复合率随时间的变化; (d) 间接复合过程中复合率随时间的变化(图片经文献[102]允许转载, 版权归2020 American Association for the Advancement of Science所有)
Figure19. The e-h recombination process in MAPbI3 systems: (a) Schematic map of the direct and by-defect e-h recombination processes. (b) e-h recombined percentage for different systems after 2 ns. The direct and by-defect e-h recombined percentages are shown by blue and green color bars. (c), (D) Time-dependent e-h recombined percentage for different systems (Reprinted with permission from Ref. [102]. Copyright 2020 American Association for the Advancement of Science)

前面已经讨论过, 在NAMD模拟中决定寿命的原因主要是NAC和退相干时间. 在MAPbI3体系中, 缺陷带来的退相干时间变化不大, 起主要作用的是NAC. 我们通过对CBM, VBM和缺陷态进行傅里叶变换来分析电声耦合的性质. 如图20所示, 我们发现在MAPbI3中与CBM, VBM和缺陷态耦合的声子都是100 cm–1以下的低频声子, 这是由于该材料的CBM和VBM都是由PbI3贡献的, 而由于这种材料硬度较低, 所以晶格PbI3贡献的都是低频声子, 而MA分子贡献的高频声子则与CBM, VBM和缺陷态没有耦合. 低频声子对应较低的原子核运动速度, 因此, 无论是否有缺陷, MAPbI3的e-h复合时间尺度总是很长. 同时, 有一些缺陷(例如Ii缺陷)会导致缺陷态在一定温度下变得局域, 这种轨道局域化会进一步使e-h复合变慢, 而这种轨道局域化也与材料的低硬度直接相关. 这种缺陷态不会产生e-h复合中心的现象保证了MAPbI3作为太阳能电池材料的良好性质, 与现有的实验结果符合得非常好[112-114].
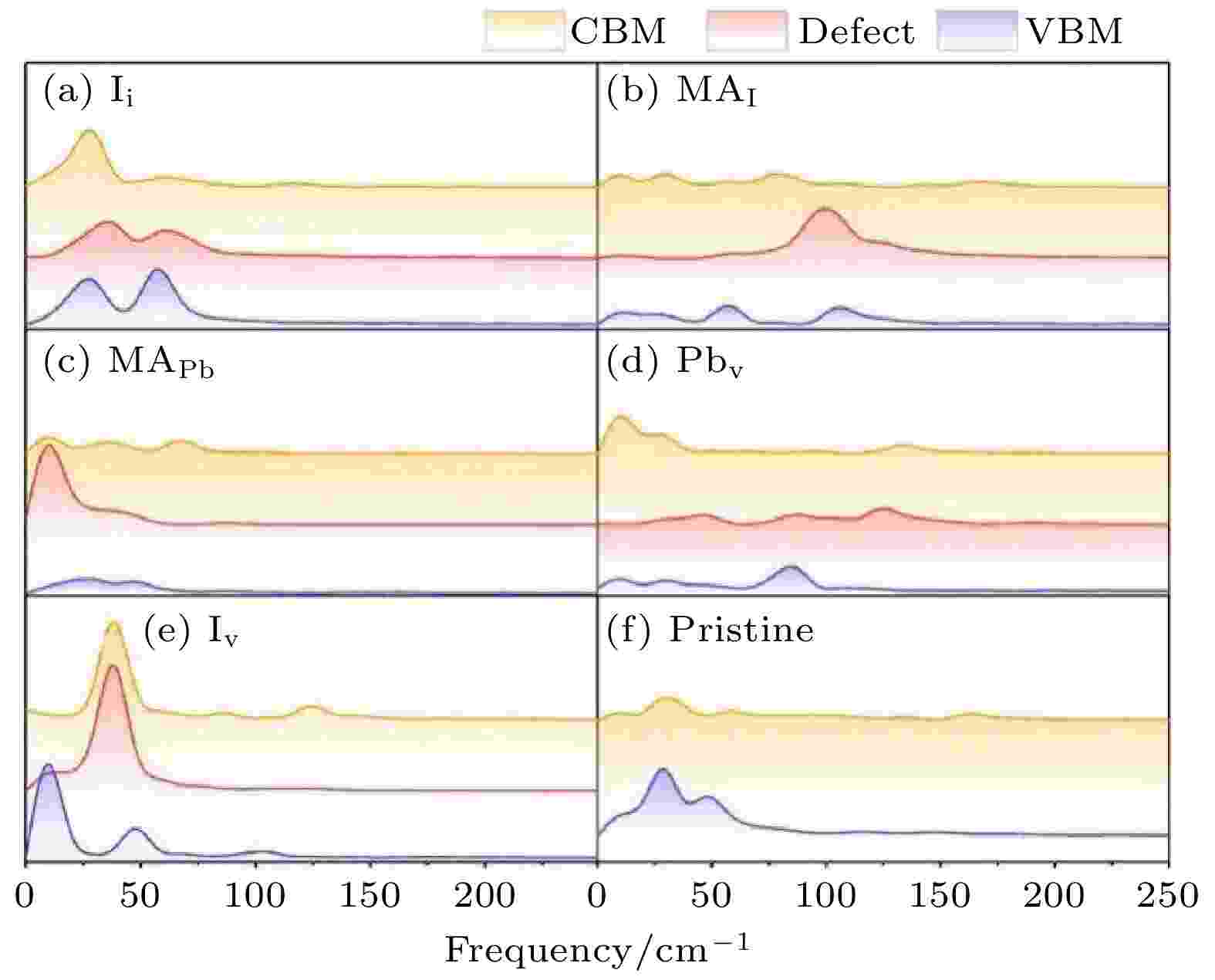图 20 不同构型的MAPbI3中VBM, CBM和缺陷态的含时能量振荡的FT谱(图片经文献[102]允许转载, 版权归2020 American Association for the Advancement of Science所有)
Figure20. The Fourier transform spectra of the autocorrelation function of the VBM, the CBM, and the defect state energies (Reprinted with permission from Ref. [102]. Copyright 2020 American Association for the Advancement of Science)

从以上对黑磷和MAPbI3的研究中可以发现, SRH理论对于硬度较低的材料似乎不再适用, 由此, 我们也大胆地猜测在硬度较低的半导体材料中, 缺陷作为e-h复合中心的作用不再显著, 由此可以推测低硬度半导体材料有可能在太阳能转化领域有很好的应用前景. 当然, 想要证实这个猜测, 还需要有进一步的实验和理论工作, 在未来的工作中, 也许可以将材料的硬度设置为一个指标, 通过高通量材料搜索的方式来寻找没有电子空穴复合中心的新能源材料.
2
4.4.衬底的声子模式对单层MoSe2中e-h复合的调控
-->

4.4.衬底的声子模式对单层MoSe2中e-h复合的调控

前面所有关于半导体e-h复合的工作都说明声子的激发和电声耦合对于e-h的复合起着至关重要的作用, 因此, 我们设想对e-h复合的调控可以从调控声子激发与电声耦合开始. 声子的激发和电声耦合的决定性因素有很多, 本文之前已经讨论过给材料施加外加应力和掺杂不同质量的元素来调控声子激发和电声耦合的方法, 在这里, 我们与南京大学王枫秋教授课题组[115]的超快光谱实验合作, 利用不同衬底对声子激发和电声耦合的影响来调控MoSe2材料中e-h复合的时间尺度. 如图21所示, 我们的实验合作者通过将单层MoSe2沉积到不同的氧化物衬底(SiO2, Al2O3和HfO2)上, 发现了e-h非辐射复合时间存在巨大的差异. 在SiO2衬底上, MoSe2的非辐射复合时间约(160 ± 10) ps, 而在HfO2上这个时间减少到(20 ± 4) ps. 我们利用NAMD方法模拟并解释了这个过程.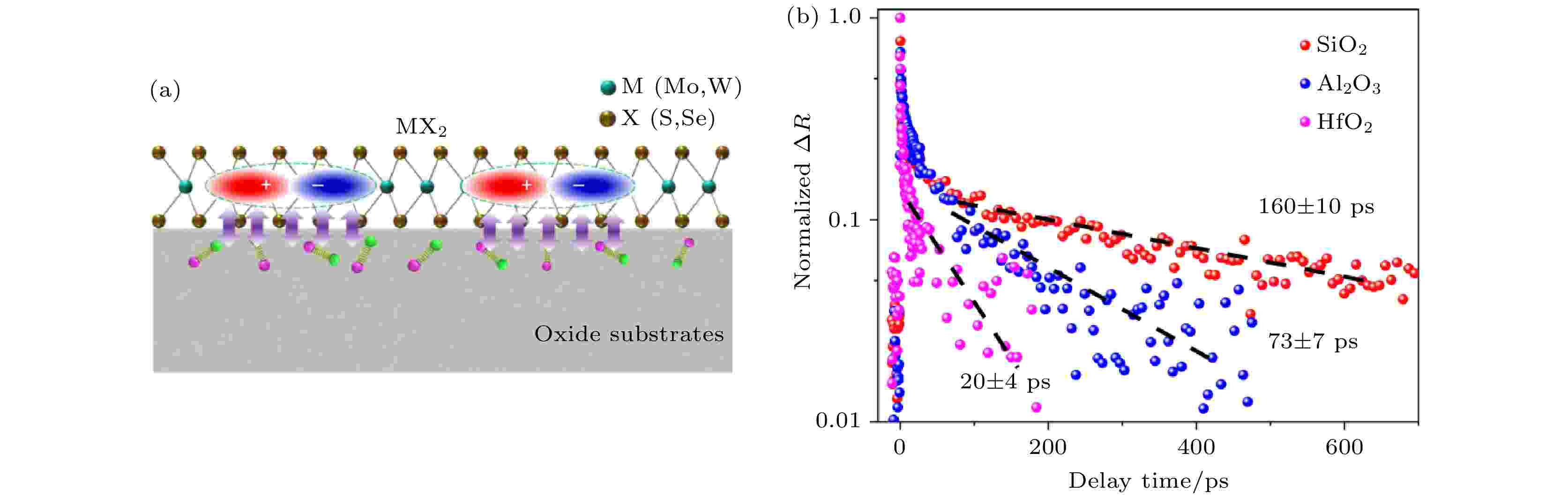
图 21 单层MoSe2在不同氧化物衬底上的超快光子动力学　(a) 界面电声耦合示意图; (b) 在不同衬底上单层MoSe2的光生载流子动力学(图片经文献[106]允许转载)
Figure21. Ultrafast photocarrier dynamics of monolayer MoSe2 on different oxide substrates: (a) Illustration of interfacial electron–phonon (e–ph) coupling; (b) photocarrier dynamics of monolayer MoSe2 on different substrates (Reprinted with permission from Ref. [106])

从图22可以看出, 在SiO2上CBM和VBM的能量波动幅度是最小的, 最大幅度只有0.2 eV, 而Al2O3和HfO2上则分别有0.8和0.5 eV左右. 这说明SiO2上电声耦合最弱, 从FT谱可以看出, 三种不同衬底贡献的都是频率高于400 cm–1波数的声子, SiO2衬底与MoSe2的耦合在三种衬底中是最弱的, 因此衬底对电声耦合贡献非常小, 这个衬底上的e-h复合是最慢的, 非常接近于孤立的MoSe2. Al2O3与HfO2两种衬底与MoSe2的耦合要强很多, 此外, HfO2的CBM位于MoSe2的带隙中, 这使得这个电子态可以作为中间态加速e-h的复合. 因此HfO2和Al2O3衬底有效地加速了e-h复合, 而其中HfO2上e-h复合的时间尺度最短. 这里不同绝缘体衬底对电声耦合贡献与其介电常数有关. 对于半导体和绝缘体, 体系的极化很大程度上来源于离子极化, 介电常数越大, 说明体系在有电场的时候越容易产生形变, 相应的硬度也就比较低. 同样, 硬度较低的绝缘体中的声子也越容易被激发, 从而加速e-h复合过程. 在这里, 我们看到SiO2贡献的声子波数在1100 cm–1, 而Al2O3和HfO2贡献的声子波数在756和600 cm–1左右, 频率相对较低. 同时, 与SiO2相比, Al2O3和HfO2都是高介电函数绝缘体. 这项工作再次证实了电声耦合对e-h非辐射复合的决定性作用, 并提出了利用不同衬底调控e-h复合时间的方案[115].
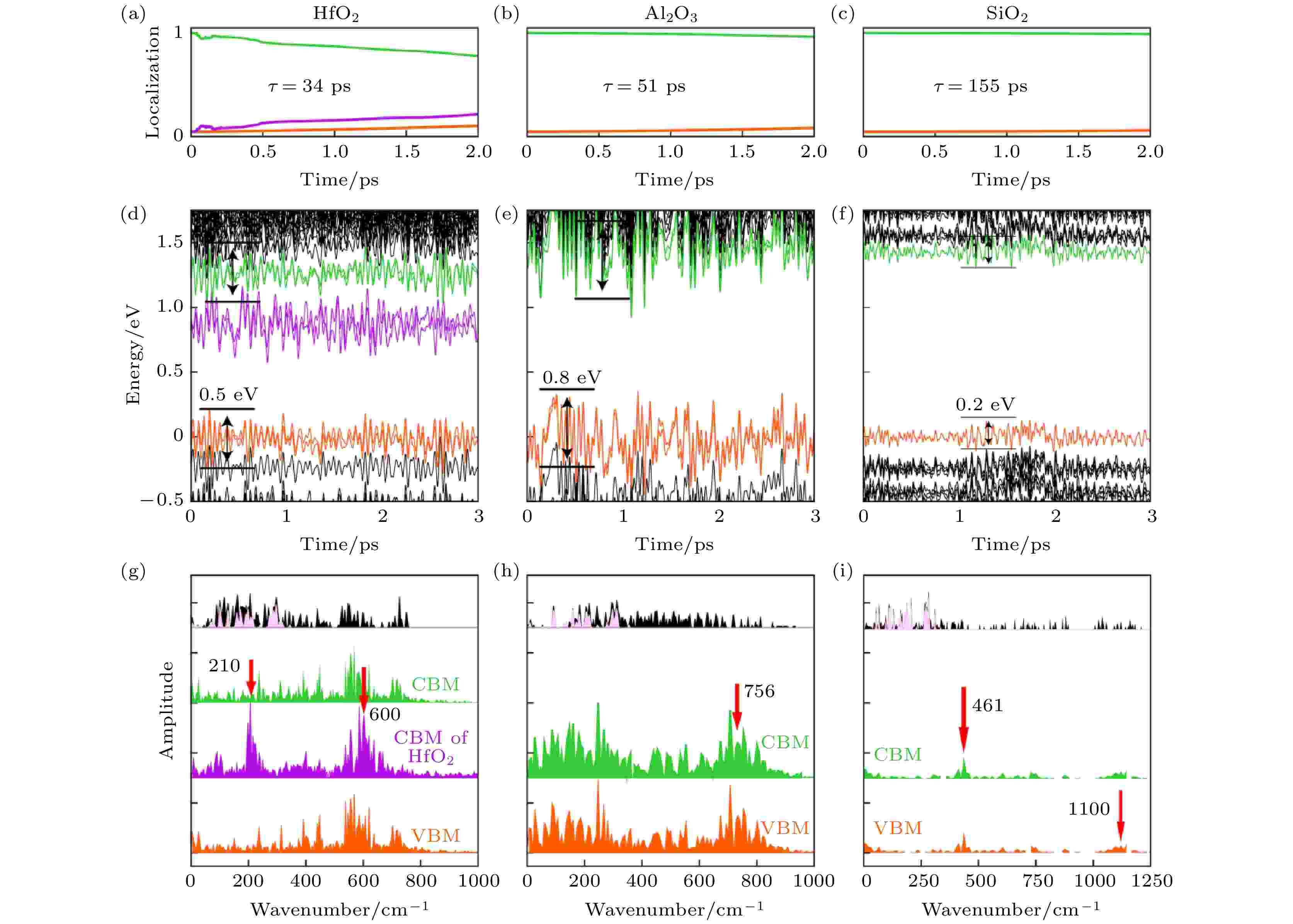图 22 在HfO2, Al2O3和SiO2衬底上单层MoSe2中e-h复合动力学　(a)—(c) 光激发电子在MoSe2上的空间分布随时间的变化; (d)—(i) CBM, VBM附近能级能量随时间的演化及其对应的FT谱, 其中红色箭头标记了主要的声子模式和对应的波数, 黑色区域和粉红色区域分别代表体系声子的总态密度以及在MoSe2上的投影(图片经文献[106]允许转载)
Figure22. The nonadiabatic molecular dynamics of e–h recombination in monolayers MoSe2 on HfO2, Al2O3 and SiO2 substrates: (a)–(c) Time-dependent electron localization on CBM of MoSe2; (d)–(i) Time evolutions of the energy states and their corresponding FT spectra, where red arrows have marked main phonon modes and its corresponding wavenumbers. The whole phonon DOS of the MoSe2-oxide substrate systems (black area) and the projection from MoSe2 (pink area) are also plotted in panels (g)–(i) (Reprinted with permission from Ref. [106])

2
4.5.半导体中e-h非辐射复合动力学小结
-->

4.5.半导体中e-h非辐射复合动力学小结

本节研究不同的半导体材料体系中e-h非辐射复合动力学过程, 包括传统的半导体材料TiO2, 新兴的二维半导体材料黑磷, 太阳能电池材料MAPbI3. 我们发现对于传统的氧化物半导体材料TiO2, SRH模型与NAMD模拟的结果符合得很好, 深能级会形成e-h复合中心. 然而, 在黑磷与MAPbI3体系中却发现SRH模型失效的情况, 在这两个体系中, 无论缺陷能级是深能级还是浅能级, 都不容易形成e-h复合中心. 我们认为这和材料的硬度低导致的低频模式激发有关, 因此, 我们预测硬度降低的半导体材料有可能不容易形成e-h复合中心, 从而在太阳能转化领域有更好的应用前景. 最后, 还提出了一些调控e-h复合的方案, 包括利用不同质量的元素掺杂、以及不同的衬底等方案.
5.磁性材料载流子动力学
自旋动力学是凝聚态物理中一个重要的领域, 对自旋电子学的发展起着重要的作用. 我们希望探索是否能利用NAMD模拟来研究激发态自旋载流子的动力学. 基于这样的想法, 我们研究了Cu掺杂单层MoS2的光激发自旋空穴流动力学过程[116].
如图23所示, 在单层MoS2中, 掺杂Cu原子取代S原子后会产生1 μB的磁矩, 这个磁矩来自于Mo原子的4d轨道上剩余的一个未配对电子. 当多个Cu杂质原子在同一层沿着Y方向排列时, 每个Cu掺杂原子上的自旋会通过超交换相互作用形成铁磁长程序. 因此, Cu掺杂后在单层MoS2带隙中引入的四条空间局域的杂质态会发生自旋劈裂(图中标记为自旋态1, 2, 3, 4), 从而光激发可以产生完全自旋极化的空穴流, 并在一定时间内弛豫到基态. 光激发自旋空穴流的寿命决定了此类材料在自旋电子学中的应用, 因此, 对激发态自旋空穴流的NAMD模拟可以为相关光学自旋器件的设计制造提供理论依据.
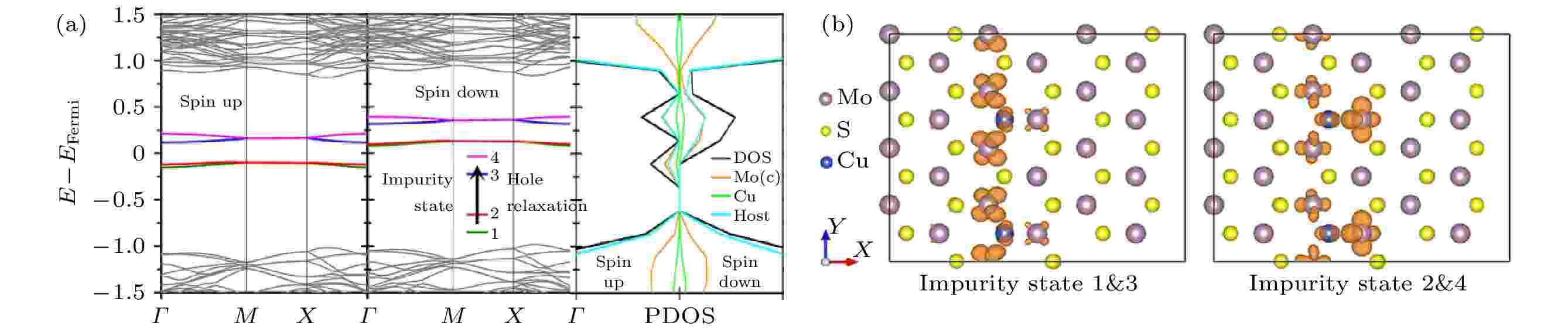图 23 (a) Cu掺杂单层MoS2体系自旋极化的能带结构和投影态密度; (b) Cu掺杂单层MoS2的杂质态轨道空间分布. 图(a)中的箭头显示了自旋极化的空穴在杂质态之间进行弛豫的过程(图片经文献[107]允许转载, 版权归2017 American Physical Society所有)
Figure23. (a) Spin-polarized band structure and the projected density of states; (b) orbital spatial distribution of the Cu doped MoS2. The process of spin hole relaxation within the impurity states is indicated by the arrow in panel (a) (Reprinted with permission from Ref. [107]. Copyright 2017 American Physical Society)

我们分别研究了温度在100和50 K下的自旋空穴动力学. 图24给出了四条杂质态在100和50 K条件下随时间变化的能级能量演化及FT谱. 杂质态的能量振荡幅度在0.19—0.30 eV之间, 比单层MoS2的CBM/VBM振荡幅度大很多, 说明杂质态的电声耦合相对比较强. 从FT谱可以得到电声耦合中的主要声子模, 如图24(b)和图24(d) 所示, 杂质态主要与240 cm–1以下的声子耦合.
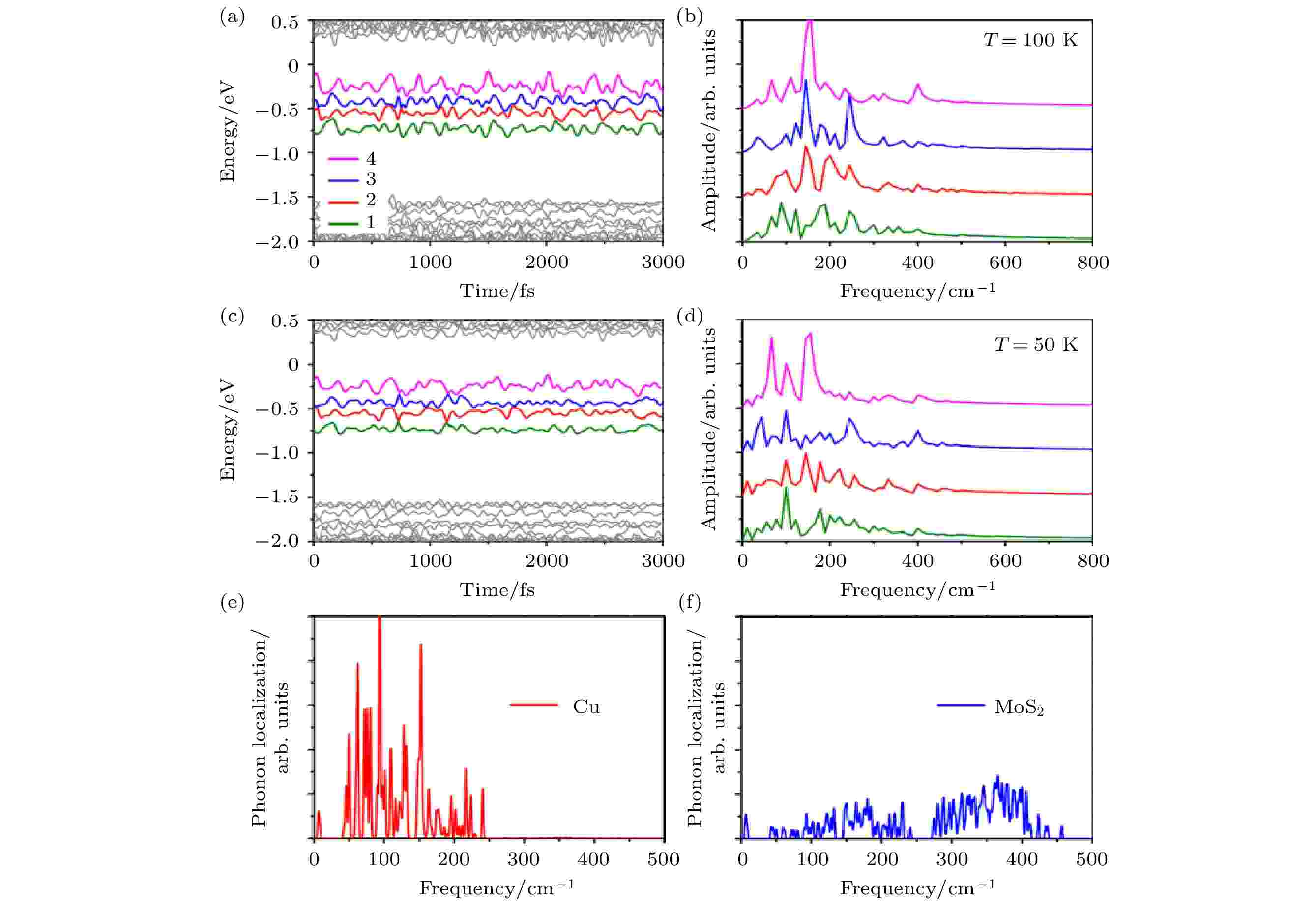图 24 在100和50 K的不同温度下, 杂质态本征能量的含时演化　((a), (c))及其自关联函数的FT谱((b), (d)), 以及每一个声子本征振动模式的空间局域度分别在Cu杂质原子和MoS2上的投影 ((e), (f))(图片经文献[107]允许转载, 版权归2017 American Physical Society所有)
Figure24. (a), (c) Time-dependent evolution of the energy of the impurity states; (b), (d) FT spectra to the autocorrelation function of the energy evolutionat 100 and 50 K, respectively; (e), (f) spatial localization of each normal phonon mode projected on the Cu impurity and MoS2 host, respectively (Reprinted with permission from Ref. [107]. Copyright 2017 American Physical Society)

光激发可以在杂质带1或者杂质带2上产生自旋极化的空穴, 一旦空穴弛豫到费米面以上, 自旋极化的空穴流就消失了. 如图25所示, 我们发现在50和100 K的温度下, 自旋空穴都是沿着相邻的能带向上逐级弛豫的. 然而, 虽然能量弛豫的特点很类似, 但是具体的时间尺度与温度有比较大的关系. 当温度从100 K降至50 K时, 空穴在带间的弛豫受到强烈的抑制. 我们认为这是由于低温下大量声子被冻结, 因而产生了自旋空穴弛豫的瓶颈.
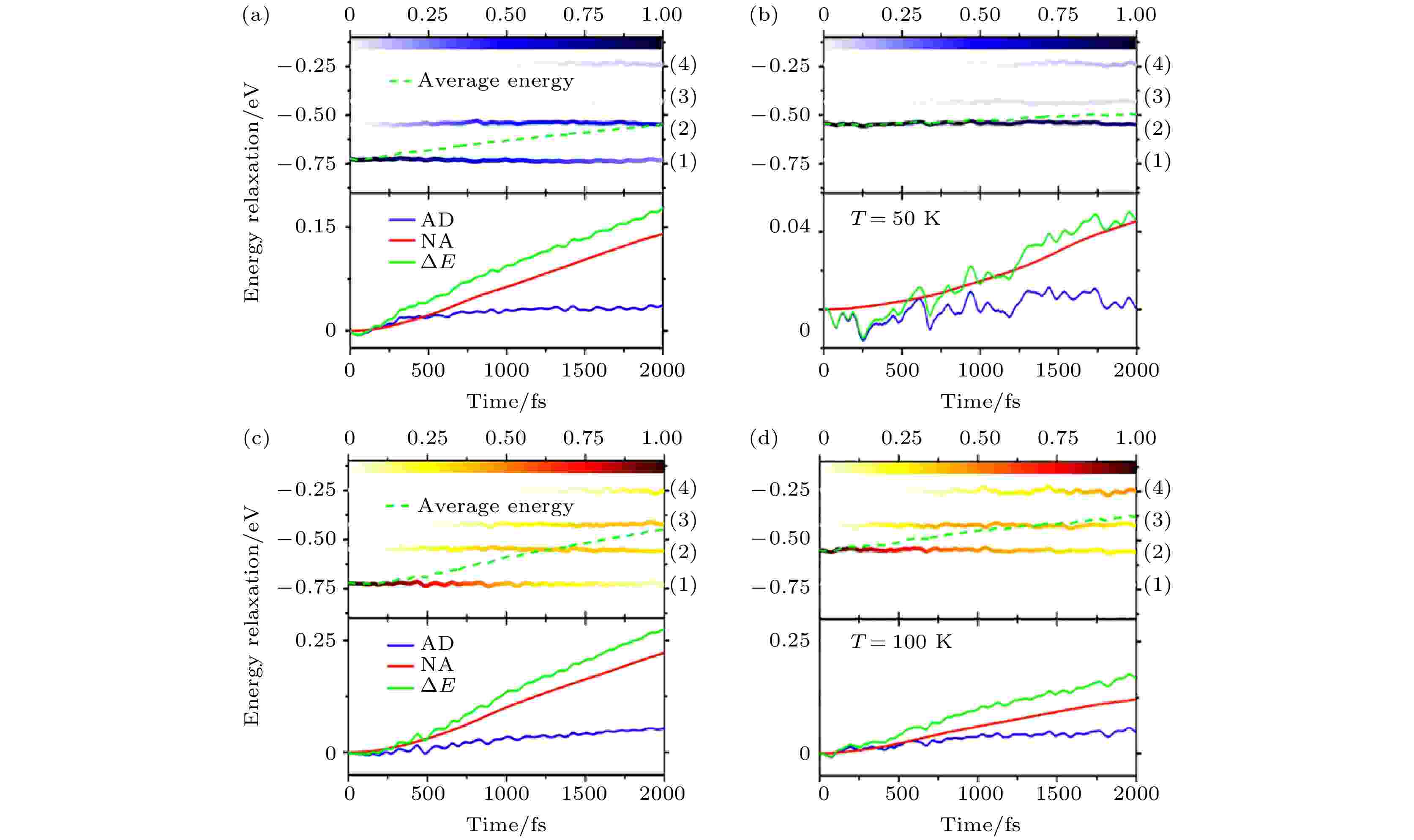图 25 50和100 K环境温度下的光激发自旋极化空穴的动力学. 图 (a), (c) 和 (b), (d) 分别是空穴的初始激发在杂质态1和杂质态2上的情况. 每个图的上半部分所示为空穴的平均能量以及空穴在每一个杂质态上的布居数; 下半部分所示为能量弛豫过程中的AD和NA过程分别做的贡献(图片经文献[107]允许转载, 版权归2017 American Physical Society所有)
Figure25. Dynamics of a photogenerated hole at 50 and 100 K, respectively. The averaged energy of the hole and the population on each impurity state are shown in the upper panel, and the AD and NA contributions to the energy relaxation are shown in the lower panel with the initial state specified at the impurity state 1 ((a), (c)) and 2 ((b), (d)) (Reprinted with permission from Ref. [107]. Copyright 2017 American Physical Society)

本工作为NAMD在激发态自旋动力学领域的初步尝试, 我们成功地研究了光激发自旋空穴流的动力学过程, 显示了本方法在激发态自旋动力学领域中的应用潜力. 值得注意的是, 这个工作中没有考虑自旋轨道耦合, 因此, 这套方案无法研究激发态载流子自旋方向的变化. 我们计划在未来的计算方法中加入自旋轨道耦合, 来研究更加丰富的光激发自旋动力学现象.
6.激子动力学
在光激发的情况下, 固体中产生的电子空穴对会通过库仑相互作用束缚在一起, 形成激子, 由于存在电子空穴相互作用, 多体效应反应了激子的本质. 激子普遍存在于绝缘体、半导体以及一些分子中, 尤其在新近发展的二维材料中, 由于缺少三维屏蔽, 激子的束缚能非常大, 多体效应尤为明显. 激子是凝聚态物理中激发态能量转移的基本单位, 对激子的描述是凝聚态物质激发态的关键.
在第一性原理计算领域, 基于多体理论的GW+BSE方法是被公认可以准确计算激子性质的方法, 其发展到应用已有几十年的时间, 在许多第一性原理计算的软件中都得到了实现(例如VASP, Berkeley GW, YAMBO等)[117-125], 并且在计算物理领域取得了巨大的成功, 成功解释了许多固体激发态性质. 这方面的代表人物是美国科学院院士Louie教授, 他们在Berkeley GW中实现了效率很高的GW算法[73].
然而, 作为常常由光激发产生的准粒子, 激子并不是一个稳定的存在, 有可能发生诸如电子空穴的解离、重组、复合, 激子声子散射, 单激子转化为多激子, 单重态裂变为三重态, 亮激子衰减为暗激子等过程. 在实际问题中, 这些激子的动力学行为往往才是决定器件与材料效率的关键. 然而, 研究动力学行为, 以10 ps时间尺度, 步长1 fs为例, 一条动力学轨迹就需要计算104量级的含时演化, 由于GW+BSE巨大的计算量, 只能被用于计算单个结构激子的波函数与束缚能, 几十年来依然难以在动力学领域有所发展.
最近, 我们引入固定介电函数近似, 在保证结果准确的基础上, 大幅度减少了计算量, 成功地将GW+BSE与NAMD结合, 在Hefei-NAMD中成功地实现了上百个原子的GW+rtBSE的含时演化, 并用这种方法研究了MoS2体系中的自旋谷激子动力学[126].
2
6.1.自旋分辨的GW+rtBSE方法
-->

6.1.自旋分辨的GW+rtBSE方法

GW+rtBSE方法中哈密顿量可以写为
$\begin{split}\left\langle {} \right.\boldsymbol{k}cv|H|{\boldsymbol{k}}'{c}'{v}'\left. {} \right\rangle =\;&\left({E}_{\boldsymbol{k}c}^{{\rm{Q}}{\rm{P}}}-{E}_{\boldsymbol{k}v}^{{\rm{Q}}{\rm{P}}}\right){\delta }_{\boldsymbol{k}{\boldsymbol{k}}'}{\delta }_{c{c}'}{\delta }_{v{v}'}\\&-{W}_{{\boldsymbol{k}}'{c}'{v}'}^{\boldsymbol{k}cv}+{v}_{{\boldsymbol{k}}'{c}'{v}'}^{\boldsymbol{k}cv}{,}\end{split}$
这里v/c分别为空穴和电子的指标, $ {E}_{\boldsymbol{k}c}^{{\rm{Q}}{\rm{P}}} $和$ {E}_{\boldsymbol{k}v}^{{\rm{Q}}{\rm{P}}} $是准粒子能级, $ |\boldsymbol{k}cv\left. {} \right\rangle ={\psi }_{\boldsymbol{k}c}({\boldsymbol{r}}_{{\rm{e}}}\left){\psi }_{\boldsymbol{k}v}^{*}\right({\boldsymbol{r}}_{{\rm{h}}}) $代表电子空穴对基组, 可以直接由KS轨道构造, 也可以将自旋轨道耦合包含在内, 采用spinor作为基组, spinor可以由自旋向上和向下的KS轨道构造, 即${\psi }_{\boldsymbol{k}n}\left(\boldsymbol{r}\right)= $$ {\psi }_{\uparrow \boldsymbol{k}n}\left(\boldsymbol{r}\right)\left|\uparrow \left. {} \right\rangle +{\psi }_{\downarrow \boldsymbol{k}n}\left(\boldsymbol{r}\right)\right|\downarrow \left. {} \right\rangle ={\displaystyle \sum }_{\sigma =\uparrow , \downarrow }|\sigma \boldsymbol{k}n\left. {} \right\rangle \otimes |\sigma \left. {} \right\rangle$, 其中$ {\psi }_{\uparrow (\downarrow )\boldsymbol{k}n}\left(\boldsymbol{r}\right)={{\rm{e}}}^{{\rm{i}}\boldsymbol{k}\cdot \boldsymbol{r}}{u}_{\uparrow (\downarrow )\boldsymbol{k}n}\left(\boldsymbol{r}\right) $是自旋向上/向下的KS轨道. (10)式中的W和v代表电子与空穴的屏蔽库仑势和交换相互作用, 可以分别写为

${W}_{\boldsymbol k'c'v'}^{\boldsymbol{k}cv} \!=\! \frac{1}{\varOmega }\sum _{\boldsymbol{G}{\boldsymbol{G}}^{{\prime}}}\frac{4{\rm{\pi }}{\varepsilon }_{\boldsymbol{G}{\boldsymbol{G}}^{{\prime}}}^{-1}\left(\boldsymbol{k}-{\boldsymbol{k}}^{\boldsymbol{{\prime}}}\right)}{\left|\boldsymbol{k}-{\boldsymbol{k}}^{{\prime}} \!+\! \boldsymbol{G}\right|\left|\boldsymbol{k}-{\boldsymbol{k}}^{{\prime}}+{\boldsymbol{G}}^{{\prime}}\right|}\left({B}_{\uparrow {\boldsymbol{k}}^{\boldsymbol{{\prime}}}{c}^{{\prime}}}^{\uparrow \boldsymbol{k}c}\left(\boldsymbol{G}\right) \!+\! {B}_{\downarrow {\boldsymbol{k}}^{\boldsymbol{{\prime}}}{{\rm{c}}}^{{\rm{{\prime}}}}}^{\downarrow \boldsymbol{k}c}\left(\boldsymbol{G}\right)\right)\left({{B}_{\uparrow {\boldsymbol{k}}^{\boldsymbol{{\prime}}}{v}^{{\prime}}}^{\uparrow \boldsymbol{k}v}}^{*}\left({\boldsymbol{G}}^{{\prime}}\right)+{{B}_{\downarrow {\boldsymbol{k}}^{{{\prime}}}{v}^{{\prime}}}^{\downarrow \boldsymbol{k}v}}^{*}\left({\boldsymbol{G}}^{{\prime}}\right)\right){,}$
${v}_{{\boldsymbol{k}}^{{\prime}}{c}^{{\prime}}{v}^{{\prime}}}^{\boldsymbol{k}cv}=\frac{1}{\varOmega }\sum _{\boldsymbol{G}\ne 0}\frac{4{\rm{\pi }}}{{\left|\boldsymbol{G}\right|}^{2}}\left({B}_{\uparrow \boldsymbol{k}v}^{\uparrow \boldsymbol{k}c}\left(\boldsymbol{G}\right)+{B}_{\downarrow \boldsymbol{k}v}^{\downarrow \boldsymbol{k}c}\left(\boldsymbol{G}\right)\right)\left({{B}_{\uparrow {\boldsymbol{k}}^{{{\prime}}}{v}^{{\prime}}}^{\uparrow {\boldsymbol{k}}^{{{\prime}}}{c}^{{\prime}}}}^{*}\left({\boldsymbol{G}}^{{\prime}}\right)+{{B}_{\downarrow {\boldsymbol{k}}^{{{\prime}}}{v}^{{\prime}}}^{\downarrow {\boldsymbol{k}}^{{{\prime}}}{c}^{{\prime}}}}^{*}\left({\boldsymbol{G}}^{{\prime}}\right)\right){,}$

这里的${\varepsilon }_{\boldsymbol{G}{\boldsymbol{G}}^{{'}}}^{-1}(\boldsymbol{k}-{\boldsymbol{k}}^{\boldsymbol{{'}}})$是介电函数的倒数, 可以由GW计算得到, G是倒空间格矢, B是布洛赫积分$ {B}_{\sigma {\boldsymbol{k}}^{\boldsymbol{{'}}}{n}^{{'}}}^{\sigma \boldsymbol{k}n}\left(\boldsymbol{G}\right)=\left\langle {} \right.{u}_{\sigma \boldsymbol{k}n}|{{\rm{e}}}^{{\rm{i}}\boldsymbol{G}\cdot \boldsymbol{r}}|{\sigma }_{\sigma {\boldsymbol{k}}^{\boldsymbol{{'}}}{n}^{{'}}}\left. {} \right\rangle $, 可以由KS基组或者spinor基组得到.
基于(10)式的BSE哈密顿量, 含时BSE方程可以写为
${\rm{i}}\hslash \frac{\partial \varPhi ({\boldsymbol{r}}_{{\rm{e}}},{\boldsymbol{r}}_{{\rm{h}}},t)}{\partial t}=H\left(\boldsymbol{R}\right(t\left)\right)\varPhi ({\boldsymbol{r}}_{{\rm{e}}},{\boldsymbol{r}}_{{\rm{h}}},t){.} $
与单粒子的非绝热分子动力学方法类似, 原子核的运动轨迹R(t)可以用第一性原理分子动力学得到. 激子态的波函数可以写为
$\begin{split}\varPhi \left({\boldsymbol{r}}_{{\rm{e}}},{\boldsymbol{r}}_{{\rm{h}}},t\right)=\;&\sum\limits_{\boldsymbol{k}}{\sum\limits_{c}}^{{\rm{e}}{\rm{l}}{\rm{e}}{\rm{c}}}{\sum\limits_{v}}^{{\rm{h}}{\rm{o}}{\rm{l}}{\rm{e}}}{A}_{\boldsymbol{k}cv}\left(t\right)\\&\times{\psi }_{\boldsymbol{k}c}\left({\boldsymbol{r}}_{{\rm{e}}}\right){\psi }_{\boldsymbol{k}v}^{*}\left({\boldsymbol{r}}_{{\rm{h}}}\right){,}\end{split}$
其中$ {\psi }_{\boldsymbol{k}c} $($ {\psi }_{\boldsymbol{k}v} $)为KS轨道基组或spinor基组, 于是含时系数演化可以写为
$\begin{split}{\rm{i}}\hslash \frac{\partial {A}_{\boldsymbol{k}cv}}{\partial t}=\,&\sum\limits_{{\boldsymbol{k}}'}{\sum\limits_{{c}'}}^{{\rm{e}}{\rm{l}}{\rm{e}}{\rm{c}}}{\sum\limits_{{v}'}}^{{\rm{h}}{\rm{o}}{\rm{l}}{\rm{e}}}\bigg(\left\langle {} \right.\boldsymbol{k}cv|H|{\boldsymbol{k}}'{c}'{v}'\left. {} \right\rangle \\& -{\rm{i}}\hslash \left\langle {} \right.\boldsymbol{k}cv|\frac{\partial }{\partial t}|{\boldsymbol{k}}'{c}'{v}'\left. {} \right\rangle \bigg) {A}_{{\boldsymbol{k}}'{c}'{v}'},\\[-12pt]\end{split}$
这里$\left\langle \boldsymbol{k}cv|H|{\boldsymbol{k}}'{c}'{v}' \right\rangle -{\rm{i}}\hslash \langle {}\boldsymbol{k}cv|\dfrac{\partial }{\partial t}|{\boldsymbol{k}}'{c}'{v}'\rangle$中的非对角元即为激子动力学中非绝热耦合矩阵元, 其中
$\begin{split}& \langle \boldsymbol{k}cv|\frac{\partial }{\partial t}|{\boldsymbol{k}}'{c}'{v}' \rangle = \\\;&\left\{\left( \langle\uparrow \boldsymbol{k}c|\frac{\partial }{\partial t}|\uparrow {\boldsymbol{k}}'{c}' \rangle + \langle \downarrow \boldsymbol{k}c|\frac{\partial }{\partial t}|\downarrow {\boldsymbol{k}}'{c}' \rangle \right){\delta }_{v{v}'} \right.\\ &+\left( \langle\uparrow \boldsymbol{k}v|\frac{\partial }{\partial t}|\uparrow {\boldsymbol{k}}'{v}' \rangle\right. \left.\left. \!+\! \langle \downarrow \boldsymbol{k}v|\frac{\partial }{\partial t}|\downarrow {\boldsymbol{k}}'{v}' \rangle \right){\delta }_{c{c}'}\right\}{\delta }_{{\boldsymbol{k}\boldsymbol{k}}'},\end{split}$
为电声耦合部分, 包含了电子与空穴的贡献. 可以注意到, 在GW+rtBSE-NAMD方法中, 非绝热耦合项不但包含电子空穴的电声耦合, 同时也包含了电子空穴屏蔽库仑势W以及交换相关势v的贡献.
由于GW的计算量非常庞大, 在动力学过程中每一步都进行GW计算是不可能实现的. 但是, 我们意识到固体材料在室温下具有较好的热稳定性, 通过理论计算, 我们验证了材料的介电性质在常温动力学过程中改变很小[126], 利用这一特点, 引入“固定介电函数”近似. 在这个近似中, 我们认为材料的介电函数在整个动力学过程中不发生变化, 这样的话, 可以只进行一次GW计算, 从中得到固体的介电函数$ {\delta }_{{\boldsymbol{G}\boldsymbol{G}}^{{\prime}}}(\boldsymbol{k}-{\boldsymbol{k}}^{{{\prime}}}) $之后, 可以利用(11)式 和 (12)式来构造每一时刻的屏蔽库仑势W以及交换相关势v, 计算GW准粒子能级与KS能级的能量差, 并通过剪刀算符得到每一时刻的准粒子能级能量, 有了W, v和准粒子能级能量, 就可以通过(13)式来构造BSE哈密顿量并研究含时激子动力学.
因此, 如图26所示，GW+rtBSE-NAMD方法的大致流程可以总结为:
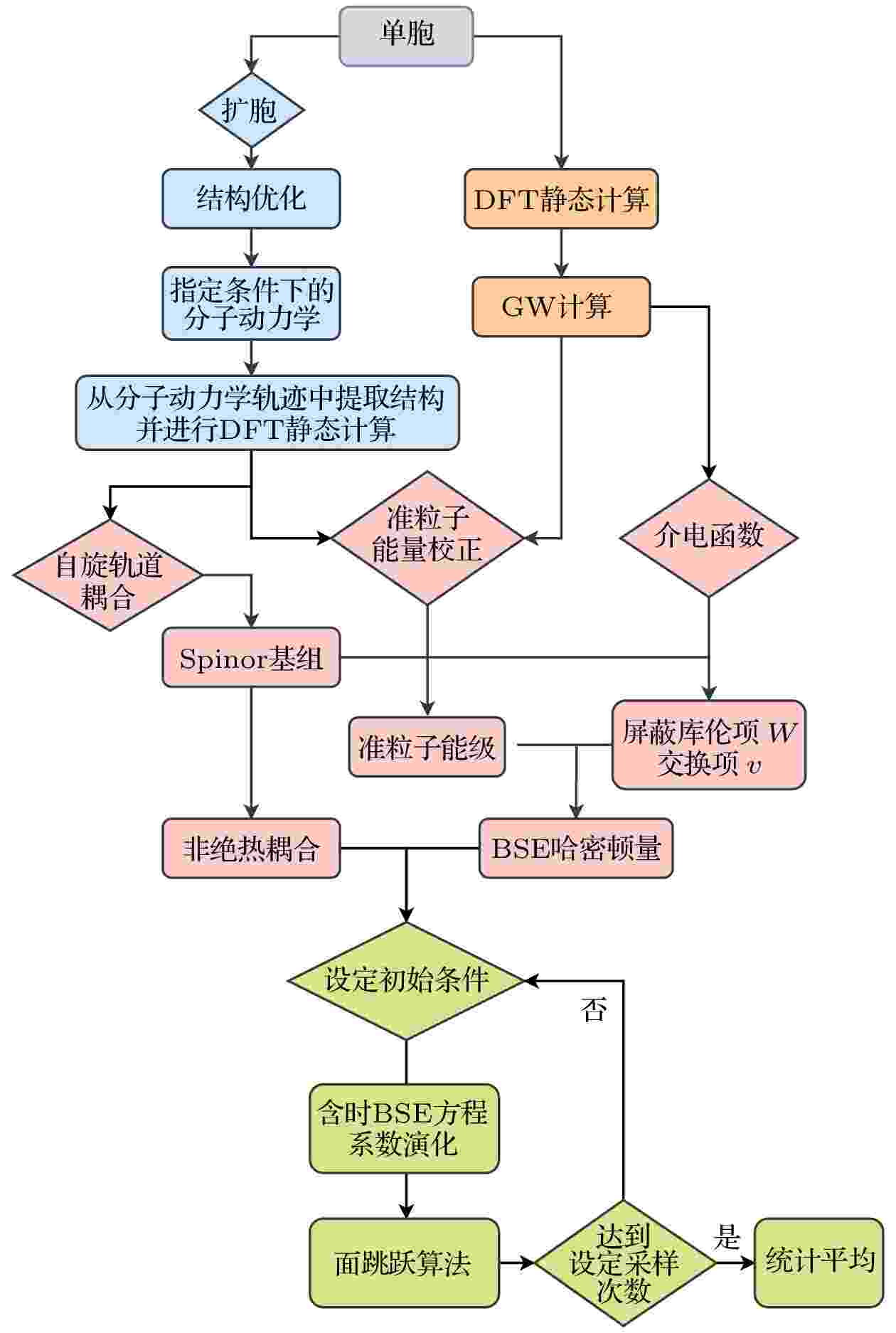图 26 GW+rtBSE程序流程图
Figure26. Work chart of GW+rtBSE package.

i) 优化零温下材料结构, 然后给系统升温至特定温度并进行一段时间的分子动力学模拟;
ii) 对分子动力学中每一步的结构进行DFT计算, 得到含时KS轨道波函数;
iii) 通过自旋向上和自旋向下的KS轨道构造含时的spinor基组;
iv) 使用零温下优化结构进行G0W0计算, 得到介电函数$\varepsilon _{\boldsymbol{GG}'} (\boldsymbol{k} - \boldsymbol{k}')$以及准粒子能级, 将准粒子能级与DFT计算得到的KS轨道能量相减, 得到G0W0计算的能量修正值;
v) 由介电函数$ {\delta }_{{\boldsymbol{G}\boldsymbol{G}}^{{'}}}(\boldsymbol{k}-{\boldsymbol{k}}^{\boldsymbol{{'}}}) $与spinor基组共同构造电子空穴屏蔽库仑势W以及交换相关势v ((11)式和(12)式);
vi) 利用剪刀算符得到分子动力学每一步的准粒子能级能量, 与屏蔽库仑势W以及交换相关势v共同构造BSE哈密顿量并进行含时演化((13)式和(15)式);
vii) 取不同的初始结构作为样本, 每个初始结构计算多条激子动力学轨线并做统计平均.
2
6.2.MoS2体系谷激子动力学研究
-->

6.2.MoS2体系谷激子动力学研究

以单层MoS2为代表的TMD材料是实现谷电子学及自旋电子学的候选材料, 由于具有六角结构, 在布里渊区的六个顶点会形成六个能谷, 成为谷电子学的基本元素. 同时, 其单层结构打破了空间反演对称性, 与自旋轨道耦合共同作用, 形成了独特的自旋-谷锁定(spin-valley locking)效应. K或K' 谷的激子可以由不同手性的圆偏光激发, 由于自旋-谷锁定效应, K或K' 谷激子也同时具有向上或向下的特定自旋方向. 激发态自旋谷激子的动力学行为是决定TMD材料谷电子学性质的基本要素.
然而, TMD材料中的自旋谷激子动力学非常复杂, 如果用左旋光激发, K谷会形成亮激子, 实验发现数皮秒之后K' 谷也会出现自旋相反的亮激子, 电子空穴的自旋方向发生了翻转, 同时动量从K变到了K' , 这个过程被称为谷激子的退极化, 前人基于模型哈密顿量的理论工作认为这个过程是由电子空穴的交换相互作用导致的[127], 然而也有人认为这是电子与声子散射的结果[128-130]; 除此以外, 亮激子也可能通过电子或空穴的自旋翻转转化为自旋禁止的暗激子, 或通过动量的改变形成电子空穴分别位于K和K' 谷的动量禁止的暗激子, 暗激子通常拥有较长的寿命, 在量子计算与玻色爱因斯坦凝聚等领域有重要应用. 如图27所示, MoS2中电子与空穴可以形成8种能量接近的电子空穴对, 其中X1, X2是亮激子, X3, X4是自旋禁止暗激子, X5, X6是动量禁止的暗激子, X7, X8是自旋、动量同时禁止的暗激子. 可以看到自旋谷激子有多条不同的弛豫通道, 电子空穴相互作用的多体效应、电声耦合和自旋轨道耦合等不同物理机制在其中相互竞争, 如何深入而准确地理解, 进而调控TMD材料中的谷激子动力学是一个非常重要而又极有挑战的科学问题.
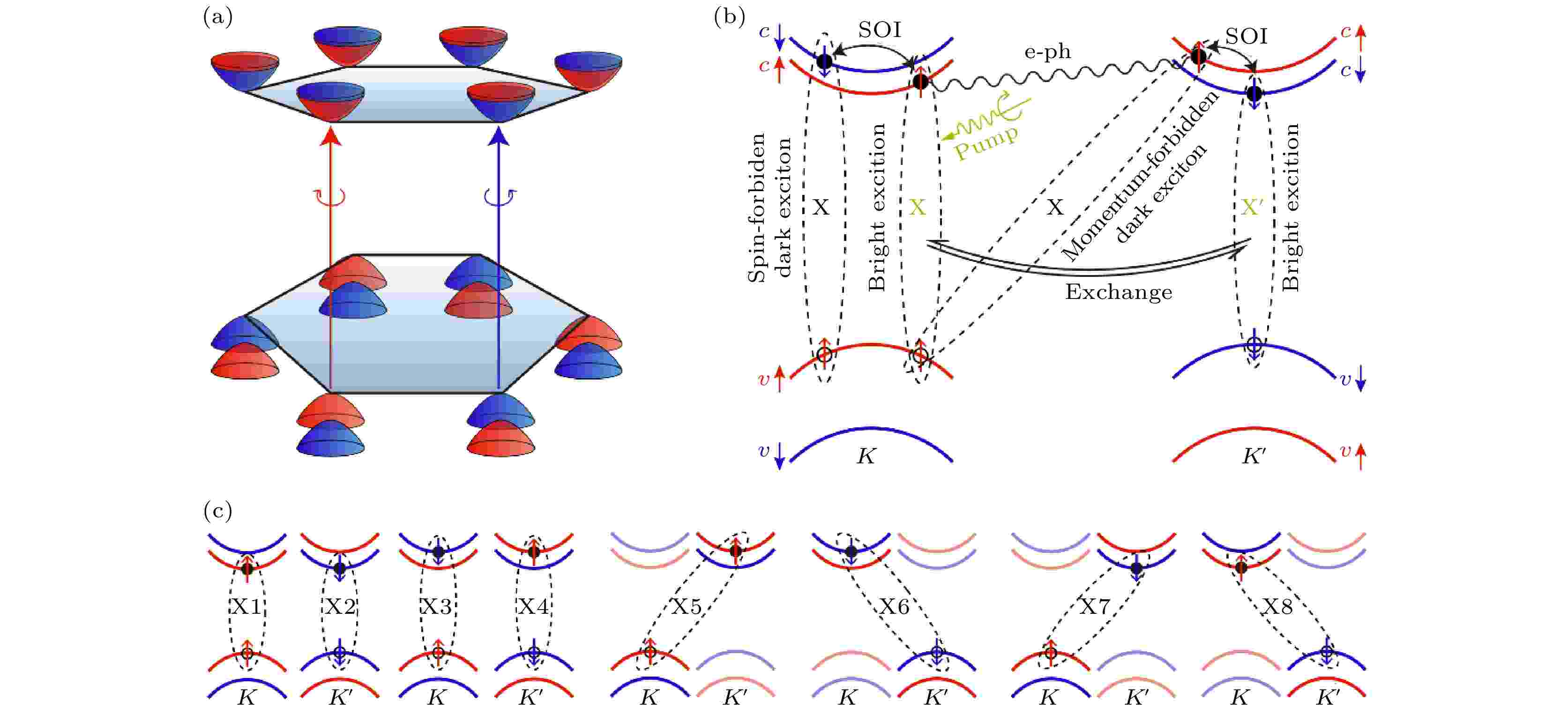图 27 MoS2自旋谷激子动力学示意图　(a) MoS2的六个自旋谷; (b)不同的激子弛豫通道; (c)8种能量最低的亮、暗激子(图片经文献[117]允许转载, 版权归2021 American Association for the Advancement of Science所有)
Figure27. Schematic showing spin-valley dynamics in TMD systems: (a) Band structure at the band edges near K and K'; (b) intervalley bright exciton transition and bright-to-dark exciton transition processes are shown; (c) e-h pairs involved during the exciton dynamics (Reprinted with permission from Ref. [117]. Copyright 2021 American Association for the Advancement of Science)

与近些年迅速发展的时间分辨超快动力学实验手段相比, 能够从第一性原理的角度研究二维材料激子时间与自旋分辨的动力学方法一直没有实现. 普遍认为能够准确描述激子的第一性原理方法是GW-BSE方法, 然而, 这种方法通常只用来计算激子的“静态”性质, 由于其巨大的计算量, 几十年来难以在动力学领域有所发展. 本工作发现可以通过引入动力学过程中固定介电函数的近似, 只进行一次GW计算, 从W项中提取介电函数矩阵, 用于构造含时BSE哈密顿量, 并将单体的含时Kohn-Sham (TDKS)方程推广为含时两体BSE方程(real-time BSE), 从而得到激子波函数和能量的含时演化. 由于固体材料在动力学过程中介电环境变化很小, 这个近似在保证结果准确度的基础上, 大幅度减少了计算量, 成功地在Hefei-NAMD中首次实现了上百个原子GW+rtBSE的含时演化, 通过与分子动力学的结合自然包含了电声耦合, 同时使用spinor基组, 包含了自旋轨道耦合效应, 该方法的发展为研究TMD材料的谷激子动力学提供了有力的工具.
通过含时激子动力学模拟，如图28所示，我们发现在K谷的亮激子(X1)被激发之后, 大约30 fs之后占据数从98%降至68%, 同时X5的占据从0%升高到30%. 说明在这个时间尺度电子被声子散射到K' 谷, 形成动量禁止的暗激子. 这样的散射能够发生也是因为CBM的自旋轨道分裂只有20 meV, 小于声子的能量. 在这个超快过程之后, X1和X5的占据数会在一个相对缓慢的时间尺度上减小, 同时X7, X8和X2的占据数会增大. 在大约4 ps之后, 体系达到平衡, 此时两个动量与自旋都禁止的激子X7, X8的占据数相对最大, 达到22%与18%, 这是由CBM的能量劈裂和暗激子缺少电子空穴的交换项造成的. 两个亮激子X1, X2的占据数为18%和15%, 剩余的占据分布在其余四个暗激子态上.
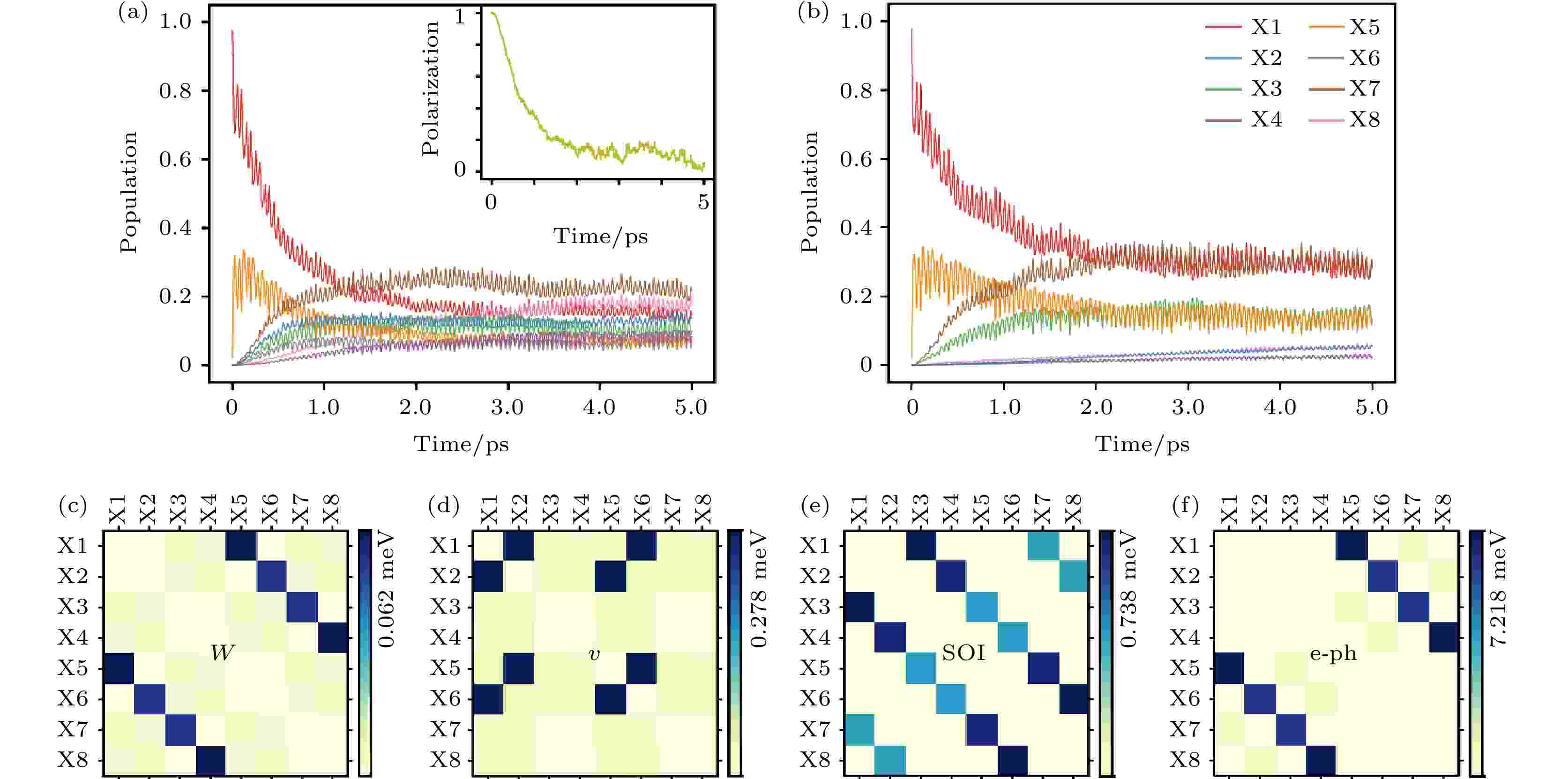图 28 MoS2材料中的含时激子动力学　(a) K谷亮激子X1激发之后, 不同激子态占据数随时间的变化; (b) 没有交换相互作用的情况下, K谷亮激子X1激发之后, 不同激子态占据数随时间的变化; 非绝热耦合矩阵中电子空穴(c)库仑相互作用(W), (d)交换相互作用(v), (e)自旋轨道耦合(SOI)以及(f)电声耦合(e-ph)的贡献(图片经文献[117]允许转载, 版权归2021 American Association for the Advancement of Science所有)
Figure28. Dynamics results and nonadiabatic couplings: (a), (b) Time evolution of the population on X1 to X8 (a) with and (b) without the e-h interaction W and v in the NAMD simulation. The time-dependent valley polarization is inserted in panel (a). (c)–(f) Averaged NACs contributed by W, v, SOI, and e-ph, respectively (Reprinted with permission from Ref. [117]. Copyright 2021 American Association for the Advancement of Science)

在GW+rtBSE方法中, 非绝热耦合项包含四部分的贡献, 分别是: i)电声耦合; ii)自旋轨道耦合; iii)电子空穴库仑相互作用(W); iv)电子空穴交换相互作用(v). 分析表明, 亮激子X1到X2的转化过程是由电子空穴的交换相互作用导致的, 是激子多体效应的直接体现, 证实了交换相互作用导致亮激子谷间散射的观点, 与之前不同实验组报道的时间分辨实验结果符合完好[76,131,132]; 同时, 自旋轨道耦合则能够让亮激子转化为自旋禁止的暗激子, 时间尺度也是皮秒量级, 而电声散射发生在飞秒量级, 时间尺度也与两个不同实验组超快光电子谱实验结果符合[133,134]. 非绝热耦合项里, 自旋轨道耦合与电子空穴交换相互作用处于一个量级, 电声耦合比这两项大一个数量级, 电子空穴库仑相互作用在这个过程中几乎不起作用. 图29给出了激子弛豫的通道与物理机制示意图.
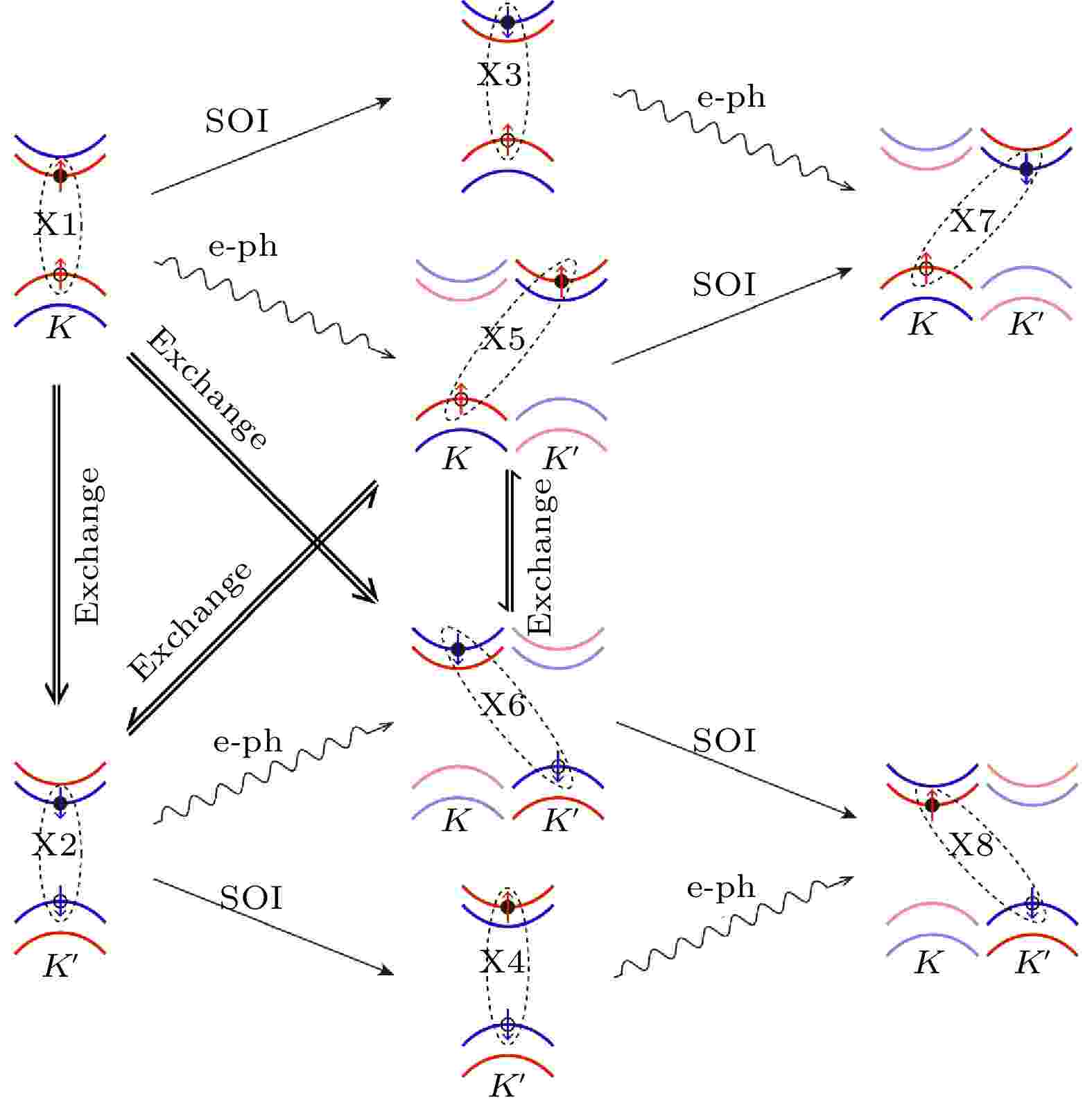图 29 材料中激子弛豫的不同通道与物理机制示意图(图片经文献[117]允许转载, 版权归2021 American Association for the Advancement of Science所有)
Figure29. Schematic map of the exciton dynamics channels and the correlated mechanisms (Reprinted with permission from Ref. [117]. Copyright 2021 American Association for the Advancement of Science)

本工作证明了单层MoS2电子空穴交换相互作用、电子声子散射、自旋轨道耦合分别是产生亮激子谷间退极化、动量禁止暗激子、以及自旋禁止暗激子的物理机制, 并得到了相应的时间尺度, 与前人的时间分辨的实验结果高度符合, 由第一性原理计算的角度首次给出了TMD材料中的谷激子动力学清晰完整的物理图像, 为实现基于二维材料的谷电子学器件提供了重要的理论依据. 同时这套方法也可以广泛应用于其他材料体系, 可以研究激子的弛豫、寿命、解离、以及与缺陷的相互作用等重要的物理问题, 为基于第一性原理的固体材料激子动力学研究领域打开了大门.
7.总结和展望
本文综述了本课题组近几年来利用Hefei-NAMD研究的凝聚态体系中的激发态动力学问题, 包括界面电荷转移、半导体e-h复合动力学以及最近发展的激子动力学, 也对激发态自旋动力学领域做了初步的探索. 在界面电荷转移动力学中, 研究了分子/半导体界面、二维TMD异质结界面以及氧化物异质结界面, 讨论了界面结构、能带匹配以及电声耦合对界面电荷转移的影响. 在半导体e-h复合的问题中, 主要探讨了e-h复合中心产生的条件, 选取了传统半导体TiO2, 二维单质半导体黑磷、以及太阳能电池材料MAPbI3来进行研究. 研究发现在硬度较低的半导体中较难形成e-h复合中心, 这主要和低频声子的激发相关. 我们也给出了一些可能的调控界面电荷转移与e-h复合动力学的方案. 另外, 尝试研究了光激发空穴流的动力学过程, 探索了NAMD在激发态自旋动力学中应用的潜力. 最后, 介绍了最近发展的GW+rtBSE方法, 以及用这种方法研究的MoS2中的自旋谷激子动力学.
值得一提的是, 凝聚态体系中的激发态动力学在第一性原理计算领域是一个刚刚兴起的方向, 我们计划在今后几年的工作中进一步开拓这个领域, 主要包括以下几个方面.
i) 开展固体材料激子动力学的研究. 成功地发展GW+rtBSE方法之后, 我们期待能够利用这个独特的工具对固体材料激子动力学开展系统性的研究工作, 计划选择典型的二维材料TMD材料、黑磷材料等体系来进行.
ii) 开展光激发自旋动力学研究. 使用光激发的手段来调控材料的磁性是超快自旋电子学中的核心概念, 利用这种手段可以实现自旋在超快时间尺度上的变化, 因此我们计划在今后的工作中开展光激发自旋动力学的研究. 计划在哈密顿量中引入自旋轨道耦合, 在电子被光激发到高能量能级之后, 在其弛豫的过程中有可能由于自旋轨道耦合而发生自旋翻转, 导致磁性的变化, 当然, 在这个过程中, 电声耦合以及自旋-声子的耦合会同时起作用, 我们计划利用第一性原理计算的手段来研究动力学过程中不同物理机制的竞争与耦合关系.
iii) 引入核量子效应. 在CPA近似的基础上, 可以通过路径积分的方法, 采用ring polymer molecular dynamics (RPMD)代替普通的第一性原理分子动力学, 引入核量子效应.
应该指出的是, 这个新兴的研究领域中, 很多其他的课题组也在进行努力, 例如, Akimov和他的合作者们[135]将SOC包含在PYXAID代码中, 他们还在小分子系统实现基于Δ-SCF的分子动力学[136]. 吕刚教授课题组[36]发展了基于TDDFT的surface hopping方法. 孟胜和Kaxiras[30]在TDAP的第一原理模拟中加入了光激发过程. 我们期待这个新兴的研究领域能够吸引越来越多的物理和化学科学家的关注与参与, 未来能够从第一性原理的角度深入理解凝聚态体系的激发态动力学及准粒子耦合过程.
相关话题/电子 过程 材料 计算 结构
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 磁场中HD分子振转跃迁的超精细结构
    摘要:HD分子红外跃迁的精密测量被用以检验量子电动力学、确定质子-电子质量比等.但HD分子的超精细结构分裂对于测量精度是一个很重要的限制因素,并可能是实验中测得ν=2—0谱带跃迁呈特殊线型的原因之一.本文分别在耦合表象和非耦合表象下计算了HD分子振转跃迁的超精细结构,并计算了不同外加磁场下HD分子( ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • X射线光电子能谱在固态锂离子电池界面研究中的应用
    摘要:固态锂离子电池因具有高安全、高能量密度等多种优势而备受关注,但目前固态锂离子电池尚未大规模商业化,主要原因是固态锂离子电池中存在的关键科学问题和技术问题尚未解决,特别是界面问题,例如界面的高电阻与不稳定性.X射线光电子能谱(X-rayphotoelectronspectroscopy,XPS) ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种铅铋合金薄膜低温相的结构及超导物性表征
    摘要:铅铋(Pb-Bi)合金超导材料被广泛研究,但对其低温物相的结构和超导物性却知之甚少.本文采用低温共沉积和低温退火的方法,在Si(111)-(7×7)衬底生长的Bi(111)超薄薄膜上制备了铅铋合金薄膜,利用扫描隧道显微术对其结构和电子学性质进行表征.通过结构表征,确定了薄膜中存在相分离,同时存 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 一种同步研究透明材料折射率和动力学特性的实验方法
    摘要:基于电磁加载装置CQ-4,建立了一种同步开展透明材料折射率和高压声速测量的实验方法.完成了聚甲基丙烯酸甲酯(PMMA)窗口材料14GPa斜波压缩实验,利用多点双光源外差位移干涉测速仪(duallaserheterodynevelocimetry,DLHV),获得了PMMA样品后表面的速度历史曲 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • NiCu双金属纳米粒子的表面偏析、结构特征与扩散
    摘要:NiCu双金属核壳纳米粒子不仅由于其优异的稳定性、选择性以及磁学和催化性能而受到广泛关注,而且可以通过改变其纳米粒子的形貌、表面元素分布和粒径大小而具有可调谐性能.采用分子动力学与蒙特罗方法并结合嵌入原子势对NiCu双金属纳米粒子的表面偏析、结构特征以及Cu吸附原子在Ni基底沉积生长与表面扩散 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • InGaN插入层对AlGaN/GaN界面电子散射的影响
    摘要:本文研究InGaN作为AlGaN/GaN插入层引起的电子输运性质的变化,考虑了AlGaN和InGaN势垒层的自发极化与压电极化对AlxGa1–xN/InyGa1–yN/GaN双异质结高电子迁移率晶体管中极化电荷面密度、二维电子气(2DEG)浓度的影响,理论分析了不同In摩尔组分下,InGaN厚 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 金刚石/铝复合材料界面性质第一性原理计算及界面反应
    摘要:采用第一性原理计算和实验相结合的方法,研究了金刚石/铝复合材料的界面性质及界面反应.计算结果表明:金刚石(100)/铝(111)界面粘附功更大,相比金刚石(111)/铝(111)的界面粘附功4.14J/m2提高了41%.同时,金刚石(100)/铝(111)界面处形成Al—C键合的趋势更强.Al ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于电化学-应力耦合模型的锂离子电池硅/碳核壳结构的模拟与优化
    摘要:硅基电极材料在应用中的一个主要问题是巨大的体积膨胀,以及由此带来的电极材料破裂、粉化.本文在有限变形假设前提下,基于电化学-力学耦合理论,研究球形Si/C核壳结构在嵌锂过程中的浓度、应力场的演化,并在此基础上讨论了核壳结构的优化设计.计算结果显示:壳层可以很好地保护硅颗粒的膨胀;然而核内产生的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 双层结构突触仿生忆阻器的时空信息传递及稳定性
    摘要:现有计算机体系架构下的神经网络难以对多任务复杂数据进行高效处理,成为制约人工智能技术发展的瓶颈之一,而人脑的并行运算方式具有高效率、低功耗和存算一体的特点,被视为打破传统冯·诺依曼计算体系最具潜力的运算体系.突触仿生器件是指从硬件层面上实现人脑神经拟态的器件,它可以模拟脑神经对信息的处理方式, ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 新型双模式加权机制及其对网络计算的影响
    摘要:高效率的网络分析方法对于分析、预测和优化现实群体行为具有重要的作用,而加权机制作为网络重构化的重要方式,在生物、工程和社会等各个领域都有极高的应用价值.虽然已经得到越来越多的关注,但是现有加权方法数量还很少,而且在不同拓扑类型和结构特性现实网络中的效果和性能有待继续提高.本文提出了一种新型的双 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.