全文HTML
--> --> -->空间环境中存在的各种高能粒子, 粒子辐照可能会影响电子设备的正常工作, 严重时甚至会导致电子器件的永久性失效, 影响航天器的可靠性和使用寿命. 粒子辐照一方面会在材料中产生电离能量损失(ionizing energy loss, IEL), 产生的电子-空穴对在材料中复合、运动, 影响材料的本征特性的同时可能会在碳化硅基器件中引起瞬态脉冲. 粒子在材料中的能量损失特性通常用线性能量传输(line energy transfer, LET)进行表征. 另一方面粒子辐照在材料中引起的非电离能量损失(non-ionizing energy loss, NIEL)会在材料中产生间隙原子-空位缺陷, 缺陷浓度的变化会导致材料的物理、化学特性发生改变[9,10]. 近年来在实验中发现高能重离子辐照会导致碳化硅器件性能退化, 严重时甚至会导致器件烧毁[11-14], 且辐照损伤与碳化硅材料有关[15]. 利用解析计算和模拟仿真对粒子辐照对碳化硅的影响进行研究, 已经取得一些进展. 郭达禧[16]等利用蒙特卡罗方法模拟了中子在碳化硅中的运输过程与位移损伤. 陈世彬等[17]运用分子动力学方法模拟了4H-SiC 材料辐照下的级联碰撞过程, 发现初级碰撞原子的能量与碳化硅中空位缺陷的数量和空间分布线性相关. 申帅帅等[18]利用Geant4软件计算了质子在碳化硅不同深度的NIEL, 发现碳化硅的抗位移损失能力强于硅, 且随质子能量增大在质子射程前端造成的位移损失更加严重. 空间环境中, 重离子通量较低, 但具有极高的能量. 虽然中子、质子辐照碳化硅发生核反应时可能产生部分重离子, 但产生的都是中低能重离子, 不足以体现更高能量的重离子在碳化硅中的能量损失特性. 现有的研究表明碳化硅器件存在严重的单粒子栅穿(single event gate rupture, SEGR)和单粒子烧毁(single event burnout, SEB)问题, 且碳化硅MOSFET和二极管存在单粒子烧毁阈值电压[19-23]. 当外加偏置电压大于烧毁阈值电压时, 碳化硅器件的外延层存在强电场, 重离子在碳化硅器件外延层中的运动会受到强电场的影响. 目前碳化硅基器件的重离子辐照机理尚不明确, 探究重离子在碳化硅器件的运输过程和能量损失具有重要意义.
针对碳化硅基器件的研究, 可以借鉴在硅基器件中使用的研究方法. Geant4是由欧洲核子中心主导开发的蒙特卡罗程序包, 可以详细模拟粒子在材料中的输运, 现被广泛应用于空间探测、空间辐射效应等研究领域. 本文首先利用蒙特卡罗方法模拟不同LET的重离子在碳化硅中的运输, 对碳化硅中能量损失的时间和空间分布等进行计算, 确定碳化硅中产生能量损失的粒子类型及电离与非电离能量损失的大小. 然后通过锎源试验和TCAD模拟得到不同漏极电压下碳化硅MOSFET内部的电场分布, 将电场分布嵌入蒙特卡罗模型, 模拟并分析不同电场对能量损失的产生及分布的影响.
2.1.模型建立
本节以碳化硅为靶材料, 利用Geant4软件对入射重离子能量及类型、物理过程、数据抽取等模块进行编程, 模拟重离子在碳化硅中的运输过程. 根据重离子在硅中的能量损失特点, 选取了三组重离子(不同种类和能量). 碳化硅靶材料的密度设置为3.2 g/cm3. 重离子从靶材表面中心垂直入射, 靶材料的厚度应足够大, 以保证重离子运动最终停止在碳化硅内. 本文选取的入射重离子描述如表1所列, 重离子在碳化硅中的射程分别使用SRIM软件[24]和Geant4软件计算得到. 从表1可以看到, 使用Geant4软件的计算结果与SRIM的计算结果有较好的一致性, 最大相差14.1%. 射程的差别主要来自在重离子能量较低时Geant4和SRIM选用物理模型的差异[24-28].| 重离子 | 能量/MeV | SiC中射程/μm@SRIM | SiC中射程/μm@Geant4 | SiC中LET /(MeV·cm2·mg–1) | Si中LET /(MeV·cm2·mg–1) |
| 铜 (Cu+) | 212 | 22.01 | 21.5 | 34.08 | 32.2 |
| 溴 (Br+) | 218 | 19.97 | 18.5 | 44.73 | 42 |
| 碘 (I+) | 270 | 19.21 | 16.5 | 69.72 | 65 |
表1选取的重离子种类、能量及其在材料中的射程
Table1.Selected heavy ion, energy and range of heavy ions in silicon carbide.
本节将碳化硅设置为一个足够大的长方体, 如图1所示. 模拟中选取三种LET值的重离子, 在同一位置入射三个相同的重离子. 图中蓝色是初级重离子的运动轨迹, 只有在射程末端能量较低无法与碳化硅相互作用产生电子时能观察到. 红色的是次级电子的运动轨迹, 大量的次级电子沿初级重离子径迹产生并在碳化硅中做无规则运动直至能量耗尽. 黑色是反应产生的极少的γ射线, 其具有较强的穿透性. 初级重离子在射程前端由于能量较高会沿初始入射方向运动, 随着能量逐渐损失重离子运动轨迹开始偏离直线方向直至能量耗尽停止运动.
图 1 不同LET的重离子入射碳化硅的径迹分布 (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mgFigure1. Track distribution of heavy ions with different LET incident on silicon carbide: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mg
2
2.2.重离子致碳化硅损伤分析
仅使用LET值衡量粒子或射线在材料中的能量损失特性太过笼统, 初级重离子的能量随着入射深度的增加而减小, 其与材料的相互作用机制及反应截面也会发生变化. 本文统计了单位深度产生的能量损失随入射深度的变化, 如图2所示. 重离子的能量和射程决定了其LET值的大小. 图2中单位深度的能量损失随入射深度的变化接近指数分布, 能量损失峰值随入射离子能量的增大向左偏移. 单位深度的能量损失在重离子射程初期随离子初始能量的增大而增大. 在入射深度大于14 μm时, 重离子初始能量越大, 在单位深度的能量损失反而越小. 初级重离子与碳化硅相互作用损失一部分能量, 同时有次级粒子产生, 模拟结果表明次级粒子中产生能量损失的主要是电子. 如图3所示, 初级重离子的能量损失随LET增大而增大, 而次级电子的能量损失在LET变化时基本保持不变, 总能量损失主要由电子和初级重离子产生. 侯东明等[29]的研究认为次级电子的能量达到材料的特定损伤阈值时, 材料出现潜径迹损伤. 潜径迹损伤在重离子径迹周围产生, 次级电子能量损失一定程度上反映了材料潜径迹损伤程度.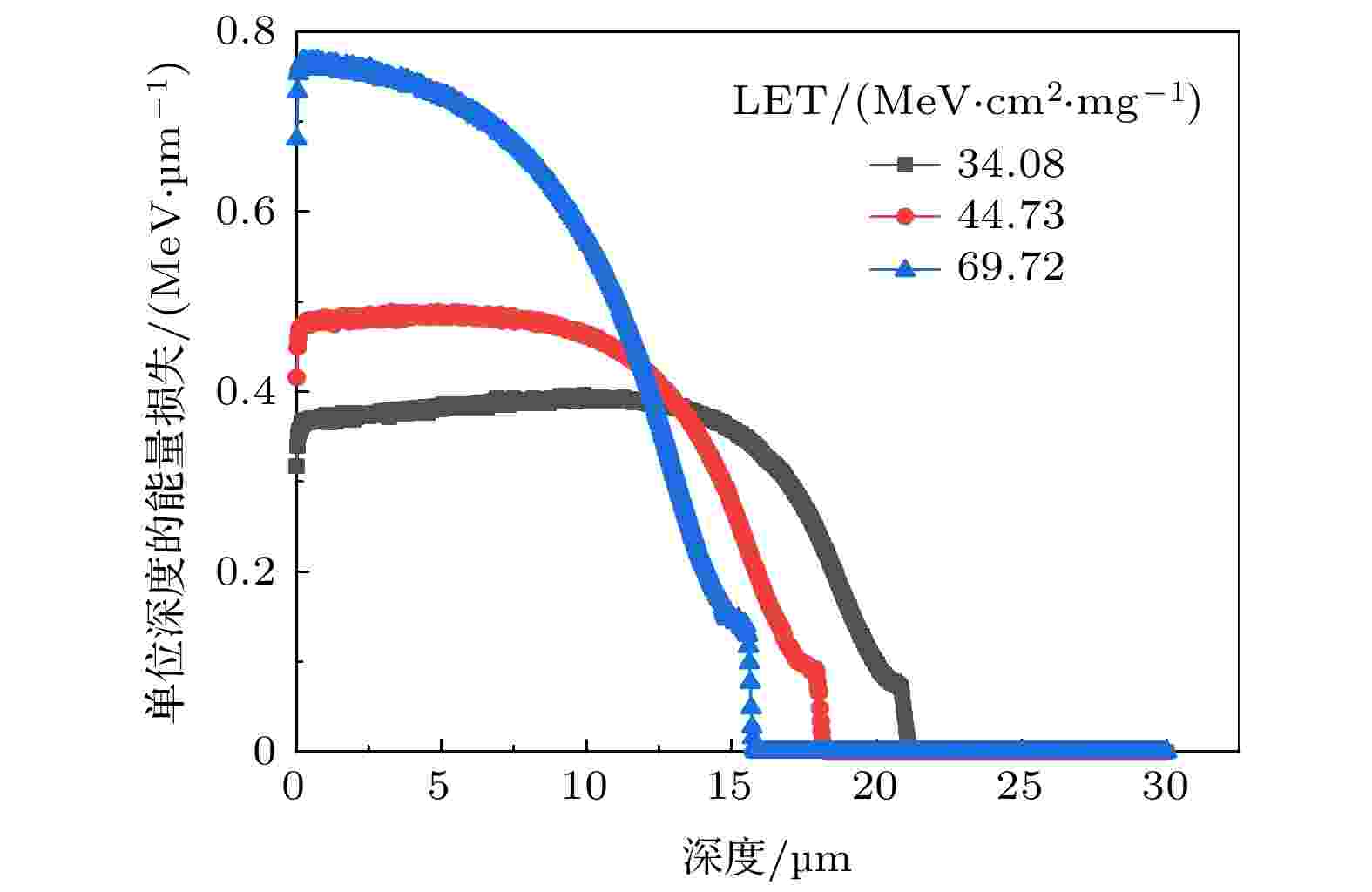
图 2 不同LET的重离子产生的能量损失随入射深度的变化Figure2. The energy loss of heavy ions with different LET changes with the depth of incidence.
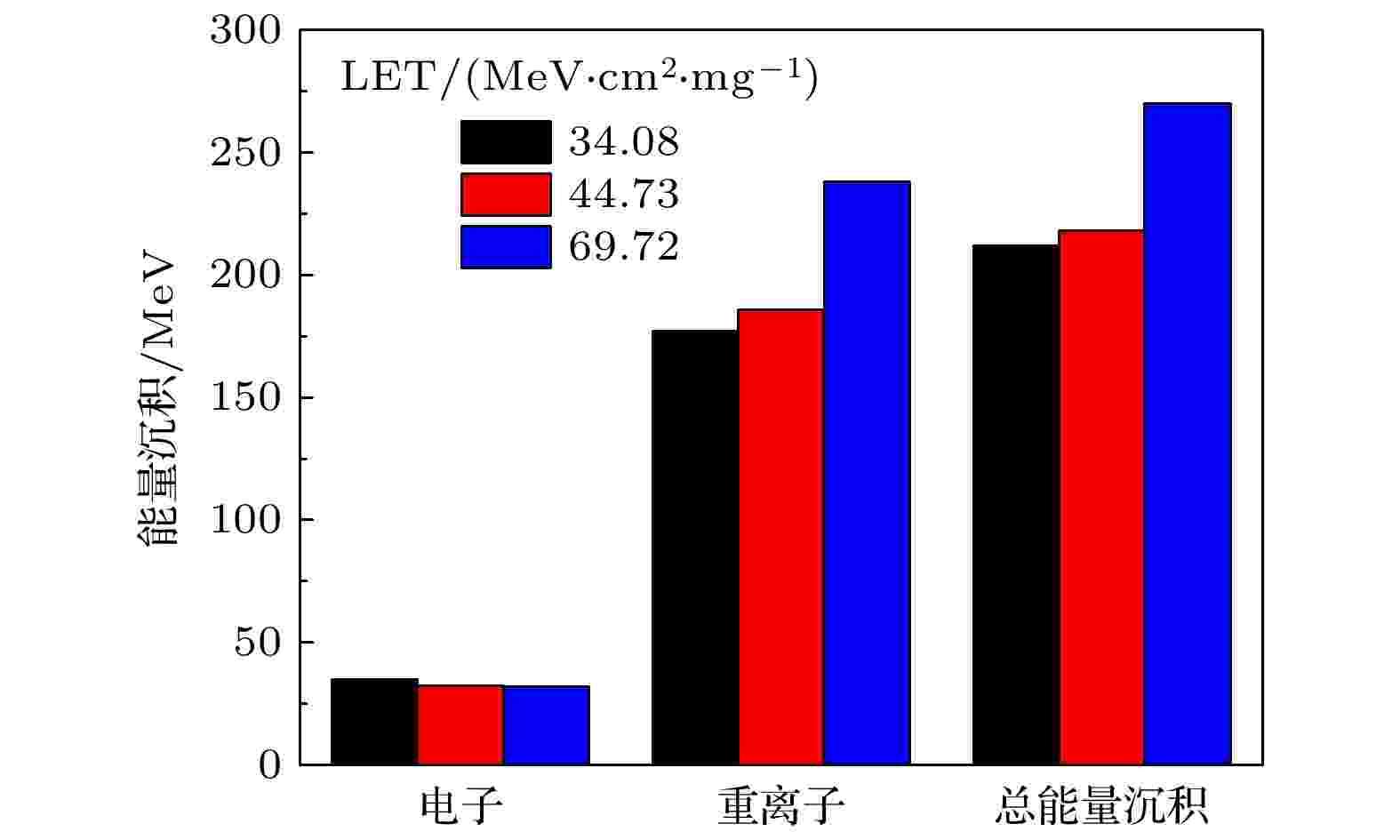图 3 不同粒子造成的能量沉积随LET的变化Figure3. Variation of energy deposition caused by different particles with LET.
图4和图5分别是不同LET下辐照产生的总能量损失和次级电子径迹的二维分布. 能量损失在重离子径迹中心分布最多, 远离径迹中心能量损失逐渐减小. 图4中统计的是多个重离子辐照碳化硅的平均能量损失. 由于重离子与碳化硅相互作用具有随机性, 重离子在射程末端可能会以一定角度偏离垂直碳化硅表面方向, 有时重离子也可能在其射程中段就开始大角度偏离垂直方向. 图4和图5所描述的能量损失和电子径迹有一部分分布在偏离碳化硅中心的区域, 重离子在射程末端能量损失分布也比较发散. 本文入射重离子数量为104个, 入射方向都一致, 足以得到较为精确的结果. 结合图4和图5, 可以发现在射程末端几乎没有次级电子产生, 这段射程内的能量损失全部来自初级重离子. 次级电子最初产生时的角度和能量大小影响着电子能损的分布, 进一步也影响着碳化硅的损伤程度. 图6是不同LET下次级电子初始状态的角度-能量分布图, 重离子入射碳化硅的方向规定为0°. 模拟结果显示, 三种LET下次级电子偏离重离子入射方向都不超过60°, 次级电子的初始能量不超过8 keV. 随着LET的增大, 次级电子的角度和能量分布越来越集中. 材料中次级电子的作用区域越集中则越有可能引起局部区域出现潜径迹损伤.
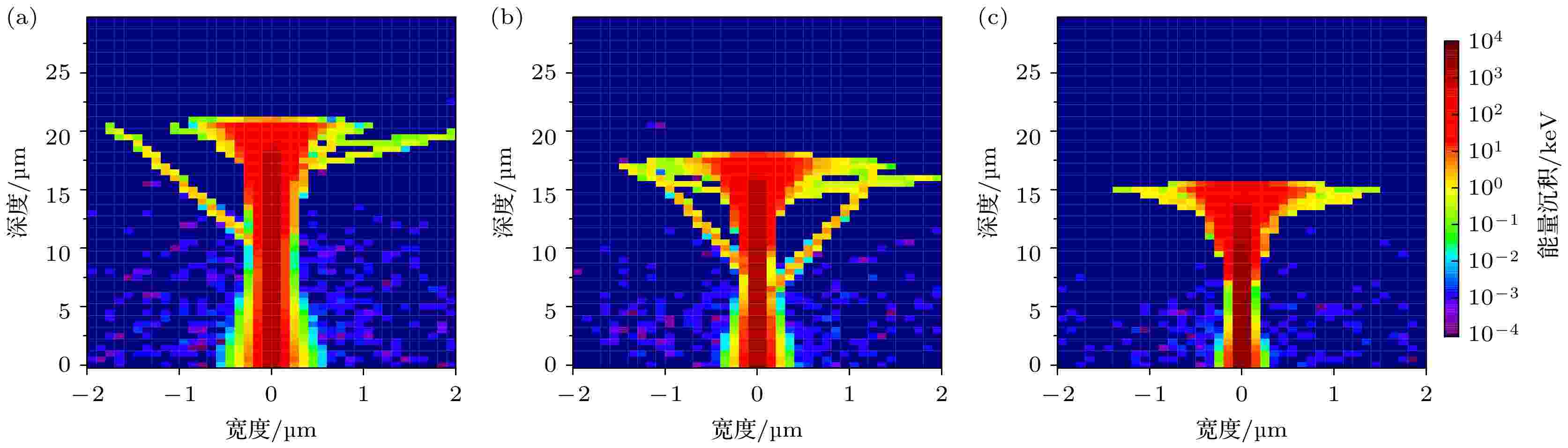图 4 不同LET下总能量损失的空间分布 (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mgFigure4. Spatial distribution of total energy loss under different LET: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mg.
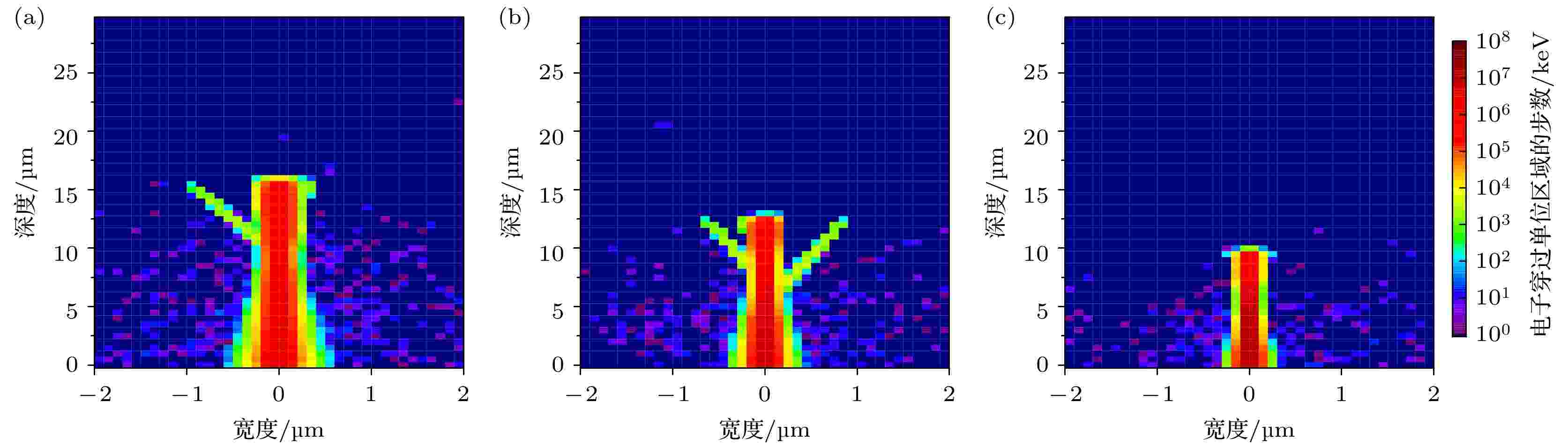图 5 不同LET下次级电子径迹的空间分布: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mgFigure5. Spatial distribution of electron tracks under different LET: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mg
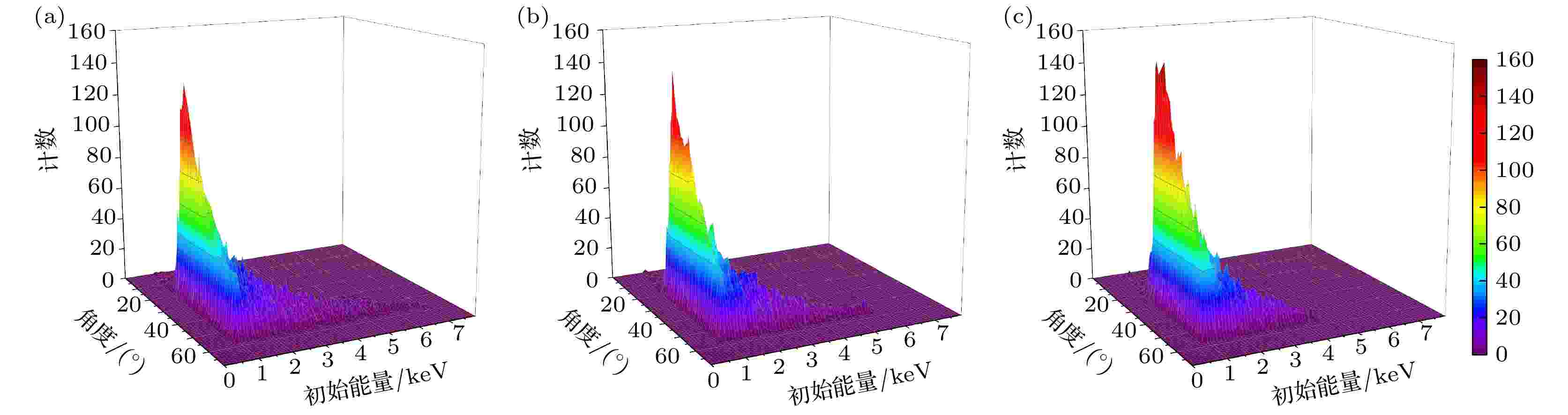图 6 不同LET下次级电子的初始能量及角度分布: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mgFigure6. The initial kinetic energy and angle distribution of secondary electron under different LET: (a) 34.08 MeV·cm2/mg; (b) 44.73 MeV·cm2/mg; (c) 69.72 MeV·cm2/mg
单个重离子在碳化硅中总能量损失随时间的变化如图7所示. 随着时间增加, 不同LET的重离子在碳化硅中的能量损失呈指数增加, 在约1.5 × 10–12 s时间内将自身能量完全损失在碳化硅中. 重离子LET的增大, 只是加剧能量损失的速率, 重离子能量完全损失所用的时间基本不变. 确定材料中电离能量损失的时间和空间分布, 是分析单粒子对器件电学性能影响的基础.
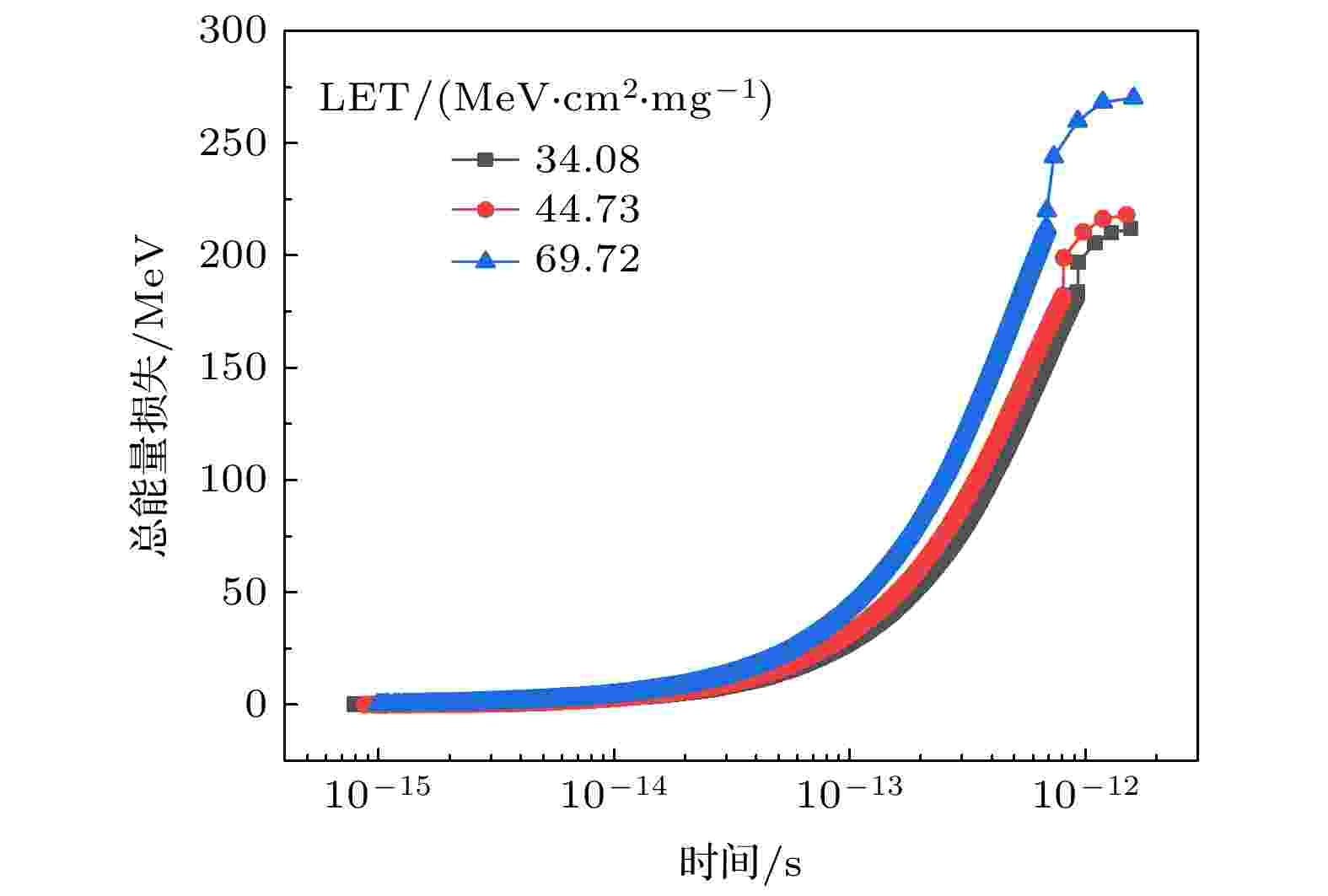图 7 总能量损失在碳化硅中的时间分布随LET的变化Figure7. Time distribution of total energy loss in SiC as a function of LET.
在统计总能量损失随时间的变化时, 也需要对非电离能损进行计算, 图8是单个重离子在碳化硅中非电离能量损失随时间的变化. 重离子在碳化硅中的非电离能损相较于图7中总能量损失所占的比例极小, 270 MeV的I离子最终在碳化硅中产生的非电离能损只有3.9 MeV, 约占总能量损失的1.44%. 值得注意的是, 非电离能损的增加主要集中在时间轴末端, 这也对应着重离子的射程末端. 我们分析在射程末端, 重离子主要是与碳原子和硅原子发生弹性和非弹性碰撞, 产生非电离能量损失. 本文计算了非电离能损随入射深度的分布情况, 如图9所示. 不同LET下重离子引起的非电离能量损失主要分布在重离子射程的末端, 而且射程末端的非电离能量损失至少比其射程前中段高一个数量级. 已有实验研究表明氮化镓的潜径迹损伤半径只有几纳米[30]. 碳化硅与氮化镓同为第三代宽禁带半导体材料, 两者的辐照损伤有一定的相似之处. 如图9所示入射重离子的LET为34.08 MeV·cm2/mg时, 单位深度产生的非电离能损在10000 eV以上. 一般来说碳原子和硅原子的位移阈能只有几十电子伏特, 非电离能损的产生对应着间隙原子-空位缺陷的形成. 随着LET值的增大, 单位深度产生的非电离能损增大, 碳化硅中产生的间隙原子-空位缺陷增多. 对于碳化硅材料, 会有一部分碳原子和硅原子的位置被撞离原本的位置成为间隙原子, 对应着出现碳空位和硅空位. 通过退火等手段可以让一些间隙原子复位, 但也可能会有部分间隙原子-空位无法复合, 形成永久性缺陷损伤. 当缺陷浓度达到一定程度时, 碳化硅材料的性质会发生改变, 进而影响碳化硅器件的性能.
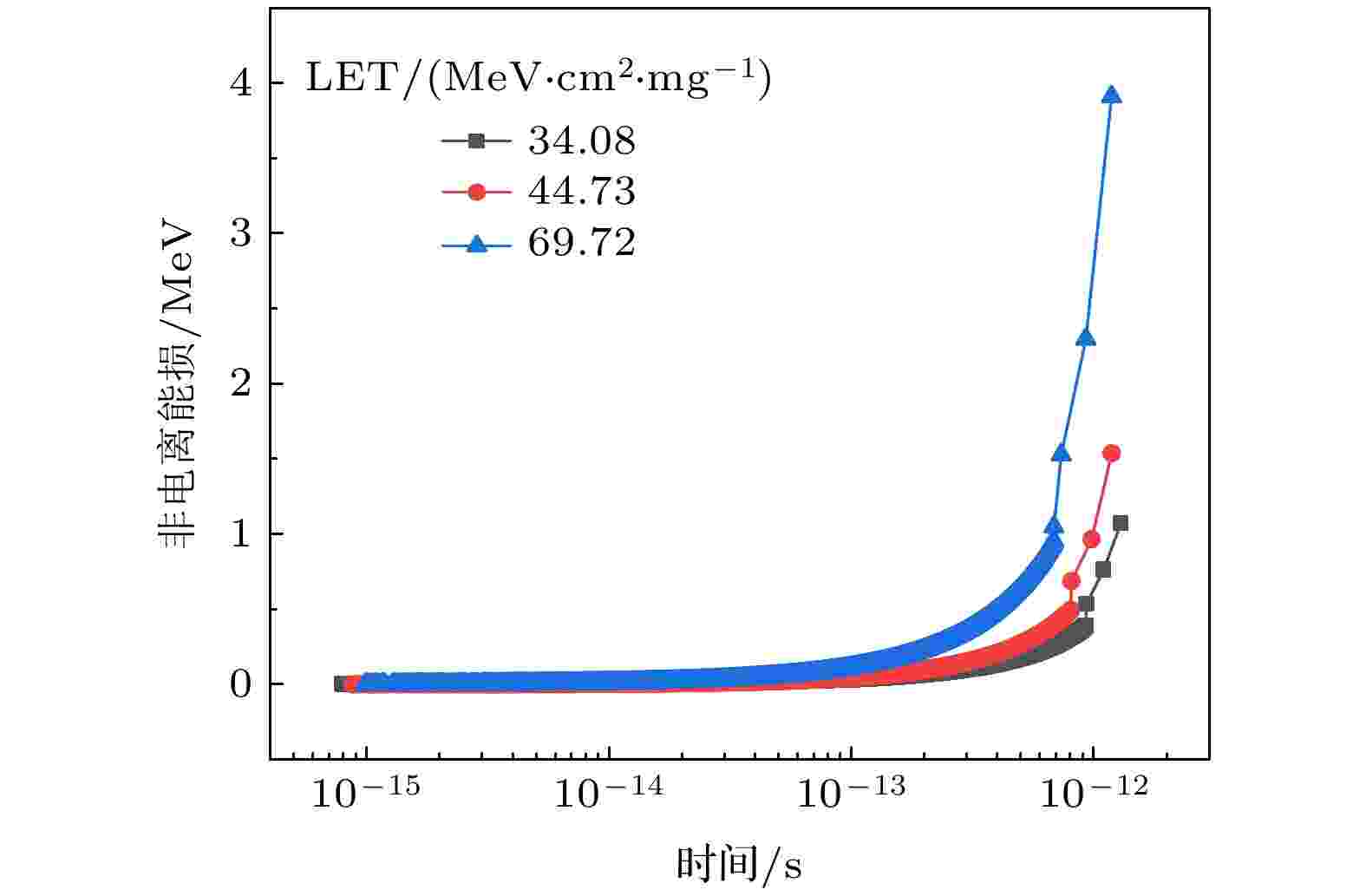图 8 非电离能量损失在碳化硅中的时间分布随LET的变化Figure8. The time distribution of non-ionizing energy loss in SiC varies with LET.
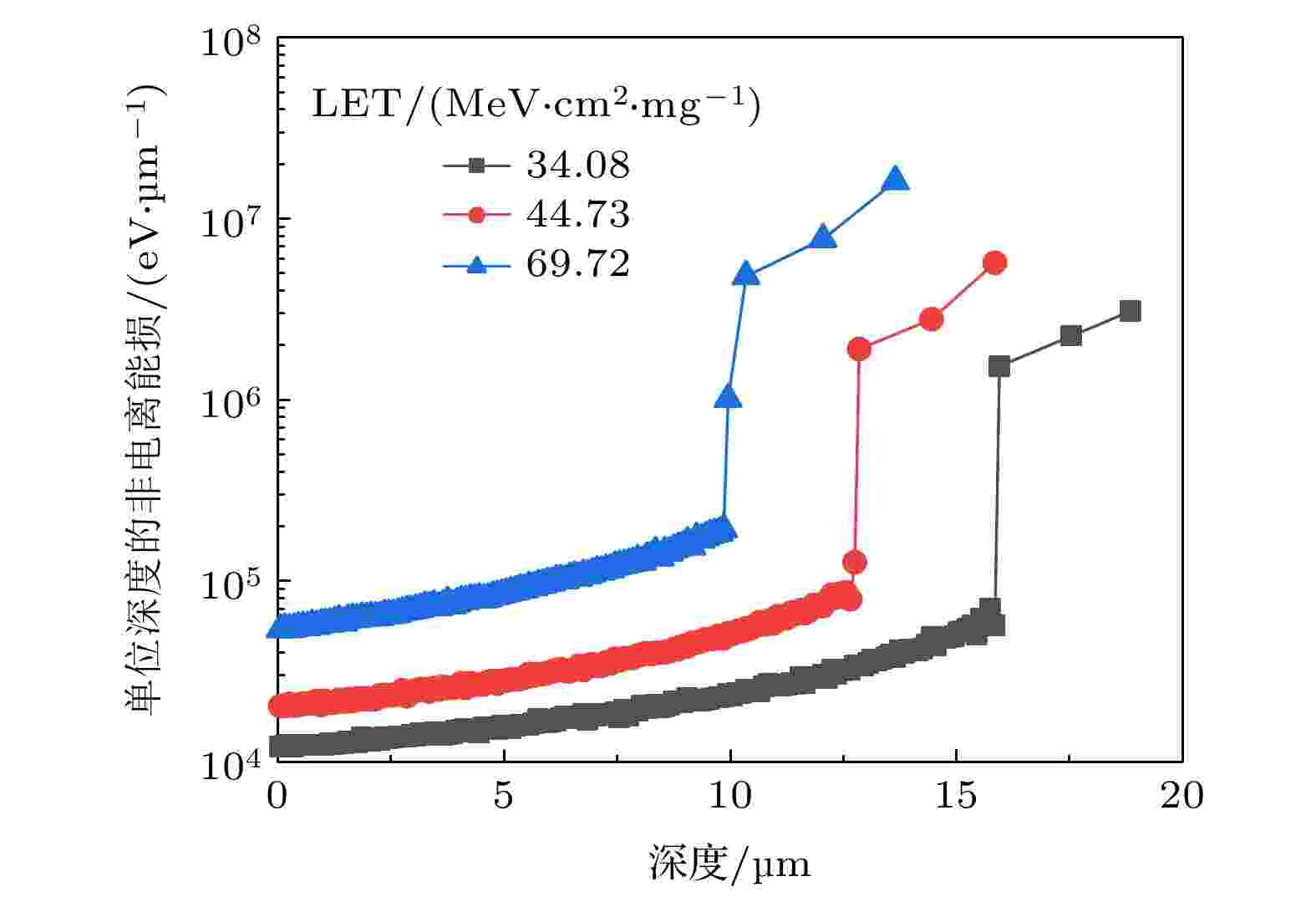图 9 不同LET下碳化硅中的非电离能量损失随深度的变化Figure9. The non-ionizing energy loss in SiC varies with depth under different LET.
能量损失在垂直于重离子径迹方向的分布一定程度上反映出碳化硅的损伤程度. 根据LET值的计算公式
图10是电荷沉积在垂直于重离子径迹方向的分布随LET的变化. 随LET的增加, 重离子径迹中心和垂直于径迹方向的能量损失都逐渐增大. 同一LET下, 不同深度处的能量损失在垂直于重离子径迹方向呈高斯线性减小, 能量损失主要集中在到重离子径迹中心距离小于0.5 μm的区域内. 结合图7和图8, 可以发现非电离能量损失在重离子的能量损失中所占的比例很小, 重离子的大部分能量损失对应着电离产生大量的电子空穴对. 潜径迹损伤对材料而言是硬损伤, 而电离能量损失引起的是瞬时高密度电荷聚集.
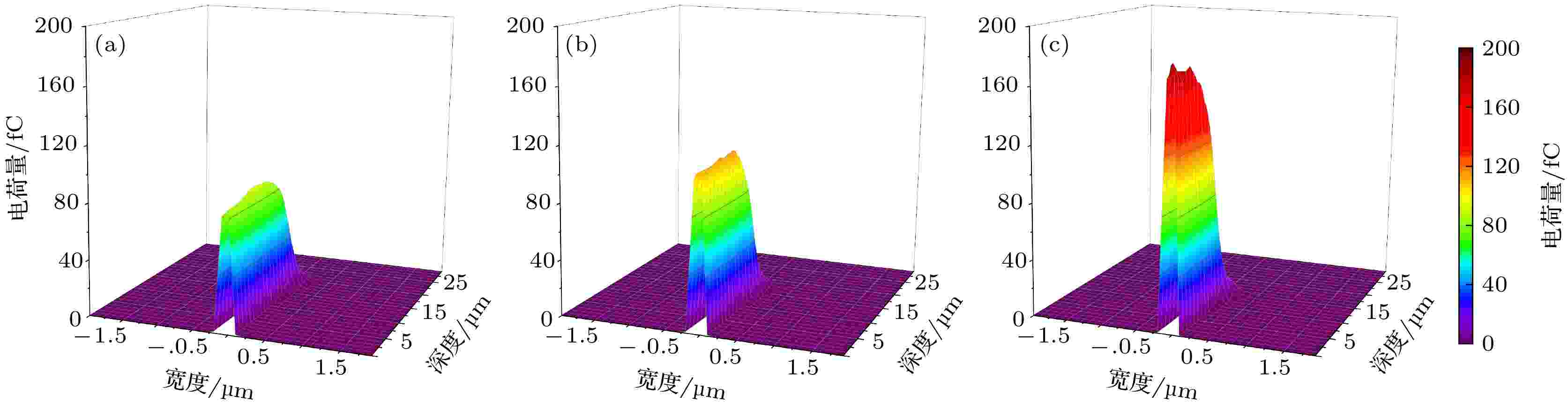图 10 不同LET下电荷沉积在垂直于重离子径迹方向的分布Figure10. Distribution of charge deposition perpendicular to the direction of heavy ion tracks under different LET.
3.1.碳化硅器件内部偏置电场分析
当漏极电压为零时, 碳化硅MOSFET内部电场也为零, 重离子产生的非电离能损不足以对碳化硅器件产生明显损伤. 当漏极电压达到烧毁阈值电压时, 碳化硅MOSFET内部有非零电场存在, 通过试验和器件仿真可以获得非零电场的大小及其在碳化硅MOSFET中的分布. 利用锎源对顶部开封后的碳化硅MOSFET进行单粒子效应试验, 选用的碳化硅器件额定电压900 V, 导通电阻120 mΩ. 锎源产生的重离子碎片LET(Si)集中在41—43 MeV·cm2/mg之间. 经探测器测量, 锎源产生的重离子注量率约为145 cm–2·s–1. 锎源试验中碳化硅MOSFET测试电路如图11所示. 图11中VDC为高压电压, C是高压电容, Rprotect是保护电阻. 数字万用表与碳化硅MOSFET串联, 实时监测器件漏端的电流变化. 试验中碳化硅MOSFET的栅极电压和源极电压始终为0 V. 当漏极电压增大至480 V时, 碳化硅MOSFET发生了单粒子烧毁. 碳化硅MOSFET发生单粒子烧毁的具体表现为瞬时漏电流呈数量级增大以及反向击穿电压小于1 V, 如图12(a)和图12(b)所示. 从图12(a)可以发现器件烧毁后输出电压几乎全部施加在保护电阻两端, 此时漏电流大小即输出电压与保护电阻的比值. 但保护电阻只能防止电路短路, 无法起到防止器件烧毁的作用. 图12(b)是辐照前后器件的击穿电压测量结果, 根据器件手册器件漏电流大于0.1 mA即被击穿. 辐照前器件的击穿电压约1200 V, 辐照后器件的击穿电压已低于1 V, 基本丧失反向击穿特性.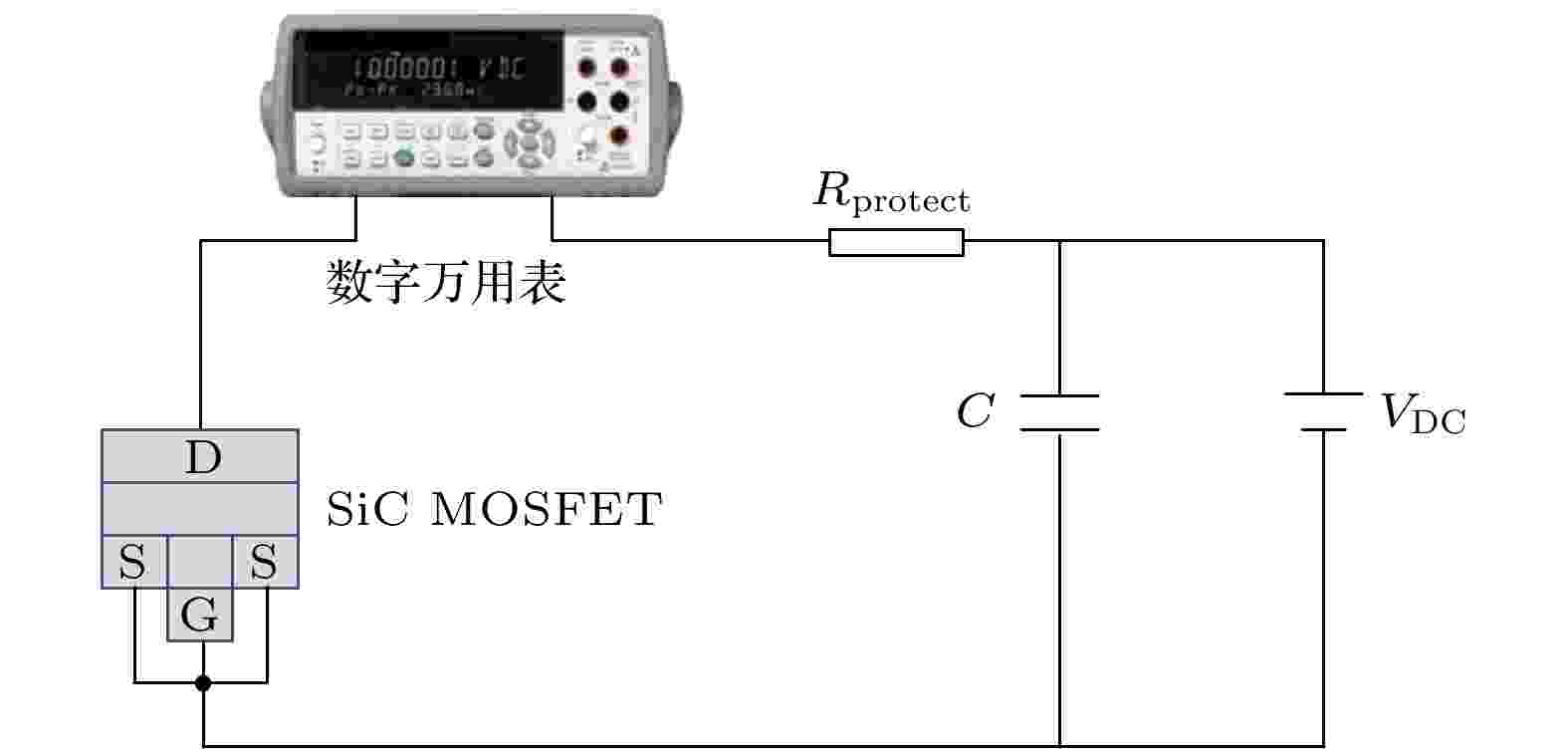
图 11 单粒子效应试验电路图Figure11. Single event effect test circuit diagram.
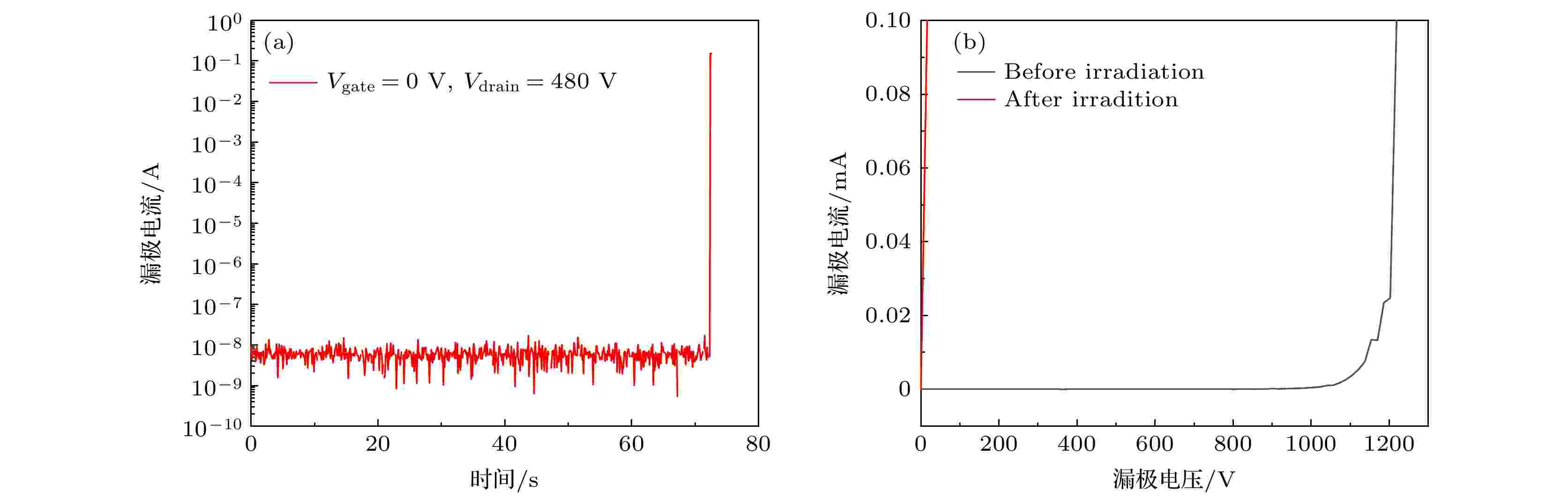图 12 碳化硅MOSFET单粒子烧毁特征 (a)烧毁时瞬态漏电流剧增; (b)击穿特性丧失Figure12. SEB characteristics of silicon carbide MOSFET: (a) Transient leakage current increases sharply when burned out; (b) loss of breakdown characteristics.
在器件栅、源、漏三端电压为0 V的试验中, 重离子累积注量为1 × 107, 试验前后碳化硅MOSFET的电学特性没有变化. 当漏极电压增大到480 V时, 器件在70 s左右便发生烧毁. 利用TCAD模拟, 得到了漏极电压为480和1000 V时碳化硅MOSFET的电场分布, 如图13所示. 可以看出, 漏极电压的增大, 对器件而言意味着外延层受到的电场增大. 碳化硅器件发生单粒子烧毁, 被认为是瞬时大电流和强电场共同作用下产生过高的功率耗散[31]. 强电场来自外部施加的漏极电压, 而大电流由粒子运动路径上沉积的电荷在强电场作用下产生.
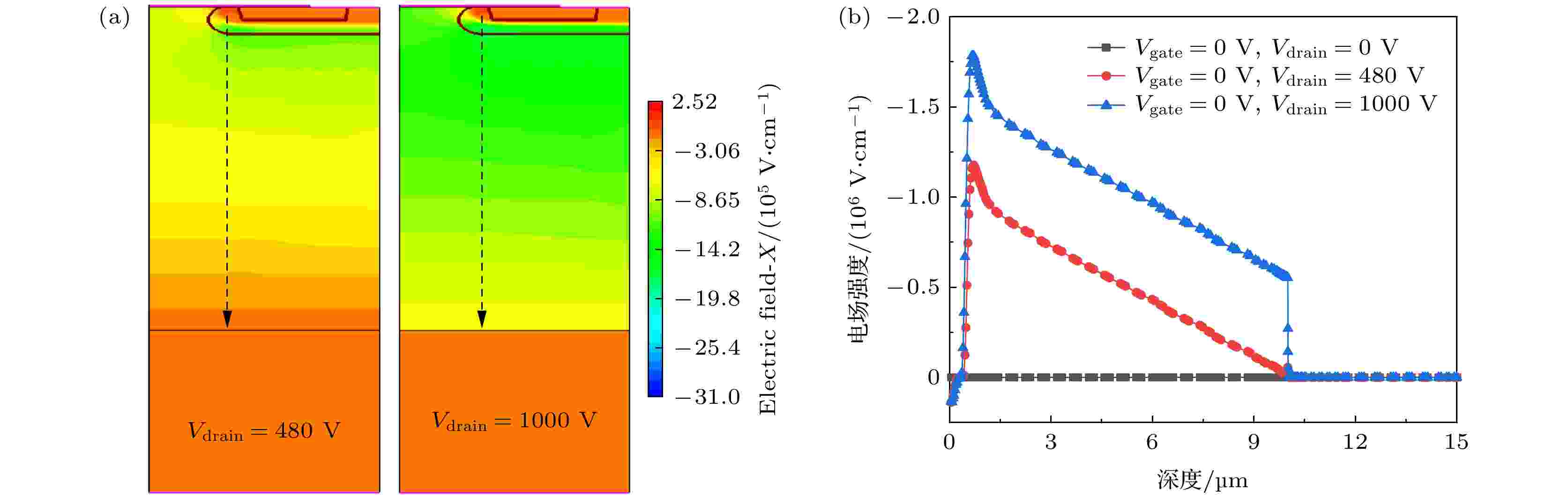图 13 不同漏极偏压下碳化硅MOSFET内部的电场分布 (a)二维分布; (b)一维分布Figure13. The electric field distribution inside the silicon carbide MOSFET under different drain bias voltages: (a) Two-dimensional distribution; (b) one-dimensional distribution.
2
3.2.偏置电场对重离子在碳化硅中能量沉积产生及分布的影响
强电场会影响电荷的运动, 但其是否会影响电荷的产生尚不清楚. 重离子在碳化硅中的运输伴随着大量次级电子的产生及运动. 重离子的初始能量较高, 但其能量会随射程的增大显著下降, 同时图6表明次级电子的初始能量较低. 电场对重离子运输过程的影响不容忽视. 对碳化硅MOSFET进行切片分析, 得到器件单胞上方金属层的厚度, 如图14(a)所示. 图14(b)是根据器件切片分析结果构建的Geant4仿真模型, 其中外延层和衬底的厚度分别设置为10和5 μm. 同时结合TCAD得到的外延层中的电场分布, 在外延层中施加一个沿器件深度方向的电场. 模拟中施加的电场大小为外延层中电场的平均值, 漏极偏置电压为480 V时外延层中沿深度方向电场平均值为–2.85 × 105 V/m, 漏极偏置电压为1000 V时外延层中沿深度方向电场平均值为–6.21 × 105 V/m.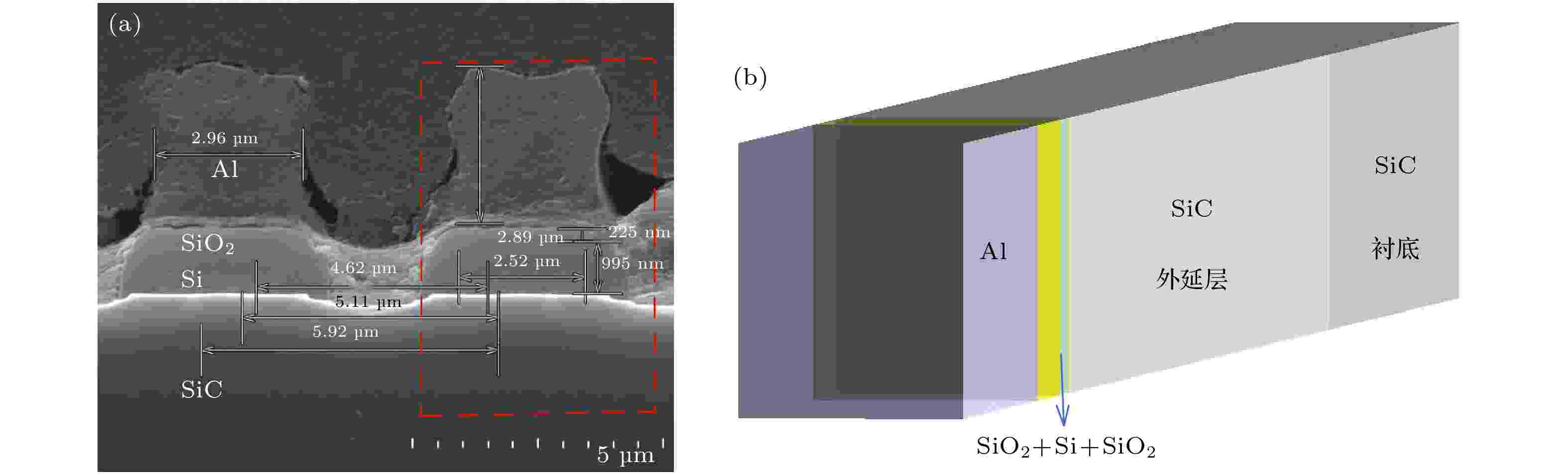
图 14 碳化硅MOSFET内部结构示意图 (a)切片分析结果; (b)Geant4仿真模型Figure14. Schematic diagram of the internal structure of silicon carbide MOSFET: (a) Slice analysis results; (b) Geant4 simulation model.
图15是不同偏置电压下碳化硅MOSFET外延层中能量沉积的二维分布. 由于受到沿深度方向的负电场作用, 电场强度越大重离子的运动越有可能往电场方向偏移, 越多的能量沉积在外延层中. 而带负电的电子初始运动方向由图6可知与深度方向的夹角较小, 且电子能量偏低, 容易受到电场影响而改变运动方向. 当大量电子运动方向趋于一致时更容易引起局部区域能量沉积过高, 进一步促进过大的瞬态电流产生. 同时强电场更容易让重离子最终停留在外延层中, 射程末端大量的非电离能损对应着外延层碳化硅材料严重的潜径迹损伤, 这可能对器件的单粒子烧毁敏感性造成影响.
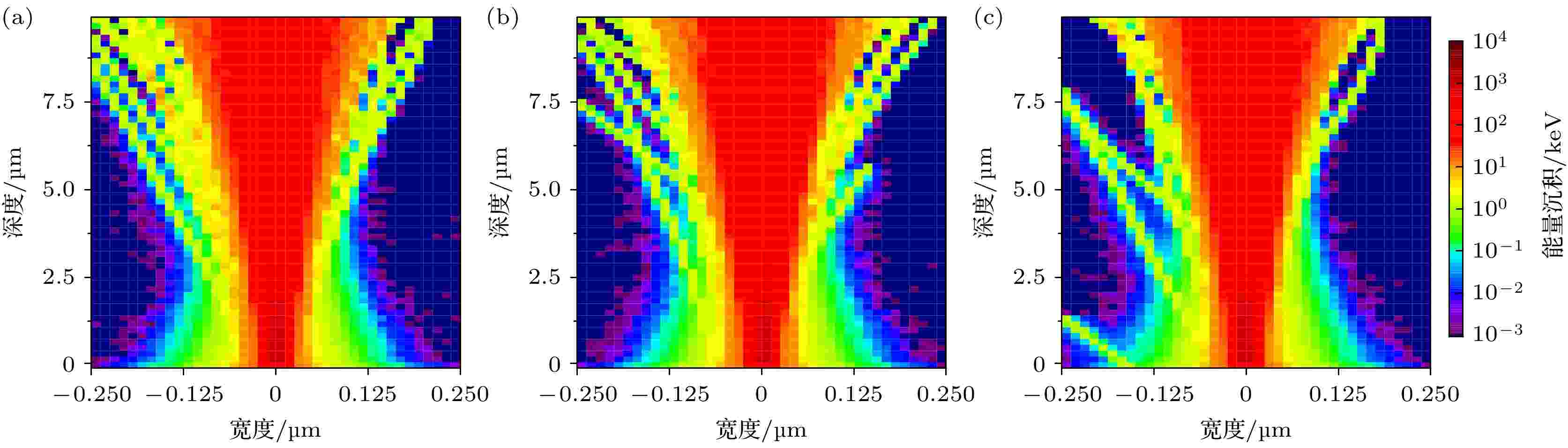图 15 不同漏极偏置电压下碳化硅MOSFET外延层的能量沉积分布 (a)VDrain = 0 V; (b)VDrain = 480 V; (c)VDrain = 1000 VFigure15. Energy deposition distribution of epitaxial layer of silicon carbide MOSFET under different drain bias voltage: (a) VDrain = 0 V; (b) VDrain = 480 V; (c) VDrain = 1000 V.
对于碳化硅器件而言, 碳化硅材料是其主要组成部分, 当器件处于高压偏置时碳化硅材料中会有强电场存在. 重离子诱导产生的大量电子空穴对在强电场作用下形成大电流, 当局部区域由于大电流、大电压同时存在而产生过多热量时, 碳化硅器件会发生烧毁. 器件材料所受到的潜径迹损伤一方面可能在材料中产生电离通道, 另一方面可能影响材料的热传导性能, 从而影响器件的单粒子烧毁敏感性. 综上所述, 碳化硅器件乃至氮化镓器件单粒子烧毁的出现, 是入射粒子诱导产生的非电离能量损失和电离能量损失共同作用的结果, 而器件的偏置电压同时影响着重离子在器件内的电荷沉积和电荷运动.
在锎源试验中确定了碳化硅MOSFET的烧毁阈值电压约为480 V, 结合TCAD模拟得到漏极偏置电压为480和1000 V时, 外延层中沿深度方向电场平均值分别为–2.85 × 105和–6.21 × 105 V/m. 利用Geant4构建碳化硅MOSFET器件模型, 在外延层中引入不同漏极偏置电压对应的电场, 发现电场强度越大重离子越有可能偏向电场方向运动, 在器件外延层中形成更多、更集中的能量沉积. 本文研究结果可用于碳化硅功率器件辐照机理分析及抗辐照加固设计方面.
