全文HTML
--> --> -->目前, SiC场效应晶体管(SiC MOSFET)器件的辐照效应引起了人们极大的关注. 2012年, Akturk等[7]利用60Co-γ射线对1200 V的SiC MOSFET功率器件开展总剂量实验, 结果表明, 当累积剂量超过100 krad (Si)时, 器件仍然具有良好的性能, 但累积剂量超过300 krad (Si)时, 栅极-漏极之间电容将发生变化并会显著影响器件的开关性能. 2016年, Pavel和Stanislav[8]利用4.5 MeV的电子对1700 V的4H-SiC MOSFET功率器件进行了总剂量实验, 结果表明, SiC MOSFET功率器件对于电子辐照十分敏感, 阈值电压随着累积剂量的增加会迅速降低. 2019年, Pavel和Stanislav [9]对不同的SiC功率器件开展了总剂量辐照实验, 结果表明, 包含氧化层的SiC器件受到辐照后更容易出现总剂量效应. 但是, 半导体器件可能在各种复杂恶劣的环境下工作, 想要精确地评估器件的抗总剂量能力, 需要掌握器件的功能退化、失效规律与累积剂量以及电压、温度等应力条件之间的关系. 根据先前的报道, MOS晶体管在辐照过程中电子空穴对的初始复合率对电场也有很强的依赖性[10]. 同时由于SiC材料具有较大的禁带宽度, 因此杂质离化能较大, SiC基器件在室温下仅有60%左右的杂质离化, 当温度达到700 K时, 所有的杂质才会全部离化, SiC器件的最高工作温度可达到800 K以上, 是一种用于高温环境的理想器件[11,12]. 因此, 在辐照过程中引入电压、温度等变量是精确评估SiC基半导体器件抗总剂量能力的必要条件.
地面模拟MOS器件的总剂量效应通常会用到高剂量率辐照配合一定条件的加速退火来等效空间辐射环境. SiC MOSFET器件在辐射后进行退火, 可以使其性能部分甚至完全恢复, 但是退火效应会受到退火时的环境温度、时间、电场等因素的影响[13,14]. 因此, 对辐照后的SiC MOSFET进行不同环境下的退火实验, 有助于深入地研究SiC MOSFET器件的退火机理.
本文利用γ射线对SiC MOSFET器件开展了不同电压、不同温度下的总剂量辐照实验; 同时也对器件辐照后的退火效应进行了研究, 并基于Arrhenius模型, 分析了阈值电压恢复时退火时间和温度之间的函数关系.
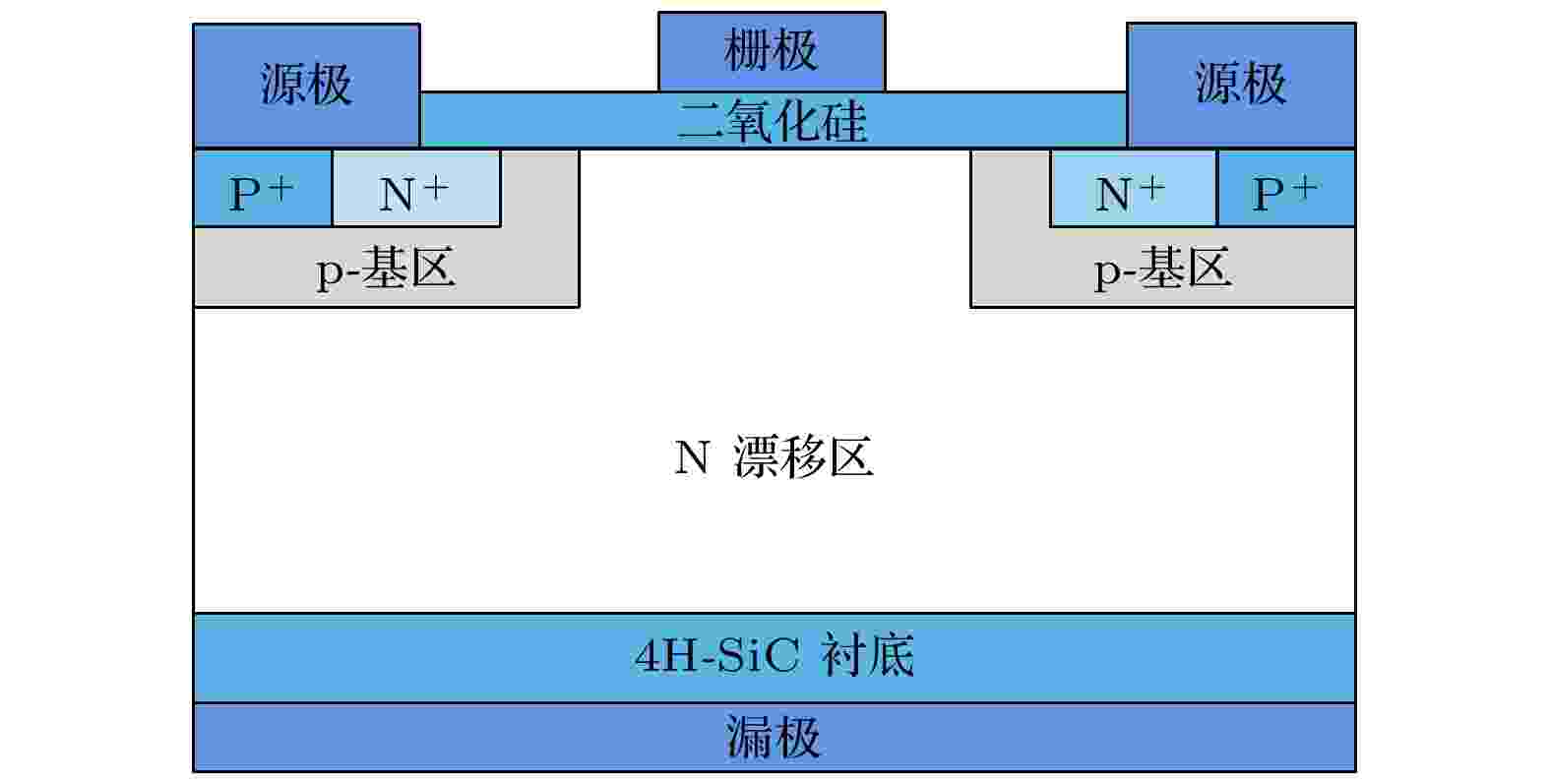图 1 4H-SiC MOSFET简化示意图Figure1. Simplified schematic diagram of 4H-SiC MOSFET.
总剂量辐照实验在60CO-γ射线源上进行, 并在辐照实验中引入了电压和温度等变量. 在探究电应力对器件辐照退化的影响时选取了栅压偏置(VGS = 5 V, VDS = 0 V)、漏压偏置(VGS = 0 V, VDS = 300 V)、零压偏置(VGS = VDS = 0 V)进行总剂量辐照实验, 在此基础上又选取了1, 3, 5, 10和20 V等不同栅压进行总剂量辐照实验; 在探究温度应力对器件辐照退化的影响时选取了室温和100 ℃两个温度变量进行总剂量辐照实验, 辐照时的剂量率都为50 rad (Si)/s. 辐照前后, 利用BC3193半导体分析仪以及B1500 A对器件的各项电学参数作出了详细的表征. 整个辐照过程中选取了50, 150, 250, 350和500 krad (Si)等5个剂量点. 为了保证实验数据的可靠性, 器件辐照后的电学参数测试都在1 h内完成.
当总剂量辐照实验完成后, 对辐照后的SiC MOSFET器件进行不同温度、不同电压下的退火实验, 整个退火过程持续一周的时间. 并在特定的时间点取下器件移位到BC3193上进行电学性能的测量.
3.1.电应力对SiC MOSFET器件总剂量效应的影响
图2和图3分别给出了SiC MOSFET器件在不同偏置条件下辐照前后的转移特性曲线、阈值电压漂移量与累积剂量的关系. 从图中的实验结果可以看出, 在500 krad (Si)的累积剂量下, 三类偏置条件下器件的转移特性曲线都有明显的向左漂移, 器件的阈值电压也有显著的减小. 与此同时, 发现实验选用的偏置电压条件对器件的辐照退化程度有很大影响, 在相同的累积剂量下, 栅压偏置下器件的辐照退化最严重. 当辐照剂量达到500 krad (Si)时, 栅压偏置下阈值电压的变化程度高达46%, 漏压偏置和零压偏置下阈值电压变化程度为24%. 以上结果表明, 对于增强型N-MOSFET器件来说, 栅极施加电场是器件总剂量辐照过程中的最恶劣偏置.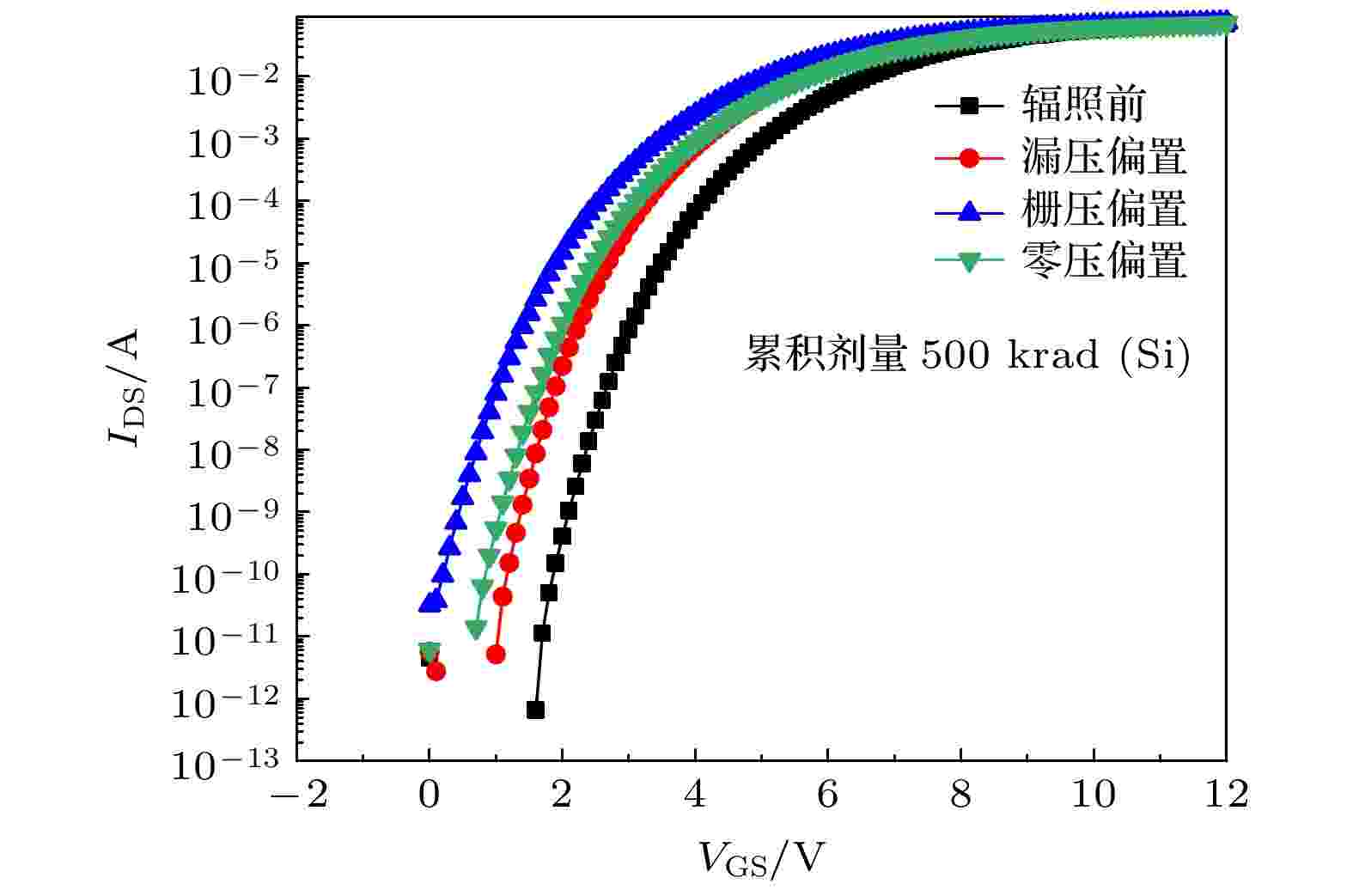
图 2 不同偏置下SiC MOSFET辐照前后转移特性曲线Figure2. Transfer characteristics of SiC MOSFET before and after irradiation under different biasing conditions.
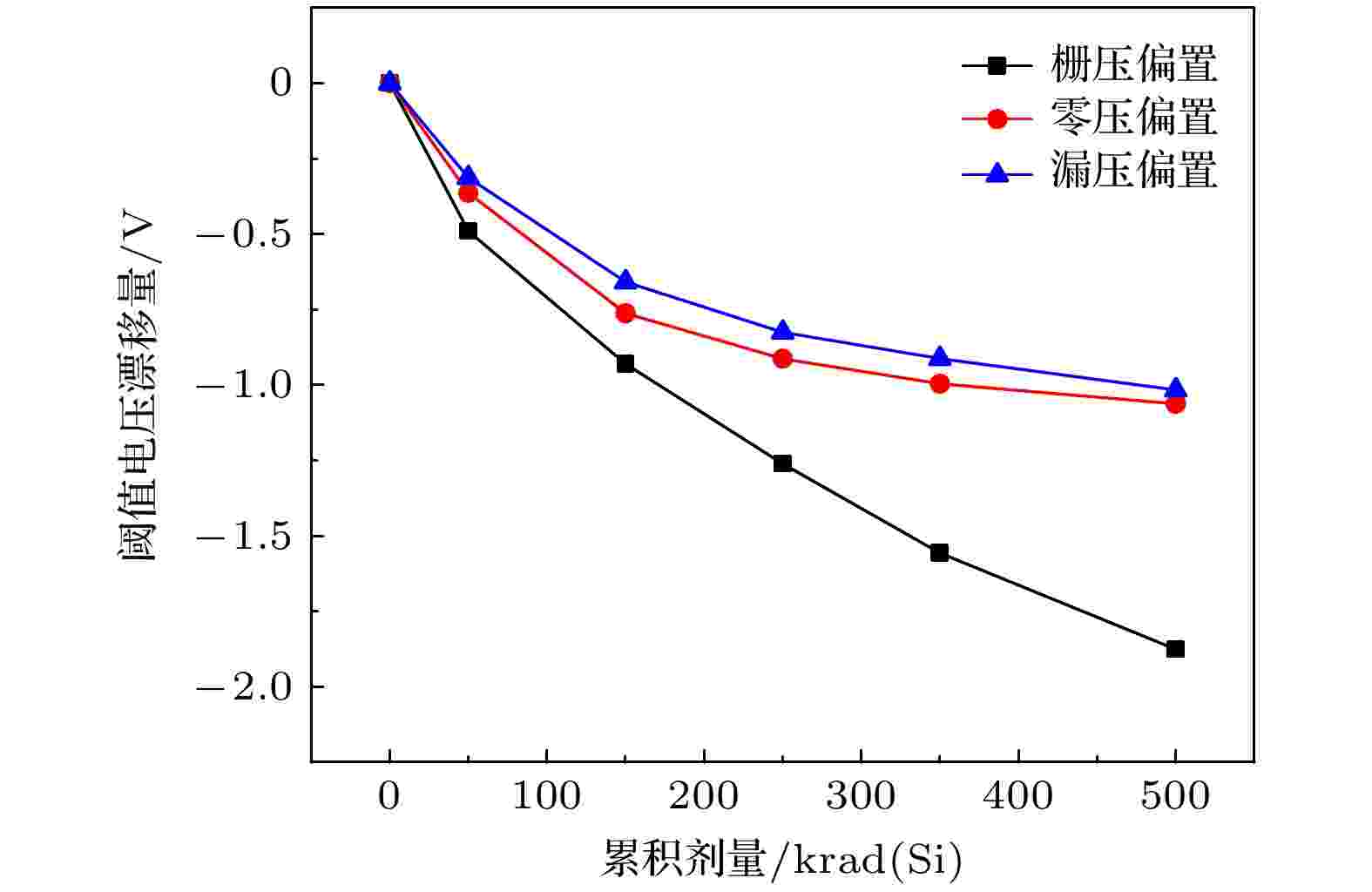图 3 不同偏置下SiC MOSFET阈值电压随累积剂量的变化Figure3. Variation of threshold voltage of SiC MOSFET with cumulative dose under different bias.
在此基础上, 为了更加深入地探索栅极电场强度对SiC MOSFET器件辐照退化的影响, 开展了不同栅压下的总剂量辐照实验. 图4是1, 3, 5, 10 和20 V等不同栅压下器件辐照前后亚阈值区域的转移曲线, 辐照累积的总剂量为500 krad(Si). 从图中结果来看, 不同栅压偏置下辐照后器件的转移曲线都向左漂移, 然而器件辐照后的退化程度并没有随着栅极电压的增加而变大. 与栅极电压为1 V时相比, 当栅极电压为3 V时器件辐照后的退化程度明显增大; 但是与栅极电压为3 V时相比, 当栅极电压为5, 10 和20 V时, 器件辐照后的退化程度明显减小, 并且随着栅压增加这种变弱的程度愈发明显. 值得注意的是, 栅压为20 V时器件辐照后的退化程度甚至要略小于栅压为1 V时的退化程度. 经过对器件阈值电压的测试发现, 当栅压为1 V时, 辐照后器件阈值降低了1.3 V, 当栅压为3 V时, 辐照后器件阈值电压减小了1.9 V, 当栅压为20 V时, 辐照后器件阈值电压减小了1.2 V.
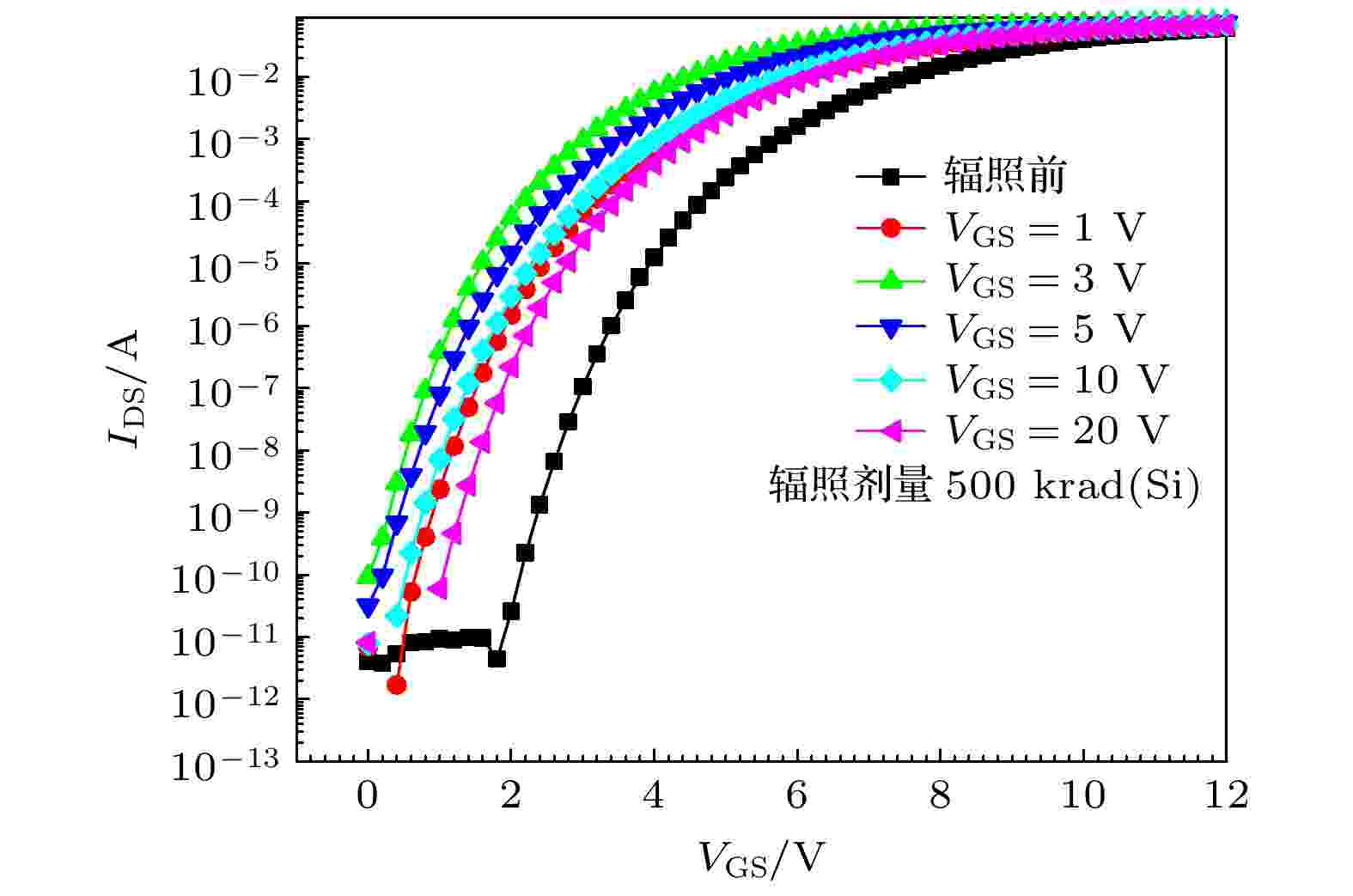图 4 不同栅压下辐照前后的亚阈值区域转移特性曲线Figure4. Transferring characteristics of subthreshold region before and after irradiation under different gate pressures.
为了解释这种总剂量辐照退化和电场之间的依赖关系, 需要从总剂量效应造成器件性能退化的物理过程来分析. 总剂量效应造成SiC MOSFET器件的退化主要是由于辐照在器件栅氧化层中感生出陷阱电荷. 当γ射线入射到SiC MOSFET中, 会在氧化层中沉积能量, 当沉积的能量大于材料的禁带宽度时, 部分被束缚的电子会吸收入射粒子沉积的能量, 使其从价带跃迁到导带, 在氧化层中产生大量的电子-空穴对. 由于电子在氧化物介质中的迁移率远大于空穴, 因此在外加电场的作用下, 电子在极短时间内(皮秒级)被扫出栅极, 在此之前空穴和电子会发生复合. 逃脱复合的空穴则会通过跃迁的方式向着SiC/SiO2界面处移动, 当空穴跃迁至SiO2界面附近时, 会在界面附近的深层陷阱中被俘获, 形成正的氧化物陷阱电荷[15-17]. 空穴跃迁过程中会释放出氢元素, 并在SiC/SiO2界面处发生作用而产生界面态陷阱. 氧化物陷阱电荷会导致SiC MOSFET器件的阈值电压负漂, 界面态电荷会导致阈值电压正漂, 可以认为阈值电压的漂移由氧化陷阱电荷和界面态电荷共同决定[18]. 所以, 对于本次研究中的N沟道MOSFET器件来说, 相对于漏压偏置和零偏, 栅极施加正的电压会增加逃脱初始复合的空穴数量, 形成的陷阱电荷浓度也会更大, 增加器件的辐照退化程度, 这也解释了为什么栅压偏置是辐照时的最恶劣偏置. 上文解释了总剂量效应会在器件栅氧化层内感生出氧化物陷阱电荷以及界面态电荷, 从而造成器件电学性能退化. 因此, 想要深入地揭示SiC MOSFET器件的总剂量效应的物理机理, 首先就是要精确地计算出γ射线辐射时在器件栅氧化层内部产生的氧化物陷阱电荷以及界面态电荷的浓度.
精确计算出两种陷阱电荷浓度的第一步是将氧化物陷阱电荷和界面态电荷对阈值电压的贡献量分离出来. 在这里用ΔVot表示氧化物陷阱电荷对阈值电压漂移做出的贡献, 用ΔVit表示界面态电荷对阈值电压漂移做出的贡献, 辐照后阈值电压的漂移量可以用(1)式表示. 本研究采用了中带电压法对器件的两种辐射感生电荷进行分离[19,20]. 中带电压Vmg就是指当费米能级与禁带中心点重合时对应的栅极电压. 此时, 由于界面态呈电中性, 不会引起阈值电压的变化. 因此, 可以认为阈值电压的漂移都是由氧化物陷阱电荷引起的, 如(2)式所示.
根据上述理论, 求出ΔVot和ΔVit后, 氧化物固定电荷浓度以及界面态电荷浓度可以通过(5)式和(6)式计算出:
基于图4所示的不同栅压下的亚阈值区域的转移特性曲线, 利用上述的中带电压法分离得到不同栅压下氧化物陷阱电荷浓度、界面态电荷浓度以及阈值电压漂移量随辐照时栅压的变化, 如图5所示. 可以看出, 相较于栅压为3 V时辐照后氧化物陷阱电荷的浓度, 在5, 10 和20 V时辐照后感生的氧化陷阱电荷浓度分别降低了22%, 37%和48%. 同时发现, 整个辐照过程界面态电荷浓度没有增加, 认为当施加的栅压超过3 V之后, 器件阈值电压的漂移量减小是由氧化物陷阱电荷浓度减小造成的.
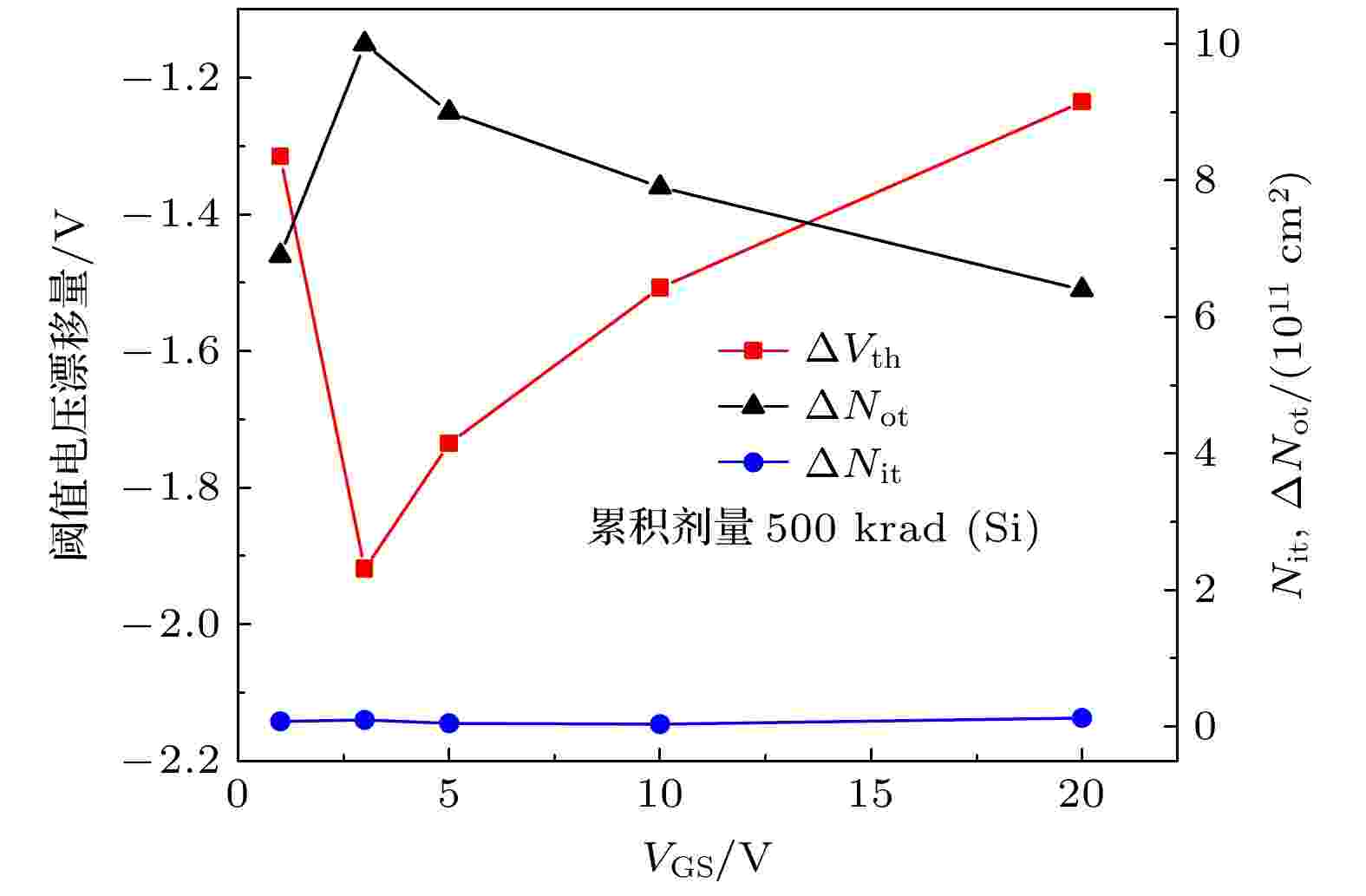图 5 辐照后阈值电压和陷阱电荷浓度随栅压的变化Figure5. Variation of threshold voltage and trap charge concentration with gate voltage after irradiation.
对于栅压和氧化物陷阱电荷俘获率之间的关系可以这样解释, 随着栅压增加, 逃脱复合的空穴比例会增加, 但空穴俘获截面会减小, 氧化层中俘获空穴的数量主要依赖于俘获截面[21,22]. 因此, 本研究表明, 在不同的栅压下进行相同累积剂量辐照, 辐照后SiC MOSFET器件的氧化物陷阱电荷浓度不会随着栅压的增大而变大, 在栅压超过3 V时, 空穴俘获截面会减小.
2
3.2.温度应力对SiC MOSFET器件总剂量效应的影响
图6(a)和图6(b)分别给出了SiC MOSFET器件在室温和100 ℃时, 辐照前后的输出特性曲线. 在辐照前后对器件的输出特性进行测试时, 分别选取了VGS = 7 V以及VGS = 9 V的测试条件. 从图6(a)和图6(b)所示的结果来看, γ射线辐照后会导致器件的漏源电流增加, 随着累积剂量的增加漏源电流的变化量逐渐增大. 图7(a)和图7(b)分别给出了SiC MOSFET器件在常温和100 ℃时, 辐照前后的亚阈值区域转移特性曲线. 从图7(a)和图7(b)可以看出, 随着累积总剂量的增加, 辐照后器件的转移特性曲线都逐渐向负电压一侧漂移, 阈值电压逐渐减小但辐照后曲线的斜率没有明显变化. 同时, 图中也反映出总剂量效应导致器件电学性能的退化会受到温度应力的影响, 主要表现为在100 ℃下辐照时器件电学性能的退化程度更低.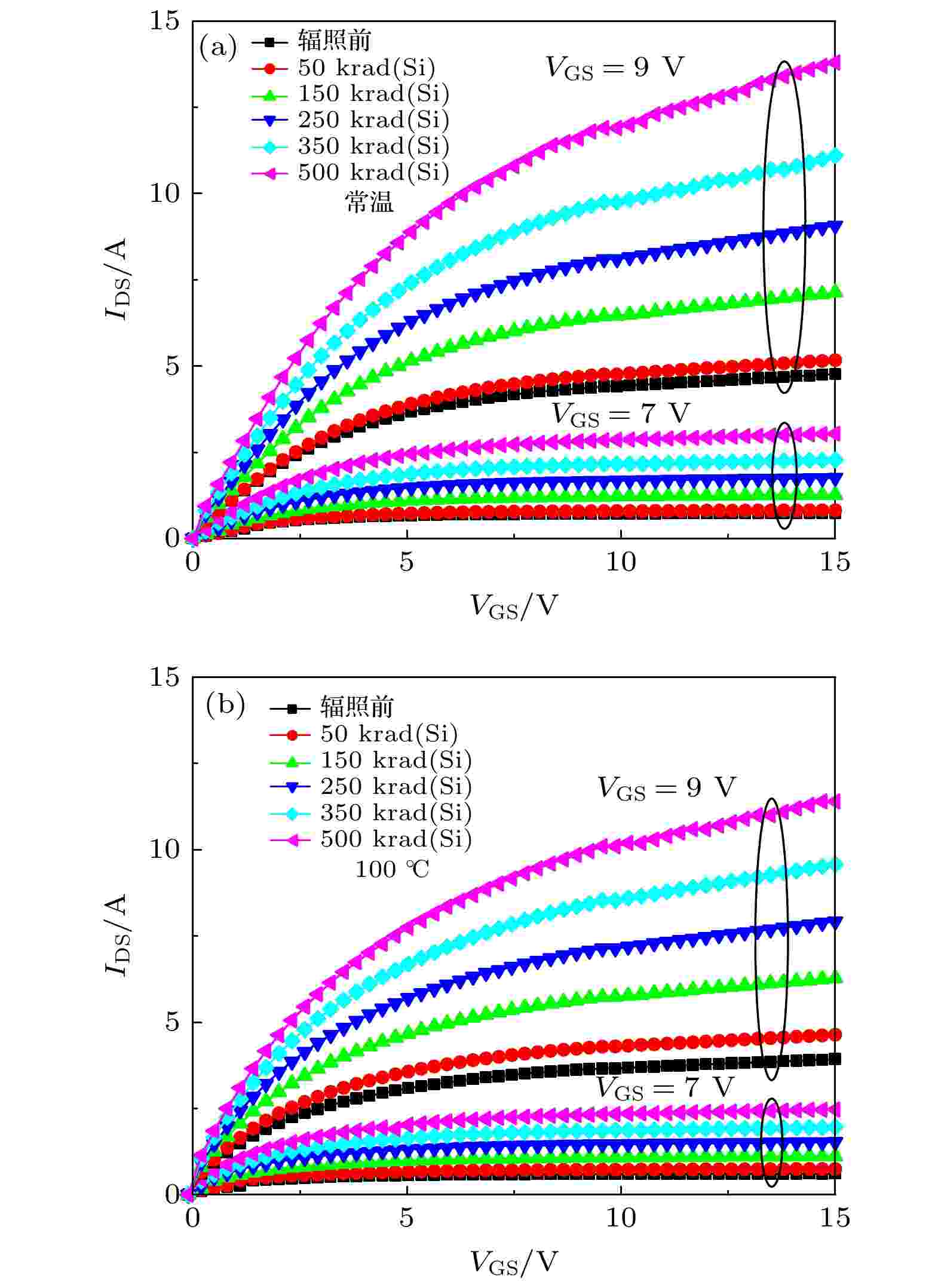
图 6 SiC MOSFET器件在辐照前后输出曲线 (a)常温辐照; (b)100 ℃辐照Figure6. Output curve of SiC MOSFET device before and after irradiation: (a) Normal temperature irradiation; (b) high temperature irradiation.
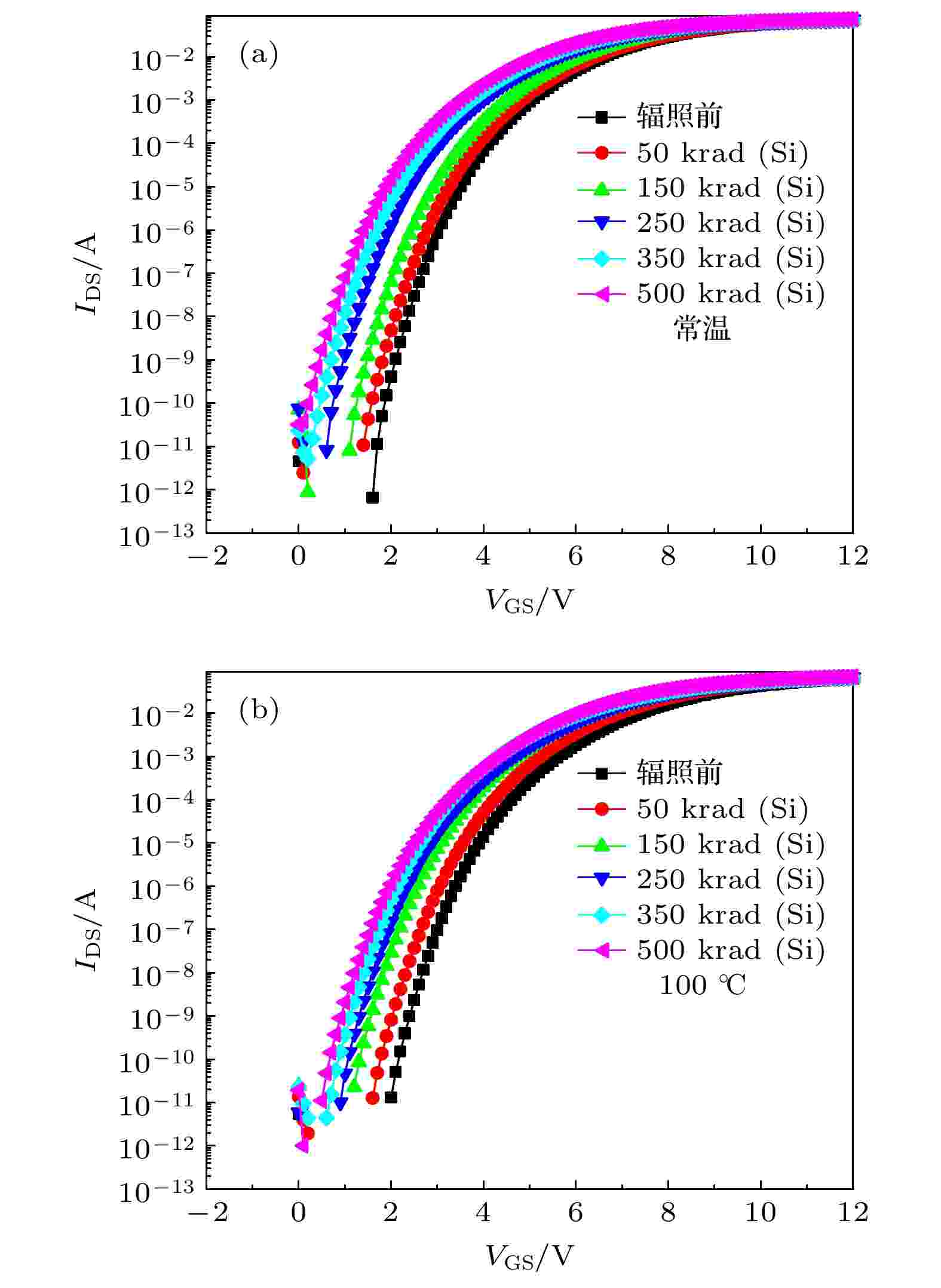图 7 SiC MOSFET器件辐照的前后转移曲线 (a)常温辐照; (b)100 ℃辐照Figure7. Transfer curve of SiC MOSFET devices before and after irradiation: (a) Normal temperature irradiation; (b) high temperature irradiation.
上述结果表明, 总剂量效应会使SiC MOSFET器件发生退化而导致器件阈值电压、漏源电流等电学参数发生变化; 相较于100 ℃, 常温环境是SiC MOSFET器件进行γ射线辐照时的恶劣辐照环境. 关于总剂量效应导致SiC MOSFET器件的退化机理在上文中已经进行了阐述, 为了解释在常温和100 ℃下辐照时, 器件退化程度存在差异的原因, 基于图7(a)和图7(b)所示的两种温度下器件辐照前后的转移特性曲线, 利用中带电压法分离得到室温和100 ℃时, 辐照感生的氧化物陷阱电荷和界面态电荷造成阈值电压的漂移量ΔVot和ΔVit, 如图8所示. 可以看出, 无论是在常温还是100 ℃的环境下辐照, 造成器件阈值电压退化的主要原因都是辐照在氧化层内感生的氧化物陷阱电荷, 但在相同的累积剂量下, 100 ℃下进行辐照时感生的氧化物陷阱电荷浓度更低一些, 所以导致在此温度下辐照时器件的退化程度更低. 分析认为, 100 ℃下辐照时, 器件在辐照过程中发生了退火效应而导致氧化物陷阱电荷浓度变低, SiC MOSFET器件辐照后存在隧穿效应以及热激发两种退火方式. 图9给出了高温辐照时隧穿效应的电荷分布情况, 当在100 ℃对器件进行辐照时, 一方面辐照会在器件的栅氧化层内感生出氧化物陷阱电荷, 另一方面沟道电子会在100 ℃的温度环境中获得足够穿过SiO2/SiC界面的能量, 在电场的作用下由沟道隧穿到氧化层内与辐照感生的氧化物陷阱电荷发生中和, 使其浓度减小, 从而造成辐照退化程度降低. 热激发退火是将氧化层中由辐照感生的氧化物陷阱电荷通过热激发的形式移除氧化层, 从而降低器件的辐照退化程度.
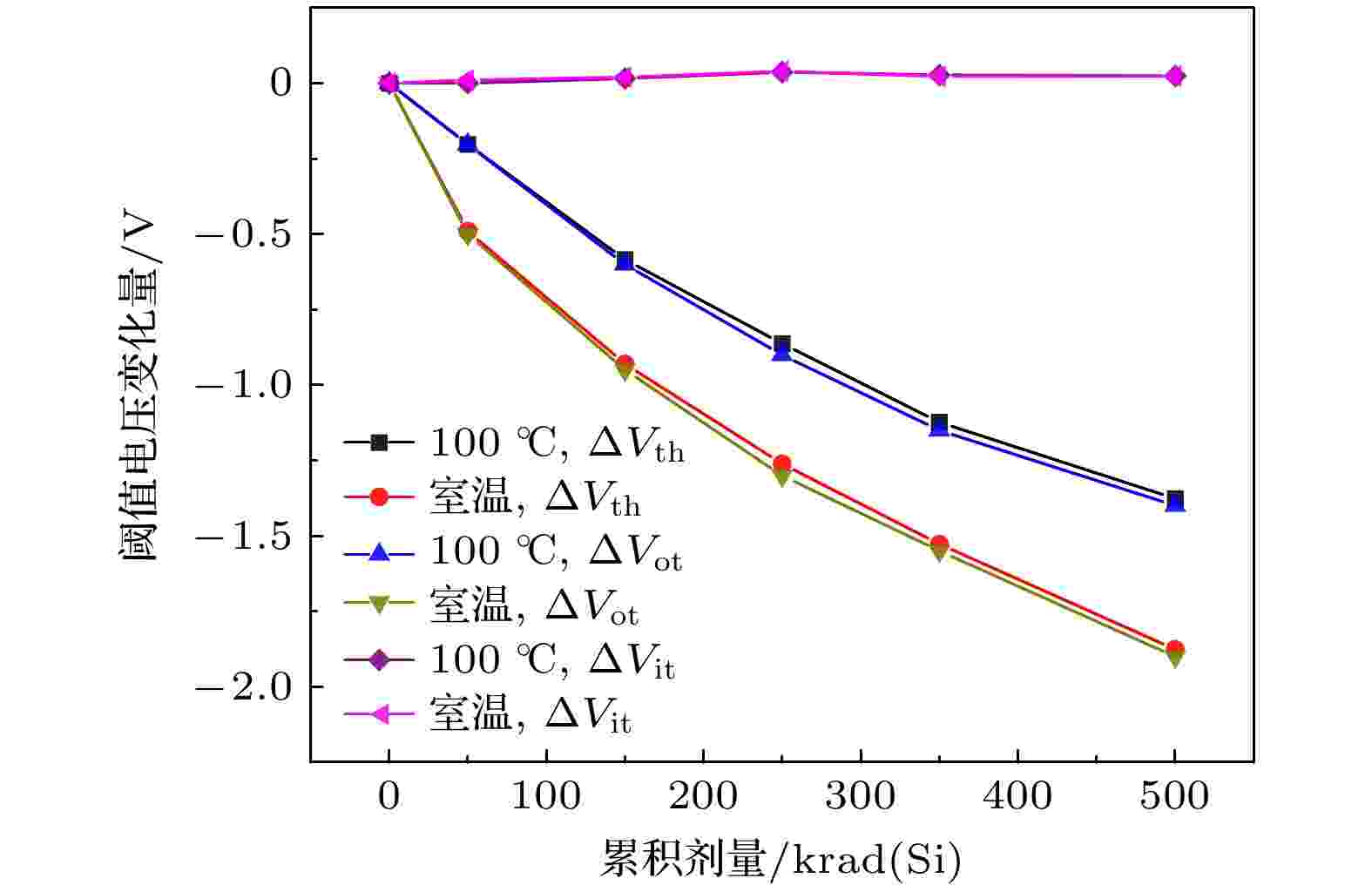图 8 不同温度下辐照时电压漂移量和总剂量的关系Figure8. Relationship between the voltage drift and the total dose during irradiation at different temperatures.
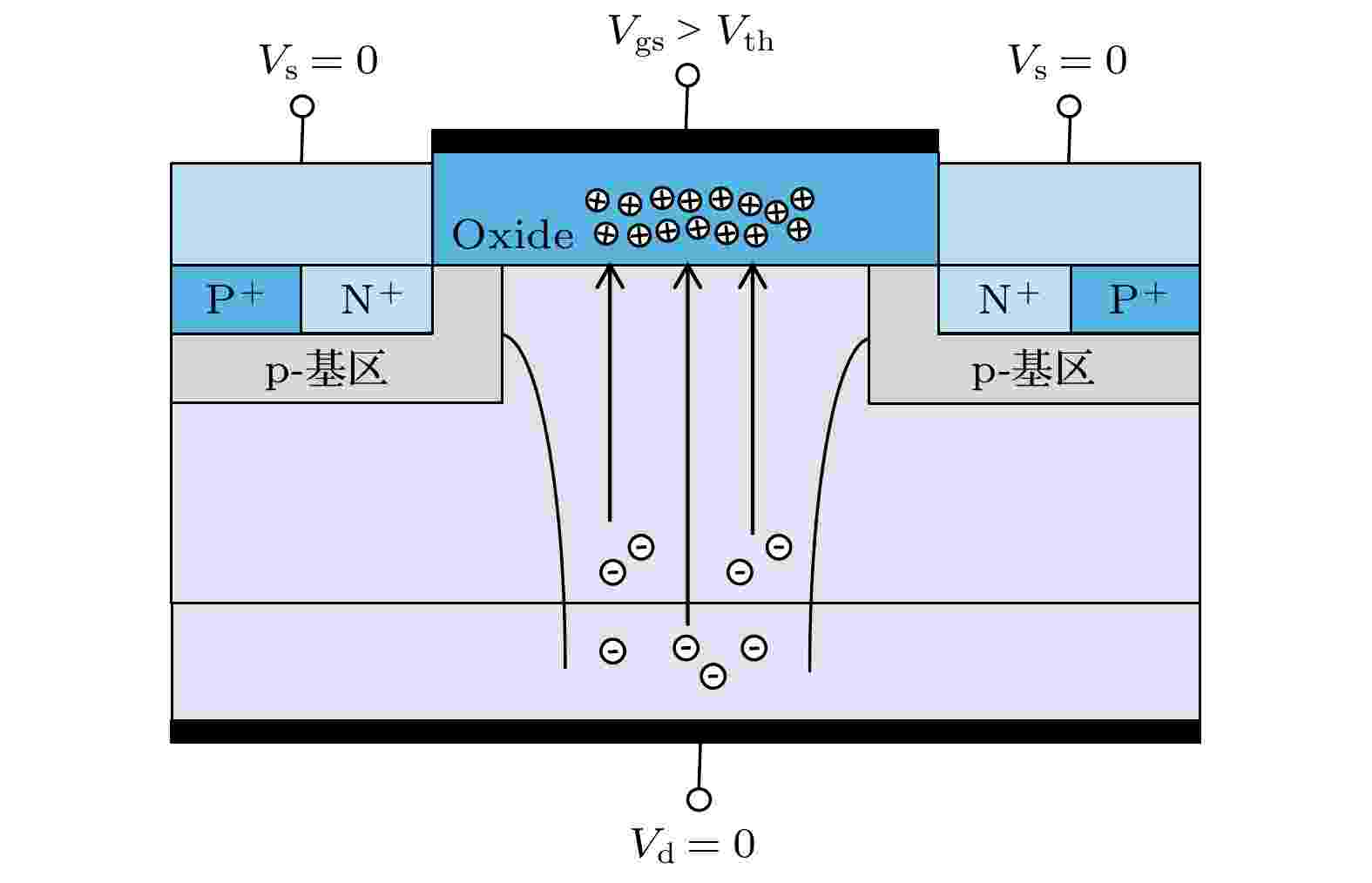图 9 SiC MOSFET器件高温辐照时隧穿效应电荷分布Figure9. Tunneling effect charge distribution in SiC MOSFET devices irradiated at high temperature.
2
3.3.退火效应
为了研究辐照后的SiC MOSFET器件的退火效应, 对辐照后的器件开展了100 ℃的恒温加速退火实验, 整个退火实验的周期为一周, 共计168 h, 并在栅极施加了5和0 V的电压, 整个退火过程中选取不同的时间点对器件的各项电学参数进行测量. 图10给出了栅压为5 V时, 在100 ℃下进行168 h退火后器件的输出特性曲线, 从图10中的结果来看, 辐照后的器件经历168 h的高温退火后曲线恢复了50%. 图11给出了在100 ℃时, 栅压为5 和0 V时退火过程中阈值电压随时间的变化曲线, 可以看出, 退火时在栅极5 V的电压会使阈值电压的恢复量更大, 退火168 h后, 栅极加电时阈值电压恢复了40%, 而不加电时阈值电压仅恢复了11%. 同时, 为了进行对比, 也开展了栅压为5 V时的常温退火实验. 图12给出了栅压为5 V时, 在100 ℃和常温下进行退火时阈值电压随时间的变化曲线, 通过对比两种温度下退火后的结果可以发现, 经历168 h的高温退火后阈值电压恢复了40%, 而经历168 h的常温退火后阈值电压仅恢复了19%.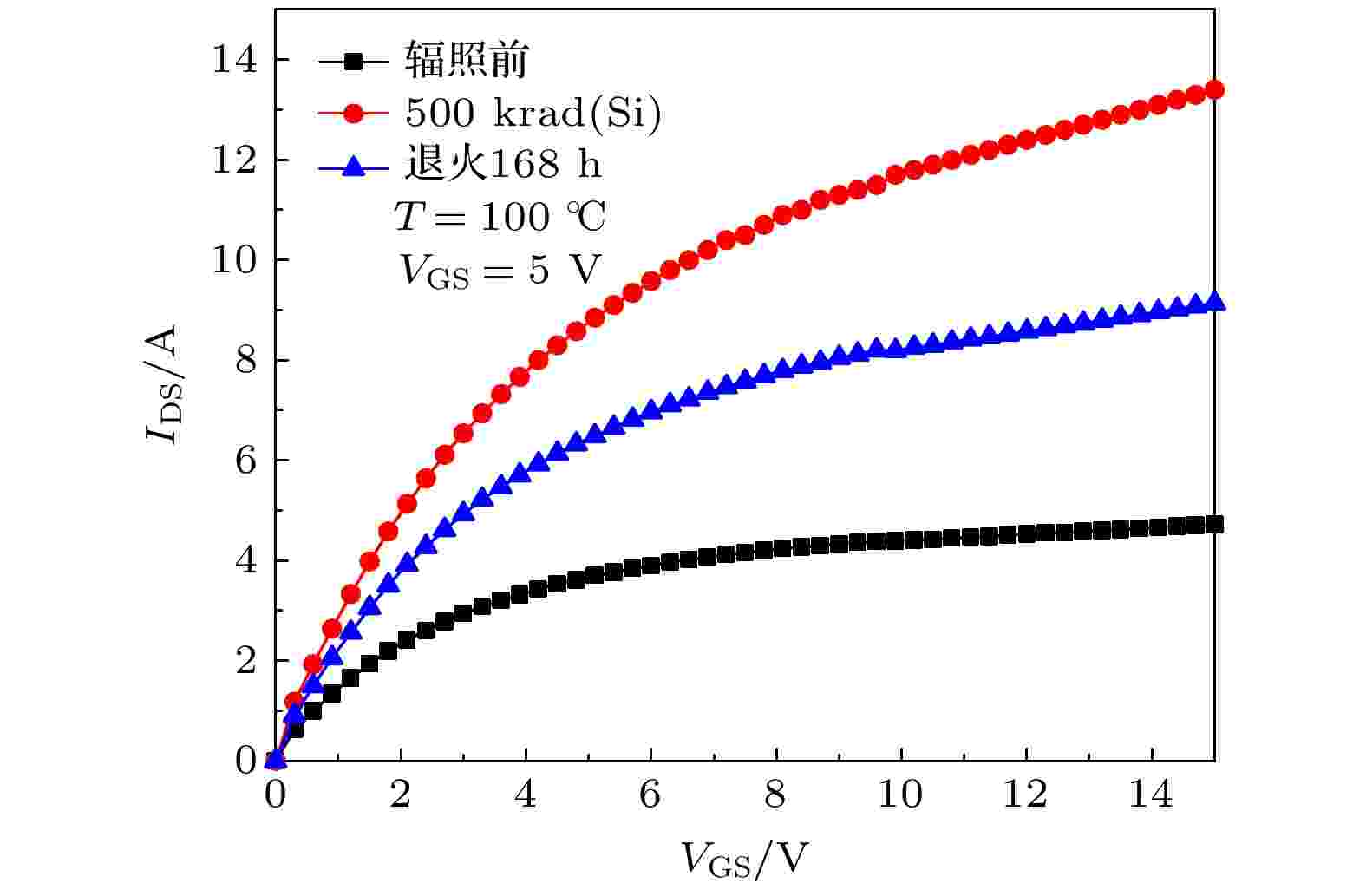
图 10 SiC MOSFET器件辐照后退火168 h后的输出曲线Figure10. Output curve of SiC MOSFET device after 168 h annealing after irradiation.
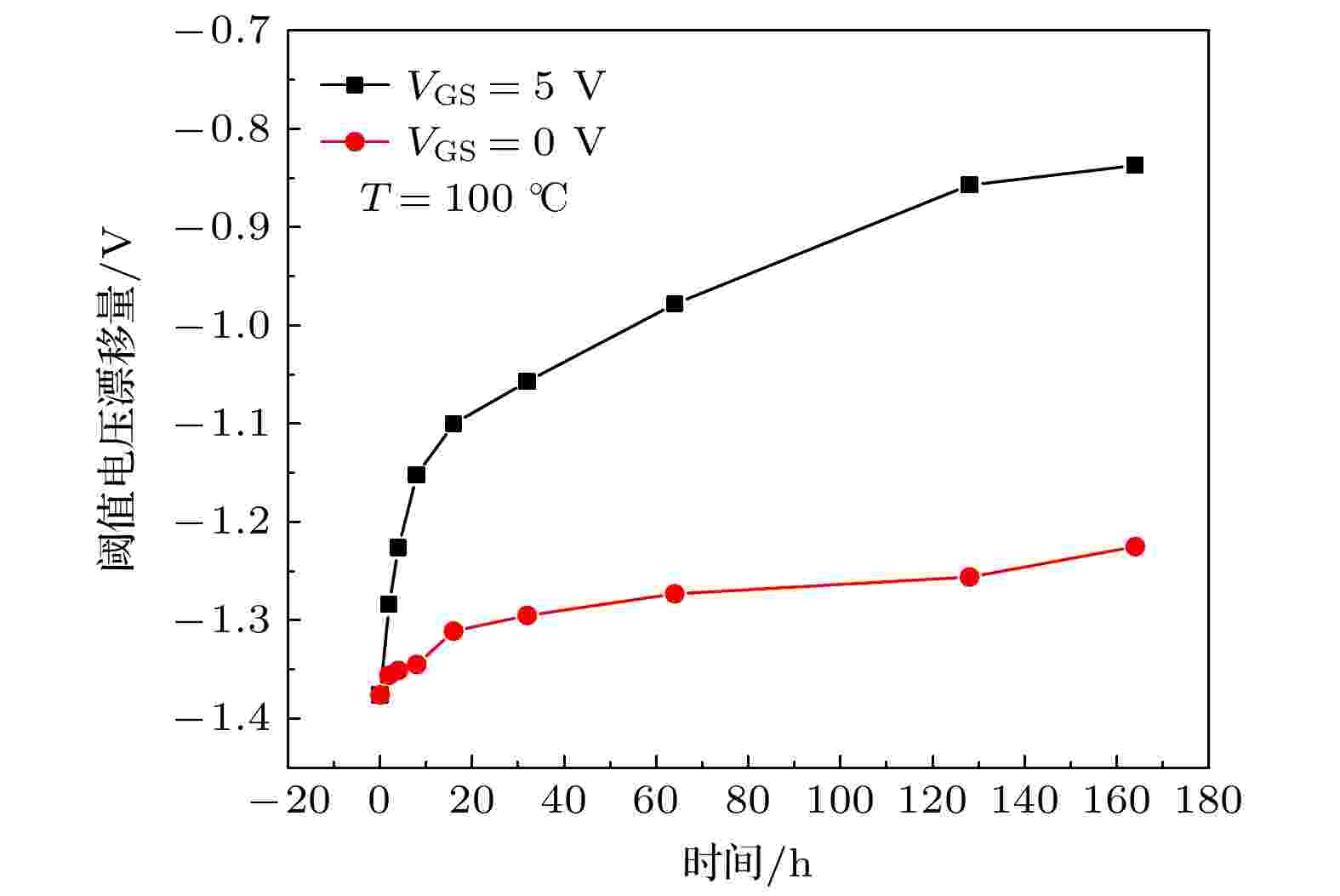图 11 栅压为5 和0 V退火时阈值电压漂移量随时间的变化关系Figure11. Relationship of threshold voltage recovery with time under different gate voltage annealing conditions.
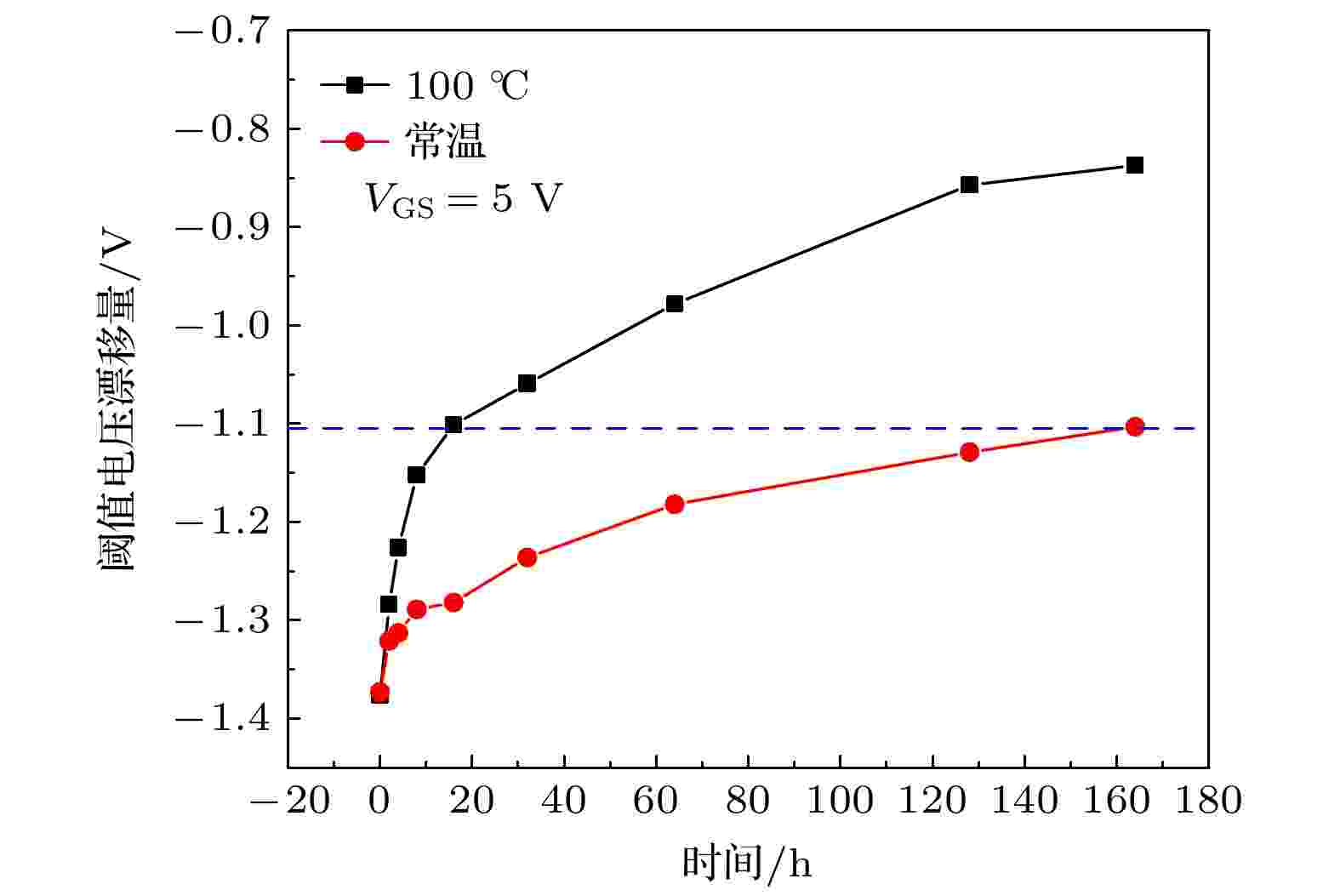图 12 常温和100 ℃退火时阈值电压漂移量随时间的变化关系Figure12. Relationship of threshold voltage recovery with time at room temperature and annealing at 100 ℃.
上一节提到了高温环境下器件辐照产生的退化会发生部分恢复, 这是由于高温环境会引发器件发生隧穿退火或热激发退火. 结合图11和图12的退火恢复情况来看, 除了高温这一重要因素外, 退火过程中给栅极施加正的电压也会极大地促进退火恢复程度. 结合两种退火恢复机理的物理过程, 说明器件100 ℃下辐照时, 主要发生的是隧穿退火而导致辐照退化程度降低.
为了更加直观地反映出辐照后的器件退火恢复程度和退火温度之间的物理关系, 本文引入了Arrhenius模型[23], 该模型是使用温度应力实验时最典型、应用最广的加速模型. 本文以相同的阈值电压恢复量作为基准, 得到温度度与时间的表达形式. 所用的阿列尼斯经验公式如下:
从(7)式可以看出, 时间t和温度T之间存在一定的函数关系. 在实验过程选取两组不同的退火温度T1, T2, 阈值电压恢复量相同时, 得到所需的时间分别为t1, t2, 如图12所示. 将实验所得的温度和时间代入(7)式, 得到如下公式:
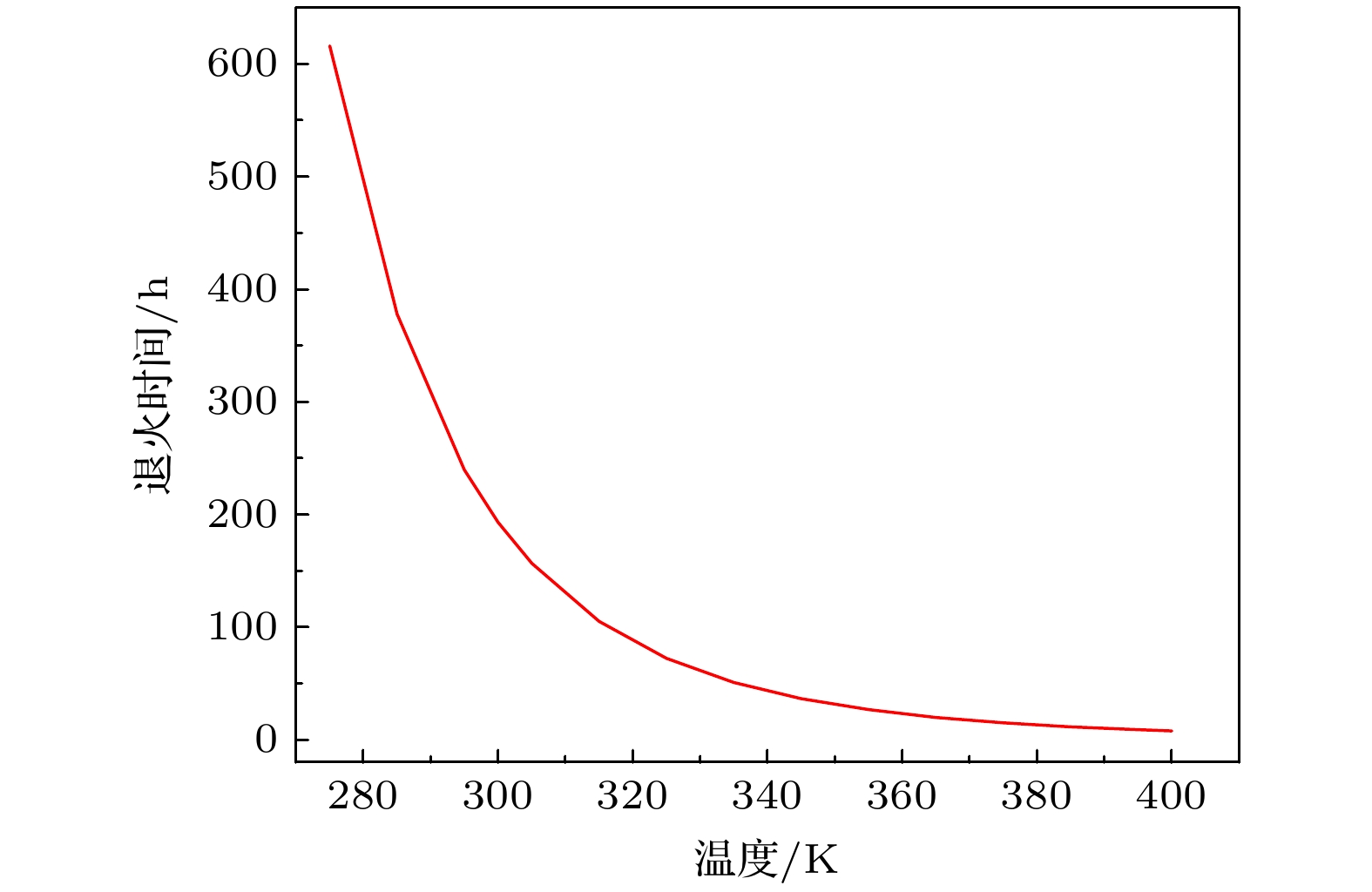图 13 阈值电压恢复时退火温度与时间的函数曲线Figure13. Function of annealing temperature and time when threshold voltage is restores.
