摘要:现存的同-离轴混合数字全息技术可同时解决同轴全息共轭像消除困难和离轴全息分辨率受限的问题, 但需预测衍射距离, 不仅复杂耗时, 且精度有限; 而远心成像技术可获得非衍射图像, 无需预测衍射距离, 并具有可消除球面像差和散焦像差等特性. 因此, 本文将远心成像技术引入同-离轴混合数字全息技术中, 提出一种远心同-离轴混合数字全息高分辨率重建方法. 该方法利用远心同-离轴混合数字全息系统, 分别采集聚焦的离轴全息图和同轴全息图; 进而将离轴全息图获得的低分辨率相位信息与同轴全息图获得的振幅信息相复合, 作为迭代恢复过程的物光复振幅初始值, 并分别在空域和频域进行约束迭代, 实现高分辨率重建. 实验结果表明, 该方法无需衍射距离等先验信息, 便可很好地消除共轭像和系统畸变的干扰, 并可充分利用图像传感器的空间带宽积, 实现物体的高分辨率重建.
关键词: 数字全息/
远心成像/
迭代恢复/
高分辨率

English Abstract

全文HTML

--> --> -->

数字全息技术^[1-3]由相机记录物光和参考光干涉图样, 并由计算机恢复待测相位, 具有全场定量、非接触、无需对样品做特殊处理等独特优点, 已作为重要成像测试手段广泛应用于生物医学、微纳制造和材料科学等领域^[4-14]. 根据物光和参考光之间是否存在夹角, 数字全息可分为离轴数字全息^[15,16]和同轴数字全息^[17,18]. 离轴数字全息可将实像项与共轭像项和零级项的频谱分离, 利用带通滤波器选取实像信息, 但是受最小记录距离的限制, 不能获得较大的数值孔径, 空间带宽积利用率低, 滤波过程损失了很多高频信息, 进而降低了成像的分辨率. 同轴数字全息可充分利用图像传感器的空间带宽积, 获得较大的数值孔径, 理论上可以获得较高的成像分辨率, 但是同轴数字全息的实像项、共轭像项和零级项重叠在一起, 无法分离出实像信息. 因此, 传统同轴数字全息一般采用相移法^[19,20]来消除共轭像, 但是相移法需要多波长拍摄或者多次拍摄, 同时对实验装置要求很高, 实验过程中实现难度较大. Gabor同轴数字全息一般采用迭代算法^[21-26]来消除共轭像, 但迭代算法对待测物体要求较高, 它受待测物体的稀疏性、弱相位波动、支持域等一系列因素的约束, 只有在满足条件的情况下, 才可以恢复出物体信息, 而待测物体自身性质无法决定, 支持域的确定也具有难度.
为兼顾离轴结构和同轴结构的优势, 2015年, Orzó^[27]提出一种同-离轴混合数字全息恢复方法, 先将离轴数字全息恢复的物光复振幅的低频成分提取出来, 再在同轴数字全息迭代的过程中进行低频替换, 实现待测物体的重建, 但当遇到强相位波动的物体时, 其迭代过程无法收敛. 2018年, 王凤鹏等^[28]也提出了一种同-离轴混合的相位恢复方法, 利用约束最优化算法^[29]从离轴数字全息图中获取物光场的近似相位分布, 并复合同轴全息图的振幅信息作为迭代过程的初始值, 进而利用迭代算法实现待测物体高分辨率重建, 但该方法因为采用平均值滤波, 依然损失了高频成分, 且需多次迭代才能达到效果, 损失了大量的时间; 同时, 其重建过程还需参考光的先验信息, 而在实验过程中很难获取准确稳定的参考光. 尤为重要的是, 以上两种方法都是在物面和全息面之间迭代完成重建工作, 从而需要精准的衍射距离; 衍射距离精准预测需利用聚焦算法, 而其成功是以大量时间消耗为代价的, 这将进一步提高重建难度, 浪费时间成本.
远心成像系统^[30-32]是传统数字全息经常采用的一种典型的光路结构, 它可以很好地抑制球面像差和散焦像差的影响, 使同轴数字全息保持最大空间带宽积; 同时, 可根据所需视场的空间分辨率调整缩放系数, 并可根据透镜焦距调整物体和图像传感器的位置, 获得聚焦的清晰图像, 从而在后期图像处理过程中无需对物光复振幅从全息面到物面进行反衍射的数值重建, 进一步避免了衍射距离预测的复杂过程, 节省了时间, 降低了重建难度. 因此, 本文将远心成像技术引入同-离轴混合数字全息技术中, 提出一种远心同-离轴混合数字全息高分辨率重建方法, 充分利用远心成像技术与同-离轴混合技术的优势, 在摈除衍射距离等先验信息以提升重建效率的同时, 抑制干扰项及系统像差, 实现高分辨率系统成像重建.

基于远心系统的远心同-离轴混合数字全息成像系统见图1. 从激光器发射出的激光, 经过准直扩束装置BE准直扩束后, 由第一分光棱镜BS1分光. 其中透射光被平面反射镜M1反射并调制倾角形成参考光, 反射光被反射镜M2再反射后经过待测物体形成物光, 物光经由透镜L1和L2构成的远心系统调制, 最后通过第二分光棱镜BS2后, 与参考光汇合并发生干涉, 在CCD成像靶面上形成全息图. 为了消除球差和散焦像差影响, 远心系统中透镜L1和L2需共轭配置形成4f系统, 待测物体S置于透镜L1的前焦面, 相机置于透镜L2的后焦面. 实验时, 先记录一幅离轴全息图, 再遮挡参考光记录一幅Gabor同轴全息图.
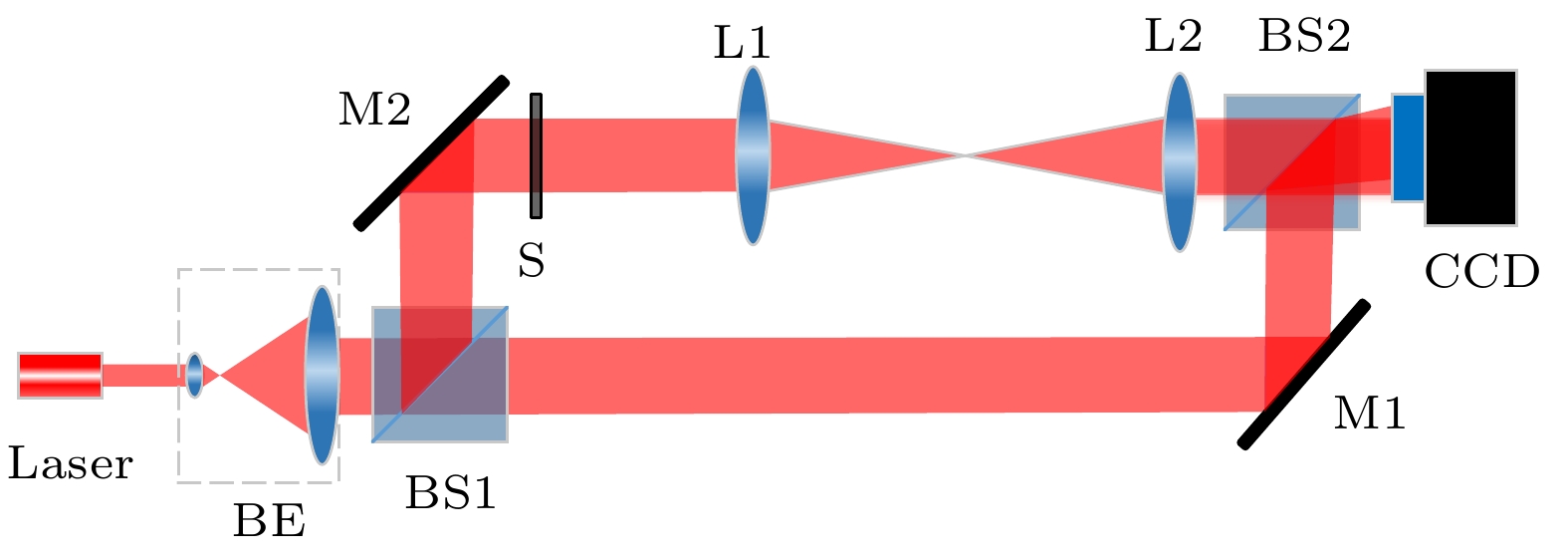图 1 远心同-离轴混合数字全息成像系统示意图
Figure1. Schematic of the telecentric in-line-and-off-axis hybrid digital holography system.

为了实现上述系统的成像重建, 提出了一种远心同-离轴混合数字全息高分辨率重建方法, 将离轴全息图获得的低分辨率相位信息与同轴全息图的振幅信息相结合作为迭代恢复过程的初始物光复振幅, 并将其在空域和频域的振幅信息作为迭代过程的振幅约束项, 同时将从离轴全息图中获取的物光复振幅低频信息作为迭代过程的频谱约束项, 最终实现物体的高分辨率重建. 重建过程如图2所示, 具体方法如下.
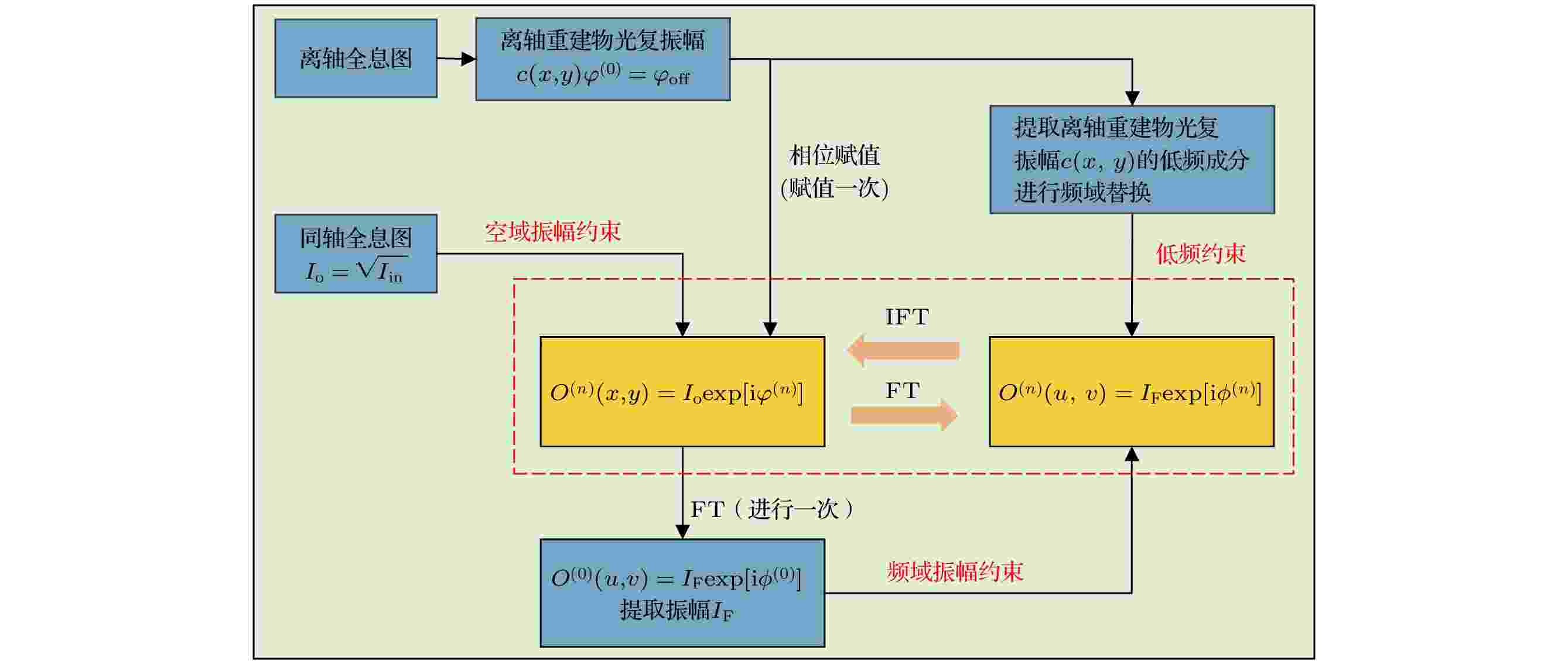图 2 远心同-离轴混合数字全息重建算法框图
Figure2. Schematic of telecentric in-line-and-off-axis hybrid digital holographic reconstruction algorithm.

1)全息图
假设物面的物光复振幅为O(x, y), 则可得到同轴全息图如下:

${I_{{\rm{in \text{-} line}}}} = {\left| {O\left( {x,y} \right)} \right|^2}. $

假设参考光复振幅为R(x, y), 则可得到离轴全息图和背景全息图如下:

$\begin{split}{I_{{\rm{off}}}} = \;&{\left| {O\left( {x,y} \right)} \right|^2} + {\left| {R\left( {x,y} \right)} \right|^2} + {O^*}\left( {x,y} \right)R\left( {x,y} \right) \\&+ O\left( {x,y} \right){R^*}\left( {x,y} \right)\\ =\;& a + 0.5b\left\{ {\exp \left[ {{\rm{i}}\left( {{\varphi _{{\rm{off}}}} + 2{\rm{\pi }}{f_{{x_0}}}x + 2{\rm{\pi }}{f_{{y_0}}}y + {\varphi _{\rm{b}}}} \right)} \right]} \right.\\&\left. { + \exp \left[ { - {\rm{i}}\left( {{\varphi _{{\rm{off}}}} \!+\! 2{\rm{\pi }}{f_{{x_0}}}x \!+\! 2{\rm{\pi }}{f_{{y_0}}}y \!+\! {\varphi _{\rm{b}}}} \right)} \right]} \right\},\\[-12pt]\end{split}$

$\begin{split} {I_{{\rm{off\_B}}}} =\;& a + 0.5b\left\{ {\exp \left[ {{\rm{i}}\left( {2{\rm{\pi }}{f_{{x_0}}}x + 2{\rm{\pi }}{f_{{y_0}}}y + {\varphi _{\rm{b}}}} \right)} \right]} \right. \\ &\left. { + \exp \left[ { - {\rm{i}}\left( {2{\rm{\pi }}{f_{{x_0}}}x + 2{\rm{\pi }}{f_{{y_0}}}y + {\varphi _{\rm{b}}}} \right)} \right]} \right\}, \end{split} $

其中, x和y为空域坐标, O*(x, y)和R*(x, y)分别为O(x, y)和R(x, y)的共轭项, I_off为离轴全息图, I_{off_B}为背景全息图, a为全息图的平均强度, b为干涉条纹的调制度, φ_off为离轴全息待测样品相位, $f_{x_0} $和$f_{y_0} $为水平方向和竖直方向的载波频率, φ_b为背景相位.
2)离轴物光场重建
分别对离轴全息图和离轴背景全息图进行傅里叶变换(FT), 可在频谱域中将零频分量和互相关项完全分离; 利用带通滤波器(BPF)选择实像项, 然后再分别进行傅里叶逆变换(IFT), 获取所需的有样品实像物光信息O_off (x, y)和背景实像物光信息 O_{off_B} (x, y), 即

$\begin{split} \;&{O_{{\rm{off}}}}\left( {x,y} \right) = {\rm{IFT}}\left\{ {{\rm{FT}}\left( {{I_{{\rm{off}}}}} \right) \times {\rm{BPF}}} \right\} \\ = \;&0.5b\{ \exp [ {\rm{i}}( {\varphi _{{\rm{off}}}} + 2{\rm{\pi }}{f_{{x_0}}}x + 2{\rm{\pi }}{f_{{y_0}}}y + {\varphi _{\rm b}} ) ] \}, \end{split} $

$\begin{split} \;& {O_{{\rm{off\_B}}}}\left( {x,y} \right) ={\rm{IFT}}\left\{ {{\rm{FT}}\left( {{I_{{\rm{off\_B}}}}} \right) \times {\rm{BPF}}} \right\} \\ =\;& 0.5b\left\{ {\exp \left[ {{\rm{i}}\left( {2{\rm{\pi }}{f_{{x_0}}}x + 2{\rm{\pi }}{f_{{y_0}}}y + {\varphi _{\rm{b}}}} \right)} \right]} \right\}. \end{split} $

应用除法算法^[33,34], 得到离轴数字全息去除背景的物光复振幅c(x, y), 即

$c\left( {x,y} \right) = {O_{{\rm{off}}}}\left( {x,y} \right)/{O_{{\rm{off\_B}}}}\left( {x,y} \right).$

提取离轴全息待测样品相位φ_off, 同时利用低通滤波器(LPF)滤出物光复振幅的低频成分O_{low_off} (u, v), 即

${\varphi _{{\rm{off}}}} = \arctan \left\{ {\frac{{\operatorname{Im} \left[ {c\left( {x,y} \right)} \right]}}{{\operatorname{Re} \left[ {c\left( {x,y} \right)} \right]}}} \right\},$

${O_{{\rm{low\_off}}}}\left( {u,v} \right) = {\rm{FT}}\left[ {c\left( {x,y} \right)} \right] \times {\rm{LPF}},$

其中, arctan为三角反正切函数; Im, Re分别为提取虚部和实部操作; u, v为频域坐标. 需要注意的是, 为了保证获取信息的一致性, LPF的外形需与所选择的BPF保持一致, 但LPF的半径不可大于BPF的半径.
3)同-离轴混合成像重建
(a) 利用同轴全息图的强度${I_0} = \sqrt {{I_{{\rm{in \text{-} line}}}}}$与第2)步获得的离轴全息待测样品相位φ_off, 组合成初始物光复振幅为O⁽⁰⁾(x, y) = I_o exp (iφ_off);
(b)将初始物光复振幅进行傅里叶变换得到频域的复振幅分布为O⁽⁰⁾(u, v) = I_F exp [i?⁽⁰⁾], 提取振幅I_F, 其中, ?⁽⁰⁾为频域初始物光相位分布;
(c) O⁽ⁿ⁾(x, y)为第n次迭代所生成的空域物光复振幅, 当n = 0时即为初始物光复振幅. 将空域物光复振幅分布O⁽ⁿ⁾(x, y) = I_o exp[iφ⁽ⁿ⁾]进行傅里叶变换获得频域物光复振幅, 用第2)步中O_{low_off}(u, v)替换它的低频成分, 并且用I_F替换它的振幅, 得到新的频域物光复振幅O⁽ⁿ⁾(u, v) = I_F exp [i?⁽ⁿ⁾], 其中, φ⁽ⁿ⁾和?⁽ⁿ⁾ 分别为空域和频域第n次迭代的相位分布;
(d)将更新后的频域物光复振幅通过傅里叶逆变换获得新的空域物光复振幅, 并用I_o替换它的振幅获得O⁽ⁿ⁺¹⁾(x, y)=I_o exp [iφ⁽ⁿ⁺¹⁾];
(e)重复步骤(c)和(d)进行迭代, 直至收敛. 输出空域物光复振幅分布, 即可得到高分辨率再现象.

为了验证所提方法的有效性, 利用计算机进行模拟仿真, 设置的初始参数为: 模拟物体为1024 × 1024的分辨率板, 设置采样频率为4.8 μm, 其中背景部分振幅透过率为0.2, 相位为0 rad, 线条和数字部分, 振幅透过率为1, 相位为–2 rad; 光波长为632.8 nm, 参考光的入射角度为21.7 mrad. 模拟生成的同轴全息图如图3(a) 所示, 离轴全息图如图3(b)所示. 由于传统的同-离轴混合算法^[27,28]无法对非衍射全息图进行重建, 因此下文分析过程只与传统同轴算法和离轴算法进行对比分析.
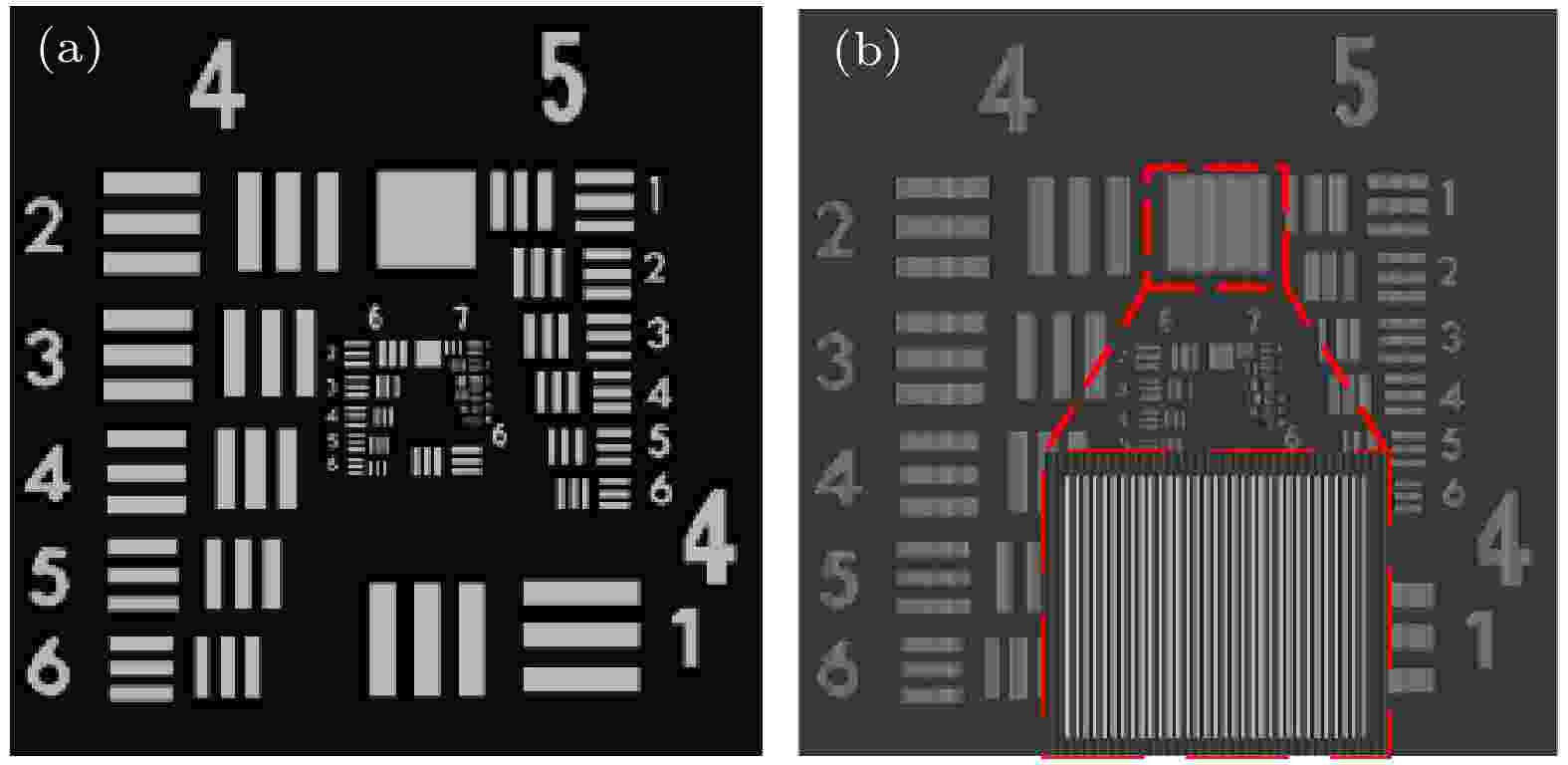图 3 (a)同轴全息图; (b)离轴全息图
Figure3. (a) In-line hologram; (b) off-axis hologram.

利用传统同轴算法^[21]对同轴全息图进行重建, 结果如图4所示. 由于重建的是无衍射过程的全息图, 振幅像不受共轭像的影响, 所以保持同轴的高分辨率特性; 但是从相位像看出, 相位值恢复并不准确, 即传统同轴算法不具有准确恢复相位信息的能力.
图 4 同轴全息图再现结果　(a)振幅像; (b)相位像
Figure4. Reconstructed results of in-line hologram: (a) Amplitude image; (b) phase image.

利用离轴频域滤波方法^[16]对离轴全息图进行重建, 结果如图5所示. 从振幅像和相位像可以看出, 信息恢复基本准确, 但是由于引入了带通滤波器, 损失了高频信息, 再现像局部放大不清晰, 数字线条轮廓模糊, 分辨率较低.
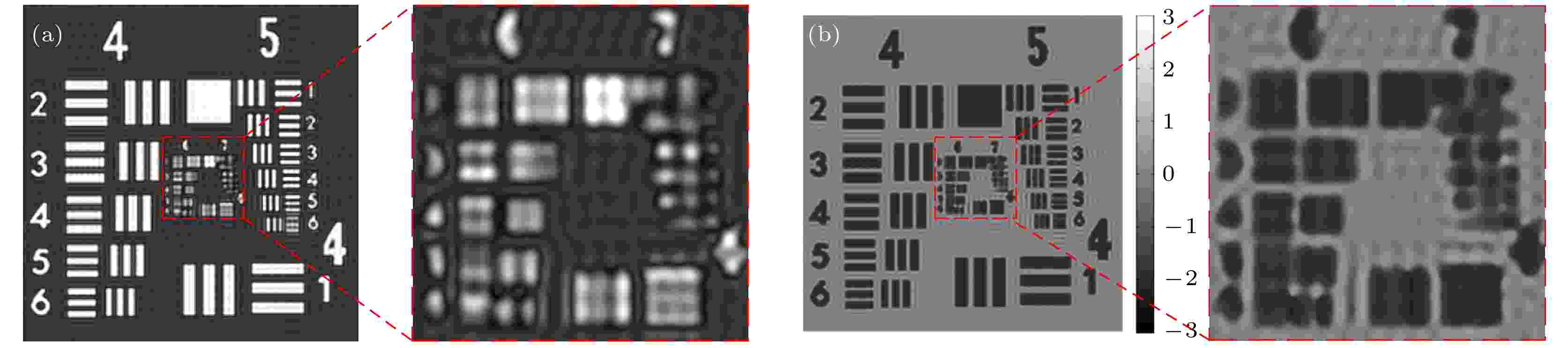图 5 离轴全息图再现结果　(a)振幅像; (b)相位像
Figure5. Reconstructed results of off-axis hologram: (a) Amplitude image; (b) phase image.

利用本文的远心同-离轴混合数字全息重建方法对全息图进行重建. 本文采用均方误差 (M_SE)对算法的收敛性进行评价, 即

${M_{{\rm{SE}}}} = \frac{1}{{M \times N}}{\sum\limits_{x = 1}^M {\sum\limits_{y = 1}^N {\left[ {{O_0}\left( {x,y} \right) - O\left( {x,y} \right)} \right]^2} } },$

其中$\displaystyle \sum$为求和符号, M和N为原始像和再现像在x和y方向上的像素数, $ O_0(x,y) $为原始像, $ O(x,y) $为再现像. 基于此, 获得的再现像均方误差随迭代次数的变化如图6所示, 其中图6(a)为振幅均方误差收敛曲线, 图6(b)为相位均方误差收敛曲线, 可以看出, 在经过15次迭代后, 两条曲线均达到了良好的收敛效果. 图7为同-离轴混合数字全息重建算法恢复的再现结果, 可以看出, 不仅振幅信息能准确恢复, 相位信息也能准确恢复, 尤其中间区域放大部分更加清晰, 肉眼即可分辨出数字和线条. 由于峰值信噪比PSNR是均方误差M_SE相对于最大信号值平方的对数表现形式, 可以有效估计重建像与原始像之间的误差, 能更加直观地衡量重建像的品质, 因此, 表1列出了不同算法重建振幅和相位的峰值信噪比, 可以看出, 相比于同轴算法和离轴算法, 混合算法均获得更高的峰值信噪比, 说明了本算法的优越性.
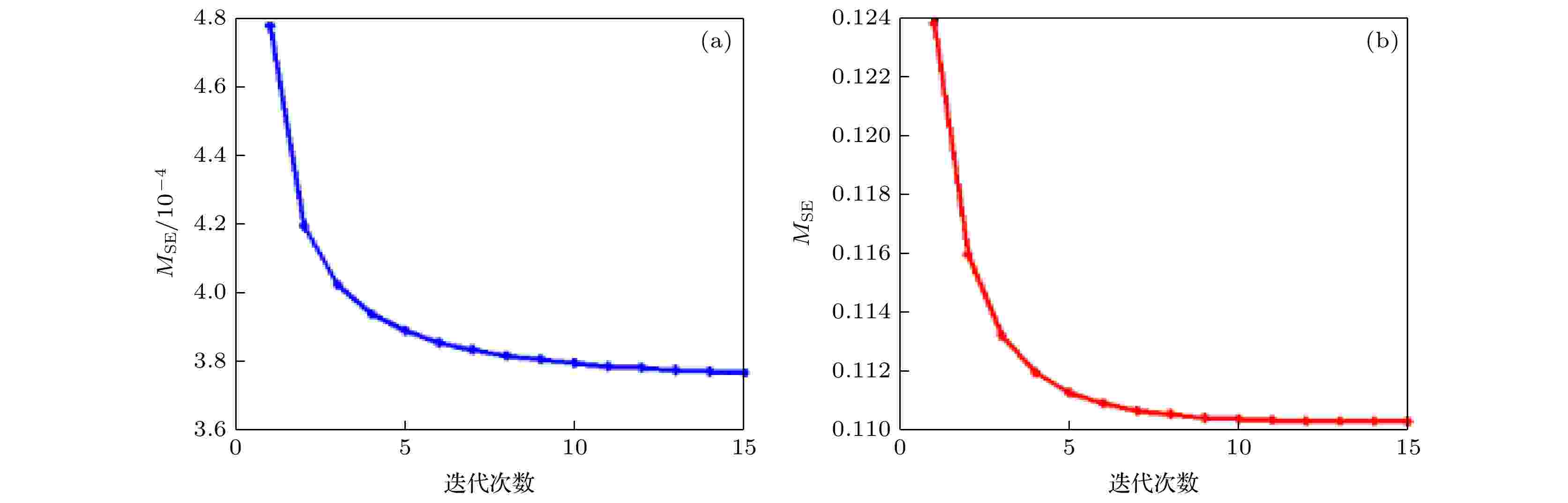图 6 再现像误差随迭代次数变化　(a)振幅均方误差收敛曲线; (b)相位均方误差收敛曲线
Figure6. Mean squared errors at each iteration: (a) Amplitude mean square error convergence curve; (b) phase mean square error convergence curve.

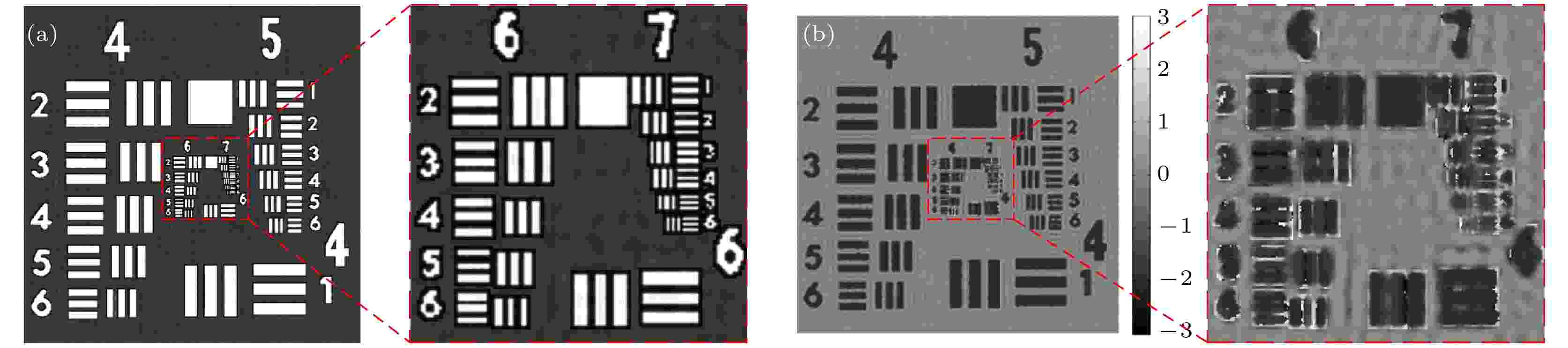图 7 同-离轴混合数字全息再现结果　(a)振幅像; (b)相位像
Figure7. Reconstructed results obtained by the in-line-and-off-axis hybrid digital holography: (a) Amplitude image; (b) phase image.

	同轴算法	离轴算法	混合算法
振幅PSNR/dB	71.55	66.54	82.37
相位PSNR/dB	43.69	55.29	57.70

表1不同算法重建振幅和相位的峰值信噪比
Table1.Peak signal-to-noise ratio (PSNR) of amplitudes and phases reconstructed by different algorithms.

为了进一步验证所提方法的有效性, 构建如图1所示的实验装置, 其中激光器为波长632.8 nm的He-Ne激光器; 构成远心系统的透镜L1的焦距为50 mm, 透镜L2的焦距为200 mm; CCD的像素数为1024 × 1280, 像素大小为4.8 μm, 因此, 本实验中理论最小分辨率为4.8 μm. 实验时, 先记录一幅离轴全息图, 再挡住参考光记录一幅Gabor同轴全息图. 考虑实际测量中无法获取实际图像, 以仿真收敛结果作为依据判断实际测量结果的收敛性, 因此, 以下实验的迭代过程均以15次迭代为结束条件.
首先, 以USAF分辨率板为待测物体进行验证, 由于该分辨率板是振幅形物体, 因此只给出振幅的重建结果. 图8(a)为同轴全息图, 图8(b)为离轴全息图, 图8(c)为传统同轴算法重建得到的振幅结果, 由于利用远心系统所拍摄的同轴全息图即为非衍射过程的强度图, 因此传统同轴方法重建的振幅结果取决于同轴全息图的强度, 可以观测到第5组第 6个元素, 线宽为8.7 μm, 但是在数字线条附近会出现模糊的虚影. 图8(d)为利用离轴频谱滤波算法对离轴全息图进行重建获得的振幅结果, 明显可见, 放大部分数字线条边界模糊, 细节部分也无法分辨, 能够分辨的第4组第1个元素, 线宽为31.3 μm, 远低于理论分辨率, 究其原因, 是因为离轴全息重建过程采用频域滤波而使高频信息丢失. 图8(e)为混合算法重建获得的振幅结果, 可看出, 放大部分数字线条的边界更加锐利, 中间细节部分更加清晰, 例如第5组中数字旁的伪影也消失不见, 从而说明本方法重建质量既远高于离轴算法, 也优于同轴算法, 且更加接近理论分辨率.
图 8 USAF分辨率板实验结果　(a)同轴全息图; (b)离轴全息图; (c) 同轴数字全息再现像; (d)离轴数字全息再现像; (e)同-离轴混合数字全息再现像
Figure8. Experimental results of USAF resolution target: (a) In-line hologram; (b) off-axis hologram; (c) amplitude reconstructed image of the in-line hologram; (d) amplitude reconstructed image of the off-axis hologram; (e) amplitude reconstructed image of the in-line-and-off-axis hybrid digital holography.

在第2个实验中, 以洋葱表皮细胞为待测物体进行实验验证, 获得的同轴全息图如图9(a)所示, 离轴全息图如图9(b)所示, 图9(c)和图9(d)为利用传统同轴算法进行重建所得到的振幅像和相位像. 从振幅恢复结果可以看出, 借助于远心系统的优势, 振幅恢复效果较好地与理论分析保持一致; 但从相位恢复结果看, 没有准确得到洋葱表皮细胞的相位信息分布, 说明传统同轴算法对于远心系统下的聚焦全息图的相位重建能力有限. 图9(e)和图9(f)为利用离轴算法重建得到的振幅像和相位像, 从重建结果可以看出, 洋葱表皮细胞虽然结构清晰可见, 但是高频信息丢失, 分辨率较低. 图9(g)和图9(h)为本文混合算法重建得到的振幅像和相位像. 从振幅恢复结果可以看出, 混合算法可以获得与同轴算法一致的分辨率, 但洋葱表皮细胞纹路边界更加清晰; 从相位像可以看出, 混合算法可以有效恢复出洋葱表皮细胞的相位信息, 且相对于离轴算法提高了细胞纹路的清晰度. 为了更好地比较, 对图9(f)和图9(h)中虚线部分进行剖面, 获得的结果如图9(i)所示, 进一步可以看出, 在细胞壁纹路处, 混合数字全息恢复结果保留了更多的高频信息, 分辨率更高.
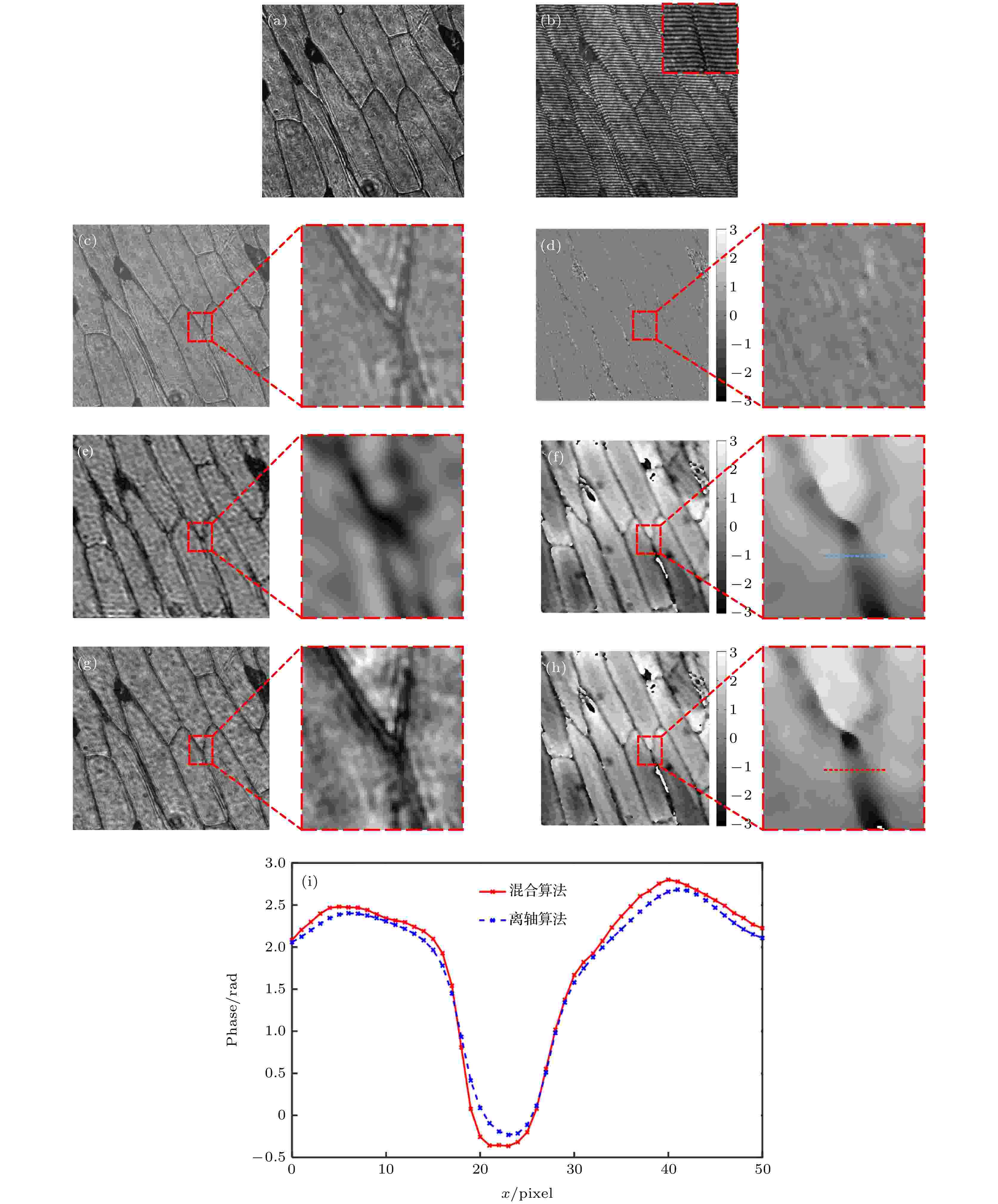图 9 洋葱表皮细胞实验结果　(a)同轴全息图; (b)离轴全息图; (c)同轴数字全息再现强度像; (d)同轴数字全息再现相位像; (e) 离轴数字全息再现强度像; (f) 离轴数字全息再现相位像; (g) 混合数字全息再现强度像; (h) 混合数字全息再现相位像; (i)相位剖面曲线
Figure9. Experimental results of onion epidermal cell: (a) In-line hologram; (b) off-axis hologram; (c) amplitude reconstructed image of the in-line hologram; (d) phase reconstructed image of the in-line hologram; (e) amplitude reconstructed image of the off-axis hologram; (f) phase reconstructed image of the off-axis hologram; (g) amplitude reconstructed image of the in-line-and-off-axis hybrid digital holography; (h) phase reconstructed image of the in-line-and-off-axis hybrid digital holography; (i) phase profile curves.

最后, 以蜜蜂翅膀为待测物体进行了实验验证. 图10(a)为蜜蜂翅膀的同轴全息图, 图10(b)为蜜蜂翅膀的离轴全息图. 图10(c)和图10(d)为利用传统同轴算法进行重建得到的振幅像和相位像, 图10(e)和图10(f)为利用离轴算法重建得到的振幅像和相位像, 图10(g)和图10(h)为本文混合算法重建得到的振幅像和相位像, 图10(i)为相位像中竖线部分蜜蜂翅膀纹路的相位刨面图. 从图10可以得到同样的结论, 即混合算法能同时实现振幅图像和相位图像的高分辨率重建, 尤其从图10(i)可以看出, 混合算法可以明显恢复出离轴算法丢失的高频信息, 明显提高了成像分辨率.
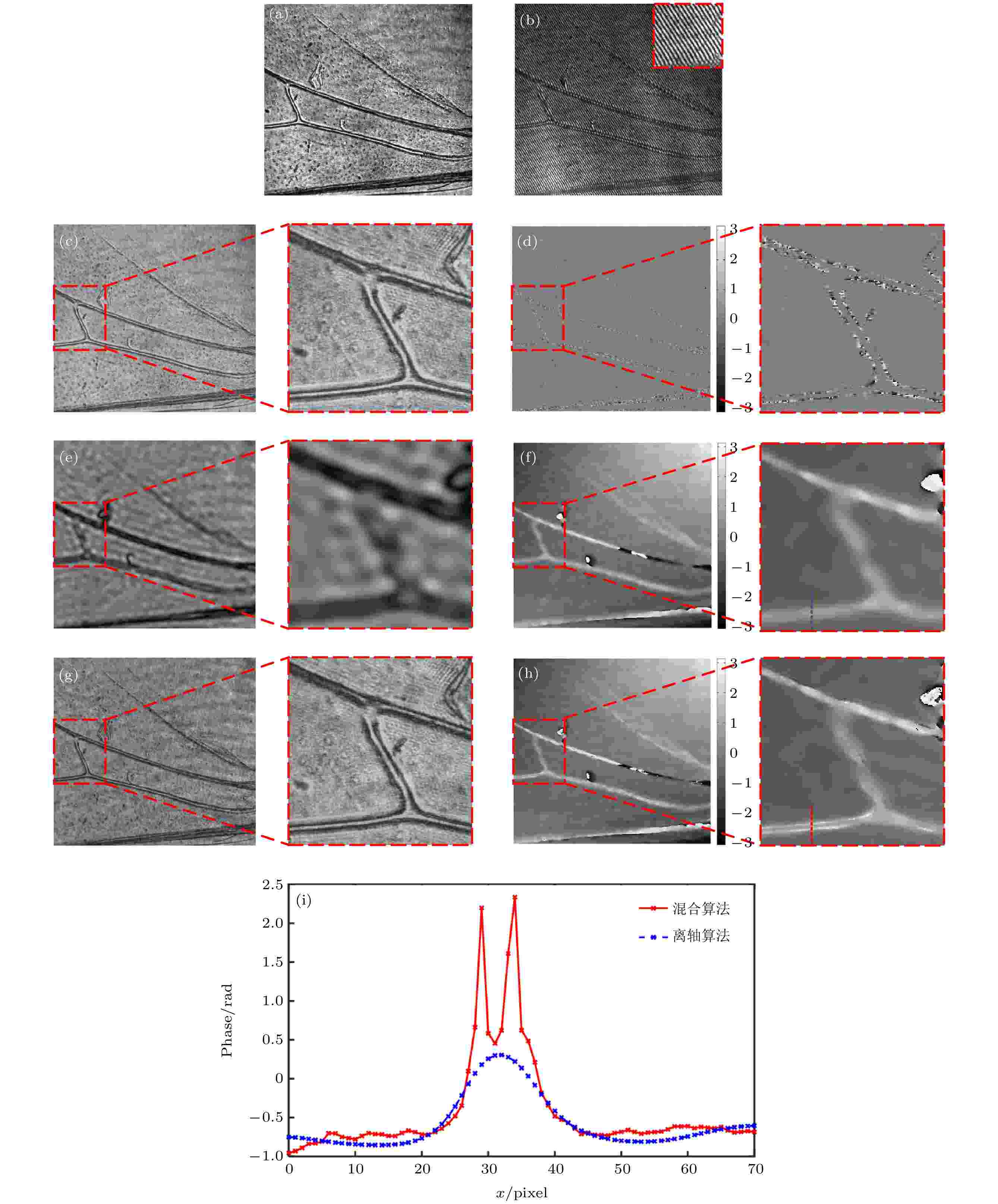图 10 蜜蜂翅膀实验结果　(a)同轴全息图; (b)离轴全息图; (c)同轴数字全息再现强度像; (d)同轴数字全息再现相位像; (e) 离轴数字全息再现强度像; (f) 离轴数字全息再现相位像; (g) 混合数字全息再现强度像; (h) 混合数字全息再现相位像; (i)相位剖面曲线
Figure10. Experimental results of bee wings: (a) In-line hologram; (b) off-axis hologram; (c) amplitude reconstructed image of the in-line hologram; (d) phase reconstructed image of the in-line hologram; (e) amplitude reconstructed image of the off-axis hologram; (f) phase reconstructed image of the off-axis hologram; (g) amplitude reconstructed image of the in-line-and-off-axis hybrid digital holography; (h) phase reconstructed image of the in-line-and-off-axis hybrid digital holography; (i) phase profile curves

本文利用远心成像技术与同-离轴数字全息技术的各自优势, 提出一种远心同-离轴混合数字全息高分辨率重建方法, 在构建实验平台基础上, 建立了成像重建模型, 并完成了模拟仿真验证与实验验证. 结果表明, 所提的远心同-离轴混合数字全息系统能够同时实现振幅图像和相位图像的高分辨率重建, 且无需衍射距离等先验知识, 从而为同-离轴混合数字全息实现生物细胞组织、空间微粒等高分辨率成像测量应用奠定了理论和实验基础.