摘要:介观尺度下颗粒布朗运动的摩擦系数符合黏性流体力学边界条件, 当颗粒尺度减小至纳米级别时, 边界条件向滑移过渡; 另一方面, 随着颗粒尺度的减小, 颗粒表面溶剂分子的吸附效应对颗粒水动力学半径的影响不可忽略. 分子动力学模拟可以捕获纳米流体中颗粒与溶剂分子相互作用的微观细节且计算精度高. 以刚性TIP4P/2005水分子模型为溶剂, 建立不同大小的Cu纳米颗粒在水中扩散的全原子模型. 采用单颗粒追踪方法对颗粒的平动和转动扩散系数进行拟合, 将摩擦因子与黏性边界条件和滑移边界条件下的结果进行比较, 并研究了溶剂在颗粒表面的吸附特性. 研究发现纳米颗粒的平转动摩擦因子均在两种边界条件所预测的理论值之间, 颗粒尺寸越小, 溶剂分子的吸附越明显, 颗粒表面的水分子层会增大颗粒的水动力学半径使得摩擦因子的计算结果偏向黏性边界, 纳米颗粒尺寸约小于5倍溶剂分子尺寸时, 需要考虑颗粒表面的溶剂层对颗粒水动力半径的影响.
关键词: 纳米颗粒/
扩散系数/
摩擦因子/
水动力学半径

English Abstract

全文HTML

--> --> -->

布朗运动是指悬浮在流体中的纳米至微米级颗粒所经历的无休止的随机运动, 在自然界中广泛存在. 关于布朗运动的起源在很长的一段时间都备受争论^[1], 直到1905年Einstein^[2]根据分子运动论原理提出了布朗动力学理论, 并建立了颗粒的扩散系数和摩擦系数的关系; Paul Langevin将随机力和黏性阻力引入牛顿第二定律^[3], 由此得到的Langevin方程以一种简洁的方式再现了Einstein的结果. 一百多年来, 布朗运动的后续研究及其推广对物理学、数学、生物学和材料科学等领域^[4,5]的发展产生了深远的影响.
Einstein的布朗动力学理论指出颗粒的随机运动是周围流体分子热运动的结果. 颗粒在周围流体分子的碰撞下产生随机运动的同时, 又受到流体分子的阻力, 由碰撞所产生的随机力和流体分子对颗粒的摩擦阻力通过涨落耗散定理约束. 颗粒的热涨落和摩擦力的关系为$D = {k_{\rm{B}}}T/f$, D为颗粒的扩散系数, k_B, T, f分别为玻尔兹曼常数、体系绝对温度、颗粒的摩擦系数. 在黏性水动力学边界条件下, 颗粒的平动摩擦系数${f_{\rm{t}}} = 6{\text{π}}\eta a$, 转动摩擦系数${f_{\rm{r}}} = 8{\text{π}}\eta {a^3}$, η为溶剂的动力学黏度, a为颗粒半径. 然而, 当研究颗粒的尺度由微米级降低至纳米级别时, 相关****^[6]发现采用黏性边界条件计算得出的旋转弛豫时间比测量值大5—10倍. 显然当研究的问题涉及微观领域, 黏性流体力学边界条件理论具有明显的局限性. 如图1(a)所示, 黏性流体力学边界条件下, 在流体中运动的球形颗粒携带着与其相接触的流体层而不发生滑移, 颗粒摩擦力来自两个部分: 颗粒正前方流体分子阻碍颗粒运动而产生的阻力和由于流体的黏性而产生的平行于颗粒运动方向的粘滞力; 滑移边界条件下(图1(b)), 摩擦力仅来自于颗粒正前方流体分子所产生的的阻力^[7]. 颗粒的旋转摩擦系数取决于绕其对称轴旋转时对周围流体产生的扰动, 黏性边界条件下, 球形颗粒会携带周围的流体旋转, 摩擦系数为$8{\text{π}}\eta {a^3}$; 而在滑移边界下, 颗粒表面与流体分子的相互作用被忽略, 没有流体分子阻碍颗粒的旋转, 因此旋转摩擦系数为0. 无论是黏性边界还是滑移边界条件, 都对流体分子与颗粒的摩擦系数作了理想假设. Richardson^[8]的研究表明, 在一个足够粗糙的表面由滑移所产生的速度场和等效光滑表面由黏性产生的速度场相近, 这表明颗粒表面粗糙程度会影响流体与颗粒的相互作用, 而且随着纳米颗粒尺寸的降低, 颗粒与溶剂相互作用对颗粒有效水动力学半径的影响不可忽略^[9]. 颗粒表面特性和电解质溶液的浓度都会影响溶剂分子在颗粒表面的吸附从而改变颗粒的有效半径^[10,11], Velasco-Velez等^[12]用X射线吸收方法和分子模拟方法研究了水分子在金颗粒表面的结构, 并指出颗粒表面悬空的氢键是水分子产生吸附的原因. Vasanthi等^[13,14]以及何昱辰和刘向军^[15]采用粗粒化模型模拟了纳米颗粒的平转动扩散特性, 计算所得的扩散系数与滑移边界条件下的结果相近, 然而粗粒化模型并不能反映颗粒表面特性和溶剂分子的真实结构. 在介观尺度的模拟方面, 耗散动力学模型和布朗动力学模型将随机力和黏性力引入颗粒的控制方程来约束颗粒的运动, 解决了由于颗粒与溶剂分子在时间和空间尺度上的差异造成计算成本过高的问题^[16], 但是由于采用粗粒化模型或者隐式溶剂模型, 忽略了溶剂分子与颗粒相互作用的微观细节.
图 1 球形颗粒在不同边界条件下的平动摩擦系数, 颗粒向右运动　(a)黏性边界条件; (b)光滑边界条件
Figure1. Translational friction coefficients of spherical particles under different boundary conditions and the particle move to the right: (a) Translational friction coefficient for stick boundary; (b) translational friction coefficient for slip boundary.

本文采用分子动力学模拟方法建立了单个Cu纳米颗粒在水溶液中扩散的全原子模型, 在原子水平上研究流体分子与纳米颗粒之间的相互作用, 在计算能力能够承受的范围内分析比较了4种不同半径的纳米颗粒在水溶液中的扩散特性. 采用单颗粒追踪算法^[17-19]并结合最小二乘法对颗粒的平转动扩散系数进行拟合, 解决了扩散系数需要对大量颗粒系综平均的问题. 将摩擦系数的计算结果与黏性边界和滑移边界条件下的结果进行比较, 讨论了颗粒表面的溶剂吸附对颗粒水动力学半径的影响. 胶体系统的粗粒化模拟过程中, 摩擦系数的选择直接决定布朗力和黏滞力的大小, 本文的结果可以为摩擦因子的选择提供支持, 而不必在黏性边界与滑移边界条件之间做出选择, 为布朗动力学和耗散动力学模型的完善提供理论依据.

2

-->

2.1.全原子模型的构建

本文建立了不同大小的单个Cu纳米颗粒在纯水溶液中扩散的全原子模型(图2(a)), Cu颗粒半径分别为0.5, 1.0, 1.5和2.0 nm, 颗粒中原子按照FCC的晶格结构排列. 初始时刻颗粒位于模拟域的中心, 模拟域的大小和总原子数目需要根据颗粒的大小进行调整, 如表1所列. 边界条件均采用周期性边界条件, 从而保证颗粒的运动为自由布朗运动. 模拟开始时颗粒的初始速度符合麦克斯韦分布, 模拟时间步长为1 fs, 系统温度均为298 K. 由于溶剂动力学黏度对颗粒摩擦系数的计算有直接的影响, 而不同水分子模型的动力学黏度相差较大, 本文中水分子的构建选用与实验符合较好的刚性TIP4P/2005模型^[20]. 除了两个氢原子和一个氧原子, 该模型在H—O—H的键角平分线上增加了一个无质量的作用位点M, 水分子结构如图2(b)所示, 其中键长b = 0.9572 ?, 键角θ = 104.52°, O和H的电荷分别为–1.1128和+0.5564 eV, 水分子的半径d = 2 ?, OM = 0.1546 ?. 水分子的键长和键角采用Shake算法固定, 因此键合势为零, 长程静电力采用PPPM算法处理^[21]. 原子间的非键合相互作用包括范德瓦耳斯相互作用和静电相互作用, 计算公式如下: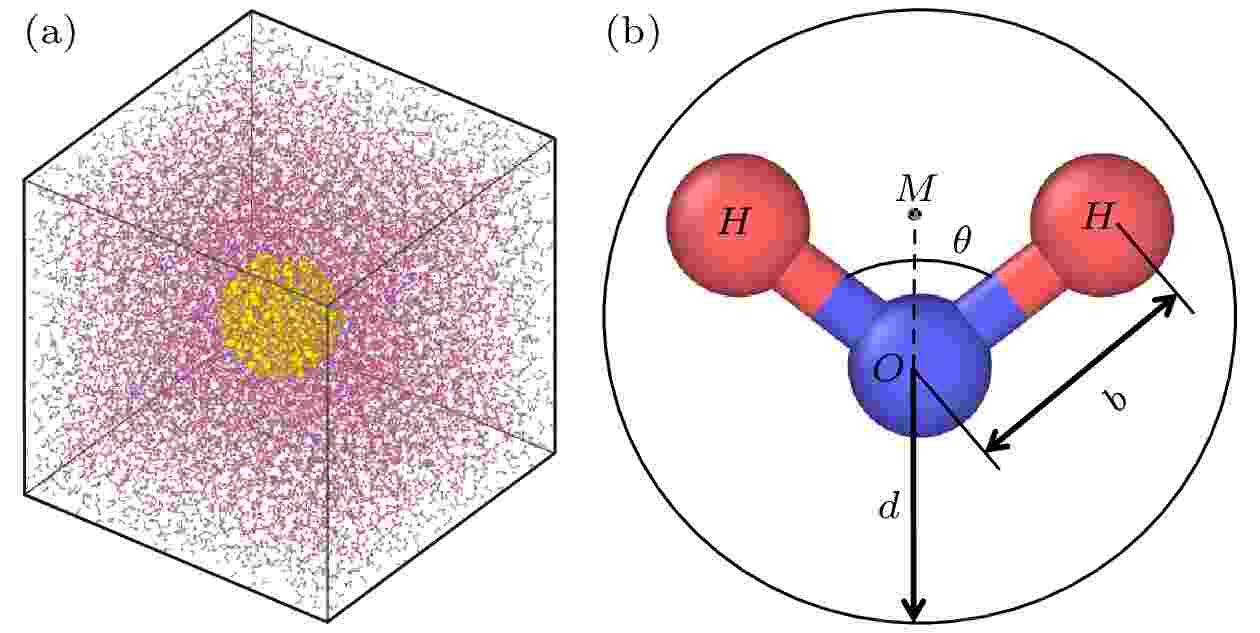
图 2 (a) Cu-H₂O纳米流体的物理模型; (b) TIP4P/2005水分子结构示意图
Figure2. (a) Physical model of Cu-H₂O nanofluid; (b) schematic diagram of TIP4P/2005 water.

颗粒半 径/nm	Cu原 子数	H2O分 子数	总原 子数	模拟域大小 Lx × Ly × Lz /?3
0.5	43	971	2956	30 × 30 × 30
1.0	351	7380	23841	60 × 60 × 60
1.5	1199	7459	23576	60 × 60 × 60
2.0	2928	14381	45972	75 × 75 × 75

表1各工况下模拟域大小与原子数目
Table1.The size of the simulation domain and number of atoms of different working conditions.

${U_{{\rm{vdw}}}} = 4\varepsilon \left[ {{{\left( {\sigma /{r_{ij}}} \right)}^{{\rm{12}}}} - {{\left( {\sigma /{r_{ij}}} \right)}^{\rm{6}}}} \right],$

${U_{{\rm{electronstatic}}}} = {q_i}{q_j}/{\rm{(4\pi }}{\varepsilon _{\rm{0}}}{r_i}_j),$

其中U_vdw代表原子间的短程引力势, U_{electronstatic}代表原子间的长程静电势, ε和σ分别代表原子的势能参数和尺寸参数, q_i和q_j为水分子中不同原子的带电量, r_ij代表原子间的距离.
颗粒与水分子的相互作用只考虑Cu原子与氧原子的范德瓦耳斯作用, Cu-H₂O纳米流体相互作用的势能参数如表2所列, 计算过程不考虑氢原子和氧原子及铜原子的范德瓦耳斯作用. 颗粒中原子间的相互作用采用适用于金属和合金的多体势(EAM)^[22], 这种EAM势在描述金属原子间的相互作用时比对势更精确, 晶体的总势能表示为

参数	取值
εo—o/eV	0.00803
σo—o/?	3.1589
εCu—o /eV	0.052
σCu—o /?	2.743

表2Cu-H₂O纳米流体势能参数
Table2.Potential energy parameter of Cu-H₂O nanofluid.

$U = \sum {{F_i}\left( {{\rho _i}} \right)} + {\varphi _i}_j\left( {{r_i}_j} \right)/{\rm{2}},$

${\rho _i} = \sum {{f_i}\left( {{r_i}_j} \right)} ,$

其中, F_i为嵌入能, 是除了第ρ_i个原子之外的所有其他原子的核外电子在第i个原子处所产生的电子云密度之和, φ_ij为对势作用项, r_ij为原子i和原子j间的距离.
系统能量最小化后, 在NPT系综下弛豫平衡, 采用Nose-Hoover方法控温控压. 目标温度和压力分别为298 K和 1 bar (1 bar = 10⁵ Pa), 时间步长为1 fs, 经过20 ps的弛豫后, 压力和温度趋于稳定. 体系稳定后, 在NVE系综下使颗粒做自由布朗运动, 总步数为6000 万步, 对应总时长为60 ns. 上述纳米流体模型的建立以及模型验证工作均采用LAMMPS软件包完成.
2 -->

2.2.水分子模型的验证

为了得到稳定的水分子体系, 需要确保系统在模拟过程中有足够的时间达到平衡. 选取随机分布的4096个水分子, 大小为49.6 ? × 49.6 ? × 49.6 ?的模拟域, 对弛豫过程中体系的温度和总能进行监测, 温度和总能随平衡时间的变化如图3(a)和图3(b)所示. 可以看出, 体系温度和总能量在300 fs左右时已经达到平衡, 总体积和密度亦趋于稳定. 由于水分子的动力学黏度对摩擦系数的计算至关重要, 本文采用green-kubo公式(5)式计算水的黏度, 该方法将流体的剪切黏度和压力张量中非对角元素的自相关函数联系起来, 通过计算压力张量的非主对角元素p_xy, p_xz, p_yz的平均值得到TIP4P/2005刚性水分子模型的剪切黏度^[23],
图 3 水分子模型的验证　(a) NPT系综下体系的温度随时间变化; (b) NPT系综下体系的总能量随时间变化
Figure3. Validation of water molecular model: (a) Curve of temperature over time; (b) total energy of the system over time.

$\eta = \frac{V}{{{k_{\rm{B}}}T}}\mathop \int \nolimits_0^\infty {\left\langle {{P_{ij}}\left( {{t_0}} \right){P_{ij}}\left( {{t_0} + t} \right)} \right\rangle _{{t_0}}}{\rm{d}}t,$

其中η为水分子的动力学黏度, V为计算域的体积, k_B为玻尔兹曼常数, P_ij为压力张量的非主对角元素.
NPT系综下平衡之后, 在NVT系综下计算体系的黏度, 经过2 ns的模拟, 得到水分子的黏度为0.825 × 10^–3 Pa·s, 该黏度与实验结果的误差约为7%^[24], 其他水分子模型(TIP3P, TIP4P, SPE/C)误差与实验结果在18%—64%之间^[23], 因此TIP4P/2005水分子模型的动力黏度已明显优于其他水分子模型.

2

-->

3.1.单颗粒布朗运动平动扩散

在统计力学中, 均方位移是指颗粒随时间运动的距离相对于参考位置的度量, Einstein在布朗运动理论中指出颗粒移动距离的平方的均值与时间呈线性关系:

$\langle {[\Delta x(t)]^2}\rangle = 2Dt,$

其中${[\Delta x(t)]^2}$为颗粒当前位置沿x方向相对于参考位置距离的平方; $\langle~ \rangle$表示体系中所有颗粒的均值; D为颗粒的扩散系数, 反映了颗粒在溶剂中扩散能力的大小.
由于布朗运动的方向具有随机性, 它的轨迹是一条由在空间随机分布的点依次连接所构成的曲线, 该曲线处处连续且处处不可导^[25]. 随着颗粒尺寸的增加, 体系内的总原子数因模拟域的增大而成倍增长, 受到计算资源的限制, 所有体系中只放置一个颗粒. 颗粒在总模拟时长内轨迹如图4所示, 蓝色代表轨迹的起点, 红色表示轨迹的终点, 模拟温度T = 298 K, 颗粒半径a = 1 nm. 从图4可以看出, 颗粒的运动方向并没有发生明显的变化, 但是轨迹同样满足处处连续且处处不可导的特征, 这是因为颗粒在运动过程中并未与其他颗粒发生碰撞. 对于单颗粒布朗运动轨迹, 采用传统的计算方法得到的扩散系数随计算时长的增加而增加, 为了准确地计算单个颗粒的均方位移, 本文采用单颗粒追踪方法并结合最小二乘法对颗粒的平动扩散系数进行拟合. 下面以半径a = 1 nm的颗粒为例说明扩散系数的拟合过程.
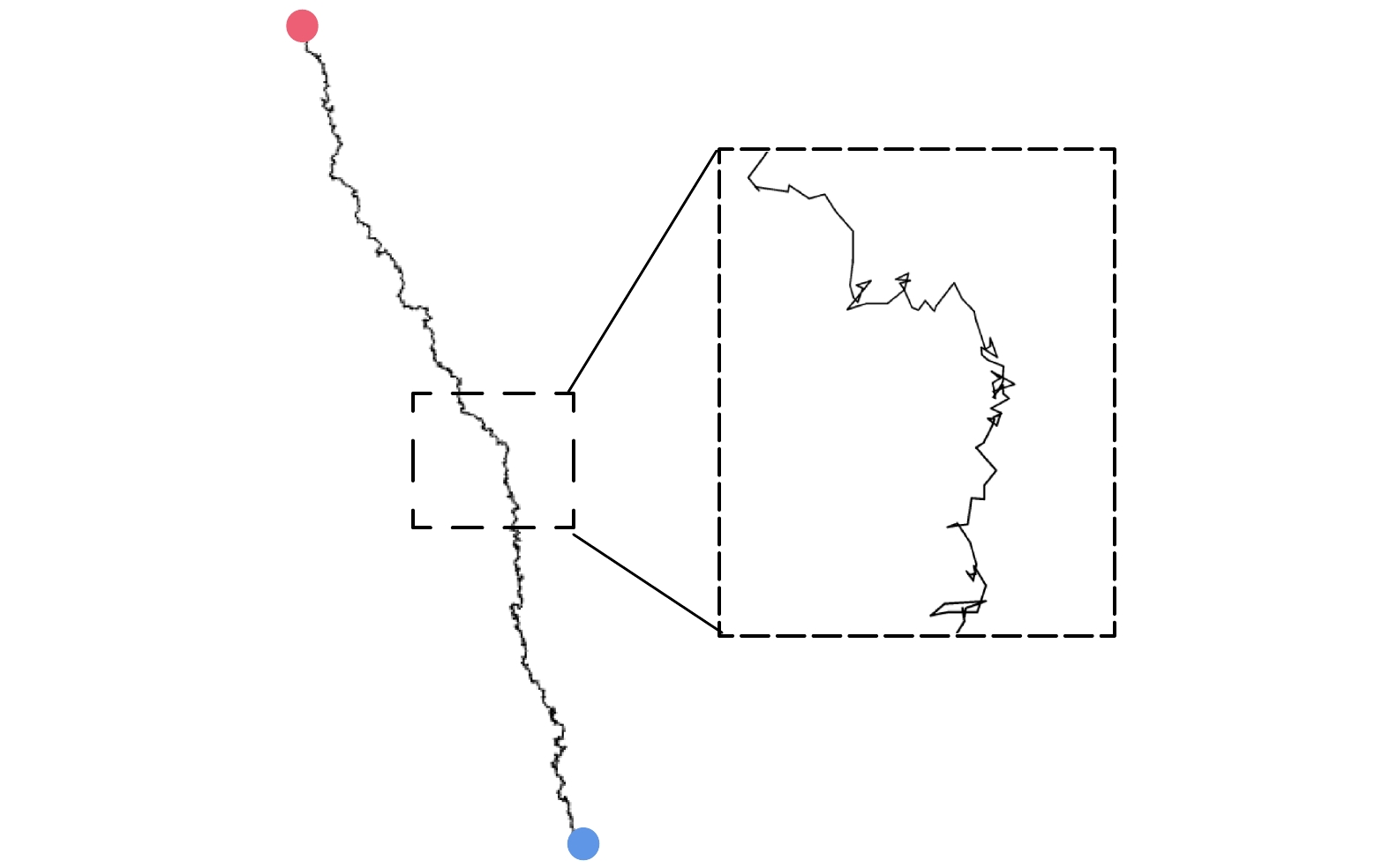图 4 单颗粒布朗运动轨迹
Figure4. Brownian motion trajectory of a single particle.

1)确定最佳关联时间. 颗粒的轨迹为含有N = 60000个数据点的连续曲线, 曲线的每一段的时间间隔为1 ps. 将该轨迹按不同的关联时间(时间间隔)N_t分成N_s = N/N_t份, 对每一段轨迹, 根据下式计算颗粒的均方位移:

$\begin{split}{\rm{MSD}} =& \frac{1}{{{N_{\rm{t}}} - n}}{\sum\limits_{i = 1}^{N - n} {({r_{i + n}} - {r_i})} ^2},\\& n = 1,2,\cdots,{N_{\rm{t}}} - 1,\end{split}$

其中N_t为每一段轨迹的关联时间, r_i为颗粒的位置坐标.
根据所求均方位移进而确定扩散系数, 然后对每一个关联时间下的N_s个扩散系数进行直方图分析. 如图5所示, 当关联时间较小时, 扩散系数呈正偏态分布, 关联时间很大时, 扩散系数呈负偏态分布, 一个呈正态分布的关联时间即是最佳关联时间^[26].
图 5 半径a = 1 nm的Cu颗粒在不同关联时间下扩散系数分布
Figure5. Diffusion coefficient distribution of Cu particles with radius a =1 nm at different correlation time.

2)确定最佳拟合点. 从(7)式可以看出, MSD曲线的第一个点代表每一段位移的平均, 而最后一个数据点没有被平均. 计算扩散系数时统计点过多或者过少都会对计算结果带来不利的影响, 因此本文计算了每一段轨迹采用不同拟合点时扩散系数D的变异系数(二阶矩/一阶矩), 变异系数最低的拟合点数目即为最佳拟合点^[27]. 图6为关联时间t = 1363 ps时得到的变异系数随拟合点变化的曲线, 可以看出, 拟合点数目在20左右时变异系数最低.
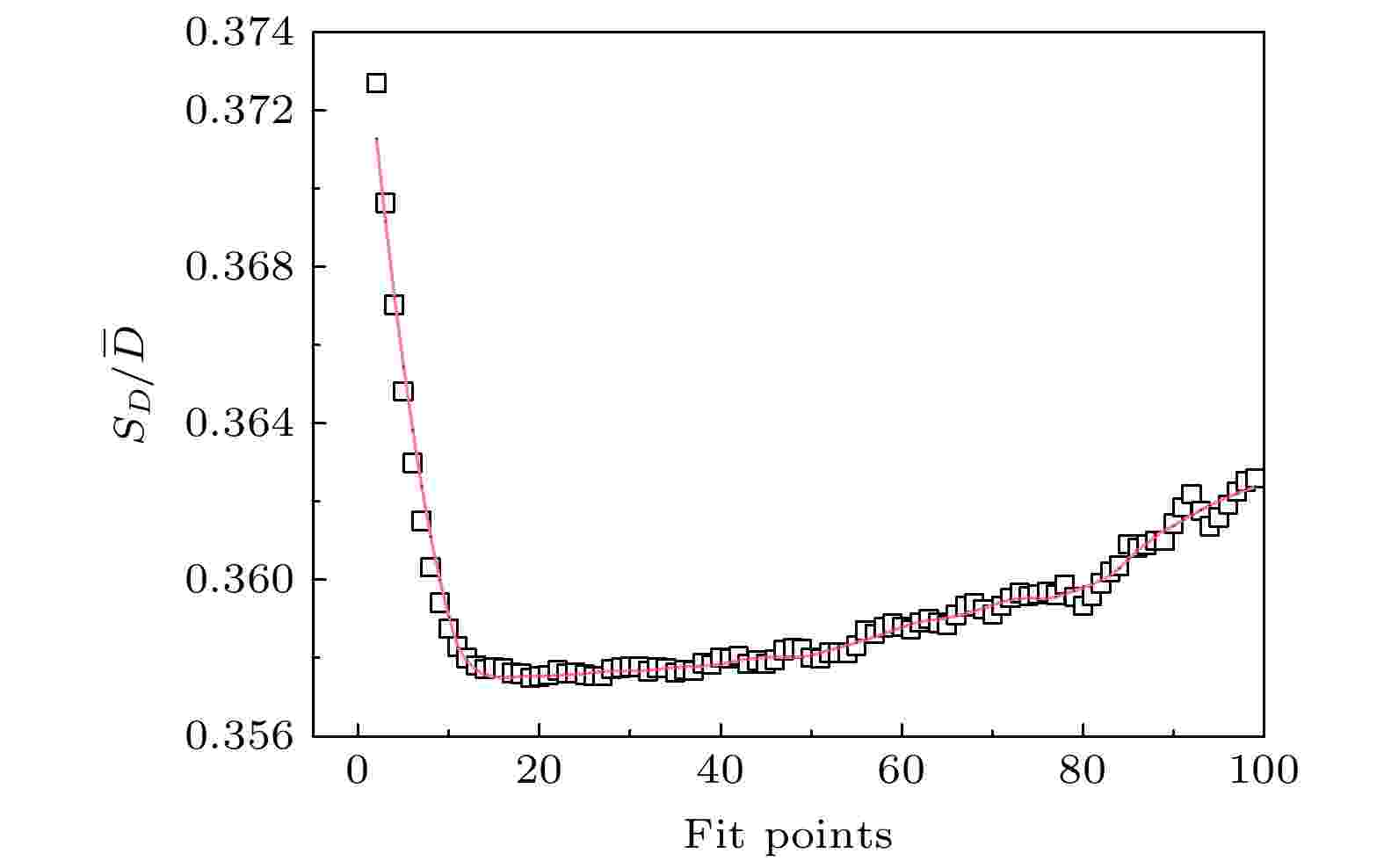图 6 半径a = 1 nm的Cu纳米颗粒在采用不同拟合点拟合时扩散系数的变异系数, 关联时间N_t = 1363 ps
Figure6. Variation coefficient of the diffusion coefficient of Cu nanoparticles with radius a =1 nm when different fitting points were used for fitting, correlation time N_t = 1363 ps.

将最佳拟合点下的扩散系数取平均可以得到半径a = 1 nm的Cu颗粒的扩散系数, 采用同样的方法可求得a = 0.5, 1.5, 2.0 nm时颗粒的扩散系数. 图7(a)表示4种颗粒的平动扩散系数, 红色曲线和蓝色曲线分别表示黏性边界条件和滑移边界条件下的预测结果, 从图7(a)可以看出, 平动扩散系数均在预测值之间. 平动扩散的摩擦因子可由$\alpha = {k_{\rm{B}}}T/{D_t}{\text{π}}\eta a$求得, 如图7(b)所示, 当半径a = 1.0, 1.5, 2.0 nm时, 摩擦因子更接近滑移边界条件; 半径a = 0.5 nm时, 摩擦因子更接近黏性边界条件. 随着颗粒尺寸的减小, 摩擦因子应逐渐趋近于4, 但对于颗粒半径为0.5和1.0 nm的颗粒, 摩擦因子有逐渐增大的趋势, 这是因为吸附在颗粒上的水分子增大了颗粒的水动力学半径, 导致计算的摩擦因子偏向黏性边界.
图 7 纳米颗粒的平动扩散特性　(a)不同尺寸Cu纳米颗粒的平动扩散系数; (b)不同尺寸Cu纳米颗粒的平动摩擦因子
Figure7. Translational diffusion characteristics of nanoparticles: (a) Translational diffusion coefficients of Cu nanoparticles with different sizes; (b) translational friction factors of Cu nanoparticles of different sizes.

2 -->

3.2.单颗粒布朗运动的旋转扩散

与平动扩散均方位移的定义类似, 颗粒的均方旋转角度可按下式定义:

${\rm{MSR}} = \langle {[\Delta \theta (t)]^2}\rangle = 4{D_\theta }t,$

其中, MSR表示颗粒的均方旋转角度, $\Delta \theta (t)$代表颗粒从初始时刻到t时刻绕某一旋转轴转过的角度, ${D_\theta }$即为颗粒的旋转扩散系数. 如图8所示, 颗粒在一个时间间隔内转过的角度为O-O轴与O'-O' 轴的夹角, 由于球形颗粒的旋转具有各向同性, 不计颗粒绕O-O轴的旋转对计算结果没有影响. 四元数可以很方便地表征空间向量在三维空间中的旋转, 本工作通过颗粒在每一个位置的四元数来计算颗粒旋转的角度. 假设颗粒在初始时刻的单位四元数q = (a₁, a₂, a₃, a₄), 将其转化为旋转矩阵R, 如(9)式所示. 在球面上任取一单位向量u, 将该单位向量右乘旋转矩阵R即可得到初始时刻的单位向量${u_{\rm{1}}}$, 同样的方法可求得向量u在其他时刻的方向向量.
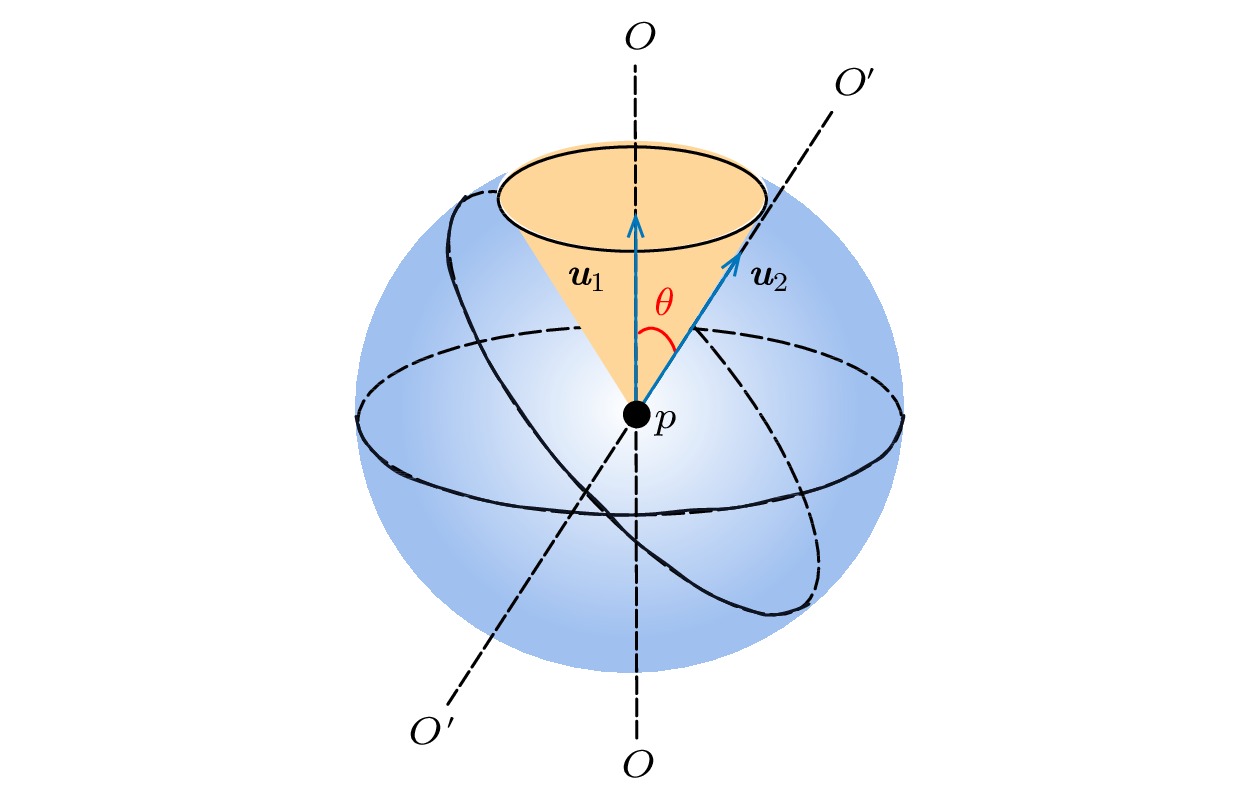图 8 颗粒旋转扩散系数计算的物理模型
Figure8. Physical model for particle rotation diffusion coefficient calculation.

$\begin{split}& {{R}} = \left[ {\begin{array}{*{20}{c}} {{\rm{1}} - {\rm{2}}({a_{\rm{3}}}^{\rm{2}} + {a_{\rm{4}}}^{\rm{2}})}&{{\rm{2}}({a_{\rm{2}}}{a_{\rm{3}}} + {a_{\rm{1}}}{a_{\rm{4}}})}&{{\rm{2}}({a_{\rm{2}}}{a_{\rm{4}}} - {a_{\rm{1}}}{a_{\rm{3}}})} \\ {{\rm{2}}({a_{\rm{2}}}{a_{\rm{3}}} - {a_{\rm{1}}}{a_{\rm{4}}})}&{{\rm{1}} - {\rm{2}}({a_{\rm{2}}}^{\rm{2}} + {a_{\rm{4}}}^{\rm{2}})}&{{\rm{2}}({a_{\rm{3}}}{a_{\rm{4}}} + {a_{\rm{1}}}{a_{\rm{2}}})} \\ {{\rm{2}}({a_{\rm{2}}}{a_{\rm{4}}} - {a_{\rm{1}}}{a_{\rm{3}}})}&{{\rm{2}}({a_{\rm{3}}}{a_{\rm{4}}} - {a_{\rm{1}}}{a_{\rm{2}}})}&{{\rm{1}} - {\rm{2}}({a_{\rm{2}}}^{\rm{2}} + {a_{\rm{3}}}^{\rm{2}})} \end{array}} \right].\end{split}$

不同于平动扩散系数, 旋转扩散系数的拟合对关联时间的选择不敏感, 因此可以直接对颗粒的MSR曲线进行拟合. 颗粒的均方旋转角度如图9所示, MSR曲线随时间单调递增, 对该曲线进行线性拟合即得到颗粒的旋转扩散系数. 图10(a)表示颗粒的旋转扩散系数随颗粒尺寸的变化, 红色曲线代表由Stokes-Einstein关系得到的颗粒在黏性边界条件下的扩散系数, 从图10(a)可以看出, 随颗粒尺寸的增加, 扩散系数逐渐趋近于黏性边界调下的结果. 图10(b)给出了旋转摩擦因子的大小, 旋转摩擦因子β可由$\beta = {k_{\rm{B}}}T/{\text{π}}\eta {a^3}$求得. 从图10(b)可以看出, 旋转摩擦因子β均在黏性边界与滑移边界所规定的范围内, 介于4—8之间, 因此更接近黏性边界条件. 颗粒尺寸越大, 边界条件越接近黏性边界, 但半径a = 0.5 nm和a = 1.0 nm的颗粒, 摩擦因子相比a = 1.5 nm和a = 2.0 nm的颗粒反而有所升高, 这是颗粒表面溶剂分子吸附的结果.
图 9 不同半径的Cu纳米颗粒的均方旋转角度
Figure9. Mean-square rotation angles of Cu nanoparticles with different sizes.

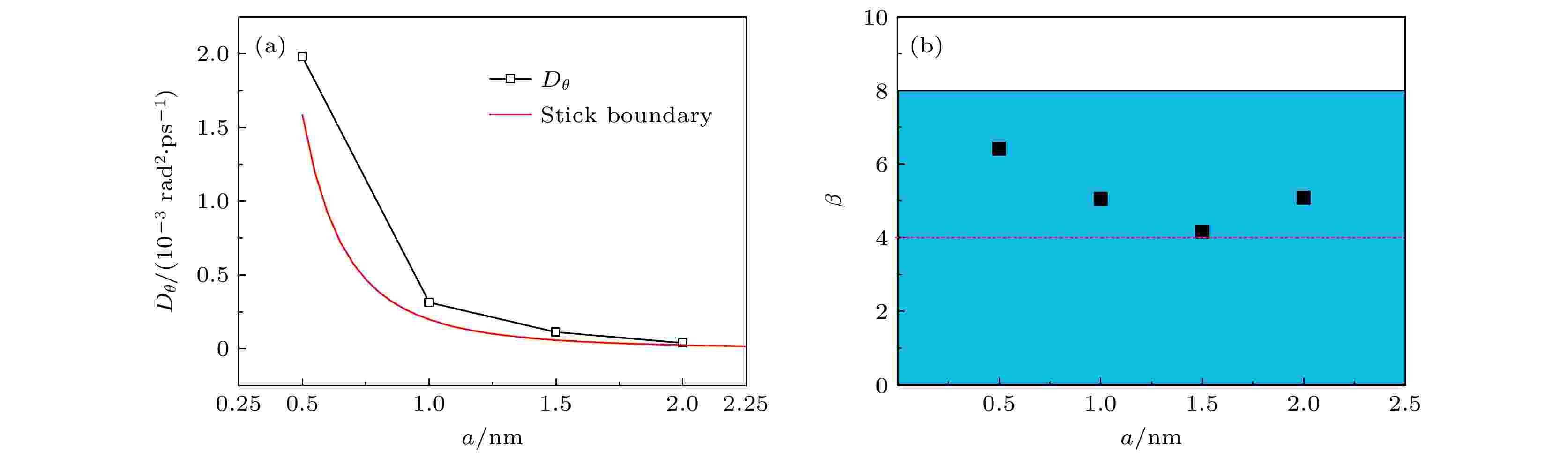图 10 颗粒旋转扩散特性　(a)颗粒的转动扩散系数; (b) 颗粒转动扩散摩擦因子
Figure10. Rotational diffusion characteristics of particles: (a) Rotational diffusion coefficients of particle; (b) rotational friction factors of particle.

2 -->

3.3.纳米颗粒表面溶剂分子的吸附特性

在滑移边界条件假设下, 纳米颗粒运动过程中表面不会携带流体分子. 然而考虑到纳米颗粒的粗糙度和固-液相互作用, 颗粒周围往往会吸附溶剂分子, 这部分溶剂分子与纳米颗粒一起做随机运动, 因此吸附的水分子层会对颗粒的有效水动力学半径产生影响. 本文统计了纳米颗粒周围水分子的分布^[28], 如图11(a)所示, 通过统计距离纳米颗粒表面为r, 厚度为dr的球壳内的原子数目, 得到了水分子的径向分布函数(RDF), RDF可用下式来计算:
图 11 纳米颗粒周围水分子的RDF　(a) RDF计算的物理模型; (b)不同尺寸的颗粒周围水分子的RDF曲线
Figure11. Radial distribution function (RDF) of water molecules around nanoparticles: (a) Physical model for RDF calculation; (b) RDF curves of water molecules around particles of different sizes.

$g(r) = \frac{{n(r)}}{{{\rho _0}{V_r}}} = \frac{{n(r)}}{{4{\rm{\pi }}{r^{\rm{2}}}{\rho _{\rm{0}}}{\rm{d}}r}},$

其中$n(r)$表示落在厚度为${\rm{d}}r$的球壳内的原子数目, V_r为球壳的体积, ${\rho _0}$表示无穷远处水分子体系的原子数密度, 随着r的增加, 球壳内原子的数密度等于溶剂分子的平均数密度, g(r)趋近于1.
图11(b)为纳米颗粒周围原子数目的径向分布函数. 可以看出, 不同尺寸的纳米颗粒周围原子数分布均在1.7 ? (略小于水分子半径)左右时达到峰值, 峰值越大, 代表溶剂分子的吸附程度越紧密, 曲线中第一个峰的高度随着颗粒尺寸的增加依次降低; 第二个峰值出现在距离表面4.3 ?处(略大于一个水分子的直径), 且峰的高度没有明显差别, 之后水分子数密度逐渐趋于标准水分子密度. 因此, 在距离颗粒表面一个水分子直径的区域内水分子排列呈现结构化, 导致颗粒周围水分子的密度大于水分子的平均密度, 固体和水分子之间悬空的氢键是导致水分子在颗粒表面产生吸附的原因^[12], 氢键存在于水分子中, 但水分子不能和金属原子之间形成氢键, 因此水分子趋于向颗粒表面靠近. 水分子在颗粒表面的吸附增大了颗粒的有效半径, 而且颗粒尺寸越小, 表面水分子层相对于颗粒的尺寸越大, 对颗粒水动力学半径的影响越大, 这是导致在转动摩擦因子的计算中, 尺寸a = 0.5和1.0 nm的颗粒摩擦因子向非滑移边界移动的原因.

本文采用分子动力学模拟方法建立了不同尺寸的单个Cu纳米颗粒在水中扩散的全原子模型, 通过单颗粒轨迹分析, 采用最小二乘法拟合了颗粒的平动和转动扩散系数, 并将摩擦因子与黏性边界与滑移边界条件下的结果作对比. 颗粒的平动和转动扩散系数随着颗粒尺寸的减小而增加, 且摩擦因子均在黏性边界条件与滑移边界条件所规定的范围内. 由于水分子之间存在氢键网络而水分子与金属原子之间无法形成氢键, 所以水分子会吸附在金属表面, 吸附在颗粒上面的水分子会增大颗粒的水动力学半径. 无论颗粒大小, 水分子的吸附现象始终存在, 对于大的颗粒, 由水分子吸附所增加的半径远小于颗粒的真实半径, 所以对颗粒有效半径的影响不够明显; 对于尺寸较小的颗粒, 由水分子吸附所增加的半径与颗粒的真实半径接近, 所以对小颗粒有效半径的影响较为显著. 因此对半径a = 0.5, 1.0 nm的颗粒, 其平动和转动摩擦因子比预测值偏大, 因为颗粒的表面水分子的吸附能力较强, 当颗粒的尺寸小于水分子半径的5倍时, 水分子吸附对颗粒有效水动力学半径的影响不可忽略.