摘要:液滴撞击固体表面是一种广泛存在于工农业生产中的现象. 随着微纳技术的发展, 纳米液滴撞击行为的定量描述有待完善. 采用分子动力学模拟纳米水滴撞击柱状粗糙铜固体表面的动态行为. 分别在液滴速度为2—15 ?/ps, 五种方柱高度和六种固体表面特征能的情况下分析液滴的动态特征. 结果表明, 随着液滴初始速度V₀的增加, 其最终稳定状态先由Cassie态(V₀ = 2—3 ?/ps)转变为Wenzel态(V₀ = 4—10 ?/ps), 然后再次呈现Cassie态(V₀ = 11—13 ?/ps). 当V₀ > 13 ?/ps时, 液滴发生弹跳. 液滴最大铺展时间t_max与V₀关系曲线中存在拐点, 并针对不同速度区域提出t_max与V₀的关系式. 随着方柱高度的增加, 液滴的稳定状态由Wenzel向Cassie态转变, 液滴稳定状态的铺展半径逐渐减小. 固体表面特征能ε_s的增大使得液滴的铺展能力增强, 液滴铺展后的回缩现象逐渐减弱直至消失.
关键词: 纳米液滴/
分子动力学模拟/
撞击/
动态行为

English Abstract

全文HTML

--> --> -->

液滴撞击固体表面的现象在工农业生产生活中广泛存在, 如喷墨打印^[1]、农药喷洒^[2]、喷雾冷却^[3]和生物打印^[4]等. 液滴撞击固体表面的动态过程主要受到液滴速度、液滴成分和固体表面润湿特性等的影响^[5]. 固体表面润湿性能的差异主要由接触角θ体现. 不同的表面可以实现自清洁^[6]、防止结冰^[7]和雾水收集^[8]等功能.
大量试验展示了宏观液滴撞击固体表面的动态行为, 并将动态过程大致分为撞击、铺展、回缩、弹跳或停留^[9-11]四个阶段. Gu等^[12]使用激光-电化学沉积的方法制备微纳复合结构的超疏水铜表面, 对液滴撞击下Cassie状态的稳定性进行了研究. Qi等^[13]研究了液滴撞击固体表面时下方气层的变化, 发现气层厚度随着温度的增加而增加、随着液滴粘度和韦伯数的增加而降低.
尽管液滴撞击固体表面的动态行为受到了众多的关注, 但由于工业生产不断向微纳领域发展, 纳米液滴与宏观液滴存在很多差异, 目前在纳米液滴撞击粗糙固体表面动态行为的研究仍不完善. 由于实物试验无法清楚地展示液滴撞击过程中更多的细节, 而采用分子动力学(MD)模拟的方法可以从原子尺度探究纳米液滴的润湿、撞击、聚并和弹跳的机理^[14-17]. Liu等^[18]通过MD模拟了纳米液滴撞击带有脊状结构的超疏水表面, 提出脊状结构能够促进液滴的弹跳并减少液滴与固体表面的接触时间, 提高弹跳速度. Wang等^[19]通过MD模拟了聚合物液滴撞击疏水表面的过程, 分析液滴内部的速度分布并提出粘性耗散机制. Yin等^[20]分析了两个等大小的液滴撞击光滑表面后的动态过程, 发现当液滴速度较高时撞击后的液滴会在交界处产生径向射流现象.
本文采用分子动力学方法模拟纳米水滴撞击柱状粗糙铜固体表面的动态行为. 在较大初始速度范围内分析液滴的动态行为, 得到最大铺展时间t_max与初始速度V₀的关系式, 并通过改变方柱高度H及固体的表面特征能${\varepsilon _{\rm{s}}}$, 探究其对液滴动态行为的影响及作用机理.

图1是纳米液滴撞击截面为正方形的柱状固体表面初始构型. 固体表面由以面心立方(FCC)方式排列的铜原子构成, 晶格常数为3.615 ?^[21]. 水分子采用TIP4P模型^[22], 氧原子电荷为–1.0484e, 氢原子电荷为+0.5242e, 键长为0.9572 ?, 键角为104.520°. 相比较其他模型, TIP4P模型能够更好地表征水的动态特性^[23]. 液滴半径为35 ?, 由5991个水分子组成. 为防止液滴初始结构中有原子重叠, 造成液滴内部相互作用过大而使计算无法收敛, 水分子之间按照体心立方(BCC)晶格排列, 晶格常数由298 K下水的密度值决定. 模型在x, y, z方向的总体尺寸分别为: 318.120, 318.120和200 ?. 足够大的模拟盒子尺寸是为了防止在模拟过程中, 模拟体系与周围的镜像体系产生联系. 初始态液滴保持静止, 其最低处与固体表面的距离为15 ?, 该距离是为确保在能量最小化和弛豫过程中两者间没有相互作用. 方柱高度H = 18.075 ?, 相邻方柱间距B = 3.615 ?, 方柱截面边长W = 7.230 ?, y方向尺寸与x方向尺寸一致.
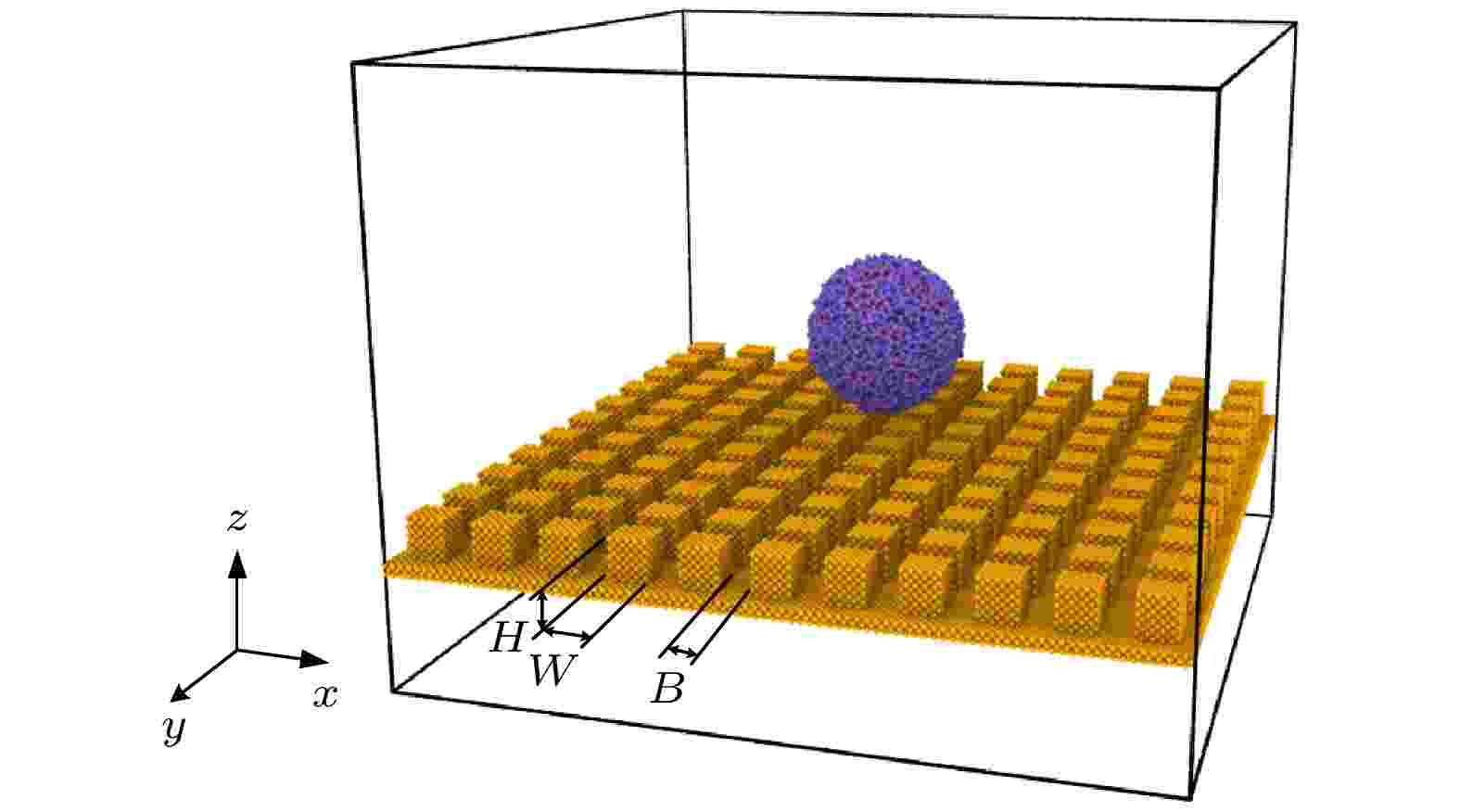图 1 模拟体系的初始构型
Figure1. Initial configuration of the simulation system.

采用大规模原子/分子并行模拟器(large-scale atomic/molecular massively parallel simulator, LAMMPS^[24])编程实现整个模拟过程. 模型的各个方向均采用周期性边界条件以消除边界影响. 为了在保证模拟结果正确的同时提高计算效率, 采用SHAKE算法对水分子的键长和键角加以约束, 同时将固体原子约束在初始平衡位置^[25-28]. 水分子与铜原子之间、铜原子与铜原子间均采用12-6 Lennard-Jones(LJ)势函数描述相互作用^[18,20]. 水分子间的相互作用为^[29]

$\begin{split}U = \;&4{\varepsilon _{{\rm{OO}}}}\left[ {{{\left( {\frac{{{\sigma _{{\rm{OO}}}}}}{{{r_{\rm{O}}}_{\rm{O}}}}} \right)}^{12}} - {{\left( {\frac{{{\sigma _{{\rm{OO}}}}}}{{{r_{\rm{O}}}_{\rm{O}}}}} \right)}^6}} \right] \\&+ \sum\limits_{{{a}} = 1}^3 {\sum\limits_{{{b}} = 1}^3 {\frac{{{q_{ia}}{q_{{{jb}}}}}}{{4\pi {\varepsilon _0}{r_{ia,}}_{{{jb}}}}}} } , \end{split}$

其中${r_{{\rm{OO}}}}$为两水分子i, j中氧原子间的距离; ${\varepsilon _{{\rm{OO}}}}$, ${\sigma _{{\rm{OO}}}}$分别为氧原子间的相互作用参数; ${r_{ia{\rm{, }}jb}}$为水分子i中电荷位置a与水分子j中电荷位置b的距离, ${q_{ia}}$, ${q_{jb}}$分别为a和b处的电荷量; ${\varepsilon _{\rm{0}}}$为真空中介电常数. 氧的相互作用参数${\varepsilon _{\rm{O}}}$ = 0.1628 kcal/mol; ${\sigma _{\rm{O}}}$ = 3.1644 ?; 铜的相互作用参数${\varepsilon _{{\rm{Cu}}}}$ = 0.2379 kcal/mol, ${\sigma _{{\rm{Cu}}}}$ = 2.3400 ?^[30].
水和铜之间的LJ相互作用参数${\sigma _{mn}}$和${\varepsilon _{mn}}$由Lorentz-Berthelot规则^[31]获得

${\sigma _{mn}} = \frac{1}{2}({\sigma _m} + {\sigma _n}), $

${\varepsilon _{mn}} = \sqrt {{\varepsilon _m}{\varepsilon _n}} , $

其中${\sigma _m}$, ${\varepsilon _m}$, ${\sigma _n}$, ${\varepsilon _n}$ 分别是原子m, n的势能参数.
模拟过程中LJ相互作用和库伦相互作用的截断半径分别取为10 ?和12 ?. 采用Velocity-Velet算法求解牛顿运动方程, 积分时间步长为1 fs, 采用PPPM算法(particle-particle particle mesh)计算长程库仑力^[32,33].
为使模拟过程更符合物理规律, 确保模拟结果的准确, 首先对非平衡态的初始体系进行能量最小化, 随后对其进行NVT 系综下的弛豫. 弛豫过程选择Nose-Hoover方法进行控温^[34,35], 目标温度为298 K. 弛豫过程中, 水分子的速度设置符合Maxwell-Boltzmann分布. 经过足够长时间的弛豫, 模拟体系达到能量稳定状态, 此时模拟区域中有气相水分子存在^[36]. 然后, 取消NVT系综, 消除对温度的控制, 对模拟体系施加NVE系综, 同时对液滴施加竖直向下的初始速度V₀, 当液滴刚接触固体表面时开始数据收集.

2

-->

4.1.液滴接触角的计算

接触角是表征固体表面性能的重要参数. 为了计算液滴在光滑铜表面的接触角, 用小立方体对模拟体系进行划分, 立方体的尺寸为1 ? × 1 ? × 1 ?. 由于液滴在x-y平面投影的对称性, 故只分析右半部分. 计算每个立方体内水分子的密度进而获得液滴密度云图, 如图2所示. 选择密度为0.5 g/cm³的等密度线作为液态-气态的分界线^[16,30] (图2中黑色曲线). 液滴的形状可假设为圆的一部分, 根据圆的方程(4)式拟合出液滴轮廓, 进而根据(5)式计算接触角θ^[30].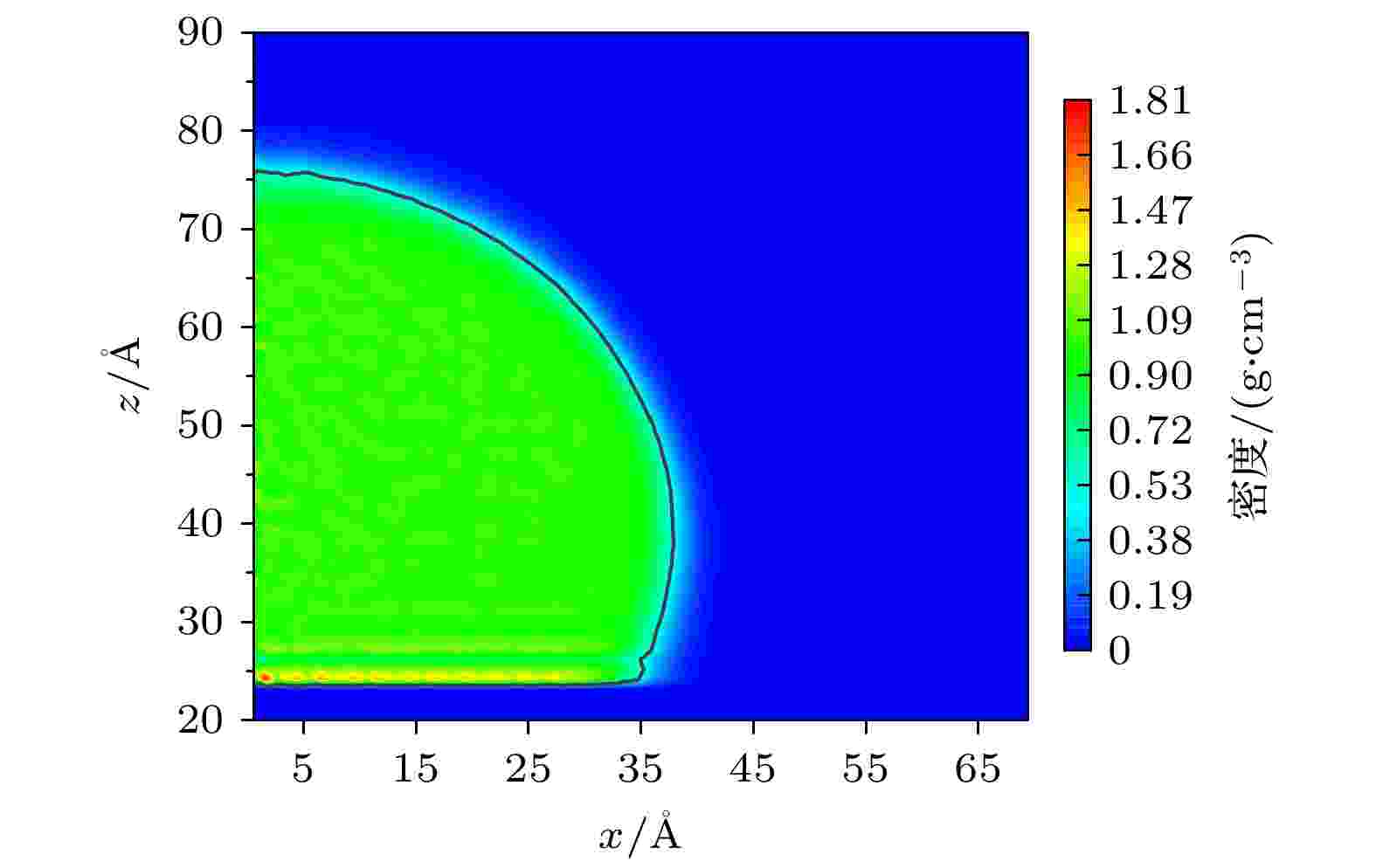

${(x - a)^2} + {(z - b)^2} = {R^2}, $

$\theta = \arcsin \left( {\frac{{b - {z_{{\rm{sub}}}}}}{R}} \right) + {90^\circ },$

其中a, b分别是圆心的x和z方向坐标; R是圆的半径; z_sub为基面位置. 计算得到θ = 108.7o. 已有试验测得液滴在光滑铜表面上的接触角为102o^[37], 模拟值与试验值相近. 误差主要来源于试验与模拟过程中铜表面的光滑程度差异.
图 2 液滴右半部分密度云图
Figure2. Density profile of the right-sided droplet.

2 -->

4.2.液滴初始半径对动态行为的影响

对半径分别为35, 40, 及45 ?的液滴在光滑表面和柱状固体表面的铺展过程进行分析. 由图3可知, 尽管液滴的半径不同, 但无量纲量R/R₀ (R是铺展半径, 即液滴与固体表面接触区域的半径; R₀是液滴初始半径)随铺展时间t的变化高度重合, 最大相对误差为6.9%. 为在保证模拟精度的同时提高计算效率, 采用R₀ = 35 ?的液滴进行进一步的研究.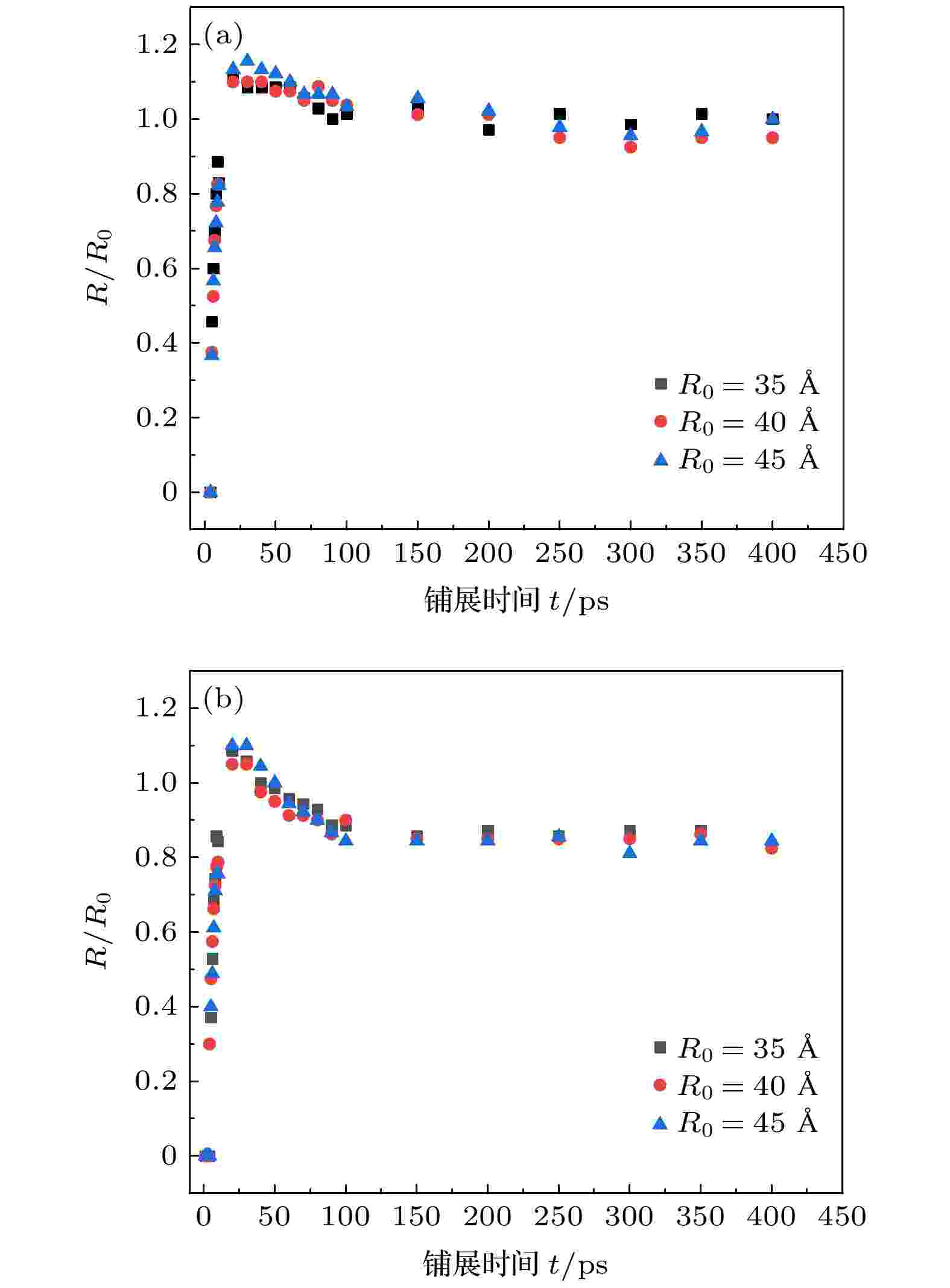
图 3 液滴尺寸对铺展时间t的影响　(a) 液滴在光滑固体表面上; (b) 液滴在柱状固体表面上
Figure3. Effects of droplets size on spreading time: (a) Droplets on the flat solid surfaces; (b) droplets on the nanopillared solid surfaces.

2 -->

4.3.初始速度的影响

由于尺度差异, 纳米液滴需要更大的初始速度V₀才能获得与宏观液滴相似的变形^[38], 也只有在高速的情况下, 纳米液滴才能与宏观或试验中的液滴有相同的韦伯数We:

$We = {{\rho {R_{\rm{0}}}V_{\rm{0}}^2}}/{\gamma }, $

其中$\rho $为液滴密度; $\gamma $为表面张力. 因此对V₀ = 2—15 ?/ps的液滴撞击柱状固体表面的动态行为进行模拟. 当液滴停留在固体表面上时, 根据液滴是否完全充满粗糙结构可以分为Wenzel态和Cassie态^[39]. 图4展示了液滴的动态行为. 将液滴铺展后小幅波动或液滴弹跳后处于匀速运动的状态定义为稳定状态(匀速运动对应图5中V₀ = 15 ?/ps的液滴在150 ps后质心高度h与t基本呈线性关系阶段). 不同V₀的液滴其稳定态的润湿模式如表1所列.
图 4 不同速度的液滴撞击柱状固体表面的动态行为
Figure4. Dynamic behaviors of droplets with various velocities impinging on nanopillared solid surfaces.

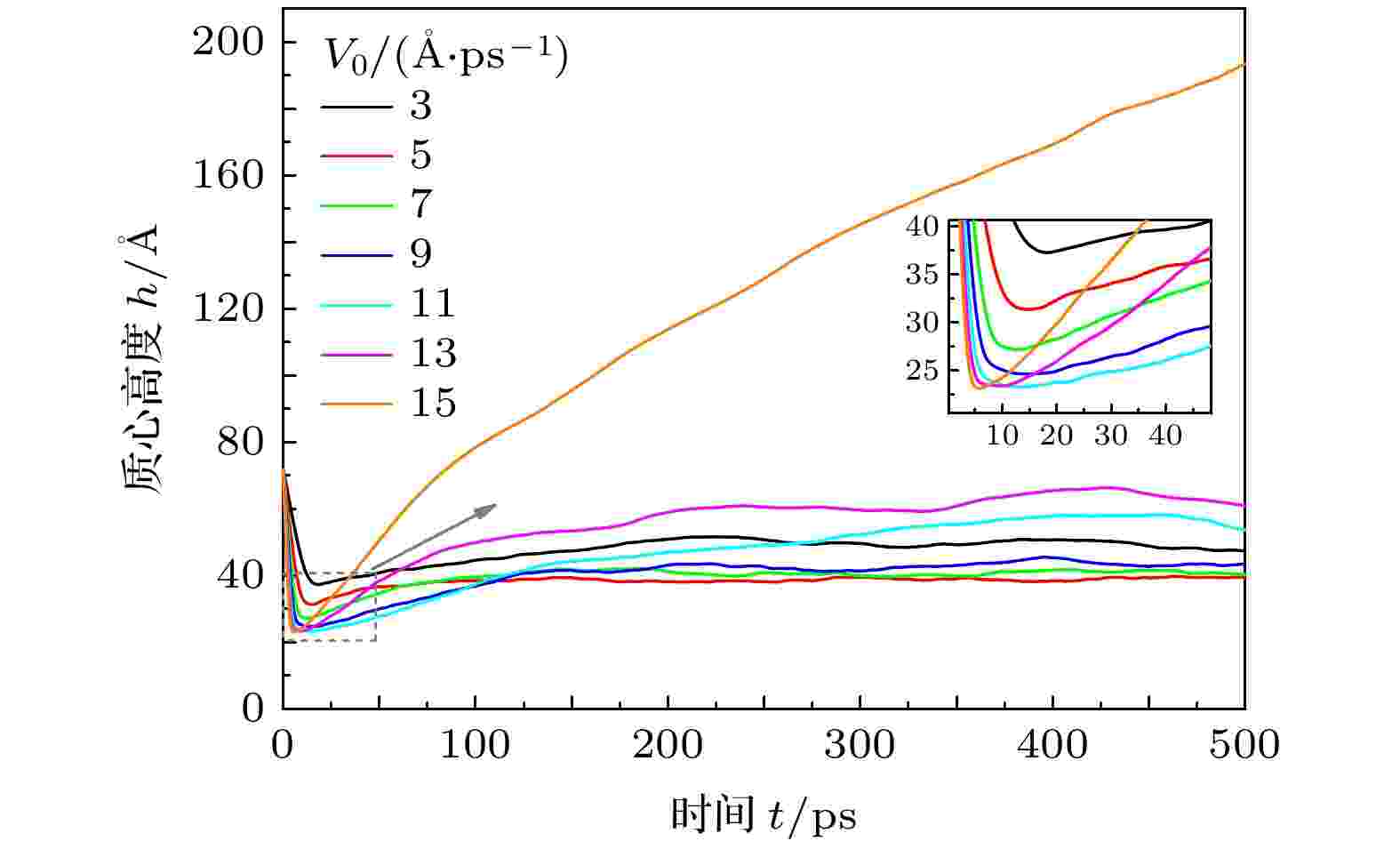图 5 液滴质心高度h随铺展时间t的变化
Figure5. Time evolution of central height of droplets with different velocities.

V0/(?·ps–1)	2—3	4—10	11—13	14—15
润湿模式	Cassie	Wenzel	Cassie	弹跳

表1液滴撞击柱状固体表面稳定状态时的润湿模式
Table1.Wetting patterns of steady state of droplets impinging on nanopillared solid surfaces.

当V₀ = 3 ?/ps时, 液滴具有的动能较小, 铺展过程中很快被消耗完, 在表面张力的作用下, 变形的液滴开始回缩, 液滴最终呈现Cassie态. 随着V₀增加至5—9 ?/ps, 具有更高动能的液滴促使铺展区域进一步扩展. 在回缩阶段, 由于液滴完全充满柱间空隙并接触固体表面底层, 固液间相互作用增强, 液滴的表面能不足以克服该相互作用, 液滴最终呈现Wenzel态. 当V₀进一步增大至11—13 ?/ps, 回缩阶段液滴的表面能虽然可以克服前述两者的吸引, 但未能克服柱状结构上表面对液滴的吸引, 从而近似球状地停留在固体表面上呈现Cassie态. 当V₀继续增加至14 ?/ps时, 液滴在130 ps时被拉伸产生显著变形, 最终完全挣脱固体表面的吸引发生弹跳. 液滴发生弹跳的临界速度为13 ?/ps. 需要指出, 尽管在V₀较大时, 有部分水分子脱离液滴主体, 以V₀ = 14 ?/ps为例对液滴前后尺寸进行计算, 液滴尺寸仅有4%的改变, 即脱离液滴主体的水分子由于占比很小, 其对液滴动态过程研究的影响可以忽略.
液滴质心高度h的变化如图5所示, 质心高度最小值h_min随着液滴初始速度V₀的增大而逐渐降低. 这是因为液滴速度的增大使其具有更大的动能进行铺展, 增大了液滴铺展面积, h_min随之减小.
图6为液滴最大铺展时间t_max随V₀的变化. t_max定义为液滴从接触固体表面至达到最大铺展状态所需时间. 根据变化规律不同, 将其按V₀大小分为低速区(0—6 ?/ps)、中速区(6—9 ?/ps)和高速区(9—15 ?/ps). t_max与V₀的关系如下式所示:
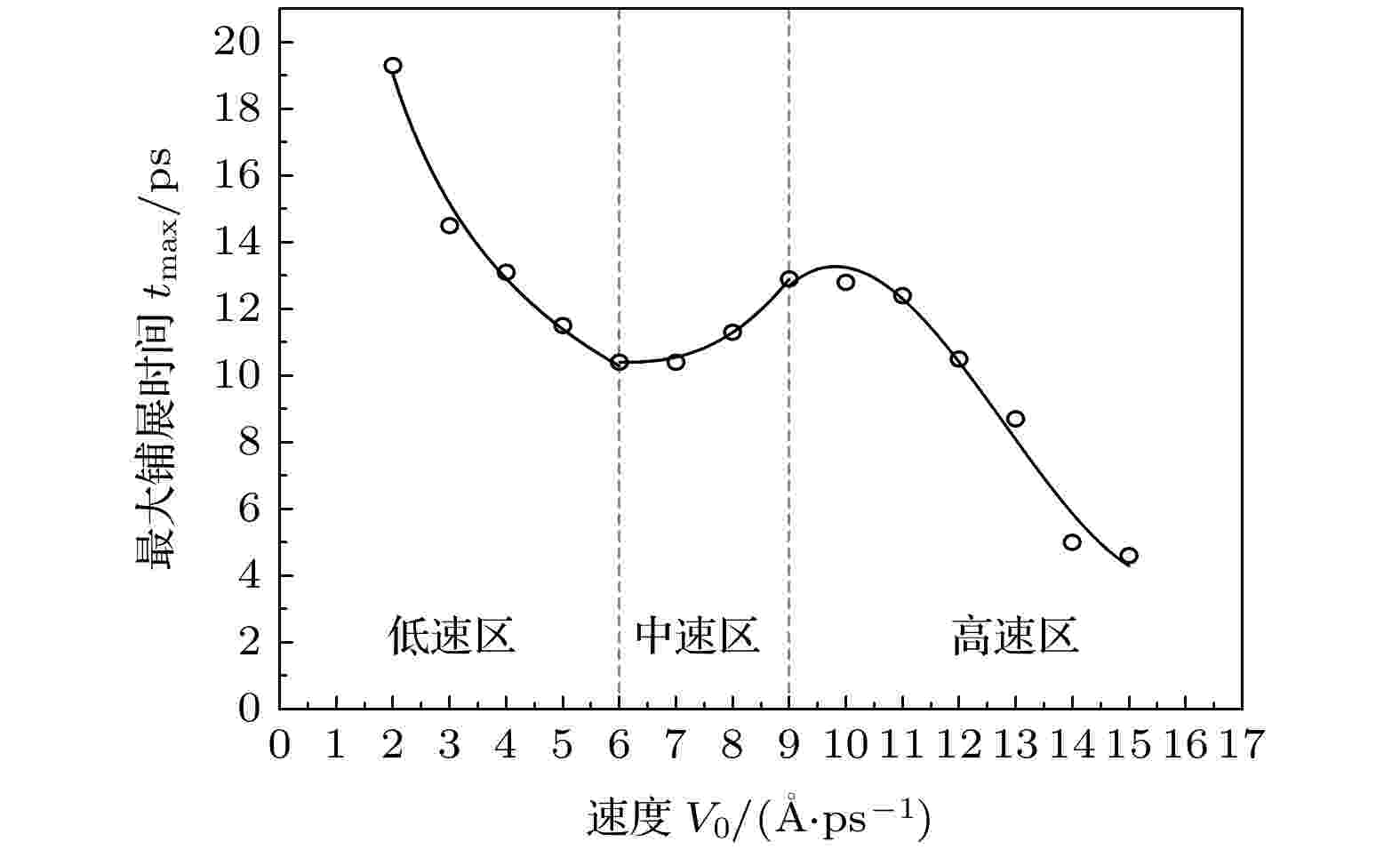图 6 最大铺展时间t_max随速度V₀的变化
Figure6. The dependence of the maximum spreading time of droplets on velocities.

${t_{\max }} =\!\! \left\{ {\begin{aligned} &{28V_0^{ - 0.559}{\rm{ }},}&{2 < {V_0} \leqslant 6~{\text{?}}{\rm{ /ps,}}}\;\; \\ &{0.157{{({V_0} - 6)}^{2.520}} + 10{\rm{ }},}&{6 < {V_0} < 9~{\text{?}}{\rm{ /ps,}}} \;\;\\ & 0.089V_0^3 - 3.412V_0^2 & {} \\&+ 41.285{V_0} - 148{\rm{,}} & 9 \leqslant {V_0} < 15~{\text{?}}{\rm{/ps }}. \end{aligned}} \right.$

V₀处于低速区的液滴, t_max随V₀的增加逐渐减小. 当V₀增加到6—9 ?/ps中速区, 图线出现拐点, t_max有增加的趋势. 为探究拐点出现的原因, V₀为2—15 ?/ps的液滴其最大铺展状态展示如图7. 速度处于2—6 ?/ps低速区的液滴撞击固体表面后在柱顶铺展, 但由于受到钉扎效应^{[40, 41]}的影响, 铺展半径几乎没有增加, 而接触角却显著增大.
图 7 不同速度液滴的最大铺展状态
Figure7. The maximum spreading states of droplets with different velocities.

V₀处于6—9 ?/ps中速区的液滴, 由于动能的增加, 液滴得以克服钉扎效应带来的铺展阻碍. 液滴开始进入并向更多的方柱间隙铺展. 由于克服钉扎效应消耗了液滴的动能, 导致液滴继续铺展的速度降低.V₀较小的液滴其动能很快被消耗尽, 而V₀较大的液滴有着相对高的动能, 其动能的耗尽需要更多的时间, 也即增加了液滴达到最大铺展状态所需时间t_max.
当V₀达到9—15 ?/ps的高速区时, 液滴开始向更多的方柱顶铺展. 虽然铺展过程中同样受到钉扎效应的阻碍, 但液滴有着足够高的动能可以将之克服. 因此t_max仍呈现下降趋势.
为定量描述液滴的动态铺展, 定义铺展半径R与初始半径R₀的比值为铺展因子β. 图8是不同V₀的液滴其β随时间t的变化. 由图8可见, 随着V₀的增加最大铺展因子β_max逐渐增大, 当V₀增大到15 ?/ps时, β_max = 1.757. 当V₀ < 9 ?/ps时, 液滴稳定态的β基本相等. 当V₀ > 9 ?/ps时, 液滴稳定态的β逐渐减小, 直到V₀增至14 ?/ps时, 弹跳离开固体表面, 此时β = 0.
图 8 不同初始速度的液滴铺展因子β随时间t的变化　(a) V₀ = 3—9 ?/ps; (b) V₀ = 11—15 ?/ps
Figure8. Time evolution of spreading factor for droplets with different velocities: (a) V₀ = 3?9 ?/ps; (b) V₀ = 11?15 ?/ps.

图9为不同V₀的液滴对应的最大铺展因子β_max, 两者近似线性关系, 拟合得到该线性方程为
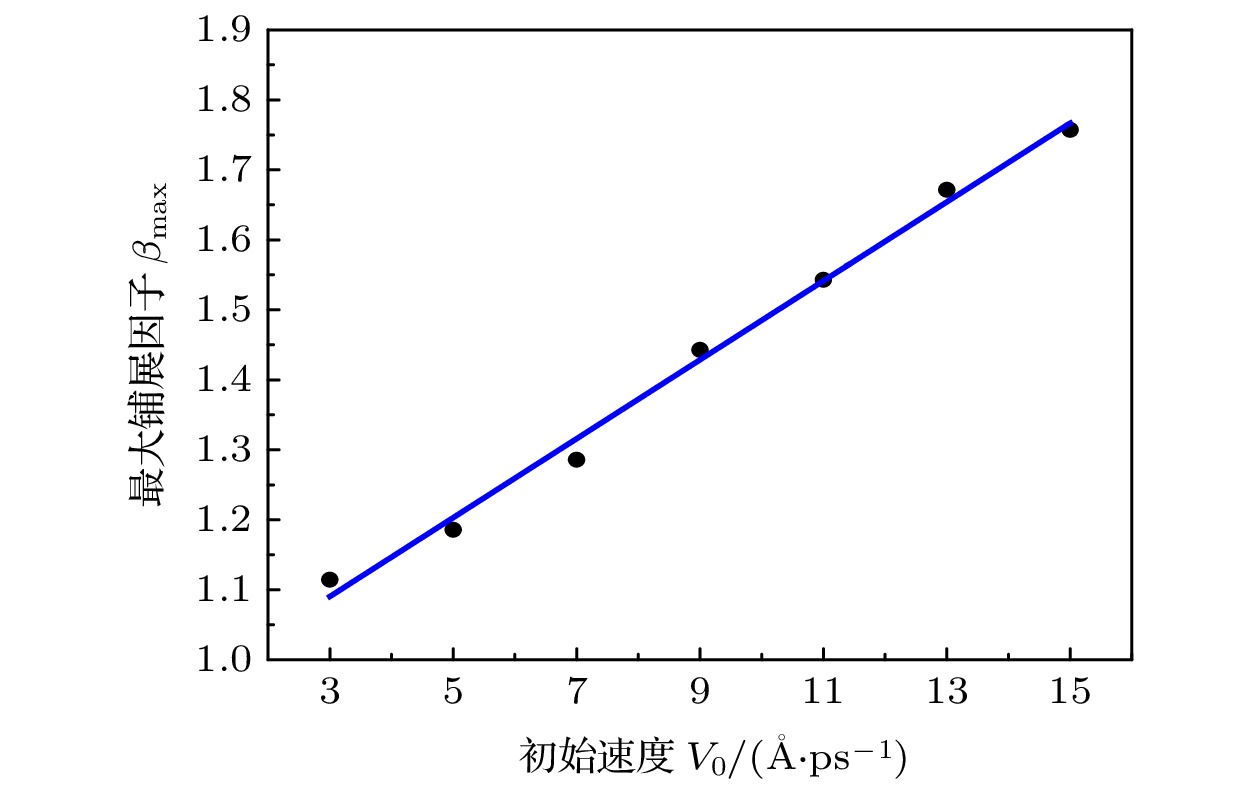图 9 不同初始速度液滴的最大铺展因子β_max
Figure9. The maximum spreading factor of droplets with different velocities.

${\beta _{{\rm{max}}}} = 0.056{V_0} + 0.921{\rm{ }}{\rm{.}}$

2 -->

4.4.方柱高度的影响

选定V₀为3 ?/ps的液滴, 改变方柱高度H, 探究其对液滴动态行为的影响. 设置方柱高度分别H₁ = 10.845 ?, H₂ = 14.460 ?, H₃ = 18.075 ?, H₄ = 21.690 ?和H₅ = 25.305 ?. 图10和表2展示了液滴撞击后的稳定状态及润湿模式. 当方柱高度为H₁和H₂时, 液滴完全充满方柱间隙, 呈现Wenzel态; 当方柱高度为H₃, H₄和H₅时, 液滴渗入方柱间隙的深度随着高度的增加而减小.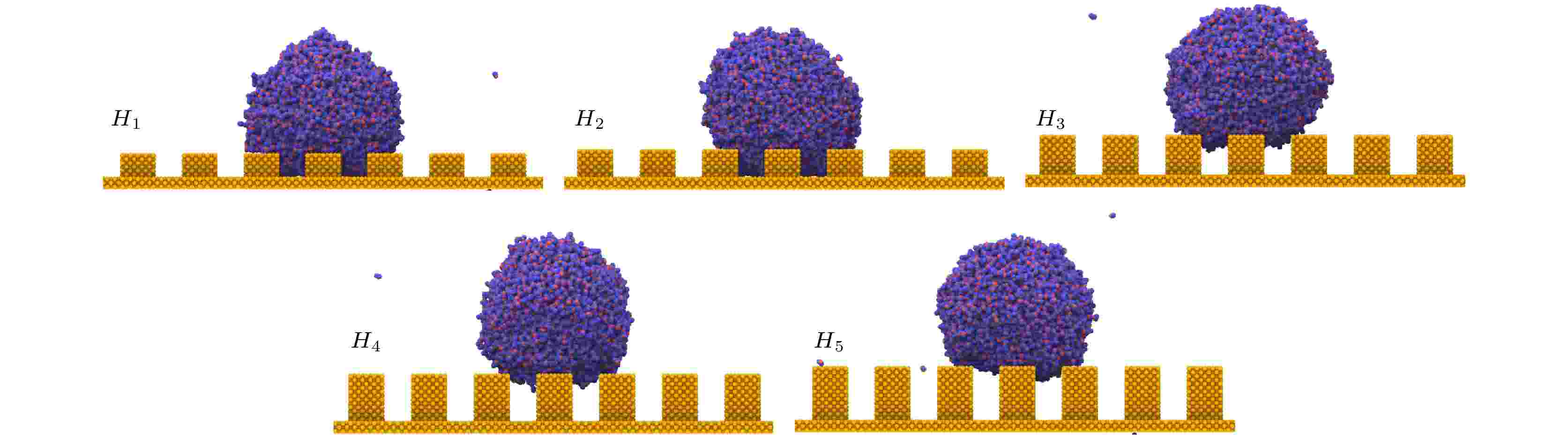
图 10 液滴撞击不同方柱高度固体表面的稳定状态
Figure10. Steady states of droplets impinging on solid surfaces with nanopillars of different height.

方柱 高度	H1	H2	H3	H4	H5
	10.845 ?	14.460 ?	18.075 ?	21.690 ?	25.305 ?
润湿 模式	Wenzel	Wenzel	Cassie	Cassie	Cassie

表2液滴撞击不同高度柱状表面后的稳定态润湿模式
Table2.Wetting patterns of steady state of droplets impinging on surfaces with different height nanopillars.

图11记录了方柱高度为H₅时, 不同时刻液滴底部的z向坐标. 在模拟过程中z_min = 20 ?. 据此, 可得到液滴渗入方柱间隙最大深度为8.920 ?, 与固体表面底层最大距离为16.385 ?, 大于LJ势的截断半径10 ?, 因此可以认为方柱高度为H₅的固体表面, 液滴的动态行为不受固体表面底层影响. 对方柱高度为H₁, H₂, H₃和H₄的表面, 假设液滴不受固体表面底层影响, 其在动态过程中与固体表面底层最大距离分别为: 1.925 ?, 5.540 ?, 9.155 ?和12.770 ?. 可见当方柱高度为H₁和H₂时, 液滴能够完全充满方柱间隙处于Wenzel态, 是因为液滴与固体表面底层的距离过近, 明显小于LJ势的截断半径, 此时固液间有着非常大的吸引力.
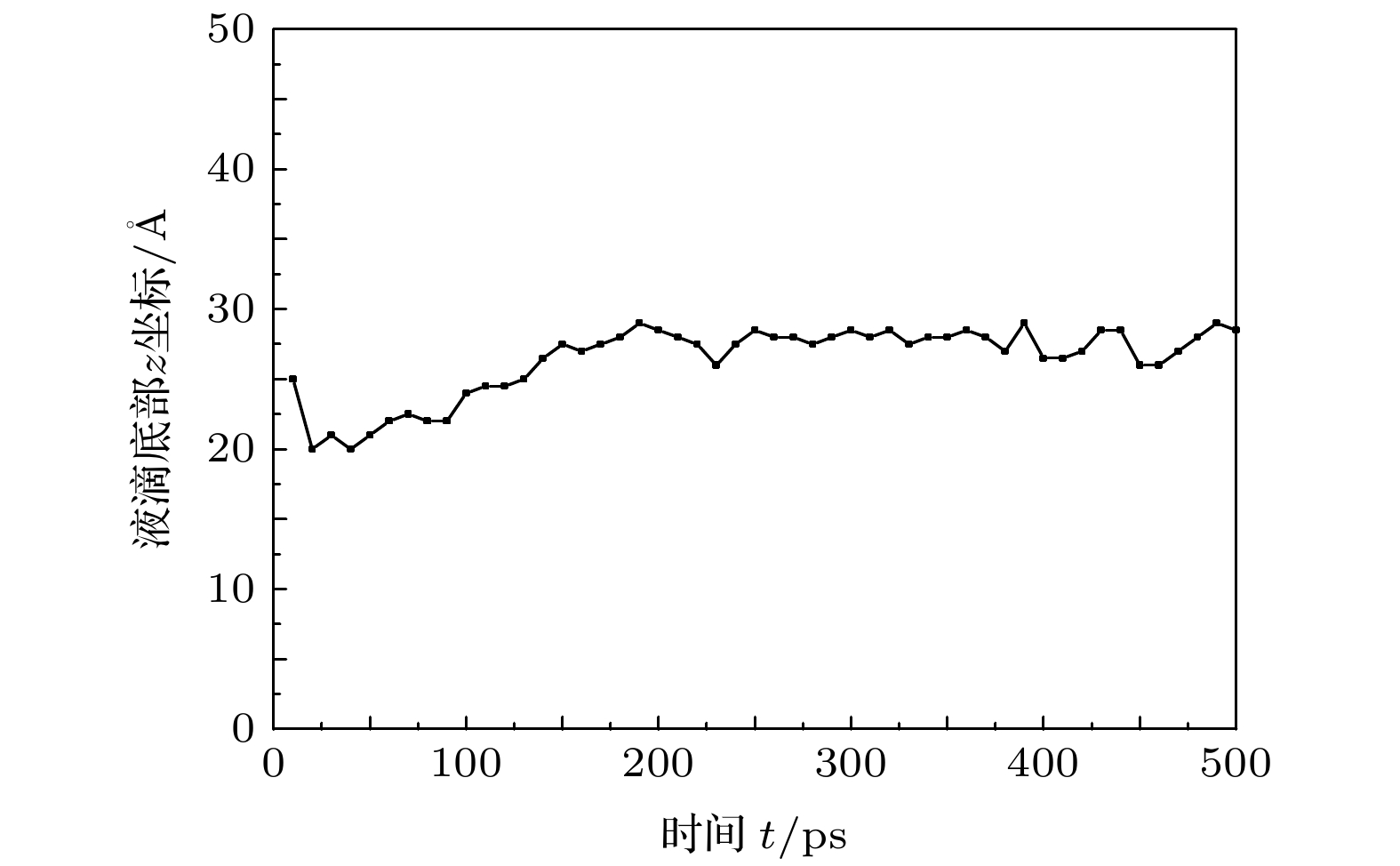图 11 不同时刻液滴底部z坐标
Figure11. Time evolution of z coordinates for the bottom of droplets.

图12展示了液滴撞击不同高度柱状固体表面时质心高度h的变化. 对于H₁和H₂, h在经历前期的下降后几乎保持水平且两者基本重合. 表明当液滴能够完全充满方柱间隙时, 方柱高度的变化对h没有影响. 但当方柱高度达到临界值18.075 ?时, 液滴最终呈现Cassie态, h有突然的增加. 当方柱高度H > 18.075 ?时, 对应液滴质心高度的增加量等于方柱高度的增加. 由图13可知, 方柱高度为H₄和H₅, 液滴达到稳态时β约为0.800, 小于其他三种情况, 表明随着H的增加, 液滴的铺展能力减小. 方柱高度的变化对β_max几乎没有影响且液滴在达到最大铺展状态前β基本一致. 因此, 方柱高度对铺展过程的影响主要作用在液滴的回缩阶段.
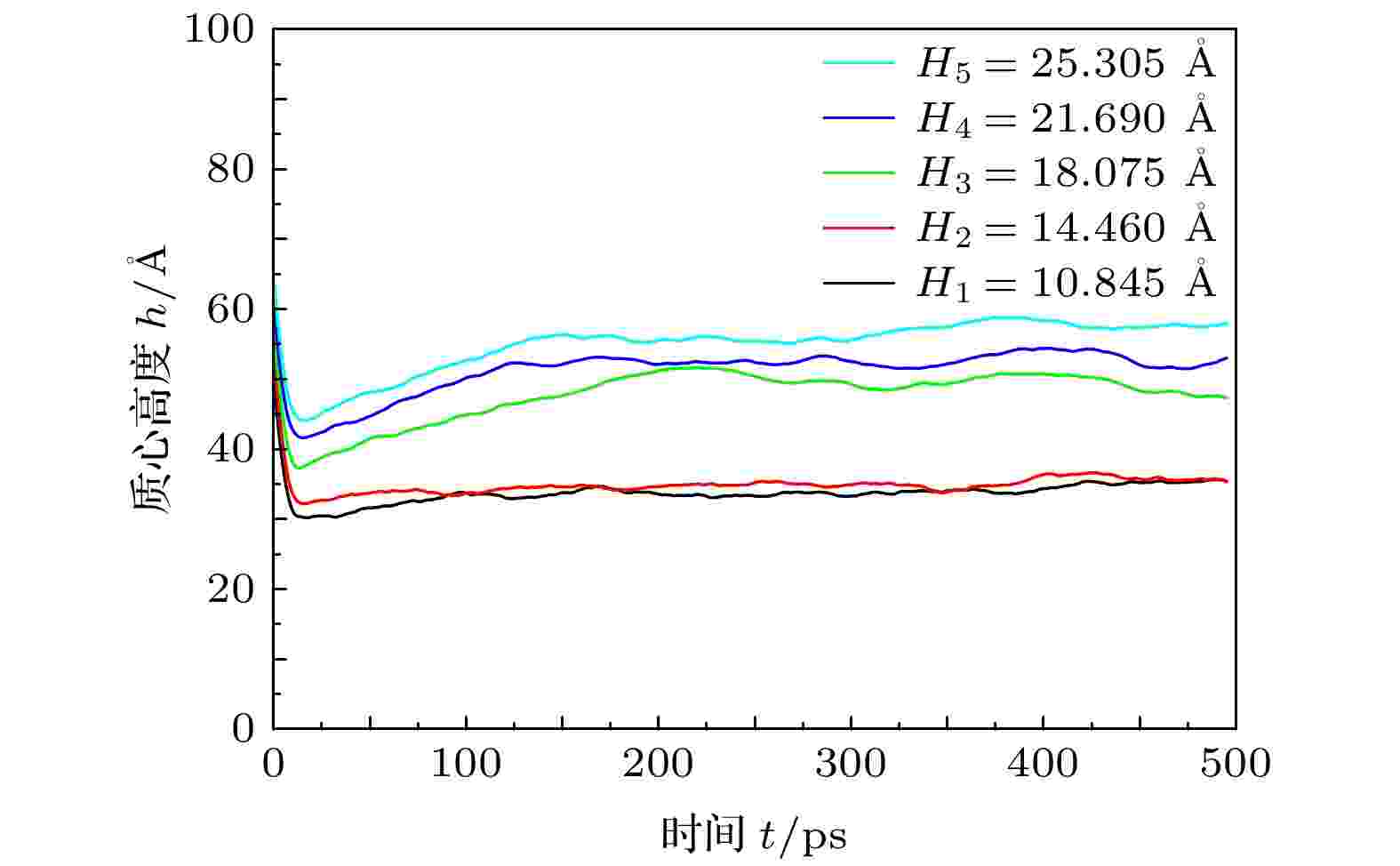图 12 不同方柱高度对液滴质心高度的影响
Figure12. Effects of nanopillars with different height on centroid height of droplets.

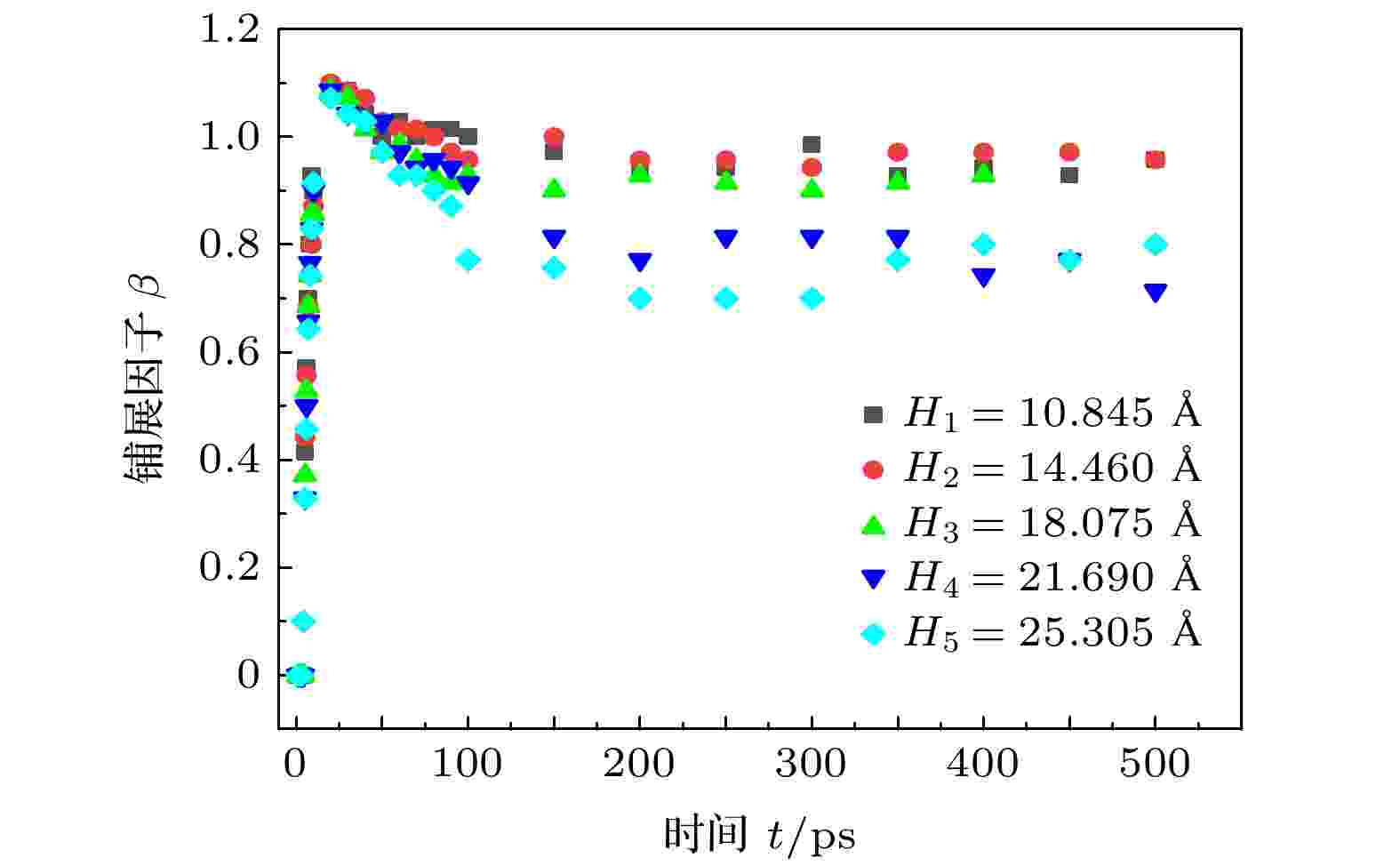图 13 方柱高度对铺展因子的影响
Figure13. Dependence of spreading factor on the height of nanopillars.

图14展示了不同高度的方柱对液滴稳定状态下铺展半径R的影响. 随着H的增加, 液滴稳定时R逐渐下降且下降程度逐渐减小, 表明H虽然对液滴的铺展过程有影响, 但影响逐渐减弱.
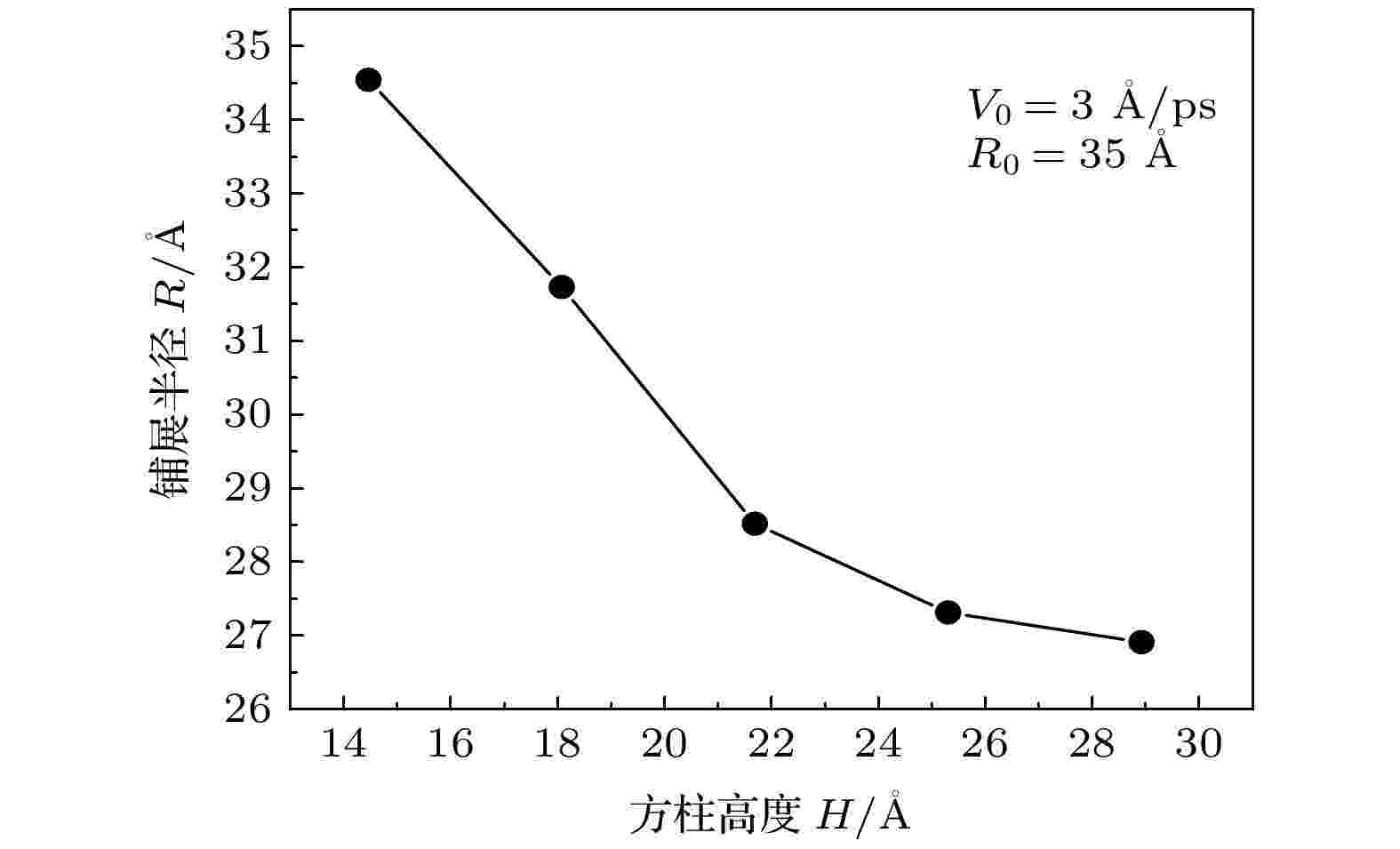图 14 方柱高度对铺展半径R的影响
Figure14. Dependence of spreading radius on the height of nanopillars.

2 -->

4.5.固体表面特征能的影响

固体的表面特征能${\varepsilon _{\rm{s}}}$是影响液滴撞击固体表面动态行为的重要因素. 为进一步探究其作用机理, 选择不同的${\varepsilon _{\rm{s}}}$进行分析, 其对应的固液间势能参数${\varepsilon _{{\rm{s \text- o}}}}$及液滴在该光滑固体表面的接触角如表3所列, ${\varepsilon _{{\rm{s\text- o}}}}$由(3)式得到.

${\varepsilon _{\rm{s}}}$/(kcal·mol–1)	${\varepsilon _{\rm{s}}}$/(kcal·mol–1)	接触角$ \theta $/$ (°) $
${\varepsilon _{{\rm{s1}}}} = 0.5{\varepsilon _{{\rm{Cu}}}} = 0.119$	0.139	125.9
${\varepsilon _{{\rm{s2}}}} = 1.5{\varepsilon _{{\rm{Cu}}}} = 0.357$	0.241	97.1
${\varepsilon _{{\rm{s3}}}} = 2.0{\varepsilon _{{\rm{Cu}}}} = 0.476$	0.278	80
${\varepsilon _{{\rm{s4}}}} = 3.0{\varepsilon _{{\rm{Cu}}}} = 0.714$	0.341	63
${\varepsilon _{{\rm{s5}}}} = 4.0{\varepsilon _{{\rm{Cu}}}} = 0.952$	0.394	45
${\varepsilon _{{\rm{s6}}}} = 5.0{\varepsilon _{{\rm{Cu}}}} = 1.190$	0.440	22

表3不同${\varepsilon _{\rm{s}}}$固体表面对应的${\varepsilon _{{\rm{s \text- o}}}}$及液滴接触角$ \theta $
Table3.Corresponding ${\varepsilon _{{\rm{s \text- o}}}}$ and contact angles of droplets for solid surfaces with different ${\varepsilon _{\rm{s}}}$.

由表3可知: 随着${\varepsilon _{\rm{s}}}$的增大, 接触角逐渐减小, 表明固体表面的润湿性能增加, 表面更有利于液滴铺展. 在此基础上进一步分析${\varepsilon _{\rm{s}}}$对液滴撞击柱状固体表面动态行为的影响. 由图15可知, 当${\varepsilon _{\rm{s}}} = {\varepsilon _{{\rm{s1}}}}$时, 液滴的质心高度h先快速减小后增大, 最后仅略低于初始高度, 说明液滴先铺展、进入方柱, 然后又回缩、退出方柱. 当${\varepsilon _{\rm{s}}}$增加到${\varepsilon _{{\rm{s2}}}}$和${\varepsilon _{{\rm{s3}}}}$时, 液滴达到最大铺展状态后h稍有增大, 之后h减小, 直至达到稳定状态. 表明液滴铺展后只有少量的回缩, 这是由于${\varepsilon _{\rm{s}}}$较大, 固体表面对液滴的吸引力较强, 致使液滴表面能很快被耗尽. 当${\varepsilon _{\rm{s}}}$继续增大到${\varepsilon _{{\rm{s4}}}}$, ${\varepsilon _{{\rm{s5}}}}$和${\varepsilon _{{\rm{s6}}}}$时, h持续减小, 没有增高的趋势, 表明此时液滴的表面张力不足以克服固液间相互作用, 液滴铺展后不回缩.
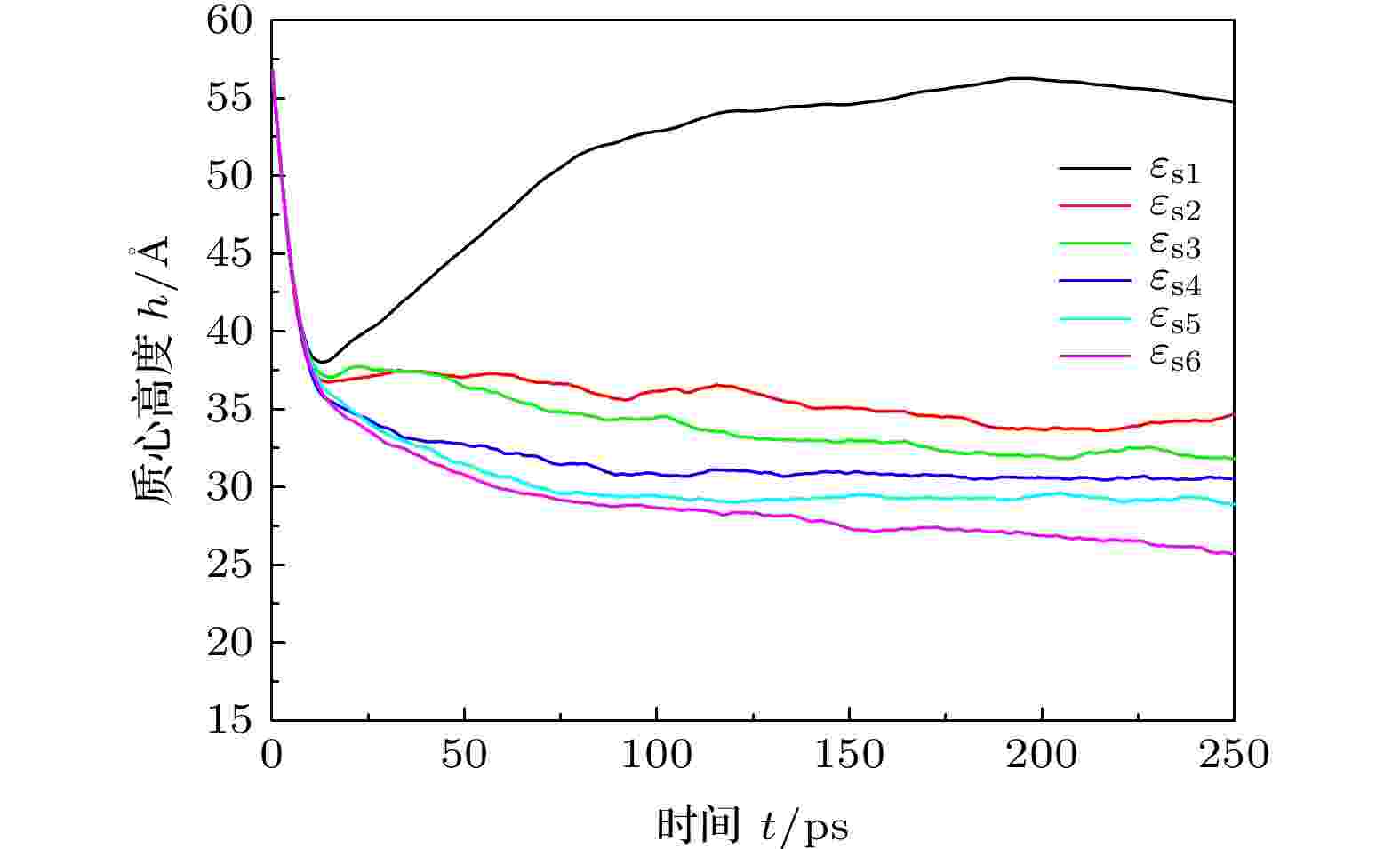图 15 液滴撞击不同特征能柱状固体表面的质心高度
Figure15. Centroid height of droplets impinging on surfaces with different characteristic energy.

图16展示了铺展因子β的变化. 当${\varepsilon _{\rm{s}}} \!\leqslant\! {\varepsilon _{{\rm{s3}}}}$时, β 在达到最大值后有减小的过程, 但该过程经历的时间随着${\varepsilon _{\rm{s}}}$的增加逐渐减小, 与上述结论相互验证.
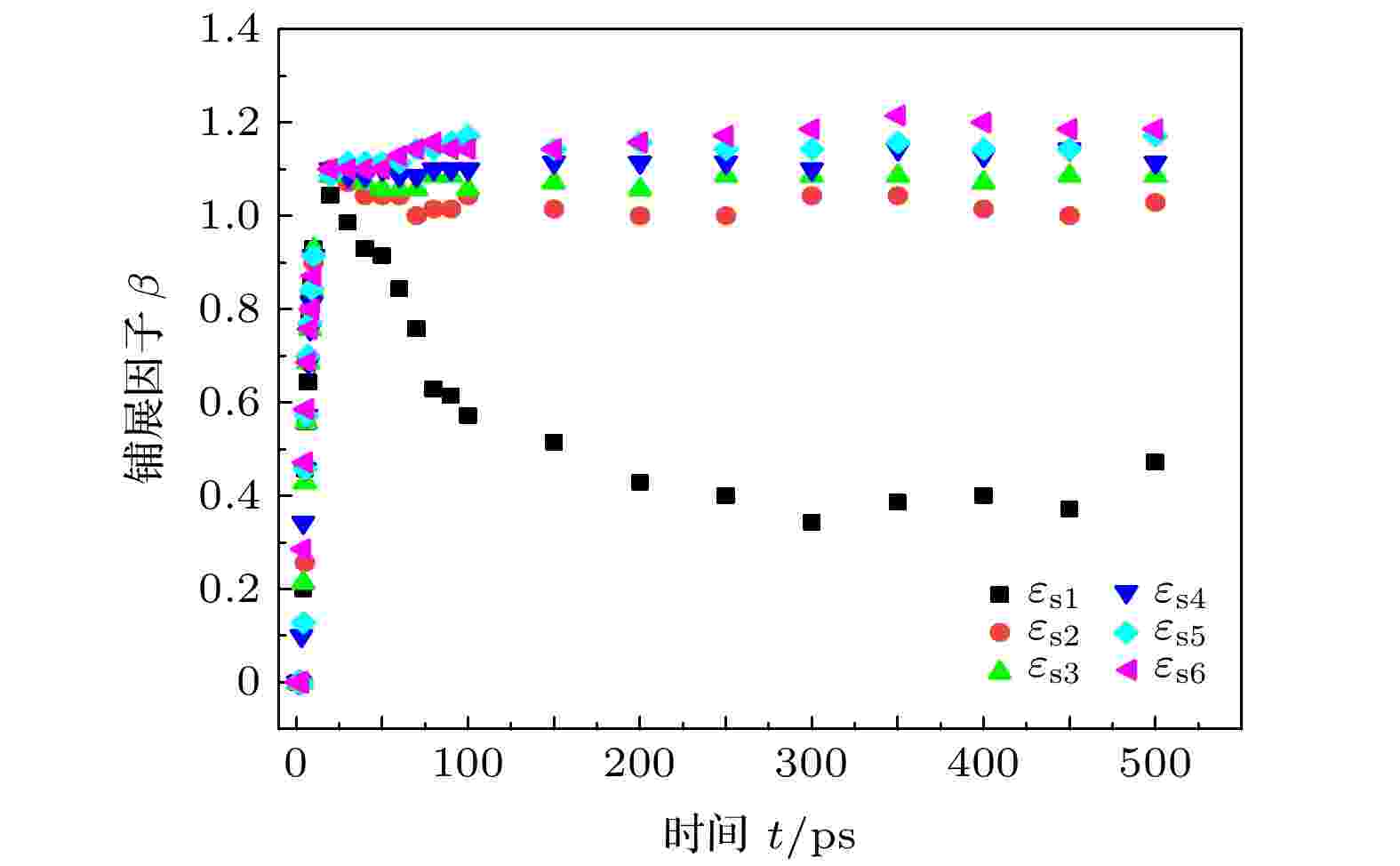图 16 液滴撞击具有不同特征能方柱表面时的铺展因子
Figure16. Time evolution of spreading factor of droplets impinging on surfaces with different characteristic energy.

不同于质心高度随${\varepsilon _{\rm{s}}}$的改变有着明显的变化, 当${\varepsilon _{\rm{s}}} \geqslant {\varepsilon _{{\rm{s2}}}}$时β间的差异较小. 特别地, 对于${\varepsilon _{{\rm{s5}}}}$和${\varepsilon _{{\rm{s6}}}}$, 液滴的质心高度是显著持续下降的, 但铺展因子仅有微弱的增大趋势. 这是因为铺展区域的增大, 液滴底部有着较大的铺展面积, 但液滴底部以上的部分由于尚未铺展, 其横截面积随着远离液滴底部而逐渐减小. 因此, 只有液滴质心高度有显著下降的情况下, 才有足够的水分子在动能和固液相互作用的驱动下完全覆盖甚至超越原有的铺展区域从而继续向外铺展, 故铺展因子β受${\varepsilon _{\rm{s}}}$的影响较小.

采用分子动力学的方法模拟纳米水液滴撞击柱状铜固体表面的动态行为. 探究了初始速度V₀、方柱高度H及表面特征能${\varepsilon _{\rm{s}}}$等对纳米液滴动态行为的影响, 得出下述结论:
1) 随着液滴撞击的初始速度增加, 液滴的稳定状态先由Cassie态转变为Wenzel态, 然后再次呈现Cassie态, 并得到液滴发生弹跳离开固体表面的临界初始速度V₀ = 13 ?/ps;
2) 首次发现液滴最大铺展时间t_max与初始速度V₀关系曲线中拐点的存在, 并提出不同速度区域中t_max与V₀的关系式;
3) 方柱高度对液滴动态过程的影响主要在液滴的回缩阶段, 但随着方柱高度的进一步增加影响逐渐减小, 方柱高度的增加有助于液滴的稳定态由Wenzel向Cassie态转变;
4) 表面特征能${\varepsilon _{\rm{s}}}$的增大有助于液滴铺展, 当表面特征能${\varepsilon _{\rm{s}}}$增大至0.714 kcal/mol时, 液滴撞击柱状固体表面后不会经历回缩阶段, 而是持续铺展直至达到稳定状态.