全文HTML
--> --> -->在元胞自动机人员疏散模型研究层面, 国外****研究起步较早并在不同疏散场景下开展了广泛的元胞自动机拓展模型研究. Miyagawa和Ichinose[1]建立了人群疏散中的多网格元胞自动机模型, 研究了人员横向移动和转弯行为对疏散过程的影响. Ji等[2]通过将元胞形状由矩形改成三角形, 使得模型中行人的运动方向由8个变为14个. Maniccam[3]将元胞形状由矩形改成六边形, 研究了元胞内临界密度的变化. Leng等[4]建立了一种基于正六边形的场域元胞模型, 研究了走廊中的行人动态特征. Jooyoung等[5]通过拓展元胞自动机模型, 模拟了不同比例的残障人群对通道疏散的影响. Hanisch等[6]利用交通研究中的元胞传输模型对公共场所行人流进行研究, Crociani等[7]提出了一种基于元胞自动机的多尺度建模方法, 用于模拟纽约市史坦顿岛渡轮运输场景. L?mmel和Fl?tter?d[8]建立了一种基于事件动态发展的元胞自动机模型, 模拟了单、双向行人流疏散场景. Kaji和Inohara [9]结合多网格元胞自动机模型和静态场模型, 研究了层流中流体的流动特征. Shi等[10]提出了一种介观疏散模型, 并开发了一套新的静态场算法用于介观尺度下人员疏散建模. 国内****主要聚焦于建筑内部微观疏散场景下的元胞自动机疏散模型研究. 胡俊等[11,12]建立了三维元胞自动机模型来研究阶梯上的行人流特征. 张磊等[13]利用元胞自动机模型对行人拥堵区域的拥挤致伤机理进行了研究. 任刚等[14]建立考虑行人行走倾向性特征的元胞自动机模型并利用复杂网络理论对行人流特征进行分析. 胥旋等[15]通过引入行人感知范围参数建立了考虑绕行行为的元胞自动机模型. 金泽人等[16]通过考虑行人基于场景的移动方向和期望速度规则拓展了场强模型. 陆卓谟和秦文虎[17]通过考虑个体的反应时间和群组运动方式等因素拓展了元胞自动机模型. 张维等[18]通过考虑人群拥挤受力作用机制, 利用改进的多格子元胞自动机模型和具有特殊赋值规律的静态场模型对出口处拥挤人群的动力学特征进行模拟. Cao等[19]建立了无能见度环境下多网格人员疏散模型, 研究了出口宽度、出口数量和初始密度对疏散时间的影响. 陈雍容[20]结合元胞自动机模型与多智能体技术建立复合疏散模型, 实现了介观疏散引导模型和微观自主疏散模型的耦合, 杨兆升等[21]将交叉口控制参数引入到基于元胞传输模型的应急疏散仿真模型中, 并应用反流策略, 对城市疏散场景下的交通分配进行优化.
总结国内外研究现状可知, 现有的元胞自动机疏散模型基本上都是微观层面的精细网格模型, 主要应用于二维平面场景, 疏散空间也多为小范围的建筑空间或局部区域, 而可应用于大范围城市区域疏散模拟的元胞自动机模型尚不成熟, 这主要是因为微观元胞自动机模型的高精度特点使其在向大尺度空间拓展时计算效率受到极大制约. 因此, 为探索元胞自动机疏散模型在大尺度空间中的适用性, 本文拟通过对疏散区域的路网道路划分微观元胞, 对特定元胞加载和卸载人员流量实现疏散生成和完成, 对道路元胞上的宏观状态量迁移实现疏散过程, 提出一种基于介观元胞自动机的城市区域应急疏散模拟方法, 以期为城市大尺度应急疏散方案论证提供科学支撑.
2.1.微观元胞自动机疏散模型
目前传统的元胞自动机疏散模型多为微观网格疏散模型, 是一类按照预定规则改变系统状态的时空离散模型, 包括有偏无后退随机行走模型[22]、场域模型[23]、多作用力模型[24]、多格子模型[25]和k近邻模型[26]等, 这些模型的核心思想都是通过个体在元胞上的迁移来实现疏散人员空间状态的改变, 相应地, 模型的关键在于计算元胞之间的迁移概率. 以经典的场域(FF)模型为例, 它通过“静态场”考虑系统结构或建筑空间构形对疏散者的影响, 通过“动态场”考虑系统中人群移动的引导效应, 然后根据(1)式计算每个元胞上的疏散个体在“静态场”
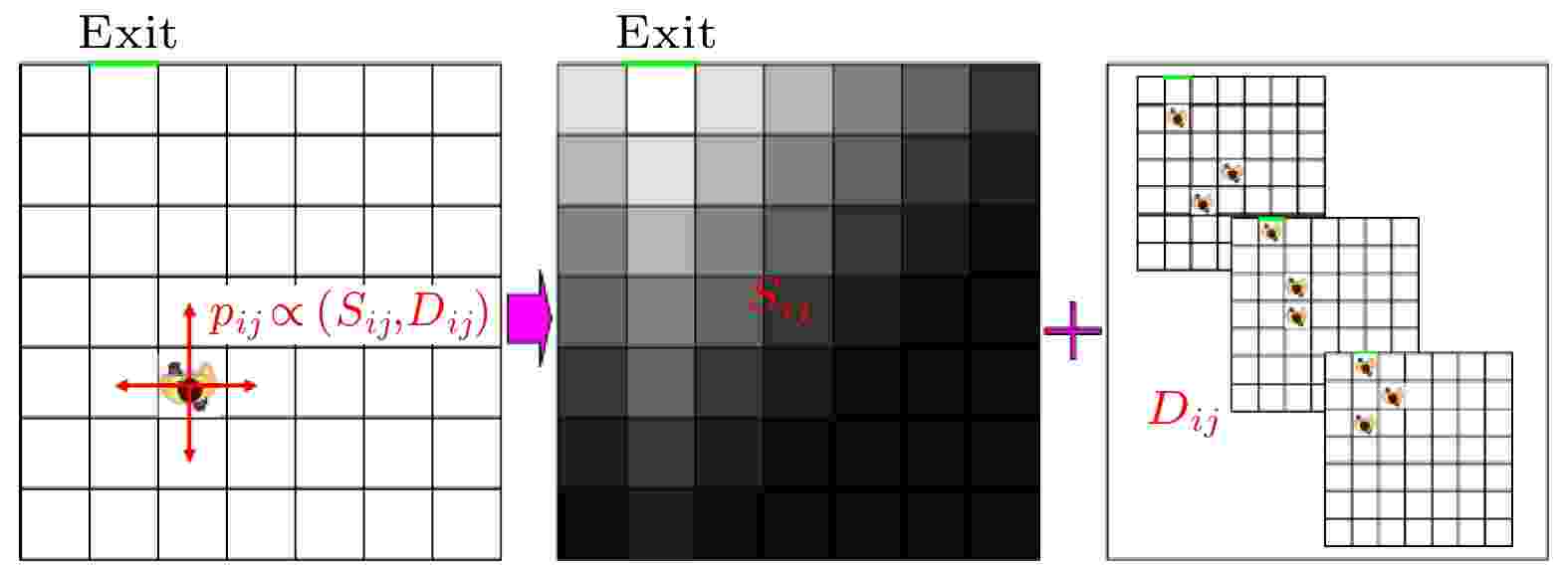图 1 场域模型中的运动过程示意图Figure1. Sketch map of the movement process in FF model.
由图1可以看出, 以场域模型为代表的元胞自动机疏散模型是典型的微观尺度模型, 随着元胞规模的增大, 模拟运算的效率将大幅下降, 因而难以适用于大尺度空间的城市区域性应急疏散模拟研究.
2
2.2.介观元胞自动机疏散模型
为实现元胞自动机技术在城市区域性应急疏散模拟中的应用, 可以维持经典元胞自动机疏散模型通过元胞间的疏散者迁移实现系统状态更新的核心思想不变, 但是在模型尺度上必须由微观转换为介观. 所谓介观, 包括两个层面: 一是在空间元胞划分上, 放弃平面网格划分的方式, 采用道路元胞切分方式, 只对疏散路网进行空间离散, 其他区域的人员向道路的转移过程通过疏散路网中特定元胞的“源加载”形式体现, 如图2所示; 二是在疏散者的元胞迁移上, 放弃个体依转移概率实现疏散运动过程的方式, 直接通过元胞对应宏观状态量的更新实现疏散群体的流动过程, 宏观状态量包括元胞上的人群数量、人群密度、疏散速度等, 如图3所示.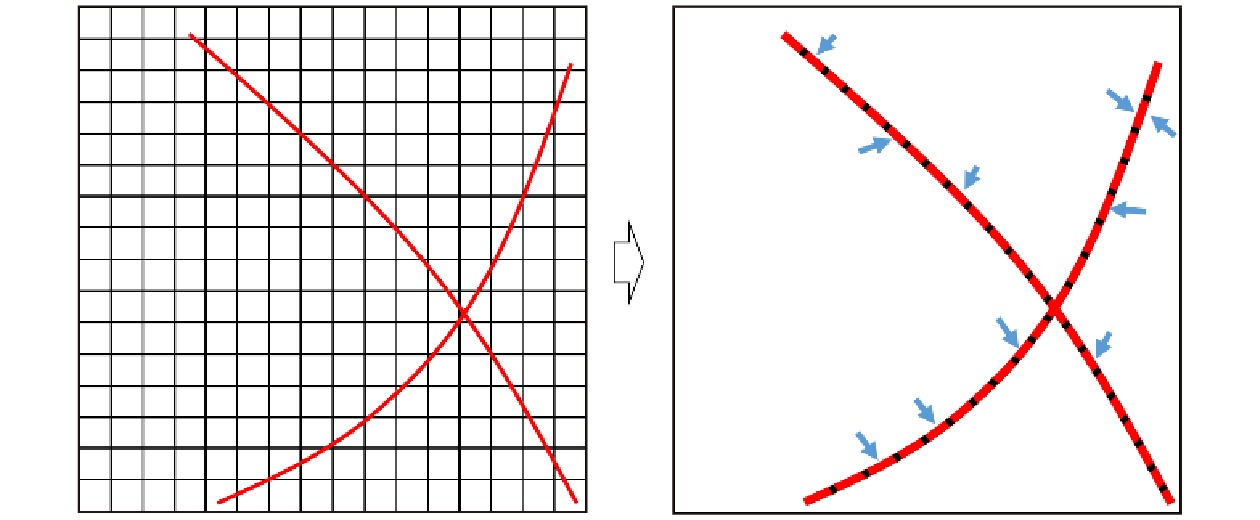
图 2 平面网格划分向道路元胞切分转变示意图Figure2. Change from plane mesh to road cell segmentation.
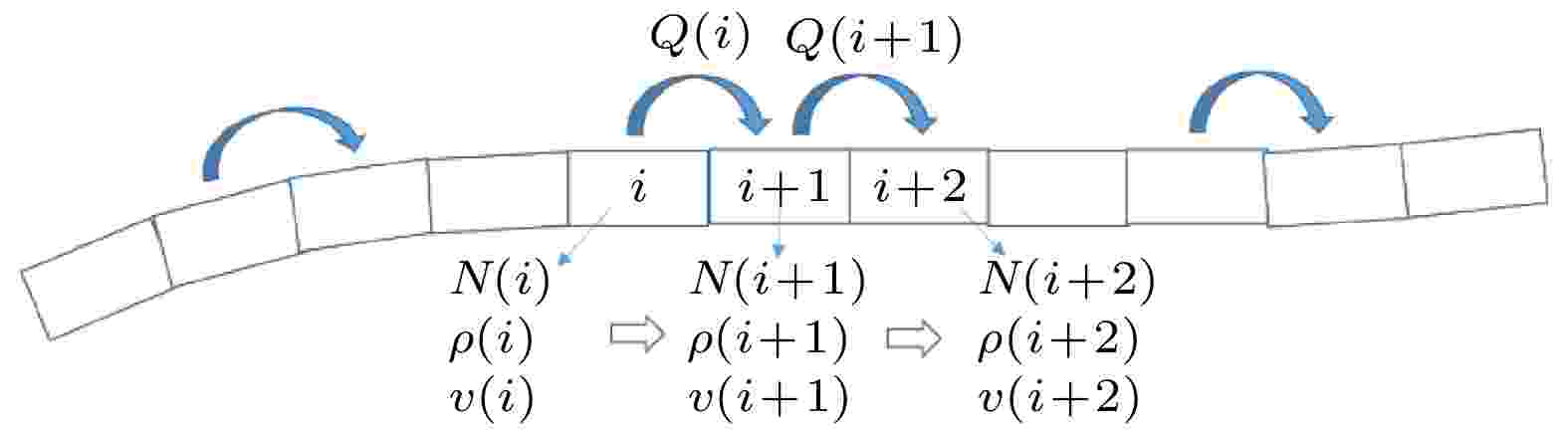图 3 疏散道路元胞间宏观状态量更新示意图Figure3. The update of macro-state variable between road cells.
根照上述思想, 构建城市区域应急疏散的介观元胞自动机模型并进行模拟研究的基本程序是:
第一步, 确定待研究的城市区域边界范围, 提取该边界范围内的疏散路网;
第二步, 对疏散道路进行元胞切分, 定位“源加载”元胞和疏散“出口”元胞;
第三步, 计算每个道路元胞和每个出口元胞之间的距离, 按照就近出口选择原则, 确定每个道路元胞疏散指向的出口元胞;
第四步, 根据流量守恒、容量限制和疏散交通流规律, 建立疏散道路元胞宏观状态量更新规则;
第五步, 设定模拟条件, 进行路网元胞状态值计算和更新, 直至疏散路网中人数降低至临界值, 疏散结束.
结合图4, 介观元胞自动机疏散模型中, 道路元胞形态本质只有两种: 一种是图4(a)所示的无外部人员加载的普通元胞; 另一种是图4(b)所示的有外部“源加载”的特定元胞. 无论是哪种元胞形态, 所遵循的规则是相似的, 并且都必须满足流量守恒、容量限制和疏散交通流规律.
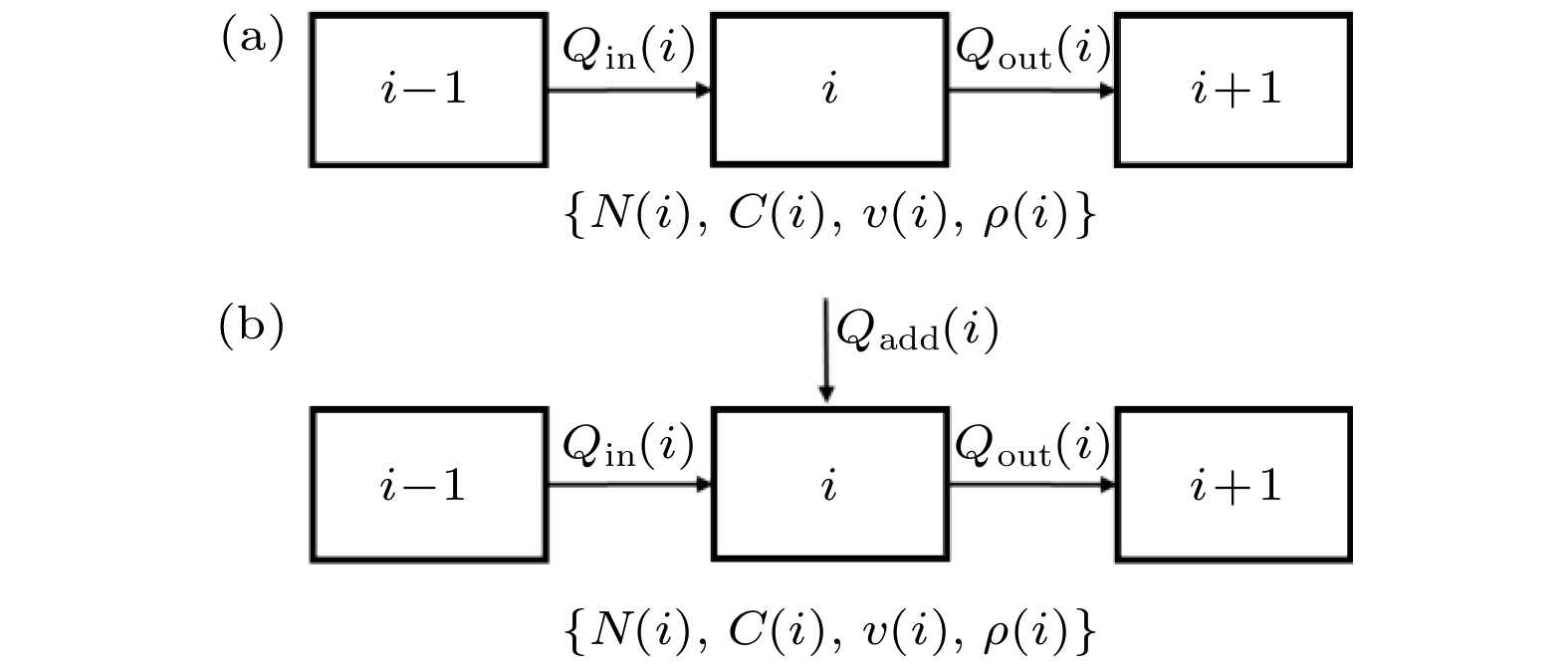图 4 疏散道路元胞间宏观状态量更新规则示意图 (a) 无加载源; (b) 有加载源Figure4. The update rule of macro-state variable between the evacuation road cells: (a) Without load source; (b) with load source.
在流量守恒方面, 元胞i中的人员数量N(i)更新需满足:
基于以上三条基本规则, 建立无加载源元胞宏观状态量更新方程如下:
3.1.城市区域选取
考虑到高校校园兼具空间范围广和人群聚集程度高的特点, 适合开展较大尺度的区域性疏散模拟研究, 选取位于武汉市洪山区街道口附近的某高校校园区域, 如图5所示, 对前文提出的介观元胞自动机疏散模型开展区域应急疏散模拟可行性研究. 该校园区域占地约675亩(450000 m2), 区域内有教学楼2栋、图书馆1个、学生宿舍楼10栋、教师宿舍楼39栋, 根据调查统计, 所有建筑满载时约容纳16838人, 而实际教学工作日时校区内人数在8200人左右. 此外, 该区域路网由8条东西道路(编号1—8)和7条南北走向道路(编号9—15)构成, 路网通往边界外部的出口有4个(星标).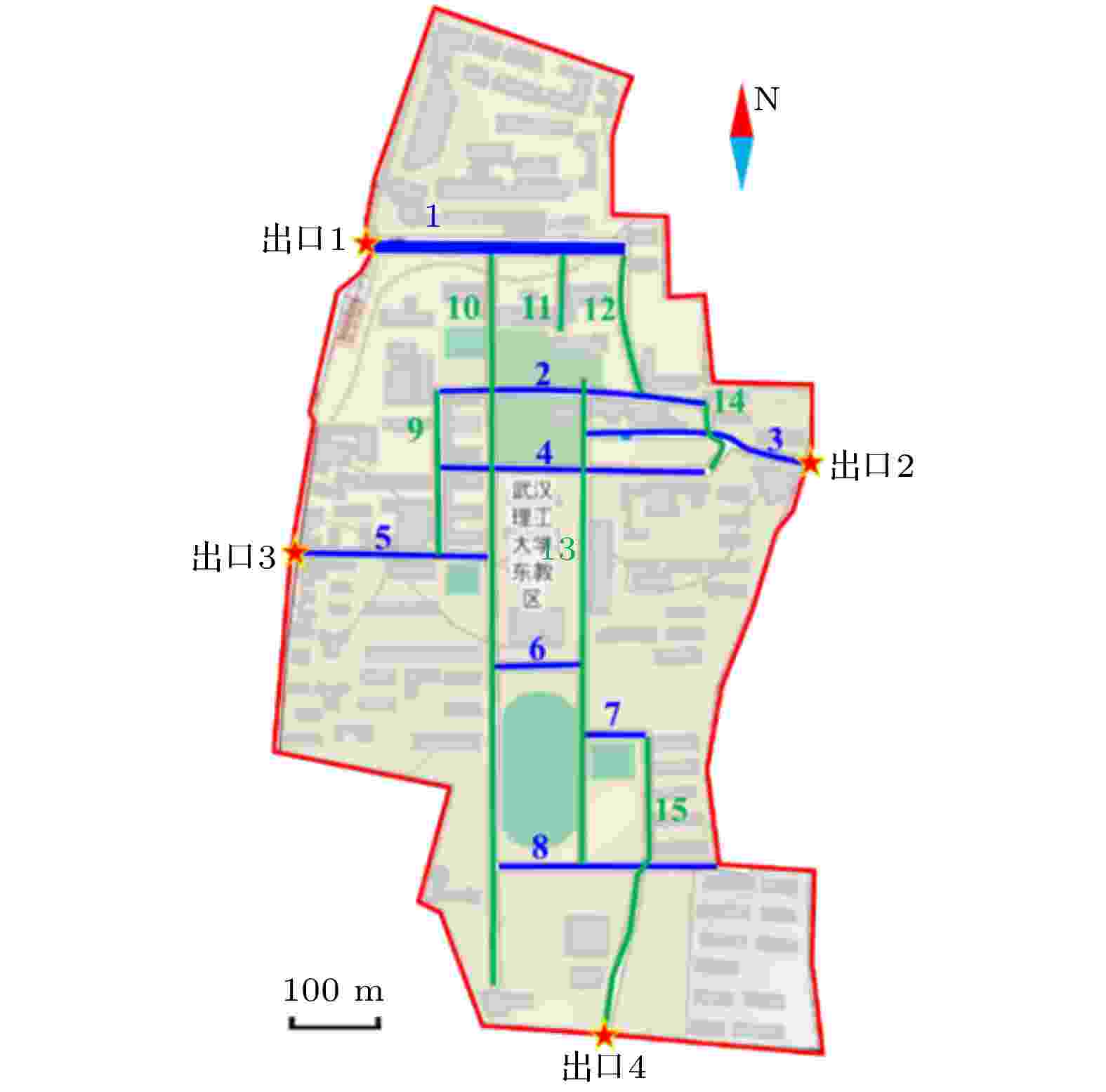
图 5 研究区域的空间范围及边界Figure5. The spatial scope and boundary of the study area.
2
3.2.路网元胞切分
沿道路网中的道路方向, 以10 m长度和6 m宽度为基本元胞尺寸, 将路网道路切分为元胞单元, 并结合教学楼、学生宿舍、图书馆和师生宿舍的位置, 选取与这些人群密集场所较近的元胞作为疏散“源加载”元胞(箭头所指元胞), 选取边界出口元胞作为疏散“出口”元胞(星标处元胞), 如图6所示.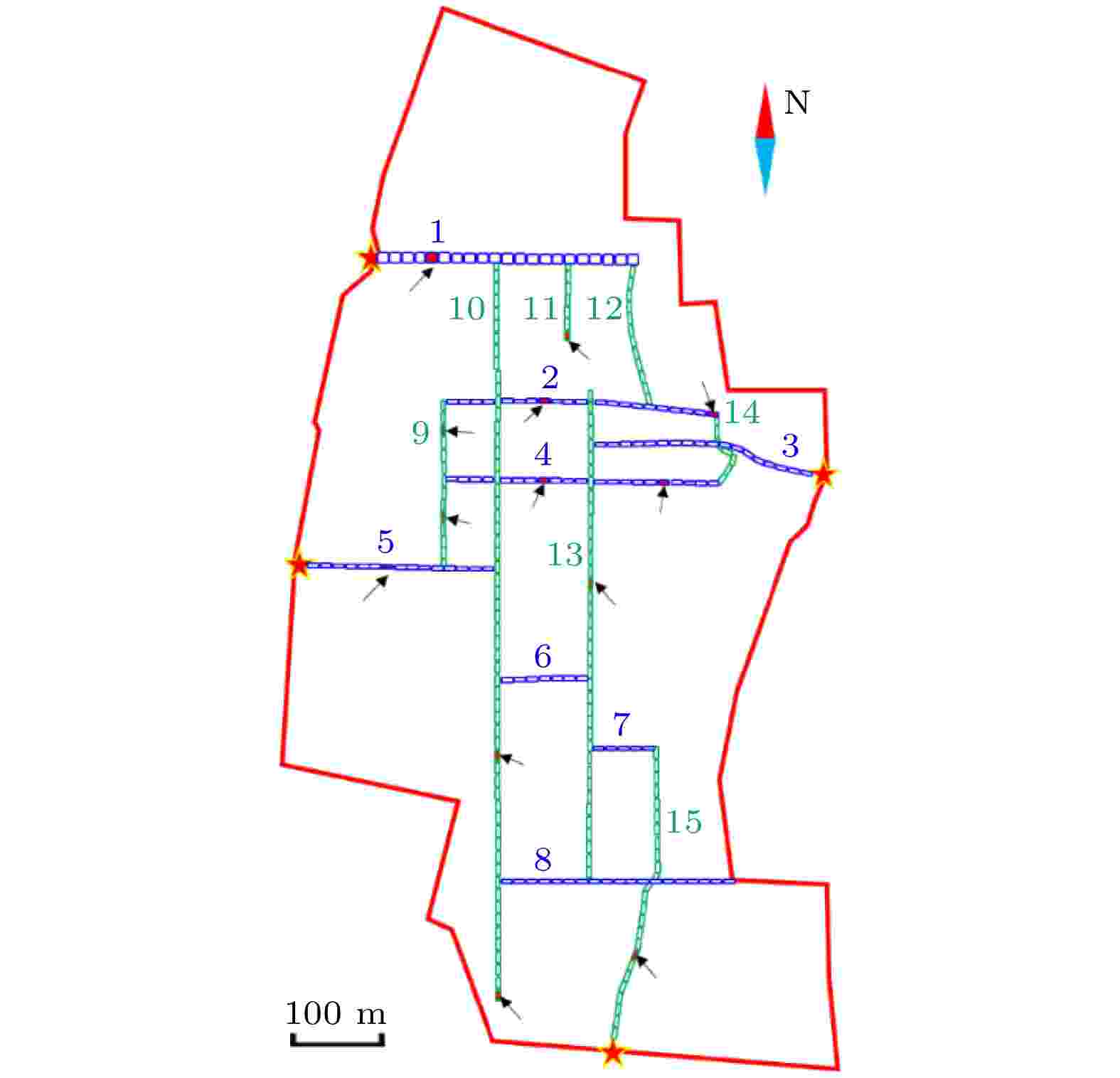
图 6 路网的元胞切分示意图Figure6. The road cell segmentation of the road network.
进一步, 按道路编号, 对每条道路从一端(西端或北端)开始向另一端(东端或南端)依次进行元胞编码, 编码后的元胞用Celli, j表示, i表示道路编号, j表示元胞在第i条道路中的次序, 本文研究区域的道路元胞编码统计信息如表1所列.
| 道路 编号 | 长/m | 宽/m | 元胞 数量 | “源加载”元胞 | “出口”元胞 |
| 1 | 280 | 12 | 28 | Cell1,8 | Cell1,1 |
| 2 | 290 | 6 | 29 | Cell2,9, Cell2,29 | — |
| 3 | 230 | 6 | 23 | — | Cell3,23 |
| 4 | 290 | 6 | 29 | Cell4,9, Cell4,17 | — |
| 5 | 200 | 6 | 20 | Cell5,9 | Cell5,1 |
| 6 | 90 | 6 | 9 | — | — |
| 7 | 68 | 6 | 7 | — | — |
| 8 | 250 | 6 | 25 | — | — |
| 9 | 180 | 6 | 18 | Cell9,5, Cell9,13 | — |
| 10 | 795 | 6 | 80 | Cell10,59, Cell10,80 | — |
| 11 | 90 | 6 | 9 | Cell11,9 | — |
| 12 | 148 | 6 | 15 | — | — |
| 13 | 530 | 6 | 53 | Cell13,21 | — |
| 14 | 70 | 6 | 7 | — | — |
| 15 | 326 | 6 | 33 | Cell15,22 | Cell15,33 |
表1区域道路元胞编码统计信息
Table1.Statistical information of regional road cellular coding.
2
3.3.疏散子网划分
将四个出口分别标记为出口1、出口2、出口3和出口4, 通过计算每个道路元胞与4个“出口”元胞间的距离, 以距离最近的出口作为该元胞疏散的目标出口, 确定4个出口覆盖的道路元胞范围, 如图7所示.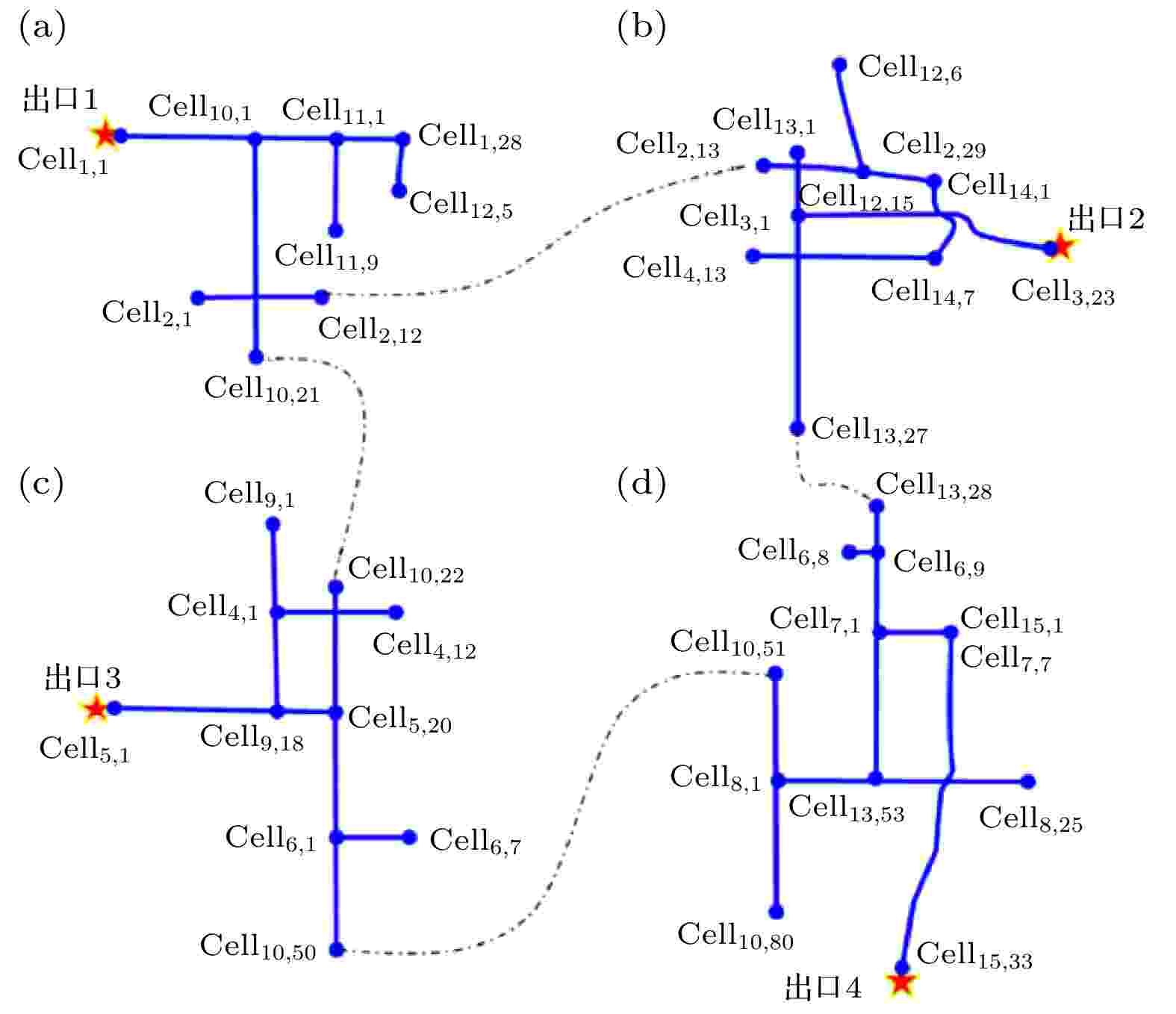
图 7 各出口覆盖疏散道路范围示意图Figure7. Evacuation range of the roads covered by each exit.
4.1.情景与参数设置
模拟情景为发生重大灾害事故时, 须迅速将校园内的人口转移疏散至安全区域, 假设疏散总需求为8200 人且疏散需求分布于13个“源加载”元胞附近的教学楼、图书馆和宿舍建筑中, 所有人员同时接受到疏散动员指令, 并通过步行方式从“源加载”元胞进入疏散路网, 模型中涉及的参数值如下表2所列.| 参数 | 含义 | 值 |
| l | 道路元胞长度 | 10 m |
| w | 道路元胞宽度 | 6 m |
| vf | 自由疏散速度 | 1.5 m/s |
| $\Delta t$ | 计算时间间隔 | 1 s |
| ρm | 拥塞临界密度 | 5 per/m2 |
表2模型参数
Table2.Model parameters.
根据实际调查确定各“源加载”元胞的加载人数, 得出各元胞实际加载人数见表3, 并依据图7的疏散子网划分, 得出各出口在疏散过程中的疏散总人数, 见表4, 考虑到人员从楼栋疏散时的瓶颈效应, 将源加载元胞的加载概率设置为梯形概率密度分布见图8, 每个“源加载”元胞在每个时间步内的加载人数为该时间步加载概率与该“源加载”元胞加载总人数之积, 各“源加载”元胞从开始加载到加载结束总时间为240个时间步, 在模拟开始后, 各“源加载”元胞开始进行人员加载, 并在第240时间步结束加载, 加载后的行人会通过道路运动到“出口”元胞, 离开校园, 当模拟中剩余人数低于0.5 人时, 判定为所有人员均疏散出校园, 疏散结束.
| “源加载” 元胞 | 加载总 人数/人 | “源加载” 元胞 | 加载总 人数/人 | |
| Cell1, 8 | 500 | Cell2, 9 | 500 | |
| Cell2, 29 | 500 | Cell4, 9 | 700 | |
| Cell4, 17 | 500 | Cell5, 9 | 900 | |
| Cell9, 5 | 800 | Cell9, 13 | 800 | |
| Cell10, 59 | 600 | Cell10, 80 | 600 | |
| Cell11, 9 | 600 | Cell13, 21 | 700 | |
| Cell15, 22 | 500 |
表3各“源加载”元胞加载人数
Table3.The number of pedestrians loaded by each ‘source loading’ cell.
| 出口 | 疏散总人数/人 |
| 出口1 | 1600 |
| 出口2 | 1700 |
| 出口3 | 3200 |
| 出口4 | 1700 |
| 总计 | 8200 |
表4各出口疏散人数
Table4.Evacuation number at each exit.
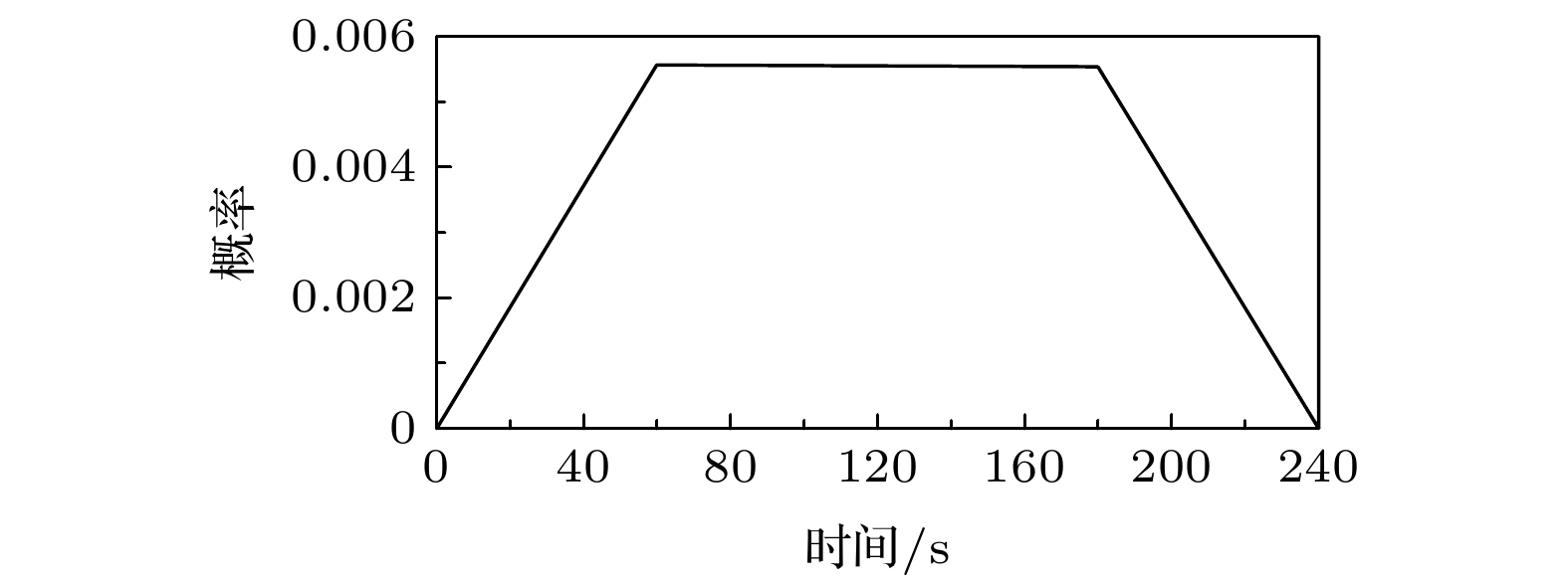图 8 “源加载”元胞加载概率密度分布图Figure8. Probability density distribution figure of “source loading”cell.
2
4.2.结果分析与讨论
依据上文给出的元胞加载数据和状态更新规则, 利用介观元胞自动机模型对该校区进行大规模疏散模拟.根据模拟结果, 绘制出各出口处疏散人数及总疏散人数随时间的变化关系情况如图9所示, 从图9中可以看出, 在40 s之后, 曲线开始呈现上升的趋势, 表示在疏散开始40 s后, 开始有行人从“源加载”元胞运动到“出口”元胞撤离出校园, 疏散人数峰值出现在250 至400 s时间段内, 观察各出口疏散人数随时间的变化关系曲线可以发现出口3和出口4的疏散人数峰值对应的时间点晚于出口1和出口2的疏散人数峰值对应的时间点, 这是由于出口3承载着较大的疏散压力, 而出口4与该疏散子网内加载元胞的距离较远, 总体上看, 该校区的疏散人数呈现先上升, 再稳定, 后下降的情况.
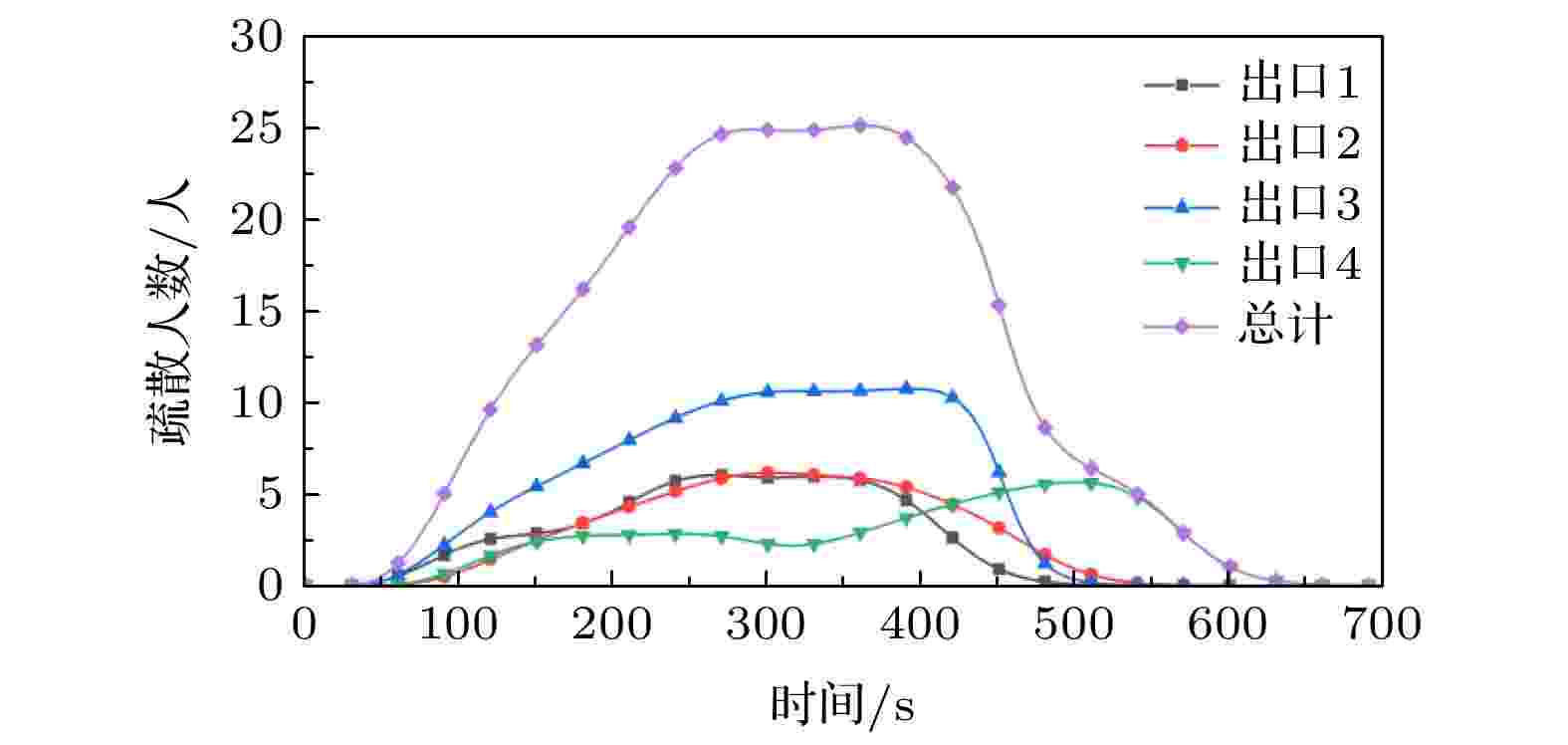图 9 各出口及总疏散人数随时间变化关系Figure9. The relationship between the exits and the total number of evacuees varies with time.
图10显示出了各出口及总疏散剩余人数随时间的变化关系情况, 各曲线总体上在疏散前期呈现出平稳的状态, 在经历过一段平稳期后曲线开始显著下降, 在疏散的后期, 下降趋势开始放缓, 疏散剩余人数逐渐趋近于0, 在672 s时刻, 总疏散剩余人数为0.4925 人, 表示所有人员均撤离出校园, 疏散结束.
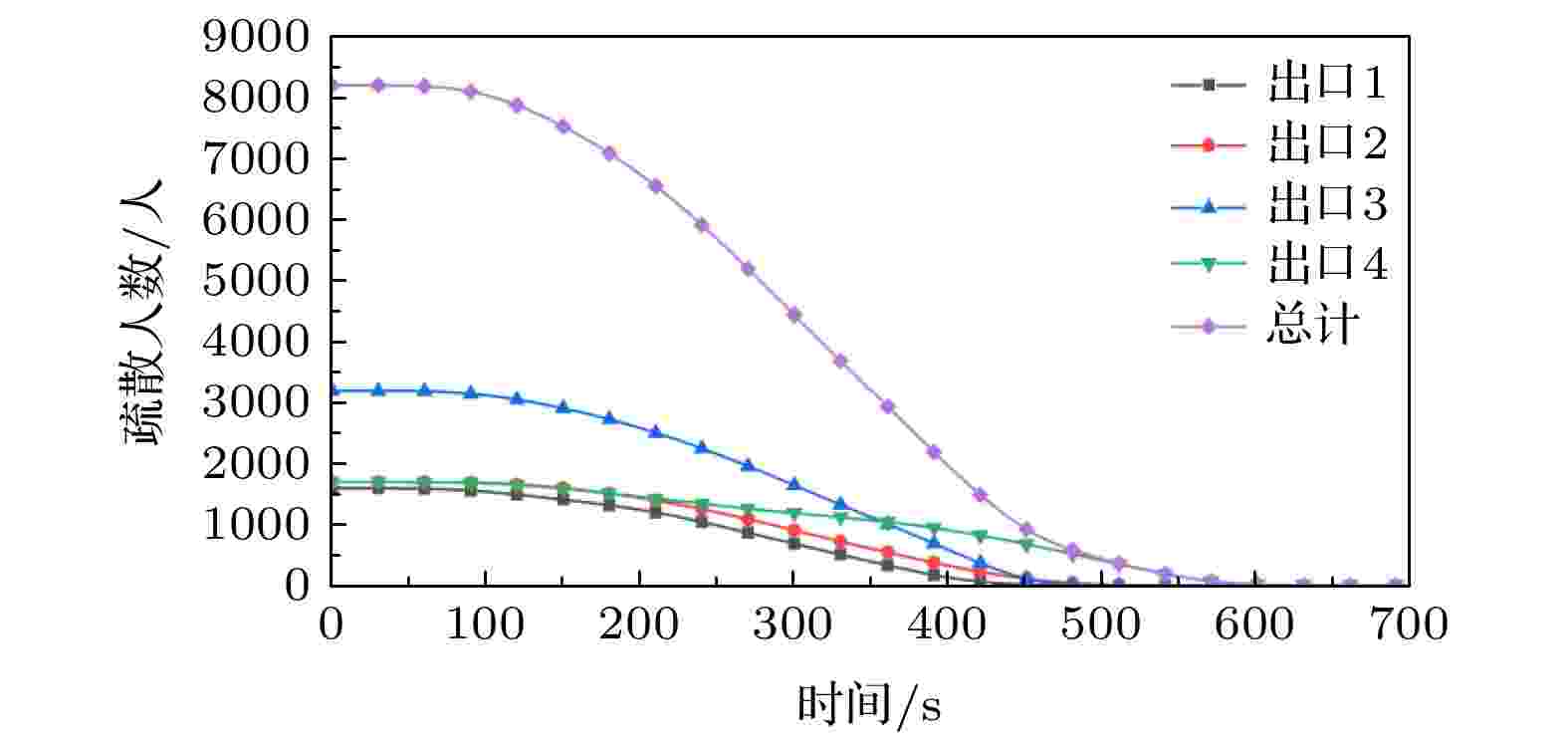图 10 各出口及总疏散剩余人数随时间变化关系Figure10. The total number of remaining evacuees at each exit varies with time.
为了进一步了解元胞状态的微观变化情况, 选取8个“观测”元胞, 观测元胞内人员数量和人员速度随时间的变化情况, 各“观测”元胞的具体位置见图11, 选取的8个“观测”元胞分别分散在四个疏散子网中, 包括1个“源加载”元胞, 1个出口元胞, 4个道路节点元胞和2个道路元胞.
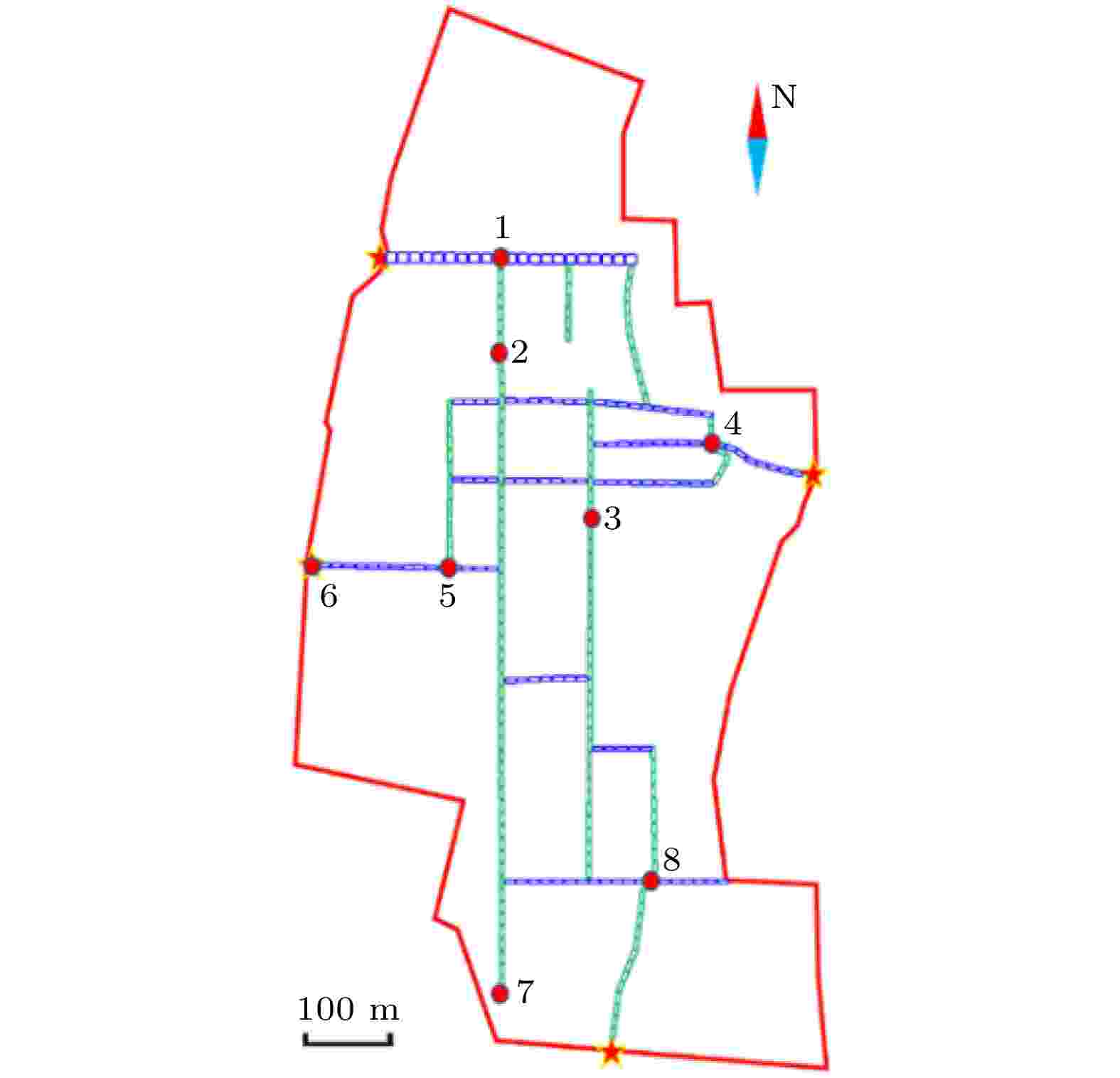图 11 “观测”元胞的位置分布Figure11. The location distribution of “observed”cellular
图12和图13显示出了选取的8个元胞的元胞内人数和速度随时间的变化关系, 从图中可以看出元胞7作为“源加载”元胞, 其人数变化和元胞加载概率密度分布图类似, 呈现出严格的梯形变化, 而元胞6作为“出口”元胞, 人数峰值出现在420 s时刻, 晚于其他“观测”元胞的人数峰值时间, 元胞5为出口3前的道路节点元胞, 承载的疏散压力较大, 人数峰值也远高于其他“观测”元胞, 最高人数接近120 人, 其对应位置处的速度也为8个“观测”元胞中最低, 略高于1 m/s, 各“观测”元胞在疏散过程中速度均在1 至1.5 m/s范围内波动.
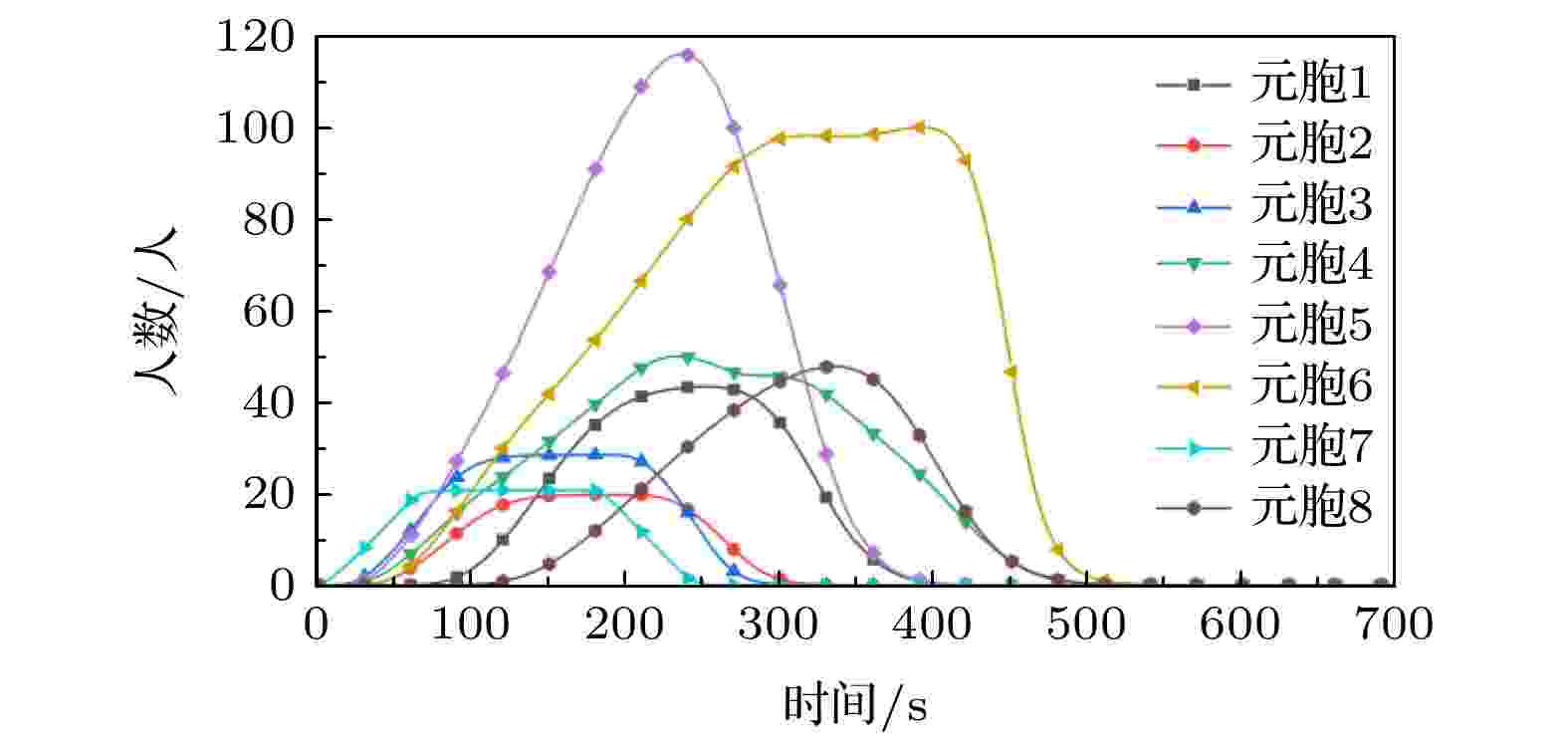图 12 各“观测”元胞人数随时间的变化Figure12. Changes in the number of “observed” cells over time.
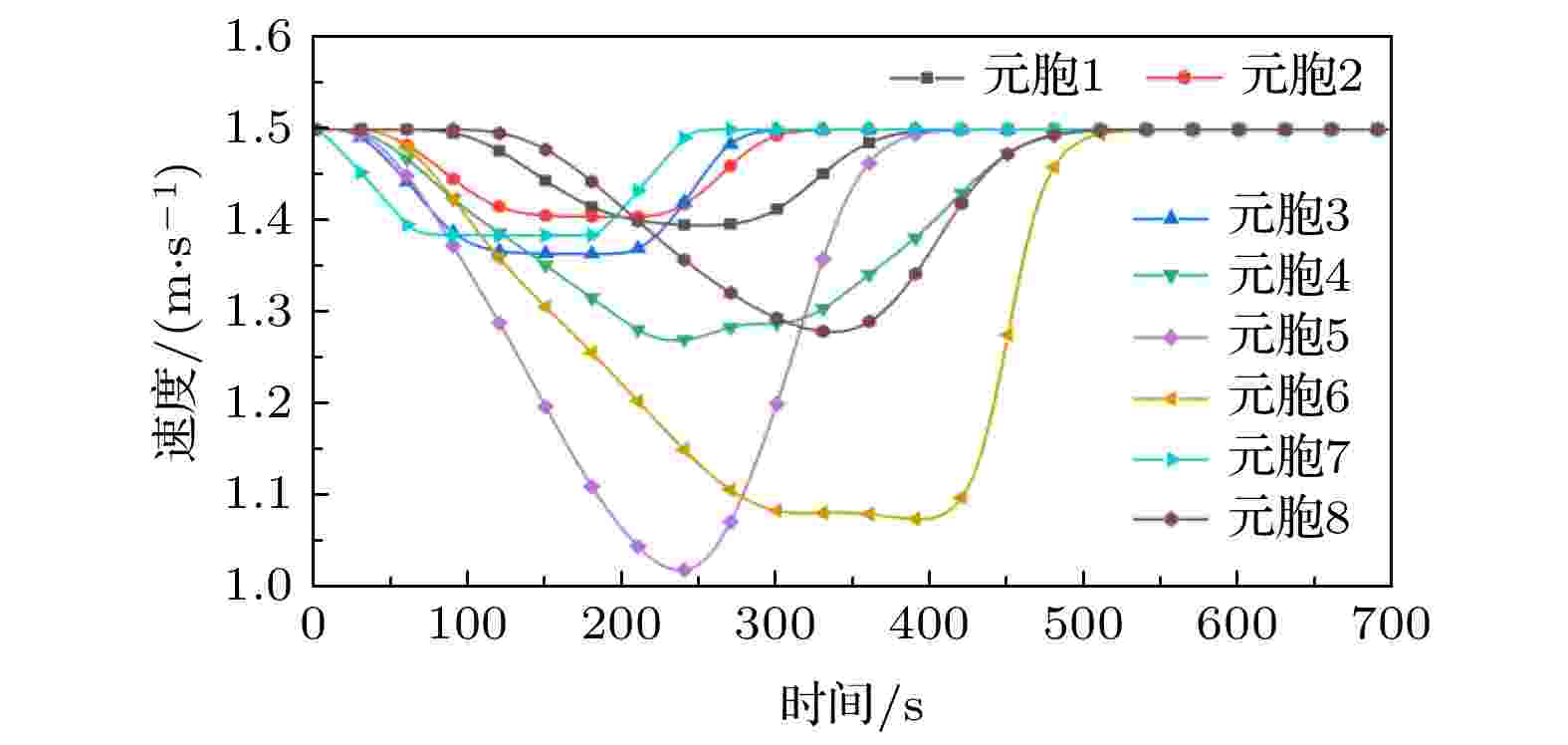图 13 各“观测”元胞速度随时间的变化情况Figure13. Variations of cell velocity with time in each observed cell.
图14为各元胞在以100 s为时间间隔的时间节点人员数量分布图, 可以观察出在200至400 s时间段内各道路人员数量较高, 各出口承载了较大的疏散压力, 在500 s时刻, 出口1、出口2和出口3出口元胞人数较少, 而出口4仍然还有一定数量行人未完成疏散, 在600 s时刻, 疏散场景内只剩余少量人员, 疏散接近尾声.
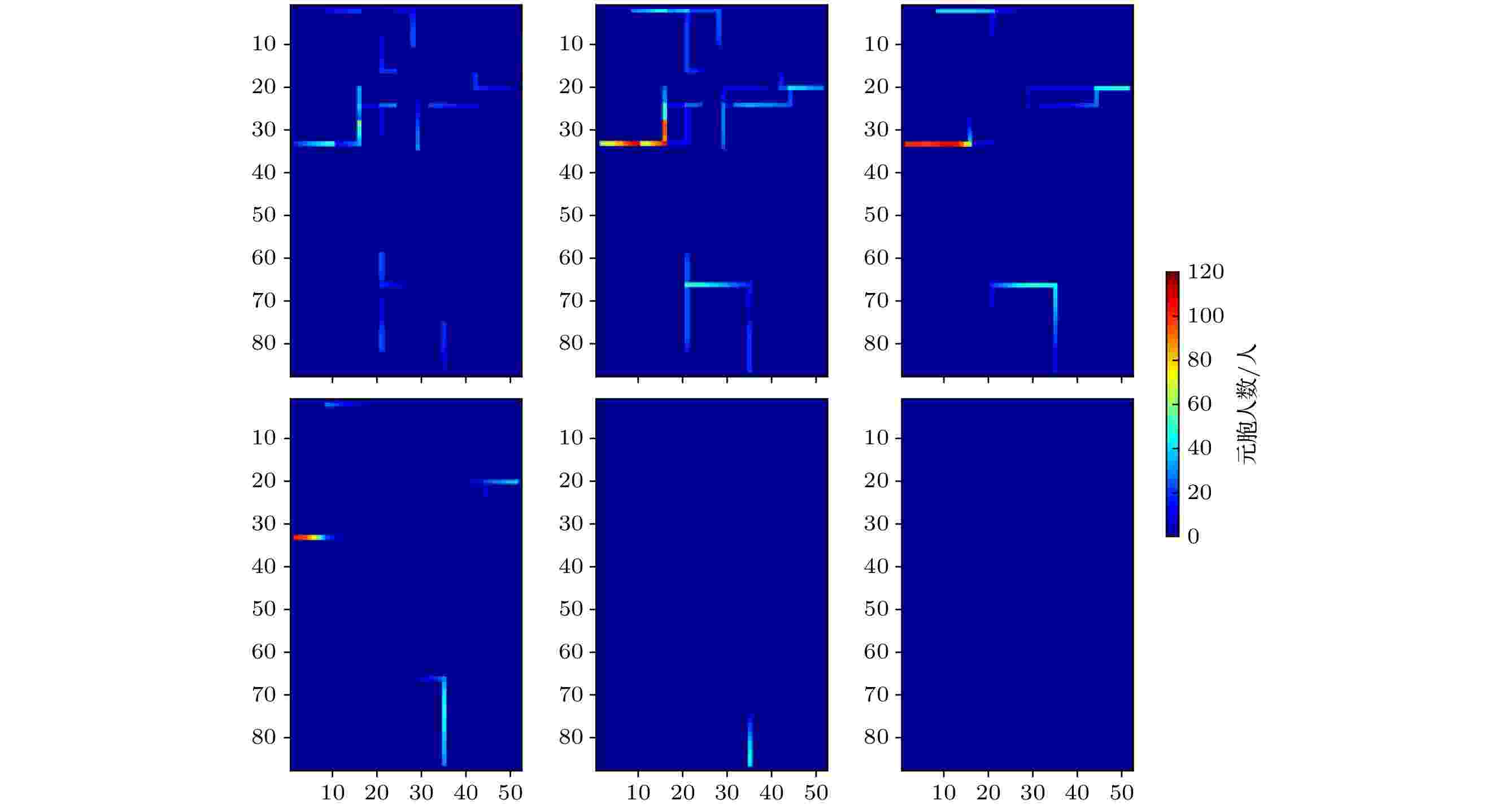图 14 空间人员数量分布图 (a) t = 100 s; (b) t = 200 s; (c) t = 300 s; (d) t = 400 s; (e) t = 500 s; (f) t = 600 sFigure14. Spatial staffing distributions: (a) t = 100 s; (b) t = 200 s; (c) t = 300 s; (d) t = 400 s; (e) t = 500 s; (f) t = 600 s.
2) 模拟疏散总时间为672 s, 在250 至400 s时间段内, 达到了总疏散人数的峰值, 且在该时段位于道路交叉口的“观测”元胞5位置处元胞峰值人数接近120 人, 在实际疏散过程中, 要避免出现人员过于密集造成踩踏事故;
3) 通过模拟发现, 出口3所在疏散子网内存在较多生活场所及设施, 元胞加载人数最多, 路网承受的疏散压力最大, 因此, 在考虑实际疏散问题时, 可以对该区域内人员进行分流, 降低局部路网疏散压力;
4) 通过分析模拟结果, 可以发现出口4疏散人数不多, 但是在四个出口中所需疏散时间最久, 这是由于人员加载场所与出口之间距离较远导致, 因此, 在实际疏散中可以考虑在人员密集场所与校区出口之间规划出一条捷径, 以加快疏散速度, 降低疏散时间.
