摘要:小液滴撞击壁面现象在喷雾冷却等领域都有广泛应用. 为研究小液滴(微米)撞击热壁面(非沸腾区)传热过程, 建立了二维液滴撞壁瞬态模型, 并采用相场方法对小液滴换热过程中对流热通量和导热热通量的大小进行了对比. 研究结果表明: 液滴撞击壁面初期形成“冷斑”, 有利于小液滴与壁面的传热; 小液滴撞击壁面过程中热通量峰值存在于三相接触点附近, 数量级在10⁵—10⁶ W/m²; 小液滴撞击壁面过程中受壁面浸润性和液滴尺寸对传导热通量的影响较为显著, 而速度和液滴尺寸对对流热通量的影响较为显著; 大多数情况下, 小液滴撞击壁面传导热通量数量级在10³—10⁵ W/m², 对流热通量数量级在10⁴—10⁶ W/m², 对流热通量大于传导热通量, 在整个换热过程中占据主导地位.
关键词: 小液滴/
撞击壁面/
传热特性/
相场方法

English Abstract

全文HTML

--> --> -->

喷雾冷却^[1,2]技术被广泛应用于微通道冷却^[3]、电池组散热^[4]和空冷机组^[5,6]等众多领域. 小液滴的尺寸^[7,8]、与固体热壁面的撞击速度^[9,10]等相关参数都对固体热壁面的散热有很大的影响. 因此, 有必要对液滴撞击热壁面(非沸腾区)时的热力学特性进行研究.
关于液滴撞击热壁面已经取得许多研究成果. Pasandideh-Fard等^[11]采用实验和数值模拟的方法, 研究了液滴(毫米级)撞击热壁面(50 ℃)的换热过程. 结果表明, 在高撞击速度的情况下, 速度对撞击传热速率的影响并不显著. 他们还发现, 在固定的雷诺数下, 冷却效率随韦伯数的增加而增加, 但在较大的韦伯数下, 冷却效率仅取决于普朗特数, 与液滴冲击速度或大小无关. Lee等^[12]采用空气加热器阵列对冷却剂PF-5060的单液滴撞击壁面的热通量进行了测量, 结果表明, 液滴撞击壁面蒸发传热分为两部分: 瞬态传热系数和恒定传热系数. Hase和Weigland^[13]对高雷诺数下液滴变形引起的传热强化进行了数值研究, 结果表明, 运动液滴的传热与雷诺数和韦伯数均有关. Berberovic等^[14]采用仿真的方法研究了液滴撞击热壁面的流体流动和传热过程, 发现固液界面的温度分布对固体壁面的传热影响较小. 叶学民等^[15]对液滴铺展换热行为进行了数值计算, 计算结果显示运动液滴壁面热通量的倒数呈单峰分布. Guggilla等^[16]利用红外热成像技术和高速成像技术, 对毫米级(2.8 mm)液滴撞击壁面进行了研究. 实验结果表明, 液滴在撞击壁面的过程中, 三相接触线附近区域传热速率最高, 从而验证了三相接触线在液滴与壁面换热中的意义. Gelissen等^[17]采用数值模拟的方法研究了气相条件下液滴撞击对热壁面的影响. 模拟结果表明, 在液滴撞击过程中, 壁面的润湿性会影响壁面的冷却. 亲水润湿条件将导致固体的冷却速率更高, 而疏水性润湿条件会使冷却速率降低, 壁面冷却速率同样受壁面粗糙度的影响. 黄龙等^[18]采用CLSVOF方法对液滴撞击壁面传热特性进行了研究, 发现大尺寸液滴有利于壁面的传热.
从目前的文献来看, 大多数研究都是针对毫米级液滴撞击热壁面时传热特性的研究, 但是微米级小液滴的传热特性是截然不同的. 本文采用相场方法对微小液滴在热壁面的传热特性以及在该过程中对流和传导热的主导作用进行了研究, 并分析了液滴尺寸、撞击速度及壁面浸润性对液滴撞击壁面热通量的影响. 本文结果将有助于丰富喷雾强化传热过程的机理及指导喷雾冷却的实际应用.

本文基于相场方法对液滴撞壁传热传质过程进行仿真计算. 为了简化物理模型, 本文做出以下假设: 1)初始时刻液滴为球形; 2)流体均视为不可压缩; 3)气相视为理想气体; 4)忽略热辐射影响; 5)液滴撞击过程中质量保持恒定.
2

-->

2.1.几何模型及参数

数值计算所采用模型如图1所示. 计算域为一个150 μm × 100 μm的长方形, 包括100 μm × 100 μm的空气域和50 μm × 100 μm的固体域, 液滴的直径为D₀, 具有一定初速度U₀, 考虑重力G的影响, 初始时刻空气速度为0 m/s, 液滴温度为283 K, 空气温度为300 K, 壁面温度为313 K. 设置液态水的定压比热容c_p为4182 J/kg·K, 导热系数k为0.6 W/m·K, 动力粘度μ为0.001 Pa·s. 计算域的左侧边界为对称轴, 右侧和上方均为开放边界, 确保了计算域内部与外部区域的连通性, 中间壁面设置为无滑移热壁面, 根据仿真需要对壁面浸润性进行调节.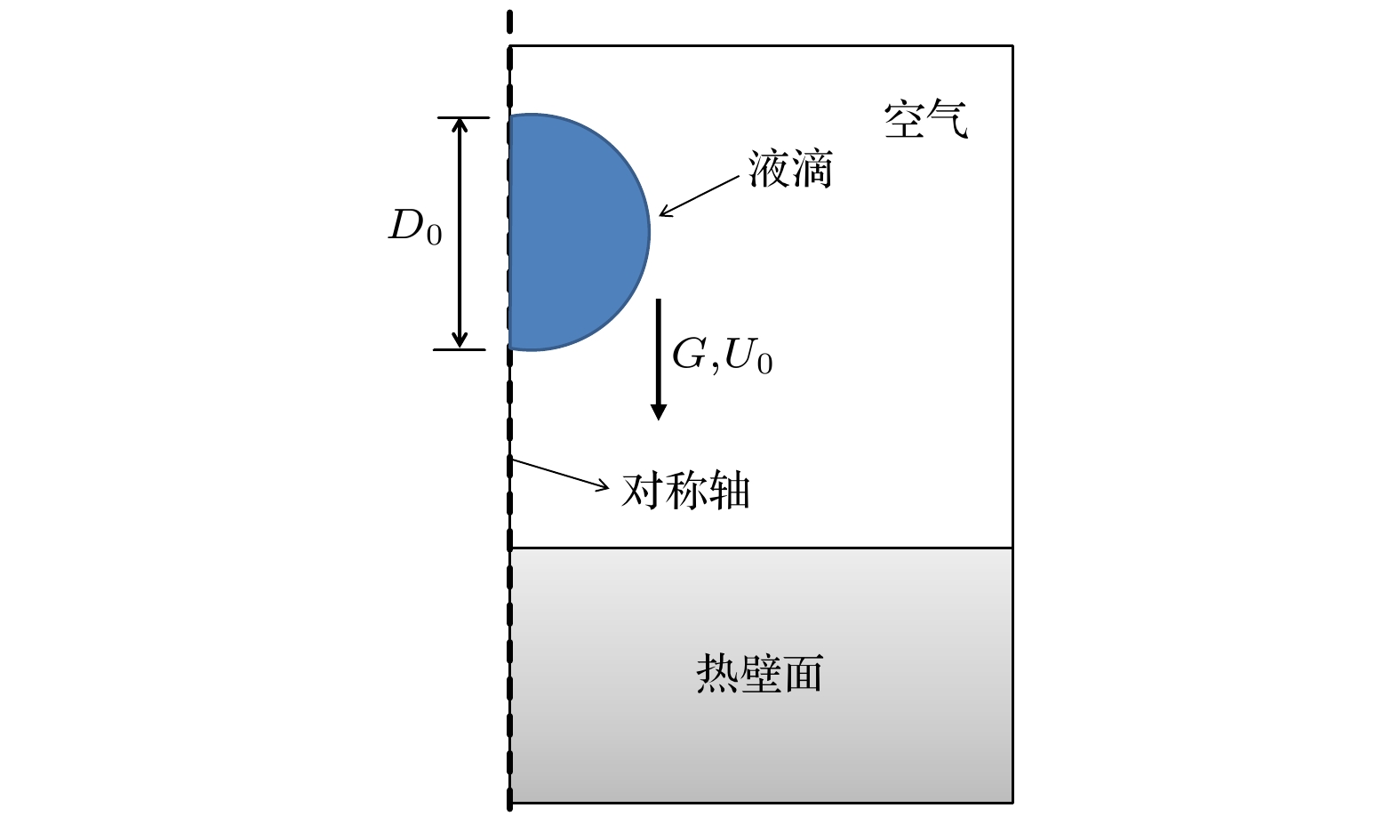
图 1 计算物理模型
Figure1. Computational physical model.

2 -->

2.2.控制方程

基于相场模型, 计算所采用控制方程主要包括: 对流Cahn-Hilliard方程^[19]、连续性方程、N-S方程、能量守恒方程, 具体如下:

$\frac{{\partial \alpha }}{{\partial t}} + \nabla \cdot (u\alpha ) = \nabla \cdot (M\nabla \varphi ),$

$\varphi = \frac{1}{2}\alpha (\alpha - 1)(2\alpha - 1) - {\varepsilon ^2}\Delta \alpha ,$

$\rho \nabla \cdot u = 0,$

$\rho \frac{{\partial u}}{{\partial t}} + \rho \left( {u \cdot \nabla } \right)u = - \nabla P + F + \rho g,$

$\rho {c_{\rm{p}}}\frac{{\partial T}}{{\partial t}} + \rho {c_{\rm{p}}}u \cdot \nabla T + \nabla \cdot q = {Q_{\rm{e}}},$

$q = - k\nabla T,$

上式中, α为保守变量, t为时间, u为流体速度, M为迁移率, φ为化学势, ρ为流体介质密度, P为压力, F为粘性力, g为重力加速度, c_p是定压比热容, Q_e是源项, T是温度, k是导热系数.
本文中温度梯度、传导热通量和对流热通量分别采用以下公式进行计算:

${\rm{grad}}\,T = \frac{{{\rm{d}}T}}{{{\rm{d}}\delta }},$

${q_{{\rm{cond}}}} = kt\,{\rm{grad}}\,T,$

${q_{{\rm{conv}}}} = h\Delta T.$

式中, gradT为温度梯度, dT为温度差, dδ为法向垂直距离, q_cond为传导热通量, q_conv为对流热通量, h为对流换热系数.
2 -->

2.3.模型验证

模型采用非结构性网格, 并选取了50 × 100, 80 × 250, 140 × 420, 160 × 500及200 × 600六种不同密度的网格进行无关性验证. 计算工况为: 液滴的直径为20 μm, 液滴温度为283 K, 环境空气温度为300 K, 壁面温度为313 K, 静态接触角为90°. 图2分别展示了五种网格密度下液滴撞击壁面后壁面热流密度随时间的变化, 为便于分析, 横坐标采用无量纲时间, 纵坐标壁面热流密度取对数值.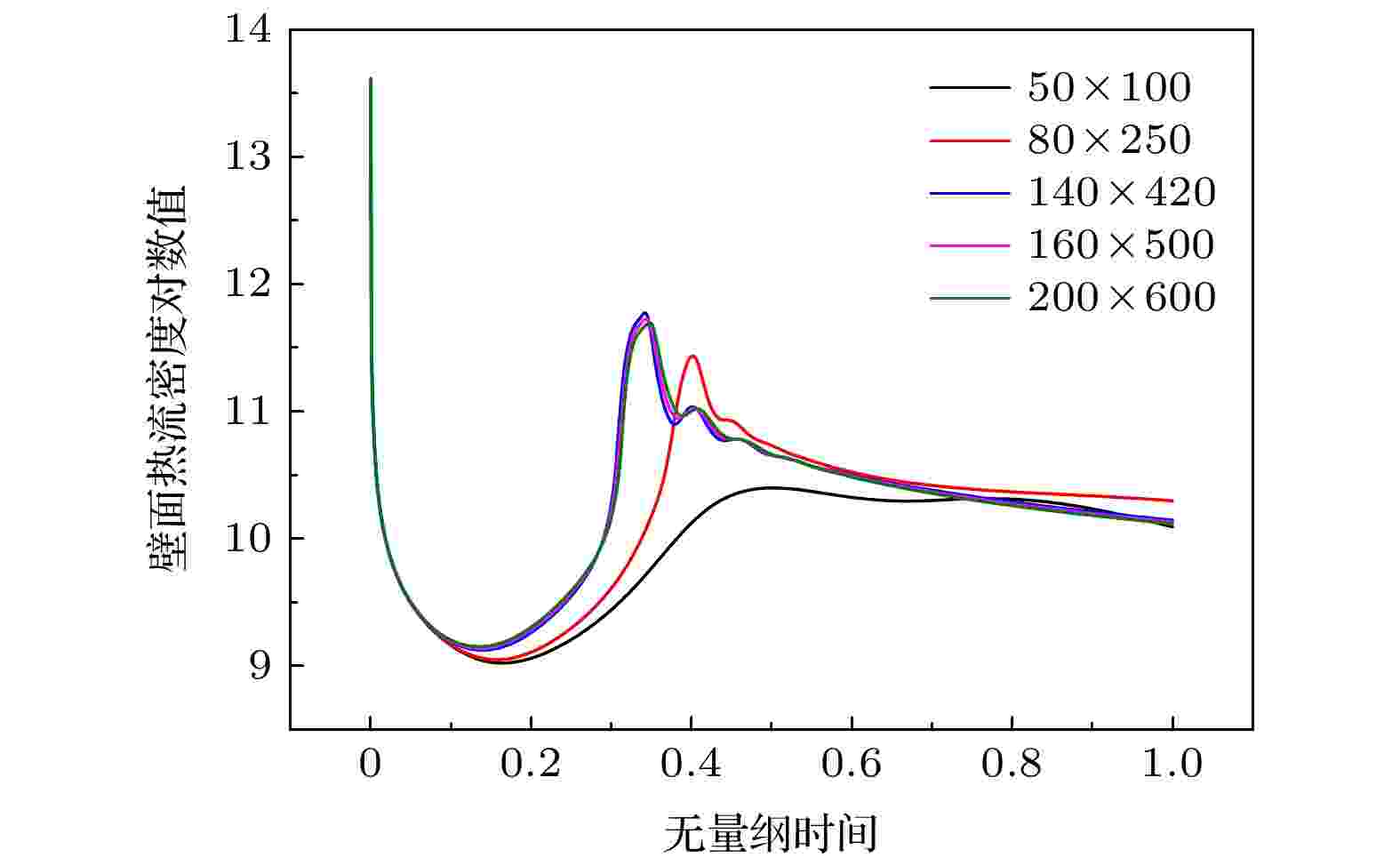
图 2 网格无关性验证
Figure2. Grid independence verification.

从图2可以看出, 在液滴撞击壁面过程中, 随着时间的推移, 壁面(固液及气液交界面)热流密度(对流热流密度与传导热流密度之和)均是先增大后减小, 且均存在一个峰值. 横向对比发现, 随着网格数量的增加, 壁面热流密度逐渐增大. 当网格密度为140 × 420时, 随着网格数的增加, 网格数对壁面热流密度的影响较小. 综合考虑计算工时和精度, 本文仿真采用的网格密度为160 × 500.
为验证本文算法的可行性, 计算结果与Van等^[20]的实验进行对比, 具体工况为: 液滴直径为60 μm, 撞击速度为0.74 m/s. 如图3所示, 模拟结果与实验结果基本一致, 本文所采用模型对液滴撞壁过程的数值模拟是有效的.
图 3 实验结果与模拟结果对比
Figure3. Comparison of experimental results and simulation results.

2

-->

3.1.温度场及流场分布

图4展示了直径为50 μm的液滴不同时刻撞击壁面的温度场及流场云图. 为了更好地进行图像描述, 图4中给出了代表位置刻度的横纵标尺, 且每幅图均分为左右两部分. 图像左侧上部分为液滴撞击热壁面流场图, 下部分为热壁面的温度场分布, 图像右侧为液滴撞击热壁面的整体温度场分布. 需要指出的是, 液滴尺寸太小导致宏观壁面温度变化较小, 图像右侧壁面处温度场分布不明显. 为了更好地展示微小液滴的冷却作用, 图像左侧下部分温度场分布采用与图像右侧不同的温度场标尺(图像左下侧温度场图例标尺最小间隔为0.01 ℃, 图像右侧温度场图例标尺最小间隔为5 ℃). 设置液滴初始速度为1 m/s, 静态接触角为90°, 表面张力系数为0.0728 N/m. 初始时刻为30 μs, 最后时刻为180 μs, 时间间隔为30 μs. 从图4可以看出, 在30 μs时刻, 液滴在初速度和重力的共同作用下垂直向下运动, 空间中的流场沿液滴运动方向竖直向下, 而且到达壁面后向外进行扩散, 液滴运动带动周围空气流动且形成一个涡旋, 涡旋将增强液滴与空气的对流换热; 液滴撞击壁面前期会破环壁面的温度场分布, 随着液滴的下落, 液滴下方的温度场将会被“压缩”, 相比其他位置具有更大的温度梯度; 此时壁面的温度场分布与空气中的温度场分布类似, 液滴下方的温度梯度更大. 液滴撞击壁面60 μs时, 进行铺展运动, 可发现与液滴接触的壁面区域温度明显低于未接触区域, 而且液滴内部与气液界面附近均触线涡旋, 涡旋将增强固液及气液的对流换热; 随着时间的发展, 液滴的铺展-回缩(震荡)行为逐渐减弱, 趋于稳态加热阶段, 固液界面的传热逐渐增强, 液滴的温度逐渐升高, 壁面的温度梯度也逐渐减小.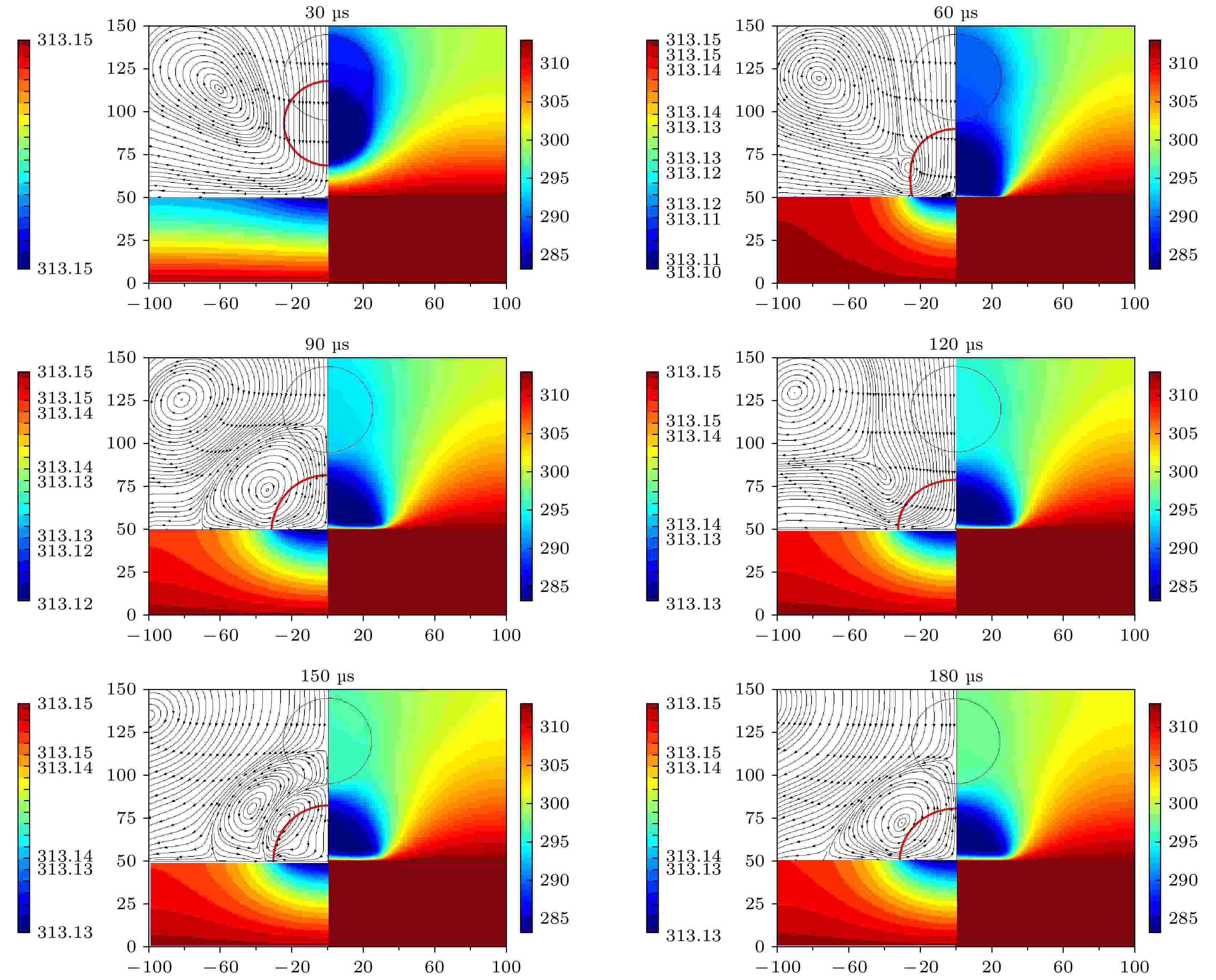
图 4 不同时刻温度场及流场分布
Figure4. Temperature field and flow field distribution at different times.

微米液滴在撞击热壁面初期, 因浸润作用会附着在热壁面上, 其底部(固液界面处)出现明显的低温区域, 同时在液滴三相接触线附近的热壁面形成一圈明显的环状低温带, 在这里称之为“冷斑”. 冷斑的存在会使液滴附近热壁面温度降低, 增大壁面温差, 从而增大热流密度, 起到强化导热的作用, 并将在短时间内加快壁面和液滴的传热速率. 但由于液滴的尺寸非常小, 壁面的温降幅度较小, 最大在0.05 K左右.
2 -->

3.2.热流密度分布

为探究液滴撞击过程对壁面的影响, 分别监控了六个壁面位置热流密度分布, 不同位置间隔为10 μm, 具体位置如图5(g)所示. 图5(a)展示了固液界面热流密度沿径向的分布, 从图5(a)可以看出, 除30 μs时刻外, 壁面热流密度随径向距离变化的趋势均是先增大后减小, 最后趋近于零. 随着时间的变化, 壁面热流密度峰值逐渐减小. 对比图4中各图可以发现, 壁面热流密度峰值均出现在三相接触点附近, 随着三相接触点的变化而变化, 存在明显的三相接触点效应. 纵向对比图5(a—f)可以发现, 离固液界面距离增大, 热流密度数值逐渐减小, 极大值逐渐消失, 三相接触点效应越来越弱. 当距离为30 μm时, 开始发生了一个转变, 如图5(d)所示; 90 μs时刻壁面热流密度整体超过60 μs时刻, 如图5(d—f)所示. 这一现象表明, 离固液界面距离大时, 壁面热流密度呈现出延迟效应, 而且距离越大, 延迟效应越明显.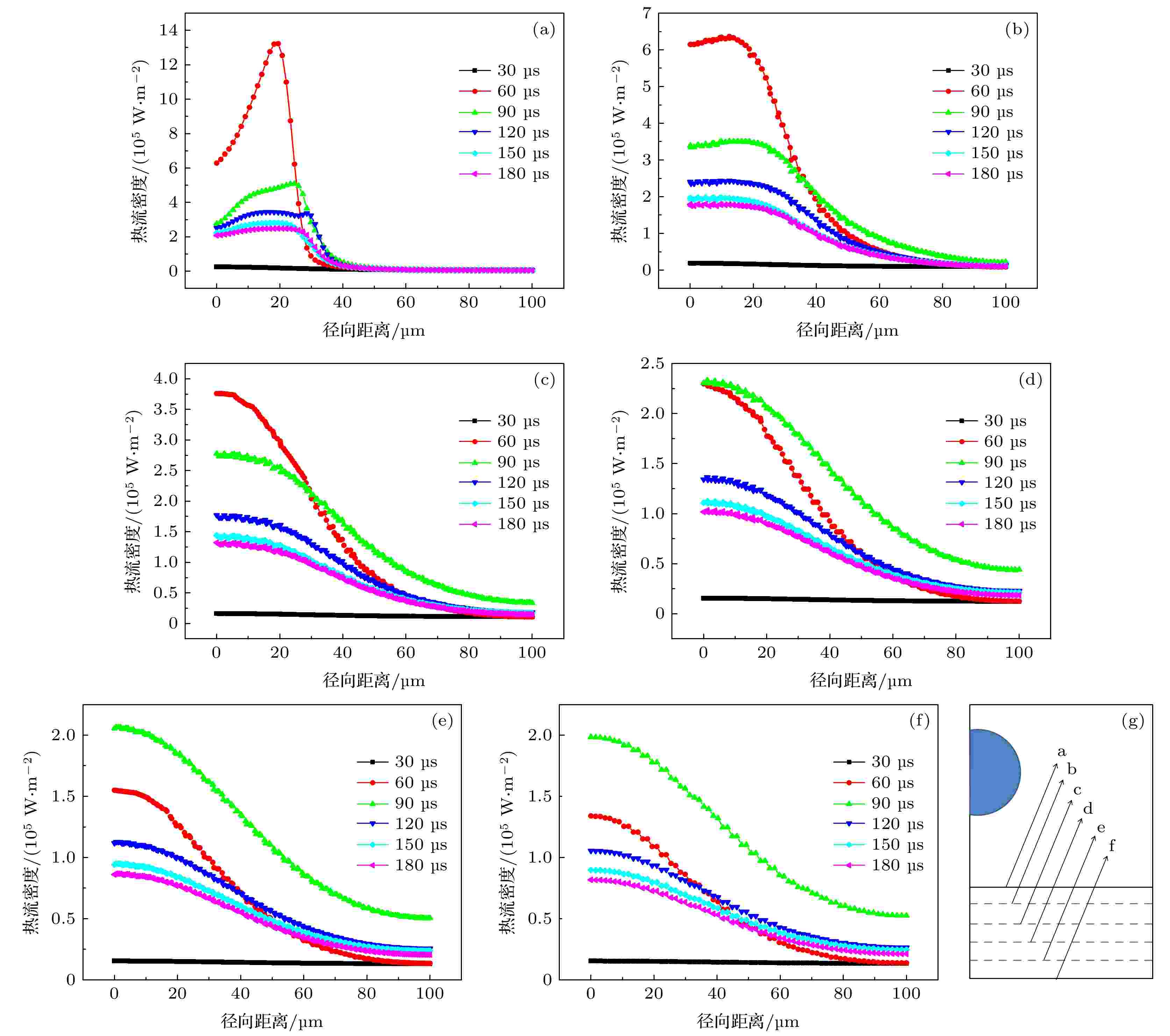
图 5 壁面不同位置热流密度分布, 与固液界面垂直距离分别为　(a) 0 μm, (b) 10 μm, (c) 20 μm, (d) 30 μm, (e) 40 μm, (f) 50 μm, (g)具体位置示意图
Figure5. The heat flux distribution at different positions on the wall, the vertical distances from the solid-liquid interface are respectively (a) 0 μm, (b) 10 μm, (c) 20 μm, (d) 30 μm, (e) 40 μm, (f) 50 μm, (g) Specific location diagram

2 -->

3.3.速度对对流和传导热通量的影响

图6展示了不同初始速度下热通量随时间的变化趋势(图中虚线之前是液滴撞壁之前, 虚线之后是撞壁之后), 初始速度分别为0.5, 1, 2 m/s. 从图6(a)可以看出, 液滴初始速度为0.5 m/s, 撞击时刻发生在90 μs左右, 撞击后传导和对流热通量均显著增加, 而且传导热通量增加幅度远远高于对流热通量. 撞击时刻后, 对流热通量随时间的变化呈现出明显的多峰分布, 而传导热通量则呈现出明显的单峰分布. 对比图4中各图可知, 液滴撞壁对流热通量变化受铺展-回缩行为影响较大, 随着液滴的铺展, 对流热通量逐渐增大, 随着液滴的回缩, 对流热通量逐渐减小. 而传导热通量几乎在第一次铺展-回缩过程完成后达到峰值, 之后随着时间的推移逐渐减小. 对比图6(a—c)可以发现, 液滴撞击壁面传导热通量量级在10⁴—10⁵ W/m², 对流热通量量级在10⁵—10⁶ W/m². 随着液滴初始速度的增加, 对流热通量数值显著增大, 传导热通量数值保持稳定; 液滴撞击壁面过程中, 对流热通量峰值均高于传导热通量. 对于传导热通量, 液滴撞击速度对其变化影响较小; 对于对流热通量, 撞壁时刻后对流热通量由递增逐渐变为递减.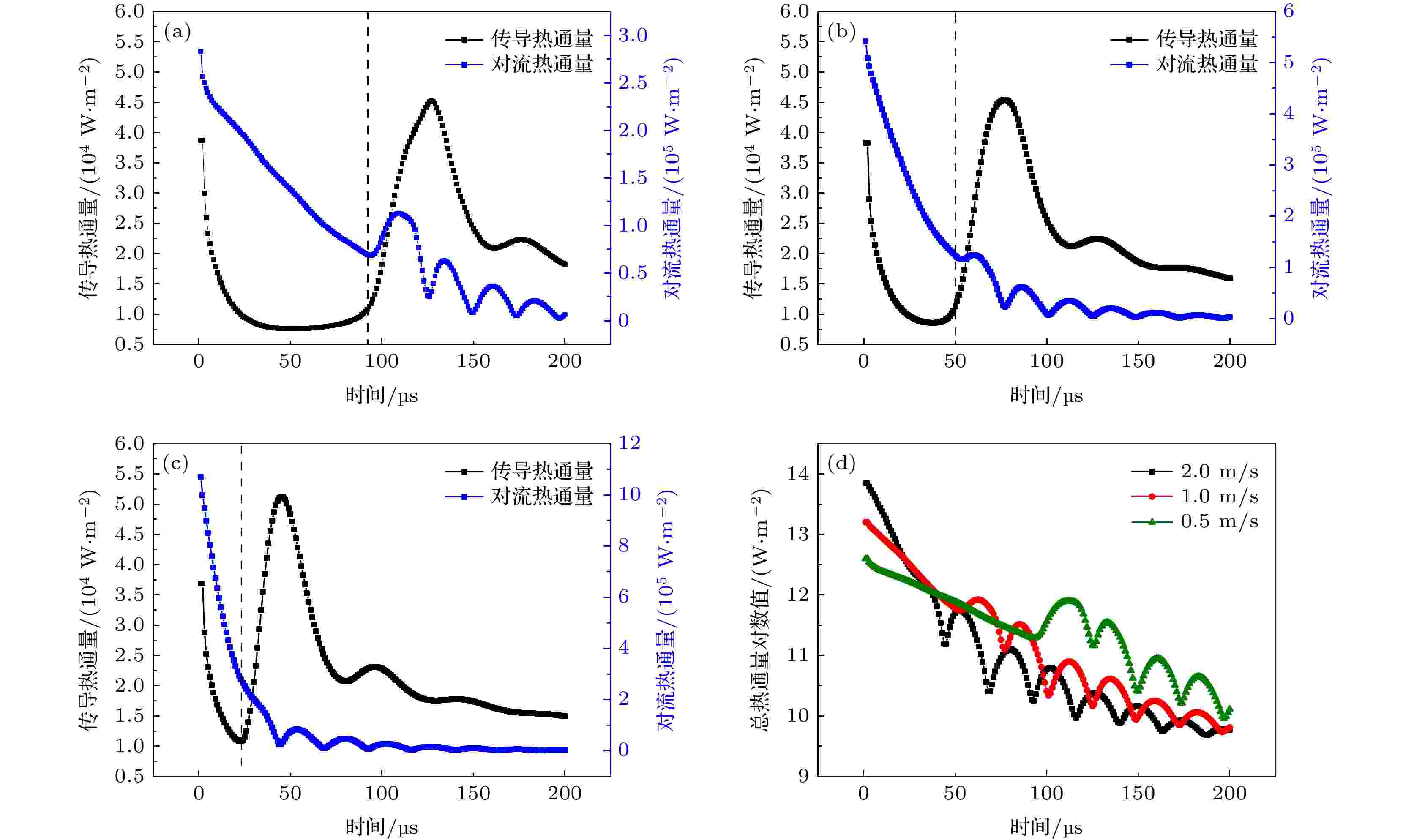
图 6 不同速度下传导及对流热通量随时间的变化　(a) 0.5 m/s; (b) 1 m/s; (c) 2 m/s; (d)不同速度下总热通量随时间的变化
Figure6. Conductive and convective heat flux changes with time at different speeds: (a) 0.5 m/s; (b) 1 m/s; (c) 2 m/s; (d) total heat flux changes with time at different speeds.

图6(d)展示了不同初始速度下液滴撞击壁面过程中总热通量对数值随时间的变化趋势. 可以看出, 三种情况下曲线均呈现多峰分布, 总体趋势均随时间逐渐降低. 随着液滴初始速度的增大, 液滴的峰值总热通量逐渐增大, 总热通量衰减速度逐渐增大. 造成上述现象的原因是, 液滴撞击热壁面之后, 由于液滴与壁面存在较大的温差, 根据公式(8)和(9)可知, 传导热通量和对流热通量会迅速升高, 且随着初始速度的增大, 对流换热得到加强, 但传导换热强度基本保持不变. 实际上, 对流换热是热对流和热传导同时参与的换热过程, 所以在热通量数值上, 对流热通量要大于传导热通量.
2 -->

3.4.壁面浸润性对对流和传导热通量的影响

壁面浸润性对液滴撞壁传热特性有一定的影响. 通常情况下, 采用静态接触角(θ)来表征壁面浸润程度. 当θ < 90°时, 认为壁面为亲水壁面; 当θ = 90°时, 认为壁面为普通壁面; 当θ > 90°时, 认为壁面为疏水壁面. 图7展示了不同浸润性条件下热通量随时间的变化趋势, 选取静态接触角分别为45°, 90°, 135°.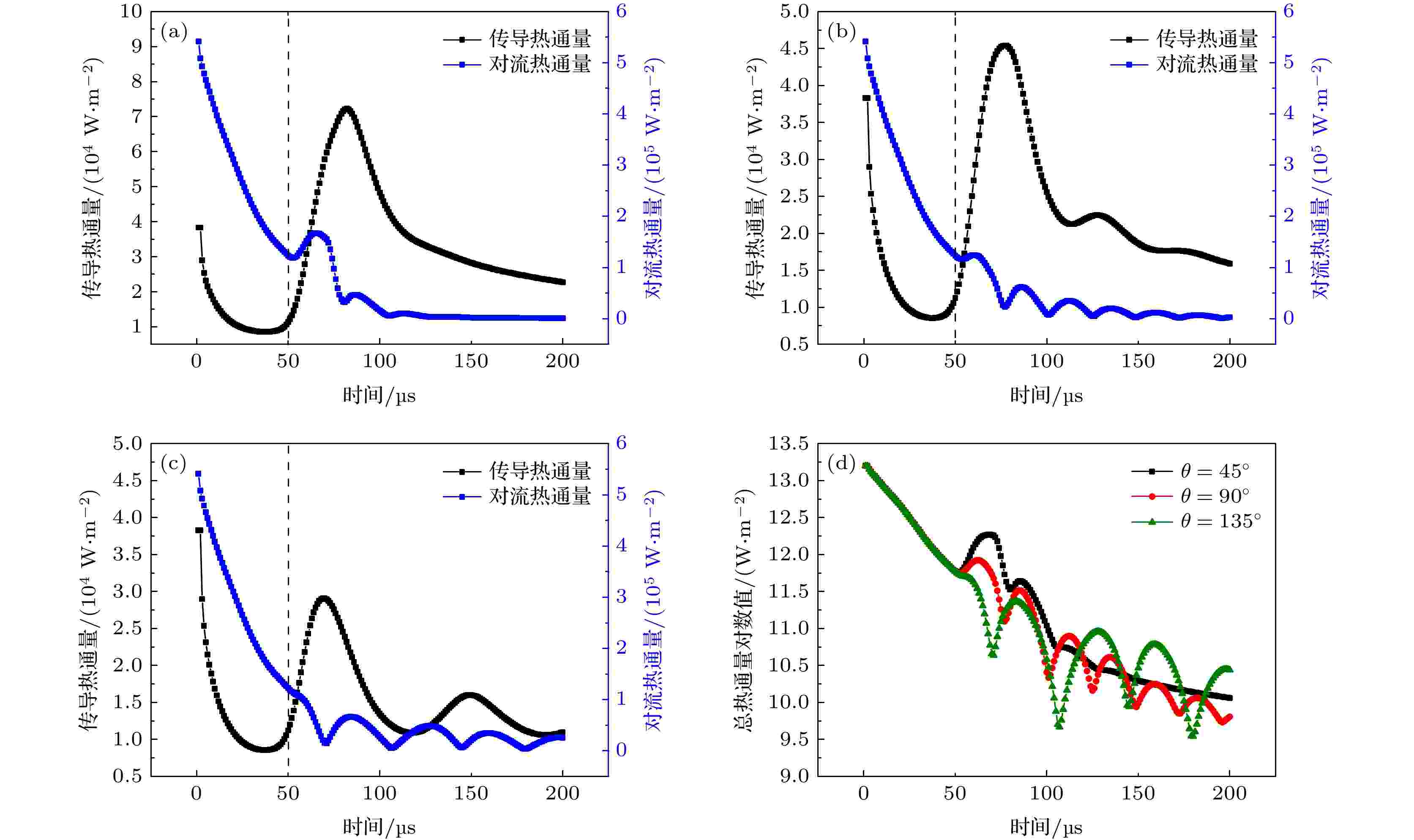
图 7 不同浸润性下传导及对流热通量随时间的变化　(a) θ = 45°; (b) θ = 90°; (c) θ = 135°; (d)不同浸润性下总热通量随时间变化
Figure7. Conduction and convective heat flux changes with time under different wettability: (a) θ = 45°; (b) θ = 90°; (c) θ = 135°; (d) total heat flux varies with time under different wettability.

分析图7(a—c)可知, 液滴撞击壁面传导热通量量级在10³—10⁴ W/m², 对流热通量在10⁴—10⁵ W/m². 随着静态接触角的增大, 传导热通量的峰值逐渐减小; 当θ = 45°时, 传导热通量呈现单峰分布, 随着壁面疏水性的增强(θ = 135°), 传导热通量显示出了双峰分布; 随着静态接触角的增大, 液滴撞击壁面后对流热通量多峰分布趋势越来越明显.
图7(d)展示了不同浸润条件下液滴撞击壁面过程总热通量随时间的变化. 从图7(d)可以看出, 液滴撞击壁面后, 亲水壁面条件下总热通量显著升高, 随着壁面疏水性的增加, 总热通量升高趋势逐渐降低, 峰值逐渐减小, 但多峰分布趋势越来越显著. 造成上述现象的原因是, 在液滴撞击热壁面过程中, 静态接触角越大, 意味着壁面疏水性越强, 液滴越不易铺展, 固液接触面接越小, 峰值对流热通量和传导热通量均减小, 总热通量峰值也减小. 疏水性越强, 壁面具有的表面能越大, 液滴撞击壁面后越容易出现铺展回缩行为, 固液接触面积随着液滴的铺展回缩而增大或减小, 使得对流热通量与传导热通量多峰分布越来越明显.
2 -->

3.5.液滴尺寸对对流和传导热通量的影响

图8展示了不同液滴尺寸下热通量随时间的变化趋势, 所选液滴直径分别为20, 30, 50 μm. 从图8中可以看出, 液滴撞击壁面传导热通量量级在10³—10⁴ W/m², 对流热通量在10³—10⁵ W/m². 随着液滴直径的增大, 传导热通量与对流热通量均提高, 传导热通量最大值由3.5 × 10⁴ W/m²增加到5 × 10⁴ W/m², 对流热通量最大值由3.5 × 10⁴ W/m²增加到5.5 × 10⁵ W/m², 对流热通量增幅远远大于传导热通量. 当液滴直径为20 μm时, 液滴撞击壁面后峰值传导热通量在1.25 × 10⁴ W/m²左右, 峰值对流热通量在1 × 10⁴ W/m²左右, 说明传导热通量在大部分时刻均大于对流热通量. 随着液滴直径的增大, 液滴撞击壁面后传导热通量逐渐增大, 对流热通量增长率逐渐减小, 其多峰分布趋势越来越明显, 传导热通量单峰分布趋势越来越显著.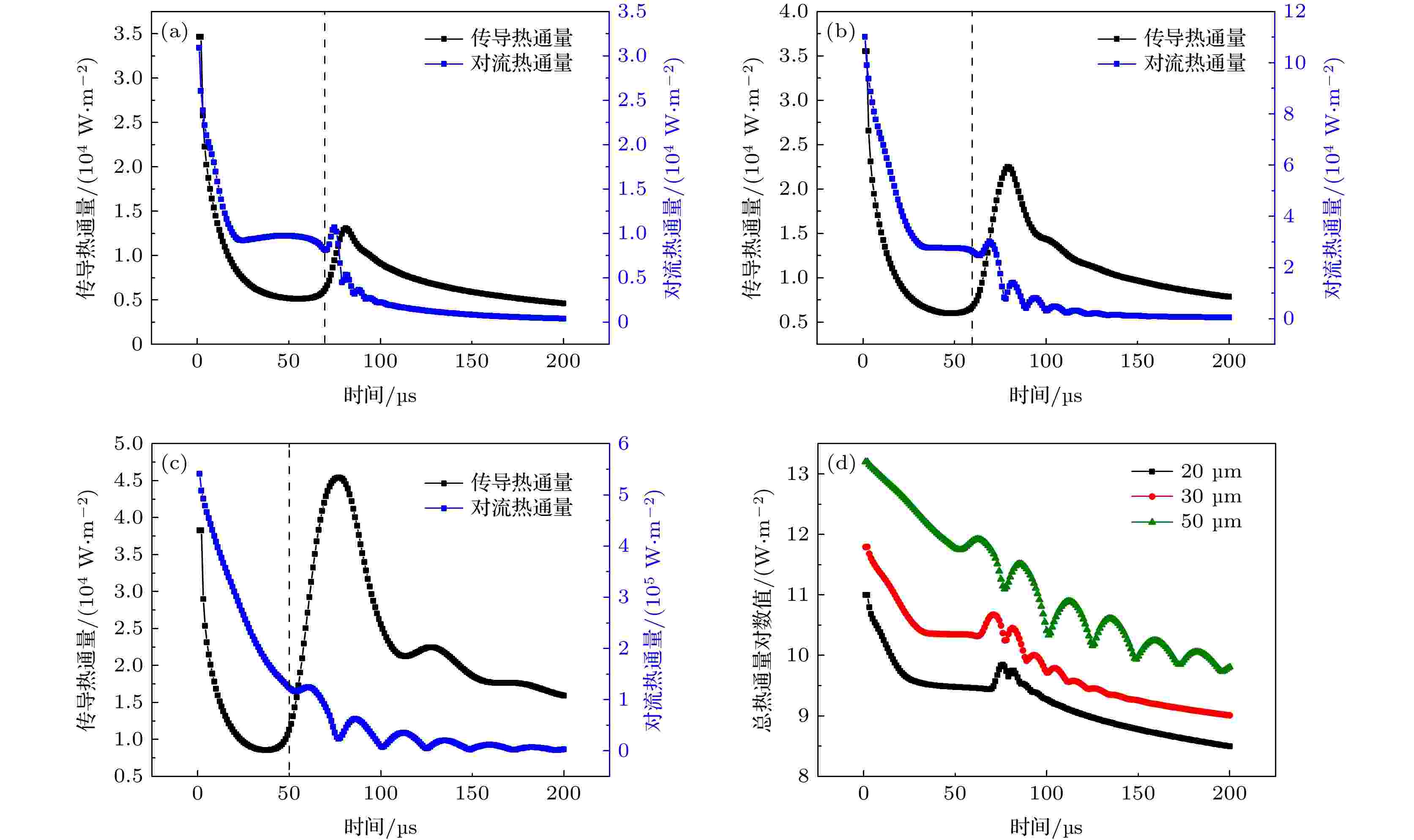
图 8 不同液滴尺寸下传导及对流热通量随时间的变化　(a) 20 μm; (b) 30 μm; (c) 50 μm; (d)不同液滴尺寸下总热通量随时间变化
Figure8. Conduction and convection heat flux changes with time under different droplet sizes: (a) 20 μm; (b) 30 μm; (c) 50 μm; (d) total heat flux changes with time under different droplet sizes.

图8(d)呈现了不同液滴直径下液滴撞击壁面总热通量随时间的变化. 由图8(d)可知, 三种情况下液滴撞击壁面后总热通量均显著增加, 而且随着液滴直径的增大, 峰值热通量逐渐增大; 液滴直径越大, 总热通量多峰分布越明显, 对比图8(a)—图8(c)可知, 液滴撞击壁面总热通量分布趋势与对流热通量分布趋势相似. 这表明, 在液滴撞击壁面换热过程中, 对流热通量占主导地位, 而且随着液滴直径增大, 对流热通量对总热通量的贡献越来越大.

采用相场方法对微米液滴撞击壁面模型进行数值模拟, 获得了速度、浸润性和液滴尺寸对液滴撞击壁面传热特性的影响规律, 结论如下:
1)液滴撞击壁面过程中固液界面存在明显的三相接触点效应, 热流密度峰值均出现在三相接触点附近; 与固液界面距离越远, 三相接触点对热流密度的影响越小, 而且热流密度出现延迟效应.
2)随着初始速度的增加, 对流热通量显著增加, 传导热通量基本不变; 初始速度增大, 峰值热通量及总热通量近似保持恒定, 速度效应并不显著.
3)随着壁面亲水性的增加, 传导热通量逐渐增大, 对流热通量变化较小; 壁面亲水性越强, 液滴撞击壁面过程中峰值热通量越大, 总热通量也越大.
4)随着液滴尺寸的增大, 传导热通量与对流热通量均显著增加, 对流热通量增加幅度更大; 液滴尺寸越大, 液滴撞击壁面过程中峰值热通量越大, 总热通量也越大.