摘要:本文模拟研究了氙气中X射线加热产生辐射激波的发光特性. 辐射激波采用Zinn模型计算, 并在模型中输入氙气的辐射不透明度和状态方程参数. 研究发现, 辐射激波伴随着丰富的光学演化过程, 激波对外辐射强度表现出两个明显的亮度峰值和一个亮度极小值, 辐射光谱也经常偏离黑体辐射光谱. 对氙气不同位置光学特性的分析可知, 激波和内部高温区的辐射吸收系数的动态演化导致了辐射激波的发光位置和辐射强度的变化.
关键词: 辐射激波/
辐射光谱/
氙气/
辐射流体力学

English Abstract

全文HTML

--> --> -->

辐射激波一般是非常强的激波, 波阵面处介质强压缩导致的辐射效应已经可以影响激波的宏观性质, 需要采用辐射流体力学理论描述这一现象. 辐射激波在天体物理和惯性约束聚变中都受到广泛关注. 在超新星爆发^[1]、天体喷流^[2]、吸积盘^[3]等活动中, 辐射对激波的能量损失和流体不稳定性的发展有重要影响. 在间接驱动惯性约束聚变中, 靶丸受X射线照射产生的强激波也伴随辐射效应, 导致能量的损失和激波结构的改变^[4].
近年来, 利用大型激光装置创造的高能量密度条件可以产生高强度的辐射激波^[5-7], 开展相关天体物理现象的实验模拟研究^[8]. 实验中一般通过激光辐照固体靶产生高温等离子体, 靶物质压缩或加热实验气体产生辐射激波^[9,10]. 不同靶物质与实验气体的作用方式不同, 塑料靶主要通过靶物质激波推动和压缩气体产生辐射激波; 而高Z金属靶辐射的X射线可以快速加热周围的气体, 演化出辐射激波. 实际应用中经常设计混合材料的固体靶, 以产生特定的辐射激波^[11]. 目前开展的实验中已经对辐射激波的形态结构^[12,13]、辐射光谱^[14,15]、激波参数^[16-18]和不稳定性发展^[6,19]等特征进行了广泛的研究. 利用辐射激波产生的高温高压条件也可以研究极端状态下的物质性质^[20], 并获取相应的状态方程^[21]和辐射不透明度^[22]数据.
辐射激波的理论研究也一直在发展中. Sew和Guess^[23]发现辐射效应将导致激波阵面的展宽. Zel’dovich和Raizer^[24]指出激波发出的辐射将加热上游的介质形成波前结构, 并导致激波阵面后形成一个温度尖峰. Drake^[25]使用半解析方法发现光学厚介质中辐射激波的波前包括扩散区和透射区, 且扩散区的特征不完全依赖于激波下游的性质. McClarren等^[26]指出当激波上游为光学薄介质时, 波前不会形成, 激波发出的辐射将离开系统, 导致激波后的密度要高于光学厚的情况. Mabey等^[27]发展了光学厚介质中辐射激波下游温度的计算方法, 为实验中激波温度的评估提供依据.
本文使用模拟方法研究辐射激波发光特性的动态演化及其形成机制. 目前的实验研究难以测量辐射激波内部的光学特征, 而理论研究多局限于特定条件下的激波性质, 很少关注激波的演化过程, 已发表文献中对辐射激波光学特征的演化多是一些定性描述, 缺乏定量、清晰的研究结果. 本研究关注X射线加热氙气形成的辐射激波, 在这一条件下激波的演化过程和发光现象非常丰富, 研究结果有助于理解辐射激波的物理过程，并为相关实验设计提供理论支撑. 本文第2节分别介绍计算模型(2.1), 计算程序中输入的氙气参数(2.2), 以及程序和参数的校验方法(2.3); 第3节是本文的研究结果和讨论; 第4节是全文总结.

2

-->

2.1.计算模型

本文对辐射激波的模拟使用Zinn^[28]提出的一维辐射流体力学模型(本文称为Zinn模型). 该模型的气体动力学和辐射输运过程均在球对称的拉格朗日坐标下求解. 模型假设介质处于局部热平衡状态, 并采用多群近似求解辐射输运过程. 这一方法在辐射能流的计算中充分利用了计算网格的球对称特征, 并对高温区和周围介质的辐射能流区分处理, 大大加快了计算速度.
Zinn模型采用有限差分格式, 将空间划分为一系列同心球层, 并假设每一球层的密度、温度等力学量是均匀分布的. 辐射输运过程求解中, 由P₁点传输到P₂点辐射的谱强度可以表示为(由忽略散射项的积分形式辐射输运方程求得)

$ {I}_{\vartheta }\left({{P}}_{2}\right)={I}_{\vartheta }\left({{P}}_{1}\right){\rm{e}}^{-{\mu }_{\rm{a}}'\Delta s}+{B}_{\vartheta }\left(1-{\rm{e}}^{-{\mu }_{\rm{a}}'\Delta s}\right) $

其中$ {I}_{\vartheta } $为辐射的谱强度, $ \vartheta $表示辐射频率, $ \Delta s $为P₁和P₂间的距离, ${\mu }_{\rm{a}}'$为考虑受激发射的辐射吸收系数, $ {B}_{\vartheta } $为平衡辐射的谱强度.
辐射的谱能流$ {F}_{\upsilon } $定义在球层边界, 同一位置向外和向内的谱能流可分别表示为:

$\begin{split}&{F}_{\upsilon }^+=2{\rm{\pi }} \int _{0}^{{\rm{\pi }}/2}{I}_{\vartheta }\left(\theta \right){\rm{sin}}\theta {\rm{cos}}\theta {\rm{d}}\theta , \\&{F}_{\upsilon }^-=-2{\rm{\pi }}\int_{{\rm{\pi }}/2}^{{\rm{\pi }}}{I}_{\vartheta }\left(\theta \right){\rm{sin}}\theta {\rm{cos}}\theta {\rm{d}}\theta .\end{split}$

其中θ为半径方向与特定辐射方向的夹角. 将$ {I}_{\vartheta } $的表达式代入, 并根据球对称几何关系可以得到任一球层通过内边界向内的辐射谱能流$ {F}_{1}^{-} $和通过外边界向外的辐射谱能流$ {F}_{2}^{+} $($ {F}_{1}^{-} $和$ {F}_{2}^{+} $均略去下标$ \vartheta $)的表达式. 由于计算过程比较繁琐, 此处略去具体的表达式和推导过程, 这些都可在文献[28]中找到.
本模型的一个重要假设是空间中每一点的辐射谱强度都可以用双值阶梯函数来表示, 即来自核心高温区的辐射取大的强度值$ {I}_{\rm{a}} $, 核心区以外的辐射取较小强度值$ {I}_{\rm{b}} $. 将这两个辐射谱强度值代入球层内外边界辐射谱能流的表达式, 联立消去辐射谱强度变量便可得到$ {F}_{1}^{-} $与$ {F}_{2}^{+} $的递推关系. 其中$ {F}_{1}^{-} $仅与其外层向内的辐射谱能流$ {F}_{2}^{-} $有关, 可以从最外层(辐射谱能流一般为零)逐层向内求解. 将计算得到的一系列向内的辐射谱能流代入, 并从核心(半径和辐射谱能流均为零)逐层向外求解$ {F}_{2}^{+} $, 这样就得到了系统对外的辐射谱能流. 当两个相邻的球层均为光学厚介质(光学厚度大于2)时, 上述辐射输运过程可以简化为扩散近似来求解.
本模型计算每一时间步辐射输运的同时, 进行一步或多步流体计算. 流体求解过程中, 首先根据密度、内能和状态方程求解每一球层的压强$ {P}_{i} $和粘性压$ {Q}_{i} $, 然后根据这些压强值求解每一层在流体时间步$ {\Delta t}_{\rm{H}} $中产生的加速度, 通过加速度可以计算该层在$ {\Delta t}_{\rm{H}} $后的位移、速度和内能, 进一步得出其他流体参量.
2 -->

2.2.气体参数

在模型计算过程中需要输入气体的状态方程与辐射不透明度参数, 这些参数的准确性对于得到可靠的计算结果非常重要. 本文使用的氙气辐射不透明度数据采用DCA/UTA不透明度程序计算^[29]. 该程序中原子的能级结构采用细致组态近似(detailed configuration accounting, DCA), 在计算谱线跃迁时, 使用UTA(unresolved transition array)统计模型近似考虑细致能级的谱线结构^[30,31]. 这套程序计算的不透明度结果与其他理论和实验结果进行了大量比较^[29,32], 证实其计算结果是可信的, 且具有较高的精度. 本文计算得到两个密度下的氙气不透明度数据如图1所示.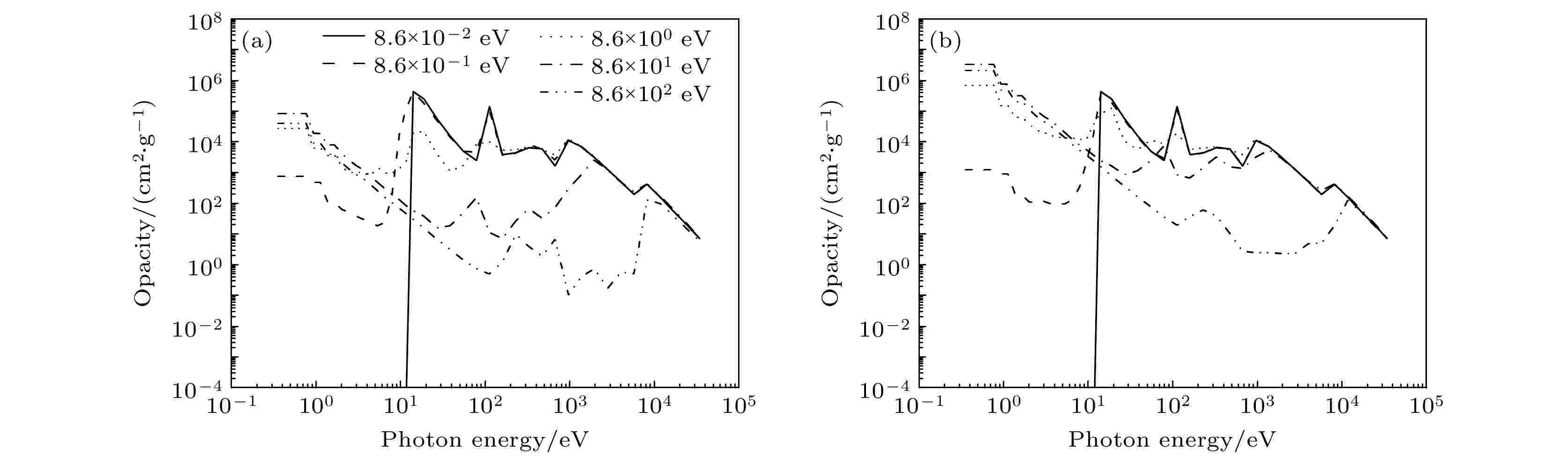
图 1 不同气体密度时氙气的辐射不透明度随光子能量的变化　(a) ρ = 5.33 × 10^–7 g/cm³; (b) ρ = 5.33 × 10^–3 g/cm³. 不同曲线类型表示不同的温度 (1 eV = 11610 K)
Figure1. Opacity data of xenon at the density of 5.33 × 10^–7 g/cm³ (a) and 5.33 × 10^–3 g/cm³ (b), lines with different style represent different temperature.

氙气状态方程数据的计算结合化学模型^[33]与平均原子模型, 其中平均原子模型的原子结构用哈特里-福克-斯莱特(HFS)自洽场方法计算^[34]. 计算中, 当温度低于2.6 eV时采用化学模型, 温度高于8.6 eV时采用平均原子模型, 两个温度之间的区域采用插值数据. 化学模型基于经验势和液体变分微扰理论计算了氙分子间相互作用能, 考虑了四级电离, 并基于正则分布和NIST公开数据库^[35]提供的原子激发能级计算了离子组分内部的电子热激发能. 计算得到的状态方程参数如图2所示.
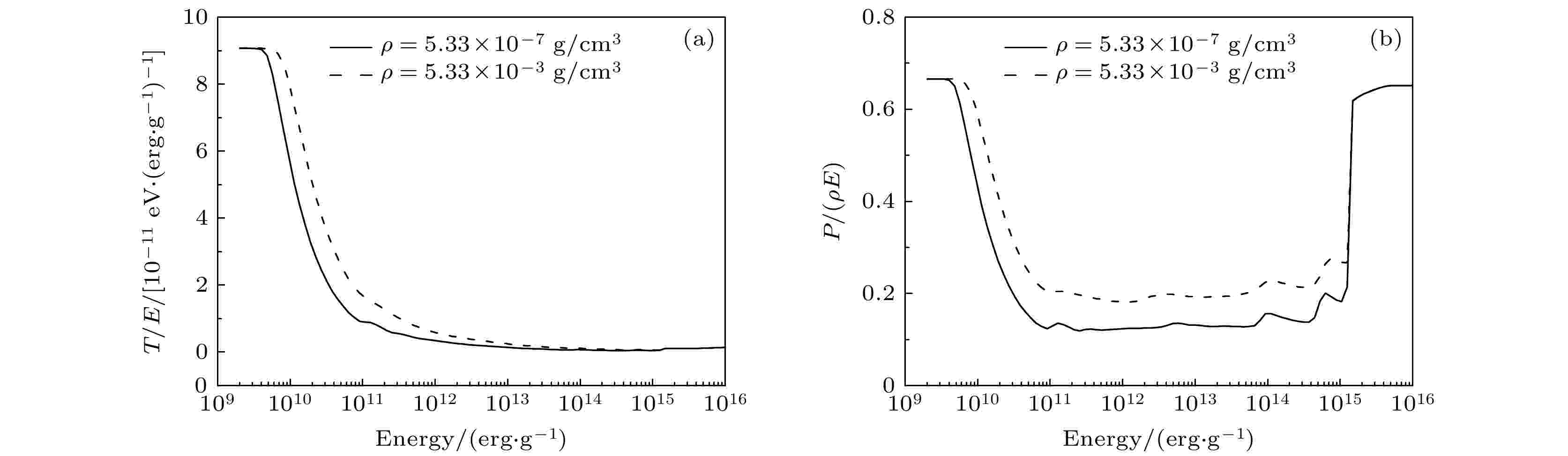图 2 氙气的状态方程数据　(a)温度(T, 单位为eV)与比内能(E, 单位为erg/g (1 erg/g = 10^–7 J/g))之比随E的变化; (b)压强(P, 单位dyn/cm² (1 dyn/ cm² = 10^–5 N/ cm²))与E和密度($ \rho $, 单位g/cm³)乘积之比随E的变化. 参数使用比值形式是为方便程序计算
Figure2. Equation-of-state data of xenon: (a) Variation of the ratio between temperature (T, in eV) and specific inertial energy (E, in erg/g) with E; (b) variation of ratio between pressure (P, in dyn/cm²) and the multiplication of E and density ($ \rho $, in g/cm³) with E. The parameters are shown by ratios for computation convenience.

2 -->

2.3.模型校验

为了验证所用程序和氙气物性参数的可靠性, 本文模拟了Vinci等^[17]和Koenig等^[18]对氙气中辐射激波的实验测量结果. 这些实验中激波产生的原理是: 激光照射到靶材上, 产生烧蚀激波, 靶材的设计避免了X射线加热, 这样烧蚀激波作为活塞, 推动氙气产生辐射激波. 实验中分别测量了0.1和0.2个标准大气压(atm)下氙气中辐射激波的平均速度和温度.
Zinn模型对0.1 atm氙气的计算中, 辐射激波的温度在1 ns时达到最大值, 约为20 eV (由380— 460 nm波段的辐射反推, 其他可见光波段的计算结果差异不大), 在实验测量中这一数值约为18 eV (文献[17]的图3), 模拟计算2—4 ns的激波平均速度为63 km/s, 与实验测量值65 km/s也很接近. 在0.2 atm的计算中, 辐射激波的最高温度和平均速度分别为13 eV和38 km/s, 与实验中的两次测量值9 eV, 45 km/s和11 eV, 41 km/s (文献[18]的表2)相差不多. 以上对比表明, 本文使用的模型和气体参数在实验涉及的氙气物性参数范围内是较为可靠的.
Zinn模型不包含激光与靶物质的相互作用过程, 因此在计算中对实验情形做了简化. 激波通过最内层球面的高速膨胀产生(相当于烧蚀激波的推动), 形成稳定的激波后, 计算激波各参量并与实验情况作对比. 在实验中, 氙气激波既有在烧蚀激波推动下向前的运动, 又有横向的扩张. 本文模型仅描述一维球对称扩张的情形, 并选取最内层驱动球面的半径为0.15 cm, 与实验情况类比相当于某个立体角所截取的波阵面的运动和扩张过程. 模拟中激波的横向尺度在7 ns内扩张1.33倍, 实验中的横向扩张是1.67倍. 原文中也曾使用一维程序进行模拟, 即使完全不考虑横向扩张过程, 仍然可以模拟激波的发光特征^[17,18], 因此就一维模拟而言, 本文计算更接近实验中辐射激波的扩张过程. 模型计算的多个参量都与实验测量值接近也证明了模型对激波物理过程描述的合理性.

本文研究的辐射激波由X射线加热氙气产生. 模拟设置中, 激光能量以内能的形式加载到核心球内, 核心球的半径取0.03 cm, 能量加载使用高斯函数, 总能量为250 J, 持续时间为1 ns. 在这一条件下, 核心球的温度可以被加热到100 eV以上. 本研究不涉及激光与靶物质的耦合过程, 但通过能量加载函数来代替靶物质X射线向气体中传输能量的过程. 对于不同初始条件的计算表明, 只要总能量不变且核心球能够被加热到100 eV以上, 激光能量加载函数和核心球半径的小幅调整, 对辐射激波演化过程的影响不大, 表明本文的计算结果是稳定的. 核心球和周围氙气密度均取2.58 × 10^–2 g/cm³, 对应常温时的压力约为4.5 atm. 以上条件参考神光II装置的激光参数^[5].
为了研究能量输入后氙气中激波的演化过程, 图3给出了几个典型时刻激波的密度(图3(a))和温度(图3(b))分布. 早期(< 3 ns)的气体密度扰动很小, 激波还未形成, 但中心温度高达几十电子伏(eV), 形成一个高温区. 此时高温区的扩张并未伴随明显的流体效应, 主要通过辐射加热周围介质, 形成高速扩张的热波^[36]. 一段时间后(20 ns), 流体扰动赶上热波阵面并以激波的形式进入周围的氙气中, 此时激波阵面与高温区表面重合, 高温区的密度明显降低. 刚形成的辐射激波(20 ns之前)上游存在一个温度低于1 eV的预加热区, 这便是波前结构, 波前随着激波温度的降低很快消失. 随着激波进一步向外扩张, 激波阵面逐渐与高温区表面分离, 形成了温度的双台阶状分布(1 μs以后的温度分布形状), 高温区和激波的温度也不断下降.
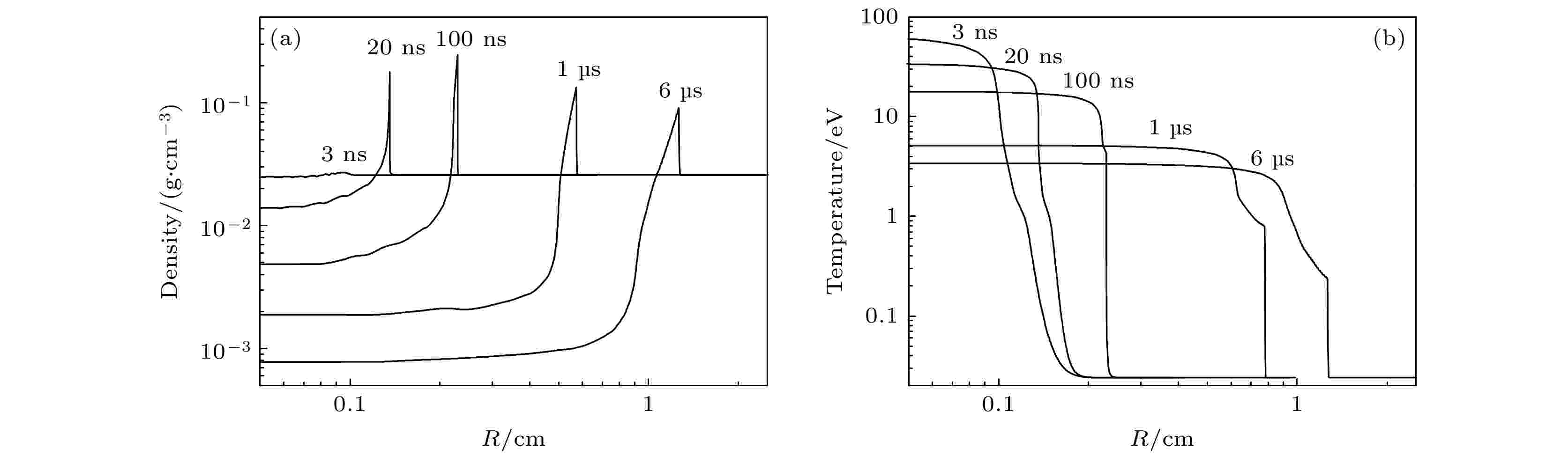图 3 不同时刻氙气中的密度(a)和温度(b)的位置分布
Figure3. Variation of density (a) and temperature (b) with position at different times in xenon.

根据氙气对外的辐射能流可计算其等效温度$ {T}_{\rm{eff}} $, 选取光学厚边界(将345 nm—420 nm波段的辐射吸收系数从最外层向内累加到1的球层)为气体发光位置, 在这一位置将不同波段的对外辐射谱能流按谱积分得到总能流S, 利用$ S=\sigma {T}_{\rm{eff}}^{4} $可以计算$ {T}_{\rm{eff}} $, 其中$ \sigma $是斯提芬-玻尔兹曼常数. 图4给出了等效温度的时间变化曲线, 30 ns—1 μs的数值抖动是高温区边界的空间网格分辨率不够导致的. 等效温度的变化过程表现出两个明显的峰值和一个极小值, 其中第一个峰值的等效温度(约3 eV)要高于第二个峰值(约1.5 eV). 下面详细研究激波演化过程中氙气的辐射特征及对应的物理过程.
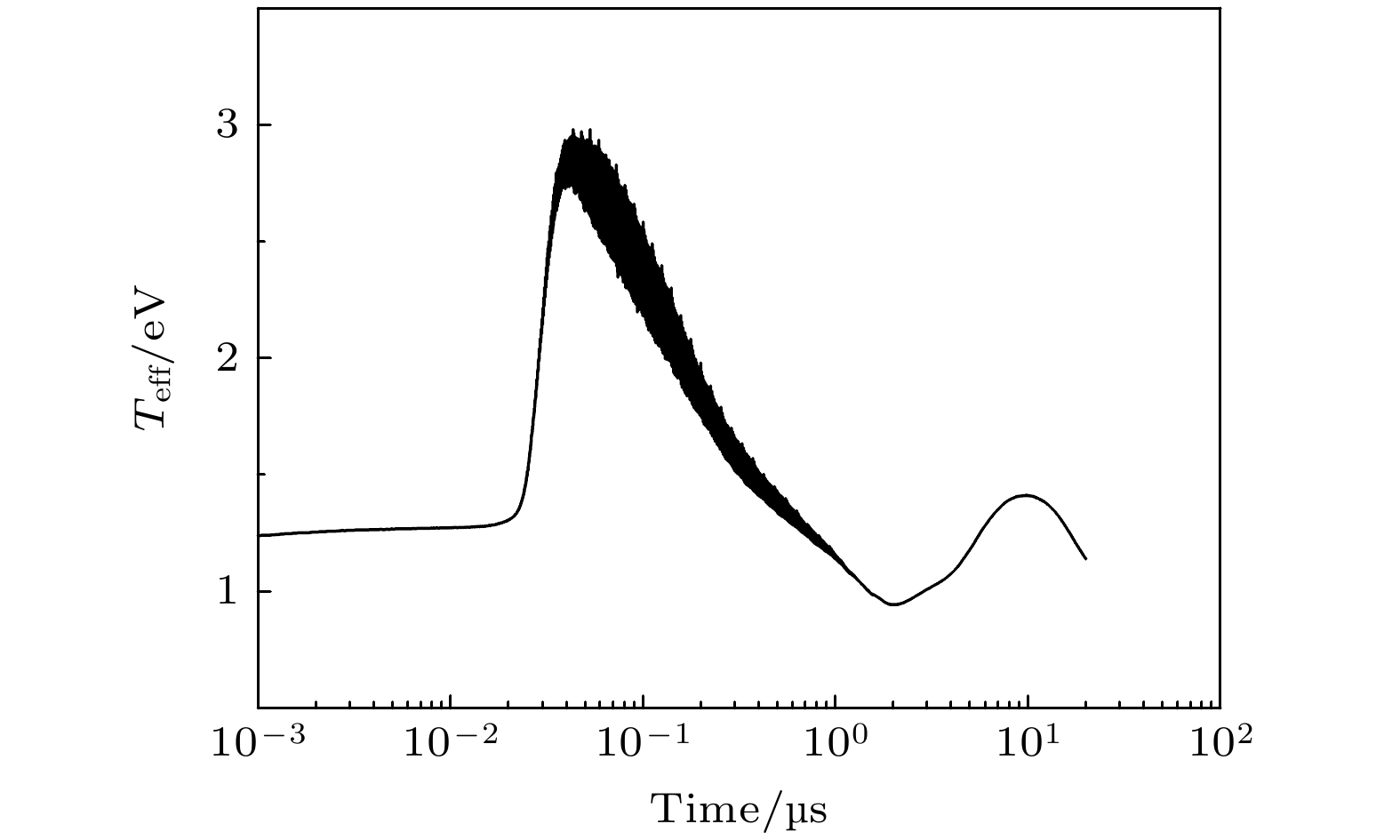图 4 氙气中辐射激波等效温度($ {T}_{\rm{eff}} $, eV)的时间演化曲线
Figure4. Time evolution of the effective temperature ($ {T}_{\rm{eff}} $, in eV) of radiative shock in xenon.

图5给出了高温氙气对外辐射光谱的时间演化过程, 计算的波长覆盖100—3600 nm. 从图5看出不同波段辐射能流的演化规律也与等效温度类似, 即存在两个辐射强度的峰值, 并在2 μs左右所有波段的辐射都减弱. 为了研究氙气辐射光谱的特征, 图6截取1 μs (图6(a))和6 μs (图6(b))两个时刻氙气的对外辐射光谱(实线), 并与相同等效温度下的黑体辐射光谱(虚线)作比较. 对比发现这两个时刻高温氙气的辐射光谱明显偏离黑体辐射光谱, 且不同时刻辐射光谱的形状也不一致. 由于计算模型使用多群近似, 每个能群内的辐射强度被平均化处理, 计算的辐射光谱不能显示气体辐射的精细结构, 但相对黑体辐射光谱的偏离是明显的.
图 5 辐射激波不同波段辐射能流的时间演化, 图像亮度代表辐射能流大小
Figure5. Time evolution of radiation flux at different wavelength of the radiative shock, and the radiation flux are represented by the brightness of the figure.

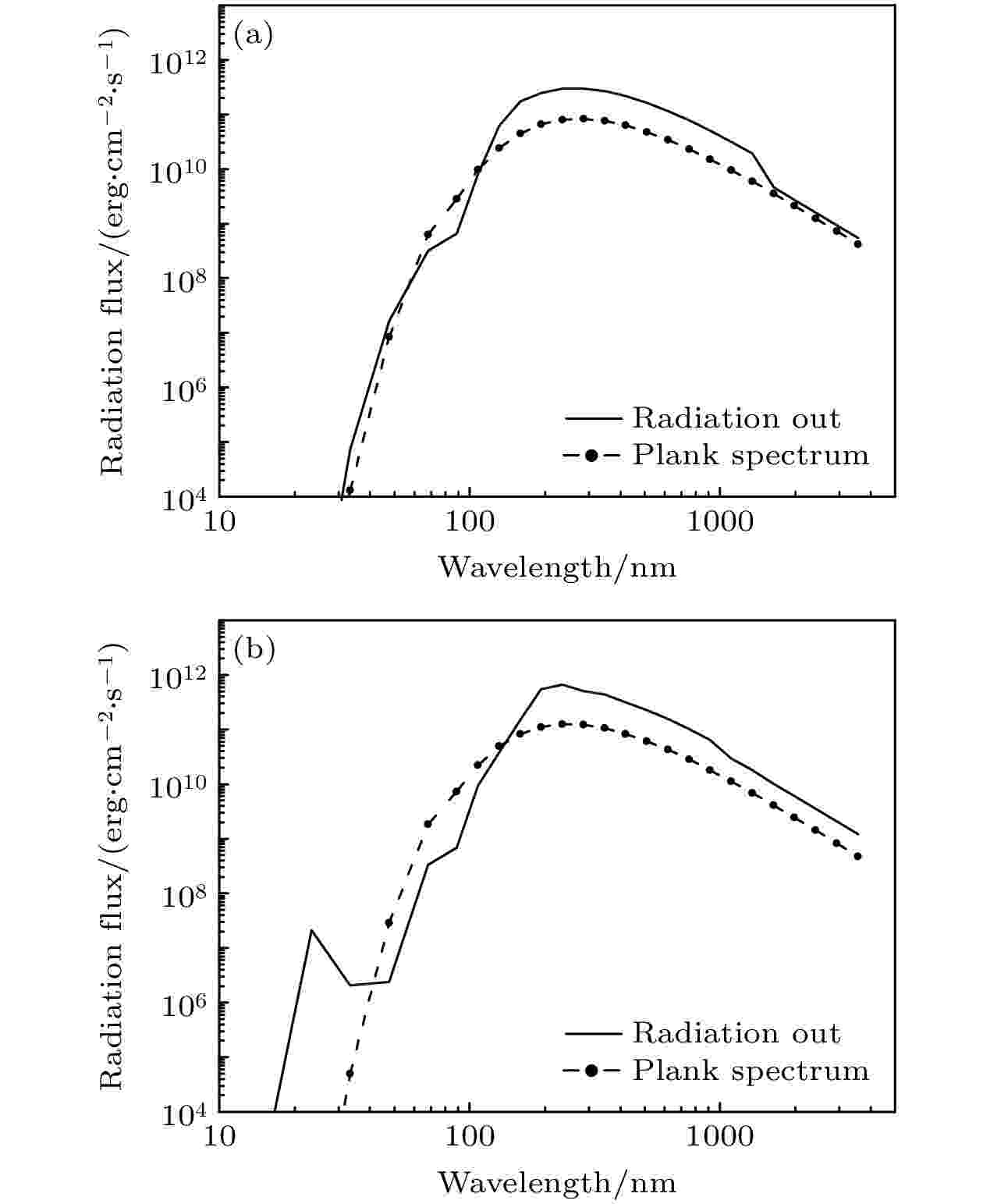图 6 不同时刻氙气的对外辐射光谱与相同等效温度下的黑体辐射光谱的比较　(a) 1 μs; (b) 6 μs
Figure6. Spectrums radiated from radiative shock in xenon and spectrums of blackbody radiation at the same effective temperature at different time: (a) 1 μs; (b) 6 μs.

为了研究氙气辐射光谱的形成机制, 图7给出了不同时刻中心高温区表面(虚线)和激波表面(点线)的黑体辐射光谱, 并与激波的对外辐射光谱(实线)作比较, 图8则给出了这些时刻380—460 nm波段辐射吸收系数的空间分布. 在辐射激波扩张过程中, 随着高温氙气不同位置温度和密度的变化, 这些位置的光学厚度也发生改变. 氙气的对外辐射光谱受辐射激波不同位置的辐射和吸收效应共同影响而偏离黑体辐射光谱, 并表现出观察到的强度变化.
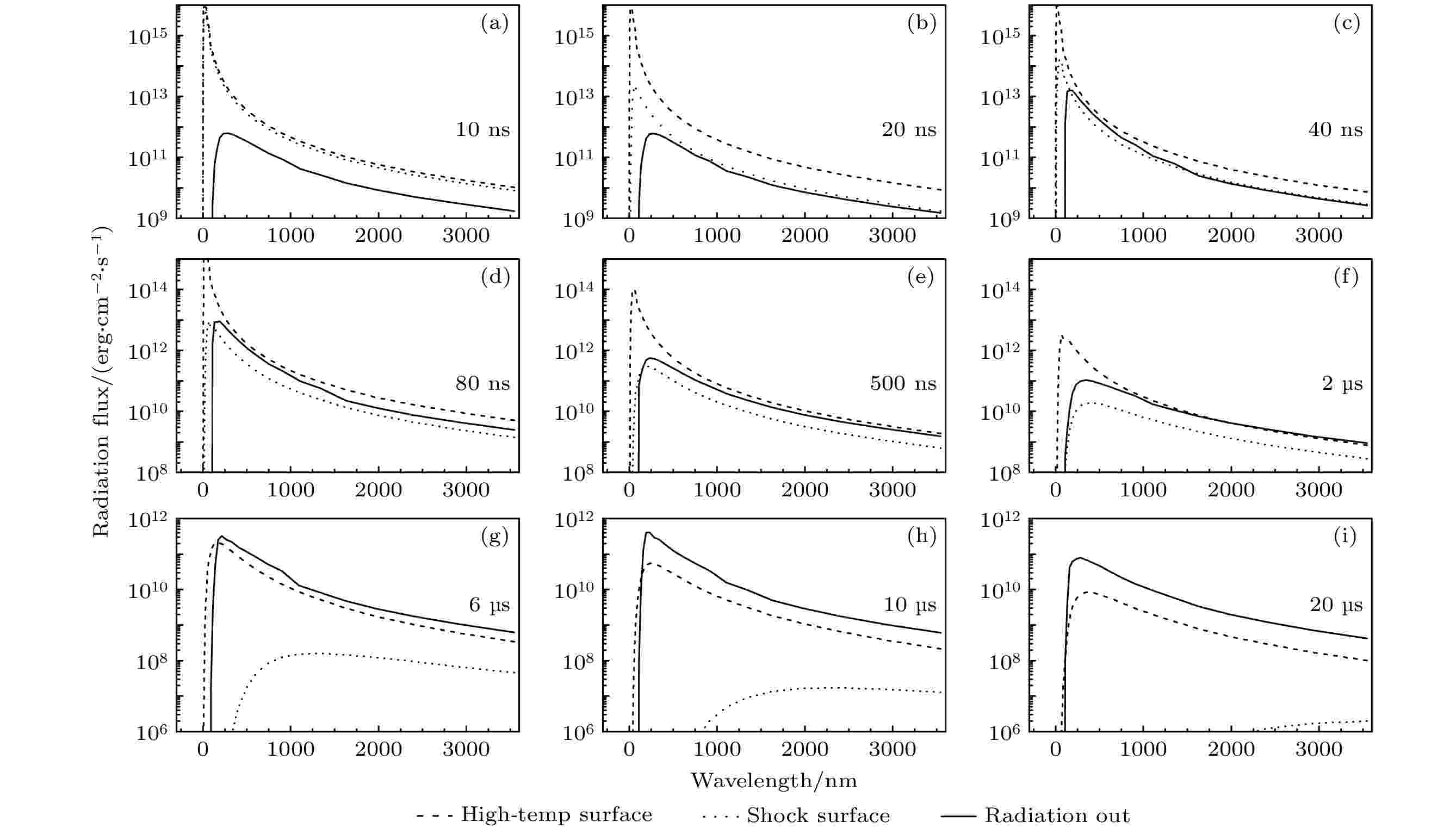图 7 高温区表面(虚线)、激波表面(点线)的黑体辐射光谱与氙气对外辐射光谱(实线)的比较.　(a)?(i)代表不同时刻的计算结果, 辐射能流统一投影到激波表面以避免球几何发散带来的影响
Figure7. Comparison among the blackbody spectrums at the surface of high-temperature-core (dash line), at the surface of the shock (dotted line), and the radiation spectrum outward-emitted by the radiative shock (solid line). (a)?(i) represent the result at different time, and all the radiation fluxes are projected on the shock surfaces to eliminate the spherical spreading effect.

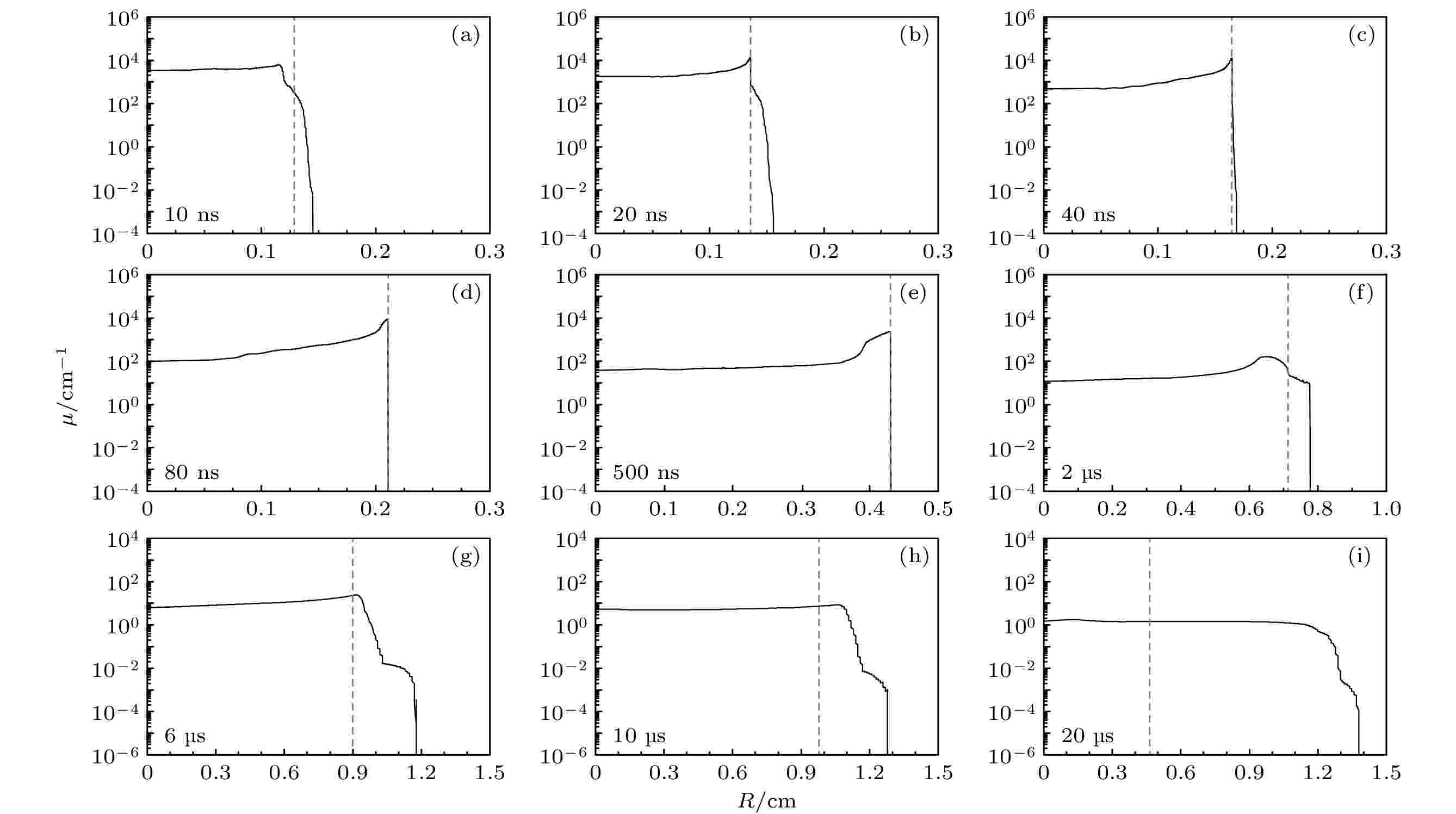图 8 380?460 nm波段的辐射吸收系数随位置的分布, 虚线为由外向内累积光学厚度为1的位置.　(a)?(i)代表不同时刻, 时间与图7相同
Figure8. Variation of absorption coefficient at 380?460 nm with position, the dash line mark the position where the optical depth equal to 1 from outside-in. Panel (a)?(i) are the same time as in Fig. 7.

刚形成的激波(10 ns)位于高温区的外表面, 激波表面和内部的温度很高, 是光学厚的, 只有激波表面的辐射可以透出. 此时激波的波前对辐射有较强的吸收(图8(a)), 使对外辐射强度弱于激波表面辐射(图7(a)). 一段时间后(20 ns), 波前吸收变得很弱, 激波表面的辐射可以透出, 对外辐射光谱与激波表面的黑体辐射光谱接近(图7(b)). 在40 ns 时刻, 激波对400 nm—1500 nm波段的吸收弱于其他波段, 使得这段辐射略强于激波表面辐射, 对外辐射能谱也偏离黑体辐射光谱(图7(c)). 这段时间由于波前吸收的减弱, 激波对外辐射呈增强趋势, 对应图4等效温度第一个峰值的上升段. 注意在不同阶段, 氙气对于高能光子(波长在100 nm以下)的吸收始终很强.
激波在之后的扩张过程中逐渐变得透明, 使得激波后的部分辐射也可以透出, 对外辐射开始强于激波表面的辐射(图7(d)和图7(e)). 到2 μs时刻, 激波除对高能光子外几乎变得完全透明, 高温区表面的辐射可以透出(图8(f)), 使得对外辐射能谱与高温区表面的黑体辐射光谱接近(高能光子除外), 气体发光面过渡到高温区表面(图7(f)). 这段时间激波区域的辐射强度随温度的下降而不断降低, 对外辐射强度整体呈减弱趋势, 对应图4等效温度第一个峰值的下降段.
随着温度的降低, 高温区表面也开始变得透明(图8(g)), 内部的部分辐射可以透出, 使对外辐射强于高温区表面的辐射(图7(g)). 随着高温区内部的辐射不断透出, 氙气的对外辐射又开始增强(图7(h)), 对应图4等效温度第二个峰值的上升段. 最后, 高温区温度降低导致的辐射减弱效果超过辐射吸收系数降低导致的辐射增强效应, 对外辐射又开始降低(图7(i)), 对应图4第二个峰值的下降段.
为了对比不同压强下氙气的对外辐射特征, 本工作还调整参数计算了辐射激波的光学演化过程. 研究发现, 压强在0.45—8 atm范围内, 激波发光特性演化的主要过程是类似的, 只是特征时间与发光强度有所差异. 所以, 以上的研究结果具有普遍意义.

本文使用Zinn模型研究了氙气中X射线加热产生辐射激波的发光特性及其演化过程. 首先构建了一套氙气的辐射不透明度与状态方程参数, 并通过对比实验数据, 验证了模型和氙气参数的合理性.
模拟研究发现, X射线加热的氙气中形成了热波、辐射激波、以及激波与内部高温区的分离等现象. 伴随着这些过程, 氙气的对外辐射表现出两个亮度峰值和一个亮度极小值. 且不同时刻的辐射光谱分布经常偏离黑体辐射光谱. 这是由气体中不同位置的辐射吸收系数随时间的演化造成的.
刚形成的辐射激波位于高温区的外表面, 激波阵面以内是光学厚的. 此时氙气的发光面位于激波表面, 但波前对辐射有强烈的吸收. 随着波前吸收的减弱, 气体对外辐射逐渐增强并达到第一个峰值. 之后, 随着激波的扩张, 其温度不断降低, 对外辐射也不断减弱. 温度降低也导致激波逐渐变得透明, 波阵面后的部分辐射可以透出. 激波变得完全透明时, 发光面过渡到内部高温区表面, 高温区内部仍然是光学厚的. 随着温度的进一步降低, 高温区表面也逐渐变得透明, 内部的辐射可以透出, 气体辐射强度随之增强并到达第二个峰值. 最后, 温度降低导致内部辐射强度衰减, 气体对外辐射强度再次降低. 以上便是氙气中辐射激波的演化过程, 在这些过程中氙气对波长100 nm以下的辐射始终是不透明的, 而对400 nm—1500 nm波段的吸收经常弱于其他波段.
本文的研究结果表明, 辐射激波的对外发射光谱并不严格符合黑体辐射光谱, 在黑体辐射假设下的计算中需要考虑这一偏离造成的误差. 在实验诊断中, 由于高温气体的发光位置是动态变化的, 根据外部光学测量反推的物理量只是气体不同区域对外辐射叠加后的等效值.