摘要: 腔增强吸收光谱技术作为一种高灵敏的痕量气体测量技术, 其吸收光谱的浓度反演是极其关键的环节. 为消除因吸收截面和仪器响应函数的不确定性引入的测量误差, 本文提出了一种基于标准样品吸收光谱的浓度回归算法, 该方法在浓度反演过程上进行优化, 采用标准气体样品吸收光谱直接拟合未知浓度气体吸收光谱. 采用中心波长在440 nm处的蓝色发光二极管(LED)作为光源, 建立了一套非相干光腔增强吸收光谱技术(IBBCEAS)系统, 实测腔镜反射率为99.915%, 利用NO
2 气体的实测吸收光谱对该算法的有效性进行了验证. 与常规吸收截面回归算法比较, 结果表明本文提出的标准样品回归算法具有显著的优越性, 测量精度提升约4倍. 利用改进的算法结合标准样品配制的多个NO
2 气体对实验系统性能进行了深入评估, 测量结果与理论值具有很好的一致性. Allan方差分析显示在积分时间为360 s的情况下, NO
2 检测限可达到5.3 ppb (1 ppb = 10
–9 ).
关键词: 非相干宽带腔增强吸收光谱 /
NO2 /
可见光谱 /
多元线性回归 English Abstract NO2 gas detection based on standard sample regression algorithm and cavity enhanced spectroscopy Bian Xiao-Ge Zhou Sheng Zhang Lei He Tian-Bo Li Jin-Song Department of Physics and Materials Science, Anhui University, Hefei 230601, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 61905001, 41875158, 61705001, 61705002, 61675005), the National Key R&D Project of China (Grant No. 2016YFC0302202), the Natural Science Foundation of Anhui Province, China (Grant Nos. 1908085QF276, 1808085QF198, 1508085MF118), and the Natural Science Foundation of the Higher Education Institutions of Anhui Province, China (Grant No. KJ2018A0034)Received Date: 13 August 2020Accepted Date: 13 September 2020Available Online: 21 February 2021Published Online: 05 March 2021Abstract: Cavity-enhanced absorption spectroscopy is a highly sensitive trace gas measurement technology, and the algorithm for retrieving gas concentrations is critical. The absorption cross-section is traditionally used to retrieve the concentration. However, the absorption cross-section used in the fitting process is affected not only by the response function of the instrument and the light source, but also by temperature and pressure. The uncertainty of the absorption cross-section will influence the accuracy of the result. Therefore, in order to eliminate the measurement error introduced by the uncertainty of the absorption cross-section and the instrument response function, a concentration regression algorithm based on the absorption spectrum of the standard sample is proposed. The process of concentration inversion is optimized. The absorption spectrum of standard gas is used to fit the unknown spectrum. In order to verify the effectiveness of the algorithm, the incoherent cavity enhanced absorption spectroscopy (IBBCEAS) system based on a blue light-emitting diode (LED) operating at 440 nm is established to analyze the absorption spectrum of NO2 ; and the fitting effect, measurement accuracy and stability are compared with the counter parts from the traditional absorption cross-section method. In the experiment, the measured reflectance of the cavity mirror is 99.915%. Compared with the conventional absorption cross-section regression algorithm, the standard sample regression algorithm proposed in this paper shows good results, in which the measurement accuracy is increased by about quadruple. The Allan deviation shows that a detection limit of 5.3 ppb can be achieved at an integration time of 360 s. Finally, the performance of the experimental system is evaluated by measuring the NO2 with different concentrations prepared by standard samples. The result shows good agreement with the theoretical value, which indicates that the improved spectral analysis algorithm is feasible and reliable for gas detection. This method can be used not only to measure NO2 , but also to detect other gases, which shows great potential applications in monitoring the industrial emissions, atmospheric chemistry and exhaled breath analysis.Keywords: incoherent broadband cavity enhanced absorption spectroscopy /NO2 /visible spectrum /multiple linear regression 全文HTML --> --> --> 1.引 言 近年来大气环境问题形势严峻, 大气污染物排放量居高不下. 大气污染俨然成为了第一大环境污染问题, 大气污染监测成为环境监测中不可缺少的一部分[1 ] . 基于激光光谱技术的痕量气体成分识别与高灵敏度检测逐渐成为大气污染物检测中的重要研究方向. 光谱检测技术因其具有高灵敏度、实时、可在线测量的优点, 被认为是一种比较具有前景的测量方法. 但大气中污染气体的浓度通常是ppb (part per billion)量级的, 常规的吸收光谱技术需要很长的吸收程长才能满足测量的要求, 系统体积庞大. 近年来, 基于高精密光学谐振腔的吸收光谱技术, 如积分腔输出光谱(ICOS)和腔增强吸收光谱(CEAS), 因为具有灵敏度高、响应快等优点, 在气体分析领域得到了广泛应用[2 ,3 ] . 1998年, Engeln等[4 ] 率先提出了腔增强吸收光谱技术的概念, 可以在腔长不足1 m的情况下, 实现几公里的有效吸收程长, O’Keefe[5 ] 在此基础上, 以可调谐半导体激光器为相干光源, 提出了积分腔输出光谱, 并在腔镜上采用压电陶瓷来控制腔长. 但激光器发出的激光是窄带光谱线, 不适合短波长区域的测量, 使得相干腔增强吸收技术的发展受到了限制, 基于这一点, Fiedler等[6 ] 使用高压氙灯为光源结合高精细光学腔测量了苯和氧在600 nm附近的吸收光谱, 由此非相干宽带腔增强吸收光谱(IBBCEAS)技术在大气测量方面得到迅猛的发展. 目前, IBBCEAS已经被广泛应用于NO2 [7 ] , HONO[8 ] , SO2 [9 ] , CHOCHO[10 ] , I2 [11 ] 等气体的检测, 如Jordan和Osthoff[12 ] 使用长度约1 m的光学腔在361—388 nm波段处监测痕量气体NO2 , 反射率超过99.98%, 测量精度达到210 ppt (1 ppt = 1 ng/L); 段俊等[13 ] 在约365 nm附近的气体中进行测量, 使用的光学腔为55 cm, 最大反射率约99.983%, NO2 的测量精度为340 ppt; 梁帅西等[14 ] 在438—465 nm波长范围内测量气体, 其有效腔长为70 cm, 此时反射率最大达到99.9942%, NO2 的测量精度可达29 ppt; 吴涛等[15 ] 在353—376 nm的测量范围内, 得到最高反射率为99.917%, 两块反射镜相距1.76 m, NO2 的检测极限为1.8 ppb (1 ppb = 10–9 ); 凌六一等[16 ] 使用长度为70 cm的光学腔, 镜片反射率在390 nm处最大, 为99.962%, 对应的探测灵敏度为1.9 ppb. 除了检测气体浓度, IBBCEAS技术还被应用于不同气体的瑞利散射截面[17 ] 以及气溶胶消光的测量[18 ] .x x 9 cm–3 , 氮氧化物的去除率较高, 最适宜消除氮氧化物污染, 若外加适当条件, 氮氧化物能重新建立平衡, 从整体上降低氮氧化物浓度[19 ] , 基于此, 实时监测大气中氮氧化物的含量成为治理大气污染的一种辅助手段. 此外, 大气中的NOx [20 ] .2 吸收光谱测量技术中浓度反演方法通常是将待测气体的吸收光谱与吸收截面拟合得到浓度值, 但拟合过程中要用到的吸收截面不仅会受到仪器响应函数和激光光源的影响, 它本身也会受温度[21 ] 和压力[22 ] 等的影响, Bogumil等[23 ] 在380—460 nm范围内对不同温度下NO2 截面研究发现了温度越低吸收就越强. Mellqvist和Rosen[24 ] 也通过研究得到了温度升高时气体吸收谱线的峰值减小、峰谷值增加的结论. 吸收截面的不确定性会降低反演结果的精确度. 针对上述情况, 本文在浓度反演过程上进行优化, 提出了一种基于标准样品吸收的浓度回归算法, 利用标准气体的吸收光谱直接拟合待测气体谱线, 反演出相应的浓度, 该方法可以有效消除因吸收截面不确定性和仪器响应函数误差性所带来的影响, 同时还可以消除长期外场连续测量时受环境因素(尤其是恶劣条件下)变化引起的光源漂移的影响, 提高浓度结果的精准度. 为了验证算法的有效性, 搭建了IBBCEAS系统对NO2 气体的吸收光谱进行分析, 并在拟合效果、测量精确度和稳定性三个方面与传统吸收截面方法进行对比, 最后对算法的稳定性进行了性能评估.2.实验装置 实验中所搭建的IBBCEAS系统的装置如图1 所示, 该系统由电流控制器、光源准直器件、滤光片、谐振腔、光纤耦合器、光纤跳线和光谱仪组成. 电流控制器(DC4104)是一个多通道LED驱动器, 通过前面板上的旋转器和按钮控制为LED光源加载相应的驱动电流, 在控制器和LED光源之间有接头集线器(DC4100-HUB)和带有M8 × 1传感环形连接器的连接线缆进行连接. 使用峰值波长为440 nm, 半高半宽为18 nm的蓝色LED作为光源, 但由于LED发出的光束具有较大的发散性, 不能直接用作激发光源, 需要利用光学准直器件将光以最大效率耦合进入光腔中, 准直后的杂散光经过滤光片消除后直接进入由一对高反射率镜面组成的高精密光腔中, 两块反射镜之间的距离为50 cm, 腔镜的反射率在430—450 nm范围内大于99.9%. 气体样品的进样流速由质量流量控制器控制, 腔体内壁涂有聚四氟乙烯材料以减少吸附作用. 通过腔体的光直接经过FiberPort耦合器(PAF2-4 E)并与SMA接头的光纤耦合进入0.4 nm分辨率的微型光纤光谱仪(Ocean Optics)中, 最终采用自行编写的LabVIEW软件实现数据采集和光谱分析功能.图 1 实验装置图Figure1. Schematic of experimental setup.3.信号处理方法 HITRAN数据库给出了NO2 波长在250—650 nm之间的吸收截面, 如图2(a) 中蓝线所示. 但是NO2 在415 nm以下会发生光化学解离现象[25 ] , 导致信号强度降低, 而图2(a) 中红线所示的LED发射光谱的中心波长在440 nm, 不会受到NO2 光化学解离的影响, 是较合适的用于NO2 检测的光源. 利用光功率计测量了在不同注入电流下的LED发射功率, 结果如图2(b) 所示. 从图中可以看到电流与输出功率呈正相关, 线性拟合相关系数高达0.99793. 由于驱动板加载的电流限制, 最大输出电流为700 mA, 对应的输出最大功率为73.1 mW.图 2 (a) NO2 吸收截面(蓝线)与LED发射光谱(红线); (b) LED输出功率与电流关系Figure2. (a) NO2 absorption cross-section (blue line) and LED emission spectrum (red line); (b) relationship between LED output power and current.图3 给出了两种算法的浓度反演流程图, 左边是传统的标准吸收截面回归法, 右边为本文提出的基于标准样品回归法. 为了验证标准样品回归法反演待测气体浓度的有效性, 利用搭建的IBBCEAS系统对NO2 气体吸收光谱进行了测量. 整个实验过程中, 温度稳定在26 ℃, 工作电流控制在300 mA, 以保证光源输出和信号光强的稳定性.图 3 拟合流程图Figure3. Flow chart of fitting.3.1.标准吸收截面回归法 3.1.标准吸收截面回归法 腔增强吸收光谱技术采用两块高反射率腔镜组成高精度光学腔, 测量在腔内经过多次反射后从后腔镜透射的积分光强. 通过测量腔内气体对光的选择性吸收引起的光强变化得到吸收系数, 最终确定待测气体浓度. 吸收系数可以通过如下公式获得:λ 为波长, I 0 和I 分别是以N2 为背景的吸收光强以及腔内含有待测气体时的光强, ${\alpha _{{\rm{Ray}}}}\left( \lambda \right)$ 为待测气体的瑞利散射系数, $R\left( \lambda \right)$ 是与波长相关的反射率, d 是腔长.[26 ] , 可以是通过已知浓度的气体来获得镜片反射率, 也可以利用O2 –O2 吸收进行标定. Washenfelder等[27 ] 用N2 和He的Rayleigh散射差异大的特性来确定反射率, 该方法操作简单. 本文就是利用这两种气体的消光程度的差异性对腔镜反射率进行了标定. N2 和He的吸收光谱与反射率关系可用(2 )式表示[28 ] :${I_{{{\rm{N}}_{\rm{2}}}}}\left( \lambda \right)$ 和${I_{{\rm{He}}}}\left( \lambda \right)$ 分别表示腔内充满N2 和He时测到的光强, $\alpha _{{\rm{Ray}}}^{{{\rm{N}}_{\rm{2}}}}\left( \lambda \right)$ 和$\alpha _{{\rm{Ray}}}^{{\rm{He}}}\left( \lambda \right)$ 分别是N2 和He散射产生的瑞利散射系数, 可根据瑞利散射截面和分子数密度计算得到. $\sigma _{{\rm{Ray}}}^{{{\rm{N}}_{\rm{2}}}}\left( \lambda \right)$ 和$\sigma _{{\rm{Ray}}}^{{{\rm{N}}_{\rm{2}}}}\left( \lambda \right)$ 利用Sneep和Ubachs[29 ] 以及Shardanand和Rao[30 ] 等测量得到的数据, 经过插值的方法得到需要的波长区域的吸收截面值.2 (99.999%)和He(99.999%)的光强变化, 利用(2 )式对腔镜的反射率进行了标定. 根据LED发光谱的中心波长位置选择了反射率的标定范围为430—450 nm, 图4(a) 给出了计算得到的与波长相关的反射率曲线, 在440 nm处的反射率达到0.99915, 相应的腔损耗(1–R (λ ))达到851 ppm (1 ppm = 1 mg/L)以及有效长度d /(1–R (λ ))为0.5 km.图 4 (a)随波长变化的反射率曲线; (b)腔损耗(黑线)和有效路径长度(绿线)Figure4. (a) Mirror reflectivity as a function of wavelength; (b) cavity loss (black line) and corresponding effective path length (green line).1 )式可以计算得到待测气体的吸收系数, 并根据最小二乘法拟合原理得到待测气体的浓度值[31 ] ,${\sigma _i}$ 和${N_i}$ 为待测气体i 的吸收截面和数浓度. 浓度拟合的原则以“残差平方和最小”来确定, 并利用python软件进行处理. 吸收截面$\sigma \left( \lambda \right)$ 由高分辨率吸收截面与仪器函数经过卷积得到[32 ] , 如图5 所示.图 5 NO2 吸收截面的卷积Figure5. Convolution of the NO2 absorption cross-section.2 样品, 并将实测吸收系数与标准吸收截面分别进行拟合. 拟合结果及其相应的残差如图6 所示. 实测谱线与拟合得到的谱线差异明显, 尤其是在高浓度的情况下. 通过比较拟合残余量可以看到, 随着NO2 浓度的升高, 拟合残差也会增加. 这种有较大拟合残差的光谱拟合效果, 反演得到的浓度也会有较大的不确定性. 表1 给出了各个浓度的光谱拟合残差及其标准偏差, 并选择拟合结果较好的445 nm附近的峰值求其信噪比(幅值/标准偏差). 根据统计结果可以看出, 信噪比随着浓度的增加呈现上升趋势, 但变化不明显.图 6 NO2 拟合结果 (a)实测吸收系数与标准吸收截面拟合; (b)拟合残差Figure6. The results of NO2 fitting: (a) Fitting between the measured absorption coefficient and the standard absorption cross section; (b) fitting residuals.浓度/ppm 7.86 5.08 3.28 2.07 1.42 0.75 标准偏差/(10–6 cm–1 ) 12.35 8.13 5.27 3.44 2.62 1.57 信噪比 11.23 11.08 10.95 10.38 9.72 8.94
表1 不同NO2 浓度对应的拟合残差的标准偏差和信噪比Table1. Standard deviation and signal-to-noise ratio of fitting residuals corresponding to different NO2 concentrations.3.2.标准样品回归法 -->3.2.标准样品回归法 吸收系数的值会受到多个变量取值的影响, 但这种影响大致会呈现线性关系. 本文以多元线性回归(MLR)法[33 ] 为理论依据, 提出了一种新的浓度反演方法, 利用标准气体的吸收光谱直接拟合未知谱线, 进而反演气体未知浓度. MLR算法表示了输入变量(X 1 , X 2 , ···, X n Y 之间的关系:α , β 1 , β 2 , ···, β n ε 为随机误差项. 基于这一理论做出了如图7 所示的多元线性拟合示意图, MLR算法充分利用了整个吸收光谱, 不是简单的吸收峰对比, 可以有效降低测量误差.图 7 多元线性拟合示意图Figure7. Multiple linear fitting diagram.2 中的NO2 )吸收光谱为X 轴作为参考, 待测样品实验光谱为Y 轴, 进行线性拟合, 线性相关度能达到0.95603, 比例因子为0.77511, 根据C Sample = C Reference × Slope, 可以得到待测气体浓度为7.75 ppm, 由于噪声等影响, 误差在1.4%以内. 光谱拟合表达式[34 ] 为${\alpha _{{\rm{ref}}}}\left( \lambda \right)$ 表示的是标准浓度下得到的吸收系数, K 0 为背景偏移量, K 1 是基于最小二乘法拟合估计得到的比例系数, $\alpha \left( \lambda \right)$ 为待测的气体吸收系数. 这种标准样品回归法在一定程度上消除了气体吸收截面因实验环境、仪器响应函数等因素的不确定性对浓度反演结果带来的影响.图8 所示为以浓度为10 ppm的NO2 气体吸收光谱与不同浓度下实测吸收系数的拟合效果以及相应的浓度残差对比图(图8(b) —图8(g) ), 对应的标准偏差和信噪比列在表2 中. 从图8(a) 中可以看出, 实验观察到的光谱与理论拟合得到的光谱符合度较高, 从而得到的拟合残差余量(实测值-理论值)及其标准偏差都整体有所降低, 该方法的拟合效果优于传统浓度反演方法. 通过对两种方法的信噪比结果分析, 改进的算法灵敏度能提升4倍左右, 而在0.75 ppm浓度下灵敏度只提升了2.81倍, 可能是气体浓度偏低, 噪声信号过大, 影响了信噪比.图 8 NO2 拟合结果 (a)实测吸收系数与标准气体吸收系数拟合; (b)?(g)拟合残差Figure8. The results of NO2 fitting: (a) Fitting of absorption coefficient between measured and standard gas; (b)?(g) fitting residuals.浓度/ppm 7.86 5.08 3.28 2.07 1.42 0.75 标准偏差/(10–6 cm–1 ) 2.7 1.67 1.36 0.78 0.62 0.59 信噪比 52.6 49.9 44.6 42.7 37.4 25.1
表2 不同NO2 浓度对应的拟合残差的标准偏差和信噪比Table2. Standard deviation and signal-to-noise ratio of fitting residuals corresponding to different NO2 concentrations.图9(a) , 浓度反演结果基本上都会略高于理论标准线(红色实线), 但浓度偏移量均有所差异, 如图9(b) 所示. 随着浓度增加, 绝对误差也会整体呈现上升趋势, 但最大偏移量不会超过0.44 ppm, 特别是标准样品回归法, 最大偏移量低于0.1 ppm, 最小也不到0.03 ppm. 为了更能反映测量的准确度, 图9(c) 给出了两种结果的相对误差, 吸收截面法计算得到的误差率主要集中在5%—8%之间, 而标准样品回归法的误差率均小于4%, 通过误差率的对比可以看出标准样品回归法反演的结果精确度要高于传统吸收截面法.图 9 浓度值对比 (a)浓度计算结果; (b)绝对误差; (c)相对误差Figure9. Concentration comparison: (a) The calculated value of concentration; (b) absolute error; (c) relative error.3.3.性能评估 -->3.3.性能评估 利用Allan方差分析评估了搭建的痕量NO2 气体测量系统的稳定性, 结果如图10 所示. 连续测量标准NO2 浓度, 记录约2 h, 并用(6 )式确定其Allan方差(图10(b) ):图 10 系统稳定性评估 (a) 2 h的浓度数据; (b) Allan偏差图; (c)直方图分析Figure10. System stability assessment: (a) Concentration data recorded for 2 hours; (b) Allan deviation plots; (c) histogram analysis.t 为时间, N 为采集的光谱序列数, X i t )是从i 到N 的序列中的NO2 浓度结果. 在传统Allan方差算法[35 ] 的结果中, 平均时间最大值存在“跳跃”现象, 为了消除这些“跳跃”, 选择了一种改进的算法[36 ] 来计算时间序列的Allan方差, 该算法使用了每个值的所有数据. 在360 s时NO2 的最佳精度为5.3 ppb. 为了进一步评估系统的灵敏度, 图10(c) 给出了利用直方图(Histogram)统计分析结果, 分析结果呈现出良好的高斯分布特性[37 ] , 并根据直方图的高斯分布计算其半高全宽(FWHM)为0.088 ppb.2 气体按照一定比例用N2 进行稀释, 采用标准样品回归法得到图11(a) 中的浓度梯度, 整个测量过程都是在大气压和室温下进行的. 最后一个梯度是持续性充入了流量为80 sccm (1 sccm = 1 mL/min)的纯氮气, 此时已经没有吸收峰轮廓, 只剩下背景噪声信号, 对应的1δ = 5.37862 × 10–7 . 将各个浓度梯度求其平均值和标准偏差并以误差棒的形式显示在图11(b) 中, 呈现很高的线性相关性.图 11 (a) NO2 气体的不同浓度; (b)浓度梯度平均值及标准偏差Figure11. (a) Different concentrations of NO2 ; (b) average and standard deviation of concentration gradient.4.总 结 通过采用IBBCEAS对NO2 气体的吸收进行测量, 验证了标准样品回归算法的可行性与准确度. 在标准吸收截面反演过程中, 不仅存在仪器分辨率相对较低带来的0.4%误差, 还有吸收截面卷积后的4.7%误差及环境影响因素, 而本文提出的标准样品回归算法则有效地消除吸收截面这一不确定性较高的变量, 减少了因不可控因素产生的误差. 相比于吸收截面回归法, 该方法拟合过程中的残差余量明显较低, 拟合效果更优; 浓度反演结果精准, 相对误差低于4%; 信噪比提高, 测量精度提高约4倍. 通过Allan方差分析, 在360 s的最佳采集时间下, 检测限能达到5.3 ppb. 最后利用改进的算法对配置的NO2 浓度进行性能评估, 测量结果与理论值具有很好的一致性, 说明改进的光谱分析算法对测量气体浓度比较可行可靠. 该方法有利于进一步了解大气中氮氧化物的气相转化, 对后续采用等离子体法消除大气中的氮氧化物含量具有重要意义, 同时也为今后监测烟气脱硝处理过程中的氮氧化物废弃产物含量提供了一种高效辅助诊断技术. 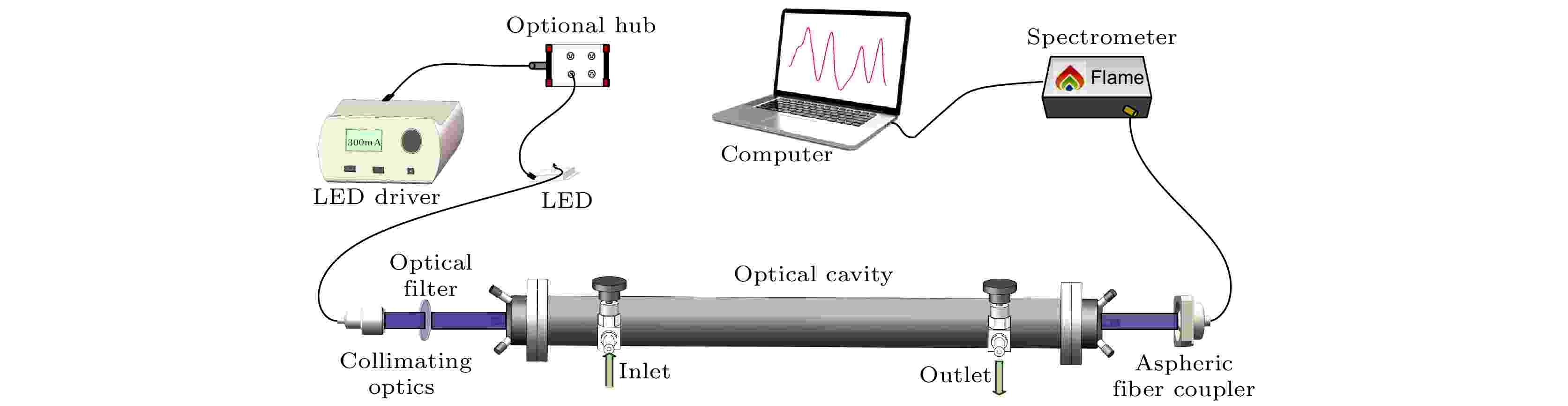 图 1 实验装置图
图 1 实验装置图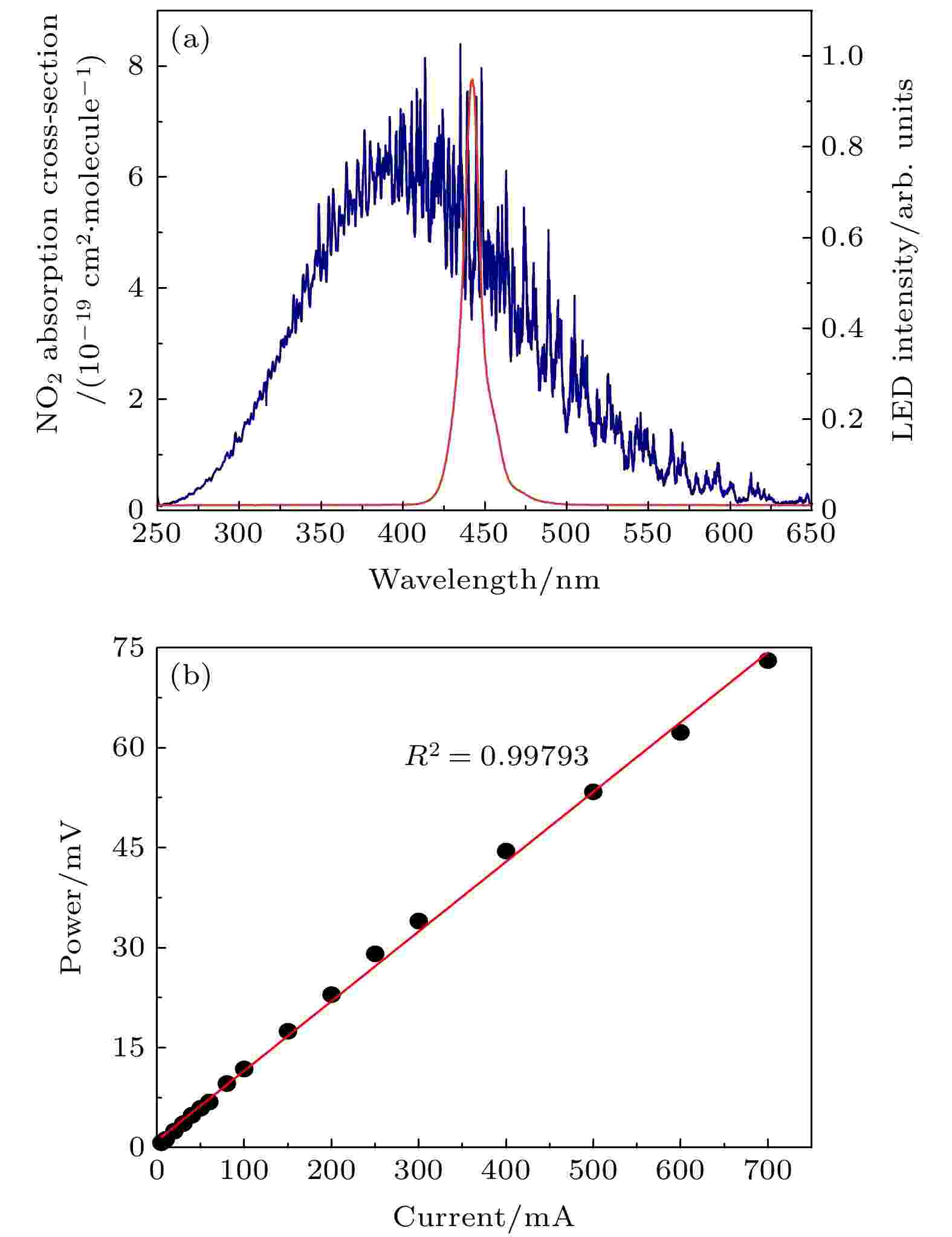 图 2 (a) NO2吸收截面(蓝线)与LED发射光谱(红线); (b) LED输出功率与电流关系
图 2 (a) NO2吸收截面(蓝线)与LED发射光谱(红线); (b) LED输出功率与电流关系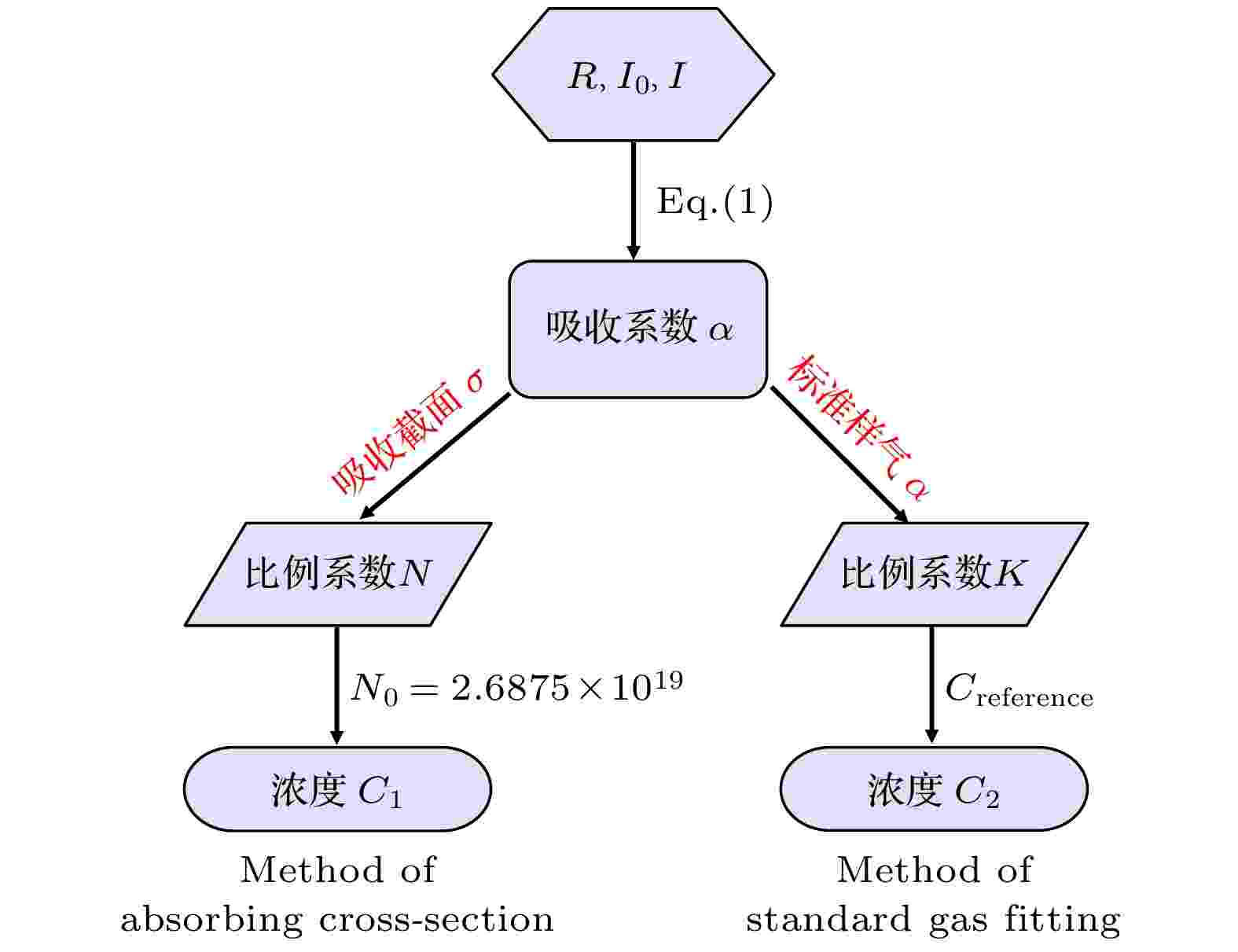 图 3 拟合流程图
图 3 拟合流程图









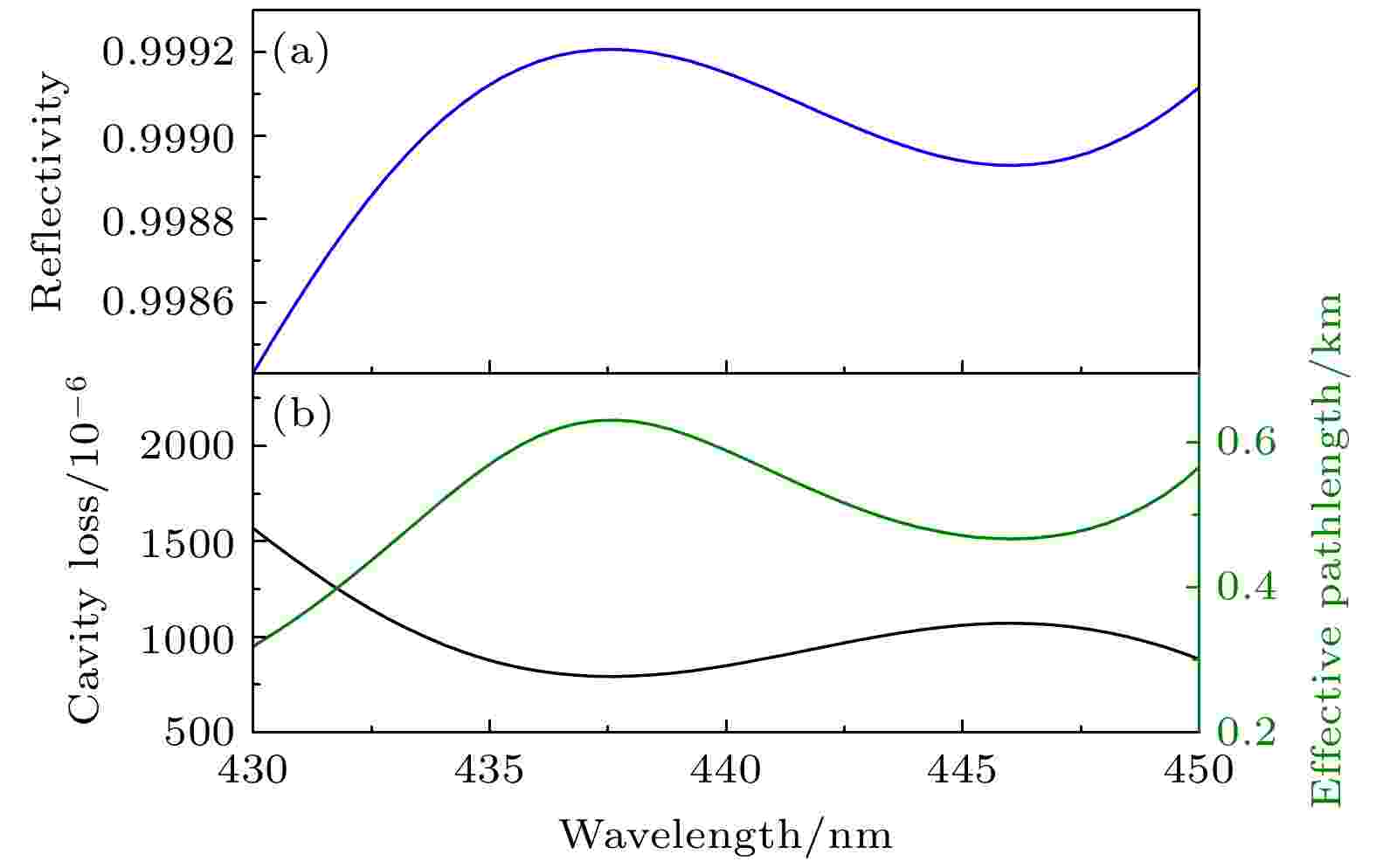 图 4 (a)随波长变化的反射率曲线; (b)腔损耗(黑线)和有效路径长度(绿线)
图 4 (a)随波长变化的反射率曲线; (b)腔损耗(黑线)和有效路径长度(绿线)


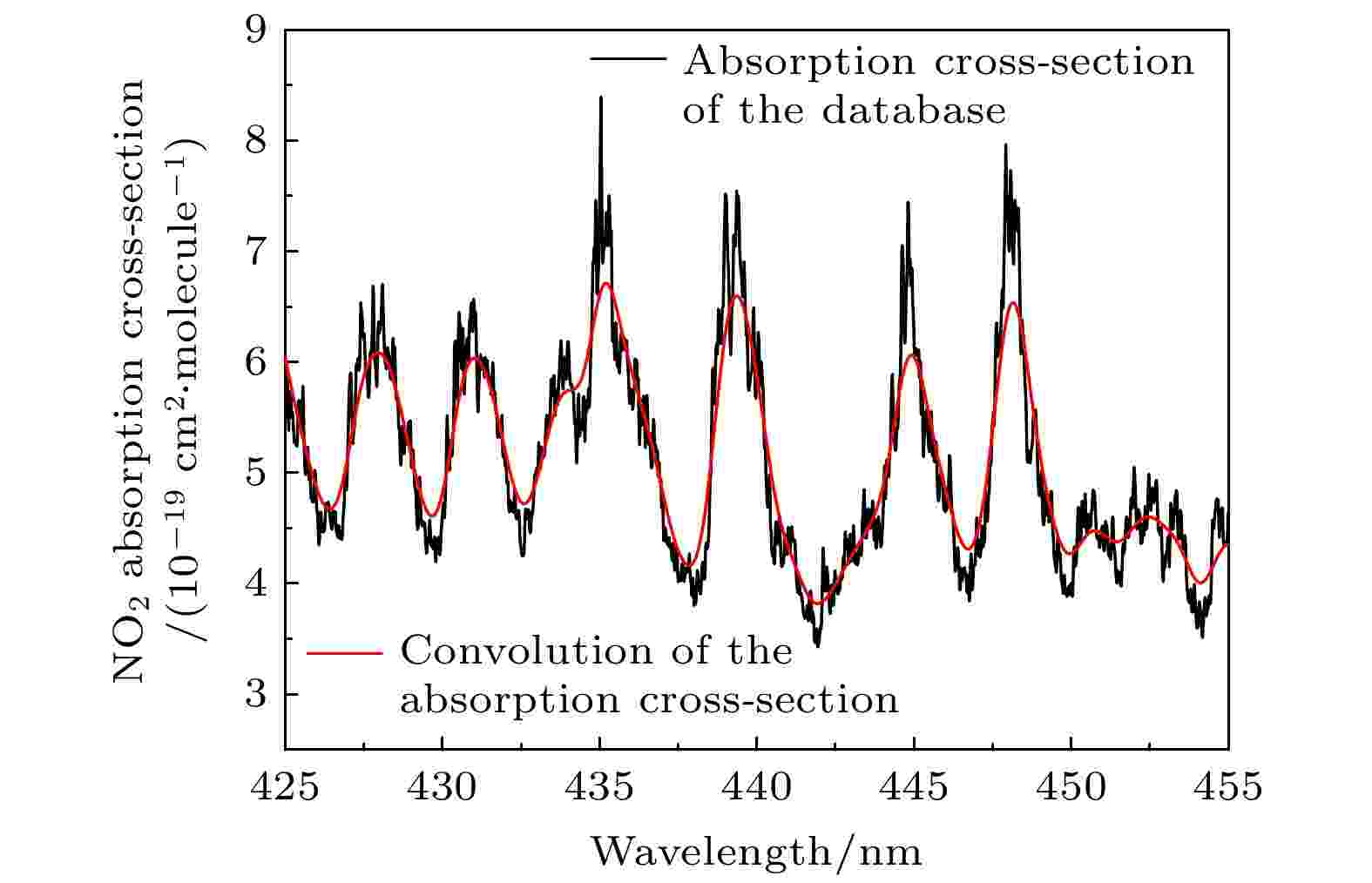 图 5 NO2吸收截面的卷积
图 5 NO2吸收截面的卷积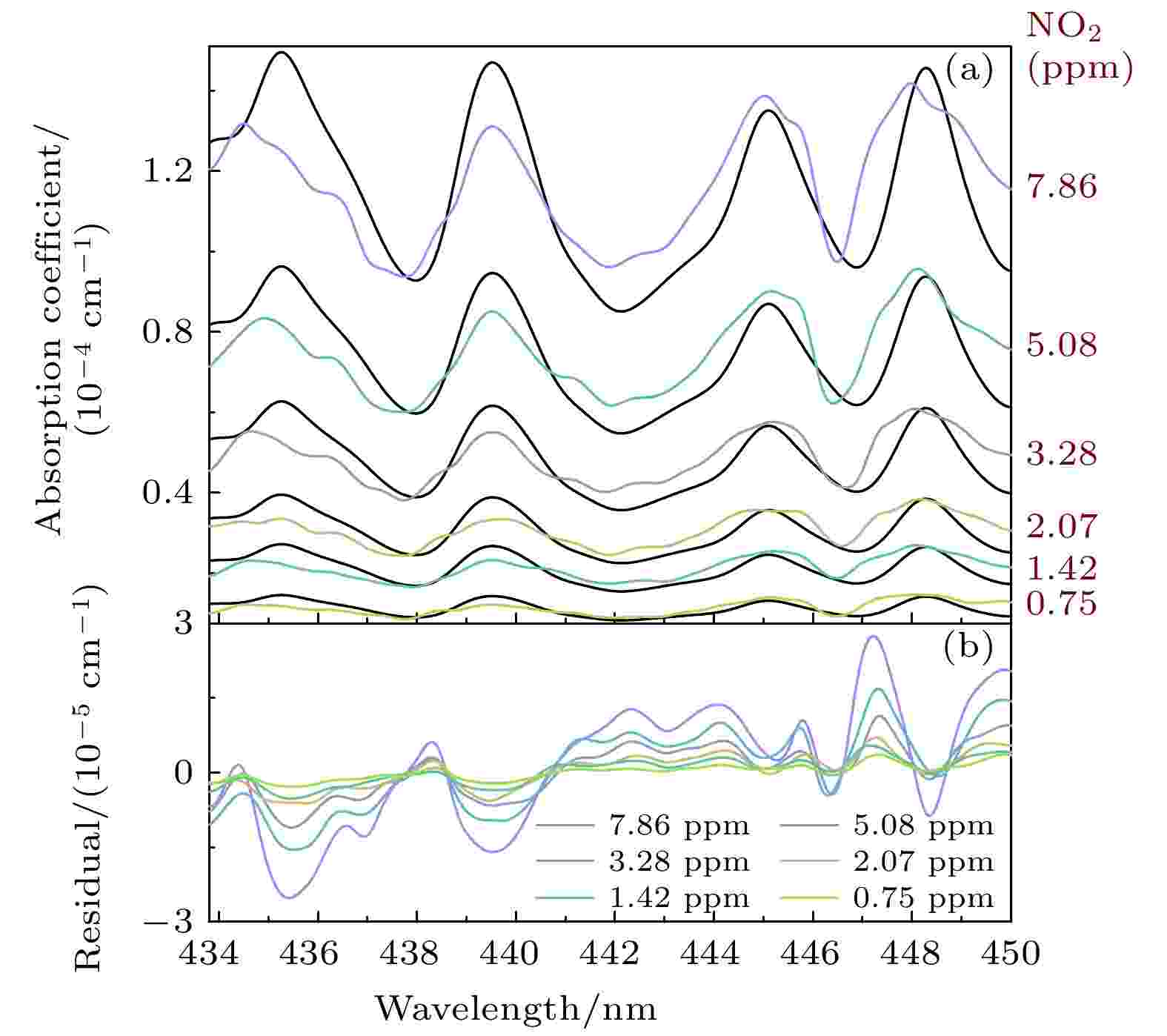 图 6 NO2拟合结果 (a)实测吸收系数与标准吸收截面拟合; (b)拟合残差
图 6 NO2拟合结果 (a)实测吸收系数与标准吸收截面拟合; (b)拟合残差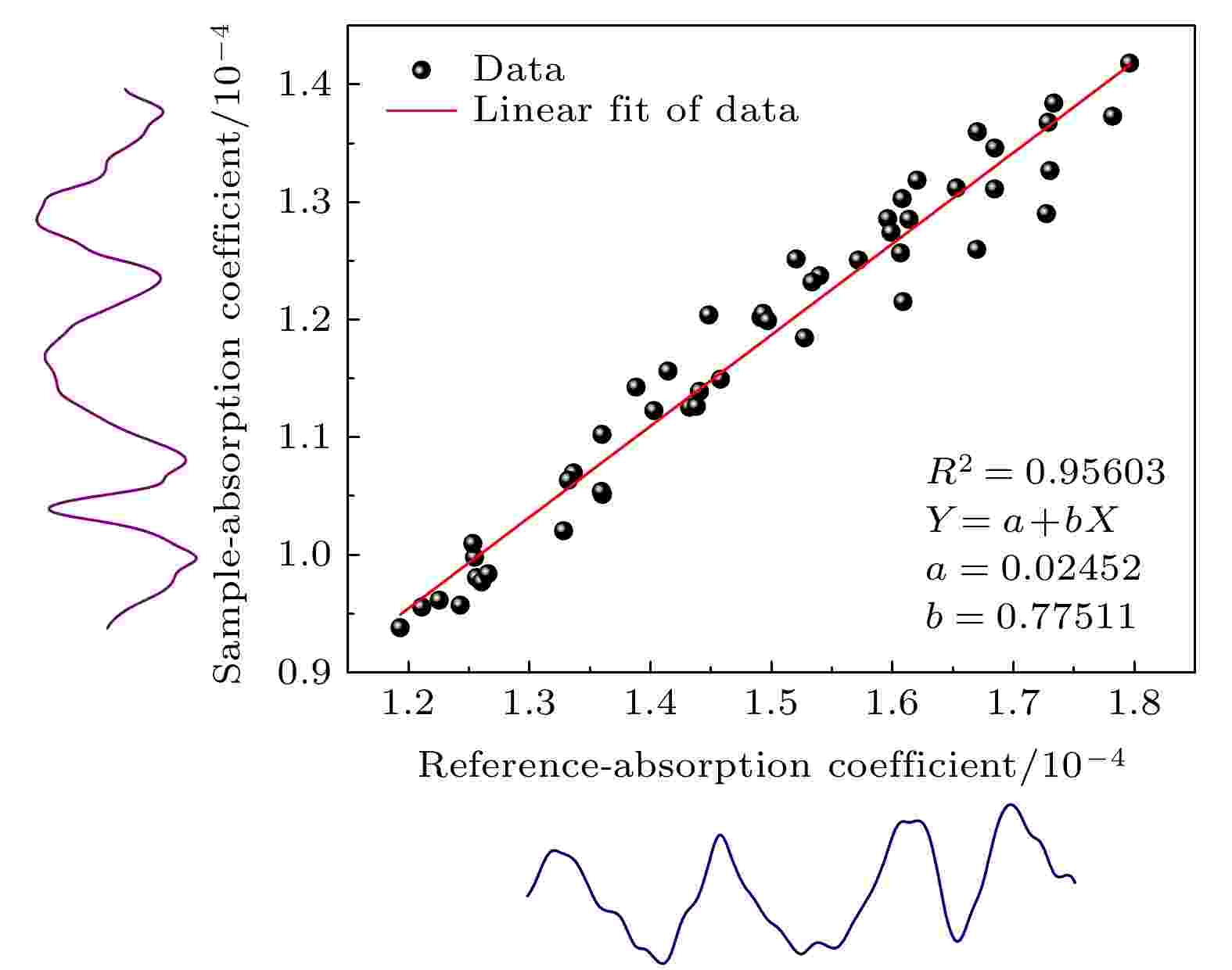 图 7 多元线性拟合示意图
图 7 多元线性拟合示意图

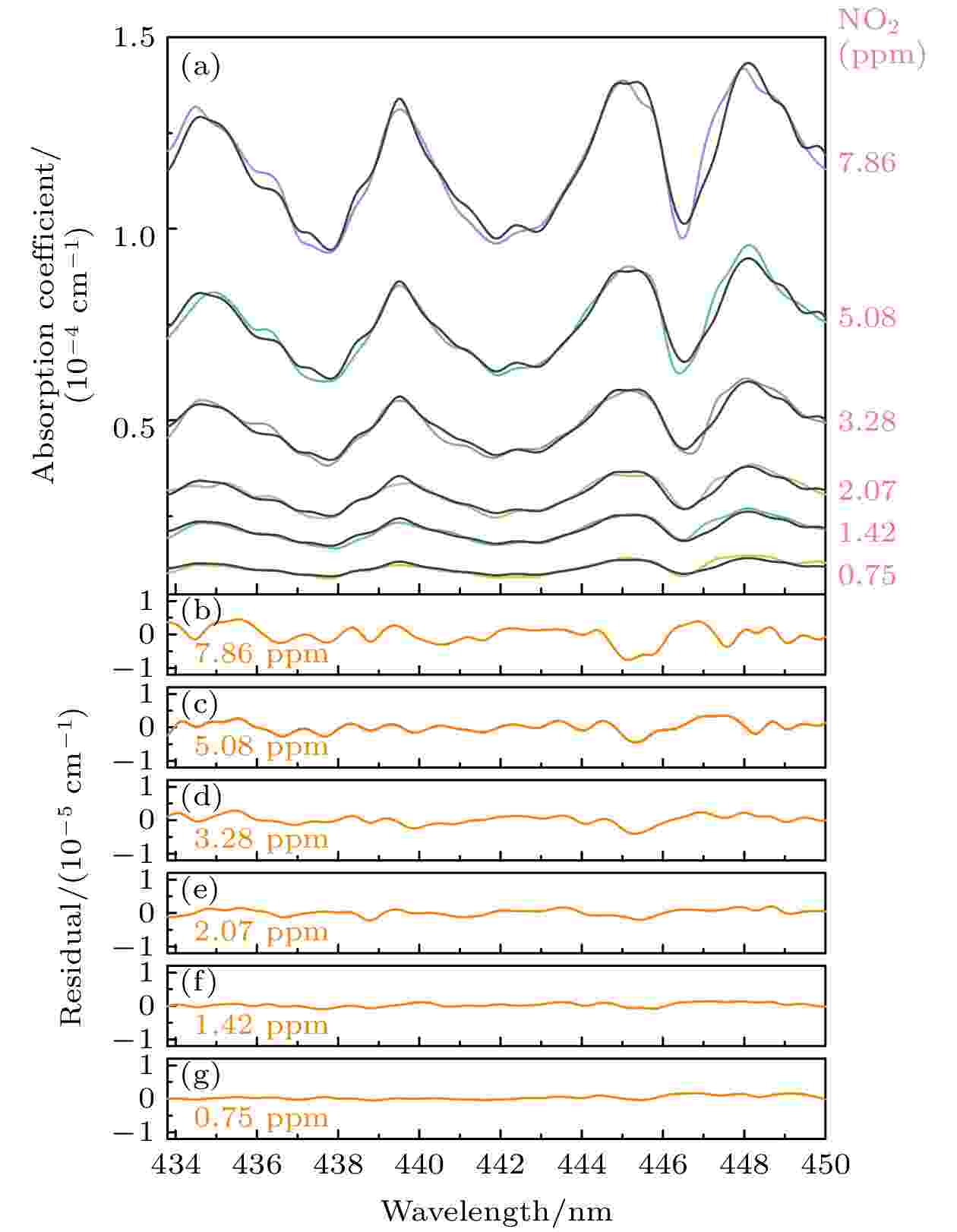 图 8 NO2拟合结果 (a)实测吸收系数与标准气体吸收系数拟合; (b)?(g)拟合残差
图 8 NO2拟合结果 (a)实测吸收系数与标准气体吸收系数拟合; (b)?(g)拟合残差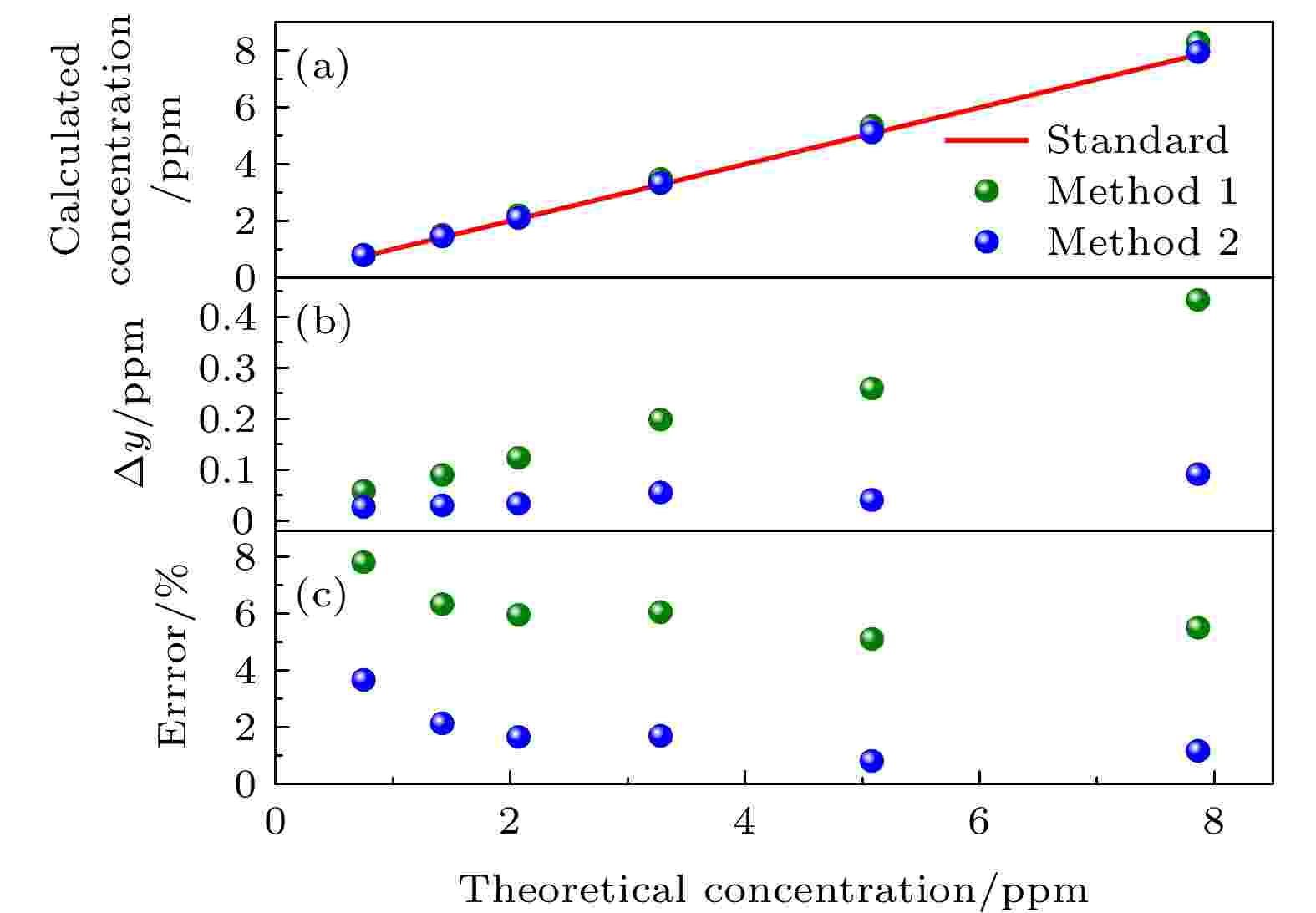 图 9 浓度值对比 (a)浓度计算结果; (b)绝对误差; (c)相对误差
图 9 浓度值对比 (a)浓度计算结果; (b)绝对误差; (c)相对误差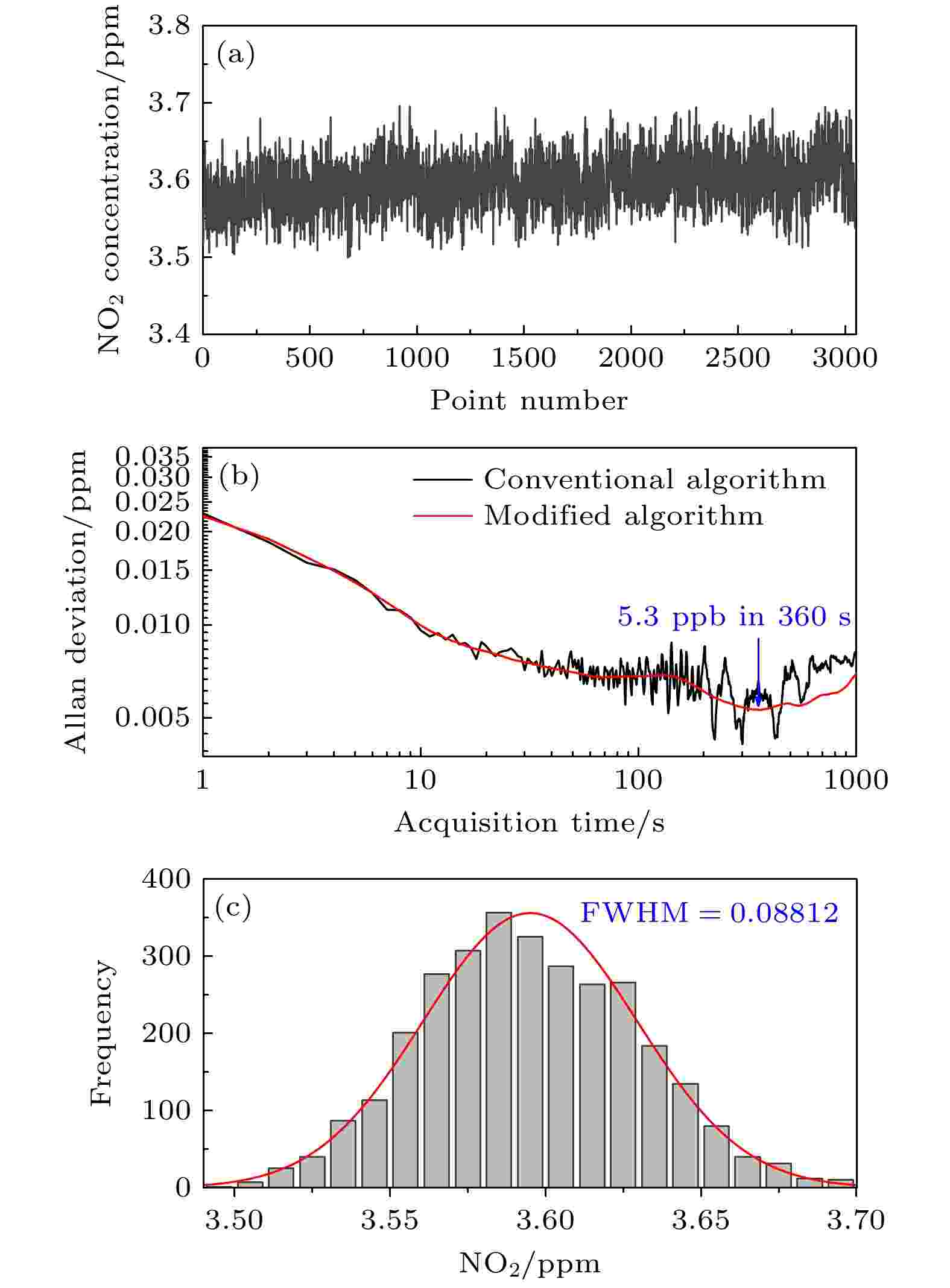 图 10 系统稳定性评估 (a) 2 h的浓度数据; (b) Allan偏差图; (c)直方图分析
图 10 系统稳定性评估 (a) 2 h的浓度数据; (b) Allan偏差图; (c)直方图分析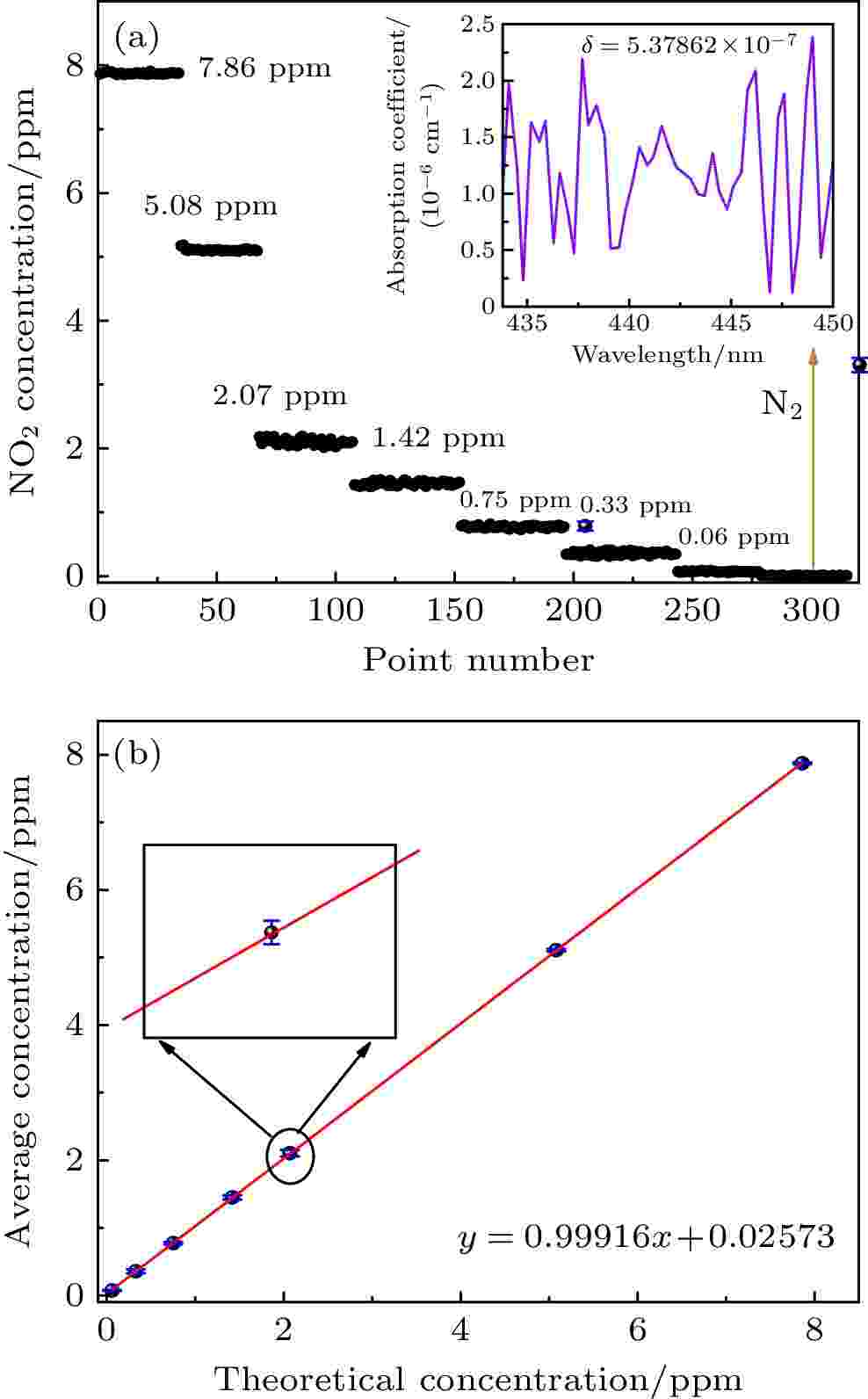 图 11 (a) NO2气体的不同浓度; (b)浓度梯度平均值及标准偏差
图 11 (a) NO2气体的不同浓度; (b)浓度梯度平均值及标准偏差