摘要:超疏水表面液滴的振动特性与接触线的移动、液滴体积、基底振幅等因素密切相关. 本文在基底振幅较小且恒定的条件下, 研究了超疏水表面液滴的共振振幅、模式区间、共振频率等振动特性及其与液滴体积(20—500 μL)的关系. 此外, 将基于一般性疏水表面建立的Noblin共振频率计算模型应用于超疏水表面, 并提出“虚驻点”的概念, 借此对模型进行了误差分析和修正. 研究表明: 1)共振时, 液滴高度变化率即比振幅随体积增大而增大, 随阶数增大而减小; 2)各模式区间的起止频率首尾相接, 其范围随体积增大而减小; 3)液滴体积越大, 共振频率越小, 随着阶数增大, 共振频率f与体积V的关系趋于f -V^–0.4, 不同于一般性疏水表面上的f -V^–0.5; 4)直接应用Noblin模型计算共振频率会产生较大误差, 主要原因在于液滴表面波波段数量统计存在较大偏差, 而修正后的模型可以准确计算超疏水表面大体积液滴的共振频率.
关键词: 超疏水表面/
液滴振动/
共振频率/
模式区间

English Abstract

全文HTML

--> --> -->

液滴振动是一种常见且容易调控的动态行为, 在液滴雾化^[1]、微流控制^[2]、物质结晶^[3,4]等诸多领域发挥着重要作用. 此外, 利用液滴振动, 还可以实现平衡态接触角、表面张力、粘度等物理量的测量^[5-9], 促进内部物质混合^[10-13], 增大细胞球尺寸^[14], 等等.
对液滴振动物理特性的研究由来己久. 早在1879年, Rayleigh^[15]就从理论上研究了非黏性自由液滴的振动. 此后, 人们逐步研究了自由液滴^[16], 以及亲水、一般性疏水^[3-5,17-27]和超疏水表面上液滴/座滴^[28-32]的振动行为. 确定不同条件、不同振荡模式下座滴的共振频率具有重要意义. 2004年, Noblin等^[26]将座滴等效成水池中的液体, 结合水池一维表面波的本征频率公式, 给出了一般性疏水表面上大体积液滴的共振频率公式, 与实验结果较为吻合. 2006年, Lyubimov等^[27]报导了半球形液滴的受迫振动行为, 在忽略黏性耗散的情况下给出了相应的共振频率计算公式. 2009年, Ilyukhina等^[28]建立了适用于描述任意浸润性表面的接触线固着的小体积液滴振动模型, 理论上可以计算超疏水表面上液滴的共振频率. 但实际上, 由于超疏水表面粘滞力很小, 液滴的接触线常处于移动状态, 与模型假定的接触线固着并不相符. 2012年, Mettu和Chaudhury^[32]报导了超疏水表面小体积(1—20 μL)液滴的振动行为, 他们采用白噪声混频信号来驱动液滴振动, 利用傅里叶转换同时获取液滴在各个频率下的振幅, 通过这种间接测量手段来确定共振频率, 其实验结果与基于一般性疏水表面建立的Noblin模型^[26]理论值较为符合. 2014年, 周建臣等^[31]在保持基底振幅恒定的情况下, 通过调节频率变化直接测量了超疏水表面小体积(9 μL)液滴的共振频率, 发现测量结果满足Rayleigh公式, 这与之前Ramos等^[36]得出的超疏水表面球形液滴可近似看作自由液滴的结论相一致. 然而, 作者没有对大体积液滴的振动行为, 及其共振频率是否满足Noblin模型进行研究.
总体而言, 目前对超疏水表面液滴的振动特性认识还不充分, 尤其是大体积液滴(大于20 μL)的共振频率、振幅变化等问题还未见报导. 此外, 以往的研究总是忽略了振动模式(阶数)对应的频率区间问题. 液滴会随频率变化做不同阶数的振动, 而每种振动阶数都不只对应一个频率点, 而是一个频率区间, 这里我们称其为“模式区间”. 处于不同振动阶数的液滴的某些性质, 如内部流场特征^[33,34], 会存在明显差异, 因此, 了解模式区间的变化规律具有重要意义, 而这方面的内容目前也未见报导.
基于以上背景, 本文在保持基底振幅恒定的条件下, 研究了超疏水表面液滴的振动特性及其与液滴体积(20—500 μL)的关系. 首先对不同体积液滴的幅频关系进行了实验测量, 从中提炼出了共振振幅、模式区间、共振频率等参量的变化规律; 继而针对共振频率进行了理论研究, 重点研究了Noblin模型的适用性和修正问题. 通过引入“虚驻点”对液滴的几何特征进行分析, 阐明了Noblin模型误差产生的原因及其随液滴体积变化的机制, 并在此基础上建立了修正模型. 实验证明, 使用修正模型可以准确计算超疏水表面大液滴的共振频率.

如图1所示, 采用美瑞克RK1212BL(20 W)音频信号发生器产生正弦信号, 将信号输出至扬声器以产生简谐振动, 通过调节输出电压来调节扬声器振幅. 实验中, 频率调节范围为30—350 Hz. 利用烷基化二氧化硅溶胶, 结合提拉和水洗工艺在单凹玻片基底上制备超疏水二氧化硅薄膜^[35], 其表面水接触角为162° ± 2°, 滚动角为5° ± 2°. 将镀膜后的玻璃片固定在扬声器振膜上, 再将水滴置于凹面中间使其做受迫振动. 与Noblin等^[26]的实验一样, 本研究采用带凹面的基底, 目的是防止液滴在振动过程中滚落. 所用单凹玻片凹面处的曲率很小, 曲率半径高达106.8 mm, 而本研究中最大液滴(500 μL)的宽度仅为12.6 mm, 因此, 液滴可近似看作是在平面基底上振动. 采用高速摄像机以每秒2000帧的速度拍摄液滴的振动行为; 使用Adobe Photoshop软件对振动瞬态图像进行叠加, 判断振动阶数; 使用Adobe Illustrator软件测量液滴的轮廓长度.
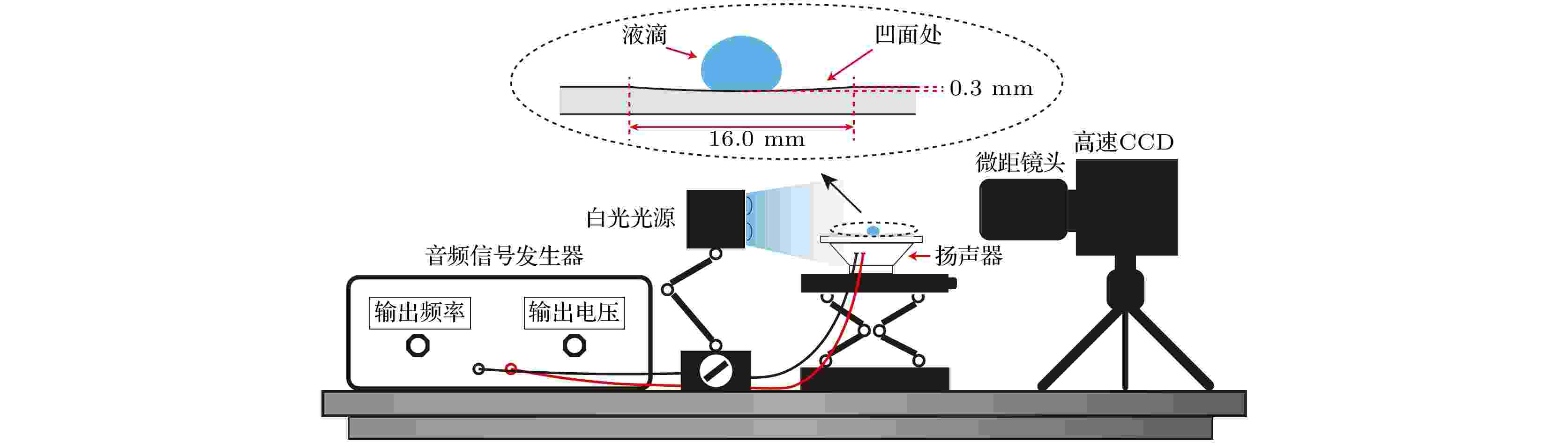图 1 实验装置示意图, 图中玻片凹面处的曲率大小与实际情况相同.
Figure1. Sketch of experiment set, with the curvature of the concave area equal to that of the real substrate.

2

-->

3.1.模式区间和共振振幅

如果液滴振动剧烈, 引起了接触线的大幅振荡, 那么在接触线滞后阻力等因素的影响下, 液滴振动频率会趋于基底振动频率的一半^[5,17,19,31], 在这种情况下, 液滴有时会做非轴对称的星形振动^[5,17,19]. 如果振动比较轻微, 接触线保持固着或者仅轻微振荡, 液滴则会做与基底同频的轴对称振动. 本研究发现, 超疏水表面的大体积液滴很容易在剧烈振动下失稳, 因此, 通过调节电压使得基底处于小幅振动, 并观测到在这种情况下, 不同体积(20—500 μL)液滴皆与基底同频振动, 且始终呈现为轴对称的形态. 由于振动的轴对称性, 只考察液滴在侧视平面内的振动.
在振动中, 液滴表面有些点的位置不随时间变化, 被称作“驻点”. 驻点数量会随频率增加, 如图2所示. 一般把驻点数量的一半定义为振动阶数, 并用于划分振动模式. 本研究对阶数的定义略有不同, 下面以图3为例进行说明. 若接触线固着, 液滴底部会存在两个驻点, 如同左边液滴的情形. 而本实验中可以观察到接触线的小幅移动, 如同右边液滴的情形. 后者相对于前者, 底部驻点消失, 按照通常的定义, 振动模式由3阶降为2阶. 然而, 由于接触线位移很小, 两个液滴的形态差异并不明显, 因此, 为便于比较, 仍将右边液滴的振动称为3阶振动. 换言之, 本文在讨论实验中的液滴振动, 以及接触线移动的Noblin模型时, 设定振动阶数n与驻点数k的关系为n = k/2 + 1, 而在讨论接触线固着的Noblin模型时, 仍然沿用阶数的一般定义(n = k/2).
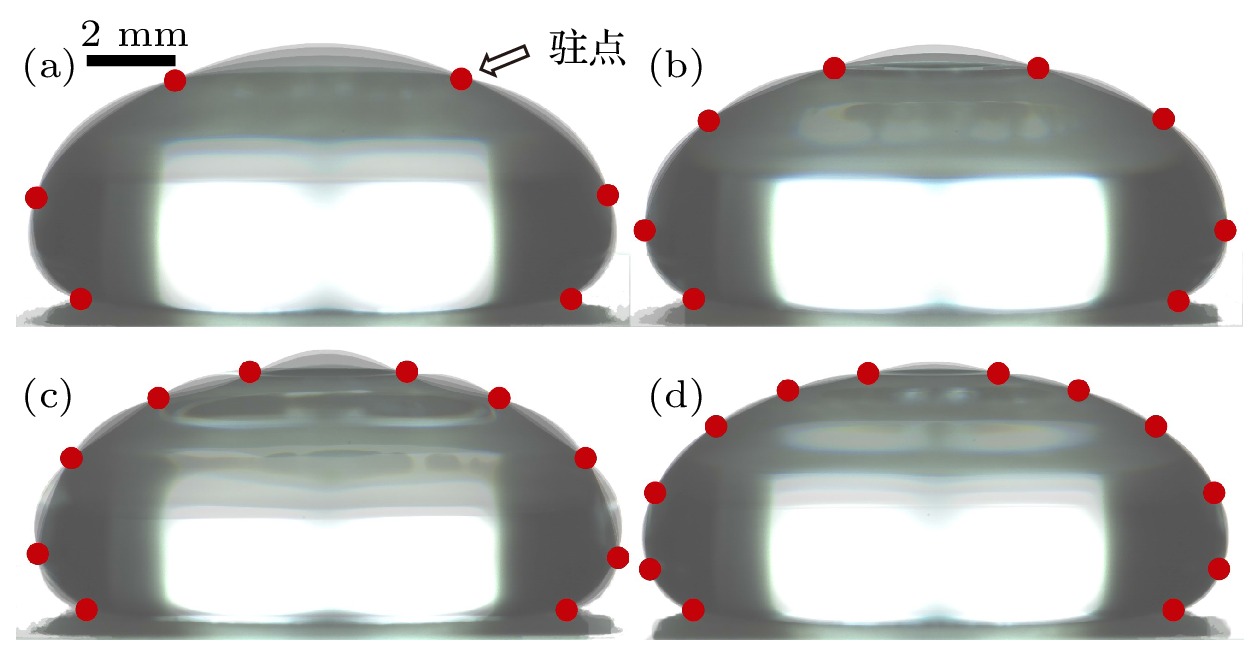图 2 500 μL液滴在不同频率下的振动瞬态图像叠加(接触线位移非常小, 近似认为三相线处为驻点)　(a) 30 Hz; (b) 50 Hz; (c) 70 Hz; (d) 100 Hz
Figure2. Snapshot-superimposed images of an oscillated droplet (500 μL) under different frequencies: (a) 30 Hz; (b) 50 Hz; (c) 70 Hz; (d) 100 Hz.

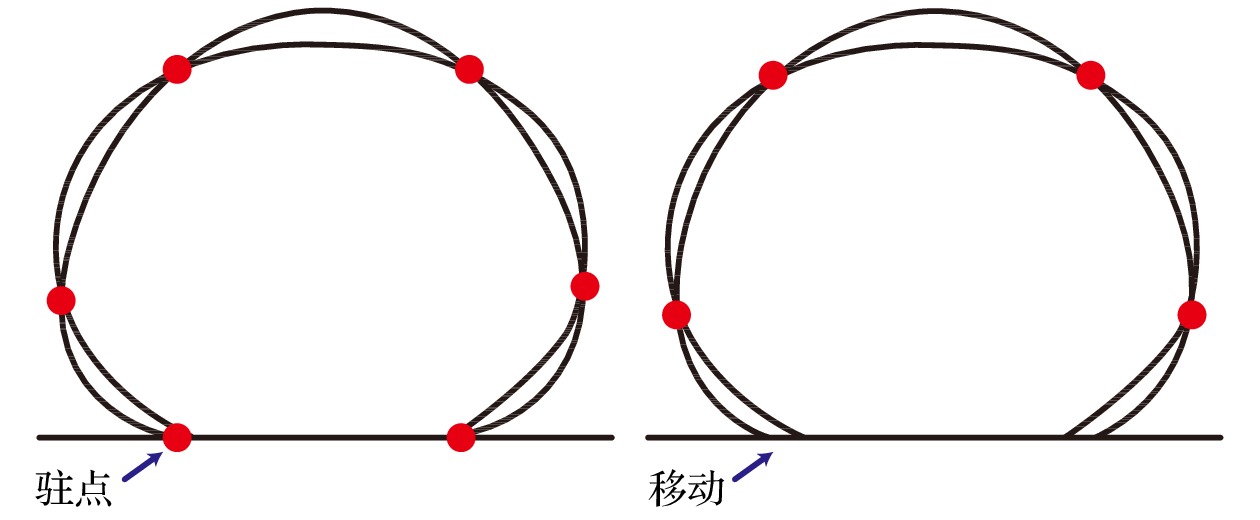图 3 接触线固着(左)和移动(右)模式下驻点数分别为6和4的液滴振动示意图
Figure3. Schematics of droplet oscillations under pinned (left) and moving (right) contact lines, with the quantity of stationary points being 6 and 4, respectively.

为描述液滴振动的剧烈程度, 引入一个无量纲参量—液滴比振幅, 定义为液滴在振动过程中最大和最小高度之差$ \Delta h $与液滴静止时的高度h之比. 根据扬声器在不同频率下的响应选择合适的输入电压(0.004—1.441 V), 来确保基底振幅(约16 μm)不随频率变化, 排除基底振幅变化对结果的影响. 图4(a)—4(d)展示了4种不同体积液滴的比振幅随频率的变化, 可以看出, 整体上, 振动阶数随振动频率增大而增大, 而每种模式的振动都对应着一个频率区间(模式区间), 区间的两端大致位于幅频曲线的极小值处, 也就是说, 液滴刚进入或离开某个模式区间时, 振幅最小. 图4(e)总结了不同体积液滴的3—5阶振动模式区间, 可以看出, 各阶振动模式区间首尾相接, 起止频率随体积增大而减小, 区间范围也随体积而减小.
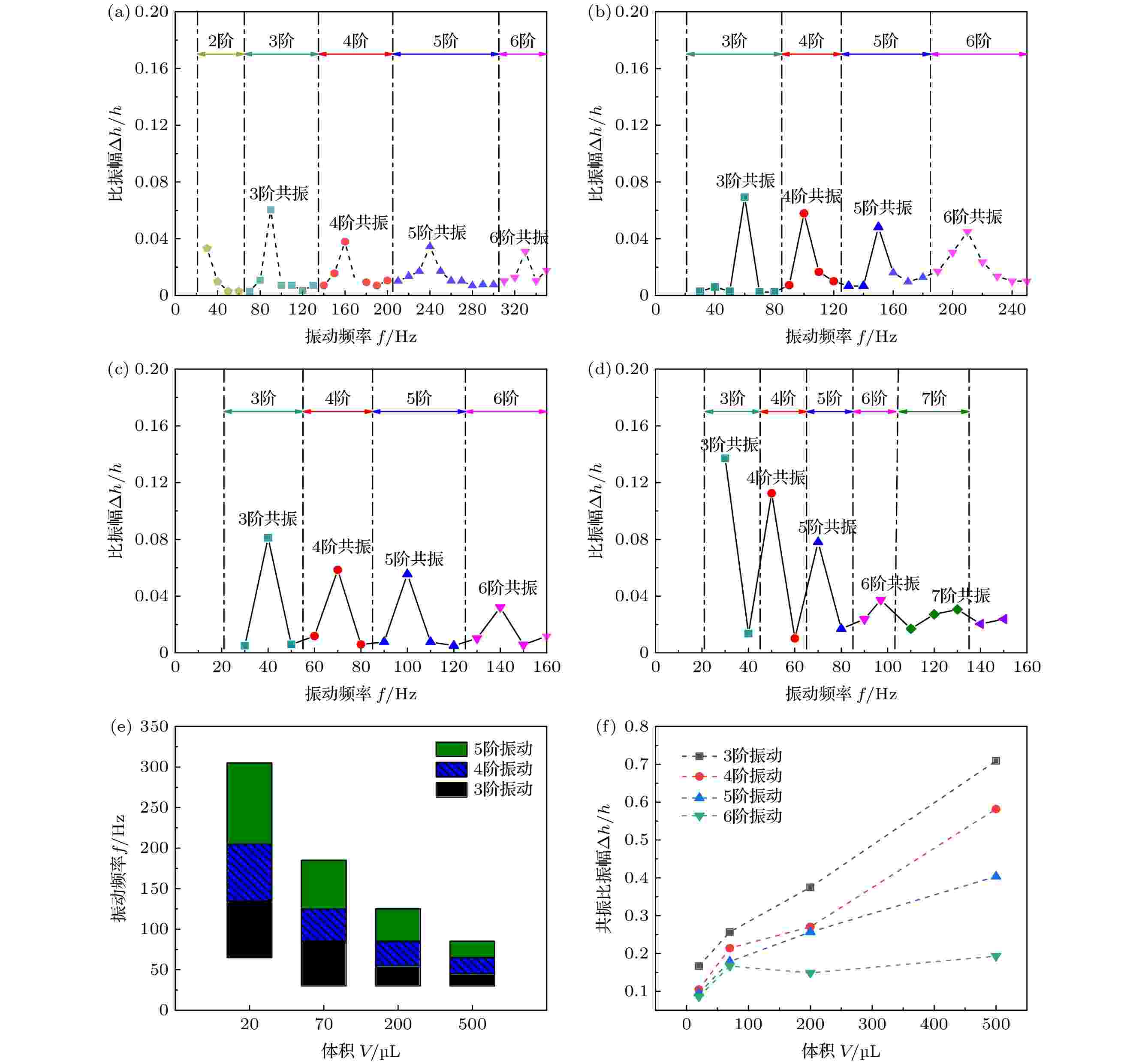图 4 不同体积液滴的幅频关系　(a) 20 μL, (b) 70 μL, (c) 200 μL, (d) 500 μL; 模式区间(e), 共振比振幅(f)与液滴体积的关系
Figure4. Droplet amplitudes versus oscillation frequencies for different droplet volumes: (a) 20 μL; (b) 70 μL; (c) 200 μL; (d) 500 μL; mode ranges (e) and resonance amplitudes (f) versus droplet volumes.

在图4(a)—4(d)中, 每个模式区间内都有一个比振幅极大值, 对应的频率即为该振动模式中的共振频率. 对于同一体积, 液滴的共振比振幅随阶数增大而减小; 对于同一阶数, 共振比振幅随体积增大而增大, 如图4(f)所示. 前人在针对亲水表面液滴以及超疏水表面小体积液滴的研究中也发现了类似规律^[8,26,32], 然而, 有些研究忽视了基底本身振幅随频率的变化^[26,32], 因此所得到的结果难以准确反映出液滴振幅随频率和阶数的变化规律. 相比之下, 本文通过调节电压使基底振幅在各个频率下保持恒定, 排除了基底振幅变化的干扰, 从而使得具体结果和相关规律具有较高的准确性和可靠性.
2 -->

3.2.理论和实验共振频率

超疏水表面的球形微液滴可以近似看作自由液滴, 它们的本征频率可以用Rayleigh公式来估算^[31,36]. 而本研究涉及的液滴体积较大, 受到较强的重力作用, 这些液滴明显偏离球形, 不能再视为自由液滴, 因此Rayleigh公式不再适用. 而Noblin等提出的共振频率计算模型适用于大体积液滴^[26], 因此采用这种模型用于共振频率的理论计算.
Noblin模型描述的是球冠/半球形液滴, 即一般性疏水表面上的液滴. 该模型将静止液滴轮廓弧长p设定为表面波总长度, 相邻两驻点包含1/2个波段, 并根据接触线移动与否, 将液滴振动分为两种类型: 接触线固着型和接触线移动型, 如图5所示. 在此基础上, 根据驻点数量确定表面波的波段数量N, 再利用表面波总长p求出波段平均长度, 并将其定义为表面波的平均波长$ \bar {\lambda } $:
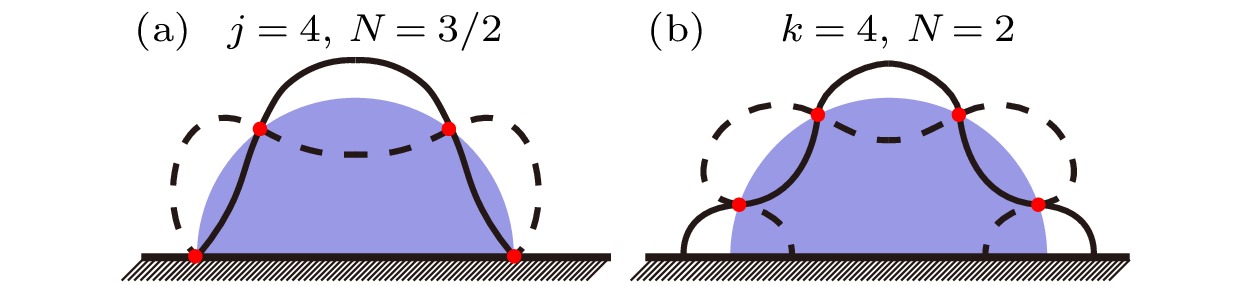图 5 Noblin模型示意图　(a)接触线固着型; (b)接触线移动型, 其中蓝色区域表示静止液滴, 实线、虚线分别为液滴处于最大和最小高度时的轮廓
Figure5. Illustrations of two types of Noblin models: (a) Fixed contact line; (b) mobile contact line, where the blue areas represent the static droplets, the solid and dashed curves represent droplet profiles at the maximum and minimum heights, respectively.

$\bar {\lambda }= {p}/{N}. $

对于接触线固着和移动模型, 表面波波段数量N与驻点数的关系分别为

$N= ({j-1})/{2}, $

$N= {k}/{2}, $

其中, j, k分别为这两种模型中的驻点数. 需要指出的是, 式(3)意味着将图5(b)中最下方驻点与基底之间的波段数量视为1/4, 尽管Noblin等在文章中并未对该细节进行说明.
在此基础上, Noblin等将座滴的表面波等效为水池中液体的表面波, 把式(1)计算出的表面波平均波长代入用来计算水池中液体一维表面波本征频率f的公式^[37]:

$\left\{ \begin{aligned}&{f^2} = \frac{{gq}}{{4{\pi ^2}}}\left[ {1 + {{\left( {\frac{q}{k}} \right)}^2}} \right]{\rm{tanh}}\left( {qh} \right),\\&{\kappa ^{ - 1}} = {\left( {\frac{\gamma }{{\rho g}}} \right)^{\frac{1}{2}}},\\&q = {{2\pi }}/{\lambda },\end{aligned} \right.$

并将计算得到的f视作液滴共振频率的理论值. 其中, g为重力加速度, $ {\kappa }^{-1} $, $ \gamma $, $ \rho $分别为液体的毛细长度、表面张力和密度, h为水池中水深(用液滴平均高度${V}/({{\text{π}}{a}^{2}})$代替, V, a分别为液滴体积和接触半径), $ \lambda $和q分别为水池中液体表面波的波长(用座滴表面波平均波长$ \bar {\lambda } $代替)和波矢. 值得一提的是, 这种等效体的思路在科学研究中应用广泛, 其本质在于借用成熟的、易测量的研究体系来模拟复杂的实际研究对象, 基于各种设定和近似来测量或计算出所研究对象的参数或特性. 例如, 在液体弹珠(空气环境中表面附着颗粒的液滴)有效表面张力问题的研究中, 常把液体弹珠等效成同体积的裸液滴, 利用裸液滴的表面张力测量手段得到液体弹珠的有效表面张力, 对此, 李晓光等人近期进行了深入探讨^[38-41].
本研究将超疏水表面上的液滴等效成水池中的液体, 将相关液滴参数代入Noblin模型来计算共振频率. 具体来说, 量取4种不同体积液滴静止状态的总弧长和俯视图半径, 分别利用接触线固着和移动模型计算出3—6阶共振频率理论值. 从图6(a)可以看出, 理论和实验共振频率有一定偏差, 但整体规律一致, 都随体积增大而减小, 随阶数增大而增大. 从图6(b)可以看出, 共振频率f与体积V近似满足$ f-{V}^{a} $(a为曲线斜率), 并且随着阶数增大, 实验曲线和理论曲线的斜率逐渐接近, 都趋于–0.4. Noblin等^[26]用一般性疏水表面作基底, 也发现了$ f-{V}^{a} $的关系, 然而在他们的研究中, 随着阶数的增大, a趋于–0.5. 斜率的差异说明, 当表面浸润性不同时, 液滴共振频率随体积变化的规律也有所不同.
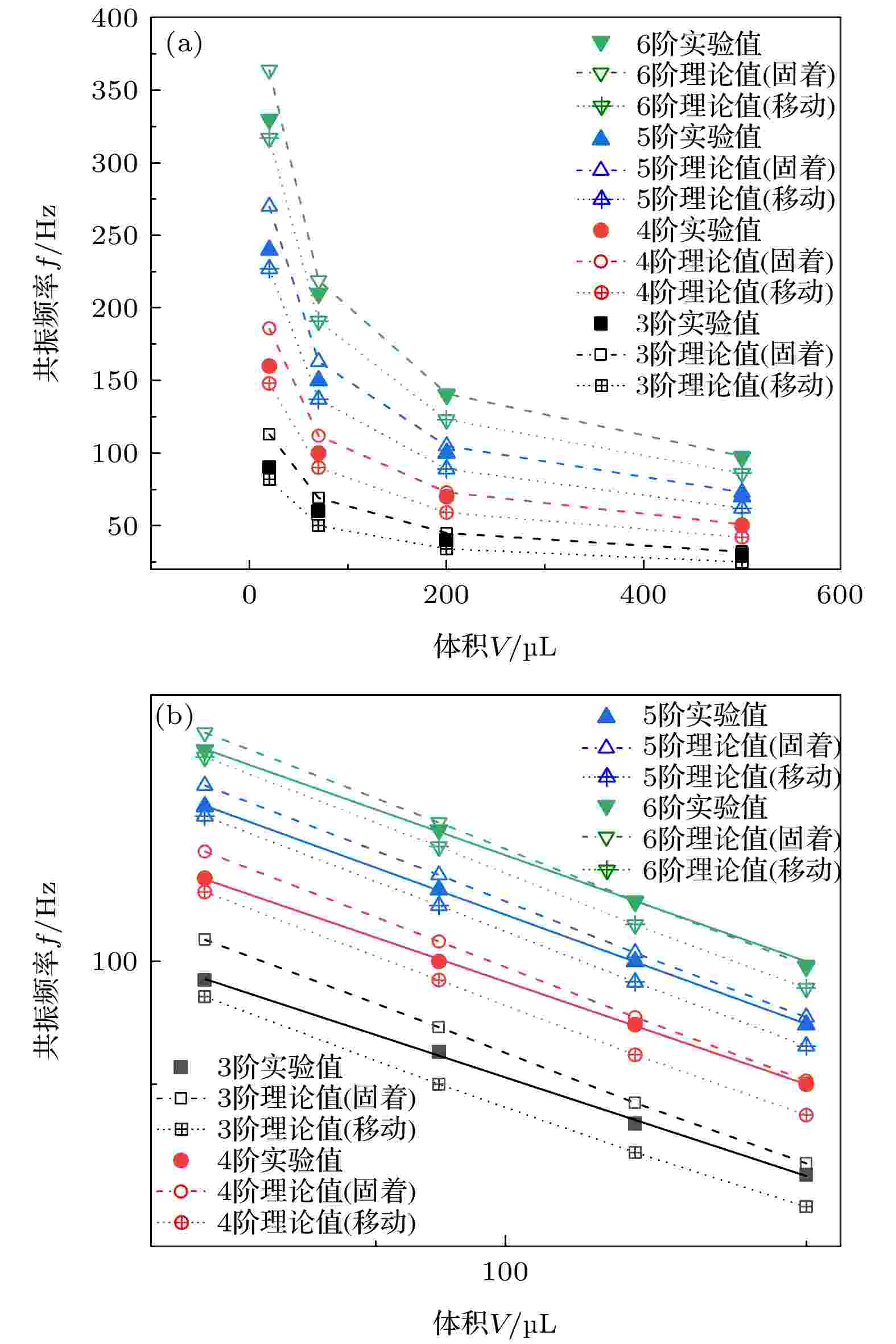图 6 普通坐标系(a)和双对数坐标系(b)中液滴3—6阶振动的共振频率与体积的关系曲线
Figure6. Theoretical and experimental resonance frequencies versus droplet volumes under oscillation mode numbers ranging from 3 to 6: (a) General coordinate system; (b) logarithmic coordinate system.

2 -->

3.3.共振频率理论模型的误差与修正

从图6还可以看出, 相对于实验测量的共振频率, 基于接触线固着模型的理论值偏大, 而基于接触线移动模型的理论值偏小. 这说明对超疏水表面上的液滴直接套用Noblin模型会产生特定误差. 分析原因, 主要有两方面因素需要考虑, 一是液滴的平均高度, 二是液滴表面波的波长. Noblin模型在建立过程中将体积与底面积之比定义为液滴“平均”高度, 实为有效高度, 用于等效水池中的液体深度. 这一设定其实是将球冠/半球形液滴等效成了圆柱体. 按照该思路, 对于超疏水表面球形/椭球形液滴有效高度的求算, 应该用体积除以俯视图面积而不是底面积, 所以, 本研究将俯视图面积代入计算. 然而, 由于液滴并不关于俯视图截面严格上下对称, 所以算得的有效高度与Noblin模型的设定并不完全一致. 为检验有效高度的影响, 将不同体积液滴的实际高度和有效高度分别代入式(4), 发现双曲正切函数tanh(qh)这一项在所有情况下都大于0.999(极限值为1), 实际高度和有效高度的差异所引起的共振频率f的变化在0.1 Hz量级, 与共振频率的大小相比可以忽略不计. 这意味着在分析Noblin模型适用性时, 可以忽略有效高度这一因素.
对表面波波长这一因素的分析, 也需要围绕几何特征来展开. 对于接触线固着模型, 基底上存在驻点, 该驻点与上方相邻驻点间包含了1/2个波段(图5(a)). 超疏水表面上液滴的接触线会随液滴一起振动, 因此基底上并不存在驻点. 然而, 将横向和纵向形变最大时的两个液滴轮廓向基底下方延长, 交汇处可形成“虚驻点”, 如图7所示. 可以认为, 虚驻点与上方相邻的实驻点间包含1/2个波段, 该波段以基底为界分成两个部分(A, B). 这意味着, 基底与上方驻点间(B部分)的波段数量实际不足1/2, 所以, 直接采用Noblin接触线固着模型, 波段数量会比实际偏多, 导致由式(1)得到的平均波长偏小, 继而使得由式(4)计算出的共振频率偏大.
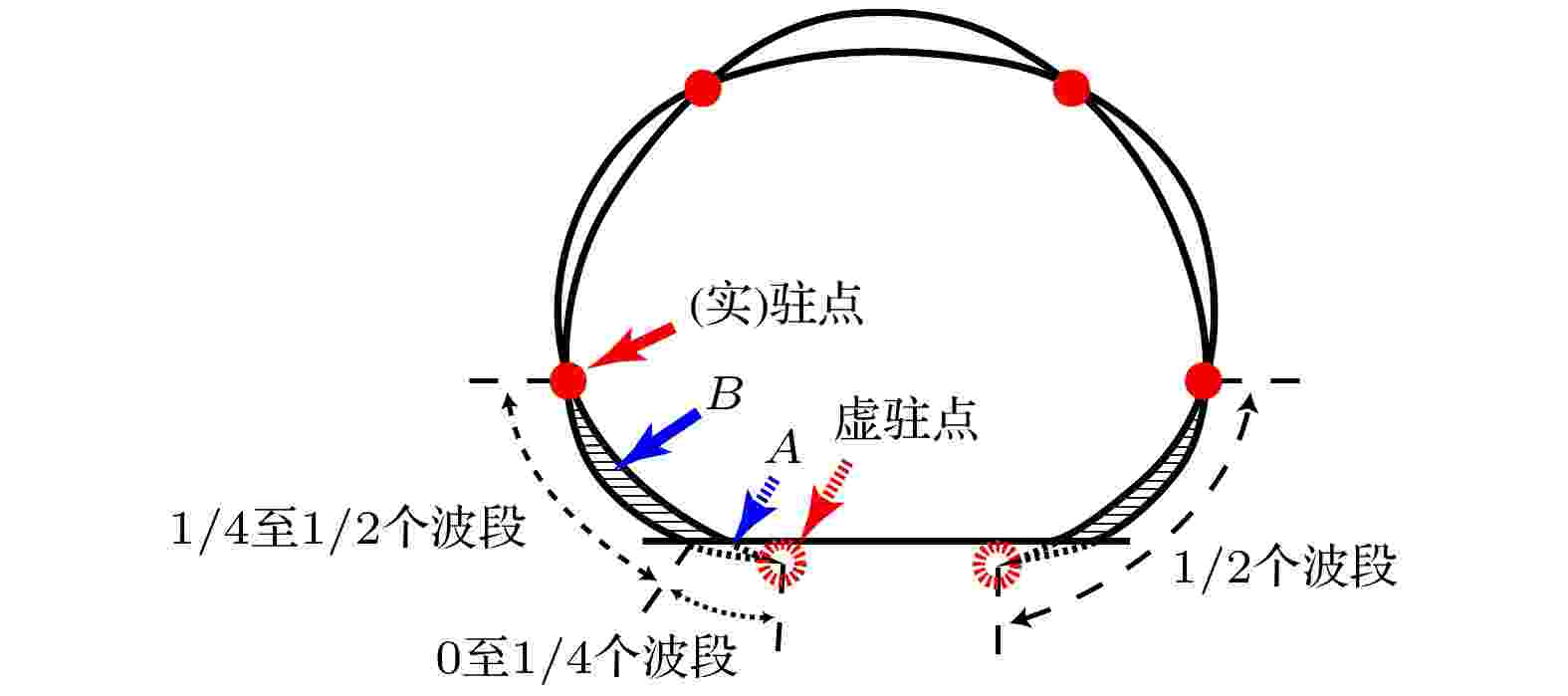图 7 超疏水表面液滴表面波的结构示意图
Figure7. Schematic of the surface wave structure of a droplet on a superhydrophobic surface.

对于接触线移动模型, 如前所述, 式(3)意味着该模型将基底至上方最近邻驻点间的波段数量设定为1/4, 这可以结合一般性疏水基底上液滴表面波的形状(图5(b))来理解. 当接触角约为90°时, 波段弧线与基底正交, 可以认为基底将一个1/2波段截去了一半, 所以基底与上方最近邻驻点间只有1/4个波段. 然而, 在超疏水表面上, 由于接触角较大, 虚驻点的位置又很靠近边缘, 所以基底只将1/2波段截去了一小半(图7, 区域A), 在基底之上余留了一大半(图7, 区域B), 也就是说, 基底与上方最近邻驻点间的波段数量大于1/4. 所以, 直接采用Noblin接触线移动模型, 波段数量会比实际偏少, 导致由式(1)得到的平均波长偏大, 继而使得由式(4)计算出的共振频率偏小.
此外, 以实验值为标准, 接触线固着模型的相对误差随体积增大而减小, 而接触线移动模型的情况则刚好相反(图8). 以20 μL和500 μL液滴的3阶振动为例, 对二者使用固着模型时产生的相对误差分别为26%和7%; 使用移动模型时分别为9%和17%. 这主要是因为, 随着体积增大, 接触线移动变得困难, 其长度变化率会逐渐减小. 根据图7, 当接触线长度变化率较小时, 区域B所占的比例较大, 包含的波段数接近1/2, 也就是接近接触线固着模型对波段数的设定, 所以, 此时采用固着模型误差较小. 反之, 当接触线长度变化率较大时, 区域B所占比例较小, 包含的波段数接近接触线移动模型设定的1/4个波段, 所以, 此时采用移动模型误差较小.
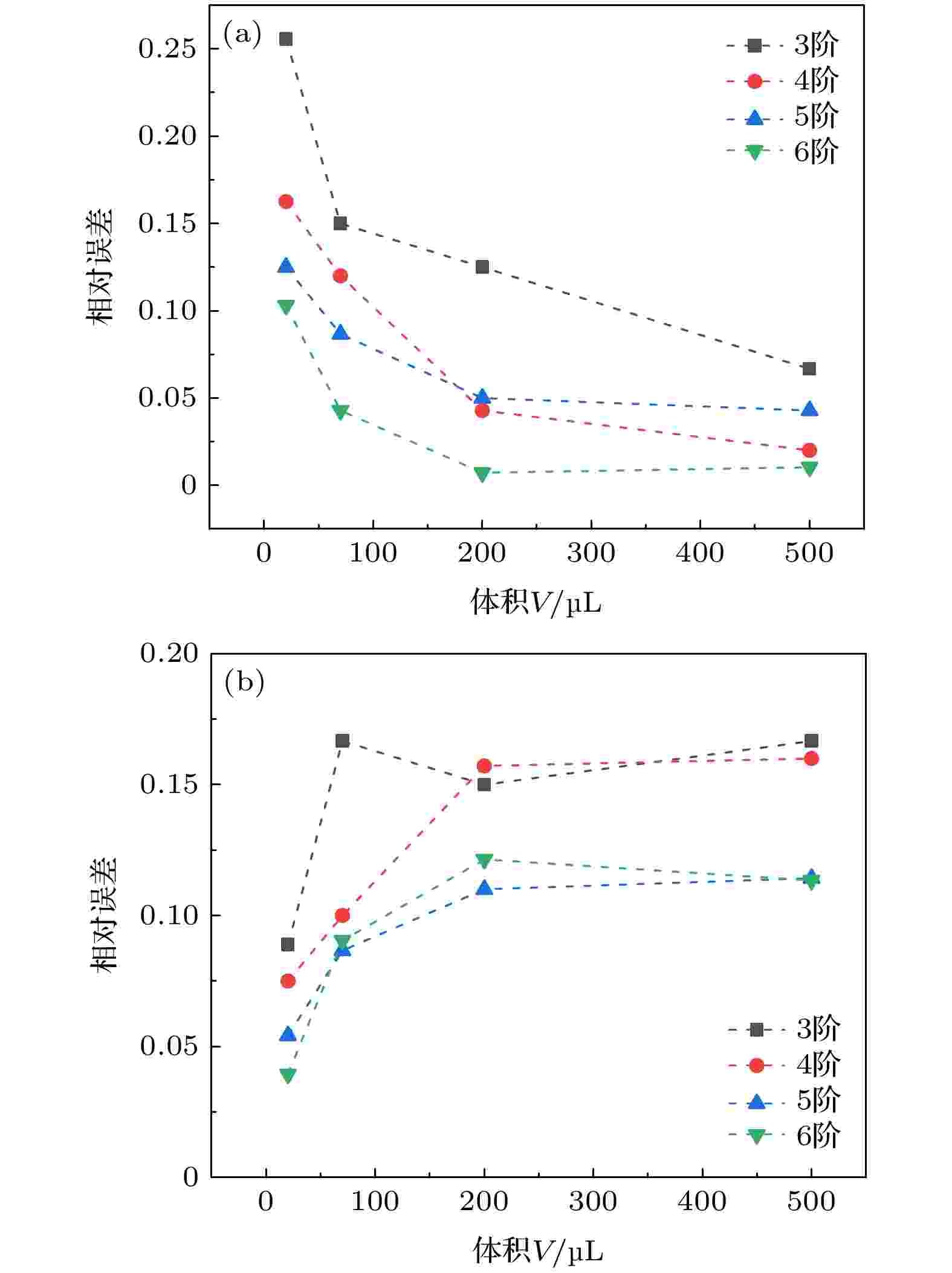图 8 利用Noblin接触线固着模型(a)和移动模型(b)求得的共振频率的相对误差与体积的关系
Figure8. Relative errors of resonance frequencies, obtained from the two types of Noblin models, versus droplet volumes: (a) Fixed-contact-line model; (b) mobile-contact-line model.

综上, 将两种Noblin模型直接应用于超疏水表面上的液滴, 产生的误差都来源于对表面波波段数量的判定, 此外, 无论哪一种模型, 产生的最小误差都已经接近10%(3阶振荡时). 为此, 引入两个修正系数/几何因子$ \alpha $和$ \beta $来对波段数量进行修正, 以期提高模型的适用性. 如图9所示, 设定区域A和B分别包含$ \alpha $和$ \beta $个1/4波段, 由于整个区域包含1/2个波段, 所以$ \alpha +\beta =2 $. 由于接触角很大, 接触线移动范围较小, 所以区域B占比总是比区域A大, 因此有: $ 0<\alpha <1 $, $ 1<\beta <2 $.
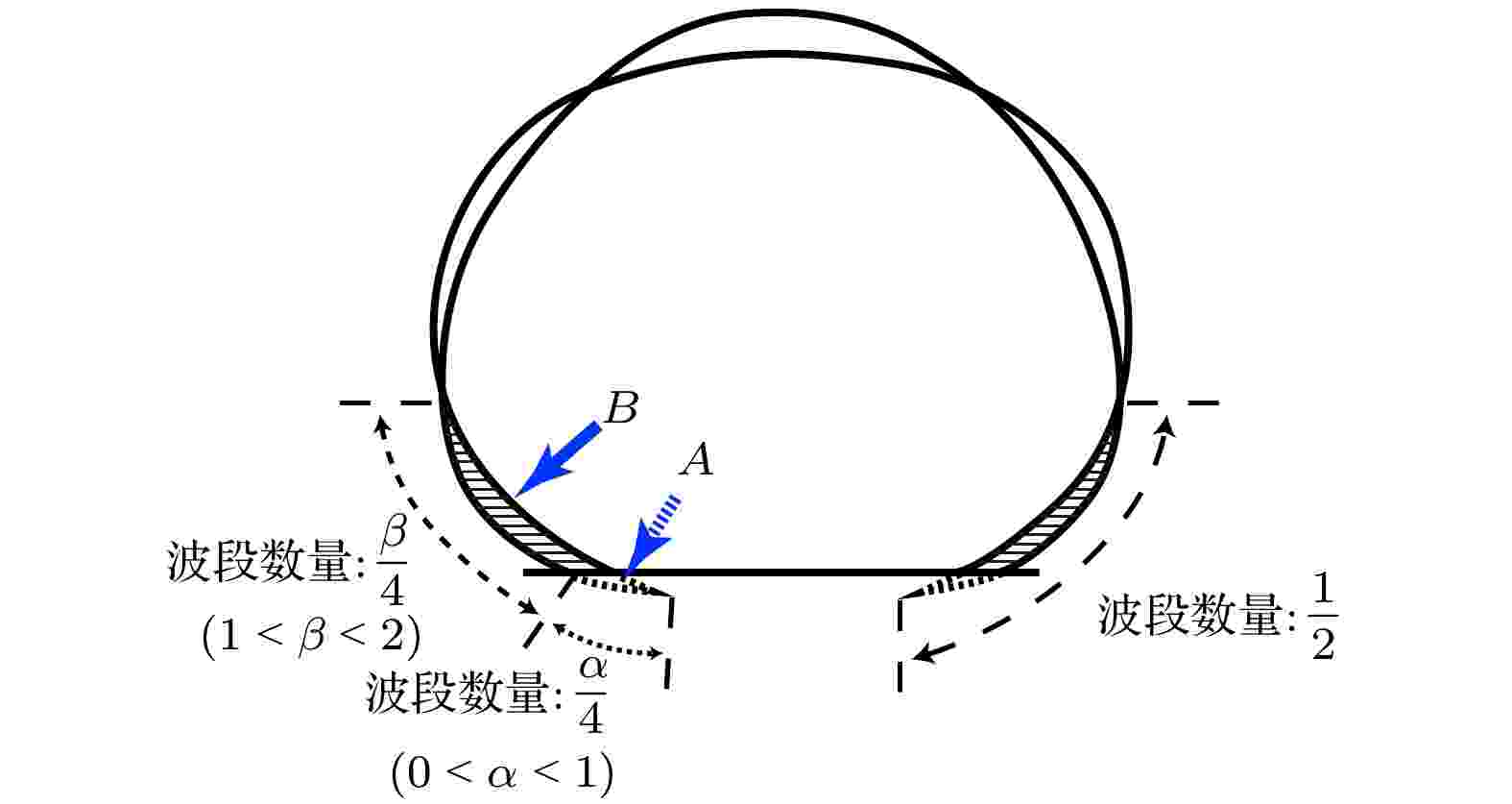图 9 包含修正系数$ \alpha$和$\beta $的表面波结构示意图
Figure9. Schematic of the surface wave structure with correction coefficients ($ \alpha\;{\rm{and}}\;\beta $) involved.

如前文所述, 接触线固着模型统计的波段数偏多, 即多统计了图中区域A包含的“虚”波段数, 因此, 应将其减去:

$ N={N}_{\rm{fixed}}-2\times {\alpha }/{4}= {(j-\alpha -1)}/{2},$

其中, j, $ {N}_{\rm{fixed}} $和N分别为该模型的驻点数、及修正前后的总波段数.
相应的, 接触线移动模型统计的波段数偏少, 具体说来是对区域B的波段数估计不足, 因此, 应予以补足:

$N={N}_{\rm{mobile}}+2\times \left(\frac{\beta }{4}-\frac{1}{4}\right)=\frac{k+\beta -1}{2},$

其中, k, $ {N}_{\rm{mobile}} $和N分别为该模型的驻点数、及修正前后的总波段数.
至此, 只需将式(2)和(3)分别替换为式(5)和(6), 就完成了对两种Noblin模型的修正. 实际上, 虽然式(5)和(6)分别是对两种不同模型的修正, 但都描述了真实的波数, 因此完全等价. 对同一个液滴振动, k = j – 2, 将其代入式(6)即可得到与式(5)相同的表达式. 也就是说, 对于超疏水表面接触线移动较小的液滴振动, 计算其理论共振频率时, 既可以采用修正后的Noblin接触线移动模型, 也可以采用修正后的固着模型, 其结果是一样的, 只要知道$ \alpha $或$ \beta $的数值, 即可计算求解出唯一的共振频率值, 下面以$ \alpha $为对象进行讨论.
利用实验测得的共振频率, 可以反向推出四个体积、四个振动模式对应的$ \alpha $值, 如表1所示. 继而, 对所得$ \alpha $值进行指数拟合, 就可以得到各个振动模式下$ \alpha $随体积连续变化的曲线(图10(a)), 及其对应的函数表达式(3—6阶):

液滴体积/μL	振动阶数
	3	4	5	6
20	0.73573	0.68488	0.69771	0.71784
70	0.47875	0.55128	0.49756	0.32655
200	0.46078	0.22800	0.33208	0.09438
500	0.32044	0.16831	0.33258	0.13569

表1不同体积及阶数对应的修正系数$ \alpha $
Table1.Values of correction coefficient $ \alpha $ under different droplet volumes and oscillation mode numbers.

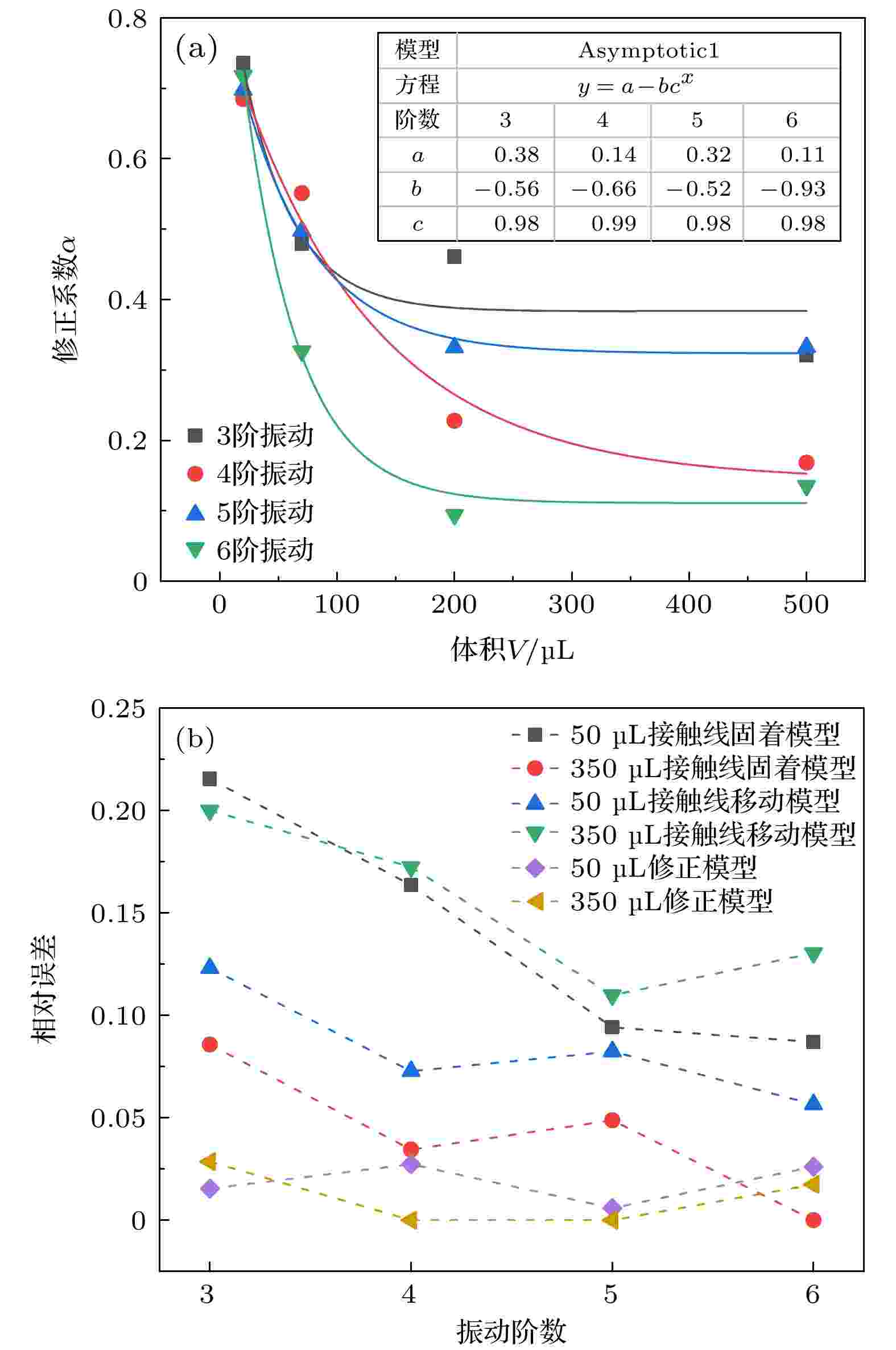图 10 (a)修正系数$ \alpha $的拟合曲线; (b)修正前后Noblin模型的相对误差
Figure10. (a) Fitted curves of the correction coefficient $ \alpha $; (b) Relative errors of resonance frequencies from pristine and modified Noblin models.

$\begin{split}&\alpha =0.38+0.56\times {0.98}^{V}, ~~ \alpha =0.14+0.66\times {0.99}^{V}, \\&\alpha =0.32+0.52\times {0.98}^{V}, ~~ \alpha =0.11+0.93\times {0.98}^{V}.\end{split}$

为了检验修正模型的有效性, 补充测量了体积为50和350 μL的液滴的3—6阶共振频率, 并利用上述函数关系求出$ \alpha $值, 继而求出相应的理论共振频率. 结果发现, 以实验值为标准, 理论值的相对误差最大不超过3%, 且受体积影响很小. 相比之下, 直接运用修正前的Noblin模型, 产生的相对误差远大于修正后的结果, 最大误差更是达到了20%以上, 而且误差受体积影响较大(图10(b)). 以上结果说明, 修正模型可以大幅度提高大体积液滴共振频率理论值的精确度, 相比原始的Noblin模型更适用于超疏水表面.

本文揭示了超疏水表面液滴的共振振幅、模式区间、共振频率等振动特性及其与液滴体积(20—500 μL)的关系. 发现共振时液滴的变形程度总体上随体积增大而增大, 随阶数增大而减小. 指出每个振动阶数都对应一个频率区间即模式区间, 其范围随体积增大而减小. 重点研究了共振频率, 发现共振频率随体积变化的指数关系不同于一般性疏水表面上的结果. 在理论共振频率的研究方面, 发现将基于一般性疏水表面建立的两种Noblin模型直接应用于超疏水表面会产生较大误差, 其中, 接触线固着模型得到的共振频率偏大, 接触线移动模型得到的共振频率偏小, 前者的误差随体积增大而减小, 后者的误差随体积增大而增大. 提出了“虚驻点”的概念用于表面波形状分析, 基于此揭示了上述误差及其变化的来源: 采用固着模型时, 由于接触线实际发生了移动, 导致统计的波段数量偏多; 采用移动模型时, 由于接触角远大于Noblin模型中的接触角(约90°), 导致统计的波段数量偏少. 为此引入了几何因子对波段数量进行修正, 利用修正后的模型计算共振频率误差明显减小, 最大相对误差不超过3%.