摘要:Mojette变换是一种最小冗余采样的离散Radon变换, 能够用较少角度的投影数据进行精确的计算层析(computed tomography, CT)重建, 为少量投影角度CT技术的实现提供了一种新思路. 投影角度的空间布局决定了层析重建最少所需投影的数量. 为了获得Mojette变换层析技术中的最优投影空间角度布局方案, 本文对三维Mojette变换数学模型及其精确重建条件进行了研究. 以此为基础, 在考虑实际探测器像素数目受限的条件下, 提出了确定最优投影角度的方法. 研究结果表明: 所有探测器围绕被测物体在同一水平面内进行平行投影采集是最优的投影角度布局方案, 此时投影模型为二维Mojette变换, 所需的投影角度和探测器像素数最少, 投影角度范围最小; 若在实际的测量中该投影条件无法满足, 则投影矢量中|p_i|和|q_i|的值越小越好. 该研究可为实际层析系统的建立提供理论基础.
关键词: 计算层析/
三维Mojette变换/
精确重建条件/
投影角度

English Abstract

全文HTML

--> --> -->

计算层析(computed tomography, CT)技术, 是一种由低维投影数据重建高维目标的技术, 已广泛应用在Terahertz波检测^[1]、量子态^[2]、医学三维成像^[3]、风洞^[4]、地质探测、激光打靶和燃烧场三维成像和检测等领域中^[5-7]. 它利用探测器采集测试目标在多个角度的二维投影, 并结合层析理论进行三维重建. 在实际应用中, 由于探测对象或测量环境的影响, 经常会遇到投影采集角度受限制的问题^[8]. 如何利用有限角度投影进行精确层析重建, 对于层析成像技术的发展和应用, 具有非常重要的意义.
传统的基于Radon变换的层析技术很难在极少角度采样的情况下获得较好的重建结果. Mojette变换是一种最小冗余采样的离散Radon变换, 可以根据多个投影之间的相互独立特性对投影个数、投影角度等进行变化, 通过改变不同投影矢量下的采样率来控制冗余度的大小, 因此可以在最大程度上避免投影信息的重复和冗余采样^[9]. Mojette变换的理论基础由Katz^[10]提出的离散角度概念以及Herman^[11]提出的迭代算子共同构筑而成, 该变换利用满足Katz引理的稀疏角度即可被精确重建, 其重建所需的数据采集量远小于Radon变换所需的数据量^[12-14]. 基于Mojette变换的层析重建能够显著减少所需的投影角度和投影射线条数, 其重建所需的数据采集量远小于Radon变换所需的数据量, 在稀疏角度下具有良好的重建性能. 并且实际的Radon变换投影可以转换为Mojette投影, 为基于Mojette变换的实际投影层析重建提供可能^[15,16].
Mojette变换层析理论中的可精确重建条件以及最少投影角度布局对于实际层析系统的建立以及提高重建精度具有非常重要的指导意义^[17]. 在传统的基于二维Radon变换^[18,19]和二维Mojette变换的层析重建技术^[20,21]中, 探测器放置在被测物体周围同一水平面内, 进行平行投影的采集. 当实际测量环境中水平面内投影角度受限时, 可以在三维空间中进行投影采集, 此时层析投影模型为三维Radon变换或三维Mojette变换. Cai等^[22]利用数值计算的方法讨论了基于三维Radon变换层析技术中投影角度的三维空间分布对重建精度的影响. 目前, 从理论上分析和解释层析系统中投影角度的最优布局方案, 特别是对三维Mojette变换以及相应的层析重建理论的相关研究仍较少.
为了在理论上获得Mojette变换层析技术中的最优投影角度空间布局方案, 本文将建立三维Mojette变换数学模型, 并且利用基于角的重建(corner based inversion, CBI)算法对精确重建条件进行研究. 以此为基础, 结合实际探测器像素数目受限条件, 提出并确定最优投影角度方案.

在三维直角坐标系$(x, y, z)$中, 三维Mojette变换的投影方向用三维离散向量${\xi _i} = ({p_i}, {q_i}, {r_i})$来表示, 其中${p_i} \in Z$, ${q_i} \in {Z^ + }$和${r_i} \in Z$分别表示投影向量在x, y和z轴的分量, 投影方向限制在y轴正向, 并且$i = 1, 2, \cdots, N$表示投影角度数. 如图1所示, 投影向量${\xi _i} = ({p_i}, {q_i}, {r_i})$对应的投影角度由方位角${\varphi _i}$和天顶角${\theta _i}$确定, ${\varphi _i} = {\tan ^{ - 1}}\left({\dfrac{{q_i}}{{p_i}}}\right)$, ${\theta _i} = {\tan ^{ - 1}} \left(\dfrac{{r_i}}{\sqrt {{p_i}^2 + {q_i}^2}}\right)$. 投影探测平面垂直于投影向量. 将被测三维物体$f(x, y, z)$均匀划分为分辨率为$P \times Q \times R$的离散网格$f(k, l, m)$.
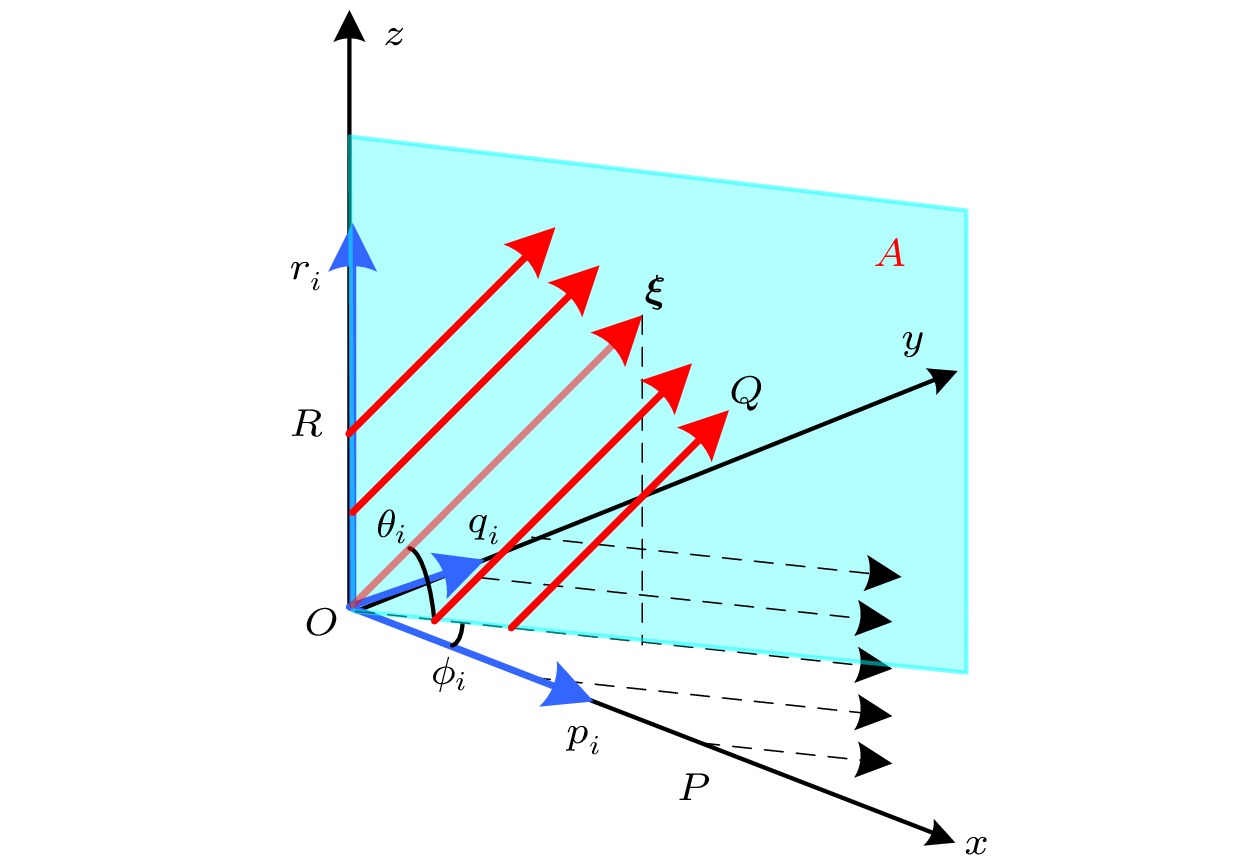图 1 三维Mojette变换示意图
Figure1. Schematic diagram of three-dimensional Mojette transform.

当${p_i} = 0$, 或${q_i} = 0$, 或${r_i} = 0$时, 三维Mojette变换等效为相应方向上的二维Mojette变换. 以${r_i} = 0$为例, 三维Mojette变换等效为m组水平方向上的二维Mojette变换, 其投影方程为

$\begin{split}[Mf]({b_1},m) =\;& \sum\limits_{k = 1}^P {\sum\limits_{l = 1}^Q {f(k,l,m)} } \Delta [{b_1} - {q_i}(k - 1) \\&- {p_i}(l - 1) - po1],\\[-12pt]\end{split}$

其中po1为一个修正值, 使投影像素的序号从1开始, 当${p_i} > 0$时, $po1 = 1$, 当${p_i} < 0$时, $po1 = - (Q - 1) \cdot {p_i} + 1$. 每行投影像素数目${B_1}$和相邻像素间隔${h_1}$分别为

$ \begin{split}&{B}_{1}=(Q-1)\left|{p}_{i}\right|+(P-1)\left|{q}_{i}\right|+1, \\ &{h}_{1}=\frac{1}{\sqrt{{p}_{i}{}^{2}+{q}_{i}{}^{2}}}.\end{split}$

当${p_i} \ne 0$, ${q_i} \ne 0$, 并且${r_i} \ne 0$时, 如图1所示, 三维Mojette变换可以看成一组在平行于平面A的平面内的二维Mojette变换结果. 探测平面上每行像素的Mojette变换投影值为在该行像素所对应的平面A内投影射线经过中心的所有网格数值的积分, 投影的行数由平行于平面A的平面数决定. 因此, 三维Mojette变换可以分解为两次二维Mojette变换:
步骤1　矢量$({p_i}, {q_i})$确定了$(x, y)$平面内的投影方向, 沿该方向的二维Mojette变换决定了最终三维Mojette变换投影的行数, 行数和相邻行之间的间隔由(2)式确定. 根据二维Mojette变换的要求, ${p_i}$和${q_i}$互质, 即${\rm{GCD}}({p_i}, {q_i}) = 1$.
步骤2　在矢量$({p_i}, {q_i})$和${r_i}$构成的二维平面A内, 以${\xi _i}$为投影方向进行二维Mojette变换, 其结果决定了三维Mojette变换投影的列数和最终的投影值.
由于第1次二维Mojette变换投影矢量$({p_i}, {q_i})$的长度为$\sqrt {p_i^2 + q_i^2}$, 并且其投影间隔为${h_1} = {1 / {\sqrt {p_i^2 + q_i^2} }}$, 因此可得$({p_i}, {q_i})$方向的投影整数为$p_i^2 + q_i^2$. 平面A内水平方向的网格数为$(x, y)$平面内的离散网格沿$( - {q_i}, {p_i})$方向进行二维Mojette变换后的投影数, 可以表示为$b' = (P - 1)\left| {{p_i}} \right| + (Q - 1)\left| {{q_i}} \right| + 1$, 垂直方向的网格数为R. 在平面A内以投影方向$(p_i^2 + q_i^2, {r_i})$进行二维Mojette变换, 要求${\rm{GCD}}(p_i^2 + q_i^2, {r_i}) = 1$.
三维Mojette变换投影的列数${B_2}$和相邻投影间隔${h_2}$分别为

$\begin{split} &{B_2} = (b' - 1)\left| {{r_i}} \right| + (R - 1)(p_i^2 + q_i^2) + 1, \\& {h_2} = \frac{1}{{\sqrt {{r_i}^2 + {{(p_i^2 + q_i^2)}^2}} }}. \end{split} $

根据以上分析, 三维Mojette变换可表示为

$\begin{split}\;& [Mf]({b_1},{b_2}) \\= \;&\sum\limits_{m = 1}^R \sum\limits_{k{{ = }}1}^P \sum\limits_{l = 1}^Q f(k,l,m) \Delta [{b_1}- {q_i}(k - 1) \\& - {p_i}(l - 1) - po1] \Delta [{b_2} - {r_i}(n - 1) \\& - (p_i^2 + q_i^2) (m - 1) - po3], \end{split} $

其中$n = - {q_i}(l - 1){{ + }}{p_i}(k - 1){{ + }}po2$, po1, po2和po3为投影像素序号的修正值, 取值分别为

$\begin{split} &po1 = \left\{ {\begin{array}{*{20}{l}} 1, & {p_i} > 0, \\ - {p_i}(Q - 1) + 1,& {p_i} < 0, \end{array}} \right. \\ &po2 = \left\{ {\begin{array}{*{20}{l}} {q_i}(Q - 1) + 1,& {p_i} > 0, \\ {q_i}(Q - 1) - {p_i}(P - 1) + 1, & {p_i} < 0, \end{array} } \right. \\& po3 = \left\{ {\begin{array}{*{20}{l}} 1,& {r_i} > 0, \\ - {r_i}(b' - 1) + 1, & {r_i} < 0. \end{array}} \right. \end{split} $

利用(4)式和(5)式计算一个$P = Q = R = 10$的全1矩阵在投影矢量$({p_i},\; {q_i},\; {r_i}) = (1,\; 1,\; 3)$和$({p_i},\; {q_i},\; {r_i}) = (1,\; 2,\; 3)$时的三维Mojette变换, 投影归一化结果如图2(a)所示. 图2(b)为全1矩阵在该投影角度下的视觉投影显示结果. 可以看出, 两种投影结果在像素数目、投影分布上完全相同, 验证了该三维Mojette变换数学模型的正确性.
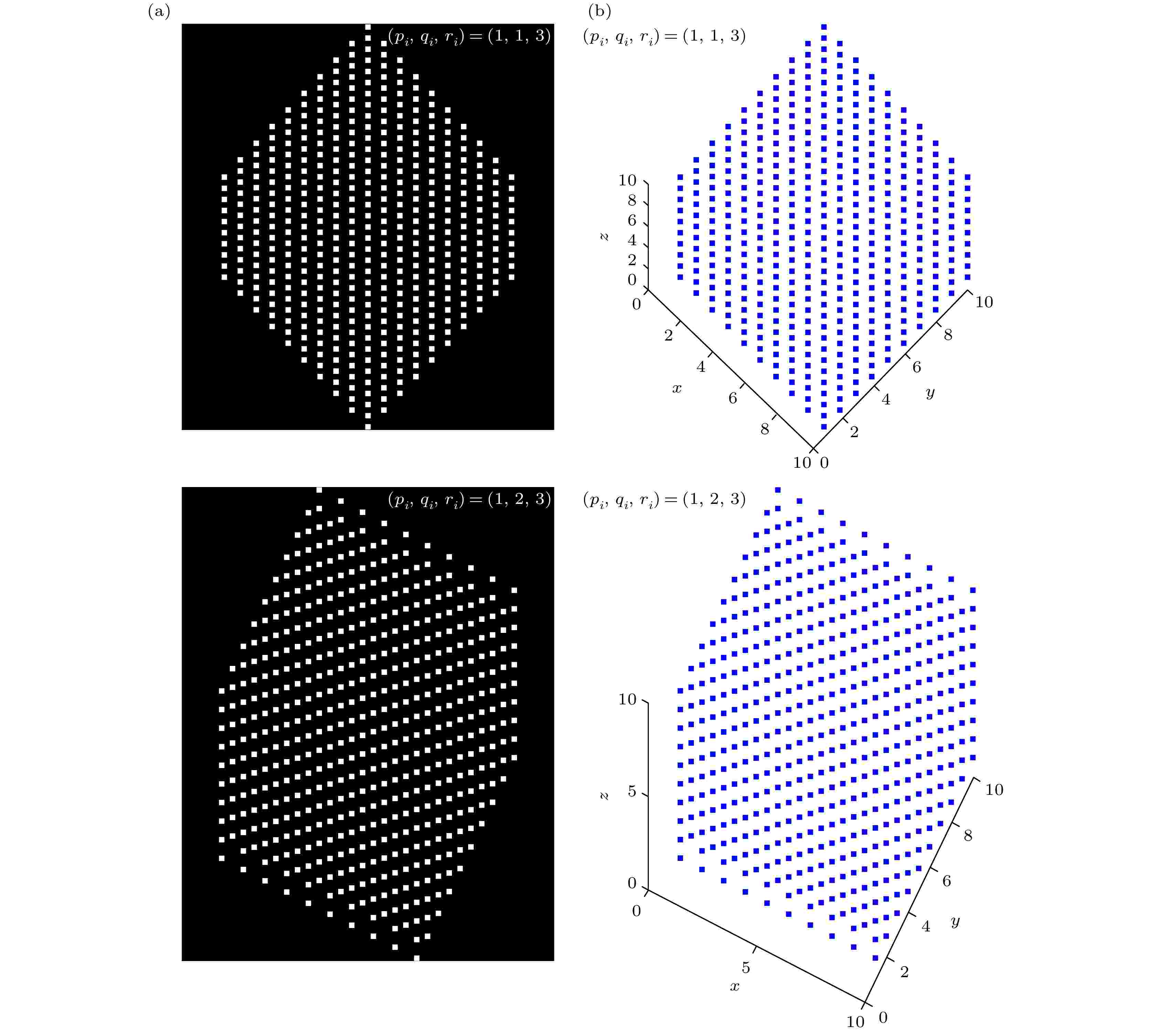图 2 (a)三维Mojette变换投影; (b)视觉投影
Figure2. (a) Three-dimensional Mojette transform projection; (b) visual projection.

1978年Katz^[10]给出一个约束投影角度数量上界的公式, 即著名的Katz引理, 该定理指出对于一簇互质的投影矢量对$({p_i}, {q_i})$, 如果重建图像的分辨率$P \times Q$满足关系

$\sum\limits_{i = 1}^N {\left| {{p_i}} \right|} \geqslant P,\;{\rm{or}}\;\sum\limits_{i = 1}^N {\left| {{q_i}} \right|} \geqslant Q,$

则最少可通过N个投影角度即可完成精确重建. (6)式为二维Mojette变换的精确重建条件. 根据不同重建图像分辨率$P \times Q$和投影角度数的要求, 可以选择合适的投影矢量$({p_i}, {q_i})$完成精确重建.
从几何角度出发, 二维Mojette变换的精确重建条件可理解为: 若所有投影矢量的绝对和超出被测区域, 则该图像可被精确重建. 将该结论推广至三维情况, 可得三维Mojette变换的精确重建条件为

$\sum\limits_{i = 1}^N {\left| {{p_i}} \right|} \geqslant P,\;{\rm{or}}\;\sum\limits_{i = 1}^N {\left| {{q_i}} \right|} \geqslant Q,\;{\rm{or}}\;\sum\limits_{i = 1}^N {\left| {{r_i}} \right|} \geqslant R.$

为了验证该精确重建条件的正确性, 利用CBI算法进行层析重建^[10,12]. CBI算法是Mojette变换最基本的重建理论. 与各种迭代类、变换类算法不同, 该算法是一种精确的求解线性方程组的算法, 二维图像中所有像素点的值被依次精确重建出来. CBI算法能够准确验证线性方程组的可解性, 其重建结果可以准确说明Mojette变换的精确重建条件是否成立, 并且通过CBI验证的精确重建条件对共轭梯度算法、反投影算法等均适用^[11,14].
利用CBI算法进行三维Mojette变换重建时, 除了对待重建三维物体进行正常投影外, 在相同投影条件下对与重建物体相同维度的三维全1矩阵和索引矩阵进行投影. 全1矩阵投影的作用是: 通过投影可以从投影向量值中看出某投影矢量下的射线穿过的像素中心点的个数, 当投影向量值中的分量为1时, 说明该投影射线穿过的路径上只有一个像素点值的贡献, 可直接求解出变量值. 当向量值中有多个1存在时, 可依次进行重建. 索引矩阵投影的作用是: 索引矩阵中的像素点值从左上角的(1, 1, 1)点赋值为0开始, 从左向右、从前到后、从上至下像素点以此递增, 每次加1, 遍历至右下角最后一个像素点时, 该点的值为$P \times Q \times R - 1$. 设置索引矩阵的目的在于, 在全1矩阵的投影向量值中找到投影值为1的分量时, 可以让计算机理解该投影对应的像素点的位置. 其逆变换的求解过程是一种串行求解模式, 即每次迭代求出全1矩阵投影值为1所对应的一批像素点, 再根据这些像素点求出的值来更新被测物体、全1矩阵、索引矩阵投影, 从而产生出投影值即为点值的像素点, 重复这一步骤, 直至所有的待求点与探测器像元上更新完毕后的一个投影值一一对应, 迭代结束.
选择经典的Shepp-Logan模型进行数值模拟实验以验证精确重建条件的正确性. 模拟三维物体的分辨率为P = Q = R = 48, 所有水平二维平面为相同的48 × 48的Shepp-Logan模型分布, 如图3(a)所示. 对表1中列出的不同投影矢量条件下的三维Mojette变换投影及重建进行数值仿真.

条件	投影矢量	(7)式是否满足	是否能精确重建
Case 1	(15, 1, 1), (13, 1, 1), (9, 1, 1), (7, 1, 1), (4, 1, 1)	√	是
Case 2	(15, 1, 1), (13, 1, 1), (9, 1, 1), (7, 1, 1), (3, 1, 1)	×	否
Case 3	(1, 15, 1), (1, 13, 1), (1, 9, 1), (1, 7, 1), (1, 4, 1)	√	是
Case 4	(1, 15, 1), (1, 13, 1), (1, 9, 1), (1, 7, 1), (1, 4, 1)	×	否
Case 5	(1, 1, 15), (1, 1, 13), (1, 1, 9), (1, 1, 7), (1, 1, 5)	√	是
Case 6	(1, 1, 15), (1, 1, 13), (1, 1, 9), (1, 1, 7), (1, 1, 3)	×	否

表1模拟仿真中采用的不同投影矢量
Table1.Projection vectors used in simulation.

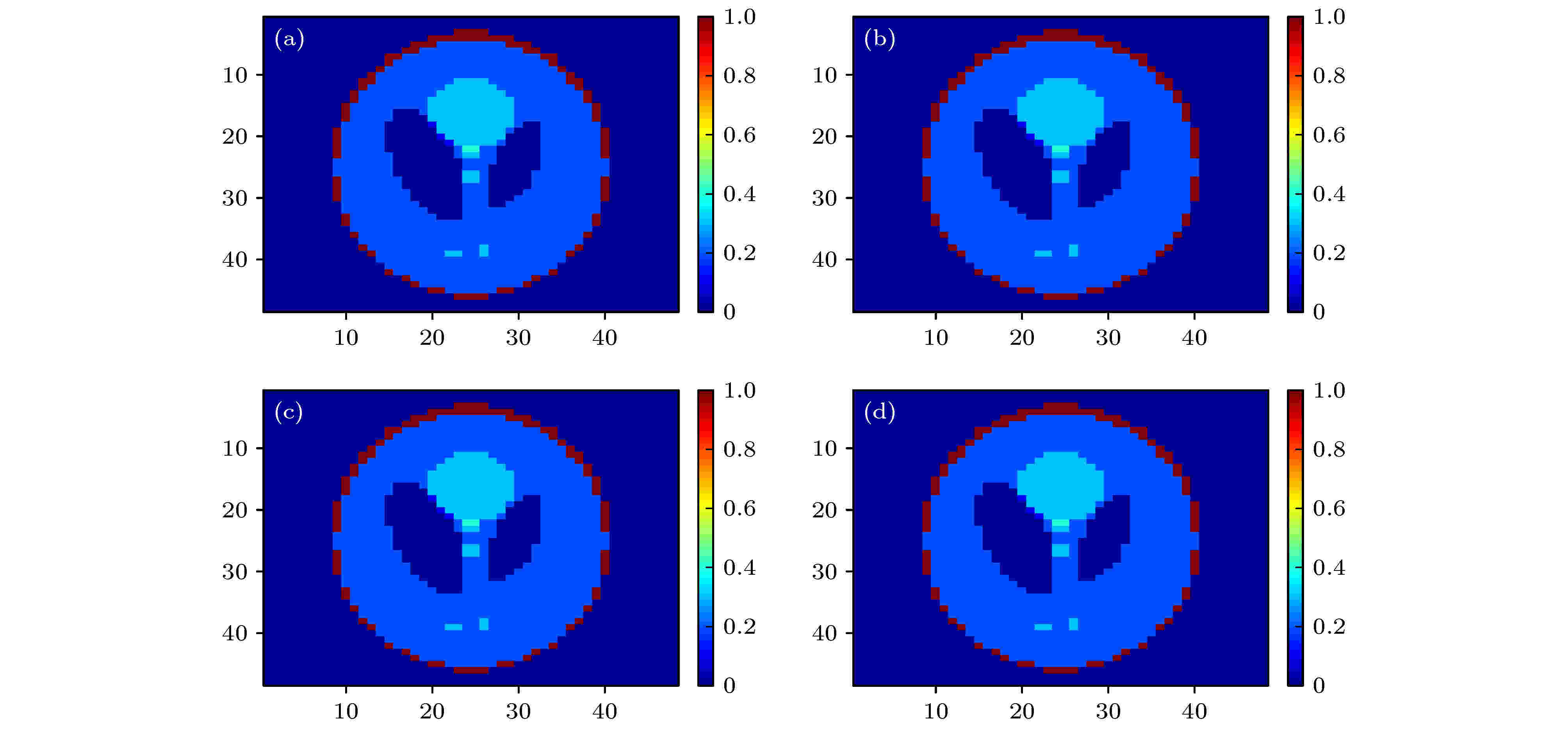图 3 满足精确重建条件下不同投影矢量的重建结果　(a) 模拟物体; (b) Case 1; (c) Case 3; (d) Case 5
Figure3. Reconstruction results of different projection vectors under accurate reconstruction condition: (a) Simulative object; (b) Case 1; (c) Case 3; (d) Case 5.

图3(b)—(d)分别为Case 1, Case 3和Case 5三种满足精确重建条件时的重建结果. 可以看出, 当选取的投影矢量满足精确重建条件时, 都可以进行精确的层析重建. 在相同的投影角度数下, 即使一个投影矢量发生变化使得精确重建条件不满足, 就得不到正确的重建结果. 数值模拟实验验证了精确重建条件的正确性.

由上述三维Mojette变换投影模型可知, 投影向量的选择决定了投影采集所需探测器的像素数目和像素大小. 对于三维Mojette变换在水平和垂直方向的投影间隔不同的问题, 在实际的投影探测中可以使用定制的成像镜头, 使水平和垂直方向的放大率不同, 可实现行和列上相邻两个像素的间隔不同. 因此, 本文只讨论探测器像素数目的影响. 由于实际探测器的像素个数有限, 则满足精确重建条件的实际投影向量和投影角度数应符合以下条件:

$(Q - 1)\left| {{p_i}} \right| + (P - 1)\left| {{q_i}} \right| + 1 \leqslant {B_1},\tag{8a}$

$\left\{ \begin{aligned} &(P - 1)\left| {{p_i}} \right|\left| {{r_i}} \right| + (Q - 1)\left| {{q_i}} \right|\left| {{r_i}} \right| \\ &+ (R - 1)({p_i}^2 + {q_i}^2) + 1 \leqslant {B_2},\;\;{\kern 1pt} \left| {{r_i}} \right| \ne 0,\\ &{ \qquad\quad \quad R \leqslant {B_2},\quad \quad \quad \quad \quad \quad {\kern 1pt}\;\;\left| {{r_i}} \right| = 0,} \end{aligned} \right. \tag{8b}$

$\sum\limits_{i = 1}^N {\left| {{p_i}} \right|} \geqslant P,\;{\rm{or}}\;\sum\limits_{i = 1}^N {\left| {{q_i}} \right|} \geqslant Q,\;{\rm{or}}\;\sum\limits_{i = 1}^N {\left| {{r_i}} \right|} \geqslant R,\tag{8c}$

$\min (N),\tag{8d}$

$\begin{split}\;&{\rm{GCD}}({p_i},{q_i}) = 1,~~{\rm{GCD}}({p_i}^2 + {q_i}^2,{r_i}) = 1,\\ \;& \qquad {p_i} \in Z,~~~~{q_i} \in {Z^ + },~~~~{r_i} \in Z\end{split}\tag{8e}$

其中$({B_1}, {B_2})$为实际探测器的像素数.
确定最优投影向量的具体步骤如下.
步骤1　确定满足(8a)式、(8b)式和(8e)式的所有投影矢量$({p_i}, {q_i}, {r_i})$.
步骤2　根据(8c)式, 要满足精确重建条件有三种方案, 即$\displaystyle \sum\limits_{i = 1}^N { | {{p_i}} |} \!\geqslant\! P$, $\displaystyle \sum\limits_{i = 1}^N { | {{q_i}} |} \!\geqslant\! Q$或$\displaystyle\sum\limits_{i = 1}^N { | {{r_i}} |} \!\geqslant\! R$, 与其对应的条件是选取的投影矢量中${p_i}$, ${q_i}$或${r_i}$的绝对值越大, 投影角度数越少. 且要保证投影像素数最少, 则在投影矢量的一个分量保持较大值时, 其他两个分量的值尽可能小. 因此, 将步骤1所确定的所有投影矢量对${p_i}$, ${q_i}$或${r_i}$的绝对值进行降序排序, 从大到小选取投影矢量, 直至满足(8c)式, 则可确定投影角度数和其对应的投影矢量.
步骤3　选择步骤2中确定的三种方案投影角度数的最小值, 其投影矢量即为最优的投影角度布局方案. 或者在实际的测量系统中, 根据测试条件对投影角度的限制, 选择三种方案中最好实现的一种为最优投影角度布局方案.
以$P = Q = R = 64$, 像素数为1024 × 2048的探测器为例对最优投影角度的布局进行说明. 当$\left| {{r_i}} \right| = 0$时, 最少需要5个投影角度可实现精确重建. 若要求投影像素数最少, 则选取的投影矢量为[(15, 1, 0), (–15, 1, 0), (14, 1, 0), (–14, 1, 0), (13, 1, 0)](方案1)或[(1, 15, 0), (–1, 15, 0), (1, 14, 0), (–1, 14, 0), (1, 13, 0)] (方案2), 其空间分布如图4(a)和图4(b)所示, 该条件下探测器限制在较小的角度范围内. 该投影矢量方向的二维Mojette变换投影结果如图5(a)和图5(b)所示, 投影像素数分别为64 × 1009, 64 × 1009, 64 × 946, 64 × 946和64 × 883. 若探测器角度范围不受限制, 选取投影矢量为[(15, 1, 0), (–15, 2, 0), (14, 5, 0), (–14, 9, 0), (13, 11, 0)] (方案3)或[(1, 15, 0), (–2, 15, 0), (5, 14, 0), (–9, 14, 0), (11, 13, 0)] (方案4), 空间分布如图4(c)和图4(d)所示. Mojette变换投影如图5(c)和图5(d)所示, 投影像素数分别为64 × 1009, 64 × 1072, 64 × 1198, 64 × 1450和64 × 1513.
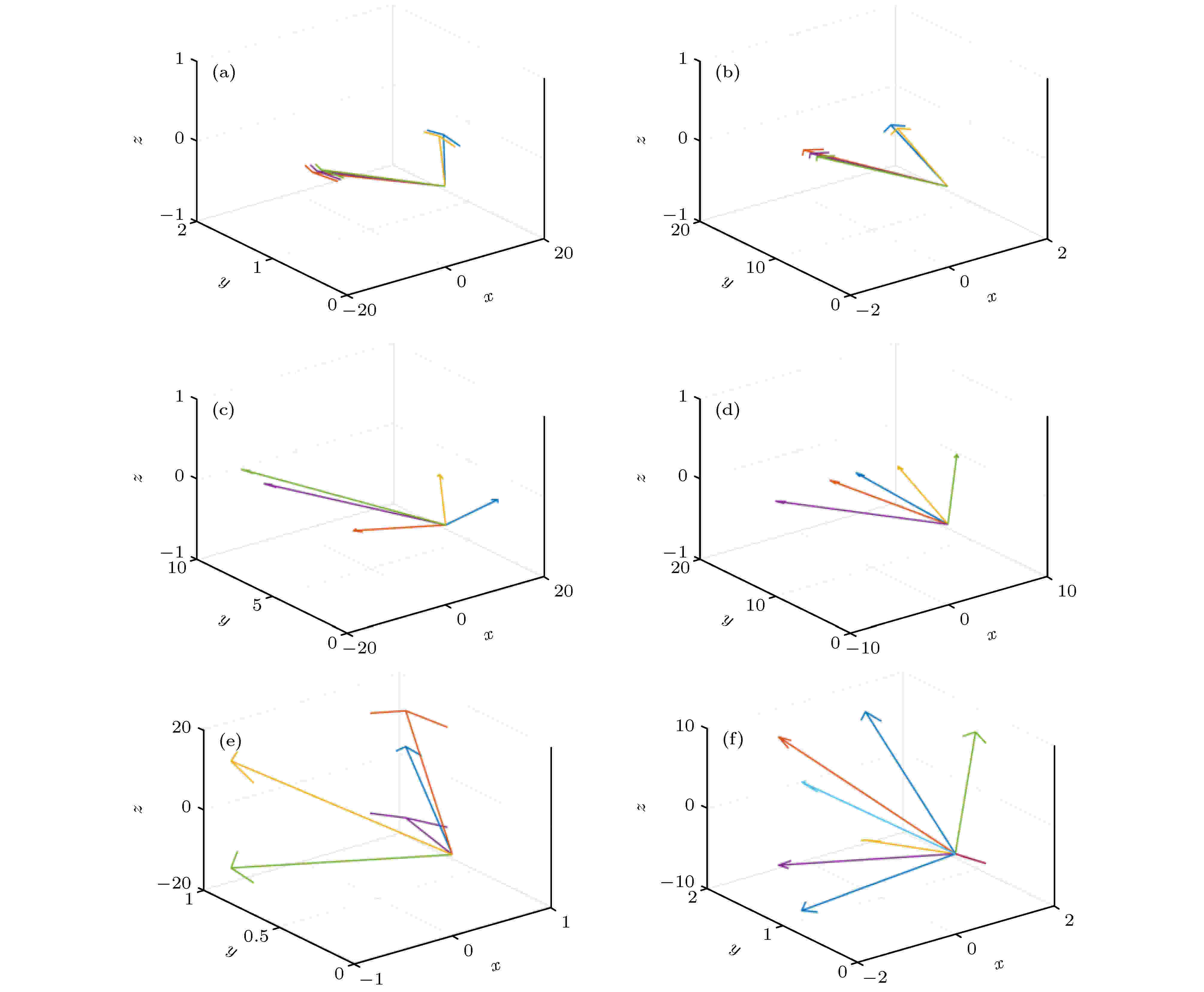图 4 不同投影矢量对应的投影角度空间分布　(a)方案1; (b)方案2; (c)方案3; (d)方案4; (e)方案5; (f)方案6
Figure4. Spatial distribution of projection angles corresponding to different projection vectors: (a) Scheme 1; (b) Scheme 2; (c) Scheme 3; (d) Scheme 4; (e) Scheme 5; (f) Scheme 6.

图 5 不同投影矢量对应的投影结果　(a)方案1; (b)方案2; (c)方案3; (d)方案4; (e)方案5; (f)方案6
Figure5. Projections corresponding to different projection vectors: (a) Scheme 1; (b) Scheme 2; (c) Scheme 3; (d) Scheme 4; (e) Scheme; (f) Scheme 6.

当$\left| {{r_i}} \right| \ne 0$时, 若要满足条件$\displaystyle\sum\limits_{i = 1}^N {| {{p_i}} |} \!\geqslant\! P$或$\displaystyle \sum\limits_{i = 1}^N {| {{q_i}} |} \!\geqslant\! Q$, 则最少的投影角度数为11; 而满足条件$\displaystyle\sum\limits_{i = 1}^N {| {{r_i}} |} \!\geqslant\! R$时最少的投影角度数为5, 对应的投影矢量为[(1, 1, 5), (1, 1, 15), (–1, 1, 15), (1, 1, –15), (–1, 1, –15)] (方案5), 空间分布如图4(e)所示. 该投影矢量方向的三维Mojette变换投影结果见图5(e), 投影像素数分别为127 × 757, 127 × 2017, 127 × 2017, 127 × 2017和127 × 2017.
若选取的投影矢量中$\left| {{p_i}} \right| > 1$或$\left| {{q_i}} \right| > 1$, 此时对应的$\left| {{r_i}} \right|$变小, 则所需最少投影角度数会增多. 例如满足精确重建条件的另一组投影矢量为[(1, 2, 9), (–1, 2, 9), (1, 2, –9), (–1, 2, –9), (2, 1, 9), (–2, 1, 9), (2, 1, –9), (–2, 1, –9)] (方案6), 空间分布如图4(f)所示. 对应的投影结果如图5(f)所示.
图4和图5的结果综合表明: 在探测器像素数受限的条件下, 最优的投影角度布局方案为水平面投影, 即基于二维Mojette变换的层析重建, 此时所需投影角的数目最少. 并且不论投影角度是否受限, 其所需的投影探测器的像素数都比三维布局方案的少. 这种方式与传统层析技术中所选取的探测器的空间布局方案完全一致. 当投影矢量无法满足水平面投影时, 要选择$\displaystyle\sum\limits_{i = 1}^N {\left| {{r_i}} \right|} \!\geqslant\! R$为精确重建条件, 并且选择$\left| {{p_i}} \right|$和$\left| {{q_i}} \right|$的值越小, 所需的投影角度数和探测器的像素数越少.

为了解决计算层析技术中投影采集角度受限制的问题, 利用有限角度的投影实现高精度的层析重建, 本文在建立三维Mojette变换数学模型及其精确重建条件的基础上, 对Mojette变换层析技术中的最优投影空间角度布局方案进行了研究. 在综合考虑精确重建条件和实际探测器像素数目受限的条件下, 提出了确定最优投影角度的方法. 研究结果表明: 1)若要求层析采集系统中投影角度数和投影像素数尽可能少, 则探测器要分布在被测物体周围的同一水平面内进行平行投影的采集, 此时层析模型为二维Mojette变换及重建; 2)当投影条件受限, 无法实现水平面投影采集时, 则投影矢量中$\left| {{p_i}} \right|$和$\left| {{q_i}} \right|$的值越小越好. 该投影角度布局方案与传统的层析系统中探测器的空间布局方案完全一致, 本文首次从理论上说明了这种布局方案的优越性.