摘要: 在跨流域复杂流动问题的模拟中, 基于求解速度分布函数演化方程的气体动理论方法的效率问题一直受到工程应用领域关注. 研究提升气体动理论方法在定常流动模拟中的计算效率具有重要意义. 为了提升定常流动计算收敛速度, 本文提出了一种耦合宏观方程数值本构关系的气体动理论加速收敛方法. 通过求解Boltzmann模型方程, 将应力、热流高阶项的数值解与宏观方程耦合, 实现了宏观方程的封闭; 另一方面, 宏观方程的计算结果被用来更新Boltzmann模型方程的当地平衡态速度分布函数中的宏观物理量, 以此构造求解Boltzmann模型方程的全隐式数值格式. 通过跨流域方腔流动、超声速圆柱绕流及双圆柱干扰绕流案例的数值模拟, 对方法进行了广泛考核. 计算结果与常规气体动理论统一算法、直接模拟蒙特卡罗法符合良好, 证明该方法很好地描述了稀薄流动中的非线性本构关系, 以及激波、强壁面剪切、流动分离等强非平衡特征. 进一步, 对于低努森数
Kn 的流动, 方法能显著加速收敛过程, 提升计算效率; 随着努森数
Kn 增加, 气体对流输运效应减弱, 方法的加速收敛效果降低. 与此同时, 如何减少内迭代耗时, 进一步提升效率有待更多研究.
关键词: 气体动理论统一算法 /
本构关系 /
加速收敛 /
耦合算法 English Abstract Method of accelerating convergence for gas kinetic algorithm based on digital constitutive relation of macroscopic equations Pi Xing-Cai 1 ,Zhu Lian-Hua 2 ,Li Zhi-Hui 1,3 ,Peng Ao-Ping 1 ,Zhang Yong-Hao 2 1.Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China Fund Project: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11902339)Received Date: 24 April 2020Accepted Date: 10 June 2020Available Online: 10 October 2020Published Online: 20 October 2020Abstract: In the simulation of complex multi-scale flows covering various flow regimes, the computational efficiency of gas kinetic method by which the evolution equation of velocity distribution function is solved directly is the key to engineering applications. In order to accelerate simulation for steady flows, a gas kinetic algorithm accelerated by utilizing the macroscopic conservative equations with a digital constitutive relation is developed. In this algorithm, the contribution of the high-order terms of stress and heat flux in macroscopic conservative equations is determined by the gas kinetic solution. Meanwhile, the solution of the macroscopic conservative equations provides the macroscopic quantities for the equilibrium distribution function in the Boltzmann model equation, where a fully implicit scheme to solve the Boltzmann model equation is developed. Extensive validations are performed for the cavity flow, the supersonic flow around the cylinder, and the interactive rarefied flow around two side-by-side cylinders. The results from the above method are in good agreement with the results from the conventional gas kinetic unified algorithm and the direct simulation Monte Carlo method. It can be concluded that the nonlinear constitutive relation of rarefied flow can be well captured by the present method. And the ability of this method to simulate complex flows such as shock wave, strong wall shear and flow separation is demonstrated. Furthermore, the present method has shown to be much faster than the conventional gas kinetic unified algorithm, especially for the low-Kn flows. As the value of Kn increases, the acceleration rate decreases, because the effect of flow convection becomes weak. Meanwhile, more effort is needed to reduce inner loop iterations to improve its efficiency. Keywords: gas kinetic unified algorithm /constitutive relation /convergence accelerated method /coupled method 全文HTML --> --> --> 1.引 言 在超声速稀薄气体动力学数值计算领域, 基于Boltzmann方程[1 ,2 ] 或Shakhov方程[3 ] 、ES-BGK方程[4 ] 等模型方程的数值方法获得了广泛的关注, 如基于离散速度坐标法[5 ,6 ] 的气体动理论统一算法(gas kinetic unified algorithm, GKUA)[7 -10 ] 、统一气体动理学格式(unified gas kinetic scheme, UGKS)[11 ] , 以及渐近保持格式[12 ,13 ] 、矩方法[14 ] 、离散Boltzmann方法(discrete Boltzmann method, DBM)[15 ,16 ] 等. 特别是GKUA, 在大型航天器、飞船返回舱再入过程模拟等工程问题中获得了成功应用[17 -21 ] . 基于离散速度坐标法的各类算法需要求解包括时间、位置空间及速度相空间的高维偏微分方程组, 导致其计算量大. 为了使该类方法获得更广泛应用, 提升计算效率是核心研究主题.22 ])通过构造新的离散平衡态速度分布函数解析表达形式, 建立了严格保守恒的数值方法, 使得该方法能以较少的离散速度点实现方程求解. 文献[23 ]采用叉树数据结构对UGKS的离散速度空间进行优化以提高计算效率; 第二类(如文献[24 ])对模型方程进行了隐式处理, 并引入演化时间平均界面通量, 通过对控制方程矩阵进行近似LU分解实现了隐式UGKS, 还包括GKUA基于LU-SGS构造的有限体积隐式数值格式, 成功应用于航天器再入解体物的绕流分析[25 -27 ] ; 第三类(如文献[28 ])开展了Shakhov模型方程与N-S方程的耦合求解, 并将其应用于低速稀薄气体流动分析, 实现了任意压力比下的狭缝稀薄流模拟; 第四类(如文献[29 ])对求解线化Boltzmann模型方程的离散速度坐标法进行Fourier稳定性分析, 获得了方法在连续流域收敛变慢的原因, 并进一步构造了不同阶数的Hermite矩方程用于算法加速收敛. 另外, 文献[30 ,31 ]采用UGKS获得网格界面的守恒量数值通量, 并用数值通量构造宏观演化方程, 通过同步求解构造的宏观演化方程获得宏观量并用于预测当地平衡态速度分布函数, 大幅度提升了传统UGKS的效率.[32 ] 、Grad13方程的正则化[33 ] 以及在广义流体力学方程的基础上提出了非线性耦合本构关系(nonlinear coupled constitutive relations, NCCR)[34 ,35 ] . 这些理论模型成功开展了一维激波结构、二维及三维高超绕流等问题的模拟分析[36 ] . 值得关注的是, 通过数值的方式封闭非守恒量输运方程也是描述近空间飞行出现的非线性稀薄效应的一个新思路. 例如, 文献[37 ]基于求解辐射输运方程的加速算法思想[38 ] 构造了求解线化Boltzmann方程的通用协同迭代格式(general synthetic iteration scheme, GSIS). 该方法通过协同迭代宏观输运方程及Boltzmann模型方程, 实现了库叶特流动、方腔稀薄流动等的快速收敛. GSIS方法的核心在于通过对Boltzmann模型方程求高阶矩, 建立宏观守恒量及非守恒量的输运方程. 通过Chapman-Enskog展开将非守恒量宏观输运方程的应力、热流高阶项剥离出来, 并利用数值求解Boltzmann模型方程给定高阶项的值, 由此实现非守恒量宏观输运方程的封闭并加速收敛过程. 最近, 文献[39 ]将GSIS拓展到非线性气体动理论方程的加速收敛算法应用研究中, 并实现了低速流动问题100迭代步收敛, Kn = 0.01的超声速圆柱绕流问题提升10余倍计算效率的效果. 为了更全面地验证协同迭代方法的有效性, 基于相同的思路, 本文在气体动理论统一算法(GKUA)框架下, 构造了耦合宏观方程本构关系的加速收敛方法. 在控制方程方面, 采用Boltzmann模型方程描述强非线性稀薄流动问题, 且简化了宏观输运方程中应力、热流高阶项的构造方式; 在数值格式方面, 改进了具有捕捉强间断能力的隐式气体动理论数值格式; 并且, 利用多块对接网格技术提高处理复杂问题的能力. 本文的研究工作将进一步验证方法的有效性并展示了其向工程应用领域拓展的能力.2 节将构建加速收敛方法的理论模型; 第3 节将对数值求解方法进行描述; 第4 节通过方腔流、超声速圆柱绕流及双圆柱干扰绕流模拟, 对本文理论算法模型进行验证分析; 第5 节将对研究内容进行总结.2.理论模型 本研究以Shakhov模型方程为例, 构造加速收敛方法的理论模型. 此构造方式同样适用于其他模型方程. Shakhov模型方程的速度分布函数$f(t, {x}, {\xi })$ 满足关系[3 ] t 为时间, x $\upsilon $ 为碰撞频率, $\rho $ 为密度, T 为温度, R 为气体常数, q $p = \rho RT$ . 对于单原子气体, 普朗特数$Pr = 2/3$ . 气体分子热运动速度C ${\xi }$ 与宏观速度U 1 )进行速度相空间降维,${F} = \left( {{f_1},{f_2}} \right),\;{{F}^N} = \left( {f_1^N,f_2^N} \right),$ 下标J 为离散速度坐标点的索引.3 )构造格心型有限体积格式, 可得I 为物理空间网格单元索引, 符号“$ \stackrel{-}{} $ ”表示物理量在网格单元的均值, $N\left( I \right)$ 为网格I 的邻近网格单元索引, ${\xi _{J, n}}$ 为${{\xi }_J}$ 在界面$\left( {I, K} \right)$ 的法向分量, ${S_{I, K}}$ 为界面$\left( {I, K} \right)$ 的面积, ${\tilde{ F}_{I, J, K}}$ 为分布函数在界面的重构量, ${\varOmega _I}$ 为第I 网格单元的体积(二维: 面积). 分布函数的重构可以采用经典的CFD重构格式, 如NND格式, 也可采用考虑气体分子碰撞迁移物理过程, 具有渐近保持特性的重构方式, 如DUGKS的重构方式[40 ,41 ] . 为了简化问题, 本研究采用经典的CFD重构格式进行界面重构. 界面数值通量的计算采用具有迎风特性的Steger-Warming矢通量分裂方法:${ {{{\tilde{ F}}_{I, J, K}}} \big|_{\rm{L}}}$ 为左界面重构分布函数, ${ {{{\tilde{ F}}_{I, J, K}}} \big|_{\rm{R}}}$ 为右界面重构分布函数.4 )将面临对流项数值稳定性条件——CFL条件, 以及当流动趋近于连续流时的刚性源项导致的时间步长限制. 采用LU-SGS进行隐式格式构造可以显著增加时间步长, 提升计算效率[7 ,19 ,26 ] . 方程(4 )在$n + 1$ 时刻具有如下形式:n 时刻残差:6 )的左端项引入${\left. {\bar{ F}_{I, J}^N} \right|^{n + 1}} = {\left. {\bar{ F}_{I, J}^N} \right|^n}, {\left. {{\upsilon _I}} \right|^{n + 1}} = {\left. {{\upsilon _I}} \right|^n}$ , 可得关于差量9 )左端项的差量的界面重构方式不影响计算结果. 因此, 一阶迎风格式是最好的选择, 即依据离散速度坐标点的方向, 选择界面迎风侧的网格单元均值作为界面值. 由此可获得关于差量的线性方程组, 可方便地使用LU-SGS方法数值求解上述方程组, 获得$ n+1 $ 时刻的差量解${ {\Delta \bar{ F}} |^{n + 1}}$ , 进而通过数值积分获得$ n+1 $ 时刻的流场宏观物理量.Kn 的降低, 其迭代步数依旧会增加, 收敛速度变慢. 文献[29 ]对求解线化Boltzmann模型方程的离散速度坐标法开展误差传递分析, 得出努森数Kn 降低将导致误差传递矩阵的谱半径逐渐趋近于1. 这是导致收敛变慢的主要原因. 另外, 有研究认为, 隐式格式构造中引入的简化假设${\left. {\bar{ F}_{I, J}^N} \right|^{n + 1}} = {\left. {\bar{ F}_{I, J}^N} \right|^n}$ 对收敛具有负面影响[30 ] .[37 -39 ] , 本研究通过构造并协同迭代求解一套与Boltzmann模型方程相容的宏观守恒方程来实现流场扰动加速传递及耗散. 通过对方程(1 )求碰撞不变量$\varphi = \left( {1, {\xi }, 0.5{\xi ^2}} \right)$ 的矩, 可得模型方程对应的质量、动量及能量守恒的宏观守恒方程如下:${C_V}$ 为定容热容.10 )并不封闭. 为了实现输运方程的理论表达形式封闭并具有良好的数学性质, 已有研究者提出了一系列的理论形式, 如正则化Burnett方程、R-13方程以及NCCR模型[32 -35 ] . 尽管做了相应的简化, 这些理论形式依旧相当复杂, 数值稳定性仍然需要进一步优化. 近年来数值求解Boltzmann模型方程的气体动理论方法同样体现出巨大的潜力. 利用气体动理论方法数值求解非线性应力、热流, 并结合经典CFD在计算效率、数值稳定性方面的优势, 从数值层面描述非线性本构关系并封闭宏观守恒方程组(10 )无疑是新的途径.f 和非守恒量${\sigma _{ij}}$ 及${q_i}$ 具有多尺度特性. 它们的多尺度展开形式为$\mu $ 为黏性系数, $\kappa $ 为热传导系数. (14 )式及(15 )式即为N-S方程的线性本构关系式. 为了保持宏观守恒方程与模型方程的一致性, 应力及热流的高阶项必须在计算中予以考虑. 值得一提的是, 在数值计算过程中, 来自壁面的扰动是通过边界层的剪切作用向主流区及远场传递并在沿途进行耗散. 耗散(包括物理耗散及数值耗散两个部分)对流场收敛及数值稳定性都有积极作用. 在宏观方程的求解过程中, 保持一阶应力、热流项表达式具有的耗散性质可更好地利用宏观方程扰动传递快的优势, 加速收敛. 对于超声速绕流, 增加宏观方程的耗散对数值稳定性更为重要.[37 ,39 ] :${\rm{Ho}}{{\rm{T}}_\sigma }$ 及${\rm{Ho}}{{\rm{T}}_q}$ 获取方法如下:${ {\sigma _{ij}^{(1)}} |^ * }$ , ${ {q_i^{(1)}} |^ * }$ 表示将Shakhov模型方程的宏观守恒量代入(14 )式及(15 )式获得的一阶应力及热流.10 )获得的宏观量对方程(6 )中的当地平衡态速度分布函数及碰撞频率进行预测, 并重新构造隐式格式, 可将方程(9 )改进为如下形式:$\upsilon _I^ * $ , ${\left. {\bar{ F}_{I, J}^N} \right|^*}$ 为通过宏观方程预测的碰撞频率及当地平衡态速度分布函数.3.数值方法 对模型方程进行无量纲化, 引入特征长度L , 特征温度${T_0}$ , 特征黏性系数${\mu _0}$ , 特征速度${C_{m\infty }} = \sqrt {2 R{T_0}}$ , 特征数密度${n_0}$ , 特征压力$0.5{n_0}mC_{m\infty }^2$ , 特征热流$0.5{n_0}mC_{m\infty }^3$ 及特征速度分布函数${{{n_0}}/{C_{m\infty }^3}}$ . Shakhov模型方程(1 )的黏性系数采用如下指数律:$\omega = 0.81$ . 因此, 无量纲碰撞频率$\overset{\lower0.5 em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\upsilon } $ 等于:$ { \frown}$ ”. 若无特别说明, 后续量都为无量纲量.2 节介绍的理论模型, 耦合宏观方程本构关系的加速收敛方法使用开源代码OpenCFD-EC2 D[42 ] 的核心代码进行宏观方程数值格式构建; 使用本课题组GKUA核心代码进行气体动理论相关算法构建; 将二阶NND格式用于Shakhov模型方程及宏观方程的界面物理量重构; 界面通量采用Steger-Warming矢通量分裂方法计算; 使用完全漫反射边界条件确定壁面反射速度分布函数. 其求解流程如下.[43 ] $\Delta \xi < \dfrac{1}{3}\sqrt {{T_{\min }}} $ . 目前, 常用的数值积分方法包括: Gauss-Hermite积分法, Gauss-Legendre积分法及Newton-Cotes积分法. 由于精确求解高阶Hermite多项式较为困难, 限制了Gauss-Hermite积分点的分布范围, 因此Gauss-Hermite方法主要应用于低马赫数流动. 高马赫流动模拟中普遍采用Gauss-Legendre积分法或Newton-Cotes积分法[19 ] .k 时间步的速度分布函数$ {f}^{k} $ 及宏观流动物理量$ {W}^{k} $ .18 )式及(19 )式获得高阶应力项$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{\sigma } $ 及高阶热流项$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{q} $ .$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{\sigma } $ 及热流项$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{q} $ 数值解代入(16 )式及(17 )式, 求解由方程(10 )式、(16 )式及(17 )式构成的方程组, 获得预测的宏观流动物理量$ {\left({W}^{k+1}\right)}^{*} $ . 即将高阶应力项$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{\sigma } $ 及热流项$ {\mathrm{H}\mathrm{o}\mathrm{T}}_{q} $ 视作宏观方程的固定源项, 迭代求解直至宏观方程收敛到特定精度或达到指定的迭代步数.$ {\left({W}^{k+1}\right)}^{*} $ 演化更新当地平衡态速度分布函数及碰撞频率, 并采用LU-SGS方法求解构造的隐式方程(20 ), 获得第k +1步的离散速度分布函数$ {f}^{k+1} $ 及宏观流动物理量$ {W}^{k+1} $ .$ {\upsilon }^{k} $ 与$ {\upsilon }^{k+1} $ 的相对偏差均值作为收敛判断标准:I 为物理空间网格索引, ${\rm{Nu}}{{\rm{m}}_{{\rm{cell}}}}$ 为物理空间总网格数, $\Delta t$ 为时间步长. 若还未达到收敛标准, 继续进行第2—5步迭代.4.算例验证 24.1.方腔流动 4.1.方腔流动 对于方腔流动, 主流区黏性特性能否准确描述对流场计算结果, 尤其是温度场的影响尤为明显. 因此, 被广泛用于算法验证. 为了与已有研究成果对比, 本文以方腔边长为参考长度分别计算了努森数Kn = 1.000, 0.075, 0.010的方腔稀薄流动. 努森数Kn 定义为[44 ,45 ] :L = 1的方块区域, 所有壁面的无量纲温度均为$ {T}_{\mathrm{w}}=1.0 $ , 上壁面无量纲速度$ {U}_{\mathrm{w}}=0.15 $ , 其余壁面无量纲速度为0. 物理空间网格为65 × 65, 在[–5.67, 5.67] × [–5.67, 5.67]的速度相空间采用32 × 32个Gauss-Hermite离散速度坐标点. 图1 绘出了各状态的温度场对比情况(“GKUA”表示常规GKUA结果; “Coupled”表示本文提出的耦合加速收敛方法结果). 通过对比可以看出两者良好符合, 反映了方腔内的流动从左侧的低温膨胀过渡到右侧的高温压缩的变化过程, 这样的过程对稀薄效应越强的流动状态表现越突出. 为了定量分析, 图2 绘出了中心线的速度分布计算结果与常规GKUA及文献[45 ]结果的对比情况. 计算结果准确反映了壁面速度滑移随稀薄程度的增加而增大以及整个流域的非线性分布规律.图 1 方腔流温度分布计算结果 (a) Kn = 1 ; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: 彩色背景及黑色实线; Coupled: 红色虚线)Figure1. Temperature distribution in cavity flow: (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: coloured background and black solid lines; Coupled: red dashed lines).图 2 方腔中心线上的速度场 (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01Figure2. Velocity profiles at the central lines of the cavity: (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01.图3 给出了耦合加速收敛方法计算收敛曲线与常规GKUA对比情况. 可知, 在小努森数Kn 情况下本方法能大幅度减少计算收敛的迭代步数. 随着努森数Kn 增大, 加速收敛效果逐渐减弱. 表1 列出了本文提出的耦合加速收敛算法的迭代步数与常规GKUA的迭代步数对比情况. 其中, Kn = 0.01的加速比达到47倍. 分析认为, 随着努森数Kn 增大, 扰动传递由宏观对流主导逐渐转换为由分子碰撞扩散效应主导, 这削弱了借助宏观方程加速收敛的优势. 需要指出的是, 由于该算例采用的宏观方程求解器为适于高速可压缩流动问题的数值格式, 其在低速弱可压的方腔流模拟中收敛较慢. 因此, 从计算耗时角度看, 耦合加速收敛方法的优势受到严重影响. 但是, 从减少气体动理方法的迭代步数来看, 该方法的效果可观, 验证了耦合本构关系思路的有效性.Kn 迭代步数(收敛标准: 10–7 ) 加速比 GKUA Coupled 0.010 8000 170 47.00 0.075 2300 300 7.60 1.000 1200 1100 1.09
表1 耦合加速收敛方法与常规GKUA的收敛情况对比Table1. Convergence comparison between the conventional GKUA and the coupled acceleration method.图 3 耦合加速收敛方法与常规GKUA的计算收敛历史Figure3. The convergence history between coupled acceleration method and the conventional GKUA.4.2.超声速圆柱绕流 -->4.2.超声速圆柱绕流 为了进一步探讨本文发展的耦合加速收敛方法对超声速稀薄绕流问题的模拟能力, 本文计算了来流马赫数Ma = 5的圆柱超声速稀薄绕流. 相较于低速流动, 超声速绕流存在着强剪切边界层、激波以及流动分离, 将导致速度分布函数严重偏离Maxwell平衡态分布. 激波结构、壁面物理量的结果对比可以有效反映耦合加速收敛方法描述强非平衡物理特征的准确性. 为了与已有研究成果对比, 以圆柱半径为参考长度, 本文计算了来流努森数Kn = 0.01, 0.10的超声速稀薄绕流. 努森数Kn 定义如下[31 ,44 ] :$ {T}_{\mathrm{w}}=1.0 $ . 本文的计算区域为: 圆柱半径R = 1; 计算域远场半径R f = 11; 物理空间网格: 周向82 × 径向80, 第一层网格高度0.0002, 并按双曲正切函数tanh增长. 在[–15, 15] × [–15, 15]的速度相空间采用100 × 100个Gauss- Legendre离散速度坐标点. 图4 绘出了Kn = 0.01案例的压力场、温度场和马赫数场的结果及其与常规GKUA果的对比. 结果显示, 采用本文提出的耦合加速收敛方法计算获得的流场与常规GKUA计算获得的流场符合良好, 包括激波厚度、尾流区大小等细节. 图5 绘出了Kn = 0.1案例的压力场、温度场及马赫数场的结果及其与常规GKUA果的对比. 同样, 两种方法获得的结果符合良好. 并且, 对比Kn = 0.01及Kn = 0.1案例的流场结果可知, 增大稀薄程度可使激波层、边界层变厚, 降低物理量的梯度, 有利于减小不同格式的数值黏性差异导致的结果差异. 图6 给出了本文的耦合加速收敛方法获得的壁面物理量与常规GKUA及DSMC获得的壁面物理量对比情况. 其中, Kn = 0.01案例的DSMC 计算结果由 DS2 V 软件[46 ] 计算得到, Kn = 0.1案例的计算结果源自参考文献[31 ]. 横坐标θ = 180°对应于圆柱迎风面驻点. 可以看出, 三种方法获得的压力符合良好, 并且气体稀薄程度增加将导致激波强度变弱, 进而增大压力系数; 热流结果总体符合, 但头部驻点的差异略有增大; 三种方法获得的壁面剪切应力符合良好. 图7 给出了耦合加速收敛方法的收敛历史及其与GKUA的对比情况. 可以看出, 本方法能大幅度加快收敛速度. 对于Kn = 0.01的案例, 迭代步数加速约7.5倍, 计算耗时提升约7.3倍(GKUA耗时116 h, Coupled耗时15.9 h); 对于Kn = 0.1的案例, 迭代步数加速约2.85倍, 计算耗时提升约2.7倍(GKUA耗时77 h, Coupled耗时28.6 h). 另外, 数值实验发现, 采用更稀疏的网格有利于提升加速收敛效果, 但是, 对壁面物理量计算结果有负面影响. 分析认为, 稀疏网格有利于宏观方程的内迭代收敛, 并利于发挥宏观方程在扰动传递方面的优势, 促进整体收敛. 另一方面, 相较于只存在一阶空间导数的气体动理论方法, 宏观方程存在的二阶导数项导致数值求解宏观方程在网格无关性方面的要求高于气体动理论方法.图 4 Kn = 0.01圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数 (GKUA: 彩色背景及白实线; Coupled: 红色虚线)Figure4. (a) Pressure, (b) temperature, (c) Mach number distribution around cylinder for Kn = 0.01 (GKUA: coloured background and white solid lines; Coupled: red dash lines).图 5 Kn = 0.1圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)Figure5. (a) Pressure, (b) temperature, (c) Mach number distribution around cylinder for Kn = 0.1 (GKUA: coloured background and white solid lines; Coupled: red dash lines).图 6 圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力Figure6. (a) Pressure, (b) heat flux, and (c) shear stress profile along the wall surface of cylinder.图 7 耦合加速收敛方法与常规GKUA的超声速圆柱绕流计算收敛情况对比Figure7. Comparison of the convergence history of supersonic flow around the cylinder between the coupled acceleration method and the conventional GKUA.4.3.并列双圆柱干扰绕流 -->4.3.并列双圆柱干扰绕流 为了进一步验证耦合加速收敛方法对复杂流场的处理能力, 本文对并列双圆柱干扰绕流进行了模拟. 相较于单体绕流, 并列双圆柱干扰绕流存在着激波融合、干扰及边界层相互影响. 为了与已有研究成果对比, 以圆柱半径为参考长度, 本文计算了来流努森数Kn = 0.1, 马赫数Ma = 2的超声速双圆柱干扰绕流. 努森数Kn 定义与上一案例相同. 无量纲壁面温度等于来流静温, 即$ {T}_{\mathrm{w}}=1.0 $ . 利用多块对接网格技术, 并列双圆柱物理空间网格布局如图8 所示. 两个半径为1的圆柱的圆心距离为4, 上下布置于计算域中. 在[–6, 6] × [–6, 6]的速度相空间里布置了40 × 40个Gauss- Legendre离散速度点. 图9 绘出了压力场、温度场及马赫数分布的耦合加速收敛方法计算结果及其与常规GKUA计算结果的对比情况. 结果显示, 采用本文提出的方法计算获得的流场与常规GKUA计算获得的流场符合良好, 包括激波、尾流区及双圆柱干扰区等特殊区域. 为了定量对比, 图10 给出了本文方法获得的上圆柱壁面压力、热流及剪切应力结果及其与常规GKUA结果、文献[47 ]给出的DSMC结果的对比情况. 横坐标θ = –180°—180°对应于从圆柱迎风面顶点沿逆时针分布的壁面位置. 结果显示, 本文提出的方法获得的壁面压力、剪切应力与常规GKUA获得的结果以及DSMC结果符合良好. 在热流方面, 本文方法和常规GKUA, DSMC结果整体符合良好, 在头部略有差异. 由此可以看出, 本文方法能够准确反映常规GKUA在描述跨流域复杂流动问题的特性. 图11 给出了耦合加速收敛方法的收敛历史及其与GKUA的对比情况. 其迭代步数加速约9.3倍, 计算耗时提升约2.5倍(GKUA耗时42.7 h, Coupled耗时16.8 h). 对比上一案例可知, 本案例离散速度空间大小缩小约6倍, 导致宏观方程内迭代耗时的占比增大, 影响了计算耗时的优化效果.图 8 并列双圆柱多块网格布局Figure8. The multi-blocks mesh layout for two side-by-side cylinders.图 9 并列双圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)Figure9. (a) Pressure, (b) temperature, (c) Mach number field for two side-by-side cylinders (GKUA: coloured background and white solid lines; Coupled: red dash lines).图 10 上圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力Figure10. (a) Pressure, (b) heat flux, and (c) shear stress profile along the surface of upper cylinder.图 11 耦合加速收敛方法与常规GKUA的并列双圆柱超声速绕流计算收敛情况对比Figure11. Comparison of the convergence history of supersonic flow around two side-by-side cylinders between the coupled acceleration method and the conventional GKUA.5.结 论 为了提高气体动理论数值方法的计算效率, 针对近空间飞行环境的稀薄气体非平衡流动特点, 本文利用宏观方程在扰动传播、演化方面的优势, 构造了基于耦合宏观方程本构关系的气体动理论加速收敛方法, 以加速气体动理论方法的收敛速度. 通过理论建模及数值验证得到如下结论.Kn = 0.01的方腔流动, 本方法相较常规GKUA的加速比为47. 随着稀薄程度增加, 气体对流输运效应减弱, 宏观方程对迭代的加速效果降低.Kn 小于0.5的案例中都能实现加速收敛效果. 








































































 图 1 方腔流温度分布计算结果 (a) Kn = 1 ; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: 彩色背景及黑色实线; Coupled: 红色虚线)
图 1 方腔流温度分布计算结果 (a) Kn = 1 ; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: 彩色背景及黑色实线; Coupled: 红色虚线)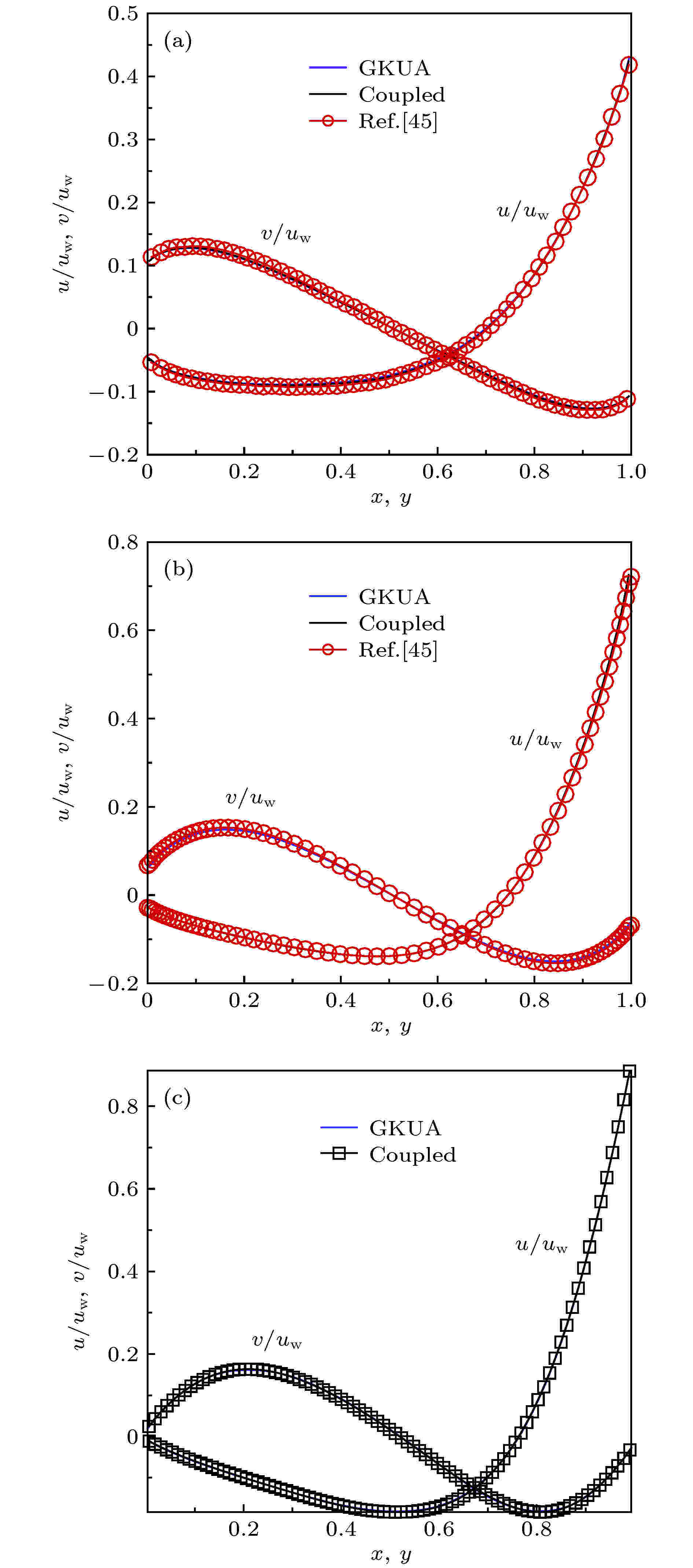 图 2 方腔中心线上的速度场 (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01
图 2 方腔中心线上的速度场 (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01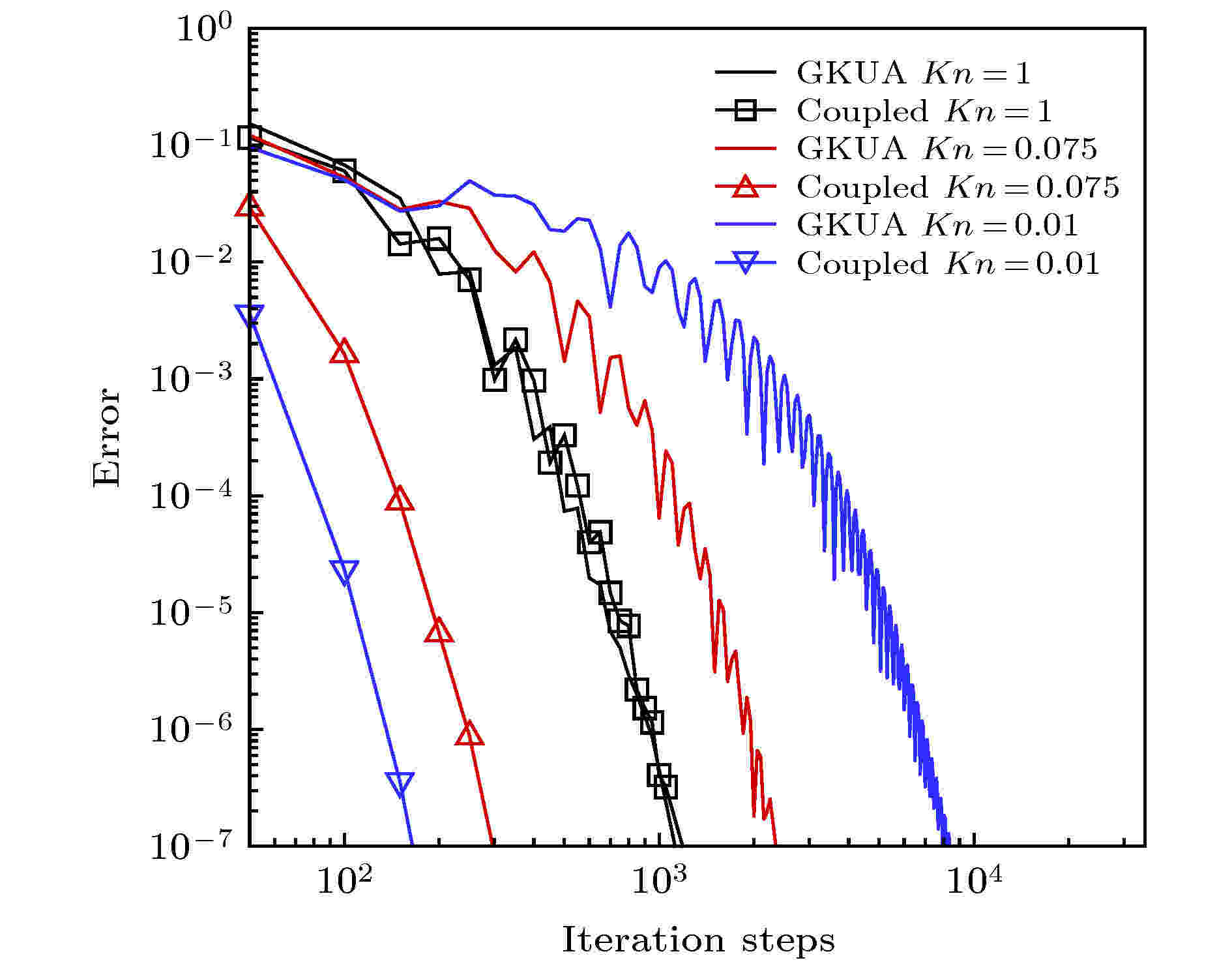 图 3 耦合加速收敛方法与常规GKUA的计算收敛历史
图 3 耦合加速收敛方法与常规GKUA的计算收敛历史
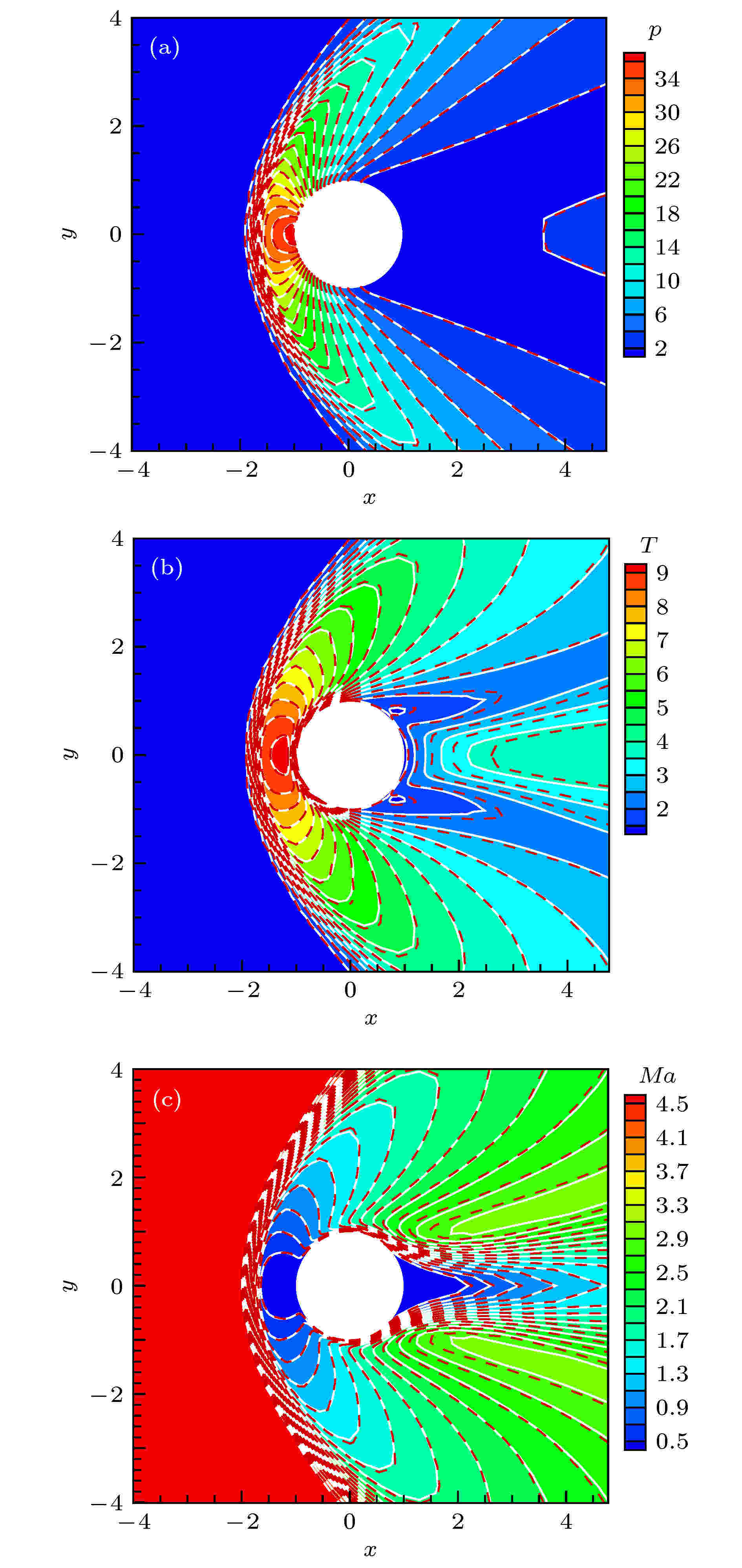 图 4 Kn = 0.01圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数 (GKUA: 彩色背景及白实线; Coupled: 红色虚线)
图 4 Kn = 0.01圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数 (GKUA: 彩色背景及白实线; Coupled: 红色虚线)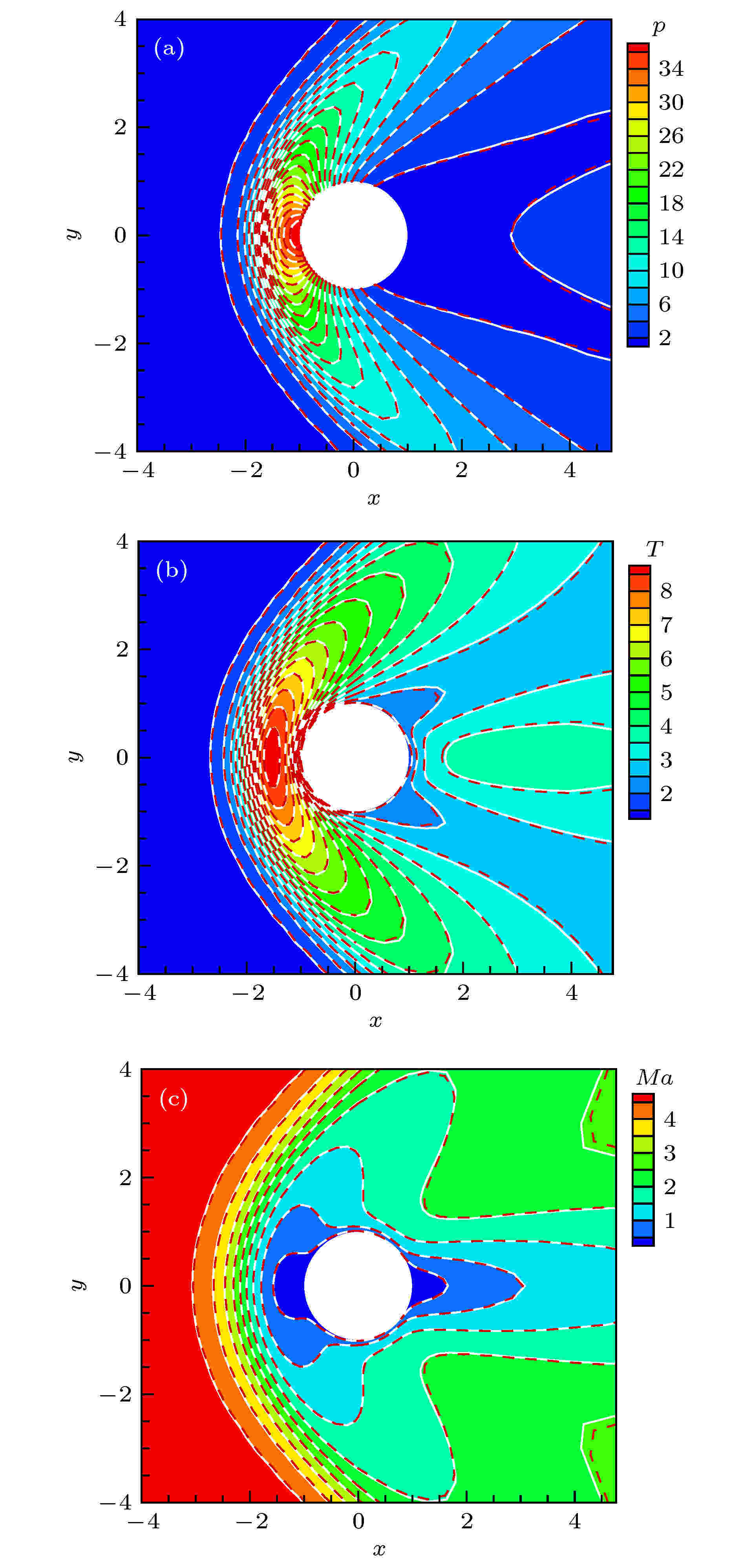 图 5 Kn = 0.1圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)
图 5 Kn = 0.1圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)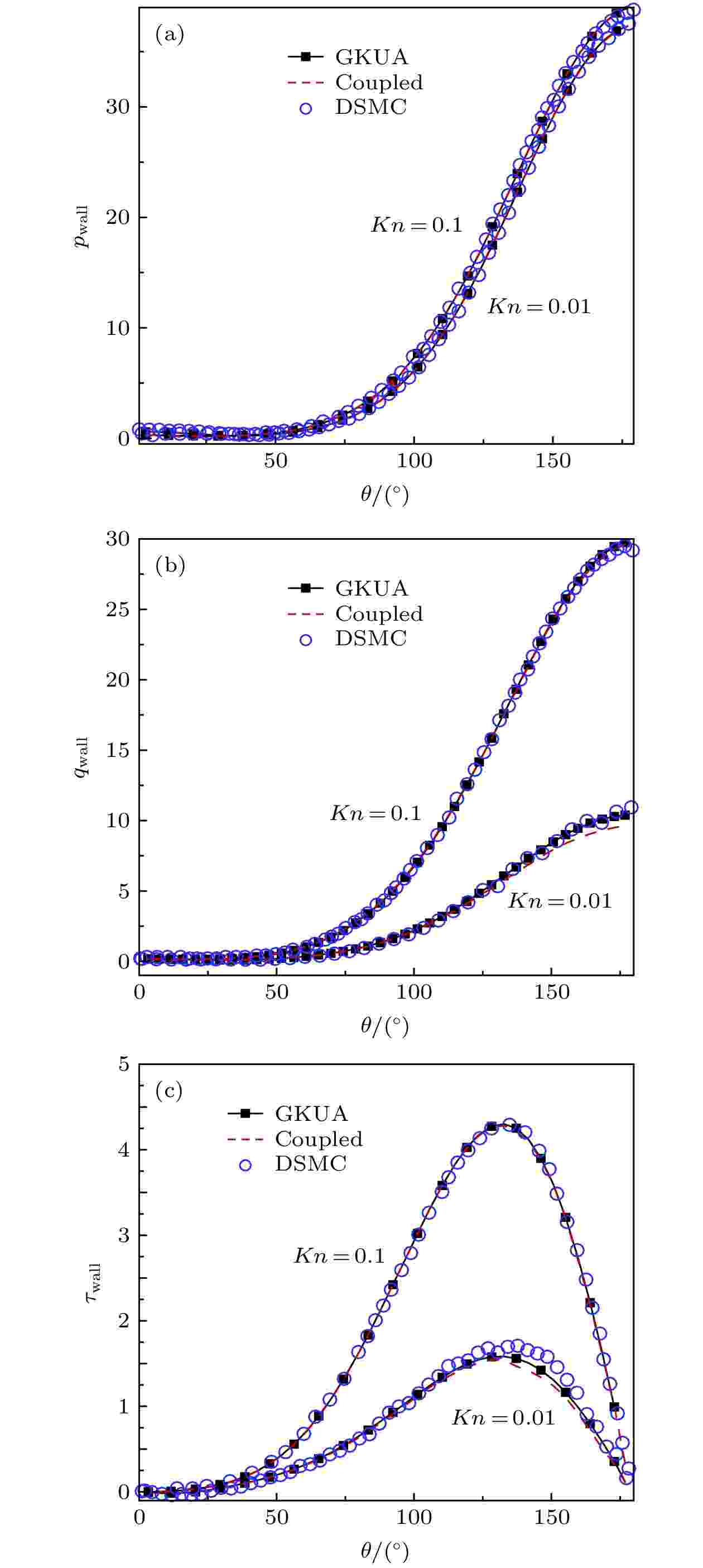 图 6 圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力
图 6 圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力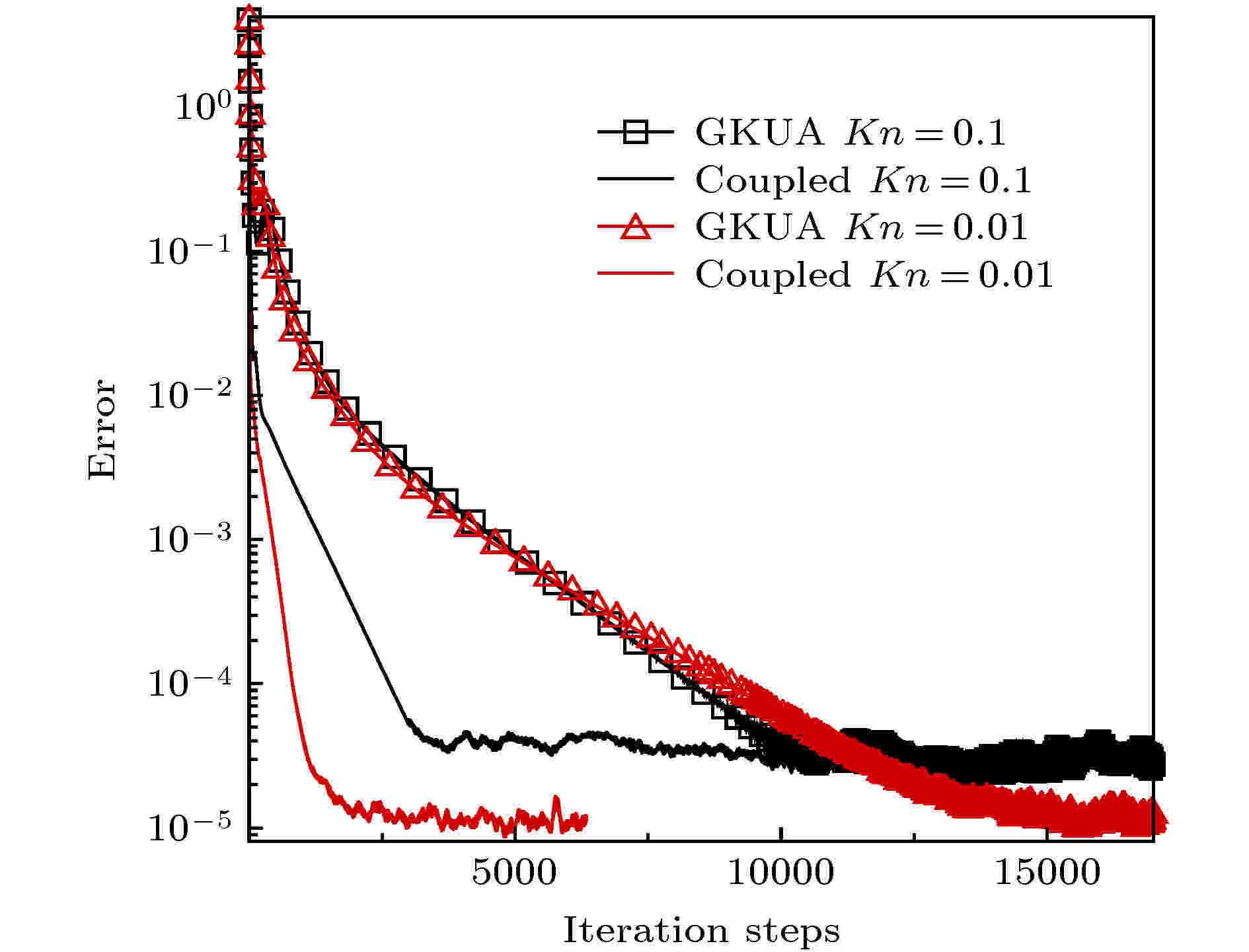 图 7 耦合加速收敛方法与常规GKUA的超声速圆柱绕流计算收敛情况对比
图 7 耦合加速收敛方法与常规GKUA的超声速圆柱绕流计算收敛情况对比
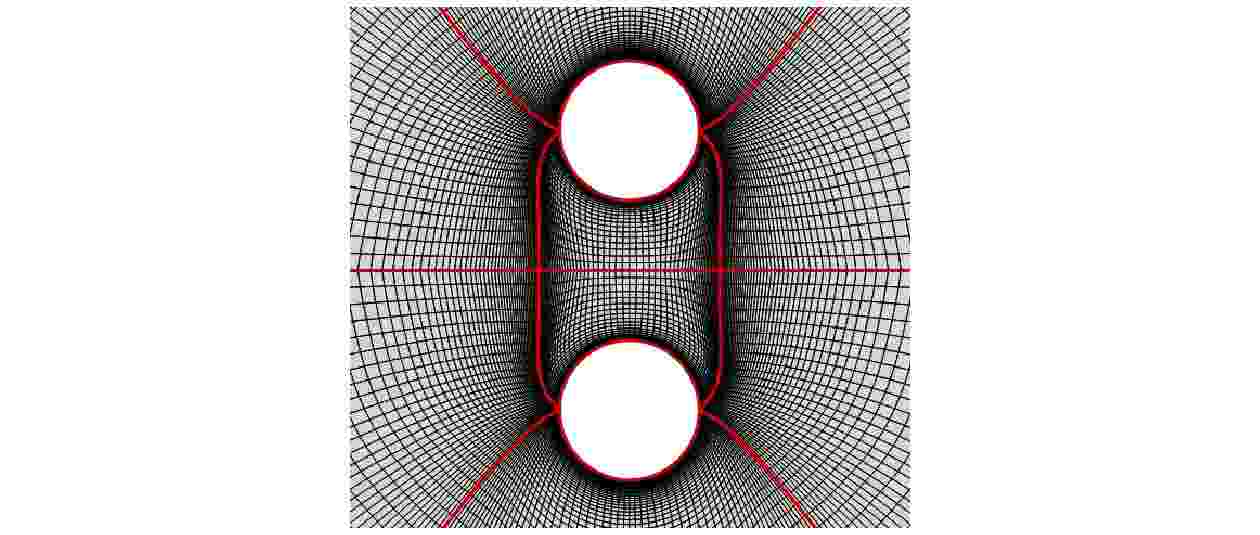 图 8 并列双圆柱多块网格布局
图 8 并列双圆柱多块网格布局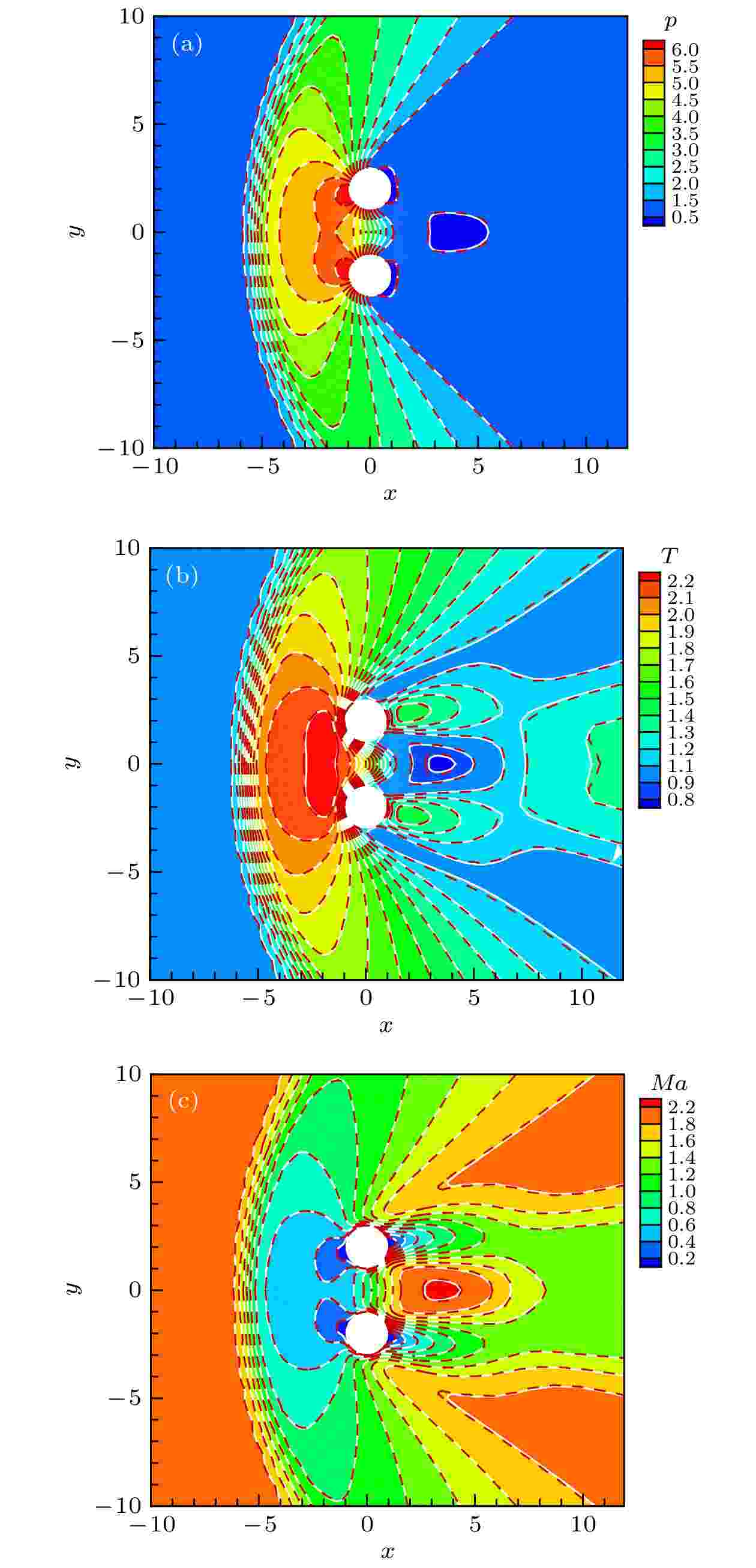 图 9 并列双圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)
图 9 并列双圆柱绕流流场对比 (a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)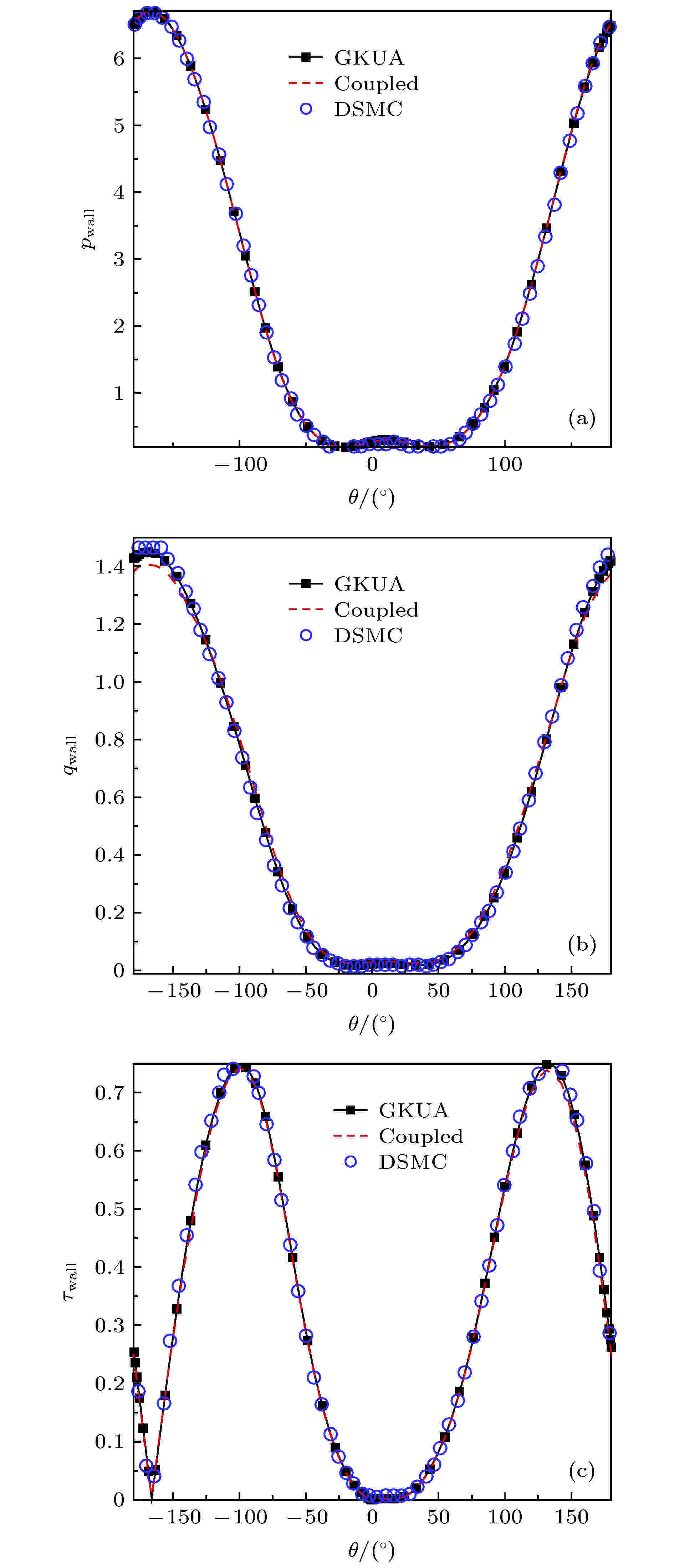 图 10 上圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力
图 10 上圆柱壁面的 (a) 压力, (b) 热流, (c) 剪切应力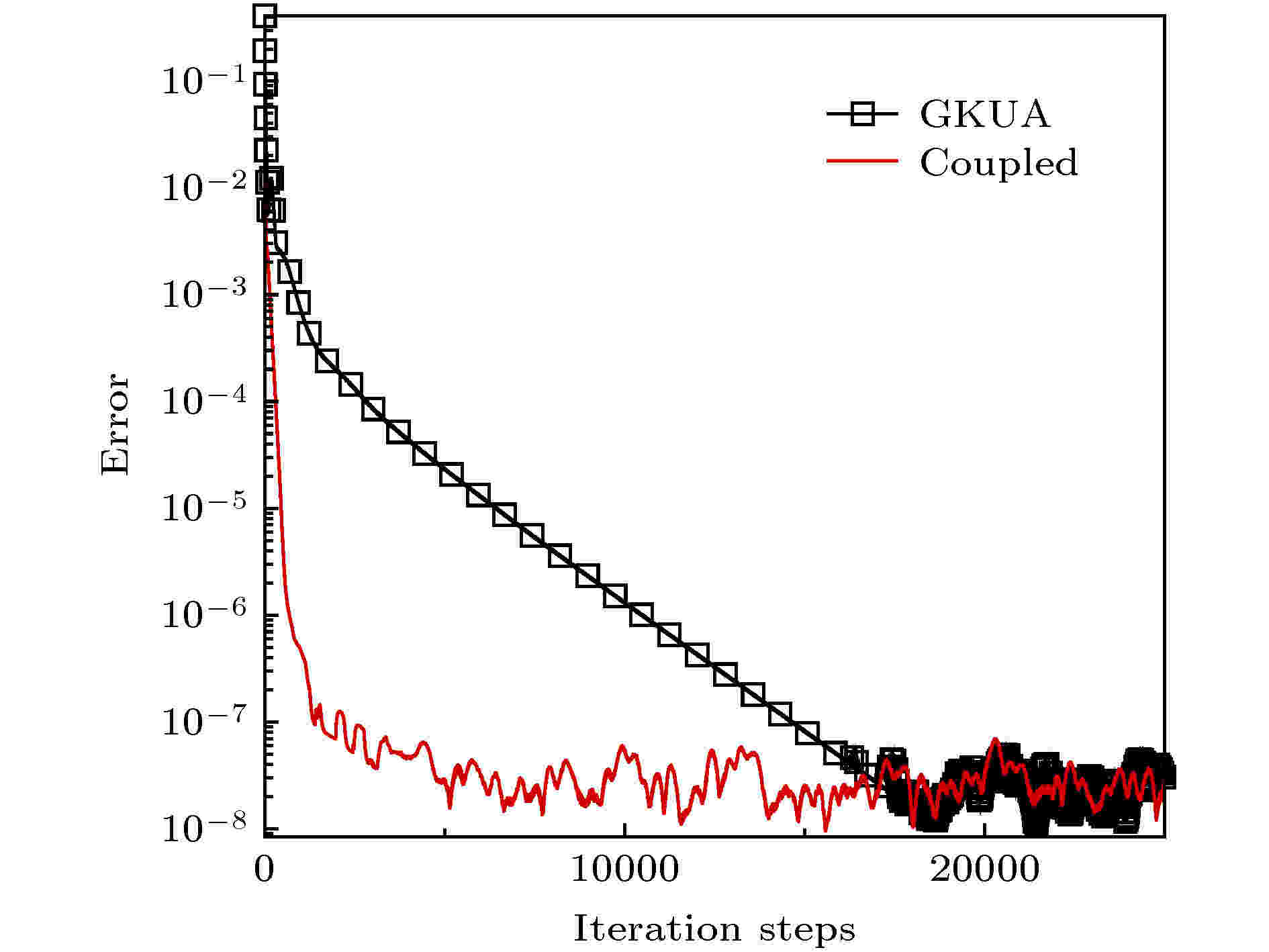 图 11 耦合加速收敛方法与常规GKUA的并列双圆柱超声速绕流计算收敛情况对比
图 11 耦合加速收敛方法与常规GKUA的并列双圆柱超声速绕流计算收敛情况对比