基于希尔伯特变换的结构光照明快速三维彩色显微成像方法

全文HTML

--> --> -->

1.引　言

生物结构在不同尺度、不同维度和不同部位的观察与形态分析, 为科学研究提供最直接的证据, 在众多学科领域扮演了不可或缺的角色. 目前生物结构的二维形态观察手段已非常成熟, 但三维技术手段却相对滞后. 三维光学成像技术具有非接触、快速、精确等优点, 是获取样品表面形态特征的一种重要手段, 也是真实物体三维数字化的基础, 在生物医学、精密测量等领域发挥着重要作用.
色彩信息是描述生物体特征的一个重要物理量, 生物体表面色彩的不同色相、饱和度和明度在很大程度上反映了其微观结构和光学性质的不同. 例如昆虫体表的结构色大都是由其表面的微纳结构产生, 结构色已成为昆虫分类和物种鉴定的一个重要指征^[1-3]. 以激光扫描共聚焦显微镜为代表的点扫描显微成像技术具有三维层析成像能力^[4-6], 结合多通道融合技术可以获得三维荧光样品的伪彩图像^[7,8], 但是受制于滤光片的有限带宽, 激光共聚焦扫描显微镜无法复原样品的真实全彩色信息.
而作为一种宽场显微技术, 结构光照明显微(structured illumination microscopy, SIM)可以实现超分辨成像^[9-11]以及三维光切片成像^[12-15], 在生物医学等领域已经获得了广泛的应用. 光切片SIM成像首先由牛津大学的Neil等^[12]提出, 使用面阵相机采集3幅固定相移差的原始图像并通过均方根(root mean square, RMS)运算重构出样品去除离焦背景的光切片图像. 其基本原理是显微物镜有一定的景深, 因此CCD相机得到的图像实际上是焦面信息和离焦背景的叠加. 在显微成像时, 高频信息会随着离焦距离的增加而快速衰减, 只有焦面的信息才会保持不变. SIM使用具有不同相位的高空间频率正弦条纹对样品进行照明, 因此只有焦平面附近才会出现条纹, 而离焦区域的条纹会迅速衰减变为均匀的宽场照明, 这相当于对焦面的目标进行了编码, 而离焦背景保持不变, 这也是使用不同相位的结构光照明样品时, 离焦背景保持不变的原因^[16-19]. 2015年, 我们使用彩色数字相机记录白光或多色结构光照明获得的彩色图像, 使用基于色相(hue)、饱和度(saturation)、明度(value)空间的HSV彩色光切片算法(HSV color space-root mean square algorithm, HSV-RMS), 实现了高分辨全彩色快速三维成像^[20]. 通过多视场拼接技术, 2019年我们进一步实现了厘米量级昆虫样品的高分辨率全彩色三维成像^[21].
HSV-RMS方法需要采集3幅固定相移差的图像并通过RMS算法计算重构出一幅消除离焦背景的光切片图像, 因此需要采集3倍于普通宽场成像的图像数据, 而且其彩色图像重构过程需要在H, S, V 3个通道中分别进行3次RMS运算以及2次RGB和HSV空间的图像转换, 计算耗时较大. 2015年, 我们课题组提出了一种基于希尔伯特变换的快速SIM三维成像方法, 只需采集2幅任意相移差的原始图像便可以重构出一幅光切片图像^[19], 但是该技术当时局限于单色三维成像, 无法恢复样品的彩色信息. 鉴于此, 本文将希尔伯特变换的快速光切片算法与彩色结构光照明光切片技术结合, 提出一种新的基于希尔伯特变换的结构光照明快速三维彩色显微成像方法(Hilbert-transform-based color optical sectioning method, HT-COS), 相比于HSV-RMS方法, HT-COS的图像采集量减少了1/3, 图像重构时间节约了约28%. 该方法有望进一步扩展SIM技术的适用领域, 在生物学、材料科学研究中获得重要应用.

2.SIM光切片算法

2.1.RMS光切片算法

-->

2.1.RMS光切片算法

RMS层析解码算法需要通过改变结构光场的相位获取3幅子图像, 相邻子图像之间的加载条纹相位差通常需严格匹配至2π/3, 继而通过特定的公式提取出焦面信息, 这是目前应用最为广泛的方法, 由Neil等^[12]首先提出.
假设所使用的结构照明正弦条纹光场强度分布满足:

${I_{\sin }}(x,y) = 1 + m\cos (2{\text{π}}px + {\varphi _0}),$

其中, m为正弦条纹的调制度, p为条纹的空间频率, φ₀为条纹的初相位. 使用3幅相移差为2π/3的结构照明光场对样品进行照明, 可得采集到的3幅图像的表达式为

$\begin{split} {I_0}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0})] \\ &+ {I_{{\rm{out}}}}(x,y), \\ {I_{2{\text{π}}/3}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0} + 2{\text{π}}/3)] \\ & + {I_{{\rm{out}}}}(x,y), \\ {I_{4{\text{π}}/3}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0}+ 4{\text{π}}/3)] \\ & + {I_{{\rm{out}}}}(x,y), \\[-13pt]\end{split} $

其中, I_in表示样品的焦面图像信息, I_out表示离焦部分的图像信息, 只有焦面图像I_in受到了正弦条纹光场的调制, 对采集到的3幅图像两两相减可得去除离焦背景的3幅结构照明图像:

$\begin{split} & \Delta {I_1} = {I_0}(x,y) - {I_{2{\text{π}}/3}}(x,y) \\ =\;& m{I_{{\rm{in}}}}(x,y)\Big[ \frac{3}{2}\cos (2{\text{π}}px + {\varphi _0}) + \frac{{\sqrt 3 }}{2}\sin (2{\text{π}}px + {\varphi _0}) \Big], \\ & \Delta {I_2} = {I_{2{\text{π}}/3}}(x,y) - {I_{4{\text{π}}/3}}(x,y) \\ =& - \sqrt 3 m{I_{{\rm{in}}}}(x,y)\sin (2{\text{π}}px + {\varphi _0}), \\ & \Delta {I_3} = {I_{4{\text{π}}/3}}(x,y) - {I_0}(x,y) \\ =&- m{I_{{\rm{in}}}}(x,y)\Big[\frac{3}{2}\cos (2{\text{π}}px \!+\! {\varphi _0}) \!-\! \frac{{\sqrt 3 }}{2}\sin (2{\text{π}}px \!+\! {\varphi _0}) \Big].\end{split} $

此时, 样品的焦面信息I_in仍然受到正弦条纹光场的调制, Neil等^[12]提出的RMS算法正是对(3)式得到的3幅图像进行均方根计算, 即:

$\begin{split} &\sqrt {\frac{{\varDelta _1^2(x,y) + \varDelta _2^2(x,y) + \varDelta _3^2(x,y)}}{3}} \\=\; & \frac{{3\sqrt 2 }}{2}m{I_{{\rm{in}}}}(x,y),\end{split}$

因此,

${I_{{\rm{in}}}}(x,y) \!=\! \frac{{\sqrt 2 }}{{3m}}\sqrt {\varDelta _1^2(x,y) + \varDelta _2^2(x,y) + \varDelta _3^2(x,y)} .$

除了2π/3相移, 相移量为π/2的正弦条纹结构光也可实现光切片图像重建, 相比2π/3相移量, 在利用数字微镜器件(digital micro-mirror device, DMD)投影产生结构光照明的SIM系统中, 相移量为π/2的条纹通常可以实现更高的条纹频率, 进而获得更优的光切片效果^[15]. 此时, (2)式可写作:

$\begin{split} {I_0}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0})]\\ & + {I_{{\rm{out}}}}(x,y),\\ {I_{{\text{π}}/2}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 \!+\! m\cos (2{\text{π}}px \!+\! {\varphi _0} \!+\! {\text{π}}/2)] \\ & + {I_{{\rm{out}}}}(x,y),\\ {I_{\text{π}}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0} + {\text{π}})] \\ & + {I_{{\rm{out}}}}(x,y).\end{split} $

由(6)式可以看出, I₀和I_π之和恰好可以消除含有条纹的调制项, 而两者的差可以消除离焦背景, 类似于(3)式, 可以构造得到

$\begin{split} &{I_0}(x,y) + {I_{\text{π}}}(x,y) - 2{I_{{\text{π}}/2}}(x,y) \\=\; & 2m{I_{{\rm{in}}}}(x,y) \cdot \sin (2{\text{π}}px + {\varphi _0}), \\ & {I_0}(x,y) - {I_{\text{π}}}(x,y)\\=\; & 2m{I_{{\rm{in}}}}(x,y) \cdot \cos (2{\text{π}}px + {\varphi _0}).\end{split} $

对(7)式进行RMS运算, 可以得到

${I_{{\rm{in}}}}(x,y) \!=\! \frac{1}{{2m}}\sqrt {{{({I_0} + {I_{\text{π}}} - 2{I_{{\text{π}}/2}})}^2} + {{({I_0} - {I_{\text{π}}})}^2}} .$

2.2.基于希尔伯特变换的光切片算法

-->

2.2.基于希尔伯特变换的光切片算法

希尔伯特变换是信号分析处理领域的一种常用方法, 以一维信号为例, 希尔伯特变换实质上是信号$x(t)$

与1/(πt)的卷积运算, 即:

$\hat x(t) = x(t) \otimes \frac{1}{{{\text{π}}t}} = \frac{{\rm{1}}}{{\text{π}}}\int {\frac{{x(\tau )}}{{t - \tau }}} {\rm{d}}\tau,$

其中, 符号$ \wedge $

表示希尔伯特变换算符. 以一维正弦信号$x(t)$

= sint为例, 对其取希尔伯特变换并进行傅里叶变换, 可得

$\begin{split} {\rm{FFT}}\left\{ {\left. {\hat x(t)} \right\}} \right.\;& = - {\rm{i}} \cdot {\rm{FFT}}\left\{ {\left. {\sin (t)} \right\}} \right. \cdot {\rm{FFT}}(1/({\text{π}}t))\\& = - {\rm{i}} \cdot {\rm{FFT}}\left\{ {\left. {\sin (t)} \right\}} \right. \cdot \operatorname{sgn} (\omega ) \\& = - \frac{{\delta \left( {\omega + 1/2{\text{π}}} \right) + \delta \left( {\omega - 1/2{\text{π}}} \right)}}{2},\end{split} $

其中, FFT为快速傅里叶变换算符; $\omega $

为频谱空间的坐标; sgn($\omega $

)为signum函数,

${\rm{sgn}} (\omega ) = \left\{ {\begin{aligned} &{1,\qquad \;\;\omega {{ > 0,}}} \\ & {0,\qquad \;\;\omega {{ = 0,}}} \\ &{ - 1,\quad\;\;\; \omega {\rm{ < 0}}.} \end{aligned}} \right.$

由此可得, 一维正弦信号$x(t)$

= sint的希尔伯特变换为

$\begin{split}\hat x(t)\; & = {\rm{i}} \cdot {\rm{FFT}}\left\{ { - \frac{{\delta (\omega + 1/2{\text{π}}) + \delta (\omega - 1/2{\text{π}})}}{2}} \right\} \\ & = - \cos t.\\[-10pt]\end{split}$

显然, 正弦信号和其希尔伯特变换结果的平方和为1, 恰好可以消除正弦条纹. 两幅相移差为$\Delta \varphi $

的正弦结构光照明图像可表示为

$\begin{split} {I_0}(x,y) = \; &{I_{{\rm{in}}}}(x,y)[1 \!+\! m\cos (2{\text{π}}px \!+\! {\varphi _0})] \!+\! {I_{{\rm{out}}}}(x,y), \\ {I_{\Delta \varphi }}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px+ {\varphi _0} + \Delta \varphi )] \\ & + {I_{{\rm{out}}}}(x,y). \\[-10pt] \end{split} $

将两幅图像相减, 首先消除了离焦背景的影响, 并令y = ${y_0}$

, 则该位置的一维信号可以表示为

$\begin{split}\Delta I(x,{y_0}) =\; & 2m\sin (\Delta \varphi /2){I_{{\rm{in}}}}(x,{y_0})\\ & \times\sin (2{\text{π}}px + {\varphi _0} + \Delta \varphi /2).\end{split}$

对(7)式进行希尔伯特变换, 然后取其频谱, 可得

$\begin{split} &{\rm{FFT}}\left\{ {\Delta \hat I(x,{y_0})} \right\} \\ =\; & \frac{{ - C}}{2}\left[ {{{\tilde I}_{{\rm{in}}}}\left( {{k_x} - p,{y_0}} \right){{\rm{e}}^{{\rm{i}}{\varphi _{\rm{s}}}}} + {{\tilde I}_{{\rm{in}}}}\left( {{k_x} + p,{y_0}} \right){{\rm{e}}^{ - {\rm{i}}{\varphi _{\rm{s}}}}}} \right] \\ =\; & - C\left[ {{{\tilde I}_{{\rm{in}}}}\left( {{k_x},{y_0}} \right) \otimes \frac{{\delta ({k_x} \!-\! p){{\rm{e}}^{{\rm{i}}{\varphi _{\rm{s}}}}} \!+\! \delta ({k_x} \!+\! p){{\rm{e}}^{ - {\rm{i}}{\varphi _{\rm{s}}}}}}}{2}} \right],\end{split} $

其中C = $2 m\sin (\Delta \varphi /2)$

, ${\varphi _{_{\rm{s}}}}$

=${\varphi _0} + \Delta \varphi /2$

, 由(15)式可得

$\Delta \hat I(x,{y_0}) = - C{I_{{\rm{in}}}}(x,{y_0})\cos (2{\text{π}}px + {\varphi _{\rm{s}}}).$

对比(14)式与(16)式可知, 经过希尔伯特变换之后, 正弦结构光照明图像产生了π/2的相移, 二者的平方和可以去除焦平面上的正弦结构图样. 以上分析为y = ${y_0}$

处的一维信号分析, 在y方向上所有位置全部进行上述运算, 则可实现整幅二维图像的图像重构处理, 进而获得焦平面上去除正弦结构条纹的光切片图像, 即:

${I_{{\rm{in}}}}(x,y) = \sqrt {\Delta I{{(x,y)}^2} + \Delta \hat I{{(x,y)}^2}} .$

基于希尔伯特变换的快速层析算法仅需两幅任意相移差的子图像即可完成图像的解码重构, 实验中以某一个成像平面为例, 其具体过程简述为: 先将在该平面获取的不同初相位结构光照明的子图像进行相减, 获得仅含焦面编码信息的新图像; 再将新图像沿着与编码条纹空间频率方向进行希尔伯特变换并与子图像差值取平方和, 即可获得有效解码后的层析图像. 以横条纹(即y方向强度为正弦分布)为例, (17)式可写作:

${I_Z} = \sqrt {{{({I_0} - {I_{\Delta \varphi }})}^2} + {{{\rm{\{ H}}{{\rm{T}}_x}({I_0} - {I_{\Delta \varphi }}){\rm{\} }}}^2}},$

其中, ${I_0}$

和${I_{\Delta \varphi }}$

为采集到的两幅相移差为$\Delta \varphi $

的结构光照明图像, ${\rm{H}}{{\rm{T}}_x}$

表示在x方向进行希尔伯特变换, ${I_Z}$

为该焦平面上的去除条纹的光切片图像.
相对于传统的RMS解码算法, 基于希尔伯特变换的快速层析解码算法具有明显的优势^[19]: 首先, 快速层析解码算法需要两幅原始图像即可完成层析图像重构, 将图像采集量减小了33%. 其次, 快速层析解码算法对相移误差不敏感, 微小的相移误差并不影响三维重构效果, 避免了传统RMS解码算法在子图像加载条纹相位差不匹配时带来的残余条纹问题.
2

2.3.基于希尔伯特变换的彩色光切片算法

-->

2.3.基于希尔伯特变换的彩色光切片算法

基于HSV-RMS方法, 将采集到的3幅固定相移差的原始彩色图像转换至HSV空间, 并在相应的通道利用RMS算法进行光切片处理, 随后将处理完成的结果转换至RGB空间进行存储并显示. 这一方法能够复原样品表面的全彩色信息, 已经成功应用于昆虫结构色的研究中^[20,21]. 然而该方法需采集3幅固定相移差的原始图像, 并且在HSV空间的三通道要进行3次RMS运算, 另外还需要在HSV空间和RGB空间进行两次转换, 对于需要视场拼接的大尺寸样品而言, HSV-RMS方法的图像采集数据量大, 图像处理算法更耗时. 为此本文提出HT-COS方法.
使用彩色相机采集得到2幅相移差为π的原始彩色图像, 首先利用(19)式得到消除条纹的均匀照明的宽场图像${I_{{\rm{wide}}}}{\rm{(RGB)}}$

; 将原始图像转换为灰度图像, 并利用(18)式计算得到光切片灰度图像${I_z}({\rm{gray}})$

, 而宽场图像${I_{{\rm{wide}}}}{\rm{(RGB)}}$

则携带有样品的全部色彩信息, 二者相乘的结果为: 宽场图像的色彩将赋予光切片图像, 进而快速地获得样品的彩色光切片图像, 算法流程图如图1(a)所示. 沿样品轴向进行扫描, 并对每一层的重构结果进行叠加, 将得到样品的三维彩色光切片图像.

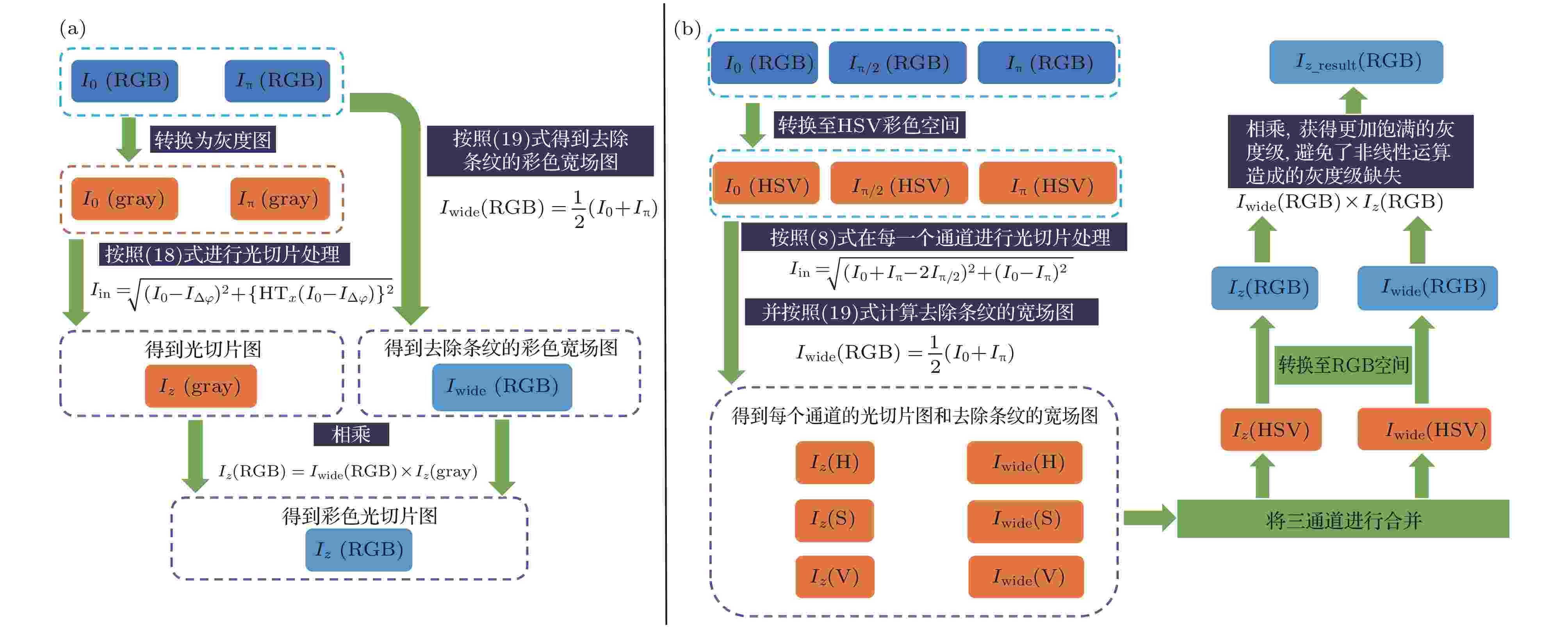图 1 HT-COS算法流程图和HSV-RMS算法流程图对比　(a) HT-COS算法流程图; (b) HSV-RMS算法流程图
Figure1. Flowchart diagram comparison between HT-COS algorithm and HSV-RMS algorithm: (a) HT-COS algorithm; (b) HSV-RMS algorithm.

${I_{{\rm{wide}}}}{\rm{(RGB)}} = ({I_0} + {I_{\text{π}}})/2.$

2.4.相移误差对HSV-RMS算法以及HT-COS算法的影响对比

-->

2.4.相移误差对HSV-RMS算法以及HT-COS算法的影响对比

RMS算法对原始图像的相移差有着严格要求, 相移的微小误差便会影响到三维重构的效果, 导致光切片图像中出现明显的残余条纹, 而残余条纹的出现会在很大程度上影响对样品真实结构的观察与判断, 以π/2相移的3幅原始正弦条纹图像为例, 假设图像在采集过程中由于环境振动引入了相移误差?φ, 那么这3幅原始图像可以写作:

$\begin{split} {I_0}(x,y) =\;& {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0})] \\ &+ {I_{{\rm{out}}}}(x,y), \\ {I_{{\text{π}}/2}}(x,y) =\;& {I_{{\rm{in}}}}(x,y)[1 \!+\! m\cos (2{\text{π}}px \!+\! {\varphi _0} \!+\! {\text{π}}/2 \!+\! \Delta \varphi )] \\ & + {I_{{\rm{out}}}}(x,y), \\ {I_{\text{π}}}(x,y) =\;& {I_{{\rm{in}}}}(x,y)[1 \!+\! m\cos (2{\text{π}}px \!+\! {\varphi _0} \!+\! {\text{π}} \!+\! \Delta \varphi )] \\ & + {I_{{\rm{out}}}}(x,y).\\[-12pt]\end{split} $

将(20)式代入(8)式, 可以求得经RMS算法重构的图像为

$I_{{\rm{in}}}^\Delta \!\approx\! \sqrt 2 m{I_{{\rm{in}}}}(x,y)\sqrt {{{\cos }^2}(2{\text{π}}px \!+\! {\varphi _0}) \!+\! {{\cos }^2}\Delta \varphi } .$

由此可知, 当原始图像的相移差存在?φ的误差时, RMS算法计算得到的光切片图像中将存在残余条纹. 由图1(b)可知, HSV-RMS算法在得到光切片图像后, 还需利用(19)式计算得到的去除条纹的宽场图, 此时宽场图中也将出现少量的残余条纹:

$\begin{split} &I_{{\rm{wide}}}^\Delta ({\rm{RGB}}) \\\approx\;& \frac{1}{2}[ {I_{{\rm{in}}}} + {I_{{\rm{out}}}}+ \cos (2{\text{π}}px + {\varphi _0})(1 - \cos \Delta \varphi )].\end{split}$

在HSV-RMS算法后续图像处理过程中, (21)式和(22)式相乘, 会使二者的残余条纹被进一步放大, 进而导致最终的彩色光切片图像中出现严重的残余条纹:

$\begin{split} & I_{{\rm{in}}}^\Delta I_{{\rm{wide}}}^\Delta \approx \frac{{\sqrt 2 }}{2}m{I_{{\rm{in}}}}\sqrt {{{\cos }^2}(2{\text{π}}px + {\varphi _0}) + {{\cos }^2}\Delta \varphi } \\ &\times \left[ {2({I_{{\rm{in}}}} \!+ {I_{{\rm{out}}}}) \!+ m{I_{{\rm{in}}}}{{\cos }^2}(2{\text{π}}px \!+\! {\varphi _0}){{(1 \!-\! \cos\Delta \varphi )}^2}} \right].\end{split} $

在基于希尔伯特变换的光切片算法中, 当两幅相移差为π的结构光照明图像中存在相移误差?φ时, (14)式可以写作:

$\Delta {I^\Delta }(x,{y_0}) = {C^\Delta }{I_{{\rm{in}}}}(x,{y_0})\sin \left( {2{\text{π}}px + {\varphi _0} + \varphi _{\rm{s}}^\Delta } \right).$

对其进行希尔伯特变换可得

$\Delta {\hat I^\Delta }(x,{y_0}) = - {C^\Delta }{I_{{\rm{in}}}}(x,{y_0})\cos \left( {2{\text{π}}px + {\varphi _0} + \varphi _{\rm{s}}^\Delta } \right).$

其中$C^{?} \!=\! 2 m\sin [(\Delta \varphi \!+\! {\text{π}})/2]$

, $\varphi _{\rm{s}}^\Delta $

=${\varphi _0} \!+\! (\Delta \varphi \!+\! {\text{π}})/2$

, 将(24)式和(25)式代入(17)式可知, 光切片计算结果中并不会出现误差?φ的调制项, 也就不存在残余条纹.
HT-COS算法中只有(22)式计算引入的微小的残余条纹, 在最终计算得到的彩色光切片图像中可以被近似忽略:

${I_{\rm {in}}}I_{{\rm{wide}}}^{\Delta } \approx \frac{1}{2}{I_{{\rm{in}}}}[2{I_{{\rm{in}}}} + 2{I_{{\rm{out}}}} + \cos(2{\text{π}}px + {\varphi _0})(1 - \cos\Delta \varphi )].$

因此, HT-COS算法对微小的相移误差并不敏感, 不影响其三维光切片重建的效果.
为验证上述结论, 模拟了不同相移误差对三维光切片重建效果的影响, 以π/2相移的HSV-RMS算法和HT-COS算法为例, 分别假设相移误差为0.01π, 0.02π和0.05π, 数值模拟计算了HSV-RMS算法和HT-COS算法的图像重构效果, 如图2所示, 其中绿色虚线方框内为绿色实线方框区域内的放大图像. 由图2(c)—(f)可以看出, 在相移误差为0.01π时, HSV-RMS算法光切片图像中无明显残余条纹, 当相移误差为0.02π时, HSV-RMS算法复原的光切片图像出现了明显的残余条纹, 而当相移误差增大为0.05π时, 残余条纹非常严重. 如图2(g)—(j)所示, HT-COS算法复原算法对相移误差并不敏感, 在相移误差为0.01π和0.02π时, 复原的光切片图像中并没有出现残余条纹, 当相移误差增加至0.05π时, 图像中出现了极少量的残余条纹. 因此本文提出的HT-COS算法具有更高的鲁棒性, 特别适用于存在机械振动等噪声干扰的实验环境.

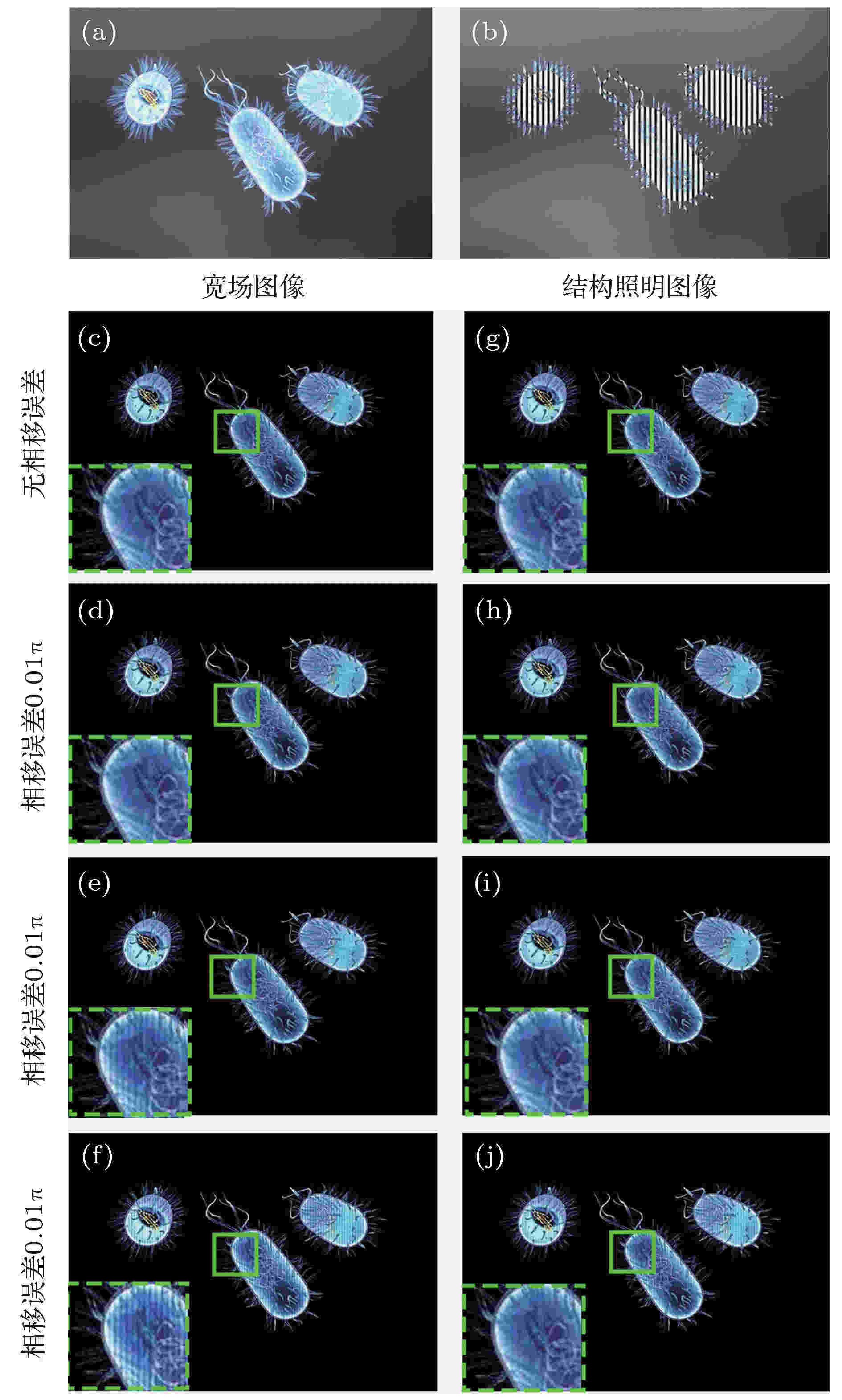图 2 相移误差对三维光切片图像的影响　(a)含有离焦背景的宽场图像; (b)结构光照明图像; (c)?(f)在不同的相移误差下, HSV-RMS算法所复原的彩色光切片图像; (g)?(j) 不同相移误差下, HT-COS算法所复原的彩色光切片图像
Figure2. Effect of phase-shift error on optical sectioning images: (a) Wide-field image with defocused background; (b) structured illumination image; (c)?(f) three-dimensional (3D) color optical sectioning images processed by HSV-RMS algorithm under different phase-shift errors; (g)?(j) 3D color optical sectioning images processed by HT-COS algorithm under different phase-shift errors.

2

2.5.噪声对HSV-RMS算法和HT-COS算法的影响对比

-->

2.5.噪声对HSV-RMS算法和HT-COS算法的影响对比

假设实验中采集的结构光照明图像中, 存在有随机分布的高斯噪声N(x, y), 3幅π/2相移的原始图像可以写作:

$\begin{split} {I_0}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0})]\\ &+ {I_{{\rm{out}}}}(x,y) + {N_1}(x,y), \\ {I_{{\text{π}}/2}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0} + {\text{π}}/2)] \\ & + {I_{{\rm{out}}}}(x,y) + {N_2}(x,y), \\ {I_{\text{π}}}(x,y) =\; & {I_{{\rm{in}}}}(x,y)[1 + m\cos (2{\text{π}}px + {\varphi _0} + {\text{π}})]\\ & + {I_{{\rm{out}}}}(x,y) + {N_3}(x,y).\\[-13pt]\end{split}$

当利用RMS算法进行光切片处理时, 根据(7)式, 对(27)式的三项进行循环相减操作, 可得

$\begin{split}& {I_0} + {I_{\text{π}}} - 2{I_{{\text{π}}/2}} + ({N_1} + {N_3} - 2{N_2}) \\ \approx\;& {I_0} + {I_{\text{π}}} - 2{I_{{\text{π}}/2}} + 2{N_{\rm C}},\\ & {I_0} - {I_{\text{π}}} + ({N_1} - {N_3}) \approx {I_0} - {I_{\text{π}}} + {N_{\rm C}}, \end{split} $

其中, N_C表示均值噪声^[22], 并有

$\left\{ {\begin{aligned} &{{N_i} + {N_j} \approx 2{N_{\rm{C}}},}\\ &{{N_i} - {N_j} \approx {N_{\rm{C}}},}\end{aligned}} \right.\;\;\;\;i \ne j.$

求取(28)式两项的平方和, 有

$\begin{split} &{({I_0} + {I_{\text{π}}} - 2{I_{{\text{π}}/2}} + 2{N_{\rm{C}}})^2} + {({I_0} - {I_{\text{π}}} + {N_{\rm{C}}})^2} \\ \approx\; & [{({I_0} + {I_{\text{π}}} - 2{I_{{\text{π}}/2}})^2} + {({I_0} - {I_{\text{π}}})^2}] + 5{N_{\rm{C}}}^2 \\ =\; & 4{m^2}{I_{{\rm{in}}}}^2 + 5{N_{\rm{C}}}^2.\end{split} $

利用(8)式计算可得在噪声环境下的光切片为

${I_{{\rm{in}}}}({\rm {noise}}) = \sqrt {{I_{{\rm{in}}}}^2 + \frac{{5{N_{\rm{C}}}^2}}{{4{m^2}}}} .$

由此可知, RMS算法计算得到光切片图像的信噪比与结构照明光场的调制度有关, 调制度越高, 信噪比越高.
当利用希尔伯特变换的方法进行光切片处理时, 相移差为π的两幅图像相减可得

$\begin{split}& \Delta I({\rm {noise}}) = {I_0} \!-\! {I_{\text{π}}} \\\approx{}& 2m\cos (2{\text{π}}px \!+\! {\varphi _0}) \!+\! N_{\rm C}.\end{split}$

对(32)式进行希尔伯特变换可得

$\Delta \hat I({\rm {noise}})= - 2m\sin (2{\text{π}}px + {\varphi _0}) + N_{\rm C}.$

将(32)式和(33)式代入(17)式, 可得噪声环境下的光切片图像为

${I_{{\rm{in}}}}({\rm {noise}})=\sqrt{{I^2_{{\rm{in}}}} + \dfrac{{N_{\rm{C}}^2}}{{2{m^2}}}} .$

对比(31)式和(34)式, 希尔伯特变换方法在噪声环境下求得的光切片图像同样与结构照明条纹的对比度有关, 调制度越高信噪比越高. 在同样的噪声参数下, RMS算法得到的光切片图像中的噪声项大于希尔伯特变换的方法, 因此, 希尔伯特变换算法相比于RMS算法, 具有更强的抗噪能力.
在图3中, 模拟了均值为0, 方差分别为0.01, 0.02和0.03时的高斯噪声对HSV-RMS算法以及HT-COS算法在彩色光切片处理时的影响, 所用正弦结构照明条纹的调制度m=0.8. 高斯噪声方差为0.01时, 结构光照明图像, HSV-RMS算法得到的光切片图像, HT-COS算法得到的光切片图像的峰值信噪比(peak signal-to-noise ratio, PSNR)分别为25.74, 22.93以及23.69; 当方差为0.03时, PSNR分别为23.62, 18.81以及21.91; 当方差为0.05时, PSNR分别为22.21, 17.35和20.51.

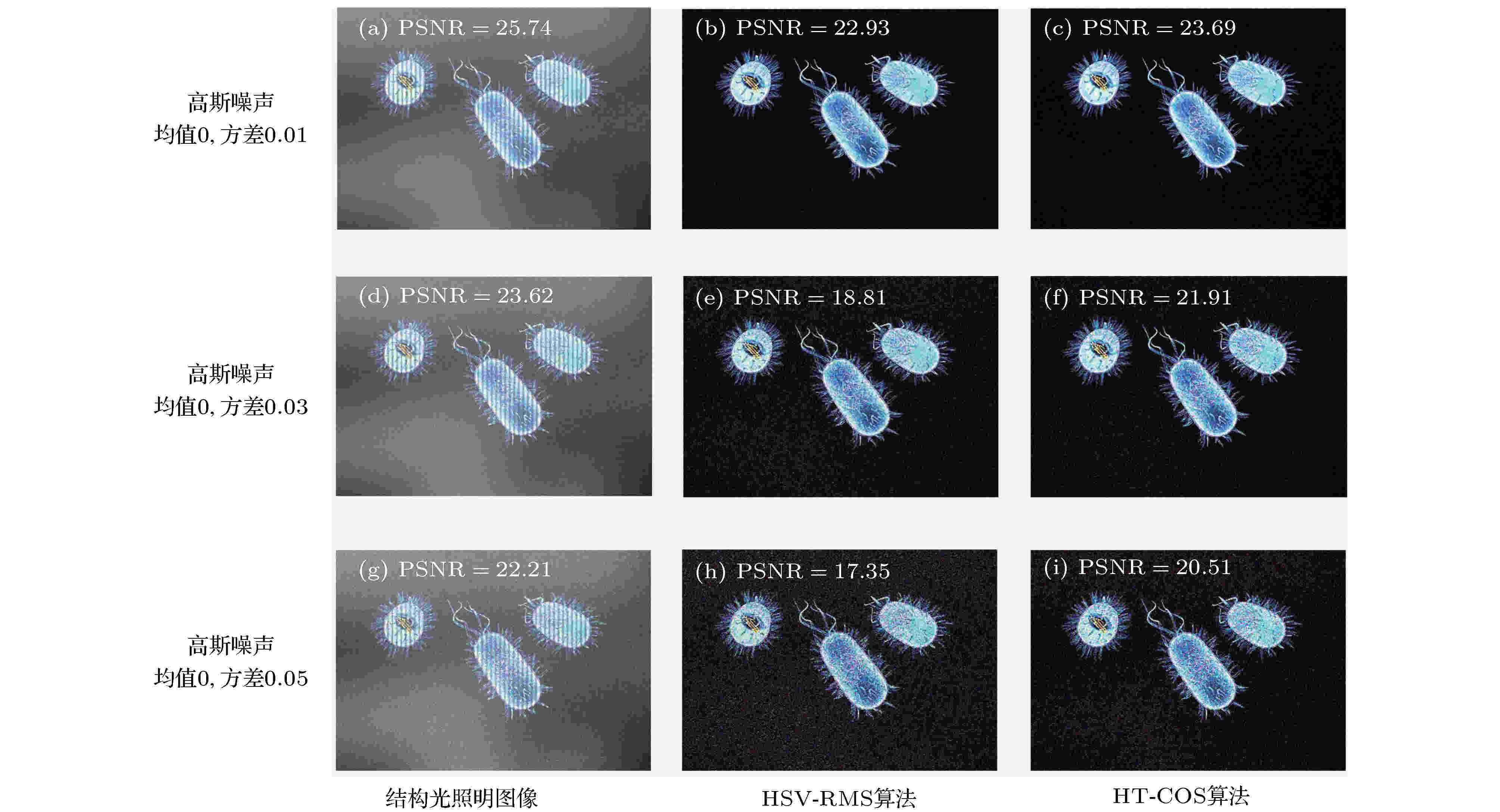图 3 高斯噪声对光切片重构图像的影响　(a)?(c) 高斯噪声方差为0.01时的结构光照明图像、HSV-RMS算法得到的光切片图像及HT-COS算法得到的光切片图像; (d)?(f) 高斯噪声方差为0.03时的结果; (g)?(i) 高斯噪声方差为0.05时的结果
Figure3. Influence of Gaussian noise on the reconstructed optical sectioning images. Structured illumination image, optical sectioning images calculated by the HSV-RMS algorithm and HT-COS algorithm, respectively, under the conditions of the Gaussian noise with variances of (a)?(c) 0.01, (d)?(f) 0.03, and (g)?(i) 0.05.

2

2.6.HSV-RMS算法和HT-COS算法色彩复原保真度对比

-->

2.6.HSV-RMS算法和HT-COS算法色彩复原保真度对比

在无噪声和无相移误差的条件下, 理论模拟了HSV-RMS算法和HT-COS算法计算所得彩色光切片图像的色彩复原保真度, 如图4所示. 图4(a)为原始的宽场图像, 为了更加直观地说明问题, 专门设计了一个含有4个色块的图像, 其中4个色块的RGB值分别为(77, 187, 95), (230, 34, 207), (198, 209, 55)和(106, 56, 56). 图4(b)和图4(c)分别为HSV-RMS算法和HT-COS算法计算得到的彩色光切片图像, 图4(d)—(f)分别为3幅图像中各色块的RGB值. 与原始图像比, HSV-RMS算法和HT-COS算法计算得到的彩色光切片图像的色彩保真度均达到99.4%以上, 证明HT-COS算法和HSV-RMS算法都可以准确复原样品的三维全彩色光切片图像.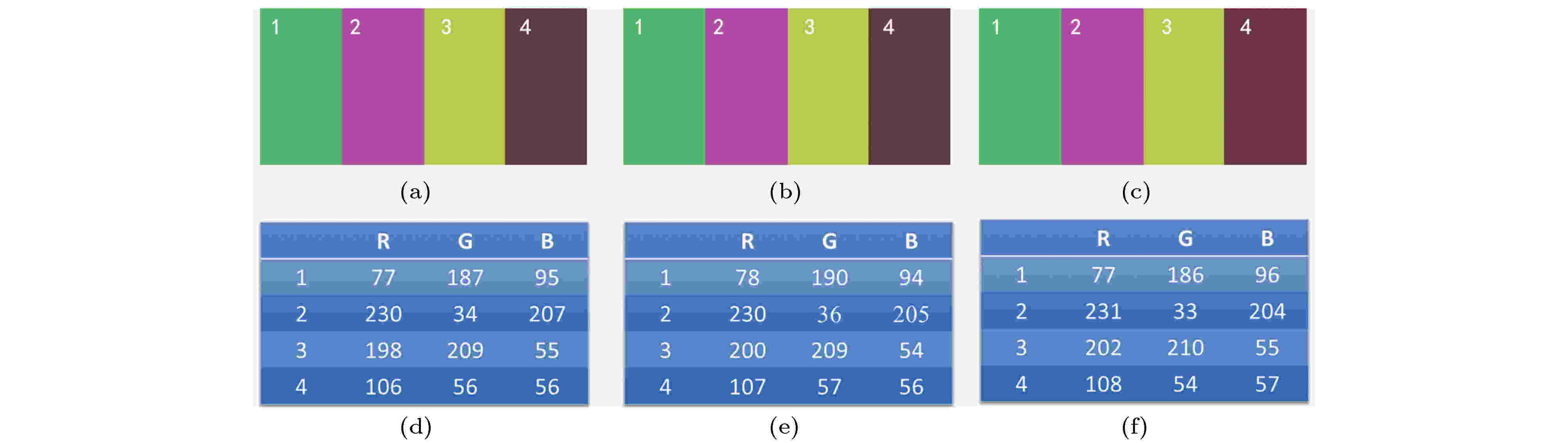

图 4 HSV-RMS算法和HT-COS算法的色彩复原保真度比较　(a)?(c)分别为原始图像、HSV-RMS算法处理后的光切片图像及HT-COS算法处理后的光切片图像; (d)?(f) 3幅图像各色块内的RGB值
Figure4. Comparison of color restoration fidelity between HSV-RMS algorithm and HT-COS algorithm: (a)?(c) Raw image, optical sectioning image calculated by HSV-RMS algorithm and optical sectioning image calculated by HT-COS algorithm, respectively; (d)?(f) RGB values for the four different regions of each image.

3.实验结果

3.1.实验系统

-->

3.1.实验系统

本文所有实验是均在自行设计的基于DMD和发光二极管(light emission diode, LED)照明的SIM系统上进行的, 如图5所示. 高亮度白光LED或者特定波长LED发射的光束经过特殊设计的全内反射(total internal reflection, TIR)棱镜后照射DMD芯片, 经过DMD调制后的正弦条纹结构光场再经过TIR棱镜之后经由投影系统和物镜透射至样品表面, 样品的反射光或激发荧光经过二向色滤光片或50/50滤光片后被彩色相机收集. 样品被固定在三维电动位移台上, 用来实现轴向扫描和X-Y方向的视场拼接. 硬件同步控制、图像采集和处理软件均基于C++自行设计开发.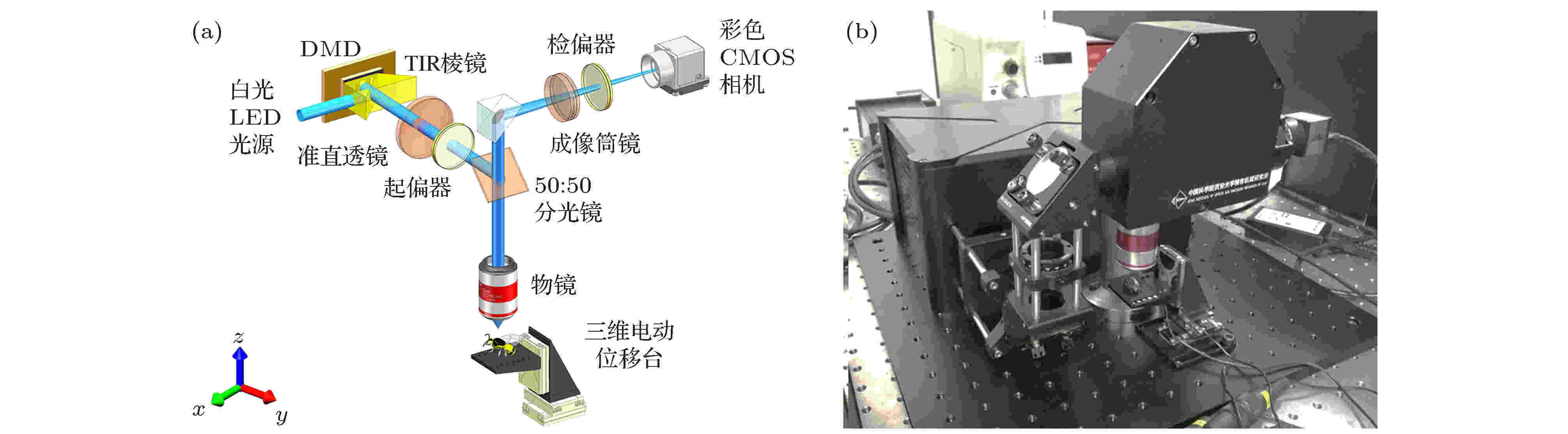

图 5 结构光照明彩色光切片实验光路及系统图　(a) 系统光路原理图; (b)系统实物图
Figure5. Schematic diagram of structured illumination color optical sectioning system: (a) Light-path diagram; (b) apparatus diagram

2

3.2.荧光样品实验

-->

3.2.荧光样品实验

我们选取具有宽光谱自发荧光(405 nm激发波长)的花粉样品进行彩色三维成像实验, 使用波长为405 nm的紫光LED光源和长通二向色镜(LP425 nm). 在样品的每层以20 ms曝光时间分别采集相移差为π/2的3幅原始结构光照明图像, 利用HSV-RMS算法进行处理. 随后从采集的原始图像中选取相移差为π的两幅图像, 再利用HT-COS算法进行处理. 实验的结果如图6所示. 图6(a)为HSV-RMS算法处理后的三维彩色光切片图像, 图6(b)为HT-COS算法处理后的结果, 显然两种算法都可以得到样品的彩色三维荧光图像.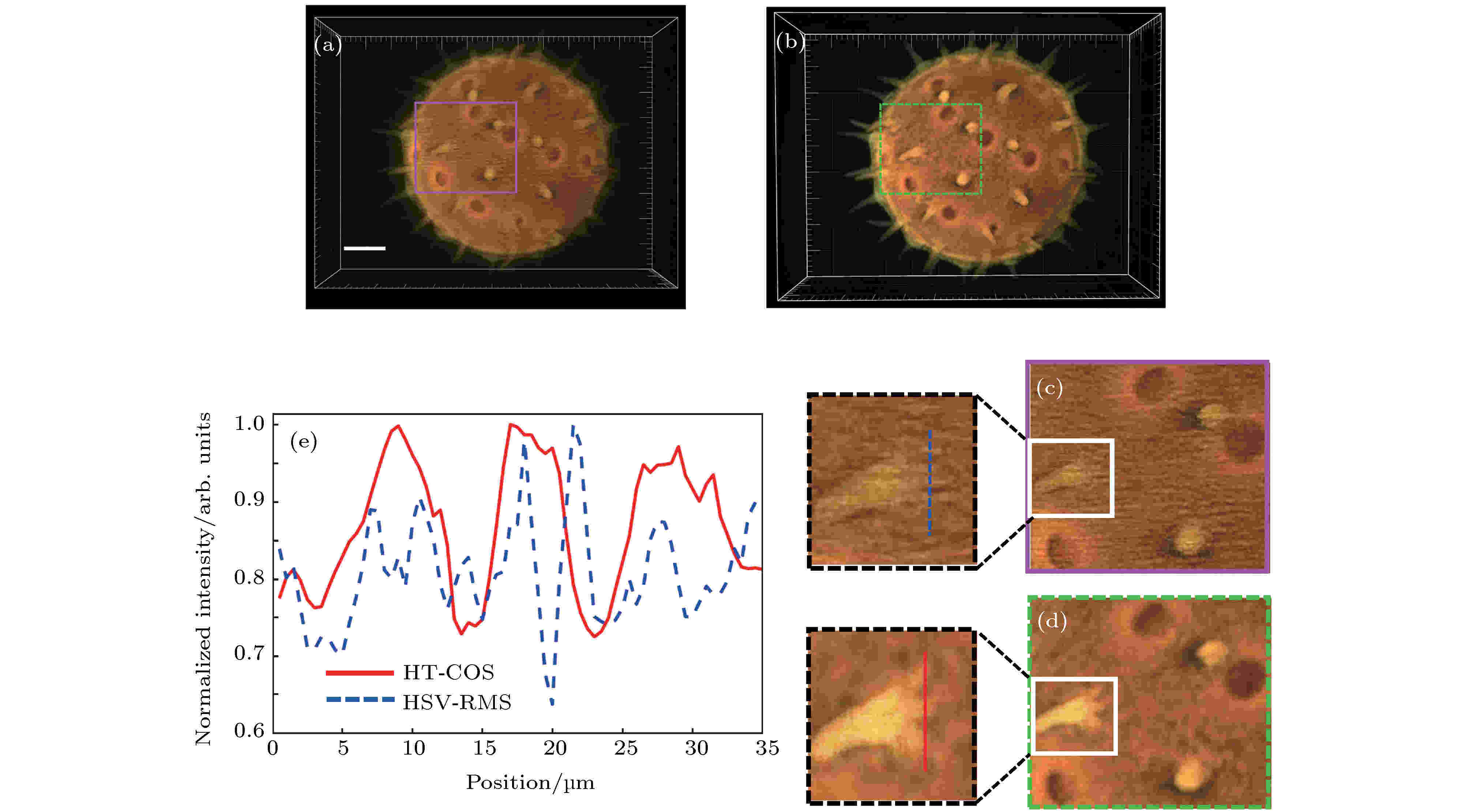

图 6 HSV-RMS算法和HT-COS算法重构的花粉彩色三维光切片图像效果对比　(a) HSV-RMS算法重构的三维图像; (b) HT-COS算法重构的三维图像; (c) 图(a)紫色方框区域的放大图像; (d) 图(b)绿色方框区域内的放大图像; (e) 图(c)中蓝色虚线和图(d)中红色实线上的强度分布; 标尺: 30 μm
Figure6. Comparison of reconstructed result of pollen grain between HSV-RMS algorithm and HT-COS algorithm: (a) 3D reconstructed color image from HSV-RMS algorithm; (b) 3D reconstructed color image from HT-COS algorithm; (c) the enlarged image in the purple rectangular box in panel (a); (d) the enlarged image in the green rectangular box in (b); (e) normalized intensity distribution of the line-scan in panel (c) and (d), i.e. the “root-shaped” structure. Scale bar: 30 μm

但由于HSV-RMS算法对3幅原始图像的相移差有严格的要求, 实验中的微小振动就会造成相移差的变化, 进而导致重构的光切片图像中产生残余条纹, 对三维重建产生影响, 为了实验验证这一结论, 在实验中加入了微小的相移扰动. 图6(c)和图6(d)对比了HSV-RMS算法和HT-COS算法重构结果中的残余条纹. 图6(c)为图6(a)中紫色方框内的放大图像, 可以看出, 图6(c)中存在比较明显的残余条纹; 图6(d)为图6(b)中绿色方框内的放大图像, 其中几乎没有残余条纹. 图6(e)中曲线的强度分布也验证了HSV-RMS算法存在明显的残余条纹, 花粉尖刺根部的“根状”结构被淹没在残余条纹之中, 而经由HT-COS重构的光切片图像则没有残余条纹, “根状”结构清晰可见, 这一实验结果进一步证实了HT-COS算法鲁棒性更高的结论.
2

3.3.反射式样品实验

-->

3.3.反射式样品实验

为了进一步证明HT-COS算法在图像采集和重构的速度优势, 对一种中华虎甲背部某区域进行了高分辨率三维成像. 首先将光路中的二向色镜替换为50∶50分束镜, 将405 nm波长LED替换为高亮度白光LED, 并分别采用HSV-RMS算法和HT-COS算法对原始图像进行处理, 结果如图7所示. 该中华虎甲的三维尺寸大约为19.5 mm × 8.3 mm × 6.6 mm, 对其整体进行了三维成像(使用4 ×, NA = 0.2物镜拍摄, 空间分辨率1.5 μm), 共采集84个视场进行拼接, 如图7(a)所示. 根据统计, 使用4 ×, NA = 0.2物镜对样品进行三维成像时, 共拼接84个视场(14行 × 6列, 单视场尺寸2.5 mm × 2.5 mm), HSV-RMS算法所需原始图像的总图像采集时间约为1767 s, 即84视场 × ((10 ms曝光时间 + 0.031 ms DMD刷新时间) × 3幅相移图像(相移差π/2) × 350层 + 30 ms位移台稳定时间 × 349次轴向移动) + 83次横向移动 × 30 ms位移台稳定时间, 而HT-COS算法只需要两步相移(相移差π), 因此图像采集时间为1472 s, 提升约16.7%. 两种方法的图像处理时间分别为13608和9744 s, 可知HT-COS算法是具有更快的图像处理速度, 提升约28.4% (Windows 7 SP1, 16GB RAM, Intel core i5-3470@3.2 GHz, Matlab R2017a). 表1对比了两种方法的图像采集时间和图像处理时间, HT-COS算法84个视场的图像采集时间和图像处理时间分别减少了295和3864 s, 这一提升对于需要视场拼接的高分辨率三维成像而言是十分可观的. 因此HT-COS算法更加适用于大尺寸样品的高分辨率三维成像, 可以大幅减小实验所需时间.

	视场个数	图像采集总时间/s	图像处理总时间/s	图像数据容量/GB	三维数据总像素数/pixels
HSV-RMS算法	84	1767	13608	1000	10¹⁰
HT-COS算法	84	1472	9744	670	10¹⁰

表1两种SIM彩色光切片算法的性能比较
Table1.Performance comparison of two algorithms for color optical sectioning SIM.

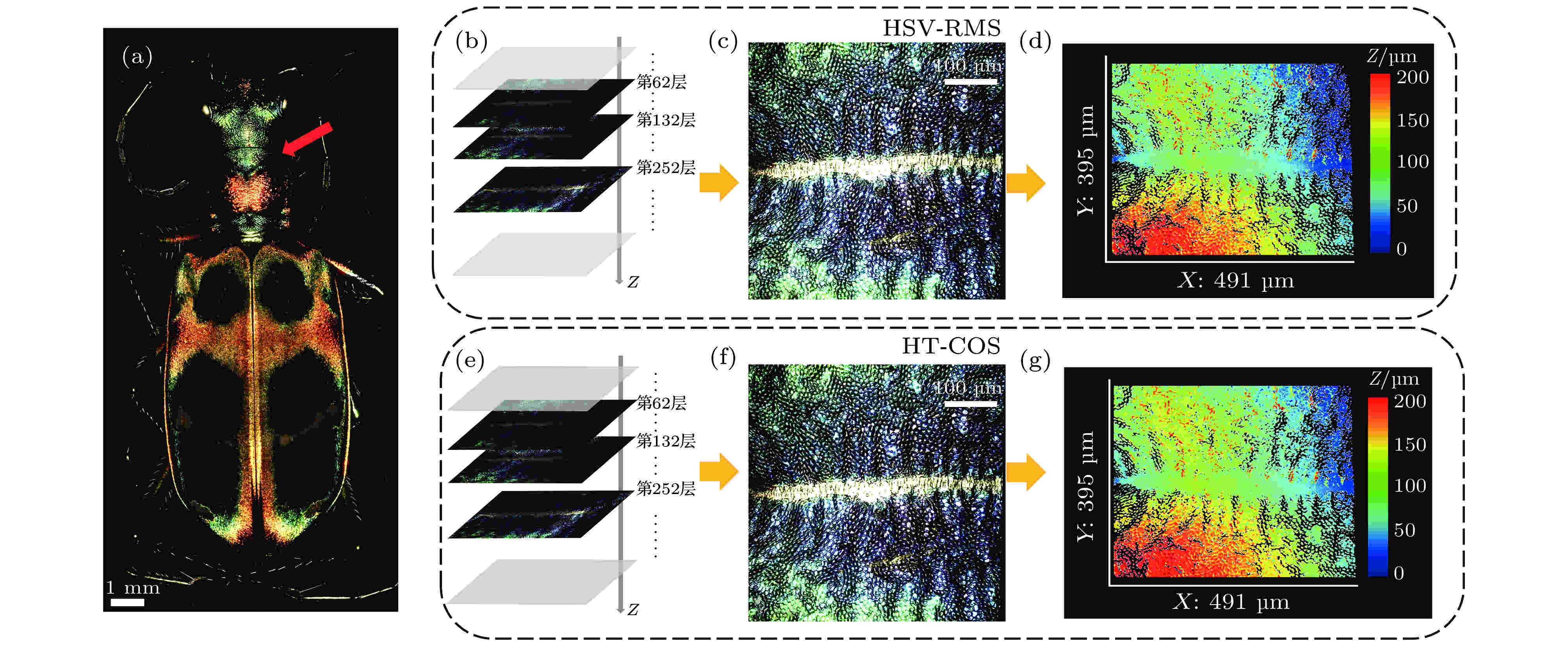图 7 一种中华虎甲背部的三维彩色SIM成像结果　(a) 该中华虎甲样品完整三维图像的二维最大值投影, 使用4 ×, NA = 0.2物镜拍摄, 共拼接84个视场, 单视场轴向扫描350层; (b) 样品轴向进行三维叠加重构的示意图, 每一层都是经过HSV-RMS算法处理后的光切片图; (c) 图(a)中红色箭头所指区域局部放大的三维光切片最大值投影图像, 使用HSV-RMS算法进行图像处理, 20 ×, NA = 0.45物镜拍摄; (d) 图(c)的三维形貌分布; (e) 样品轴向进行三维叠加重构的示意图, 每一层都是经过HT-COS算法处理后的光切片图; (f)图(a)中红色箭头所指区域局部放大的三维光切片最大值投影图像, 使用HT-COS算法进行图像处理, 20 ×, NA = 0.45物镜拍摄; (g) 图(f)的三维形貌分布
Figure7. 3D color imaging result of a Chinese tiger beetle: (a) Maximum intensity projection image of the tiger beetle under 4 ×, NA = 0.2 objective lens, the 3D volume is rendered from 84 data sets stitching and sliced 350 layers; (b) schematic diagram of 3D reconstruction in axial direction after imaging processing with HSV-RMS algorithm; (c) maximum intensity projection images of the area pointed by the red arrow in panel (a) processed with HSV-RMS algorithm. The images are captured under 20 ×, NA = 0.45 objective lens; (d) 3D height map of panel (c); (e) schematic diagram of 3D reconstruction in axial direction after imaging processing with HT-COS algorithm; (f) maximum intensity projection images of the area pointed by the red arrow in (a) processed with HT-COS algorithm. The images are captured under 20 ×, NA = 0.45 objective lens; (g) the 3D height map of panel (f).

在样品某区域(图7(a)中红色箭头指向区域)利用20×, NA = 0.45物镜进行局部放大并进行了两种方法的比较实验. 对比图7(c)和图7(f)可以看出, 在没有相移误差的条件下, HT-COS算法在图像对比度、色彩还原度以及图像分辨率方面与HSV-RMS算法相比并无明显差异.
由于SIM三维光切片成像结果消除了离焦背景的干扰, 因此在恢复物体表面三维形貌高度中具有十分显著的优势, 利用“shape from focus”算法, 可以在横向实现高分辨率的形貌解析度^[21,23,24]. 对于三维图像中的某一点(x, y, z), 其在每一层光切片图像中都对应同一个像素坐标(x, y), 根据光切片层数的不同, 该像素坐标(x, y)的光强也不同, 只有当该点处于焦面位置时才有光强的最大值. 通过寻找亮度的最大值, 即可获得该点的高度信息, 即:

$h(x,y) = {\arg _z}\max [I(x,y,z)],$

其中, h(x, y)代表(x, y)坐标处的高度; I(x, y, z)代表(x, y, z)处的光强; arg_zmax代表取光强最大时的轴向位置, 即高度信息. 利用(35)式分别计算图7(c)和图7(f)的三维形貌分布并进行定量对比, 图7(d)和图7(g)是对应的三维形貌分布图, 图中不同的颜色代表不同的高度. 两种算法计算得到的形貌分布完全一致, 但HT-COS算法具有更快的图像处理速度, 因此更适合大尺寸物体的三维成像.

4.结　论

本文提出了一种基于希尔伯特变换的结构光照明快速彩色三维显微成像方法(HT-COS), 与已有的HSV-RMS算法相比, HT-COS算法图像采集量减少了1/3, 图像处理时间节约了约28%. 实验结果表明, 该方法在图像对比度、色彩还原度及形貌高度恢复等方面与HSV-RMS算法并无明显差异, 该方法对大尺寸样品的高分辨率三维彩色成像具有重要的意义, 将进一步扩展SIM的应用范围.
感谢中国科学院动物研究所白明研究员提供的昆虫样品.

本站小编 Free考研考试/2021-12-29

English Abstract

Fast structured illumination three-dimensional color microscopic imaging method based on Hilbert-transform

Corresponding author:Yao Bao-Li, yaobl@opt.ac.cn;Lei Ming, ming.lei@mail.xjtu.edu.cn

全文HTML

2.1.RMS光切片算法

2.2.基于希尔伯特变换的光切片算法

2.3.基于希尔伯特变换的彩色光切片算法

2.4.相移误差对HSV-RMS算法以及HT-COS算法的影响对比

2.5.噪声对HSV-RMS算法和HT-COS算法的影响对比

2.6.HSV-RMS算法和HT-COS算法色彩复原保真度对比

3.1.实验系统

3.2.荧光样品实验

3.3.反射式样品实验

相关话题/图像 结构 实验 计算 信息

领限时大额优惠券,享本站正版考研考试资料!

马约拉纳零能模的非阿贝尔统计及其在拓扑量子计算的应用

两种Ge-Sb-Se薄膜的光学性质及微观结构

深海海底反射区声场角谱域分布结构分析及在声纳波束俯仰上的应用

分子动力学模拟冷却速率对非晶合金结构与变形行为的影响

膜间相互作用、开弦对产生和增强效应及其可能的实验探测

Re对Ni<sub>3</sub>Al微观结构及力学性质影响的第一原理研究

磁电势垒结构中光场辅助电子自旋输运特性

平面复合金属微纳结构的圆二色性研究

真空沟道结构GaAs光电阴极电子发射特性

确定大气边界层顶高度的新方法及数值实验