摘要:提出一种综合利用区域逼近法和柯西拟合法精确获取Ge₂₀Sb₁₅Se₆₅薄膜和Ge₂₈Sb₁₂Se₆₀薄膜透射光谱范围内任意波长处折射率与色散的多点柯西法, 并从理论上证明了该方法的准确性. 实验上, 采用磁控溅射法制备了这两种Ge—Sb—Se薄膜, 利用傅里叶红外光谱仪测得了透射光谱曲线, 运用分段滤波的方法去除噪声, 然后使用多点柯西法得到了这两种薄膜在500—2500 nm波段的折射率、色散、吸收系数和光学带隙. 结果表明Ge₂₈Sb₁₂Se₆₀薄膜的折射率和吸收系数大于Ge₂₀Sb₁₅Se₆₅薄膜, Ge₂₈Sb₁₂Se₆₀薄膜的光学带隙小于Ge₂₀Sb₁₅Se₆₅薄膜. 最后, 利用拉曼光谱对两种薄膜的微观结构进行了表征, 从原子之间的键合性质解释了这两种硫系薄膜不同光学性质的原因.
关键词: 红外硫系薄膜/
柯西模型/
光学性质/
微观结构

English Abstract

全文HTML

--> --> -->

硫系薄膜具有较宽的红外透过光谱范围, 到目前为止, 已广泛应用于超快全光开关器件、静电复印/平板印刷的感光组件、红外传感、红外热成像、全息存储、能量传输、红外光波导等领域^[1-4]. 随着硫系薄膜在诸多技术领域中的应用日益广泛, 薄膜制备水平不断提升, 各种特殊用途对薄膜制备技术和薄膜材料也提出了更高的要求. 精确获取硫系薄膜的光学参数对于研究人员和技术人员设计和制造高质量的红外微光学器件至关重要.
为了准确而有效地获得薄膜材料的折射率, 研究人员开发出诸如椭圆偏振法^[5-7]、棱镜偶合法^[8-10]和透射光谱法^[11-13]等方法. 其中一些方法虽然能获取薄膜的折射率等光学常数, 但也存在不足之处, 如: 椭圆偏振法建模要求较高, 棱镜耦合法测试薄膜的折射率范围受到限制等. Swanepoel方法能基于薄膜的透射光谱获得薄膜的折射率、厚度等, 许多研究人员用该方法分析薄膜的光学特性^[14-19], 但是他们只利用了有限个峰谷处波长的折射率, 再选用Cauchy, Sellmeier等模型来获取全波段的折射率, 需要根据材料特性的不同选取不同的模型, 而选取模型的准确与否会严重影响结果的准确性, 能在模型未知的情况之下准确获取薄膜光学参数显得非常迫切.
针对上述问题, 本文提出综合利用改进的Swanepoel法^[20]和区域逼近法^[21]研究薄膜的光学特性. 首先, 理论上分析了该方法的计算精度; 接着, 利用此方法, 根据透射光谱的实验数据, 得到Ge₂₀Sb₁₅Se₆₅和Ge₂₈Sb₁₂Se₆₀薄膜的折射率、色散、吸收系数和光学带隙. 最后通过拉曼光谱对两种薄膜的微观结构进行了表征, 并从原子之间键合性质的角度解释了这两种硫系薄膜具有不同光学特性的原因.

2

-->

2.1.理论模型

单层硫系薄膜在高效太阳能电池、光流控传感芯片等方面具有巨大的应用价值. 如图1所示, 在透明厚的二氧化硅基底上有单层透明薄膜. 薄膜参数包括: 厚度d, 吸收系数α和复折射率N = n － ik, 其中n是折射率的实部, k是消光系数, 可以用吸收系数表示为k = αλ/(4π), 其中λ是光波长. 透明衬底折射率为s, 吸收系数α_s = 0, 厚度比薄膜厚度d大两个数量级. 周围空气的折射率n₀ = 1.
图 1 镀在透明二氧化硅玻璃衬底上的薄膜结构示意图
Figure1. Schematic of the structure of a thin film coated on a transparent silica glass substrate.

2 -->

2.2.折射率获取方法及拟合模型

3 -->

2.2.1.改进的Swanepoel方法

改进的Swanepoel方法用来获取薄膜透射光谱切点处的折射率. 薄膜的透射曲线T可以表示为

$T = \frac{{Ax}}{{B - Cx\cos \varphi + D{x^2}}},$

其中A = 16n²s, B = (n + 1)³(n + s²), C = 2(n² – 1)(n² – s²), D = (n – 1)³(n – s²), φ = 4πnd/λ, x = e^–αd, λ是光波长, φ是相位, s是玻璃衬底折射率, x是与膜的厚度d和吸收系数α有关的参数. 我们在透射谱线基础上得到上下两条包络线T_M和T_m, 然后得到该薄膜在各个切点位置处对应的折射率n:

$\begin{split}n ={}& \Bigg[ 2s\frac{{{T_{\rm{M}}} - {T_{\rm{m}}}}}{{{T_{\rm{M}}}{T_{\rm{m}}}}} + \frac{{{s^2} + 1}}{2} \\ &+ \sqrt {{{\left( {2s\frac{{{T_{\rm{M}}} - {T_{\rm{m}}}}}{{{T_{\rm{M}}}{T_{\rm{m}}}}} + \frac{{{s^2} + 1}}{2}} \right)}^2} - {s^2}}\;\Bigg]^{1/2}, \end{split}$

式中s是玻璃衬底的折射率, 再根据折射率和波长与厚度之间的关系式

$d = \frac{{{\lambda _1}{\lambda _2}}}{{2({\lambda _1}{n_2} - {\lambda _2}{n_1})}},$

得到各个切点位置处对应的薄膜厚度值d, (3)式中${\lambda _1}$和${\lambda _2}$是相邻的两个波峰或波谷附近切点位置对应的波长, ${n_1}$和${n_2}$分别是${\lambda _1}$和${\lambda _2}$处的折射率.
3 -->

2.2.2.区域逼近法

区域逼近法用来获取薄膜透射光谱任意波长处的折射率. 在(1)式中, x可以通过(4)式确定:

$x = \frac{{{E_{\rm{M}}} - {{[E_{\rm{M}}^2 - {{({n^2} - 1)}^3}({n^2} - {s^4})]}^{1/2}}}}{{{{(n - 1)}^3}(n - {s^2})}},$

其中

${E_{\rm{M}}} = \frac{{8{n^2}s}}{{{T_{\rm{M}}}{T_{\rm{s}}}}} + ({n^2} - 1)({n^2} - {s^2}),$

T_M是T的上切线包络线. 另外, 在干涉条纹的基本公式

$2nd = m\lambda $

中的厚度d可以通过改进的Swanepoel方法获得. 在确定干涉级数m后, 波长λ处折射率n由(5)式获得, 利用以上方法得到多个波长处的折射率.
3 -->

2.2.3.折射率拟合模型

利用上述方法获得离散的折射率后, 采用以下几种模型: Cauchy, Sellmeier, Conrady和Herzberger^[22-25]得到薄膜全波段的折射率, 具体形式见表1.

名称	模型
Cauchy	$n = A + \dfrac{B}{{{\lambda ^2}}} + \dfrac{C}{{{\lambda ^4}}}$
二阶归一化标准Sellmeier	$n = \sqrt {1 + \dfrac{{A \cdot {\lambda ^2}}}{{{\lambda ^2} - B}} + \dfrac{{C \cdot {\lambda ^2}}}{{{\lambda ^2} - D}}} $
三阶归一化标准Sellmeier	$n = \sqrt {1 + \dfrac{{A \cdot {\lambda ^2}}}{{{\lambda ^2} - B}} + \dfrac{{C \cdot {\lambda ^2}}}{{{\lambda ^2} - D}} + \dfrac{{E \cdot {\lambda ^2}}}{{{\lambda ^2} - F}}} $
二阶非标准形式的Sellmeier	$n = \sqrt {A + \dfrac{{B \cdot {\lambda ^2}}}{{{\lambda ^2} - C}} + D \cdot {\lambda ^2}} $
Conrady	$n = A + \dfrac{B}{\lambda } + \dfrac{C}{{{\lambda ^{3.5}}}}$
Herzberger	$n = A + B \cdot {\lambda ^2} + C \cdot {\lambda ^2} + \dfrac{D}{{\left( {{\lambda ^2} - 0.028} \right)}} + \dfrac{E}{{{{\left( {{\lambda ^2} - 0.028} \right)}^2}}}$

表1六种折射率模型
Table1.Six models of refractive index.

2 -->

2.3.模拟仿真

为了精确获取两种Ge-Sb-Se硫系薄膜的光学特性, 利用文献[26]中已知性质的单层透明薄膜对折射率和色散进行优化模拟仿真. 在(1)式中代入文献[26]中已知的薄膜属性: $s = 1.51$, d = 1000 nm, $n = \dfrac{{3 \times {{10}^5}}}{{{\lambda ^2}}} + 2.6$, $\lg \alpha = \dfrac{{1.5 \times {{10}^6}}}{{{\lambda ^2}}} - 8$, 得到图2. T_M和T_m为上下包络线, “■”为上下包络线与透射曲线的切点.
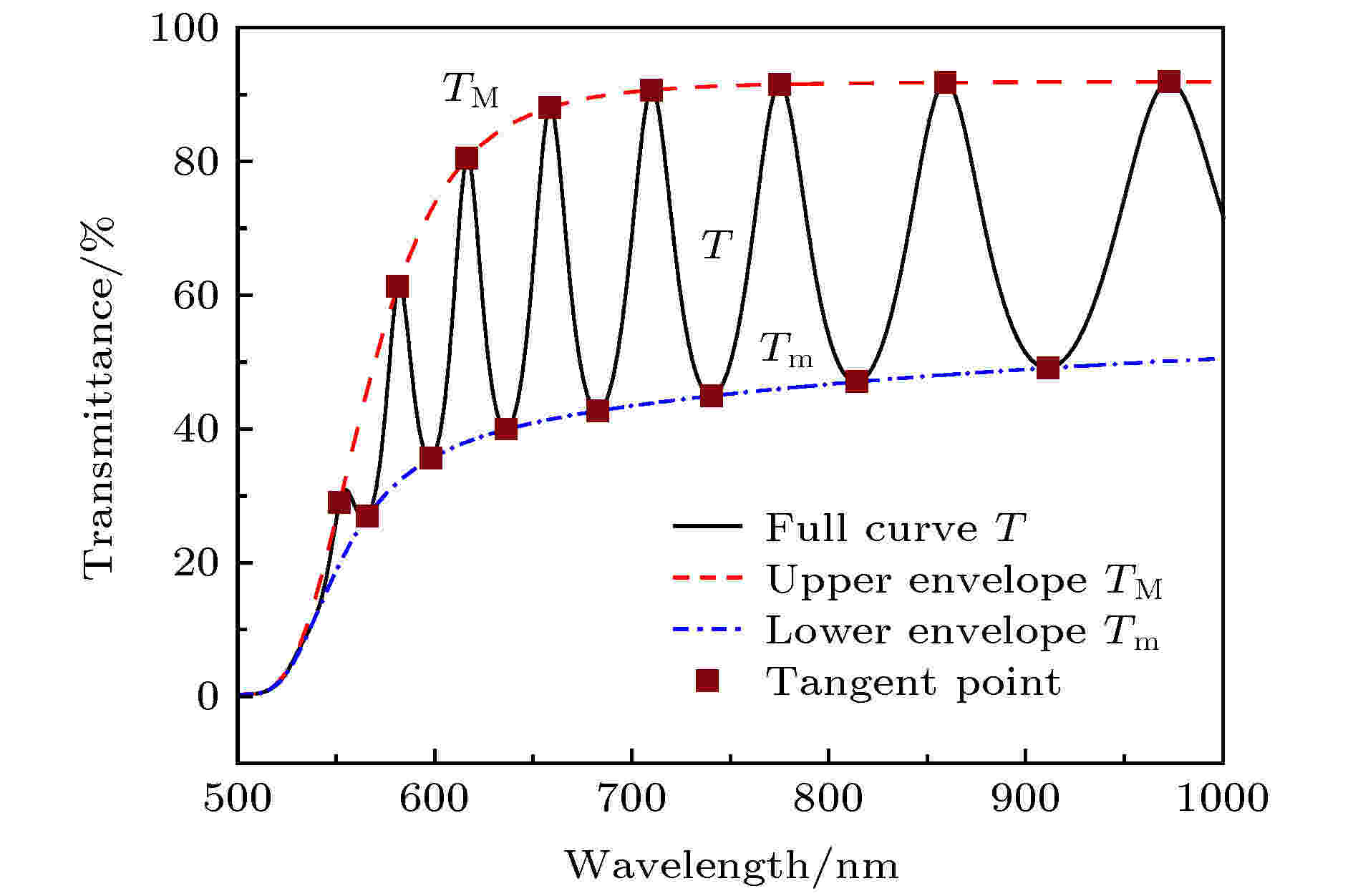图 2 在有限玻璃基板上的Si-H薄膜的透射率曲线
Figure2. Transmittance curve of Si-H thin film on finite glass substrate.

由图2数据以及(2)式和(3)式可以获得薄膜透射光谱切点处的折射率, 结果列于表2.

λ	TM	Tm	n	d	m0	m	n0	d0
972.4	0.9202	0.5007	2.9173		6.001	6.0	2.9169	1000.0
911.2	0.9199	0.4904	2.9613		6.501	6.5	2.9611	1000.0
859.0	0.9193	0.4801	3.0066	1000.0	7.002	7.0	3.0062	1000.0
814.1	0.9183	0.4697	3.0527	1000.4	7.501	7.5	3.0526	1000.1
774.9	0.9165	0.4591	3.0996	1000.1	8.002	8.0	3.0993	1000.0
740.5	0.9134	0.4485	3.1471	999.5	8.502	8.5	3.1468	1000.0
710.0	0.9080	0.4376	3.1951	999.7	9.002	9.0	3.1947	1000.0
682.8	0.8984	0.4260	3.2435	999.4	9.502	9.5	3.2430	999.9
658.4	0.8818	0.4132	3.2921	1000.2	10.002	10.0	3.2917	1000.0
636.3	0.8530	0.3982	3.3410	999.3	10.503	10.5	3.3402	999.9
616.3	0.8050	0.3796	3.3898	999.6	11.003	11.0	3.3893	999.9
598.1	0.7252	0.3546	3.4335	1020.4	11.483	11.5	3.4387	1001.6
581.3	0.6127	0.3191	3.4878	1000.6	12.002	12.0	3.4874	1000.0
565.9	0.4595	0.2678	3.5368	981.9	12.502	12.5	3.5365	1000.0
551.7	0.2879	0.1965	3.5856	1001.6	13.001	13.0	3.5857	1000.1
注: $ \qquad \quad \overline d = 1000.2;{\sigma _1} = 7.58;\overline {{d_0}} = 1000.1;{\sigma _0} = 0.40$.

表2由图2中数据获得的λ, T_M和T_m的值以及通过改进后的Swanepoel方法计算的n和d值
Table2.Values of λ, T_M, and T_m obtained in Fig. 2 and the values of n and d calculated by the improved Swanepoel method

表2中的切点处波长的折射率用表1中的模型拟合, 获得薄膜500—1000 nm波段的折射率(各个模型的系数详见附录表A1). 得到六种色散模型拟合后的折射率曲线后再由(6)式可以获得色散数据, 与真实的折射率以及色散作对比, 如图3. 材料色散为
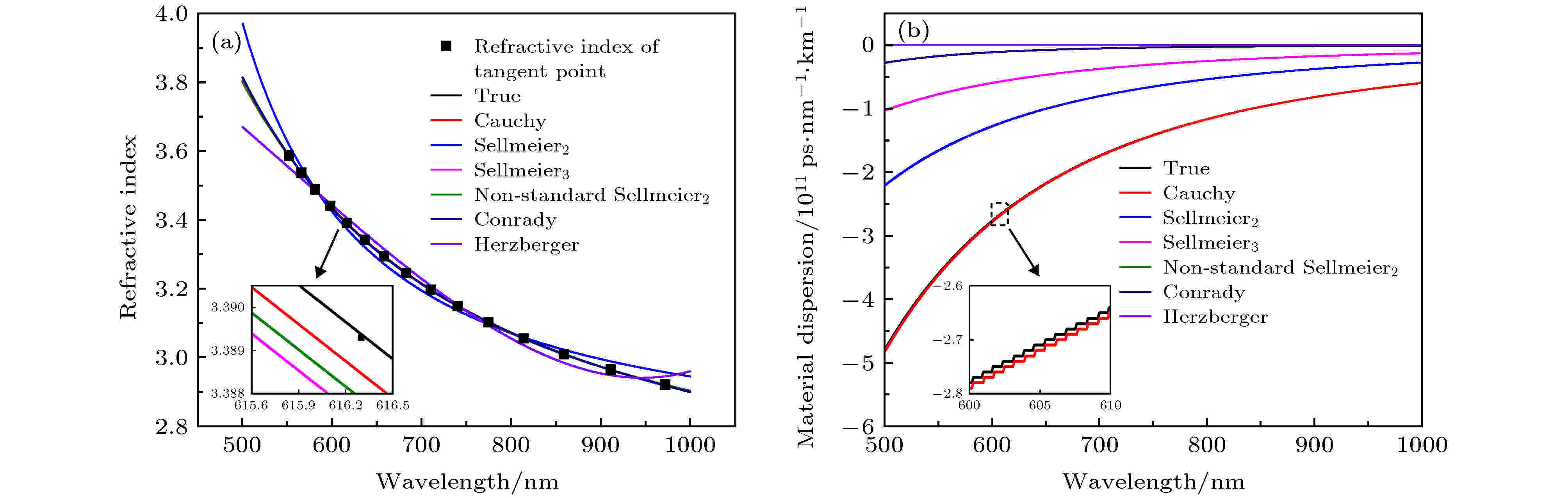图 3 六种不同模型得到的薄膜折射率和色散比较
Figure3. Comparison of refractive index and dispersion of thin film obtained by six different models.

	A	B	C	D	E	F
Cauchy	2.6006	2.9900 × 105	2.4107 × 108
二阶归一化标准Sellmeier	6.0592	1.3837 × 105	0.5371	1.3837 × 105
三阶归一化标准Sellmeier	11.1212	6.4542 × 104	5.9297	6.4455 × 104	–11.3546	–4.9139 × 104
二阶非标准形式的Sellmeier	–30.1052	36.8509	4.3322 × 104	–0.0079
Conrady	2.3534	502.8603	1.2718 × 109
Herzberger	4.3450	–3.1408 × 10–8	1.7525 × 10–12	3.0038 × 105	9.0228 × 1010

表A1六种模型的系数
TableA1.Coefficients of six models.

${D_{\rm{m}}} = - \frac{\lambda }{c}\frac{{{{\rm{d}}^2}n}}{{{\rm{d}}{\lambda ^2}}}.$

由图3可以看出, Cauchy色散模型计算的折射率和色散的精度明显优于其他模型.
由于改进的Swanepoel方法只能获得切点处的折射率, 所以很难通过柯西模型精确地获取全波段的折射率和色散特性曲线. 因此我们提出了一种先利用区域逼近法获得多个波长处的折射率, 然后再通过柯西模型更精确地获取薄膜500—1000 nm波长的折射率和色散的多点柯西法. 利用此方法, 得到了n和λ之间的函数关系:

$n = {\rm{2}}.{\rm{3234}} + \frac{{{\rm{4}}.{\rm{7593}} \times {\rm{1}}{{\rm{0}}^{\rm{4}}}}}{{{\lambda ^{\rm{2}}}}} + \frac{{{\rm{3}}.{\rm{0409}} \times {\rm{1}}{{\rm{0}}^{{\rm{10}}}}}}{{{\lambda ^4}}}.$

为了比较本文提出的多点柯西法与各种模型获得的薄膜折射率精度, 我们把Δn_Cauchy, Δn_Sel2, Δn_Sel3, Δn_Sel2非, Δn_Conrady, Δn_Herzberger和Δn_MCM表示为n_Cauchy, n_Sellmeier2, n_Sellmeier3, n_{Sellmeier2非}, n_Conrady, n_Herzberger和n_MCM与真实折射率${n_{{\rm{tr}}}}$的差值(详细数据见附录表A2). 图4(a)表示Δn_Cauchy, Δn_Sel2, Δn_Sel3, Δn_Sel2非, Δn_Conrady和Δn_Herzberger与Δn_MCM随波长变化的对比关系.
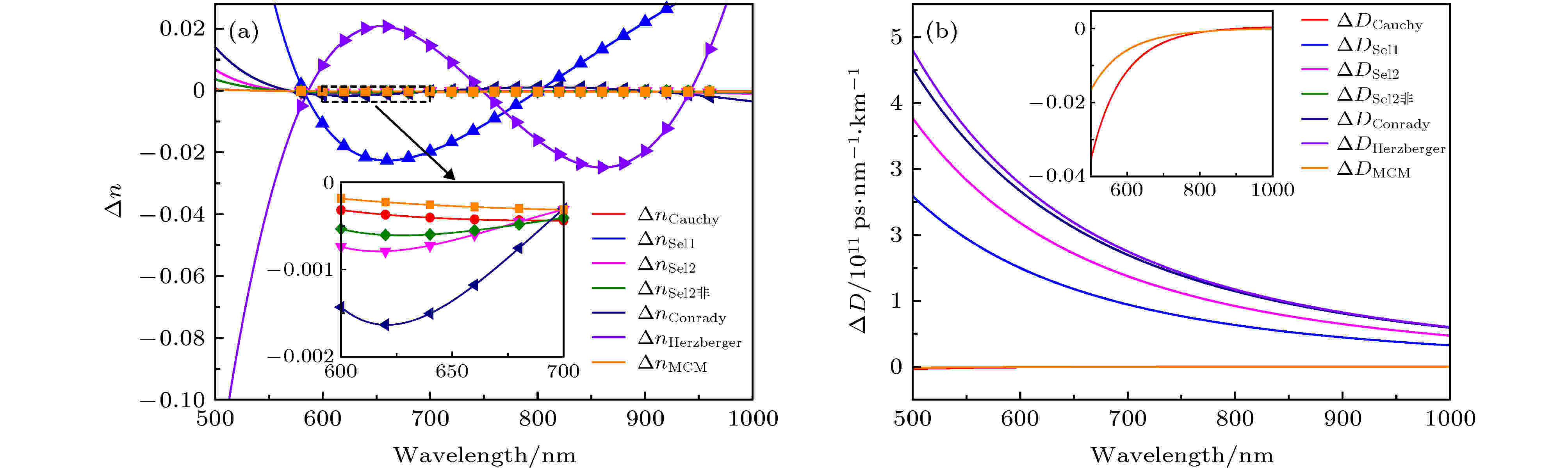图 4 六种色散模型(包含多点柯西法)得到的折射率和色散与真实值差值随波长变化关系　(a)折射率差与波长的关系; (b)色散差与波长的关系
Figure4. Relation between the refractive index and the dispersion obtained by six dispersion models (include MCM) and the true value as a function of wavelength: (a) Δn vs. wavelength; (b) ΔD vs. wavelength.

λ	Δncauchy	ΔnSel2	ΔnSel3	Δnsel2非	ΔnConrady	ΔnHerzberger	ΔnMCM
580	–0.0002	0.0018	–0.0005	–0.0003	–0.0007	–0.0050	–0.0001
600	–0.0003	–0.0107	–0.0007	–0.0005	–0.0014	0.0081	–0.0002
620	–0.0004	–0.0180	–0.0008	–0.0006	–0.0016	0.0162	–0.0002
640	–0.0004	–0.0216	–0.0007	–0.0006	–0.0015	0.0201	–0.0003
660	–0.0004	–0.0226	–0.0006	–0.0005	–0.0012	0.0207	–0.0003
680	–0.0004	–0.0218	–0.0005	–0.0005	–0.0008	0.0186	–0.0003
700	–0.0004	–0.0197	–0.0003	–0.0004	–0.0003	0.0146	–0.0003
720	–0.0004	–0.0167	–0.0002	–0.0003	0.0001	0.0091	–0.0003
740	–0.0004	–0.0131	–0.0001	–0.0003	0.0005	0.0028	–0.0003
760	–0.0004	–0.0090	0.0000	–0.0002	0.0008	–0.0038	–0.0003
780	–0.0004	–0.0047	0.0000	–0.0002	0.0010	–0.0103	–0.0003
800	–0.0004	–0.0002	0.0000	–0.0002	0.0011	–0.0160	–0.0003
820	–0.0004	0.0043	0.0000	–0.0002	0.0011	–0.0207	–0.0003
840	–0.0003	0.0089	0.0000	–0.0002	0.0009	–0.0238	–0.0003
860	–0.0003	0.0134	–0.0001	–0.0002	0.0007	–0.0249	–0.0003
880	–0.0003	0.0178	–0.0002	–0.0002	0.0004	–0.0236	–0.0003
900	–0.0003	0.0222	–0.0003	–0.0002	–0.0001	–0.0196	–0.0003
920	–0.0002	0.0264	–0.0004	–0.0003	–0.0006	–0.0123	–0.0003
940	–0.0002	0.0305	–0.0006	–0.0004	–0.0012	–0.0014	–0.0003
960	–0.0002	0.0345	–0.0007	–0.0004	–0.0019	0.0134	–0.0003
$\begin{aligned}{\text{注}}:\; & \Delta {n_{{\rm{Cauchy}}}} = 0.0003;\sigma {n_{{\rm{Cauchy}}}} = 0.0002;\Delta {n_{{\rm{Sel2}}}} = 0.0253;\sigma {n_{{\rm{Sel2}}}} = 0.0273;\\ &\Delta {n_{{\rm{Sel3}}}} = 0.0006;\sigma {n_{{\rm{Sel3}}}} = 0.0010;\Delta {n_{{\rm{Sel}}2{\simfont\text{非}}}} = 0.0005;\sigma {n_{{\rm{Sel}}2{\simfont\text{非}}}} = 0.0005;\\ & \Delta {n_{{\rm{Conrady}}}} = 0.0016;\sigma {n_{{\rm{Conrady}}}} = 0.0022;\Delta {n_{{\rm{Herzberger}}}} = 0.0226;\sigma {n_{{\rm{Herzberger}}}} = 0.0225;\\ & \Delta {n_{{\rm{MCM}}}} = 0.0002;\sigma {n_{{\rm{MCM}}}} = 0.0001 .\end{aligned}$

表A2利用六种模型和多点柯西法得到的折射率与真实值的差
TableA2.Difference between refractive index obtained by using six models, MFM, and real value.

通过图4(a)可以看出, Δn_Sellmeier, Δn_Condary和Δn_Herzberger的值均大于Δn_Cauchy的值, 这表明用Cauchy色散模型比用Sellmeier, Condary和Herzberger色散模型得到的折射率值更加精确. 此外, 可以明显看出Δn_MCM的值在大部分波长处均小于Δn_Cauchy且波动较小, 这表明用多点柯西法比用柯西模型得到的全波段折射率精度高.
为了比较多点柯西法和各种模型获得色散数据的精度, 我们利用计算得到的500—1000 nm波段的色散和真实值做差, 得到图4(b), 由图可以明显看出 ΔD_MCM 的平均值和方差都小于其他色散模型.
多点柯西法是基于薄膜透射光谱确定薄膜光学常数的一种方法, 因此要使用该方法获得待测薄膜的光学常数, 待测薄膜应该满足以下两个条件: 1)薄膜在待测波长处透明或半透明, 可测量得到其透过率数据; 2)薄膜的厚度保持在600 nm以上确保其透射光谱中包含6个以上的干涉峰谷.

实验中采用磁控溅射法^[27,28]在二氧化硅玻璃衬底上制备了两种组分的Ge-Sb-Se薄膜, 并用傅里叶红外光谱仪获得它们的透射光谱.
2

-->

3.1.样品制备

Ge-Sb-Se薄膜制备以两面抛光的块体硫系玻璃样品为靶材. 根据Ge₂₀Sb₁₅Se₆₅或Ge₂₈Sb₁₂Se₆₀玻璃的化学组分和目标质量, 计算各以单质形式加入的原料质量, 其中Ge, Sb, Se的纯度均为99.999%. 高纯的Ge, Sb, Se单质的称重过程在干燥、洁净的手套箱中进行, 以防止原料被氧化. 原料混合后装入内表面预先洗净并烘干的石英试管, 采用德国莱宝PT50型真空泵对石英试管进行抽真空, 同时对装有原料的石英试管进行预加热至100 ℃以除去原料中的水, 当真空度达1.0 × 10^–3 Pa以下时用氢氧焰封接熔断, 再放入摇摆炉中升温至1000 ℃后熔制10 h, 取出在水中淬冷后放入退火炉中缓慢退火至室温以减少玻璃内部的应力. 最后将玻璃加工成Ф50 mm × 1.5 mm两面抛光的样品作为薄膜制备的靶材.
实验中采用磁控溅射法在二氧化硅玻璃衬底上制备Ge-Sb-Se薄膜. 制备过程中, 真空腔内的压力 ≤ 10^–5 Pa且温度保持在25 ℃左右, 溅射功率范围为20—40 W, 衬底的旋转速度为5 r/min. 为了使薄膜结构更加稳定, 将薄膜放入退火炉, 在玻璃转化温度(T_g)以下40 ℃退火15 h.
2 -->

3.2.样品测试

1) 组分测试
薄膜样品的组分采用Tescan VEGA 3SBH型扫描电子显微镜配置的能谱仪 (energy dispersive spectrometer, EDS)测得, 结果表明磁控溅射法制备的Ge-Sb-Se薄膜和玻璃靶材的组分偏差比保持在3%以内.
2) 透射光谱获取
使用带有显微成像装置HYPERION 3000的傅里叶红外光谱仪Bruker VERTEX 70测试薄膜的透射光谱.
3) 拉曼测试
采用英国的Renishaw inVia型显微拉曼光谱仪测试拉曼光谱, 激发波长为785 nm, 测试功率为0.1 mW.

2

-->

4.1.透射光谱滤波

薄膜透过率获取的准确与否会影响光学参数计算结果的准确性. 为了提高薄膜透过率测试的准确性, 采取了以下措施: 1)多次重复测量同一位置的透射光谱, 以减少获取薄膜透过率时的误差; 2)采用分光光度计、傅里叶红外光谱仪等多个设备测量薄膜同一位置的透射光谱, 比较测试结果; 3)利用平移匹配法校正透射光谱, 在校正后的透射谱基础上, 准确获取薄膜的折射率.
实验得到的薄膜透过率曲线数据通常会存在许多噪声, 如图5的Ge₂₈Sb₁₂Se₆₀薄膜实验数据. 这些噪声会导致折射率的计算结果存在不同程度的误差, 因此需要对实验的透过率曲线数据进行去噪声处理. 常用的滤波方法有adjacent averaging, Savitaky-Golay, percentile filter和FFT filter^[29-32]. 图5(a)—图5(d)分别为用以上四种方法对同一组实验数据进行去噪声处理后的对比图.
图 5 五种滤波方法去噪声比较　(a) Adjacent averaging方法; (b) Savitaky-Golay方法; (c) percentile filter方法; (d) FFT filter方法; (e)分段拟合法
Figure5. Comparison of five filtering methods to reduce noise: (a) Adjacent averaging method; (b) Savitaky-Golay method; (c) percentile filter method; (d) FFT filter method; (e) piecewise fitting method.

通过比较图5(a) —图5(d)可知, 用以上方法滤波后的透射曲线均出现不同程度的失真情况, 进而导致无法精确地获取薄膜的折射率和色散参数, 为此采用一种能够精确滤除薄膜透射光谱曲线中的噪声的方法. 首先, 以半高宽为界限对测得的透过率谱线进行分段, 分成若干个波峰和波谷, 然后, 利用函数模型$T \!=\! a\cos ({{n}/{\lambda}}) \!+\! b$对上述波峰和波谷进拟合, 其中a, b为待求解的拟合参数, λ表示波长, 这里的n选用四阶柯西模型$n \!=\! {c}/{{{\lambda ^2}}} \!+\! {d}{\lambda } \!+\! e$, 其中c, d, e也是待求解的拟合参数, 获取每一段的拟合残差$\theta '$与设定阈值$\theta $比较, 将大于$\theta $的数据段再次按半高宽分段拟合, 循环处理至所有段的拟合残差都小于$\theta $时, 将拟合后的数据拼接在一起得到一条理想光滑的透射光谱曲线, 结果如图5(e)所示.
2 -->

4.2.折射率及色散分析

利用改进的Swanepoel方法获得了两种薄膜分段滤波后透射率曲线的上和下切线包络, 如图6(a)和图6(b)所示, 并通过计算得到两种薄膜的厚度分别为1200.0和1400.0 nm.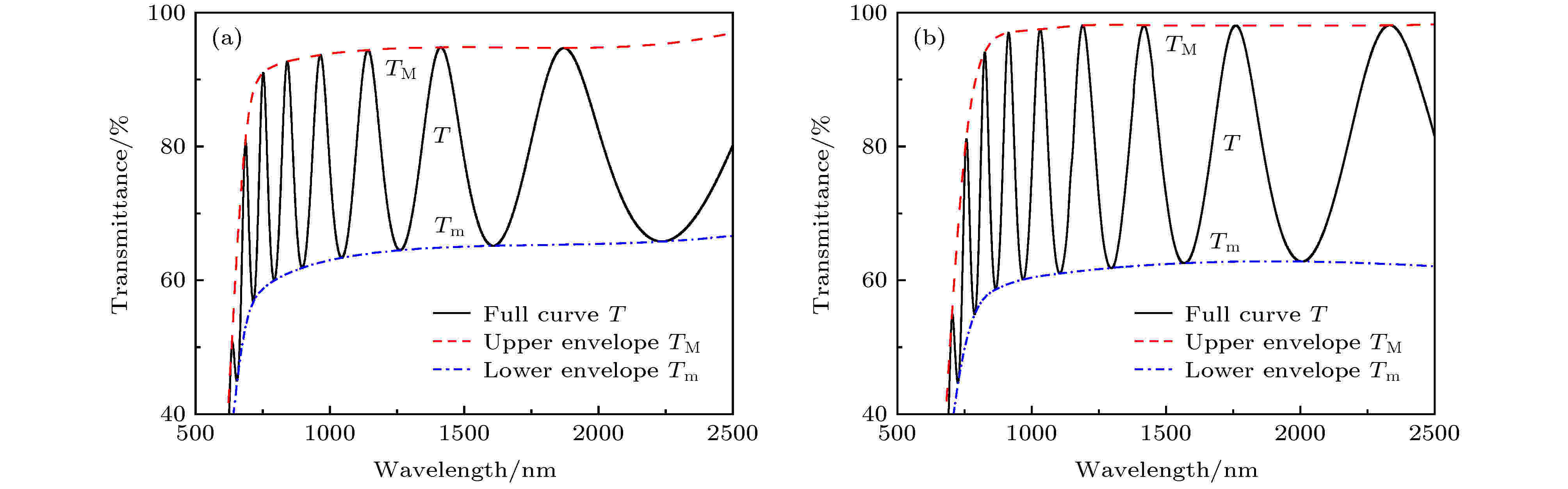
图 6 利用改进的Swanepoel方法获得的具有上下切线包络的透射曲线　(a) Ge₂₀Sb₁₅Se₆₅薄膜; (b) Ge₂₈Sb₁₂Se₆₀薄膜
Figure6. Transmission curve with upper and lower tangent envelopes obtained by using the improved Swanepoel method: (a) Ge₂₀Sb₁₅Se₆₅ film; (b) Ge₂₈Sb₁₂Se₆₀ film.

由区域逼近法计算得到多个波长处折射率后, 利用柯西模型拟合得到两种薄膜的折射率方程如下:

${n_{\rm G{\rm{e}}20}} = {\rm{2}}.{\rm{3234}} + \frac{{{\rm{4}}.{\rm{7593}} \times {\rm{1}}{{\rm{0}}^{\rm{4}}}}}{{{\lambda ^{\rm{2}}}}} + \frac{{{\rm{3}}.{\rm{0409}} \times {\rm{1}}{{\rm{0}}^{{\rm{10}}}}}}{{{\lambda ^4}}},$

${n_{\rm G{\rm{e}}28}} = {\rm{2}}.{\rm{4467}} + \frac{{{\rm{6}}.{\rm{3766}} \times {\rm{1}}{{\rm{0}}^{\rm{4}}}}}{{{\lambda ^{\rm{2}}}}} + \frac{{{\rm{3}}.{\rm{1509}} \times {\rm{1}}{{\rm{0}}^{{\rm{10}}}}}}{{{\lambda ^4}}}.$

利用(8)和(9)式计算两种硫系薄膜多个波长处的折射率, 数据列于表3. 由(8)和(9)式求得500—2500 nm波长的折射率和色散曲线, 如图7所示.

波长/nm	Ge20Sb15Se65薄膜					Ge28Sb12Se60薄膜
	Texp	TM	m	n		Texp	TM	m	n
600	0.2449	0.2682	8.7331	2.6902		0.0009	0.0253	13.3793	2.8670
620	0.3463	0.4036	8.0131	2.6530		0.0417	0.0726	12.7620	2.8259
640	0.4987	0.5496	7.4160	2.6208		0.1107	0.0957	12.2073	2.7902
660	0.4749	0.6845	6.9106	2.5929		0.2449	0.2519	11.7057	2.7592
680	0.7724	0.7891	6.4760	2.5685		0.2914	0.3957	11.2495	2.7320
700	0.6566	0.8552	6.0972	2.5472		0.5222	0.5266	11.0259	2.7081
750	0.9088	0.9096	5.7634	2.5041		0.7469	0.7853	10.1068	2.6597
800	0.6160	0.9219	5.4665	2.4720		0.6155	0.9123	9.3455	2.6233
900	0.6199	0.9321	4.9602	2.4285		0.8667	0.9681	8.1494	2.5735
1000	0.7666	0.9388	4.5433	2.4014		0.7547	0.9735	7.2448	2.5420
1100	0.8085	0.9429	4.1932	2.3835		0.6124	0.9773	6.5316	2.5210
1200	0.7580	0.9455	3.8945	2.3711		0.9678	0.9805	5.9523	2.5062
1300	0.6850	0.9472	3.6364	2.3622		0.6186	0.9813	5.4709	2.4955
1400	0.9418	0.9480	3.4109	2.3556		0.9556	0.9806	5.0638	2.4875
1500	0.7814	0.9482	3.2121	2.3506		0.7282	0.9801	4.7145	2.4813
1600	0.6521	0.9479	3.0356	2.3466		0.6430	0.9800	4.4112	2.4765
1700	0.7244	0.9474	2.8776	2.3435		0.8853	0.9800	4.1452	2.4726
1800	0.8914	0.9470	3.1213	2.3410		0.9383	0.9801	3.9099	2.4694
1900	0.9384	0.9470	2.9544	2.3389		0.7164	0.9801	3.7002	2.4668
2000	0.8249	0.9476	2.8046	2.3372		0.6282	0.9800	3.5121	2.4647
2100	0.7121	0.9491	2.6694	2.3358		0.6868	0.9800	3.2838	2.4628
2200	0.6614	0.9518	2.5468	2.3345		0.8411	0.9801	3.1325	2.4613
2300	0.6679	0.9559	2.4349	2.3335		0.9705	0.9804	2.9947	2.4599
2400	0.7188	0.9617	2.3326	2.3326		0.9441	0.9809	2.8686	2.4588

表3多点柯西法获得的两种薄膜多个波长处的折射率
Table3.Refractive index at multiple wavelengths of two thin films obtained by MCM.

图 7 Ge-Sb-Se薄膜的折射率和色散　(a)折射率与波长的关系; (b) 色散与波长的关系
Figure7. Refractive index and dispersion of Ge-Sb-Se films: (a) Refractive index vs. wavelength; (b) dispersion vs. wavelength.

薄膜折射率主要取决内部离子的极化率和介质密度. Ge离子的极化率高于Se离子的极化率, Ge原子逐渐代替Se原子将导致离子极化程度增加; 而且在Sb含量相对固定时, 随着Ge含量增加, 薄膜密度先减小后增加, 最小值出现在完全化学计量配比的组分Ge_20.83Sb₁₅Se_64.17处^[33]. 综合因素导致了Ge₂₈Sb₁₂Se₆₀薄膜的折射率大于Ge₂₀Sb₁₅Se₆₅薄膜.
在该光谱范围内, 两种薄膜的折射率随着波长的增加而减小, 色散参数D在该光谱范围内小于0, 所以光在两种薄膜内的传输速度是长波比短波传输得更快, 且在同波长下光在Ge₂₀Sb₁₅Se₆₅薄膜内传输的速度快于Ge₂₈Sb₁₂Se₆₀薄膜.
2 -->

4.3.吸收系数及光学带隙分析

将表3中的n及T_M数据代入(4)式可得x为

$x = \frac{{\dfrac{{8{n^2}s}}{{{T_{\rm{M}}}}} + ({n^2} - 1)({n^2} - {s^2}) + {{\left\{ {{{\left[ {\dfrac{{8{n^2}s}}{{{T_{\rm{M}}}}} + ({n^2} - 1)({n^2} - {s^2})} \right]}^2} - {{({n^2} - 1)}^3}({n^2} - {s^4})} \right\}}^{1/2}}}}{{{{(n - 1)}^3}(n - {s^2})}}, $

然后将x和$\overline {{d_1}} $代入$x = {{\rm{e}}^{ - \alpha d}}$中可求得薄膜的吸收系数为

$\alpha = - \frac{{\ln x}}{{{d_1}}}.$

最后对得到的离散的吸收系数进行插值得到该薄膜的吸收系数关于波长的变化曲线, 如图8(a)所示. 根据该结果, 可以将透射曲线分为三个吸收区域: 强吸收区域(500—760 nm)、弱和中等吸收区域(760—1400 nm)以及透明区域(> 1400 nm). 对于间接跃迁型非晶半导体材料, 在材料的强吸收区域的吸收系数和光子能量之间的关系满足Tauc^[34]公式:
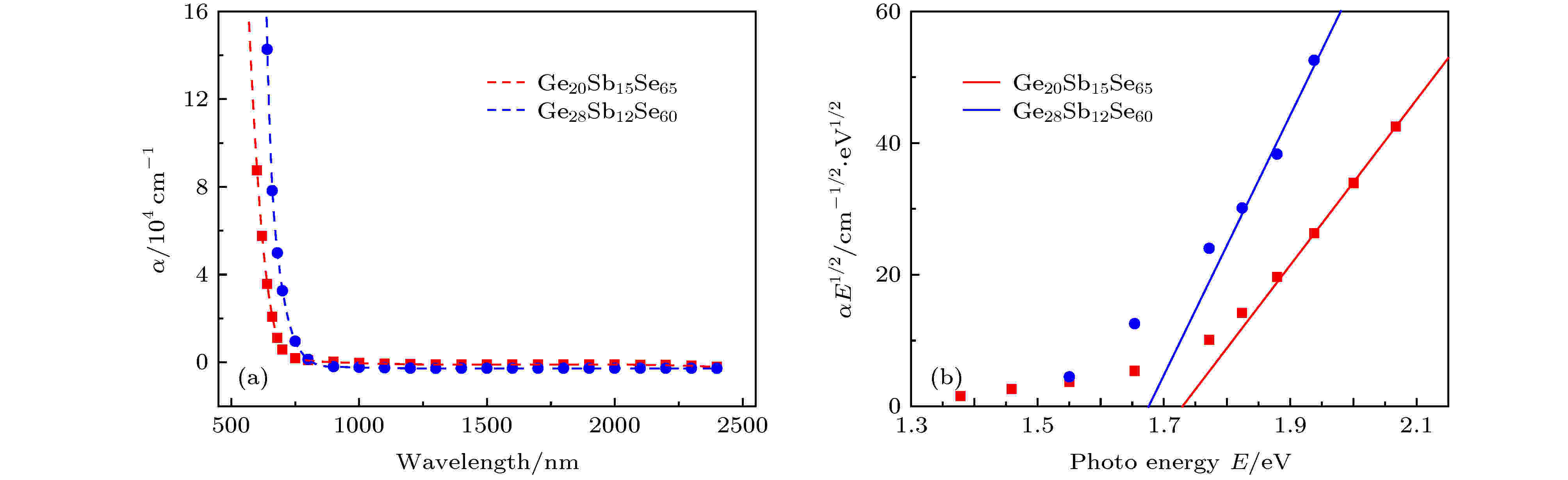图 8 Ge-Sb-Se薄膜的吸收特性　(a) 吸收系数与波长的关系; (b) 强吸收区域中吸收系数与光子能量乘积的平方根与光子能量之间的关系
Figure8. Absorption characteristics of Ge-Sb-Se films: (a) Absorption coefficient vs. wavelength; (b) square root of the product of the absorption coefficient and photon energy vs. the photon energy in the strong absorption region.

${(\alpha E)^{1/2}} = k(E - {E_{\rm{g}}}),$

其中k是与薄膜的组分组成有关的常数, E为光子能量, E_g为光学带隙, 是$E \propto {(\alpha E)^{1/2}}$直线在E轴上的截距, 通过线性拟合可得到如图8(b)所示结果, 并且得到两个拟合方程: ${(\alpha E{}_{{\rm{g}}1})^{1/2}} = 125.6 \times $$(E_{{\rm{g}}1} - 1.729) $; ${(\alpha E{}_{g2})^{1/2}} = 197.2 \times (E{}_{g2} - 1.675)$. 当${(\alpha E)^{1/2}} = 0$时, E_g1 = 1.729 eV, 相应的波长为717.2 nm; E_g2 = 1.675 eV, 相应的波长为740.3 nm.
2 -->

4.4.拉曼结构分析

拉曼光谱采用英国雷尼绍公司的inVia显微拉曼光谱仪(Raman)测得, 激光波长选定为785 nm, 测试功率为0.1 mW. 测试结果表明, 拉曼光谱中有150—180 cm^–1, 180—240 cm^–1和240—300 cm^–1三个主要特征带, 如图9所示. 1) 180—240 cm^–1特征带中的203 cm^–1和其肩峰215 cm^–1分别对应共顶点和共边GeSe_4/2四面体中的Ge—Se键振动峰^[35]. 而且195 cm^–1对应SbSe_3/2三角锥结构中的Sb—Se键振动峰^[36], 由于其振动峰与Ge—Se振动峰重叠在一起, Sb—Se振动峰不能清楚地在拉曼光谱中显示出来. 2) 240— 300 cm^–1振动带归因于Se链或者Se环结构中的Se—Se键振动^[37]. 3) 150—180 cm^–1振动带归因于Ge—Ge (约170 cm^–1)和Sb—Sb (约160 cm^–1)同极键^[38]. 表4显示了拉曼峰所对应的振动模式.

拉曼峰位/cm–1	振动模式
160	Se2Sb-SbSe2结构中的Sb—Sb同极键的振动
170	Ge2Se6/2结构中的Ge—Ge同极键的伸缩振动
197	SbSe3/2三角锥结构中的Sb—Se键的E1模式振动
203	共顶角GeSe4/2四面体中的Ge—Se键的V1模式振动
215	共边GeSe4/2四面体中的Ge—Se键振动
235	Sen环结构中的Se—Se键振动
256	Sen链结构中的Se—Se键振动
270	Ge-GemSe4-m结构中的Ge—Ge同极键的振动
303	GeSe4四面体的F2型不对称振动

表4Ge-Sb-Se薄膜拉曼光谱中对应的振动模式
Table4.Vibration modes in the Raman spectrum of Ge-Sb-Se system.

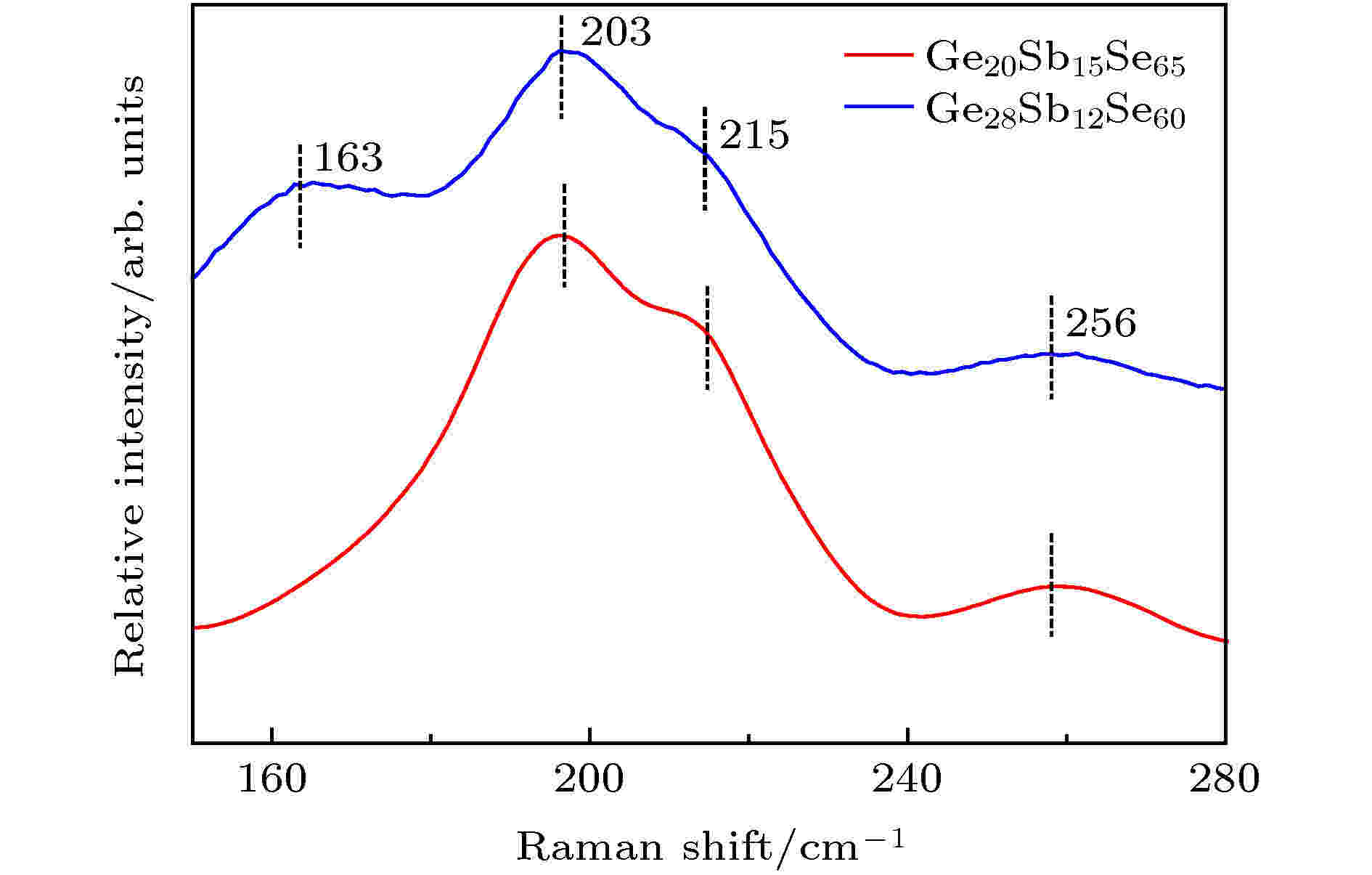图 9 Ge-Sb-Se薄膜的拉曼光谱
Figure9. Raman spectrum of Ge-Sb-Se film.

随着Ge含量的增加, 180—240 cm^–1振动带强度增大, 是由于振动带中GeSe_4/2四面体结构中的Ge—Se键数量的增加. 而240—300 cm^–1振动带的强度随着Ge含量的增加而减小, 这是由于更多的Sb(Ge)与Se成键, 逐渐消耗Se原子, 使得Se—Se结构单元的浓度降低. 另一方面150—180 cm^–1振动带十分明显, 这是由于Se已经完全被Ge和Sb消耗完, 得不到Se原子的Ge和Sb原子将分别形成Ge—Ge键和Sb—Sb键, 因此150—180 cm^–1振动带强度增大. 考虑同极键(Ge—Ge, Sb—Sb, Se—Se)为Ge—Sb—Se薄膜系统中的错键, 错键随Ge含量的增加先减小后增加, 其最小值出现在完全化学计量配比的组分Ge_20.83Sb₁₅Se_64.17中^[33]. Ge₂₈Sb₁₂Se₆₀薄膜中的错键(Ge—Ge, Sb—Sb)比Ge₂₀Sb₁₅Se₆₅薄膜中的多, 带尾更宽, 光学带隙更小.

本文利用多点柯西法系统研究了Ge₂₀Sb₁₅Se₆₅薄膜和Ge₂₈Sb₁₂Se₆₀薄膜的光学特性和微观结构. 理论上利用Cauchy, 二阶归一化Sellmeier, 三阶归一化Sellmeier, 二阶非标准形式Sellmeier, Conrady和Herzberger六种模型分析比较了薄膜折射率和色散计算精度, 结果表明本文提出的先利用区域逼近法计算得到多个波长处的折射率, 再利用柯西模型计算硫系薄膜全波段折射率和色散的多点柯西法更为精确. 实验上获得了这两种薄膜在500—2500 nm波段的透射光谱, 利用模型$T = a\cos \left( {\dfrac{n}{\lambda }} \right) + b$分段滤波后, 再利用上述方法精确得到两种薄膜的光学参数. 结果表明Ge₂₈Sb₁₂Se₆₀薄膜的折射率大于Ge₂₀Sb₁₅Se₆₅薄膜, 这是前者的极化率和密度较大导致的. 两种薄膜的折射率都随着波长的增加而减小, 所以光在两种薄膜内的传输速度是长波比短波传输得更快. 另外, Ge₂₈Sb₁₂Se₆₀薄膜的光学带隙为1.675 eV, 小于Ge₂₀Sb₁₅Se₆₅薄膜的1.729 eV, 两者相应的波长分别为740.3和717.2 nm. 最后拉曼光谱分析表明Ge₂₈Sb₁₂Se₆₀薄膜中的错键(Ge—Ge, Sb—Sb)比Ge₂₀Sb₁₅Se₆₅薄膜中的多, 带尾更宽, 光学带隙更小.