摘要:提出了一种基于电光调制光学频率梳的光谱干涉测距方法. 理论分析了电光调制光学频率梳的数学模型和光谱扩展原理, 并分析得出了光谱干涉测距方法的非模糊范围和分辨力的影响因素. 在实验中, 使用三只级联的电光相位调制器调制单频连续波激光生成了40多阶高功率梳齿状边带, 并通过单模光纤和高非线性光纤对电光调制器输出的激光进行光谱扩展, 得到重复频率为10 GHz, 光谱宽度达30 nm的光学频率梳. 将该光频梳作为光谱干涉测距装置的光源, 可以实现无“死区”的绝对距离测量. 另外, 使用等频率间隔重采样和二次方程脉冲峰值拟合算法对测量结果进行数据处理, 可以修正系统误差, 提升测距精度. 实验结果表明, 在1 m的测量范围内, 使用该装置可以在任意位置达到 ± 15 μm以内的绝对测距精度.
关键词: 光学频率梳/
电光调制/
光谱干涉/
绝对测距

English Abstract

全文HTML

--> --> -->

近年来, 高端装备制造的发展, 比如卫星编队飞行、大飞机、大型科研装置的制造与加工安装, 对高精度的大尺寸测量提出了需求. 另一方面, 在超快激光和光学频率梳(optical frequency comb, 以下简称“光频梳”)发明之后, 科学家们也一直在探究他们的应用. 自从2000年Minoshima和Matsumoto发明了一种基于超快激光纵模自拍频的相位法测距技术之后^[1], 20年来, 科学家对基于超快激光和光频梳的绝对测距技术进行了广泛的研究, 陆续提出了几种测距方法. 具体可以分为基于时域脉冲的测距方法和基于频域特征的测距方法两大类. 其中扫描位移台干涉、调节腔长干涉和双光梳异步光学采样是三种主要的基于时域脉冲的测距手段^[2-7], 他们依靠脉冲在空间上的相遇会产生互相关干涉条纹, 通过解算互相关条纹就可以判断脉冲的位置, 进而解算出待测距离; 而频域法又可以分为多波长干涉法和光谱干涉法两类, 多波长干涉法是通过光频梳不同纵模之间的波长差组建合成波长, 检测合成波长的相位变化来求解被测距离, 最典型的是纵模自拍频合成波长法^[1]和多外差合成波长法^[8-10]. 光谱干涉法又被称为色散干涉法^[11-16], 光频梳中不同的纵模代表不同波长的激光信号, 这些信号在经过相同的测量臂后一起与参考臂的信号相干涉, 不同波长的光干涉时的相位不同, 导致干涉后的条纹亮度就不同, 将干涉后的光频梳放在光谱仪上观察, 会看到光频梳光谱中出现一个类似正弦调制的包络, 这个包络的频率正与被测距离相关, 解算出包络的频率, 就可以推算出待测距离. 光谱干涉测距方法相对于扫描位移台干涉、调节腔长干涉这两种时域干涉方法, 结构中不需要可动部件, 可靠性好; 相对于双光梳异步光学采样法和多外差方法, 系统仅需一台光频梳, 而且测量装置简单, 测量结果直观、易解算. 所以近些年来光谱干涉测距方法得到很多科学家们的重视. 2006年, Joo与Kim^[12]提出通过光谱频域干涉实现绝对测距的方案, 并在0.89 m测量范围内取得了约1.46 mm非模糊范围和约7 nm的分辨力. 2015年, van den Berg等^[13]使用虚拟成像相控阵高分辨力光谱仪解析出1 GHz钛宝石激光器的每个梳齿, 并在实验中结合了光谱干涉测量法、白光干涉测量法和多波长干涉测量法, 在50 m的测量范围内达到了10^–8量级的相对测距不确定度. 随后, 中国科学院周维虎团队^[14,15]基于飞秒激光光谱干涉技术研制出了飞秒激光跟踪仪, 实现了微米级的三维坐标测量. 2017年Lesundak等^[16]使用法布里-珀罗腔将一个1 GHz重复频率的光频梳滤波为56 GHz重复频率的光频梳, 在减少了测距非模糊范围的同时也消除了测距“死区”, 并于实验中得到了50 m范围内与参考干涉仪相比0.5 μm的测距一致性. 这些研究验证了光谱干涉技术的测距能力, 并证明了该方法可以投入工业应用的潜力.
现在的光学频率梳一般是通过将超快激光器锁定住重复频率和偏移频率来产生的. 而超快激光器又主要有固体激光器、可饱和吸收体锁模激光器和光纤锁模激光器等几种类型, 他们都是根据锁模原理直接生成脉宽极窄的激光脉冲, 对应的光谱宽度也能达到数十乃至数百纳米以上的半高全宽. 这些锁模机制的超快激光器经过长时间的研究其稳定性也有很大提高. 不过基于锁模激光器的光频梳的稳定性还有待发展, 其目前所采用的一些主流的频率锁定机构在应对一些环境变化或者振动等条件下有可能会失去其锁频状态, 剧烈的变化还有可能导致模式“失锁”, 在工业现场的大规模应用还存在挑战. 然而, 基于电光调制的光学频率梳生成技术在近些年得到比较快的发展, 电光调制光频梳因生成机理不同, 不存在锁模激光器所有的“失锁”状态, 且其重复频率易于锁定和溯源, 有望解决光频梳运行稳定性的问题. 1993年, Kourogi等^[17]开始尝试使用铌酸锂(LiNbO₃)相位调制器在一个输出波长为1.5 μm的半导体激光器周围调制出多根梳齿, 得到了类似光频梳的基本频域特征, 随后, 基于强度调制器和基于相位调制器的光频梳生成技术被陆续提出并得到广泛的研究^[18-22]. 科学家们还发现, 通过将调制器级联可以生成更多的梳齿和更宽的光谱, 并且光谱平坦度可以通过不同形式调制器组合的方式得到优化^[23], 这使得电光调制光频梳在精密光谱学等领域得到很高的重视. 2013年, Wu等^[24]发现可以通过单模光纤将电光调制光频梳的时域脉冲压缩到ps量级, 压缩后的光频梳脉冲经过高非线性光纤可以完成超连续谱的生成. 2014年, Yang等^[25]开始将电光调制光梳应用到测距中, 使用双电光调制光频梳通过合成波长测距法在10 m范围内得到15 μm的测距精度. 2018年, 本课题组提出三电光调制光频梳绝对测距方案, 使用粗精结合的外差合成波长测距方案将测距系统的非模糊范围提升到百米以上, 同时绝对测距精度保持在1 μm以内^[10]. 电光调制光频梳生成简单、易维护, 不存在传统锁模激光器的“失锁”情况, 可长时间运行. 但如果使用上述基于双光频梳或三光频梳的测距方法就会失去成本优势, 且数据处理过程比较复杂. 如果能将电光调制光频梳与光谱干涉测距方法结合起来, 将会极大提高整套系统的运行稳定性, 并有效降低成本, 是非常值得研究的课题.
本文提出了一种基于电光调制光学频率梳的光谱干涉测距方法, 使用三组级联的相位调制器对一个单频连续波激光器进行光谱调制得到光学频率梳, 并通过单模光纤和高非线性光纤对生成的光频梳进行光谱展宽, 得到重复频率为10 GHz, 光谱全宽约30 nm的电光调制光学频率梳. 将该光频梳作为光源引入到光谱干涉测距系统中, 在光谱仪上采集干涉信号, 并使用等频率间隔重采样和脉冲二次方程拟合等算法对测距结果进行处理, 在绝对测距验证实验中得到了优于 ± 15 μm的测距不确定度.

一束单频连续波激光通过电光晶体, 如果在晶体两端加载电学信号, 根据克尔效应, 输出的激光就会被调制上相关的微波信号, 在光谱上的表现就是激光的中心频率周围会出现等频率间隔分布的边带信号, 而这个频率间隔就等于所加载的电学信号的频率. 巧合的是, 光学频率梳的光谱模型也是一系列等频率间隔分布的纵模梳齿, 所以可以使用电光调制技术来生成光学频率梳. 电光调制光频梳的生成原理如图1所示.
图 1 电光调制光频梳生成示意图 (PS: 移相器)
Figure1. Schematic setup of the electro-optic (EO) comb generation (PS, phase shifter).

单频连续波激光可以被表示为

${E_0}(t) = {E_{\rm{o}}}{{\rm{e}}^{{\rm{j}}{\omega _0}t}}, $

其中${E_0}$表示光在时域中的强度, ${\omega _0}$表示光的频率. 当其经过第一个相位调制器后, 其激光电场变为

$E(t) = {E_0}(t){{\rm{e}}^{{\rm{j}}[{\chi _1}\sin ({\omega _{\rm{m}}}t + \Delta {\phi _1})]}}, $

其中${\chi _1}$为相位调制器的调制系数, 和信号源供给电压与调制器的半波电压之比相关; ${\omega _{\rm{m}}}$为调制信号的角频率; $\Delta {\phi _1}$是信号源的相位, 这个相位可以通过图中所示的移相器改变. 将(2)式根据贝塞尔级数进行展开, 得

$E(t) = {E_0}(t)\sum\limits_{a = - \infty }^{ + \infty } {{{\rm{J}}_a}({\chi _1})} {{\rm{e}}^{{\rm{j}}a({\omega _{\rm{m}}}t + \Delta {\phi _1})}}, $

其中a表示贝塞尔级数的阶数, 同时也是电光调制光频梳梳齿的阶数. 将(1)式代入, 并进一步整理为傅里叶级数的形式, 得

$E(t) = \sum\limits_{a = - \infty }^{ + \infty } {[{E_0}{{\rm{J}}_a}({\chi _1})} {{\rm{e}}^{{\rm{j}}a\Delta {\phi _1}}}]{{\rm{e}}^{{\rm{j}}({\omega _0} + a{\omega _{\rm{m}}})t}}, $

再对其进行傅里叶变换, 每阶梳齿的功率就可以表示为

$F[\omega - ({\omega _0} + a{\omega _{\rm{m}}})] = \sum\limits_{a = - \infty }^{ + \infty } {[{E_0}{{\rm{J}}_a}({\chi _1})} {{\rm{e}}^{{\rm{j}}a\Delta {\phi _1}}}], $

可以看出, 每阶梳齿的功率与调制系数和调制信号的相位有关, 如果调整输入信号的电压或者调节移相器, 可以改变各阶信号的功率. 但是根据贝塞尔函数的性质, 阶数越高, 梳齿的强度值越弱, 所以经过单个相位调制器生成的梳齿数量是有限的. 如果要增加生成的梳齿数量, 可以通过级联多个电光调制器. 种子光源经过3个级联的相位调制器后, 输出的光信号在频域上可以表示为

$\begin{split} & F\{ \omega - [{\omega _0} + (a + b + c){\omega _{\rm{m}}}]\} \\ =\;& \sum\limits_{c = - \infty }^{ + \infty } {} \sum\limits_{b = - \infty }^{ + \infty } {} \sum\limits_{a = - \infty }^{ + \infty } {\big[{E_0}{{\rm{J}}_a}({\chi _1}){{\rm{J}}_b}({\chi _2}){{\rm{J}}_c}({\chi _3})}\\ & \times {{\rm{e}}^{{\rm{j}}(a \cdot \Delta {\phi _1} + b \cdot \Delta {\phi _2} + c \cdot \Delta {\phi _3})}}\big], \end{split}$

其中b和c代表光频梳梳齿的阶数, ${\chi _2}$和${\chi _3}$分别表示第二和第三个电光调制器的调制系数, $\Delta {\phi _2}$和$\Delta {\phi _3}$分别表示输入到第二和第三个电光调制器的微波信号的相位. 可以看到, 级联多个电光调制器后, 光谱形状的调节自由度更高, 可以通过分别调配输入到每个电光调制器上的微波信号的功率和相位, 来使高阶的梳齿也具有相对较高的功率, 进而使得光谱顶部更加平坦.
经过多个相位调制器的级联, 具有多根梳齿的光频梳生成了, 但经电光调制器调制出的边带(梳齿)数量毕竟有限, 致使此时光频梳光谱宽度比较窄, 不利于光谱干涉测距方法的应用, 所以需要对输出的电光调制光频梳光谱进行扩展. 光谱扩展的第一步是进行色散补偿, 实验证明, 电光调制器与单模光纤的色散系数是相反的^[24], 所以可以将电光调制光频梳的输出信号接入单模光纤进行色散补偿. 色散补偿后每根梳齿的线宽都将得到收缩, 进而这些梳齿的峰值功率会升高, 在光纤中传播时会由于四波混频等非线性效应产生新的频率成分. 但单模光纤的非线性效应比较微弱, 产生的新频率成分数量较少且功率较低. 为了有效进行光谱扩展, 就需要使用高非线性光纤, 并且在高非线性光纤之前最好先使用光功率放大器来进一步放大峰值功率. 通过使用上述非线性扩谱技术, 光频梳光谱宽度一般可被扩展数倍以上. 另外还值得注意的是, 电光调制光频梳光源内的大部分时候光都不是脉冲形式. 在光源的前半段, 光的时域形式只是有着多个频率成分的连续波激光, 只在扩谱模块的光纤内最后一部分才可能产生脉冲.

2

-->

3.1.光谱干涉测距原理

据前文所述, 光谱干涉现象产生的物理原因是光谱内的各阶频率成分的光进入干涉仪发生干涉, 不同频率的光在相同距离下相位变化不一样, 干涉后的强度也不一样, 组合起来就有了光谱干涉条纹. 光谱干涉测距装置使用迈克耳孙干涉仪, 光频梳$E(t)$被分为参考臂${E_{\rm{ref}}}(t) = \alpha E(t)$和测量臂${E_{\rm{meas}}}(t) = \beta E(t - \tau )$两部分, 其中$\alpha $和$\beta $分别表示参考臂和测量臂的分光比, $\tau $表示光在测量臂往返运行的时间. 在这个时间内, 光的相位变化为

$\varphi = 2{\text{π}}\nu \cdot \tau = \omega \cdot \tau, $

其中$\nu $和$\omega $分别代表光的频率和角频率. 通过傅里叶变换, 在频域内, 参考光和测量光可以分别表示为

${E_{{\rm{ref}}}}(\omega ) = \alpha E(\omega ), $

及

${E_{\rm{meas}}}(\omega ) = \beta E(\omega )\exp( - {\rm{i}}\omega \tau ), $

将参考臂和测量臂合束后送入光谱仪内, 两路光会在光谱仪的传感器上发生干涉, 干涉信号可以表示为

$\begin{split} & I(\omega ) = {({E_{\rm{ref}}}(\omega ) + {E_{\rm{meas}}}(\omega ))^2} \\=\; & {E^2}(\omega )[{\alpha ^2} + {\beta ^2} + 2\alpha \beta \cos (\tau \omega )], \end{split}$

从(10)式可以看到, 干涉后的信号包含一个强度为$({\alpha ^2} + {\beta ^2}){E^2}(\omega )$的直流分量和信号表达式为$2\alpha \beta {E^2}(\omega )\cos (\tau \omega )$的交流分量. 直流分量的强度是固定的, 且不带有距离信息, 可以不去解算. 而交流信号被信号光的运行时间$\tau $调制了. 对(10)式做傅里叶变换, 可将光谱干涉信号转换到伪时域中, 得

$\begin{split}& I(t) = {\rm{FT}}[I(\omega )] \\={}& {I_0}(t) \otimes \Big[\frac{1}{2}\delta ({{t}} - \tau ) + \delta ({{t}}) + \frac{1}{2}\delta ({{t + }}\tau )\Big],\end{split}$

在伪时域中, $ \pm \tau $的位置会各出现一个脉冲, 解算出脉冲峰值点对应的横坐标, 就可求出光在测量臂的传输时间$\tau $.
在传统的激光测距系统中, 解算出激光传播时间后将其乘以传输介质里的光速就可以直接得出待测距离. 但光频梳的重复频率一般较高, 所以测距时还需考虑“非模糊范围”的问题. 因为光频梳在时域上是等间隔的脉冲周期, 相邻脉冲之间的空间距离为

${L_{\rm{pp}}} = c/({n_{\rm{g}}} \cdot {f_{\rm{rep}}}), $

其中c表示真空中的光速, ${n_{\rm{g}}}$为光传播介质(此时指的是空气)的群折射率, ${f_{\rm{rep}}}$为光频梳的重复频率. 如果脉冲在空间中传播的距离大于${L_{\rm{pp}}}$, 就意味着这个脉冲进入到了下一个周期中, 这会导致测距结果出现歧义. 另一方面, 在频域的包络信号解调时, 因为光频梳的光谱是由一根根离散分布间隔为${f_{\rm{rep}}}$的梳齿组成的, 所以无论光谱仪对光谱的采样率有多高, 光频梳对光谱包络信号的采样率只有${f_{\rm{rep}}}$. 根据奈奎斯特采样定律, 超出${f_{\rm{rep}}}/2$的调制频率就无法解调出来, 所以解调出来的测量光传输时间

$\tau \leqslant {n_{\rm{g}}}{L_{\rm{pp}}}/c, $

即最多解调出光在${L_{\rm{pp}}}/2$内往返的时间, 如果待测距离超过${L_{\rm{pp}}}/2$, 就需要预先知道被测距离是在几个${L_{\rm{pp}}}/2$内, 待测距离可以表示为

$L = (k{\rm{c}})/(2{n_{\rm{g}}} \cdot {f_{\rm{rep}}}) \pm (c\tau )/(2{n_{\rm{g}}}), $

其中k为自然数, 代表已知的周期数.
2 -->

3.2.光谱干涉测距非模糊范围及精度理论分析

在上一节提到, 光谱干涉测距的非模糊范围与光频梳相邻脉冲的间距(${L_{\rm{pp}}}$)有关, 同时也与光谱仪的采样率密切相关. 如上一节所述, 光频梳的梳齿对光谱干涉调制包络的采样率就等于光频梳的重复频率, 即${f_{\rm{rep}}}$. 依据傅里叶变换性质, 将包络信息转换成伪时域后时间范围为$[ - 1/2{f_{{\rm{rep}}}}, \;1/2{f_{{\rm{rep}}}}]$, 最大可测的无歧义距离为

${L_{\max }} = (c/2{n_{\rm{g}}}) \cdot (1/2{f_{\rm{rep}}})={L_{\rm{pp}}}/4.$

从另一个角度分析, 解调出的距离是测量脉冲和离他最近的参考脉冲的光程差, 所以在测量脉冲位于相邻参考脉冲的正中间的时, 可以得到最大可测量值, 即${L_{\rm{pp}}}/4$. 当脉冲远离这个位置后, 实测的距离值开始下降, 显示如图2中纵坐标所示.
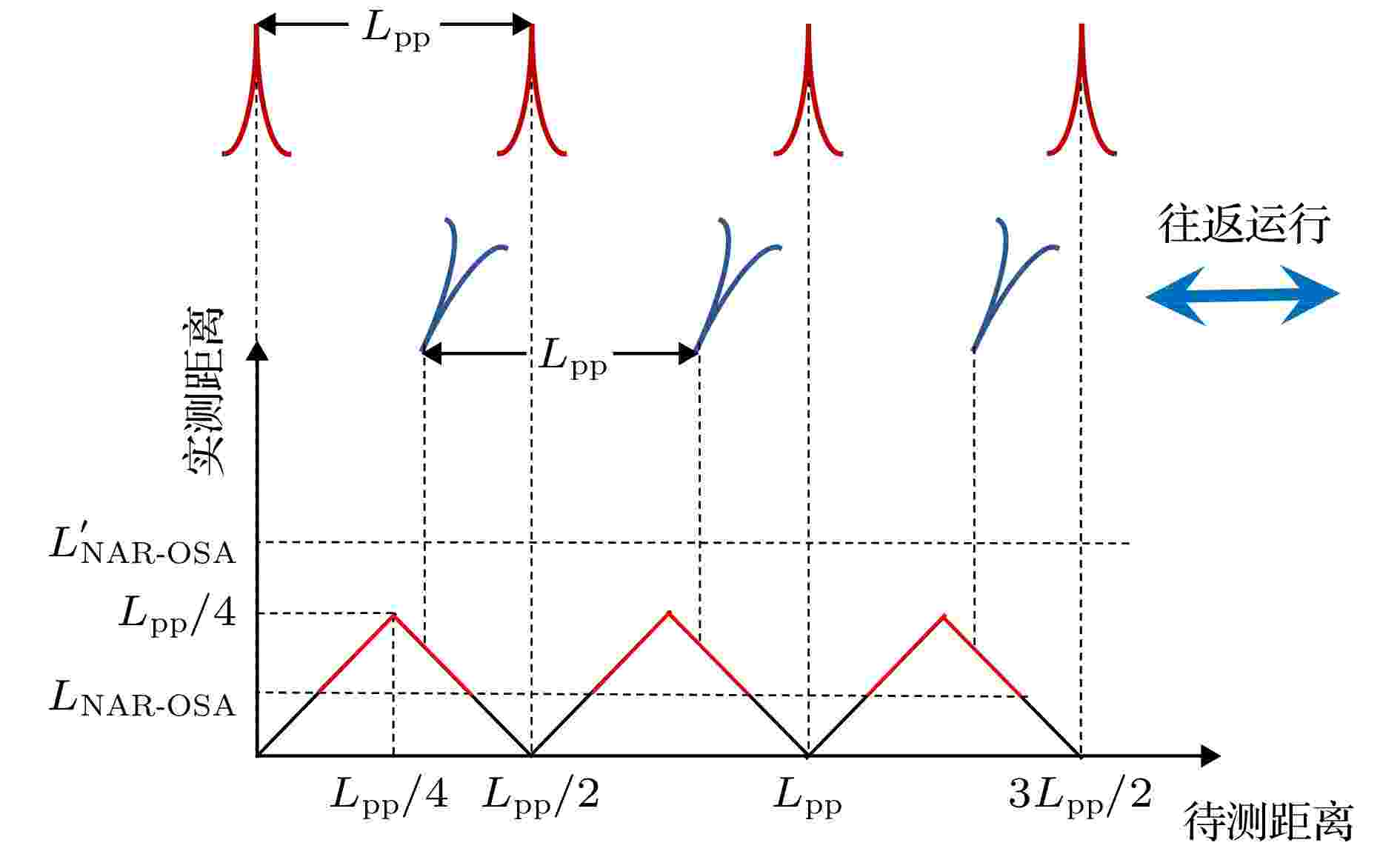图 2 光谱干涉测距非模糊范围理论示意图
Figure2. Schematic diagram of the non-ambiguous range of spectral interference ranging.

上述分析是建立在光谱仪分辨力足够高, 以至于能采集到光频梳的每根梳齿的基础上. 事实上, 常规的商用光谱仪波长分辨力为十皮米量级, 而常见的超快激光器主要工作在中近红外波段, 他们的重频一般在数十兆赫兹至数百兆赫兹量级, 在这个分辨力下很难采到光频梳的梳齿. 在此情况下, 限制非模糊范围的因素就是光谱仪的频率分辨力(也是光谱仪的最高频率采样率). 假设光谱仪可分辨的最小频率间隔为${f_{\rm{s}}}$, 且${f_{\rm{s}}} > {f_{\rm{rep}}}$, 此时由光谱仪分辨力决定的最大可测的无歧义距离为

${L_{{\rm{NAR}}\text-{\rm{OSA}}}} = (c/2{n_{\rm{g}}}) \cdot (1/2{f_{\rm{s}}})=c/4({n_{\rm{g}}} \cdot {f_{\rm{s}}}), $

此时${L_\text{NAR-OSA}} < {L_{\rm{pp}}}/4$, 非模糊范围就是$L_\text{NAR-OSA}$, 那么图2中所示红色部分的距离信息就测不出来了, 也就是说在这种情况下存在测距“死区”. 但如果光谱仪频率分辨力足够高, ${f_{\rm{s}} } \leqslant {f_{\rm{rep}}}$, 那么由光谱仪频率分辨力决定的理论测距结果不低于${L_{\rm{pp}}}/4$, 如图中$L_{{\rm{NAR}}\text-{\rm{OSA}}}^{\prime}$, 那么非模糊范围仍然是${L_{\rm{pp}}}/4$, 此时理论上就不存在测距“死区”. 总结来说, 当${f_{\rm{s}}} > {f_{\rm{rep}}}$时, 非模糊范围为${L_{{\rm{NAR}}\text-{\rm{OSA}}}}$, 存在测距“死区”; 而当${f_{\rm{s}} } \leqslant {f_{\rm{rep}}}$时, 非模糊范围为${L_{\rm{pp}}}/4$, 不存在测距“死区”.
根据傅里叶变换的性质, 变换后横坐标的分辨力(即时间分辨力)等于采样率与采样点数的商, 可以表述为

${R_t} = \dfrac{t_{\rm{s}}}{N_{\rm{s}}}, $

其中${t_{\rm{s}}}$表示采样率, ${N_{\rm{s}}}$表示采样点数. 在光谱宽度一定的情况下, 采样率和采样点数的商也是定值. 假设光频梳的中心波长为1550 nm, 光谱仪的波长采样率为x nm, 暂不考虑介质折射率, 那么在光频梳中心频率周围光谱仪的频率采样率为

$\begin{split}{f_{\rm{s}}} \; &= \frac{c}{{1550~{\rm{nm}}}} - \frac{c}{{(1550 + x)~{\rm{nm}}}} \\&\approx \bigg[\frac{{3 \times {{10}^8}}}{{1550 \times {{10}^{ - 9}}}} - \frac{{3 \times {{10}^8}}}{{(1550 + x) \times {{10}^{ - 9}}}}\bigg]\;{\rm{Hz}}\\& = 3 \times {10^{17}} \times \Big(\frac{1}{{1550}} - \frac{1}{{1550 + x}}\Big)\;{\rm{Hz}},\end{split}$

又因为光谱仪的采样率要远小于光频梳的中心频率, 则有

${f_{\rm{s}}} \approx 3 \times {10^{17}} \times \frac{x}{{{{1550}^2}}}\;{\rm{ Hz}} \approx (1.25 \cdot x) \times {10^{11}}\;{\rm{ Hz}}, $

此时, 光谱仪的时间采样率为

${t_{\rm{s}}} = 1/{f_{\rm{s}}} \approx \frac{8}{x} \times {10^{ - 12}}\;{\rm{ s}}, $

再假设光频梳的光谱宽度为M nm, 那么采样点数

${N_{\rm{s}}} = M/x, $

则时间分辨力为

${R_t} = {t_{\rm{s}}}/{N_{\rm{s}}} = \frac{8}{x} \cdot \frac{x}{M} \times {10^{ - 12}}\;{\rm{ s = }}\frac{8}{M} \times {10^{ - 12}}\;{\rm{ s}}, $

那么距离分辨力为

${R_L} = c \cdot {R_t} \approx \frac{{2.4}}{M} \times {10^{ - 3}}\;{\rm{ m}}.$

从(23)式可以看出, 在当前的光谱干涉距离解算方法中, 光频梳的光谱宽度是测距分辨力的惟一影响因素. 不过, 分辨力实际上影响的是傅里叶变换后伪时域里采样点的间隔, 如果系统分辨力低, 则意味着伪时域中脉冲上采样点稀少. 如果只取脉冲最高位置附近采样点作为测量结果必然会造成明显的测距误差. 但如果先对脉冲做一个波形拟合再取拟合后的顶点, 那么测量精度就有机会得到明显改善.
除了分辨力之外, 光谱干涉的测距精度还要受光谱仪采样方式的影响, 光谱仪的采样是按照等波长间隔采样的, 而我们使用的傅里叶变换等数据处理算法是根据等频率间隔采样来计算的. 光的波长与频率并不是线性的, 所以如果直接对光谱仪采样结果做傅里叶变换分析就会引入采样误差. 为了解决这个问题, 我们课题组提出过一种对光谱仪采样结果进行等频率间隔重采样的方法^[26]. 图3表述了光谱仪采样及等频率间隔重采样的过程. 在光谱仪等波长间隔重采样的情况下, 采集到的光谱干涉条纹不是恒定周期的信号, 如图3(a)所示; 直接将图3(a)的横坐标换算成频率的话, 换算出的频率值${f_{15}}$, ${f_{14}}$, ···, ${f_1}$不是等间隔排列的, 如图3(b)所示. 需要注意的是, 波长和频率是负相关的, 所以图3(b)中的波形和图3(a)是镜像对称的; 接着将横坐标进行线性排列, 干涉条纹的波形就变成了标准的正弦形式, 如图3(c)所示; 最后对图3(c)里的正弦波形进行等频率间隔重采样, 如图3(d)所示. 此时, 对重新采集到的信号数列做傅里叶变换处理, 就可以得到不失真的测距结果.
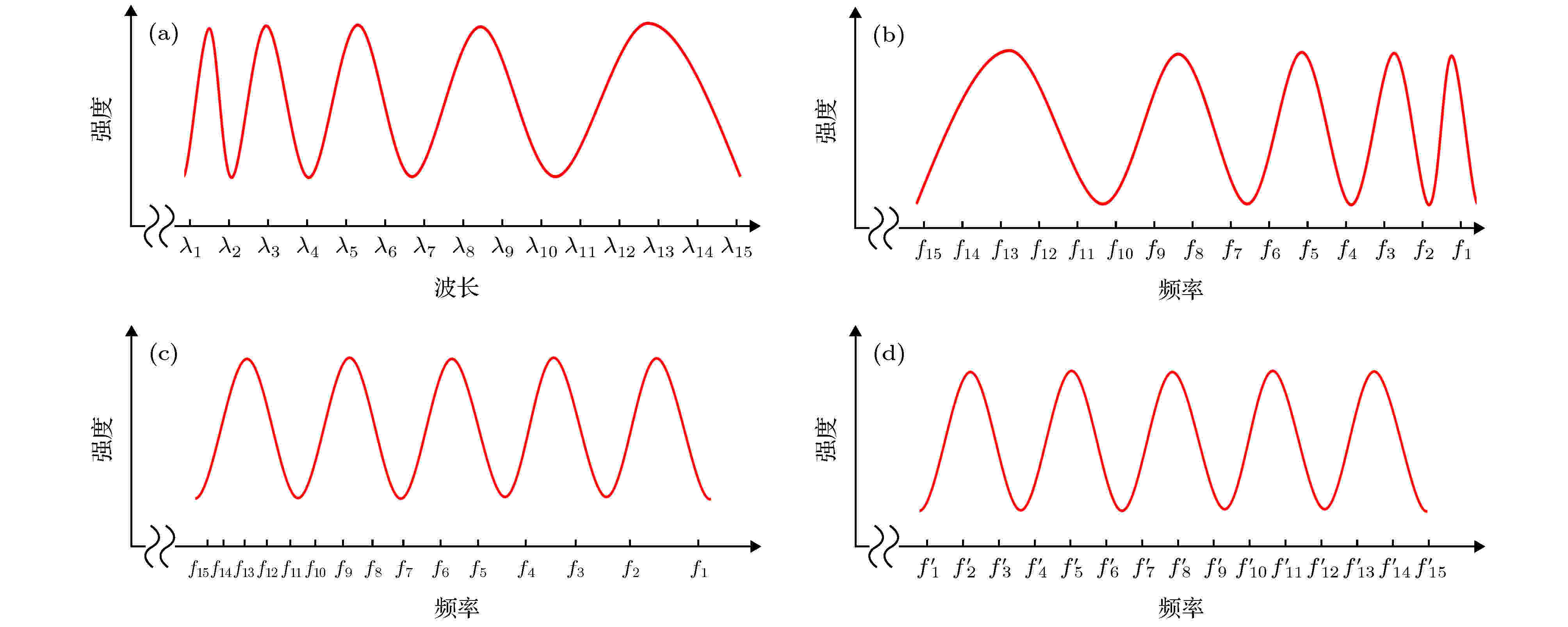图 3 等频率间隔重采样处理示意图　(a)光谱仪等波长间隔采样得到的信号; (b)对横坐标进行波长-频率变换后的信号; (c)对横坐标进行线性坐标转换后的信号; (d)对转换后的信号进行等频率间隔重采样的结果
Figure3. Schematic diagram of equal frequency interval resampling: (a) Signal obtained by spectrometer with equal wavelength interval sampling; (b) the signal after wavelength-frequency transformed; (c) the signal after linear coordinate transformation on the abscissa; (d) the signal after equal frequency interval resampling.

根据前文针对光谱干涉测距方法的非模糊范围和测距精度问题做的理论分析, 对应到现有的商用光谱仪来讨论, 常用的光谱仪其波长采样率最高在皮米或数十皮米量级, 那么在1550 nm波长附近对应频率采样率${f_{\rm{s}}}$在10⁸—10⁹ Hz量级. 如果需要光谱干涉装置工作在无“死区”状态下, 使用的光频梳的重复频率至少要高于10⁸—10⁹ Hz量级. 考虑到在工程实际中, 采样率一般要求达到被测信号频率的5倍以上, 则实际使用光频梳的重复频率就需要达到10⁹ Hz乃至10¹⁰ Hz量级, 才可进行无“死区”测距. 对应到现有的基于锁模激光器的商用光频梳来说, 光纤锁模激光器的腔体内需要一段增益光纤, 其重复频率最高只能达到10⁸ Hz量级; 而固体激光器可以使用短腔长将重复频率升至GHz量级, 但现阶段制作高重频的固态激光器价格较高, 市场上大多数商用锁模激光器的重复频率还都在10⁷—10⁸ Hz量级. 然而, 使用电光调制光频梳就没有这个问题. 受益于电子工业的发展, 电光器件的输入电信号大多可以在kHz到GHz量级任意调制, 很多商用电光调制器的最高工作频率能达到10 GHz以上, 以这些电光调制器为基础制作的光学频率梳就可以具有足够高的重复频率来实现无“死区”的光谱干涉测距.
另外, 根据前文的分析, 光谱宽度决定了光谱干涉测距的分辨力, 越宽的光谱就会有越高的分辨力. 电光调制光频梳的宽度是由级联调制器的个数、电光调制器的输入功率与非线性扩谱的结果来共同决定的. 虽然决定因素较多, 但总体来说, 电光调制光频梳的光谱宽度与光频梳制作的成本是正相关的. 然而, 即使刚开始通过傅里叶计算得到的系统分辨力不高, 我们仍有机会通过脉冲波形拟合等办法来提高测距精度^[26]. 所以在具体的实验设计中需要平衡考虑成本与精度, 以设计出更符合应用需要的测距仪器.

2

-->

4.1.光谱干涉测距实验

光谱干涉测距装置见图4, 其包括光源部分和测距部分两大模块. 光源部分的核心是三只级联的电光相位调制器(EOspace PM-5SE-10-SRF2W), 电光调制器将种子光源(RIO ORION, 中心波长1543.7 nm, 输出功率7 mW)调制出多个边带, 形成光学频率梳. 电光调制器的调制电压由一个定制的微波信号源(湖南全波段 MW1956H, 10 GHz输出频率)经移相器(北京谷波 GDL22-T50)输入, 通过调整移相器的输出相位或者改变信号源的输出功率来改变输出光频梳梳齿的数量和梳齿的功率分布. 为了保证光频梳重复频率的稳定性, 定制的信号源直接以铷原子钟(SRS FS725)的输出信号作为频率基准源, 以实现光频梳重复频率对原子钟频率的溯源.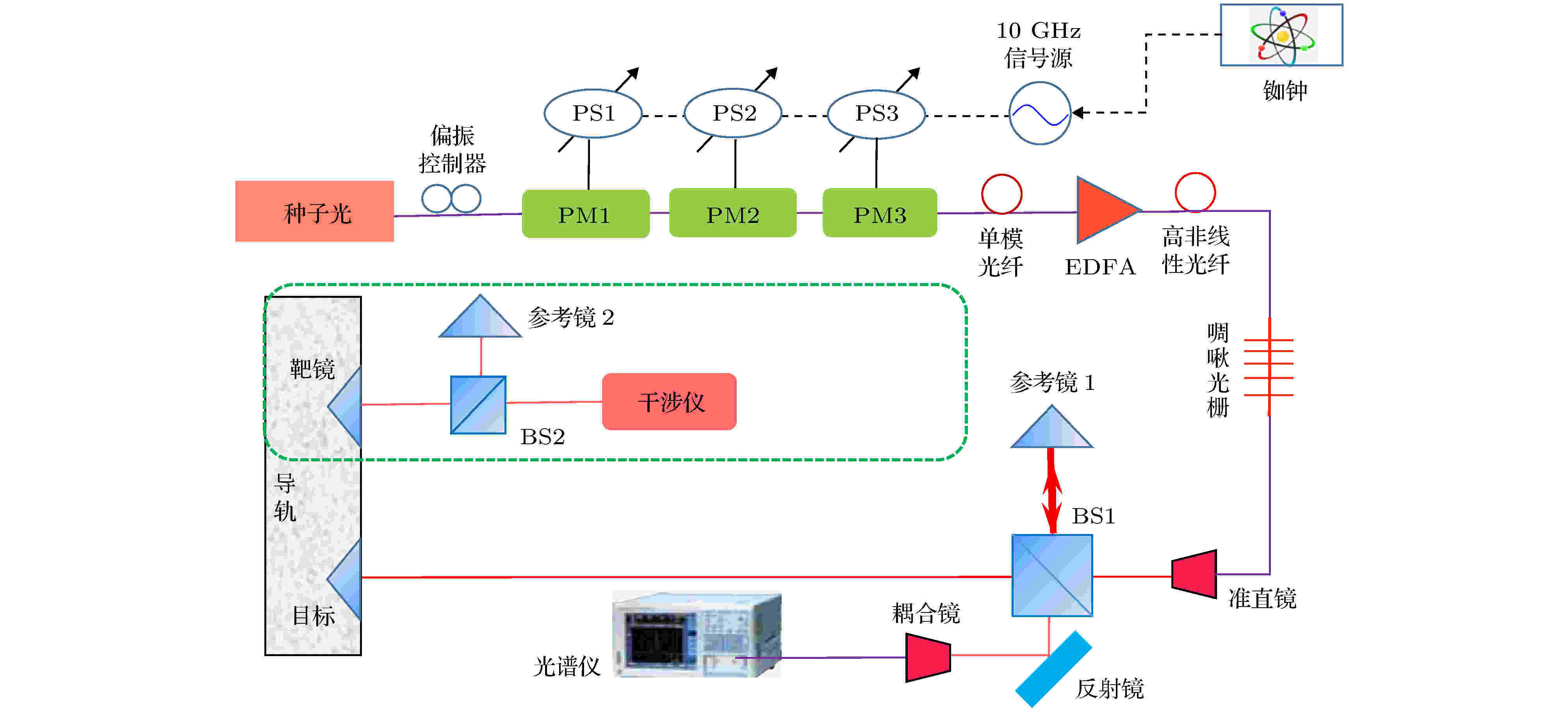
图 4 电光调制光频梳光谱干涉测距结构图(BS, 分光棱镜; EDFA, 掺铒光纤放大器)
Figure4. Experimental setup of EO comb dispersion interferometry (BS, beam splitter; EDFA, erbium doped fiber amplifier).

种子源经过级联的电光调制器后输出的信号如图5(a)所示, 此时, 超过40根功率较高且相对平坦的梳齿被调制出来. 输出的光频梳以种子光源的频率(1543.7 nm)为中心频率, 以微波调制频率(10 GHz)为重复频率对称分布, 高功率梳齿所在的光谱宽度约为4 nm. 接下来, 对初步生成的光频梳进行光谱扩展, 使用的单模光纤(Corning G.652)长度为2.4 km, 该型光纤在1550 nm波长附近的色散系数约为18 (ps/nm)·km. 单模光纤输出的光先进入掺铒光纤放大器(erbium doped fiber amplifier, EDFA, 上海瀚宇 MARS), EDFA将总功率提升到840 mW再进入到高非线性光纤. 实验中使用的高非线性光纤(OFS HNLF Zero-Slope)长为850 m, 非线性系数约为10.8 W^–1·km^–1, 扩谱后的光谱全宽接近30 nm, 如图5(b)所示. 实验中发现, 光谱宽度与高非线性光纤的长度直接相关, 更长的光纤可以获得更宽的光谱, 但也要EDFA有足够的输出功率来支撑. 可以看到, 扩展后的光谱呈现中间高, 两边低的形态, 尤其是初始光谱所在的波段功率特别高, 相比扩谱产生的新频率成分的功率高出10 dB以上, 换算成线性坐标就是将近10倍, 这将严重影响光谱包络信号的识别与提取. 为了使输出光谱相对平坦, 定制了一个基于啁啾光纤光栅的带阻滤波器, 其阻带中心频率为1543 nm, 在4.8 nm的带宽内光反射率达到了92.5%, 其余波长几乎无衰减, 经过带阻滤波器后的光频梳光谱如图5(c)所示. 但因为主要功率都集中在滤波器的阻带上, 经滤波器后的输出光功率将明显衰减. 另外可以看到, 经过高非线性光纤的光谱长波部分比短波部分的基底功率要高. 在 图5(c)中没有采集到的长波方向, 与主光谱间隔约100 nm的波段也有一些频率成分, 但功率相对较低. 所以光源内或许存在一些受激拉曼散射效应, 但该效应不影响测距, 且拉曼效应的光谱不与主光谱连接, 不方便处理干涉条纹, 所以本系统不对其进行采集.
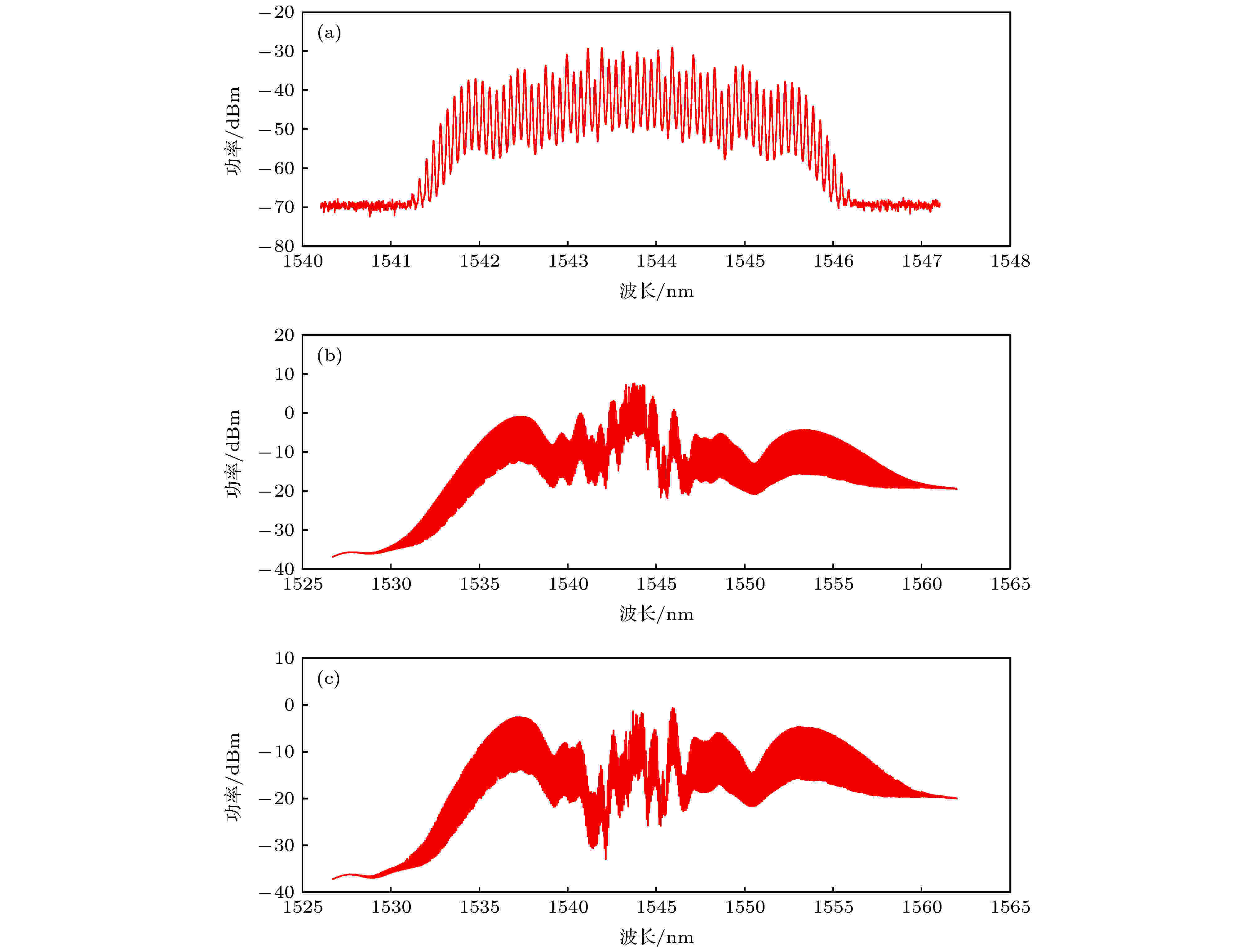图 5 电光调制光频梳光谱图　(a)电光调制器输出的光频梳光谱; (b)经过扩谱后的光频梳光谱; (c)经过带阻滤波后的光频梳光谱
Figure5. The spectrum of EO comb: (a) The spectrum of EO comb generated by cascaded EO modulators; (b) the EO comb spectrum after spectrum expansion; (c) the EO comb spectrum after band elimination filter.

理论上说, 电光效应和非线性效应都会受光的偏振态和相位的影响, 所以光源内的偏振扰动和相位变化会对光谱的稳定性尤其是光谱的宽度产生影响. 在级联电光调制器部分, 在种子光源和电光调制器之间加了偏振控制器, 电光调制器之间使用保偏光纤连接, 并在每个电光调制器和信号源之间都加了移相器, 这样可以方便偏振态和相位的调控和维护. 在光谱扩展部分, 由于使用了很长的单模光纤, 偏振扰动不可避免, 不过我们使用的EDFA有自动功率控制的功能, 使其可以满足无论输入光功率和偏振态有何变化, 它都能输出固定功率, 而且输出光的偏振态也基本是固定的. 所以在这一部件上完成了对偏振变化的“免疫”, 所以没有在这部分使用偏振控制器. 然而, 调节相位调制器前端的移相器仍然能改变进入到高非线性光纤的光的相位, 这样可以通过调节移相器来完成相位匹配, 以达到更好的非线性扩谱效果.
而测距部分主要由一套迈克耳孙干涉光路构成. 啁啾光纤光栅滤波后的光经准直镜转化为空间光, 再由分光棱镜转化为参考光和测量光, 测量反射镜安置在导轨上, 而参考反射镜固定不动. 参考反射镜与测量反射镜的回光再经分光棱镜合束送入到光谱分析仪(横河 AQ6370D)中, 光谱仪上显示的就是被光谱干涉条纹调制后的光谱. 图6显示的就是参考镜和测量镜在不同相对距离的情况下被调制后的光谱图, 为了方便后续数据处理, 将纵坐标(功率)转换为线性坐标, 此时有效的光谱宽度还有约26 nm, 对应测距分辨力约为92.3 μm. 从图6可以看出, 参考镜和测量镜的相对位置不同, 光谱上光谱干涉包络的频率也不同, 解调出这个包络频率, 就可以解算出被测距离. 不过在解算出距离之前, 还要使用前文所述的等频率间隔重采样算法进行预处理.
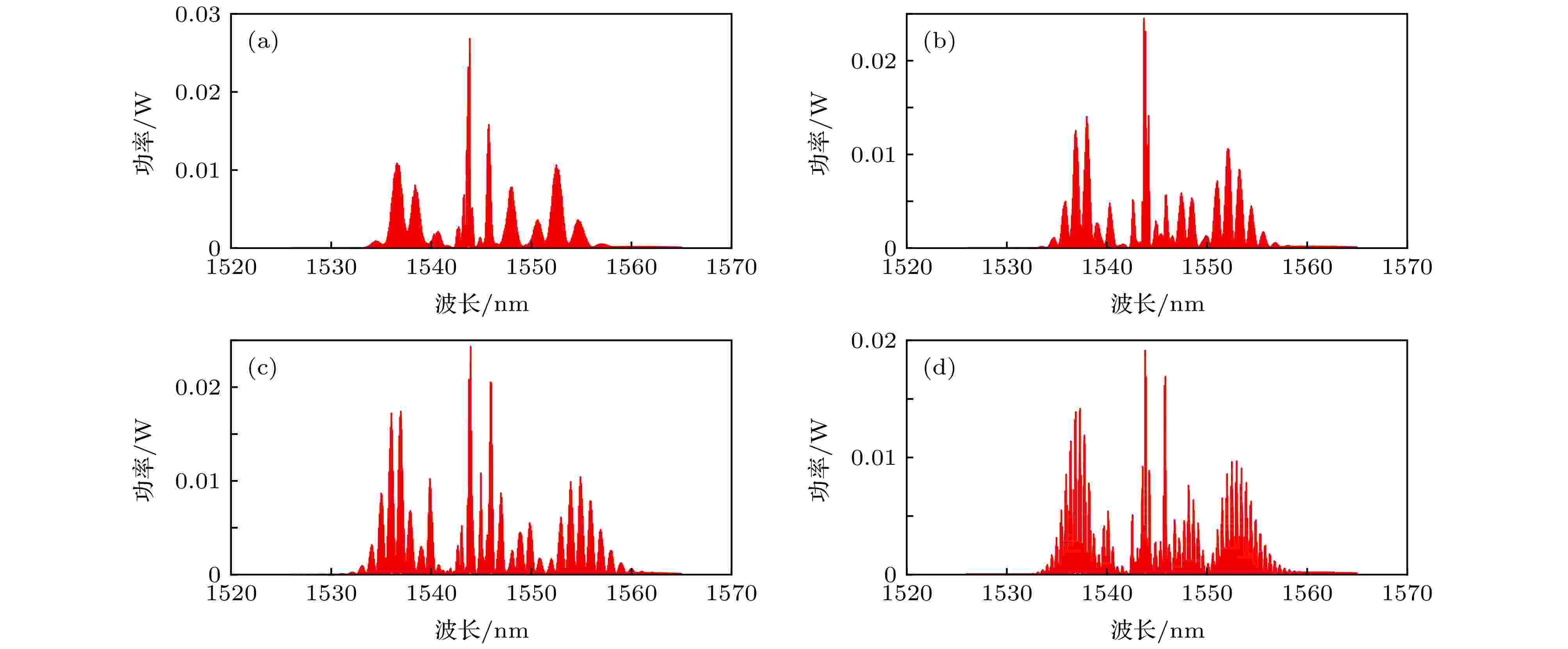图 6 参考臂与测量臂在不同相对位置下的光谱干涉图　(a)相对位置0.3 mm; (b)相对位置0.6 mm; (c)相对位置1 mm; (d)相对位置2 mm
Figure6. Spectral interferogram of reference arm and measuring arm at a relative position of (a) 0.3 mm, (b) 0.5 mm, (c) 1 mm, (d) 2 mm.

图7显示了在参考臂与测量臂的相对位置为2 mm的时候进行等频率间隔重采样的数据处理过程. 首先使用寻峰算法得到干涉光谱上的包络信号, 如图7(a)所示. 如果直接对包络信号进行快速傅里叶变换(fast Fourier transform, FFT), 解算后将得到如图7(c)所示的结果. 可以看到FFT后的脉冲有一些展宽, 脉冲峰值的位置也未必准确. 将图7(a)中的光谱横坐标转换成频率, 并按照等频率间隔进行重新采样, 得到图7(b)所示的频域信号, 再对这个信号进行FFT处理, 并将横坐标换算为距离, 就可以得到图7(d)所示的结果. 此时, 脉冲形状相对7(c)中有了明显的改善, 峰值位置也有所修正.
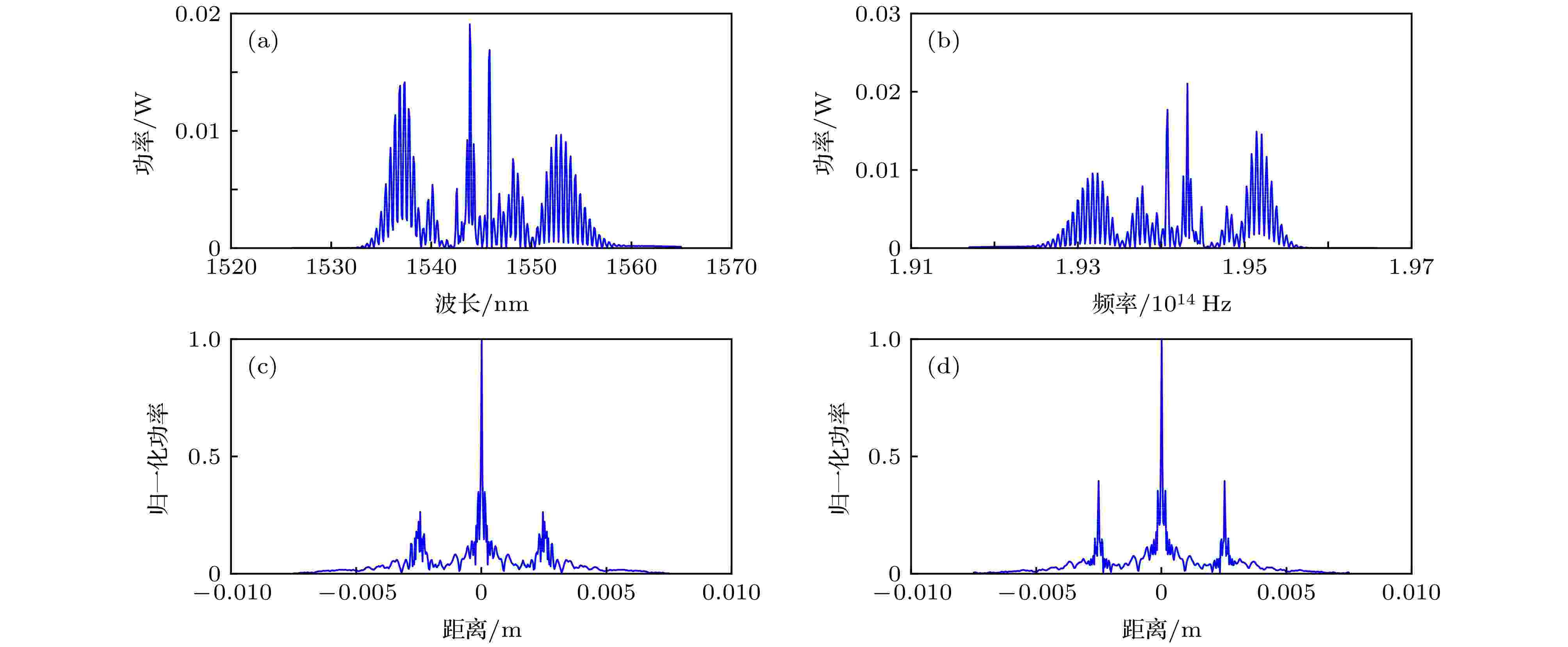图 7 等频率间隔重采样数据处理过程图　(a)寻峰算法处理后的光谱干涉图; (b)横坐标转化成频率后的光谱干涉图; (c)对图(a)做傅里叶变换后的结果; (d)对图(b)做傅里叶变换后的结果
Figure7. Data processing of equal frequency interval resampling. (a) Spectral interferogram processed by peak seeking algorithm; (b) spectrum interferogram after the abscissa is converted into frequency; (c) Fourier transform of panel (a); (d) Fourier transform of panel (b).

另外, 依据前文所述, 由于分辨力不足, 如果直接取脉冲峰值附近的数据点作为测距结果将会造成很大的测量误差. 在实验中, 将脉冲峰值前后三个数据点合起来做一元二次方程拟合, 提取拟合后曲线的峰值点作为最终测量点, 测距结果将会得到进一步修正(如图8所示).
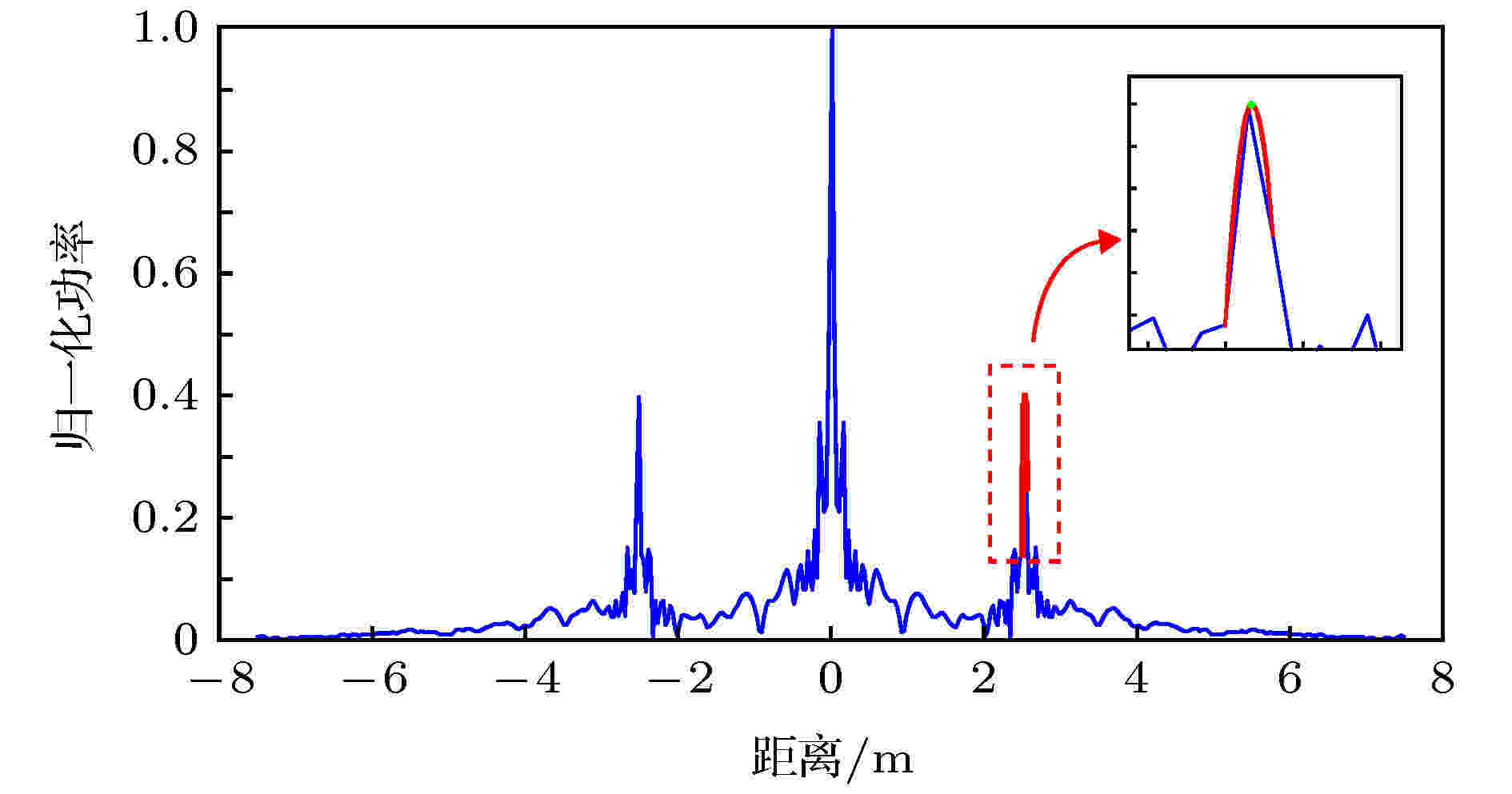图 8 脉冲峰值数据二次方程拟合过程图(插图是对脉冲及拟合曲线的放大)
Figure8. Peak position fitting according to quadratic equation. The inset is an enlargement of the pulse and the fitted curve.

2 -->

4.2.光谱干涉测距实验结果

在本系统10 GHz的光频梳重复频率下, 测距非模糊范围约为7.5 mm. 在实验中, 发现在非模糊范围的起始位置, 因为光谱宽度的问题, 无法提取到一个完整周期的包络信号. 无法提取信号的光程范围与系统的分辨力在数值上是相等的. 也就是说, 在非模糊范围的起始阶段也存在一段的“死区”, 其长度等于系统原本的分辨力. 但过了这段距离之后就可以通过等频率间隔重采样和脉冲二次方程拟合的方法来对测量数据做处理, 测距精度就不再受上述分辨力的制约.
在测距能力的验证实验中, 首先调节导轨, 使参考臂与测量臂相等, 将这个点设定为起始点. 然后每移动1.4 mm测一组数据, 每组数据测量5次. 环境温度、湿度和气压信息由传感器测定, 结果分别为温度20.83 ℃, 空气湿度41.22%, 气压1005.12 hPa. 根据改进的艾德伦公式进行空气折射率计算^[27], 得到群折射率约为1.00026528. 测量结果与参考干涉仪(雷尼绍 XL-80)数值的对比如图9所示. 其中红色叉号表示单次测量数值与干涉仪参考值对比的误差, 蓝色圆圈表示在该位置所有测量数据平均值与干涉仪参考值对比的误差, 蓝色线段的长度表示该位置所有测量结果的二倍标准差. 可以看到, 经过数据处理后, 在一个非模糊范围内可以实现 ± 15 μm的绝对测距精度. 另外可以看到, 在7 mm的位置时, 有一个测量数据相对其他数据发生明显的跳变, 致使该位置上的二倍标准差显著增加. 在工程上, 可以通过3σ准则将这个数据删去. 不过在1.4 mm的位置上仍然可以观察到类似的跳变. 在图9还可以看出, 如果除去这些过分明显的跳变, 测距结果的重复性精度基本稳定在4 μm以内. 在任何激光测距系统中, 空气湍流、目标振动、热变化等问题带来的一些非高斯噪声皆有可能引起数据跳变, 进而增加测距不确定度. 而在该系统中数据跳变幅度这么大其实是系统初始的测距分辨力不高遗留下的问题. 在数据处理中, 通过使用二次方程拟合算法提高了伪时域脉冲峰值提取精度, 但是脉冲上的信号点毕竟比较少, 如果信号点位置发生跳动, 拟合的结果仍会受之影响. 此外, 前文提到, 如果光的相位发生抖动, 光谱宽度也会有所变化, 进而也有可能增加测量结果的不确定度. 不过在实验过程中, 没有观察到光谱宽度有明显变化, 光谱宽度的轻微变化引起的测距不确定度包含在了上述4 μm的重复性精度以内.
图 9 一个非模糊范围内光谱干涉绝对测距实验结果
Figure9. Experimental results of spectral interferometry in a non-ambiguous range.

下一步, 我们在导轨上验证了跨非模糊范围的绝对测距能力, 在1 m范围内每隔0.1 m测一个组数, 每组数据同样测量5次. 7.5 mm的非模糊范围足够大, 可以提前估算待测距离在第几个非模糊范围内. 与参考干涉仪对比的绝对测距结果如图10所示, 可以发现在跨非模糊范围的测距中, 测距不确定度依然没有明显变化, 仍约为 ± 15 μm.
图 10 跨非模糊范围光谱干涉绝对测距实验结果
Figure10. Experimental results of spectral interferometry beyond serial non-ambiguous ranges.

2 -->

4.3.光谱干涉测距结果的不确定度分析

根据(14)式, 光谱干涉测距的合成不确定度可以表示为

$\begin{split}& {u_L} = \\& \sqrt{{{\bigg[ {\frac{c}{{2n_{\rm{g}}^2}}\Big(\frac{k}{{{f_{{\rm{rep}}}}}} \!+\! \tau\Big){u_{{n_{\rm{g}}}}}} \bigg]}^2} \!+\! {{\bigg( {\frac{{c \cdot k}}{{2{n_{\rm{g}}}f_{{\rm{rep}}}^2}}{u_{{f_{{\rm{rep}}}}}}} \bigg)}^2} \!+\! {{\Big( {\frac{c}{{2{n_{\rm{g}}}}}{u_\tau }} \Big)}^2}} \\\;& = \sqrt {{{\left( {\frac{L}{{n_{\rm{g}}^{}}}{u_{{n_{\rm{g}}}}}} \right)}^2} + {{\left( {\frac{{c \cdot k}}{{2{n_{\rm{g}}}f_{{\rm{rep}}}^2}}{u_{{f_{{\rm{rep}}}}}}} \right)}^2} + {{\left( {\frac{c}{{2{n_{\rm{g}}}}}{u_\tau }} \right)}^2}},\end{split}$

其中${u_{{n_{{\rm g}}}}}$, ${u_{{f_{\rm{rep}}}}}$和${u_\tau }$分别代表空气群折射率、光频梳重复频率和激光传输时间的不确定度, 根据(24)式可以看出, 最终的合成不确定度正与这三个因素有关, 本节就对这三个因素引起的不确定度变化做具体介绍.
(24)式中, 根号内第一项与空气折射率的不确定度有关, 改进的艾德伦公式自身的相对测量不确定度约为$3 \times {10^{-8}}$, 温度、湿度和气压传感器的测量不确定度分别为0.05 ℃, 0.1%和5 Pa, 代入艾德伦公式换算出最终空气折射率的测量不确定度为$1.16 \times {10^{-7}}L$. 根号内第二项与重复频率的不确定性有关, 本装置中的电光调制光频梳直接溯源到铷钟, 铷钟的频率稳定性为10^–11量级, 所以重复频率的频率稳定性也基本能达到相同量级. 另一方面, 由于本系统的重复频率较高, 在10⁹量级, 使得根号内第二项的系数非常小. 综合来看, 重复频率的不确定性影响要远小于空气折射率, 所以第二项可以忽略. 第三项与传播时间的不确定度有关, 而传播时间的不确定度与光速的乘积正好等于测量距离的不确定度, 根据第4.2节的实验结果, 测量距离的不确定度约为15 μm. 因此光谱干涉测距的标准合成不确定度约为$\sqrt {{{(15\;{{\text{μ} \rm m}})}^2} \!+\! {{(1.16 \!\times\! {{10}^{ - 7}}L)}^2}} $.

本文提出了一种基于电光调制光学频率梳光谱干涉法进行绝对距离测量的方法, 从理论上分别分析了电光调制光频梳的数学模型和光谱扩展方法, 以及光谱干涉测距方法的非模糊范围和分辨力. 系统论述了该方案的优势, 相比于其他电光调制光频梳测距方法, 该方法结构简单、现象直观、数据易处理; 而相比传统的基于锁模激光器的光学频率梳的光谱干涉方法, 该方法中的光源易生成、寿命长, 重复频率能稳定溯源到原子钟. 虽然光谱宽度会受光相位变化的影响, 但容易维护, 并且没有大范围的测量“死区”. 在实验中, 使用三组级联的电光调制器调制种子光源, 初步生成了具有数十根梳齿的光频梳. 接着使用单模光纤和高非线性光纤分别对该光频梳进行色散补偿和光谱扩展, 最后生成了光谱宽度达30 nm, 重复频率为10 GHz的电光调制光频梳. 将其作为光源引入光谱干涉绝对距离系统, 使用等频率间隔重采样算法将光谱仪采样方式引起的系统误差做修正, 并使用二次方程脉冲峰值拟合算法来提升系统的测距精度. 在1 m范围的绝对测距验证实验中, 得到了 ± 15 μm的测量不确定度.
得益于近些年科学家的探索, 电光调制光频梳的低成本、高稳定性和重频调节的高自由度得到了充分的证实, 很有工业应用的潜力; 而光谱干涉测距方法是当前被报道的所有基于光频梳的测距方法中最便捷、成本最低、复现性最好的绝对测距手段之一. 一段时间以来, 光谱干涉方法的应用一直受到测量“死区”的限制, 若想消除这个“死区”, 需要对光谱仪或光源做进一步的改进, 客观上升高了系统的成本. 这套基于电光调制光频梳的光谱干涉测距方法可以将两者的优势相结合, 并且利用电光调制光频梳的高重频来消除测距“死区”, 不需增加系统成本, 也能同时保障测距系统运行的稳定性. 然而, 本系统中电光调制光频梳的光谱宽度比较窄, 客观上限制了系统的测距分辨力. 不过可以通过更高的电光调制频率, 更多的级联调制器, 更大的调制功率或者更充分的非线性扩谱来提高光源的光谱宽度, 但这也会造成系统成本的上升. 未来还需研究成本更低的电光调制光频梳光谱扩展方法. 另外, 由于本系统对光谱仪的带宽和分辨力要求不是很高, 如果未来对本系统进行仪器化研发, 还可以使用一些成本更低的光栅和图像传感器来代替商用光谱仪^[15], 以尽可能平衡仪器性能与系统成本.