摘要:直接吸收光谱(DAS)可直接测量分子吸收率函数, 并通过拟合吸收率函数确定待测气体参数. 波长调制-直接吸收光谱(WM-DAS)在DAS基础上, 结合了波长调制光谱(WMS)中谐波分析思想, 利用傅里叶变换复现吸收率函数, 可有效提高吸收率函数的测量精度. 本文利用WM-DAS方法结合长光程气体吸收池, 在室温低压条件下, 对CO分子1567 nm处R5—R11近红外弱吸收谱线吸收率函数进行了精确复现, 其拟合残差标准差低至3 × 10^–5, 随后根据测得的吸收率函数对谱线的碰撞展宽、Dicke收敛以及速度依赖的碰撞展宽系数等光谱参数进行了高精度标定, 并将其与高灵敏度的连续波腔衰荡光谱(CW-CRDS)测量结果进行了比较, 实验结果表明该方法与CW-CRDS测量结果具有高度一致性, 更具有系统简单、测量速度快、对环境要求低等优点.
关键词: 波长调制-直接吸收光谱/
腔衰荡光谱/
吸收率函数/
碰撞展宽系数/
Dicke收敛系数

English Abstract

全文HTML

--> --> -->

气体分子吸收谱线的物理常数(如碰撞展宽系数^[1], 线强度^[2]等)是测量气体浓度、温度等不可或缺的参数, 它可通过拟合测得的分子吸收率函数得到, 因此, 吸收率函数的测量精度决定了谱线物理常数的标定精度. 目前, 常用的气体分子吸收率函数测量方法主要有傅里叶变换红外吸收光谱^[3,4]和可调谐激光二极管吸收光谱(TDLAS)^[5-7], 其中TDLAS采用窄带激光扫描分子吸收谱线, 具有波长选择性强、测量速度快、灵敏度高等优点. TDLAS中常用的直接吸收光谱(DAS)^[8-11]可直接测量吸收率函数, 通过拟合吸收率函数确定待测气体参数或谱线光谱常数, 其物理概念清晰、操作简单, 在强吸收谱线光谱常数标定和气体参数测量中得到广泛应用.
尽管DAS在气体参数测量和谱线参数标定等方面具有操作简单、物理概念清晰等优点, 但诸如“振动噪声”、“暗噪声”、“光噪声”和“比例噪声”等限制了DAS测量精度的进一步提高^[12,13], 难以用于弱吸收条件(如气体浓度低、谱线强度弱等)气体参数或谱线光谱常数的高精度测量. 为此, 科研工作者常采用延长有效吸收光程的方法以提高气体分子对激光的吸收作用^[14-19], 进而提高吸收率函数的测量信噪比. 基于几何光学的Herriott^[14-17]和White^[18,19]等多次反射池通过增加激光反射次数延长吸收光程, 如反射100次即可将10 cm长吸收池的有效吸收光程提高到10 m左右, 在痕量气体监测、弱吸收谱线参数标定等领域得到广泛应用. 与此同时, 为进一步提高吸收率函数的测量精度, 科研工作者进行了诸多研究, 如采用稳定光强的方法以减小光强波动对吸收率函数测量的影响^[20], 或采用基于物理光学的腔增强吸收光谱^[21-23]或连续波腔衰荡光谱(CW-CRDS)^[24-26]将有效吸收光程提高到数km以上, 但该类方法对环境要求高, 系统操作复杂.
与上述延长吸收光程、稳定光强等研究方法不同, Du等^[27]将波长调制光谱(WMS)谐波分析思想引入到DAS中, 通过傅里叶变换中特征频谱复现分子吸收率函数, 即波长调制-直接吸收光谱法(WM-DAS). 该方法融合了DAS (免标定、可测量吸收率函数)和WMS (高信噪比、抗干扰能力强)的优点, 将吸收率函数测量信噪比提高了约1个量级, 其拟合残差标准差低至约1 × 10^–5量级^[28,29]. 该方法可高精度标定分子谱线的光谱常数, 如碰撞展宽系数、温度指数、线强度等, 即使在弱吸收条件下仍能测得吸收率函数的精细结构, 可实现高精度的Rautian^[30]和Galatry^[31]线型函数中的Dicke收敛系数、Speed-dependent Voigt^[32]线型函数中的速度依赖的碰撞展宽系数等参数的精确测量.
考虑到WM-DAS的优点, 本文利用高信噪比的WM-DAS方法结合长光程Herriott池, 在室温低压条件下, 对CO分子1567 nm处R5—R11近红外弱吸收谱线(约2 × 10^–23 cm^–1/(mol·cm^–2))的吸收率函数进行了高精度复现, 同时根据测得的吸收率函数标定了谱线碰撞展宽、Dicke收敛和速度依赖的碰撞展宽等系数, 并将测量的吸收率函数、标定的光谱参数及其不确定度与高灵敏度的CW-CRDS测量结果进行了比较.

实验系统如图1所示, 虚线方框内为WM-DAS^[27-29]系统, 其他部分与CW-CRDS^[24-26]系统共用. 两系统的气体池通过聚四氟管线联通, 待测气体经过干燥和过滤后进入气体池中, 两气体池内的气体压力、温度、浓度均相同. 两系统共用一个中心波长1567 nm的分布反馈半导体激光器(电流、温度调谐范围分别为18—100 mA, 10—40 ℃, 功率约7 mW), 激光束通过光隔离器以减少对激光器的光反馈. 输出激光分为两束, 一束通过声光调制器进入衰荡腔, 另一束进入Herriott池^[14-17], 并通过程序控制激光控制器的外调制开关, 以实现WM-DAS和CW-CRDS分时测量. 激光绝对波长和相对波长分别采用波长计(Bristol 671A)和干涉仪(Thorlabs, 自由光谱区30 GHz)进行标定. Herriott池由一对间隔约1 m、曲率半径2 m的镀银反射镜(反射率约98%)组成, 总光程约为120 m. 激光光束在Herriott池内经过多次反射后由入射孔出射, 经探测器接收并通过高速采集卡采集.
图 1 WM-DAS与CW-CRDS的系统原理图(LC, 激光电流和温度控制器; FI, 光纤隔离器; AOM, 声光调制器; APD, 雪崩光电二极管; PD, 光电二极管; DDG, 数字延迟发生器; PZT, 压电换能器; WM, 波长计)
Figure1. System schematic diagram of WM-DAS and CW-CRDS. LC, laser current and temperature controller; FI, fiber isolator; AOM, acousto-optic modulator; APD, avalanche photodiode; PD, photodiode; DDG, digital delay generator; PZT, piezoelectric transducer; WM, wavelength meter.

衰荡腔(腔长约0.5 m)由一对高反射率(反射率高于99.99%)镜片组成. 通过PZT扫描腔长, 使腔长扫描范围大于一个自由光谱区, 以确保任意波长的激光均可耦合进腔内. 腔另一端的出射光由光电探测器接收, 当探测器达到预设触发电平时, 由数字延迟发生器发送脉冲信号, 使声光调制器失去能量, 从而关闭进入腔内的激光以形成单指数衰减信号. 采用高速数据采集卡同时采集脉冲信号和单指数衰减信号, 并利用计算机对实验数据实时处理, 快速拟合^[24]得到衰荡时间. 采用步进式扫描激光电流来改变激光波长, 从而得到随波长改变的衰荡时间τ(v), 采集多个扫描周期并平均以提高信噪比. 随后, 通过公式${1 / {(c\tau \left( \nu \right)}}) = \kappa \left( \nu \right) + {\kappa _0}$将衰荡时间τ(v)转换为吸收系数κ(v), 其中c为光速, κ₀表示镜面反射率、散射、吸收等导致的损耗^[24-26], 再对1/(cτ(v))拟合即可得到谱线参数.

WM-DAS考虑了激光输出光强和波长的非线性, 建立了激光波长与光强之间的关系^[27]. 在WM-DAS方法中, 定义x = cos(ωt + η), 其中t为扫描时间, ω为正弦调制信号的角频率, η为基倍频初始相位角, 激光光强I和激光波长v可表示为

$\begin{split} I\left( x \right) =\; & \sum\limits_{k = 0}^\infty {{A_k} \cdot \cos \left[ {k \cdot \left( {\arccos x \pm \eta } \right)} \right]} \\&\pm \sum\limits_{k = 0}^\infty {{B_k} \cdot \sin \left[ {k \cdot \left( {\arccos x \pm \eta } \right)} \right]} , \end{split}$

$\begin{split} v\left( x \right) = \; & {\nu _0} + {a_1}x + {a_2} \Big[ \left( {2{x^2} - 1} \right)\cos {\varphi _2} \\ & \pm 2x\sin {\varphi _2}\sqrt {1 - {x^2}} \Big], \end{split}$

式中, v₀为激光中心波长, a₁和a₂为调制深度, A_k和B_k是k次特征频率的傅里叶系数的实部和虚部. 根据(1)和(2)式可重构出光强I与波长v的关系, 其中‘－’和‘+’分别代表光强上升沿和下降沿. 根据Beer-Lambert定律可得到吸收率函数如下^[27-29]:

$\alpha (v) = - \ln \left( {\frac{{{I_{\rm t}}\left( \nu \right)}}{{{I_0}\left( \nu \right)}}} \right) = PS\left( T \right)XL\varphi \left( v \right), $

式中, I_t(v)和I₀(v)分别为重构的透射光强和入射光强. P (atm)为气体压力(1 atm = 1.01325 × 10⁵ Pa), S (cm^–2·atm^–1)为谱线强度, T(K)为气体温度, X为气体摩尔分数, L (cm)为光程, φ(v) (cm)为线型函数, 可以用Voigt^[27-30], Rautian^[31], Galatry^[32], Speed-dependent Voigt^[33,34]等线型来描述.
其中Voigt线型(VP)可以表示为^[27-30]

${\varphi _{\rm{V}}}(x,y) = A{\rm{Re}}\left[ {W\left( {x,y} \right)} \right], $

$W\left( {x,y} \right) = \frac{{\rm{i}}}{{\text{π}}}\int_{ - \infty }^{ + \infty } {\frac{{\exp \left( { - {t^2}} \right)}}{{x + {\rm{i}}y - t}}{\rm{d}}t} , $

式中W(x, y)为误差函数^[33], $A = {{\sqrt {{{\ln 2} / {\text{π}}}} }}/{{{\gamma _{\rm{D}}}}}, $ $y = \sqrt {\ln 2} \dfrac{{{\gamma _{\rm{c}}}}}{{{\gamma _{\rm{D}}}}}, \; x = \sqrt {\ln 2} \dfrac{{\nu - {\nu _0}}}{{{\gamma _{\rm{D}}}}}$. 这里, $ {\gamma _{\rm{c}}} = {\gamma _{\rm{s}}}{p_1} + $$ \gamma _0{p_2} $, 其中γ_s是待测气体分子的自身碰撞展宽系数, γ₀是背景气体分子对待测气体分子的碰撞展宽系数, p₁是待测气体分压, p₂是背景气分压; γ_D是多普勒半宽, ${\gamma _{\rm{D}}} = 3.581 \times {10^{ - 7}}{\nu _0}\sqrt{{T}/{M}} $, 其中M是相对分子质量, T为气体温度. 当背景气体的分子质量大于待测气体分子质量时, φ(v)可采用Rautian线型(RP)描述^[31]:

${\varphi _{\rm{R}}}(x,y,z) = A{\rm{Re}} \left[ {\frac{{W\left( {x,y + z} \right)}}{{1 - \sqrt {\text{π}} zW\left( {x,y + z} \right)}}} \right], $

式中$z = \sqrt {\ln 2} \dfrac{{{\beta _0}{p_2}}}{{{\gamma _{\rm{D}}}}},\;\beta = {\beta _0}{p_2} $. 这里, β₀(cm^–1·atm^–1)代表碰撞导致的收窄系数(Dicke收敛系数). 当背景气体的分子质量小于待测气体分子质量时, φ(v)可采用Galatry线型(GP)描述^[32]:

$\begin{split} & {\varphi _{\rm{G}}}(x,y,z)= \\\;& A{\rm{Re}} \left[ {\int_0^{ + \infty } {\exp \left( { - {\rm{i}}xt - yt - \frac{{zt - 1 + {{\rm{e}}^{ - zt}}}}{{2{z^2}}}} \right){\rm{d}}t} } \right].\end{split}$

与GP和RP相比, Speed-dependent Voigt线型(SDVP)^[33,34]的精度更高, 其表达式为

${\varphi _{{\rm{SDV}}}}({z_ - },{z_ + }) = A{\rm{Re}} \left[ {w\left( {{\rm{i}}{z_ - }} \right) - w\left( {{\rm{i}}{z_ + }} \right)} \right],$

式中w(z)和z_±表达式如下:

$w\left( z \right) = \frac{{\rm{i}}}{{\text{π}}}\int_{ - \infty }^\infty {\frac{{{{\rm{e}}^{ - {t^2}}}}}{{z - t}}{\rm{d}}t}, $

${z_ \pm } = \pm \sqrt \delta + \frac{1}{{\sqrt 2 }}\eta + {\rm{i}}\chi \frac{1}{{\sqrt 2 \eta }},$

$\eta = \sqrt {\sqrt {{{\left( {\theta + \chi } \right)}^2} + {\chi ^2}} + \theta + \delta }, $

其中, $\theta = \dfrac{{{\gamma _{\rm{c}}}}}{{{\gamma _2}}} - 1.5, \; \chi = \dfrac{{\nu - {\nu _0}}}{{{\gamma _2}}},\; \delta = \dfrac{1}{{4\ln 2}}{\left( {\dfrac{{{\gamma _{\rm{D}}}}}{{{\gamma _2}}}} \right)^2}$. γ₂代表速度依赖的碰撞展宽, 若γ₂趋近于0, 则SDVP可简化为VP. 测量光谱的信噪比(SNR)定义为α_max/σ_SD, 即吸收率函数峰值α_max与其拟合残差(Res)标准差(SD) σ_SD的比值.

实验中采用WM-DAS对CO分子1567 nm附近的R5—R11谱线进行了测量. Herriott池有效光程120 m, 气体温度、压力和CO浓度分别为288 K, 18 kPa和0.1% (背景气N₂). 激光扫描频率、扫描范围分别为1 kHz, 0.4 cm^–1, 单次实验共采集100个正弦波周期(用时0.1 s), 同时采集相应的干涉仪信号(?)进行激光波长标定, 如图2所示, 其中蓝色曲线为透射光强信号, 红色曲线为波长标定结果. 蕴含气体吸收率函数信息的透射光强信号傅里叶系数为A_k和B_k, 将A_k和B_k及通过干涉仪标定的激光波长系数a₁, a₂和η等参数代入(1)—(3)式中即可复现吸收率函数.
图 2 测量的100个正弦波周期的激光光强及激光相对波长标定结果(FSR为自由光谱范围), 以及蕴含气体吸收率函数信息的透射光强傅里叶变换(FFT)系数
Figure2. Measured transmitted intensities of 100 periods of sinusoidal waves and fitted frequency (FSR, free spectral range), and fast Fourier transform (FFT) coefficients A_k and B_k of transmitted light intensity.

图3(a)展示了WM-DAS方法对R10谱线的测量结果, 为便于与CW-CRDS比较, 将WM-DAS所测吸收率(α)转换为吸收系数(κ). CW-CRDS方法采用步进式扫描激光波长, 间隔约0.002 cm^–1, 扫描范围约0.4 cm^–1, 共扫描100次, 用时约20 min. 图3(b)展示了CW-CRDS测量结果, 由于测量的吸收系数仅与衰荡时间相关而与光强无关^[24-26], 残差波动小, 测量数据更加平滑, 可以清晰看出VP拟合残差中“w”形的精细结构, 其原因在于VP未考虑Dicke收敛效应^[31,32], 观察到该精细结构也说明了CW-CRDS具有很高的灵敏度. 与此相比, WM-DAS通过提取周期性正弦信号的整数倍特征频谱来复现气体吸收光谱, 可有效减小或消除振动、电磁等多种噪声干扰^[12,13], VP拟合残差中也可清晰地观察到“w”形的精细结构, 这验证了本文WM-DAS测量结果与CW-CRDS相一致. 与VP不同, RP考虑了Dicke收敛效应, 拟合时可以消除“w”形残差. 从RP拟合结果可知, WM-DAS和CW-CRDS两种方法测得的吸收率函数拟合残差标准差相差约2.5倍, 相应的SNR(1σ)相差约2.5倍, 但WM-DAS的测量时间(0.1 s)远小于CW-CRDS (20 min), 在大量的谱线参数标定以及工业现场的气体快速监测中更有优势.
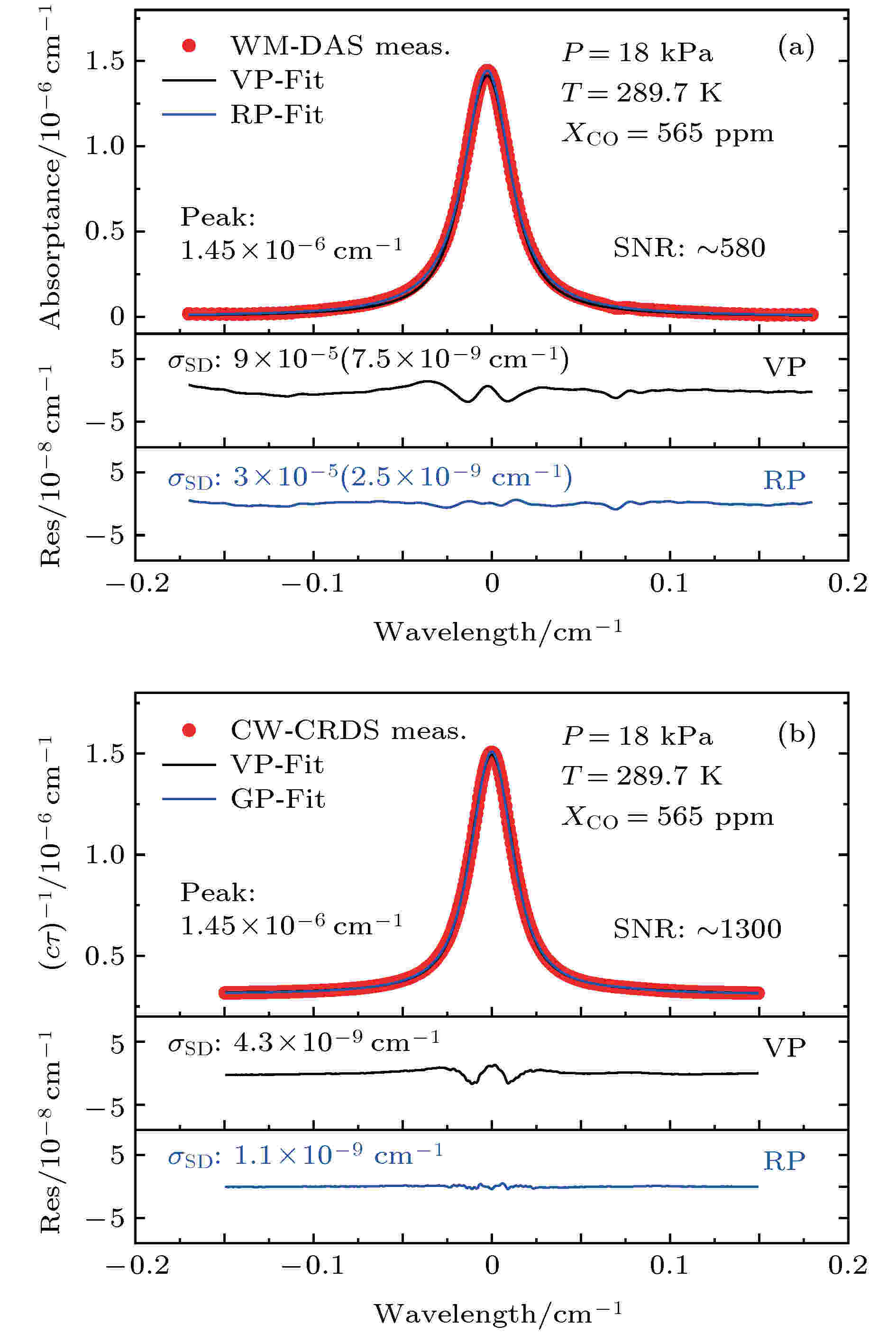图 3 测量的CO光谱及其最佳Voigt和Rautian线型拟合结果(X_CO, c, τ和σ_SD分别为CO浓度、光速、衰荡时间和残差的标准差) (a) WM-DAS; (b) CW-CRDS
Figure3. Measured absorption function of CO and the best fits of Voigt and Rautian profile (X_CO, c, τ, and σ_SD represent the CO concentration, light velocity, ring down time and standard deviation of the residual, respectively): (a) WM-DAS; (b) CW-CRDS.

为了进一步验证WM-DAS的测量精度, 利用该方法对不同压力下CO分子R5—R11谱线的光谱参数进行了测量, 并与CW-CRDS测量结果进行对比, 其中, 碰撞展宽(γ_c)及速度依赖的碰撞展宽(γ₂)选用SDVP^[33,34]的拟合结果, Dicke收敛(β)选用RP^[31,32]的拟合结果. 气体温度为288 K, 温度波动小于0.3 K, CO浓度为0.5% (背景气为N₂), 压力范围1—25 kPa. 图4(a)和图4(b)给出了不同压力下, 两种方法对CO分子R10谱线的γ_c及γ₂和β测量结果, 测量数据的拟合线性度分别达到0.9998 (γ_c)和0.98 (γ₂和β), 这说明两方法测量数据有较好的一致性. 在上述参数中, β和γ₂数值远小于碰撞展宽γ_c, 对光谱信噪比有较高的要求, 因而其测量误差略大于γ_c. 事实上, 虽然WM-DAS的SNR低于CW-CRDS的SNR, 但是WM-DAS测量速度更快测量点更多, 每个测量点仅需1 s (信号采集和数据处理), 测量过程受环境温度、气压波动影响更小, 因而β和γ₂的线性拟合结果与CW-CRDS相一致.
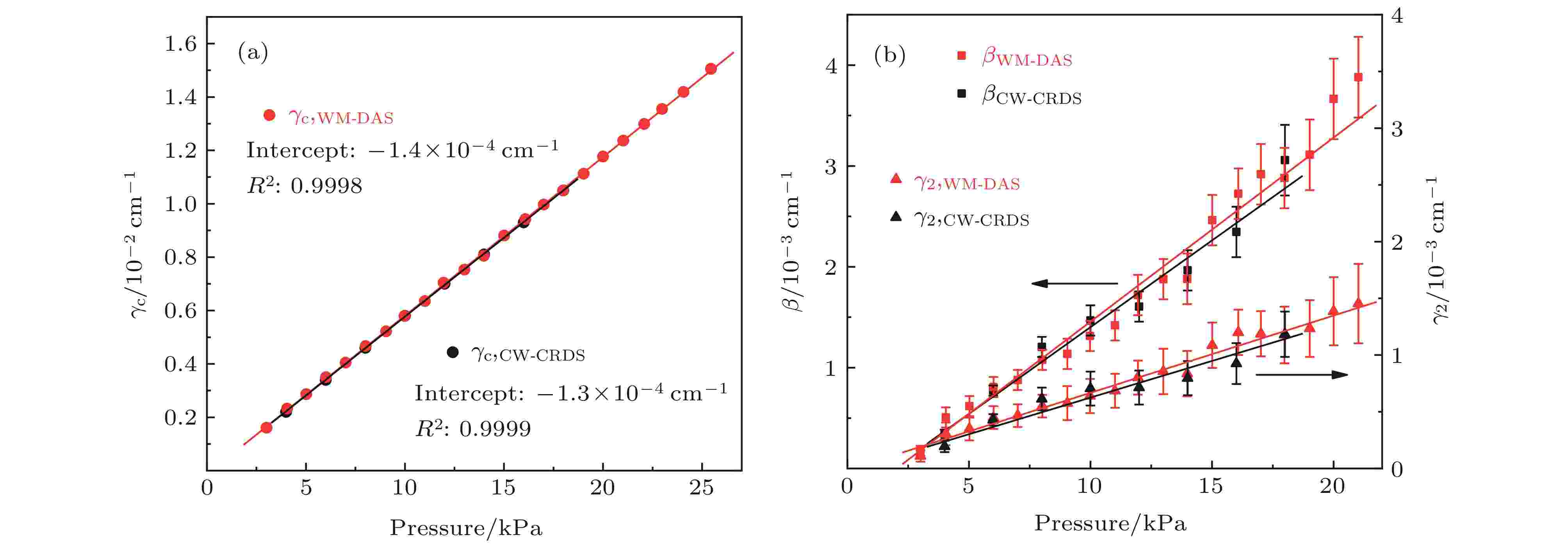图 4 不同压力下测得的光谱参数(WM-DAS为红色, CW-CRDS为黑色) (a) γ_c (圆); (b) β (正方形), γ₂ (三角)
Figure4. Measured spectral parameters for various pressures (WM-DAS (red), CW-CRDS (black)): (a) γ_c (dot); (b) β (square), γ₂ (triangle).

表1列出了WM-DAS和CW-CRDS两种方法采用四种线型(VP, GP, RP, SDVP)拟合得到的碰撞展宽系数γ₀(T₀), Dicke收敛系数β₀(T₀)和速度依赖的碰撞展宽系数γ₂(T₀). 测量不确定度主要来源于气体温度(< 0.2 K)、压力(< 30 Pa)、浓度(< 50 ppm)以及吸收率函数拟合误差, 经计算得到γ₀(T₀)总的不确定度范围约为0—1% (CW-CRDS)和0—1.5% (WM-DAS). 其中, 两种方法采用VP拟合的γ₀(T₀)的相对误差均不超过1%, 采用精度更高的RP/GP/SDVP拟合的γ₀(T₀)的相对误差仅略大于1%, 主要是由Dicke收敛系数及速度依赖的碰撞展宽系数的拟合不确定引起的. 由于β₀(T₀)和γ₂(T₀)值比γ₀(T₀)小, 对光谱信噪比要求更高, 因此CW-CRDS测得的β₀(T₀)和γ₂(T₀)的不确定度范围为5%—15%, 与文献[35]的测量结果0.7%—14%相接近. 相比之下, WM-DAS通过提取特征频率复原吸收率函数, 并通过快速测量大量的数据点来降低不确定度, β₀(T₀)和γ₂(T₀)不确定度范围达到10%—20%.

v0/cm–1	Transition	E′′/cm–1	?	γ0(T0)/10–2 cm–1·atm–1				β0(T0)/10–2 cm–1·atm–1			γ2(T0)/10–2 cm–1·atm–1
				CRDS	WM	HT		CRDS	WM		CRDS	WM
6371.299	R5	57.670	VP	6.26b	6.23b	6.29a		—	—		—	—
			GP	6.43b	6.48b			2.84c	2.90d		—	—
			RP	6.47b	6.50b			2.57c	2.67d		—	—
			SDVP	6.50b	6.55b			—	—		0.87c	0.77d
6374.406	R6	80.735	VP	6.10b	6.08b	6.12a		—	—		—	—
			GP	6.20b	6.30b			2.65c	2.71d		—	—
			RP	6.25b	6.30b			2.38c	2.46d		—	—
			SDVP	6.26b	6.36b			—	—		0.69c	0.73d
6377.407	R7	107.642	VP	5.97b	5.94b	5.99a		—	—		—	—
			GP	6.07b	6.12b			2.22c	2.48d		—	—
			RP	6.10b	6.17b			2.06c	2.36d		—	—
			SDVP	6.25b	6.24b			—	—		0.71c	0.71d
6380.301	R8	138.390	VP	5.89b	5.88b	5.89a		—	—		—	—
			GP	6.04b	6.02b			2.20c	2.27d		—	—
			RP	6.06b	6.09b			2.14c	2.14d		—	—
			SDVP	6.11b	6.15b			—	—		0.70c	0.64d
6383.090	R9	172.978	VP	5.80b	5.78b	5.80a		—	—		—	—
			GP	5.91b	6.03b			2.08c	2.11d		—	—
			RP	5.94b	6.03b			1.89c	1.85d		—	—
			SDVP	5.97b	6.09b			—	—		0.61c	0.63d
6385.771	R10	211.404	VP	5.72b	5.68b	5.73a		—	—		—	—
			GP	5.91b	5.89b			2.27c	2.29d		—	—
			RP	5.92b	5.91b			1.98c	1.86d		—	—
			SDVP	5.98b	5.96b			—	—		0.62c	0.65d
6388.347	R11	253.667	VP	5.62b	5.58b	5.67a		—	—		—	—
			GP	5.91b	5.80b			2.62c	2.21d		—	—
			RP	5.93b	5.82b			2.15c	2.00d		—	—
			SDVP	5.95b	5.89b			—	—		0.77c	0.67d
注: WM代表WM-DAS, HT表示HITRAN[36];a表示相同温度(T0 = 288 K)下HITRAN的数据, 空气为背景气;b不确定度 0—1%;c不确定度 5%—15%;d不确定度 10%—20%.

表1WM-DAS和CW-CRDS测量的光谱参数及其不确定度
Table1.Measured spectroscopic parameters and uncertainties.

为了进一步评价WM-DAS和CW-CRDS两种方法的测量下限, 在相同条件下, 分别对WM-DAS和CW-CRDS进行了Allan方差^[37]分析, 实验结果如图5所示. 其中CW-CRDS采用固定中心波长的测量方式, 积分时间约25 s时(固定波长下的衰荡时间采集速度约为0.01 s, 25 s相当于平均2500次), 基于CW-CRDS的CO检测限可到30 ppb ($1~{\rm{ppb}} = {{1~{\rm{μg}}}}/{{\rm{L}}}$), 这与文献[38]检测限相一致, 这验证了本文CW-CRDS测量结果的可靠性. 与此相比, 积分时间约100 s时, 基于WM-DAS的CO检测限可到80 ppb, 略高于CW-CRDS, 对应的吸收系数约2 × 10^–10 cm^–1.
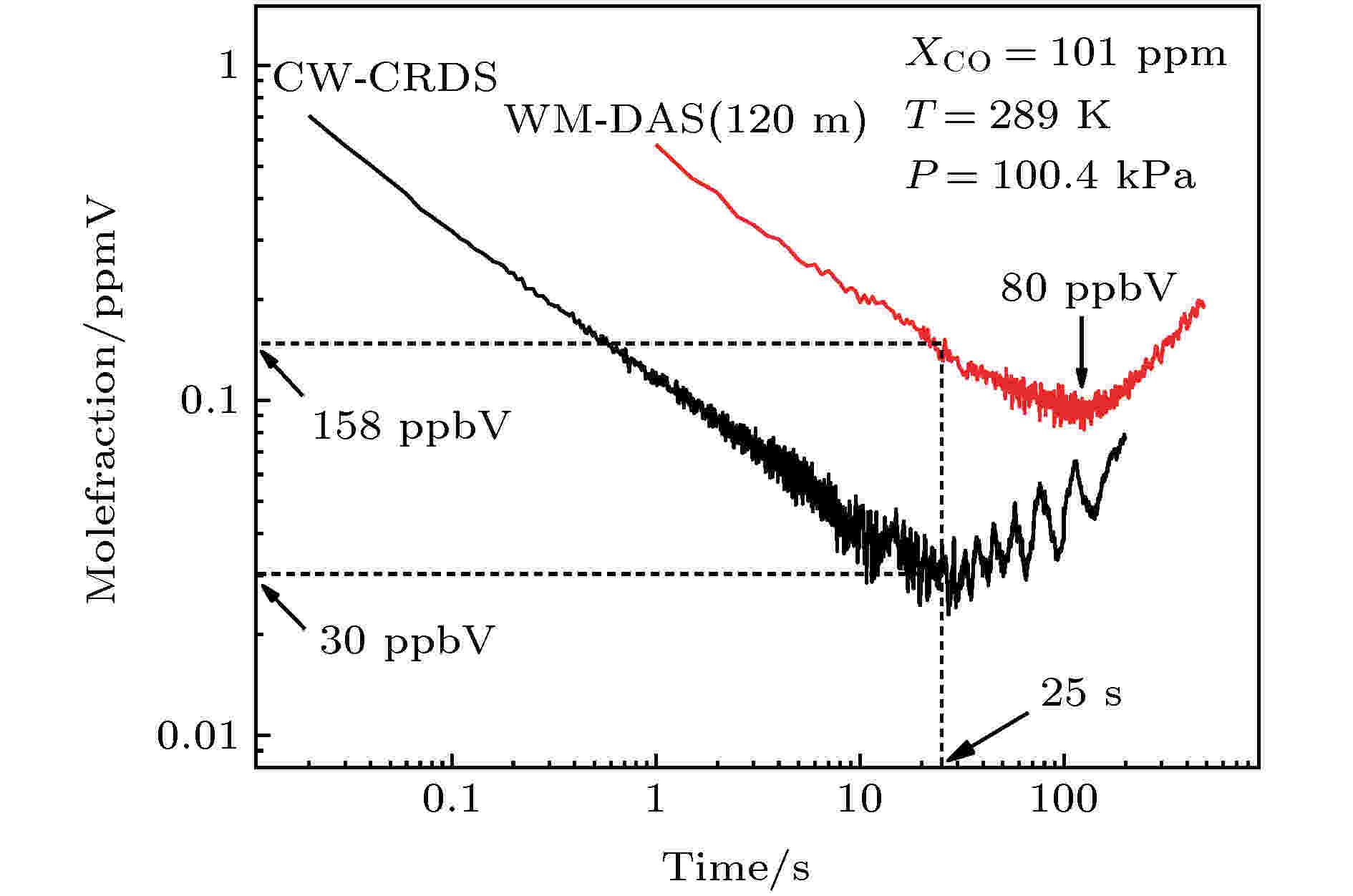图 5 两种方法测量的Allan方差
Figure5. Allan variance measured by the two methods.

本文利用免标定、高信噪比的WM-DAS方法结合长光程Herriott池, 在低压常温条件下, 对CO分子1567 nm附近7条近红外弱吸收谱线(R5—R11)的吸收率函数进行了测量, 光谱拟合残差标准差低至3 × 10^–5. 随后, 采用不同的线型函数对测得的吸收率函数进行拟合得到了谱线光谱参数及其测量不确定度, 并将其与高灵敏度的CW-CRDS测量结果进行比较. 实验结果表明: CW-CRDS方法测得的吸收率函数信噪比约为长光程WM-DAS方法的2.5倍, 两种方法测得的谱线物理参数具有高度一致性, 其中VP线型拟合的碰撞展宽系数的相对误差小于1 %. 与此同时, 基于WM-DAS方法的CO的检测限达到80 ppb, 对应的吸收系数低至2 × 10^–10 cm^–1, 略高于CW-CRDS方法, 但其测量速度更快, 并且具有系统简单、成本低、可长期稳定运行的优点, 预期可为弱吸收谱线的测量提供新的测量方法.