摘要: 少模光纤的受激布里渊散射对于分布式温度/应变传感具有重要应用价值. 本文提出一种纤芯折射率呈M型分布的少模光纤, 详细研究了光学模式LP
01 和LP
11 模式内及模式间的布里渊增益谱. 研究结果表明: LP
01 -LP
11 模式对的布里渊增益谱中, 其相邻两个布里渊散射峰的频率间隔较宽、增益峰值较大且峰值相差较小. 通过优化光纤结构参数, 提高了基于LP
01 -LP
11 模式对布里渊增益谱的温度和应变传感性能, 最小误差分别为0.23 ℃和5.67 με. 该研究对探究少模光纤中模式内及模式间的受激布里渊散射特性具有一定的指导意义, 对提升同时温度和应变传感测量的性能具有一定参考价值.
关键词: M型少模光纤 /
受激布里渊散射 /
布里渊增益谱 /
传感 /
温度和应变 English Abstract Inter-mode stimulated Brillouin scattering and simultaneous temperature and strain sensing in M-shaped few-mode fiber Li Xue-Jian Cao Min Tang Min Mi Yue-An Tao Hong Gu Hao Ren Wen-Hua Jian Wei Ren Guo-Bin Key Laboratory of All Optical Network and Advanced Telecommunication Network, Ministry of Education, Institute of Lightwave Technology, Beijing Jiaotong University, Beijing 100044, China Received Date: 15 January 2020Accepted Date: 12 March 2020Published Online: 05 June 2020Abstract: Stimulated Brillouin scattering (SBS) in a few-mode fiber (FMF) is of significance for the distributed temperature and strain sensing. An FMF with M-shaped refractive index distribution (M-FMF) is proposed in order to improve the performance of simultaneous temperature and strain sensing based on SBS. Propagation of four optical modes is supported by the M-FMF, so that the Brillouin gain spectrum (BGS) can be obtained by both intra-mode and inter-mode SBS. The BGSs produced by the interactions of LP01 -LP01 mode pair, LP01 -LP11 mode pair, and LP11 -LP11 mode pair are analyzed, respectively. Meanwhile, the temperature and strain sensing performance based on the BGS of LP01 -LP11 mode pair are studied in detail. Considering a common step-index FMF, only one obvious scattering peak is usually present in the BGS obtained from the interaction between different optical mode pairs, therefore, it is inconvenient to achieve multi-parameter sensing measurement. In this paper, the BGS of LP01 -LP11 mode pair has two scattering peaks, which are contributed by the acousto-optic coupling between the acoustic modes L1n (n = 1, 2) and the optical modes LP01 and LP11 . The two Brillouin scattering peaks have large gain values of 0.1004 m–1 ·W–1 and 0.0463 m–1 ·W–1 , respectively. More importantly, the gain difference between two Brillouin scattering peaks is small, and the frequency interval is 75 MHz, which can be applied to simultaneous temperature and strain sensing. The influences of the refractive index and the fiber core radius on the BGS of LP01 -LP11 mode pair are studied. By selecting the optimal structure parameters, we discuss the effect of temperature and strain on the BGS of LP01 -LP11 mode pair. The errors for simultaneous temperature and strain measurement are reduced to 0.23 ℃ and 5.67 με. Compared with other reported results, our obtained temperature and strain sensitivity are high and sensing errors are low in the considered M-FMF. In other words, based on the BGS of LP01 -LP11 mode pair, the performance of temperature and strain sensing are improved in the M-FMF. This work is of great significance for studying intra-mode and inter-mode SBS in an FMF. Moreover, the results also provide a guideline for further improving the performance of simultaneous temperature and strain sensing.Keywords: M-shaped few mode fiber /stimulated Brillouin scattering /Brillouin gain spectrum /sensing /temperature and strain 全文HTML --> --> --> 1.引 言 随着光纤通信技术的发展, 单模光纤(single mode fiber, SMF)的传输容量已经不能满足通信系统对容量的需求[1 ] . 为了解决这一问题, 研究人员提出基于少模光纤(few mode fiber, FMF)的模分复用技术[2 ] . 受激布里渊散射(stimulate Brillouinscattering, SBS)是光纤中抽运波、散射波和声波之间相互作用的一种非线性效应. 当抽运光功率超过SBS阈值时, 抽运光通过电致伸缩效应产生声波, 声波调制折射率产生折射率光栅导致抽运波发生散射. 当光栅运动方向与抽运光同向时, 产生的散射光为频率下移的斯托克斯光; 反之当光栅运动方向与抽运光反向时, 产生的散射光为频率上移的反斯托克斯光. 在标准单模光纤中, 斯托克斯光的频移量在11 GHz附近.同时, 根据斯托克斯光与抽运光的传播方向是否一致, 可将SBS分为前向SBS和后向SBS. SBS一方面会限制光纤传输系统的信道功率, 引入大量噪声, 影响整个系统的性能, 另一方面其特性又被广泛应用于光纤激光器[3 -5 ] 、光纤传感器[6 ] 、布里渊放大器[7 ] 、慢光技术[8 ,9 ] 、微波信号处理[10 ,11 ] 和脉冲布里渊显微镜 [12 ,13 ] 等领域.[14 ] , 研究主要包括布里渊增益谱(Brillouin gain spectrum, BGS)[15 ,16 ] 、布里渊频移[17 ,18 ] (Brillouin frequency shift, BFS)、SBS阈值[19 -21 ] 以及增强[22 ] 或抑制[23 ] SBS效应等方面. 基于不同光纤结构 [24 ,25 ] 、不同掺杂浓度[26 ,27 ] SMF中SBS特性的温度和应变传感已经被大量地研究报道.[28 ] 、四模圆芯少模光纤[29 ] 、大模场面积的双包层光纤[30 ] 、渐变折射率分布光纤[31 ] 、阶跃型少模光纤[32 -34 ] 以及多模光纤[35 ] 等. 基于少模光纤中SBS特性的温度和应变传感应用被广泛研究. 2009年, Zou等[36 ] 利用熊猫型保偏光纤(polarization-maintaining fiber, PMF)中BFS和双折射系数实现了对温度和应变的同时传感测量, 温度和应变误差分别为0.08 ℃和3 με, 但是PMF的偏振对准较难实现, 整个系统较为复杂. 2016年, Xu等[37 ] 研究了在反抛物型少模光纤中基于基模模内SBS的温度、应变布里渊传感器, 温度和应变的误差分别为0.85 ℃和17.4 με. 2016年, Zhou等[38 ] 研究了基于渐变折射率分布少模光纤的布里渊传感器, 其温度和应变的误差分别为1.8 ℃和4 με. 2015年, Li等[39 ] 基于少模光纤中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模内的SBS特性, 设计了一种温度和应变的光纤传感器, 得到了温度和应变的误差分别为0.8 ℃和20.1 με. 2019年, Fang等[40 ] 研究了基于椭圆纤芯少模光纤中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模内SBS特性的温度和应变传感, 得到了温度和应变的误差分别为0.28 ℃和5.81 με, 但其系统较为复杂.[37 -40 ] , 但不同光学模式之间相互作用的SBS特性及其规律还需深入研究, 其传感性能还有待进一步提高.${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 与${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 的模间后向SBS特性, 以实现温度和应变的同时传感测量、提升测量的灵敏度和降低误差为目的, 本文设计了一种纤芯折射率呈M型分布的少模光纤(M-shaped index few mode fiber, M-FMF), 该光纤能够支持四种光学模式(${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{02}}}}$ )的传导, 分析了不同光学模式模式内和模式间相互作用的BGS, 探究了光纤结构参数(半径和折射率)对BGS的影响. 研究表明基于${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 与${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 的模间SBS特性可实现同时温度和应变传感测量, 提高温度和应变灵敏度, 降低误差.2.基本原理 光纤中的SBS是一种光学模式与声学模式的相互耦合效应. 采用线偏振模(linearly polarized mode, LP)近似, 对光纤中抽运波和散射波的光学模式(${\rm{L}}{{\rm{P}}_{mn}}$ )进行分析. 在圆均匀光波导中, 线偏振模的横向电场分布满足标量Helmoholtz方程:$\nabla _t^2 = {\partial ^2}/\partial {r^2} + \left( {1/r} \right)\partial /\partial r + \left( {1/{r^2}} \right){\partial ^2}/\partial {\theta ^2}$ 是柱坐标系下的拉普拉斯算子, $f\left( {r, \theta } \right)$ 表示光学模式的横向场分布, $n\left( {r, \theta } \right)$ 表示光纤的折射率分布, k 是与波长$\lambda $ 相关的光波数, $\beta $ 是光学模式的传播常数.${{\rm{L}}_{mn}}$ )可以通过声学标量模方程求解[14 ] :${\xi _m}\left( {r, \theta } \right)$ 是第m 个声学模式的位移场分布, q 表示声学模式的传播常数, $\varOmega _m^{}$ 是第m 个声学模式的角频率, $V_{\rm l}^{}\left( {r, \theta } \right)$ 表示声波的纵向声速. 在后向SBS过程中, 激励的声学模式、抽运波的光学模式和散射波的光学模式相互作用, 满足相位匹配, 即$q = {\beta _1} + {\beta _2}$ , 其中${\beta _1}$ 和${\beta _2}$ 分别表示抽运波和散射波的传播常数.1 )式和(2 )式中光纤折射率$n(r,\theta)$ 和纵向声速$V_{\rm{l}}^{}\left( {r, \theta } \right)$ 不仅与掺杂元素Ge/F的掺杂浓度有关, 同时也与外界温度和应变有关[25 ] :${\omega _{{\rm{Ge}}}}$ 和${\omega _{\rm{F}}}$ 分别表示掺杂元素Ge/F的掺杂浓度, 单位为${\rm{wt}}.\% $ ; $\Delta T$ 和$\Delta S$ 分别表示温度和应变的变化, 单位分别是℃和με.m 个声学模式的非线性耦合强弱通过光学模式和声学模式的重叠积分表征, 即声光有效面积$A_m^{{\rm{ao}}}$ , 表示为${f_1}\left( {r, \theta } \right)$ 和${f_2}\left( {r, \theta } \right)$ 分别表示抽运波和散射波中光学模式的场分布, ${\xi _m}\left( {r, \theta } \right)$ 表示第m 个声学模式的位移场分布.$f\left( {r, \theta } \right)$ 以及声学场${\xi _m}\left( {r, \theta } \right)$ 可以分解为cosine项和sine项, 因此根据(5 )式可知, 光学模式对$ {\rm{L}}{\rm{P}}_{{m_1} {n_1}}$ -$ {\rm{L}}{\rm{P}}_{{m_2} {n_2}}$ 和声学模式${{\rm{L}}_{mn}}$ 之间的耦合作用遵循以下原则: 声学模式的方位角模式数必须等于两个光学模式的方位角模式数之和(或差且不为负), 即$m=|m_1\pm m_2|$ .$g_{\rm{B}}^m\left( v \right)$ 表示总的BGS, ${\omega _m}$ 是BGS的半高全宽, ${v_m}$ 是第m 个声学模式的频率, 即BFS, ${g_m}$ 是布里渊增益系数, 单位为${\rm{m/W}}$ , ${n_{\rm{p}}}$ 和${n_{\rm{s}}}$ 分别表示抽运波和散射波中光学模式的有效折射率, ${p_{12}}$ 是介质的弹光系数, c 是光速, ${\rho _0}$ 是密度. 本文中$\lambda $ = 1550 nm, ${p_{12}}$ = 0.271, ${\rho _0}$ = 2202 ${\rm{kg/}}{{\rm{m}}^{\rm{3}}}$ , ${\omega _m}$ = 35 MHz[27 ] .3.分析与讨论 23.1.布里渊增益谱 3.1.布里渊增益谱 在SI-FMF中, 基模与高阶模的模式内及模式间相互作用得到的BGS通常只存在一个明显的散射峰. 对于如图1 插图所示的阶跃型少模光纤, 其${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式间相互作用的BGS中, 声学模式${{\rm{L}}_{{\rm{11}}}}$ , ${{\rm{L}}_{{\rm{12}}}}$ 和${{\rm{L}}_{{\rm{13}}}}$ 对应散射峰的峰值分别为0.098, 0.0019和0.0013 ${\rm{m}}^{ - 1}\cdot {\rm{W}}^{-1}$ , 相邻两个散射峰的频率间隔分别为46和73 MHz. 总的BGS只存在一个峰值较大的散射峰, 高阶声模对应散射峰的增益峰值较小, 因此不利于多参数传感的测量.图 1 SI-FMF中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS (插图为SI-FMF的结构分布)Figure1. The BGS of ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ mode pair in SI-FMF (Inset: The structure of SI-FMF).${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 与$ {\rm{L}}{{\rm{P}}_{{\rm{11}}}} $ 模式间SBS的同时温度及应变的传感, 本文设计了一种纤芯折射率呈M型分布的少模光纤, 如图2(a) 所示. 该光纤的结构参数分别为r 1 = 4 μm; r 2 = 6 μm; r clad = 62.5 μm; n 1 = 1.454; n 2 = 1.4557; n clad = 1.444; 其中n 1 , n 2 , r 1 和r 2 分别表示纤芯第一层和第二层的折射率和半径. 该光纤支持四种光学模式: ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{02}}}}$ , 其横向场分布如图2(b) —图2(e) 所示.图 2 M-FMF的结构分布以及光学模式的模场分布 (a) M-FMF的结构分布; (b) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ ; (c) ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ ; (d) ${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ ; (e) ${\rm{L}}{{\rm{P}}_{{\rm{02}}}}$ Figure2. The structure of M-FMF and the field distribution of optical modes in M-FMF: (a) The structure of M-FMF: (b) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ ; (c) ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ ; (d) ${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ ; (e) ${\rm{L}}{{\rm{P}}_{{\rm{02}}}}$ .${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 模式内耦合所激励的声学模式类型是${{\rm{L}}_{0 n}}$ , 由${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式内耦合所激励的声学模式类型是${{\rm{L}}_{0 n}}$ 和${{\rm{L}}_{2 n}}$ , 由${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式间耦合所激励的声学模式类型是${{\rm{L}}_{1 n}}$ , 其中n = 1, 2, 3, ···. 根据相位匹配, 不同光学模式对激励声学模式的传播常数q 不同: q = 11.7746 × 106 rad/m (LP01 -LP01 ); q = 11.7631 × 106 rad/m (LP01 -LP11 ); q = 11.7515 × 106 rad/m (LP11 -LP11 ).1 )式和(2 )式中求得的光学模式的场分布和声学模式的位移场分布代入(5 )式, 可以得到光纤中不同光学模式对与所激励声学模式之间的声光有效面积. 声光有效面积越小, 表示抽运波中的光学模场、散射波中的光学模场与声学模场重叠越好, 则声光耦合强度越强, 布里渊增益峰值也越大. 表1 给出了${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 三种情况下模式耦合的声光有效面积.LP01 -LP01 LP01 -LP11 LP11 -LP11 m = 0m = 1m = 0m = 2Lm 1 251.63 208.71 156.24 180.74 Lm 2 162.48 449.52 1.65 × 103 1.09 × 103 Lm 3 2.12 × 105 4.54 × 104 3.82 × 103 1.11 × 104
表1 不同光学模式对与声学模式之间相互耦合的声光有效面积(单位: μm2 )Table1. Acousto-optic effective area by the coupling between different optical mode pairs and acoustic modes (in μm2 ).6 )式中, 再结合(7 )式和(8 )式, 可得到不同光学模式对的BGS, 其中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 三种模式对的BGS如图3 所示. 图3 中, 虚线表示总的BGS, 由于不同声学模式对应的BFS不同, 总的BGS由多个散射峰组成. 对于${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 模式对的BGS, 其声学模式${{\rm{L}}_{{\rm{01}}}}$ 和${{\rm{L}}_{{\rm{02}}}}$ 对应散射峰的频率间隔为64 MHz, 与其相比, ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS中声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的频率间隔为76 MHz, 其对应散射峰的增益值分别为0.1004 m–1 ?W–1 和0.0463 m–1 ?W–1 , 峰值相差较小; 声学模式${{\rm{L}}_{{\rm{13}}}}$ 对应散射峰的峰值仅为0.00045 m–1 ?W–1 , 对声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的分析不造成影响. 同时, 本文也研究了${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ 和${\rm{L}}{{\rm{P}}_{02}}$ 模式内和模式间, 以及与${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式间的布里渊增益特性, 分别得到其相互作用的BGS, 但这些模式对的BGS均存在散射峰的峰值较小、峰值相差较大或频率间隔较小的特性, 不利于温度和应变的传感研究. 此外, 在BGS中, 当相邻散射峰的频率间隔较小时, 随着温度和应变的变化, 相邻散射峰的频率间隔可能小于其线宽, 不利于测量散射峰的频率. 因此本文选取${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS进行温度和应变的传感分析, 首先分析改变纤芯半经r 1 , r 2 和纤芯折射率n 1 , n 2 对其BGS的影响, 如图4 所示.图 3 不同光学模式对的BGS (a) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}\text-{\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ ; (b) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ ; (c) ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ Figure3. The BGS of different optical mode pairs: (a) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}\text-{\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ ; (b) ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ ; (c) ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ .图 4 M-FMF的结构对${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对BGS的影响 (a) n 1 ; (b) n 2 ; (c) r 1 ; (d) r 2 Figure4. The BGS of ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ mode pair in M-FMF versus: (a) n 1 ; (b) n 2 ; (c) r 1 ; (d) r 2 .图4(a) 中, 随着n 1 的增大, 声学模式${{\rm{L}}_{{\rm{11}}}}$ 对应散射峰的频率变化较小, 峰值先减小后增大; 声学模式${{\rm{L}}_{{\rm{12}}}}$ 和${{\rm{L}}_{{\rm{13}}}}$ 对应散射峰的频率均向低频移动, ${{\rm{L}}_{{\rm{12}}}}$ 模式对应散射峰的峰值逐渐增大, ${{\rm{L}}_{{\rm{13}}}}$ 模式对应散射峰的峰值几乎不变. 但当n 1 ≥ 1.452时, 由于${{\rm{L}}_{{\rm{13}}}}$ 模式与基模之间的耦合强度变小, 因此其散射峰逐渐消失, 此外${{\rm{L}}_{{\rm{11}}}}$ 模式和${{\rm{L}}_{{\rm{12}}}}$ 模式对应散射峰的频率间隔逐渐减小. 图4(b) 中, 随着n 2 的增大, 三个声学模式对应的散射峰都向低频移动且峰值逐渐减小, 彼此频率间隔逐渐增大. 图4(c) 中, 随着r 1 的增大, 声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的峰值变化较小, 但二者频率间隔逐渐减小. 图4(d) 中, 随着r 2 的增大, 声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的峰值逐渐减小, 其频率间隔逐渐增大. 因此相邻两个声学模式对应散射峰的峰值和频率间隔可以通过光纤结构来控制, 以满足温度和应变传感测量的要求, 本文选取M-FMF的最优结构参数来研究温度和应变传感, 即r 1 =4 μm, r 2 =6 μm, r clad =62.5 μm; n 1 = 1.454, n 2 = 1.4557, n clad = 1.444.3.2.布里渊传感性能 -->3.2.布里渊传感性能 基于${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS, 采用优化结构的M-FMF, 研究了温度和应变同时传感的性能. 由${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对激励的声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 的位移场分布如图5 所示, 其中${{\rm{L}}_{{\rm{11}}}}$ 模式主要分布在纤芯第二层, ${{\rm{L}}_{{\rm{12}}}}$ 模式主要分布在纤芯的第一层.图 5 ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对激励的声学模式的位移场分布 (a) ${{\rm{L}}_{{\rm{11}}}}$ ; (b) ${{\rm{L}}_{{\rm{12}}}}$ Figure5. The displacement field distribution of acoustic mode excited by the interaction of ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ mode pair: (a) ${{\rm{L}}_{{\rm{11}}}}$ ; (b) ${{\rm{L}}_{{\rm{12}}}}$ .${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 相互作用得到的BGS主要包含两个声学模式对应的散射峰. 根据(3 )式和(4 )式, 温度和应变会引起纤芯折射率和纵向声速的变化, 改变声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 的分布特性, 导致${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的BFS随温度和应变发生变化, 且散射峰BFS变化的频移量不同, 因此可通过测量两个散射峰BFS变化的频移量实现温度和应变的同时传感. 声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的BFS与温度$\Delta T$ 和应变$\Delta S$ 之间呈线性关系[41 ] , 即(9 )式, 同时温度和应变会造成不同散射峰BFS变化的频移量不同, 因此, 对于不同散射峰, 其温度系数和应变系数不同. 根据(10 )式, 可通过测量BGS中两个声学模式对应散射峰变化的频移量得到外界温度和应变的改变量, 实现温度和应变的同时传感.$C_T^{{{\rm{L}}_{11}}}C_S^{{{\rm{L}}_{12}}} - C_T^{{{\rm{L}}_{{\rm{12}}}}}C_S^{{{\rm{L}}_{{\rm{11}}}}} \ne 0$ 时, 由(9 )式可得$C_T^{{{\rm{L}}_{1 n}}}$ 和$C_S^{{{\rm{L}}_{1 n}}}$ (n = 1, 2)分别表示声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的温度和应变系数, $\Delta {v_{{{\rm{L}}_{1 n}}}}$ (n = 1, 2)表示声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰BFS的频移量, $\Delta T$ 和$\Delta S$ 分别表示温度和应变的变化量, 单位分别为℃和με.图6 表示${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS随温度和应变的变化, 其中虚线表示${{\rm{L}}_{{\rm{11}}}}$ 模式对应的散射峰, 实线表示${{\rm{L}}_{{\rm{12}}}}$ 模式对应的散射峰. 可以发现, 随着温度(应变)的增加, 两个散射峰均向高频移动, ${{\rm{L}}_{{\rm{11}}}}$ 模式对应散射峰的峰值逐渐增加, 而${{\rm{L}}_{{\rm{12}}}}$ 模式对应散射峰的峰值逐渐减小. 由于随着温度和应变的增加, 声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 逐渐向纤芯中心靠拢, 且${{\rm{L}}_{{\rm{11}}}}$ 模式的峰值逐渐减小, ${{\rm{L}}_{{\rm{12}}}}$ 模式的峰值逐渐增大, 而光学模式的模场分布几乎不变, 导致$A_{{{\rm L}_{11}}}^{{\rm{ao}}}$ 逐渐减小, $A_{{{\rm L}_{12}}}^{{\rm{ao}}}$ 逐渐增大, 得到其散射峰的峰值变化刚好相反. 图7 表示声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的BFS随温度和应变的变化. 可以发现, 两个散射峰的BFS随温度和应变呈线性变化, 通过线性拟合得到对应于声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 的温度和应变系数, 即$ C_T^{{{\rm L}_{11}}} $ = 4.3400 ${\rm{MHz}}/{^\circ {\rm{C}}}$ , $ C_T^{{{\rm L}_{12}}} $ = 3.9315 ${\rm{MHz}}/{^\circ {\rm{C}}}$ , $ C_S^{{{\rm L}_{11}}} $ = 0.19373 MHz/με, $ C_S^{{{\rm L}_{12}}} $ = 0.17715 MHz/με.图 6 ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS随温度和应变的变化 (a) BGS随温度的变化; (b) BGS随应变的变化Figure6. The BGS of ${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ mode pair versus: (a) Temperature; (b) strain.图 7 声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰的BFS随温度和应变的变化 (a) BFS随温度的变化关系; (b) BFS随应变的变化关系Figure7. The BFS corresponding to ${{\rm{L}}_{{\rm{11}}}}$ and ${{\rm{L}}_{{\rm{12}}}}$ acoustic modes versus: (a) Temperature; (b) strain.10 )式, 当散射峰BFS的频移量等于BFS精度时, 可得到温度和应变的误差δT 和δS . 一般假定BGS中散射峰BFS的精度为0.1 MHz[25 ] , 因此, 将声学模式${{\rm{L}}_{{\rm{11}}}}$ 和${{\rm{L}}_{{\rm{12}}}}$ 对应散射峰BFS的频移量$\Delta {v_{{{\rm{L}}_{{\rm{11}}}}}}$ = $\Delta {v_{{{\rm{L}}_{{\rm{12}}}}}}$ = 0.1 MHz代入(10 )式, 得到温度和应变的误差分别为δT = 0.23 ℃, δS = 5.67 με. 表2 列出了不同研究报道中基于SBS的温度/应变系数和误差[25 -27 ,37 -40 ] , 其中$C_T^i$ 和$C_S^i$ (i = 1, 2)分别表示对应于不同散射峰的温度和应变系数. 与之相比, 本文所研究的温度和应变的传感性能更优越, 灵敏度更高, 温度和应变误差更小. 这是由于随着温度、应变的增大, 光学模式和声学模式的有效折射率和有效声速逐渐增大, BFS与二者成正比, 且M-FMF中模式有效折射率和有效声速随温度和应变的变化率更大, 故温度和应变的灵敏度较高.Fiber $C_T^1$/MHz·℃–1 $C_T^2$/MHz·℃–1 $C_S^1$/MHz·℃–1 $C_S^2$/MHz·℃–1 δT /℃ δS /με M-FMF 4.3400 3.9315 0.19373 0.17715 0.23 5.67 M-SMF[25 ] 1.5187 1.1642 0.06640 0.05280 0.47 12.30 SSMF[26 ] 1.1900 1.1500 0.06228 0.05009 0.93 19.48 SMF[27 ] 1.1900 1.1190 0.03560 0.04030 0.90 28.80 IPGIF[37 ] 0.74323 0.9016 0.04202 0.03825 0.85 17.40 GIFMF[38 ] 5.2700 4.300 0.23700 0.18900 1.80 41.00 c-core FMF[39 ] 1.0169 0.9909 0.05924 0.04872 1.20 21.90 e-core FMF[40 ] 1.2420 1.2780 0.06130 0.03640 0.37 7.61
表2 不同研究报道中基于SBS的温度应变系数和误差Table2. The coefficients and errors of temperature and strain based on SBS in different literatures.4.结 论 普通阶跃型少模光纤中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式间的BGS只存在一个明显的散射峰, 不利于实现同时温度和应变传感. 针对此种情况, 本文设计了一种纤芯折射率呈M型分布的少模光纤, 计算了不同光学模式对与所激励声学模式的声光有效面积, 并由此分析对比了四种光学模式(${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ , ${\rm{L}}{{\rm{P}}_{{\rm{21}}}}$ 和${\rm{L}}{{\rm{P}}_{{\rm{02}}}}$ )模式内和模式间的BGS, 表明${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对的BGS中相邻散射峰的频率间隔较宽、增益峰值较大且峰值相差较小, 更有利于实现温度和应变的同时传感. 通过分析光纤结构(半径和折射率)对${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ -${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式对BGS中相邻散射峰的峰值增益和频率间隔的影响, 优化光纤结构, 提高了基于M-FMF中${\rm{L}}{{\rm{P}}_{{\rm{01}}}}$ 与${\rm{L}}{{\rm{P}}_{{\rm{11}}}}$ 模式间SBS的温度和应变同时传感的性能, 得到温度和应变的误差分别为0.23 ℃和5.67 με. 



















































































 图 1 SI-FMF中
图 1 SI-FMF中











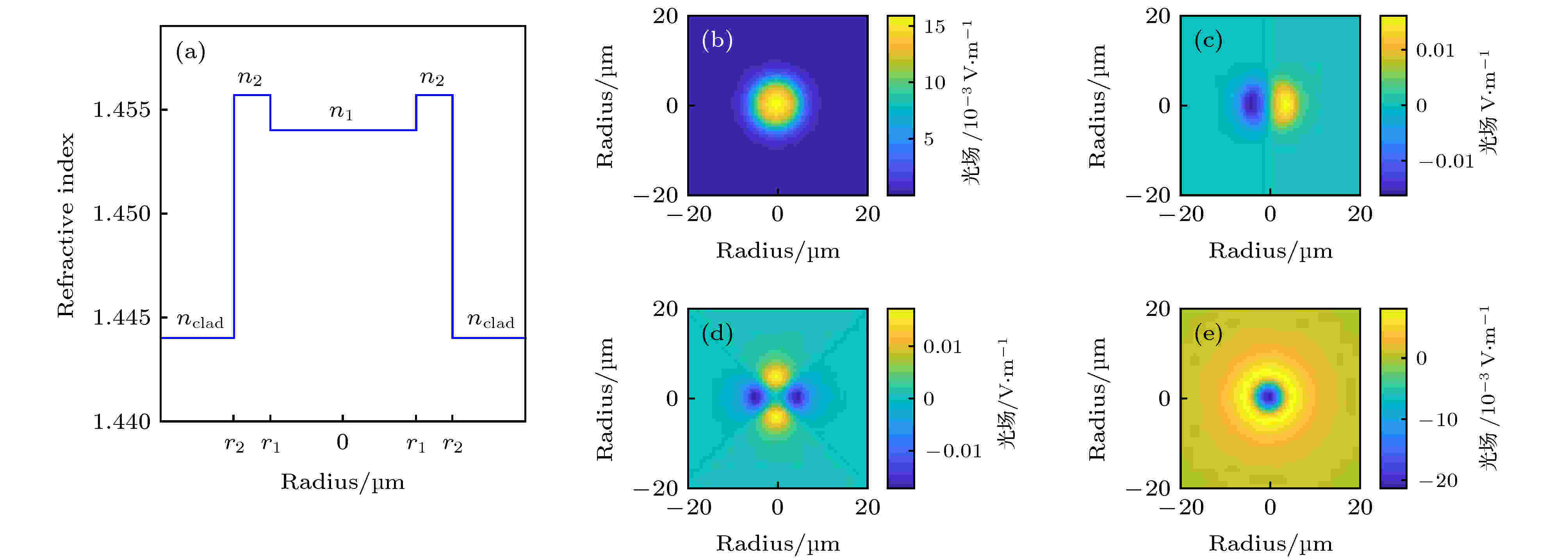 图 2 M-FMF的结构分布以及光学模式的模场分布 (a) M-FMF的结构分布; (b)
图 2 M-FMF的结构分布以及光学模式的模场分布 (a) M-FMF的结构分布; (b) 
























































































































































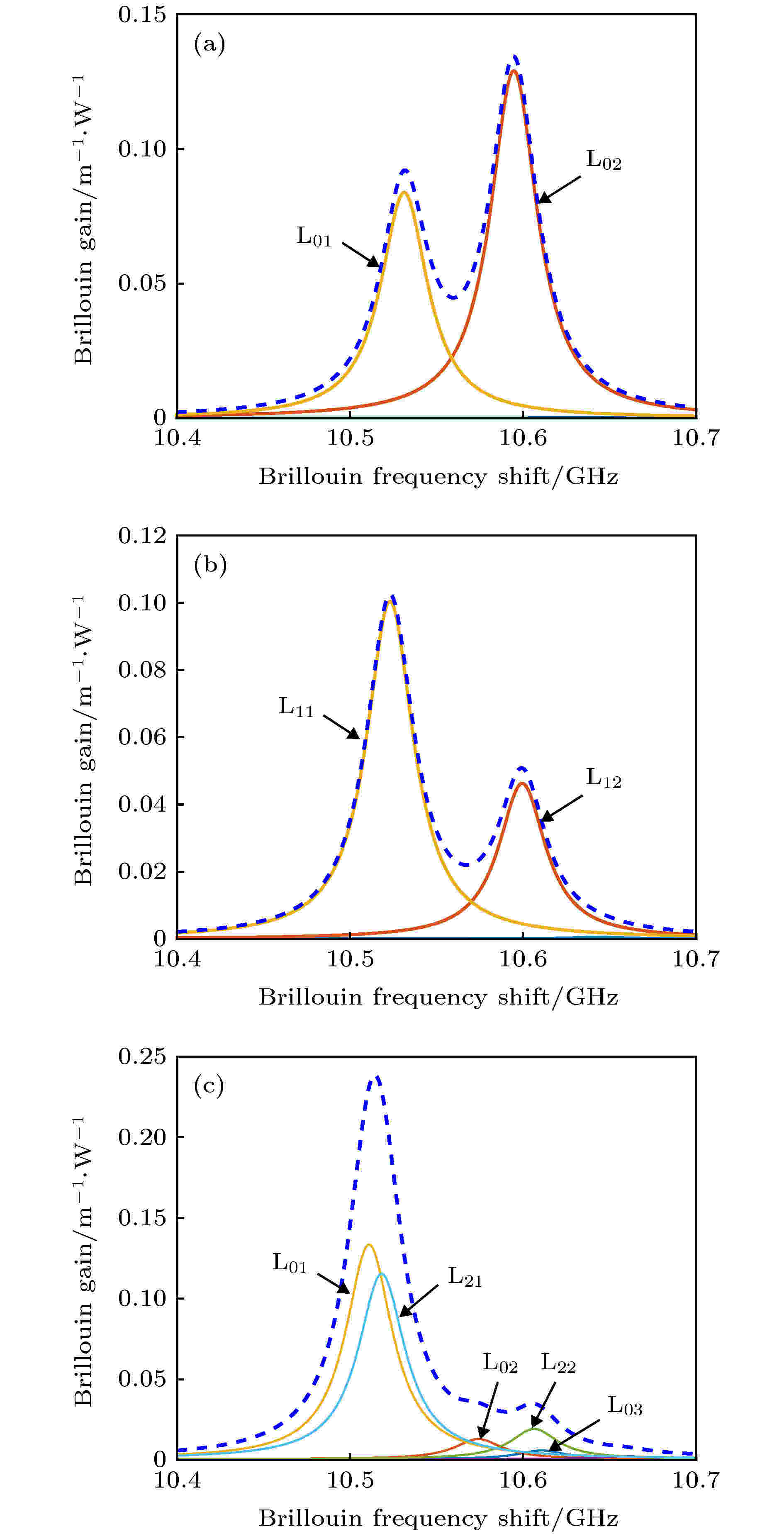 图 3 不同光学模式对的BGS (a)
图 3 不同光学模式对的BGS (a) 





















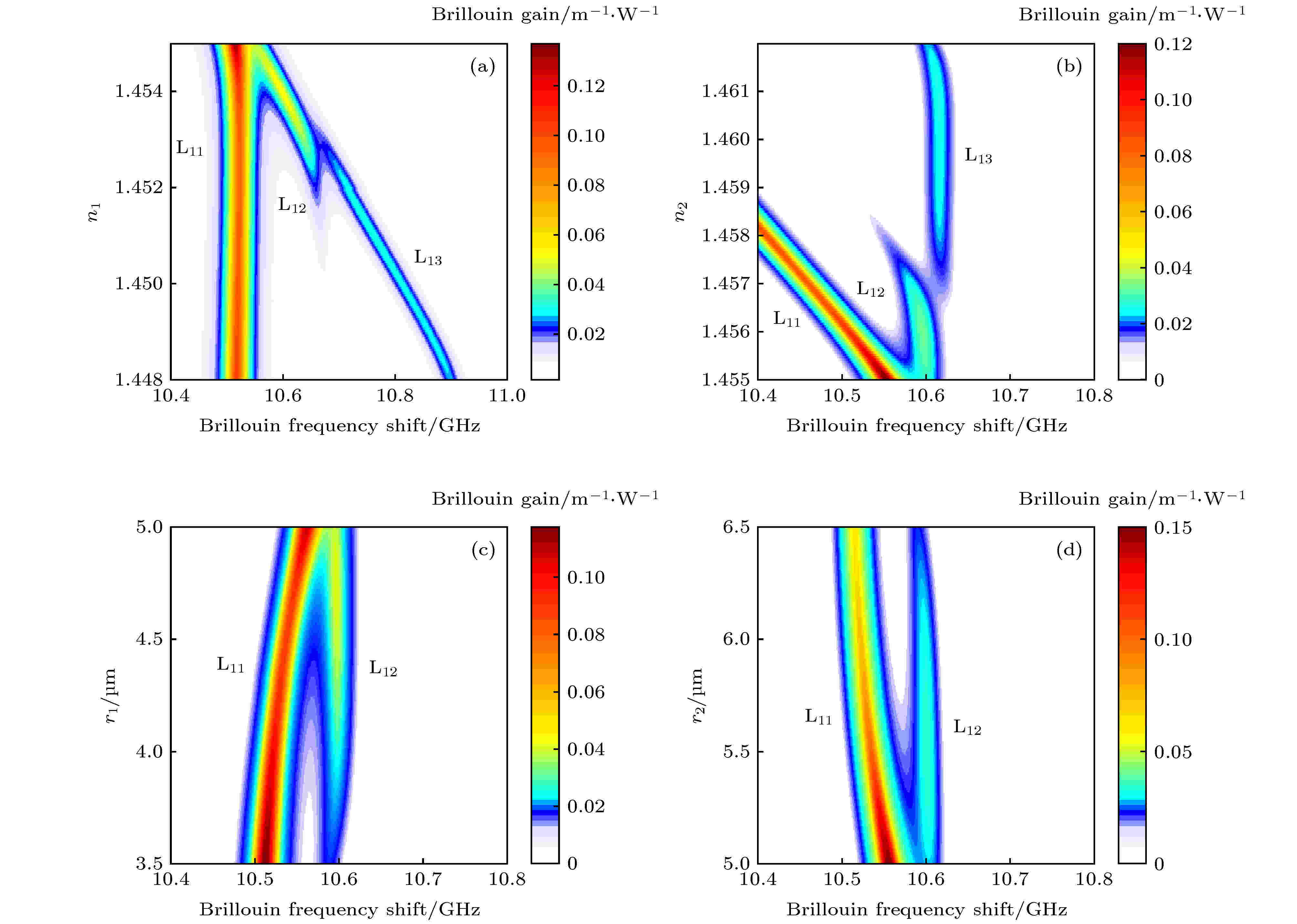 图 4 M-FMF的结构对
图 4 M-FMF的结构对





































































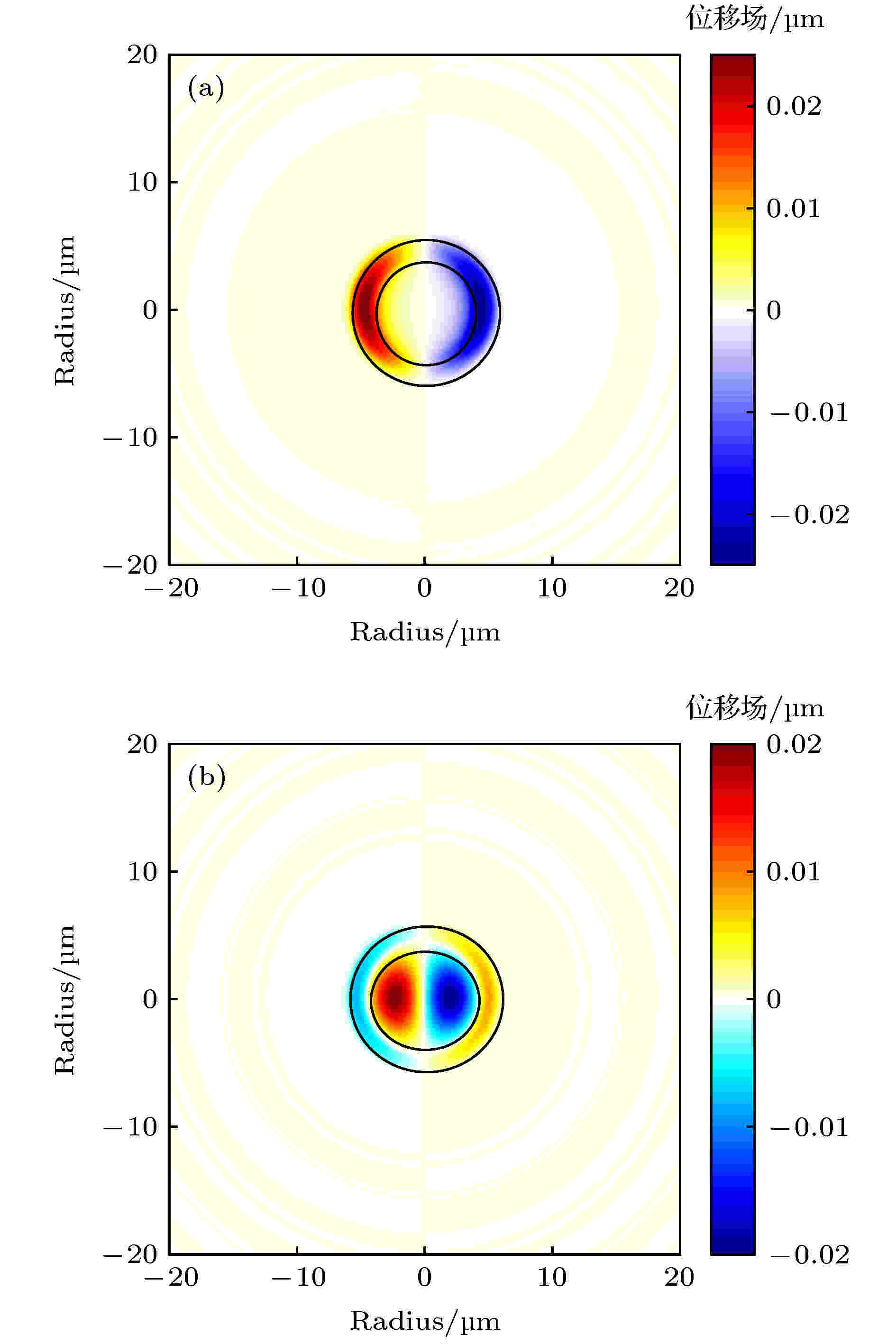 图 5
图 5 































































































































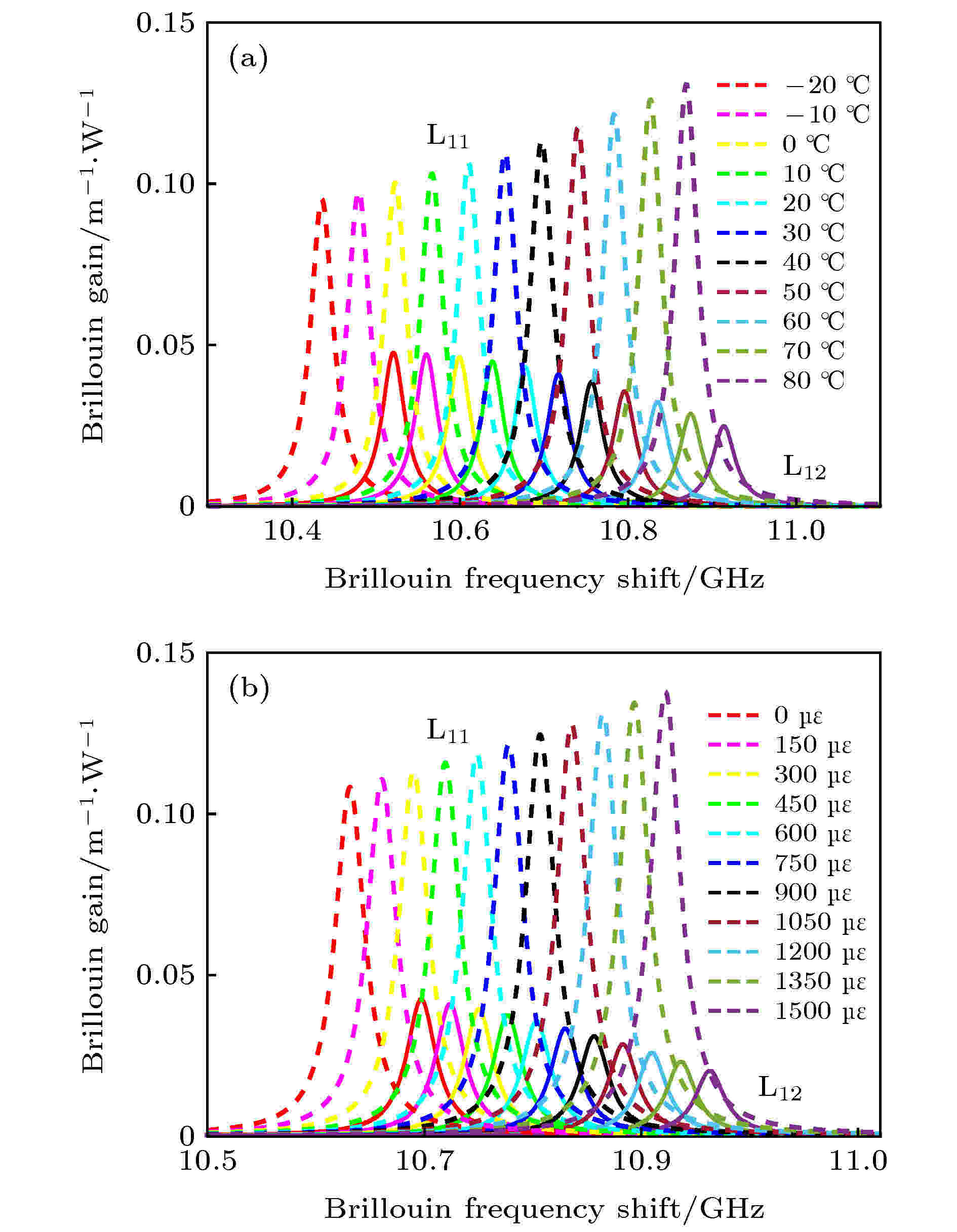 图 6
图 6 



 图 7 声学模式
图 7 声学模式





























































