摘要:在有对称性保护的条件下, 拓扑能带绝缘体等自由费米子体系的拓扑不变量可以在能带结构计算中得到. 但是, 为了得到强关联拓扑物质态的拓扑不变量, 我们需要全新的理论思路. 最典型的例子就是分数量子霍尔效应: 其低能有效物理一般可以用Chern-Simons拓扑规范场论来计算得到; 霍尔电导的量子化平台蕴含着十分丰富的强关联物理. 本文将讨论存在于玻色和自旋模型中的三大类强关联拓扑物质态: 本征拓扑序、对称保护拓扑态和对称富化拓扑态. 第一类无需考虑对称性, 后两者需要考虑对称性. 理论上, 规范场论是一种非常有效的研究方法. 本文将简要回顾用规范场论来研究强关联拓扑物质态的一些研究进展. 具体内容集中在“投影构造理论”、“低能有效理论”、“拓扑响应理论”三个方面.
关键词: 强关联系统/
拓扑序/
对称保护拓扑态/
拓扑量子场论

English Abstract

全文HTML

--> --> -->

在凝聚态物理中, 绝大多数金属/绝缘体等凝聚态材料可以在朗道-费米液体理论框架下得到很好的解释^[1]. 相互作用的电子会形成十分丰富的对称破缺序, 比如超导序、各种密度波序. 数学上, 假设哈密顿量的对称性G自发破缺到基态的对称性H. “序参量”$ \phi $是在实空间中的局域连续函数(从实空间到$ G/H $的映射). 对称破缺序的低能有效拉格朗日量可以根据对称性的要求表达成$ \phi $的泛函, 比如: $ {\cal{L}}[\phi]\sim (\partial \phi)^2+\phi^2+\phi^4\cdots\, $. 通过对该量子场论做重整化、线性响应等标准微扰计算, 我们可以系统地研究对称破缺相与相变.
由于在解释和预言实验方面的巨大成功, 对称破缺机制几乎成了固态物理的“标准模型”. 但是, 上个世纪八十年代强关联凝聚态实验的重大发现—分数量子霍尔效应(FQH)—让我们看到了超越此“标准模型”的可能性. FQH基态的拓扑性质, 比如拓扑激发“任意子”的统计性质和基态简并度^[2], 本质上与对称破缺毫无关联. 我们甚至没法定义一个局域函数作为序参量来刻画与区分不同的FQH态. 同时, FQH的低能有效理论是拓扑量子场论—Chern-Simons理论^[3]. 比如, 对于填充数$\nu= 1/k $的劳夫林(Laughlin)态, 其低能有效理论是$ U(1)_k $ Chern-Simons理论. 作用量可写为

$ S = \frac{k}{4{\text{π}}} \int a \wedge {\rm d}a ,$

其中场量$ a_\mu $是$ U(1) $规范场. 该规范理论在(2+1)维^①闭合流形上的大规范不变性要求系数k必须量子化为整数: $ k\in {\mathbb{Z}} $. S是一个拓扑量子规范理论, 明显不同于$ {\cal{L}}[\phi] $. 从传统的微扰重整化技术来看, 我们很难想象一个只含有电子算符的量子多体系统会“流动到”一个含有演生规范场的拓扑量子场论. 需要注意的是, 这里的Chern-Simons理论是所谓的流体力学构造^[3], 具有严格的系数(即k)量子化要求, 不同于Zhang等^[4]的复合玻色子场论、Lopez和Fradkin^[5]以及Jain^[6–8]的复合费米子场论.
作为拓扑序理论的先驱, Wen^[9,10]指出FQH不是简单的“填能级+微扰”能够解释的费米子系统^[11], 而是一种完全超越传统固态物理框架的强关联物质形态. 他把FQH等一大类超越对称破缺机制的量子多体态所含有的“刚性”、“序”称为“拓扑序”^[10](注: 为了与近年来出现的容易混淆的术语区分开, 本文暂称之为“本征拓扑序”, intrinsic topological order, iTO). iTO的提出使我们对超越对称破缺序的量子多体物理的理解有了飞跃式发展. 同时, 拓扑量子场论和共形场论的引进, 极大地促进了凝聚态物理与数学物理等学科的交流. 但是问题在于, iTO的确切的定义是什么? 是不是有能隙的超越对称破缺机制的多体态都是iTO? 比如, 霍尔丹(Haldane)自旋链^[12]是不是iTO呢? 当然现在我们已经知道, 细究此类凝聚态物理的问题需要借助量子信息科学中的一些非常深刻的概念和方法. Chen等^[13], Verstraete等^[14]和Vidal^[15]借助量子信息中的 “有限深度的量子电路”来重新认识有能隙的多体态. 首先, 自旋系统的每个格点上的自旋子空间提供了一个有限维度的“子空间”. 比如, 自旋-$ 1/2 $的体系的每个格点上的子空间维度是$ 2 $. 我们从具有这种希尔伯特空间的局域可分解的性质的多体态出发, 使用空间局域幺正算符(LU)将有能隙的多体态作绝热幺正变换. 如果多体态可以通过有限次数的LU操作变换成平凡的直积态, 那么该多体态就是短程纠缠态. 否则, 该多体态是长程纠缠态. 在热力学极限下, 我们需要非常小心定义“有限次数”: 先取热力学极限, 再取次数的极限. 然后, 如果任意次数LU都无法连接到直积态, 那么该多体态是长程纠缠态. SPT和iTO^②分别是短程纠缠态和长程纠缠态.
在有限多次的LU操作下, 霍尔丹自旋链的基态波函数(比如AKLT严格可解模型的基态波函数^[16])可以变换成平凡的直积态, 因而霍尔丹相是短程纠缠态. 但是从对称保护的意义上来看, 霍尔丹相仍然是“非平凡”的, 这是因为连接霍尔丹相与平凡的直积态之间的所有绝热路径(注: 路径就是一连串LU操作)都破坏特定的对称性, 比如自旋旋转对称性或者时间反演对称性($ {\mathbb{Z}}^T_2 $). 像霍尔丹相这种非平凡的短程纠缠态被称为“对称保护拓扑态”(SPT)^[17–19]. 因为体内每个格点上的自旋都是整数, 所以边缘上出现的半整数自旋表明一维体内有非平凡的SPT序. 但如果自旋对称性被破坏, 分数化的边界自旋就不再存在. SPT的体态有能隙, 体内的激发都是系统本身的玻色子(及其组合)激发或者自旋翻转等. 这些激发被称为平凡激发. 但是SPT边界上会有非平凡的量子态出现(以量子反常体现). 在不破坏对称性的条件下, SPT的边界态无法单独成为一个可以被格点正规化的量子理论. 除霍尔丹自旋链^[12]之外, 与SPT序有关的具体模型已经有很多研究, 比如掺杂的霍尔丹链^[20]、二维CZX自旋模型^[21]、二维玻色整数量子霍尔态^[22–24]、二维莱温-顾(Levin-Gu)自旋模型^[25]、二维自旋量子霍尔效应^[26]、三维拓扑顺磁体^[27]、三维玻色拓扑绝缘体(BTI)^③[28]等.
SPT研究领域的最重要的进展之一是文献[29,30]提出的统一的分类与表征方法. 具体来讲, 霍尔丹相只是SPT大家族的冰山一角. 正如抽象数学“群论”被用于分析对称破缺序, 代数拓扑里面的“群的上同调论”^[29,30]被发现可以用来构造SPT的严格可解模型的配分函数, 并在给定空间维度D和对称群G的条件下给出SPT的不等价类(亦即SPT的分类). 具体来讲, 给定G之后, 我们可以用G的上同调群$ H^{D + 1} [G, U(1)] $的群元$ \omega $来标记SPT的不等价类. 在群上同调的框架下, 我们可以用定义在离散时空格点上的非线性西格玛模型来研究SPT的体内的基态和边界的低能激发态. 正如物理其他领域一样, 用不同的角度不同的方法去理解SPT物理是非常有价值的. 群上同调的构造办法非常系统化. 另一方面, 由于群上同调的格点模型代表SPT不动点的物理, 不动点模型的自旋之间的相互作用十分复杂(比如: 可能是六个相邻自旋或者更多的相互作用). 群上同调理论关于连续自旋幺正对称群的计算非常复杂, 对反幺正对称性的SPT的分类也不完全^[28,31]. 然而这两种类型的对称性是实际量子自旋材料中常见的对称性. 另外, 给定一个“非不动点”的基态波函数, 群上同调方法不方便直接用于判断出该基态是否是SPT、是哪一个SPT.
与SPT相反, iTO^[10,32–35]具有长程纠缠, 不需要对称性的保护, 支持非平凡的拓扑激发(比如二维iTO中的任意子). iTO的边界上会有“引力反常”(比如一维手征流). iTO的典型例子是手征自旋液体^[2]、toric code自旋模型^[36]、Kitaev蜂窝格子自旋模型^[36]、莱温-文(Levin-Wen)弦网自旋模型^[37,38]、Dijkgraaf-Witten模型^[39]等. iTO和SPT有重要的对偶关系^[25,40]; 通过研究iTO序我们可以间接探索新的SPT序. 当iTO具有某种对称性G, 我们称这种iTO为SET(symmetry-enriched topological phases, 对称富化拓扑态)^[13]. 从这个定义上来看, 分数量子霍尔效应可以看成含有二维手征iTO和$ U(1) $对称群的SET序. SET的研究也与寻找拓扑量子自旋液体^[41,42]紧密联系: 通过研究任意子激发携带的分数化量子数, 我们可以分类与刻画不同的自旋液体态. 二维SET的张量范畴数学框架最近也有非常系统的研究^[43–47]. 三维iTO含有圈激发(loop excitations), 因而有必要研究三维SET甚至无能隙的自旋液体态中对称性如何分数化^[48–60].
SPT, iTO和SET都是强关联拓扑物质态. 我们不可能通过能带结构的分析来实现完整的分类和表征. 寻找这些拓扑物质态的“拓扑不变量”需要新的思路. 人们在研究铜氧高温超导的过程当中已经发展了许多非常有效的理论研究方法^[11,61–63]. 规范场论就是其中一种. 作为粒子物理标准模型的理论基础, 规范场论在高能物理中占据着至关重要的地位. 在凝聚态物理特别是强关联物理中, 规范结构通常以低能下的演生的动力学自由度出现. 在长波低能下, 我们可以构造出具有动力学的阿贝尔规范结构甚至非阿贝尔规范结构. 近年来凝聚态物理中的拓扑物质态为研究具有拓扑性质的规范场论提供了一个非常重要的平台. 同时, 数学物理、高能物理里有许多与实际(3 + 1)维时空的粒子物理并无直接关系、但仍具有十分重要的理论价值的研究成果. 令人振奋的是, 这些研究成果十分巧妙地应用到了凝聚态特别是强关联拓扑物质态中, 比如在研究拓扑物质态的边界态的量子反常、体内的拓扑量子场论、编织统计、拓扑量子计算等方面的应用.
本文将简要回顾近年来SPT，iTO和SET这些拓扑物态的规范场论的研究进展. 本文具体内容主要在“投影构造理论”(第2章)、“低能有效理论”(第3章)、“拓扑响应理论”(第4章)这三大块. 在“投影构造理论”中, 我们将物理自由度分成多个“部分子”, 这些部分子之间在紫外有强烈的规范涨落. 在“低能有效理论”中, 我们使用流体力学方式的办法来得到拓扑物质态的低能有效规范场论. 在这些场论里的规范场是有动力学的. 在“拓扑响应理论”中, 我们通过施加外部规范场来探测拓扑物质态中的对称性的性质. 这些拓扑响应理论里的规范场是静止的，没有动力学. 第5章是简短的总结与展望.

2

-->

2.1.部分子之间的规范涨落与玻色型整数量子霍尔效应

“投影构造”(projective/parton construction)已经广泛用于重费米子、高温超导等强关联问题^{[7,61,64–81]}. 最近该方法也用在了构造SPT态的问题上^[27,82–86]. 在这种构造当中, 玻色子/自旋算符可以分解成多个费米子(也可能是玻色型)算符(被称为“部分子”, parton)的乘积. 部分子形成各种平均场的量子态(常称为“拟设”, ansatz). 由于部分子形成的希尔伯特空间比原始玻色子/自旋空间的“物理希尔伯特”空间($ {\mathcal{H}}_{\rm {phys}.} $)大, 我们需要最后通过投影算符将部分子重新“粘”在一起, 恢复物理希尔伯特空间.
在这种构造方法中, 一个难点在于如何处理部分子之间的规范涨落. 实际上, 当我们在格点上写下部分子的作用量时, 和部分子耦合的那些规范场并没有麦克斯韦项(Maxwell项)出现. 这说明, 在格点上(紫外), 部分子之间的规范涨落的强度是无穷大的! 但是, 如果部分子形成的平均场量子态恰巧能给规范场一个能隙, 那么规范涨落就被压制了^④. 在二维SPT的投影构造中, 我们可以假设部分子填充陈-能带(Chern band), 从而自然地给规范涨落提供一个Chern-Simons能隙^[87]. 即使陈数(Chern number)为零, 由于二维的纯紧致化量子电动力学(QED)没有库仑相, 规范场耦合常数将始终流到强耦合区域的瞬子激增(instanton proliferation)态, 导致无能隙的光子从激发谱中消失. 所以, 在二维SPT的投影构造中, 规范涨落是相对容易处理的. 然而, 三维体系的部分子之间的规范涨落是一个复杂的问题. 三维没有陈氏能带可以让部分子填充, 同时三维QED可以处在库仑相也可以处在磁荷凝聚(monopole condensation)相. 为了让体内既有能隙也可能支持非平凡的SPT序, 我们在文献[84,85]中使用了双荷子(dyon)凝聚这种方式来做投影构造. 本文将在第2.5节中介绍三维的投影构造.
文献[83]研究了对称群为$ U(1) $, $ SO(3) $, $ SU(2) $的二维SPT的低能有效场论和基态波函数的投影构造. 这里的投影构造的基本思路如下: 考虑部分子形成了各种各样的陈-能带, 然后通过投影算符恢复物理希尔伯特空间. 文献[86]对此投影构造做了蒙特卡罗方法计算, 从多个角度验证了投影后的态是非平凡SPT. 如图1所示, 投影后的态的拓扑纠缠熵为零, 说明没有本征拓扑序. 这种SPT也被称为“玻色型整数量子霍尔态”(BIQH), 对称群是$ U(1) $, 其霍尔电导量子化为偶数(单位为: ${e^2}/{h} $): $ \sigma_{xy} = 0, \pm2, \pm4, \cdots $. 为理解为什么$ \sigma_{xy} $量子化为偶整数, Senthil和Levin^[23]借助著名的“劳夫林论证”(Laughlin's argument)的基本思想^[88]提供了一个十分简单的图像: $ \sigma_{xy} $必须量子化为整数, 以保证体内没有分数激发; 而且$ \sigma_{xy} $必须是偶数, 以保证体内不存在费米子激发.
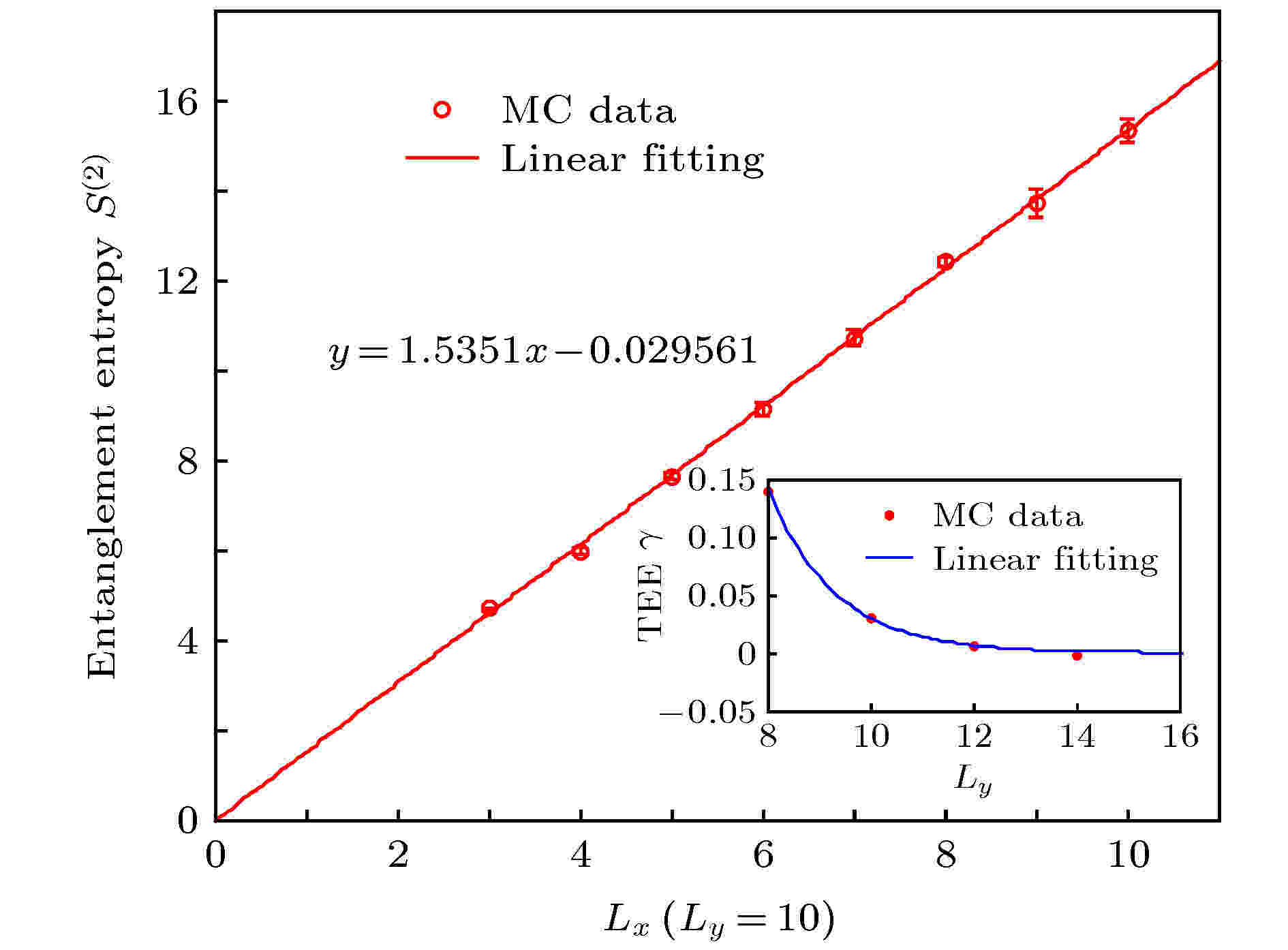图 1 蒙特卡洛验证投影后得到的SPT波函数的拓扑纠缠熵为零, 摘自文献[86]
Figure1. Monte Carlo verification of vanishing topological entanglement entropy of the SPT wave function obtained from the projective construction

2 -->

2.2.部分子的拟设与Hubbard相互作用

文献[83,86]做了初步的投影构造研究. 本文将讨论一些更加典型的例子, 澄清一些具体技术细节. 首先考虑两种不同“味”(flavor)的自旋–1/2的费米子: $ f_{1\sigma} $和$ f_{2\sigma} $. 这里的“味”指标可以是双层二维系统的层指标, 也可以代表不同最外层轨道. 这些费米子可以看成上面所说的物理自由度分解开形成的部分子; 也可以将其直接看成是真实存在的费米子; 然后施加适当的Hubbard相互作用, 可以将这个费米子系统的希尔伯特空间投影到“物理自由度”组成的$ {\mathcal{H}}_{\rm {phys}.} $.
首先, 我们假设两个味的费米子以各种填充方式形成能带绝缘体. 考虑表1里的四种拟设($ A1, A2, A3, A4 $). 在该表格里, 每个元胞里的费米子填充数完全由陈-能带数目决定. 也就是说, 费米子不再填充其他任何能带. 这样一来, 我们可以直接从该表格读出每种费米子总的粒子数目. 比如, 拟设$ A1 $里的费米子总粒子数分别为

拟设	完全被$f_1$填充的陈-能带	完全被$f_2$填充的陈-能带	自旋矢量$q^T_s$	电荷矢量$q^T_c$
$A1$	$\uparrow+, \downarrow+, \uparrow-, \downarrow-$ $(2, 2)$	$\uparrow+, \downarrow+, \uparrow-, \downarrow-$ $(2, 2)$	$\left(\dfrac{1}{2}~~-\dfrac{1}{2}~~\dfrac{1}{2}~~-\dfrac{1}{2}~~\dfrac{1}{2}~~-\dfrac{1}{2}~~\dfrac{1}{2}~~-\dfrac{1}{2}\right)$	$(1~~1~~1~~1~~1~~1~~1~~1)$
$A2$	$\uparrow+, \downarrow-$ $(1, 1)$	$\uparrow+, \downarrow-$ $(1, 1)$	$\left( {1}/{2}~~- {1}/{2}~~ {1}/{2}~~ -{1}/{2}\right)$	$(1~~1~~1~~1)$
$A3$	$\uparrow+, \downarrow-$ $(1, 1)$	$\downarrow+, \uparrow-$ $(1, 1)$	$\left(1/{2}~~- {1}/{2}~~- {1}/{2}~~ {1}/{2}\right)$	$(1~~1~~1~~1)$
$A4$	$\uparrow+, \downarrow-$ $(1, 1)$	无	$\left( {1}/{2}~~- {1}/{2}\right)$	$(1~~1)$

表1二维投影构造中的部分子的拟设. $ A1, A2,\cdots, A4 $代表四种拟设. 每条完全填充的能带由箭头和正负号标记. 箭头表示自旋方向, 正负号代表陈数为1或–1. A1一共有8条填满的陈-能带. A2和A3都有4条填满的陈-能带. A4只用到了f₁, 一共有两条陈-能带被填满. 括号里成对的数字表示单个元胞里的费米子f₁或f₂的填充数: (自旋向上的费米子数目, 自旋向下的费米子数目).
Table1.Parton ansatzes in the two-dimensional projective construction. $ A1,A2, \cdots, A4 $ stand for four different ansatzes respectively. Each fully occupied band is labeled by a pair of arrow and plus/minus sign. The arrow represents the spin eigenvalue of $ S^z $, and $ \pm $ represents Chern number $ \pm1 $. In A1, there are 8 fully occupied Chern bands; There are 4 fully occupied Chern bands in each of A2 and A3. In A4, flavor index is not involved, so only one flavor, say, $ f_1 $ is taken into account. And there are two filled Chern bands. A pair of integers denote the filling number of either $ f_1 $ and $ f_2 $ in each unit cell: (fermion number with up spin, fermion number with down spin).

$ \begin{aligned} N^{f1}_ \uparrow \; &= N^{f1}_ \downarrow = N^{f2}_ \uparrow = N^{f2}_ \downarrow \\ &= \frac{1}{2} N^{f1} = \frac{1}{2}N^{f2} = 2 N_{\rm cell} = 2 N_{\rm latt}/q.\end{aligned} $

其中$ N_{\rm cell} $是总的元胞数目, $ N_{\rm latt} $是总的格点数目, q是单个元胞对应的不等价格点个数. 拟设$ A2 $里的费米子总粒子数分别为:

$ \begin{aligned}N^{f1}_ \uparrow \;&= N^{f1}_ \downarrow = N^{f2}_ \uparrow = N^{f2}_ \downarrow \\ &= \frac{1}{2}N^{f1} = \frac{1}{2}N^{f2} = N_{\rm cell} = N_{\rm latt}/q.\end{aligned} $

拟设$ A3 $里的费米子总粒子数分别为:

$ \begin{aligned}N^{f1}_ \uparrow \;&= N^{f1}_ \downarrow = N^{f2}_ \uparrow = N^{f2}_ \downarrow\\ &=\frac{1}{2}N^{f1} = \frac{1}{2}N^{f2} = N_{\rm cell} = N_{\rm latt}/q.\end{aligned} $

拟设$ A4 $里的费米子总粒子数分别为:

$ N^{f1}_ \uparrow = N^{f1}_ \downarrow = \frac{1}{2}N^{f1} = N_{\rm cell} = N_{\rm latt}/q .$

在投影之前, 表1的任意一个拟设都可以用如下的Chern-Simons理论来刻画^[89]:

$ S = \int \frac{{{K_{IJ}}}}{{4{\text{π}} }}{a^I} \wedge {\rm d}{a^J} + \frac{{q_c^I}}{{2{\text{π}} }}{A^c} \wedge {\rm d}{a^I} + \frac{{q_s^I}}{{2{\text{π}} }}{A^s} \wedge {\rm d}{a^I} + \cdots .$

其中, 省略号包含所有含有比Chern-Simons项更高阶的动量的作用量, 比如麦克斯韦项. 要注意的是, 麦克斯韦 项一般情况下可以忽略. 但是个别情况下, 我们需要保留麦克斯韦项. 我们用指标$ I, J = 1, 2, 3, 4, \cdots $表记第I或第J条完全被填满的能带. 第I条能带对应的粒子流$ J^I_\mu $: $ J^I_\mu = \dfrac{1}{2{\text{π}}}\partial_\nu a^I_\lambda \epsilon^{\mu\nu\lambda}\, $. 用微分形式可以简写为: $ J^I = \dfrac{1}{2{\text{π}}}*{\rm d}a^I $. 其中$ * $代表Hodge对偶算符. 显然, $ f_1 $费米子的总粒子数流$ J^{f1}_\mu $是所有由$ f_1 $占据的能带贡献的流的总和. 比如拟设$ A1 $中$ J^{f1}_\mu = J^1_\mu+ $$J^2_\mu+J^3_\mu+J^4_\mu$. 同样, $ f_2 $费米子的总粒子数流$ J^{f2}_\mu = J^5_\mu+J^6_\mu+J^7_\mu+J^8_\mu $. $ A^c_\mu $代表通常的外电磁场, 耦合到费米子流, 用于计算电磁响应. $ A^s_\mu $是外加的“自旋规范场”. 该规范场耦合到自旋$ S^z $形成的流. 电荷矢量$ \{q^I_c\} $和 自旋矢量$ \{q^I_s\} $分别决定每个能带对应的$ {U}(1)_C $ (代表电荷守恒的对称群)荷 和$ {U}(1)_{S^z} $(代表自旋z方向守恒的对称群)荷.
具体来讲, 对于$ A1 $来讲, 相应的K为:

$K = \left( {\begin{array}{*{20}{c}}1&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0\\0&0&{ - 1}&0&0&0&0&0\\0&0&0&{ - 1}&0&0&0&0\\0&0&0&0&1&0&0&0\\0&0&0&0&0&1&0&0\\0&0&0&0&0&0&{ - 1}&0\\0&0&0&0&0&0&0&{ - 1}\end{array}} \right) .$

其中, 能带指标$ I = 1, 2, \cdots, 8 $与表1中的能带从左到右依次对应. $ A2 $和$ A3 $共享同一个矩阵K:

$ K = \left( {\begin{array}{*{20}{c}}1&0&0&0\\0&{ - 1}&0&0\\0&0&1&0\\0&0&0&{ - 1}\end{array}} \right) . $

最后, 拟设$ A4 $的K为:

$ K = \left( {\begin{array}{*{20}{c}}1&0\\0&{ - 1}\end{array}} \right) .$

表1里的费米子都是自由的. 在这些自由费米子模型的基础上, 我们考虑如下形式的Hubbard相互作用(脚标i代表空间格点):

$\begin{split}\;& {H_{{\rm{int}}}} = {U_1}\sum\limits_i {{{({n_{i1}} - {n_{i2}})}^2}} \\&+ {U_2}\sum\limits_i {\left[ {{{({n_{i1 \uparrow }} - {n_{i2 \downarrow }})}^2} + {{({n_{i1 \downarrow }} - {n_{i2 \uparrow }})}^2}} \right]} \\& + {U_3}\sum\limits_i {\left[ {{{({n_{i,1 \uparrow }} - {n_{i2 \uparrow }})}^2} + {{({n_{i1 \downarrow }} - {n_{i2 \downarrow }})}^2}} \right]} \\& + {U_4}\sum\limits_i {\left[ {{{({n_{i1 \uparrow }} + {n_{i2 \downarrow }} - 1)}^2} + {{({n_{i1 \downarrow }} + {n_{i2 \uparrow }} - 1)}^2}} \right]} \\& + {U_5}\sum\limits_i {{{({n_{i1}} + {n_{i2}} - 1)}^2}} + {U_6}\sum\limits_i {{{({n_{i1}} - 1)}^2}} \\&+ {U_7}\sum\limits_i ( {n_{i1 \uparrow }} - {n_{i1 \downarrow }}{)^2}. \\[-15pt]\end{split}$

其中的带有各种脚标的算符n是格点i上相应费米子的粒子数算符. 这些相互作用在强耦合的极限下将限制每个格点上低能下可容许的费米子占据状态. 表2里列出了所有相互作用在强耦合极限下形成的低能希尔伯特空间, 亦即$ {\mathcal{H}}_{\rm phys.} $. 为了让每个格点上都能够同时处于该空间里然后做投影构造, 我们需要要求实空间里各种费米子总的填充数也满足一定要求. 因此, 在选择“拟设”和“相互作用”的时候, 一定要注意拟设里的晶格选择和能带填充设计是否自动满足了该表格里的要求. 如果没有得到满足, 则我们需要把部分高能态考虑进来.

U	任意一个格点上的物理希尔伯特空间基矢$ [f_1]n_{i, 1 \uparrow}, n_{i, 1 \downarrow}, n_{i, 2 \uparrow}, n_{i, 2 \downarrow}[f_2] $	费米子填充总数要求
$U_1$	$(0, 0, 0, 0)$, $(0, 1, 0, 1)$, $(0, 1, 1, 0)$, $(1, 0, 0, 1)$, $(1, 0, 1, 0)$, $(1, 1, 1, 1)\, $	$N^{f1}=N^{f2} $
$U_2$	$(0, 0, 0, 0)$, $(0, 1, 1, 0)$, $(1, 0, 0, 1)$, $(1, 1, 1, 1)\, $	$N^{f1}_{\uparrow} = N^{f2}_{\downarrow}, $ $N^{f1}_{\downarrow}=N^{f2}_{\uparrow}$
$U_3$	$(0, 0, 0, 0)$, $(0, 1, 0, 1)$, $(1, 0, 1, 0)$, $(1, 1, 1, 1)\, $	$N^{f1}_{ \uparrow}=N^{f2}_{ \uparrow}, $ $N^{f1}_{ \downarrow}=N^{f2}_{\downarrow}$
$U_4$	$(0, 0, 1, 1)$, $(0, 1, 0, 1)$, $(1, 0, 1, 0)$, $(1, 1, 0, 0)$	$N^{f1}_{\uparrow}+N^{f2}_{\downarrow}=N_{\rm latt}$, $N^{f2}_{\uparrow}+ N^{f1}_{\downarrow}=N_{\rm att}$
$U_5$	$(1, 0, 0, 0)$, $(0, 1, 0, 0)$, $(0, 0, 1, 0)$, $(0, 0, 0, 1)$	$ N^{f1} + N^{f2}=N_{\rm latt}$
$U_6$	$(1, 0)$, $(0, 1)$	$ N^{f1} =N_{\rm latt}$
$U_7$	$(0, 0)$, $(1, 1)$	$N^{f1}_{\uparrow} = N^{f1}_{\downarrow }$

表2在大U极限下, 实空间每个格点上的不消耗U能量的占据状态形成了物理希尔伯特空间. 我们需要对费米子的总的填充数做限制. 限制之后, 所有格点都能够同时处于物理希尔伯特空间.
Table2.At large U limit, the physical Hilbert space is formed by those occupancy bases without energy cost. We should restrict the total particle number of each flavor properly such that Hilbert space of every site is always in the physical Hilbert space

2 -->

2.3.投影后的态的量子霍尔“电”导

在开始做投影之前, 我们需要小心定义各种霍尔“电”导来确定投影之后的态的拓扑性质. 首先, 我们这里需要同时考虑施加外电磁场和所谓的“自旋规范场”. 前者最小耦合于电流, 后者最小耦合于自旋流(z分量). 由于两种外场和两种响应流的出现, 为了不产生歧义, 我们需要小心定义关于电导的术语. 新定义的术语需要明确体现出外场和响应流两个信息. 最一般的响应理论由如下这个拉格朗日量给出:

$ \begin{align} &{\cal{L}}_{\rm Resp.} = \frac{1}{2} \begin{pmatrix} A^c_\mu& A^s_\mu \end{pmatrix} \begin{pmatrix} \sigma^c&\sigma^{cs}\\ \sigma^{cs}&\sigma^{s} \end{pmatrix}\partial_{\nu} \begin{pmatrix} A^c_\lambda\\ A^s_\lambda \end{pmatrix}\epsilon^{\mu\nu\lambda}\,. \end{align} $

其中, $ \sigma^c $是“量子电荷霍尔电导”, 也就是通常意义下的“量子霍尔电导”, 相应的外场和响应流分别是外电磁场和电流; $ \sigma^{cs} $在这里被称为“量子电荷-自旋霍尔电导”, 也就是平常所说的Kane-Mele模型中的“量子自旋霍尔电导”, 相应的外场和响应流分别是外电磁场和自旋流(或者交换一下: 自旋规范场和电流). $ \sigma^s $被称为“量子自旋霍尔电导”, 但不是通常意义下的量子自旋霍尔电导, 这里相应的外场和响应流分别是自旋规范场和自旋流. 对于非阿贝尔的版本的$ \sigma_s $, 读者可以参见文献[26]里的讨论, 该文章作者将$ SU(2) $的情形叫做自旋量子霍尔效应, 也是为了和通常意义下的量子自旋霍尔效应区别开. 对于一个玻色SPT, $ \sigma^{cs} $的量子化条件是$ \sigma^{cs} = {k}/{2{\text{π}}} $, 其中$ k\in{\mathbb{Z}} $. 对这个量子化条件的一个简单的物理论证, 可参见文献[51].
2 -->

2.4.几个投影波函数例子

例子1　$ |A1 U1\rangle $
我们用“拟设+Hubbard相互作用”来标记一个投影波函数. 比如$ A1 U1 $表示在拟设$ A1 $所对应的能带绝缘体上加上$ U_1 $相互作用, 并考虑大$ U_1 $的极限下得到的态. 该多体态可以写为: $ |A1 U1\rangle = P^{U_1}_G|A1\rangle $其中, $ |A1\rangle $是拟设$ A1 $的陈-能带对应的基态波函数. $ P^{U_1}_G $是投影算符, 定义为: $ P^{U_1}_G \!=\! \displaystyle\prod\nolimits_i \left(\displaystyle\sum\nolimits^6_{\ell = 1}| \varPhi_i^\ell\rangle\langle \varPhi_i^\ell|\right) $. 其中, i是空间格点坐标. 波函数$ | \varPhi_i^\ell\rangle $定义为$ | \varPhi_i^1\rangle = |0000\rangle\, , | \varPhi_i^2\rangle = |0101\rangle\, , | \varPhi_i^3\rangle = |0110\rangle\, , | \varPhi_i^4\rangle = $$|1001\rangle\, ,| \varPhi_i^5\rangle = |1010\rangle\, , | \varPhi_i^6\rangle = |1111\rangle\, $. 这里的“$ |xxxx\rangle $”对应表2中的费米子占据状态. 为了理解这个投影波函数的性质, 我们应用Chern-Simons理论来分析. 投影算符起的作用实际上是要求$ f_1 $与$ f_2 $的粒子数流处处相等, 亦即 $\displaystyle \sum\limits^4_{I = 1}J^I_\mu \!=\! \sum\limits^8_{I = 5}J^I_\mu $. 选择合适的规范, 该约束条件可以改写成 $\displaystyle \sum\limits^4_{I = 1}a^I_\mu = \sum\limits^8_{I = 5}a^I_\mu $. 因而, 这$ 8 $个规范场中只有$ 7 $个是线性独立的. 不失一般性, 我们可以将公式(2)中的$ a^8_\mu $替换掉, 得到新的Chern-Simons理论. 新的K矩阵, 矢量$ q_c $和矢量$ q_s $分别为:

$\begin{split} &\left( {\begin{array}{*{20}{c}}0&{ - 1}&{ - 1}&{ - 1}&1&1&1\\{ - 1}&0&{ - 1}&{ - 1}&1&1&1\\{ - 1}&{ - 1}&{ - 2}&{ - 1}&1&1&1\\{ - 1}&{ - 1}&{ - 1}&{ - 2}&1&1&1\\1&1&1&1&0&{ - 1}&{ - 1}\\1&1&1&1&{ - 1}&0&{ - 1}\\1&1&1&1&{ - 1}&{ - 1}&{ - 2}\end{array}} \right),\\ &\left( {\begin{array}{*{20}{c}}2\\2\\2\\2\\0\\0\\0\end{array}} \right),\left( {\begin{array}{*{20}{c}}0\\{ - 1}\\0\\{ - 1}\\1\\0\\1\end{array}} \right).\end{split}$

新的矩阵的行列式为零($ \det K = 0 $). 为了更明显看到零本征值, 我们做相似变换将$ (K, q_c, q_s) $变换到如下形式:

$ \begin{split}& K \to WK{W^{\rm T}} \\=\;& \left( {\begin{array}{*{20}{c}}0&{ - 1}&{ - 1}&{ - 1}&1&1&0\\{ - 1}&0&{ - 1}&{ - 1}&1&1&0\\{ - 1}&{ - 1}&{ - 2}&{ - 1}&1&1&0\\{ - 1}&{ - 1}&{ - 1}&{ - 2}&1&1&0\\1&1&1&1&0&{ - 1}&0\\1&1&1&1&{ - 1}&0&0\\0&0&0&0&0&0&0\end{array}} \right),\\{q_c} \to W{q_c} = \;& {\left( {\begin{array}{*{20}{c}}2&2&2&2&0&0&0\end{array}} \right)^{\rm T}},\\{q_s} \to W{q_s} =\;& {\left( {\begin{array}{*{20}{c}}0&{ - 1}&0&{ - 1}&1&0&0\end{array}} \right)^{\rm T}},\\{\text{其中}},\;W =\;& \left( {\begin{array}{*{20}{c}}1&0&0&0&0&0&0\\0&1&0&0&0&0&0\\0&0&1&0&0&0&0\\0&0&0&1&0&0&0\\0&0&0&0&1&0&0\\0&0&0&0&0&1&0\\1&1&{ - 1}&{ - 1}&{ - 1}&{ - 1}&1\end{array}} \right)\\[-45pt]\end{split}$

这里的变换矩阵$ W\in {\rm{GL}}(7, {\mathbb{Z}}) $. 需要注意的是, 为了简化符号, 在新的基底下, 我们仍然使用了旧的符号$ (K, q_c, q_s) $和$ a^I, I = 1, 2, 3, \cdots, 7 $. 在这个新的基底下, 第七个规范场$ a^7_\mu $没有Chern-Simons项. 因而我们需要考虑比Chern-Simons更高阶的规范不变项, 亦即麦克斯韦项$ \dfrac{1}{g^2}(\epsilon^{\mu\nu\lambda}\partial_\nu a^7_\lambda)^2 $. 尽管不确定g的大小, 我们知道$ (2 + 1) $维紧致量子电动力学的路径积分中的瞬子构型会导致一个有限大的光子质量(能隙)^[90–92]. 所以, 一个单纯的$ (2 + 1) $维的紧致QED始终是有能隙的. 但我们要十分小心地把这个结论用到我们的问题上来. 首先, 如果$ q_c $和$ q_s $的第7分量不为零, 那么$ a^7 $的磁通将会携带物理守恒荷—电荷和z方向的自旋. 瞬子构型使得磁通产生消失, 从而明显破坏对称荷的守恒律, 从而破坏在外加规范场(亦即$ A^c $和$ A^s $)规范变换下的不变性. 这个图像表明, 非零的物理守恒荷将修正瞬子产生算符的标度维度, 使得基态处于具有零质量光子激发的库伦相. 正好, 现在正在计算的例子中的$ q_c $和$ q_s $的第7分量都为0, 所以, 在我们讨论的具体问题里, $ a^3 $的确是有能隙. 我们可以把$ (K, q_c, q_s) $的第7行第7列都去掉, 得到:

$ \begin{split} & K = \left( {\begin{array}{*{20}{c}} 0&{ - 1}&{ - 1}&{ - 1}&1&1\\ { - 1}&0&{ - 1}&{ - 1}&1&1\\ { - 1}&{ - 1}&{ - 2}&{ - 1}&1&1\\ { - 1}&{ - 1}&{ - 1}&{ - 2}&1&1\\ 1&1&1&1&0&{ - 1}\\ 1&1&1&1&{ - 1}&0 \end{array}} \right),\\ & {q_c} = {\left( {\begin{array}{*{20}{c}} 2&2&2&2&0&0 \end{array}} \right)^{\rm T}},\\ & {q_s} = {\left( {\begin{array}{*{20}{c}} 0&{ - 1}&0&{ - 1}&1&0 \end{array}} \right)^{\rm T}} \end{split} $

这个新的K矩阵的行列式绝对值为$ 1 $, 因而$ |A1 U1\rangle $没有iTO. 对角元都是偶数, 因而$ |A1 U1\rangle $是一个玻色型的波函数. 该矩阵有三个正本征值和三个负本征值, 因而$ |A1 U1\rangle $是非手征的, 手征中心荷$ c = 0 $. 为了进一步判断该态是平凡的玻色绝缘体, 还是非平凡的SPT, 我们需要计算量子霍尔电导: $ \sigma^{c} = \sigma^s = \sigma^{cs} = 0 $. 由于所有电导都为0, 我们可以判定$ |A1 U1\rangle $是一个平凡的玻色绝缘体.
例子2　$ |A2 U1\rangle $
下面我们讨论$ |A2 U1\rangle $. 同样, 大$ U_1 $极限导致$ J^1_\mu+J^2_\mu = J^3_\mu+J^4_\mu $. 在选择合适的规范下, 该约束条件等价于: $ a^1_\mu+a^2_\mu = a^3_\mu+a^4_\mu $. 因而四个规范场不是完全独立, 我们可以把其中一个, 比如 $ a^4_\mu $消掉. 这样一来, 我们得到新的 K、$ q_c $和$ q_s $:

$K \!=\! \left(\!\!\!{\begin{array}{*{20}{c}}0&{ - 1}&1\\{ - 1}&{ - 2}&1\\1&1&0\end{array}}\!\!\!\right),{q_c}\! =\! \left( {\begin{aligned}2\\2\\0\end{aligned}} \right),{q_s} \!=\! \left( {\begin{aligned}\;0\;\\{-1}\\\;1\;\end{aligned}} \right) . $

注意, 以上新的矢量的行指标的编号从上到下依次对应着$ a^1_\mu, a^2_\mu, a^3_\mu $三个规范场. 因为新的矩阵的行列式为０($ \det K = 0 $), 我们需要用一个矩阵$ W\in {GL}(3, {\mathbb{Z}}) $做相似变换:

$\begin{split} & K \to WK{W^{\rm T}} = \left( {\begin{array}{*{20}{c}}0&1&0\\1&0&0\\0&0&0\end{array}} \right), \\& {q_c} \to W{q_c} = \left( {\begin{array}{*{20}{c}}0\\2\\0\end{array}} \right),\end{split} $

$ {q_s} \to W{q_s} = \left( {\begin{aligned}1\\0\\0\end{aligned}} \right){\rm{,}}\;　W = \left( {\begin{array}{*{20}{c}}{\rm{0}}&{\rm{0}}&{\rm{1}}\\{\rm{1}}&{\rm{0}}&{\rm{0}}\\{{\rm{ - 1}}}&{\rm{1}}&{\rm{1}}\end{array}} \right) . $

我们可以看到, 在新的基底下, $ 3\times3 $的K-矩阵可以写成泡利矩阵与零的直和: $ \sigma^x\oplus 0 $.在新的基底下, $ a^1 $和$ a^2 $之间混合在一起. 同时, $ a^3 $分别与$ a^1 $和$ a^2 $不混合, 而且$ a^3 $规范场没有Chern-Simons项$ \sim a^3\partial a^3 $. 由于$ q_c $和$ q_s $的第三分量都为零, 所以, 在我们讨论的具体问题里, $ a^3 $是有能隙的. 我们可以把$ (K, q_c, q_s) $的第三行第三列都去掉, 得到: $ K = \sigma^x\, , q_c = (0\; \; 2 ){\rm T}\, , q_s = (1\; \; 0){\rm T}\, $. 新的K表明$ |A2 U1\rangle $没有iTO, 非手征, 玻色型. 下一步, 我们可以计算各种霍尔电导: $ \sigma^{c} = \dfrac{1}{2{\text{π}}}q^{\rm T}_cK^{-1}q_c = 0, $$\sigma^{s} = \dfrac{1}{2{\text{π}}}q^{\rm T}_sK^{-1}q_s = 0\, , \sigma^{cs} = \dfrac{1}{2{\text{π}}}q^{\rm T}_cK^{-1}q_s = \dfrac{2}{2{\text{π}}} $. 由于有非零的“量子电荷-自旋霍尔电导”, $ |A2 U1\rangle $是一个受到$ {U}(1)_C\times {U}(1)_{S^z} $对称群保护的非平凡SPT.　
例子3　$ |A3 U1\rangle $
接下来我们讨论一下$ |A3 U1\rangle $. 注意到 拟设$ A3 $的自旋矢量 $ q_s = (1/2\; \; -1/2\; \; -1/2\; \; 1/2)^{\rm T} $, 在大U极限下, 我们可以得到与(11)一样的 K矩阵和 $ q_c $, 但是$ q_s = (1\; \; 0\; \; -1)^{\rm T} $. 在W的作用下, 我们得到与(12)式一样的K和$ q_c $, 但是$ q_s = (-1\; \; 1\; \; -2)^{\rm T} $. 我们注意到, $ q_s $的第三分量不再是零. 这说明, $ a^3 $的磁通将携带自旋自由度. 从而, $ a^3 $的光子仍然处于无能隙的库伦相. 接下来我们可以看到, 该无能隙的激发正好是投影之后得到的磁有序态的戈德斯通(Goldstone)模. 为了看出这一点, 我们可以对与$ a^3 $有关的项, 亦即

$ {\cal{L}}[a^3] = -\frac{2}{2{\text{π}}}A^s_\mu\partial_\nu a^3_\lambda\epsilon^{\mu\nu\lambda}+\frac{1}{g^2}(\partial_\nu a^3_\lambda\epsilon^{\mu\nu\lambda} )^2 $

做对偶变换. 用$ J^3_\mu = \dfrac{1}{2{\text{π}}}\partial_\nu a^3_\lambda \epsilon^{\mu\nu\lambda} $替换$ a^3 $: ${\cal{L}}[a^3] =$$ -2 J^{3}_\mu A^s_\mu+\theta \partial_\mu J^{3}_\mu +\dfrac{1}{g^2}(J^3_\mu)^2 $. 其中, $ \theta $是用于施加$ \partial_\mu J^{3}_\mu = 0 $这个约束条件的拉格朗日乘子. 积掉$ J^3 $可以得到:

$ {\cal{L}}\sim g^2(\partial_\mu\theta+2A^s_\mu)^2. $

这个有效理论正好是带对称性的凝聚体的有效理论, 其中 $ \theta $是戈德斯通模式. 需要强调的是, 这里的规范场$ A^s $是外加的、“非动力学的”自旋规范场, 因而戈德斯通模不会消失. 因而, $ |A3 U1\rangle $态的对称性是$ U(1)_C\times {\mathbb{Z}}_2 $.
除了$ a^3 $之外, 与$ a^1 $和$ a^2 $有关的项由Chern-Simons理论描述: $ K = \sigma^x\, , q_c = (0\; \; 2 )^{\rm T}$, $q_s = $$(-1\; \; 1)^{\rm T} $. 严格来讲, 由于$ U(1)_{S^z} $已经破缺到$ {\mathbb{Z}}_2 $, $ q_s $应该理解为对称破缺后剩余$ {\mathbb{Z}}_2 $荷, $ q_s $与$ q_s+2 $等价. 为了刻画这个态, 我们可以计算拓扑不变量: $ \sigma^{c} = \dfrac{1}{2{\text{π}}}q^{\rm T}_cK^{-1}q_c = 0$, $K^{s} = q^{\rm T}_sK^{-1}q_s = -2$, $K^{cs} = $$q^{\rm T}_cK^{-1}q_s = -2 $. 需要注意的是, 我们引入了新的符号$ K^s $和$ K^{cs} $来替代$ \sigma^{s} $和$ \sigma^{cs} $. 原因是现在自旋对称性不再是$ U(1)_{S^z} $, 无法定义与自旋有关的霍尔效应. 但物理上, 我们仍然可以用$ K^s $来描述外加的自旋$ {\mathbb{Z}}_2 $磁通的“自统计”—自己绕着自己转一圈的拓扑相位积累. $ K^s = 2 $说明这个外加的$ {\mathbb{Z}}_2 $自旋磁通可以看成一个称为“半子”(semion)的任意子(anyon). 但要注意的是, 由于无能隙的戈德斯通激发的存在, 两个$ {\mathbb{Z}}_2 $磁通之间始终存在一个对数相互作用势. 因而, 两个磁通的交换统计相位始终有一个非普适的动力学相位. 我们需要指出的是, 以上讨论的任意子及其非平凡的统计性质, 并不表示着$ |A3 U1\rangle $有iTO. 因为, 这些任意子都是外加的“非动力学的”自旋规范场$ A^s $产生的$ {\mathbb{Z}}_2 $磁通的性质, 而不是$ |A3 U1\rangle $态本身的激发的性质. 的确, 在$ |A3 U1\rangle $中, 与$ a^1, a^2 $有关的项组成的Chern-Simons项的K矩阵的行列式绝对值是1. $ {\mathbb{Z}}_2 $磁通被称为“monodromy缺陷”^[25,93].
如果我们把$ A^s $视为动力学的规范场的话, 那么, 由于希格斯机制的缘故, 戈德斯通模就不再存在. 此时的低能有效理论的K矩阵需要把$ A^s $也包括进来. 同时, $ A^s $是被Higgs到$ {\mathbb{Z}}_2 $规范群, 因而, 我们可以引进另外一个1-形式的动力学规范场B来把$ {\mathbb{Z}}_2 $放松到$ U(1) $, 从而我们可以在基矢$ (a^1, a^2, A^s, B) $下, 写出新的K矩阵:

$K = \left( {\begin{array}{*{20}{c}}0&1&{ - 1}&0\\1&0&1&0\\{ - 1}&1&0&2\\0&0&2&0\end{array}} \right),$

该矩阵的行列式绝对值为$ 4 $, 有拓扑激发.
例子4　$ |A4 U6\rangle $
如果考虑蜂窝格子的话, 拟设$ A4 $正好满足半填满(注意q = 2)的条件. $ |A4 U6\rangle $可以看成是Kane-Mele-Hubbard模型^[94–96]在半填满时的强耦合极限下的基态. 在大$ U_6 $极限下, $ a^2_\mu $可以被 $ -a^1_\mu $代替. 相应的低能有效理论对应的$ K, q_c, q_s $分别为:

$ K = 0\,,~~q_c = 0\,,~~q_s = 1. $

用与前面类似的分析办法, 我们可以得到把低能有效理论对偶到一个携带自旋量子数的凝聚体. 因而, 该投影波函数是一个自旋对称性$ U(1) $的自发破缺态, 是一个自旋能隙为零的磁有序态. $ q_c = 0 $说明激发都是电中性.
例子5　$ |A3 U4\rangle $
大$ U_4 $极限导致规范场之间的约束条件: $ a^1_\mu+a^3_\mu = 0\, , a^2_\mu+a^4_\mu = 0 $. 消掉$ a^3_\mu $和$ a^4_\mu $, 我们得到新的K, 新的$ q_c $, 和新的$ q_s $:

$ K = \left( {\begin{array}{*{20}{c}}2&0\\0&{ - 2}\end{array}} \right),~~{q_c} = \left( {\begin{aligned}0\\0\end{aligned}} \right),~~{q_s} = \left( {\begin{aligned}\;1\;\\{ - 1}\end{aligned}} \right) . $

这个矩阵正好是双半子态(double-semion state)的K矩阵. 行列式绝对值为$ 4 $, 说明有iTO. 对角元都是偶数, 说明是玻色型波函数. 这个iTO有三个非平凡拓扑激发: 半子s (拓扑自旋为i, 由准粒子矢量$ (1\; \; 0)^{\rm T} $标记), 反半子$ \overline{s} $(拓扑自旋为$ -i $, 由准粒子矢量$ (0\; \; 1)^{\rm T}$标记), 以及玻色复合粒子$ s\overline{s} $. 半子和反半子分别携带$ S_z $的物理自旋$ S_z = 1/2 $: $ S^z_{s} \!=\! \begin{pmatrix} 1, 0 \end{pmatrix} K^{-1}q_s = {1}/{2}\, , S^z_{\overline{s}} \!=\! \begin{pmatrix} 0, 1 \end{pmatrix} K^{-1}q_s \!=\! 　{1}/{2}. $
2 -->

2.5.双荷子凝聚和三维复合粒子理论

以上投影构造均是二维的情形. 正如第2.1节所述, 三维体系中关于部分子与部分子之间的规范涨落的处理将变得非常复杂. 文献[84,85]中提出的双荷子(dyon)凝聚机制可以用来得到一些非平凡的SPT. 这种双荷子凝聚机制在构造三维拓扑态中起的作用类似于复合费米子和复合玻色子理论在构造二维分数量子霍尔效应中起的作用^[4–8]. 所以, 我们把这个机制称为“三维复合粒子理论”^[84,85]. 基于该三维复合粒子理论, 我们可以构造BTI、费米型和玻色型分数拓扑绝缘体(具有$ U(1)\rtimes {\mathbb{Z}}^T_2 $的费米型与玻色型SET)等拓扑态, 也可以讨论三维iTO中的一种拓扑对称性—荷-圈激发对称性(Charge-loop excitation symmetry, Charles)^[85]. 这种对称性是二维iTO中的讨论^{[43,97–108]}的三维推广. 我们将在第2.6节中简单介绍一下Charles对称性.
考虑一个费米子(比如电子)系统^[85], 电子算符c可以写成奇数个费米型部分子($ f^i $, i = 1, 2, $ \cdots, 2 n + 1 $)的乘积: $ c = f^1 f^2\cdots f^{2 n + 1} $. 因而, 电子算符c是$ SU(2 n + 1) $规范群的一个单态. $ SU(2 n + 1) $的极大环面子群(maximal torus)是紧致的阿贝尔群$ (U(1))^{2 n} $. 其规范变换定义为: $ f^1 \;\rightarrow \;f^1 e^{i\theta_1}, \cdots, f^i \;\rightarrow \;f^ie^{i\theta_{i}-i\theta_{i-1}}, \cdots, f^{2 n + 1} \;\rightarrow $$f^{2 n + 1}e^{-i\theta_{2 n}}$. 这里的 $ \{\theta_i\} $ ($ i = 1, 2, \cdots, 2 n $)是空间格点和连续时间的任意标量函数. 这样一来, 通过应用't Hooft规范投影^[109], 电子体系的作用量在强耦合区域可以表示为相互作用的部分子与$ 2 n $个紧致的、动力学的、阿贝尔规范场$ \{a^{(i)}_\mu\} $ (i = 1, 2, $ \cdots, 2 n $). 为了表述简便, 我们称这些规范场为“内部规范场”. 与之对应, “外部规范场”特指用于探测电磁响应而施加的非动力学的电磁场. 图2给出了$ n = 1 $的情形. 波浪线代表外部规范场$ A_\mu $和两个内部规范场$ a_\mu $和$ b_\mu $(分别属于紧致规范群$ U_a(1) $和$ U_b(1) $). 部分子$ f^1 $和$ f^2 $分别携带$ U_a(1) $规范群的一个单位的规范荷和一个单位的负规范荷. 同时, 部分子$ f^3 $和$ f^2 $分别携带$ U_b(1) $规范群的一个单位的规范荷和一个单位的负规范荷. 部分子$ f^1 $, $ f^2 $, $ f^3 $分别携带电荷$ e, e, -e $.
图 2 一种将电子分成三个部分子的投影构造(即 $ n=1 $), 摘自文献[85]
Figure2. Parton decomposition of electron operators

尽管考虑到规范场的强耦合性, 规范涨落的领头效应仍然可以在考虑一些复合粒子的玻色-爱因斯坦凝聚之后做微扰计算得到. 在强耦合区域, 凝聚的复合粒子可以携带规范场的磁荷. 这个思路在$ (3 + 1) $维紧致QED、Georgi-Glashow模型、超对称杨-米尔斯理论(SUSY)中有所应用^{[90–92,109–117]}. 对于紧致阿贝尔规范理论, Fradkin和Susskind^[115]构造了磁单极子产生算符及其非零的真空期望值. 由于在磁荷凝聚相里, 试探电荷之间存在线性势能, 因而磁荷凝聚相也被称为: 禁闭相(confinement phase). 然而, 如果我们直接假设部分子之间的规范场涨落处于磁荷凝聚相, 部分子将简单地还原成电子, 我们将无法得到一个有趣的物质态(iTO或者SPT). 为了得到一个有能隙的、非平凡的拓扑态, 文献[84,85]考虑双荷子凝聚相, 也就是所谓的“倾斜禁闭相”(oblique confinement phase)^[109]. 双荷子指的是部分子和磁荷形成的复合粒子. 这里的部分子携带内部规范场的“电荷” ^⑤; 这里的磁荷是内部规范场形成的磁荷. 但我们要强调的是, 为了得到一个局域场论, 凝聚的双荷子携带的规范荷和磁荷不能属于同一个规范群. 因而, 严格来讲, 这里的被凝聚的粒子针对具体一个规范子群来讲, 并不是双荷子.
整个系统的规范群是$ U(1)_C\times U(1)_a\times U(1)_b $. 在没有考虑规范涨落的时候, 存在包括部分子在内的各种不同的粒子. 每个粒子可以用三个“电荷”和三个“磁荷”来标记. 尽管三维没有陈氏能带, 我们可以考虑新的拟设: 部分子处于三维拓扑绝缘体的状态^[118,119]. 图2中使用了规范场A、a和b. 在很多情况下, 我们需要变换一下基矢得到如下三个更加好用的规范场: $ A^{f1}_\mu = a_\mu+A_\mu, A^{f2}_\mu = -a_\mu-$$b_\mu+A_\mu$, $A^{f3}_\mu = b_\mu-A_\mu$, 如图2 所示. 按照定义, $ A^{fi} $是只耦合到$ f^i $的规范场. 在新的基矢下, 规范群可以写为: $ U(1)_{f1}\times U(1)_{f2}\times U(1)_{f3} $. 两套规范场标记方案之间满足如下变换关系:

$ \left( {\begin{array}{*{20}{c}}{{A_\mu }}\\{{a_\mu }}\\{{b_\mu }}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&1&1\\0&{ - 1}&{ - 1}\\1&1&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}{A_\mu ^{f1}}\\{A_\mu ^{f2}}\\{A_\mu ^{f3}}\end{array}} \right) .$

这里的变换矩阵属于$ {GL}(3, {\mathbb{Z}}) $群. 由于规范场有两种标记方案, 相应的规范荷和磁荷也应该满足一定的变换关系. 我们用 $ N_{a, b} $来标记 $ U(1)_{a, b} $规范群里的规范荷, 同时, 用$ N_m^{a, b} $来标记磁荷. 我们用$ N_A $和M 来标记外电磁场响应下的“裸电荷”和“磁荷”. 由于凝聚体有电荷屏蔽作用, 每个粒子实际携带的电荷Q需要在“裸电荷”上扣除掉类似Debye-Hückel的屏蔽电荷. 在新的基矢下, 我们可以用$ N^{fi} $和$ N^{fi}_m $分别标记规范荷和磁荷. 根据变换公式(19), 我们可以得到两个基矢下各种荷之间的变换:

$ \left( {\begin{array}{*{20}{c}}{{N_A}}\\{{N_a}}\\{{N_b}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&1&{ - 1}\\1&{ - 1}&0\\0&{ - 1}&1\end{array}} \right)\left( {\begin{array}{*{20}{c}}{{N^{f1}}}\\{{N^{f2}}}\\{{N^{f3}}}\end{array}} \right), $

$\left( {\begin{array}{*{20}{c}}M\\{N_m^a}\\{N_m^b}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}1&1&1\\0&{ - 1}&{ - 1}\\1&1&2\end{array}} \right)\left( {\begin{array}{*{20}{c}}{N_m^{f1}}\\{N_m^{f2}}\\{N_m^{f3}}\end{array}} \right) . $

其中两个矩阵也属于$ {GL}(3, {\mathbb{Z}}) $群. 所有磁荷的定义域都在整数域: M, $ N_m^a $, $ N_m^b $, $ N_m^{fi}\in{\mathbb{Z}} $. 然而, 当考虑强规范涨落之后, 留在激发谱上的粒子的磁荷实际可以取到的整数区间要小于整个整数域.
根据威腾效应(Witten effect)的公式^[118–120], 规范荷$ N^{fi} $ ($ i = 1, 2, 3 $)与磁荷有如下关系: $ N^{fi} = n^{fi}+\dfrac{\theta}{2{\text{π}}}N^{fi}_m $. 其中, 整数$ n^{fi} $标记相应复合粒子内粘附了多少部分子$ f^i $. $ \theta $由部分子的拟设决定. 如果$ \theta = 0 $, 那么所有部分子处于平凡能带绝缘体拟设; 如果$ \theta = {\text{π}} $, 那么所有部分子均处于非平凡的拓扑能带绝缘体拟设. 取决于$ \theta $, $ N^{f1, f2, f3} $, $N_a, N_b, N_A$既可以是整数也可以是半整数.
考虑强规范涨落之后, $ \varphi_1 $和$ \varphi_2 $两个玻色型粒子发生凝聚^⑥. 由于希格斯(Higgs)机制, 两个凝聚体提供两个独立约束条件. 六个参数最终剩下四个自由参数. 比如, 消掉$ N^a $和$ N^b $, 剩下$ (N_A, M, N^a_m, N^b_m) $. 通过分析这四个参数的取值, 我们可以判断强规范涨落(亦即投影之后)得到的态是否保持时间反演对称性、是否支持非平凡的威腾效应, 由此得到投影后的态的表征.
2 -->

2.6.荷-圈激发对称性与非阿贝尔线缺陷

文献[85]提出三维拓扑态的“荷-圈激发对称性”(简称为: $ {\mathsf{Charles}} $)的动机是推广二维iTO中的“拓扑对称性”(或称之为“任意子对称性”anyonic symmetry)^{[43,97–108]}. 二维iTO中最简单的一个例子就是Wen-plaquette格点模型^[121]实现的$ {\mathbb{Z}}_2 $ iTO里的激发e和激发m之间的交换操作. 该操作就是任意子对称群$ {\mathbb{Z}}_2 $里的非平凡操作. 在这个操作下, iTO的所有拓扑不变量(比如拓扑自旋、编织统计)保持不变. 有趣的是, 对于这个具体的例子, 我们可以通过在格点上引入缺陷—位错(lattice dislocation)来实现e-m之间的交换操作: 当e穿过一条终止于位错的割线(branch cut)的时候, e将变成m. 更有趣的是, 正由于位错起的这个作用, 位错这个缺陷可以看成一个具有非阿贝尔统计性质的点粒子. 文献里将这种缺陷称为: extrinsic twist defect. 需要注意的是, 该非阿贝尔粒子来源于外加的几何缺陷, 并不是原$ {\mathbb{Z}}_2 $ iTO的激发.
我们首先简单介绍一下二维阿贝尔iTO里任意子对称性. 二维阿贝尔iTO的低能有效理论^[89]是K-矩阵Chern-Simons理论(K是$ N\times N $整数对称矩阵, $ \text{Det}K\neq \pm1 $). 所有拓扑性质都由矩阵K决定. 如果$ K' = WKW^T $, 其中$ W\in GL(N, {\mathbb{Z}}) $, 那么$ K' $和K对应的iTO完全等价. 如果选取的W使得$ K = K' $, 那么W生成了K的自同构(automorphism). 我们用符号$ \text{Auto}(K) $来表示自同构. 但要注意的是, 在所有这样的W中, 有部分的W矩阵只是把所有非平凡的激发(任意子)上粘附平凡的局域激发, 因而实际上激发谱的标记^⑦没有任何本质的改变. 我们用符号Inner$(K) $来表示这类平凡的变换. 因而, 刻画“e-m交换”这类操作的“任意子对称群”可以定义为: $ G\equiv{\rm{Outer}}(K) =$$ {{\rm{Auto}}(K)}/{{\rm{Inner}}(K)} $, 从而把所有平凡的变换去掉.
$ {\mathsf{Outer}}(K) $可以看成对N维超方晶格的点群操作; 同时, 该超方晶格每一个格点对应着一个激发(任意子). 为了把二维的讨论推广到三维iTO, 我们基于第2.5节中的投影构造, 定义一个六维的“电荷-圈格子”(charge-loop lattice), 格点坐标为: ${V} = (N_A, {{N}}^{\rm T}_m, M, {{L}}^{\rm T}) = (N_A, N^a_m, N^b_m, M, \ell, \ell') $. 两分量整数矩阵$ {{L}} = (\ell, \ell')^{\rm T} $是纯圈激发的标记. 如果所有坐标都不为零, 那么格点代表着一种点粒子激发和圈激发的复合. 于是, 我们可以用类似二维iTO的任意子对称群的定义方式来定义三维iTO的“荷-圈激发对称性”($ {\rm{Charles}} $). $ {\rm{Charles}} $群是六维电荷-圈格子的点群的一个子群: Charles = $ \dfrac{{\rm{Auto}}(K)}{{\rm{Inner}}(K)}. $这里的K是任意整数矩阵(注: 不一定是对称的), 来自于(3 + 1)维多分量阿贝尔BF理论的系数. 这里的$ {\text{Auto}}(K) $是K的自同构的推广, 由矩阵$ {\cal{G}} = W\oplus \varOmega $生成. 其中的两个$ GL(N, {\mathbb{Z}}) $矩阵W和$ \varOmega$满足 两个条件: 第一, $ \varOmega K W^{\rm T} = K\, $; 第二, $ \varGamma(\cdots, {{{N}}_m}, \cdots) = \varGamma (\cdots, W^{-1}{{N}}_m, \cdots) $. 第二个条件中的$ \varGamma $是点粒子的自统计(要么是玻色子要么是费米子). $ {\rm{Inner}}(K) $里的群元 除了满足这两个条件之外, 还需要满足: $ W^{-1}{{N}}_m-{{N}}_m = K^{\rm T}\, (n_1, n_2)^{\rm T} $和$ \varOmega^{-1}{{L}}-{{L}} = K(n_3, n_4)^{\rm T} $. 其中, $ n_1, \cdots, n_4\in{\mathbb{Z}} $.
物理上, $ {\rm{Charles}} $群的群元$ {\cal{G}} = W\oplus\varOmega $对应着点群操作: $ ({{{N}}_m})_{\text{new}} = W^{-1} {{N}}_m, \, ({{{L}}})_{\text{new}} = \varOmega^{-1}{{L}} $. Charles群的操作不仅保证电荷-圈格子几何性质不变, 而且保证所有激发(电荷-圈的复合)的所有拓扑性质不变. 在我们考虑的具体投影构造中, 这里的拓扑性质包括点粒子的自统计、点粒子-圈激发之间编织统计(亦即Aharonov-Bohm相位)以及Debye-Hückel屏蔽电荷. 类似于二维的做法, 我们在三维也可以引入extrinsic twist defect. 通过计算发现, 点缺陷始终对应着$ {\rm{Charles}} $群的单位元. 线缺陷可以生成非平凡的群元. 类似二维的做法, 我们也可以讨论线缺陷的非阿贝尔融合规则(non-Abelian fusion rule), 如图3的(b)和(c)所示.
图 3 “Twist缺陷和拓扑激发”的融合规则示意图　(a) 二维iTO的任意子和点缺陷的融合. (b) 三维iTO的点激发与线缺陷的融合. (c) 三维iTO的圈激发与线缺陷的融合. 摘自[85]
Figure3. Diagrammatic illustration of fusion rules among twist defects and topological excitations. (a) Fusions between an anyon (quasiparticle) and a point-defect in a two-dimensional iTO. (b) Fusions between a particle excitation and a line defect in a three-dimensional iTO; (c) Fusions between a loop excitation and a line defect in a three-dimensional iTO.[85]

2

-->

3.1.三维对称保护拓扑态

对于绝大多数阿贝尔对称群, SPT的低能有效场论是一个两分量的Chern-Simons理论: $ S = \displaystyle\int \dfrac{K^{IJ}}{4{\text{π}}}{a}^I\wedge {\rm d} a^J\, , I, J = 1, 2\, $. 其中, $ a^1_\mu $和$ a^2_\mu $是两个不同的$ U(1) $规范场, 矩阵K是泡利矩阵$ \sigma^x $. K的行列式是$ -1 $, 使得SPT的体内没有拓扑激发, 也就没有iTO. 有趣的是, 这个Chern-Simons项正好是所谓的level-1的“$\rm BF $”理论^[122–126]在(2 + 1)维时空的实现. 按照$\rm BF $项的标准写法, 我们把其中一个规范场写成b. 那么上面这个Chern-Simons项就变成了: $ S = \displaystyle\int \dfrac{1}{2{\text{π}}}b \wedge {\rm d} a \, $. 鹿芫明和Vishwanath^[127]系统地研究了二维SPT的低能有效场论. 从二维SPT的Chern-Simons理论出发, 通过研究Chern-Simons理论的边界上的共形场论, 我们即可得到受阿贝尔对称群保护的二维SPT的分类. 对于绝大多数简单的阿贝尔群, 他们的分类结果和群上同调^[29,30]得出的结果是完全吻合的. 后来人们进一步发现, 单独的Chern-Simons项是不够的. 比如, 对于对称性为$ {\mathbb{Z}}_{N_1}\times {\mathbb{Z}}_{N_2}\times $${\mathbb{Z}}_{N_3} $这种对称性保护的SPT, 我们需要形式如^[128]: $ S \!=\! \displaystyle\int \sum\limits^3_I \dfrac{1}{2{\text{π}}}b^I\wedge {\rm d} a^I \!+\! \dfrac{q}{4{\text{π}}^2}a^1\!\wedge\! a^2\!\wedge\! a^3\, $这种twisted拓扑项^[40]. 其中, 三分量的level-1 $\rm BF $拓扑项保证了SPT体内没有拓扑激发. 系数q满足一定的量子化条件和周期性条件. 而周期性条件给出了相应SPT的分类. 但如果$ BF $项的level是大于1的整数, 那么该作用量可以看成DW格点模型^[39]的连续场论. 后者具有iTO, 有拓扑激发.
文献[129]提出了三维SPT(其对称性是幺正的阿贝尔幺正群; 时间反演对称性摘自[130])的低能有效理论, 并详细研究了对称操作与规范变换的定义, 见表3. SPT的低能有效理论有如下两个特点: 第一, 体内激发必须是非分数化的(亦即局域算符即可产生的), 同时, 基态在任何闭流形上必须非简并; 第二, 当且仅当对称群G没有被破坏的时候, 不同的SPT的拓扑规范场论是不等价的. 要得到正确的场论描述, 我们需要正确定义规范变换和全局对称变换, 以使得两者不冲突. 我们首先考虑如下作用量($ I = 1, 2 $):

对称群G	拓扑规范场论与分类
$\mathbb{Z}_{N_1}\times\mathbb{Z}_{N_2}$	$\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^2_Ib^I\wedge \, {\rm d}a^I+ p_1\displaystyle\int a^1\wedge a^2\wedge \, {\rm d}a^2~~(\mathbb{Z}_{N_{12}} )$ ; $\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^2_Ib^I\wedge \, {\rm d}a^I+ p_2\displaystyle\int a^2\wedge a^1\wedge \, {\rm d}a^1 ~(\mathbb{Z}_{N_{12}}) $
$\mathbb{Z}_{N_1}\times\mathbb{Z}_{N_2}\times\mathbb{Z}_{N_3} $	$\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^3_Ib^I\wedge \, {\rm d}a^I+ p_1 \displaystyle\int a^1\wedge a^2\wedge \, {\rm d}a^3~~(\mathbb{Z}_{N_{123}})$ ; $\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^3_Ib^I\wedge \, {\rm d}a^I+ p_2 \displaystyle\int a^2\wedge a^3\wedge \, {\rm d}a^1~~(\mathbb{Z}_{N_{123}}) $
$\prod^4_I\mathbb{Z}_{N_I} $	$\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^4_Ib^I\wedge \, {\rm d}a^I+p \displaystyle\int a^1\wedge a^2\wedge a^3\wedge a^4~~ ( \mathbb{Z}_{N_{1234}} )$
$\mathbb{Z}_{N_1}\times\mathbb{Z}_{N_2}\times {U}(1)$	$\dfrac{1}{2{\text{π}}}\displaystyle\int \sum^3_Ib^I\wedge \, {\rm d}a^I+p\displaystyle\int a^1\wedge a^2\wedge \, {\rm d}a^3~~ (\mathbb{Z}_{N_{12}})$

表3受到幺正阿贝尔群保护的“不可约”的三维SPT态的低能有效理论及其分类. $ a^I $和$ b^I $分别是1-形式 和2-形式$ {U(1)} $规范场. 系数p、$ p_1 $、$ p_2 $的取值满足一定的量子化条件和周期性. 系数的周期给出分类的结果.“($ {\mathbb{Z}}_{N_{12}} ) \cdots $”表示相应的分类. 其中, 符号$ N_{IJ\cdots} $表示$ N_I, N_J, \cdots $等整数的最大公约数. 受到$ {\mathbb{Z}}_N $或$ {U(1)}^k $或$ {\mathbb{Z}}_N\times {U(1)}^k $保护的SPT态都是平凡的, 因而没有列入表中.“不可约”是指对称群的所有子群都起着保护SPT的作用. 其他SPT都可以通过表格里的结果构造出来. 具体摘自[129].
Table3.A brief summary of irreducible 3D SPT phases with unitary Abelian symmetry. $ a^I $ and $ b^I $ are 1-form and 2-form $ {U(1)} $ gauge fields, respectively. “($ {\mathbb{Z}}_{N_{12}} $)$ \cdots $”denote the corresponding classifications, where $ N_{IJ\cdots} $ are greatest common divisors of $ N_I, N_J, \cdots $. SPT phases with either $ {\mathbb{Z}}_N $ or ${U(1)}^k $ or $ {\mathbb{Z}}_N\times {U(1)}^k $ are trivial and not included below. By “irreducible”, we means that all subgroups of symmetry group play nontrivial roles in protecting the nontrivial SPT phases. All other SPT's with unitary Abelian group symmetries can be obtained directly by using this table^[129].

$ S = \frac{1}{{2{\text{π}} }}\sum\limits_I^2 \int {b^I} \wedge {\rm d}{a^I} + p\int {a^1} \wedge {a^2} \wedge {\rm d}{a^2} + {S_M} .$

其中 $ \{b^I_{\mu\nu}\} $是两个2-形式的$ U(1) $规范场^⑧. $ S_{M} $是推广的麦克斯韦项, 其作用是紫外的正规子:

$ \begin{split} S_M = &\int {\rm d}^4x\bigg[\frac{1}{2\chi}(p {a}^2_\nu \partial_\lambda {a}^2_\rho\epsilon^{\mu\nu\lambda\rho}+\frac{1}{4{\text{π}}}\partial_\nu b^1_{\lambda\rho}\epsilon^{\mu\nu\lambda\rho})^2 \\ & + \frac{1}{2\chi}(-p {a}^1_\nu \partial_\lambda {a}^2_\rho\epsilon^{\mu\nu\lambda\rho}+\frac{1}{4{\text{π}}}\partial_\nu b^2_{\lambda\rho}\epsilon^{\mu\nu\lambda\rho})^2\\ &+\sum\limits_I^2 \frac{(f^I_{\mu\nu})^2}{4g^2}\bigg]\,. \\[-18pt]\end{split} $

尽管该项破坏了作用量的拓扑不变性, 该项提供了一个有限大的体内能隙, 可以正规化动量空间的积分. 该项虽然破坏了作用量的拓扑不变性, 但是提供了一个有限大的体内能隙, 可以用于正规化动量空间的积分.
公式(22)的第一项是两个level-1的BF项. 所有规范场满足如下狄拉克量子化条件: $ \displaystyle \dfrac{1}{2{\text{π}}}\int_{{\cal{M}}^2} {\rm d}{a}^I\in {\mathbb{Z}}\, , \;\; \dfrac{1}{2{\text{π}} } \int_{{\cal{M}}^3} {\rm d}b^I\in {\mathbb{Z}}\, $. 其中, $ {\cal{M}}^2 $是二维闭流形. 所有规范场的规范变换定义如下:

$a^I\rightarrow a^I+\,d\chi^I\,,\,b^I\rightarrow b^I+\,{\rm d} V^I -2{\text{π}} p \,\epsilon^{IJ3} \chi^J \,{\rm d} a^2\,. $

其中, 规范参数$ \{\chi^{I}\} $和$ \{V_{\mu}^{I}\} $分别是标量(1-形式)和矢量(2-形式). 注意到, 1-形式$ \, {\rm d}\chi^I $和2-形式$ \, {\rm d}V^I $都是闭合的(closed)但可以是非恰当的(non-exact). 具体来讲, 闭流形上的积分

$ \int_{{\cal{M}}^1} \,{\rm d}\chi^I = 2{\text{π}} n^I\,;~~\, \int_{{\cal{M}}^2} \,{\rm d}V^I = 2{\text{π}} k^I.$

其中, $ \{n^I\} $和$ \{k^I\} $代表四个独立的整数. 非零的$ n^I $和$ k^I $导致非恰当, 同时对应的规范变换通常被称为“大规范变换”. 当$ p = 0 $时, $ b^I $的规范变换和一般的BF理论一致.p的出现改变了通常的2-形式规范变换: 多出了一个依赖于p的项. 因而, 相应的Wilson算符(见图4)为:

$\begin{split}&\exp \left({{\rm i}\int_{{\cal{M}}^1} a^I}\right),\\ &\exp \left({{\rm i}\int_{{\cal{M}}^2} b^I - {\rm i} 2{\text{π}} p\int_{{\cal{V}}^3} \epsilon^{IJ3} a^J \wedge {\rm d} a^2} \right). \end{split}$

这里的$ {\cal{V}}^3 $是一个三维流形, 其边界是$ {\cal{M}}^2 $, 亦即: $ \partial {\cal{V}}^3 = {\cal{M}}^2 $. 图4(a)表示圈算符$ {\rm e}^{{\rm i}\int_{{\cal{M}}^1} a^I} $. 图4(b)表示算符$ \exp\left\{{\rm i}\displaystyle\int_{{\cal{M}}^2} b^I - {\rm i}2{\text{π}} p\displaystyle\int_{{\cal{V}}^3} \epsilon^{IJ3}a^J\wedge \, {\rm d} a^2\right\} $. 其中, 立方体表示某个任意的三维空间区域$ {\cal{V}}^3 $; 立方体内部的星代表来自$ \displaystyle\int_{{\cal{V}}^3} \epsilon^{IJ3}a^J\wedge \, {\rm d} a^2 $ in $ {\cal{V}}^3 $的贡献.
图 4 公式(26)中的规范不变的Wilson算符示意图. 摘自文献[129]
Figure4. Illustration of gauge-invariant Wilson operators in Eq. (26)

在作用量(22)中, 2-形式规范场$ b^I $的“电磁”通量给出了SPT的局域玻色子的粒子流: $ J^I_\mu = \dfrac{1}{4{\text{π}}}\epsilon^{\mu\nu\lambda\rho} \partial_\nu b^I_{\lambda\rho} $. 用微分形式可以写为: $ {*} J^I = \dfrac{1}{2{\text{π}}} {\rm d}b^I\, $, 其中, $ * $表示Hodge对偶操作. 如果对称性是$ U(1) $, 那么我们可以用$ U(1) $的外电磁场$ A^I $来耦合粒子流: $S \rightarrow S+ \displaystyle \sum\limits_I^2\dfrac{1}{2{\text{π}}}\int A^I \wedge {\rm d} b^I\, $. 但我们实际考虑的对称性是$ G = \displaystyle\prod\nolimits_I^3{\mathbb{Z}}_{N_I} $, 粒子数不严格守恒, 粒子数的变化可以是$ N_I $的整数倍. 为了使作用量在粒子数改变$ N_I $的时候不变, 我们需要限制: $\displaystyle \int_{{\cal{S}}^1}A^I = \dfrac{2{\text{π}}}{N_I}\times 0, \pm 1, \cdots $. 其中$ {\cal{S}}^1 $是一维闭流形.
为了同时使得规范变换与全局对称性操作有良好定义, 我们要求系数p有如下量子化条件和周期性: $ p = \dfrac{k}{4{\text{π}}^2}\dfrac{N_1 N_2}{N_{12}}\, $, $ k\in{\mathbb{Z}}_{N_{12}} $, $ N_{12} $是$ N_1 $和$ N_2 $的最大公约数. 整数k的周期性表示, 一共有$ {N_{12}} $种由作用量S刻画的G保护的不等价的SPT相; 每个SPT对应着$ {\mathbb{Z}}_{N_{12}} $群的群元. 平凡的态对应着单位元, 其作用量由$ k = 0\text{ mod }N_{12} $标记. 同时, 除了作用量(22), 我们也可以考虑$ a^2\wedge a^1\wedge {\rm d}a^1 $这个拓扑项, 因为$ a^1\wedge a^2\wedge {\rm d}a^2 $与$ a^2\wedge a^1\wedge {\rm d}a^1 $线性独立^⑨. 相应的系数的量子化和周期性结果不变. 于是, 总的分类是$ ({\mathbb{Z}}_{N_{12}})^2 $. 该结果和群上同调的结果是一致的: $ {H}^{4}\bigg[\displaystyle\prod\nolimits^2_I{\mathbb{Z}}_{N_I}, {U(1)}\bigg] = ({\mathbb{Z}}_{N_{12}})^2 $. 这里我们不再重复具体计算细节. 这里的计算的关键在于, 系数的量子化和周期性结果是规范变换与全局对称性的要求, 同时都和对称群G紧密相关. 如果我们完全破坏对称群, 那么p的取值结果可以通过形式上令$ N_1 = N_2 = 1 $得到: $ p = {k}/({4{\text{π}}^2})\, $. 由于此时整数k的周期是1, 所有非零的整数k都和$ k = 0 $等价. 所以, 在没有对称群保护的时候, 作用量(无论添加的是$ a^1\wedge a^2\wedge {\rm d}a^2 $还是$ a^2\wedge a^1\wedge {\rm d}a^1 $)均描述的是平凡态.
表3里的拓扑规范场论描述的是阿贝尔幺正对称群保护的SPT. 对于反幺正群—时间反演对称性, 文献[130]使用$ b\wedge b $来构造拓扑场论:

$S = \int {\sum\limits_I^4 {\frac{1}{{2{\text{π}} }}} } {b^I} \wedge {\rm d}{a^I} + \int {\sum\limits_{IJ} {\frac{{{\varLambda ^{IJ}}}}{{4{\text{π}} }}} } {b^I} \wedge {b^J} .$

其中, $ \varLambda $是$ SO(8) $群的嘉当(Cartan)矩阵:

$ \Lambda = \left( {\begin{array}{*{20}{c}}2&1&1&1\\1&2&0&0\\1&0&2&0\\1&0&0&2\end{array}} \right) .$

该场论描述的BTI不在“群的上同调”分类结果里^[31].
2 -->

3.2.$ AAB $拓扑项与Borromean Rings编织统计

二维iTO^[10,132]体内的任意子激发的编织统计以及边界态的手征中心荷c是iTO的核心拓扑不变量. 相应的代数结构是特定的模张量范畴(modular tensor category)^[10,45,97]. 二维iTO的任意子的编织统计^{[32,33,133–135]}由(2 + 1)维的拓扑量子场论—Chern-Simons规范理论来刻画. 任意子在(2 + 1)维时空中的世界线形成各种非平凡的纽结, 物理上包含了拓扑激发的编织统计信息; Chern-Simons规范理论正好可以用于刻画这些纽结的拓扑性质^[136]. 而三维iTO^[34,35]不仅有点粒子激发, 也有圈激发. 虽然我们知道三维拓扑态的点粒子的自统计只能有玻色和费米两种选项^[134,137], 但是圈激发的存在使得编织统计及其拓扑场论十分丰富. 圈激发甚至也可以有非平凡的纽结性质, 见图5. 我们可以通过研究具有圈激发的拓扑纠缠熵来分辨具有相同规范群G但闭上链$ \omega $不同的Dijkgraaf-Witten模型^[138].
图 5 三维iTO中的点激发和圈激发示意图^[138]
Figure5. Illustration of point-like excitations and loop excitations in three-dimensional iTO

我们考虑简单的阿贝尔规范群可以描述的编织过程. 点粒子-圈之间的编织过程比较简单, 如图6(a)所示. 该编织过程生成一个Hopf环链. 物理上, 我们可以用$ (3 + 1) $维电荷-N的玻色子与$ U(1) $规范场耦合来实现^[63,139]. 除了该编织统计过程, 我们可以考虑更加复杂的规范群, 比如$ G = \displaystyle\prod\nolimits_I {\mathbb{Z}}_{N_I} $. 由于有多个$ {\mathbb{Z}}_{N_I} $规范子群, 我们可以考虑“三圈编织过程”(three-loop braiding). 该编织过程涉及到三个圈激发^[140]. 它们的磁通必须属于至少两个不同的$ {\mathbb{Z}}_{N_I} $规范子群. 如果规范子群有四个或四个以上, 要完整刻画iTO, 除了三圈编织, 我们还需要考虑更加复杂的“四圈编织过程”(four-loop braiding)^[141–143]. 所有这些编织过程及其编织统计可以统一用Dijkgraaf-Witten格点模型^[39]来实现.
图 6 (a) 点粒子-圈之间的编织: 点粒子激发$ e_i $ (携带单位$ \mathbb{Z}_{N_i} $规范荷) 绕着圈激发$ m_i $(携带单位$ \mathbb{Z}_{N_i} $规范磁通)转一圈. $ e_i $的轨迹$ \gamma_{e_i} $与静止的圈$ m_i $形成一个Hopf环链. (b) 博罗梅安编织(点粒子-圈-圈编织): 点粒子$ e_k $绕着两个互相未链接的圈激发$ m_i, m_j $转一圈. $ e_k $的轨迹$ \gamma_{e_k} $与$ m_i $, $ m_j $一起形成博罗梅安环(Borromean Rings, 或更一般的Brunnian link)
Figure6. (a) Particle-loop braiding: a particle $ e_i $ travels around a loop $ m_i $ such that the braiding trajectory $ \gamma_{e_i} $ and $ m_i $ form a Hopf link. (b) Borromean-Rings braiding: a particle $ e_k $ moves around two unlinked loops $ m_i, m_j $ such that $ m_i $, $ m_j $ and the trajectory $ \gamma_{e_k} $ form the Borromean rings (or generally the Brunnian link)

在连续时空中, 我们可以使用多分量的twisted BF理论^{[40,48–50,129,130,140–156]}来实现上面提到的编织过程和编织统计. 作用量类似于(22)式, 可写为(大写字母表示规范场):

$ \begin{split} S = & \sum\limits_I \int \frac{N_I}{2{\text{π}}}B^I \wedge {\rm d} A^I + \sum\limits_{IJK}p^{IJK} \int A^I \wedge A^J \wedge {\rm d} A^K\\ &+\sum\limits_{IJKL}c^{IJKL}A^I\wedge A^J\wedge A^K\wedge A^L\,.\\[-18pt] \end{split} $

文献[157]提出了新的编织过程—“博罗梅安编织”(Borromean-Rings braiding), 如图6(b)所示. 在此编织过程中, 一个点粒子绕着两个互相未链接的圈激发转了一圈, 形成博罗梅安环或者更加一般的Brunnian link. 因为该编织过程涉及到一个点粒子和两个圈激发, 所以我们也可以称之为“点粒子-圈-圈编织”. 该编织过程的拓扑不变量是Milnor三重链接数(Milnor's triple linking number, $ \bar{\mu} $)^[158,159]. 考虑$ G = {\mathbb{Z}}_{N_1}\times{\mathbb{Z}}_{N_2}\times {\mathbb{Z}}_{N_3}$, 相应的低能有效理论包含形如$ AAB $的拓扑项:

$ S = \sum\limits_I^3 {\int {\frac{{{N_I}}}{{2{\text{π}} }}} } {B^I} \wedge {\rm d}{A^I} + \int {\frac{q}{{{{(2{\text{π}} )}^3}}}} {A^1} \wedge {A^2} \wedge {B^3} .$

其中, 系数$ q = \dfrac{2{\text{π}} N_1 N_2 N_3 k}{N_{123}} $, $ k\in{\mathbb{Z}}_{N_{123}} $. 系数的量子化和周期性来源于大规范变换的要求. 在$ A^1 A^2 B^3 $拓扑项刻画的博罗梅安编织过程中, 点粒子携带$ {\mathbb{Z}}_{N_3} $规范子群的规范荷, 两个圈激发分别携带$ {\mathbb{Z}}_{N_1} $和$ {\mathbb{Z}}_{N_2} $的磁通. 如果点粒子的空间轨迹和两个圈激发一起形成了图6(b)中的博罗梅安环, 那么相应的Milnor三重链接数$ \bar\mu = 1 $. 同时, 该编制过程贡献一个编织相位:

$ \begin{align} S_{\rm BR} = \frac{2{\text{π}} k_{ij,k}}{N_{ijk}}\bar{\mu}({m_{i}},{m_{j}},\gamma_{e_{k}}) = \frac{2{\text{π}} k_{ij,k}}{N_{ijk}} . \end{align} $

2 -->

3.3.三维对称富化拓扑态与对称性分数化

前面我们介绍了SPT和iTO的一些低能有效场论的研究. 当iTO含有对称性, 对应的拓扑态就是对称富化拓扑态(SET). 文献[48]提出三维SET的低能有效场论的构造方案, 并研究了具体的例子. 文献[49]构造了一类具有量子反常的三维SET. 文献[51]讨论了部分具有反幺正对称群的SET. 文献[160](见其附录E)讨论了同时含有空间群(比如空间旋转对称性)和内部群(比如自旋旋转对称性)的SET的低能有效理论与拓扑响应理论. 文献[50]基于^[48]提出了系统分类和表征三维SET的场论计算方法. 部分例子见表4^[50]. 符号$ G_g $代表iTO对应的规范群. 体内的iTO完全由规范群和twisted拓扑项决定. 后者由一对整数标记: 比如对于规范群$ {\mathbb{Z}}_2\times {\mathbb{Z}}_2 $, $ (q, \bar q) $ = $ (0, 0) $、$ (2, 0) $或$ (2, 2) $, 代表twisted拓扑项前面的系数. 如果标记为“–”, 那么该规范群没有非平凡的twisted拓扑项. 符号$ G_s $代表施加的全局对称性. 给定iTO和对称性, 相应的SET分类标记为: $ \mathcal{C}_1\oplus \mathcal{C}_2 \oplus\cdots $. 其中, 角标$ i = 1, 2, \cdots $用于标记携带单位规范荷的点粒子的对称性分数化(symmetry fractionalization). 给定i, 即给定点粒子的对称性分数化. 同时, $ \mathcal{C}_i $表示“圈激发的对称性分数化”的分类(一般标记为一个或多个循环群的直乘). 符号$ \oplus $表示形式上把具有不同的粒子对称性分数化的SET“放在一起”. 符号$ ({\mathbb{Z}}_n)^m $定义为m个$ {\mathbb{Z}}_n $的直乘: $ ({\mathbb{Z}}_n)^m = {\mathbb{Z}}_n\times {\mathbb{Z}}_n\cdots {\mathbb{Z}}_n $. 同时, $ k({\mathbb{Z}}_n)^m = $$ ({\mathbb{Z}}_n)^m \oplus ({\mathbb{Z}}_n)^m \oplus\cdots\oplus ({\mathbb{Z}}_n)^m $, 其中, k 表示$ ({\mathbb{Z}}_{n})^m $的个数.“gcd”是最大公约数的缩写. $ {\mathbb{Z}}_1 $表示有且仅有一种SET, 即把iTO和有对称性的平凡SPT放在(stack)一起. 例如, 当$ G_g = {\mathbb{Z}}_2 $且$ G_s = {\mathbb{Z}}_{2 n} $的时候, 分类结果是$ ({\mathbb{Z}}_2)^2\oplus {\mathbb{Z}}_1 $, 于是一共有$ 5 $个SET. 注意, 该表格的结果来源于阿贝尔规范场论计算, 没有考虑在对称操作下容许出现的拓扑激发之间的轮换, 也未考虑非阿贝尔的对称性分数化.

规范群$G_g$	twisted拓扑项	对称群$G_s$	SET分类
${\mathbb{Z}}_2$	–	${\mathbb{Z}}_{2 n + 1}$	${{\mathbb{Z}}_1}$
${\mathbb{Z}}_2$	–	${\mathbb{Z}}_{2 n}$	$ {({\mathbb{Z}}_2)^2}\oplus {\mathbb{Z}}_1$
${\mathbb{Z}}_3$	–	${\mathbb{Z}}_{3 n}$	$({\mathbb{Z}}_3)^2\oplus {\mathbb{Z}}_1 \oplus {\mathbb{Z}}_1$
${\mathbb{Z}}_3$	–	${\mathbb{Z}}_{3 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{4 n+2}$	$ ({\mathbb{Z}}_2)^2\oplus {\mathbb{Z}}_1$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{4 n}$	$ ({\mathbb{Z}}_4)^2\oplus ({\mathbb{Z}}_2)^2\oplus {\mathbb{Z}}_1 \oplus {\mathbb{Z}}_1 $
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(0, 0)	${\mathbb{Z}}_{2 n}$	$({\mathbb{Z}}_2)^6\oplus ({\mathbb{Z}}_2)^2 \oplus ({\mathbb{Z}}_2)^2 \oplus ({\mathbb{Z}}_2)^2$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(0, 0)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(2, 0)	${\mathbb{Z}}_{2 n}$	$({\mathbb{Z}}_2)^6$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(2, 0)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(2, 2)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(0, 0)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(4, 0)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(4, 4)	${\mathbb{Z}}_{2 n + 1}$	${\mathbb{Z}}_1$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(0, 0)	${\mathbb{Z}}_{4 n}$	$({\mathbb{Z}}_2)^4\times ({\mathbb{Z}}_4)^2\oplus 2({\mathbb{Z}}_4)^2\oplus4({\mathbb{Z}}_2)^2 \oplus ({\mathbb{Z}}_2)^6$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(4, 0)	${\mathbb{Z}}_{4 n}$	$({\mathbb{Z}}_2)^4\times ({\mathbb{Z}}_4)^2$
${\mathbb{Z}}_2\times {\mathbb{Z}}_4$	(4, 4)	${\mathbb{Z}}_{4 n}$	$({\mathbb{Z}}_2)^4\times ({\mathbb{Z}}_4)^2$
${\mathbb{Z}}_2$	–	${\mathbb{Z}}_{2 m + 1} \times {\mathbb{Z}}_{2 n + 1}$	$({\mathbb{Z}}_{2\gcd(2 m + 1, 2 n + 1)})^2$
${\mathbb{Z}}_2$	–	${\mathbb{Z}}_{2 m + 1} \times {\mathbb{Z}}_{2 n}$	$({\mathbb{Z}}_{\gcd(2 m + 1, 2 n)})^2 \oplus ({\mathbb{Z}}_{2\gcd(2 m + 1, 2 n)})^2 $
${\mathbb{Z}}_2$	–	${\mathbb{Z}}_{2 m} \times {\mathbb{Z}}_{2 n}$	$({\mathbb{Z}}_2)^6\times({\mathbb{Z}}_{2\gcd(m, n)})^2\oplus ({\mathbb{Z}}_{2\gcd(2 m, n)})^2 \oplus ({\mathbb{Z}}_{2\gcd(m, 2 n)})^2 \oplus ({\mathbb{Z}}_{2\gcd(m, n)})^2$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{2 n + 1} \times {\mathbb{Z}}_{2 n + 1}$	$16({\mathbb{Z}}_{2 n + 1})^2$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{2(2 n + 1)} \times {\mathbb{Z}}_{2(2 n + 1)}$	$4({\mathbb{Z}}_2)^6 \times ({\mathbb{Z}}_{2(2 n + 1)})^2\oplus 12({\mathbb{Z}}_{2(2 n + 1)})^2$
${\mathbb{Z}}_4$	–	${\mathbb{Z}}_{4 n} \times {\mathbb{Z}}_{4 n}$	$({\mathbb{Z}}_4)^6 \times ({\mathbb{Z}}_{4 n})^2\oplus 12({\mathbb{Z}}_{4 n})^2 \oplus 3[ ({\mathbb{Z}}_{4 n})^2\times ({\mathbb{Z}}_2)^6]$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(0, 0)	${\mathbb{Z}}_{2}\times {\mathbb{Z}}_2$	$({\mathbb{Z}}_2)^{18}\oplus 6({\mathbb{Z}}_2)^8 \oplus 3({\mathbb{Z}}_2)^6 \oplus 6({\mathbb{Z}}_2)^4$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(2, 0)	${\mathbb{Z}}_{2}\times {\mathbb{Z}}_2$	$({\mathbb{Z}}_2)^{18}$
${\mathbb{Z}}_2\times {\mathbb{Z}}_2$	(2, 2)	${\mathbb{Z}}_{2}\times {\mathbb{Z}}_2$	$({\mathbb{Z}}_2)^{18}$

表4部分三维SET的分类, 摘自[50].
Table4.Classification of SET examples.

在具体计算中, 我们考虑一个有全局对称性的规范场论(Symmetry-Enriched Gauge theory, SEG):

$ S = \int \sum\limits_{i = 1}^m \frac{N_i}{2{\text{π}}} b^i \wedge {\rm d}a^i+S_{c}+S_{\rm int}\,.$

规范群和对称群分别为: $ G_g = \displaystyle\prod\nolimits_{i = 1}^nZ_{N_i} $, G_s = $ \displaystyle\prod\nolimits_{i = 1}^k Z_{K_i} $. 当$ m \geqslant i\geqslant n + 1 $时, $ N_i = 1 $, 因而这些i对应的规范场都是平凡的. 这些场量的引进并不会改变SEG的iTO, 但会作为辅助的场量而提供更多可能的对称性富化方式. 我们将这些出现在level-1的$ BF $项的规范场称为“level-1规范场”. 这个技巧首先在^[48]中被提出. 外部规范场的耦合项

$ S_c = \int \sum\limits_{i = 1}^k \sum\limits_{j = 1}^m \frac{Q_{ij}}{2{\text{π}}} A^i \wedge {\rm d}b^j $

用于探测对称性. 外加规范场$ A^i $用于探测$ U(1) $的$ Z_{K_i} $子群. $ Q_{ij} $是$ k\times m $任意整数矩阵. 要注意的是, 所有外加规范场只是静态背景场, 没有动力学, 不是配分函数的组态. $ S_{\rm int} $包括所有可能的twisted拓扑项(包括所有规范场)^⑩. 作用量S的这些特点可以概括在示意图7中. 每个“layer”表示一个三维系统. 所有“layer”堆在一起并占据三维空间中同一个区域. 在没有考虑对称性的时候, 亦即在形成SEG之前, 体系只含有type-I layers, 描述纯iTO. type-II layers里面的规范场都是level-1, 是在施加对称性之后加进来的. 每一条黄色的虚线表示$ S_{\rm int} $中的某个拓扑项涉及到的layers. 需要说明的是, 图中的虚线都是连接两个layer, 实际上可以同时涉及到三个或四个. 通过该场论, 我们可以计算携带规范荷的粒子的对称荷, 从而确定粒子上的对称性分数化. 同时, 圈激发的对称式分数化由“混合多圈统计”(mixed multi-loop, MML)来确定. 要注意的是, type-II layers的层数是任意的, $ Q_{ij} $也是任意的. 也就是说, 给定规范群和对称群之后, 作用量的写法是无穷多个. 文献[48]在具体例子中选取了特定的作用量写法, 来计算对称性分数化. 文献[50]考虑了所有可能的Q和所有可能的twisted拓扑项, 并发现无穷个Q可以约化到有限个, 从而系统地得到表4中的结果.
图 7 SEG的构造图. 摘自文献[48]
Figure7. Illustration of SEG

对于含有反幺正对称群的SET, 比如时间反演, 文献[51]讨论了部分例子, 见表5. $ U(1)_C $和$ U(1)_{S^z} $分别是电荷和z方向自旋对称群. $ {\mathbb{Z}}_2 $是指绕着$ S^y $自旋轴转动$ {\text{π}} $.

投影对称群(PSG)	规范群$G_g$	对称群$G_s$	三维体内($\varSigma^3$) 的规范理论	表面($\partial\varSigma^3$)的反常 玻色理论	二维平面($\varSigma^2$)的正常Chern-Simons理论的$K_G$-矩阵
${\mathbb{Z}}_N \rtimes{\mathbb{Z}}^T_2$	${\mathbb{Z}}_N$	${\mathbb{Z}}^T_2$	$\dfrac{N}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^c_{\mu\nu}\partial_\lambda A_\rho^c+$ $\dfrac{\theta_c}{8{\text{π}}^2} \epsilon^{\mu\nu\lambda\rho}\partial_\mu A^c_\nu \partial_\lambda A^c_\rho$	${\mathbb{Z}}^T_2$破缺的 $\partial\varSigma^3$: $\dfrac{N}{2{\text{π}}}\partial_0 \phi^c \epsilon^{ij}\partial_i \lambda^c_j$	${\mathbb{Z}}^T_2$破缺的$\varSigma^2$: $\left(\begin{array}{*{20}{c}} {2 p}&N\\ N&0 \end{array}\right)$
${\mathbb{Z}}_N\!\times\!{\mathbb{Z}}^T_2$	${\mathbb{Z}}_N$	${\mathbb{Z}}^T_2$	$\dfrac{N}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^s_{\mu\nu}\partial_\lambda A_\rho^s+$ $\dfrac{\theta_s}{8{\text{π}}^2} \epsilon^{\mu\nu\lambda\rho}\partial_\mu A^s_\nu \partial_\lambda A^s_\rho$	${\mathbb{Z}}^T_2$破缺的$\partial\varSigma^3$: $\dfrac{N}{2{\text{π}}}\partial_0 \phi^s \epsilon^{ij}\partial_i \lambda^s_j$	${\mathbb{Z}}^T_2$破缺的$\varSigma^2$: $ \left({\begin{array}{*{20}{c}} 2 p &N \\ N & 0 \end{array}} \right)$
${\mathbb{Z}}_N \!\times\! [U(1)_{S^z}\rtimes{\mathbb{Z}}_2]$	${\mathbb{Z}}_N\!\times\! U(1)_{S^z}$	${\mathbb{Z}}_2$	$\dfrac{N}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^c_{\mu\nu}\partial_\lambda A_\rho^c +$ $\dfrac{\theta_0}{4{\text{π}}^2} \epsilon^{\mu\nu\lambda\rho}\partial_\mu A^s_\nu \partial_\lambda A^c_\rho$	${\mathbb{Z}}_2$破缺的$\partial\varSigma^3$: $\dfrac{N}{2{\text{π}}}\partial_0 \phi^c \epsilon^{ij}\partial_i \lambda^c_j$	${\mathbb{Z}}_2$破缺的$\varSigma^2$: $ \left({\begin{array}{*{20}{c}} 2 p_1 &N & p_{12}& 0\\ N & 0 &0 & 0\\ p_{12} & 0 &2 p_2 & 0\\ 0 & 0 &0 & 0 \end{array}} \right)$
$U(1)_C \!\times\! [{\mathbb{Z}}_N \rtimes{\mathbb{Z}}_2]$	$U(1)_C\!\times\!{\mathbb{Z}}_N$	${\mathbb{Z}}_2$	$\dfrac{N}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^s_{\mu\nu}\partial_\lambda A_\rho^s+$ $\dfrac{\theta_0}{4{\text{π}}^2} \epsilon^{\mu\nu\lambda\rho}\partial_\mu A^s_\nu \partial_\lambda A^c_\rho$	${\mathbb{Z}}_2$破缺的$\partial\varSigma^3$: $\dfrac{N}{2{\text{π}}}\partial_0 \phi^s \epsilon^{ij}\partial_i \lambda^s_j$	${\mathbb{Z}}_2$破缺的$\varSigma^2$: $ \left({\begin{array}{*{20}{c}} 2 p_1 &0 & p_{12}& 0\\ 0 & 0 &0 & 0\\ p_{12} & 0 &2 p_2 & N\\ 0 & 0 &N & 0 \end{array}} \right)$
${\mathbb{Z}}_{N_1} \!\times\! [{\mathbb{Z}}_{N_2}\rtimes{\mathbb{Z}}_2]$	${\mathbb{Z}}_{N_1}\!\times\! {\mathbb{Z}}_{N_2}$	${\mathbb{Z}}_2$	$\dfrac{N_1}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^c_{\mu\nu}\partial_\lambda A_\rho^c+$ $\dfrac{N_2}{4{\text{π}}} \epsilon^{\mu\nu\lambda\rho} B^s_{\mu\nu}\partial_\lambda A_\rho^s+$ $\dfrac{\theta_0}{4{\text{π}}^2} \epsilon^{\mu\nu\lambda\rho}\partial_\mu A^s_\nu \partial_\lambda A^c_\rho$	${\mathbb{Z}}_2$破缺的$\partial\varSigma^3$: $\dfrac{N_1}{2{\text{π}}}\partial_0 \phi^c \epsilon^{ij}\partial_i \lambda^c_j+$ $\dfrac{N_2}{2{\text{π}}}\partial_0 \phi^s \epsilon^{ij}\partial_i \lambda^s_j$	${\mathbb{Z}}_2$破缺的$\varSigma^2$: $\begin{aligned} & {}\\ & \left({\begin{array}{*{20}{c}} 2 p_1 &N_1 & p_{12}& 0\\ N_1 & 0 &0 & 0\\ p_{12} & 0 &2 p_2 & N_2\\ 0 & 0 &N_2 & 0 \end{array}} \right)\end{aligned}$

表5部分含有反幺正对称群(时间反演)的SET的体内理论与边界理论, 摘自[51].
Table5.Bulk and boundary theories of SET with anti-unitary symmetry (e.g., time-reversal symmetry).

2

-->

4.1.分数化S-对偶、分数拓扑绝缘体与堆叠操作

三维拓扑能带绝缘体^[161,162] (topological insulator, TI)是一种自由费米子系统的SPT. 其对称性是$ {U(1)}\rtimes {\mathbb{Z}}^T_2 $. 与普通绝缘体不同, TI的电磁响应理论^{[119,163,164]} 含有一个与轴子角$ \theta $有关的拓扑项:

$ S = {\rm i}\frac{\theta}{8{\text{π}}^2}\int F \wedge F+\frac{1}{2g^2}\int F\wedge * F. $

其中轴子角$ \theta = {\text{π}}\, {\rm{mod}}\, 2{\text{π}} $ (TI体内)或者$ \theta = 0\, {\rm{mod}}\, 2{\text{π}} $ (在真空). $ F = dA $是$ 2 $-形式的场张量. g是电磁耦合常数. 该响应理论的两个参数可以统一写成一个复数: 模参数(modular parameter) $ \tau = \dfrac{\theta}{2{\text{π}}}+ {\rm i}\dfrac{2{\text{π}}}{g^2} $. 威腾效应^[119,118]正是由$ \theta $项产生的: 一个外加的磁单极子(携带单位磁荷)会携带${\theta}/{2{\text{π}}} $这么多的极化电荷. 但如果S中的外电磁场A被视为具有动力学的场量, 那么S代表的物理变成了: 有$ \theta $的(3 + 1)维QED (QED$ _4 $). 该理论具有“S-对偶”^[165–167]: 配分函数$ \mathcal{Z} $在$ {\cal{S}} $和$ {\cal{T}} $操作下以模形式(modular form)变换: $ {\cal{S}}: \tau\rightarrow -\dfrac{1}{\tau} $, $ {\cal{T}}: \tau\rightarrow \tau+{1} $. 通过$ {\cal{T}} $操作, 我们知道$ \theta $在费米子体系(考虑自旋结构的流形)中周期是$ 2{\text{π}} $. 为了保持时间反演对称性, $ \theta $在TI体内的取值必须取$ {\text{π}}\text{ mod }2{\text{π}} $. S-对偶最近用在了二维凝聚态物理中, 比如一系列推广粒子-涡旋对偶的理论^[168–174]. 其中一种推导这些新的粒子-涡旋对偶的方法就是在有边界的4维时空上研究S-对偶^[174–177].
在强关联电子系统中, 尽管“电子填充能带”的图像失效, 我们仍然可以考虑受$ {U(1)}\rtimes {\mathbb{Z}}^T_2 $保护的有能隙的态. 强关联的拓扑绝缘体有两大类. 第一类是SPT, 其体内的激发仍然是平凡, 但是边界上会有对称性保护的“表面拓扑序” (surface topological order, STO)^{[28,130,178–181]}. STO可以看成反常的二维SET, 只能存在于边界上. 第二类可以叫做“分数拓扑绝缘体”(fractional TI, FTI), 其体内激发谱支持拓扑激发. 此类拓扑绝缘体可以看成三维的SET. FTI除了体内有拓扑激发之外, 其$ \theta $在一定条件下可以取分数化的值(相对于$ {\text{π}} $来讲), 而且不破坏时间反演对称性. FTI的投影构造、格点模型等方面已经有不少的研究进展^{[84,85,182–188]}. 文献[189]提出并应用“分数化的S-对偶”来研究FTI中$ \theta $的周期与时间反演不变的取值. 分数化S-对偶的$ {\cal{S}} $和$ {\cal{T}} $分别是

$ \tau\rightarrow -\frac{1}{t^4\tau}\,,\,\,\tau\rightarrow \tau+\frac{1}{t^2}. $

其中, $ 1/t $表示体内的拓扑激发携带的电荷最小单位. 一旦考虑了$ {\mathbb{Z}}^T_2 $, FTI中$ \theta $的取值规律就确定了: $ \theta ={{\text{π}}}/{t^2}\text{ mod }{2{\text{π}}}/{t^2} $. 周期$ \varDelta_\theta ={2{\text{π}}}/{t^2}. $当$ t = 1 $, 亦即体内没有电荷分数化, $ \theta $的取值变成了大家熟知的TI的结果^[119]: $ \theta = {\text{π}} \text{ mod }2{\text{π}} $. 正如FQH里的复合费米子理论提供了理解Jain态^[5–8]的思路, 这里的S-对偶理论也提供了一个理解FTI中$ \theta $的分数量子化的思路. 注意到对于任意的t, ${\cal{S}}^2 =$ $ (\mathcal{ST})^3 = 1 $, $ \tau $的所有的模不动点(modular fixed point)^[175,190]等价于: $ {i}/{t^2} $和$ {e^{i\frac{2{\text{π}}}{3}}}/{t^2} $. 前者在$ {\cal{S}} $的操作下不变, 而后者在$ \mathcal{ST} $联合操作下不变. 探索这些不动点的物理是非常有趣的, 比如当$ t = 1 $时, 这些不动点物理上控制着TI表面的相图有关^[175,191].
除了得到FTI中$ \theta $的量子化规律之外, 我们还可以把FTI分成两类: type-I FTI和type-II FTI. 两类FTI在所谓的“堆叠”(stacking)操作下(用符号$ \boxtimes $表示)有着截然不同的性质. 堆叠操作就是把两个态放在同一个三维空间区域, 并容许施加局域算符. 所有可以通过堆叠操作连接在一起的的拓扑态构成一个幺半群(monoid)^[45]—与真正的群的区别在于, 幺半“群”里不是所有元素都有逆. 在我们要讨论的(分数)拓扑绝缘体这个具体例子中, 真空或者平凡能带绝缘体是幺半群的单位元(标记为: Vac), 自由费米子的拓扑绝缘体TI和它自己互为逆元素, 所有FTI(标记为: FTI$ _t $)都没有逆元素. 两个TI堆叠在一起得到真空:

$ {\rm{TI}}\boxtimes{\rm{TI}} = {\rm{Vac}} . $

这个堆叠结果与TI的$ {\mathbb{Z}}_2 $分类结果是相符的, 也说明了TI是可逆的(invertible). 两个纯拓扑序iTO(其$ \theta $是平凡的, 取值是周期的整数倍)堆叠在一起得到新的iTO: $ {\rm{iTO}}_{t_1}\boxtimes{\rm{iTO}}_{t_2} \!=\! {\rm{iTO}}_{t_*} $, 其中$ t_* \!=\! {\mathsf{Lcm}}(t_1, t_2) $($ {\mathsf{Lcm}} $是最小公倍数). FTI和TI堆叠在一起的结果是: $ {\rm{FTI}}_{t}\boxtimes{\rm{TI}} = {\rm{iTO}}_{t} \; (t\in{\mathbb{Z}}_{\rm odd}) $或$ {\rm{FTI}}_{t} \; (t\in{\mathbb{Z}}_{\rm{even}}) $. 这个堆叠结果说明, t为奇数的FTI实际上可以看成iTO和TI的堆叠($ {\rm{iTO}}_{t}\boxtimes $$ {\rm{TI}} = {\rm{FTI}}_t\, (t\in{\mathbb{Z}}_{\rm odd}) $), 其非平凡的$ \theta $是由于TI的存在. 然而对于偶数t的FTI却显得更加基本. 因而我们把奇数t的FTI称为type-I, 而把偶数t的FTI称为type-II. 把两个FTI堆叠在一起得到: $ {\rm{FTI}}_{t_1}\boxtimes{\rm{FTI}}_{t_2} \!=\! {\rm{iTO}}_{t_*} \;(t_1, t_2 \!\in \!{\mathbb{Z}}_{\rm odd}) $或$ {\rm{FTI}}_{t_*} \; (t_1 \!\in\! {\mathbb{Z}}_{\rm odd},$$ t_2\in {\mathbb{Z}}_{\rm{even}}) $. 其中$ t_* = {\rm{Lcm}}(t_1, t_2) $. 如果$ t_1, t_2 $都是偶数, 假设$ t_i = 2^{k_i}t_i' $ ($ i = 1, 2; t_i' \in{\mathbb{Z}}_{\rm{odd}}, k_i\in{\mathbb{Z}} $), 那么$ {\rm{FTI}}_{t_1}\boxtimes{\rm{FTI}}_{t_2} = {\rm{iTO}}_{t_*}\; (k_1 = k_2) $或$ {\rm{FTI}}_{t_*}\; (k_1\neq k_2) $. 其中, $ t_* = {\mathsf{Lcm}}(t_1', t_2')2^{\max(k_1, k_2)}\, . $总的来讲, 在$ {\rm{TI}} $、$ {\rm{iTO}}_t $ ($ t\in{\mathbb{Z}}_{\rm{odd}} $)和type-II $ {\rm{FTI}}_t $之间的各种堆叠操作可以产生所有其他的拓扑态, 从而生成整个幺半群. 所以, 我们可以把这三种态称为“根态”(root phases).
2 -->

4.2.推广的Witten效应和表面量子霍尔效应

三维拓扑绝缘体(TI)中两个重要的响应现象是体内的威腾(Witten)效应和边界上的半整数霍尔电导. TI需要的对称群是$ U(1)\rtimes {\mathbb{Z}}^T_2 $, 相应的拓扑响应作用量是(34)式. 文献[51]讨论更多对称群保护的三维SPT态, 推广了威腾效应, 见表6. $ q_i = s, s-1, s-2, \cdots $, 其中, s是总自旋量子数: $ {{S}}^2 = s(s + 1) $. 表格中的各种量子霍尔效应的名称及其电导的定义已经在第2.3节中有所介绍. 如果恢复量纲, 霍尔“电”导$ \sigma^c $、$ \sigma^s $和$ \sigma^{cs} $的单位分别是: $ {e^2}/{\hbar} $、$ \hbar $和e. $ U(1)_C $和$ U(1)_{S^z} $分别是电荷和z方向自旋对称群. $ {\mathbb{Z}}_2 $是指绕着$ S^y $自旋轴转动$ {\text{π}} $. 响应作用量可以统一写为:

轴子角	对称群	三维体内($\varSigma^3$)的响应	二维表面($\partial\varSigma^3$)的反常响应	二维平面($\varSigma^2$)的响应
$ \theta_c=2{\text{π}}+4{\text{π}} k$ (带电玻色系统)	$U(1)_C\rtimes{\mathbb{Z}}^{\rm T}_2$	电荷-威腾效应: $N^c=n^c+N^c_m$	量子电荷霍尔效应 (${\mathbb{Z}}^{\rm T}_2$破缺的$\partial\varSigma^3$): $\widetilde{\sigma}^{c}=(1+2 k)\dfrac{1}{2{\text{π}}}$	量子电荷霍尔效应 (${\mathbb{Z}}^{\rm T}_2$破缺的$\varSigma^2$) $\sigma^c=2 k\dfrac{1}{2{\text{π}}}$
$ \theta_s=2{\text{π}}+4{\text{π}} k$ (整数自旋的 玻色系统)	$U(1)_{S^z} \times {\mathbb{Z}}^{\rm T}_2$	自旋-威腾效应: $N^s=\displaystyle \sum_i q_in_i^s+N^s_m\sum_{i}q_i^2$	量子自旋霍尔效应 (${\mathbb{Z}}^{\rm T}_2$破缺的$\partial\varSigma^3$): $\widetilde{\sigma}^{s}=(1+2 k)\dfrac{1}{2{\text{π} } }\displaystyle\sum_i{q_i^2}$	量子自旋霍尔效应 (${\mathbb{Z}}^{\rm T}_2$破缺的$\varSigma^2$) $\sigma^s=2 k\dfrac{1}{2{\text{π} } }\displaystyle\sum_i{q_i^2}$
$ \theta_0={\text{π}}+2{\text{π}} k$ (带电和整数自旋 的玻色系统)	$U(1)_C \!\times\! [U(1)_{S^z} \!\rtimes\! {\mathbb{Z}}_2]$	交互-威腾效应: $N^c=n^c+\dfrac{1}{2}N^s_m$; $N^s=n^s_{+}-n^s_{-}+\dfrac{1}{2}N^c_m$	量子电荷-自旋/ 自旋-电荷效应 (${\mathbb{Z}}_2$破缺的 $\partial\varSigma^3$): $\widetilde{\sigma}^{cs}=\widetilde{\sigma}^{sc}=\left(\dfrac 1 2+k\right)\dfrac{1}{2{\text{π}}}$	量子电荷-自旋/ 效应 自旋-电荷 (${\mathbb{Z}}_2$破缺的$\varSigma^2$): $\sigma^{cs}=\sigma^{sc}=k\dfrac{1}{2{\text{π}}}$

表6带整数自旋和电荷的玻色SPT的电荷和自旋响应理论^[51].
Table6.Charge and spin response of spin-1 and charge-1 boson systems.

$ S = \int \frac{\varTheta_{IJ}}{8{\text{π}}^2} {\rm d} A^{I} \wedge {\rm d} A^{J} . $

其中, $ I, J = 1, 2 $. $ A_\mu^1, A_\mu^2 $分别表示 $ A^c_\mu, A^s_\mu $. 通常的麦克斯韦项没有写进作用量, 因为麦克斯韦项只会修正体系的介电常数和磁导率, 与我们关心的拓扑性质(体内的威腾效应与边界上的霍尔效应)没有关系.
系数矩阵$ \varTheta_{IJ} $是对称的, 定义为: $ \varTheta_{11} = \theta_c $, $ \varTheta_{22} = \theta_s $, $ \varTheta_{12} = \varTheta_{21} = \theta_0 $. 表格里第一行是BTI; 第二行是拓扑顺磁体. 下面简单介绍一下第三行的物理, 亦即作用量S的非对角元

$S_0\equiv \int {\rm d}^4 x \frac{\theta_0}{4{\text{π}}^2}\partial_{\mu}A^{c}_\nu\partial_\lambda A^{s}_\rho\epsilon^{\mu\nu\lambda\rho} = \int \frac{\theta_0}{4{\text{π}}^2} {\rm d} A^{c}\wedge {\rm d} A^{s}.$

这种$ {\rm d}A^c {\rm d} A^s $的项在文献[192—194]中作为电流4-矢量的不守恒量“$ \partial J $”的期望值.
用于保护非对角元拓扑项的最小对称性要求是$ U(1)_C\times[U_{S^z}(1)\rtimes{\mathbb{Z}}_2] $. 在$ {\mathbb{Z}}_2 $的非单位元的操作下, $ A_\mu^s\rightarrow -A^s_\mu $. 规范场$ A^s $相应的所谓的“电场”$ {{E}}^s $和“磁场”$ {{B}}^s $作如下变换: $ {{E}}^s\rightarrow -{{E}}^s $, ${{B}}^s\rightarrow -{{B}}^s，$ ${{E}}^c\rightarrow {{E}}^c\, , {{B}}^c\rightarrow {{B}}^c$. 从这些变换我们可以得到作用量的变换规则:

$ \begin{split} S_0 = &\int {\rm d}^4x \frac{\theta_0}{4{\text{π}}^2}\partial_{\mu}A^{c}_\nu\partial_\lambda A^{s}_\rho\epsilon^{\mu\nu\lambda\rho}\\ = &\int {\rm d}^4x \frac{\theta_0}{4{\text{π}}^2} ({{E}}^c \cdot{{B}}^s+ {{B}}^c\cdot{{E}}^s )\longrightarrow -S_0. \end{split} $

尽管有负号产生, $ \theta_0 $的周期性可以让$ -S_0 $变回$ S_0 $. 下面我们考察一下$ \theta_0 $的周期. 考虑SPT态定义在三维区域$ \varSigma^3 $, 其边界(或称为“表面”, 定义在$ z = 0 $的平面, x和y坐标有周期性边界条件)是$ \partial\varSigma^3 $. 假设该边界上$ {\mathbb{Z}}_2 $对称性被破坏, 该表面的响应理论是一个交互(mutual)Chern-Simons拓扑项: $ S_{0, \partial\varSigma^3} = \displaystyle\int\dfrac{\theta_0}{4{\text{π}}^2}A^s \wedge {\rm d} A^c $. 最近, 类似交互Chern-Simons拓扑项已应用于其他不同问题上, 比如掺杂莫特绝缘体^{[76–78,195,196]}和阻挫量子反磁体^[197]. 自旋和电荷响应流(response current)分别定义为:

$\begin{split} & J^{s, \partial \varSigma^3}_\mu\equiv \frac{\delta S_{0, \partial\varSigma^3}}{\delta A^s_\mu} = \frac{\theta_0}{4{\text{π}}^2}\partial_\nu A^c_\lambda\epsilon^{\mu\nu\lambda}, \\ & J^{c, \partial \varSigma^3}_\mu\equiv \frac{\delta S_{0, \partial\varSigma^3}}{\delta A^c_\mu} = \frac{\theta_0}{4{\text{π}}^2}\partial_\nu A^s_\lambda\epsilon^{\mu\nu\lambda}.\end{split} $

他们分别由外电场$ {{E}}^c $和自旋规范场的“电场”矢量$ {{E}}^s $诱导. 从响应流的表达式, 我们可以读出相应的自旋-电荷 和电荷-自旋 霍尔电导: $ \widetilde{\sigma}^{sc} = \widetilde{\sigma}^{cs} = $$\dfrac{\theta_0}{4{\text{π}}^2}$. 假设$ \theta_0 $的最小周期为P, 物理上, 我们可以通过在表面态上堆叠一层正常的二维霍尔态^[51,198,199]. 正常的霍尔态对应的霍尔电导的量子化条件是$ \sigma^{cs} = \sigma^{sc} = \dfrac{k}{2{\text{π}}} $, $ k\in{\mathbb{Z}} $. 因而, $ \dfrac{P}{4{\text{π}}^2} = \dfrac{k}{2{\text{π}}} $. 令$ k = 1 $, 则$ P = 2{\text{π}} $. 满足$ {\mathbb{Z}}_2 $操作下不变的$ \theta_0 $的最小值是周期的一半, 所以$ \theta_0 = {\text{π}} \text{ mod }2{\text{π}} $.
为了理解表6中的交互威腾效应, 我们首先写下三维体内($ \varSigma^3 $)的响应流方程:

$ J^s_\mu\equiv \frac{\delta S_0}{\delta A^s_\mu} = \frac{\theta_0}{4{\text{π}}^2}\epsilon^{\mu\nu\lambda\rho}\partial_\nu \partial_\lambda A^c_\rho $

和

$ J^c_\mu\equiv \frac{\delta S_0}{\delta A^c_\mu} = \frac{\theta_0}{4{\text{π}}^2}\epsilon^{\mu\nu\lambda\rho}\partial_\nu \partial_\lambda A^s_\rho.$

其中, $ J^s_\mu $和$ J^c_\mu $分别是响应自旋流和电流. 零分量$ J^s_0 $和$ J^c_0 $对应的方程是:

$J^s_0 = \frac{\theta_0}{4{\text{π}}^2}\nabla\cdot {{B}}^c,\, J^c_0 = \frac{\theta_0}{4{\text{π}}^2}\nabla\cdot {{B}}^s. $

一般来讲, 磁场是没有散度的. 但是考虑磁单极子的组态之后, 磁场是可以有散度的: $\displaystyle \int {\rm d}^3 x \nabla\cdot $${{B}}^c = 2{\text{π}} N_m^c $, 其中, $ N_m^c\in {\mathbb{Z}} $是磁荷(亦即, 磁单极子个数). 同样, 我们也可以写出自旋规范场对应的“磁单极子个数”$ N_m^s $. 根据零分量的响应方程我们可以计算出响应自旋总量和响应电荷总量: $ N^{s/c} = \displaystyle\int {\rm d}^3 x J^{s/c}_0 = \dfrac{\theta_0}{2{\text{π}}}N_m^{c/s} $. 这个响应自旋和电荷均是极化自旋云和极化电荷云, 不携带量子统计信息^[200]. $ N^{s/c} $的表达式表明, 磁单极子会诱导分数化的电荷和自旋. 但原则上, 磁单极子上还可以粘附整数个电荷($ n^c\in{\mathbb{Z}} $)和整数自旋($ n^s_{+}\in{\mathbb{Z}} $和$ n^s_{-}\in{\mathbb{Z}} $)(因为SPT是由携带整数自旋和整数电荷的玻色子构成). 所以, 加上这些整数贡献, 我们就可以得到如表6中所示的交互威腾效应的表达式: $ N^s = n^s_{+}-n^s_{-}+\dfrac{\theta_0}{2{\text{π}}}N^c_m $, $ N^c = n^c+\dfrac{\theta_0}{2{\text{π}}}N^s_m $. 其中, $ \theta_0 $的周期贡献可以吸收到粘附的电荷和自旋中去. 在$ {\mathbb{Z}}_2 $的操作下, 我们有以下变换规律: $ N^s\rightarrow -N^s $, $ n^s\rightarrow -n^s-N^c_m $, $ N^s_m\rightarrow -N^s_m $, $ n^c\rightarrow n^c+ $$N^s_m$, $ N^c\rightarrow N^c $, $ N^c_m\rightarrow N^c_m $.
2 -->

4.3.推广的Wen-Zee拓扑项

SPT的对称性除了可以是自旋旋转这种作用在内部空间的情形, 还可以是空间对称性. 比如自由费米子体系里的拓扑晶体绝缘体^[201,202]. 过去几年里, 对点群保护的SPT(缩写为pgSPT)的研究有了许多进展, 比如:^[203–208]. 其中一个思路是通过局域幺正变换把SPT变成低一维空间的SPT, 使得原SPT的空间对称性变成了低一维SPT的通常的内部对称性. 通过这种映射关系, 我们可以得到点群对称性保护的SPT的分类和表征. 这个方法的结果与更加数学化的方法^[207]相符. 文献[28]构造了包括晶体对称性在内的SPT的波函数. 该文献[160]研究了同时受到空间群和内部群保护的SPT: 两种对称群其中一个被破坏, SPT序就会被破坏. 文献[160]推导了这种SPT的拓扑响应理论: 一种推广了的Wen-Zee拓扑项^[209]. 最简单的几个例子见表7.

时空维度	空间对称群$G_s$	内部对称群$G_i$	不可约的Wen-Zee拓扑项$S$	角动量/自旋${\cal{J}}$
$(2 + 1)$维	$SO(2)$	$U(1)$	$\dfrac{k}{2{\text{π}}} \displaystyle\int \omega \wedge {\rm d}A$, $k \in \mathbb{Z}$	$\dfrac{k}{2{\text{π}}} \displaystyle\int_{M^2} {\rm d}A$
$(2 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1}$	$\dfrac{k}{2{\text{π}}} \displaystyle\int \omega \wedge {\rm d}A$, $k \in \mathbb{Z}_{N_{01}}$,	$\dfrac{k}{2{\text{π}}} \displaystyle\int_{M^2} {\rm d}A$
$(2 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2} $	$k \dfrac{ N_1 N_2}{(2{\text{π}})^2 N_{012}} \displaystyle\int \omega \wedge A^1 \wedge A^2$, $k \in \mathbb{Z}_{N_{012}}$	$k \dfrac{ N_1 N_2}{(2{\text{π}})^2 N_{012}} \displaystyle\int_{M^2} A^1 \wedge A^2$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1}$	$k \dfrac{N_0 N_1}{ (2{\text{π}})^2 N_{01}} \displaystyle\int \omega \wedge A \wedge {\rm d}A$, $k \in \mathbb{Z}_{N_{01}}$	$k \dfrac{ N_1}{ (2{\text{π}})^2 N_{01}} \displaystyle\int _{M^3} A \wedge {\rm d}A$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1}$	$k \dfrac{N_0 N_1}{(2{\text{π}})^2 N_{01}} \displaystyle\int A \wedge \omega \wedge {\rm d} \omega$, $k \in \mathbb{Z}_{N_{01}}$	$k \dfrac{ N_1}{2{\text{π}}^2 N_{01}} \displaystyle\int_{M^3} A \wedge {\rm d}\omega$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1} \times U(1)$	$k \dfrac{N_0 N_1}{(2{\text{π}})^2 N_{01}} \displaystyle\int \omega \wedge A^1 \wedge {\rm d}A^2$, $k \in \mathbb{Z}_{N_{01}}$	$k \dfrac{N_1}{(2{\text{π}})^2 N_{01}} \displaystyle\int_{M^3} A^1 \wedge {\rm d}A^2$
$(3 + 1)$维	$SO(2)$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2}$	$k \dfrac{N_1 N_2}{(2{\text{π}})^2 N_{12}} \displaystyle\int A^1 \wedge A^2 \wedge {\rm d} \omega$, $k \in \mathbb{Z}_{N_{12}}$	$k \dfrac{N_1 N_2}{(2{\text{π}})^2 N_{12}} \displaystyle\int_{M^3} {\rm d} (A^1 \wedge A^2)$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2}$	$k \dfrac{N_0 N_1}{(2{\text{π}})^2 N_{01}} \displaystyle\int \omega \wedge A^1 \wedge {\rm d}A^2$, $k \in \mathbb{Z}_{N_{012}}$	$k \dfrac{N_1}{(2{\text{π}})^2 N_{01}} \displaystyle\int_{M^3} A^1 \wedge {\rm d}A^2$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2}$	$k \dfrac{N_0 N_2}{(2{\text{π}})^2 N_{02}} \displaystyle\int \omega \wedge A^2 \wedge {\rm d}A^1$, $k \in \mathbb{Z}_{N_{012}}$	$k \dfrac{ N_2}{(2{\text{π}})^2 N_{02}} \displaystyle\int_{M^3} A^2 \wedge {\rm d}A^1$
$(3 + 1)$维	$C_{N_0}$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2} \times \mathbb{Z}_{N_3}$	$k \dfrac{N_0 N_1 N_2 N_3}{(2{\text{π}})^3 N_{0123}} \displaystyle\int \omega \wedge A^1 \wedge A^2 \wedge A^3$, $k \in \mathbb{Z}_{N_{0123}}$	$k \dfrac{ N_1 N_2 N_3}{(2{\text{π}})^3 N_{0123}} \displaystyle\int_{M^3} A^1 \wedge A^2 \wedge A^3$
$(3 + 1)$维($*$)	$SO(2)$	$U(1)$	$\dfrac{k}{2{\text{π}}} \displaystyle\int \omega \wedge {\rm d}B$, $k \in \mathbb{Z}$	$\dfrac{k}{2{\text{π}}} \displaystyle\int_{M^3} {\rm d}B$
$(3 + 1)$维($*$)	$C_{N_0}$	${\mathbb{Z}}_{N_1}$	$\dfrac{k}{2{\text{π}}} \displaystyle\int \omega \wedge {\rm d}B$, $k \in \mathbb{Z}_{N_{01}}$	$\dfrac{k}{2{\text{π}}} \displaystyle\int_{M^3} {\rm d}B$
$(3 + 1)$维($*$)	$C_{N_0}$	$\mathbb{Z}_{N_1} \times \mathbb{Z}_{N_2}$	$k \dfrac{N_0 N_1 N_2}{(2{\text{π}})^2 N_{012}} \displaystyle\int \omega \wedge A \wedge B$, $k \in \mathbb{Z}_{N_{012}}$	$k \dfrac{N_1 N_2}{(2{\text{π}})^2 N_{012}} \displaystyle\int_{M^3} A \wedge B$

表7推广的Wen-Zee拓扑项, 摘自[160].
Table7.Generalized Wen-Zee terms.

Wen-Zee拓扑项的基本特征是, 此类拓扑项是由通常的规范场与空间的规范场(比如自旋联络)的楔积(wedge product)混合形成的. 文献[209]在FQH态里讨论并提出了Wen-Zee拓扑项. 在一个最简单的例子, 比如整数量子霍尔态里, 我们可以从以下拉格朗日量出发:

$ {\cal{L}} = \frac{1}{4{\text{π}}} \epsilon^{\mu \nu \rho} \left( K_{IJ} a^I_\mu \partial_\nu a^J_\rho + 2 t_I A_\mu \partial_\nu a^I_\rho + 2 s_I \omega_\mu \partial_\nu a^I_\rho \right) .$

其中A是外加电磁场(扣除霍尔系统的原均匀磁场之后). $ t_I $和$ s_I $分别是电荷矢量分量和自旋矢量分量. $ \omega $是$ SO(2) $自旋联络. “$ \omega\wedge {\rm d} a $”就是最原始的Wen-Zee拓扑项, 描写的是外场如何耦合到每个拓扑流的自旋. 通过路径积分积掉$ a^I $, 我们可以得到拓扑响应理论:

$ {\cal{L}} = \frac{1}{4{\text{π}}} \epsilon^{\mu \nu \rho} (t_I A_\mu + s_I \omega_\mu) \left(K^{-1}\right)^{IJ} \partial_\nu (t_J A_\rho + s_J \omega_\rho).$

其中, A和$ \omega $的混合项也可以称为Wen-Zee拓扑项. 从而我们可以得到响应电流和响应自旋流:

$j_\mu = {\partial {\cal{L}} }/{\partial A^\mu} = \frac{1}{2{\text{π}}} \epsilon^{\mu \nu \rho} t_I \left(K^{-1}\right)^{IJ} \partial_\nu (t_J A_\rho + s_J \omega_\rho) .$

和

$ j_{s, \mu} = {\partial {\cal{L}} }/{\partial \omega^\mu} = \frac{1}{2{\text{π}}} \epsilon^{\mu \nu \rho} s_I \left(K^{-1}\right)^{IJ} \partial_\nu (t_J A_\rho + s_J \omega_\rho) .$

假设霍尔系统定义在一个二维闭流形上, 对响应电流的零分量作积分就得到了响应电荷总量: $ N_e = \displaystyle\int {\rm d}^2 x j_0 $; $ N_\phi = \nu^{-1} N_e - {\cal{S}} $. 其中, 总的磁通量子数$ N_\phi = \dfrac{1}{2{\text{π}}} \displaystyle\int\!\!\!\int {\rm d}A $和欧拉示性数$ N_R = \dfrac{1}{2{\text{π}}} \displaystyle\int\!\!\!\int {\rm d}\omega = $$2(1-g)$. g是二维闭流形的亏格. 霍尔态的填充数$ \nu = \mathbf{t}^T {K}^{-1} \mathbf{t} $. $ N_\phi $的第一项是霍尔态里$ N_\phi $与$ N_e $的标准关系. 但由于s矢量的存在, $ N_{\phi} $的第二项给出了一个新的贡献, 被称为“shift”: $ {\cal{S}} = (\mathbf{t}^T {K}^{-1}\mathbf{s}) \nu^{-1} N_R $.
注意到, 自旋联络可以看成对空间旋转对称性的“gauging”. 我们发现, Wen-Zee拓扑项可以推广到更加复杂的情形, 并且可以作为SPT的拓扑响应理论. 在表7中, A、$ A^I $代表内部对称群对应的外加规范场. 如果对称群是$ U(1) $, 那么外加规范场的规范群也是$ U(1) $; 如果对称群是$ {\mathbb{Z}}_N $, 那么外加规范场的规范群形式上仍然是$ U(1) $, 但其Wilson loop取值只在$ {\mathbb{Z}}_N $里面. $ N_{ij\cdot k} $是$N_i, N_j,\cdot ,$ $ N_k $的最大公约数. 推广的Wen-Zee拓扑项的整系数k用于标记不同的SPT态. 对于实际材料, 阿贝尔空间转动群$ G_s $限于$ C_2, C_3, C_4 $和$ C_6 $. 需要注意的是, 最后三行(用星号特别标记)含有$ 2 $-形式的规范场B. 拓扑响应理论里含有$ 2 $-形式的规范场, 说明相应的SPT的对称群含有1-形式的对称性^[210]. 而一般情况下, 内部对称性都是$ 0 $-形式, 比如自旋旋转对称性. 文献[157]也讨论了有高形式对称性的拓扑态, 摘自[157]的附件(Supplemental Materials). 表7里的角动量/自旋$ {\cal{J}} $是响应荷: $ {\cal{J}} \!=! \dfrac{1}{N_0}\displaystyle\int {\rm d}^Dx \dfrac{\delta S}{\delta \omega_0} $ (当$ G_s \!=\! C_{N_0} $)和$ {\cal{J}} \!=\! \displaystyle\int {\rm d}^Dx \dfrac{\delta S}{\delta \omega_0} $ (当$ G_s \!=\! SO(2) $).
物理上, 我们可以通过“旋错”(disclination)这种晶格缺陷来实现$ \omega $的非平凡磁通$\displaystyle \int {\rm d}\omega $. 在黎曼-嘉当(Riemann-Cartan)几何^[211–214]里, 挠率(torsion)和黎曼曲率分别可以用位错和旋错两种晶格缺陷来实现. 对于表7中的SPT, 空间群均是沿着某个固定轴的空间旋转, 因此在探测这种SPT序的时候, 旋错将会起到重要的作用. 下面我们详细计算一个例子来理解表7.
我们考虑对称群为$ G = C_{N_0} \times {\mathbb{Z}}_{N_1} \times {\mathbb{Z}}_{N_2} $的二维SPT. 拓扑响应理论的作用量是:

$ S = \; k \frac{N_0 N_1 N_2}{(2{\text{π}})^2 N_{012}} \int \omega \wedge A^1\wedge A^2. $

其中, $ N_{ij\dots k} \equiv {\rm{gcd}}\{N_i, N_j, \dots, N_k\} $. 整数$ k\in {\mathbb{Z}}_{N_{012}} $与SPT态一一对应. 从该作用量我们可以得到响应角动量:

$ {\cal{J}} = \frac{1}{N_0}\int_{M^2} {\rm d}^2x \frac{\delta S}{\delta \omega_0} = k \frac{N_1 N_2}{(2{\text{π}})^2 N_{012}} \int_{M^2} {\rm d}^2x \epsilon^{ij} A^1_i A^2_j. $

这个响应荷由被束缚在$ D_1 $和$ D_2 $的交点处的无能隙模式携带, 见图8(a). 对于给定的k, 该角动量取值的最小单元是:
图 8 (a) 公式(42)代表的拓扑响应现象的示意图. $ \mathbb{Z}_{N_1} $的对称性畴壁$ D_1 $和$ \mathbb{Z}_{N_2} $的对称性畴壁$ D_2 $的交点携带分数角动量$ \mathcal{J} $. $ A^1 $和$ A^2 $分别是垂直于畴壁$ D_1 $和$ D_2 $的规范联络. (b) 公式(44)代表的拓扑响应现象的示意图. 旋错线与$ \mathbb{Z}_{N_2} $对称性畴壁$ D_2 $的交点携带$ A^1 $规范场的分数规范荷$ \mathcal{Q}_1 $. $ \omega $和$ A^2 $分别是垂直于旋错线和畴壁的规范联络^[160]
Figure8. (a). Topological response for Eq. (42). The intersection of $ \mathbb{Z}_{N_1} $ and $ \mathbb{Z}_{N_2} $ symmetry domain walls $ D_1 $ and $ D_2 $ carries the angular momentum $ \mathcal{J} $. $ A^1 $ and $ A^2 $ are the gauge connections normal to the domain walls. (b). Topological response of Eq. (44). The intersection of disclination line and $ \mathbb{Z}_{N_2} $ symmetry domain walls $ D_2 $ carries the $ A^1 $ charge $ \mathcal{Q}_1 $. $ \omega $ and $ A^2 $ are the gauge connections normal to the disclination line and domain wall, respectively

$ {\cal{J}}_{\min} = k \frac{N_1 N_2}{(2{\text{π}})^2 N_{012}} \frac{2{\text{π}}}{N_1}\frac{2{\text{π}}}{N_2} = \frac{k}{N_{012}}. $

当k增加一个周期, $ {\cal{J}}_{\min} $只会改变整数大小, 因而其分数部分可以用来刻画非平凡的SPT序. 假设$ N_0 = 4, N_1 = N_2 = 8 $, 亦即$ G_s = C_4 $和$ G_i = {\mathbb{Z}}_8\times $${\mathbb{Z}}_8 $. 那么 k的最小周期是4: $ k \!\sim\! k \!+\! 4 $. $ k \!=\! 0, 1, 2, 3 $可以用于标记四种不同的SPT序. 它们的最小的正的角动量取值分别为: $ {\cal{J}}_{\min} \!=\! \hbar\, , (k \!=\! 0 , \text{平凡态}) $、$ {\cal{J}}_{\min} \!=\! \dfrac{1}{4}\hbar\, , \, \, (k = 1) $、$ {\cal{J}}_{\min} \!=\! \dfrac{1}{2}\hbar\, , (k = 2) $、$ {\cal{J}}_{\min} \!=\! \dfrac{3}{4}\hbar,$ (k = 3) . 我们也可以从拓扑响应理论的作用量中得到$ A^1 $的规范荷, 见图8(b):

$\begin{split} {\cal{Q}}_1\; & = \frac{1}{N_1} \int_{M^2} {\rm d}^2x \frac{\delta S}{\delta A^1_0} \\ &= -k \frac{N_0 N_2}{(2{\text{π}})^2 N_{012}} \int_{M^2} {\rm d}^2x \epsilon^{ij} \omega_i A^2_j, \end{split}$

$ {\cal{Q}}_1 $取值是分数化的:

$ {\cal{Q}}_1 = k\dfrac{N_0 N_2}{(2{\text{π}})^2 N_{012}} \dfrac{2{\text{π}}}{N_0}\dfrac{2{\text{π}}}{N_2} = \dfrac{k }{N_{012}} .$

表里其他例子可以用类似的方法来理解. 比如$ G = C_{N_0} \times {\mathbb{Z}}_{N_1} \times U(1) $. 我们可以考虑作用量$ S = k \dfrac{N_0 N_1}{(2{\text{π}})^2 N_{01}}\displaystyle \int \omega \wedge A^1\wedge {\rm d}A^2 $. 响应角动量$ {\cal{J}} $可写为: $ {\cal{J}} = k \dfrac{ N_1}{(2{\text{π}})^2 N_{01}}\displaystyle \int_{M^3} {\rm d}^3 x \ \epsilon^{ijk} A^1_i \partial_j A^2_k $. 其最小可取的分数值为: $ {\cal{J}}_{\min} = {k}/{N_{01}} $. 如图9(a)所示, 在$ {\mathbb{Z}}_{N_1} $对称性畴壁$ D_1 $和$ A^2 $的磁力线的交点会有分数化的$ \mathcal J $.
图 9 两个三维SPT拓扑响应现象示意图. 摘自文献^[160]
Figure9. Illustration of two examples of SPT topological response phenomena in three dimensions

另外, 我们考虑$ G = SO(2) \times {\mathbb{Z}}_{N_1} \times {\mathbb{Z}}_{N_2} $. 对于作用量$ S = k \dfrac{N_1 N_2}{(2{\text{π}})^2 N_{12}} \displaystyle\int A^1\wedge A^2 \wedge {\rm d} \omega $, 我们可以计算出 $ {\cal{Q}}_{1} = k \dfrac{ N_2}{(2{\text{π}})^2 N_{12}} \displaystyle\int_{M^3} {\rm d}^3 x \ \epsilon^{ijk} A^2_i \partial_j \omega_k $. 该电荷最小可取的分数值是$ {\cal{Q}}_{\min} \!=\! {k}/{N_{12}} $. 如图9(b)所示, 在旋错线(disclination line)与 $ {\mathbb{Z}}_{N_2} $对称性畴壁$ D_2 $的交点上会有分数化的 $ A^1 $电荷.
2 -->

4.4.SPT拓扑响应的gauged Wess-Zumino理论

在第3.1节中, 我们介绍了SPT的低能有效理论, 主要方法是规范场论. 除此之外, 还有一种非常有效的办法: 用有约束的玻色场写下的非线性西格玛模型(NL$ \sigma $M)^[215–220]. 下面我们将介绍NL$ \sigma $M中的对称性如何被直接gauge掉, 特别是如何在Wess-Zumino(WZ)^?拓扑项里对全局对称性直接gauge^?, 从而得到边界态的微扰$ U(1) $量子反常和体内的拓扑响应理论. 详细介绍可参考文献[163]. 我们主要介绍所有奇数时空维度的玻色整数量子霍尔态(BIQH)的体内和边界的构造过程.
在NL$ \sigma $M理论中^[216], d维SPT的体内理论的作用量(定义在Minkowski时空$ {\mathbb{R}}^{d, 1} $里)可写为一个包含$ \theta = 2{\text{π}} k $的$ \theta $项的$ O(d+2) $NL$ \sigma $M:

$ S_{\rm bulk}[ {{n}}] = \int {\rm d}^{d + 1}x \ \frac{1}{2g}( \partial^{\mu}{{n}})\cdot( \partial_{\mu}{{n}}) + S_{\theta}[ {{n}}]. $

其中, 拓扑项是如下$ \theta $项(注意: 不要和公式(34)中的$ \theta $项混淆):

$ S_{\theta}[ {{n}}] = \frac{\theta}{{\cal{A}}_{d + 1}}\int_{{\mathbb{R}}^{d,1}} {{n}}^*\omega_{d + 1}\,. $

时空坐标定义为 $ x^{\mu} $, $ \mu = 0, \dots, d $ ($ x^0 = t $是时间坐标). $ \theta = 2{\text{π}} k $, $ k\in{\mathbb{Z}} $. 单位向量$ {{n}}\in O(d+2) $, 其组态空间是(d + 1)维超球面$ S^{d + 1} $. 微分形式$ \omega_{d + 1} $定义为:

$ \omega_{d + 1} = \sum_{a = 1}^{d+2} (-1)^{a-1} n_a dn_1 \wedge \cdots \wedge \overline{dn_a}\wedge \cdots\wedge dn_{d+2}. $

其中$ \overline{dn_a} $的符号“$ \overline{xxx} $”表示在楔积中需要去掉该项. 超球面$ S^{d + 1} $的“面积”是$ {\cal{A}}_{d + 1} \equiv \text{Area}[S^{d + 1}] = $$\dfrac{2{\text{π}}^{({d+2})/{2}}}{\varGamma\left[({d+2}/{2})\right]} $. $ {{n}}^*\omega_{d + 1} $表示对$ \omega_{d + 1} $的拉回(pullback)操作(相应的映射$ {{n}}: {\mathbb{R}}^{d, 1}\to S^{d + 1} $). 在笛卡尔坐标系下, $ S_{\theta}[ {{n}}] $的具体表达式为:

$ \begin{align} S_{\theta}[ {{n}}] = &\frac{\theta}{{\cal{A}}_{d + 1}}\int d^{d + 1}x \epsilon^{a_1\cdots a_{d+2}} n_{a_1} \partial_{x^0}n_{a_2} \partial_{x^1}n_{a_3}\cdots \\ & \partial_{x^d}n_{a_{d+2}}.\\[-12pt] \end{align} $

另一方面, $ (d-1) $维的边界的作用量(定义在垂直于$ x^d $坐标轴的边界Minkowski时空$ {\mathbb{R}}^{d-1, 1} $上)可写为一个包含level-k WZ拓扑项的$ O(d+2) $ NL$ \sigma $M:

$ S_{bdy}[ {{n}}] = \int d^{d}x \frac{1}{2g_{bdy}}( \partial^{\mu}{{n}})\cdot( \partial_{\mu}{{n}}) + S_{\rm WZ}[ {{n}}]. $

其中, WZ拓扑项为: $ S_{\rm WZ}[ {{n}}] = \dfrac{2{\text{π}} k}{{\cal{A}}_{d + 1}}\displaystyle\int_{{\cal{B}}} \tilde{ {{n}}}^*\omega_{d + 1} $. 边界上的$ {{n}} $只有$ d-1 + 1 = d $个时空坐标. 为了得到非平凡的WZ拓扑项, 我们通常需要做一个“维度扩张”(dimension extension), 从而增加一个虚拟维度$ s\in[0, 1] $. 符号$ {\cal{B}} = [0, 1]\times {\mathbb{R}}^{d-1, 1} $表示维度扩张之后边界的$ d + 1 $维时空流形. 扩张维度之后的$ {{n}} $改写为: $ \tilde{n}_a(x^{\mu}, s) $, 并满足如下边界条件: $ \tilde{n}_a(x^{\mu}, 1) = \delta_{a, 1} $, $ \tilde{n}_a(x^{\mu}, 0) = n_a(x^{\mu}) $. 符号$ \tilde{ {{n}}}^*\omega_{d + 1} $表示对$ \omega_{d + 1} $的拉回操作(相应的映射$ {\cal{B}}\rightarrow S^{d + 1} $). 在笛卡尔坐标系下, WZ项可改写为:

$ \begin{align} S_{\rm WZ}[ {{n}}] = & \frac{2{\text{π}} k}{{\cal{A}}_{d + 1}}\int_0^1 {\rm d}s \int d^{d}x\ \epsilon^{a_1\cdots a_{d+2}} \tilde{n}_{a_1} \partial_{s}\tilde{n}_{a_2} \\ & \partial_{x^0}\tilde{n}_{a_3}\cdots \partial_{x^{d-1}}\tilde{n}_{a_{d+2}}\ . \\[-12pt]\end{align} $

为了将上面这些理论用于理解受对称群$ G = U(1) $保护的SPT, 亦即BIQH态, 我们需要定义$ U(1) $对称操作. 我们考虑$ 2 m-2 $维的BIQH, 体内由包含$ \theta $项的$ O(2 m) $ NL$ \sigma $M刻画. 尽管选择不唯一, 我们可以选择如下的组合来定义一系列玻色子场:

$ b_{\ell} = n_{2\ell-1} + i n_{2\ell}\,\ \ell = 1,\dots,m\ . $

有了常见的玻色子场, 我们就可以方便地把$ U(1) $对称操作定义为: $ b_{\ell} \to e^{i\xi}b_{\ell}, \forall \ell $, 其中$ \xi\in{\mathbb{R}} $是不依赖于时空坐标的群参数. 物理上, 我们可以将玻色子$ b_\ell $理解为m个带单位电荷的复标量场. 由于$ {{n}}\cdot {{n}} = 1 $, 玻色子场也受到一个约束条件: $\displaystyle \sum\limits_{\ell = 1}^m |b_{\ell}|^2 = 1 $. 有了对称操作的定义之后, 我们需要施加$ U(1) $电磁场A来探测SPT的拓扑响应现象. 对于$ S_{bdy} $的第一项, 我们可以根据常用的“Peierls substitution”原则, 将其改写为:

$ S_{\rm kin,gauged}[ {{n}},A] = \int d^d x \frac{1}{2g_{bdy}}\sum\limits_{\ell = 1}^{m} (D^{\mu} b_{\ell})^*(D_{\mu}b_{\ell}). $

其中, $ D_{\mu} = \partial_{\mu}- {\rm i} A_{\mu} $是通常的协变导数. 对于WZ项, gauge的过程需要新的思路. 在WZ项里正确添加规范场之后可以得到新的拓扑项, 我们称之为“gWZ项”(gauged WZ). 由于体内SPT是非平凡的, 边界理论应该不是$ U(1) $规范不变的. 由于$ S_{bdy} $的第一项是规范不变的, 我们需要考察WZ项在规范变换下如何发生变化. 文献[163]指出, 在规范变换$ b_{\ell} \to {\rm e}^{{\rm i}\xi}b_{\ell} $, $ A\to A+ {\rm d}\xi $ ($ \xi $依赖于时空坐标)下, 正确的gWZ项$ S_{g\rm WZ}[ {{n}}, A] $应作如下变化:

$ S_{g\rm WZ}[ {{n}}, A] \to S_{g\rm WZ}[ {{n}}, A] + \delta_{\xi} S_{g\rm WZ}[A,\xi]\, $

其中, $ \delta_{\xi} S_{g\rm WZ}[A, \xi] $表示gWZ项在规范变换下多出来的项. 多出来的这一项被要求只和A、$ \xi $有关, 与$ {{n}} $无关.
根据这个要求, 我们来推导正确的gWZ项. 首先, WZ项中的volume form可以分解为: $ \omega_3 = {\cal{J}}_1\wedge\mathcal{K}_2 + {\cal{J}}_2\wedge\mathcal{K}_1 $. 其中, $ {\cal{J}}_{\ell} = n_{2\ell-1}dn_{2\ell}- $$n_{2\ell}dn_{2\ell-1}$, $ \mathcal{K}_{\ell} = dn_{2\ell-1}\wedge dn_{2\ell} $. 在规范变换$ b_{\ell} \to {\rm e}^{{\rm i}\xi}b_{\ell} $下, $ \omega_3 $的改变量$ \delta_{\xi}\omega_3 $是一个全微分: $ \delta_{\xi}\omega_3 = \dfrac{1}{2}d\left[ {\cal{J}}_1\wedge d\xi + {\cal{J}}_2\wedge d\xi \right] $. 因而,

$ \delta_{\xi} S_{g\rm WZ}[ {{n}}] = \frac{2{\text{π}} k}{{\cal{A}}_{3}}\frac{1}{2}\int_{{\mathbb{R}}^{1,1}} \left( {\cal{J}}_1+ {\cal{J}}_2\right)\wedge {\rm d}\xi\,. $

为了抵消$ \delta_{\xi} S_{\rm WZ}[ {{n}}] $, 我们添加一个抵消项(counter term):

$ S^{(1)}_{ct}[ {\bf{n}},A] = -\frac{2{\text{π}} k}{{\cal{A}}_{3}}\frac{1}{2}\int_{{\mathbb{R}}^{1,1}} \left( {\cal{J}}_1+ {\cal{J}}_2\right)\wedge A\ . $

规范变化使得$ A\to A+ {\rm d}\xi $, 从而抵消掉$ \delta_{\xi} S_{\rm WZ}[ {{n}}] $. 考虑了抵消项之后, 总的gWZ项变成:

$ S_{g\rm WZ}[ {{n}}, A] = S_{\rm WZ}[ {{n}}] + S^{(1)}_{ct}[ {{n}},A]. $

但是, 规范变换同时也改变了$ {\cal{J}}_1+ {\cal{J}}_2 $ ($ {\cal{A}}_{3} = 2{\text{π}}^2 $, $ F = {\rm d}A $): $ \delta_{\xi} S_{g\rm WZ}[ {{n}}, A] = k\displaystyle\int_{{\mathbb{R}}^{1, 1}} \xi \Big(\dfrac{F}{2{\text{π}}}\Big) $. 我们发现, 加了抵消项之后, $ \delta_{\xi} S_{g\rm WZ}[ {{n}}, A] $就不再依赖于$ {{n}} $, 只与$ \xi $、A有关. 所以, (56)式是正确的gWZ作用量. 为了计算体内的拓扑响应理论, 我们知道体内的响应作用量应该是Chern-Simons理论. Chern-Simons理论在有边界的时候不是规范不变的. 在规范变换下, 体内Chern-Simons理论多出来的项将会被边界的gWZ多出来的项完全抵消. 只有完全抵消, “体内+边界”作为整体才是一个自洽地、可以在格点上定义的局域模型. 从而我们得到正确的体内拓扑响应理论:

$ S_{\rm bulk} = \int \frac{2k}{4{\text{π}}}A\wedge {\rm d}A\,. $

以上是通过计算边界的gWZ理论来确定体内的拓扑响应理论. 对于更高维度(所有偶数实空间)的BIQH, 我们需要添加更多抵消项($ S^{(1)}_{ct}[ {{n}}, A], S^{(2)}_{ct}[ {{n}}, A], \cdots $)才能得到正确的gWZ作用量, 进而得到体内Chern-Simons理论($ A\wedge {\rm d}A\wedge $${\rm d}A\cdots $)的正确的系数.

本文简要回顾了SPT、iTO和SET的规范场论的研究进展, 包括“投影构造理论”、“低能有效理论”和“拓扑响应理论”三方面的内容. 本文仅讨论了玻色系统, 费米系统具有更加复杂的数学结构和丰富的物理现象, 见最近的费米子SPT的分类进展^[221]. 另外, 对于高对称性(higher symmetry)/高形式对称性(higher-form symmetry)保护的SPT也是一个非常有趣的方向^[222].
作者特别感谢下列合作者在强关联物理和拓扑物理方面的讨论: 翁征宇、田矗舜、祁晓亮、张龙、王晴睿、马遥、刘朝星、文小刚、王浚帆(Juven Wang)、刘正鑫、梅佳伟、顾正澄、Eduardo H. Fradkin、Taylor L. Hughes、Joseph Maciejko、Matthew Lapa、简超明、宁上强、程蒙、王宇轩、陈伯安(AtMa Pak On Chan)、Shinsei Ryu(笠真生)、王华嘉、韩博、温学达、Apoorv Tiwari、何欢、郑云钦等. 本文的写作也得益于国家自然科学基金委员会资助(批准号: 11847608)的中山大学理论物理讲习班(2019.11)的所有专家带来的精彩纷呈的课程, 在此一并致谢!