摘要:节点影响力的识别和预测具有重要的理论意义和应用价值, 是复杂网络的热点研究领域. 目前大多数研究方法都是针对静态网络或动态网络某一时刻的快照进行的, 然而在实际应用场景中, 社会、生物、信息、技术等复杂网络都是动态演化的. 因此在动态复杂网络中评估节点影响力以及预测节点未来影响力, 特别是在网络结构变化之前的预测更具意义. 本文系统地总结了动态复杂网络中节点影响力算法面临的三类挑战, 即在增长网络中, 节点影响力算法的计算复杂性和时间偏见; 网络实时动态演化时, 节点影响力算法的适应性; 网络结构微扰或突变时, 节点影响力算法的鲁棒性, 以及利用网络结构演变阐释经济复杂性涌现的问题. 最后总结了这一研究方向几个待解决的问题并指出未来可能的发展方向.
关键词: 增长网络/
实时动态网络/
网络结构微扰/
节点影响力

English Abstract

全文HTML

--> --> -->

复杂网络中节点影响力的识别和预测作为复杂网络的一个热点研究领域^[1-4], 有助于我们理解很多实际系统的内在结构特征并帮助我们解决一系列自然和社会系统中的重要问题, 具有重要理论意义以及现实应用价值^[5-7]. 常见的如计算机病毒在网络上的扩散、传染病在人群中的蔓延、谣言在社会中的传播等都可以看作是服从某种规律的网络传播行为. 识别和预测节点的传播影响力, 从而有效控制和引导复杂网络的传播行为^[8]. 再如用来评估科学家的潜力, 科研成果的影响力、专利的创新性等, 也可以通过科研合作网络、引文网络、专利引用网路等的拓扑结构计算其影响力, 有助于建立更加客观和具有前瞻性的科学评价体系^[9]. 在社交网络中也可以通过网络拓扑结构计算网络中节点的影响力, 用来识别在线用户的社会影响力, 同样电商网络中也可以通过网络拓扑结构计算网络中节点的影响力, 用来评价消费者和商家的声誉, 商品的流行度和口碑等, 有助于建立客观的电子商务交易评价体系^[10]. 另外随着互联网和电子产品在全球范围内获得普及, 人们大部分的社会活动都要借助互联网和电子产品, 同时互联网也忠实地记录下人们在社会经济系统中的大量行为数据, 而海量数据的开放和使用进一步会对社会经济研究产生深远影响. 目前已经有一些开创性的工作利用国际贸易、手机记录、社交媒体、网络检索、网络购物等数据构建复杂网络, 利用网络拓扑结构计算节点的影响力, 用来评估区域经济影响力, 预测经济发展潜力, 甚至提前预测一些关键经济指标^[11,12].
采用复杂网络的方法预测节点影响力一般是基于网络拓扑结构^[13]. 基本思路是如果目标节点在网络中的拓扑特征非常显著, 我们就认为该节点在网络中具有重要作用或影响力, 从而用来预测节点实际的影响力, 如传播影响力、社会影响力、区域经济影响力. 例如最简单的网络拓扑结构方法—-度(Degree)^[14]即计算节点在网络中邻居个数. 在一个社交网络中, 有大量的邻居数目的用户(即该节点的度拓扑特征非常显著)可能有较大的社会影响力; 又如在引文网络中, 利用文章的引用次数来评价科学论文的影响力; 再如在国际贸易网络中, 通过出口国家数目度量国家的贸易影响力. 经典的网络拓扑结构方法除度外, 还有度量网络中的节点对其他节点施加影响的能力的紧密度指标(Closeness)^[15], 衡量个体社会地位的介数指标(Betweenness)^[16], 将单个节点的影响力看成是所有其他节点影响力的线性组合的特征向量指标(Eigenvector)^[17], 以及通过节点在网络中的位置来挖掘节点影响力的K- 壳(K-shell)分解方法^[18]. 不过研究者们并不满足于仅使用这些经典的指标. 例如直接改进度^[19,20]、紧密度及介数^[21,22]等经典指标, 设法降低特征向量的计算复杂度^[23], 优化K-壳分解方法^[24-26]. ?Lü等^[27]提出H-index指标可以刻画节点度到K-壳的变化, 并依据H-index选择高影响力节点, 以及探索K-壳扩展的度量指标^[28-30]. 这些都是为了使复杂网络中节点影响力预测和识别更有效. 另外还有一类基于随机游走的节点影响力排序方法如PageRank^[31,32], LeaderRank^[33]和HITS算法^[34].
然而上述的这类方法多是从某一角度对网络的某一方面的结构特征进行刻画, 如果目标网络的结构在该方面表现显著, 即可得到较好的效果^[35]. 那么这些指标在不同拓扑结构的网络的准确性又是怎样呢? Da Silva等^[36]通过随机网络、小世界网络和随机集合网络等网络理论模型以及美国航空网络的传播仿真实验, 采用皮尔逊系数, 讨论了节点的拓扑性质如度、可达性、节点强度、介数、K-壳指标与该节点传播影响力相关程度. 另外由于网络结构的异质性, 大量的节点的拓扑特征是不显著的, 这些指标在不同拓扑结构特征不显著的节点的影响力预测准确性又是怎样呢? 任卓明等^[37]对复杂网络中最小K-壳节点的传播影响力进行了分析, 发现真实网络中存在大量的K-壳值非常小的节点, 而传统的K-壳分解方法无法对这部分节点的传播影响力进行度量.
近5年来已有多篇综述文献对现有的复杂网络中节点影响力研究进行了系统的回顾, 总结了最新研究进展. 如刘建国等^[38]从网络结构和传播动力学的角度总结了节点影响力排序方法的最新研究进展, 并对各种方法的优缺点以及适用环境进行了分析. 任晓龙和吕琳媛^[39]系统地介绍了复杂网络领域具有代表性的30余种重要节点挖掘方法, 并详细比较各种方法的计算思路、应用场景和优缺点. Pei和Makse^[40]总结了识别和预测复杂网络中传播影响力的方法, 给出了在不同场景下有效识别和预测传播影响力的策略. Lü等^[3]在物理科学和复杂交叉科学的综述期刊之一Physics Reports上撰文深度总结了复杂网络中节点影响力近年来的研究现状及并讨论了发展动态. 目前这几篇综述的被引用次数都已经超过百次, 表明节点影响力依然是复杂网络的一个热点研究领域.
在这几篇综述的总结和展望中都提到一个问题: 节点影响力的识别和预测局限于特定网络拓扑结构, 一旦该方法在对应拓扑结构上不显著, 那么该方法的识别和预测的准确性就令人存疑, 并且在实际应用场景中, 几乎所有的复杂网络, 比如社会、生物、信息、技术、交通运输都在不停地演化中, 网络的规模和结构也的确是在不断变化的^[41]. 当网络规模小, 结构单一时, 我们可选择的节点影响力方法也多, 但是随着时间推移, 网络规模变得足够大, 网络结构变得更加复杂, 那么之前介绍的节点影响力算法就面临巨大的挑战和局限. 如图1所示, 我们给出一个动态复杂网络示例图, 在$ t_0 $时刻绿色节点的影响力可以用度衡量, 但在$ t_{0+l} $和$ t_{0+l+k} $时刻, 绿色节点的节点影响力就不再适合用度的方法评估.
图 1 动态网络示意图
Figure1. An example of the dynamic network

网络在演化过程中, 网络规模可能进一步增大, 结构随时发生改变, 网络结构中某种特性有可能是大体保持不变, 也有可能发生剧烈变化. 于是在本文中, 我们根据网络结构演化的特点, 分别详细讨论三类动态网络的节点影响力的研究进展. 第一类是增长网络, 节点影响力算法复杂性和时间偏见的问题. 因为涉及网络全局结构特征的算法, 虽计算复杂但预测准确性高, 为减少算法复杂性和针对不同网络规模, 我们介绍将网络全局结构特征的算法改进成局部到全局的渐进式算法; 另外在增长网络中, 我们讨论新旧节点的网络拓扑特征带有时间偏见的问题, 特别是基于引文网络和合作网络等, 评价和预测科学家和科技论文影响力尤为明显. 第二类是网络结构实时动态演化时, 节点影响力算法适应性问题. 在社交网络领域, 网络结构是实时动态变化的, 介绍了如何通过分析和预测网络结构特征的动态演化规律, 建立有针对性节点影响力的算法; 并讨论了网络结构演变过程中, 节点影响力的预测能力变化的问题. 第三类是网络随时间演化, 结构微扰或突变时, 节点影响力算法鲁棒性问题. 总结了在网络结构受到微扰或者突变时, 目前一系列关于经典的算法和设计高效的算法预测网络中超级稳定的节点和超级敏感的节点的工作; 并介绍了通过分析结构微扰或突变对网络拓扑特征的影响定量刻画国家经济复杂性的研究工作. 最后介绍了在动态网络中关于节点的动力学演化与网络结构特征的关系的研究工作.

2

-->

2.1.增长网络

增长网络最显著的特征是网络规模不断地变大, 最常见的例子比如因特网、合作网络、引文网络. 网络增长导致算法的复杂性和成本提高, 因此有必要设计针对不同算法复杂性和不同网络规模, 利用节点局部到全局信息的渐进式的算法. 像紧密度、介数还有基于矩阵特征向量等网络结构全局信息的方法计算复杂性太高导致难以在大规模网络中应用^[42], 而像度等这样局部特征的算法虽然算法复杂性低但预测的准确性低. 那么如何在网络规模增长到上千万甚至过亿节点的情况下快速而准确地预测节点影响力, Ercse-Ravasz等^[43,44]提出了如图2所示的局部介数方法, 该方法可以只计算节点的局部信息就可以预测节点的介数. Lü等^[45]也通过节点的局部特征近似计算katz指标用于复杂网络链路预测.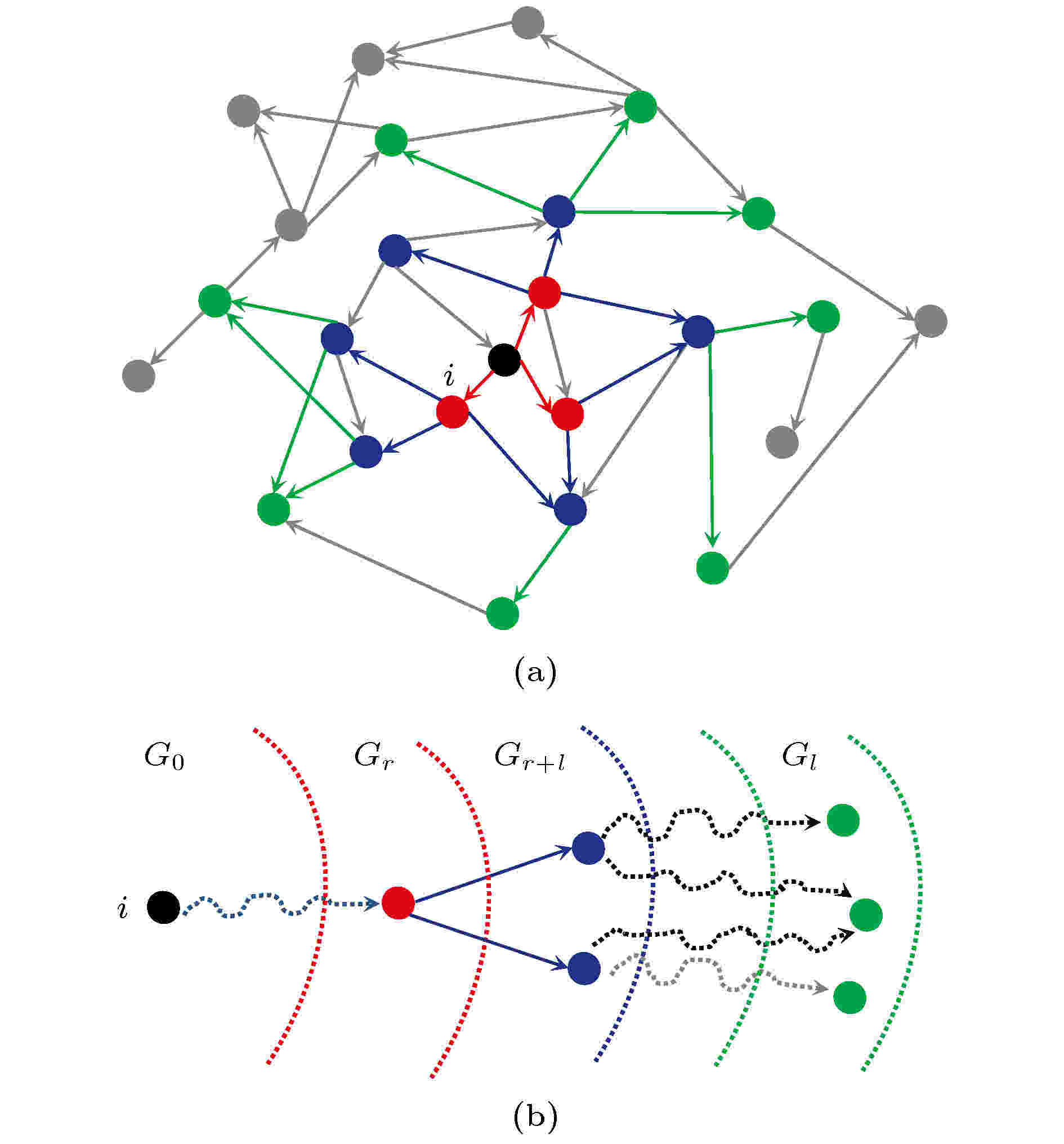
图 2 局部到全局的渐进式算法的示意图　(a) 全局算法; (b) 渐进式算法
Figure2. The diagram of local to global progressive algorithm: (a) Global algorithm; (b) The local to global progressive algorithm.

另外在增长网络中, 因为节点加入网络的先后不同, 节点影响力方法具有时间偏见, 即对旧节点更有优势. 特别是基于引文网络和合作网络等评价和预测科学家和科技论文影响力尤为明显, Mariani等^[46,47]和Wasserman等^[48]发现了PageRank算法^[31,32]在增长网络模型中存在缺陷, 即原始的PageRank算法过于偏向于旧节点, 网络中具有潜力的新节点往往会被PageRank算法压制, 进而提出了一个重标(Rescaled)的含时PageRank算法. 该算法将每个节点与其相邻时间的节点相比较, 消除了时间偏向, 弥补了PageRank算法的不足. 在该算法中, 不同时代的节点不会因为加入网络的早晚受到影响, 而且该算法相比于传统算法, 能够及早甄别出极具潜力的重要节点. 目前常见的度量影响力的算法有Citations和PageRank, 还有诸如Long Gap^[49,50], CiteRank^[51], Rescaled Citations和Rescaled PageRank^[47]等算法基于修正节点加入网络的时间的影响. Ren等 ^[52,53]利用美国电影引用数据和科学家引文数据, 分析了这6种节点影响力算法, 比较了这些算法的优劣. 虽然这些指标将每个节点与其相邻时间的节点相比较, 消除了对老的节点的时间偏向, 弥补了传统算法的不足, 仍有两个问题待解决: 1)如何修改这个方法以便在不同学科方向的论文都能够广泛适用? (不同学科的论文引用模式差别非常大, 例如在生物方面的论文引用要远远高出别的学科方向); 2)如何利用这个方法来衡量科研人员的表现, 也能更好地识别出具有潜力的科研工作者?
2 -->

2.2.实时动态网络

在实时动态网络中, 节点影响力算法的适应性问题. 现实世界的网络的统计分析表明, 大量网络的集聚性^[54]、度-度相关性^[55,56]、度分布^[57]等基本网络结构拓扑特征是随时间演化的, 诸如社交网络之类网络结构几乎是实时动态变化的, 图3给出一个实时动态网络示例图.
图 3 实时动态网络　(a) 含有一段时间的网络; (b) 动态演化网络
Figure3. An example of the time-variant dynamic network: (a) A network with a period of time; (b) the time-variant dynamic network.

在社交网络中, 大量的研究表明网络集聚性会影响网络的传播、同步、控制等功能^[58]. Klemm等^[59]研究表明集群动力学中节点的影响力是由网络拓扑结构和集群动力学机制共同决定的. Aral和Walker^[60]研究网络上的用户传播行为时, 发现有影响力的节点更具有集聚性. Centola^[61]发现传播行为在高集聚类网络中传播更快. Bond等^[62]以2010年美国大选为实例研究时发现Facebook用户的影响力与网络结构和传播机制两者都相关. 宋玉萍和倪静^[63]通过构建可变集聚系数的无标度网络模拟现实中的实时动态网络的结构演化, 以及通过采用经典传播模型进行传播影响力的仿真实验, 系统分析了在不同集聚系数的无标度网络中预测节点影响力算法的准确性. 结果发现度和介数的准确性在低集聚系数的网络中表现更好, 特征向量则在高集聚网络中更准确, 而紧密度的准确性受网络集聚系数的变化影响较小. 因此当网络的集聚系数较低时, 可选择度或者介数进行网络节点影响力评价; 反之则需要选择紧密度指标或特征向量指标. 另一方面, 传播过程的感染率越高, 度指标和介数指标越可靠, 紧密度和特征向量则相反. 另外Ma等^[64]和邵凤等^[65]也进行其他网络特征属性的研究, 结果如图4所示. 4种经典节点影响力算法 (度、紧密度、介数、特征向量中心性) 在可变度-度相关性的无标度网络中的准确性也是不同的. 另外也可以通过将实时动态网络变成高阶网络^[66,67], 这时原来网络的结构就发生改变. 如Xu等^[68]和Tao等^[69]将全球航运网络转换为高阶网络, 分析Pagerank的排序变化情况.
图 4 4种经典节点影响力算法(度、紧密度、介数、特征向量中心性)在可变度-度相关性的无标度网络中准确性, 其中β表示传播参数, r表示可变度-度相关性的无标度网络中的度- 度相关性参数, Kendall's tau值大小表示节点影响力方法的准确性
Figure4. The accuracy analysis of four centrality (degree, closeness, betweenness, eigenvector) methods on the scale-free network model with tunable assortative coefficient r and different infectious rate β.

2 -->

2.3.结构微扰或突变的动态网络

在生态网络中, 网络结构经过自然演化基本形成了稳定的结构, 但是经常可能遭遇一些自然因素, 比如极端天气、自然灾害或人为因素的干扰, 这样就会对原本稳定的网络结构造成了扰动. 还有就是交通网络, 节点代表站点, 边代表客流量, 我们知道在一般的工作日中, 由站点和客流量构成网络结构基本是固定的, 但是在周末或者节假日等会导致某些站点变得异常重要, 特别是在遭遇局部的极端天气时会导致某些站点重要性失效或者其周边可替代的节点就变得异常重要. 与交通网络类似, 还有日常生活中的电网, 由于某些节点突发原因导致级联失效. 另外在国际贸易网络中也有类似的现象, 例如遭遇局部战争、局部地区动荡或者突发的金融经济危机等, 造成网络结构发生微小扰动或者重大改变.
对于这类问题, 抽象成复杂网络问题就是网络结构在演化过程中保持某种状态, 但是随时会遇到网络中部分节点和边的状态发生变化即结构微扰或突变. 那么在这种复杂动态网络中, 如何预测节点影响力? 这就涉及到节点影响力方法的鲁棒性问题. 美国东北大学的Ghoshal和Barabasi^[70]研究了对随机网络和无标度网络结构微扰时, 通过PageRank算法的计算所得的节点影响力排序的稳定性. 结果表明PageRank面对经过微扰过的随机网络进行节点影响力排序表现很敏感, 而对经过微扰过的无标度网络的节点排序时表现很好的鲁棒性, 特别地还存在排序超级稳定(super-stable)的节点. Lü等^[71]也将结构微扰理论用于预测复杂网络连边.
最近出现一个热门领域, 即经济复杂性-基于数据驱动预测经济发展潜力^[11,12]. 其基本想法是通过国家进出口贸易数据构建一个国家-产品的二部分网络(网络中边代表国家或地区有能力生产和出口某种产品), 通过对这个二部分网络的结构特征分析, 定量刻画国家的经济复杂性. 研究结果发现未来经济的发展状况, 至少在短期内, 主要由国家产业结构复杂性所决定的. 如果想要实现持续的经济增长和繁荣, 就应该把力气花在满足自身经济复杂性涌现的条件上, 而这就取决于二部分网络的结构特征. 目前该研究主题方兴未艾, 国内外主要有意大利罗马大学Pietronero小组^[72-74]、美国麻省理工学院的Hidalgo小组^[75-77]、瑞士弗里堡大学Zhang小组^[78,79]、电子科技大学周涛小组^[11,80,81]等在这方面做了一系列的研究工作. 一般国家竞争力或影响力与其进出口的产品组合(即国际贸易网络的嵌套结构(nested structure))紧密相连. 嵌套结构的定义原本来自生态学中, 简单讲就是岛屿生物系统中, 在小岛屿中出现的物种多数也出现在物种相对丰富的大岛屿中, 这一非随机分布格局被命名为嵌套结构^[5]. 图5 给出了三个网络嵌套性分别为0, 0.5, 1的进出口网络的示意图. 这里选取经典网络的嵌套性算法NODF^[82]如下. 首先对邻接矩阵的列和行按照度降序排列, 然后按照(1)式和(2)式计算网络的嵌套性.
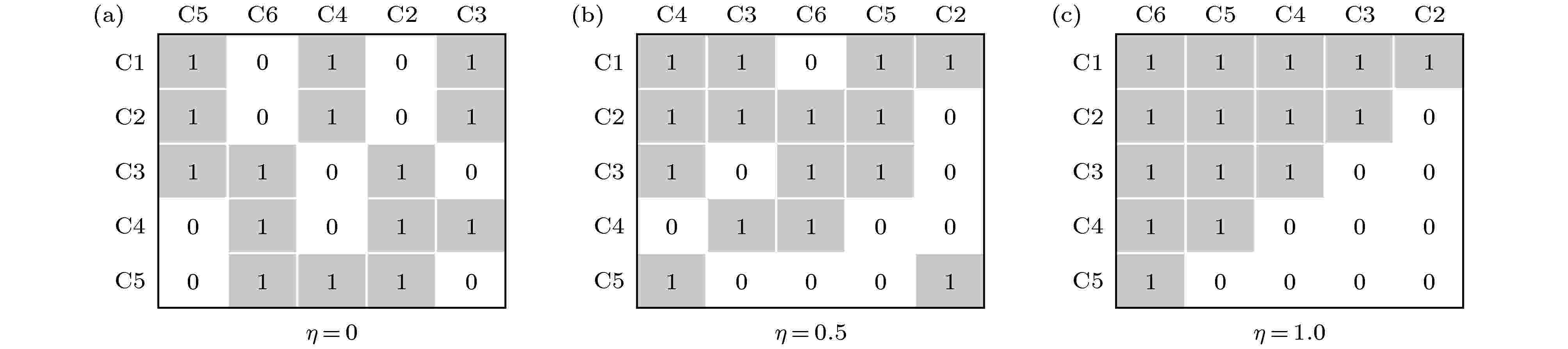图 5 邻接矩阵的嵌套性示意图　(a) 邻接矩阵的嵌套值为0; (b) 邻接矩阵的嵌套值为0.5; (c) 邻接矩阵的嵌套值为1
Figure5. The nestedness of the adjacency matrix: (a) The nestedness of the adjacency matrix is 0; (b)the nestedness of the adjacency matrix is 0.5; (c)the nestedness of the adjacency matrix is 1.

$ {\rm {NODF}}_{{ij}} = \sum\limits_{i < j} {\left\{\!\!\!\!{\begin{array}{*{20}{c}}{0,}&{{\rm{if}}{k_i} = {k_j}},\\{\frac{{\displaystyle\sum\nolimits_l {{M_{il}}{M_{jl}}} }}{{\min ({k_i},{k_j})}}},&{{\rm{otherwise}}},\end{array}} \right.} $

$ {\rm {NODF}} = \frac{\displaystyle\sum\nolimits_{i < j}{({\rm {NODF}}_{ij}^{\rm {row}}+{\rm {NODF}}_{ij}^{\rm {column}})}}{\dfrac{n(n-1)}{2}+\dfrac{m(m-1)}{2}}, \\ $

其中k为节点的度. 最终求得的邻接矩阵的嵌套值为$ [0, 1] $. 其中0表示邻接矩阵没有嵌套性质, 如图5(a), 1表示网络拥有完美的嵌套特性, 如图5(c).
嵌套结构也常用来刻画非生态系统, 例如全球或地方的经济贸易格局的演变^[83]. 图6给出了牛肉、摩托车、医疗器械三类不同商品的国际贸易网络的可视化邻接矩阵, 对应三个显著不同的嵌套特性, 图中的曲线为国际贸易中786类商品的嵌套性分布图. 随着科技进步和贸易日趋紧密, 这种贸易网络中对应的嵌套特性演化规律和机制, 以及与国家经济复杂性和影响力的映射关系. Bustos等^[84]研究发现在网络在演化过程中, 嵌套拓扑结构特性保持稳定, 但是网络中会有部分连边消失或新出现一些连边. 这一发现可以用来描述和预测国家某些新产业的出现或消失的模式, 从而找到经济发展的新动力, 为国家或地区经济的发展做出前瞻指导.
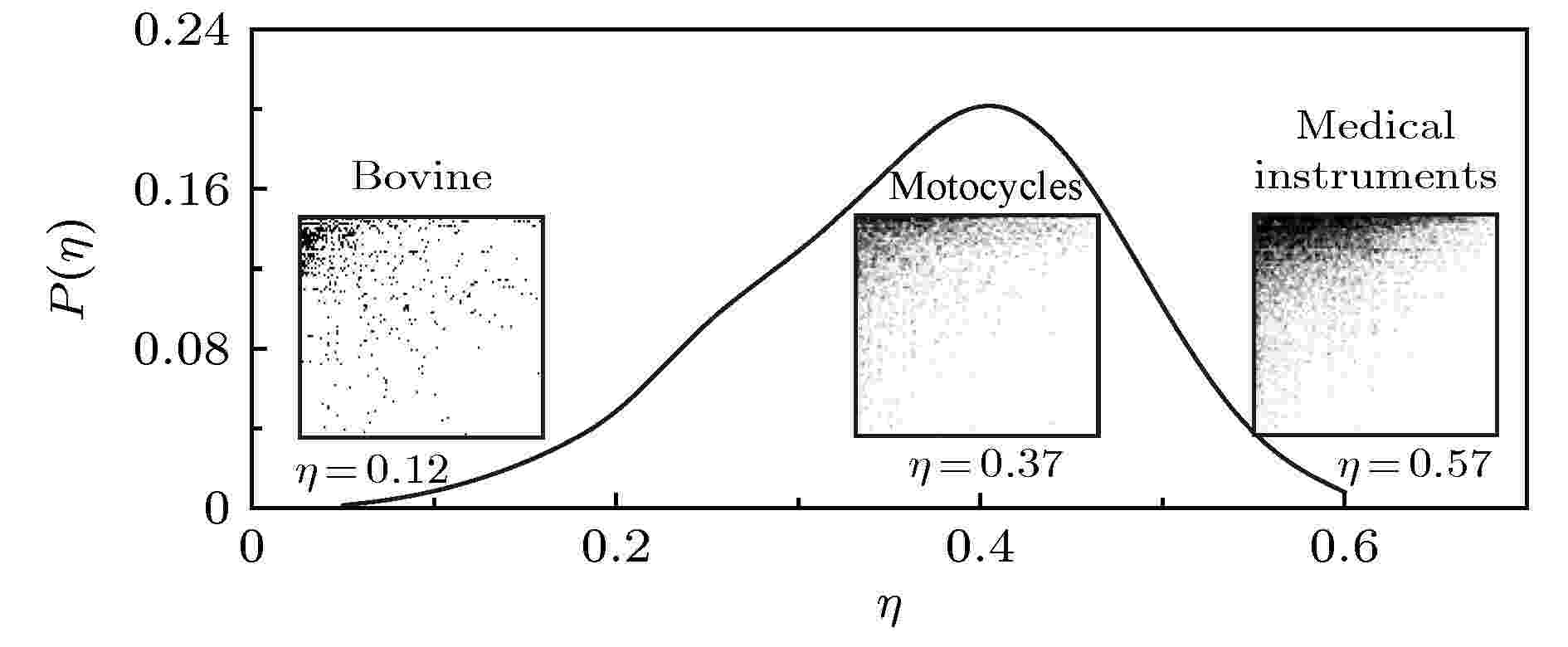图 6 786类商品国际贸易网络的嵌套性分布图, 其中子图为牛肉、摩托车、医疗器械三类不同商品的国际贸易网络的可视化邻接矩阵
Figure6. Distribution of the nestedness in the international trade networks with 786 kinds of goods. (subgraphs) The matrices are representations of the different layer of world trade networks which respectively corresponds to the network of Bovine, Motorcycles, and Medical Instruments.

就传播影响力来说, 病毒在计算机网络上的蔓延、传染病、谣言、信息在现实社会网络或虚拟的社交网络中的传播, 我们必须有效控制和引导复杂网络的传播行为趋利避害, 最好的方式就是在传播扩散之前预先推测或测定节点的传播影响力. 这时可以通过对计算机网络、现实社会网络以及虚拟的社交网络的拓扑结构特征分析, 对节点在特定结构特征中显著程度进行定量分析. 如果节点拓扑特征性质与真实的传播影响力存在拟合或相关性之类的映射关系^[85], 那么就可以采用网络结构特征来事前推测或测定节点的传播影响力. 针对真实的节点影响力, 可以采用传播动力学模仿真实的传播信息扩散过程计算传播影响力, 社会动力学过程模拟计算社会影响力, 或者通过真实的社会评价获取社会影响力, 区域经济影响力可以通过贸易流动的模拟计算. 针对不同的动力学, Barzel和Barabasi^[86,87]给出一个统一的动力学特征并分析不同动力学的与网络结构的关系. 一般动力学过程可以简化成如下描述,

$ \frac{{\rm d}{{x}_{i}}}{{\rm d}t} = W({{x}_{i}}(t))+\sum\limits_{j = 1}^{N}{{{A}_{ij}}}Q({{x}_{i}}(t),{{x}_{j}}(t)), $

其中左式为节点动力学特征随时间演化过程, 右式中$ A_{ij} $为网络的邻接矩阵, W为与节点自身相关的时间函数, Q为节点对之间相互作用的时间函数. 节点的影响力可以通过动力学仿真或数值解析获得, 公式中网络的邻接矩阵$ A_{ij} $代表是网络, 我们知道现实中网络的拓扑关系容易获得, 可以直接计算网络每个节点的拓扑结构属性. 如果这一结构特征恰好刻画实际影响力, 那么这一方法则能准确预测节点影响力.
另外也可以从从微观角度出发, 描述节点生命周期内其拓扑和动力学特征的普遍演化规律, 并给出其表达方式, 建立模型刻画节点拓扑和动力学结构特征的演化机制. 节点的拓扑和动力学特征演化特征如(4)式^[88,89]所示.

$ {{R}_{i}}(t,\Delta t) = \frac{{\rm{The}}\; {\rm{actual}}}{{{\rm{The}}\; {\rm{expected}}}} = \frac{\Delta {{f}_{i}}{{(t,\Delta t)}_{\rm a}}}{\Delta {{f}_{i}}{{(t,\Delta t)}_{\rm e}}}, $

右式中$ \Delta {{f}_{i}}{{(t, \Delta t)}_{\rm a}} $表示实际的网络节点拓扑特征在$ (t, \Delta t) $时间的变化, $ \Delta {{f}_{i}}{{(t, \Delta t)}_{\rm e}} $表示经过网络模型计算的理论值. 如果$ {{R}_{i}}(t, \Delta t) = 1 $就表明真实的动态网络与网络模型规律一致. 如果$ {{R}_{i}}(t, \Delta t) < 1 $就表明真实的动态网络节点的属性演化慢于网络模型. 如果$ {{R}_{i}}(t, \Delta t) > 1 $就表明真实的动态网络节点的属性演化快于网络模型. 我们以最简单的度和无标度网络中优先连接(preferential attachment)为例. 在实际动态演化网络中, 节点在$ \Delta t $获得度为$ \Delta {{k}_{i}}(t, \Delta t) $, 那么经过PA模型获得的节点在$ \Delta t $获得度为

$ \Delta {{k}_{i}}{{(t,\Delta t)}_{\rm {PA}}} = \frac{{{k}_{i}}(t)}{\displaystyle\sum\nolimits_{j}{{{k}_{j}}(t)}}\Delta l(t,\Delta t), $

那么度的演化动力学可以表述为

$ {{R}_{i}}(t,\Delta t) = \frac{\Delta {{k}_{i}}(t,\Delta t)}{\Delta {{k}_{i}}{{(t,\Delta t)}_{\rm {PA}}}}. $

Ren等^[90]分析了用户-电影的二部分动态网络中, 电影的流行度的演化分析, 电影的流行度可以简单定义为观众点击或观看的次数, 可以理解为电影的受欢迎程度, 即电影的影响力. 采用(6)式计算, 发现在电影刚上市时, $ {{R}_{i}}(t, \Delta t)\gg 1 $表明真实的动态网络节点的属性演化远远快于网络模型, 而后渐渐减缓到$ {{R}_{i}}(t, \Delta t) = 1 $, 表明真实的动态网络与网络模型规律一致.

本文系统总结了三类动态复杂网络中节点影响力的一些研究进展. 在增长网络中, 节点影响力的算法复杂性和时间偏见的问题; 网络结构实时动态演化时, 节点影响力的算法适应性问题; 结构微扰或突变的动态网络中, 节点影响力算法鲁棒性问题以及利用网络结构演变阐释经济复杂性涌现的问题. 可以看出目前这个方向仍然有诸多挑战有待解决. 正如本文第三节中提及的节点的动力学演化与网络结构特征的关系. 如何挖掘经典的动力学机制和网络结构特征之间的关系, 分析基于动力学模拟真实的节点影响力和基于网络结构特征挖掘的节点影响力之间的统计特性和关联关系, 并通过数学解析和数值获得节点影响力的精确解或近似解? 还有就是基于网络异质性的考虑, 分析在异质网络中, 处于“胖尾”分布的大量节点的动力学和拓扑特征的演化模式和规律, 以及在演化过程中的节点影响力的稳定性以及可预测性. 另外随着最近几年大数据变得越来越容易获得, 如何通过相互关联的动态网络增强节点影响力的可预测性和设计综合节点影响力预测算法, 这些难题的解决具有广泛应用场景. 例如通过引文网络和合作网等数据构建的多层关联网络, 建立综合影响力预测模型, 预测科学家影响力. 再如利用手机社交数据、航空网络、贸易网络等多个地理标签动态网络, 通过地理映射构建多层相互关联演化网络, 设计新的地区经济影响力预测指标, 预测地区经济发展潜力. 最后构建相互关联的动态网络模型, 系统研究对节点影响力的可预测性的影响, 从而设计综合影响力指标.