摘要: 任意矩形电路网络中的电位分布问题一直是科学研究的难题. 本研究发展了研究电阻网络的递推-变换(RT)理论使之能够用于计算任意
m ×
n 阶电路网络模型. 研究了一类含有任意边界的
m ×
n 阶矩形网络的电位分布及等效电阻, 这是一个之前一直没有解决的深刻问题, 因为之前的研究依赖于规则的边界条件或一个含有零电阻的边界条件. 其他方法如格林函数技术和拉普拉斯矩阵方法计算电位函数比较困难, 研究含有任意边界的电阻网络也是不可能的. 电位函数问题是自然科学和工程技术领域研究的一个重要内容, 如拉普拉斯方程的求解问题就是其中之一. 本文给出了含有一条任意边界的
m ×
n 矩形电阻网络的节点电位函数解析式, 并且得到了任意两节点间的等效电阻公式, 同时导出了一些特殊情形下的结果. 在对不同结果的比较研究时, 得到了一个新的数学分式恒等式.
关键词: 复杂网络 /
递推-变换理论 /
矩阵方程 /
电位函数 /
边界条件 /
分式恒等式 English Abstract Electrical properties of an arbitrary m ×n rectangular network Tan Zhi-Zhong 1 ,Tan Zhen 2 1.Department of Physics, Nantong University, Nantong 226019, China Fund Project: Project supported by the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20161278)Received Date: 28 August 2019Accepted Date: 06 November 2019Published Online: 20 January 2020Abstract: The development of natural science raises many complex new problems and requires people to find the basic method to resolve them. It was found that many problems could be resolved by building the resistor network model. In 1845, the German scientist Kirchhoff set up the node current law and the circuit voltage law.Since then the basic theory of electric circuit has been established. At present, three general theories for studying large-scale resistor networks have been developed, for example, In 2000 Cserti [Am. J. Phys. 2000, 68 , 896] set up the Green function technique to evaluate the resistance of infinite lattices. In 2004 Wu [J. Phys. A: Math. Gen. 2014, 37 , 6653] formulated a Laplacian matrix method and calculated the resistance of arbitrary finite and infinite lattices by using the eigenvalues and eigenvectors. In 2011 Tan [Resistance Network Model (Xi’an: Xidian University Press) 2011, pp16–216] proposed the recursion-transform (RT) method which depends on the one matrix along one directions and avoids the trouble of the Laplacian method that depends on two matrices along two directions. Among them, only two theories can calculate both finite and infinite networks. One is Wu's Laplacian matrix method and the other is Tan's RT method. However, there is only one way to compute a resistor network with arbitrary boundary, that is, the Tan's RT method. Potential distribution problem in arbitrary rectangular circuit network has always been a problem of scientific research. In this paper, we develop the RT-I theory of resistor networks to calculate the arbitrary m × n circuit network model. We study the potential distribution and the equivalent resistance of a class of m × n rectangular network with an arbitrary boundary, a profound problem that has not been resolved so far, because previous research depends on the boundary conditions of rules or a zero-resistance boundary condition. Other methods, such as Green function technique and Laplacian method to calculate potential function are difficult and also impossible to study the resistor network with arbitrary boundary. Potential function problem is an important research subject in natural science and engineering technology, for example, the solution of Laplace's equation is one of research work. In this paper, we present an analytical expression of the node potential function of m × n rectangular resistor network with an arbitrary boundary, and also obtainan equivalent resistance formula between any two nodes, and the results in some special cases as well. In the comparative study of different results, a new mathematical identity and several interesting inferences are discovered. Keywords: complex networks /recursion-transform theory /matrix equation /potential function /boundary conditions /fraction identity 全文HTML --> --> --> 1.引 言 德国物理学家基尔霍夫(1824—1887)创立的节点电流定律和回路电压定律为人类研究电路网络模型提供了理论基础. 现在电阻网络的研究已经不再局限于电路领域, 已经成为一种基本模型被应用于许多学科领域, 通过构建电阻网络模型进行计算机仿真研究已经成为解决一些科学问题的基本方法[1 ,2 ] . 复杂电阻网络的等效电阻解析式的获得通常比较困难, 原因在于它是一个跨学科的科学难题, 不仅需要电路理论知识, 而且需要数学理论与方法的创新[3 -6 ] . 在自然界中, 石墨烯网络的研究、一些金属化合物晶体或非金属晶体结构的研究、纳米碳管结构的研究、星际空间的宇宙尺度研究、数学中的图论研究、聚合物中的高分子结构研究、统计物理学和复杂性科学研究等, 都可能需要通过构建电阻网络模型进行模拟研究.[6 ] . 求解复杂边界条件下的拉普拉斯方程往往比较困难. 在实践研究中研究者发现可以采用模拟法通过建立电阻网络模型来研究温度场、扩散场等问题, 这是一种很有意义的模拟法. 寻找含有任意边界m × n 阶电阻网络电位问题的精确解是重要的但却是困难的. 以前的理论没有解决这样的问题, 本研究所建立的研究理论与方法能够求出多种结构电阻网络模型中各个节点的电势, 从而解出所要求解的函数方程. 因此电阻网络模型的建立与研究具有重要的理论意义与实际应用价值.[1 -43 ] , 电阻网络研究的重要进展可以概括为四个阶段. 第一阶段是1845年德国物理学家基尔霍夫(1824—1887)创立了节点电流定律和回路电压定律, 建立了电路分析的基本理论, 推动了电路理论的研究与发展; 第二阶段是2000年Cserti[3 ] (匈牙利罗兰大学) 建立了计算无限矩形网络等效电阻的格林函数技术, 该方法不适用于有限电阻网络, 格林函数技术已经得到较好的应用与发展[4 ,5 ,7 -12 ] ; 第三阶段是国际著名理论物理学家Wu[13 ] (伍法岳, 美国东北大学教授)于2004年建立了计算等效电阻的Laplacian matrix方法, 第一次系统地研究了多种拓扑结构的任意电阻网络的等效电阻, 给出了一系列理想的结论. 但是Laplacian matrix方法只适用于自由边界(规则边界)、周期边界, 零电阻边界等特殊情形的网络, 所给出的结论是由倍求和表达的结果[13 -19 ] , 在后来的研究中Laplacian matrix方法在研究电阻方面已经得到较好的应用与发展[20 -23 ] ; 第四阶段是2011年谭志中(南通大学)建立了一种“递归-变换” (recursion-transform)方法[24 ] , 该方法适用于研究含有任意边界的有限和无限的电阻网络模型, 弥补了Laplacian matrix方法的不足[25 -30 ] . “递归-变换”方法(简称RT方法)的新发展是Tan[28 -30 ] 于2015年发表的三篇论文, 该方法不仅能够计算等效电阻而且能够研究复阻抗的电特性[31 -34 ] . 特别需要说明的是, 随着研究的不断深入与发展, 谭志中的RT方法已经细化为RT-I方法和RT-V方法, 其中RT-I方法是指基于支路电流参数建立矩阵方程的方法, 而RT-V方法是指基于节点电压参数建立矩阵方程的方法[35 ,36 ] , 这两种方法构成了研究电阻网络模型的系统理论.n × m 有限电阻网络的方法只有两种, 一种是伍法岳的Laplacian matrix方法, 另外一种是谭志中的RT方法, 而能够用于研究含有任意边界电阻网络的方法只有唯一的RT方法. 因此有必要进一步介绍RT方法曾经给出的研究. 2013年Tan等[25 ] 应用RT方法研究了一个3 × n 阶cobweb模型, 并且提出了任意m × n 阶cobweb等效电阻的一个猜想, 该猜想引起了国际同行专家的高度兴趣[20 ] , 吸引了国际同行专家与我们开展合作研究[23 ,26 ,27 ] . 2014年以来我们采用RT方法发表了一系列学术论文[26 -43 ] , 解决了一系列之前没有解决的电阻网络难题. RT方法的优越性在于应用此理论所给出的等效电阻结论是由单求和表达的简单结果 (注: Wu教授建立的Laplacian matrix方法所给出的结果是由倍求和表达), 便于推广应用, 并且所得到的等效电阻公式能够有效地应用于复阻抗网络研究[32 ,33 ,37 -40 ] . 尽管前面阐述RT方法能够用于研究复杂的电阻网络模型, 但是由于时间的限制 (RT理论提出的时间不长)及电阻网络边界条件的复杂多样, 还没有来得及解决所有的问题. 例如之前的RT-I理论所研究的电阻网络都依赖于含有零电阻的边界[25 -31 ,41 -43 ] 或只是研究了特殊节点间的等效电阻[32 -34 ] . 当然, 研究复杂边界的电阻网络问题还需要技术创新, 本文正是获得了技术创新才解决了非零边界的电阻网络, 解决了以前没有解决的复杂问题.图1 所示的电阻网络, 该模型不含有零电阻边界但是含有一个任意的右边界, 研究任意节点的电位函数是一个以前从来没有解决的问题, 这主要因为以前的相关理论不能解决这样的问题(如Laplacian matrix方法[13 ] , 格林函数技术[7 -12 ] 等). 任意右边界条件代表了网络的多功能特性, 因为可以任意改变右边界而得到各种各样的几何结构, 如当${r_1} = 0$ 时得到一个扇形网络模型, 当${r_1} = {r_0}$ 时得到规则的矩形网络模型, 等等. 文献[13 ]曾经研究了当${r_1} = {r_0}$ 时的规则矩形电阻网络(${r_1} = {r_0}$ ), 为了便于本文的比较研究, 不妨首先给出文献[13 ]给出的一个结论.图 1 含有一个任意边界的矩形电阻网络, 右边界上的任意电阻为r 1 , 其他在水平和竖直方向的电阻元素分别为r 和r 0 Figure1. An arbitrary rectangular m × n resistor network with an arbitrary boundary. Bonds in the horizontal and vertical directions are resistors r and r 0 except for r 1 on the right boundary.m × n 阶矩形电阻网络模型, 如图1 所示(${r_1} = {r_0}$ ), 其中水平和竖直网格上的电阻元素分别为r 和${r_0}$ , 水平和竖直方向上的网格数分别为n 和m . 假设矩形网络的底边为X 轴, 左边界为Y 轴. 利用Laplacian matrix方法得到任意m × n 阶矩形网络二节点间的等效电阻公式:${\theta _i} = {{i{\text{π}}} / {(m + 1)}}$ , ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ , 节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 是直角坐标系中的2个任意节点.1 )式的获得是一次重要创新, 但美中不足的是该公式是由倍求和$\Big(\displaystyle\sum {\sum {{f_i}} } \Big)$ 表达的结果, 略显复杂. 本研究拟研究图1 网络模型的等效电阻与电位函数解析式, 所给出的结论都是由单求和$\Big(\displaystyle\sum {{f_i}} \Big)$ 表达的结果, 实现了理论和方法上的创新.2.RT-I理论与应用 22.1.参数定义 2.1.参数定义 为了方便研究与计算, 以及下文各种表达式的简化, 给出如下定义:29 ,36 ]中给出的定义, 可以与国际学术研究所使用的符号定义相统一.2.2.总体设计及计算思路 -->2.2.总体设计及计算思路 考虑图1 所示的任意m × n 阶矩形电阻网络模型, 其中水平和竖直方向上的网格数分别为n 和m . 水平和竖直网格上的电阻元素分别为r 和${r_0}$ , 右边界的任意电阻为${r_1}$ . 假设矩形网络的底边为X 轴, 左边界为Y 轴. 本文的研究目标是给出任意节点的电位函数解析式及任意节点间的等效电阻公式.${A_0}$ 是直角坐标系的坐标原点. 假设稳恒电流J 从节点${d_1}({x_1}, {y_1})$ 输入再从节点${d_2}({x_2}, {y_2})$ 输出. 用图2 子网络表达所有网络中的分布电流及参数符号. 设经过所有m + 1行水平电阻r 上的电流分别为$I_k^{\prime(1)}$ , $I_k^{\prime(2)}$ , $I_k^{\prime(3)}$ , ···, $I_k^{\prime(n)}$ ($0 \leqslant k \leqslant m$ ); 经过所有n + 1行竖直电阻r 0 上的电流分别为$I_k^{(1)}$ , $I_k^{(2)}$ , ···, $I_k^{(m)}$ ($0 \leqslant k \leqslant n$ ). 设任意节点$d(x, y)$ 的电位函数为$U(x, y)$ , 选择坐标原点$O(0, 0)$ 为电位参考点(因为电位函数是一种相对标量值), 计算图1 中任意节点的电位分布函数的基本思路如下.图 2 含有电流参数和方向的部分电阻网络Figure2. Segment of resistor network with current directions and parameters.$U_{(0, 0)}^{(x, y)} = U(0, 0) - U(x, y)$ , 因为电势沿着电流方向是降低的)为$1 \leqslant x \leqslant n - 1$ , $I_0^{\prime(i)}$ 是沿着下边界水平方向的电流, $I_x^{(i)}$ 是沿着竖直方向并且经过节点$d(x, y)$ 的电流. 当$x = n$ 时, 意味着计算右边界上的节点电位, 由于右边界上的电阻为${r_1}$ , 所以得到$I_x^{(i)}$ 和$I_0^{\prime(i)}$ 是解决问题的关键. 本文将发展之前所建立的RT-I方法使之能够解决以上问题. RT-I方法包含四个主要步骤: 一是在三个连续的同向轴线上建立一个关于电流参数的主矩阵方程; 二是建立关于电流参数的边界条件约束方程; 三是实施对角化矩阵变换将多元方程降低为一维的差分方程, 给出矩阵的解; 四是实施对角化矩阵逆变换解出各支路电流的解析式, 进而计算节点电位和等效电阻.2.3.递推方程建立 -->2.3.递推方程建立 矩形网络的子网络如图2 所示. 根据RT-I理论应用基尔霍夫定律分析该网络, 利用图2 中的2个网孔可以得到相关回路电压方程, 根据图2 中的6个节点可以得到6个节点电流方程. 通过消元法消去水平方向的电流参数而得到如下方程:$h = {r / {{r_0}}}$ . 如果考虑电流J 从${d_1}({x_1}, {y_1})$ 输入和从${d_2}({x_2}, {y_2})$ 输出的情形, 则上述方程可以写成矩阵形式:${{{I}}_k}$ 和${{{H}}_x}$ 分别为$m \times 1$ 阶列矩阵, 表达为$ {[ \quad ]^{\rm{T}}} $ 表示为矩阵的转置, ${({H_k})_i}$ 是矩阵${{{H}}_x}$ 中的元素伴随着电流J 从${d_1}({x_1}, {y_1})$ 输入和从${d_2}({x_2}, {y_2})$ 输出, ${\delta _{i, y}}$ 的含义是${\left. {{\delta _{i, y}}} \right|_{y = i}} \!=\! 1$ , ${\left. {{\delta _{i, y}}} \right|_{y \ne i}} \!=\! 0$ ,11 )的建立方法, 应用基尔霍夫定律分别对左边界和右边界进行网络分析, 获得如下2组约束条件方程:${h_1} = {{{r_1}} / {{r_0}}}$ , E m × m 阶恒等矩阵, 矩阵${{{A}}_m}$ 由方程(14 )给出. 由于右边界含有任意电阻, 因此关于右边界的约束方程(16 )比左边界的约束方程(15 )复杂得多.11 )—(16 )就是计算图1 所示任意m × n 网络的等效电阻所需要的全部方程(属于RT方法中的递推方法), 所有电阻网络中的电位分布和等效电阻等等问题的解决都依赖于以上方程的解. 然而, 从方程(11 )—(16 )中直接解出电流$I_k^{(i)}$ 的精确表达式是比较困难的事情. 为此这里对以上诸方程采用变换方法(属于RT方法中的变换技术)间接地解决该问题.2.4.矩阵变换方法 -->2.4.矩阵变换方法 如何获得矩阵方程(11 )的通解是解决问题的关键. 这里首先采用矩阵变换方法将复杂的矩阵方程转变成为一维的差分方程而间接地给出它的通解. 具体方法是用一个待定的m × m 阶矩阵${{{P}}_m}$ 左乘矩阵方程(11 ), 得到${{{T}}_m} = {\rm{diag}}({t_1}, {t_1}, \cdots, {t_m})$ 是一个对角化矩阵, 并且${t_i}$ ($i = 1, 2, \cdots, m$ )是矩阵${{{A}}_m}$ 的特征值. 解(18 )式得到${\theta _i} = {{i{\text{π}}} / {(m + 1)}}$ , 将(20 )式代入(19 )式计算解得${{{P}}_m}$ 是可逆的, 其逆矩阵为(可以参考文献[33 ]的研究)17 )式和(19 )式给出如下定义:${{{X}}_m}$ 是一个$m \times 1$ 阶列矩阵,13 )及(17 )式应用于(11 )式得到,21 )中的元素应用于方程(13 )及(25 )式计算得到(简记${\zeta _{{x_k}, i}} $ 为${\zeta _{k, i}} $ )25 )是一个简单易解的线性方程.17 )式所做变换相同的变换方法, 应用矩阵${{{P}}_m}$ 左乘矩阵(15 )式和(16 )式实施矩阵变换, 并且应用(19 )式和(23 )式得到,25 )—(28 )即可以解出所需要的参数$X_k^{(i)}$ (矩阵方程的特解).$X_k^{(i)}$ , 进而获得所有支路电流函数的解析式, 当然实际的求解还需要相关的计算技巧. 下文将采用RT理论中的解方程技术给出以上方程组的通解与特解.2.5.矩阵方程的解 -->2.5.矩阵方程的解 考虑电流J 从${d_1}({x_1}, {y_1})$ 输入和从${d_2}({x_2}, {y_2})$ 输出, 假设$\lambda _k^{}, \bar \lambda _k^{}$ 是方程(25 )关于${X_k}$ 的特征方程的2个根, 那么根据(25 )式的特征方程可以解得方程的特征根(4 ). 解方程(25 )可以得到如下分段函数解:$F_k^{(i)} = {{(\lambda _i^k - \bar \lambda _i^k)} / {({\lambda _i} - {{\bar \lambda }_i})}}$ 被定义在方程(5 )中.27 )式代入(29 )式消去$X_1^{(i)}$ 得到30 )和(31 )及在方程(34 )中取$k \!=\! {x_1} \!-\! 1, $ x 1 解得32 ), (33 )及(35 )解得(${x_2} \leqslant { {k}} < n$ )28 )消去$X_n^{(i)}$ 得到${q_i} = {t_i} + ({h_1} - 2)$ .$X_k^{(i)}$ , 需要数个独立的方程. 因为$X_{n - 2}^{(i)}, X_{n - 1}^{(i)}$ 满足(36 )式, 由此与方程(37 )一起联立组成含有三个未知数$X_0^{(i)}, X_{n - 2}^{(i)}, X_{n - 1}^{(i)}$ 的三个独立方程, 即38 )并不复杂, 经过适当的计算之后解得$\alpha _x^{(i)}$ 定义在(6 )式中, 并且${\zeta _{1, i}}, {\zeta _{2, i}}$ 由方程(26 )给出.39 )是一个关键的公式. 将(39 )式分别代入(34 )式—(36 )式及(28 )式, 经过一系列化简运算之后得到${h_1} = {{{r_1}} / {{r_0}}}$ , 并且${f_x}(i)$ 是一个新定义的函数,$\beta _{{x_s} \vee x}^{(i)}$ 定义在方程(7 )中.40 )式和(41 )式是关于$X_k^{(i)}$ 的矩阵方程的统一解, 定义${f_x}(i)$ 的目的在于可以统一计算相关的问题而不需要分段计算(如方程(34 )—(36 )是3个分段函数), 从而使计算的过程大大简化.2.6.计算分支电流 -->2.6.计算分支电流 根据方程(8 )和(9 )得知, 必须计算出关键的电流$I_x^{(i)}$ 及$I_0^{\prime(k)}$ . 根据方程(23 )得到${{{I}}_s} = {{P}}_m^{ - 1}{{{X}}_s}$ , 由此应用矩阵(21 )式和(22 )式计算得到8 )及(9 )的需要, 需要计算出$\displaystyle\sum\nolimits_{j = 1}^y {I_s^{(j)}} $ 的和44 )式得到${f_s}(i)$ 定义在方程(42 )中.$I_0^{\prime(k)}$ , 即43 )式代入(46 )式计算得到47 )式的分段表达式.$0 \leqslant k \leqslant {x_1}$ 时, 将(34 )式代入(47 )式化简得到48 )式中的k 从$k = 1$ 到x 求和, 得到$f_x^{}(i)$ 由(42 )式给出, 以下与此同.${x_1} \leqslant k \leqslant {x_2}$ 时, 将(35 )式代入(47 )式化简得到49 )式对(50 )式中的k 从$k = 1$ 到x 求和, 得到${x_2} \leqslant k \leqslant n$ 时, 将(36 )式代入(47 )式计算得到51 )式对(52 )式中的k 从$k = 1$ 到x 求和, 得到45 )式和(50 )式—(53 )式即为电路网络中的各支路电流分布理论公式. 获得$\displaystyle\sum {I_k^{(k)}} $ 和$\displaystyle\sum {I_y'^{(k)}} $ 是计算电位函数的预备工作, 下面将依据这些结果推导电位分布函数公式.3.电位函数解析式 23.1.电位分布函数公式 3.1.电位分布函数公式 设图1 网络中的${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 为电流输入和输出的2个任意节点(不失一般性设${x_1} \leqslant {x_2}$ ). 设一个任意节点$d(x, y)$ 的电位函数为$U(x, y)$ , 选择坐标原点${d_0}(0, 0)$ 的电位$U(0, 0)$ 为电位参考点, 则矩形网络中的任意节点的电位函数解析式为$(x, y) = (0, 0)$ 代入(54 )式时, 得到坐标原点${d_0}(0, 0)$ 的电位57 )式即为本文所选择的电位参考点, 即该节点${d_0}(0, 0)$ 位于坐标原点的参考电位为方程(57 ). 显然(57 )式的选择是科学合理的, 并且与(54 )式—(56 )式的表达结构完全自洽.3.2.电位函数证明 -->3.2.电位函数证明 选择${d_0}(0, 0)$ 为电位参考点, 设$U_{(0, 0)}^{(x, y)} = U(0, 0) - $ $U(x, y) $ . 应用(45 )式和(49 )式—(53 )式, 以及(8 )式和(9 )式推导计算电位公式.$0 \leqslant x \leqslant {x_1}$ 时, 将(45 )式和(49 )式代入(8 )式, 得到两节点${d_0}(0, 0)$ 和$d(x, y)$ 之间的电位差:${x_1} \leqslant x \leqslant {x_2}$ 时, 将(45 )式和(51 )式代入(8 )式得到两节点${d_0}(0, 0)$ 和$d(x, y)$ 之间的电位差:${x_2} \leqslant x < n$ 时, 将(45 )式及(53 )式代入(8 )式和(9 )式得到两节点${d_0}(0, 0)$ 和$d(x, y)$ 之间的电位差:$f_x^{}(i)$ 由(42 )式给出, 并且以上三式利用了下列恒等式57 )的假设及(42 )式的定义, 则坐标原点$O(0, 0)$ 的电位函数为61 )式分别代入(58 )式—(60 )式并且利用(42 )式化简即得到任意位置节点$d(x, y)$ 的电位分布函数解析式(54 )式—(56 )式.54 )式—(56 )式是本文第一次发现的关于矩形电阻网络的电位函数解析式, 是之前研究者一直没有解决的难题, 本文应用RT-I方法彻底解决了该问题, 第一次获得了含有任意边界的m × n 矩形电阻网络的电位函数解析式, 为电阻网络研究提供了新的理论工具. (54 )式—(56 )式是三个一般性结论, 为了帮助读者易于理解我们的结论, 下面给出一些具体应用.3.3.电位函数的应用 -->3.3.电位函数的应用 特别说明, 下面各种应用中出现的网络均是基于图1 结构的网络模型, 并且选择位于坐标原点${d_0}(0, 0)$ 的参考电位为方程(57 ).应用1 输入输出电流分别在左右边界上的情形. 设电流从电路网络的左边界上的节点${d_1}(0, {y_1})$ 输入而电流从右边界的节点${d_2}(n, {y_2})$ 输出, 当$0 \leqslant x \leqslant n$ 时, 由(55 )式得到任意节点$d(x, y)$ 的电位分布函数${x_1} = 0, {\rm{ }}{x_2} = n$ 时, 有$\beta _{{x_1} \vee x}^{(i)} = \alpha _{n - x}^{(i)},$ $ \beta _{{x_2} \vee x}^{(i)} = {h_1}F_n^{(i)} $ .${h_1} = 1 \Leftrightarrow {r_1} = {r_0}$ 时, 有$\alpha _{n - x}^{(i)} = $ $\Delta F_{n - x}^{(i)} + ({h_1} - 1)\Delta F_{n - x - 1}^{(i)} = \Delta F_{n - x}^{(i)} $ , 则(62 )式简化成为一个简单结论${h_1} = 1 \Leftrightarrow {r_1} = {r_0}$ 时, 输入和输出节点电流${d_1}(0, {y_1})$ 和${d_2}(n, {y_1})$ 位于同一水平线上的两端时, 由方程(63 )得到任意节点$d(x, y)$ 的电位函数,应用2 输入输出电流在对角线的情形. 设电流从电路网络的左下角的节点${d_1}(0, 0)$ 输入而从右上角的节点${d_2}(n, m)$ 输出, 当$0 \leqslant x \leqslant n$ 时, 由(55 )式得到任意节点$d(x, y)$ 的电位分布函数,${y_1} = 0, {y_2} = n$ 时, 有${C_{0, i}} = \cos \left( {\dfrac{1}{2}{\theta _i}} \right)$ , ${C_{2, i}} = \cos \left( {m + \dfrac{1}{2}} \right){\theta _i} = \cos (i{\text{π}})\cos \left( {\dfrac{1}{2}{\theta _i}} \right)$ , 则将此代入(55 )式即得到(65 )式.应用3 输入输出电流在同一竖直线上的情形. 设电流从电路网络的同一竖直线上的节点${d_1}({x_1}, {y_1})$ 输入而从上方的节点${d_2}({x_1}, {y_2})$ 输出, 当$0 \leqslant x \leqslant n$ 时, 由(54 )—(56 )式得到任意节点$d(x, y)$ 的电位函数,${C_{k, i}}$ , $\beta _{{x_k} \vee x}^{(i)}$ 分别定义在(2 )式和(7 )式之中.${C_{2, i}} = \cos \left( {m + \dfrac{1}{2}} \right){\theta _i}=$ $ \cos (i{\text{π}})\cos \left( {\dfrac{1}{2}{\theta _i}} \right)$ , 所以由(66 )式得到任意节点$d(x, y)$ 的电位分布函数,应用4 输入输出电流在左边界上的情形. 设电流从电路网络的左边界上的节点${d_1}(0, {y_1})$ 输入而电流从节点${d_2}(0, {y_2})$ 输出, 当$0 \leqslant x \leqslant n$ 时, 在(56 )式中取${x_1} = {x_2} = 0$ 得到任意节点$d(x, y)$ 的电位分布函数,${C_{k, i}}$ , $\beta _{{x_k} \vee x}^{(i)}$ 分别定义在(2 )式和(7 )式之中.68 )式得到应用5 含有2个节点输出电流的情形. 设有电流大小为J 的电流从左边界上节点${d_1}(0, {y_1})$ 输入, 再分别有电流大小为J /2的电流分别从右边界上的节点${d_2}(n, 0)$ 和${d_3}(n, m)$ 的输出. 这种情形视为2个独立电流源的作用. 那么, 2个电流输入时, 任意节点的电位是2个电位之和, 应用(62 )式得到节点$d(x, y)$ 的电位分布函数,应用6 含有4个节点输入和输出电流的情形. 设分别有电流大小为J 的电流从左边界的上下端点输入, 再分别有电流大小为J 的电流从右边界上的上下端点输出. 这种情形视为2组独立电流源的作用. 那么, 2组电流输入时, 任意节点的电位是2个电位之和, 应用(62 )式得到节点$d(x, y)$ 的电位分布函数,71 )式是由矩形网络四个角点输入与输出电流时的电位分布函数.应用7 右边界含有m + 1个输出电流的情形. 设有电流大小为J 的电流从左边界节点${d_1}(0, {y_1})$ 输入, 设$U(0, 0) = {U_0}$ , 定义在(57 )式中, 并且电流分别从右边界上的m + 1个节点${d_k}(n, {y_k})$ 输出, 每个节点输出的电流均为${J / {(m + 1)}}$ . 则任意节点$d(x, y)$ 的电位分布函数为证明 当存在m + 1个电流源时, 由于电位是标量函数, 则任意节点的电位是由m + 1个电位之代数和组成, 应用(62 )式得到节点$d(x, y)$ 的电位分布函数$\sum {_C} = \dfrac{1}{{m + 1}}\sum\limits_{k = 0}^m {\cos \left( {{y_k} + \dfrac{1}{2}} \right){\theta _i}} $ . 容易计算得到$\sum_C= 0$ , 所以将此代入(73 )式化简即得到(72 )式.应用8 含有m + 1个输入和输出电流的情形. 设分别有电流大小为${J / {(m}} + 1)$ 的电流从左边界上m + 1个节点${d_k}(0, {y_k})$ 输入, 重新定义$U(0, 0) = {U_0}$ , $U(n, 0) = - {U_0}$ , 并且电流分别从右边界上的m + 1个节点${d_k}(n, {y_k})$ 输出, 每个节点输出的电流均为${J / {(m}} + 1)$ . 则任意节点$d(x, y)$ 的电位分布函数为证明 当存在m + 1个电流源时, 由于电位是标量函数, 则任意节点的电位是由m + 1个电位之代数和组成, 应用(62 )式得到节点$d(x, y)$ 的电位分布函数$\displaystyle\sum_C = 0$ , 所以代入(75 )式得到57 )式得到${U_{(0, 0)}} = 0$ , 即(76 )式是以${U_{(0, 0)}} = 0$ 为参考点为条件的结果. 当考虑$U(0, 0) = {U_0}$ , $U(n, 0) = - {U_0}$ 时, (76 )式应该改写成$U(n, 0) = - {U_0}$ , 从而由(77 )式得到${U_0} = \dfrac{{nr}}{{2(m + 1)}}J$ , 将此代入(77 )即式得到(74 )式.74 )式是一个与y 无关, 仅仅与x 有关的函数. 说明在命题条件下矩形网络在同一竖直轴线上的电位都相同, 这是一个很有趣的问题.4.矩形网络的等效电阻公式 24.1.一个总的等效电阻公式 4.1.一个总的等效电阻公式 在图1 所示的含有一个任意右电阻边界条件的m × n 电路网络中, 其中水平和竖直方向上的网格数分别为n 和m . 水平和竖直网格上的电阻元素分别为r 和${r_0}$ , 右边界的任意电阻为${r_1}$ . 设矩形网络的底边为X 轴, 左边界为Y 轴. 则任意两节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 间的等效电阻公式为${C_{k, i}}$ , $F_k^{(i)}$ 分别定义在(2 )式和(5 )式之中, 并且参数$\beta _{k, s}^{(i)}$ 由(7 )式得到78 )式的推导过程如下.图1 电路网络中任意两节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 之间的等效电阻, 应用欧姆定律得到55 )式中分别取$(x, y) = ({x_1}, {y_1})$ 和(x , y ) = $ ({x_2}, {y_2})$ 得到81 )和(82 )代入(80 )式化简即得到(78 )式.78 )式是图1 所示的含有一个任意右边界条件的m × n 电路网络的一个总的等效电阻公式, 由本文第一次获得. 由于右边界是一个任意电阻, 并且节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 是两个任意节点, 所以(78 )式包含了一系列特殊情形的等效电阻, 作为公式的应用, 下面将给出(78 )式的若干有趣的推论.4.2.电阻公式(78 )式的应用 -->4.2.电阻公式(78 )式的应用 Case 1 一个半无穷网络的电阻公式. 在图1 所示的含有一个任意右电阻边界条件的m × n 电路网络中, 当$n \!\to \!\infty $ , ${x_1}, {x_2}\! \to\! \infty $ 但${x_1} \!-\! {x_2}$ 为有限值, 并且竖直轴方向的网格数也为有限时(上下有限, 左右无限), 称该网络为一个半无穷矩形网络, 其任意二节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 间的等效电阻为83 )式是根据(78 )式取极限得到的.Case 2 当${h_1} = 1$ (${r_1} = {r_0}$ )时, 图1 的网络退化为一个规则的矩形网络, 根据(78 )式得到图1 所示的标准边界的矩形网络任意二节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 之间的等效电阻$\beta _{k, s}^{(i)}$ 退化为$\beta _{k, s}^{(i)} = \Delta F_{{x_k}}^{(i)}\Delta F_{n - {x_s}}^{(i)}$ .Case 3 当${h_1} = 0$ 时, 图1 的网络退化为扇形网络, 如图3 所示. 此时右边的零电阻边界塌陷为一个节点, 根据(78 )式得到任意两节点${d_1}({x_1}, {y_1})$ 和${d_2}({x_2}, {y_2})$ 之间的等效电阻公式图 3 一类任意m × n 阶Fan电阻网络模型Figure3. An arbitrary m × n Fan resistor network.$\beta _{k, s}^{(i)}$ 退化为$\beta _{k, s}^{(i)} = \Delta F_{{x_k}}^{(i)}F_{n - {x_s}}^{(i)}$ .27 -29 ]曾经研究了Fan网络的等效电阻, 但是这里给出的电阻公式与他们的结果不同, 因为文献[27 -29 ]研究Fan网络时是沿着经度(半径)方向建立矩阵方程, 而本文是沿着纬度(圆弧)方向建立矩阵方程. 这说明沿着不同轴线建立方程可以得到不同的等效电阻表达式.Case 4 当两个节点都处在相同竖直轴线上时, 根据(78 )式得到图1 网络中任意两节点${d_1}(x, {y_1})$ 和${d_2}(x, {y_2})$ 之间的等效电阻公式${d_1}$ 和${d_2}$ 分别在相同轴线上的上下边界上时, (86 )式可以进一步简化为33 ]曾经专门研究了Case 4的问题, 并且得到的结果与(86 )式完全一致, 但是这里给出的电阻公式是一般结果(78 )式的特殊情形, 这也就间接验证了本研究的正确性.Case 5 当两个节点在相同的水平轴线上时, 根据(78 )式得到图1 网络水平轴线上任意两节点${d_1}({x_1}, y)$ 和${d_2}({x_2}, y)$ 之间的等效电阻公式$ \beta _{k, s}^{(i)} = \Delta F_{{x_k}}^{(i)}\left[ {\Delta F_{n - {x_s}}^{(i)} + ({h_1} - 1)\Delta F_{n - {x_s} - 1}^{(i)}} \right].$ Case 6 当${h_1} = 1$ , 节点${d_1}$ = $(0, {y_1})$ 位于左边界上, 并且节点${d_2}$ = $(n, {y_2})$ 位于右边界上, 根据(78 )式得到图1 网络中任意两节点${d_1}(0, {y_1})$ 和${d_2}(n, {y_2})$ 之间的等效电阻公式Case 7 当${d_1} = ({x_1}, 0)$ 位于底边界上, 而${d_2} = ({x_2}, m)$ 位于上边界上, 根据(78 )式得到图1 网络中任意两节点${d_1}({x_1}, 0)$ 和${d_2}({x_2}, m)$ 之间的等效电阻公式Case 8 当${h_1} = 1$ 时, 并且节点${d_1} = (0, 0)$ 和${d_2} = (n, m)$ 分别位于一对对角线上时, 根据(78 )式得到图1 网络中任意两节点${d_1}(0, 0)$ 和${d_2}(n, m)$ 之间的等效电阻公式91 )式是一个规则连接的m × n 矩形网络最大分离节点间的等效电阻公式. 这是一个很有趣的问题, 该问题曾经被文献[15 ,16 ]深入研究, 但是这里给出的(91 )式比较简单, 更加有利于进行渐进性问题的研究.78 )式, 但是这些公式仍然比较复杂而不容易理解. 为了帮助读者进一步理解和验证所得结论的正确性, 下面将给出(78 )式在$m = 1$ 时的一个最简单情形下的结果.Case 9 当$m = 1$ 时, 图1 退化为一个含有任意右边界的1 × n 电阻网络, 如图4 所示. 如此情形下有${\theta _i} = {{i{\text{π}}} / {(m + 1)}} = {{\text{π}} / 2}$ , 并且图 4 一类含有任意右边界的1 × n 阶电阻网络Figure4. 1 × n resistor network with an arbitrary right boundary.${A_k}$ 和${B_k}$ 是图4 中的任意节点, 其中k 表示从左向右计数的第k 个网格, 根据(78 )式得到如下一系列结论.${A_0} = (0, 0)$ , ${B_k} = (k, 1)$ , 根据(78 )式得到$0 \leqslant k \leqslant n$ , 参数$\Delta F_k^{}$ 及$\alpha _x^{(i)}$ 定义在方程(6 )中, 即$\alpha _x^{} = \Delta F_x^{} + ({h_1} - 1)\Delta F_{x - 1}^{}$ . 在${h_1} = 1$ 的条件下, 根据(93 )式和(94 )式得到${h_1} = 1$ 时, 分别设$k = 0$ 和n , 根据(95 )式和(96 )式得到97 )式—(99 )式的正确性可以从文献[24 ]中的结论得到验证. 当然, 当分别取$n = 0, 1, 2$ 时可以直接验证以上诸公式的正确性. 事实上, 由于本文的推导过程和计算过程都是精确的和自洽的, 因而所得结论必然是正确的. 从以上1 × n 阶电阻网络的研究发现: 一个简单的1 × n 电阻网络都能给出7个不同情形的等效电阻公式, 显然一个任意m × n 电阻网络的等效电阻公式(78 )式是一个多功能的普适公式, 具有重要的应用价值.Case 10 当${h_1} = 1$ , $n = 0$ 时, 图1 退化成为一个线性串联电阻结构. 根据(78 )式得到${\theta _i} = {{i{\text{π}}} / {(m + 1)}}$ . 众所周知线性串联电阻${d_1}(0, {y_1})$ 和${d_2}(0, {y_2})$ 之间点间有$\left| {{y_2} - {y_1}} \right|$ 个电阻元素, 其等效电阻为100 )式和(101 )式得到102 )式是一个很有趣的恒等式, 该恒等式可以利用文献[13 ]的理论给予证明, 但是这里是采用物理方法而不是数学方法得到的.4.3.一个新的分式恒等式 -->4.3.一个新的分式恒等式 (1 )式是由文献[13 ]在${r_1} = {r_0}$ 情形下给出的矩形网络的等效电阻, 而本文给出了相同条件电阻网络相应的等效电阻公式(84 )式, 既然是同一个矩形电阻网络模型, 在相同的坐标规定下两者的等效电阻必然相等. 比较(1 )式与(84 )式得到$m, n, {x_1}, {x_2}$ 及y 都是自然数, 并且$0 \leqslant {x_1}, {x_2} \leqslant n$ , $0 \leqslant {y_1}, {y_2} \leqslant m$ . ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ ,$ {C_{1, i}} = $ $ \cos \left( {{y_1} + {1}/{2}} \right){\theta _i}$ , ${C_{2, i}} = \cos \left( {{y_2} + {1}/{2}} \right){\theta _i}$ . $F_k^{(i)} = {{(\lambda _i^k - \bar \lambda _i^k)} / {({\lambda _i} - {{\bar \lambda }_i})}}$ , $\Delta F_k^{(i)} = F_{k + 1}^{(i)} - F_k^{(i)}$ , 以及103 )式是一个很有趣的分式恒等式, 本文是第一次发现, 而且是采用物理方法而非数学方法得到的复杂分式恒等式, 所以是一个很有意义的工作. 这一恒等式的发现为数学工作者提供了新的数学工具. 由于(103 )式比较复杂, 下面将给出它的一些特殊推论.推论1 当${y_1} = {y_2} = y$ 时, ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ , ${\theta _i} = {{i{\text{π}}} / {(m + 1)}}$ . 由(103 )式得到${\lambda _i}, {\bar \lambda _i}$ 及$F_k^{(i)}$ 出现在(103 )式中.推论2 当${x_1} = {x_2} = x$ 时, ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ , ${\theta _i} = {{i{\text{π}}} / {(m + 1)}}$ . 由(103 )式得到推论3 当$m = 1, {y_1} = 0, \;\;{y_2} = 1$ 时, 得到${\theta _i} = {{\text{π}} / 2}$ , ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ , 由(103 )式得到${\lambda _i}, {\bar \lambda _i}$ 由(104 )式简化得到推论4 当$m = 1, {y_1} = 0, {y_2} = 1$ 并且 x 1 = x 2 = x 时, ${\phi _j} = {{j{\text{π}}} / {(n + 1)}}$ , 由(107 )式得到103 )式中继续取一些特殊坐标(xi , yi )值, 还可以推导出一系列有趣的简单恒等式, 这里不再举例.5.结 论 进一步发展了之前建立的研究电路网络的RT-I理论[28 -30 ] , 借助于图1 的任意矩形电路网络模型阐述了RT-I方法的基本过程. 本文克服了之前的RT-I理论研究电阻网络都依赖于含有零电阻的边界[25 -31 ] 或者要求规则边界[32 -34 ] 的缺点, 通过技术创新解决了非零边界的电阻网络问题, 解决了以前从来没有解决的图1 网络问题. 关键创新点是建立了计算沿着水平方向电流的方法, 给出了任意的水平电流公式(48 )式—(53 )式. 事实上, 任意边界的网络才是现实中的实际电路网络模型, 因此本文建立的理论推广了之前的理论而成为更具一般性的普适方法. 新的RT-I理论可以计算复杂电路网络中任意节点的电位解析式, 能够自然地得到电路中的电流分布, 自然地得到任意节点间的等效电阻公式.54 )式—(56 )式, 然后得到了含有一个任意边界的m × n 阶电阻网络的任意节点间的等效电阻公式(78 )式. (78 )式是一次理论上的创新, 包含了一系列的特殊结论. 对于规则的m × n 阶矩形电阻网络, 文献[13 ]给出的结论(1)是由倍求和表达的结果, 而本文给出的规则矩形网络的等效电阻公式(84 )式是由单求和表达的结果, 根据两种不同方法对同一问题得到的结论的等价性, 得到了一个有趣的分式恒等式(103 )式, 问题的有趣之处就在于这是通过物理方法而不是数学方法得到的, 这为数学研究者提供了一个新的研究课题. 作为电阻网络公式(78 )式的应用及对公式的理解, 本文给出了一系列有趣的特殊推论. 









 图 1 含有一个任意边界的矩形电阻网络, 右边界上的任意电阻为r1, 其他在水平和竖直方向的电阻元素分别为r和r0
图 1 含有一个任意边界的矩形电阻网络, 右边界上的任意电阻为r1, 其他在水平和竖直方向的电阻元素分别为r和r0
























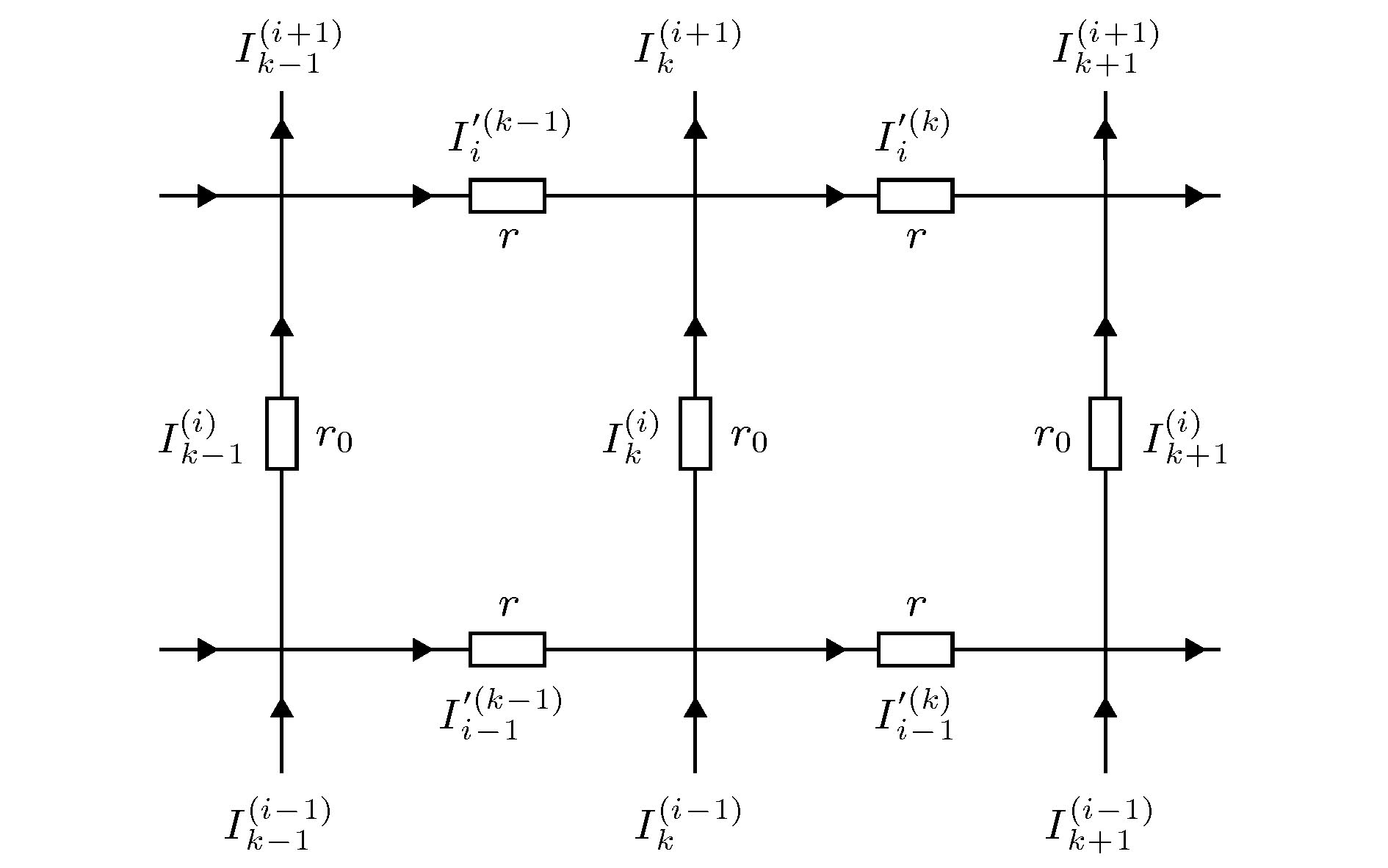 图 2 含有电流参数和方向的部分电阻网络
图 2 含有电流参数和方向的部分电阻网络




































































































































































































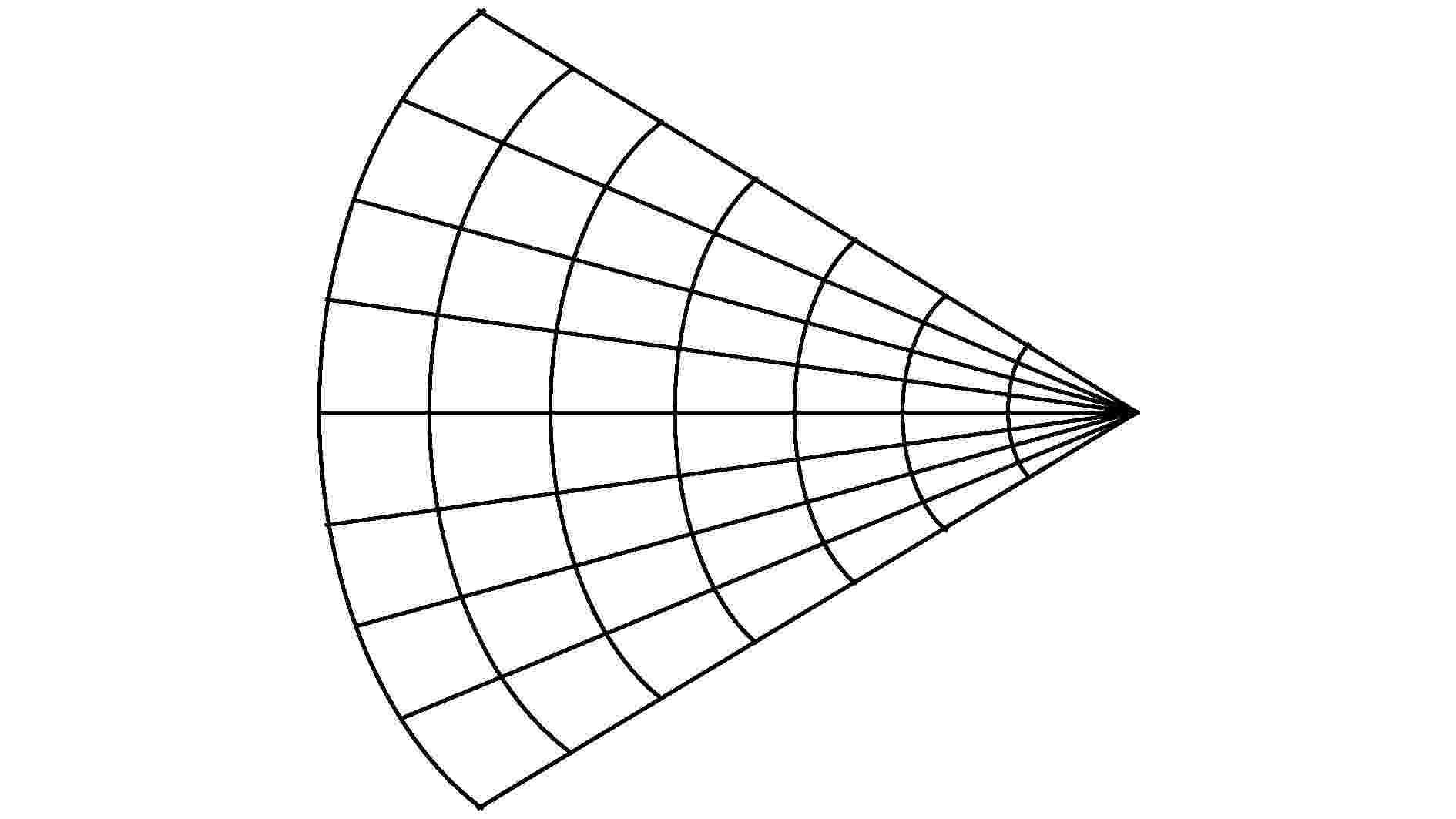 图 3 一类任意m × n阶Fan电阻网络模型
图 3 一类任意m × n阶Fan电阻网络模型



























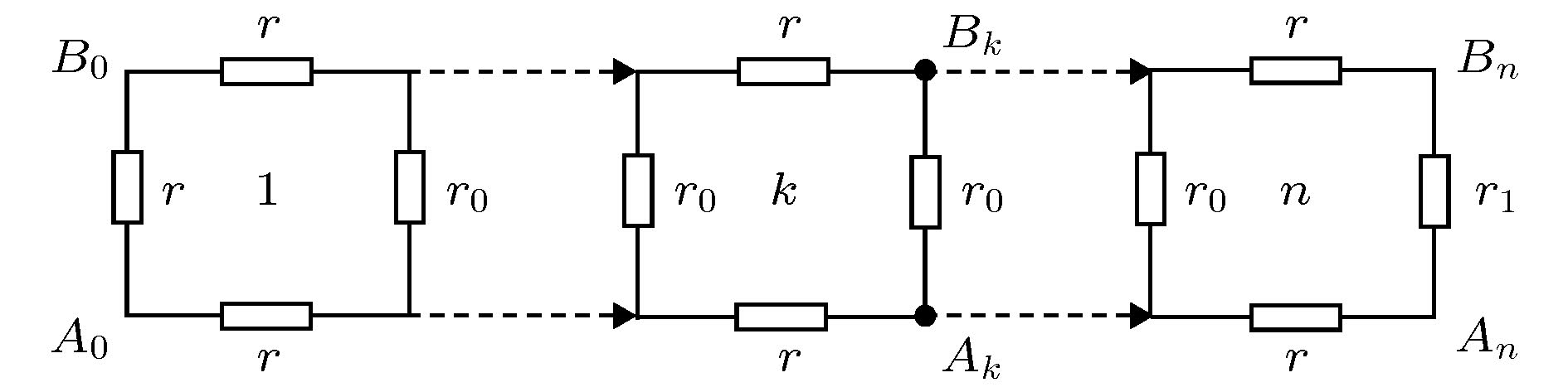 图 4 一类含有任意右边界的1 × n阶电阻网络
图 4 一类含有任意右边界的1 × n阶电阻网络









































