摘要:设计了一种由包裹有机玻璃涂层的四棱柱形压电材料按正方形晶格周期性连接在四个环氧树脂短板上构成的1×5新型二维压电声子晶体板, 并利用超元胞法结合有限元方法分别计算了完美声子晶体板和缺陷声子晶体板的能带结构和传输损失. 通过改变施加在压电散射体上下表面的电边界条件, 形成点缺陷波导, 以限制弹性波能量流, 该声子晶体板克服了材料参数和结构参数已确定的情况下振动波导方向不可变的局限性. 压电效应有利于完全带隙的扩大, 当缺陷态的频率出现在带隙内时, 缺陷态响应频率范围随之扩大, 因此可以收集更宽频率范围的机械能. 用振动能量回收电路连接缺陷处压电片上下表面的电极, 能够将振动所产生的机械能转化为电能.
关键词: 声子晶体/
有限元法/
点缺陷/
振动能量回收

English Abstract

全文HTML

--> --> -->

声子晶体是声波或弹性波在其中以一定的特性传播的周期性复合材料, 其最主要的特性是存在能够阻止声波或弹性波在一定频率范围内传播的声子带隙^[1,2]. 当声子晶体的固有周期性被打破时, 就会产生缺陷态, 此时声波或弹性波的分布将局限于点缺陷处或沿线缺陷传播^[3-6]. 由于带隙和缺陷态的存在, 声子晶体具有许多潜在的应用前景, 可以广泛地应用到声波导、便携式设备和无线传感器等器件中^[7-9], 同时这些装置的能源供给需求也在不断增长, 因此研究如何从装置本身周围振动环境中回收能量, 是方便且具有潜力的自供电方式^[10-13]. 基于机械或声学振动原理的材料应用中, 经常使用压电、压阻、磁致伸缩等各类功能性材料, 其中压电材料的能量回收技术主要是将机械或声学振动引起散射体形变所产生的应变能转换为电能, 通过外接电路回收的电能, 既可以储存在电容中, 又可以直接为负载供电^[14-27].
压电材料可将机械应变能转化为电能, 电能可被传感器和无线发射机等电子设备储存和利用. 在利用压电材料获取能量的研究中, Poulin等^[21]将压电式能量回收和电磁式能量回收方法为便携式电子元器件供电的能力进行了对比, 得出压电系统可以获得更高的能量密度, 更适合在微机电系统中应用; Roundy和Leland^[22]比较分析了压电、电磁和静电能量回收效率, 发现压电式能量回收装置的相对功率密度更高; Lu等^[23]根据机电耦合效应, 设计出了压电发电机在微机电系统中的应用模型, 发现增加压电材料的振动频率可以提高输出功率; Horowitz等^[24]和Liu等^[25]使用机电谐振器作为声能收集装置, 该装置的原理是在谐振器的谐振腔内产生振动压力来引起压电材料的振动, 从而实现了声能到电能的转换; Wu等^[26]用声子晶体材料研制了一种声能采集器, 该采集器的原理是在完美声子晶体板中移除一个杆从而产生点缺陷以充当共振腔, 在共振腔上端覆盖一层聚偏氟乙烯压电声子晶体薄膜进行能量收集, 研究发现当入射声波的频率达到4.2 kHz时, 压电声子晶体薄膜输出电压达到最大; Qi等^[27]在具有硅橡胶涂层的铝板上植入压电声子晶体板, 使振动的能量集中在压电片上, 然后在压电片的电极处外接电路将振动的机械能转化为电能; Gao等^[28]实现了低频声能量的采集, 设计了由八个多腔环氧树脂声子晶体单胞组成的正方形超胞, 由于超胞结构与各单胞结构存在单方向三重共振并相互耦合而产生的复合单极三重共振, 从而形成能量集中; Park等^[29]将具有单一缺陷的二维八角形压电声子晶体作为高密度弹性能量收集的超材料, 通过尺寸优化和系统设计, 使带隙达到最大, 与无压电声子晶体材料的情况相比, 具有压电声子晶体板的超材料的输出功率在微瓦级放大了20倍以上. 本研究组^[30]曾提出一种二维三组元压电声子晶体模型, 该模型实现了对多条完全带隙的主动调控, 据此设计了可切换路径的压电声子晶体板波导, 同时通过施加不同的电边界条件, 使得振动能量局域到点缺陷处, 但振动能量的回收并没有进一步研究.
由于振动存在不同的频率, 仅通过改变压电材料的形状和尺寸来回收压电声子晶体的固有频率所对应的能量是非常困难的, 在这种情况下, 能量回收系统结构的设计应具有可调固有频率的功能. 基于以上考虑, 本文新设计了一种1 × 5型二维三组元压电声子晶体板, 通过改变施加在压电散射体上下表面的电边界条件, 形成可调路径的点缺陷波导; 同时分析了压电效应对缺陷态的影响; 最后, 利用振动能量回收电路连接压电片上下表面的电极, 将机械能转化为电能. 以上研究可为便携式电子元器件提供新的可参考供电模式.

图1为1 × 5超元胞二维压电声子晶体板及其初基原胞示意图, 其中图1(a)为超胞平面图, 图1(b)为原胞立体图, 图1(c)为原胞平面图, 图1(d)为第一布里渊区及不可约布里渊区. 该单胞结构由包裹有机玻璃涂层的四棱柱形压电材料按正方形晶格周期性连接在四个环氧树脂短板上构成, x-y平面位于板的中间平面上, z轴沿着厚度方向. 研究采用沿[001]方向极化且具有高机电耦合系数的压电材料0.27 PIN-0.4 PMN-0.33 PT作为中心散射体, 该结构参数定义如下: 晶格常数为a, 环氧树脂连接板的长度和高度分别为l₁和d; 四棱柱压电散射体的深度和高度分别为l₂和h₁; 有机玻璃涂层的长度和高度为l₃和h₂. 图1计算所需的压电材料和弹性材料的参数分别由表1和表2给出.
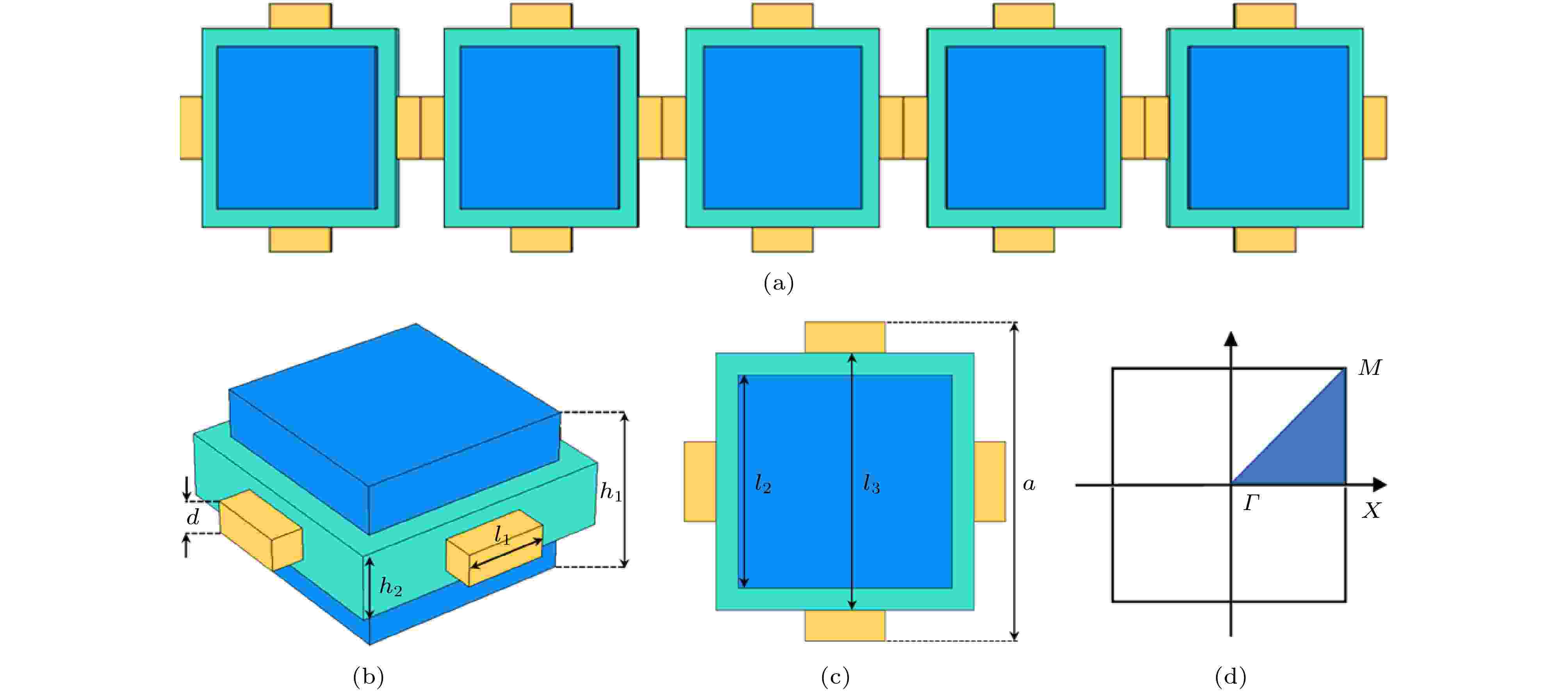图 1 1 × 5超元胞二维压电声子晶体板及其初基原胞示意图　(a) 1 × 5超胞; (b)原胞立体图; (c)原胞平面图; (d)第一布里渊区(阴影部分为不可约布里渊区)
Figure1. 1 × 5 supercell two-dimensional piezoelectric phonon crystal plate and its primary cells: (a) The supercell plan; (b) the protocell stereogram; (c) the protocell floor plan; (d) the first Brillouin zone (the shadow part is the irreducible brillouin zone).

密度ρ/kg·m–3	弹性常数Cij/1010 N·m–2							压电常数e/C·m–2				介电常数ε/10–11 F·m–1
	C11	C12	C13	C33	C44	C66		e15	e31	e33		ε11	ε33
8189	12.2	11.3	10.8	11.2	6.9	6.2		16.0	–2.7	18.6		4193	585

表1压电材料0.27PIN-0.4PMN-0.33PT的参数
Table1.Piezoelectric material parameters of 0.27PIN-0.4PMN-0.33PT.

	密度ρ/kg·m–3	杨氏模量E/1010 Pa	剪切模量μ/1010 Pa
有机玻璃	1142	0.200	0.072
环氧树脂	1180	0.435	0.159

表2弹性材料参数
Table2.Material parameters of elastic materials.

利用有限元软件COMSOL Multiphysics 5.3^[31]研究声子晶体的能带结构和传输特性. 有限元方法是随着电子计算机的发展而迅速发展起来的一种现代计算方法, 该方法不仅计算精度高, 而且能适应各种复杂形状, 因而成为行之有效的工程分析手段. 基于有限元法的压电控制方程为^[17]:

$\rho \frac{{{\partial ^2}{u_j}}}{{\partial {t^2}}} = \frac{{\partial {T_{ij}}}}{{\partial {x_i}}},$

$\frac{{\partial {D_i}}}{{\partial {x_i}}} = 0\;\;\left( {i,j = 1,2,3} \right),$

其中ρ为压电材料的密度, u_j是位移, t是时间, x_i (i = 1, 2, 3) 分别对应坐标变量x, y和z, T_ij和D_i为应力和电位移并分别遵守位移u_j和电位φ作为变量的压电本构关系^[17]:

${T_{ij}} = {C_{ijkl}}\frac{{\partial {u_k}}}{{\partial {x_k}}} + {e_{lij}}\frac{{\partial \varphi }}{{\partial {x_l}}},$

${D_i} = {e_{ikl}}\frac{{\partial {u_k}}}{{\partial {x_l}}} - {\varepsilon _{il}}\frac{{\partial \varphi }}{{\partial {x_l}}},$

(3)式和(4)式中, C_ijkl, e_lij和ε_il分别是弹性常数、压电常数和介电常数. 在压电散射体的表面区域上, 存在两种不同类型的电边界条件^[12], 如果表面是自由表面, 则称为开路状态, 表面上电位移的法向分量D_z = 0; 如果表面覆盖一层薄金属膜并接地, 称为短路状态, 上下表面的电势差$\varphi = 0$. 声波速度取决于材料的结构特性, 比如压电材料, 因此可通过控制波速来达到调控压电声子晶体能带结构的目的. 由于结构具有二维周期性, 根据Bloch定理, 将周期性边界条件施加在单位原胞的四个边界处, 位移场为^[18]

$u\left( r \right) = {u_k}\left( r \right){{\rm{e}}^{{\rm{i}}{{k}} \cdot {{r}}}},$

式中u和r分别为位移和位置矢量, k为Bloch波矢. 通过改变第一布里渊区中的k的值并求解由有限元算法产生的特征值问题, 即可获得色散关系以及本征模式. 压电声子晶体具有正压电效应, 当受到谐波激励时, 正负电荷会分别向压电层上下表面流动形成电势差; 电流、电荷和电压均为时间函数, 这些周期函数将取决于声子晶体结构的机械振动模态; 压电散射体与外部阻抗相连, 流向外部阻抗的电流会与电极表面电荷产生差值, 将电荷表示为时间谐波函数, 即电流振幅I等于频率f乘以电荷Q^[19]:

$I = fQ,$

纯负载电阻R_L电路的电流I与电压V关系为

${R_{\rm{L}}} = \frac{V}{I}.$

由于外部阻抗是纯电阻, 所以输出电压和电流具有相同的相位. 输出功率可定义为

$P = \frac{1}{4}(V{I^*} + I{V^*}).$

输出功率的外负载电阻取决于压电材料的振动频率.
为验证能带的数值仿真结果, 同时计算了所设计声子晶体模型的传输损失谱, 对应计算的结构如图2所示. x方向上为5个单元组成的有限周期性结构; y方向上, 在模型两侧施加Bloch周期性边界条件并将波矢k沿着$\varGamma \to X$方向扫描; 将完美匹配层(PML)应用于有限结构的x方向右端, 以防止能量反射. 由加速度激励源提供的单频率入射平面波从有限结构的左边界入射, 沿x方向传播, 传输损失T定义为
图 2 用于计算传输损失的有限结构
Figure2. The finite structure for the calculation of the transmission loss.

$T = 20{\rm{log}}\frac{{{d_{{\rm{out}}}}}}{{{d_{{\rm{in}}}}}},$

式中d_in为在有限结构左侧施加的位移加速度激励, d_out为在右侧拾取的位移加速度激励.

2

-->

3.1.缺陷态能带结构

本文设计的由包裹有机玻璃涂层的四棱柱形压电材料按正方形晶格周期性连接在四个环氧树脂短板上构成的二维压电声子晶体板, 结构参数取值为: a = 20 mm, h ₁ = 10 mm, h ₂ = 4 mm, l ₁ = 5 mm, l ₂ = 16 mm, l ₃ = 18 mm, d = 2 mm. 采用超晶胞法结合有限元方法来模拟无限长压电声子晶体板波导并计算能带结构, 超晶胞包含5个单位单元. 在超晶胞的x和y方向施加Bloch周期性边界条件, 将中间压电散射体的z方向设置成开路电边界条件, 两侧压电散射体的z方向设置成短路电边界条件, 从而形成电边界缺陷. 图3给出了1 × 5超晶胞完美声子晶体板和缺陷态声子晶体板周期性结构的色散关系, 通过对比, 可以看到缺陷态声子晶体板能带结构在900—1300 m/s之间存在三个频散曲线, 即缺陷频带. 图4为完美声子晶体板和缺陷声子晶体板的传输损失对比示意图, 可以看出该传输损失谱中存在的频率衰减范围与图3中的完全带隙的频率范围相符合, 很好地验证了能带结构的数值结果, 并且在0—1550 m/s频率范围内, 压电声子晶体板传输损失谱存在三个明显的能量衰减区域, 其能量衰减频率范围分别是180—750, 1031—1289和1408—1507 m/s, 当引入点缺陷时, 第一和第三完全带隙的频率范围几乎保持不变, 而在第二个能量衰减区域中的1248 m/s附近出现峰值, 表明峰值是由电边界缺陷造成的.
图 3 完美和缺陷周期性结构压电声子晶体板的能带结构示意图
Figure3. Schematic diagram of energy band structure of piezoelectric phononic crystal plate with perfect and periodic defect structures.

图 4 完美和缺陷周期性结构压电声子晶体板传输特性对比示意图
Figure4. Schematic diagram of transmission characteristics of piezoelectric phonon crystal plates with perfect and periodic defect structures.

本文设计的1 × 5新型二维压电声子晶体板超元胞总共有的三种点缺陷振动模式, 即点缺陷分别位于超元胞中间位置(模式A)、左二或右二位置(模式B)和任意端位置(模式C). 为了进一步说明峰值是由点缺陷造成的这一事实, 计算了电边界缺陷位置为模式B和模式C时的能带结构和传输损失, 计算结果如图5所示. 图6给出了超元胞三种不同点缺陷位置的传输特性对比结果. 通过对比发现, 位于超元胞中间位置的点缺陷即模式A的峰值频率为1248 m/s, 模式B点缺陷的峰值频率为1139 m/s, 模式C点缺陷的峰值频率为1050 m/s, 可见点缺陷的位置越靠近中心, 其峰值频率越大, 表明峰值变化是由引入点缺陷所造成的.
图 5 1 × 5超元胞的两种不同点缺陷位置传输损失和能带结构　(a)点缺陷为模式B; (b)点缺陷为模式C
Figure5. The position transmission loss and band structures of two different defects in the 1 × 5 supercells: (a) The point defect is at pattern B; (b) the point defect is at pattern C.

图 6 超元胞的三种不同点缺陷位置的传输特性对比
Figure6. Comparison diagram of transmission characteristics of three different defect locations of the supercell.

图7给出了上述三种处于不同电边界缺陷位置峰值频率的位移矢量场, 三种模式都是良好的振动模态, 其弹性能量主要限制在开路电边界缺陷处, 中心压电散射体的有效弹性刚度通过消除切向电场而减小, 因此可以将弹性波限制在点缺陷周围. 压电散射体在z轴方向上有一个振幅很大的振动, 且带动了包覆层和连接板的z方向振动, 从而产生大幅变形, 以得到最大的应变, 因此振动能量将局域在上下表面开路条件的压电散射体中, 更强烈地限制在缺陷处, 利用压电散射体在z方向上(面外波)振动导致声子晶体板形变从而将机械动能转化为电能进行能量回收.
图 7 压电声子晶体板缺陷态处于三种不同位置的位移矢量场
Figure7. Displacement vector fields of piezoelectric phonon crystal plates with defect states at three different positions.

2 -->

3.2.压电常数对带隙特性的影响

压电材料具有正压电效应, 当受到外界压力作用时会在上下两端面间形成电势差, 而压电常数e''是反映力学量(应力或应变)与电学量(电位移或电场)间相互耦合的线性响应系数, 对带隙的位置和宽度有着很大的影响, 从而导致缺陷态频率发生改变. 假定压电常数e'' = e/e', 对于真实的压电材料属性, 设定e'' = 1, 对于没有压电效应的情况, e'' = 0. 本文计算了点缺陷处于超元胞中间位置的压电声子晶体的压电常数 e''从0 (无压电)逐渐改变为1 (实际值)的传输损失谱, 结果如图8所示. 第一和第三完全带隙的频率范围几乎保持不变, 而随着第二个能量衰减区域中压电常数的增大, 对应的峰值频率也越来越大.
图 8 压电常数对声子晶体板传输特性的影响
Figure8. Influence of piezoelectric constant on the transmission characteristics of phonon crystal plates.

为了进一步分析, 图9给出了第五条带隙和第六条带隙边缘随压电常数的变化情况. 结果表明: 随着压电常数增大, 第五带隙下边缘大致保持不变, 而带隙上边缘随着耦合强度的增加而上移; 第六完全带隙的下边缘随着压电常数的增大而向上移动, 致使缺陷态频率提高, 这是因为较低的频带边缘上的模式主要为压电散射体的平移振动或不受压电效应影响的弹性材料的振动, 上边缘模式是压电柱的扭曲振动. 因此, 可以得出结论: 压电效应对完整带隙有显著影响, 并有利于缺陷态的形成和扩大.
图 9 压电常数e''对第五和第六完全带隙上边缘和下边缘(即缺陷态)的影响
Figure9. Effect of piezoelectric constant e'' on upper and lower edge (i.e. defect state) of fifth and sixth complete bandgap.

2 -->

3.3.振动能量回收能力分析

前面已经证明了通过改变电边界条件可以将压电声子晶体振动的机械能集中到点缺陷处, 并且当点缺陷处于超元胞不同位置时对应的峰值振动频率也发生了改变, 本节旨在对比三种局域到不同点缺陷处的机械能转化为电能并进行回收的能力. 图10给出了振动能量集中在压电声子晶体板三种不同位置时回收装置整流电路原理图, 前端信号发生器连接激振器, 利用机械振动使后端的压电声子晶体板获得一定形式和大小的振动量, 根据压电效应, 压电散射体的形变将产生的正负电荷积聚在晶体的上下表面形成电势差, 表面电极上的电压与应力的关系为^[8]
图 10 振动能量回收整流电路原理图
Figure10. Vibration energy recovery circuit diagram.

$V = eh{\bar \sigma _{\max }},$

其中e是0.27PIN-0.4PMN-0.33PT压电陶瓷的压电常数, h为压电层的厚度, ${\bar \sigma _{\rm max }}$为整个压电层自由面上的横向应力取平均值. 压电散射体在共振频率处发生共振所产生的是交流电压, 因此用整流电路连接压电片上下表面的电极将交流电变成直流电, 输出的电能就可以为直流负载供电. 图11给出了交流电压的波形图, 图12给出了结构发生共振时, 负载电阻R_L两端的功率随激励交流电压源的变化, 可以看出负载电阻R_L两端的功率随共振频率处的电压增大而增大, 对比三种模式缺陷态回收电能的能力发现, 当缺陷态处于超元胞中间位置, 即模式A时, 其振动能量回收能力为三种方式中最大的, 是缺陷态为模式C的能量的两倍多.
图 11 压电散射体上下表面电压波形图
Figure11. Voltage waveform of upper and lower surface of piezoelectric scatterer.

图 12 三种不同点缺陷位置的电阻R输出功率随激励电压的变化示意图
Figure12. Schematic diagram of resistance R output power varying with excitation voltage at three different defect positions

在完美压电声子晶体板中通过改变电边界条件来引入缺陷态, 可以将振动所产生的机械能局域到点缺陷处, 利用正压电效应将压电散射体中正负电荷积聚在晶体的上下表面, 从而形成电势差, 实现机械能到电能的转换, 这种机电转换方式更加绿色环保. 本文设计了一种由包裹有机玻璃涂层的四棱柱形压电材料按正方形晶格周期性连接在四个环氧树脂短板上构成的1 × 5新型二维压电声子晶体板, 并利用超元胞法结合有限元法分别计算了完美声子晶体板和缺陷态位于超元胞三种不同位置的声子晶体板的能带结构和传输损失. 通过改变施加在压电散射体上下表面的电边界条件, 形成点缺陷波导, 限制弹性波能量流. 当电边界缺陷在超元胞三种不同位置时, 对应的峰值频率也发生改变, 压电效应有利于收集更宽频率范围的机械能, 为了对比三种局域到不同点缺陷处的机械能转化为电能进行回收的能力, 用回收电路分别连接到三种不同电边界缺陷处的压电片上下表面的电极, 将振动的机械能转化为电能, 为负载供电, 发现当缺陷态处于超元胞中间位置时, 其振动能量回收能力为三种方式中最大的, 是缺陷态处于超元胞任意端位置的能量的两倍多.