摘要:在不改变结构的情况下实现声学超材料对外部响应的可调性, 一直是声学超材料所面临的挑战之一. 因此, 本文提出了以磁流变弹性体(MRE)作为单、双包覆层的声学超材料元胞结构, 研究其在磁场作用下的可调带隙以及传输谱特性. 通过改变作用于包覆层MRE的磁场强度, 控制MRE的剪切模量, 使声学超材料的带隙和传输谱在磁场作用下具有可调性. 应用有限元法对两种声学超材料的带隙及传输谱特性进行了仿真分析. 仿真结果表明, 在磁场作用下, 两种声学超材料的带隙频率和宽度随着磁场强度的增强而增加; 传输谱随着磁场强度的增强其最大衰减频率向高频移动, 最大衰减量也随之增加. 同时, 采用质量-弹簧模型对声学超材料的带隙频率进行了估算, 仿真结果与估算结果具有很好的一致性. 此外, 讨论了芯体、壳体的材料参数以及填充率对带隙和传输谱特性的影响. 这些研究可为声学超材料对弹性波的主动控制, 以及为新型隔振、抑振结构的开发和应用提供理论基础.
关键词: 声学超材料/
磁流变弹性体包覆层/
带隙和传输谱特性/
磁场强度

English Abstract

全文HTML

--> --> -->

声学超材料是一种典型的人工周期结构, 其可呈现出如负质量密度^[1,2]、负体积模量^[3-5]、负泊松比^[6]、零折射率^[7]等天然材料所不具备的超常物理性能, 所以近年来声学超材料受到了广泛关注^[8-11]. 这些超常物理性能, 使声学超材料具有许多潜在的应用, 如波导^[12]、弹性波聚焦^[13,14]、声隐身^[15-19]、反常多普勒效应^[20]等. 近年来, 随着对声学超材料研究的深入, 进一步拓展了声学超材料在声学拓扑绝缘体^[21]、声场的精确控制^[22]以及声慢波传输和相位操控^[23]等方面的应用.
声学超材料的研究起源于声子晶体, 许多****已对声子晶体的带隙特性进行了深入的研究^[24-26]. 2000年, Liu等^[27]提出了局域共振声子晶体, 利用其对声波的局域效应成功实现了低频带隙. 2004年, Li等^[28]利用局域共振机理设计了一种具有等效质量密度和等效体积模量同时为负值的复合介质, 提出了声学超材料的概念. 基于局域共振机理的声学超材料结构中起主要作用的是局域共振单元, 当弹性波的频率与局域共振单元的共振频率接近时, 声学超材料能够产生弹性波低频带隙, 在带隙频率范围内不允许弹性波透过. 由于结构中的振动和噪声通常是以弹性波的形式进行传播, 这使声学超材料在低频隔振与噪声控制上具有良好的应用前景.
然而, 传统声学超材料一旦结构设计好后, 其响应频率即随之确定, 不具有带隙可调性, 因此限制了声学超材料的实际应用. 为了能够使声学超材料适应不同的工作环境, 应设计具有参数可调的声学超材料结构. 声学超材料的参数调节可分为被动与主动调节. 被动调节的主要实现方式是改变或设计声学超材料的几何结构. Goffaux等^[29]借助于方形散射体的旋转来进行带隙调节, Bertoldi等^[30]通过改变晶格与散射体形状来调节带隙. Zhou等^[11]提出了多包覆层局域共振单元结构, 来拓展声学超材料的低频带隙, 并对包覆数量与厚度对带隙和传输谱的影响进行了讨论. Larabi等^[31]采用有限时域差分法对多包覆层局域共振单元结构的带隙特性进行了研究, 对比了包覆层的奇、偶数对带隙特性的影响. Lewińska等^[32]研究了采用黏弹性材料作为多包覆层的局域共振声学超材料, 研究发现改变包覆层参数不但影响带隙频率, 还影响带隙频率内弹性波的衰减量. 基于Mie共振机理的声学超材料也具有重要的应用. Gao等^[33]设计了一种基于单级Mie共振的低频声波能量吸收器, 该吸收器能够实现低频声波的高吸收特性, 同时具有良好的鲁棒性. Cheng等^[34]设计了一种具有Mie共振的超稀疏声学超表面, 实现了低频声波的强反射. Zhu等^[35]设计了一种高局域偶极Mie共振声学超表面, 实现了深亚波长尺度下声波的定向传感.
参数的主动调节, 主要通过智能材料改变局域共振单元的共振频率来实现. Chen等^[36,37]采用压电片作为局域共振单元, 通过外加电场控制声学超材料结构中的弹性波传播, 实现了声学超材料的带隙控制, 拓宽了带隙频率. Xiao等^[38]研制了一种由电场控制的薄膜声学超材料, 他们将薄膜上电极与另一侧网状电极构成电容器, 采用调节其上的电压改变薄膜的共振频率和相位的方式, 实现声波传输过程中带隙的主动调节. 贺子厚等^[39]采用压电质量块嵌入弹性薄膜方法设计了一种可调控薄膜声学超材料, 通过改变压电质量块和外接电路的参数来调整共振频率, 实现对隔声性能的调控. Shen等^[40]设计了一种主动声学超表面, 该声学超表面由$4 \times 4$阵列的压电片植入环氧树脂基体中构成一个超元胞结构, 通过调整超元胞宽度与晶格常数的比值可以完全控制由结构衍射引起的栅瓣. Zhou等^[41]研究了电流变材料包覆层初始应力对带隙的影响, 还通过外部电场获得了声学超材料的可调带隙. 同样还可以通过改变作用于磁流变材料的外部磁场来调节声学超材料的带隙结构. 磁流变弹性体(MRE)是磁流变材料的一种, 其特点是可通过控制作用于材料的磁场大小连续控制材料的力学性能, 具有响应快、可逆性好、可控能力强等特点^[42-44]. Chen等^[45]设计了一种磁-声学超材料结构, 将MRE作为薄膜覆盖于铝制环上, 通过改变结构外部磁场控制声学超材料的带隙频率. Xu等^[46]采用MRE作为三维声学超材料局域共振单元的包覆层, 在外部磁场作用下声学超材料的带隙频率和宽度可调.
为了进一步研究声学超材料的可调带隙和传输谱特性, 本文设计了以MRE为包覆层的两种声学超材料元胞结构, 一种是以MRE作为单包覆层的元胞结构, 另一种是以MRE作为双包覆层的元胞结构; 分析了磁场强度、芯体与壳体材料参数、填充率等对两种元胞结构构成的声学超材料带隙特性以及传输谱特性的影响.

2

-->

2.1.声学超材料结构

两种声学超材料的元胞结构如图1所示, 第一种声学超材料元胞结构为单层MRE包裹纯铁圆柱体(芯体)组成局域共振单元结构, 如图1(a)所示, 将其植入基体材料, 按周期结构排列可构成单包覆层MRE声学超材料; 第二种声学超材料元胞结构为内层MRE (内包覆层)包裹纯铁圆柱体 (芯体), 在内层MRE外包裹一层纯铁圆柱壳体, 在圆柱壳体外再包裹一层MRE (外包覆层), 构成双包覆层MRE局域共振单元结构, 如图1(b)所示, 同样将其植入基体材料按周期结构排列, 构成双包覆层MRE声学超材料. 两种声学超材料的基体材料均为环氧树脂, 且局域共振单元均按照正方晶格结构排列. 第一不可约布里渊区如图1(c)所示. 构成声学超材料的具体材料参数如表1所列.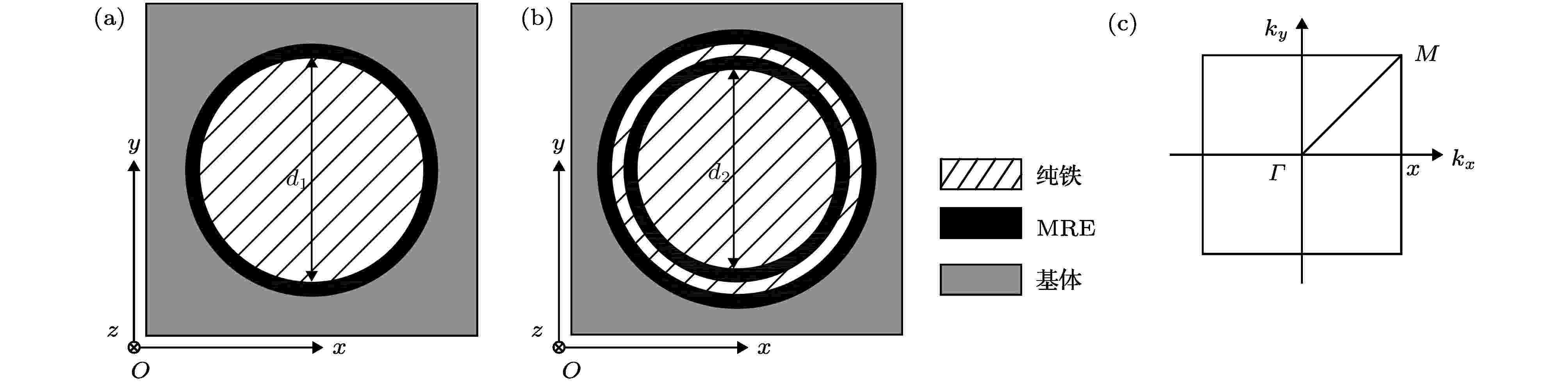
图 1 MRE包覆层声学超材料元胞结构和不可约布里渊区　(a) 单包覆层MRE声学超材料; (b) 双包覆层MRE声学超材料; (c) 正方晶格第一不可约布里渊区
Figure1. Schematic of the MRE acoustic metamaterial cells and the irreducible first Brillouin zone: (a) Single-layer MRE acoustic metamaterial; (b) double-layer MRE acoustic metamaterial; (c) the irreducible first Brillouin zone of square lattices.

材料	密度$\rho /{\rm{kg}} \cdot {{\rm{m}}^{ - 3}}$	拉梅常数
		λ/GPa	μ/GPa
纯铁	7900	115.38	76.92
环氧树脂	1180	4.52	1.59
MRE	3009	6.26×10-3	0.4×10-3

表1构成MRE声学超材料的材料参数
Table1.Material properties of the MRE acoustic metamaterials.

单包覆层MRE声学超材料的芯体直径${d_1} = {\rm{34\;mm}}$, MRE包覆层厚度为${\rm{2\;mm}}$. 双包覆层MRE声学超材料的芯体直径${d_2} = {\rm{30\;mm}}$, 壳体厚度为${\rm{2\;mm}}$, 内、外MRE包覆层的厚度均为${\rm{2\;mm}}$, 声学超材料的晶格常数为${\rm{50\;mm}}$.
2 -->

2.2.磁流变弹性体

磁流变弹性体, 采用磁偶极子模型^[47], 铁磁颗粒密度${\rho _{{\rm{Fe}}}} =$ 7.89 × 10³ kg/m³, 硅橡胶密度${\rho _{\rm{r}}} = $ 1.2 × 10³ kg/m³, MRE的拉伸性能与剪切性能相似, 取其泊松比为0.47. 外磁场对剪切模量的改变量为^[48]

$\Delta G = 36\phi {\mu _{\rm{f}}}{\mu _0}{\beta ^2}{H^2}{\left( {{R/d}} \right)^3}\zeta ,$

式中$\phi $是在硅橡胶基体中的铁磁颗粒的体积比, R是颗粒半径, d表示链中的两个颗粒之间的距离, ${\mu _0}={{4{\text{π}} \times 1}}{{\rm{0}}^{ - 7}}\;{\rm{H/m}}$是真空磁导率, H为外部磁场强度, $\zeta = 1.202$, $\beta \approx 1$, ${\mu _{\rm{f}}} = 1$是相对磁导率. 假设${d/R} = 2.5$, $\phi = 27\% $, 并采用典型的弹性参数${G_0} = {\rm{0}}{\rm{.4\;MPa}}$^[46,48], $G = {G_0} + \Delta G$.
2 -->

2.3.仿真方法

对于多层局域共振单元模型, 其弹性波的传播方程为

$\rho {\ddot u_i} \!=\! \sum\limits_{j = 1}^3 \bigg[ \frac{\partial }{{\partial {x_i}}}\Big(\lambda \frac{{\partial {u_j}}}{{\partial {x_j}}} \Big) \!+\! \frac{\partial }{{\partial {x_j}}} \Big(\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} \!+\! \mu \frac{{\partial {u_j}}}{{\partial {x_i}}} \Big) \bigg],$

式中$i, j = 1, 2, 3; $${u_i}$为i方向位移; ${u_1}$, ${u_2}$, ${u_3}$分别与${u_x}$, ${u_y}$, ${u_z}$对应, ${x_1}$, ${x_2}$, ${x_3}$分别与x, y, z对应; $\rho $为密度; $\lambda , {\rm{ }}\mu $为Lame常数.
对于二维声学超材料结构, 假设弹性波在xoy平面内传播时, 介质的位移只与x, y坐标有关, 而与z坐标无关. 此时描述xoy平面内与z方向上的波动方程可以解耦, 分别称作xy模式和z模式. 在xy模式下弹性波的传播方程为

$\begin{split} \rho \frac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} = \, &\frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial {u_x}}}{{\partial x}} + \lambda \frac{{\partial {u_y}}}{{\partial y}}} \right) + \frac{\partial }{{\partial y}}\bigg(\mu \frac{{\partial {u_x}}}{{\partial y}} \\ & + \mu \frac{{\partial {u_y}}}{{\partial x}} \bigg) + 2\frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial {u_x}}}{{\partial x}}} \right), \\ \rho \frac{{{\partial ^2}{u_y}}}{{\partial {t^2}}} = \, & \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial {u_x}}}{{\partial x}} + \lambda \frac{{\partial {u_y}}}{{\partial y}}} \right) + \frac{\partial }{{\partial x}}\bigg(\mu \frac{{\partial {u_y}}}{{\partial x}} \\ & + \mu \frac{{\partial {u_x}}}{{\partial y}} \bigg) + 2\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial {u_y}}}{{\partial y}}} \right).\end{split} $

由于声学超材料为周期结构, 需满足布洛赫定理

${{u}}\left( {{{x}},t} \right) = {\bar{ u}}\left( {{{x}},t} \right){{\rm{e}}^{{\rm{i}}\left( {{{kX}} + \omega t} \right)}},$

式中${{k}}$为波矢, $\omega $为角频率, t为时间, ${\bar{ u}}$为${{x}}$的周期函数, ${\bar{ u}}$可表示为

${\bar{ u}}\left( {{{x}}{\rm{,}}t} \right) = {\bar{ u}}\left( {{{x}} + {{{R}}_n},t} \right),$

式中${{{R}}_n}$为晶格向量.
根据方程(3)—(5)可计算xy模式下声学超材料的带隙结构. 本文采用有限元软件COMSOL Multiphysics?计算MRE声学超材料的带隙结构. 在COMSOL Multiphysics?软件中, 以单个元胞为研究对象, 在元胞的x和y方向施加Floquet周期性边界条件, 网格采用自由三角形网格, 网格尺寸为细化, 波矢${{k}}$沿第一布里渊区进行参数化扫描, 计算得到带隙结构.

2

-->

3.1.单包覆层MRE声学超材料带隙特性

3 -->

3.1.1.磁场强度对带隙特性的影响

单包覆层MRE声学超材料, 其元胞结构如图1(a)所示, 当外部磁场作用时, MRE包覆层的剪切模量可随磁场变化, 因此其带隙结构可以通过改变磁场强度进行调节. 图2为MRE包覆层在没有磁场(H = 0 kOe), 以及磁场强度为H = 6 kOe作用下的带隙结构, 以说明磁场对带隙结构的影响.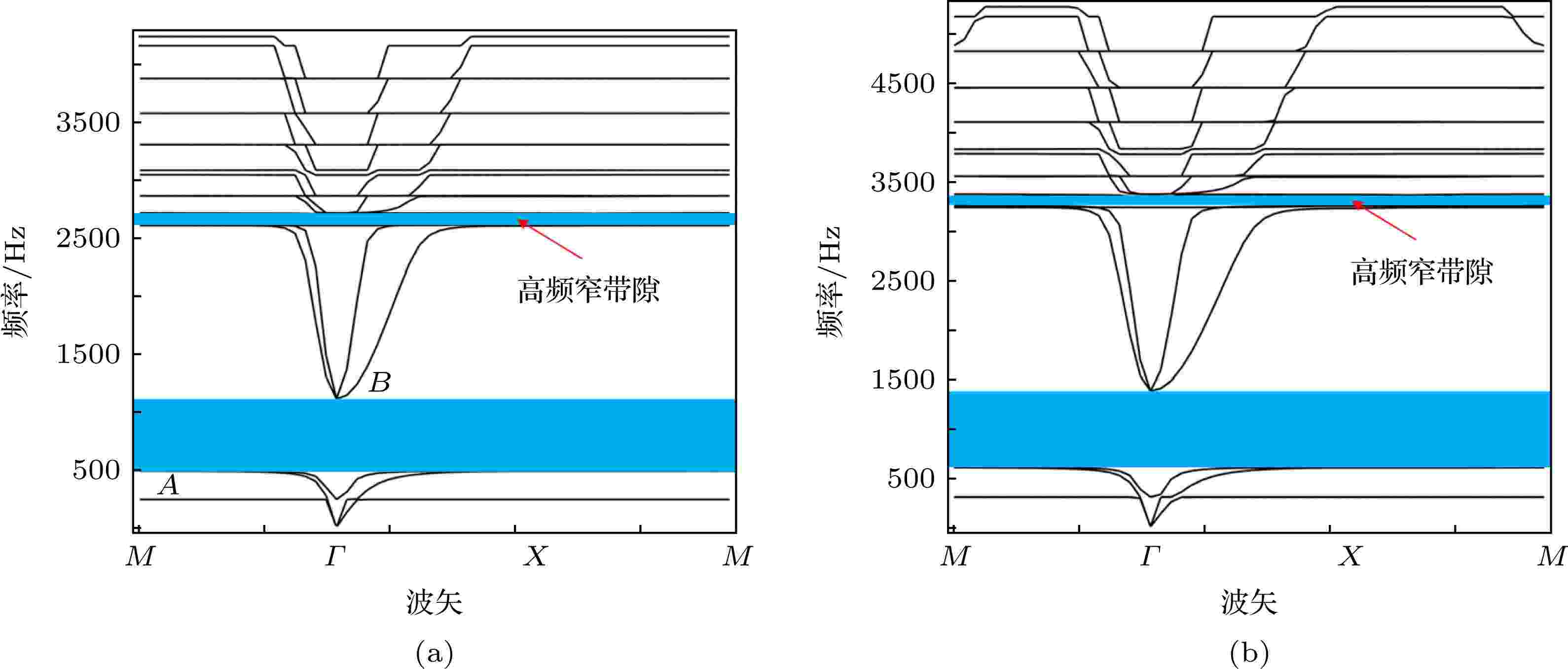
图 2 单包覆层MRE声学超材料带隙结构　(a) 磁场强度H = 0; (b) 磁场强度H = 6 kOe
Figure2. The band gap structures of single-layer MRE acoustic metamaterial: (a) Magnetic field intensity of H = 0; (b) magnetic field intensity of H = 6 kOe.

对于单包覆层MRE声学超材料我们关注其第一阶带隙, 因为第一阶带隙频率较低, 且带隙较宽. 如图2(a)所示, 当没有外部磁场作用时, 带隙频率为488—1114 Hz; 当磁场强度为H = 6 kOe时, 带隙结构如图2(b)所示, 带隙频率为607—1368 Hz. 由以上计算可知, 有磁场作用于包覆层MRE时, 声学超材料带隙的下边界与上边界频率都随之升高. 在图2中还可以看到在高频处还有一窄带隙, 但由于其频率高, 且带隙窄, 很难将其应用于实际工程领域.
由图2还可以发现, 声学超材料的带隙为多条平直线, 具有典型的局域共振特性. 为了进一步理解声学超材料的带隙机理, 下面讨论在图2(a)中带隙边界处标出的A, B两点的位移向量场. 图3为A, B两点的位移向量场, 由图3(a)中可以看到, 在带隙下边界的A点处, 当弹性波在声学超材料中传播时为芯体在振动, 而基体保持静止; 由图3(b)中可以看到, 在带隙上边界处B点, 为基体在振动, 芯体只有轻微振动, 且芯体与基体运动方向相反, 此时, MRE包覆层可以视为弹簧, 而芯体与基体可视为集中质量, 芯体与基体以相对振动的方式发生共振. 图3中的箭头表示基体和芯体的相对运动方向.
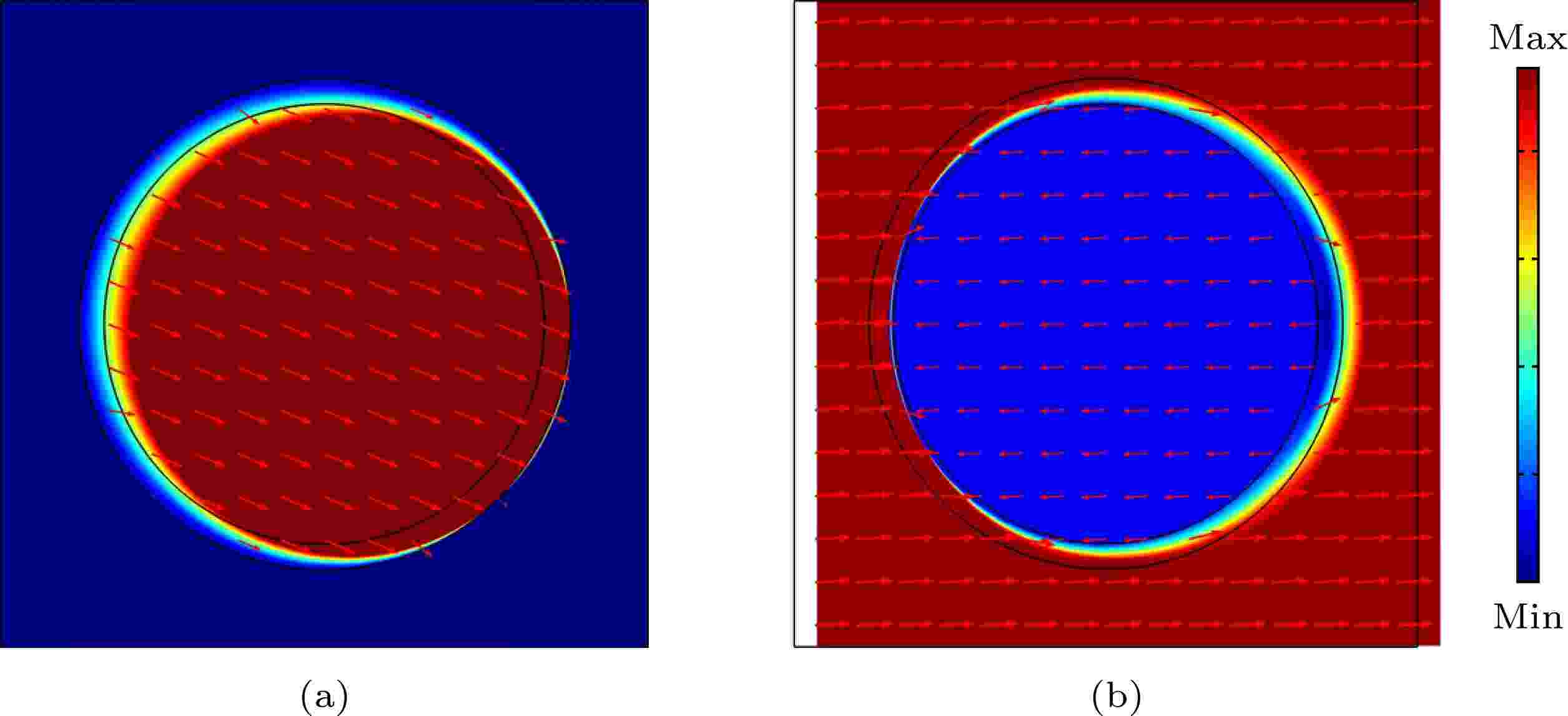图 3 单包覆层MRE声学超材料带隙边界位移场　(a) 带隙下边界; (b) 带隙上边界
Figure3. Displacement field of the band gap boundaries of the single-layer MRE acoustic metamaterial: (a) The lower boundary of the band gap; (b) the upper boundary of the band gap.

根据位移向量场, 单包覆层MRE声学超材料可简化为图4所示的质量-弹簧模型^[49]来描述其带隙下边界和上边界的振动模式. 其中${m_1}$为元胞的芯体质量, ${m_2}$为基体质量, 弹簧k为MRE包覆层的等效刚度, 其具体定义见文献[49]. 在带隙下边界处, ${m_1}$在弹簧k的作用下, 发生共振(对应图3(a)). 在带隙上边界处, m₁和m₂在弹簧k的作用下, 以相对振动的方式发生共振(对应图3(b)).
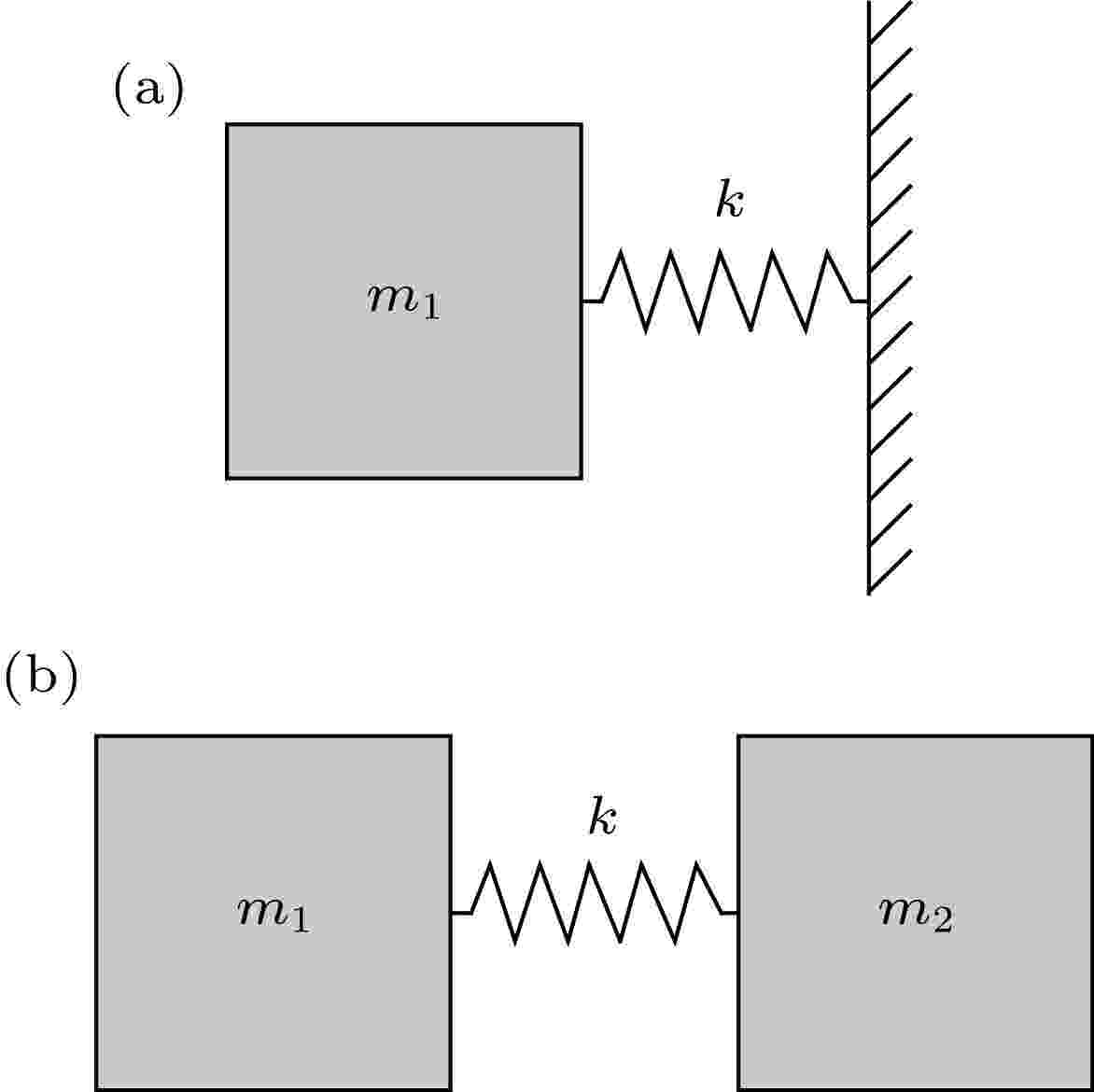图 4 单包覆层MRE声学超材料的质量-弹簧模型　(a) 带隙下边界; (b) 带隙上边界
Figure4. The mass-spring model of single-layer MRE acoustic metamaterial: (a) Lower boundary of band gap; (b) upper boundary of band gap.

在该等效模型下, 单包覆层MRE声学超材料的低频带隙下边界${f_{\rm{L}}}$和上边界${f_{\rm{U}}}$可由以下公式估算:

${f_{\rm{L}}} = \frac{1}{{2{\text{π}}}}\sqrt {\frac{k}{{{m_1}}}} ,$

${f_{\rm{U}}} = \frac{1}{{2{\text{π}}}}\sqrt {\frac{{k\left( {{m_1} + {m_2}} \right)}}{{{m_1}{m_2}}}} .$

由(6)和(7)式可知${f_\alpha } \propto \sqrt k $, ($\alpha = {\rm{L, U}}$), 在声学超材料中, 包覆层的剪切模量G可通过文献[49]的方法将其计算为包覆层的等效刚度k, 所以${f_\alpha } \propto \sqrt G $, 因此,

${{{f_\alpha }}/{f_\alpha ^0}} = \sqrt {{G/{{G_0}}}} ,$

$f_\alpha ^0$为磁场强度$H = {\rm{0\;kOe}}$时的带隙边界.
由以上仿真结果可知, 单包覆层MRE声学超材料可以通过改变磁场强度来改变其带隙结构. 现在分析磁场强度连续变化时声学超材料的带隙变化情况. 磁场强度由0—10 kOe连续变化时, 单包覆层MRE声学超材料的带隙变化如图5(a)所示, 其带隙频率从488—754 Hz变化到1114—1723 Hz. 由此可知, 随着磁场强度增强, 带隙下边界与上边界频率都呈上升趋势, 但其上边界频率变化较大, 宽度增加, 这是因为MRE的剪切模量随着磁场强度增强而增加. 图5(b)为随着磁场强度增强, 由(8)式计算的${{{f_\alpha }}/{f_\alpha ^0}}$随磁场强度变化曲线与有限元法计算的${{{f_\alpha }}/{f_\alpha ^0}}$随磁场强度变化曲线的对比图, 从图中可以看出, 有限元计算结果与质量-弹簧模型方法具有很好的一致性.
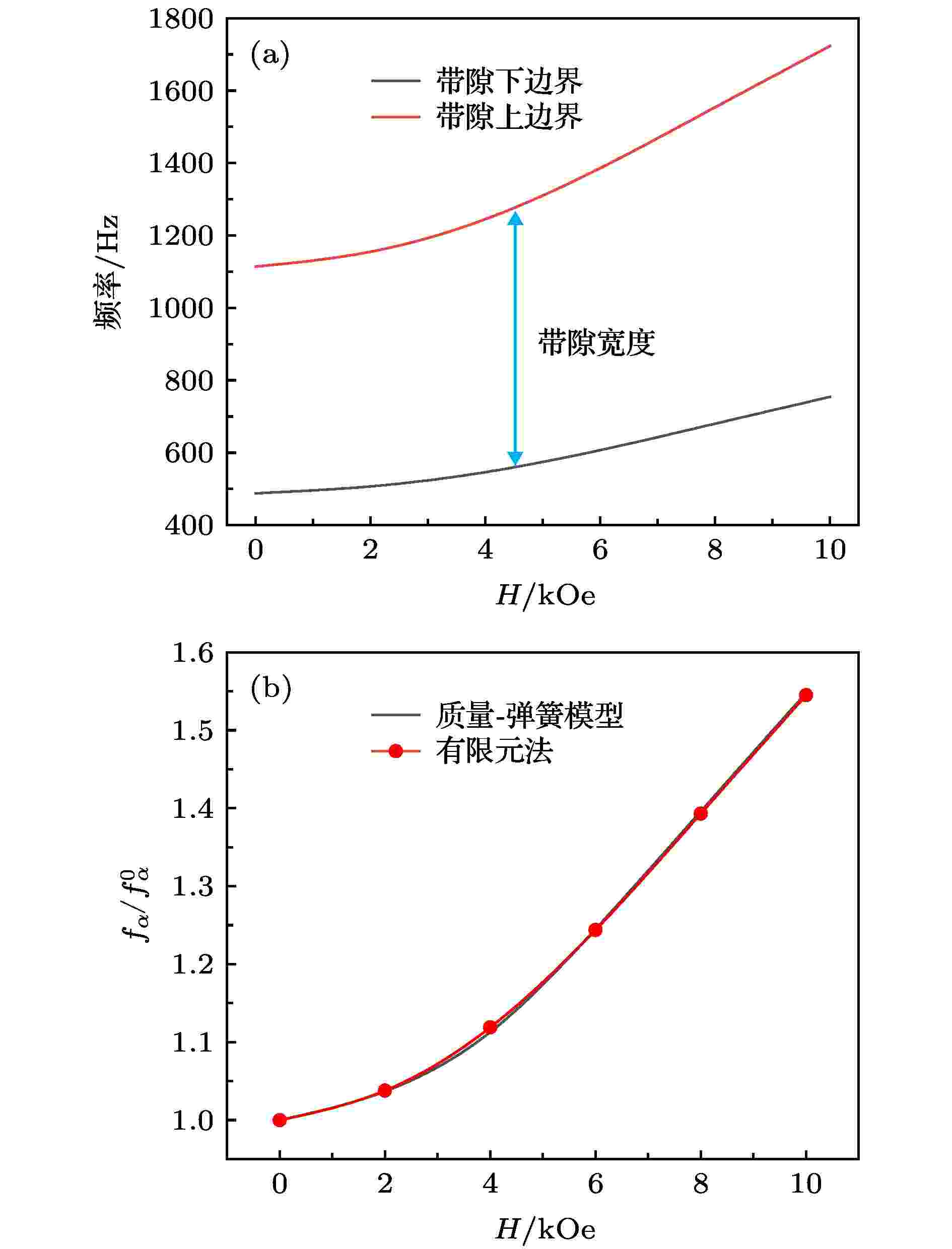图 5 单包覆层MRE声学超材料带隙随磁场强度变化及有限元法与质量-弹簧模型对比　(a) 磁场强度H = 0—10 kOe; (b) 有限元法与质量弹簧-模型对比
Figure5. Dependence of the band gap boundaries on the applied magnetic field of single-layer MRE acoustic metamaterial and a comparison of the FEM and the mass-spring model for (a) magnetic field intensity of H = 0–10 kOe, (b) comparison of the FEM and mass-spring model.

3 -->

3.1.2.芯体质量和填充率对带隙特性的影响

对声学超材料带隙特性研究的主要目标是降低带隙频率拓展带隙宽度, 声学超材料的带隙主要与芯体与壳体材料、包覆层参数以及填充率等参数相关. 前面分析了MRE包覆层在磁场作用下对带隙特性的影响, 下面分析材料和结构参数对带隙特性的影响.
芯体采用的材料参数如表2所列. 当芯体选用表2中的材料时, 单包覆层MRE声学超材料的带隙变化如图6(a)所示. 随着芯体质量增加, 带隙上、下边界频率都呈下降趋势. 根据位移向量场以及质量-弹簧模型, 在带隙的下边界处主要为芯体在振动, 所以芯体质量${m_1}$对带隙下边界频率影响较大. 在带隙上边界处为芯体与基体以相对运动的方式发生共振, 因此芯体质量${m_1}$和基体质量${m_2}$对带隙上边界频率都有较大影响. 而且从(6)式和(7)式中也可以看到, 随着芯体质量${m_1}$的增加, 带隙下边界与上边界频率均会逐渐下降, 但上边界频率下降趋势小于下边界频率, 带隙宽度增加.

材料	密度ρ/kg·m–3	弹性参数
		弹性模量E/GPa	泊松比$\upsilon $
钨	19100	344	0.28
铅	11600	16	0.42
铜	8950	115	0.32
钛	4540	102	0.3
铝	2730	68	0.33

表2材料参数
Table2.The material parameters.

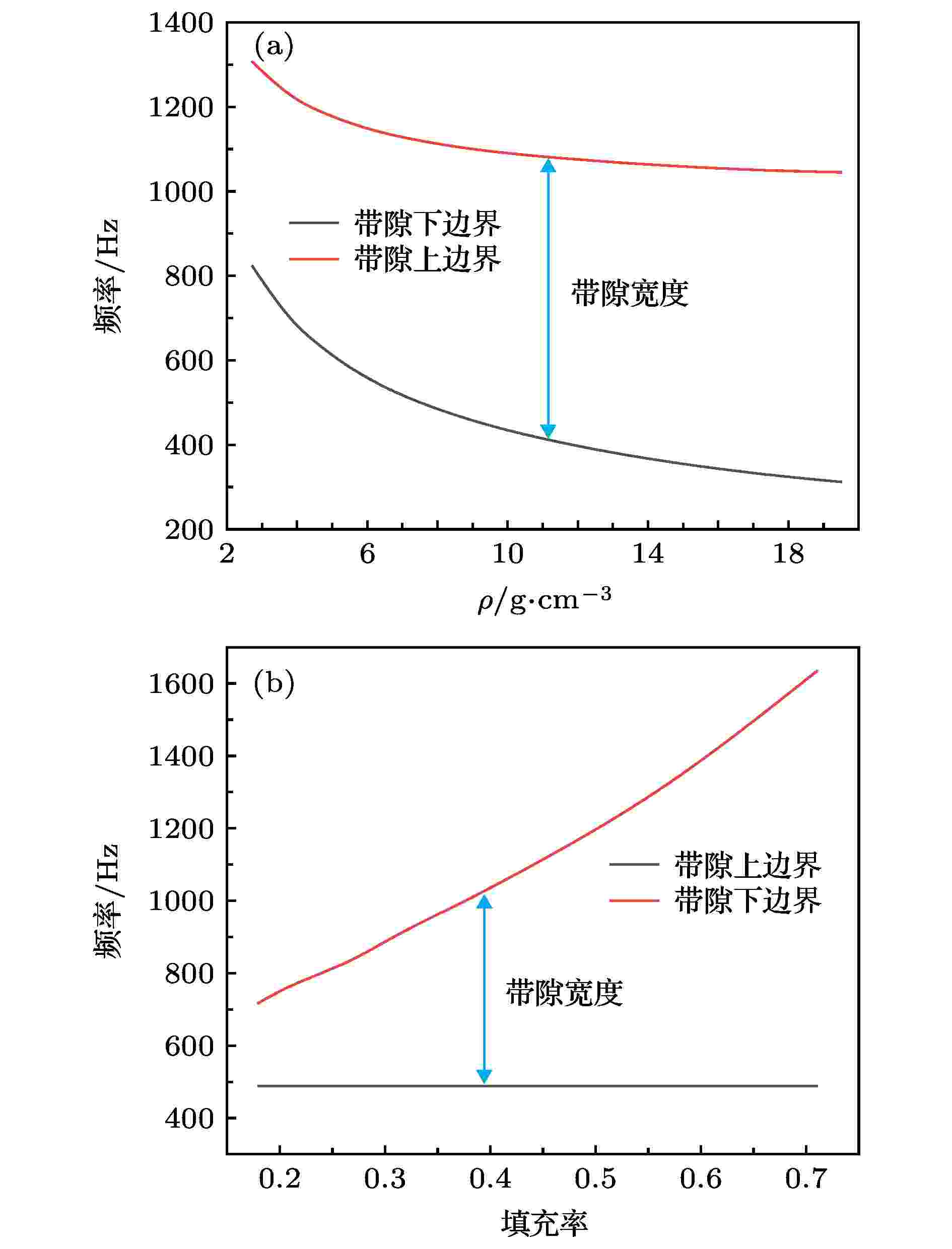图 6 单包覆层MRE声学超材料带隙随材料和结构参数变化　(a) 随芯体质量增加变化; (b) 随填充率增加变化
Figure6. The band gap of single-layer MRE acoustic metamaterial changes with (a) the core mass and (b) the filling rate.

对于二维声学超材料, 填充率是局域共振单元在声学超材料元胞中所占的面积比. 本文采用改变晶格常数的方式改变声学超材料的填充率, 这样可以保证局域共振单元的结构参数不发生改变. 在局域共振单元结构参数不变的情况下, 改变晶格常数也就是改变基体质量.
单包覆层MRE声学超材料带隙随填充率变化如图6(b)所示, 从图中可以看到, 随着填充率的增加, 带隙的下边界频率基本没有变化, 上边界频率逐渐升高, 带隙宽度增加. 这是因为随着填充率的增加, 基体质量逐渐减小, 即${m_2}$质量减小, 因此带隙上边界频率升高, 而带隙下边界频率只与芯体质量相关, 所以下边界频率基本没有变化.
2 -->

3.2.双包覆层MRE声学超材料带隙特性

3 -->

3.2.1.磁场强度对带隙特性的影响

双包覆层MRE声学超材料的元胞结构如图1(b)所示, 图7为双包覆层MRE声学超材料在没有磁场($H = {\rm{0\;kOe}}$), 以及磁场强度为$H = {\rm{6\;kOe}}$作用下的带隙结构, 以说明磁场对双包覆层MRE声学超材料带隙结构的影响.
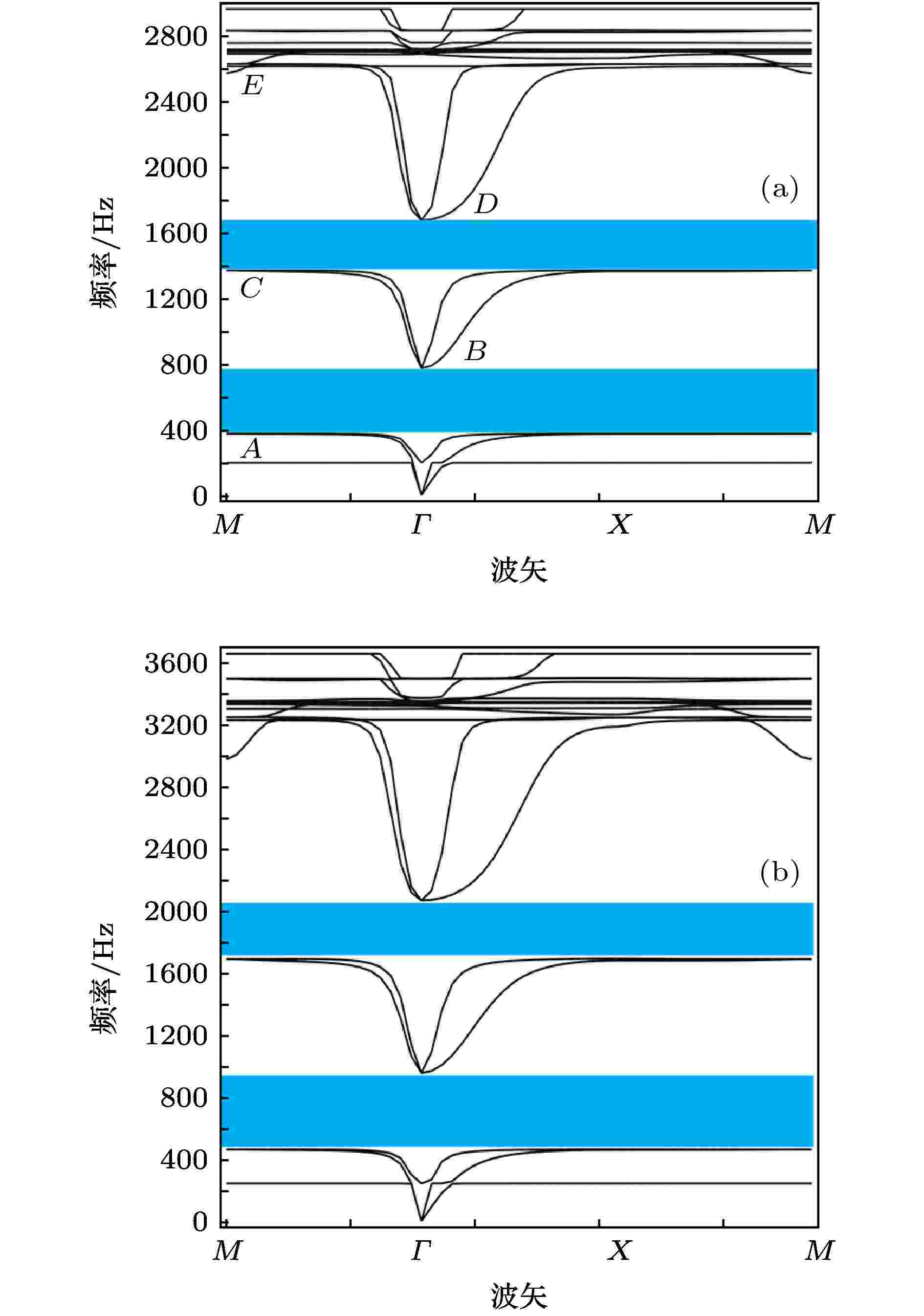图 7 双包覆层MRE声学超材料带隙结构　(a) H = 0; (b) H = 6 kOe
Figure7. The band gap structures of the double-layer MRE acoustic metamaterial: (a) H = 0; (b) H = 6 kOe.

与单包覆层MRE声学超材料相比, 双包覆层MRE声学超材料有两阶宽频带隙, 在单包覆层MRE声学超材料中存在的高频窄带隙消失. 如图7(a)所示, 当没有磁场(H = 0 kOe)作用时, 双包覆层MRE声学超材料的第一阶带隙频率为374—771 Hz, 第二阶带隙频率为1365—1670 Hz. 当磁场强度为H = 6 kOe时, 带隙结构如图7(b)所示, 此时第一阶带隙频率为465—959 Hz, 第二阶带隙频率为1698—2077 Hz, 与没有磁场作用时相比, 第一阶与第二阶带隙频率升高, 宽度增加.
下面进一步考察第一阶与第二阶带隙边界处的位移向量场, 图7(a)中标识的A, B, C, D, E点的位移向量场如图8所示. 图8(a)为第一阶带隙下边界A点的位移向量场, 在第一阶带隙下边界处为芯体在振动, 而基体保持静止; 第一阶带隙上边界B点处, 位移向量场如图8(b)所示, 芯体与基体的运动方向相反, 其与单包覆层MRE声学超材料的带隙上边界处位移向量场相似; 第二阶带隙下边界C点的位移向量场如图8(c)所示, 最大位移发生在包覆层位置, 壳体与芯体的运动方向相反; 第二阶带隙上边界D点的位移向量场如图8(d)所示, 为壳体与基体的运动方向相反, 可以看出壳体、芯体和基体相当于集中质量, 而包覆层相当于弹簧. 图7中E点的位移向量场如图8(e)所示, 从图中可以看到, 基体与芯体都不运动, 仅内、外包覆层扭转运动, 由于没有水平和竖直方向运动, 因此不能产生带隙, 所以高频窄带隙消失.
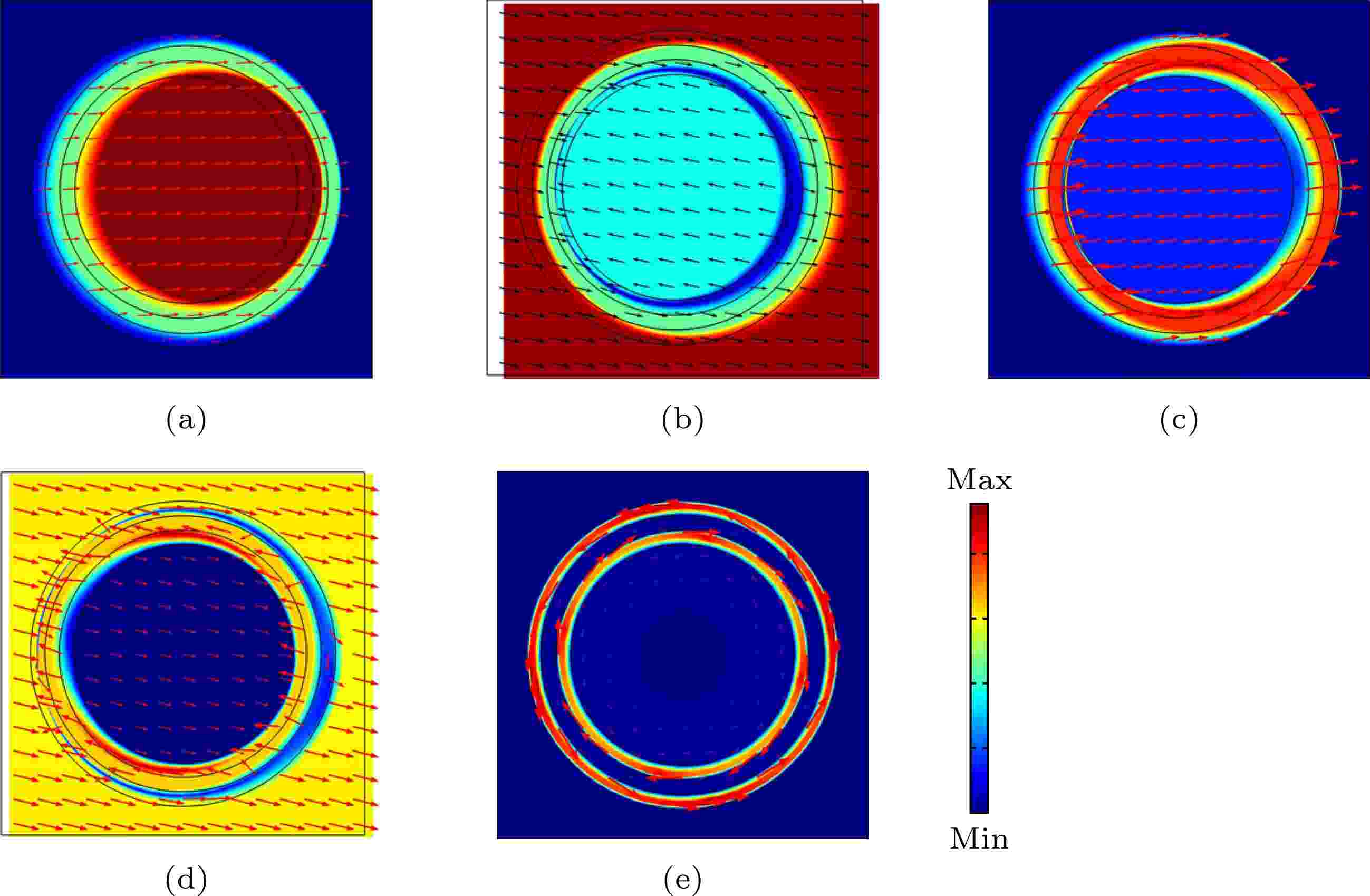图 8 双包覆层MRE声学超材料带隙边界处位移向量场　(a) 第一阶带隙下边界; (b) 第一阶带隙上边界; (c) 第二阶带隙下边界; (d) 第二阶带隙上边界; (e) 图7(a)中E点
Figure8. Displacement field of the band gap boundaries of the double-layer MRE acoustic metamaterial: (a) The lower boundary and (b) the upper boundary of the first band gaps; (c) the lower boundary and (d) the upper boundary of the second band gap; (e) point E in Fig.7 (a).

由以上分析可知, 声学超材料的带隙数量随着包覆层数量的增加而增多, 这是因为存在更多的局域共振模式. 带隙数量增多可以使声学超材料更好地应用于振动与噪声的控制.
由双包覆层MRE声学超材料的位移向量场, 可将双包覆层MRE声学超材料简化为如图9所示的质量-弹簧模型^[50], 可以用质量-弹簧模型进一步估算其带隙频率. 其中${m_1}$为元胞的芯体质量, ${m_2}$为壳体质量, ${m_3}$为基体质量, 弹簧${k_1}$和${k_2}$分别为MRE内、外包覆层的等效刚度, 其具体定义见文献[50]. 在双包覆层MRE声学超材料的两阶带隙下边界处, ${m_1}$和${m_2}$在弹簧${k_1}$和${k_2}$的作用下, 发生共振. 在两阶带隙上边界处, ${m_1}$, ${m_2}$和${m_3}$在弹簧${k_1}$和${k_2}$的作用下, 以相对振动的方式发生共振.
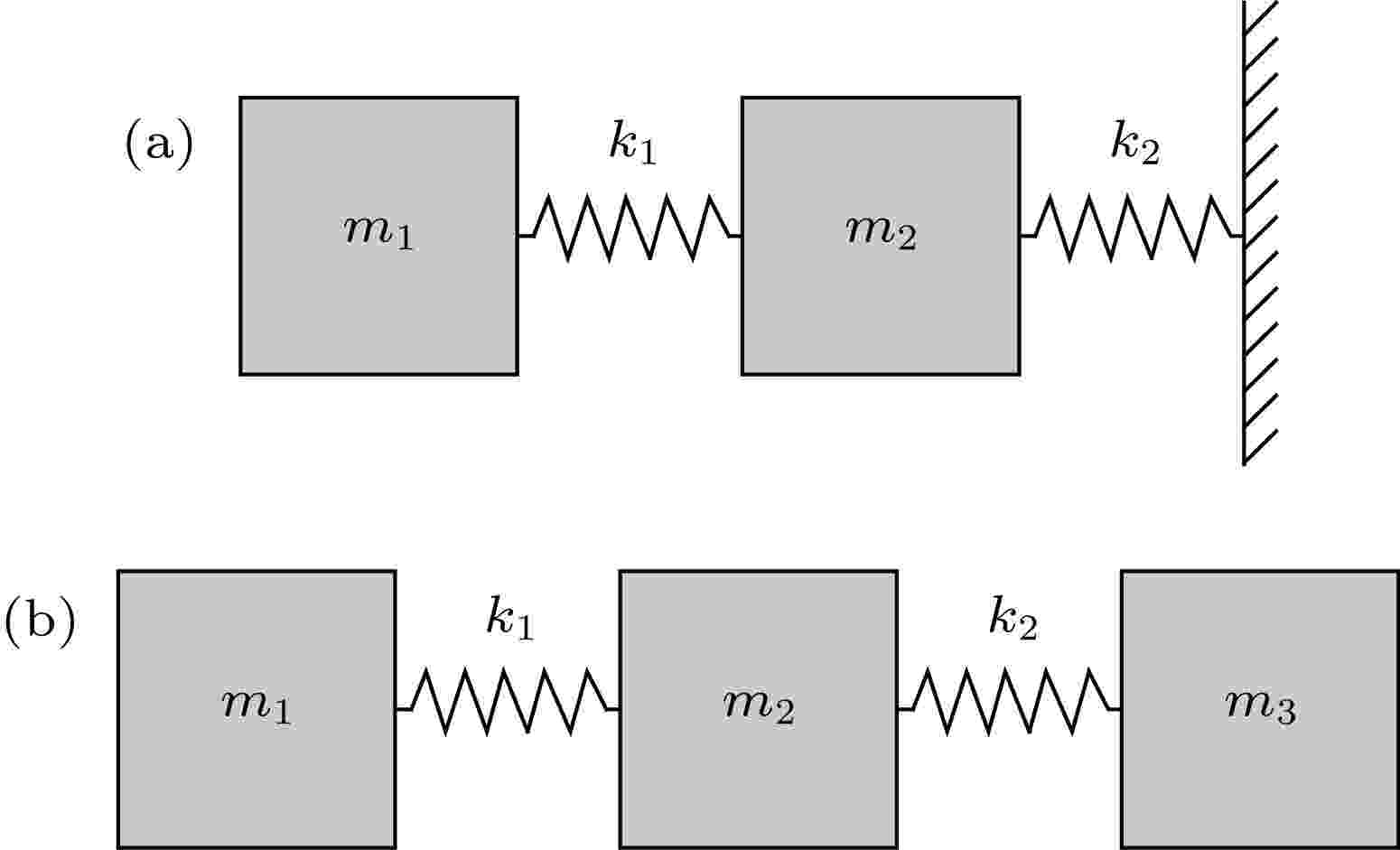图 9 双包覆层MRE声学超材料质量-弹簧模型　(a) 第一阶与第二阶带隙下边界; (b) 第一阶与第二阶带隙上边界
Figure9. The mass-spring model of the double-layer MRE acoustic metamaterial: (a) Lower boundary of the first and second band gap; (b) upper boundary of the first and second band gap.

图9(a)中质量-弹簧模型的刚度矩阵和质量矩阵为:

${{{K}}_1} = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - {k_1}} \\ { - {k_1}}&{{k_1} + {k_2}} \end{array}} \right],$

${{{M}}_1} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0 \\ 0&{{m_2}} \end{array}} \right].$

第一阶与第二阶带隙的下边界频率为

$\left| {{{{K}}_1} - f_{\rm{L}}^2{{{M}}_1}} \right| = 0.$

图9(b)中质量-弹簧模型的刚度和和质量矩阵为:

${{{K}}_2} = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{ - {k_1}}&0 \\ { - {k_1}}&{{k_1} + {k_2}}&{ - {k_2}} \\ 0&{ - {k_2}}&{{k_2}} \end{array}} \right],$

${{{M}}_2} = \left[ {\begin{array}{*{20}{c}} {{m_1}}&0&0 \\ 0&{{m_2}}&0 \\ 0&0&{{m_3}} \end{array}} \right].$

第一阶与第二阶带隙的上边界频率为

$\left| {{{{K}}_2} - f_{\rm{U}}^2{{{M}}_2}} \right| = 0.$

当磁场强度由0—10 kOe连续变化时, 双包覆层MRE声学超材料的带隙变化如图10(a)所示, 第一阶带隙频率从374—771 Hz变化到575—1187 Hz; 第二阶带隙频率从1365—1670 Hz变化到2099—2567 Hz. 由此可知, 随着磁场强度增强两阶带隙下边界与上边界频率都呈上升趋势, 带隙宽度增加, 这是因为内、外包覆层MRE的剪切模量随着磁场强度增强而增加.
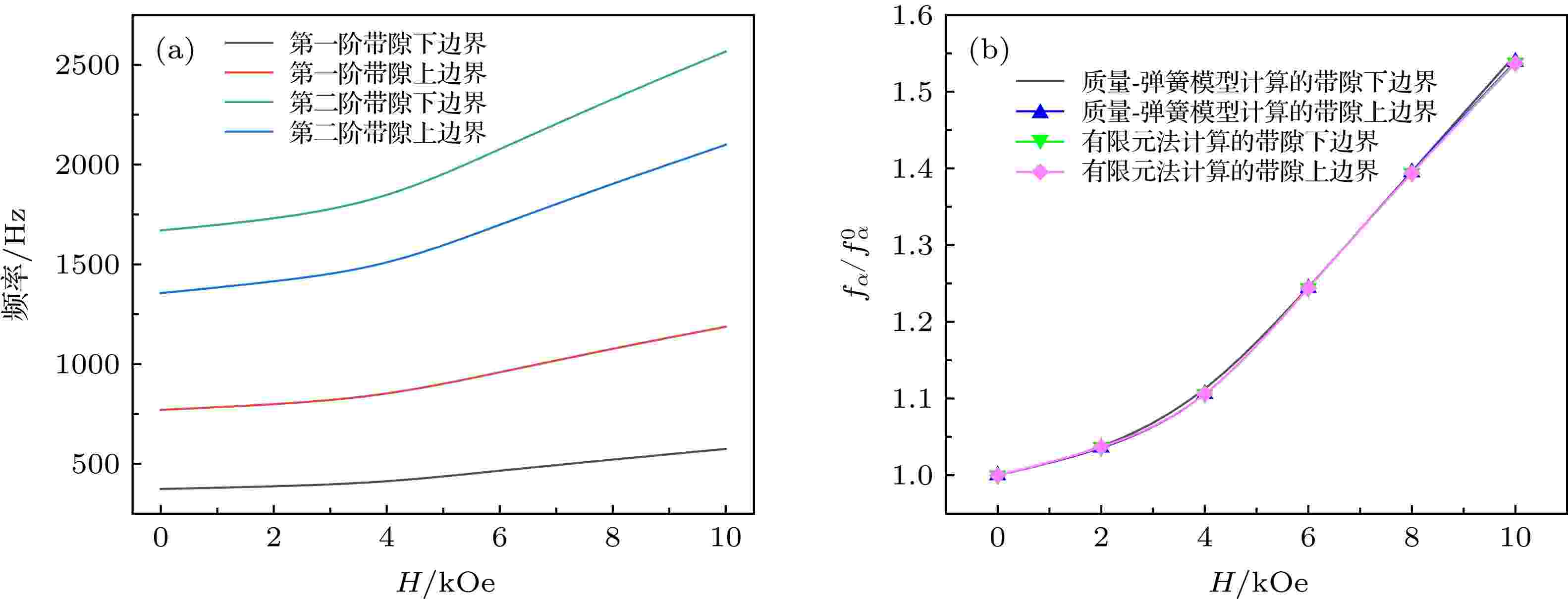图 10 双包覆层MRE声学超材料带隙随磁场强度变化及有限元法与质量-弹簧模型对比　(a) 磁场强度H = 0—10 kOe; (b) 有限元法与质量-弹簧模型对比
Figure10. Dependence of the band gap boundaries on the applied magnetic field of double-layer MRE acoustic metamaterial and a comparison of the FEM and mass-spring model for (a) magnetic field intensity of H = 0–10 kOe, (b) comparison of the FEM and mass-spring model.

由质量-弹簧模型计算的双包覆层MRE声学超材料的${{{f_\alpha }}/{f_\alpha ^0}}$随磁场强度变化曲线与有限元方法计算的${{{f_\alpha }}/{f_\alpha ^0}}$随磁场强度变化曲线的对比如图10(b)所示, 由对比图可以看到, 双包覆层MRE声学超材料的有限元计算结果与质量-弹簧模型方法也具有很好的一致性.
3 -->

3.2.2.芯体与壳体质量和填充率对带隙特性的影响

双包覆层MRE声学超材料的两阶带隙间存在带隙间隔(通带), 我们应该尽量缩小两阶带隙间的通带, 拓展其带隙宽度. 下面分析芯体质量、壳体质量、填充率对带隙频率以及两阶带隙间通带的影响.
当声学超材料的结构参数不变, 根据质量-弹簧模型, 芯体质量为${m_1}$, 壳体质量为${m_2}$. 采用控制变量法, 当壳体质量${m_2}$(选取密度较大的金属钨)不变时, 首先分析芯体质量${m_1}$变化对带隙的影响. ${m_1}$分别选取表2中的材料时, 声学超材料的带隙变化如图11(a)所示, 从图中可以看到, 当${m_1}$质量较小时, 带隙间通带宽度较窄, 第一阶带隙宽度较宽, 第二阶带隙宽度较窄. 随着芯体质量${m_1}$增加, 第一阶带隙的上边界频率和第二阶带隙的下边界频率都在逐渐减小, 而第一阶带隙的上边界频率减小幅度更大, 使带隙间的通带加宽. 结合位移向量场和质量弹簧模型的分析可知, 这是因为芯体质量主要影响第一阶带隙频率, 对第二阶带隙影响较小.
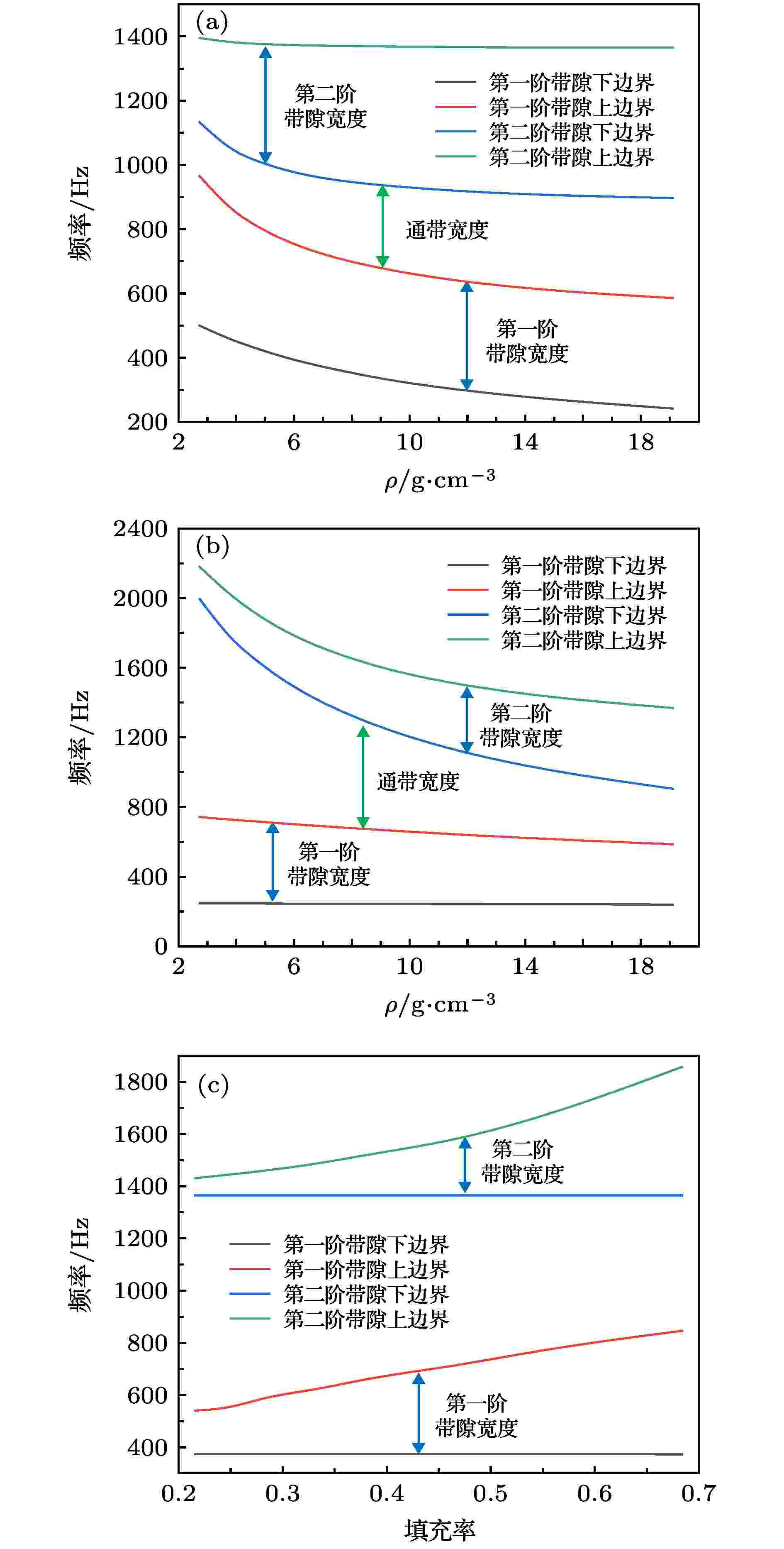图 11 双包覆层MRE声学超材料带隙随材料和结构参数变化　(a) 芯体质量增加; (b) 壳体质量增加; (c) 填充率增加
Figure11. The band gap of double-layer MRE acoustic metamaterial changes with (a) the core mass, (b) the shell mass, (c) the filling rate.

当芯体质量${m_1}$(材料为金属钨)不变, 壳体${m_2}$分别选取表2中的材料, 声学超材料的带隙变化如图11(b)所示, 从图中可以看到, 第一阶带隙的下边界频率基本不随壳体质量${m_2}$改变而变化, 第一阶带隙的上边界频率随壳体质量${m_2}$增加而有所降低; 第二阶带隙下边界频率和上边界频率都随着壳体质量${m_2}$增加而逐渐降低, 且带隙宽度增加. 由于第二阶带隙的下边界频率减小幅度大于第一阶带隙的上边界频率, 因此随着壳体质量${m_2}$增加, 带隙间的通带逐渐减小. 这是因为, 由于芯体质量$ {m_1} $不变, 所以第一阶带隙变化较小, 而壳体质量${m_2}$主要影响第二阶带隙, 致使第二阶带隙频率和宽度变化较大.
同样通过改变晶格常数, 对双包覆层MRE声学超材料带隙随填充率变化情况进行分析, 得到的结果如图11(c)所示. 随着填充率增加, 第一、二阶带隙的下边界频率基本保持不变, 第一阶带隙上边界频率有缓慢增加, 而第二阶带隙的上边界频率增加速度较快. 这是由于改变晶格尺寸, 相当于改变基体质量${m_3}$, 根据双包覆层MRE声学超材料的质量-弹簧模型, 改变基体质量主要影响第一阶与第二阶带隙的上边界频率. 增大填充率相当于减小基体质量, 因此第一阶与第二阶带隙上边界频率升高.
2 -->

3.3.传输谱

虽然声学超材料在其带隙频率范围内有完美的弹性波屏蔽效果, 但这是基于无限周期结构的结果. 而在实际应用中, 只能取有限周期结构, 这使得带隙频率范围内的某些弹性波无法被完全衰减, 仍然可以透过有限结构. 因此对于有限周期声学超材料还需要反映其结构中弹性波的传输特性. 下面采用$8 \times 8$周期结构对单、双包覆层MRE声学超材料的传输谱特性进行分析.
在声学和振动工程中, 传输谱的计算一般采用如下定义:

$T = 20\log \left( {\frac{{{p_2}}}{{{p_1}}}} \right),$

式中${p_1}$为入射端激励物理量, ${p_2}$为出射端激励物理量, 本文采用入射端和出射端加速度响应来研究声学超材料的传输谱特性.
3 -->

3.3.1.单包覆层MRE声学超材料传输谱特性

3 -->

3.3.1.1.磁场强度对传输谱的影响

图12(a)为磁场强度分别为0, 4, 6, 8 kOe时, 单包覆层MRE声学超材料的传输谱. 从图中可以发现, 在带隙频率范围内, 弹性波具有较大程度的衰减, 在高频窄带隙处同样存在传输损失. 同时随着磁场强度增强, 传输谱的最大衰减频率向高频移动, 与磁场强度增强带隙频率升高相一致. 从图中还可以看到, 随着磁场强度增强传输损失也呈增加趋势. 这是由于磁场强度增强, 改变了MRE的剪切模量, 使其对弹性波的阻抗效应增大. 因此, 使用MRE作为声学超材料的包覆层不但在磁场作用下使声学超材料的带隙频率和宽度可调, 还可以增大对弹性波的衰减作用, 使声学超材料具有更好的传输特性.
图 12 单包覆层MRE声学超材料传输谱变化　(a) 磁场强度为0, 4, 6, 8 kOe; (b) 芯体材料分别为铝、钛、铜、铅和钨; (c) 填充率增加
Figure12. Transmission spectra of single-layer MRE acoustic metamaterial change with (a) At magnetic field intensity of 0, 4, 6, and 8 kOe, (b) core materials for aluminum, titanium, copper, lead, and tungsten, (c) the filling rate.

3 -->

3.3.1.2.芯体材料和填充率对传输谱的影响

当芯体分别选用表2中的材料时, 单MRE声学超材料的传输谱如图12(b)所示, 可以看到材料的密度从小到大变化时, 传输谱的最大衰减频率由高频向低频移动, 与带隙频率随芯体质量变化趋势一致. 芯体材料不同时, 最大衰减量不同, 芯体材料为铅时衰减量最大, 材料为钨时衰减量最小. 从图中可以发现, 随着材料的弹性模量增加最大衰减量呈减小趋势, 这是由于随着芯体材料变硬, 对弹性波阻抗效应变小所致. 因此可以得出, 当其他参数不变时, 单包覆层MRE声学超材料传输谱的最大衰减量与芯体材料的弹性模量相关, 当芯体材料的弹性模量较小材料较软时, 最大衰减量增加; 当芯体材料的弹性模量较大材料较硬时, 最大衰减量减小.
图12(c)为不同填充率单包覆层MRE声学超材料的传输谱, 可以看到, 随着晶格常数增大填充率减小, 传输谱的最大衰减频率没有变化. 这是因为, 随着填充率减小带隙下边界频率基本没有变化, 而传输谱的最大衰减量发生在带隙的起始频率处. 但是, 传输谱的最大衰减量随着晶格常数增大填充率减小而减小, 这是由于填充率减小晶格常数变大, 基体质量增加, 发生局域共振时使局域共振单元的振幅减小, 削弱了其对弹性波的衰减.
3 -->

3.3.2.双包覆层MRE声学超材料传输谱特性

3 -->

3.3.2.1.磁场强度对传输谱的影响

图13(a)为磁场强度分别为0, 4, 6, 8 kOe时, 双包覆层MRE声学超材料的传输谱. 从图中可以发现, 在第一阶与第二阶带隙频率范围内, 弹性波具有较大程度衰减, 在带隙起始频率处衰减最大, 与单包覆层MRE声学超材料传输谱类似; 随着磁场强度增强, 传输谱的最大衰减频率向高频移动, 这也与磁场强度增强时带隙频率升高相一致. 从图13(a)中还可以看到, 随着磁场强度增强传输损失也呈增加趋势, 这也是因为磁场强度增强使MRE阻抗增强的原因.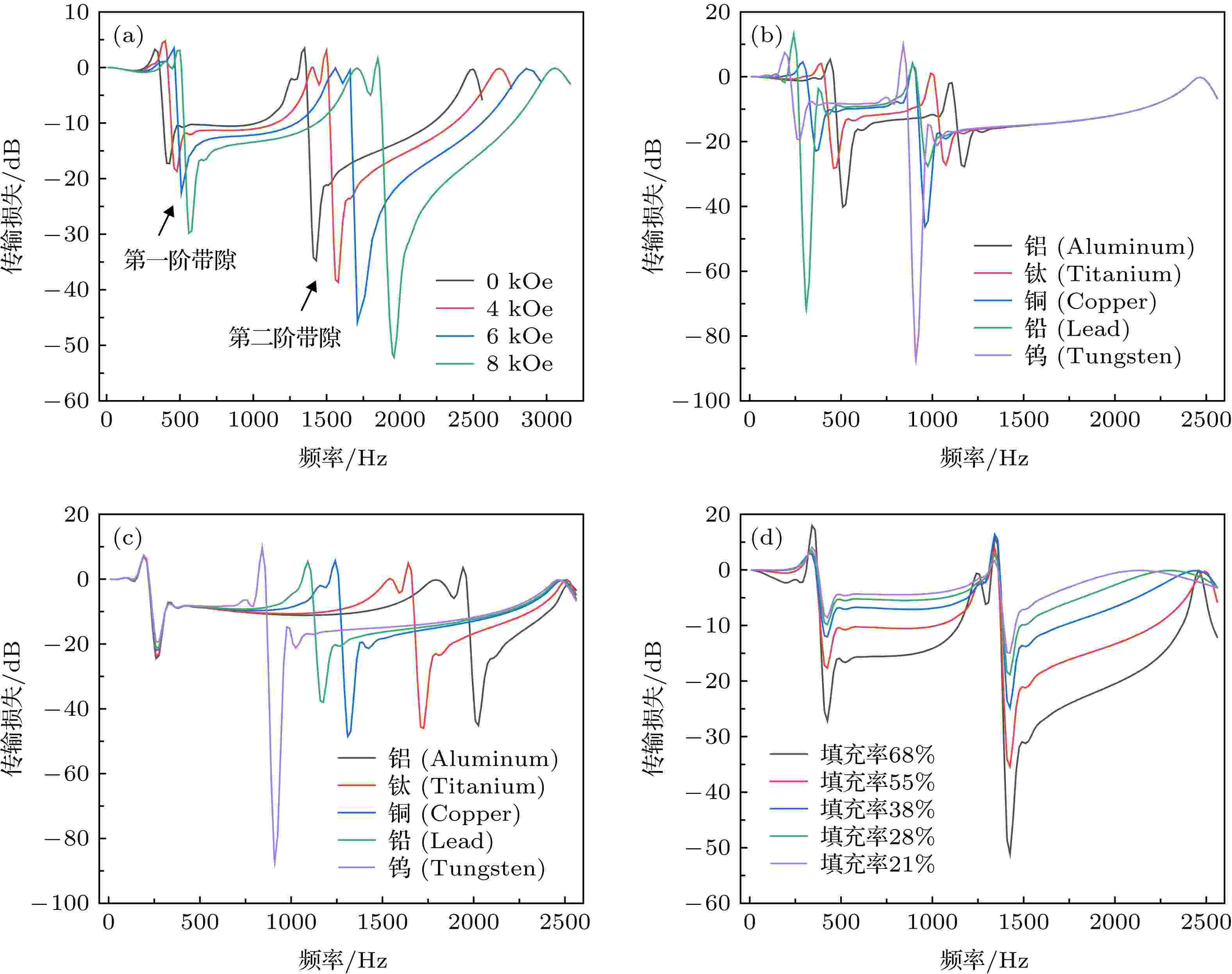
图 13 双包覆层MRE声学超材料传输谱变化　(a) 磁场强度为0, 4, 6, 8 kOe; (b) 芯体材料分别为铝、钛、铜、铅和钨; (c) 壳体材料分别为铝、钛、铜、铅和钨; (d) 随填充率变化
Figure13. Transmission spectra change of double-layer MRE acoustic metamaterial: (a) At the magnetic field intensity of 0, 4, 6, and 8 kOe; (b) with the core materials for aluminum, titanium, copper, lead, and tungsten, (c) with the shell materials of aluminum, titanium, copper, lead, and tungsten, (d) with filling rate.

3 -->

3.3.2.2.芯体与壳体材料和填充率对传输谱的影响

采用控制变量法, 当壳体材料不变时(材料为金属钨), 芯体选用表2中的材料时, 双包覆层MRE声学超材料的传输谱如图13(b)所示. 从图中可以看到, 传输谱的最大衰减频率随着芯体密度增加向低频移动, 与带隙频率变化趋势相同. 同时, 第一阶带隙的最大衰减量, 随着芯体材料弹性模量的增加而减小, 这与单包覆层MRE声学超材料传输谱的最大衰减量随材料弹性模量的变化趋势相同; 第二阶带隙的最大衰减量随着芯体材料弹性模量的增加而增大. 由此可以得出, 当壳体材料参数不变时, 芯体材料的弹性参数主要影响第一阶与第二阶带隙的传输损失, 且与第一阶带隙的传输损失成反比, 与第二阶带隙的传输损失成正比.
当芯体材料不变时(材料为金属钨), 壳体为表2中材料时, 双包覆层MRE声学超材料的传输谱如图13(c)所示. 从图中可以看到, 第一阶带隙的最大衰减频率没有变化, 这是由于芯体质量不变第一阶带隙的下边界频率基本没有变化, 而声学超材料的最大衰减频率发生在带隙的起始频率处; 第二阶带隙的最大衰减频率随着壳体材料密度增加向低频移动, 这也与壳体材料密度增加带隙频率变化趋势一致. 同时, 由于芯体材料不变, 第一阶带隙的最大衰减量基本没有变化, 第二阶带隙的最大衰减量只有当壳体材料为钨时衰减较大, 而壳体材料为其他四种材料时最大衰减量相差不大. 由双包覆层MRE声学超材料的位移向量场可知, 在第二阶带隙边界处主要为壳体和包覆层振动, 由于壳体较薄, 质量较轻, 因此除材料钨以外, 另外四种材料对弹性波的衰减量相差不大.
图13(d)为不同填充率时双包覆层MRE声学超材料的传输谱. 从图中可以看到, 随着晶格常数增大填充率减小, 第一阶带隙与第二阶带隙的最大衰减频率没有变化, 这是因为随着填充率变化, 第一阶与第二阶带隙的下边界频率基本不变. 同时, 最大衰减量随着填充率减小而减小, 这也是由于填充率减小, 晶格常数变大, 基体质量增加, 发生局域共振时使局域共振单元的振幅减小, 削弱了对弹性波的衰减.

本文深入分析了单、双包覆层MRE声学超材料在磁场作用下的可调带隙以及传输谱特性. 通过改变作用于MRE包覆层的磁场强度可以调节单、双包覆层MRE声学超材料的带隙结构. 随着磁场强度增强, 单、双包覆层MRE声学超材料的带隙频率和带隙宽度都随之增加. 采用质量-弹簧模型对单、双包覆层MRE声学超材料的带隙频率进行了计算, 仿真结果与两种质量-弹簧模型的计算结果具有很好的一致性. 同时对单、双包覆层MRE声学超材料在磁场作用下的传输谱特性进行了分析, 随着磁场强度增强, 单、双包覆层MRE声学超材料传输谱的最大衰减频率向高频移动, 同时最大衰减量也随之增加. 讨论了单、双包覆层MRE声学超材料的芯体、壳体的材料参数以及填充率对带隙以及传输谱的影响. 结果表明, 芯体和壳体的质量主要影响带隙频率和带隙宽度. 对于单包覆层MRE声学超材料, 随着芯体质量增加其带隙频率下降, 带隙宽度增加. 对于双包覆层MRE声学超材料, 当壳体质量不变, 随着芯体质量增加, 两阶带隙间的通带宽度逐渐增加, 两阶带隙的宽度增大, 带隙频率降低; 当芯体质量不变, 随着壳体质量增加, 两阶带隙间的通带宽度逐渐减小, 第一阶带隙宽度减小, 第二阶带隙宽度增大, 带隙频率降低. 芯体和壳体的弹性参数主要影响传输谱的传输损失. 单包覆层MRE声学超材料, 芯体材料的弹性参数与带隙的传输损失成反比. 双包覆层MRE声学超材料, 芯体材料的弹性参数与第一阶带隙的传输损失成反比, 第二阶带隙的传输损失成正比; 壳体材料弹性参数对传输损失的影响较小. 随着填充率增大, 单、双包覆层MRE声学超材料的带隙频率和宽度都相应增加; 传输谱最大衰减频率不变, 传输损失增大. 声学超材料的带隙和传输谱特性研究, 可为声学超材料在低频振动与噪声控制方面提供理论基础.