摘要:利用强场近似理论开展了基于正交偏振场的双光学控制脉冲与氦原子相互作用产生高次谐波和阿秒脉冲发射的理论研究. 这里的正交偏振场由具有一定时间延迟、振幅相等且呈正交偏振的两束线偏振脉冲构成, 双光学控制脉冲是在正交偏振场的驱动脉冲电场方向附加一束线偏振二次谐波脉冲. 研究发现, 若合理地调整正交偏振场中两束线偏振脉冲之间的时间延迟及附加二次谐波场与驱动脉冲电场之间的相对相位, 可得到效率较高且在整个平台区及截止位置附近皆连续的高次谐波发射谱, 傅里叶变换后实现了143 as孤立短脉冲的辐射. 相比于利用两束反旋圆偏振脉冲附加二次谐波场的双光学控制方案, 该方案不仅克服了对入射驱动脉冲脉宽和强度的限制, 而且避免了偏振门前端光学周期引起的气体介质电离不利于谐波相位匹配的弊端.
关键词: 高次谐波/
阿秒脉冲/
正交偏振场/
双光学控制

English Abstract

全文HTML

--> --> -->

阿秒脉冲开辟了探索原子和分子内部超快电子动力学的新途径和前所未有的时间分辨研究^[1-3], 是当前科学中较受关注的前沿课题之一. 强激光场与原子或分子体系相互作用产生的高次谐波发射是当前获得极紫外波段阿秒脉冲链或孤立阿秒脉冲唯一有效手段^[4-6]. 该过程通常由众所周知的半经典三步模型给出合理解释^[7,8]: 电子首先隧穿通过由原子势和强电场形成的势垒, 电离后的电子随后被强电场加速并获得很大能量, 最后被拉回到母离子附近与其复合, 并发出频率等于$\hbar {\omega _{{\rm{max}}}} = {I_{\rm p}} +$$ 3.17{E_{{\rm{kin}}}} $的谐波光子. 这里I_p是原子的电离势, E_kin为电子与原子基态复合时具有的动能.
基于高次谐波产生, 孤立阿秒脉冲已在少数实验室通过少周期驱动脉冲振幅控制方案^[9,10]、电离控制方案^[11]、偏振控制方案^[12-14]、阿秒灯塔^[15]以及双色脉冲方案^[16,17]实现. 迄今为止, 瑞士苏黎世联邦理工学院Gaumnitz等^[18]利用振幅控制技术已实现了最短43 as孤立短脉冲的产生.
偏振控制方案主要是利用高次谐波强度对激光偏振状态敏感的特性获得孤立阿秒脉冲产生. 基于偏振脉冲的椭偏率为0.2时的高次谐波强度比线偏振光情形减少一个数量级, Corkum等^[12]提出利用两束反向旋转的圆偏振脉冲作为驱动脉冲用于高次谐波发射, 通过调整两束反旋脉冲之间的时间延迟控制驱动脉冲光场在脉冲中心的半个光学周期的时间窗口形成线性偏振的偏振门, 从而可获得单一阿秒脉冲的发射. 该方案于2006年在实验上首次实现, 且获得了能量为70 pJ, 脉宽为130 as的孤立短脉冲^[19]. 实际上, 这种方案具有一定局限性, 在偏振门到达前的圆偏振光或者椭圆偏振光引起的气体介质电离同时限制了驱动激光的脉冲持续时间和强度.
鉴于Corkum等^[12]提出的偏振控制方案在高次谐波产生过程中的局限性, 本文提出了一种新的偏振控制方案, 即将驱动脉冲激光的偏振态从线性偏振变化到椭圆偏振之后再回到线性偏振. 该技术可通过以下方式实现, 将一束线偏振脉冲激光传播通过石英晶体, 它将分成具有不同传播速度, 相同或不同电场强度的两束线性正交偏振脉冲. 若合理调整石英晶体光轴与入射脉冲偏振方向之间的夹角以及石英晶体的厚度, 可得到两束具有相同电场强度, 垂直偏振方向且具有一定时间延迟的输出脉冲(通过改变石英晶体的厚度和角度, 理论上可以得到任意时间延迟的两束正交偏振脉冲). 该合成电场在脉冲的前沿和后沿呈现出线性偏振而在脉冲的中间部分呈现出椭球偏振的特点. 由于椭球偏振场不能获得有效高次谐波发射, 因此谐波产生主要来源于脉冲前沿和后沿的线偏振部分电场, 我们称之为正交偏振控制方案. 这里, 由于x方向电场结束时y方向电场强度也已减弱, 原子的低电离概率与原子基态布居衰退共同作用使得y方向产生的谐波强度明显低于x方向, 这样仅需考虑脉冲前沿的线偏振电场贡献给高次谐波产生, 因此有望得到有效孤立阿秒脉冲的产生. 在此基础上, 考虑到脉冲激光两个相邻半个光学周期峰值振幅差异对高次谐波超连续谱的影响, 我们在上述偏振控制脉冲电场的x方向附加了一束二次谐波脉冲, 其目的是使两个相邻半个光学周期电场的振幅发生急剧变化, 使得来自最高半个光学周期及第二高半个周期之间增加的截止位置差支持获得超短阿秒脉冲产生的宽带极紫外(extreme ultra-violet, XUV)连续谱. 由于本文方案同时利用了正交偏振控制和二次谐波控制, 因此称其为基于正交偏振场的双光学控制方案. 很显然, 该方案与Zhao等^[20]提出的双光学控制方案不同. 他们的方案是在两束反向旋转的圆偏振控制脉冲的驱动脉冲电场方向附加一束二次谐波脉冲, 其目的是将脉冲中间部分线性偏振的偏振门从半个光学周期调整到一个光学周期, 在一定程度上释放了入射脉冲的持续时间和强度限制, 因此他们利用脉宽为7 fs入射驱动脉冲最终得到了67 as的孤立短脉冲. 然而, 在两束反旋圆偏振脉冲电场中附加二次谐波的双光学控制方案大幅增加了实验操作的困难, 更重要的是, 偏振门前端的椭球偏振激光场引起气体介质电离不利于谐波在传播过程中的相位匹配条件. 研究发现, 当采用惰性气体原子作为谐波产生介质时, 只有当靶原子电离概率为百分之几时才能实现谐波的相位匹配条件. 为了满足该条件, 在偏振控制方案中需要采用较弱的入射驱动脉冲, 从而限制了偏振门内产生谐波的截止位置和强度. 我们提出的方案在谐波传播这个环节与电离控制方案相似, 都是基于被强电场诱导的瞬时相位匹配^[21], 即介质被驱动脉冲前沿电场电离且产生一个致密的等离子体, 该等离子体抑制随后产生的XUV脉冲与驱动脉冲之间的相位匹配, 由瞬时相位匹配引起高次谐波时间限制的实验证据在文献[22—24]中被报道.

本文采用 Lewenstein 强场近似模型理论数值模拟了氦原子在双光学控制脉冲辐照下的高次谐波发射谱^[25-27], 由于激光脉冲的椭偏率随时间变化, 因此需要分别计算x, y两个不同方向上的偶极矩. 先前研究工作已经表明, 沿y方向谐波谱的强度远低于沿x方向的谐波谱强度^[28]. 因此, 我们只需要计算x方向上的谐波发射谱. 在外部场中电子的含时偶极矩^[29]可以描述为(除非特殊说明, 否则本文中均采用原子单位):

$\begin{split}{d_{nl}}\left( t \right) \approx\, & {\rm{i}}\mathop \int \nolimits_{ - \infty }^t {\rm{d}}t'{\left[ {\frac{{\text{π}}}{{\varepsilon + {\rm{i}}\left( {t - t'} \right)/2}}} \right]^{3/2}}\\& \times{d_x}^{\rm{*}}\left[ {{{{p}}_{{\rm{st}}}}\left( {t',t} \right) - {{A}}\left( t \right)} \right] \\& \times\exp \left[ { - {\rm{i}}{S_{{\rm{st}}}}\left( {{{{p}}_{{\rm{st}}}},{t^{\rm{'}}},t} \right)} \right]{{d}}\left[ {{{{p}}_{{\rm{st}}}}\left( {t',t} \right) - {{A}}\left( {t'} \right)} \right] \\& \times{{E}}\left( {t'} \right)g\left( t \right) + {\rm{c}}.{\rm{c}}..\end{split}$

这里ε是一个非常小的正数; ${{A}}\left( t \right)$和${{E}}\left( t \right)$是脉冲激光的矢势和电场; ${d_x}^{\rm{*}}\left[ {{{{p}}_{{\rm{st}}}}\left( {t',t} \right) - {{A}}\left( t \right)} \right]$代表电子从连续态跃迁回基态的过程, ${{d}}\left[ {{{{p}}_{{\rm{st}}}}\left( {t',t} \right) - {{A}}\left( {t'} \right)} \right]$代表的是电子的电离过程; 基态布居数$g\left( t \right) = $${\rm{exp}}[ - \mathop \int \nolimits_{ - \infty }^t {\omega _{{\rm{ADK}}}}\left( {t''} \right){\rm{d}}{t^{{\rm{''}}}}]$, 其中电离速率${\omega _{{\rm{ADK}}}}\left( {t''} \right)$由Ammosov-Delone-Krainov (ADK)理论计算而得^[30].
在(1)式中, 与电子定态相位相关的正则动量p_st和准经典作用量S_st表示如下:

${{{p}}_{{\rm{st}}}}\left( {t',t} \right) = \frac{1}{{t - t'}}\mathop \int \nolimits_{t'}^t {{A}}(t''){\rm{d}}t'',$

$\begin{split}{S_{{\rm{st}}}}\left( {{{{p}}_{{\rm{st}}}},{t^{\rm{'}}},t} \right) = & \left( {t - {t^{\rm{'}}}} \right){I_{\rm{p}}} - \frac{1}{2}{p_{{\rm{st}}}}^2\left( {t',t} \right) \left( {t - t'} \right) \\ &+ \frac{1}{2}\mathop \int \nolimits_{t'}^t {A^2}({t^{''}}){\rm{d}}t'',\end{split}$

而类氢原子电偶极近似值可以表示为

${{d}}\left( {{p}} \right) = {\rm{i}}\frac{{{2^{7/2}}{{\left( {2{I_{\rm{p}}}} \right)}^{5/4}}}}{{\text{π}}}\frac{{{p}}}{{{{\left( {{p^2} + 2{I_{\rm{p}}}} \right)}^3}}}.$

根据ADK隧穿电离理论模型, 在(1)式中基态电子的耗尽情况可以根据如下电离速率的公式计算给出:

${\omega _{{\rm{ADK}}}}\left( t \right) = {\omega _{\rm{p}}}{\left| {{C_{{n^*}}}} \right|^2}{\left( {\frac{{4{\omega _{\rm{p}}}}}{{{\omega _t}}}} \right)^{2{n^*} - 1}}{\rm{exp}}\left( { - \frac{{4{\omega _{\rm{p}}}}}{{3{\omega _t}}}} \right),$

这里${\omega _{\rm{p}}} = {I_{\rm{p}}}$, 价电子的有效主量子数${n^{\rm{*}}} = $$ Z{\left( {\dfrac{{{I_{{\rm{ph}}}}}}{{{I_{\rm{p}}}}}} \right)^{1/2}}$, ${\omega _t} = \dfrac{{\left| {E\left( t \right)} \right|}}{{\sqrt {2{I_{\rm{p}}}} }}$及${\left| {{C_{{n^{\rm{*}}}}}} \right|^2} = \dfrac{{{2^{2{n^{\rm{*}}}}}}}{{{n^{{{*\varGamma }}\left( {{n^{\rm{*}}} + 1} \right){\varGamma}\left( {{n^{\rm{*}}}} \right)}}}},$ 其中Z是氦原子的净电荷, I_ph是氢原子的电离势.
偶极加速度由含时偶极矩$a\left( t \right) = \dfrac{{{{\rm{d}}^2}}}{{{\rm{d}}{t^2}}}{d_{nl}}\left( t \right)$给出. 通过对偶极加速度做傅里叶变换可以求得单个原子高次谐波发射谱的强度

${P_{\rm{A}}}\left( \omega \right) = {\left| {\frac{1}{{{t_{\rm{f}}} - {t_{\rm{i}}}}}\frac{1}{{{\omega ^2}}}\mathop \int \nolimits_{{t_{\rm{i}}}}^{{t_{\rm{f}}}} a\left( t \right){{\rm{e}}^{ - {\rm{i}}\omega t}}{\rm{d}}t} \right|^2},$

其中t_f是电子与原子核的复合时刻, t_i是电子的电离时刻. 最后通过叠加谐波谱上超连续谐波可合成超短阿秒脉冲, 其公式为

$I\left( t \right) = {\left| {\mathop \sum \nolimits_q {a_q}{{\rm e}^{ - {\rm{i}}q\omega t}}} \right|^2},$

式中q为谐波阶次, ${a_q} = \mathop \int \nolimits^ a\left( t \right){{\rm e}^{ - {\rm{i}}q\omega t}}{\rm{d}}t$.

在本文数值模拟计算中, 组合脉冲电场由具有一定时间延迟的正交线偏振电场叠加其二次谐波场构成. 椭偏率随时间变化的组合脉冲电场形式为${{E}}\left( t \right) = {E_{{\rm{drive}}}}\left( t \right){{x}} + {E_{{\rm{gate}}}}\left( t \right){{y}}$, 其中控制脉冲和驱动脉冲电场的具体形式分别为

${E_{{\rm{gate}}}}\left( t \right) = {E_0}{f_y}\left( t \right)\cos \left( {{\omega _0}t + {\phi _{{\rm{CEP}}}}} \right),$

${E_{{\rm{drive}}}}\left( t \right) = {E_0}{f_x}\left( t \right)\cos \left( {{\omega _0}t \!+ {\phi _{{\rm{CEP}}}} \!+ {\phi _{{\rm{td}}}}} \right) + {E_{{\rm{second}}}}\left( t \right),$

${E_{{\rm{second}}}}\left( t \right) = a{E_0}{f_x}\left( t \right){\rm{cos}}\left( {2{\omega _0}t + {\phi _{{\rm{CEP}}}} + {\phi _{{\rm{td}}}} + \varphi } \right),$

式中E₀和ω₀分别表示钛宝石脉冲激光通过石英晶体后的两束等振幅正交线偏振电场的峰值强度和频率, 初始载波包络相位${\phi _{{\rm{CEP}}}} = 0$. 正交线偏 振场的脉冲包络函数${f_x}\left( t \right) = {{\rm{e}}^{ - 2{\rm{ln}}2{{\left( {t + td/2} \right)}^2}/\tau _x^2}}$和${f_y}\left( t \right) = {{\rm{e}}^{ - 2{\rm{ln}}2{{\left( {t - td/2} \right)}^2}/\tau _y^2}}$, 其中τ_x和τ_y分别是正交线偏振场x和y方向电场的脉冲宽度(半高全宽), td是x和y方向电场峰值之间的时间延迟, 由此导致两束脉冲之间的相位差${\phi _{{\rm{td}}}} = td \times {\omega _0}$. 附加二次谐波场公式(10)中的a为比例系数, 表示与x方向钛宝石脉冲电场峰值强度的比值, φ为x方向两束线偏振脉冲之间的相位差.
图1(a)展示了入射线偏振脉冲激光传播通过石英晶体后得到的具有一定时间延迟、正交偏振方向且振幅相等的两束线偏振脉冲随时间的变化. 这里两束线偏振脉冲电场峰值之间的时间延迟取为1.9T₀ (T₀是钛宝石脉冲的光学周期), 两束脉冲的峰值振幅E₀取为0.2 a.u., 入射脉冲的脉宽取为4 fs. 图中的红色实线、蓝色实线和绿色实线依此给出了总电场、x方向和y方向线偏振电场随时间的变化. 从图1(a)可以看出, x方向电场的前沿和y方向电场的后沿是线性偏振的, 而中间部分电场是椭球性随时间变化的椭圆偏振场. 很显然, 在该电场作用下, 只有脉冲前沿的光脉冲能够产生有效高次谐波发射. 考虑到脉冲激光两个相邻半个光学周期峰值振幅差异对高次谐波超连续谱的影响, 在图1(a)的基础上附加了二次谐波脉冲, 如图1(b)所示. 这里二次谐波脉冲与基频脉冲之间的相位差取为0.5π, 二次谐波脉冲的峰值强度取为0.3E₀, 脉宽同样取为4 fs. 为了细致地分析附加二次谐波脉冲后电场的变化情况, 图1(c)和图1(d)分别给出了附加二次谐波场前后x方向驱动脉冲光强随时间的变化. 由于y方向线偏振脉冲与x方向线偏振脉冲之间的时间延迟取为1.9T₀, 图1(c)和图1(d)中只有A, B, C, D四个峰值区域是处于线偏振区域. 对比图1(c)和图1(d)可以发现, 附加二次谐波场后, A的峰值强度不变, B的强度明显变小, 而C的峰值强度大幅增加, D的强度基本不变. 此时, 从A和B附近电离的电子概率很小, 对谐波谱有很小的影响. 谐波产生主要来源于从C附近电离电子在随后电场D作用下加速而得到的, 因此有望得到效率较高且呈现宽带超连续特点的谐波谱. 相比较而言, 在图1(c)中电场作用下, 由于峰值B和C电离的电子在随后半个光学周期电场作用下对谐波谱皆有重要贡献, 因此将会得到具有干涉特征的不规则结构谐波谱.
图 1 (a)驱动脉冲电场中未加二次谐波场、(b)加入二次谐波场情况下, 偏振控制脉冲总电场(红色曲线)、控制(绿色曲线)及驱动脉冲电场(黑色曲线)随时间变化三维图; (c)未加入二次谐波场、(d)加入二次谐波场情况下, 驱动脉冲电场光强随时间变化曲线图
Figure1. Three-dimensional diagrams for the total electric field (red line), gating field (black line) and driving field (green line) in polarization gating pulse as a function of time: (a) Orthogonal polarization field; (b) double optical gating field. The change of laser intensity in x-polarized direction with time: (c) Orthogonal polarization field; (d) double optical gating field.

图2中红色实线给出了双光学控制脉冲电场辐照氦原子得到的高次谐波发射谱. 从图2可以看出, 谐波频谱的截止频率接近160次谐波, 且整个平台区及截止位置都呈现规则分布的超连续特点. 作为比较, 也给出了未叠加二次谐波场的正交偏振控制脉冲与氦原子相互作用得到的高次谐波发射谱, 如图2中黑色实线所示. 数值模拟过程中除驱动脉冲电场中未加入二次谐波电场外, 其余脉冲电场参数不变. 从图2可以明显的看出, 谐波频谱的截止频率虽达到了185次, 但具有规则结构的平台宽度约为35次, 特别需要注意的是整个谐波平台效率低了2个数量级. 可见, 二次谐波电场的加入, 不仅拓宽了平台区超连续谱的带宽, 且大幅提高了谐波谱平台的效率, 与上述通过电场分析预测的结果是一致的.
图 2 脉宽为4 fs的偏振控制脉冲激光与氦原子相互作用得到的高次谐波发射谱, 其中红线对应于双光学控制方案, 黑线对应于正交偏振控制方案
Figure2. High order harmonic generation from helium atom irradiated by the polarization gating pulse with 4 fs pulse width. Red line corresponds to the double optical gating scheme; black line corresponds to the orthogonal polarization gating scheme.

接下来我们从电场、原子电离速率以及半经典三步模型理论详细分析上述谐波谱所呈现出来的特点. 图3(a)和图3(b)分别展示了附加二次谐波场前后x和y方向线偏振电场及原子电离速率随时间的变化. 图中黑色曲线是x方向驱动脉冲电场, 红色曲线是y方向控制脉冲电场, 蓝色填充区域是由ADK模型计算得到的氦原子电离速率(填充区域面积物理意义为电子的电离量). 可以看到, 电场峰值位置D以后的脉冲激光具有椭球性质, 不能用来产生有效高次谐波发射. 图3(c)和图3(d)分别给出了利用半经典三步模型理论计算得到的附加二次谐波场前后不同时刻电离电子的复合时刻及该时刻电子具有的动能. 其中黑色点线表示的是电子的电离时刻, 红色点线表示的是复合时刻. 从图3(b)和图3(d)可以看出, 未叠加二次谐波场时, 在电场峰值位置A, B和C附近电离的电子与母离子复合时能够产生最大截止位置时的谐波次数分别为75次、150次和185次. 由于峰值A附近电子电离量几乎为0, 故对谐波形成贡献不大, 而另外两个峰值B, C位置电离的电子产生谐波相互干涉仅能得到约35次超连续谱的谐波谱. 相反, 图3(a)和图3(c)给出了附加二次谐波场的双光学控制方案下的结果, 从图3(c)可以看出, 电场峰值对应的电离时刻有A, B和C, 而在图3(a)可以明显看到, 峰值A和B附近电子的电离量几乎为0, 所以它们对谐波谱基本没有贡献, 高次谐波的产生主要来源于从峰值位置C附近电离电子在随后电场的加速下得到的. 由于二次谐波场的增加, C的峰值强度大幅增加, 从图3(a)可以看到, 峰值C附近电子的电离量明显高于没有附加二次谐波场的情形, 因此得到了图2中红色曲线所展示的超连续谱带宽大幅增加且谐波谱平台区效率提高2个数量级的结论.
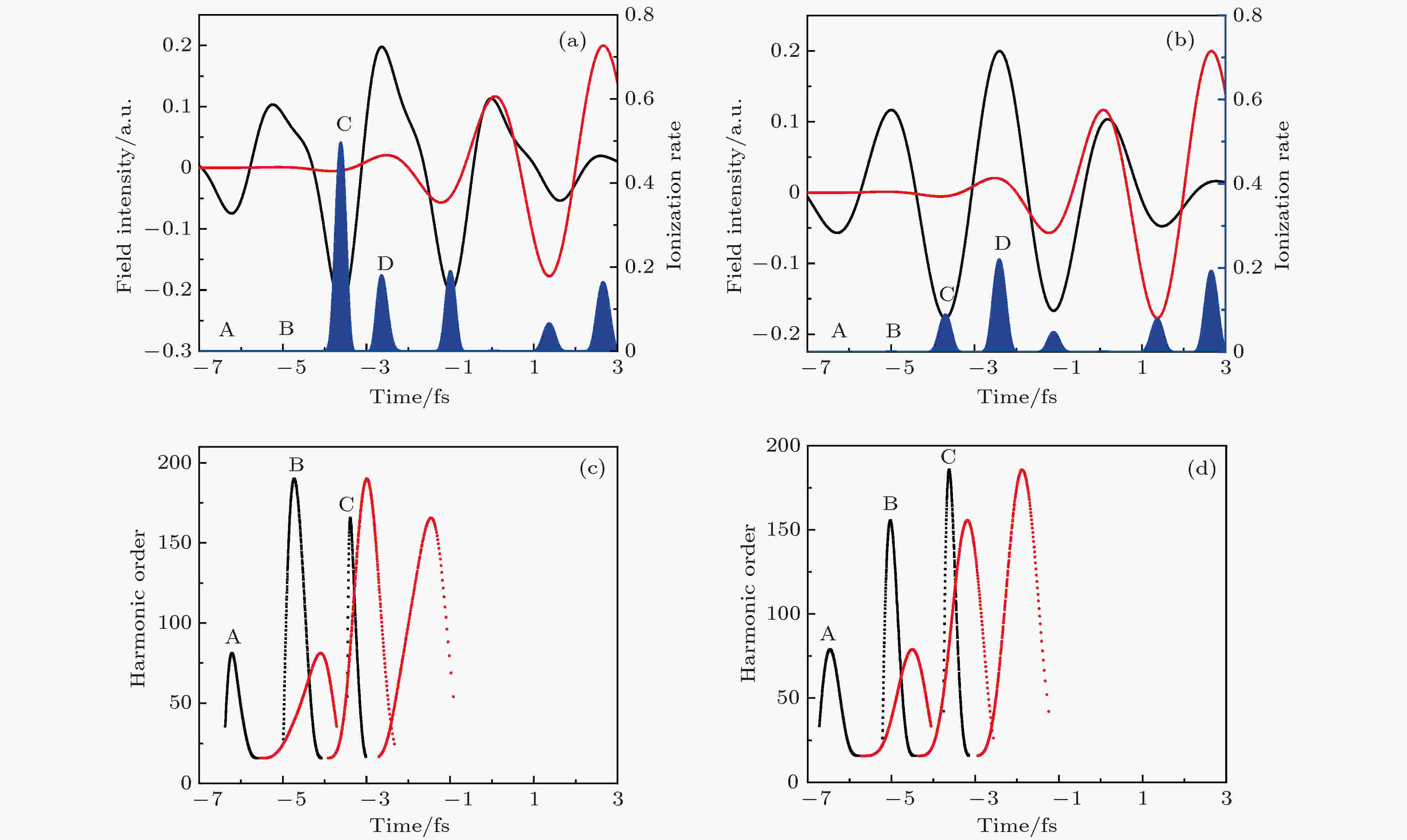图 3 (a)双光学控制方案、(b)正交偏振控制方案下, x方向驱动脉冲电场(黑色)、y方向控制脉冲电场(红色)及氦原子电离速率(蓝色填充区域)随时间的变化; (c)双光学控制方案、(d)正交偏振控制方案下, 高次谐波次数随电离(黑色点线)和复合时刻(红色点线)的变化
Figure3. Variations of the amplitude of x-polarized (black curve) and y-polarized field (red curve), and the ionization rate of the helium atom (filled blue region) with time: (a) Double optical gating scheme; (b) orthogonal polarization gating scheme. Evolution of the harmonics with ionization (black) and recombination (red) time in the x polarized field case: (c) Double optical gating scheme; (d) orthogonal polarization gating scheme.

需要强调指出的是, 两种方案下在峰值位置D附近电离电子对谐波谱的贡献. 这里谐波产生效率主要由电子电离产额以及电场椭偏率两个因素决定. 从图3(a)和图3(b)可以看到虽在峰值位置D附近原子电离有一定布居, 然而电子回核过程中受到椭圆偏振场作用, 很难回到核附近与核复合, 因此在三步模型图中没有得到峰值D附近电场对谐波谱的贡献. 为了证实电离电子不能回到母核附近的结论, 图4给出了双光学控制方案(两种方案下电场变化不大, 只说明一种情况)下电子电离后回核的最近距离图, 其中红线和黑线分别为驱动脉冲电场和原子的电离概率随时间的变化, 蓝色填充区域为电子电离速率随时间的变化, 绿色点线为电子回核最近距离. 可以看到, 在D峰附近电离电子, 由于受到弱椭偏率电场作用, 根据经典力学计算只能回到离核最近距离为20—25 a.u.的位置, 因此在该区域原子虽有电离, 电离电子却无法回到原子核附近与之复合. 另外, 从图4中黑色曲线可以看到, 在时间3 fs时原子的电离概率已经达到了60%, 此时x方向驱动脉冲电场已基本结束, y方向电场强度也已减弱, 原子基态布居衰退及y方向电场强度减弱引起的原子低电离概率共同作用使得y方向产生的谐波强度将明显低于x方向, 因此我们只需考虑x方向谐波的产生.
图 4 双光学控制方案中, 驱动脉冲电场(红色曲线)、氦原子的电离率(蓝色填充区域)、电离概率(黑色曲线)和电子回核最近距离(绿色曲线)随时间的变化
Figure4. In the case of double optical gating scheme, driving pulse field (red line), the ionization rate of helium atom (filled blue region) and the closest distance of electron to nucleus (green line) as a function of time.

为了进一步说明图2中谐波谱平台及截止位置呈现规则分布特点的原因, 我们利用小波变换方法计算了双光学控制方案中驱动脉冲辐照下氦原子高次谐波发射的时频分析图像, 如图5所示. 图中平台上的谐波主要由长短两个量子轨迹构成, 长轨迹对应于–1.5 fs附近时刻的发射峰, 短轨迹对应于–2.5 fs附近时刻的发射峰, 这两个辐射时段与图3(c)中从C峰附近电离电子的复合时刻完全一致, 两个轨迹干涉后得到了图2中规则分布的谐波谱平台结构.
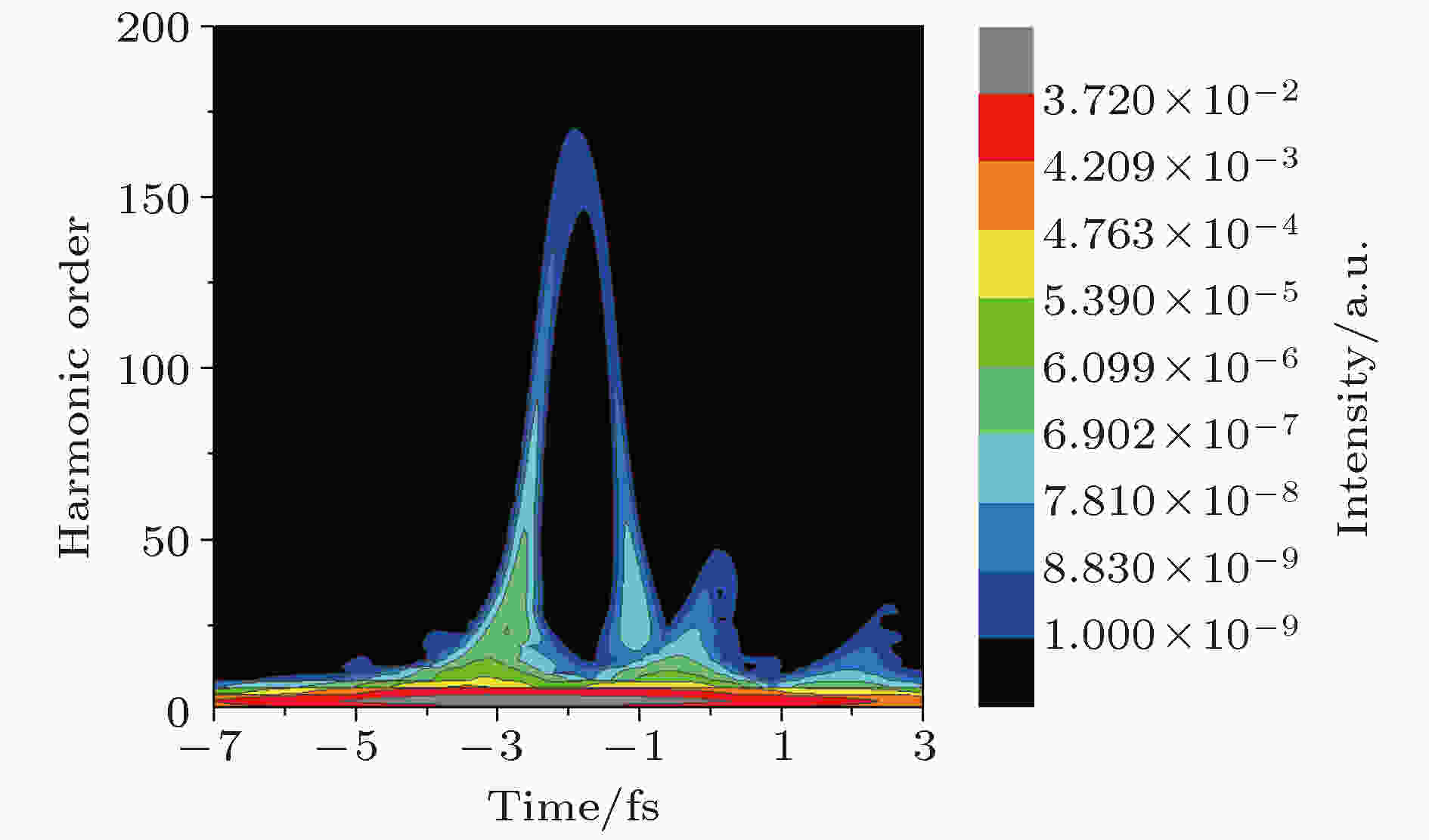图 5 双光学控制方案中谐波发射的时频分析图像
Figure5. Time-frequency analysis of harmonic emission in double optical gating scheme.

图6(a)和图6(b)分别展示了双光学控制方案和正交偏振控制方案中叠加谐波谱上呈规则分布谐波生成的阿秒脉冲时域图. 在双光学控制方案情况下, 如图6(a)所示, 通过叠加谐波谱平台上的50到150次超连续谐波, 得到了一个附带弱脉冲的孤立阿秒脉冲, 附带弱脉冲的强度约为主脉冲强度的10%. 这里的主脉冲A对应着谐波发射的短轨迹, 其半高全宽为145 as, 而附带的弱脉冲B对应着谐波发射的长轨迹. 可见, 在本文双光学控制方案中, 即使不考虑谐波传播效应也可以得到孤立阿秒脉冲的产生. 而在未加二次谐波脉冲的正交偏振控制方案情况下, 如图6(b)所示, 通过叠加谐波谱平台上150到185次谐波, 得到了包含长短量子轨迹阿秒脉冲链, –2.3 fs附近的阿秒脉冲A′对应着谐波发射的短轨迹, 其半高全宽为143 as, –1.5 fs附近的阿秒脉冲B′对应着谐波发射的长轨迹, 其半高全宽为141 as, 同时我们发现在C′位置处存在一个很微弱的脉冲, 依据图4给出的电子离核最近距离的经典力学计算(假设电子隧穿时刻的初始速度为零), 电离电子是不能回到母离子附近的. 然而强场近似模型计算中电子隧穿时刻的初始速度可以不为0, 从而可以补偿椭球偏振激光场导致的位置偏移, 这样电子仍然可以回到原子核发生复合. 不过电子的初始速度不为零时原子的电离概率较低, 因此得到了微弱的脉冲辐射. 另外, 当采用双光学偏振脉冲控制方案时, 单一阿秒脉冲的强度提高了1个数量级, 这与上述原子电离概率的分析结果是一致的. 可见, 利用附加二次谐波脉冲的双光学控制方案, 可以实现效率较高的孤立阿秒脉冲产生.
图 6 阿秒脉冲产生时域图　(a)双光学控制方案; (b)正交偏振控制方案.
Figure6. Attosecond pulse generation from (a) double optical gating scheme and (b) orthogonal polarization gating scheme.

本文利用三维强场近似理论开展了脉宽为4 fs 的正交偏振控制脉冲叠加二次谐波场获得强度较高孤立阿秒脉冲的研究. 不同于通常偏振控制脉冲方案中电场的变化从椭圆偏振到线性偏振再回到椭圆偏振的特点, 我们提出的正交偏振控制方案中电场的变化具有从线性偏振到椭圆偏振再回到线性偏振的特点. 该方案克服了传统偏振控制方案中偏振门到达前圆偏振光或者椭圆偏振光引起气体介质电离不利于谐波在传播过程中相位匹配条件的缺点. 二次谐波脉冲的加入调整了驱动脉冲电场的光强分布, 从而得到了效率较高且在整个平台区及截止位置都呈现出超连续特性的谐波谱.