摘要: 超声调制光学成像技术是一种新型的生物组织光学检测技术, 在癌症的早期检测方面具有巨大的潜力, 但该技术在信噪比和成像对比度方面存在不足. 在超声调制光学成像技术的基础上, 结合高灵敏度的激光回馈技术提出了超声调制激光回馈技术, 建立了含微泡介质的蒙特卡罗光子传输模型, 通过仿真和实验研究了超声微泡造影剂增强超声调制激光回馈成像对比度的作用机理. 结果表明, 在透明溶液中, 超声微泡造影剂可以增强超声调制激光回馈信号, 并产生谐波调制, 通过检测回馈基波和谐波信号增强量的方法可提高成像对比度; 而在仿生物组织环境中, 超声微泡造影剂可显著衰减超声调制激光回馈信号, 通过检测回馈基波和谐波信号衰减量的方法可提高成像对比度.
关键词: 声光成像 /
激光回馈 /
包膜微泡 /
对比度增强 English Abstract Mechanism of contrast-enhancement in ultrasound-modulated laser feedback imaging with ultrasonicmicrobubble contrast agent Zhou Bo-Rui 1,2 ,Tan Yi-Dong 2 ,Shen Xue-Ju 1 ,Zhu Kai-Yi 2 ,Bao Li-Ping 3 1.Department of Electronic and Optical Engineering, Army Engineering University of PLA, Shijiazhuang 050051, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51722506)Received Date: 20 May 2019Accepted Date: 16 August 2019Available Online: 01 November 2019Published Online: 05 November 2019Abstract: Ultrasound-modulated optical imaging technology is a new type of biological tissue optical detection technology, and sensitive to the change of scattering coefficient and absorption coefficient of biological tissue. This technology is a non-ionizing and non-invasive pathological detection method, which has great potential application in early detection of cancer. However, ultrasound-modulated optical imaging technology is insufficient in signal-to-noise ratio (SNR) and imaging contrast. Frequency-shifted laser feedback technology with microchip laser is a new type of highly sensitive interference technology, whose gain coefficient for weak optical signal can reach 106 . This technology can greatly improve the SNR of imaging. Combined with the high sensitive laser feedback technology, the ultrasound-modulated laser feedback technology is proposed. The SNR of this technology is better than that of the traditional ultrasound-modulated optical imaging technology. The increase in SNR can achieve greater depth of detection in biological tissue imaging, but there is no significant improvement in imaging contrast. In order to improve the contrast of biological tissue imaging and achieve high resolution imaging of thick biological tissue, we use ultrasound microbubble contrast agent in ultrasound-modulated laser feedback imaging technology. We establish a Monte Carlo photon transport model with microbubbles in order to study the mechanism of contrast enhancement in ultrasound-modulated laser feedback imaging with microbubbles. Finally, we establish an experimental system to verify the correctness of the simulation results. Experimental and simulation results show that in the transparent solution, the ultrasonic microbubble contrast agent can enhance the ultrasound-modulated laser feedback signal and generate harmonic modulation, which can improve the imaging contrast by detecting the enhancement of the fundamental and harmonic signals of the feedback. In the scattering medium, the ultrasonic microbubble contrast agent can significantly attenuate the ultrasound modulated laser feedback signal, and the imaging contrast can be improved by detecting the attenuation of the fundamental and harmonic signal.Keywords: acousto-optic imaging /laser feedback /capsule microbubbles /contrast-enhancement 全文HTML --> --> --> 1.引 言 以超声调制光学层析成像技术[1 ] (ultrasound-modulated optical tomography, UOT)和光声层析成像技术[2 ] (photoacoustic tomography, PAT)为代表的生物组织光子检测技术是将光学、超声学相结合逐渐发展起来的一种新型生物组织检测技术. 该技术敏感于生物组织的散射系数、吸收系数变化, 是一种无电离辐射、非入侵的病理学检测手段, 因此人们又常称其为“光活检”(optical biopsy)技术, 在乳腺癌等癌症的早期检测方面有着巨大的应用潜力, 目前已成为生物组织成像领域的研究热点.[3 ] . 而后, 利用CCD等阵列型探测器, 调制信号的信噪比得到有效提高, 但采集速度受限, 实时性较差, 且算法较为复杂[4 ] ; 结合光折变晶体或空间烧孔效应的UOT可以极大提高检测系统的灵敏度和集光度. 2012年, Zhang等[5 ] 和Suzuki等[6 ] 分别利用空间烧孔效应和光折变晶体提高了UOT的信噪比, 实现了9 cm生物组织仿体的透射探测. 但这两种方法实验系统复杂, 均难以在保证高灵敏度条件下进一步提高成像速度. 因此, 生物组织对入射光的强散射带来的信噪比、对比度不足以及实验系统复杂带来的成像速度低是限制UOT技术发展的主要瓶颈.6 量级)的特点, 借助锁相放大器对超声调制频率处的信号进行解调, 可以极大地提高ULFI的信噪比.[7 ] . 超声微泡造影剂可作为血球示踪剂用于人体微小血管成像和组织血流灌注检测, 其结合超声成像技术后在血管显像效果方面具有CT, MRI等其他检测方法无法比拟的优势. 活性靶向微泡造影剂结合超声成像可实现精准的靶向成像[8 ,9 ] , 同时利用微泡空化爆破形成的射流还可进行细胞灭活[10 ] .[11 ] 、超声调制相干光成像[12 ,13 ] 、超声调制非相干光成像[14 ] 中实验验证了微泡增强超声调制信号的效果. 针对传统UOT在信噪比和成像对比度方面的问题, 利用ULFI技术信噪比高且超声微泡造影剂能提高成像对比度的特性, 提出了实现生物组织大探测深度清晰成像的方案. 为获得一种极大提升ULFI成像对比度的方法, 本文将对微泡造影剂增强ULFI对比度的机理进行研究.2.ULFI技术及微泡增强ULFI对比度的机理 22.1.超声调制激光回馈成像技术 2.1.超声调制激光回馈成像技术 图1 所示为ULFI技术原理图. 微片激光器输出频率为$\omega $ 的激光, 在聚焦超声焦点位置被驱动频率为$\varOmega $ 的聚焦超声调制, 经被测物体反射或散射后频率为$\omega + \varOmega $ 的调制光返回激光谐振腔内, 与激光器内部的光场混合, 从而引起激光器输出光功率(光强)调制, 交流光电探测器PD直接检测激光器输出的调制光功率, 可以反映被测物体信息, 通过位移台移动被测物体可实现扫描成像.图 1 ULFI技术原理图Figure1. Schematic of ULFI technology.[15 ,16 ] ${I_{\rm{s}}}$ 为激光器稳态输出功率; $\kappa $ 为回馈水平(即回到谐振腔内的光子数与激光输出光子数之比); M 为超声调制效率(其大小与超声声压正相关); $\varOmega $ 为超声驱动频率; $G\left( \varOmega \right)$ 为激光移频回馈增益因子, 其大小与超声驱动频率$\varOmega $ 和激光器弛豫振荡频率有关, 当超声频率与激光器弛豫振荡频率一致时, $G\left( \varOmega \right)$ 可达106 ; $\phi $ 为相位因子, 其与激光回馈外腔长度有关; ${\phi _{\rm{s}}}$ 为初始相位.$\varOmega $ 有关的信号增益$G\left( \varOmega \right)$ , 并且通过锁相放大器提取特定频率$\varOmega $ 的信号, 可以剔除未调制光子产生的直流背景噪声, 因此ULFI系统的噪声来源主要为探测器噪声${I_{{\rm{PD}}}}$ 和激光器量子噪声${I_\nu }$ , 信噪比可表示为$G\left( \varOmega \right)$ , 因此在同等条件下ULFI系统可获得更高的信噪比.2.2.基于微泡的ULFI对比度增强机理分析 -->2.2.基于微泡的ULFI对比度增强机理分析 微泡加入待探测区域后, 将在超声场的作用下改变被测介质物理特性, 微泡、光场、声场之间相互作用情况如图2 所示. 一方面, 加入微泡造影剂后被测介质散射系数增高, 引起回馈水平$\kappa $ 下降, 其下降程度与被测介质散射特性、微泡浓度$\rho $ 和微泡的平均动态半径$\bar R$ 有关, 可以表示为$\kappa (\rho,\bar R)$ ; 另一方面, 置于超声场中的微泡相当于强散射源, 向四周产生散射声场, 对光子产生附加调制, 提高声光调制效率, 散射声场在频率$\varOmega $ 处的散射声压大小表示为${P_{\rm{mb}}}\left( \varOmega \right)$ , 微泡附加声光调制效率表示为$\gamma \left( {{P_{{\rm{mb}}}}\left( \varOmega \right)} \right)$ . 根据驱动超声的声压和频率, 微泡会产生线性或非线性的振荡. 当微泡非线性振荡时, 散射声场中除了与驱动超声频率$\varOmega $ 相同的基波外, 还包含频率为$2\varOmega,3\varOmega, \cdots,k\varOmega $ 的谐波. 考虑超声场中微泡的作用, 由(1 )式可得到微泡作用下的超声调制回馈系统的调制光功率为图 2 微泡、光场、声场相互作用示意图Figure2. Schematic diagram of interaction among microbubbles, light field and sound field.${\phi _k}$ 为初始相位.${{\left| {{I_{\rm{ob}}} - {I_{\rm{b}}}} \right|} / {{I_{\rm{b}}}}}$ . 其中${I_{{\rm{ob}}}}$ 为目标区域信号强度, ${I_{\rm{b}}}$ 为背景信号强度. 在背景信号强度${I_{\rm{b}}}$ 不为零且其大小一定的情况下, 使得${I_{{\rm{ob}}}} \gg {I_{\rm{b}}}$ 或${I_{{\rm{ob}}}} \ll {I_{\rm{b}}}$ 都可明显增大$\left| {{I_{{\rm{ob}}}} - {I_{\rm{b}}}} \right|$ , 即提高图像对比度. 根据(3 )式看出, 由于$G\left( {k\varOmega } \right)$ 只与激光器工作状态有关, 因此回馈光信号$\Delta I$ 由回馈水平$\kappa (\rho,\bar R)$ 以及调制效率$M\left( {{P_{{\rm{dri}}}}} \right)$ 和微泡附加调制效率$\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 决定. 由于加入微泡造影剂降低回馈水平$\kappa (\rho,\bar R)$ 的同时增强声光调制效率$M\left( {{P_{{\rm{dri}}}}} \right)$ 和微泡附加调制效率$\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ , 因此, 当$M\left( {{P_{{\rm{dri}}}}} \right)$ 和$\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 的增强作用大于$\kappa (\rho,\bar R)$ 的衰减作用时, $\Delta I$ 相比于未加微泡时表现为增强; 相反, 当$\kappa (\rho,\bar R)$ 的衰减作用大于$M\left( {{P_{{\rm{dri}}}}} \right)$ 和$\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 的增强作用时, $\Delta I$ 相比于未加微泡时表现为减弱. 由上述分析可知, 加入微泡引起$\Delta I$ 的变化增强了ULFI对比度.3.含微泡介质的蒙特卡罗光子传输模型的建立和微泡增强ULFI对比度仿真 ULFI对比度增强取决于微泡造影剂与超声场和光子的相互作用, 该作用决定了超声调制激光回馈光信号的强弱. 由(3 )式可知, $\Delta I$ 的大小由$M\left( {{P_{{\rm{dri}}}}} \right)$ , $\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 和$\kappa (\rho,\bar R)$ 共同决定. $M\left( {{P_{{\rm{dri}}}}} \right)$ , $\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 与${P_{{\rm{dri}}}}$ , ${P_{{\rm{mb}}}}\left( {k\varOmega } \right)$ 有关, 其仿真涉及微泡的超声动力学模型[17 -19 ] 和声光调制模型[20 ] ; $\kappa $ 与散射介质的散射特性、吸收特性有关, 其仿真涉及微泡的光散射模型和光子在散射介质内的传输模型[21 -24 ] . 为了系统描述上述过程, 在仿真声场中微泡的半径变化、动态微泡的光散射特性的基础上, 建立了涉及微泡-光子-超声场相互作用的蒙特卡罗模型.3.1.微泡对声光调制的影响 3.1.微泡对声光调制的影响 所用SonoVue? 超声微泡是典型的脂质包膜微泡, 因而使用修正Herring模型[19 ] 描述单个SonoVue? 微泡在声场中的振动:r 处的散射声压可近似表示为[19 ] ${\rho _{\rm{L}}}$ 为微泡所处溶液的密度, R 为微泡在超声场中的动态半径, ${R_0}$ 为微泡的初始半径, $\chi $ 为包膜弹性系数, $\sigma $ 为界面张力, ${P_0}$ 为环境气压, ${P_{{\rm{dri}}}}$ 为超声驱动声压, $\gamma $ 为微泡内气体的多方指数, $\mu $ 为微泡所处溶液的流体黏滞系数, ${\mu _{{\rm{sh}}}}$ 为微泡包膜的黏滞系数, c 为溶液中的声速, $\varepsilon $ 为微泡包膜厚度.4 )式可求得不同声压条件下微泡半径随时间变化的数值解. 对于初始半径为1.25 μm的微泡, 在频率为3 MHz、声压为160 kPa的超声驱动下, 其半径随时间变化如图3 所示, 仿真参数设置如表1 所列. 从图3(b) 微泡半径变化频谱图可以看出, 驱动声压160 kPa下微泡振荡产生了明显的谐波信号. 再根据求得的不同声压下微泡半径随时间的变化曲线, 按(5 )式计算得到了驱动声压在0—160 kPa范围内该微泡散射声压随驱动声压变化的曲线, 如图4 所示.图 3 微泡的超声动态特性 (a)微泡半径变化曲线; (b)微泡半径变化频谱图Figure3. Ultrasonic dynamics of microbubble: (a) Curve of microbubble radius; (b) spectrogram of microbubble radius.${\rho _{\rm{L}}}/{\rm{kg}} \cdot {{\rm{m}}^{ - 3}}$ ${P_0}/{\rm{kPa}}$ $\sigma /{\rm{N}} \cdot {{\rm{m}}^{ - 1}}$ $\chi /{\rm{N}} \cdot {{\rm{m}}^{ - 1}}$ $c/{\rm{m}} \cdot {{\rm{s}}^{ - 1}}$ $\varepsilon /{\rm{nm}}$ ${\mu _{{\rm{sh}}}}/{\rm{Pa}} \cdot {\rm{s}}$ $\gamma $ 998 1010 0.051 0.26 1500 5 0.003 1.07
表1 Rayleigh-Plesset方程仿真参数Table1. Rayleigh-Plesset equation simulation parameters.图 4 微泡散射声压曲线Figure4. Curves of microbubble scattering acoustic pressure.图4 可以看出, 由于微泡作用使得散射声压随驱动声压增强而增强. 按照文献[20 ]的结论可知, 在较低声压条件下, 声光调制效率与声压正相关. 因此可以得到微泡声光调制效率$\gamma \left( {{P_{{\rm{mb}}}}\left( {k\varOmega } \right)} \right)$ 与${P_{{\rm{mb}}}}\left( {k\varOmega } \right)$ 正相关、${P_{{\rm{mb}}}}\left( {k\varOmega } \right)$ 与${P_{{\rm{dri}}}}$ 正相关, 聚焦超声换能器产生的声光调制效率$M\left( {{P_{{\rm{dri}}}}} \right)$ 与${P_{{\rm{dri}}}}$ 正相关, 即存在微泡的情况下, 随着${P_{{\rm{dri}}}}$ 的增强, 声光调制效率总体表现为增强.3.2.微泡对光散射特性的影响 -->3.2.微泡对光散射特性的影响 微泡半径随时间变化导致微泡光散射特性变化, ULFI系统为了契合生物组织光学窗口使用了波长为1064 nm的Nd:YVO4 微片激光器, 激光器波长与SonoVue? 微泡在超声场中受迫振荡时动态半径处于同一数量级, 因此可使用Mie散射理论研究动态微泡的光学性质. 当超声场与微泡发生作用时, 微泡的半径$R\left( t \right)$ 、相对折射率$n\left( t \right)$ 将随时间发生周期性变化,导致微泡群的散射系数${\mu _{\rm{s}}}\left( {t,R} \right)$ 和各向异性因子$g\left( {t,R} \right)$ 以及Mie散射效率${Q_{{\rm{sca}}}}\left( {t,R} \right)$ 随时间周期性变化.[25 ] ${\rho _{{\rm{mb}}}}$ 为微泡溶液浓度, ${Q_{{\rm{sca}}}}\left( {t,R} \right)$ 为微泡的Mie散射效率, 微泡相对折射率${n_{{\rm{mb}} \text{-} {\text{水}}}}\left( {t,R} \right)$ 可以近似表示为[25 ] ${n_{{\rm{mb}} \text{-}{\text{水}}}}\left( {t,R} \right) \approx \!\sqrt {1 + 3A{p_{\rm G}}\left( {t,R} \right)/\bar RT} /{n_{{\text{水}}}}$ , 其中${p_{\rm G}}\left( R \right)$ 为微泡内气体的压力, $\bar R$ 为气体摩尔常数, T 为热力学温度. 利用Mie散射仿真软件求得了微泡散射系数随声压变化的曲线, 如图5 所示.图 5 微泡群散射系数变化曲线Figure5. Curves of microbubbles scattering coefficient.图5 可以看出, 微泡群的总散射系数随驱动声压的增加而增加, 最大可以达到1%浓度的脂肪乳剂在1064 nm波长下散射系数的2.5倍. 为了进一步研究微泡对光的散射特性, 在前述理论的基础上建立了涉及微泡-光子-超声场相互作用的蒙特卡罗模型, 并对如下四种介质进行仿真: 1) 0.9%的氯化钠溶液无微泡; 2) 0.9%的氯化钠溶液加入微泡; 3) 1%的脂肪乳剂无微泡; 4) 1%的脂肪乳剂加入微泡. 仿真中超声声压为160 kPa、频率为3 MHz, 微泡初始半径为1.25 μm、浓度为108 个/mL. 在蒙特卡罗仿真中, 介质的散射系数、吸收系数、各向异性因子决定光子在介质内单步行进的方向和步长, 根据微泡在超声中的光散射特性, 重新定义了蒙特卡罗仿真中光子步长的选取方法, 光散射参数的选择流程图如图6 所示, 其中$\xi \in \left[ {0,1} \right]$ 为一个满足均值分布的随机数.图 6 蒙特卡罗仿真光散射参数的选择流程图Figure6. Flow chart of optical scattering parameters selection in Monte Carlo simulation.${\mu _{\rm{a}}}=0.1/{\rm{cm}}$ 、吸收系数${\mu _{\rm{s}}}=0.0001/{\rm{cm}}$ 、各向异性因子$g=0$ ; 对于1%的脂肪乳剂溶液, 取散射系数${\mu _{\rm{a}}}=0.1/{\rm{cm}}$ 、吸收系数${\mu _{\rm{s}}}=10/{\rm{cm}}$ 、各向异性因子$g=0.76$ . 四种条件下对106 个光子进行蒙特卡罗仿真, 所得到的背向散射光子分布如图7 所示. 其中蓝色为未调制的背景光子, 红色为调制光子, 绿色为微泡附加调制的光子. 表2 为四种介质中, 取收集孔径为5 mm, 收集角为5o时得到的未调制光子数、调制光子数和微泡附加调制光子数.图 7 蒙特卡罗仿真背向散射光斑图 (a) 0.9% NaCl; (b) 0.9% NaCl添加微泡; (c) 1%的脂肪乳剂; (d) 1%的脂肪乳剂添加微泡Figure7. Monte Carlo simulation of backscattered spot patterns: (a) 0.9% NaCl; (b) 0.9% NaCl with microbubbles; (c) 1% intralipid; (d) 1% intralipid with microbubbles.溶液种类 背向散射光子数 $\dfrac{{{\simfont\text{调制}} + {\simfont\text{附加调制}}}}{{\simfont\text{未调制}}}$ 调制 未调制 附加调制 0.9%的NaCl溶液 9354 45080 0 20.75% 0.9%的NaCl、微泡混合液 9379 46070 4607 30.36% 1%的脂肪乳剂溶液 843 52966 0 1.59% 1%的脂肪乳剂、微泡混合液 97 52685 7 0.20%
表2 蒙特卡罗仿真结果Table2. Results of Monte Carlo simulation.图7(a) 、图7(b) 和表2 结果分析可知: 微泡造影剂作用在0.9%的氯化钠溶液中时, 会产生散射声场, 提高基波声光调制效率的同时引入谐波调制, 总调制光子数(调制光子数与附加调制光子数之和)明显增多, 而光子与微泡的相遇概率较低(根据微泡密度计算约为0.39%), 微泡Mie散射造成的回馈水平下降几乎可以忽略不计, 因此微泡造影剂在0.9%的氯化钠溶液中的作用表现为对超声调制激光回馈信号的增强, 通过检测加入微泡后超声调制激光回馈基波和谐波信号的增强量, 可提高透明介质中ULFI对比度.图7(c) 、图7(d) 和表2 结果分析可知: 微泡造影剂作用在1%的脂肪乳剂溶液中时, 由于光子穿透强散射介质会发生多次散射, 实际光程远大于样品物理尺寸, 微泡引起的散射系数增高在强散射介质中体现十分显著. 虽然微泡造成的散射声场提高了调制效率, 但由于微泡造成光散射系数增强, 出射的调制光子数十分有限, 样品回馈水平极低, 信号淹没于激光器量子噪声和探测器噪声中, 无法探测到明显的基波调制信号和谐波调制信号. 因此, 微泡造影剂在1%的脂肪乳剂溶液中的作用表现为对超声调制激光回馈信号的显著减弱, 并且随着驱动声压的增大, 有无微泡时的超声调制激光回馈信号的差值会逐渐增大, 通过检测微泡后超声调制激光回馈基波和谐波信号的衰减量, 可提高生物组织或强散射介质中ULFI对比度.4.实验验证 为了验证仿真结果, 搭建如图8 所示实验系统. 实验所用激光器为全固体Nd:YVO4 微片激光器, 单纵模线偏振输出, 波长为1064 nm、激光功率20.2 mW. 输出激光经分束比为4 ∶ 1的分束镜BS分束, 约4 mW的激光入射光电探测器PD用以检测回馈信号, 约16 mW的激光经透镜L准直后入射样品槽. 水浸聚焦超声换能器(I3-10SF20, EasyNDT)焦距为2 cm, 驱动频率3 MHz, 超声换能器沉浸于样品槽内. 硅胶软管穿过样品槽, 用以导入微泡, 其内径为3 mm、外径为4 mm, 距离样品槽激光入射表面2.5 cm, 软管连接微量推进泵(LSP01-2A, LongerPump? ), 用以控制微泡溶液流速. 超声方向、光束方向和硅胶软管互相垂直, 相交位置为超声焦点. 信号发生器(33250A, Agilent)通道一产生3 MHz驱动信号, 经功率放大器(LZY-22+, Mini Circuits)放大后送入聚焦超声换能器; 光电探测器PD输出的测量信号和信号发生器通道二产生的3 MHz参考信号同时输入锁相放大器(HF2L1, Zurich Instruments)进行解调, 得到超声驱动频率处及其倍频处的信号强度. 微泡使用SonoVue? 超声微泡造影剂(Bracco Imaging B.V., Switzerland), 溶液未稀释时微泡浓度约为108 个/mL. 微泡制备过程为: 先使用注射器将5 mL生理盐水注入含有微泡冻干粉和SF6 气体的小瓶中, 而后持续振荡30 s. 完成制备后将装有微泡的注射器安装在微量推进泵上, 以缓慢速度推进保持微泡溶液流动性.图 8 实验系统Figure8. Experiment system.实验1 样品槽内盛装去离子水, 浸没聚焦超声换能器, 硅胶软管内分别通入0.9%的氯化钠溶液和使用0.9%的氯化钠溶液配制的微泡造影剂(浓度约为108 个/mL), 使用微量推进泵以10 μL/s的速度推动溶液在硅胶软管内缓慢流动. 图9 给出了超声换能器驱动声压在0—160 kPa范围内逐渐增加时锁相放大器的输出信号. 由图9 分析可以得到: 1)在较低声压状态下, 加入微泡后溶液散射系数提高, 微泡溶液中的ULFI信号低于0.9%的氯化钠溶液的ULFI信号; 2)随着声压不断提高, 声光调制效率引起的信号增强大于散射引起的信号衰减, 微泡溶液中的ULFI信号逐渐高于0.9%氯化钠溶液中的ULFI信号; 3) 0.9%氯化钠溶液中的二次谐波信号、三次谐波信号始终淹没于噪声中, 微泡溶液中的二次谐波信号、三次谐波信号强度相较基波信号强度低一个数量级.图 9 微泡溶液和0.9%NaCl溶液中的声压-ULFI信号曲线 (a)总曲线; (b)基波信号; (c)二次谐波信号; (d)三次谐波信号Figure9. Acoustic pressure-ULFI signal curve of the microbubble solution and 0.9% NaCl solution: (a) Total curve; (b) fundamental signal; (c) second harmonic signal; (d) third harmonic signal.实验2 配置1%浓度的脂肪乳剂用以模拟生物组织光学特性, 替代实验1中的去离子水填充样品槽, 浸没聚焦超声换能器, 硅胶软管内分别通入1%的脂肪乳剂和1%的脂肪乳剂、微泡造影剂混合液(微泡浓度约为108 个/mL), 使用微量推进泵以10 μL/s的速度推动. 图10 给出了超声换能器驱动声压在0—160 kPa范围内逐渐增加时锁相放大器的输出信号. 由图10 分析可以得到: 1)硅胶软管内通入1%浓度的脂肪乳剂时, 驱动声压逐渐增强的同时基波信号不断增强, 而谐波信号始终淹没于噪声中; 2)硅胶软管内通入脂肪乳剂、微泡造影剂混合液时, 驱动声压不断提高, 基波信号、谐波信号始终淹没于噪声中; 3)对比有无微泡造影剂的ULFI信号, 可以发现微泡造影剂在1%浓度的脂肪乳剂中对信号有极强的衰减能力, 并且随着声压增大, 加入微泡和无微泡时的信号之差不断增大.图 10 1%的脂肪乳剂溶液和微泡、脂肪乳剂混合溶液中的声压-ULFI信号曲线Figure10. Acoustic pressure-ULFI signal curves of 1% intralipid solution and microbubble intralipid mixed solution.5.结 论 ULFI技术是一种高信噪比、高灵敏度的超声调制光学成像技术, 有望实现生物组织光学波段大探测深度清晰成像. 为获得一种极大提升ULFI成像对比度的方法, 本文对微泡造影剂增强ULFI对比度机理进行了研究, 建立了含微泡介质的蒙特卡罗光子传输模型, 并通过仿真和实验对该机理进行了验证. 机理分析表明: 微泡对于光波有散射作用, 会提高介质散射系数, 降低回馈水平; 对于超声波, 会增加散射声场, 激发出谐波信号, 提高声光调制效率. 微泡的光学散射特性和声学增强特性共同作用, 决定ULFI信号变化. 在透明介质(如0.9% NaCl溶液)中, 光子与微泡相遇概率较低, 散射效果不明显, 声光调制效率的增强占主导地位, 因此表现为ULFI信号的增强, 通过检测ULFI基波和谐波信号增强量的方法可提高成像对比度; 在仿生物组织环境(1%脂肪乳剂溶液)中, 光子发生多次散射和吸收, 背向散射光程远大于实际探测深度, 微泡的光散射特性表现显著, 回馈水平的降低占主导地位, 因此表现为对ULFI信号的显著衰减, 并且随着驱动声压提高, 有无微泡时ULFI信号差异不断增大, 通过检测ULFI基波和谐波信号衰减量的方法可极大提高成像对比度. 


 图 1 ULFI技术原理图
图 1 ULFI技术原理图






























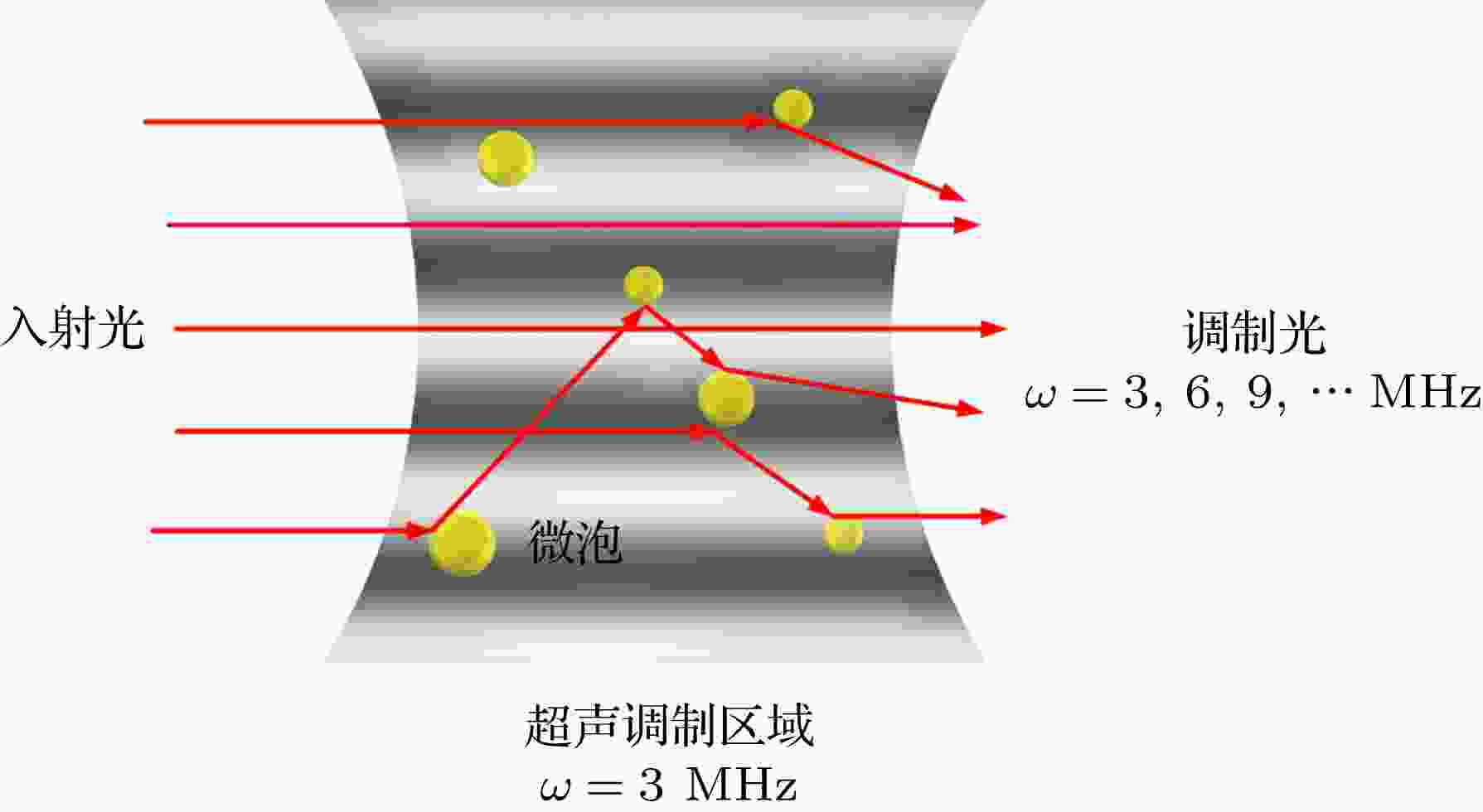 图 2 微泡、光场、声场相互作用示意图
图 2 微泡、光场、声场相互作用示意图

































































































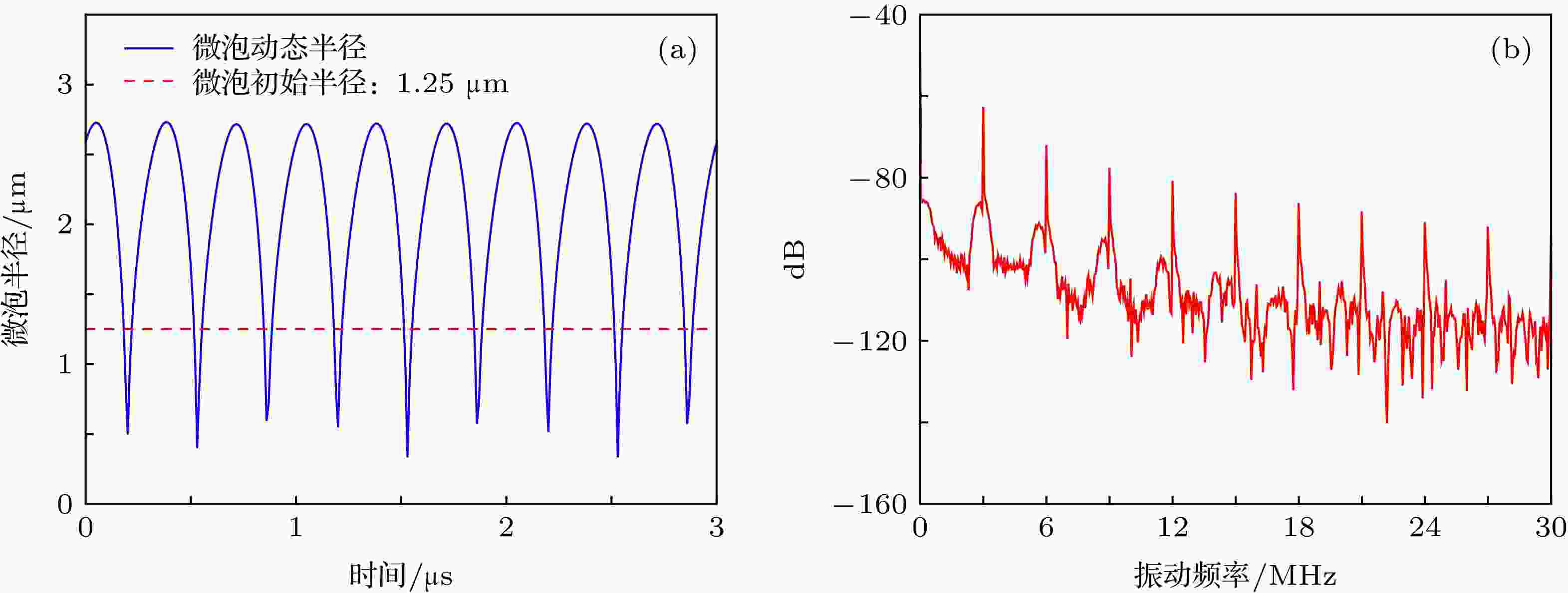 图 3 微泡的超声动态特性 (a)微泡半径变化曲线; (b)微泡半径变化频谱图
图 3 微泡的超声动态特性 (a)微泡半径变化曲线; (b)微泡半径变化频谱图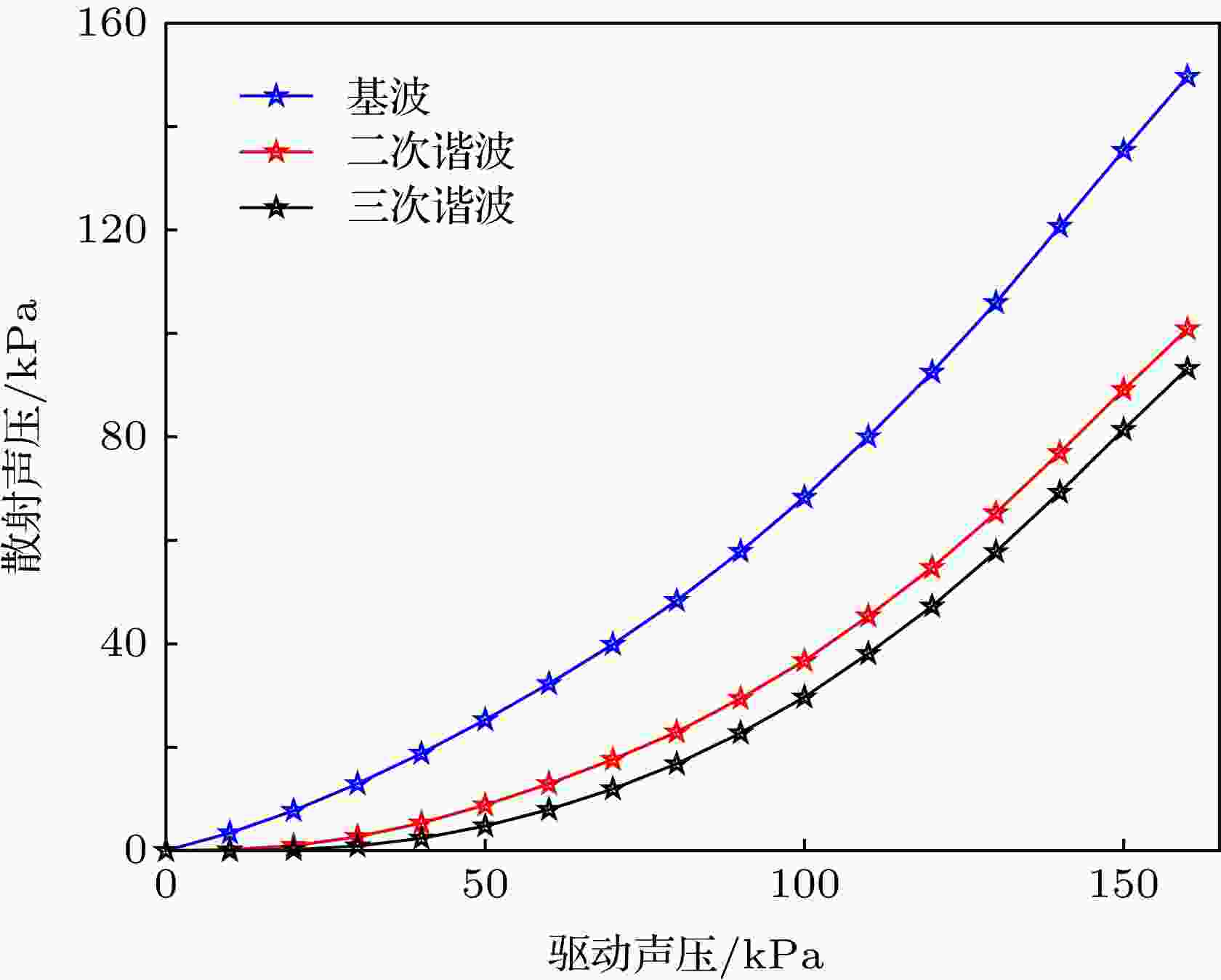 图 4 微泡散射声压曲线
图 4 微泡散射声压曲线

























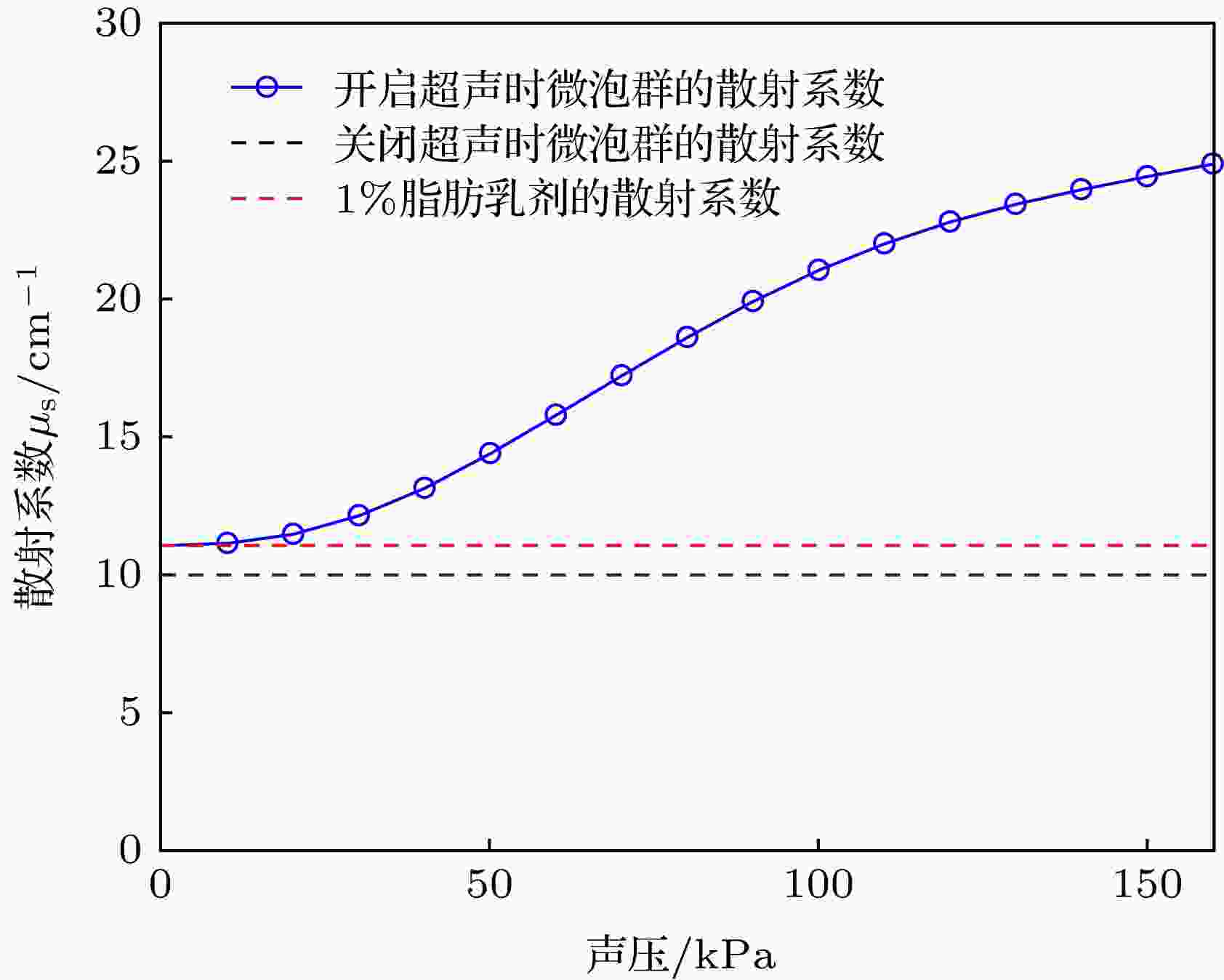 图 5 微泡群散射系数变化曲线
图 5 微泡群散射系数变化曲线
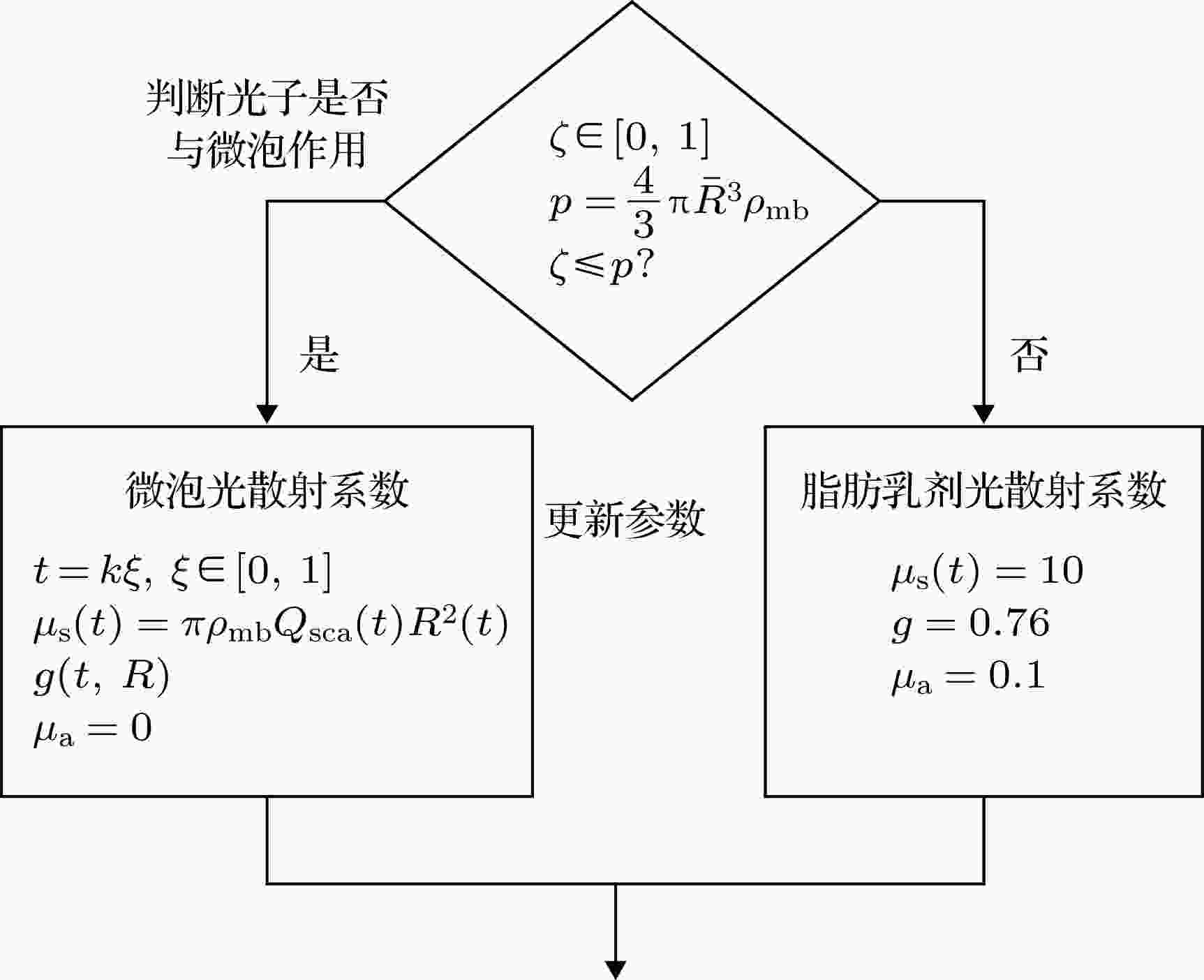 图 6 蒙特卡罗仿真光散射参数的选择流程图
图 6 蒙特卡罗仿真光散射参数的选择流程图







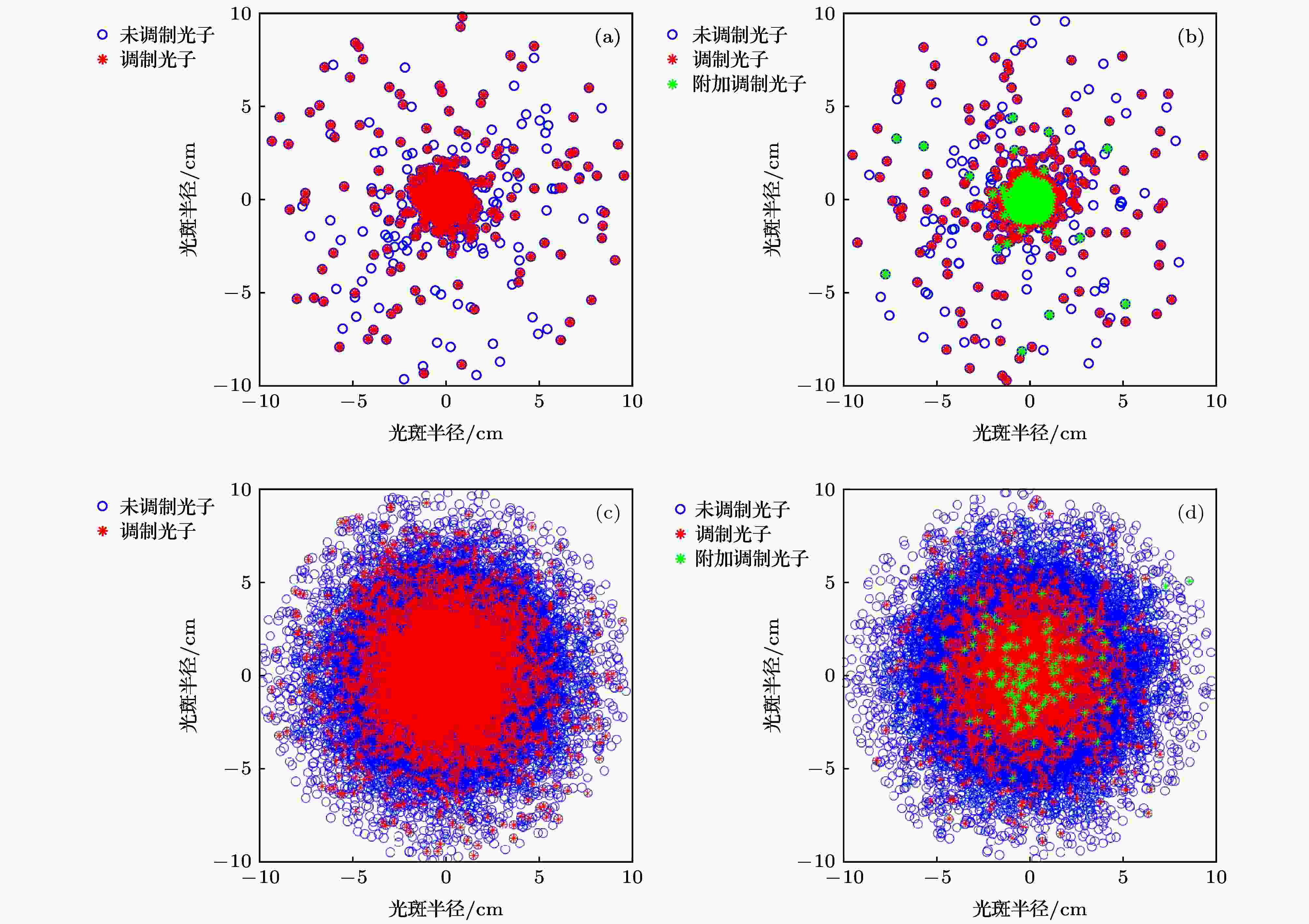 图 7 蒙特卡罗仿真背向散射光斑图 (a) 0.9% NaCl; (b) 0.9% NaCl添加微泡; (c) 1%的脂肪乳剂; (d) 1%的脂肪乳剂添加微泡
图 7 蒙特卡罗仿真背向散射光斑图 (a) 0.9% NaCl; (b) 0.9% NaCl添加微泡; (c) 1%的脂肪乳剂; (d) 1%的脂肪乳剂添加微泡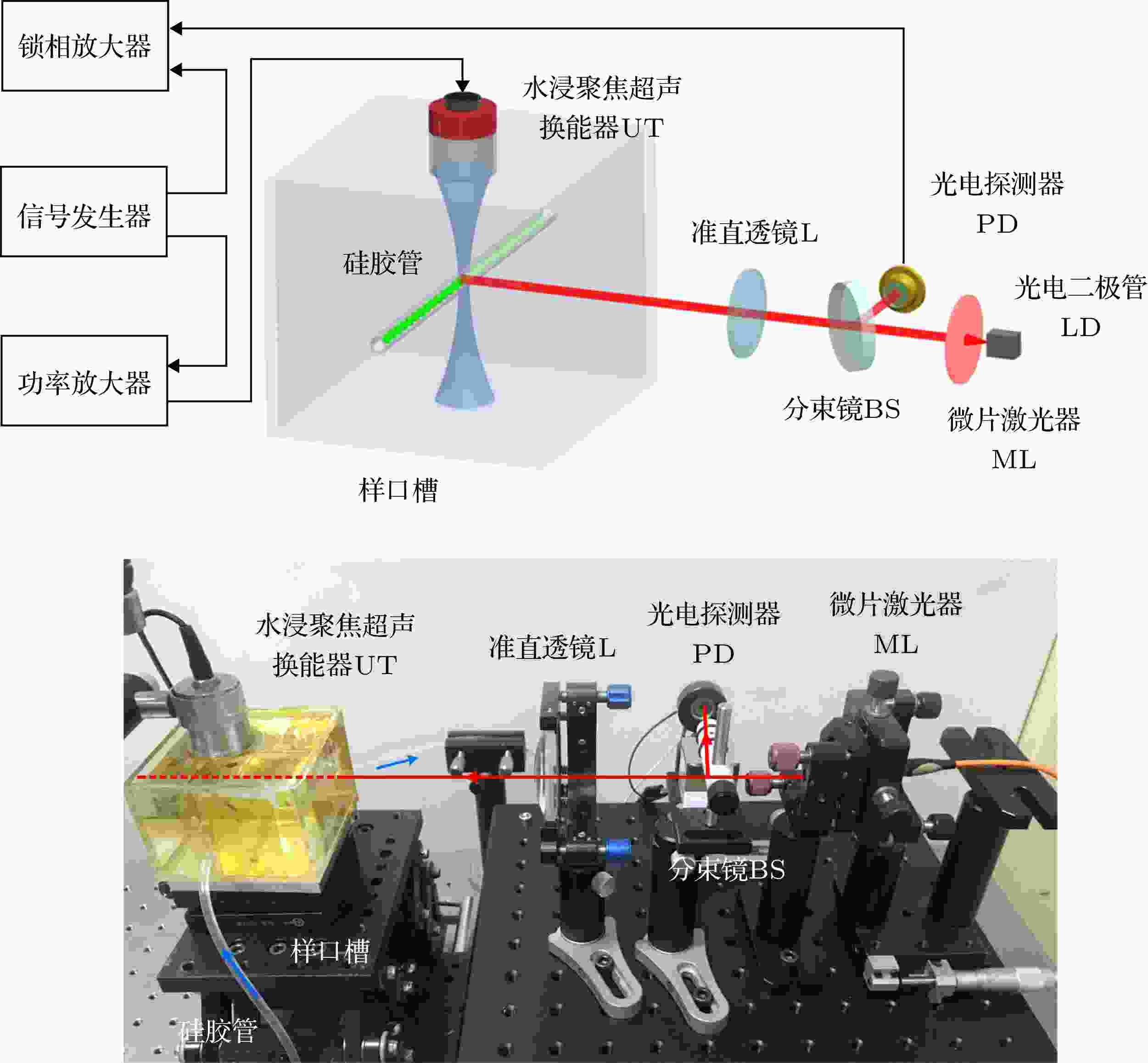 图 8 实验系统
图 8 实验系统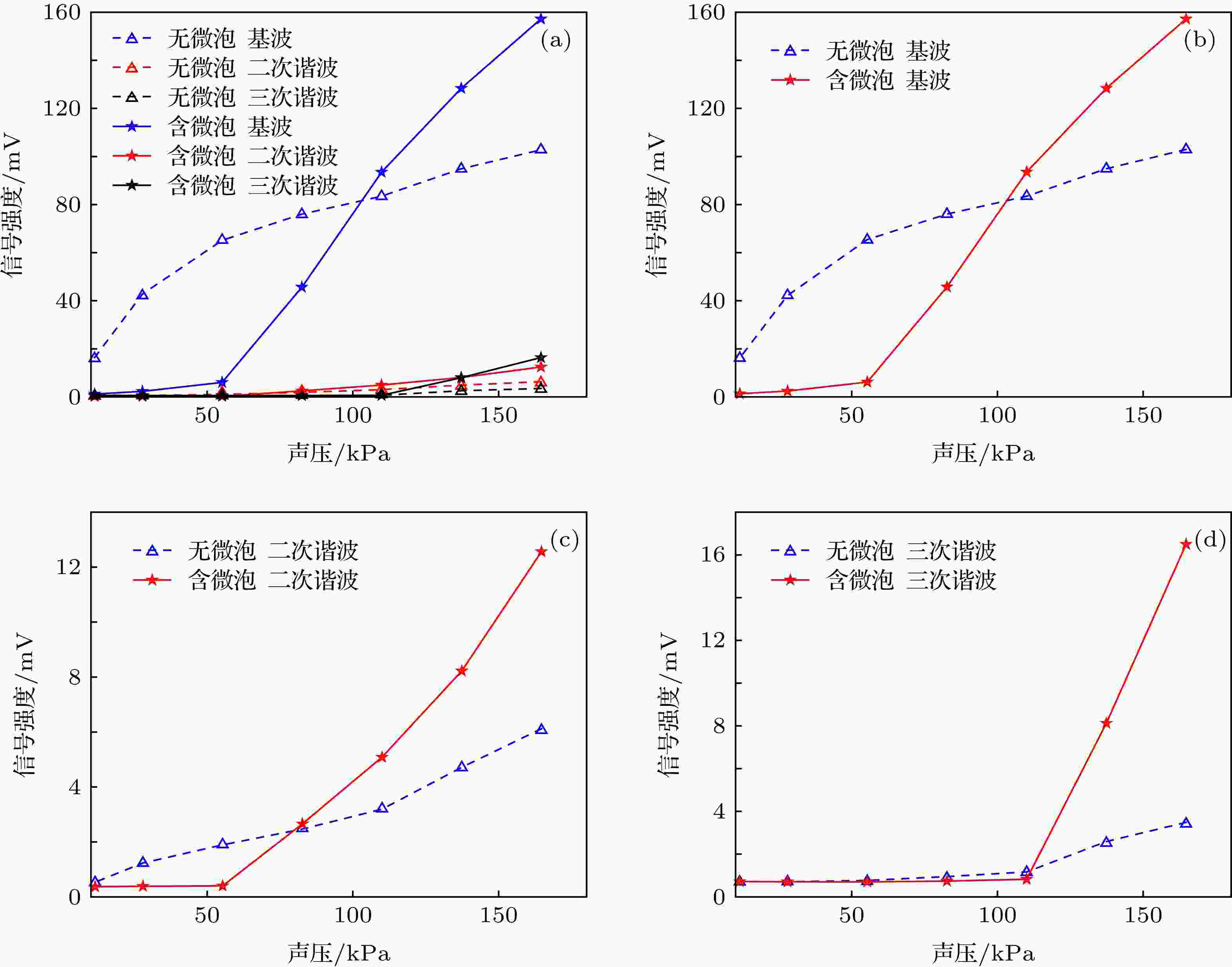 图 9 微泡溶液和0.9%NaCl溶液中的声压-ULFI信号曲线 (a)总曲线; (b)基波信号; (c)二次谐波信号; (d)三次谐波信号
图 9 微泡溶液和0.9%NaCl溶液中的声压-ULFI信号曲线 (a)总曲线; (b)基波信号; (c)二次谐波信号; (d)三次谐波信号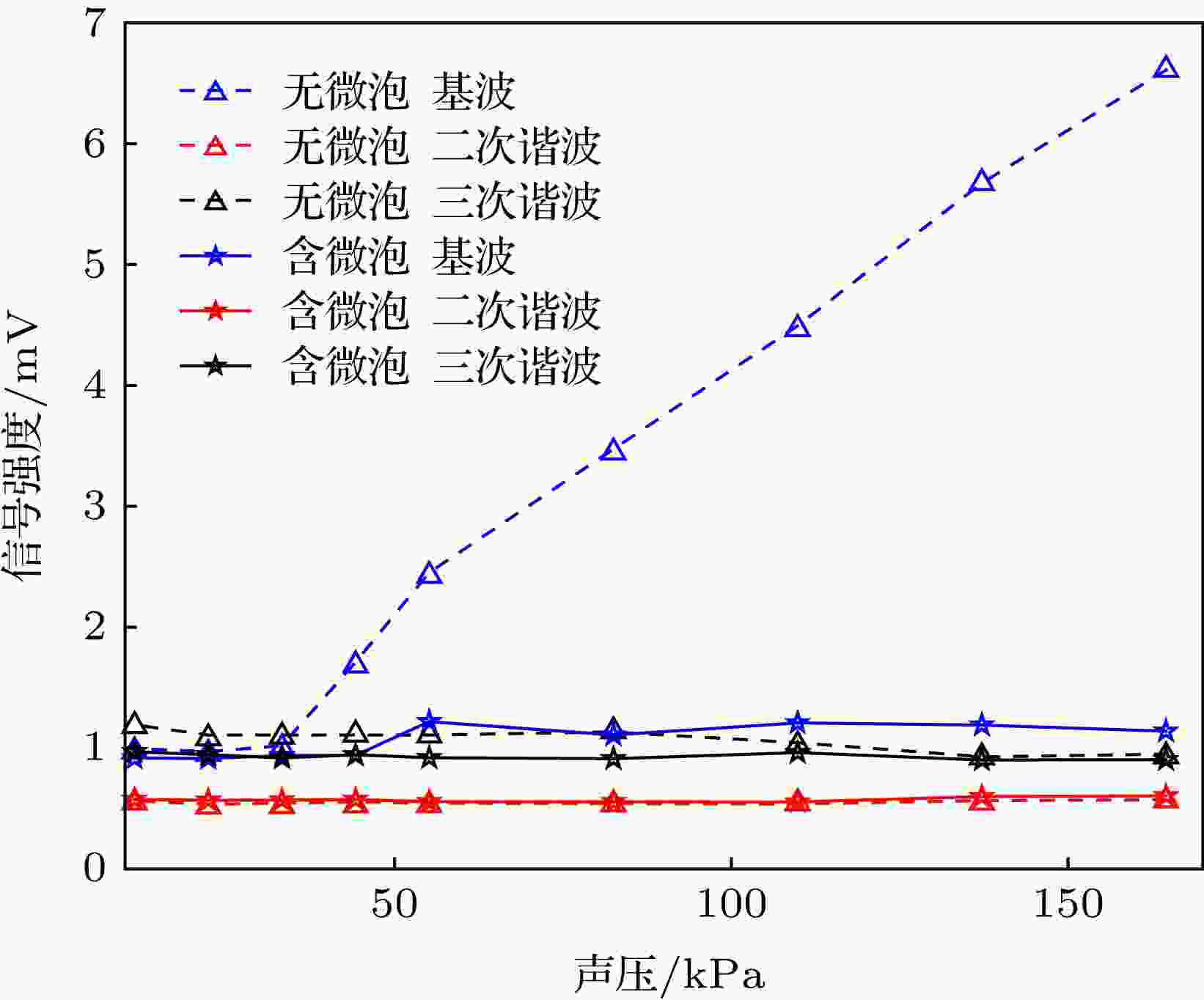 图 10 1%的脂肪乳剂溶液和微泡、脂肪乳剂混合溶液中的声压-ULFI信号曲线
图 10 1%的脂肪乳剂溶液和微泡、脂肪乳剂混合溶液中的声压-ULFI信号曲线