摘要:当两个晶格常数或晶格转角不同的二维材料叠加在一起时会出现周期性的莫尔条纹结构, 这种莫尔超晶格形成了一个新的二维周期势, 可以大大改变原有体系的物理性质. 最近石墨烯与石墨烯、石墨烯与六方氮化硼形成的莫尔超晶格提供了一个非常有趣的体系, 在该体系中石墨烯的电子能带结构发生了根本性的改变, 在原本的能谷处产生了额外的超晶格小能带, 由此产生了十分丰富的强关联效应和拓扑效应. 本文介绍关于石墨烯莫尔超晶格体系拓扑性质的理论和实验研究进展, 主要包括双层石墨烯的畴壁拓扑态、转角双层石墨烯的小能带拓扑态、ABC堆叠三层石墨烯以及转角双层堆叠双层石墨烯的拓扑性质等, 最后介绍利用近场光学技术研究石墨烯莫尔超晶格体系的能带结构和新奇拓扑性质.
关键词: 石墨烯/
莫尔超晶格/
拓扑/
近场光学

English Abstract

全文HTML

--> --> -->

拓扑绝缘体等拓扑材料和量子自旋霍尔效应、量子反常霍尔效应等新奇物理现象的发现是当代凝聚态物理最重要的进展之一^[1,2]. 1982年Thouless等^[3]指出二维电子系统的量子霍尔效应态来源于其电子态波函数的拓扑性质, 可以用一个拓扑不变量陈数(Chern number)来描述, 不同的陈数对应于不同的量子霍尔电导台阶. 量子霍尔效应属于外加磁场打破时间反演对称性(time reversal symmetry)而产生的拓扑性质, 后来人们又找到了陈数以外的拓扑不变量来刻画具有时间反演对称的绝缘体系统的拓扑性质, 这类材料使用Z₂拓扑不变量来描述, 分为拓扑绝缘体和普通绝缘体两类^[1,2], Z₂拓扑绝缘体可以从二维拓展到三维. 此外, 在金属中也有一些特殊的体系具有内禀的拓扑性质, 比如Dirac半金属^[4,5]、Weyl半金属 ^[6]等. 通过各种电学、磁学等手段对这些拓扑材料进行调控以研究它们的性质是目前凝聚态物理的重要研究方向.
堆叠二维层状材料构成的莫尔(Moiré)超晶格体系为拓扑物理的研究增添一个新的自由度, 带来了许多新奇的拓扑性质, 尤其是通过外加电压连续调控拓扑相变和拓扑物态的可能性. 最近实验和理论上的研究表明, 通过改变石墨烯超晶格层与层之间的堆叠角度以及调节外加偏置电压, 可以使得狄拉克点附近价带和导带的陈数发生变化, 甚至在拓扑平庸和非平庸态之间发生转变^[7-9]. 在转角双层石墨烯中, 利用垂直的外加电场可以控制带宽和能带的陈数, 在不同方向的偏置电压下与两个小能谷相关的能带陈数可以在0, ± 1之间改变. 同时, 转角双层石墨烯的魔角^[10,11]附近也已经观察到了绝缘态和超导态, 这使其有望成为将拓扑与强关联效应相结合的体系. 对于本身具有平带的ABC堆叠三层石墨烯, 当施加偏置电压时其孤立的价带会与导带分离, 价带变得更加平坦, 通过不同的偏压还可以使孤立的价带具有非零的陈数, 使其具有可调节的能带拓扑结构. ABC堆叠三层石墨烯中的库仑相互作用和动能之间的竞争关系可以通过原位调节发生变化, 还可以期待在材料中实现拓扑与强关联相结合的性质^[12-15]; 转角双层堆叠双层石墨烯(twisted bilayer-bilayer graphene, TBBG)也受到了广泛的关注, 最近的研究表明其具有电调控的强关联绝缘体、超导态^[16-18]和理论上预测的拓扑性质^[19]. 国内****利用多种测量手段对石墨烯莫尔超晶格体系进行研究也获得了许多重要的进展, 包括使用输运技术观测到的强关联态^[13]和超导态^[18], 利用红外光谱对朗道能级^[20]和热载流子^[21]的研究, 利用近场光学技术对一维拓扑边缘态的成像^[22], 使用ARPES研究非公度超晶格中的准晶结构^[23], 在STM的研究中发现了巨大的赝磁场等诸多新奇性质^[24,25]. 此外, 理论上对该体系拓扑物理的研究也在为人们探索新的拓扑性质提供帮助^[26,27]. 因此, 二维莫尔超晶格体系有可能给拓扑物理的研究带来巨大进展.
本文结合早期理论研究介绍石墨烯中内禀拓扑性质的来源, 然后讨论双层石墨烯畴壁中导电通道的拓扑来源, 进而讨论转角双层石墨烯如何在小能带(minibands)中获得拓扑性质、ABC三层堆叠石墨烯能带的陈数及其电学调控、AB-AB和AB-BA转角双层堆叠双层石墨烯中拓扑和强关联态的研究. 最后本文将介绍利用近场光学技术研究石墨烯莫尔体系的能带和拓扑性质, 包括通过研究等离激元的色散关系与衰减等性质来研究小能带的带间跃迁, 以及利用近场光学成像技术研究双层石墨烯畴壁中受拓扑保护的一维电子态及其对等离激元的散射.

2

-->

2.1.石墨烯拓扑性质的来源

单层石墨烯具有蜂窝晶格结构^[28] (图1(a))和非常独特的电子特性^[29-31]. 作为一种零带隙半导体, 它的导带与价带在六角形布里渊区的相邻两角处(即K和–K点)呈锥形接触, 对应于简并且不等价的能谷, 同时具有空间反演对称性(inversion symmetry)与时间反演对称性. 石墨烯的拓扑性质从它出现开始就受到人们的广泛关注, 包括对其量子霍尔效应的测量^[32,33]、量子自旋霍尔效应^[34]和量子反常霍尔效应的预言^[35]、能谷拓扑性质的研究等.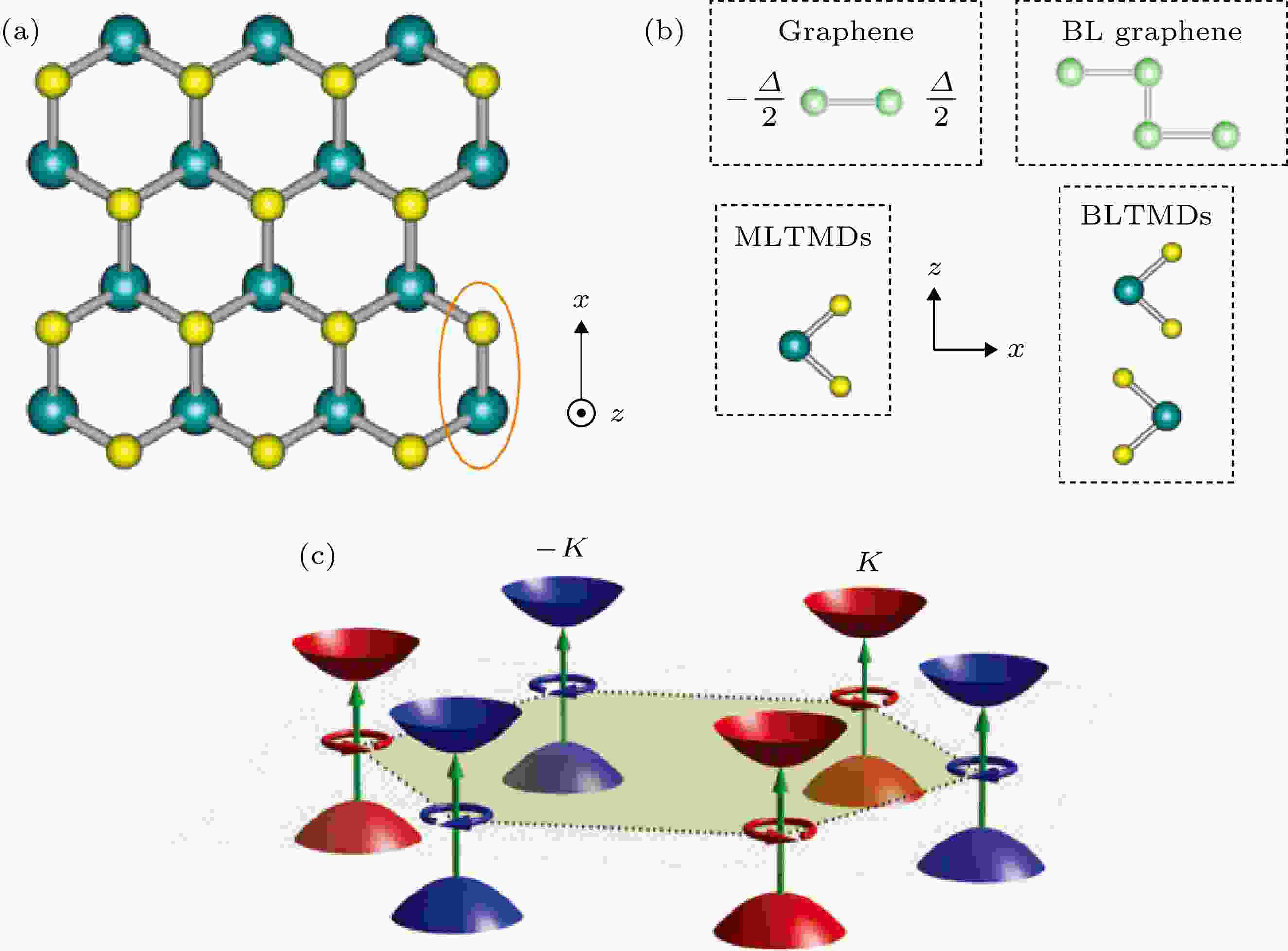
图 1 (a) 石墨烯、单层过渡金属硫族化合物(TMDs)等材料的二维蜂窝晶格; (b)当单层石墨烯与h-BN基底产生相互作用, 空间反演对称性就会被破坏, 单层TMDs不具有空间反演对称性结构, 在双层石墨烯和双层TMDs中反演对称性可以通过施加z方向的电场打开或关闭; (c) 反演对称性破缺的狄拉克体系在能谷处打开能隙, 箭头表示能谷光学跃迁, 圆形箭头表示不同的圆偏振光^[28]
Figure1. (a) 2D hexagonal lattice, representing graphene, monolayer transition metal dichalcogenides (TMDs), etc; (b) In monolayer graphene, inversion symmetry is broken when monolayer graphene interacts with h-BN substrate. The monolayer TMDs have structures that lack inversion symmetry. Inversion symmetry in bilayer graphene and TMDs can be switched on/off by an electric field applied in the z-direction; (c) An energy gap is opened in Dirac systems with broken inversion symmetry. The arrows indicate interband transitions at different valleys, and the circular arrows represent different circularly polarized light^[28].

空间反演对称性破缺的石墨烯体系具有内禀的非零贝里曲率(Berry curvature)和能谷陈数(valley Chern number)^[36,37], 这是该体系拓扑性质的来源. 六方氮化硼(h-BN)基底与单层石墨烯的相互作用可以打破空间反演对称性^[36,38,39], 从而使石墨烯在狄拉克点处打开一个能隙. 由于h-BN与石墨烯晶格不匹配而形成的莫尔条纹会使石墨烯能带的能谷处产生超晶格小能带, 这在莫尔体系中是很普遍的, 导致了各种有趣的效应^[20,40-45], 通过光谱和输运方法都可以对超晶格小能带进行定量测量^[42,46-50]. 此外, 在AB堆叠双层石墨烯中加入偏置电压也可以打破空间反演对称性—该体系中上层的A亚晶格位于下层的B亚晶格之上, 当施加偏置电压时体系的层与层之间会出现能量差Δ (图1(b)右图), 能量差Δ与单层石墨烯和h-BN基底相互作用产生的能量差相似, 可以破坏体系的空间反演对称性. 理论计算表明空间反演对称性破缺的、具有能隙的单层石墨烯(图1(b)左图)的贝里曲率和轨道磁矩为^[36]:

${{{\varOmega}} _{\rm{c}}}({{k}}) = - {{z}}\frac{{2{a^2}{t^2}\varDelta }}{{{{\left( {4{a^2}{t^2}{k^2} + {\varDelta ^2}} \right)}^{3/2}}}}{{{\tau}} _z},$

${{m}}({{k}}) = - {{z}}\frac{{2{a^2}{t^2}\varDelta }}{{4{a^2}{t^2}{k^2} + {\varDelta ^2}}}\frac{e}{{2\hbar }}{{{\tau}} _z},$

其中${{{\varOmega}} _{\rm{c}}}({{k}})$和${{m}}({{k}})$分别为贝里曲率和轨道磁矩, 其中${{{\tau}} _z} = \pm 1$是能谷系数, a是晶格常数, t是有效最近邻跃迁积分, $\varDelta $表示能隙. 理论计算表明价带的贝里曲率绝对值相同符号相反, 轨道磁矩在导带和价带中具有相同的值, 对于低导带和高价带之间的跃迁, 在能谷处的狄拉克点附近可以得到近乎完美的圆偏振光选择规律(图1(c)). 上述性质在空间反演对称性破缺的狄拉克体系中是普遍存在的.
时间反演对称性决定两个不等价能谷的贝里曲率绝对值相同、符号相反, 两个不同能谷之间的能带相互连接, 因此系统总的陈数(贝里曲率在整个布里渊区内的积分)为零^[51]. 但是考虑到两个能谷间的距离很远, 散射作用很弱, 可以只对于单一能谷定义一个能谷陈数, 在空间反演对称性破缺的狄拉克体系中能谷陈数可以是非零的, 基于能谷陈数可以对能谷电子进行拓扑分析^[20,52-56], 这种意义下的能谷拓扑属于一种拓展的拓扑概念.
除去打破空间反演对称性以外, 更早期的工作表明自旋轨道耦合相互作用可以在石墨烯内引入拓扑性质, 即量子自旋霍尔效应^[34,57]. 自旋轨道耦合作用相当于对材料内的运动电子引入一个等效磁场, 这可以使能带在狄拉克点自发地打开一个能隙, 此时时间反演对称性并未被打破, 体系的陈数为0, 因此不具有与量子霍尔态相同的拓扑性质(后者具有非零的陈数). 于是人们对于这个体系存在的新的拓扑性质定义出了拓扑不变量Z₂, 取值只为1或0, 对于石墨烯的量子自旋霍尔态Z₂ = 1不同于量子霍尔效应, 量子自旋霍尔效应中边缘态同时具有两种自旋极化且运动方向相反的电子通道, 总电荷电流为零, 但自旋电流不为零; 时间反演对称性保护导致自旋相反的电子不会受到非磁性杂质的散射, 因此边缘态是无耗散的. 石墨烯的自旋轨道耦合作用非常弱, 只能在狄拉克点打开一个非常小的能隙, 因此目前在实验上还没有观测到石墨烯的量子自旋霍尔效应, 而这一效应在(Hg, Cd)Te/HgTe/(Hg, Cd)Te(量子阱)中得到了实验证实^[58].
2 -->

2.2.二维过渡金属硫族化合物(TMDs)的能谷拓扑性质

二维TMDs材料具有与石墨烯类似的蜂窝晶格结构, 单层TMDs材料缺乏空间反演对称性, 因此具有内禀的能谷对比的非零贝里曲率, 而双层TMDs材料与双层石墨烯一样, 可以通过层间偏压来打破空间反演对称性, 从而产生能谷对比的贝里曲率、轨道磁矩和光学圆二色性. 这个体系中过渡金属的d轨道电子导致其自旋轨道耦合作用比石墨烯大得多, 在重金属原子的d轨道上产生的带边电子和空穴具有强自旋轨道耦合. 二维TMDs材料提供了一个独特的体系来探索自旋和能谷之间的相互作用, 即自旋-能谷耦合, 它可以导致自旋指数与能谷指数在能带边缘处发生锁定(一个能谷只会被某一种自旋的电子所占据), 因此不同的能谷可以根据能谷光学选择规则进行选择性地激发. 此外能谷间的散射需要同时进行自旋翻转, 能谷间自旋弛豫是缓慢的^[59], 这提供了一个自旋和能谷极化的保护. 在二维TMDs中能谷霍尔效应的产生还伴随着自旋霍尔效应^[60].

拓扑和强关联是现代凝聚态物理学的两个重要主题. 最近有许多工作表明, 基于石墨烯的转角莫尔超晶格系统中存在可以使拓扑和强关联态同时实现的拓扑平带, 并可以简单地用电场控制能带拓扑结构和强关联效应. 在转角双层石墨烯、ABC堆叠三层石墨烯和转角双层堆叠双层石墨烯等体系中, 垂直的外加电场可以控制带宽, 甚至还可以控制能带的陈数, 根据特定体系和垂直电场的不同, 与两个微能谷相关的能带陈数可以是 ± 0, ± 1, ± 2和 ± 3, 这些石墨烯莫尔超晶格体系或许有希望实现许多迷人的拓扑现象, 例如(分数)量子反常霍尔效应等.
2

-->

3.1.转角双层石墨烯中的畴壁拓扑态

机械剥离的双层石墨烯天然存在AB和BA堆叠, 当一块样品中同时存在两种堆叠时, 就会在AB-BA堆叠的交界处产生畴壁. 在外加偏置电压下双层石墨烯在狄拉克点打开能隙并获得非零的能谷陈数, 堆叠的次序会导致能谷陈数发生改变, 畴壁两侧AB和BA两种不同堆叠区域在某一特定能谷的能谷陈数符号相反, 所以畴壁上存在无能隙的一维拓扑电子态^[51,61-64]. 这种拓扑手性模形成一维导电通道^[51,63] (图2(a)), 电流的传播方向由偏置电压V_i的符号和能谷指数决定, 图2(b)和图2(c)分别为层间正偏置电压和负偏置电压的情况.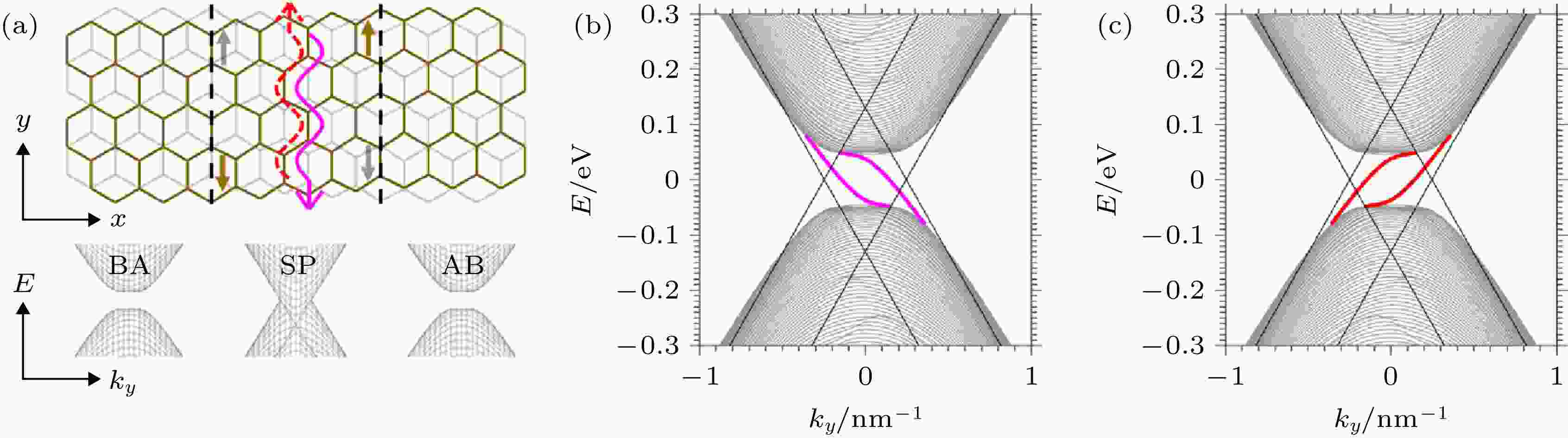
图 2 (a) 双层石墨烯中剪切型畴壁的示意图与BA、鞍点(Saddle point, SP)和AB堆叠的能带结构. 红色和粉色的箭头表示束缚在畴壁上的手性拓扑模; (b), (c) 在正(负)层间偏压${V_{\rm{i}}}$作用下K谷畴壁的能带结构^[61]
Figure2. (a) Schematic representation of a shear domain wall in bilayer graphene and the band structure of BA, Saddle point (SP), and AB stacking. Red and magenta wavy arrows represent chiral topological modes bound to the domain wall; (b), (c) Band structure of the wall under a positive (negative) interlayer bias ${V_{\rm{i}}}$ for the K valley^[61].

在小角度的转角双层石墨烯中晶格弛豫使得样品重构成一系列的AB和BA堆叠区域^[16], 不同堆叠区域的畴壁形成一个三角网格, 畴壁上的一维拓扑态也就形成了一个三角网格的导电通道, 具有新奇的输运性质^[16]. 由于畴壁一维拓扑态使得畴壁区域的局域光电导发生增强, 在近场光学实验中可以观测到这种畴壁拓扑态及其对等离激元的散射^[65].
2 -->

3.2.转角双层石墨烯中小能带的拓扑性质

最近在转角双层石墨烯的魔角^[10,11]附近观察到了绝缘态和超导态, 类莫特(Mott)绝缘体的行为和超导现象的产生意味着该体系具有强关联的物理行为, 转角双层石墨烯中转角产生的长周期莫尔条纹重构了电子能带结构, 费米能级附近产生非常平坦的小能带(图3), 电子态密度出现峰值, 库仑相互作用的影响变得很重要, 此时库仑排斥作用远大于电子动能, 导致出现每个莫尔点阵都只有一个电子占据的Mott绝缘状态^[66,67]. Mott绝缘体在强关联物理中起着核心作用, 掺杂的Mott绝缘体常被哈伯德模型所描述^[68], 而哈伯德模型会引起其他相关的现象, 如反常磁性, 甚至高温超导性^[69]. 这些实验发现大大打破了人们对石墨烯体系的预期, 引起了对层状转角莫尔体系的广泛研究.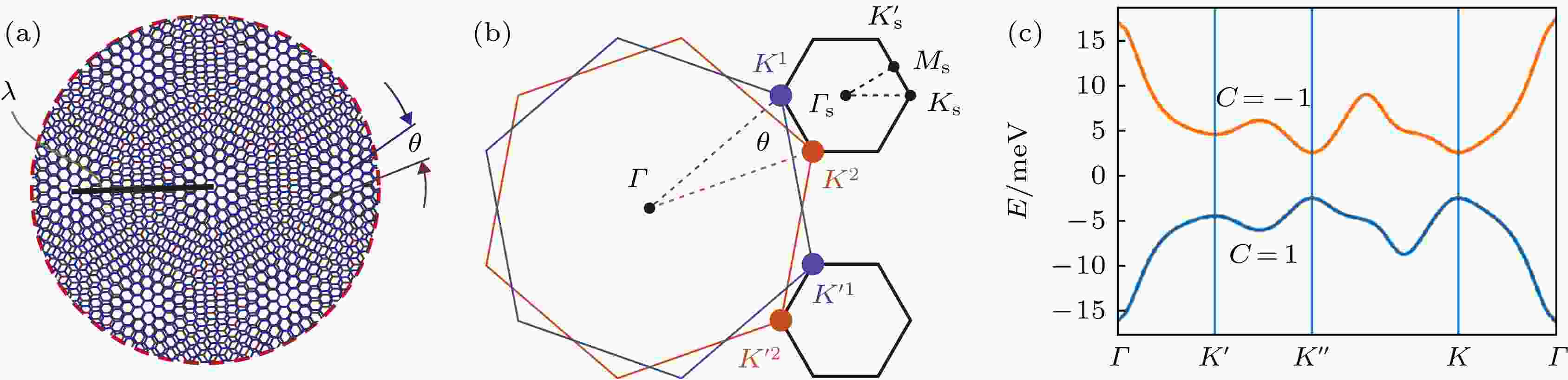
图 3 (a)转角双层石墨烯莫尔超晶格示意图^[10]; (b)小布里渊区示意图, ${K_{\rm{s}}}$, ${K'_{\rm{s}}}$和${\varGamma _{\rm{s}}}$代表小布里渊区中的点^[10]; (c)与h-BN对齐的转角双层石墨烯中小能带处的能带结构, ${\theta _{\rm{M}}} = 1.20^\circ $^[8]
Figure3. (a) The Moiré superlattice as seen in twisted bilayer graphene^[10]; (b) schematic representation of the mini Brillouin zone. ${K_{\rm{s}}}$, ${K'_{\rm{s}}}$ and ${\varGamma _{\rm{s}}}$ denote points in the mini Brillouin zone^[10]; (c) band structure for valley + of the twisted bilayer graphene aligned with h-BN in the mini Brillouin zone ${\theta _{\rm{M}}} = 1.20^\circ $^[8].

在普通的单层石墨烯或AB堆叠双层石墨烯中, 不论是与h-BN基底的相互作用还是偏置电压均未打破体系的时间反演对称性, 不同能谷的能谷陈数符号相反, 由于两个能谷在动量空间是相互连接的, 导带(或价带)总的陈数为零. 但转角双层石墨烯中的莫尔超晶格势使得每个能谷处的小能带都与其他能带分离开, 于是不同能谷间的小能带不再相互连接, 打破空间反演对称性后每个小能带都具有非零的陈数(图3(c))^[8].
考虑与h-BN对齐的、层间转角接近魔角的转角双层石墨烯, 顶部h-BN层和顶部石墨烯层的扭转角度${\theta _{{\rm{hBN}}}}$接近于零, 底部的h-BN衬底与底部石墨烯层是错位的. 顶部h-BN对顶层石墨烯有两种影响: 一是在顶层石墨烯与h-BN产生的相互作用, 二是h-BN与石墨烯晶格失配所产生的莫尔势, 它远小于转角双层石墨烯莫尔势^[70], 因此可以近似忽略.
图3(c)为根据标准连续模型^[70]计算得到的与h-BN对齐的转角双层石墨烯体系小能带处的能带结构, 由于莫尔势的周期远远大于晶格常数, 所以其代表莫尔势的能带结构区域在动量空间会非常小. 同时, 在小能带区域存在与六角布里渊区相似的能谷和相应的狄拉克点, 通过石墨烯与h-BN基底的相互作用, 可以打开小能带中能谷位置上狄拉克点的能隙. 除此之外, 小能带与上下其他能带是分离的, 因此可以定义其陈数, 计算得出在能谷的导带和价带上分别具有陈数C = 1, –1. 理论预言可以通过控制系统的陈数和填充数而获得量子反常霍尔效应、自旋极化的量子谷霍尔绝缘体等不同的效应^[17], 实验上初步观测到了相关的迹象^[71].
2 -->

3.3.ABC堆叠三层石墨烯

ABC堆叠三层石墨烯与六方氮化硼衬底(ABC TG/h-BN)对齐的体系(图4(a))中利用莫尔超晶格实现了一种可以调节的Mott绝缘体, 其库仑相互作用和动能之间的竞争关系可以通过原位调节发生变化^[13,14], 该体系最有趣也是最重要的一点是它可能包含的拓扑和强关联性质.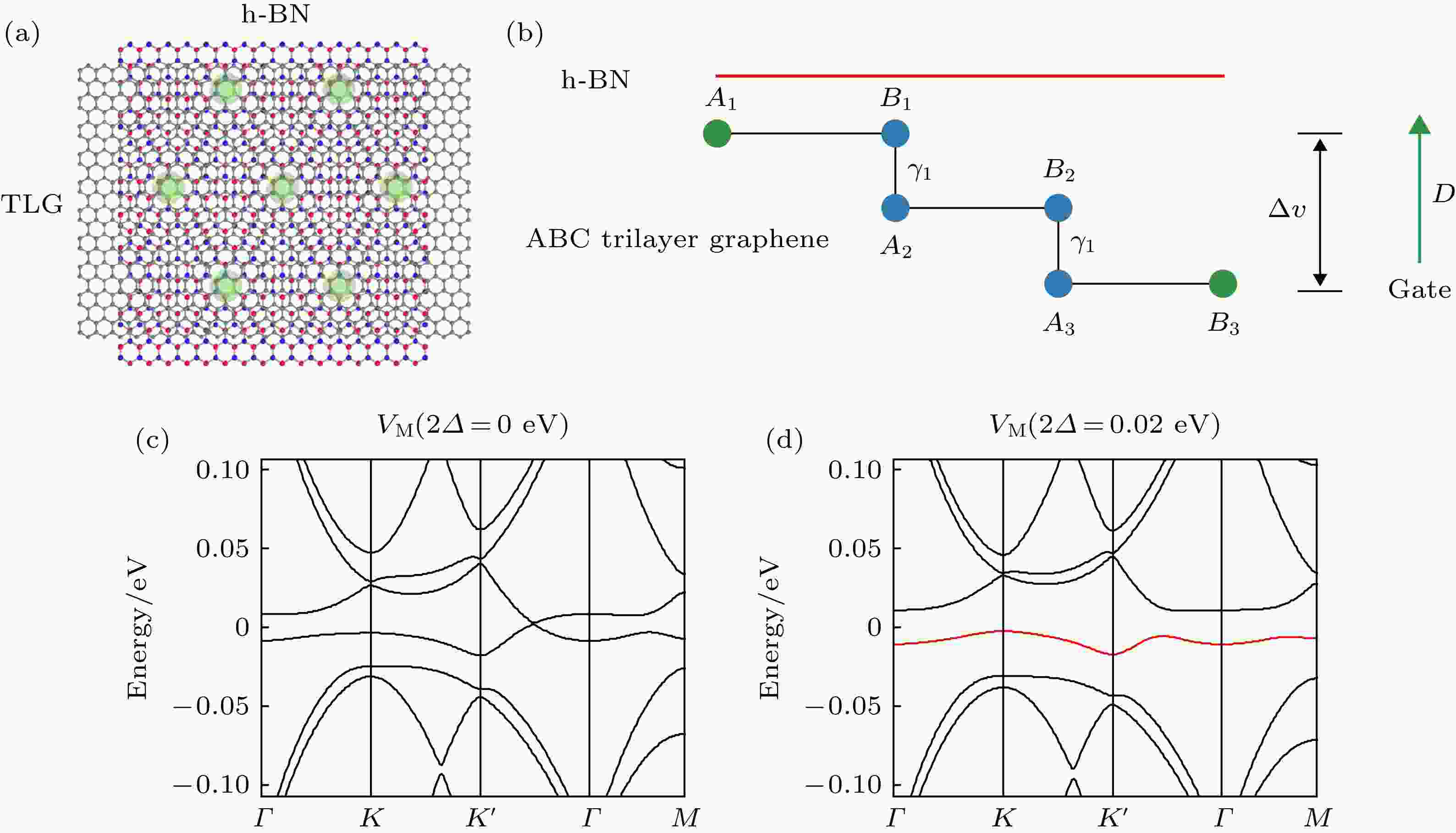
图 4 (a) ABC TLG/h-BN的莫尔超晶格示意图, 为了图像清晰, 只显示了顶部h-BN和底部石墨烯最上层的原子^[13]; (b) ABC堆叠三层石墨烯/h-BN体系示意图, 垂直电场使顶部和底部石墨烯层之间的电子能量差为$\Delta V$^[12]; (c), (d)分别为没有和有垂直电场时的小布里渊区处的能带图; (d)垂直电场在顶部和底部石墨烯层之间产生20 mev的电位差, 导致了一个带宽减小的孤立的空穴型小能带, 增强了强关联作用, 从而生成了可调节的Mott绝缘体态^[13]
Figure4. (a) Schematic of ABC TLG/h-BN Moiré superlattice. Only atoms of the top h-BN layer and the bottom graphene layer are shown for clarity^[13]; (b) illustration of the ABC stacked trilayer graphene/h-BN system. A vertical electric field introduces an energy difference $\varDelta V$ for electrons between the top and the bottom graphene layer^[12]; (c), (d) energy dispersion of the two electron and hole minibands without and with a vertical electrical field, respectively. The vertical electrical field in (d) generates a potential difference of 20 meV between the top and bottom graphene layers, leading to an isolated hole minibands with strongly suppressed bandwidth. The reduced electronic bandwidth relative to the Coulomb interaction enhances the electron correlation, and leads to the tunable Mott insulator states^[13].

Zhang等^[7]对AB堆叠双层石墨烯和ABC TG/h-BN进行了计算, 这种n层石墨烯的单个能谷+K的有效哈密顿量为

${H_ + }\left( {{k}} \right) = \left( {\begin{array}{*{20}{c}}{\dfrac{U}{2}}&{A{{\left( {{k_x} - {\rm{i}}{k_y}} \right)}^n}}\\{A{{\left( {{k_x} + {\rm{i}}{k_y}} \right)}^n}}&{ - \dfrac{U}{2}}\end{array}} \right),$

这里U是质量项, $A = {{{v^n}}}/{{\gamma _1^{n - 1}}}$, $v \approx {10^6}$m/s是石墨烯狄拉克点的电子速度, ${\gamma _1} \approx 380\;{\rm{meV}}$是层间耦合参数(图4(b)). n代表层数, 对于n = 1的单层石墨烯, U是两个子晶格之间的能量差. 对于n = 2的AB堆叠双层石墨烯和n = 3的ABC堆叠三层石墨烯, U为顶层与底层的能量差. 而在双层石墨烯和三层石墨烯中, 垂直电场可以很容易地控制U ^[13]. (3)式本质与Xiao等^[36]和Yao等^[37]的模型相同, 具有内禀的贝里曲率, 在施加垂直电场时可以打开能隙, 使价带和导带具有非零的陈数.
ABC堆叠三层石墨烯的电子具有三次方的能量色散和非常大的有效质量^[72-76] (即能带非常平), 因此ABC TLG/h-BN异质结构中的莫尔超晶格^{[38,46-48,77-79]}可以产生非常平坦的小能带, 这有利于强关联现象的出现. 位移场D为上下石墨烯层间的电子提供了一个能量差$\Delta V$, 如图4(b)所示, 当施加偏压时, 孤立的价带会与导带分离(图4(c)和图4(d)), 价带变得更加平坦. 通过不同的偏压, 还可以使孤立的价带具有非零的陈数, 使其具有可调节的能带拓扑结构^[7,14].
实验上已经观测到了ABC TLG/h-BN异质结构中的Mott态^[13], 每个填充的小能带在一个莫尔原胞中包含4个电子(自旋和能谷简并), Mott绝缘态出现在1/4和1/2填充处, 分别对应于每个位置的一个电子和两个电子. Mott能隙可以通过垂直电场调制, 同时电子掺杂可以通过门电压调节来填充从一个Mott绝缘态到另一个Mott绝缘态的能带(图5(a)). 理论预言D < 0时空穴小能带为拓扑非平庸态(即陈数C ≠ 0), D > 0时为拓扑平庸态(C = 0)^[14]. 最近的实验在ABC TLG/h-BN中观测到霍尔电阻在h/2e² 量子化, 对应于C =2 的陈绝缘体态(图5(a)), 这个拓扑态表现出强铁磁性(图5(b))^[14].
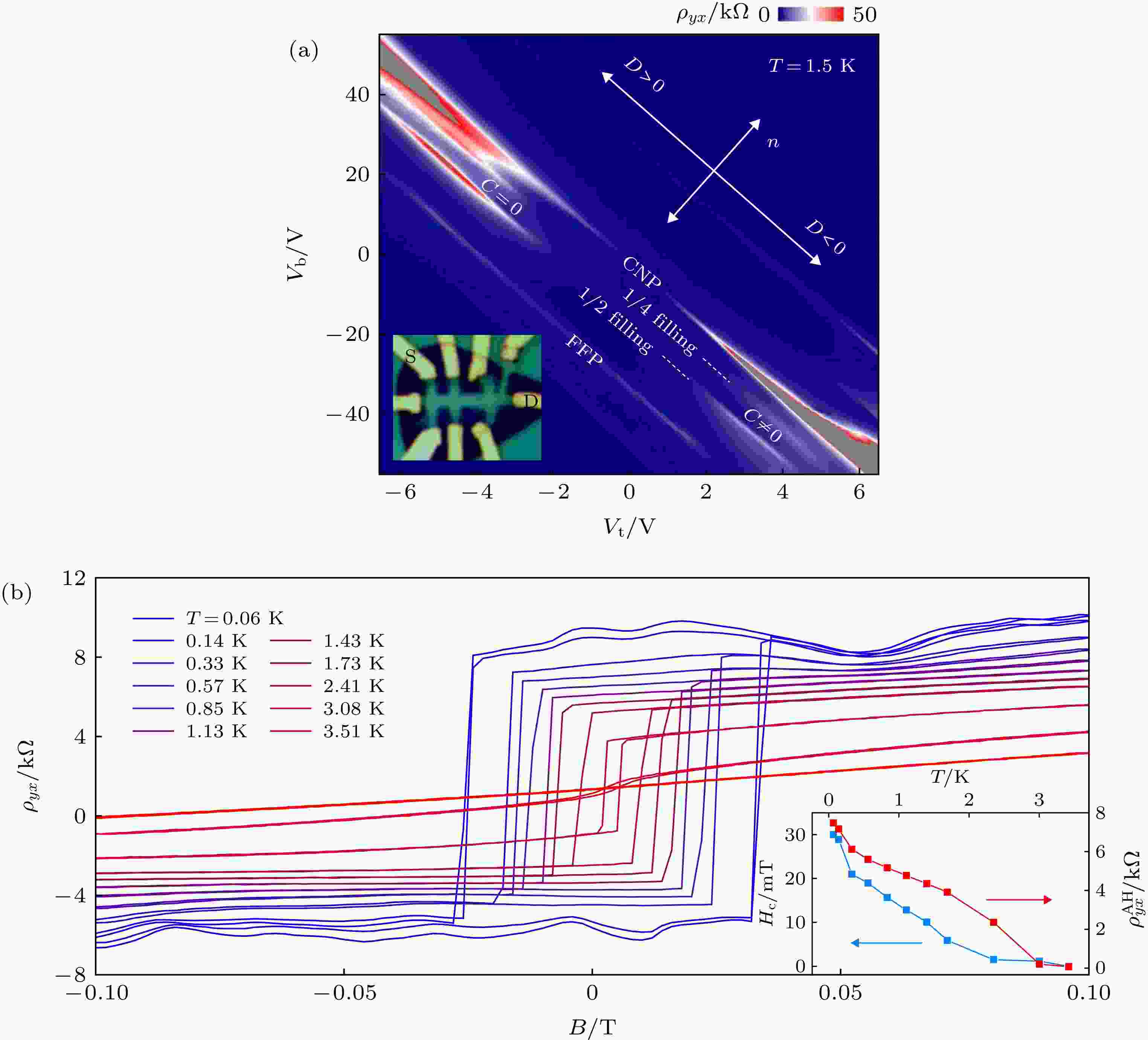图 5 ABC TLG/h-BN, 纵向电阻率图和不同磁场下的霍尔电阻率图　(a) T = 1.5 K时以${V_{\rm{t}}}$和${V_{\rm{b}}}$为函数的纵向电阻率图, 箭头分别表示掺杂(n)和电位移场(D)的方向. 理论预言D < 0时空穴小能带为拓扑非平庸态(即陈数C ≠ 0), D > 0时为拓扑平庸态(C = 0); (b)在1/4填充和D = –0.5 V/nm时不同的温度下的霍尔电阻${\rho _{yx}}$, 显示出清晰的反常霍尔效应(AH)的信号并伴随着很强的磁滞回线. 在温度T = 0.06 K时, 横向电阻$\rho _{yx}^{{\rm{AH}}} = 8\;{\rm{k}}\Omega $和矫顽场${H_{\rm{c}}} = 30\;{\rm{mT}}$. 插图: 矫顽场和AH信号与温度的函数^[14]
Figure5. ABC TLG/h-BN, color plot of the longitudinal resistivity and Magnetic field dependent ${\rho _{yx}}$: (a) Longitudinal resistivity as a function of ${V_{\rm{t}}}$ and ${V_{\rm{b}}}$ at T = 1.5 K. The arrows show the direction of changing doping (n) and displacement field (D), respectively. It was predicted theoretically that the hole miniband is topological (Chern number C ≠ 0) for D < 0 and trivial (C = 0) for D > 0; (b) magnetic field dependent ${\rho _{yx}}$ at 1/4 filling and D = –0.5 V/nm at different temperatures. The Hall resistivity displays a clear AH signal with strong ferromagnetic hysteresis. At the base temperature of T = 0.06 K, the AH signal can be as high as $\rho _{yx}^{{\rm{AH}}} = 8\;{\rm{k}}\Omega $ and the coercive field is ${H_{\rm{c}}} = 30\;{\rm{mT}}$. Inset: Extracted coercive field ${H_{\rm{c}}}$ and AH signal $\rho _{yx}^{{\rm{AH}}}$ as a function of temperature^[14]

3 -->

3.4.转角双层堆叠双层石墨烯(TBBG)

最近研究发现TBBG具有与转角双层石墨烯相似的性质, 包括电调控的强关联绝缘体、超导^[16-18]和理论预言的拓扑性质^[19]. TBBG具有两种不同的堆积形式, 分别为AB-AB与AB-BA堆积, 这两种不同的堆积方式具有相似的能带结构, 但与之相关的陈数则完全不同. 特别是在没有外加垂直电场的情况下, 当费米能级处于能隙时AB-AB体系是一个平庸的绝缘体, AB-BA则是一个能谷霍尔绝缘体. 而当施加垂直电场后AB-AB体系的陈数不再为0^[19].
实验上, 在大转角(1.23°)且每个莫尔原胞填充为1/4, 以及小转角(0.84°)且原胞填充数较高时, 都出现了多种强关联态. 能带计算结果表明, 通过施加电位移场小转角TBBG电荷中性点附近的能带会出现多平带状态, 每一个平带对应于不同的填充情况, 又对应着多种强关联效应^[17]; 在不同的填充下, 体系的自旋和能谷带来的四重简并也会对应于不同的极化状态. 对于不同的电位移场, 外加磁场可以诱导体系从自旋极化到能谷极化之间的转变, 也会导致塞曼效应和能谷塞曼效应的竞争^[17].

利用散射型扫描近场光学显微技术(s-SNOM)可以对石墨烯莫尔体系进行纳米空间分辨率的光学研究^[65,80-82]. 石墨烯莫尔体系的许多重要物理性质的能量范围都在红外波段, 例如拓扑效应、强关联效应、带间跃迁、等离激元等, 但是传统光学研究手段受到衍射极限的限制在中红外波段只能达到几微米(半波长)的空间分辨率, 这对于研究石墨烯莫尔体系(莫尔条纹的周期在几纳米到几百纳米左右)是远远不够的.
如图6(a)所示, s-SNOM是基于原子力显微镜(AFM)的, 将红外光照射在曲率半径为20 nm左右的金属化针尖尖端, 在避雷针效应作用下针尖下方会产生强烈增强的局域光场, 由于针尖与样品的距离远小于波长, 这个局域光场携带有近场光学信息, 近场信号是由样品的局域介电函数以及针尖与样品的耦合决定的, 该近场信号经过针尖散射变为可被探测的远场信号. s-SNOM的空间分辨率通常由针尖曲率半径决定, 可以达到10 nm量级的空间分辨率, 样品表面的局域电磁场带有材料自身的电子结构、准粒子激发、局部应力响应等信息, 因此s-SNOM可以在高空间分辨率下研究材料的局域性质. 由于近场信号与样品的局域介电函数直接相关, s-SNOM的一个重要应用是研究材料的空间不均匀性、相分离和相变. 例如金属与绝缘体的介电函数差别非常大, 导致了s-SNOM信号的巨大差异, 因此利用s-SNOM可以观察材料金属绝缘体相变的变化过程^[83], 并得到纳米级空间分辨的局域介电函数.
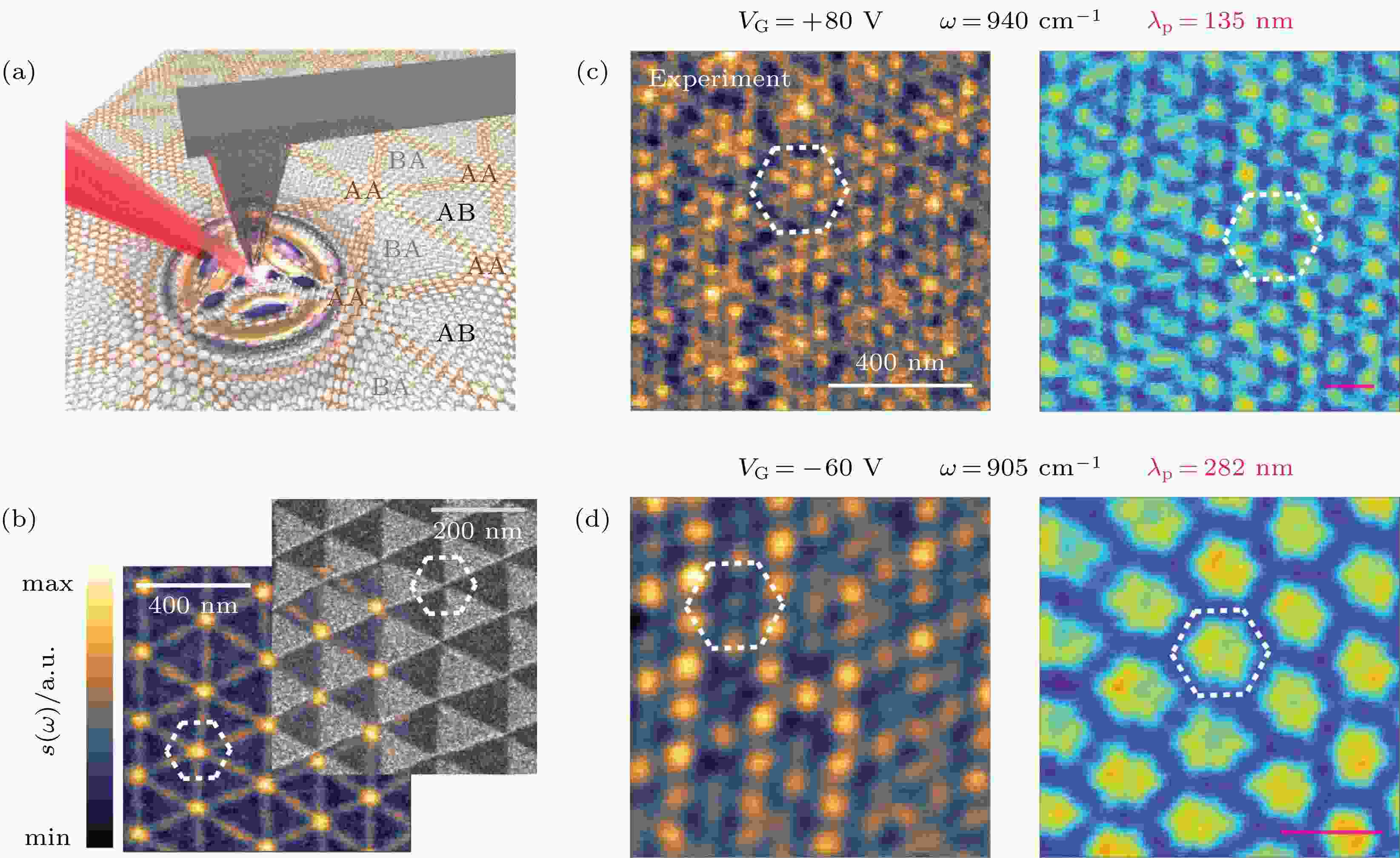图 6 (a) 红外s-SNOM实验技术示意图. AB、BA和AA表示双层石墨烯堆积方式的周期性改变; (b) (左)显示转角双层石墨烯中由畴壁晶格形成的纳米光子晶体. 这种反差是由于畴壁的局部光学导电性增强造成的. (右)转角双层石墨烯样品的暗场TEM图像; (c), (d) 分别为${\lambda _{\rm{p}}}$ = 135 nm和282 nm时获得的红外s-SNOM图像^[65]
Figure6. (a) Schematic of the IR s-SNOM experimental technique. AB, BA, and AA label periodically occurring stacking types of graphene layers; (b) (Left) isualizing the nano-light photonic crystal formed by the domain wall in twisted bilayer graphene. The contrast is due to enhanced local optical conductivity at domain wall. (Right) Dark-field TEM image of a twisted bilayer graphene sample; (c), (d) IR s-SNOM images obtained for ${\lambda _{\rm{p}}}$ = 135 nm and 282 nm, respectively^[65].

极化激元是物质中极化电荷与光场耦合后集体振荡形成的、光与物质的耦合模式, 比较典型的有金属中的等离激元、极性晶体中的声子极化激元、半导体激子极化激元等. 石墨烯是一种优良的能够传播等离激元的介质, 其等离激元特性很容易由载流子密度^[84,85]和介电环境^[80,86]控制. 但极化激元自身带有非常大的动量$q$, 不能与在自由空间中传播的光发生耦合; s-SNOM的针尖可以使散射光具有额外的动量, 可以避免极化激元与自由传播光之间的动量失配^[84], 从而实现极化激元的激发. s-SNOM可以扫描探测在样品表面激发的极化激元的性质, 并可以呈现出具有纳米级分辨率的极化激元图像. 在石墨烯中, 等离激元被其晶界和畴壁散射, 并与传播向边界的等离激元发生干涉形成干涉条纹, s-SNOM可以探测到等离激元的干涉条纹^[84,85].
石墨烯莫尔体系的近场光学研究已经取得了许多进展. 在双层转角石墨烯中, 由于晶格重构引起的畴壁(也称为孤子)会将AB和BA堆叠区域分开^[65,87], 形成周期性的三角网状格子(图6(b)), 格子的大小和周期性由堆叠角度控制. 在s-SNOM实验中, 双层石墨烯中的表面等离激元会被畴壁散射^[22,61], 类似于单层石墨烯中等离激元被晶界散射^[88]. 由于两侧区域中能谷陈数的反转, 畴壁中存在无能隙的手性一维电子态, 这些手性一维态本质是一种拓扑现象并受拓扑保护 ^[59], 可以无耗散地在畴壁中传播并保留相关的能谷指数, 能谷指数相反的电子相向运动. 这种畴壁一维拓扑态可以在s-SNOM实验中观测到^[61,64]: 一维拓扑态会引起畴壁上光电导的局域增强, 从而增强了畴壁区域对于红外光的响应, 表现为s-SNOM成像中畴壁区域明显的亮条纹(图6(b)左图). 畴壁与其他区域光电导的不同会导致样品表面传播的等离激元在畴壁处产生散射和干涉, 形成干涉图像; 在不同的门电压下石墨烯的等离激元波长会产生改变, 在被畴壁散射后可以形成多种不同的干涉图像^[65](图6(c) 和图6(d)), 所以晶格重构后的双层转角石墨烯可以看作是一种天然的新型等离激元光子晶体.
利用s-SNOM对等离激元的测量能够获得石墨烯莫尔超晶格电子能带结构的重要信息. 由莫尔超晶格势引入的小能带会带来额外的带间跃迁通道, 影响光学电导率, 最终影响等离激元的波长、振幅、耗散等性质, 基于这个原理, 最近的一个工作通过s-SNOM实验得到石墨烯/h-BN 莫尔能带的信息^[80].
图7显示计算得到的石墨烯/h-BN 莫尔能带, 当载流子密度较低时费米能级无法接触到小能带区域(图7(b)), 光电导主要由γ点处的狄拉克点提供; 当载流子密度提高时(图7(c)), 费米能级接触到小能带区域, 箭头处产生的额外光学跃迁通道会改变材料的光学电导率^[80]. 图8展示了在不同的载流子密度下, 石墨烯与石墨烯/h-BN等离激元具有相似的波长, 但振幅和衰减率不同, 这是由于后一系统中带间跃迁所带来的额外的等离激元能量耗散通道所导致的. 实验测量和分析显示, 石墨烯与石墨烯/h-BN中等离激元行为的差异来源于后者小能带区域带间跃迁的贡献^[80].
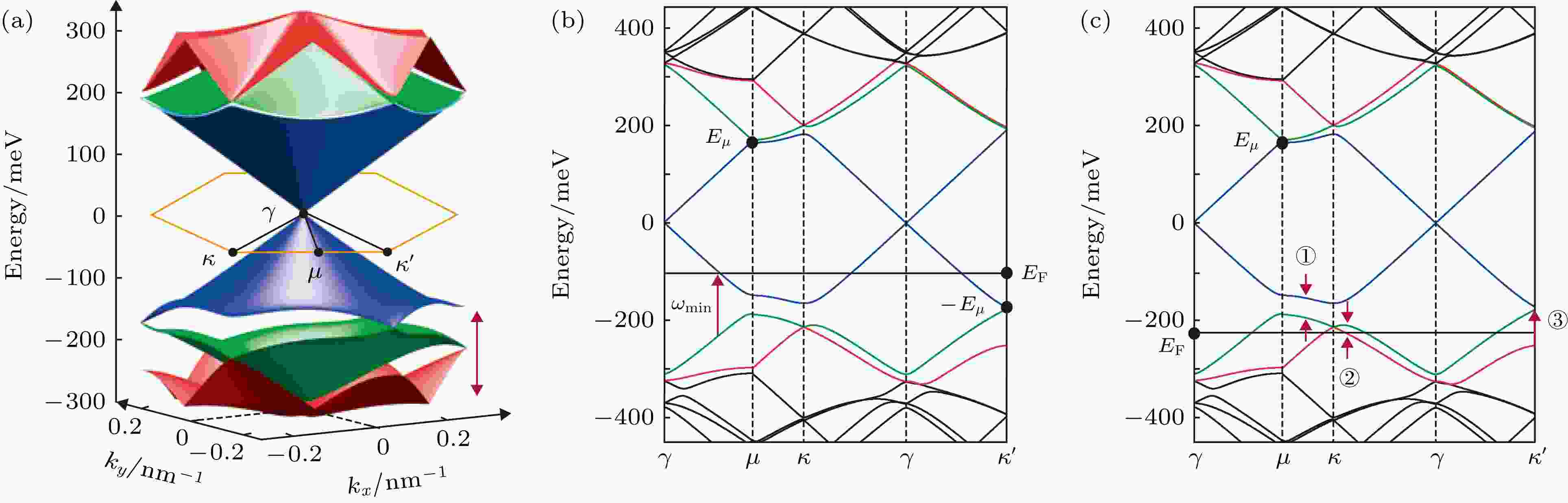图 7 (a) 通过唯象模型得到的石墨烯/h-BN电子能带结构的三维表示; (b) ${E_{\rm{F}}}$小于${E_\mu }$~170 meV时的光学跃迁; (c) ${E_{\rm{F}}}$大于${E_\mu }$时莫尔势导致多个额外的光学跃迁通道, 这些跃迁提高电导率, 同时对等离激元波长产生了一个额外的带间跃迁贡献^[80]
Figure7. (a) 3D representation of the electronic band structure of graphene/h-BN obtained from the phenomenological model; (b) Optical transitions at 170 mev, for a magnitude of the ${E_{\rm{F}}}$ smaller than ${E_{\rm{\mu }}}$; (c) For a magnitude of ${E_{\rm{F}}}$ larger than ${E_\mu }$ one finds multiple additional channels for optical transitions, all initiated by the moirépotential. These transitions enhance the conductivity and also yield an interband contribution to the plasmonic wavelength in addition to intraband contribution^[80].

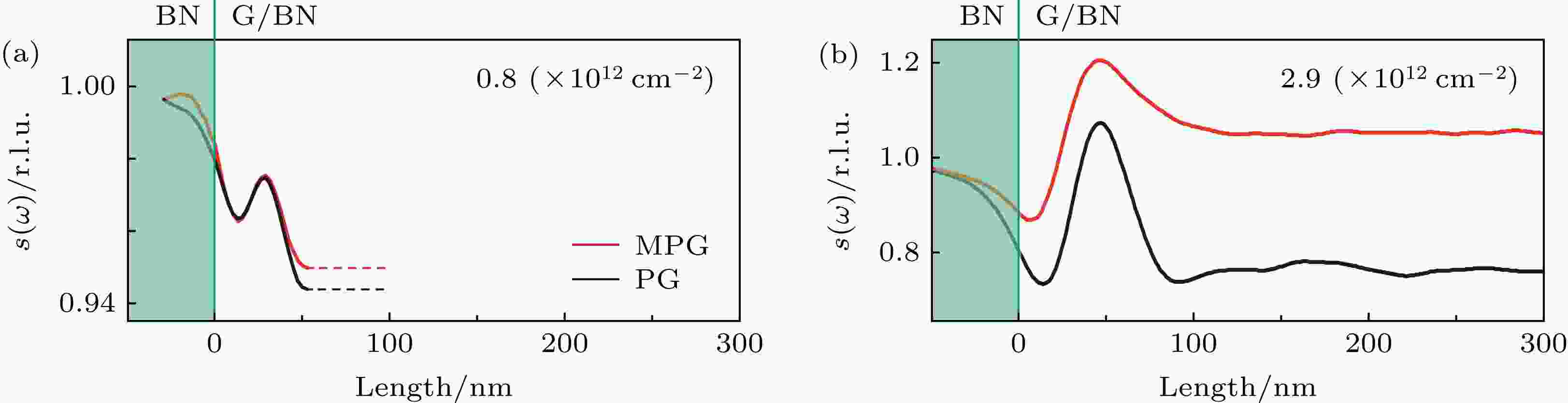图 8 不同载流子密度下莫尔石墨烯和普通石墨烯的等离激元谱线^[80]　(a) 0.8 × 10 ¹²cm^–2; (b) 2.9 × 10¹² cm^–2
Figure8. Plasmonic line-profiles for both Moiré graphene and plain graphene at different carrier densities^[80]: (a) 0.8 × 10¹² cm^–2; (b) 2.9 × 10¹² cm^–2.

对于石墨烯莫尔体系, 不同的转角和堆叠会产生不同的能带结构及其内禀的拓扑和强关联性质, 这将使相关光学研究变得更加困难. 但通过施加不同的入射光频率和电压调控, 并分析s-SNOM测量得到的光谱信息、等离激元干涉条纹的振幅及相位等, 可以在纳米空间分辨率下获得被测样品的介电函数、带间跃迁、能带结构等重要物理信息, 这对于研究石墨烯莫尔体系的小能带和平带的性质具有重要意义.

石墨烯莫尔超晶格体系的最新进展为拓扑物理的研究带来了新的活力, 该体系中能带陈数、填充数以及能带宽度的连续电学调控使得拓扑和强关联这两个凝聚态物理学重要主题结合在了一起, 这不仅带来了更加丰富的物理现象, 也为拓扑物理研究提供了新的思路. 在未来几年中, 石墨烯莫尔超晶格体系(尤其是魔角附近和超小角度体系)的能带结构、超导态和各种拓扑态(例如陈绝缘体和量子反常霍尔态)的形成机制、拓扑和强关联同时存在带来的新奇物理效应等都是非常重要但目前尚未理解的研究课题, 利用电场、磁场、应变和异质结构等手段调控和构造各种新的量子态也将是非常有意义的努力方向. 实验方面, 可以预期几乎所有实验技术在这个体系中都可能会揭示令人惊奇的新物理效应. 近场光学技术作为石墨烯莫尔体系研究的一个重要实验手段, 可以在纳米空间分辨率下提供该体系的许多重要物理信息. 可以预见, s-SNOM技术今后将为石墨烯莫尔体系中各种新奇的拓扑态、拓扑现象和强关联效应等研究带来更多的进展.