摘要:基于宽带光源微光学元件(如集成导光板)在衍射色散方面的设计需求, 本文构建了宽带光源微光学元件衍射理论分析模型, 探讨分析了衍射光谱的色度规律特性, 提出并定义了能准确定量衡量衍射光束色散程度的色散量C, 同时明确给出了零色散的边界判据点. 通过对研制的矩形位相光栅进行测试分析, 所得的光谱色度特性规律与理论分析结果相一致, 实验结果验证了本文提出的色散度判据参量C和零色散边界点的正确性. 本文提出的宽带光源色散度判据参量C、零色散边界判据点, 不仅为集成导光板结构参数的设计提供指导, 而且也能为其他宽带微光学元件的设计过程中探讨色散特性时提供指导.
关键词: 微光学元件/
宽带光源/
无色散/
集成导光板

English Abstract

全文HTML

--> --> -->

众所周知, 衍射微光学元件在窄带光源方面应用广泛^[1-6]. 随着微结构制作工艺的快速发展及微光学元件的集成化, 衍射微光学元件在宽带光源方面的应用也日益广泛, 如将微透镜阵列^[7]、径向光栅^[8]、非对称的衍射光筛^[9]、折射率及高度相互匹配的多层衍射元件^[10]、高深宽比不同占空比的亚波长矩形光栅^[11]等应用于光耦合、光束整形和无色散方面. 本课题组研究设计的一体化导光板也是宽带光源折衍整形、无色散元件^[12], 通过优化设计一体化导光板上下表面的微结构参数及微结构阵列分布方式, 将位于导光板一侧的由点光源白光发光二极管(LED)组成的灯带整形成高亮度、高光能利用率的均匀白光面光源^[13]. 为了提高背光模组的光能利用率等性能参数, 国内外研究机构在研究设计新型集成导光板时, 已将其结构特征尺寸由数十微米发展到微米、亚微米级别, 其设计理论由几何光学到物理光学甚至到矢量理论. 如, 本课题组于2004年就提出上表面熔合二元光学衍射元件阵列的新型导光板^[14]; 清华-富士康纳米科技研究中心提出由应力双折射材料构成的偏振型导光板^[15]; 韩国BK21中心提出上表面为二维光栅点阵型的导光板^[16]; 荷兰的飞利浦欧洲研究院在导光板上表面设置亚波长浮雕光栅^[17,18].
随着新型集成导光板的结构特征尺寸由数十微米向微米、亚微米级别发展, 衍射色散现象必然会成为研究设计无色散LED背光模组的一个突出问题. 故在研究设计新型集成LED背光模组时, 需要预判LED背光模组的出射光场无色散时对应的集成导光板结构特征尺寸的边界点, 以此确定是否需要考虑衍射色散现象. 然而, 研究衍射光学元件的色散问题一般是针对窄带光源的; 针对微光学元件在宽带光源光照条件下的衍射光谱色散特性的一般性规律分析讨论尚未见报道. 因此, 基于研究设计新型集成导光板方面的实际所需, 本文探究在宽带光源照射条件下的微光学元件的衍射光谱色散规律特性, 摸索衍射光束无色散边界条件, 为新型集成导光板的参数设计提供指导.

2

-->

2.1.宽带光源微光学元件衍射理论模型

本文以典型的一维矩形位相光栅(rectangular phase grating, RPG)及普遍使用的白光LED光源为模型, 分析讨论微光学元件在宽带光源光照条件下的菲涅尔衍射光谱色度特性, 并摸索衍射光束无色散时的边界条件.
当LED线光源与光栅的相对位置和角度不同时, 接收面的衍射光谱也不同. 光栅的任一点位置都可接收到整个LED线光源所发出的光; 而光栅的不同位置所接收到的LED线光源的光束是不尽相同的, 衍射的光谱也是不同的. 因此, 当考虑所有的情况时, 理论模型将很复杂. 本文将上述物理模型进行简化, 仅讨论LED线光源平行于光栅且位于其中间位置, LED全部光束照射至光栅中间时的光束衍射情况. 构建的理论分析模型如图1所示, 其中, a, d, Δh分别为矩形位相光栅的脊宽、周期、槽深; z表示观察距离; D为白光LED与矩形位相光栅的距离; l为LED的线宽(本文仅探讨一维线宽情况); θ为入射光束锥角(指的是LED光源全线宽l发射的光束相对于矩形位相光栅中央被照点的张角); y轴箭头朝里.
图 1 宽带光源微光学元件衍射理论模型图(宽带光源为白光LED, 微光学元件为矩形位相光栅)
Figure1. Diffraction theoretical model under the broadband light source illumination. The broadband light source is a white LED, and the microstructure array is the RPG.

由于菲涅耳衍射理论只适用于单色平行光束, 为了探讨矩形位相光栅在白光LED宽带光源光照下的菲涅耳衍射光谱特性, 将其入射光束进行两个方面的简化: 第一, 将光束锥角为θ的LED光源全线宽l发射的入射光束等价成由很多束不同入射方向(不同入射方向具有不同光强度)光束锥角δ极小的近似细平行光束构成(细光束的宽度为Δl), 即该理论模型的入射光束可视为由很多束不同入射方向的细平行光束构成; 第二, 由于白光LED是宽光谱特性的, 基于色度学的色光匹配混合原理^[19], 将白光LED等价分解成红、绿、蓝三基色的混合光. 因此, 该简化模型称为宽带光源微光学元件衍射理论模型, 其入射光束最终简化等效成由很多束不同入射方向不同强度的三基色细平行光束的叠加.
2 -->

2.2.宽带光源微光学元件衍射光场

当宽带光源微光学元件衍射理论模型的入射光束简化之后, 根据菲涅耳衍射理论, 分别计算很多束不同入射方向、不同强度的三基色细平行光束在矩形位相光栅衍射后的光场分布; 然后再综合分析在观察平面上三基色光叠加后的光场及色度特性.
本文应用的白光LED线宽l = 2.5 mm, 假定细光束的锥角δ = 0.5°, LED入射光束锥角θ与D (LED与光栅的距离)直接相关, 即θ = 2 arctan[l/(2D)]. 白光LED的色品坐标为x = 0.2966, y = 0.2983, 计算其可由色度量为R = 0.7325, G = 0.9249, B = 1.2195的三原色光(R)-(λ_R = 700 nm), (G)-(λ_G = 546.1 nm), (B)-(λ_B = 435.8 nm)混合而成^[19]. 单束平面波复振幅^[20]、一维矩形位相光栅的复振幅透过率^[20]、菲涅耳衍射区传递函数^[21]的表达式分别如(1), (2), (3)式所示. 联立(1), (2), (3)三个表达式, 利用卷积定理, 可计算得单色细平行光束经矩形位相光栅衍射后的频谱复振幅如(4)式所示.

${U_0}\left( {{x_0},{y_0}} \right) = A\exp \left[ {{\rm{j}}2{\text{π}}\left( {{f_\alpha }{x_0} + {f_\beta }{y_0}} \right)} \right],$

$\begin{split} t( {{x_0},{y_0}} ) =\, & \Big[\big( {{\rm{e}}^{{\rm{j}}{\phi _2}}} - {{\rm{e}}^{{\rm{j}}{\phi _1}}} \big){\rm{rect}} \Big( \frac{{{x_0}}}{a} \big) \\ & \times\frac{1}{d}{\rm{comb}}\Big( \frac{{{x_0}}}{d} \Big) + {{\rm{e}}^{{\rm{j}}{\phi _1}}}\Big] \\ & \times{\rm{rect}}\left( {\frac{{{x_0}}}{W}} \right){\rm{rect}}\left( {\frac{{{y_0}}}{L}} \right),\end{split}$

$H\left( {{f_x},{f_y}} \right) = \exp \left( {{\rm{j}}kz} \right)\exp \left[ { - {\rm{j}}{\text{π}}\lambda z\left( {f_x^2 + f_y^2} \right)} \right],$

$\begin{split} & U\left( {{f_x},{f_y}} \right) = F\left\{ {{U_0}\left( {{x_0},{y_0}} \right)} \right\} * F\left\{ {t\left( {{x_0},{y_0}} \right)} \right\} \cdot H\left( {{f_x},{f_y}} \right) \\ = \, & \bigg\{ \left( {{{\rm{e}}^{{\rm{j}}{\phi _2}}} - {{\rm{e}}^{{\rm{j}}{\phi _1}}}} \right)\frac{{aAWL}}{d}\sum\limits_{n = - \infty }^\infty \sin {\rm{c}}\left( {\frac{{an}}{d}} \right)\sin c\left[ {W\left( {{f_x} - \frac{n}{d} - {f_\alpha }} \right)} \right]\sin {\rm{c}}\left[ {L\left( {{f_y} - {f_\beta }} \right)} \right] \\& + {{\rm{e}}^{{\rm{j}}{\phi _1}}}AWL\sin {\rm{c}}\left[ {W\left( {{f_x} - {f_\alpha }} \right)} \right]\sin {\rm{c}}\left[ {L\left( {{f_y} - {f_\beta }} \right)} \right] \bigg\} \times \exp \left( {{\rm{j}}kz} \right)\exp \left[ { - {\rm{j}}{\text{π}}\lambda z\left( {f_x^2 + f_y^2} \right)} \right], \\\end{split} $

其中, f_α = cosα/λ, f_β = cosβ/λ, α, β分别为入射细平行光束与x轴、y轴的夹角; f_x = x/(λz), f_y = y/(λz)分别是观察平面的频谱坐标; A为入射细平行光束的振幅; ?₁, ?₂分别为矩形位相光栅每个周期内的两部分位相延迟; W, L分别是衍射孔径的宽和长. 在本文中, β = 90°, A的取值由三原色光色度量(R, G, B)和LED朗伯光源出光角(即90°–α)决定, W = Δl.
由(4)式可知, 一维矩形位相光栅将入射光调制成2 |n|+1束光输出, 可依次推导出细平行光束的各级衍射光的峰值位置x_n、各级次光强的半高全宽Δx、观察平面上零级(n = 0)光束的能量计算表达式、第n能级光束的能量计算表达式分别如(5)—(8)式所示:

${x_n} = \left( {{{n\lambda z} / d}} \right) + z \cdot \cos \alpha,$

$\Delta x = {{0.886\lambda z} / W},$

$\begin{split}{E_{n = 0}} =\, & \Big[{{\left( {{a / d}} \right)}^2} + {{\left( {1 - {a / d}} \right)}^2} + 2\left( {{a / d}} \right)\left( {1 - {a / d}} \right) \\ & \times \cos \left( {{\phi _2} - {\phi _1}} \right)\Big]{A^2}WL,\\[-15pt]\end{split}$

${E_n} = 2\left[ {1 - \cos \left( {{\phi _2} - {\phi _1}} \right)} \right]{\left( {{a / d}} \right)^2}\sin {{\rm{c}}^2}\left( {{{an} / d}} \right){A^2}WL.$

最后, 结合上述LED光源两方面的简化分解, 联立观察平面衍射光场的频谱复振幅分布公式(4)、各级衍射光的峰值位置x_n计算式(5)、各级次光强的半高全宽Δx计算式(6)、各级衍射光束能量计算式(7)和(8), 即可综合求解得LED宽带光源经矩形位相光栅衍射后观察平面上的三原色光的零级、± 1级的相对衍射光强分布.
假定, 矩形位相光栅的占空比r = a/d = 0.5, 槽深Δh = 1 μm, 材料的折射率为1.5, 观察距离z为明视距离250 mm. 当LED入射光束锥角θ和矩形位相光栅周期d分别为(7.5°, 4 μm), (7.5°, 8 μm), (7.5°, 40 μm), (14.5°, 4 μm), (102.5°, 4 μm)时, 计算求得零级、± 1级三衍射级次相对光强I分布, 如图2所示.
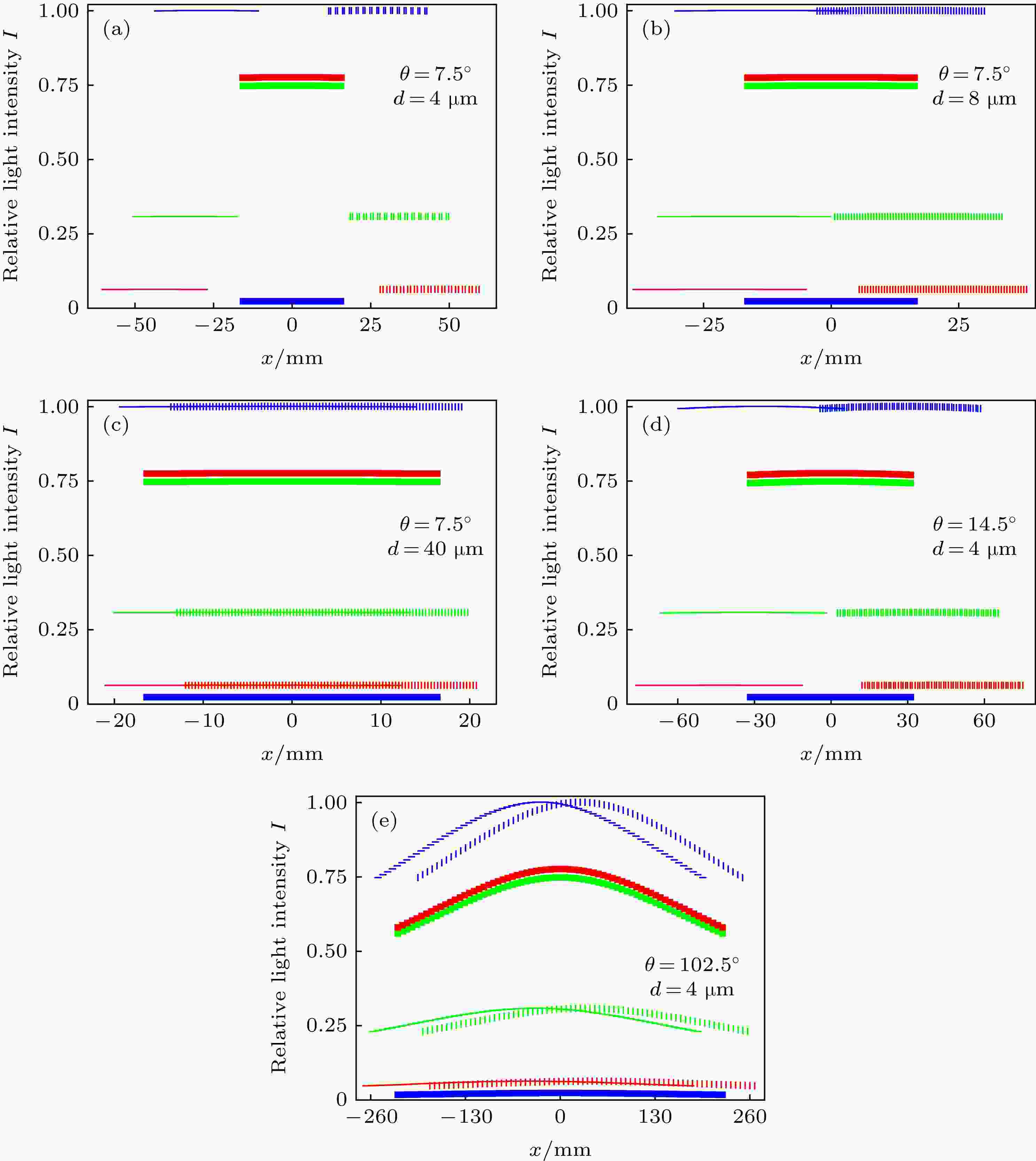图 2 零级、± 1级三衍射级次的相对光强分布　(a)?(e)入射光束锥角θ和光栅周期d分别分别为(7.5°, 4 μm), (7.5°, 8 μm), (7.5°, 40 μm), (14.5°, 4 μm), (102.5°, 4 μm); 图中红色、绿色、蓝色线分别代表三原色的红光、绿光、蓝光; 零级、+1级、–1级分别用粗横线、竖短线、细横线表示
Figure2. Relative light intensity distributions of zero, positive and negative one order of diffraction beams of three primary colors, where the RPG period d and the cone angle of incident beam θ of (a)?(e) are (7.5°, 4 μm), (7.5°, 8 μm), (7.5°, 40 μm), (14.5°, 4 μm) and (102.5°, 4 μm) respectively. The red, green, blue line represents the red, green, blue light of three primary colors respectively. The zero, positive and negative one order beam is represented by the thick horizontal, vertical short and thin horizontal line respectively.

由图2可知, 当LED入射光束锥角θ、矩形位相光栅周期d都比较小时, 三原色衍射光束明显展开, 衍射光谱的色散明显; 其中红光展宽最明显. 由图2(a)—(c)可知, 随着矩形位相光栅周期d的增大, 衍射光谱的色散减弱, 三原色光的 ± 1级衍射光束由最初的完全分开变成开始交叠、最终几乎完全交叠; 由图2(a)、图2(d)、图2(e)可知, 随着LED入射光束锥角θ增大, 衍射光谱的色散减弱, 三原色光的 ± 1级衍射光束由最初的完全分开变成开始交叠、最终几乎完全交叠.
2 -->

2.3.色散量C定义

为了便于理论分析及后续的实验测试, 本文提出色散量C这一参量对衍射光谱的色散进行讨论. 色散量C的定义如(9)式所示, 其中, Δx_r表示 ± 1级的红光束远心端点和零级光束中点的距离, 零级光束宽度Δx₀表示蓝、绿、红光的零级光束宽度的平均值, 相关参量的示意图如图3所示. 由图3可知, Δx_r/Δx₀的最小值等于0.5, 为了使得衍射光谱无色散时对应的色散量C也恰好为0, 因此, 色散量C的定义式中减去了一个常数0.5.
图 3 色散量C的相关定参量示意图, 其中红线、黑线分别代表红色光束、零级光束
Figure3. Relevant parameters of the dispersion parameter C. Where the red, black line respectively represents the red, zero order light beam.

$C = \left( {{{\Delta {x_r}} / {\Delta {x_0}}}} \right) - 0.5.$

由(9)式可知, 色散量C无量纲, C ≥ 0. 当C数值越大, 表明衍射光束的色散越明显; 数值越小, 则表明衍射光束的色散越小. 当蓝、绿、红三原色光的 ± 1级衍射光束完全交叠, 全部成为零级光, 此时为无色散的理想状态, 即色散量C为最小值(0). 当C = 0.5时, 红光 ± 1级衍射光刚开始交叠; C越小, ± 1级衍射光交叠得越多; 当C < 0.3时, 表明衍射光谱色散已比较小. 因此, 在设计宽带无色散器件的过程中, 就是要通过改变结构参数或光照条件使得色散量C尽可能地小; 初步设定色散量C = 0.3为零色散的边界点.
根据理论模型及色散量C的定义, 首先探讨LED入射光束锥角θ = 7.5°, 14.5°, 102.5°时, 矩形位相光栅周期d对色散量C的影响; 然后探讨光栅周期d = 4, 8, 40 μm时, LED入射光束锥角θ对色散量C的影响. 计算所得的关系曲线如图4所示.
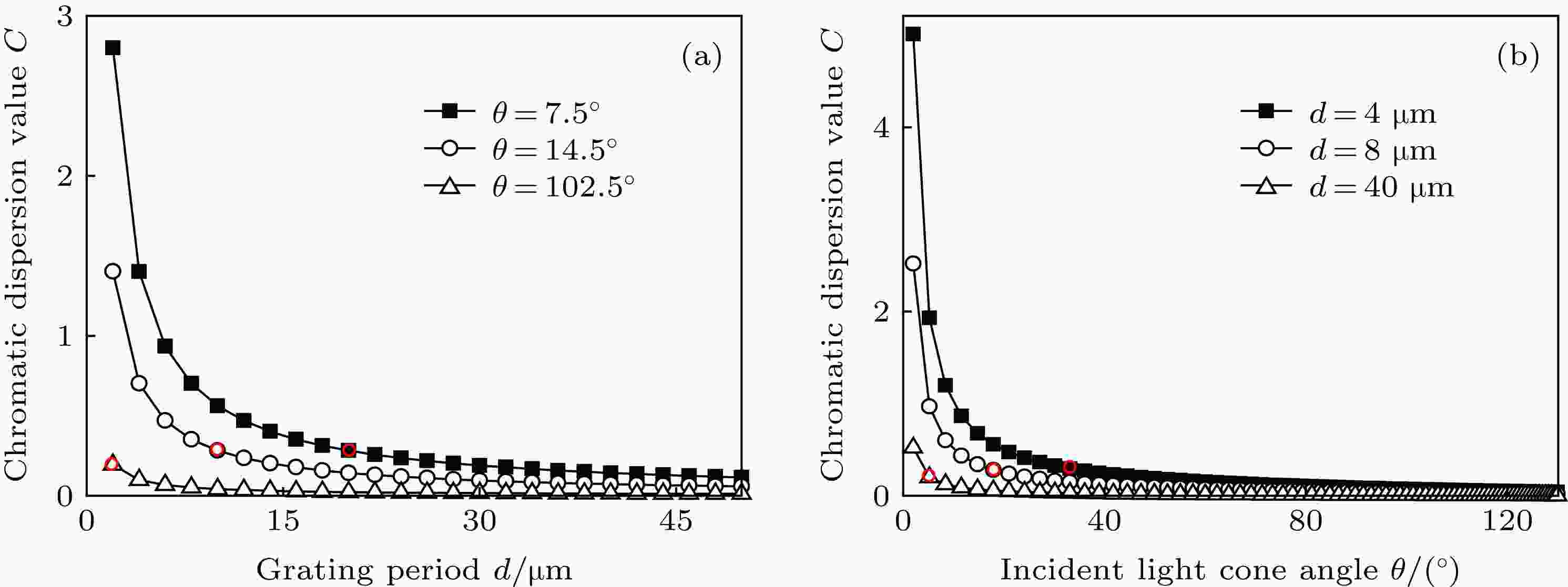图 4 色散量C与矩形位相光栅周期d, LED入射光束锥角θ的关系　(a)矩形位相光栅周期d; (b) LED入射光束锥角θ; 其中红圆圈表示零色散的边界点
Figure4. Influences of grating period d and incident light cone angle θ on the dispersion parameter C. (a), (b) is the calculated relationship curve between C and d, or θ respectively, where the red circles represent the zero-dispersion boundary points.

由图4可以看出, 白光LED光束经矩形位相光栅衍射后的色散量C随着入射光束锥角θ和光栅周期d的增大而快速单调递减. 由图4(a)中的红圆圈可知, 当LED入射光束锥角θ分别为7.5°, 14.5°, 102.5°, 光栅周期d对应为20, 10, 2 μm时, 色散量C都已经小于0.3, 衍射光谱色散已不明显, 即有零色散的边界点(θ, d): (7.5°, 20 μm), (14.5°, 10 μm), (102.5°, 2 μm). 由图4(b)中的红圆圈可知, 当光栅周期d分别为4, 8, 40 μm, LED入射光束锥角θ对应为33.1°, 17.9°, 5.2°时, 色散量C都已经小于0.3, 衍射光谱色散已不明显, 即有零色散的边界点(θ, d): (33.1°, 4 μm), (17.9°, 8 μm), (5.2°, 40 μm). 因此, 无论是增大入射光束锥角θ还是光栅周期d, 只要这两参数匹配使得色散量C小于0.3, 即可实现出射光束零色散.
2 -->

2.4.物理机理

上述物理模型(宽带光源微光学元件衍射理论模型)中, 对衍射光谱的色散量C起主要影响的物理参量是入射光束锥角θ和微结构阵列周期d. 增大入射光束锥角θ意味着降低入射光束的空间相干性, 衍射光谱色散变弱; 增大微结构阵列周期d, 衍射光束色散度自然降低. 无论是增大入射光束锥角θ还是微结构阵列周期d, 使得 ± 1级衍射红光完全交叠(即C = 0), 如图2(e)所示, 则衍射光束全部为零级白光, 实现了无色散.
传统的色散概念, 如角色散率、线色散率, 是用来表示光束经折射或衍射后的角度、位移变化随波长变化的关系, 当物理模型有解析表达式时可求得角色散率、线色散率等; 本文定义的色散量C更适用于宽带光源难以存在精确解析表达式的物理模型, 其不仅计算过程简单、无需求导, 而且可通过实验结果直接验证.

本文应用微纳加工技术制作一款光栅周期d = 4 μm、占空比为0.5、光栅槽深为1 μm的矩形位相光栅样品, 用来搭建图1所示的宽带光源微光学元件衍射理论模型, 进而测试验证上述理论分析结果的正确性.
样品的制作工艺步骤主要包括光刻、湿法蚀刻、电铸、紫外线压印. 在SiO₂衬底上采用电子束曝光方法将所设计的矩形光栅图案制作成掩膜版, 再通过紫外曝光光致抗蚀剂的方法将掩膜版上的二元精细图文转移至光刻胶版上, 这时光强度为450 μW/cm², 曝光时间为65 s. 然后用浓度为0.01 g/mL的NaOH溶液作为显影液, 显影4 s. 然后将光刻胶版表面的浮雕光栅进行表面金属化, 形成金属导电层, 为在后续的电铸过程中作为阴极使用. 本文应用银镜反应原理在矩形光栅的光刻胶版上镀一层银, 用银氨络合物和葡萄糖溶液浸泡光刻胶版的同时并摇匀, 使得光栅表面附着一层薄薄的银层. 接着运用电铸工艺将金属层加厚至数十微米后剥离, 用碱液将残留在金属版上的光刻胶清洗干净, 得到了金属版的矩形光栅. 最后, 在金属版的矩形光栅制备好之后, 采用紫外线压印工艺方法复制转印出所需的矩形位相光栅样品, 所采用的UV胶折射率为1.5.
运用激光显微镜测试样品, 所得的结构如图5所示; 从测试结果可知, 矩形位相光栅样品的实际结构参数与设计值一致.
图 5 矩形光栅样品的结构测试图　(a)光刻显影后; (b)紫外线压印后
Figure5. Structural testing diagrams of the RPG sample:　(a) After being developed; (b) the structural testing diagrams of the final sample after UV stamping.

运用单个白光LED(色品坐标x = 0.2966, y = 0.2983; 线宽l = 2.5 mm)制作的矩形位相光栅样品、BM-7亮度计等搭建测试装置, 用来测试分析矩形位相光栅的光谱色度值.
首先, 移开光栅, 直接用亮度计在观测平面测量白光LED光源中心点的亮度值、色坐标, 分别为8311.8 cd/m²和x = 0.2919, y = 0.2735. 接着, 使LED光束透过光栅, 改变LED光源和矩形位相光栅间的距离D, 即改变入射光束锥角θ, 用人眼在观测平面观察实验光束的变化, 同时用亮度计测量观察平面上光束中点的亮度值、色坐标; 进而判断衍射光束的色散情况. 表1是不同入射光束锥角θ所对应的衍射光束中点的亮度值和色坐标的测试值.

θ	102.68o	64.01o	45.24o	34.71o
Luminance L (cd/m2)	6105.6	5161.2	4018.2	3262.1
Chromaticity Coordinate	x = 0.2978 y = 0.2828	x = 0.3024 y = 0.2798	x = 0.3074 y = 0.2779	x = 0.3025 y = 0.2770

表1不同入射光束锥角θ在观察平面中点所对应的衍射光谱的亮度值和色坐标
Table1.Luminance and chromaticity coordinate of the center diffraction spectrum with different θ.

在实验过程中, 用人眼可观察到, 随着入射光束锥角θ逐渐减小, 在观测平面观察到的实验光束则逐渐由白光变为彩虹光束, 即由无色散变成有色散. 当入射光束锥角θ > 34.71°时, 衍射光束为白光, 衍射光谱几乎无色散; 从表1的色坐标测试值也可得到验证. 当入射光束锥角θ = 34.71°时, 人眼已经在光束边缘处观测到彩虹光, 如图6(a)所示, 即衍射光束由零色散变成有色散; 而表1亮度计测试的色坐标仍位于白光区域, 是由于人眼对于色散的辨识度比亮度计更加精准. 这与上述理论分析的零色散边界点(θ = 33.1°, d = 4 μm)吻合, 进一步表明理论分析中设定色散量C = 0.3为零色散的边界点是可行的.
图 6 实验光束观测图　(a)零色散边界点(θ = 34.71°, d = 4 μm); (b) θ = 3.58°, d = 4 μm
Figure6. Observation diagram of the diffraction beam:　(a) At zero-dispersion boundary point (θ = 34.71°, d = 4 μm); (b) θ = 3.58°, d = 4 μm.

为了验证色散量C定义的正确性, 本文将色散量C的测试结果与理论结果进行对比分析. 因为只有入射光束锥角θ足够小时, 色散才明显, 才能观察到 ± 1级衍射的红光; 所以选取一些小的入射光束锥角θ来测试色散量C; 此处也是通过改变LED光源至矩形位相光栅的距离D来改变入射光束锥角θ. 如当入射光束锥角θ = 3.58o时, 观察平面上的光束分布如图6(b)所示, 衍射光谱具有明显的彩虹色, 色散度高; 中心点色坐标为x = 0.2453, y = 0.1679, 明显偏离白光. 接着, 根据(2)式对实际测量值进行计算, 得到色散量C的实验测试计算值. 将色散量C的实验测试计算值与理论计算值进行对比, 如图7所示.
图 7 色散量C的理论值和测试值与入射光束锥角θ关系曲线的对比
Figure7. Contrast curves of the relationship between the test and theoretical value of C with θ.

从图7中可以看出, 色散量C的实际测试值与理论计算值非常接近, 绝对误差小于0.1, 相对误差百分比小于3.3%. 该误差有可能是因为理论计算模型的量化取值、操作人眼的观察光束的误差而引起的, 故该误差在可接受范围内. 实验结果表明, 本文定义的色散量C不仅可以较准确定量地衡量宽光谱光束经矩形位相光栅衍射后的色散程度, 而且其具体数值可通过理论计算、或是实验直接快速测得.

基于宽带光源下微光学元件(如集成导光板)在衍射色散方面的设计需求, 本文以矩形位相光栅、白光LED为例, 构建了宽带光源微光学元件衍射的理论分析模型, 探讨分析了衍射光谱的色度特性, 提出了能准确定量衡量衍射光束色散程度的色散量C, 并明确给出了零色散的边界判据点C = 0.3. 探究发现白光LED光束经矩形位相光栅衍射后的色散量C随着入射光束锥角θ和光栅周期d的增大而快速减小; 无论是增大入射光束锥角θ还是光栅周期d, 只要两参数匹配使得色散量C ≤ 0.3即可实现出射光束零色散, 给出了物理机理分析. 同时还应用微纳加工技术制作了结构参数与设计值相一致的矩形位相光栅, 测试了不同入射光束锥角θ下的衍射光场的亮度值、色坐标, 进而计算得到相应的色散量C; 实验结果与理论分析结论一致, 表明本文提出的色散度判据参量C以及零色散边界点的正确性. 上述研究成果, 不仅为本课题组研究设计的集成导光板提供指导, 而且也能为其他宽带衍射元件设计过程中探讨色散特性时提供指引.