摘要: 高斯混合模型被广泛应用于统计压缩感知中信号先验概率分布的建模. 利用高斯混合模型对图像的概率分布进行建模时, 通常需要先对图像分块, 再对图像块的概率分布进行建模. 本文提出卷积高斯混合模型对整幅图像的概率分布进行建模. 通过期望极大化算法求解极大边缘似然估计, 实现模型中未知参数的估计. 此外, 考虑到在整幅图像上计算的复杂度较高, 本文在卷积高斯混合模型和压缩测量模型中引入循环卷积, 所有的训练和恢复过程都可以利用二维快速傅里叶变换实现快速运算. 仿真实验表明, 本文所提的MMLE-convGMM算法的恢复性能要优于传统的压缩感知算法的恢复性能.
关键词: 卷积高斯混合模型 /
统计压缩感知 /
期望极大化算法 /
卷积稀疏编码 English Abstract Statistical compressive sensing based on convolutional Gaussian mixture model Wang Ren 1 ,Guo Jing-Bo 2 ,Hui Jun-Peng 1 ,Wang Ze 1 ,Liu Hong-Jun 1 ,Xu Yuan-Nan 1 ,Liu Yun-Fo 1 1.China Academy of Launch Vehicle Technology R&D Center, Beijing 100076, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 51677094)Received Date: 24 March 2019Accepted Date: 20 June 2019Available Online: 01 September 2019Published Online: 20 September 2019Abstract: Statistical compressive sensing needs to use the statistical description of source signal. By decomposing a whole image into a set of non-overlapping or overlapping patches, the Gaussian mixture model (GMM) has been used to statistically represent patches in an image. Compressive sensing, however, always imposes compression on the whole image. It is obvious that the entire image contains much richer information than the small patches. Extending from the small divided patches to an entire image, we propose a convolutional Gaussian mixture model (convGMM) to depict the statistics of an entire image and apply it to compressive sensing. We present the algorithm details by learning a convGMM from training images based on maximizing the marginal log-likelihood estimation. The learned convGMM is used to perform the model-based compressive sensing by using the convGMM as a model of the underlying image. In addition, aiming at the problem of high-dimensional image that makes learning, estimation and optimization suffer high computational complexity, all of the training and reconstruction process in our method can be fast and efficiently calculated in the frequency-domain by two-dimensional fast Fourier transforms. The performance of the convGMM on compressive sensing is demonstrated on several image sets.Keywords: convolutional Gaussian mixture models /statistical compressive sensing /expectation maximization /convolutional sparse coding 全文HTML --> --> --> 1.引 言 压缩感知[1 ,2 ] 实现了以远低于奈奎斯特的采样频率去采样稀疏信号, 并以高概率实现原信号的准确恢复. 贝叶斯压缩感知[3 ] 从统计学的角度描述了信号的压缩采样与恢复过程. 根据稀疏贝叶斯学习理论, 需要对信号的先验分布进行建模. 高斯混合模型(Gaussian mixture models, GMM)因其具有强大且灵活的拟合能力被广泛应用于信号先验分布的建模中[4 -6 ] . 从主成分分析(principal components analysis, PCA)的角度来说, GMM模型中每一类高斯分布的协方差矩阵的PCA基张成了信号稀疏分解的子空间[7 ] . 压缩感知自提出以后被广泛应用于物理成像领域, 如光谱成像[8 ] 、太赫兹成像[9 ] 、图像加密[10 ] 、图像重建[11 ,12 ] 等.[13 ] . 一种直观的想法是能不能直接对整幅图像的先验分布进行建模, 但该想法实现的困难体现在两方面: 一是整幅图像的信息量相比于图像块要丰富得多, 拟合其先验分布函数的难度会大大增加, 简单的GMM对于整幅图像先验分布函数的建模效果不佳; 二是整幅图像的维数比图像块的维数大得多, 若对整幅图像的概率分布进行建模, 计算量将大大增加.[14 ] 和解卷积网络(deconvolutional networks, DN)[15 -17 ] 中得到启发, 利用多个滤波器(filter)与特征图(feature map)卷积的线性加权求和来拟合整幅图像的细节信息. 从图像块到整幅图像建模的关键是使用了解卷积网络. 从直观的角度来说, 解卷积神经网络中滤波器的作用类似于传统压缩感知中的稀疏基. 同时, 本文将GMM与解卷积网络相结合, 使得该模型兼具了多个解卷积网络线性加权的灵活性.[18 ] , 所有的训练和恢复过程都可以利用二维快速傅里叶变换(two-dimensional fast Fourier transforms, 2D-FFTs)实现快速运算.2.convGMM 令X $p\left( {{{X}}\left| z \right.} \right)$ 服从高斯分布, $p\left( z \right)$ 表示第z 个高斯分布所占的权重. 使用GMM时需要先将整幅图像分割成多个图像块, 再对每一图像块的概率分布函数进行建模.X $ * $ 表示二维卷积算子, ${\tilde {{F}}_z}$ 表示卷积滤波器(卷积核或者字典), $\tilde {{S}}$ 表示特征图, ${{{M}}_z}$ 描述的是不同卷积网络的背景. 多个${{{M}}_z}\;(z = 1, \cdots ,K)$ 的线性加权用来描述图像的背景信息, 多个滤波器与特征图卷积${\tilde {{F}}_z} * \tilde {{S}}\;(z = 1, \cdots ,K)$ 的线性加权求和用来拟合图像的细节信息. I ${{\textit{π}}_z}$ 表示第z 个卷积网络所占的权重.X ${{x}} = {\rm{vec}}\left( {{X}} \right)$ , 则它的分布为${{{\mu}} _z} = {\rm{vec}}\left( {{{{M}}_z}} \right)$ ; ${\rm{vec}}\left( {{{\tilde {{F}}}_z} * \tilde {{S}}} \right) = {{{F}}_z}{{s}} = {{S}}{{{f}}_z}$ , ${{{F}}_z}$ 和S ${{s}} = {\rm{vec}}\left( {\tilde {{S}}} \right)$ , ${{{f}}_z} = {\rm{vec}}\left( {{{\tilde {{F}}}_z}} \right)$ , 即将特征图$\tilde {{S}}$ 和卷积滤波器${\tilde {{F}}_z}$ 写成向量形式.3 )式中的卷积是循环卷积, 而不是线性卷积. 使用循环卷积的目的是为了在整幅图像上实现快速有效的运算. 如果图像的大小为${{X}} \in {\mathbb{R}^{{N_1} \times {N_2} \times {N_{\rm{c}}}}}$ (对于灰度图像N c = 1, 对于彩色图像N c = 3), 每个滤波器的大小为${\tilde {{F}}_z} \in {\mathbb{R}^{{n_1} \times {n_2} \times {N_{\rm{c}}}}}$ (一般情况下${n_1} \ll {N_1},{n_2} \ll {N_2}$ ), 则在循环卷积的框架下特征图$\tilde {{S}}$ 与图像X $\tilde {{S}} \in {\mathbb{R}^{{N_1} \times {N_2} \times {N_{\rm{c}}}}}$ . 根据卷积滤波器${\tilde {{F}}_z}$ 与卷积矩阵${{{F}}_z}$ 之间的对应关系, 卷积矩阵${{{F}}_z}$ 是一个有着循环块的块循环矩阵:${{{F}}_{z,j}},j = 0,1, \cdots ,{N_2} - 1$ 是1个${N_1} \times {N_1}$ 的循环矩阵, 根据BCCB的性质, 可得${{{W}}_{{N_1}}}$ 表示${N_1} \times {N_1}$ 大小的离散傅里叶变换矩阵, $ \otimes $ 表示Kronecker积, ${{{\varDelta }}_z} = {\rm{diag}}\left( {{{\hat {{f}}}_z}} \right)$ , ${\hat {{f}}_z} = \left( {{{{W}}_{{N_2}}} \otimes {{{W}}_{{N_1}}}} \right){\tilde {{f}}_z}$ , ${\tilde {{f}}_z}$ 是卷积矩阵${{{F}}_z}$ 的第一行. 因此, 循环卷积运算${{{F}}_z}{{s}} = {\rm{vec}}\left( {{{\tilde {{F}}}_z} * \tilde {{S}}} \right)$ 可以利用(8 )式中的一次二维快速傅里叶逆变换(two-dimensional inverse fast Fourier transforms, 2D-IFFTs)、两次2D-FFTs和频域上简单的分量式运算实现快速运算. 为了表示简洁, 这里令${{{W}}_{\rm 2d}} = {{{W}}_{{N_2}}} \otimes {{{W}}_{{N_1}}}$ 表示相应维度的2D-FFTs矩阵, 则(8 )式可以简写为N 幅图像共同被K 组卷积滤波器${\tilde {{F}}_z}\left( {z = 1,2, \cdots ,K} \right)$ 与特征图的循环卷积表示;$\tilde {{S}}$ 没有标注下标z 并不是表示每幅图像只对应一个特征图, 相反每幅图像都有特定的K 个特征图, 每个特征图都有各自的后验分布, 如(11 )和(12 )式所示. 省去下标z 的原因是所有特征图的先验分布相同.3.从训练集中学习convGMM 考虑从一组训练图像集$\left\{ {{{{X}}_i}} \right\}_{i = 1}^N$ 中学习所提出的convGMM, 记该模型中待估计的参数为$\varTheta = \left\{ {{{\textit{π}} _z},{{{\mu}} _z},{{{f}}_z}} \right\}_{z = 1}^K$ .$p\left( {z,{{s}},{{x}}} \right)$ 和后验分布$p\left( {z,{{s}}\left| {{x}} \right.} \right)$ .9 )式中${{{F}}_z}$ 的频域性质, 可得${{{\bar \varDelta }}_z}$ 表示${{{\varDelta }}_z}$ 的共轭, ${\left| {{{{\varDelta }}_z}} \right|^2} = {\rm{diag}}\left( {{{\left| {{{\hat {{f}}}_z}} \right|}^2}} \right)$ , (11 )式最后一行的参数满足11 )式可得信号x x z , s $\left\{ {{z_i},{{{s}}_i}} \right\}$ 看作隐变量, 基于MMLE从训练数据集中学习convGMM:$p\left( {{z_i},{{{s}}_i},{{{x}}_i}\left| \varTheta \right.} \right)$ 由(10 )式给出. 通过EM算法[19 ] 求解上述的目标函数, 具体步骤如下.16 )的后验分布$p\left( {{z_i},\;{{{s}}_i}\left| {{{{x}}_i},\;{\varTheta ^{(t - 1)}}} \right.} \right)$ , 求解对数似然函数$\ln p\left( {{z_i},{{{s}}_i},{{{x}}_i}\left| \varTheta \right.} \right)$ 的期望.$\varTheta $ 无关项的和, $\rho _{iz}^{(t - 1)} = {\rho _z}\left( {{{{x}}_i},{\varTheta ^{(t - 1)}}} \right)$ . 为了表示简洁, 这里省略了期望${\mathbb{E}_{{z_i},{{{s}}_i}\left| {{{{x}}_i},{\varTheta ^{(t - 1)}}} \right.}}\left( \cdot \right)$ 的下标.19 )式最后一行的期望, $\mathbb{E}\left[ {{\left( {{{{x}}_i} - {{{\mu}} _z} - {{{F}}_z}{{{s}}_i}} \right)}^\prime }{{\left( {\gamma {{I}}} \right)}^{ - 1}}\right. \;\cdot$ $ \left( {{{{x}}_i} - {{{\mu}} _z} - {{{F}}_z}{{{s}}_i}} \right) \Bigr]$ , 从而完成整个期望的计算. 但在 卷积运算转化为乘积运算的过程中, ${\rm{vec}}\left( {{{\tilde {{F}}}_z} * \tilde {{S}}} \right) = $ $ {{ F}_z}{ s}$ , 大的卷积矩阵${{{F}}_z} \in $ $ {\mathbb{R}^{({N_1} \cdot {N_2}) \times ({N_1} \cdot {N_2})}}$ 是由小的卷积滤波器${\tilde {{F}}_z} \in {\mathbb{R}^{{n_1} \times {n_2}}}$ 按照循环卷积的对应关系生成的, 且${{{F}}_z}$ 中大部分元素都是0. 所以在接下来EM算法的M-step中, 本文不能直接更新${{{F}}_z}$ , 而应更新滤波器${\tilde {{F}}_z}$ . 在本步中需要将(19 )式最后一行的${{{F}}_z}$ 转化为用${\tilde {{F}}_z}$ (或${{{f}}_z}$ , 因为${{{f}}_z} = {\rm{vec}}\left( {{{\tilde {{F}}}_z}} \right)$ )来表示. 为了使后续的结论更加具有普适性, 这里将协方差矩阵$\gamma { I}$ 拓展为任意矩阵${{\varGamma}} $ 的一般情形. (19 )式最后一行可进一步化简为20 )式的最后一行的两项都含有卷积矩阵${{{F}}_z}$ , 现将它们转化成用卷积滤波器${{{f}}_z}$ 来表示:${{\varXi}} _{iz}^{(t - 1)}$ 是满足${{{F}}_z}{{\xi}} _{iz}^{(t - 1)} = {\rm{vec}}\left( {{{\tilde {{F}}}_z} * \tilde {{\varXi}} _{iz}^{(t - 1)}} \right) = $ ${{ \Xi}} _{iz}^{(t - 1)}{{{f}}_z}$ 关系的卷积矩阵, 类似于(6 )式中卷积运算到乘积运算的转化. 若考虑特殊情形${{\varGamma}} = \gamma {{I}}$ , 则20 )式最后一行的第二项为${{\varGamma}} = \gamma {{I}}$ , 则${\left[ \cdot \right]_{l,:}}$ 和${\left[ \cdot \right]_{:,j}}$ 分别表示矩阵的第l 行和第j 列; ${\left[ {{{Q}}_z^{(t - 1)}} \right]_{\left\{ l \right\},\left\{ j \right\}}}$ 是矩阵${{Q}}_z^{(t - 1)}$ 沿着主对角线的子矩阵, 它的行索引$\left\{ l \right\}$ 是由${{{f}}'_z}$ 在行向量${\left[ {{{{F}}_z}} \right]_{l,:}}$ 中的位置决定, 列索引$\left\{ j \right\}$ 是由${{{f}}_z}$ 在列向量${\left[ {{{{{F}}'}_z}} \right]_{:,j}}$ 中的位置决定; ${{\varPsi}} _z^{(t - 1)} = \sum\limits_j {{{\left[ {{{Q}}_z^{(t - 1)}} \right]}_{\left\{ j \right\},\left\{ j \right\}}}} $ .22 )和(24 )式代入(19 )和(20 )式中, 可得对数似然函数的期望为25 )式来更新参数${\varTheta ^{(t)}}$ , ${\varTheta ^{(t)}} = \mathop {\arg \max }\limits_\varTheta ll\left( {\varTheta \left| {{\varTheta ^{(t - 1)}}} \right.} \right)$ , 可得12 )—(14 )式和(26 ), (27 )式之间交替迭代组成了整个MMLE-convGMM算法的迭代过程. 根据EM算法的性质[19 ] , 边缘似然函数$\displaystyle\sum\limits_{i = 1}^N {\ln \displaystyle\sum\limits_{z = 1}^K {{\textit{π}} _z^{(t)}{\cal N}\left( {{{{x}}_i}\left| {{{\mu}} _z^{(t)},{{{R}}_z}\left( {{\varTheta ^{\left( t \right)}}} \right)} \right.} \right)} } $ 将随迭代次数逐渐增加直至收敛.4.基于convGMM的压缩测量 在压缩测量过程中, 本文考虑将原图像与随机核矩阵进行循环卷积, 再依据采样率对循环卷积的结果进行降采样. 该过程的模型为$\tilde {{\varPhi}} $ 表示随机卷积核, 它与图像的大小相同; ${{\cal P}_{{\Omega}} }$ 表示在索引集${{\Omega}} $ 下的降采样算子; Y N 28 )式向量化:${{{P}}_{{\Omega}} }$ 是降采样算子${{\cal P}_{{\Omega}} }$ 对应的降采样矩阵, ${{\varPhi}} $ 是由卷积核$\tilde {{\varPhi}} $ 生成的有着循环块的块循环矩阵, 其结构如(7 )式所示, 故${{\varPhi}} $ 可表示为${{{\varDelta }}_{{\rm{CS}}}} = {\rm{diag}}\left( {{{{W}}_{{\rm{2d}}}}\tilde { \phi} } \right)$ , $\tilde{ \phi} = {\rm{vec}}\left( {\tilde {{\varPhi}} } \right)$ .图1 所示, 本文的目标是基于极大后验估计, 从压缩测量结果y x 图 1 基于convGMM的压缩测量Figure1. Structure of convGMM with application to compressive sensing.z , s x y z , s x y ${{{\bar \varDelta }}_{{\rm{CS}}}}$ 表示${{{\varDelta }}_{{\rm{CS}}}}$ 的共轭. 值得注意的是上述这些参数均可利用2D-FFTs实现快速运算.32 )式的最后一行可得y y z , s x 43 )式可得信号x x $\hat {{x}}$ 表示从压缩测量结果y $\dfrac{{\partial MSE}}{{\partial \hat {{x}}}} = 0$ , 可得x ${\mathbb{E}_{{{x}}\left| {{{y}},\varTheta } \right.}}\left( {{x}} \right)$ 恰好是最小均方误差(minimum mean square error, MMSE)意义下的估计[20 ] , 即5.计算复杂度分析 由于本文所提的convGMM对整幅图像的概率分布进行建模, 因而存在矩阵维数大, 计算复杂的问题, 为了提高MMLE-convGMM算法运算的效率, 本文做了如下两个重要的降低计算复杂度的工作.2 )和(3 )式), 因而循环卷积运算${{{F}}_z}{{s}} = {\rm{vec}}\left( {{{\tilde {{F}}}_z} * \tilde {{S}}} \right)$ 可以利用有着循环块的块循环矩阵的数学性质, 基于(8 )式中的一次2D-IFFTs、两次2D-FFTs和频域上简单的分量式运算实现快速运算. 计算复杂度从$O\left( {{{\left( {{N_1} \cdot {N_2}} \right)}^2}} \right)$ 减小到$O\left( {\left( {{N_1} \cdot {N_2}} \right){{\log }_2}\left( {{N_1} \cdot {N_2}} \right)} \right)$ .3 节convGMM模型的训练中, (12 )—(14 )式中参数的计算, 以及第4 节从压缩测量结果y x 48 )式中参数的计算, 均可利用(8 )式中的2D-FFTs和2D-IFFTs实现快速运算.27 )式中矩阵求逆的计算复杂度较大. 令${{\varXi}} _{iz}^{(t - 1)}$ 的大小为$\left( {{N_1}\! \cdot \!{N_2}} \right) \!\times\! \left( {{n_1} \!\cdot \!{n_2}} \right)$ , 则矩阵A $\left( {{N_1} \!\cdot \!{N_2} \!+\! {n_1} \cdot {n_2}} \right) \!\times\! \left( {{N_1} \cdot {N_2}\!+\! {n_1} \!\cdot \!{n_2}} \right)$ . 如果直接对(49 )式求逆, 则利用Cholesky分解, 其计算复杂度为$O\left( {{{{{\left( {{N_1} \cdot {N_2} + {n_1} \cdot {n_2}} \right)}^3}}/ 3} + {{\left( {{N_1} \cdot {N_2} + {n_1} \cdot {n_2}} \right)}^2}} \right)$ .A M 50 )和(52 )式可以看出, 计算${ A^{ - 1}}$ 的主要计算量在于求${{A}}_{22}^{ - 1}$ , ${\left( {{{{A}}_{22}} - {{{A}}_{21}}{{A}}_{11}^{ - 1}{{{A}}_{12}}} \right)^{ - 1}}$ 和${{A}}_{11}^{ - 1}$ . 由于矩阵${{{A}}_{11}}$ 是对角矩阵, ${{A}}_{11}^{ - 1}$ 的计算量可以忽略. 矩阵${{A}}_{22}^{ - 1}$ 和${\left( {{{{A}}_{22}} - {{{A}}_{21}}{{A}}_{11}^{ - 1}{{{A}}_{12}}} \right)^{ - 1}}$ 的大小都为$\left( {{n_1} \cdot {n_2}} \right) \times \left( {{n_1} \cdot {n_2}} \right)$ , 他们求逆的复杂度为$O\left( {{{{{\left( {{n_1} \cdot {n_2}} \right)}^3}} / 3} + {{\left( {{n_1} \cdot {n_2}} \right)}^2}} \right)$ . 在卷积网络中滤波器的大小${\tilde {{F}}_z} \in {\mathbb{R}^{{n_1} \times {n_2}}}$ 远小于图像的大小${{X}} \in $ ${\mathbb{R}^{{N_1} \times {N_2}}} $ . 利用上述的矩阵分块求逆和Woodbury矩阵恒等式, 矩阵A $O\left( {{{{{\left( {{N_1} \cdot {N_2} \!+ \! {n_1} \cdot {n_2}} \right)}^3}}/ 3} \!+ \!{{\left( {{N_1} \cdot {N_2} + {n_1} \cdot {n_2}} \right)}^2}} \right)$ 降低到$O\left( {{{{{\left( {{n_1} \cdot {n_2}} \right)}^3}} / 3} + {{\left( {{n_1} \cdot {n_2}} \right)}^2}} \right)$ .6.仿真结果及分析 本节将在三个标准数据集上验证MMLE-convGMM算法的有效性. 此外, 还与其他的压缩感知算法相比较, 包括基于GMM的MMLE-GMM算法[6 ] , 贪婪算法中的正交匹配追踪算法(orthogonal matching pursuit, OMP)[21 ] , 凸优化算法中的YALL1算法[22 ] 以及通过极小化l 2,1 范数求解群基追踪(group basis pursuit)问题的广义交替投影(generalized alternating projection, GAP)算法[23 ] . 每一种算法的恢复性能通过峰值信噪比(peak signal to noise ratio, PSNR)来评价. 对于OMP, YALL1和GAP, 这里选取离散余弦变换(discrete cosine transform, DCT)矩阵作为稀疏基, 记为“DCT-OMP”,“DCT- YALL1”和“DCT-GAP”. 此外, 文献[24 ]还提供了KSVD-YALL1算法用于整幅图像的恢复, 该算法首先利用KSVD算法在图像块上学习稀疏表示的字典, 再将图像块上学习的稀疏字典构建出整幅图像的稀疏字典, 因此本文也增加了KSVD-YALL1算法作为比较.6.1.CIFAR-10数据集 6.1.CIFAR-10数据集 首先在CIFAR-10数据集[25 ] 上验证MMLE-convGMM算法的有效性. CIFAR-10数据集是由10类$32 \times 32$ 大小的自然图像组成的数据集, 每一类图像有60000张, 其中50000张训练图像、10000张测试图像. 这里随机从中选取了3000张图像(每一类图像约300张)并将其转化为灰度图像用于压缩感知. 基于第4节的压缩测量方法, 首先将每张图像与高斯核矩阵做循环卷积, 再对卷积的结果进行降采样. 采样率(sampling rate)定义为压缩采样数m 与图像的像素n 之比, 这里设定采样率从0.05增加到0.4, 增加的步长为0.05, 即${m/ n} \in \left\{ {0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4} \right\}$ . 压缩测量噪声的标准差设为$\sigma = {10^{ - 4}}$ .图2 给出了在CIFAR-10图像中, 不同压缩感知算法恢复出图像的PSNR随采样率的变化情况, 可以看出MMLE-convGMM明显优于传统的压缩感知算法, MMLE-GMM算法的性能次之. DCT-YALL1与DCT-GAP两大类凸优化算法的恢复性能相当. 贪婪算法DCT-OMP的计算速度较快, 但其恢复性能比凸优化算法要差.图 2 CIFAR-10图像, 不同算法下恢复图像的PSNR随采样率的变化Figure2. Averaged PSNR of reconstructed images from CIFAR-10 dataset as a function of sampling rate.6.2.Caltech 101数据集 -->6.2.Caltech 101数据集 为了进一步在大一些的图像数据集上测试MMLE-convGMM算法的有效性, 本节选取Caltech 101数据集[26 ] . Caltech 101数据集由101类自然图像所组成, 每一类图像有40—800张, 且每一张图像的大小约为$300 \times 200$ . 这里选取其中“飞机”图像, 共800张. 首先将它们转化为灰度图像, 再将其统一成$128 \times 128$ 的像素. 所有其他的设置, 包括采样率、测量矩阵、噪声水平同CIFAR-10数据集的仿真. 图3 是不同压缩感知算法的恢复PSNR随着采样率的变化情况. 此外, 在图4 中展示了随机选取的12张Caltech 101“飞机”图像在不同算法下的恢复情况, 采样率设定为0.4.图 3 Caltech 101图像, 不同算法下恢复图像的PSNR随采样率的变化Figure3. Averaged PSNR of reconstructed images from Caltech 101 dataset as a function of sampling rate.图 4 采样率为0.4时, 12张Caltech 101“飞机”图像在不同算法下的恢复情况 (a)原图像; (b) MMLE-convGMM下的恢复图像; (c) MMLE-GMM下的恢复图像; (d) KSVD-YALL1下的恢复图像; (e) DCT-YALL1下的恢复图像; (f) DCT-GAP下的恢复图像; (g) DCT-OMP下的恢复图像Figure4. Reconstructed performance comparison of 12 randomly selected “airplane” images from Caltech 101: (a) Original images; (b) images reconstructed by MMLE-convGMM; (c) images reconstructed by MLE-GMM; (d) images reconstructed by KSVD-YALL1; (e) images reconstructed by DCT-YALL1; (f) images reconstructed by DCT-GAP; (g) images reconstructed by DCT-OMP. All of the sampling rates are 0.4.图3 和图4 可以看出, 类似于CIFAR-10的仿真结果, MMLE-convGMM算法明显优于其他的压缩感知恢复算法, 且在采样率为0.4时, 恢复图像的PSNR达到了28 dB.6.3.CelebA数据集 -->6.3.CelebA数据集 最后在含有更大图像的CelebA (Large-scale CelebFaces Attributes)数据集[27 ] 上验证MMLE-convGMM算法的有效性. CelebA数据集含有超过200000张的名人图像, 每幅图像有40个属性注释. 该数据集中的图像包含了各种人物的姿势和背景. 这里将图像统一为$256 \times 256$ 的像素. 图5 是CelebA图像的恢复PSNR随着采样率的变化情况. 图6 展示了随机选取的CelebA图像的恢复情况, 采样率设定为0.4, 可以看出MMLE-convGMM算法在大图像数据集上有着很好的恢复效果. 当采样率为0.4时, 恢复图像的PSNR为30 dB.图 5 MMLE-convGMM算法恢复CelebA图像的PSNR随采样率的变化Figure5. Averaged PSNR of reconstructed images from CelebA dataset as a function of sampling rate by MMLE-convGMM.图 6 随机选取的CelebA图像的恢复情形 (a)原图像; (b) MMLE-convGMM算法恢复的图像, 采样率为0.4Figure6. Reconstructed performance of randomly selected CelebA face images: (a) Original images; (b) images reconstructed by MMLE-convGMM. The sampling rates are 0.4.7.结 论 本文提出了convGMM对整幅图像的概率分布进行建模, 该模型不仅利用了解卷积神经网络的思想, 对于整幅图像先验分布的建模具有非常好的效果, 而且兼具GMM的灵活性. 对于convGMM中未知参数的学习, 本文提出了通过EM算法求解MMLE. 基于后验分布的期望从压缩测量结果中估计原信号, 且该估计是最小均方误差意义下的估计. 为解决对整幅图像直接进行计算时的维数较大、计算复杂度较高的问题, 在convGMM和压缩测量模型中都使用了循环卷积, 所有的训练和恢复过程都可以利用2D-FFTs实现快速运算. 仿真实验表明, 本文所提的MMLE-convGMM算法明显优于传统的压缩感知算法. 















































































































 图 1 基于convGMM的压缩测量
图 1 基于convGMM的压缩测量





































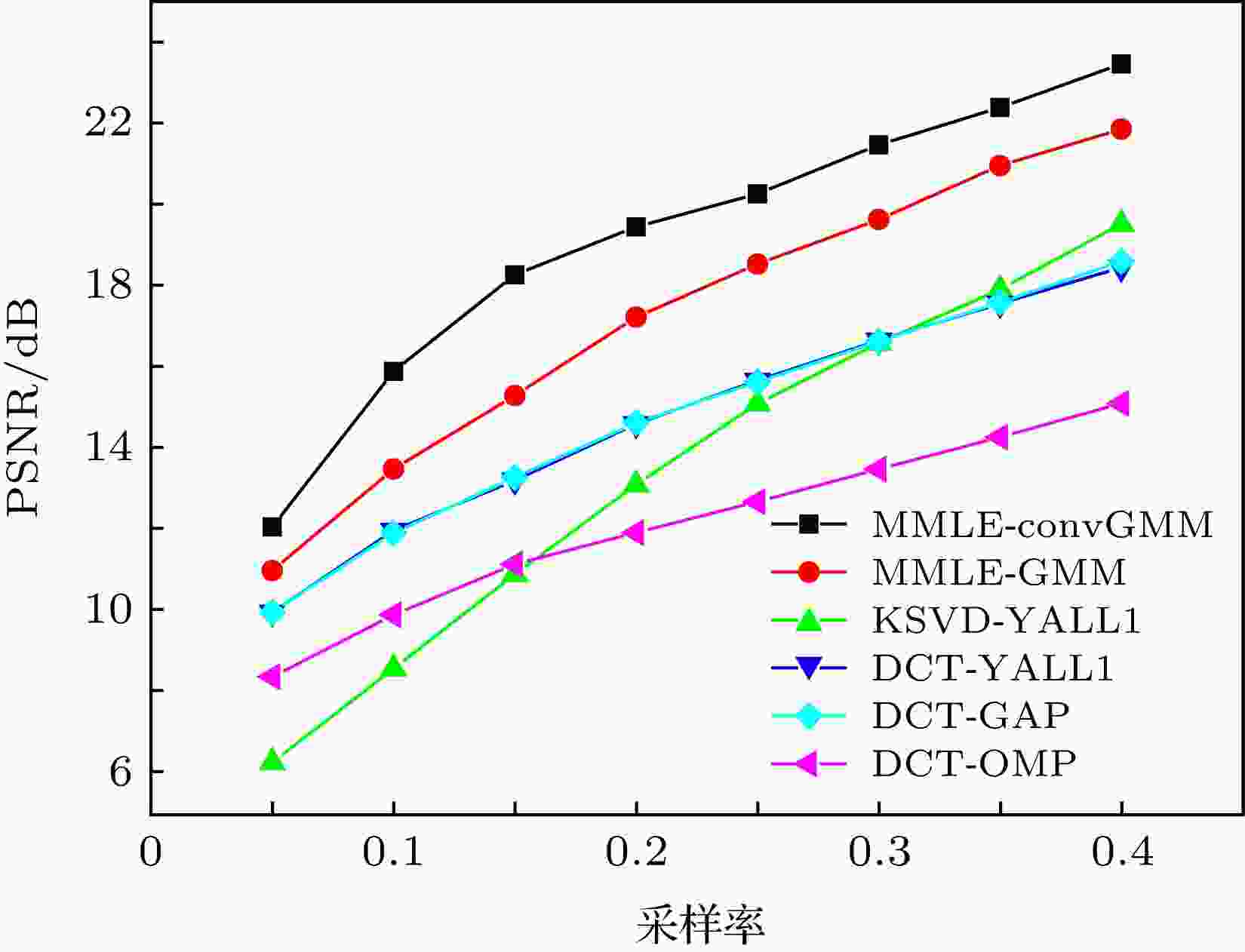 图 2 CIFAR-10图像, 不同算法下恢复图像的PSNR随采样率的变化
图 2 CIFAR-10图像, 不同算法下恢复图像的PSNR随采样率的变化

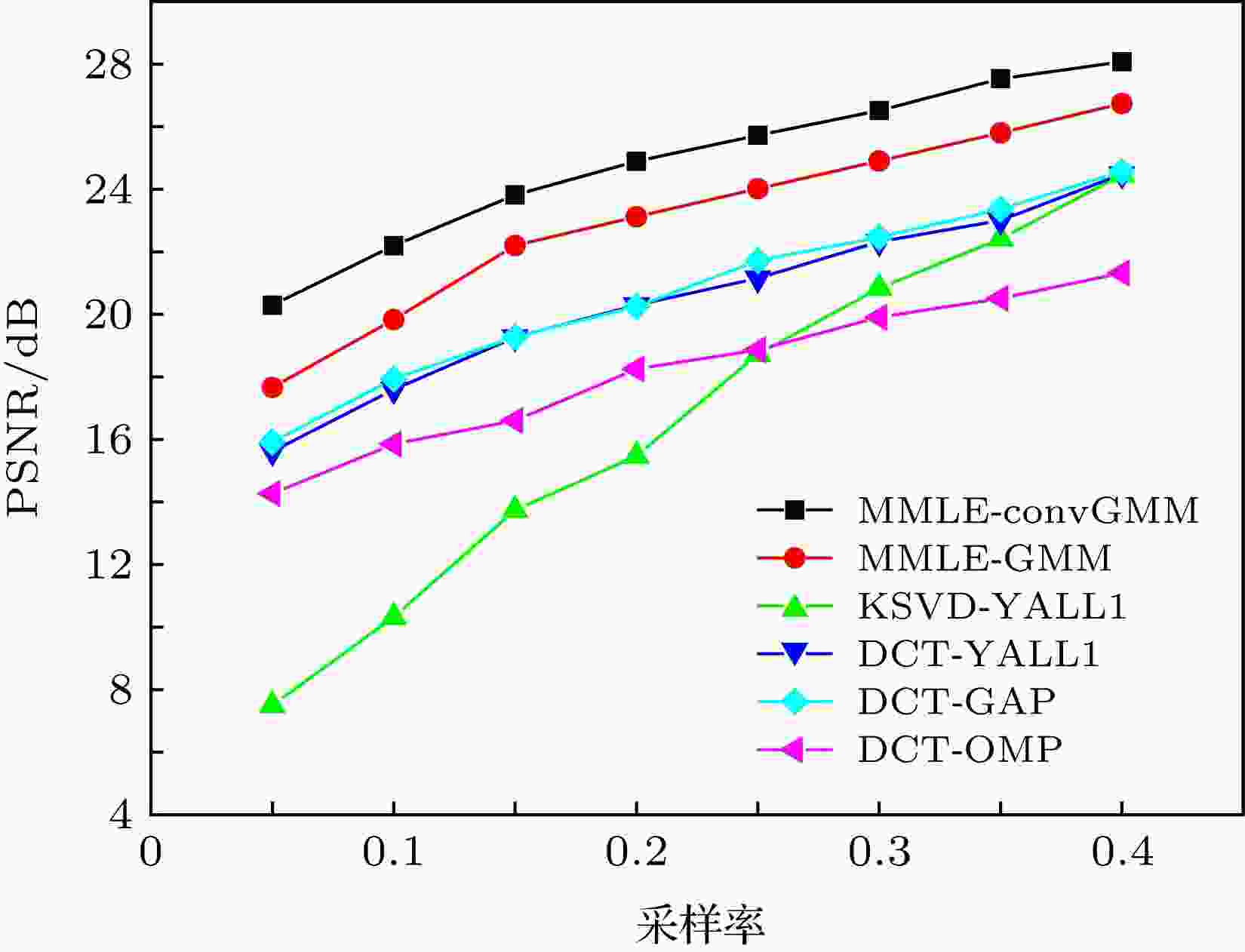 图 3 Caltech 101图像, 不同算法下恢复图像的PSNR随采样率的变化
图 3 Caltech 101图像, 不同算法下恢复图像的PSNR随采样率的变化 图 4 采样率为0.4时, 12张Caltech 101“飞机”图像在不同算法下的恢复情况 (a)原图像; (b) MMLE-convGMM下的恢复图像; (c) MMLE-GMM下的恢复图像; (d) KSVD-YALL1下的恢复图像; (e) DCT-YALL1下的恢复图像; (f) DCT-GAP下的恢复图像; (g) DCT-OMP下的恢复图像
图 4 采样率为0.4时, 12张Caltech 101“飞机”图像在不同算法下的恢复情况 (a)原图像; (b) MMLE-convGMM下的恢复图像; (c) MMLE-GMM下的恢复图像; (d) KSVD-YALL1下的恢复图像; (e) DCT-YALL1下的恢复图像; (f) DCT-GAP下的恢复图像; (g) DCT-OMP下的恢复图像
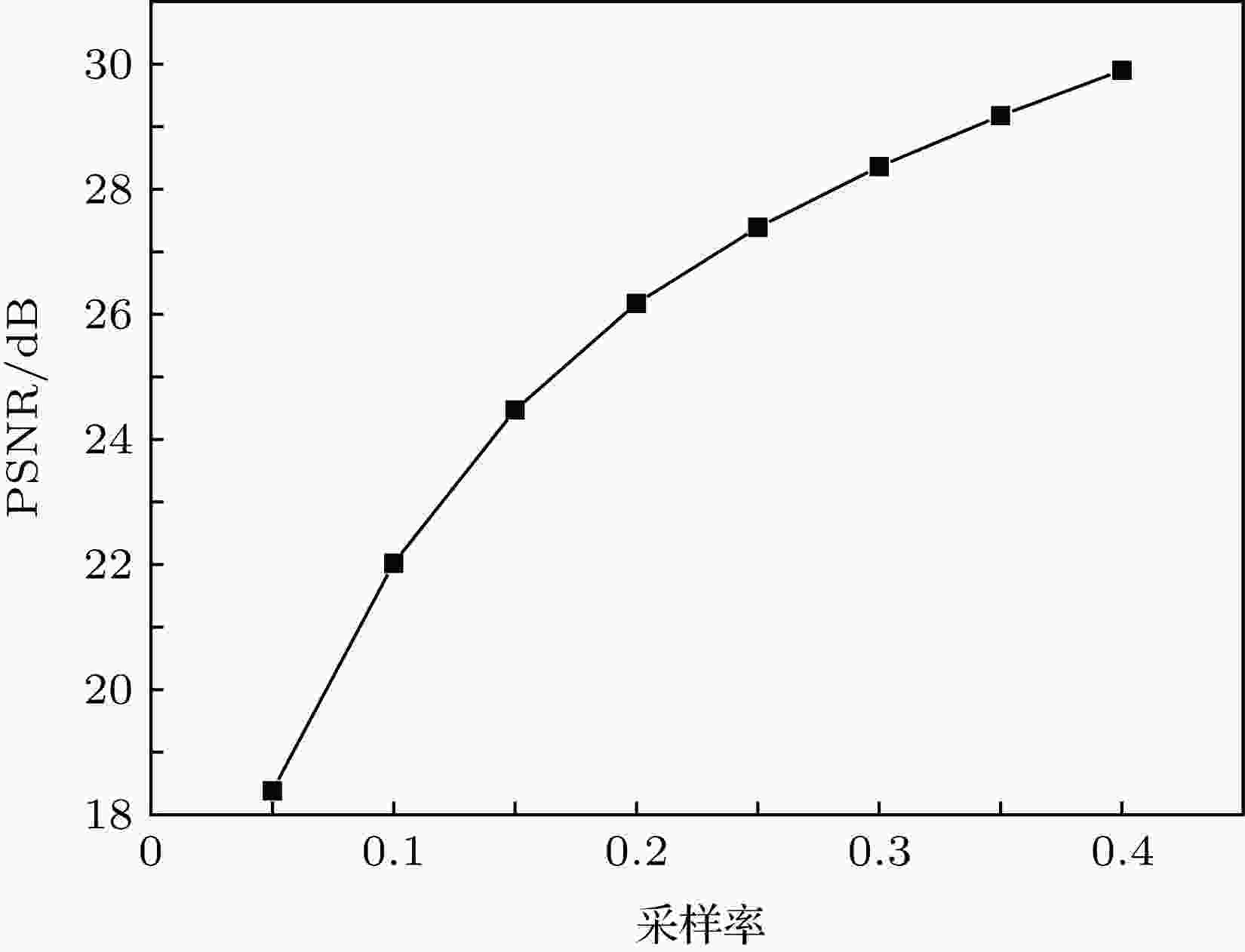 图 5 MMLE-convGMM算法恢复CelebA图像的PSNR随采样率的变化
图 5 MMLE-convGMM算法恢复CelebA图像的PSNR随采样率的变化 图 6 随机选取的CelebA图像的恢复情形 (a)原图像; (b) MMLE-convGMM算法恢复的图像, 采样率为0.4
图 6 随机选取的CelebA图像的恢复情形 (a)原图像; (b) MMLE-convGMM算法恢复的图像, 采样率为0.4