摘要:针对超材料吸波频带窄的问题, 采用金属螺旋环超表面与碳纤维吸波材料相复合的方式, 设计了宽频高性能复合吸波体. 研究发现, 在碳纤维吸波材料中引入双层螺旋环超表面能显著增强吸收峰值和吸波带宽, 且适当增加螺旋环初始线长和吸收层厚度有利于提高复合吸波体的吸波性能, 9.2—18.0 GHz频段的反射损耗均优于–10 dB (带宽达8.8 GHz), 吸收峰值达–14.4 dB. 利用S参数计算得到螺旋环-碳纤维复合吸波体的等效电磁参数和特征阻抗呈现多频点谐振特性, 通过构建双层螺旋环超表面等效电路模型, 定量计算了复合吸波体的电磁谐振频点, 发现由等效电路模型获得的谐振频点计算值与仿真值基本相符, 说明该复合吸波体多频点电磁谐振是宽频电磁损耗的主要机制.
关键词: 螺旋环超表面/
电磁谐振/
等效电路/
微波损耗机制

English Abstract

全文HTML

--> --> -->

高性能吸波材料在电磁兼容、电磁辐射防护、特种装备反探测等方面能发挥重要作用, 将传统吸波材料与超材料复合是吸波材料发展的重要方向^[1-5]. Landy等^[6]在2008年就设计了由开口环形金属图案阵列、损耗电介质和金属微带线组成的X波段超材料吸波体, 对11.65 GHz处的入射电磁波的吸收率接近100%. 基于超材料研发的复合吸波体具有厚度薄、质量轻、吸收强、吸收频带可调^[7-20]等优点, 但由单一尺寸金属图案单元构成的超材料吸波体一般仅在某频点对电磁波具有强吸收, 难以满足实际应用的宽频吸波要求.
为拓宽超材料吸波体的吸收频带, 通常是将不同尺寸的金属图案组合而使多个吸收峰相互叠加^[21-23]. 程用志^[24]分别将两个和四个不同尺寸的十字型金属图案组合, 得到了具有双频点与四频点(3.76, 3.98, 4.18, 4.34 GHz)强吸收的吸波体, 且临近的吸收峰能相互叠加, 半峰高的宽度(吸收率超过50%的带宽)分别达410和810 MHz.
研制宽频吸波材料的另一种有效方法是将超材料与传统吸波材料相复合^[25,26]. Sun等^[27]将基于方环图案的超材料吸波体与泡沫吸波材料复合, 总厚度为4 mm时复合吸波体反射损耗优于–10 dB的带宽达2 GHz. 徐永顺等 ^[28]将基于单层螺旋图案的超材料嵌于两层磁性吸波材料中, 复合吸波体反射损耗优于–10 dB的频段为6.69—13.8 GHz, 带宽达7.11 GHz.
本文将双层螺旋结构的超表面与填充短切碳纤维的吸波材料复合, 研究螺旋环结构的线长、线宽特征尺寸及介质层厚度对复合吸波体反射率的影响规律, 利用全波仿真软件分析复合吸波体电磁场和表面电流密度的分布, 并通过构建双层螺旋超表面/碳纤维吸波体复合结构的等效电路模型, 探讨复合吸波体的多频点谐振特性及微波损耗机理, 可为基于超表面的宽频高性能复合吸波材料提供设计参考.

设计的螺旋环超表面-碳纤维复合吸波体结构如图1所示. 结构单元的尺寸为10 mm × 10 mm, 螺旋环初始长度a = 2.5 mm, 线宽度b = 0.25 mm, 厚度d = 0.01 mm, 螺旋环末段金属线沿反螺旋方向伸出引脚, 可利用尖端效应增强相邻螺旋环单元之间耦合. 螺旋环材质为铜, 电导率σ = 5.8 × 10⁷ S/m. 两种电磁参数不同的理想碳纤维吸波材料用两种长度的T700短切碳纤维制得, 相对磁导率均为1, 其介电频谱如图2所示, 上层电介质厚度h为优化参量.
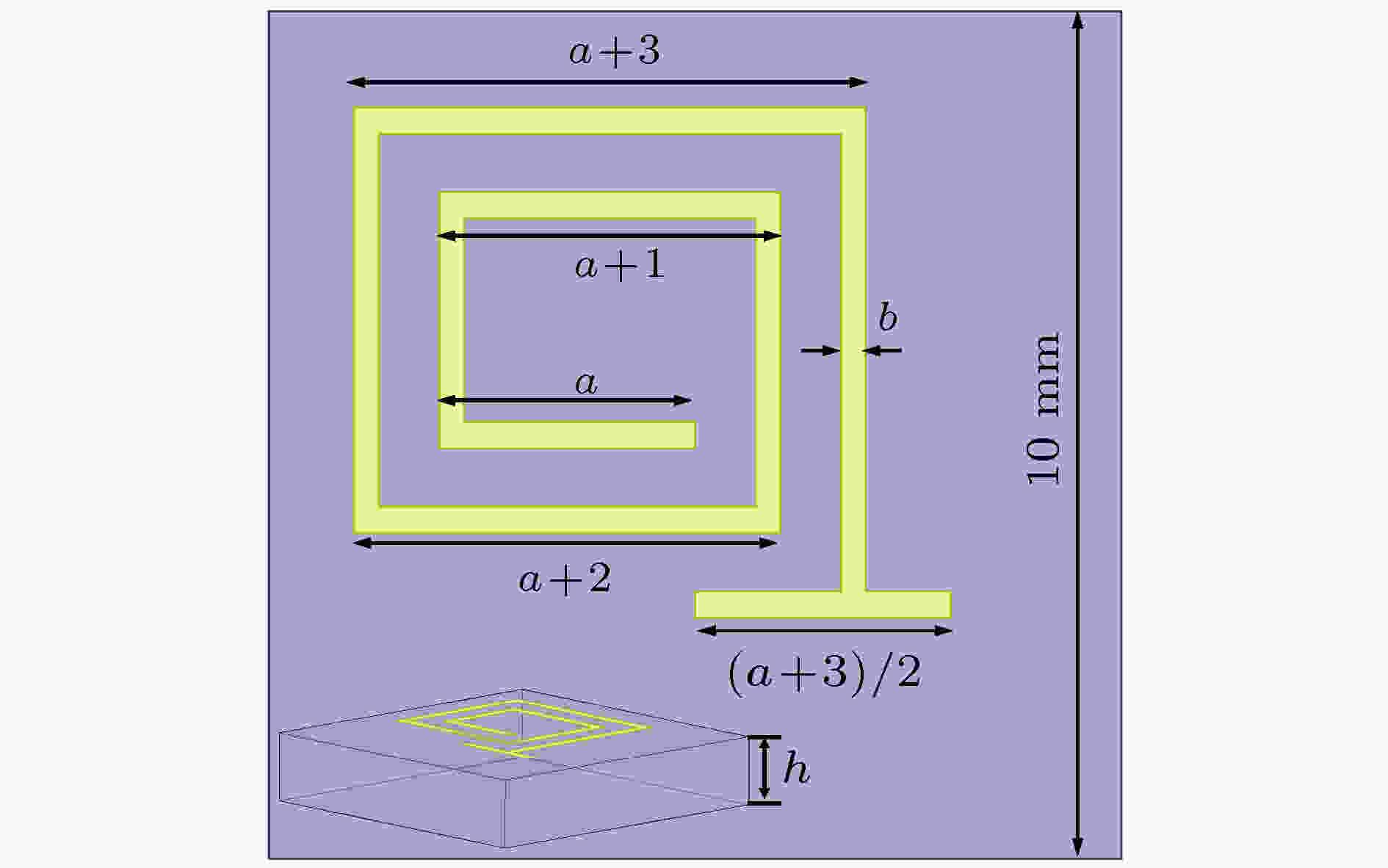图 1 螺旋环-碳纤维复合吸波体结构示意图
Figure1. Structure schematic diagram of spiral-ring with carbon fiber composite microwave absorber.

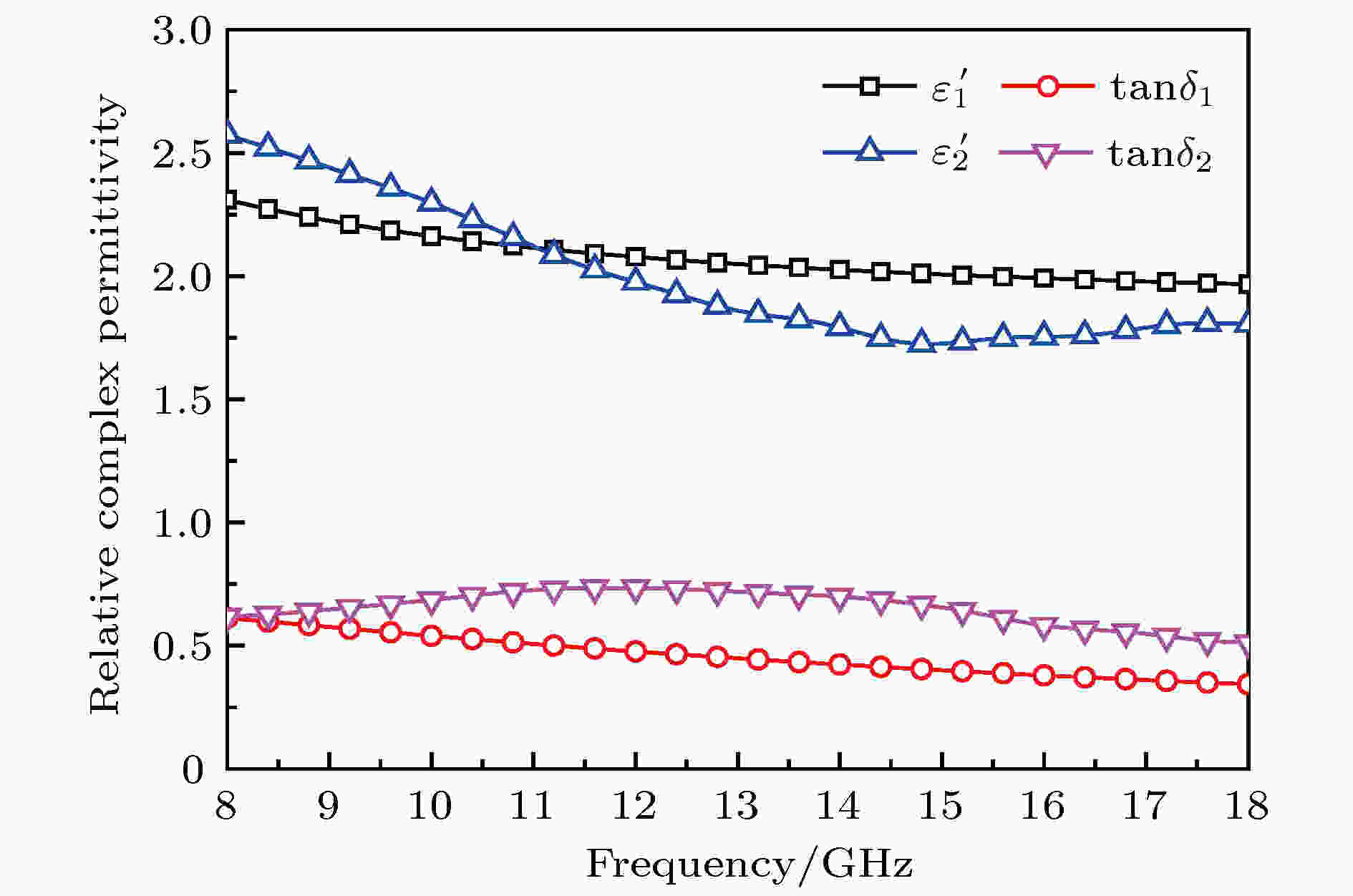图 2 碳纤维损耗层复相对介电常数频谱
Figure2. Relative complex permittivity of carbon fiber.

由于吸波体实物是由大量的单个吸波体单元在横、纵两个方向周期性排列形成的一个二维结构. 在HFSS仿真软件中, 选择由“主边界”和“从边界”构成的“主从边界条件”, 在该边界条件下, 相邻的边界之间的电场存在相位差, 可用于对无限阵列的仿真模拟. 如图3所示, 在平行于xoy平面的端口处均设置Floquet端口激励, 电磁波垂直入射, 其余四个平面设置为两对主从边界条件, 以此模拟二维周期性结构. 扫描频率范围设置为8.0—18.0 GHz.
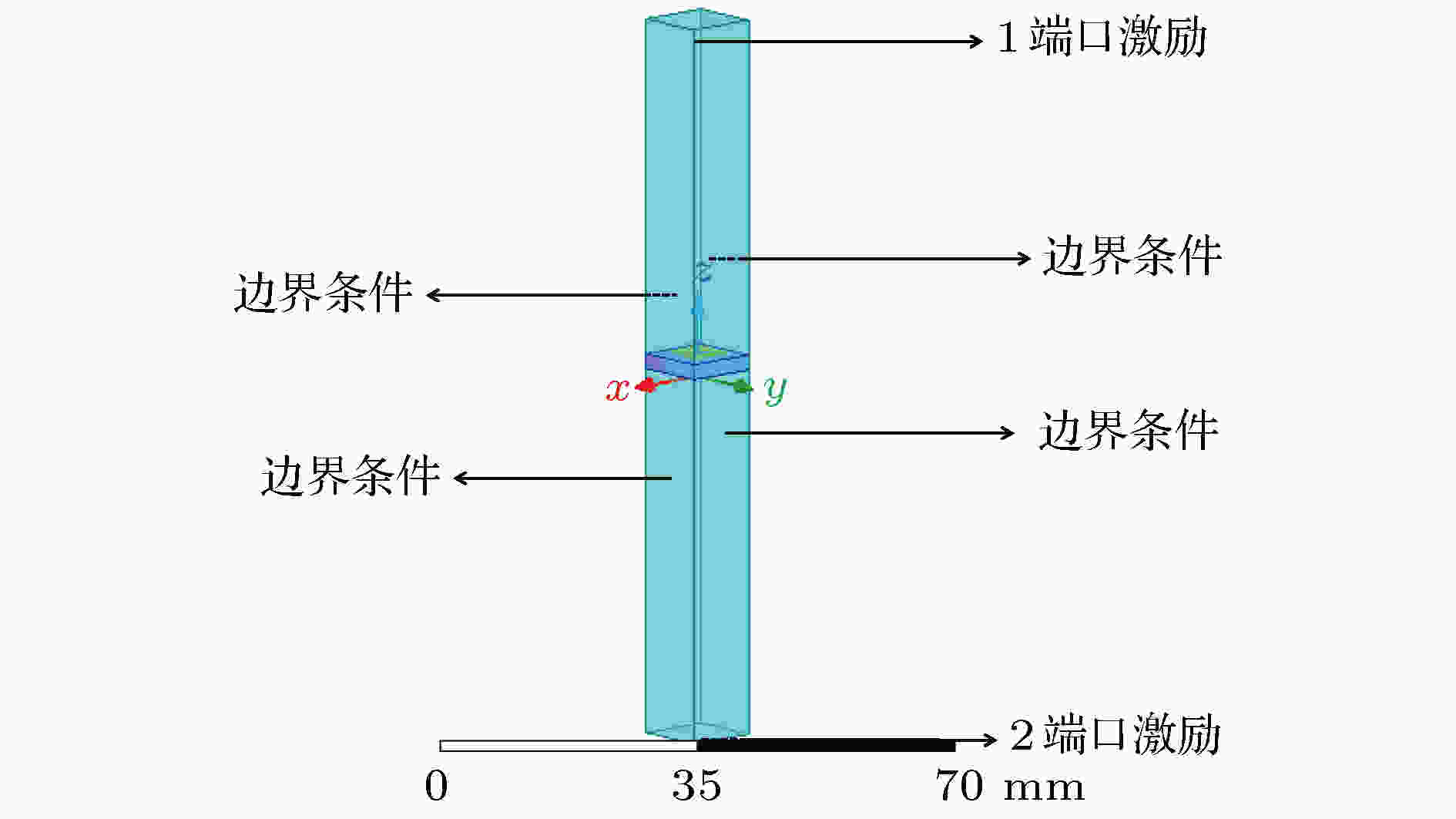图 3 仿真模型边界条件与激励设置
Figure3. Settings of boundary conditions and incentive settings for the simulation model.

设计的双层金属螺旋环与碳纤维吸波材料复合结构、双层碳纤维吸波材料及介质基板FR-4上的双层金属螺旋环复合结构(总厚度均为3.1 mm)的吸波性能如图4所示. 可见, 双层碳纤维吸波体在18 GHz频点处的峰值反射损耗仅为–7.5 dB; FR-4上的双层金属螺旋环复合结构呈现谐振型多峰值的吸波特性; 双层碳纤维吸波层插入螺旋环后, 呈现明显的宽频吸波特性, 9.2—18.0 GHz频段的反射损耗均优于–10 dB(带宽达8.8 GHz), 吸收峰值达–14.4 dB.
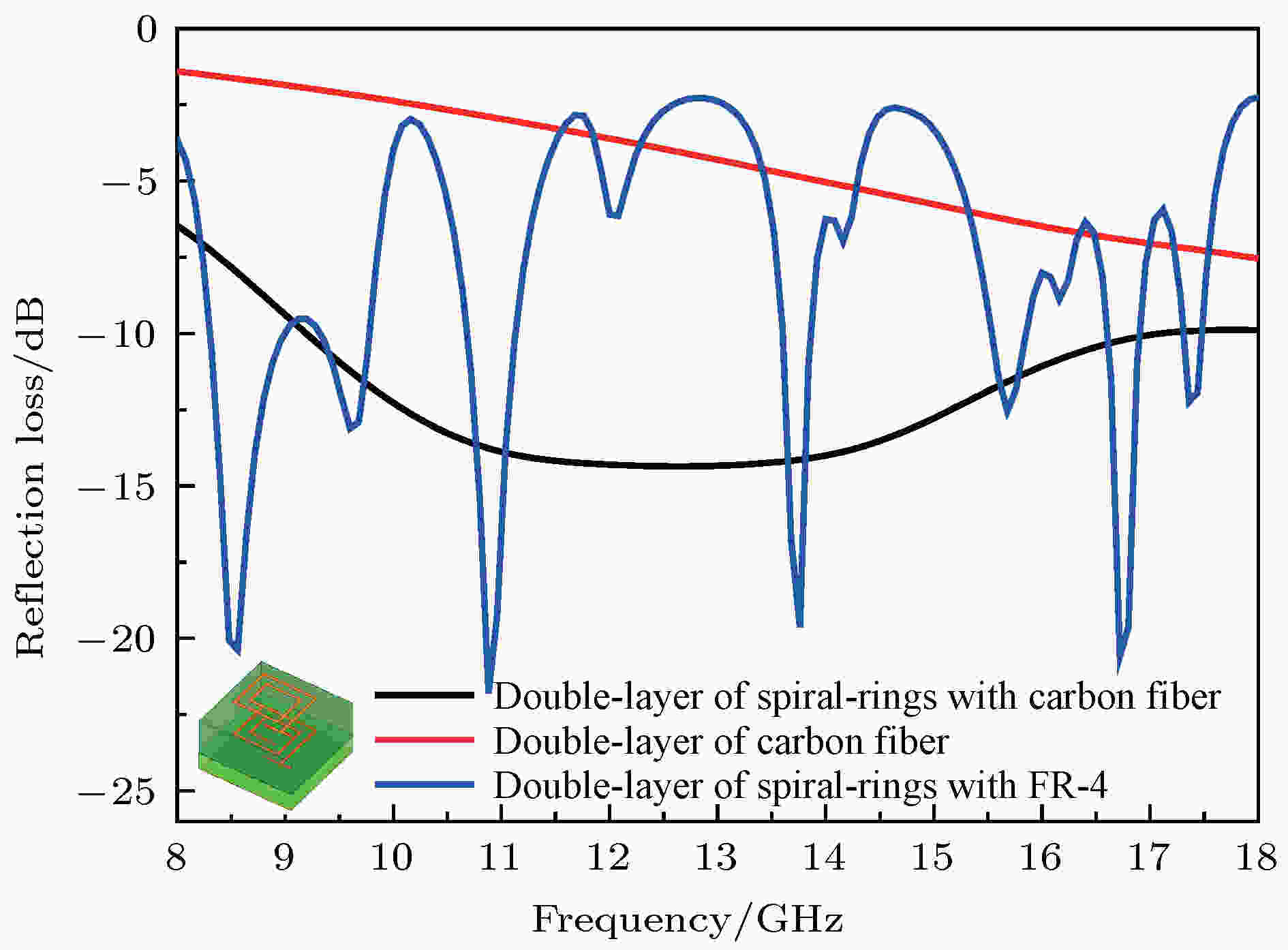图 4 双层金属螺旋环-碳纤维复合吸波体的反射损耗
Figure4. Reflection loss of double layers metal spiral-ring with carbon fiber composite microwave absorber.

螺旋环初始线长a、线宽b和上层吸波材料厚度h对复合吸波体反射率的影响规律见图5. 初始线长a对复合吸波体反射率的影响显著, 随a逐渐增加, 吸收峰值有所增加, 优于–10 dB的吸收带宽显著增加; 且随a增加, 吸收峰对应的频率向低频移动, 即在不增加吸波层厚度的前提下能增强低频段微波的吸收. 线宽b对复合吸波体微波反射率的影响较小; 而增加吸收层厚度h能有效增强低频段电磁波的吸收. 经优化设计发现, 当螺旋结构尺寸为a = 3.0 mm, b = 0.3 mm, h = 2.1 mm时的螺旋形超材料与短切碳纤维吸波材料组成的复合吸波体性能最佳, 反射损耗优于–10 dB的频段为9.20—18.00 GHz, 吸收峰值达–14.36 dB.
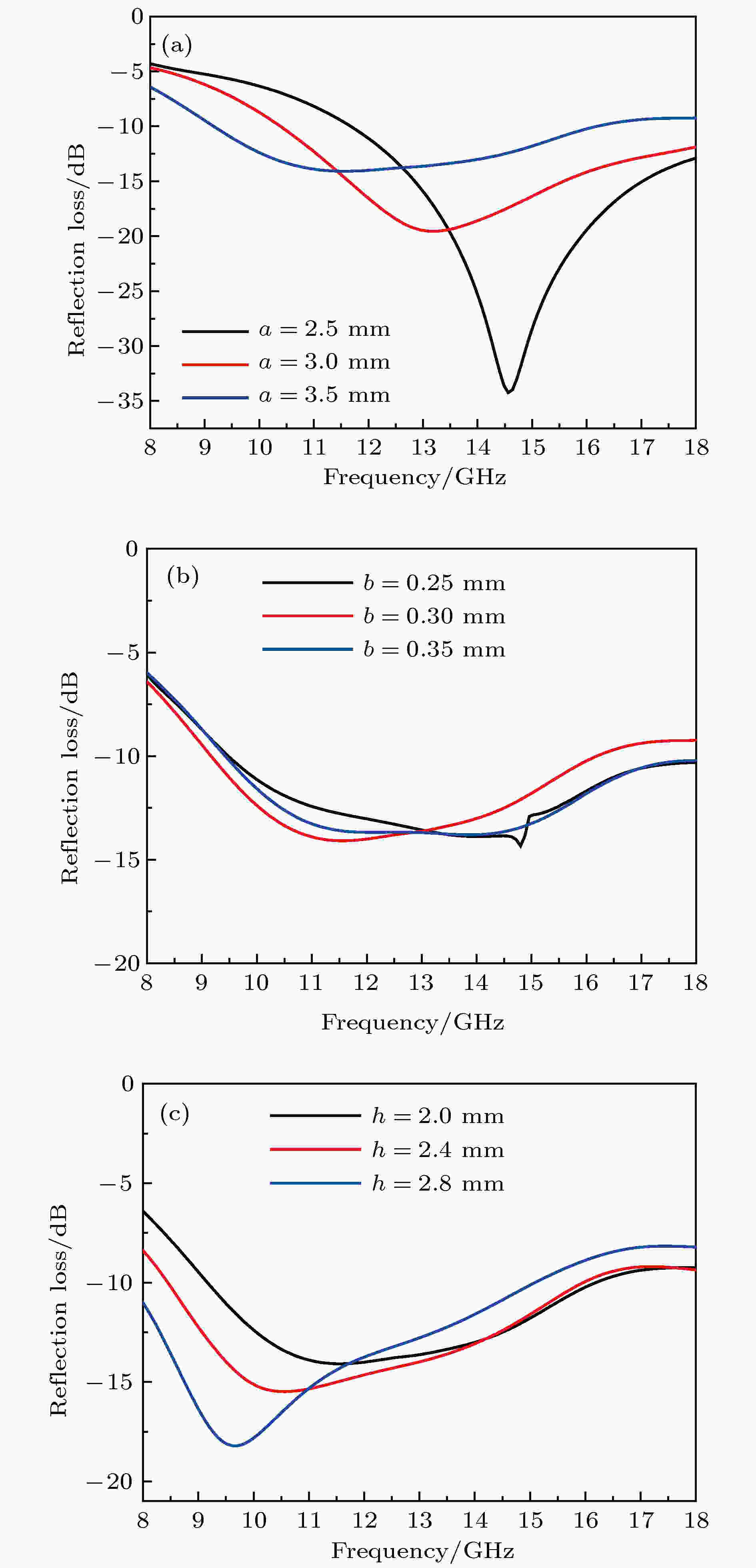图 5 螺旋环结构参数对双层螺旋环-碳纤维复合吸波体反射损耗的影响　(a)初始线长; (b)线宽; (c)损耗层厚度
Figure5. Effects of structure parameters of spiral-ring on the reflection loss of double layers metal spiral-ring with carbon fiber composite microwave absorber: (a) Initial length of line; (b) width of line; (c) thickness of upper dielectric layer

利用S参数可算得双层螺旋环超表面与碳纤维吸波材料复合结构的复折射率n及复阻抗Z, 计算公式如下^[29]：

$n = \frac{1}{{kd}} \cdot \left( {{\rm{arccos}}\left( {\frac{{1 - S_{11}^2 + S_{21}^2}}{{2{S_{21}}}}} \right) + 2m{\text{π}}} \right),$

$Z = \pm \sqrt {\frac{{{{\left( {1 + {S_{11}}} \right)}^2} - S_{21}^2}}{{{{\left( {1 - {S_{11}}} \right)}^2} - S_{21}^2}}},$

式中k是波矢, d是复合吸波体的厚度, S₁₁和S₂₁分别为反射系数和透射系数, m为考虑反余弦函数解的多值性引入的整数, Z为复阻抗. 由复折射率n与复阻抗Z可进一步计算得到复合吸波体的等效复电磁参数, 计算式如下：

${\varepsilon _{{\rm{eff}}}} = \frac{n}{Z},$

${{\mu} _{{\rm{eff}}}} = n \cdot Z.$

S参数的幅值与相位如图6所示.
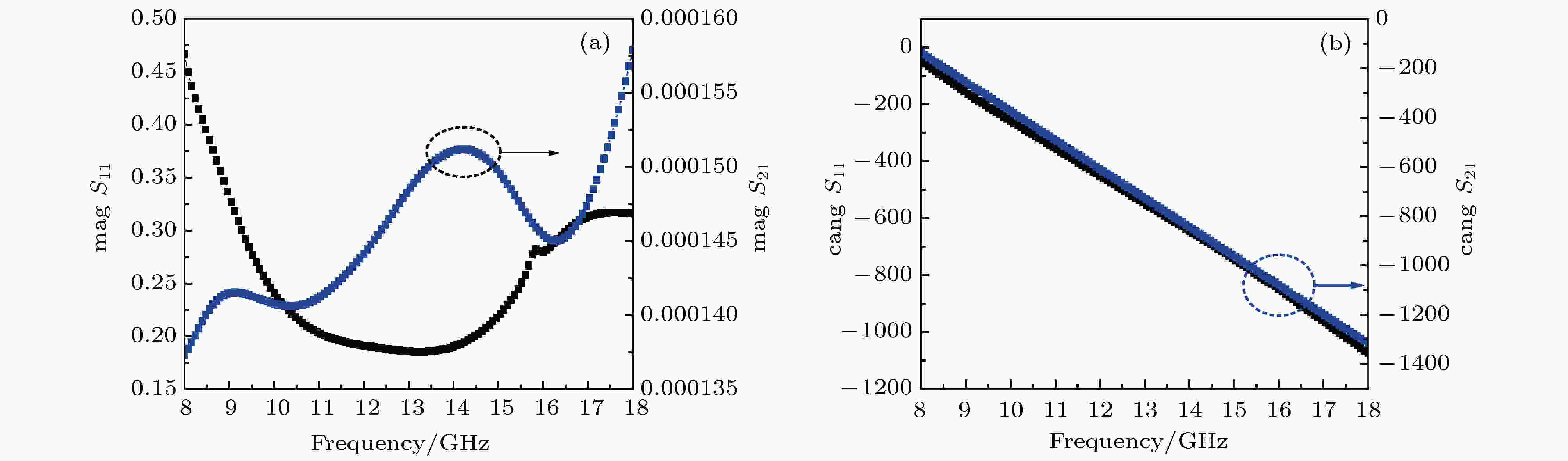图 6 复合吸波体S参数的(a)幅值和(b)相位的频谱特性
Figure6. Spectrum feature of composite microwave absorber’s S parameter: (a) Amplitude; (b) phase

根据(1)—(4)式, 结合S参数, 计算得到特征阻抗、介电常数、磁导率以及复折射率的频谱特性如图7所示.
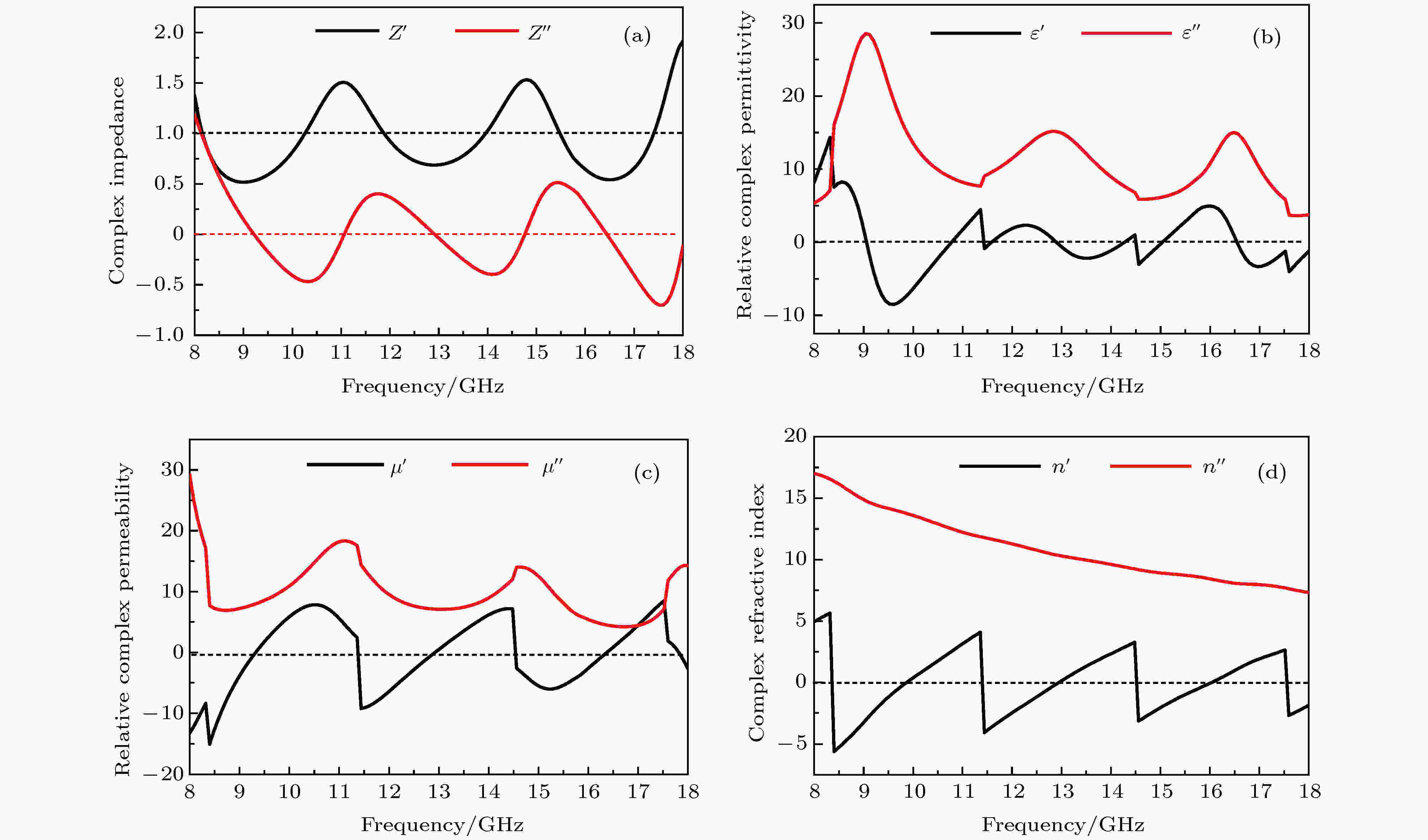图 7 复合吸波体的(a) 复阻抗Z、(b) 复介电常数、(c)复磁导率和(d)复折射率的频谱特性
Figure7. Spectrum feature of composite microwave absorber: (a) Complex impedance Z; (b) relative complex permittivity; (c) relative complex permeability; (d) complex refractive index

可见, 复合吸波体的特征阻抗、复电磁参数均出现明显的谐振特性. 复阻抗的实部Re(Z)在1附近振荡变化, 虚部Im(Z)在0附近振荡变化, 与自由空间的复阻抗Z₀ = 1+0j较为接近, 能保证良好的阻抗匹配而使入射电磁波能进入复合吸波体. 复合吸波体的等效复介电常数、等效复磁导率在8—18 GHz频段具有多个电磁谐振峰：在f₀₁ = 9.04 GHz, f₀₂ = 12.80 GHz, f₀₃ = 16.48 GHz处发生电谐振, 在f₀₄ = 11.12 GHz, f₀₅ = 14.64 GHz处发生磁谐振复折射率实部在8—18 GHz频段存在多个取负值的频段.
图8为电场强度矢量E的分布图, 在低频点f₀₁ = 9.04 GHz、中频点f₀₂ = 12.80 GHz、高频点 f₀₃ = 16.48 GHz三个频点处, 与单一的电损耗吸波材料相比, 螺旋环超材料吸波体的引入使吸波体内部的电场强度矢量E的模提高了一个数量级. 从螺旋环超表面复合吸波体等效介电常数频谱曲线可以发现, 引入螺旋环超表面后的复合吸波体相对介电常数虚部显著增强, 8—18 GHz范围的平均值由0.96增加到11.66, 表明对微波能量的损耗能力显著增强.
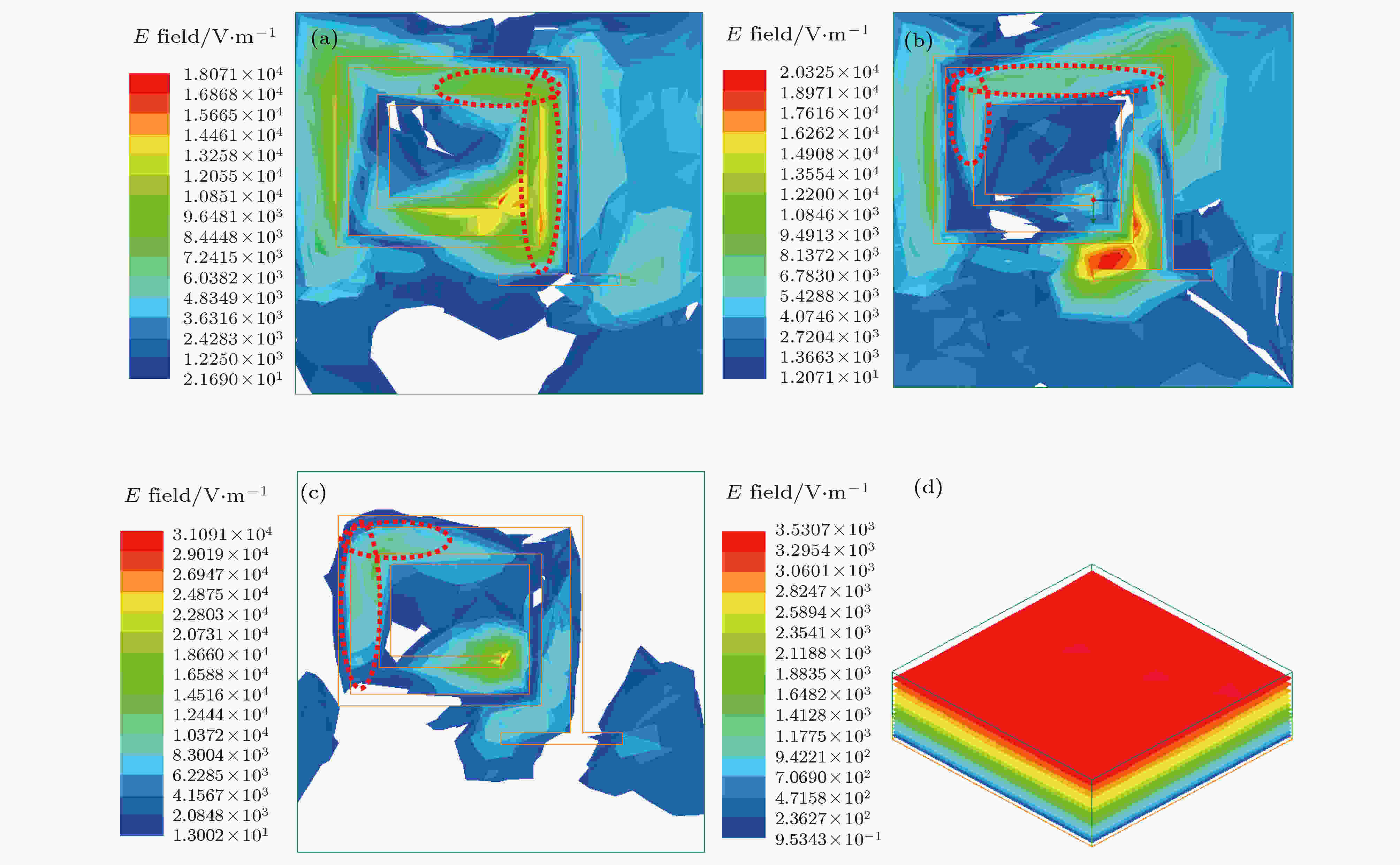图 8 电场强度E幅值分布俯视图　(a) f₀₁ = 9.04 GHz; (b) f₀₂ = 12.80 GHz; (c) f₀₃ = 16.48 GHz; (d)等厚度有耗介质(f₀₃ = 16.48 GHz)
Figure8. Top view of electric field amplitude E distribution: (a) f₀₁ = 9.04 GHz; (b) f₀₂ =12.80 GHz; (c) f₀₃ = 16.48 GHz; (d) dielectric with dielectric loss with the same thickness (f₀₃ = 16.48 GHz)

进一步提取了复合吸波体在8—18 GHz频段两个磁谐振频点(f₀₄ = 11.12 GHz, f₀₅ = 14.64 GHz)的电流密度J矢量分布图. 如图9所示, 上、下金属环上的电流密度J矢量方向以及下金属环与底部金属接地铜板上的电流密度J矢量的方向分别相反, 导致磁谐振发生而吸收微波电磁能量. 在上述谐振频点, 电场强度(见图8)和表面电流密度(见图9)主要分布于红色虚线框所示区域的上下层螺旋线之间, 且随谐振频率升高, 电场和磁场能量分布愈集中.
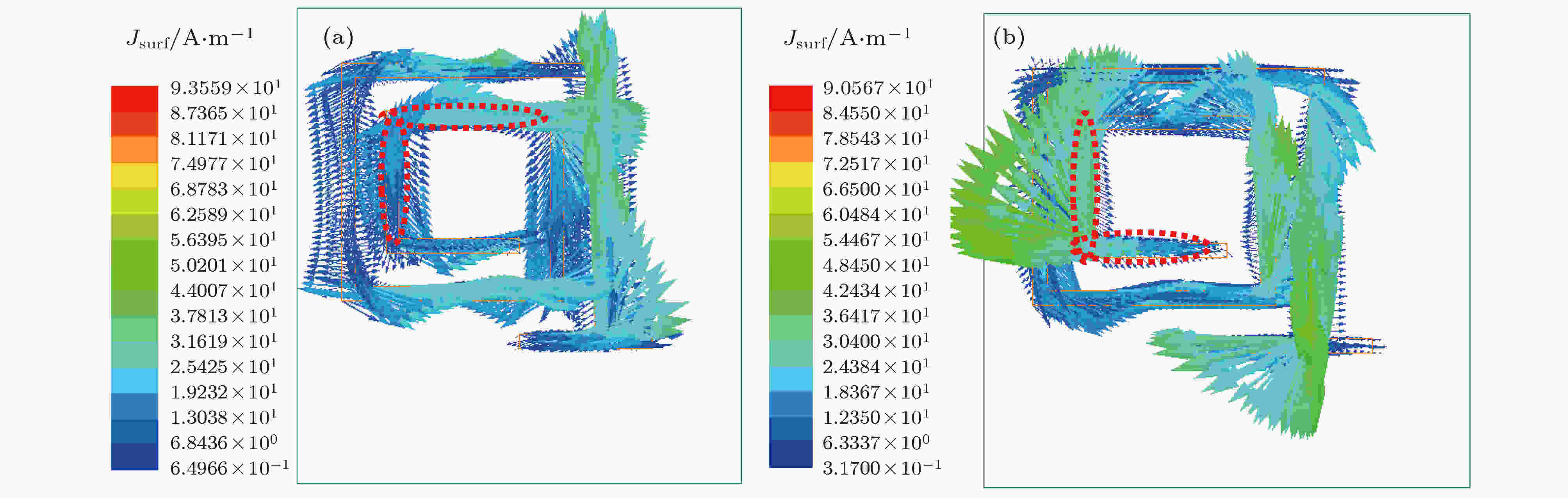图 9 表面电流密度矢量J分布俯视图　(a) f₀₄ = 11.12 GHz; (b) f₀₅ = 14.64 GHz
Figure9. Top view of distribution for surface current density J : (a) f₀₄ = 11.12 GHz; (b) f₀₅ = 14.64 GHz

上下层螺旋环长直导线的间距$D = h = 2.1\; \times $$ {10^{ - 3}}\;{\rm{m}} $, 螺旋环导线的截面等效圆半径$r = $$ \sqrt {\dfrac{{{S_{\text{金属线截面}}}}}{\text{π}}} = \sqrt {\dfrac{{0.01 \times {{10}^{ - 3}} \cdot b}}{\text{π}}} \; \approx\; 3.01 \times {10^{ - 5}}$ m, 满足近似条件：$D \gg r$. 利用等效电路法将上、下金属螺旋环每一组尺寸相同、沿电磁波入射方向正对的两组金属螺旋线等效为平行板电容器和双长直导线电感, 电感L为

$L = \frac{{{{\textit{μ}} _0}{{\textit{μ}} _{\rm{r}}}l}}{{\text{π}}} \cdot \left[ {{\rm{ln}}\left( {\frac{D}{r}} \right) + \frac{1}{{4{{\textit{μ}} _{\rm{r}}}}}} \right],$

式中${{\textit{μ}} _{\rm{0}}}$是真空磁导率, ${{\textit{μ}} _{\rm{r}}}$是介质材料的相对磁导率, L是双长直导线的线长.
值得注意的是, 图8和图9中电场与磁场在金属线之间的分布是不均匀的, 部分空间没有场的分布; 因此, 实际的等效电容C_e与等效电感L_e应小于相应的理想值C, L. 从而提出等效修正因子$k = {k_c} \cdot {k_l}$, 其中${k_c} = \displaystyle\frac{{{C_{\rm{e}}}}}{C}$, ${k_l} = \displaystyle\frac{{{L_{\rm{e}}}}}{L}$. k值越接近于1, 说明等效L-C电路模型拟合程度越高.
在L-C谐振电路中, 谐振频率f与电容值C_e、电感值L_e的关系是

$f = \frac{1}{{2{{\text{π}}} \cdot \sqrt {{L_{\rm{e}}} \cdot {C_{\rm{e}}}} }}.$

综合以上各式可以得到第i个谐振频率的表达式

${f_i} \approx \frac{c}{{2\sqrt {{\text{π}}} }} \cdot \frac{1}{{\sqrt {k{\varepsilon _{\rm{r}}}{{\mu} _{\rm{r}}}} }} \cdot \frac{1}{{\sqrt {\dfrac{b}{h} \cdot {\rm{ln}}\left( {\displaystyle\frac{h}{r} + \displaystyle\frac{1}{{4{{\mu} _{\rm{r}}}}}} \right)} }} \cdot \frac{{\rm{1}}}{{{a_i}}}.$

利用(7)式可得复合吸波体的谐振频点, 取$c = 3 \times {10^8}\; {{\rm{m/s}}}$, $b = 0.3\;{\rm{m}}$, $h = 2.{\rm{1}}\; {{\rm{mm}}}$, $r \approx 3.01 \times $ $ {10^{ - 2}}\;{{\rm{mm}}}$, 计算结果如表1所列.

编号i	等效电磁参数谐振 频点f0i/GHz	相对介电 常数εr	等效电容器/电感线 长度ai/mm	修正因子k = 1时近似 谐振频点fi/GHz	修正因子 k	f0i与fi的 相对误差
1	9.04	2.216	8.0	9.12	1.02	0.88%
2	12.80	2.054	6.5	11.66	0.83	–8.91%
3	16.48	1.985	5.0	15.42	0.88	–6.43%
4	11.12	2.110	7.0	10.68	0.92	–3.96%
5	14.64	2.009	5.0	15.33	1.10	4.71%

表1复合吸波体谐振频点的等效电路模型计算值
Table1.Calculation results of resonance frequency of composite microwave absorber.

根据表1的计算结果可得f_0i与f_i (k = 1)的变化趋势对比图, 如图10所示. $i \in \left\{ {1,\;2,\;3} \right\}\;$时为电谐振频点计算结果对比, 当$i \in \left\{ {4,\;5} \right\}$时为磁谐振频点计算结果对比. 发现将金属螺旋环结构长度相同、上下排列的两金属线等效为平行板电容器C和双长直载流直导线电感器L, 不同尺寸的金属线构成谐振频率f不同的L-C振荡电路, 计算的谐振频点与仿真所得的谐振频点较吻合, 说明含螺旋形超表面的复合吸波体的多频点电磁谐振是其宽频吸波性能增强的主要原因.
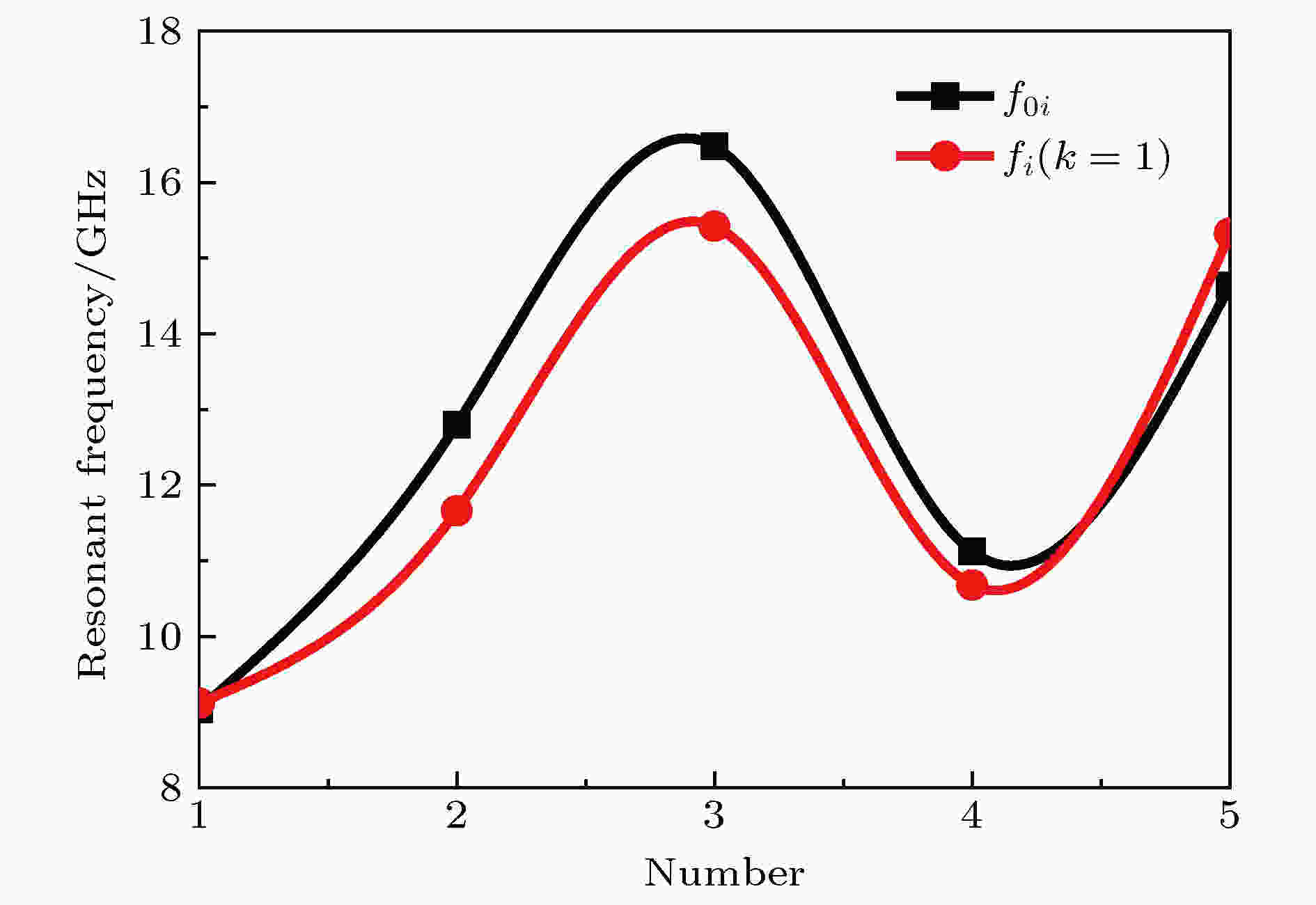图 10 复合吸波体f_0i与f_i (k = 1)的对比
Figure10. Comparison of f_0i and f_i (k = 1) .

1)在双层碳纤维吸波材料中引入双螺旋环超表面层, 得到的复合吸波体吸收峰值达–14.4 dB, 9.2—18.0 GHz的反射损耗均优于–10 dB.
2)单元结构参数中螺旋环初始线长a对复合吸波体的反射率影响显著, 随a适当增加, 吸收峰值和吸收带宽均显著增加, 且吸收峰频点向低频移动; 线宽b对复合吸波体的反射率影响较小, 适当增加吸收层厚度h能有效增强低频段的反射损耗.
3)基于L-C等效电路模型计算的复合吸波材料在X波段和Ku波段的多个电、磁谐振频点, 与仿真获得的谐振频点基本相符, 说明多频点电磁谐振是复合吸波体的宽频吸波性能增强的主要原因, 且通过调节螺旋形超材料金属图案的结构参数可以对谐振频点进行调控.