删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

过渡金属硼碳化物<i>TM</i><sub>3</sub>B<sub>3</sub>C和<i>TM</i>

本站小编 Free考研考试/2021-12-29
摘要:在过渡金属轻元素化合物中, 寻找新的硬质或者超硬材料是当前的一个研究热点. 目前寻找范围多集中在过渡金属硼化物、碳化物和氮化物等二元体系, 三元相的研究则相对较少. 本文以已知Nb3B3C和Nb4B3C2结构为模板, 采用元素替代法构建了29种TM3B3C (TM为过渡金属元素)结构和29种TM4B3C2结构, 采用基于密度泛函理论的第一性原理计算方法, 成功找到了热力学、动力学以及力学都稳定的Ta3B3C和Ta4B3C2两种新相. 结构搜索计算确认了这两相为全局能量最优结构. 能带结构和态密度的计算显示这两相均为导体, 导电性主要源于Ta原子的d电子. 这两种新相的硬度大约为26 GPa, 说明Ta3B3C和Ta4B3C2属于高硬度材料, 但不是超硬材料.
关键词: 硬质材料/
第一性原理计算/
稳定性/
硬度

English Abstract


全文HTML

--> --> -->
1.引　言
硬质或者超硬材料(维氏硬度大于40 GPa)因其具有高的硬度和强度、良好的抗摩擦磨损能力以及优异的化学稳定性等特点, 在地质勘探、航空航天、机械加工等领域发挥着重要的作用[1]. 传统超硬材料存在于轻元素B, C, N, O结合所形成的强共价键化合物, 比如早期发现的金刚石和立方BN, 以及后期预测或实验合成的c-BC2N, c-BC5, B6O, C3N4等[2-4]. 该体系内除了涌现的这些新型超硬材料以外, 已有的金刚石和立方BN的研究最近又有了很大进展[5-7]. 燕山大学田永君课题组[5-7]以洋葱结构纳米颗粒为前驱物, 成功地合成了纳米孪晶的金刚石和立方BN, 使得两者硬度均有了较大幅度的提高. 上述传统超硬材料优势是具有很高的硬度, 但是缺点在于合成条件(温度和压力)往往比较苛刻.
寻找合成条件温和的新型硬质或者超硬材料, 是材料研究领域的一个热点. 基于材料硬度测试方法, 可知超硬材料应具有较强的抵抗弹性变形和塑性变形的能力. 过渡金属具有较高的价电子密度从而具有较高的弹性模量, 比如金属锇的体弹模量和金刚石的相当, 具有极强的抗压缩变形能力, 但是其硬度仅有4 GPa, 远低于金刚石的硬度. 这源于过渡金属单质中, 原子间为金属键, 缺乏化学键的方向性, 不能有效阻止位错的产生和移动(塑性变形). 如能在过渡金属结构中引入轻质非金属元素(B, C, N等), 则可以在保持高价电子密度的同时, 形成短而强的方向性共价键, 从而可以抵抗塑性变形, 进而提高材料硬度. 这正是第二类硬质(超硬)材料—过渡金属轻元素化合物的设计思路[8].
过渡金属轻元素化合物的研究主要集中于硼化物、碳化物和氮化物. 过渡金属硼化物体系中, 2005年Cumberland等[9]成功合成了硬质材料OsB2, 其硬度超过20 GPa. 2007年Chung等[10]采用电弧熔炼的方法成功得到了ReB2. 需要特别指出的是, 上述两种过渡金属硼化物都是在常压条件下就可以获得. 最近W-B体系内的稳定化合物也得到了充分研究和预测[11,12]. 过渡金属碳化物体系中, 比较常见的化合物有TiC, ZrC, HfC, VC, NbC, TaC等. 过渡金属氮化物体系中, 2004年著名高压科学家毛河光课题组[13]采用高温高压方法成功合成了PtN2. 随后不久过渡金属氮化物OsN2和IrN2也被成功合成[14], 这些过渡金属氮化物均为极难压缩材料. 关于过渡金属轻元素化合物的更多信息, 可参阅综述文献[2, 15, 16].
从以上文献可以看出, 过渡金属轻元素化合物的研究主要集中于二元相, 三元相的研究则相对少见. 鉴于B, C, N三种元素在周期表中位置相邻、原子大小相似、核外电子排布相近, 因此过渡金属轻元素三元化合物的存在是完全可能并且合理的. 相对二元相, 三元相成分的复杂性决定了其结构和性能的多样性和可调性. 2001年, Hillebrecht和Gebhardt[17]以Nb, B和C作为原料, 以Al-Cu合金作为助溶剂, 成功得到了Nb3B3C和Nb4B3C2晶体. 考虑到不同过渡金属元素的价电子排布相似、原子大小相近, 因此有理由相信, 具有和Nb3B3C和Nb4B3C2化合物相同结构的其他过渡金属TM3B3C和TM4B3C2 (TM = transition metals)化合物应该存在, 这样的稳定化合物期待我们去探索发现.
随着计算理论的不断优化与完善, 通过计算预测稳定相来指导实验合成, 取得了很多成功的先例. 结构预测的方法可以大致分为两种: 1)以已知结构为基础, 以化学成分相近的元素进行替代的方式, 产生新结构, 结构优化之后, 获得最低能量的最优结构. 这种方法的优点在于构建结构模型简单, 计算量小. 但缺点是依赖于已知结构, 有可能会漏掉能量更低的全局最优结构. 2)基于最新发展的遗传算法[18]和粒子群优化算法[19]结合第一性原理计算来预测结构. 该类方法在寻找某种成分的全局最优结构方面, 已经有了很多成功的例子, 发表了多篇高水平论文. 但缺点在于计算量很大, 在不确定某种成分是否存在新稳定结构的前提下, 盲目进行结构搜索, 很多情况下往往会无功而返.
本文将上述两种结构预测方法结合使用. 这是因为周期表中相近元素具有相同结构的可能性大(类质同晶现象), 因此首先采用第一种方法, 以Nb3B3C和Nb4B3C2结构为基础, 用其他过渡金属原子TM替代结构中的Nb原子, 构建多种成分的TM3B3C和TM4B3C2结构模型. 采用基于密度泛函理论的第一性原理计算方法, 通过计算所建结构的形成焓、声子谱和弹性常数, 判断其热力学、动力学和力学稳定性, 初步筛选出稳定的TM3B3C和TM4B3C2化合物. 对这些初步确定为稳定的化学组分TM3B3C和TM4B3C2, 采用第二种结构预测方法, 寻找该组分的全局最优结构, 确认第一种方法找到的稳定结构拥有全局能量最小值.
2.计算方法
本文第一性原理计算采用基于密度泛函理论的平面波赝势方法, 具体计算由VASP (Vienna ab-initio simulation package)软件包[20]来完成. 交换关联采用广义梯度近似(GGA)下的Perdew-Burke-Ernzerhof泛函进行处理. Nb, Ta, B, C原子的4p64d45s, 5p65d36s2, 2s22p, 2s22p2电子作为价电子处理. 平面波截断能设为600 eV. 布里渊区积分采用Monkhorst-Pack形式的特殊K点方法, K点精度设置为$2{\text{π}}$ × 0.03 ?–1. 在结构优化过程中, 未做任何限制, 即晶胞参数和原子位置均可被优化. 优化过程中能量迭代收敛标准为1 × 10–5 eV/atom. 弹性常数的计算采用应力应变方法[21]. 声子谱的计算采用有限位移法, 由VASP软件和PHONOPY软件[22]结合计算完成.
3.计算结果与讨论
2
3.1.结构搜索及热力学稳定性
-->

3.1.结构搜索及热力学稳定性

Nb3B3C和Nb4B3C2同属正交晶系, 空间群皆为Cmcm (No. 63). 表1列出了优化之后Nb3B3C和Nb4B3C2的结构参数. 可以看出计算的晶格参数比文献中实验值稍大, 这也是GGA泛函的一贯问题, 但误差在1%以内, 说明了本文计算方法的可靠性以及计算结果的可信性.
模型 晶系和空间群 晶格参数(?, degree) 原子坐标
Nb3B3C Orthorhombic Cmcm a = 3.284, 3.265a, b = 28.877, 28.710a, c = 3.144, 3.129a, α = β = γ = 90 Nb1 (4c) (0, 0.2128, 0.25), Nb2 (4c) (0, 0.3620, 0.25), Nb3 (4c) (0, 0.4532, 0.25), B1 (4c) (0, 0.1120, 0.25), B2 (4c) (0, 0.0155, 0.25), B3 (4c) (0, 0.0790, 0.25), C (4c) (0, 0.2878, 0.25)
Nb4B3C2 Orthorhombic Cmcm a = 3.257, 3.229a, b = 37.874, 37.544a, c = 3.153, 3.133a, α = β = γ = 90 Nb1 (4c) (0, 0.1621, 0.75), Nb2 (4c) (0, 0.2805, 0.75), Nb3 (4c) (0, 0.3946, 0.75), Nb4 (4c) (0, 0.4642, 0.25), B1 (4c) (0, 0.0854, 0.75), B2 (4c) (0, 0.0118, 0.25), B3 (4c) (0, 0.0602, 0.25), C1 (4c) (0, 0.2202, 0.75), C2 (4c) (0, 0.3383, 0.75)
Ta3B3C Orthorhombic Cmcm a = 3.267, b = 28.688, c = 3.133, α = β = γ = 90 Ta1 (4c) (0, 0.2121, 0.25), Ta2 (4c) (0, 0.3619, 0.25), Ta3 (4c) (0, 0.4531, 0.25), B1 (4c) (0, 0.1130, 0.25), B2 (4c) (0, 0.0155, 0.25), B3 (4c) (0, 0.0791, 0.25), C (4c) (0, 0.2874, 0.25)
Ta4B3C2 Orthorhombic Cmcm a = 3.243, b = 37.609, c = 3.141, α = β = γ = 90 Ta1 (4c) (0, 0.1615, 0.75), Nb2 (4c) (0, 0.2806, 0.75), Nb3 (4c) (0, 0.3945, 0.75), Nb4 (4c) (0, 0.4641, 0.25), B1 (4c) (0, 0.0861, 0.75), B2 (4c) (0, 0.0118, 0.25), B3 (4c) (0, 0.0602, 0.25), C1 (4c) (0, 0.2202, 0.75), C2 (4c) (0, 0.3380, 0.75)
注: a文献[17]中的实验值.


表1Nb3B3C, Nb4B3C2, Ta3B3C和Ta4B3C2晶体的结构参数
Table1.Structural parameters of the Nb3B3C, Nb4B3C2, Ta3B3C and Ta4B3C2 configurations.

Nb3B3C晶体结构如图1(a)和图1(b)所示. 从图中可以看出, 该结构晶胞可以划分为两类区域: Nb-C区和Nb-B区. 在Nb-C区中, Nb原子和C原子形成岩盐矿NaCl型结构, C原子位于Nb原子所形成的八面体中心, 每个C原子配位数为6, 形成6个Nb—C键, 键长范围在2.142—2.273 ?之间, 与二元化合物Nb2C中Nb—C键长(2.191—2.218 ?)相当. 在Nb-B区中, Nb原子和B原子形成AlB2型结构, B原子位于6个Nb原子所形成的三棱柱中心, Nb—B键长范围在2.394—2.456 ?之间, 与二元化合物中NbB2中Nb—B键长2.428 ?相当. B原子的排列类似石墨中碳原子分布方式, 呈蜂窝状, 每个B原子除了与三棱柱顶角的6个Nb原子成键以外, 还与相邻的3个B原子成键, 因此B原子的配位数为9.
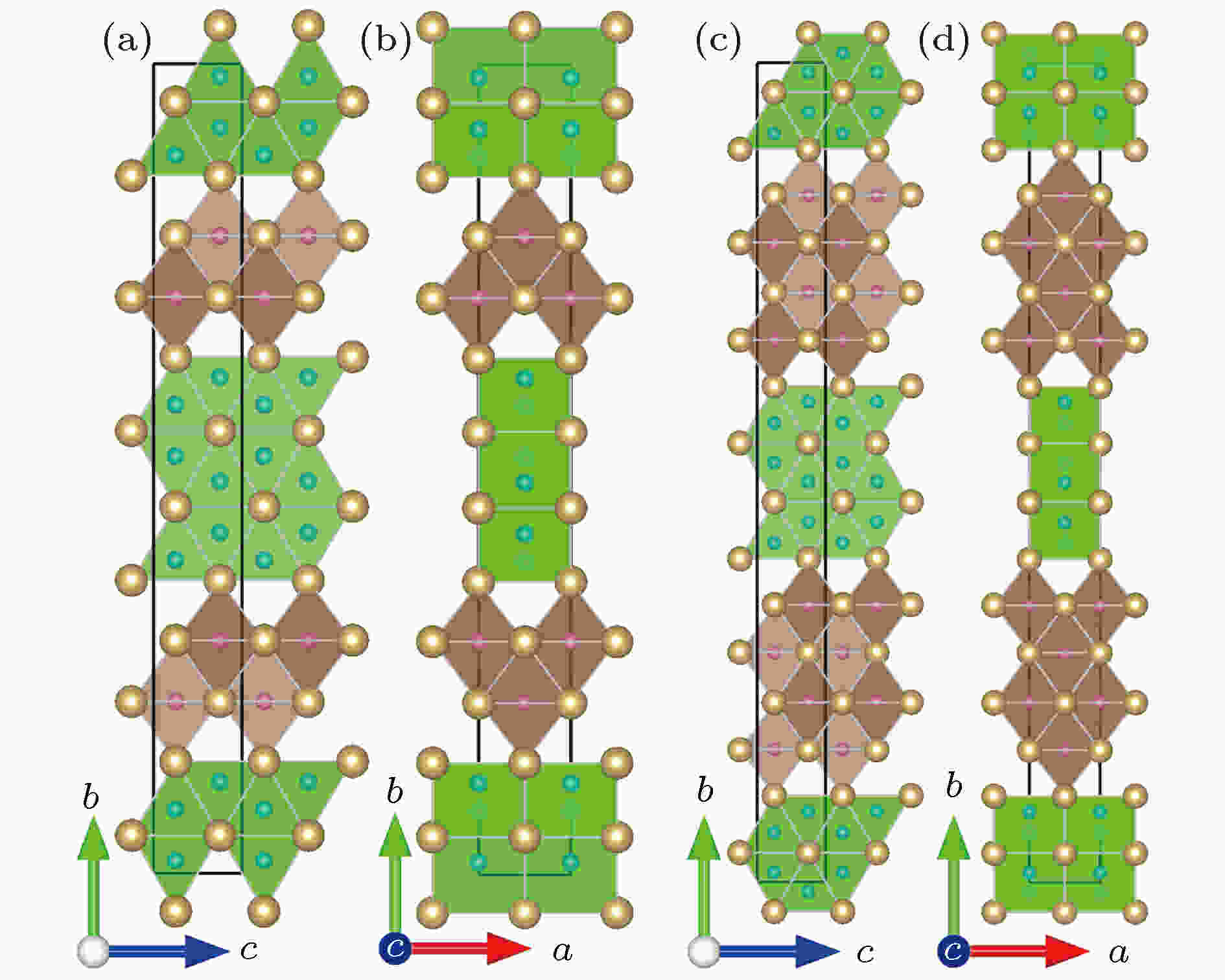图 1 (a), (b) Nb3B3C和(c), (d) Nb4B3C2的晶体结构(棕球, Nb原子; 蓝球, B原子; 粉球, C原子; Nb6B三棱柱和Nb6C八面体分别用绿色和褐色表示)
Figure1. Crystal structures of the (a), (b) Nb3B3C and (c), (d) Nb4B3C2. The light brown, blue and pink spheres represent Nb, B and C atoms, respectively. The Nb6B trigonal prisms and Nb6C octahedrons are painted green and dark brown.

如图1(c)和图1(d)所示, Nb4B3C2结构中原子排列方式和Nb3B3C结构中相似, 基本组成单元相同, 区别在于Nb-C区中八面体层数的不同. 由于这种结构的相似性, 使得两种结构中键长相近, 从而造成两种结构晶格参数a和c数值也相近.
本文选择元素周期表第Ⅲ, Ⅳ, Ⅴ周期中除La系以外的所有过渡金属(TM = Sc—Zn, Y—Cd, Hf—Hg)作为替代元素, 替代Nb3B3C和Nb4B3C2结构中Nb原子, 形成29种TM3B3C和29种TM4B3C2. 首先讨论这29种TM3B3C化合物的热力学稳定性. 对于一个热力学稳定的三元化合物来说, 不能分解成相应单质、二元相以及其他三元相的任意组合. 但是分解产物的组合方式往往有很多种, 计算判断比较繁琐复杂. 因此首先通过判断TM3B3C化合物相对于三种单质材料的稳定性, 从而先排除一部分不稳定的TM3B3C相. 三种单质材料生成三元TM3B3C相的化学反应方程式如下:
$3 \times TM + 3 \times {\rm{boron}} + 3 \times {\rm{carbon}} \leftrightarrow T{M_3}{{\rm{B}}_3}{\rm{C}}{{.}}$
对于该化学反应, 可以通过下式来判断化学反应的方向:
$\begin{split}\Delta {H_{{\rm{elements}}}} = &\left( {7 \times {H_{TM_3{\rm{B}}_3{\rm{C}}}} - 3 \times {H_{TM}}} \right.\\&\left. { - 3 \times {H_{{\rm{boron}}}} - {H_{{\rm{carbon}}}}} \right)/7,\end{split}$
式中, $\Delta {H_{{\rm{elements}}}}$是三种单质生成TM3B3C化合物的形成焓; $ H_{TM_3{\rm{B}}_3{\rm{C}}}$, HTM, Hboron和Hcarbon分别是三元TM3B3C、单质TM、单质硼以及石墨的焓值(单位: eV/atom). 如果$\Delta {H_{{\rm{elements}}}}>0$, 则意味着化学反应向左进行, 三元相TM3B3C是不稳定的, 意味着容易相分离; 否则就说明化学反应可以向右进行, 三元TM3B3C相对其三种单质材料来说是稳定的. 形成焓的计算结果列于表2中, 相对于单质而言, 有16种TM3B3C相是不稳定的, 首先被排除. 剩下的13种TM3B3C相倾向于不分解, 集中于第IIIB—VIIB族(Re除外)过渡金属元素. 但是这13种相对单质的稳定相, 还可能分解为单质、二元相以及三元相的任意组合. 因此对每种TM-B-C组分, 通过在无机晶体结构数据库(ICSD)和美国材料基因组计划所建的材料数据库(materials project网站)[23]搜索其相应的各种单质、二元相和三元相, 任意组合形成TM3B3C组分. 在各种任意组合中, 焓值总和最低的那一组称之为TM3B3C相的最稳定竞争组合. 采用如下公式计算这13种相对单质稳定TM3B3C相的热力学稳定性:
TM TM3B3C TM4B3C2
$\Delta {H_{{\rm{elements}}}}$ $\Delta {H_{{\rm{comp}}}}$ 最稳定竞争组合 $\Delta {H_{{\rm{elements}}}}$ $\Delta {H_{{\rm{comp}}}}$ 最稳定竞争组合
Sc –0.637 0.071 6ScB2 + Sc4C3 + Sc2C = 4Sc3B3C –0.520 0.144 10ScB2 + 4Sc4C3 + Sc2BC2 = 7Sc4B3C2
Ti –0.896 0.019 9TiB2 + TiC + Ti8C5 = 6Ti3B3C –0.863 0.018 9TiB2 + 7TiC + Ti8C5 = 6Ti4B3C2
V –0.687 0.101 3VB + C = V3B3C –0.628 0.092 18VB + 7C + V6C5 = 6V4B3C2
Cr –0.294 0.159 3CrB + C = Cr3B3C –0.194 0.178 9CrB + 4C + Cr3C2 = 3Cr4B3C2
Mn –0.100 0.195 3MnB + C = Mn3B3C 0.024
Fe 0.002 0.139
Co 0.094 0.255
Ni 0.296 0.456
Cu 0.738 0.959
Zn 0.713 0.929
Y –0.385 0.089 9YB2 + 5Y2C + Y2B3C2 = 7Y3B3C –0.283 0.160 6YB2 + 8Y2C + 3Y2B3C2 = 7Y4B3C2
Zr –0.851 0.019 3ZrB2 + 2ZrC + Zr = 2Zr3B3C –0.838 0.020 3ZrB2 + 4ZrC + Zr = 2Zr4B3C2
Nb –0.698 –0.023 3NbB + C = Nb3B3C –0.661 –0.002 C + 6Nb3B3C + Nb6C5 = 6Nb4B3C2
Mo –0.257 0.175 3MoB + C = Mo3B3C –0.155 0.202 3MoB + C + MoC = Mo4B3C2
Tc –0.005 0.326 12TcB2 + 11C + 3Tc7B3 = 11Tc3B3C 0.138
Ru 0.211 –0.369
Rh 0.230 –0.406
Pd 0.552 0.744
Ag 1.027 1.295
Cd 0.846 1.112
Hf –0.920 0.016 3HfB2 + 2HfC + Hf = 2Hf3B3C –0.922 0.018 3HfB2 + 4HfC + Hf = 2Hf4B3C2
Ta –0.704 0.003 3Ta3B4 + C + 3TaC = 4Ta3B3C –0.691 –0.010 3Ta3B4 + C + 7TaC = 4Ta4B3C2
W –0.094 0.227 3WB + C = W3B3C –0.007 0.273 3WB + C + WC = W4B3C2
Re 0.281 0.425
Os 0.590 0.755
Ir 0.604 0.758
Pt 0.708 0.855
Au 1.096 1.310
Hg 1.186 1.333


表2不同成分TM3B3C和TM4B3C2的形成焓(eV/atom)
Table2.Calculated formation enthalpies of different TM3B3C and TM4B3C2 phases (eV/atom).

$\Delta {H_{{\rm{comp}}}} = {H_{TM_3{\rm{B}}_3{\rm{C}}}} - {H_{{\rm{comp}}}},$
式中, $\Delta {H_{{\rm{comp}}}}$是最稳定竞争组合生成TM3B3C化合物的形成焓, Hcomp是最稳定竞争组合的焓值(单位: eV/atom). 如果$\Delta {H_{{\rm{comp}}}}>0$, 则意味着三元相TM3B3C是不稳定的, 会分解成最稳定竞争组合; 否则就说明相对所有可能分解产物, 三元TM3B3C化合物都能稳定存在. 形成焓$\Delta {H_{{\rm{comp}}}}$计算结果列于表2中, 每种成分TM3B3C的最稳定竞争组合也列于表2中. 从表2可以看出, 热力学稳定的TM3B3C相只有Nb3B3C一种, 这和实验上已经合成了Nb3B3C相[17]的结果是一致的, 也说明了本文计算结果的准确性和可靠性. 但同时注意到, Ta3B3C相的形成焓$\Delta {H_{{\rm{comp}}}}$虽为正值, 但和最稳定竞争组合的焓差只有0.003 eV/atom. 密度泛函理论第一性原理只能计算绝对零度下材料的结构和性能, 因此如果考虑温度因素, 形成能完全有可能变成负值. 采用准谐近似方法[22,24]计算了0—2000 K下Ta3B3C相及其最稳定竞争组合相的自由能, 如图2所示. 当温度超过约250 K后, Ta3B3C相的自由能开始低于其最稳定竞争组合相, 因此采用现代材料合成方法, Ta3B3C相是完全可以在高温下合成得到.
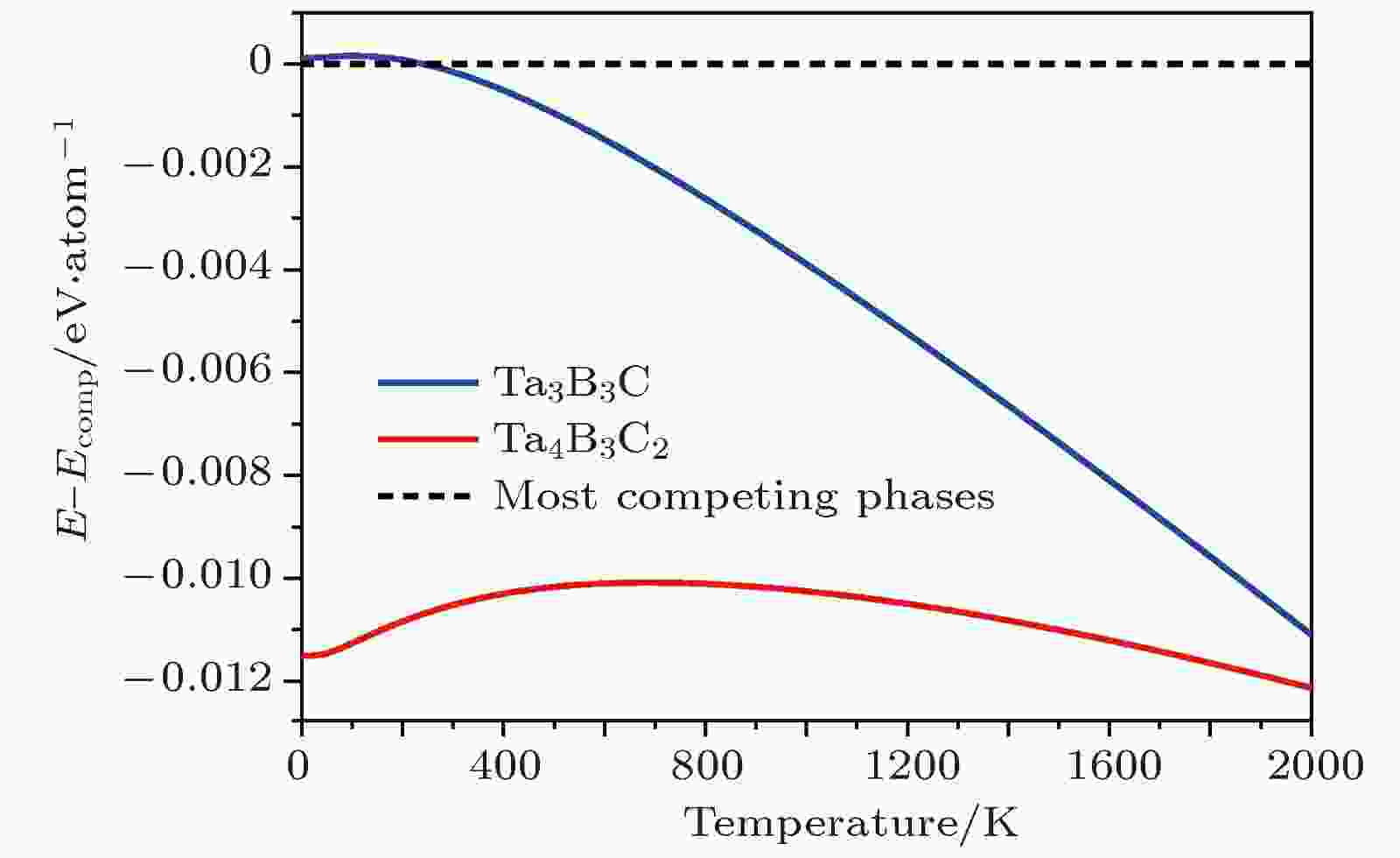图 2 不同温度下Ta3B3C, Ta4B3C2相分别和其相应最稳定竞争组合相的自由能之差
Figure2. Energy differences of Ta3B3C and Ta4B3C2 phases with respect to their most competing phases as a function of temperature.

采用上述类似方法, 也计算了29种TM4B3C2相的形成焓, 结果见表2. 相对于单质, 有18种TM4B3C2相倾向于分解, 只有11种TM4B3C2相对于单质可以稳定存在, 集中于第IIIB—VIB族过渡金属元素. 但相对于最稳定竞争组合, 只有Nb4B3C2和Ta4B3C2是热力学稳定的. 图2显示Ta4B3C2相在整个高温区间(0—2000 K)都可以稳定存在. 相对Ta3B3C相来说, Ta4B3C2相与其相应最稳定竞争相组合的焓差更大, 因此意味着Ta4B3C2相要比Ta3B3C相具有更好的稳定性.
通过以上计算, 本文成功预测了Ta3B3C和Ta4B3C2两相可以热力学稳定存在. 本文的预测是基于Nb3B3C和Nb4B3C2结构进行的, 因此所得的Ta3B3C和Ta4B3C2两相均为这两种结构. 对于Ta3B3C和Ta4B3C2组分而言, 有可能会存在能量更低的更稳定结构. 基于遗传算法的USPEX软件[18]和基于粒子群优化算法的CALYPSO软件[19]是当前流行的结构预测软件, 在结构预测领域已经有了很多成功的先例. 为了确保结果的可靠性, 采用这两种预测软件搜索全局最稳定结构. 采用USPEX和CALYPSO建立候选结构, 每一代生成50个结构, 结构优化由VASP软件来完成, 如果每一代能量最低结构连续20代保持不变, 则认为结构搜索收敛, 找到了全局能量最低结构. 两种软件的计算搜索结果都显示基于Nb3B3C和Nb4B3C2的Ta3B3C和Ta4B3C2结构均为能量最低结构, 从而确定了Nb3B3C和Nb4B3C2型结构为Ta3B3C和Ta4B3C2组分的基态结构. 其结构信息列于表1中, 由于Ta—B和Ta—C的键长分别稍短于Nb—B和Nb—C的键长, 使得Ta3B3C和Ta4B3C2的晶格参数稍小于相应的Nb3B3C和Nb4B3C2的数值.
2
3.2.动力学和力学稳定性
-->

3.2.动力学和力学稳定性

为了验证Ta3B3C和Ta4B3C2结构的动力学稳定性, 计算了其声子色散曲线, 绘制于图3中. 在整个布里渊区范围内均未见任何虚频, 这表明这两个结构在动力学上是稳定的.
图 3 (a) Ta3B3C和(b) Ta4B3C2结构的声子色散曲线
Figure3. Phonon dispersion curves of (a) Ta3B3C and (b) Ta4B3C2 structures.

力学稳定性是材料存在的另一个必要条件. 力学稳定性意味着晶体在发生形变时, 应变能为正值. 力学稳定性可以通过检验弹性常数是否满足特定的条件来判断[25]. 对于Ta3B3C和Ta4B3C2所属的正交晶系, 稳定结构的9个独立弹性常数需满足如下条件: C11 > 0, C44 > 0, C55 > 0, C66 > 0, C11C22 > $C_{12}^2 $, ${C_{11}}{C_{22}}{C_{33}} + 2{C_{12}}{C_{13}}{C_{23}} -{C_{11}}C_{23}^2 - $${C_{22}}C_{13}^2 - {C_{33}}C_{12}^2 > 0$. 计算的Ta3B3C和Ta4B3C2结构弹性常数列于表3中, 可见都符合上述条件, 因此Ta3B3C和Ta4B3C2结构都是力学稳定的.
结构 弹性常数 力学性能a 硬度
C11 C22 C33 C44 C55 C66 C12 C13 C23 B G B/G HChen HTian
Ta3B3C 569.6 514.4 563.5 194.1 180.0 261.8 187.1 147.3 173.9 295.9 200.8 1.47 25.3 25.3
Ta4B3C2 581.1 535.3 602.1 197.3 185.1 275.8 200.3 146.0 170.2 305.7 209.0 1.46 26.2 26.2
Nb3B3C 544.3 479.8 522.8 181.5 171.9 245.3 170.9 132.9 162.2 275.3 189.7 1.45 24.8 24.7
Nb4B3C2 551.5 499.2 548.5 184.0 175.1 257.1 183.2 132.7 157.8 282.9 195.8 1.44 25.5 25.4
TaB2 302 200 1.51 24.4 24.5
NbB2 287 195 1.47 24.8 24.8
TaC 324 215 1.51 25.6 25.9
NbC 239 161 1.48 21.6 21.4
SiC 213 187 1.14 33.6 32.2
Al2O3 232 147 1.58 18.7 18.7
TiN 259 180 1.44 24.3 24.0
注: a二元相力学性能数据来自Materials Project网站.


表3Ta3B3C, Ta4B3C2结构的弹性常数、体弹模量、剪切模量和维氏硬度 (GPa)
Table3.Calculated elastic constants Cij, bulk modulus B, shear modulus G, Vickers hardness HV of Ta3B3C and Ta4B3C2 configurations (GPa).

2
3.3.力学性能
-->

3.3.力学性能

多晶材料的弹性模量可以由单晶体的弹性常数计算得到. 体弹模量B和剪切模量G可分别由以下公式得到[26]:
$B = \left( {1/2} \right)\left( {{B_{\rm{V}}} + {B_{\rm{R}}}} \right),\;G = \left( {1/2} \right)\left( {{G_{\rm{V}}} + {G_{\rm{R}}}} \right),$
其中, 下标V和R分别代表Voigt和Reuss方法.
BV, BR, GV和GR可由以下公式得到:
$\begin{split}&{{B_{\rm{V}}} = (1/9)\left[ {{C_{11}} + {C_{22}} + {C_{33}} + 2\left( {{C_{12}} + {C_{13}} + {C_{23}}} \right)} \right],}\\&{G_{\rm{V}}} = (1/15)[{C_{11}} + {C_{22}} + {C_{33}} + 3({C_{44}} + {C_{55}} + {C_{66}}) - ({C_{12}} + {C_{13}} + {C_{23}})],\\&{B_{\rm{R}}} = [{C_{11}}\left( {{C_{22}} + {C_{33}} - 2{C_{23}}} \right) + {C_{22}}\left( {{C_{33}} - 2{C_{13}}} \right) - 2{C_{33}}{C_{12}} + {C_{12}}\left( {2{C_{23}} - {C_{12}}} \right) + {C_{13}}\left( {2{C_{12}} - {C_{13}}} \right) \\& \qquad + {C_{23}}\left( {2{C_{13}} - {C_{23}}} \right)]^{ - 1} \times \left[ {{C_{13}}\left( {{C_{12}}{C_{23}} - {C_{13}}{C_{22}}} \right)} \right. + {C_{23}}\left( {{C_{12}}{C_{13}} - {C_{23}}{C_{11}}} \right) \left. { + {C_{33}}\left( {{C_{11}}{C_{22}} - {C^2}_{12}} \right)} \right],\\&{B_{\rm R}} = [{C_{11}}\left( {{C_{22}} + {C_{33}} - 2{C_{23}}} \right) + {C_{22}}( {C_{33}} - 2{C_{13}}) - 2{C_{33}}{C_{12}} + {C_{12}}\left( {2{C_{23}} - {C_{12}}} \right) + {C_{13}}(2{C_{12}} - {C_{13}}) \\&\quad\quad + {C_{23}}\left( {2{C_{13}} - {C_{23}}} \right){]^{ - 1}} \times \varDelta,\\&{G_{\rm{R}}} = 15\{ 4[{C_{11}}\left( {{C_{22}} + {C_{33}} + {C_{23}}} \right) + {C_{22}}\left( {{C_{33}} + {C_{13}}} \right) + {C_{33}}{C_{12}} - {C_{12}}\left( {{C_{23}} + {C_{12}}} \right) - {C_{13}}\left( {{C_{12}} + {C_{13}}} \right)\\&\quad\quad - {C_{23}}\left( {{C_{13}} + {C_{23}}} \right)]/\varDelta + 3\left[\left( {1/{C_{44}}} \right) + \left( {1/{C_{55}}} \right) \right. \left.+ \left( {1/{C_{66}}} \right) \right]{\} ^{ - 1}},\end{split}$

其中, $\varDelta \; =\; C_{13}(C_{12}C_{23} \; ?\; C_{13}C_{22}) \; +\; C_{23}(C_{12}C_{13}$$ \; ?\; C_{23}C_{11})\; +\; C_{33}(C_{11}C_{22} \; ? \; C^2_{12}) $ .
Ta3B3C和Ta4B3C2结构的体弹模量B和剪切模量G见表3. 为了比较, Nb3B3C和Nb4B3C2结构的计算数据也一并给出. 对同一成分来说, TM4B3C2结构的B和G值均稍大于TM3B3C结构; 对不同成分来说, Ta3B3C (Ta4B3C2)结构的B和G值均稍大于Nb3B3C (Nb4B3C2)结构, 这源于Ta-B-C中稍短的键长, 这说明新发现的Ta-B-C相抵抗弹性变形的能力要强于相应的已知Nb-B-C相. 根据Pugh经验判据[27], B/G的比值可用来判断一个材料是脆性还是韧性. 若B/G > 1.75, 表明材料是韧性的; 反之表明材料是脆性的. 根据这个判据可知, Ta3B3C, Ta4B3C2结构和已知的超硬或者硬质材料相同, 属于脆性材料.
为了探索Ta3B3C和Ta4B3C2相作为硬质材料的可行性, 计算了其硬度. 计算方法采用中国科学院金属研究所陈星秋公式[28]和燕山大学田永君公式[1]:
${H_{{\rm{Chen}}}} = 2{\left( {{k^2}G} \right)^{0.585}} - 3,$
${H_{{\rm{Tian}}}} = 0.92{k^{1.137}}{G^{0.708}},$
(6)和(7)式中, HChen和HTian是分别根据陈星秋和田永君硬度公式计算得到的维氏硬度, k为剪切模量G和体弹模量B的比值.
计算的Ta3B3C, Ta4B3C2, Nb3B3C, Nb4B3C2结构以及一些已知二元相的硬度值列于表3中. 两种硬度计算方法的结果很相近, 都显示本文新发现的Ta-B-C三元相硬度约为26 GPa, 稍高于已知Nb-B-C三元相. 26 GPa的硬度值表明Ta3B3C和Ta4B3C2相都不是超硬材料, 但也属于高硬度材料. 其硬度值和相应的二元相TaB2, TaC相近, 高于Al2O3和TiN材料, 但低于SiC材料.
2
3.4.电学性能
-->

3.4.电学性能

图4给出了Ta3B3C和Ta4B3C2结构的能带结构和态密度(DOS)图. 能带结构图中, 费米面横穿过能带, 导带和价带互相交叠, 这说明两相均为导体. 从DOS图可以看出, 费米面上的电子态主要是Ta原子的d电子, 因此其导电性主要源于Ta原子的d电子. 由于这两相具有类似的结构, 因此其态密度图很相似. 其价带部分可以看成由9个电子态峰组成, 除了峰2和峰3为Ta原子和B原子的电子贡献以外, 其他7个电子态峰均含有三种原子的电子. 对B原子和C原子来说, 从–14 eV到–10 eV的峰1, 主要来源于2s轨道上的电子, 而–10 eV到费米能级的能带区域则主要来源于2p电子. 从–10 eV到费米能级的能带区域看, Ta原子的d电子与B原子的p电子, 以及Ta原子的d电子与C原子的p电子之间均发生了较强的杂化, 这说明Ta和B以及Ta和C之间是很强的共价结合.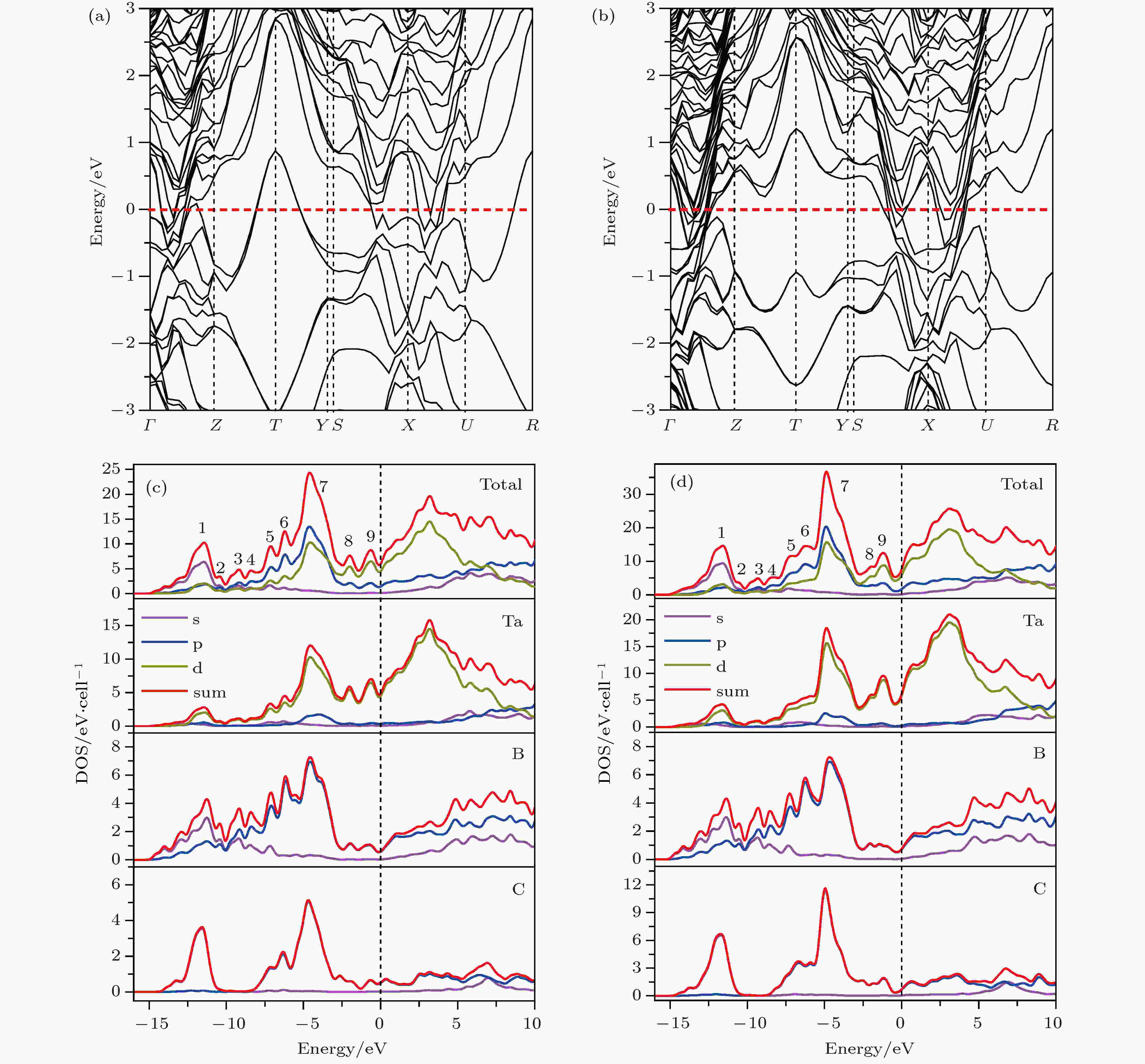
图 4 (a), (c) Ta3B3C和(b), (d) Ta4B3C2结构的能带结构和态密度图
Figure4. Band structures and density of states of (a), (c) Ta3B3C and (b), (d) Ta4B3C2 structures.

4.结　论
本文基于密度泛函理论第一性原理计算方法, 以Nb3B3C和Nb4B3C2结构为模板, 采用元素替代法和结构搜索法相结合, 成功预测了两种稳定的Ta3B3C和Ta4B3C2新相. 其中Ta3B3C结构虽不是绝对零度下的基态稳定相, 但高温下可以稳定存在. Ta3B3C和Ta4B3C2新相的维氏硬度大约为26 GPa, 表明这两相虽没有达到超硬材料的标准, 但也属于高硬度材料. 这两相还是导电的脆性材料. 另外其他诸如光学、热学等性能期待后续的挖掘和研究. 相对二元相, 三元相具有更大范围的成分以及性能可调性, 因此我们期待Ta3B3C和Ta4B3C2相是新型可调多功能硬质材料. 同时本文的研究思路和计算方法, 后续可以扩展到更多已知材料体系, 从而可以预测甚至合成更多的稳定新相.
相关话题/结构 材料 计算 金属 电子
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于二维材料MXene的仿神经突触忆阻器的制备和长/短时程突触可塑性的实现
    摘要:兼具长时程可塑性与短时程可塑性的电子突触被认为是类脑计算系统的重要基础.将一种新型二维材料MXene应用到忆阻器中,制备了基于Cu/MXene/SiO2/W的仿神经突触忆阻器.结果表明,Cu/MXene/SiO2/W忆阻器成功实现了稳定的双极性模拟阻态切换,同时成功模拟了生物突触短时程可塑性的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Helmholtz腔与弹性振子耦合结构带隙
    摘要:为提高Helmholtz型声子晶体低频隔声性能,设计了一种Helmholtz腔与弹性振子的耦合结构,通过声压场及固体振型对其带隙产生机理进行了详细分析,建立了相应的弹簧-振子系统等效模型,并采用理论计算和有限元计算两种方法研究了各结构参数对其带隙的影响情况.研究表明,该结构可等效为双自由度系统 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于共心球透镜的多尺度广域高分辨率计算成像系统设计
    摘要:针对实时广域高分辨率成像需求,充分利用具有对称结构的多层共心球透镜视场大且各轴外视场成像效果一致性好的特点,设计基于共心球透镜的多尺度广域高分辨率计算成像系统.该系统基于计算成像原理,通过构建像差优化函数获得光学系统设计参数,结合球形分布的次级相机阵列进行全局性优化,提高系统性能的同时有效简化 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 基于高折射率液体填充的花瓣形微结构光纤可调滤模特性
    摘要:提出一种新型的可调滤模光纤结构,利用纤芯模式与微结构包层形成的超模群之间的耦合实现选择性滤模,采用花瓣形包层结构使包层中传输的模式更容易产生高的泄漏损耗;提出以液体填充包层介质柱,使包层形成的超模群有效折射率区间可以通过环境温度来调节,从而达到可调选择性滤模目的.利用液体柱的LP11模所形成的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 太赫兹液晶材料与器件研究进展
    摘要:液晶是一种性能优异的可调控光电功能材料,基于液晶的太赫兹器件有着广泛的应用前景,但高性能太赫兹功能器件的研发仍处于初级阶段.本文综述了太赫兹领域液晶材料与器件的研究现状,探讨了液晶技术与太赫兹技术相结合的发展趋势.关键词:液晶/太赫兹波/超材料/石墨烯EnglishAbstractResear ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 硅纳米结构晶体管中与杂质量子点相关的量子输运
    摘要:在小于10nm的沟道空间中,杂质数目和杂质波动范围变得十分有限,这对器件性能有很大的影响.局域纳米空间中的电离杂质还能够展现出量子点特性,为电荷输运提供两个分立的杂质能级.利用杂质原子作为量子输运构件的硅纳米结构晶体管有望成为未来量子计算电路的基本组成器件.本文结合安德森定域化理论和Hubba ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ce-La-Th合金高压相变的第一性原理计算
    摘要:采用第一性原理计算对Ce0.8La0.1Th0.1在高压下fcc-bct的结构相变、弹性性质及热力学性质进行了研究讨论.通过对计算结果的分析,发现了合金在压力下的相变规律,压强升高到31.6GPa附近时fcc相开始向bct相转变,到34.9GPa时bct相趋于稳定.对弹性模量的计算结果从另一角 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • GaAs纳米线晶体结构及光学特性
    摘要:采用分子束外延技术在N-型Si(111)衬底上利用自催化生长机制外延砷化镓(GaAs)纳米线,对生长的纳米线进行扫描电子显微镜测试,纳米线垂直度高,长度直径均匀度好.对纳米线进行光致发光(photoluminescence,PL)光谱测试,发现低温10K下两个发光峰P1和P2分别位于1.493 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 超薄柔性透射型超构材料吸收器
    摘要:设计并加工了一种超薄柔性透射型吸收器,总体厚度为0.288mm,可实现柔性弯曲,容易做到与曲面目标共形.该吸收器由三层结构组成,底层是金属光栅,中间为介质层,表面单元由两条平行放置的尺寸不同的金属线组成.仿真和实验结果表明,对横电波在5和7GHz的吸收分别达到97.5%和96.0%,对横磁波在 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 螺旋锥束计算机断层成像倾斜扇束反投影滤波局部重建算法
    摘要:螺旋锥束计算机断层成像(CT)作为常用的临床诊断工具,如何尽可能地减少其辐射剂量是热点研究领域之一.局部成像利用准直器减小射线直照区域,能够有效降低CT辐射剂量.然而,局部成像会造成投影数据横向截断,产生局部重建问题.现有螺旋反投影滤波(BPF)算法只能实现局部曲面重建,难以实现局部体区域重建 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.