删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

Hg<sup>+</sup>离子5d<sup>10</sup>6s <sup>2</sup>S<sub>1/2<

本站小编 Free考研考试/2021-12-29
摘要:本文首先在Dirac-Hartree-Fock近似下理论评估了Hg+离子5d106s 2S1/2→5d96s2 2D5/2钟跃迁的质量位移(mass shift, MS)和场位移(field shift, FS)在其同位素位移(isotope shift, IS)中的相对贡献, 发现MS远小于FS而可以被忽略. 在此基础上, 通过系统地考虑该原子体系中主要的电子关联效应, 计算了这条钟跃迁FS的精确值以及涉及到的上下两个能级的超精细结构常数, 并得到了几种稳定汞同位素离子该跃迁的IS和超精细结构分裂. 其中, 计算的199Hg+和198Hg+离子之间的钟跃迁频率偏移与已有实验测量值相比误差为2%左右. 最终, 本文给出了汞离子7种常见同位素该谱线的绝对频率值, 为实验上的谱线测量提供了有效的理论依据.
关键词: 超精细结构/
同位素位移/
多组态Dirac-Hartree-Fock方法/
汞离子光钟

English Abstract


全文HTML

--> --> -->
1.引　言
在星载原子钟中, 传统原子钟(铷钟、铯钟和氢钟)会因原子之间和原子与器壁的碰撞产生多普勒频移, 使跃迁谱线比较宽, 而利用电磁场约束粒子的离子钟则避免了这些因素, 使其具有较高的频率准确度和稳定度. 在离子钟中, 汞离子具有最高的基态超精细能级跃迁频率, 并对温度和空间磁场的敏感度较低, 稳定度指标与主动型氢钟相当, 且重量轻(约3 kg)、体积小[1,2], 所以是理想的星载原子钟, 可用于导航二期后续、深空导航等项目[3]. 精确的汞离子钟还可以作为精密测量平台探测精细结构常数$\alpha $是否随时间变化[4]或轻夸克质量与量子色动力学标度因子比率[5], 在低能区检验标准模型, 探索新物理.
自然界中稳定存在的汞天然同位素共有7种, 分别为196Hg, 198Hg, 199Hg, 200Hg, 201Hg, 202Hg和204Hg. 表1给出了它们的相关参数, 包括同位素质量数、相对原子质量、元素丰度、均方根核电荷半径、核自旋、核磁偶极矩和核电四极矩. 其中, 199Hg和201Hg的核自旋不为零而使其能级具有超精细结构.
Isotopes’ mass numberRelative atomic mass[6]Abundance[7]R/fm[8]I/$\hbar$$\mu $/nm[9]Q/barn[9]
196195.9658326 (32)0.15%5.43850+––
198197.96676860 (52)10.04%5.44630+––
199198.96828064 (46)16.94%5.44741/2–+0.5058855(9)–
200199.96832659 (47)23.14%5.45510+––
201200.97030284 (69)13.17%5.45813/2––0.5602257(14)+0.387(6)
202201.97064340 (69)29.74%5.46480+––
204203.97349398 (53)6.82%5.47440+––


表17种天然汞同位素及相关参数
Table1.Related parameters of seven natural mercury isotopes.

199Hg+是光钟的重要候选离子[10,11], 对于199Hg+离子5d106s 2S1/2(F = 0)→5d96s2 2D5/2(F = 2) 态跃迁谱线的实验测量, Rafac等[12]、Bergquist等[13]和Oskay等[14]已经将测量精度提高到了10–17量级. 其中, Oskay等[14]给出绝对频率精度最高, 为1064721609899144.94 (97) Hz, 可以作为光学频率基准, 199Hg+也被列入新的秒定义候选离子. 198Hg+离子5d106s 2S1/2→5d96s2 2D5/2态跃迁谱线也有实验精确测量, 其值为35514.304(6) cm–1[15]. 对于无超精细结构的202Hg+和198Hg+离子, 它们约194 nm的深紫外光可被用来对四极阱中的199Hg+和201Hg+离子进行光抽运[1,5]. 另外, 在激光电离分离汞同位素离子技术中[16,17], 需要通过参考具体同位素频移来调谐用于光电离的激光, 选择性地电离制备特定的汞同位素离子. 但是对于汞同位素离子5d106s 2S1/2和5d96s2 2D5/2等能级及能级之间跃迁同位素位移(isotope shift, IS)的研究则缺少相关理论和高精度的实验结果.
本文中我们利用相对论多组态Dirac-Hartree-Fock(MCDHF)方法计算了钟跃迁谱线的IS以及相关两个能级的超精细结构常数, 与已有实验值比较, 我们的IS计算精度已经达到2%左右. 在此基础上, 获得了其他6种汞同位素离子相对于199Hg+钟跃迁频率的偏移量, 并理论预言了各种汞同位素可能的钟跃迁绝对频率值. 该理论计算结果可以为实验测量其他汞同位素离子跃迁谱线提供参考, 大幅减小实验扫谱范围, 降低实验难度, 为实现不同汞同位素离子的光学频率标准提供帮助. 另外, 汞离子IS为研究汞原子核的结构、性质及核子相互作用规律提供了必要的理论参数[18].
2.研究方法
2
2.1.多组态Dirac-Hartree-Fock方法
-->

2.1.多组态Dirac-Hartree-Fock方法

在MCDHF方法下, 原子态波函数$\varPsi$是由线性的组态波函数$\varPhi$展开的[19], 即
$\varPsi \left( {\gamma PJ{M_J}} \right) = \sum\limits_i {{c_i}\varPhi \left( {{\alpha _i}PJ{M_J}} \right)} .$
其中: ci是混合系数; ${\alpha _i}$是附加量子数, 它与宇称P、总角动量J及其z方向的分量MJ一起使描述的组态波函数具有唯一性. 理论上, 用无限个组态波函数去展开这个原子态波函数就能得到体系真实的原子态波函数. 但是, 实际计算中只能选择有限个组态波函数, 其数目多少和选择方式决定了对电子关联的描述程度.
在自洽场(self-consistent field, SCF)过程中, 基于变分原理, 混合系数和单电子相对论轨道通过求解MCDHF方程来同时优化. 在得到单电子轨道基后, 进一步扩大组态空间, 利用相对论组态相互作用(relativistic configuration interaction, RCI)方法可以包含更多电子关联效应. 另外, 在RCI计算中还能包括Breit相互作用[20]和量子电动力学(quantum electrodynamics, QED)修正[21,22]. 本文的计算利用了基于MCDHF方法发展的GRASP程序包[23].
2
2.2.超精细结构理论
-->

2.2.超精细结构理论

原子核的电磁多极矩与电子之间的超精细相互作用可以表示为
${H_{{\rm{hfs}}}} = \sum\limits_{k \geqslant 1} {{{{T}}^{\left( k \right)}} \cdot {{{M}}^{\left( k \right)}}} .$
其中, T(k)和M(k)分别是电子和原子核空间的k阶球张量算符[24]. k = 1表示磁偶极超精细相互作用, k = 2表示电四极超精细相互作用. 进一步, 磁偶极和电四极超精细结构常数A, B可以分别表示为[25]
$\begin{split}& {A_J} = \frac{{{\mu _I}}}{I}\frac{1}{{{{\left[ {J\left( {J + 1} \right)} \right]}^{{\rm{1/2}}}}}}\left\langle {\gamma J\left\| {{{{T}}^{\left( 1 \right)}}} \right\|\gamma J} \right\rangle , \\& {B_J} = 2{Q_I}{\left[ {\frac{{J\left( {2J - 1} \right)}}{{\left( {J + 1} \right)\left( {2J + 3} \right)}}} \right]^{1/2}}\left\langle {\gamma J\left\| {{{{T}}^{\left( 2 \right)}}} \right\|\gamma J} \right\rangle.\end{split}$
相应的磁偶极和电四极超精细相互作用的一阶能量修正可表示为
$\begin{split}& {W_{M1}}\left( {J,J} \right) = \frac{1}{2}{A_J}C, \\& {W_{E2}}\left( {J,J} \right) = {B_J}\frac{{\frac{3}{4}C\left( {C + 1} \right) - I\left( {I + 1} \right)J\left( {J + 1} \right)}}{{2I\left( {2I - 1} \right)J\left( {2J - 1} \right)}},\end{split}$
其中C = F(F + 1) – J(J + 1) – I(I + 1).
2
2.3.IS理论
-->

2.3.IS理论

早期处理原子结构时, 把原子核看成是质量无穷大的点电荷. 但实际上, 原子核是有限质量的质子和中子组成的量子体系, 其内部结构不同也影响着核外电子, 进而造成不同同位素之间原子能级存在不同程度的位移, 这一位移量被称为IS. IS分为质量位移(mass shift, MS)和场位移(field shift, FS)[20,26,27]. 对于较轻元素, 依赖于核有限质量的MS贡献较大. 对于较重元素, 依赖于核电荷分布的FS贡献较大, 后面的讨论将细致比较两者在汞离子IS中占的实际比重.
对于质量为M的原子核, 在($\alpha $Z)4m2/M近似下[28-30](其中m是电子质量), MS对应的哈密顿量为
$ \begin{split} {H_{{\rm{MS}}}} & = {H_{{\rm{NMS}}}} + {H_{{\rm{SMS}}}},\\ {H_{{\rm{NMS}}}}& = \frac{1}{{2M}}\sum\limits_{j = 1}^N \left( {{p}}_j^2 - \frac{{\alpha Z}}{{{r_j}}}{{{\alpha }}_j} \cdot {{{p}}_j}-\right.\\&\quad \left. \frac{{\alpha Z}}{{{r_j}}}\left( {{{{\alpha }}_j} \cdot {{C}}_j^1} \right){{C}}_j^1 \cdot {{{p}}_j} \right), \\ {H_{{\rm{SMS}}}}&=\frac{1}{{2M}}\sum\limits_{j \ne k}^N \left( {{{p}}_j} \cdot {{{p}}_k} - \frac{{\alpha Z}}{{{r_j}}}{{{\alpha }}_j} \cdot {{{p}}_k}-\right. \\&\quad \left. \frac{{\alpha Z}}{{{r_j}}}\left( {{{{\alpha }}_j} \cdot {{C}}_j^1} \right){{C}}_j^1 \cdot {{{p}}_k} \right). \end{split} $
其中, Z为核电荷数; $\alpha$为精细结构常数; ${{{\alpha }}_j}$为4 × 4的Dirac矩阵; pj为四维形式的电子动量算符. MS算符可以分为单体部分, 即正规质量偏移(normal mass shift, NMS)和两体部分, 即特殊质量偏移(specific mass shift, SMS), 分别对应HNMS和HSMS. NMS和SMS因子的形式分别为
$\begin{split}& {K_{{\rm{NMS}}}} = M\left\langle {\varPsi \left\| {{H_{{\rm{NMS}}}}} \right\|\varPsi } \right\rangle , \\& {K_{{\rm{SMS}}}} = M\left\langle {\varPsi \left\| {{H_{{\rm{SMS}}}}} \right\|\varPsi } \right\rangle.\end{split}$
对于FS, 不同同位素之间FS造成的能级频率位移$\delta \nu $可表示为[31,32]
$\delta \nu = \frac{{2{\text{π}}}}{{3h}}Z\left( {\frac{{{e^2}}}{{4{\text{π}}{\varepsilon _0}}}} \right)\Delta {\left| {\varPsi \left( 0 \right)} \right|^2}\delta \left\langle {{r^2}} \right\rangle. $
其中, ${\left| {\varPsi \left( 0 \right)} \right|^2}$为电子在原子核内的概率; $\delta \left\langle {{r^2}} \right\rangle $为两同位素原子核电荷半径的均方根平方之差[33].
3.结果和讨论
2
3.1.5d106s 2S1/2→5d96s2 2D5/2钟跃迁FS和MS的相对大小
-->

3.1.5d106s 2S1/2→5d96s2 2D5/2钟跃迁FS和MS的相对大小

首先, 在单组态近似下计算了汞的7种同位素相对199Hg+离子的5d106s 2S1/2→5d96s2 2D5/2跃迁的MS和FS, 结果如图1所示. 由于实验测量的汞不同同位素的原子核均方根半径的平方随中子数增加而线性变化[8], 从图1中可以看出其同位素的FS也与同位素的质量数大致呈现线性关系. 另外, 也观察到汞不同同位素的MS基本相同. 值得注意的是, 对于Hg+离子的这条钟跃迁谱线, MS远小于FS, 其对IS的贡献远小于1%. 因此, 在IS的计算中可以忽略MS.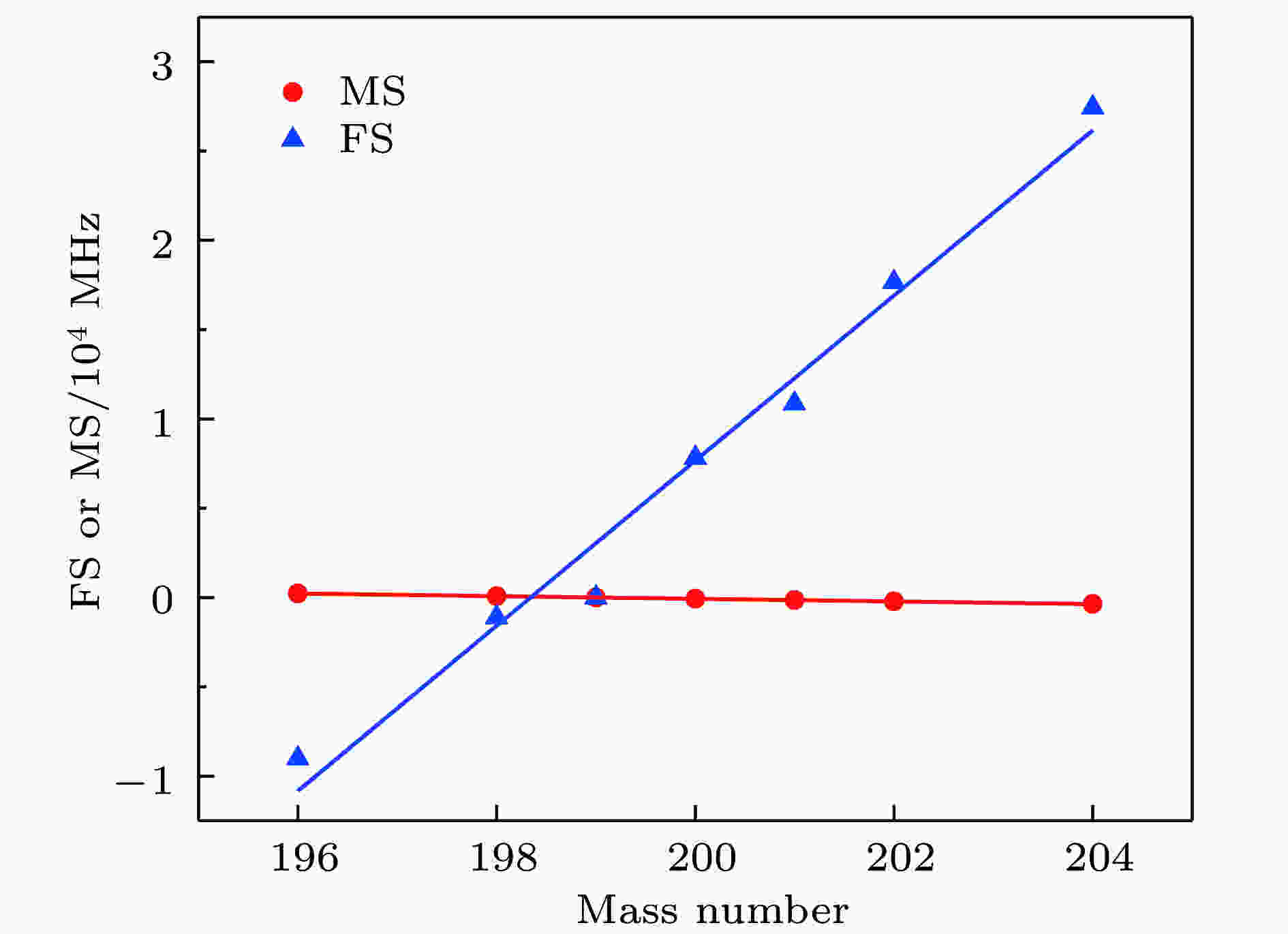
图 1 汞同位素离子5d106s 2S1/2→5d96s2 2D5/2跃迁相对于199Hg+离子的FS和MS随质量数变化的趋势
Figure1. Trends of field shift and mass shift for the 5d106s 2S1/2→5d96s2 2D5/2 transition in mercury isotope ions with respect to 199Hg+ as the increase of mass number.

2
3.2.5d106s 2S1/2→5d96s2 2D5/2钟跃迁FS的理论计算
-->

3.2.5d106s 2S1/2→5d96s2 2D5/2钟跃迁FS的理论计算

为了获得Hg+离子5d106s 2S1/2→5d96s2 2D5/2钟跃迁FS的准确结果, 需要考虑体系中的电子关联效应. 本文采用活动空间方法[34]产生组态空间来系统地捕获电子间的关联. 选取5d106s和5d96s2为参考组态, 把5d和6s电子看成价电子(V), 其他电子为芯电子(C). 组态空间利用限制性单双激发(SrD)方式扩展, 即活动的原子芯轨道中最多只允许一个电子激发出去, 而价电子可以被同时激发两个. 这样, 包括了芯电子与价电子(CV)和价电子之间的关联(VV). 为了使能量本征值和IS收敛, 关联轨道(virtual orbitals)是逐层加入的, 而且在SCF计算中每次只优化最新加入的轨道. 另外, 为了全面考虑原子芯电子(C)和价电子(V)之间的关联效应, 在逐层加入关联轨道的同时, 也逐层打开参考组态中占据的原子芯轨道(active orbitals), 即打开的原子芯轨道上的电子也可以被激发到价轨道或虚轨道上. 为了表述计算得到的原子态波函数的品质, 在表2中给出了具体的计算模型以及能量本征值随组态空间扩大的变化. n代表虚轨道最大的主量子数, DF代表单组态近似模型, NCF列两组数字分别代表参考组态5d106s 2S1/2和5d96s2 2D5/2在每个计算模型下组态的数目, Energy eigenvalue列下的两组值分别对应这两个组态的能量本征值.
nActive orbitalsVirtual orbitalsNCFEnergy eigenvalue/104 Hartrees
DF1/1–1.964857825739/–1.964840329639
75d6s7s, 6p, 6d, 5f, 5g310/1631–1.964887721767/–1.964870006459
85spd6s8s, 7p, 7d, 6f, 6g4047/19457–1.964907829871/–1.964890991924
94spdf5spd6s9s, 8p, 8d, 7f, 7g29884/151235–1.964927346267/–1.964910124355
103spd4spdf5spd6s10s, 9p, 9d, 8f, 7g69579/334460–1.964929839430/–1.964912598231
113spd4spdf5spd6s11s, 10p, 10d, 9f, 7g103101/480763–1.964930723063/–1.964913507368


表2电子关联对能量本征值的影响
Table2.Effect of electron correlations on energy eigenvalues.

如表2所示, 计算是从DF近似(单组态近似)出发, 然后产生了5层虚轨道, 其中前3层轨道角动量包括spdfg, 最后两层轨道角动量为spdf. 对于主量子数大于8且角动量为g的轨道以及角动量全部为h的轨道, 计算结果显示它们的影响较小, 所以在虚轨道中不用添加. 在扩充虚轨道的同时, 我们还同时逐层打开了原子芯轨道直到n = 3.
表3给出了汞同位素离子相对199Hg+离子的FS收敛情况，第一列与表2的计算模型对应. 可以大致看出，随着越来越多的电子关联被考虑，汞同位素离子的FS趋向收敛. 比如，对于196Hg+离子，n = 8时的FS与n = 9相比相差3.28%，而n = 9时的FS与n = 10相比仅相差0.12%.
n196Hg+198Hg+200Hg+201Hg+202Hg+204Hg+
DF–9.01296–1.114767.8096210.855317.663427.4329
7–9.20985–1.139117.9802311.092518.049328.0321
8–8.81504–1.090287.6381310.616917.275526.8305
9–9.11351–1.127207.8967410.976417.860527.7389
10–9.12483–1.128607.9065610.990117.882727.7734
11–9.14646–1.131277.9253011.016117.925027.8392


表3汞同位素离子相对199Hg+离子5d106s 2S1/2→5d96s2 2D5/2钟跃迁的场位移 (单位: GHz)受电子关联的影响
Table3.Effect of electron correlations on the FS (in GHz) of the 5d106s 2S1/2→5d96s2 2D5/2 transition in mercury isotope ions (relative to 199Hg+).

2
3.3.Hg+离子5d106s 2S1/2和5d96s2 2D5/2态的超精细结构常数
-->

3.3.Hg+离子5d106s 2S1/2和5d96s2 2D5/2态的超精细结构常数

使用上述计算FS的模型, 也计算了Hg+离子5d106s 2S1/2和5d96s2 2D5/2能级的磁偶极(A)和电四极(B)超精细结构常数, 其随电子关联的变化趋势展示在表4中. 为了反映同位素效应, 同位素的质量数标记在超精细结构常数的左上角. 另外, 原子态的角动量也标记在右下角. 可以看出, 随着组态空间的扩大, 磁偶极(A)和电四极(B)超精细结构常数均趋于收敛. 例如, 199Hg+ 5d106s 2S1/2态在n = 8时的磁偶极常数A与n = 9时的差别为4.43%, 而n = 9时的A值比n = 10的结果只大1%. 表4中最后4行给出了文献中已知的理论和实验值, 与文献[35]和[36]中理论结果相比, 在n = 11模型下的计算结果更接近文献[37]中的实验值, 其中, 计算的199Hg+和201Hg+离子5d106s 2S1/2态磁偶极超精细结构常数A与实验值的误差分别为1.67%和1.48%. 另外, 还得到了199Hg+和201Hg+离子5d96s2 2D3/2态的磁偶极超精细结构常数分别为2735.73 MHz和–1009.86 MHz, 201Hg+离子电四极超精细结构常数为841.17 MHz.
n199A1/2199A5/2201A1/2201A5/2201B5/2
DF36812.0986.665–13585.7–364.216796.132
739090.51263.67–14426.7–466.447755.219
838761.2795.021–14305.1–293.490765.173
940556.1951.973–14967.5–353.908936.169
1040967.0951.669–15119.2–351.307961.161
1141133.9963.552–15180.8–355.692966.809
Ref. [38]963.5–355.7839.4
Ref. [37]40460–14960
Ref. [35]423661315–15527–482859
Ref. [36]41477–15311


表4199Hg+和201Hg+ 离子5d106s 2S1/2和5d96s2 2D5/2态的磁偶极(A单位: MHz)和电四极(B单位: MHz)超精细结构常数
Table4.Magnetic dipole A (in MHz) and electric quadrupole B (in MHz) hyperfine interaction constants for the 5d106s 2S1/2 and 5d96s2 2D5/2 states of 199Hg+ and 201Hg+.

2
3.4.超精细结构下5d106s 2S1/2→5d96s2 2D5/2钟跃迁的IS
-->

3.4.超精细结构下5d106s 2S1/2→5d96s2 2D5/2钟跃迁的IS

图2描述了198Hg+和199Hg+离子超精细结构下5d106s 2S1/2→5d96s2 2D5/2钟跃迁的IS. 其中, ISS代表精细结构下能级的IS, HFSS代表超精细结构能级劈裂. 利用上面n = 11时计算的FS和超精细结构常数, 得到了199Hg+与198Hg+离子跃迁谱线的ISS之差为1.13 GHz, 199Hg+离子F = 2到F = 0超精细分裂(HFSS之差)为29.16 GHz, 因此这两个同位素钟跃迁的偏移(ν1与ν2之差)为这两项值之和, 即30.30 GHz, 该值即为199Hg+与198Hg+离子在超精细结构下的IS. 已知实验测量的199Hg+离子光钟钟跃迁频率为1064721609899144.94(97) Hz[14], 以及198Hg+离子光钟钟跃迁频率为1064.6919524 THz[15], 可以得到199Hg+与198Hg+ 离子5d106s 2S1/2→5d96s2 2D5/2钟跃迁的频率IS实验值为29.66 GHz, 我们的理论结果与其符合的很好, 两者差别仅为2.16%.
图 2 199Hg+和198Hg+离子的超精细能级结构图
Figure2. Hyperfine level structure diagram of 199Hg+ and 198Hg+.

从计算中发现, Hg+离子能级的IS在104 GHz量级, 而超精细结构分裂在1～10 GHz量级. 但是对于跃迁IS, 其值是上能级5d106s 2S1/2和下能级5d96s2 2D5/2的IS之差, 该值与超精细结构分裂在相同的数量级. 结合表3中FS的计算结果也可以看出, 对于汞元素的几种同位素, 它们的FS都小于29.16 GHz的超精细结构分裂, 这导致计算IS时, 超精细结构的影响需要重点考虑.
在同时考虑了5d106s 2S1/2→5d96s2 2D5/2跃迁的IS和超精细结构, 给出了汞7种同位素离子该谱线的绝对频率值, 如表5所示. 其中, 201Hg+离子对应的跃迁是5d106s 2S1/2(F = 1)→5d96s2 2D5/2(F = 1), 199Hg+离子的是5d106s 2S1/2(F = 0)→5d96s2 2D5/2(F = 2). 除了199Hg+和198Hg+离子外, 其他汞同位素离子目前均没有相应实验测量值, 也没有其他理论计算结果来进行比较, 有待将来实验验证我们的理论计算结果.
Ions196Hg+198Hg+199Hg+200Hg+201Hg+202Hg+204Hg+
ν/GHz1064683.301064691.31*1064721.61[14]1064700.371064719.891064710.371064720.28
*Experiment value is 1064691.95 GHz[15].


表5汞同位素离子5d106s 2S1/2→5d96s2 2D5/2跃迁谱线的绝对频率值
Table5.Absolute frequency values of the 5d106s 2S1/2→5d96s2 2D5/2 transition in mercury isotope ions.

4.结　论
本文首先在Dirac-Hartree-Fock近似下, 发现汞离子IS中FS要远大于MS. 进一步, 忽略MS的影响, 利用MCDHF方法, 我们考虑了原子体系中主要的电子关联效应, 获得了汞同位素离子5d106s 2S1/2→5d96s2 2D5/2钟跃迁在超精细结构下的IS. 其中, 计算的199Hg+和198Hg+离子的IS与实验值仅相差2.16%. 最后, 我们也理论预言了汞7种同位素5d106s 2S1/2→5d96s2 2D5/2钟跃迁谱线的绝对频率值. 本文的计算结果对进一步的实验测量工作提供了有价值的参考数据, 同时也对后续汞原子核相关性质的研究提供了理论依据.
相关话题/结构 计算 电子 实验 质量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 中性原子量子计算研究进展
    摘要:相互作用可控、相干时间较长的中性单原子体系具备在1mm2的面积上提供成千上万个量子比特的规模化集成的优势,是进行量子模拟、实现量子计算的有力候选者.近几年中性单原子体系在实验上取得了快速的发展,完成了包括50个单原子的确定性装载、二维和三维阵列中单个原子的寻址和操控、量子比特相干时间的延长、基 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 纳米结构超疏水表面冷凝现象的三维格子玻尔兹曼方法模拟
    摘要:采用三维多相流格子玻尔兹曼方法(latticeBoltzmannmethod,LBM),对纳米结构超疏水表面液滴的冷凝行为进行模拟研究.通过Laplace定律和光滑表面的本征接触角理论对三维LBM模型进行定量验证.模拟分析了超疏水表面纳米阵列的几何尺寸和润湿性的局部不均匀性对冷凝液滴形核位置和 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • Ce和O空位共掺杂TiO<sub>2</sub>的电子结构与光学性质
    摘要:采用基于密度泛函理论加U的计算方法,研究了Ce和O空位单(共)掺杂锐钛矿相TiO2的电子结构和光吸收性质.计算结果表明,Ce和O空位共掺杂TiO2的带隙中出现了杂质能级,且带隙窄化为2.67eV,明显比纯TiO2和Ce,O空位单掺杂TiO2的要小,因而可提高TiO2对可见光的响应能力,使TiO ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 聚甲基丙烯酸甲酯间隔的金纳米立方体与金膜复合结构的表面增强拉曼散射研究
    摘要:金属纳米颗粒与金属薄膜的复合结构由于其局域表面等离子体和传播表面等离子体间的强共振耦合作用,可作为表面增强拉曼散射(SERS)基底,显著增强吸附分子的拉曼信号.本文提出了一种聚甲基丙烯酸甲酯(PMMA)间隔的90nm金纳米立方体与50nm金膜复合结构的SERS基底,通过有限元方法数值模拟,得到 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 表面形貌对热阴极电子发射特性的影响
    摘要:为了研究热阴极表面形貌对电子发射能力的影响,使用飞秒激光微纳加工技术在光滑的热阴极表面制备不同尺寸和形状的周期性条纹结构,并使用相同的制备工艺对阴极进行除气和激活.测试结果显示:阴极表面周期性条纹结构可有效增强阴极的电子发射能力,正交双向条纹结构表面阴极的发射电流密度高于单向条纹结构表面阴极的 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 氢化二维过渡金属硫化物的稳定性和电子特性: 第一性原理研究
    摘要:用氢对单层二维过渡金属硫化物(TMDs)进行功能化是调节单层TMDs电子性质的既有效又经济的方法.采用密度泛函理论,对单层TMDs(MX2(M=Mo,W;X=S,Se,Te))的稳定性和电子性质进行理论研究,发现在单层MX2的层间有一个比其表面更稳定的氢吸附位点.当同阳离子时,随着阴离子原子序 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 类KBe<sub>2</sub>BO<sub>3</sub>F<sub>2</sub>结构硼酸盐深紫外非线性光学材料的研究进展
    摘要:利用非线性光学(NLO)晶体材料和变频技术,可以把波长范围有限的激光光源扩展到紫外、深紫外区,这已成为深紫外光源的热点研究方向.然而,目前限制深紫外全固态激光器发展和应用的关键问题是缺乏能够在该波段进行频率转换并且产业化应用的NLO晶体材料.因此,该领域的各国科学家都在积极探索并发展新一代的深 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 二维应变作用下超导薄膜LiFeAs的磁性和电子性质
    摘要:基于密度泛函理论的第一性原理计算,研究了二维应变作用下LiFeAs超导薄膜的磁性结构、电子能带和态密度变化,分析了应变对其超导电性的作用.结果显示,对体系施加1%—6%的二维平面张、压应变均不改变其基态条形反铁磁性结构,费米面附近的电子态密度主要来自于Fe-3d轨道电子以及少量的As-4p电子 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 微结构气体探测器中紫外激光束的信号和指向精度实验研究
    摘要:在气体探测器研究中,利用266nm紫外激光的双光子电离物理机制使气体电离产生可测量的信号,是一种重要的标定方法.随着微结构气体探测器(MPGD)的不断发展,用紫外激光标定来实现较高精度位置分辨率成为了一种研究需求,对此有两个关键技术问题需要解决:实验研究激光可测信号大小以及激光指向精度.分析和 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29
  • 太赫兹量子级联激光器中有源区上激发态电子向高能级泄漏的研究
    摘要:利用热力学统计理论和激光器输出特性理论,建立了太赫兹量子级联激光器(THzQCL)有源区中上激发态电子往更高能级电子态泄漏的计算模型,以输出功率度量电子泄漏程度研究分析了晶格温度和量子阱势垒高度对电子泄漏的影响.数值仿真结果表明,晶格温度上升会加剧电子泄漏,并且电子从上激发态泄漏到束缚态的数量 ...
    中科院物理研究所 本站小编 Free考研考试 2021-12-29

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.