删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

微磁检测应力和塑性区的磁弹塑耦合理论

本站小编 Free考研考试/2022-01-01


引 言


钢铁材料因其具有良好的力学以及机械性能, 被广泛应用于重大机械、土木交通工程、管道输运等领域. 长期服役中钢铁类构件或结构的突发破坏导致恶性工程事故频发, 探索针对钢铁材料应力状态和塑性变形的无损检测方法, 有望通过结构局部危险点的及时发现来有效预防结构整体垮塌事故, 具有重大的研究价值和现实意义. 常规无损检测方法有超声检测、磁粉检测、涡流检测、渗透检测以及射线检测等, 这些检测方法多被应用于已成形宏观裂纹的检测. 微磁检测方法, 如磁记忆检测方法, 被认为可以实现材料应力集中或塑性变形等早期损伤的无损检测[1-6]. 微磁检测方法通过测量材料表面的非线性磁场分布, 确定材料的早期损伤或者缺陷的位置和尺寸. 微磁检测信号主要源于材料内部各位置处磁特性的改变, 进而在宏观损伤、局部外形轮廓等几何形貌等的漏磁效应下在材料表面形成具有非线性分布的磁场信号[3]. 材料各位置处的磁特性表现为该位置处磁场和磁化之间的非线性且存在磁滞效应的映射关系, 又称材料的磁学本构. 内部位错等微缺陷、局部微观组织等材料构成的空间差异或变化都会影响内部各位置处磁特性的变化[7-8]; 材料内部各位置处温度、应力、塑性变形等物理场的空间分布性差异也会使得材料在各位置处表现出差异明显的磁场?磁化映射规律[3], 产生磁特性的差异. 因此, 微磁检测方法中非线性磁信号的成因较复杂.

本文涉及的理论研究是在忽略微缺陷和微观组织变化, 以及温度等物理场均匀的假设下进行的, 以探讨弹塑性变形对材料内部各位置处磁特性的改变, 进而通过磁场模拟分析弹塑性变形对表面微磁信号的影响. 从微磁检测的基本原理可以得出, 厘清铁磁材料内部应力、缺陷与微磁信号之间的对应关系是实现微磁检测工程应用的关键问题[3,9]. 这部分研究主要包含铁磁材料自身应力、应变、磁场与磁化间的定量关系, 即力-磁本构关系, 以及缺陷信息、检测参数与微磁信号间的对应关系, 即检测信号分析. 在力磁本构关系方面, 美国****Jiles[10]于1995年基于有效场理论及不可逆磁化的接近原理, 提出了铁磁材料应力磁化的Jiles本构关系, 并在2003年, 通过瑞利定律对Jiles本构关系进行了应力项修正[11]. 2011年, Li和Xu[12]通过考虑应力磁化行为的拉压不对称性对Jiles本构关系进行了细节修正. 上述这些研究结果[10-12]定性上无法描述压应力作用下材料磁化强度改变量为负的实验现象, 拉应力下磁化强度预测结果也与经典实验结果[13]存在30%左右误差. Shi等[14]基于热力学原理以及不可逆磁化的接近原理, 建立了铁磁材料的力磁耦合本构关系. 与Jiles本构关系及其修正本构关系相比, 新提出本构关系的预测结果与经典实验结果吻合, 解决了压应力情形磁化强度预测结果与实验数据的异号矛盾. 上述提到的本构关系多针对处于弹性阶段的材料开展研究, ****们也针对塑性变形的影响机制展开了研究. 2011年Wang等[15]基于塑性变形钉扎效应提出考虑塑性效应的力磁耦合本构, Li等[16]基于此开展了类似研究. 最近, 时朋朋重新研究了塑性变形引起的有效场分量表达式, 纠正了已有研究中的磁化项[15-16], 建立了铁磁材料的磁弹塑性耦合本构[17].

在检测信号分析方面, ****通过结合力磁本构、力学分析、磁学分析研究微磁信号的影响因素及影响规律. Wang等[18-19]采用磁荷密度与局部应力集中呈线性关联的假设, 采用磁荷模型对材料表面一维薄层或二维矩形应力集中区诱发的微磁信号进行了模拟, 也通过考虑应力集中处的磁导率的变化分布规律, 系统地分析了应力集中宽度、埋深位置等对微磁信号的影响[20], 相关结果对微磁检测方法的量化研究具有一定意义. 针对已有磁偶极子理论不能分析应力相关微磁信号的缺点, 结合力磁耦合本构的磁偶极子理论模型被建立, 以适用于描述微磁方法中应力载荷对磁信号的影响[21]. Shi等[22]实验测量了碳钢材料在弹性载荷、塑性变形的联合作用下试件表面的磁信号变化, 并结合弹塑性磁化本构关系和磁偶极子对实验规律进行了解释. 针对微磁检测实验信号的精确定量分析, 还需要借助精细的力磁耦合本构关系以及力学、静磁场的有限元分析方法实现[23-24], 研究表明合理的力磁耦合本构关系在实现微磁信号定量化分析上的重要性. 基于改进力磁本构关系的检测信号分析模型已被成功用于研究损伤识别[25]、环境磁场方向效应[26]、磁热弹塑性耦合现象[27]以及疲劳[28]等问题.

鉴于上述提到的检测信号分析模型多针对材料处于弹性阶段的情形, 实际工程中的结构和材料残余应力和塑性有可能联合存在, 该情形下微磁信号规律的理论研究较少. 本文介绍了铁磁材料微弱环境磁场下的磁弹塑性本构进展, 及其在微磁信号分析方面的应用. 力磁本构关系方面, 构建了受弹塑性载荷铁磁材料的理想磁化本构显式解析式, 分析了恒定微弱磁场下的应力磁化行为. 检测信号分析方面, 建立并求解了微弱磁场下铁磁试件中弹性应力或塑性区诱导的表面磁信号的二维分析模型. 结合实验结果证实磁信号二维分析模型在刻画弹塑性因素对微磁信号影响规律方面的定量能力, 进而对微磁信号的特征量与局部弹性应力或塑性区的尺寸间的相互关系进行了分析.


1.
微弱磁场环境下的磁弹塑性力磁本构



1.1
磁弹塑等效场模型


在恒定的磁场和等温环境下, 具有残余塑性应变的各向同性铁磁材料承受外部载荷作用下, 材料的磁化状态将在外加磁场、弹性应力、塑性变形等的联合作用下发生变化. 材料所受到的有效场可以表示为







$$ {H_{{
m{total}}}}{text{ = }}{H_H}{text{ + }}H_sigma ^e{text{ + }}H_sigma ^p $$
(1)

其中$ {H_H} $, $ H_sigma ^e $, $ H_sigma ^p $分别表示环境磁场引起的有效场、应力相关力磁耦合效应导致的等效场以及塑性变形引起的等效场.

外加环境磁场相关的赫姆霍兹自由能密度函数为







$$ {A_H} = {mu _0}HM - frac{{{mu _0}}}{2}{N_d}{M^2} + TS $$
(2)

其中$ {mu _0} $表示真空磁导率, $ H $表示环境磁场, $ M $表示磁化强度, $ {N_d} $表示退磁因子, $ T $表示温度, $ S $表示熵.

等温条件下, 外加磁场作用的有效场可以表示为其相关赫姆霍兹自由能密度函数关于磁化强度的微分







$$ {H_H}{text{ = }}frac{1}{{{mu _0}}}frac{{{text{d}}{A_H}}}{{{text{d}}M}}{text{ = }}H - {N_d}M $$
(3)

参考已有文献[17], 考虑畴壁钉扎对磁化强度的影响, 存在塑性变形时, 其相关的钉扎能密度可以表示为







$$ E_sigma ^p = int {xi {mu _0}left( {H + M}
ight)bvarepsilon _p^n{text{d}}M} $$
(4)

其中$ xi $表示磁矩和磁感应强度的线性比例因子, $ b $反映钉扎密度与塑性的比例因子, $ {varepsilon _p} $是塑性变形, $ n $表示钉扎密度关于塑性变形的指数.

塑性变形导致的有效场分量可以表示为







$$ H_sigma ^p = - frac{1}{{{mu _0}}}frac{{partial E_sigma ^p}}{{partial M}} = - k'varepsilon _p^nleft( {H + M}
ight) $$
(5)

其中$ k'{text{ = }}xi b $. 值得注意的是, 这里采用的有效场分量表达式对参考文献[15]中的有效场分量表达式进行了修正.

这里考虑应力相关力磁耦合效应导致的等效场. Kuruzar 和Cullity[29]的实验结果表明, 铁磁材料的磁致伸缩应变是磁化强度的偶函数. 本文磁致伸缩应变$ lambda left( {sigma ,M}
ight) $表达式如下







$$ lambda left( {sigma ,M}
ight){text{ = }}frac{{{M^2}}}{{M_{{
m{ws}}}^2}}{lambda _{{text{wall}}}}left( sigma
ight) - vartheta frac{{Delta {M^2}}}{{Delta M_s^2}}{lambda _{{text{rotation}}}} $$
(6)

其中$ Delta M{text{ = }}left| M
ight| - {M_0} $, $ Delta {M_s}{text{ = }}{M_s} - {M_0} $. 等号右端第一项表示铁磁材料磁致伸缩应变由于磁畴壁移过程导致的增大, 等号右端第二项表示磁化强度超过饱和磁化强度之后磁畴转动导致的磁致伸缩应变减少量. ${M_{{
m{ws}}}}$表示无应力作用下的饱和壁移磁化强度; $ {M_0}left( sigma
ight) $表示与应力相关的饱和壁移磁化强度; $ {M_s} $表示饱和磁化强度; $ vartheta $是阶跃函数, 当$ M < {M_0} $时, $ vartheta {text{ = }}0 $; 当$ M geqslant {M_0} $时, $ vartheta {text{ = }}1 $. $ {lambda _{{text{wall}}}}left( sigma
ight) $表示不同应力作用下的饱和壁移磁致伸缩, $ {lambda _{{text{rotation}}}} $表示磁化强度超过与应力相关的饱和壁移磁化强度后, 磁畴旋转引起的磁致伸缩减小.

参考已有研究[30], $ {lambda _{{text{wall}}}}left( sigma
ight) $, $ {lambda _{{text{rotation}}}} $以及$ {M_0}left( sigma
ight) $的具体表达式可确定为







$$left. begin{array}{l} {M_0} = gleft( sigma
ight){M_{{
m{ws}}}} {lambda _{{text{wall}}}} = gleft( sigma
ight){lambda _s} hfill {lambda _{{text{rotation}}}} = k{lambda _s} hfill end{array}
ight} $$
(7)

其中假设饱和壁移磁化强度随应力的变化满足函数$ gleft( sigma
ight) = 1 - tanh left( {beta sigma /{sigma _s}}
ight) $, $ ;beta $描述磁化随应力的变化速率; $ {sigma _s} $表示材料的屈服强度; 假定饱和壁移磁致伸缩随应力的变化也满足该函数关系; $ {lambda _s} $表示饱和磁致伸缩应变, $ k $为磁致伸缩应变下降段和饱和磁致伸缩量的比值. 这些参数$ beta $乃至特征函数$ gleft( sigma
ight) $均可以通过实验进行测量, 即由不同应力下的饱和壁移磁化强度数据进行函数拟合准确得到.

铁磁材料力磁耦合本构关系可以通过热力学理论推导. 在等温环境下, 通过力磁耦合能$ G $可以建立力磁耦合热力学关系式如下[30]







$$left. begin{array}{l}lambda = frac{{partial G}}{{partial sigma }}{mu _0}H_sigma ^e = frac{{partial G}}{{partial M}}end{array}
ight} $$
(8)

其中$ H_sigma ^e $是应力引起的有效场.

利用方程(6) ~ 式(8)可以得出应力引起的有效场可以表示为







$$ begin{split} H_sigma ^e =& frac{{2{lambda _s}}}{{{mu _0}M_{ws}^2}}left[ {sigma - frac{{{sigma _s}}}{beta }ln Bigg( cosh frac{{beta sigma }}{{{sigma _s}}}} Bigg)
ight]M hfill & - vartheta frac{{2{lambda _{{text{rotation}}}}}}{{{mu _0}Delta M_s^2}}sigma Delta M hfill end{split} $$
(9)

联立求解方程(1), (3), (5)和(9), 可以获得铁磁材料在环境磁场、应力以及塑性变形联合作用下的有效场总和.


1.2
微弱磁场下的理想磁化


考虑在恒定的磁场和等温环境下, 具有残余塑性应变的各向同性铁磁材料承受外部载荷作用. 力磁效应平衡下, 铁磁材料的无磁滞理想磁化$ {M_{an}} $可表示为







$$ {M_{an}} = {M_s}fleft( {{H_{{
m{total}}}}}
ight) $$
(10)

其中$ f $表示磁化强度与有效场${H_{{
m{total}}}}$之间的非线性关系.

对于磁各向同性材料, 磁化强度$ {M_{an}} $和有效场${H_{{
m{total}}}}$之间满足经典郎之万函数







$$ {M_{an}} = {M_s}left[ {coth left( {{H_{{
m{total}}}}/a}
ight) - a/{H_{{
m{total}}}}}
ight] $$
(11)

其中$ a $是单位为A/m的磁化模型参数.

对于地环境磁场下的微磁检测方法, 材料磁化强度$ M < 0.2{M_s} $. 当材料的磁化强度$ M < 0.2{M_s} $, 朗之万函数线性简化后导致的计算误差不超过2.5%. 此时, 可以利用郎之万函数的线性简化使得磁化强度与有效场之间的关系更加简洁







$$ {M_{an}} = {M_s}{H_{{
m{total}}}}/left( {3a}
ight) $$
(12)

联立方程(1), (3), (5)和(9), 有效场和为







$$ begin{split} {H_{{
m{total}}}} =& left( {1 - k'varepsilon _p^n}
ight)H - left( {{N_d} + k'varepsilon _p^n}
ight){M_{an}} hfill & {text{ + }}frac{{2{lambda _s}}}{{{mu _0}M_{{
m{ws}}}^2}}left[ {sigma - frac{{{sigma _s}}}{beta }ln Bigg(cosh frac{{beta sigma }}{{{sigma _s}}}} Bigg)
ight]{M_{an}} hfill & - vartheta frac{{2{lambda _{{text{rotation}}}}}}{{{mu _0}Delta M_s^2}}sigma left( {{M_{an}} - {M_0}}
ight) hfill end{split} $$
(13)

联立方程式(12)和式(13), 可以获得如下弹塑性作用下理想磁化的显式解析式







$$ begin{split} &{M_{an}} = &frac{{left( {1 - k'varepsilon _p^n}
ight)H{text{ + }}vartheta dfrac{{2{lambda _{{text{rotation}}}}}}{{{mu _0}Delta M_s^2}}sigma {M_0}}}{{dfrac{{3a}}{{{M_s}}} + {N_d} + k'varepsilon _p^n - dfrac{{2{lambda _s}}}{{{mu _0}M_{{
m{ws}}}^2}}left[ {sigma - dfrac{{{sigma _s}}}{beta }ln Bigg(cosh dfrac{{beta sigma }}{{{sigma _s}}}} Bigg)
ight]{text{ + }}vartheta dfrac{{2{lambda _{{text{rotation}}}}}}{{{mu _0}Delta M_s^2}}sigma }}end{split} $$
(14)

方程(14)是理想磁化强度的显式表达式, 在已知环境磁场、应力以及塑性变形的情况下, 可以直接求得材料的理想磁化强度. 相比已有力磁本构关系, 本研究建立的显式解析形式的理想磁化更加简洁, 有助于提升对磁记忆微磁检测中力磁耦合效应的理解和应用.


1.3
微弱磁场下的应力磁化


本节通过引入接近原理考虑应力变化对材料磁化强度的影响[10, 30]. 应力加载历史对铁磁材料磁化强度的影响可以通过如下表达式描述







$$ frac{{{text{d}}M}}{{{text{d}}sigma }} = frac{sigma }{{Exi '}}left( {{M_{an}} - M}
ight) + cfrac{{{text{d}}{M_{an}}}}{{{text{d}}sigma }} $$
(15)

其中$ c $反映磁畴壁的柔性系数, $ xi ' $是与能量相关的系数, $ E $是弹性模量.

利用低磁化状态下的瑞利定律对上式中的应力项进行修正, 通过参数$ eta $考虑应力对不可逆磁化改变量的影响, 得到包含线性修正项的磁化强度的微分表达式







$$ frac{{{text{d}}M}}{{{text{d}}sigma }} = frac{{sigma pm eta E}}{{Exi '}}left( {{M_{an}} - M}
ight) + cfrac{{{text{d}}{M_{an}}}}{{{text{d}}sigma }} $$
(16)

方程式(14)和式(16)构成了微弱环境磁场下铁磁材料的力磁耦合关系, 以考虑恒定微弱磁场下应力变化对材料磁化强度的影响.


2.
微磁检测信号分析的磁弹塑耦合模型



2.1
磁信号分析方法的介绍


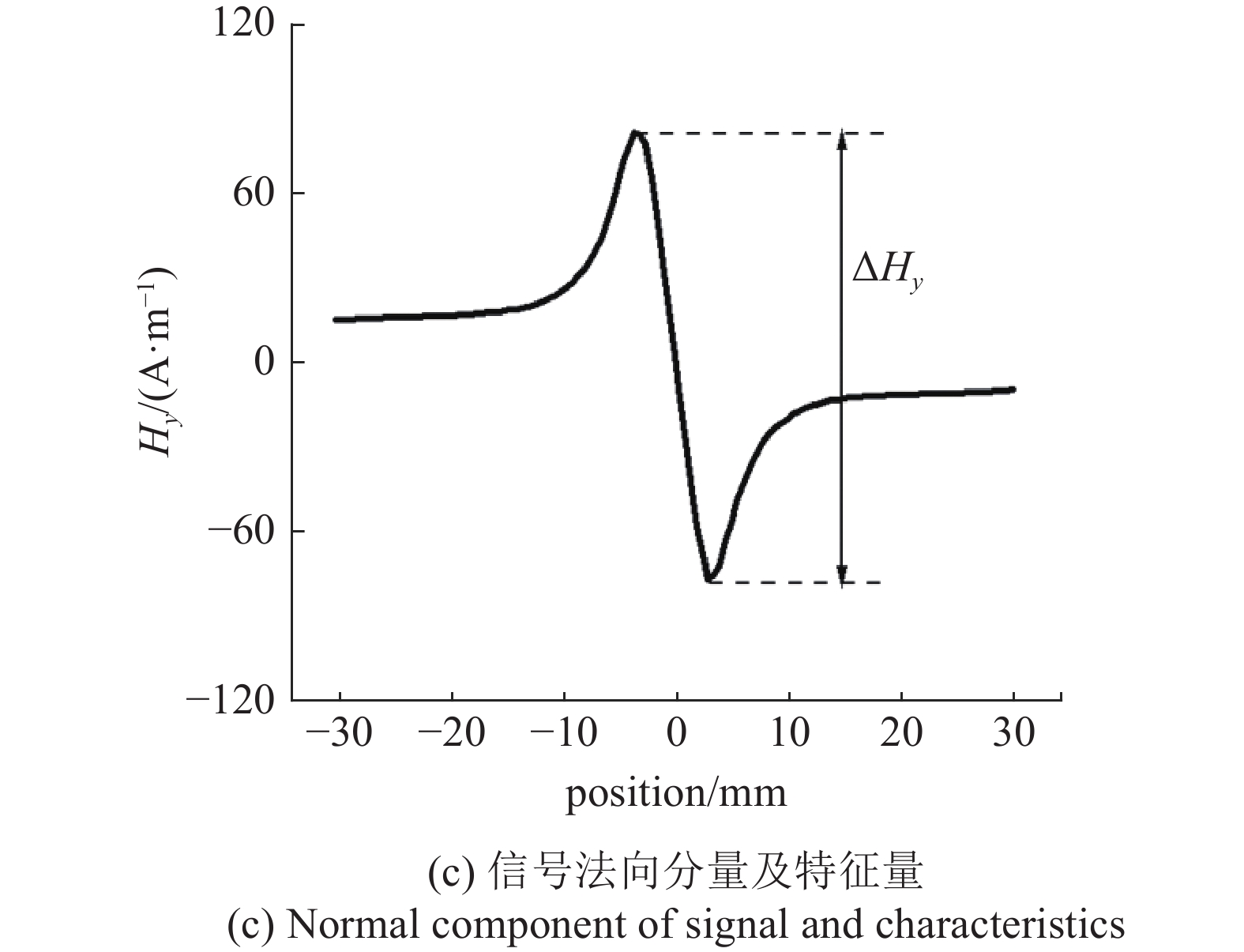
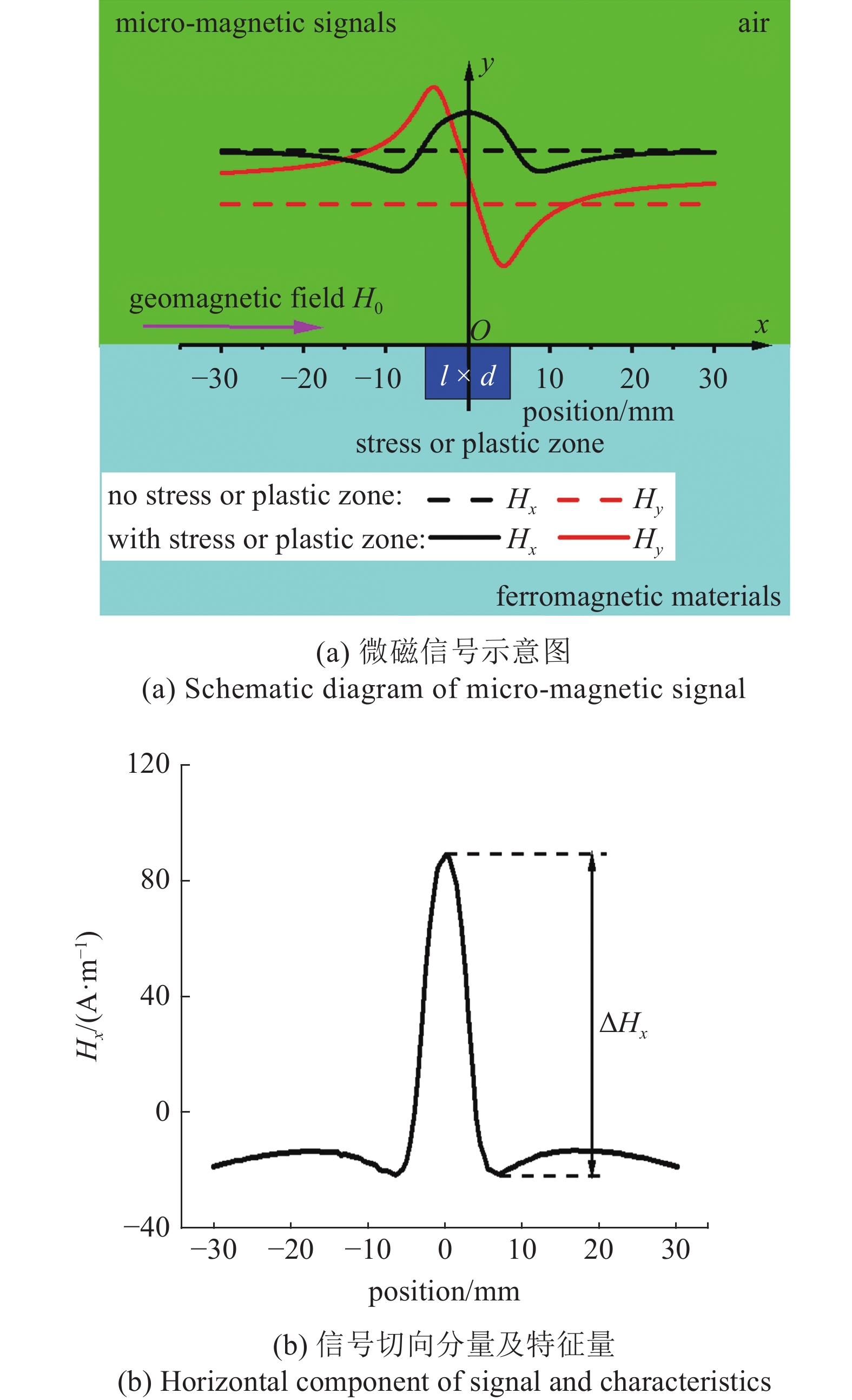
图1(a)所示为铁磁材料表面某区域存在应力集中或塑性变形时, 铁磁材料表面微磁信号的示意图. 在应力和塑性变形作用时, 应力集中或塑性区的磁畴将产生有规律地取向变化, 发生磁化状态的改变, 进而在材料表面附近产生微磁信号. 为能定量描述这些因素对微磁信号的影响, 定义并计算如图1(b)和图1(c)所示的微磁信号特征量, 分别为切向信号的峰谷值$ Delta {H_x} $, 法向信号的峰谷值$ Delta {H_y} $.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1" />



图
1
弹性应力或塑性区诱导微磁信号及其信号特征量的示意图



Figure
1.
Schematic diagram of the micro-magnetic signal induced by elastic stress or plastic zone and its signal characteristics



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-1-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure1-1" />




下载:
全尺寸图片
幻灯片


分析铁磁材料引起的微磁信号, 需要求解空间的磁场分布. 假设固定地点地磁场环境随时间变化不大时, 忽略铁磁介质表面的传导电流, 铁磁介质处于恒定微弱地磁场的环境中. 这样, Maxwell基本方程可以简化为$ nabla cdot {boldsymbol{B}} = 0 $, $ nabla times {boldsymbol{H}} = {bf{0}} $. 需要基于Maxwell方程对材料附近的空气区域内的磁场进行求解, 以实现该处的磁信号的分析与显示. 考虑到材料和空气之间的界面磁导率存在跳变, 界面满足如下磁场跳变方程$ {H_{1 t}} = {H_{2 t}} $, $ {B_{1 n}} = {B_{2 n}} $. 距离铁磁材料较远的区域, 磁场与空气环境磁场相同, 满足磁场边界条件$ {boldsymbol{H}} = {{boldsymbol{H}}_0} $, 其中$ {{boldsymbol{H}}_0} $为环境磁场. 环境中的空气介质满足的磁学本构关系为$ {boldsymbol{B}} = {mu _0}{boldsymbol{H}} $, 其中$ {mu _0} $为空气磁导率. 无应力集中或塑性变形的区域, 处于磁场环境中铁磁介质的电磁本构关系为$ {boldsymbol{B}} = {mu _0}left( {{boldsymbol{H}} + chi {boldsymbol{H}}}
ight) $, 其中$ chi $表示铁磁材料的磁化率. 如图1 a所示, 铁磁材料某一表面区域存在应力集中或塑性变形. 应力集中区或塑性区中的铁磁介质满足的磁学本构关系为$ {boldsymbol{B}} = {mu _0}left[ {{boldsymbol{H}} + {boldsymbol{M}}left( {{boldsymbol{H}},sigma ,{varepsilon _p}}
ight)}
ight] $, 其中$ {boldsymbol{M}} $表示铁磁材料在磁弹塑性耦合作用下产生的磁化强度改变量. 由上文所述的微弱磁场作用下的应力磁化模型, 可计算获得恒定环境磁场下磁化强度$ {boldsymbol{M}} $随应力或塑性值的变化曲线, 进而完成应力集中或塑性变形区中的铁磁介质磁学本构的计算.

本文首先通过MATLAB编程采用常微分方程的欧拉数值格式求解由方程式(14)和式(16)构成的微弱环境磁场下铁磁材料的力磁耦合关系, 以得到恒定微弱磁场下应力和塑性变形导致的材料磁化强度的变化. 然后采用静磁场有限元程序结合本节上述所示的磁弹塑性耦合作用下铁磁介质本构关系进行计算, 实现弹性应力或塑性区诱导微磁信号的有限元数值求解.


2.2
有限元求解方法的验证


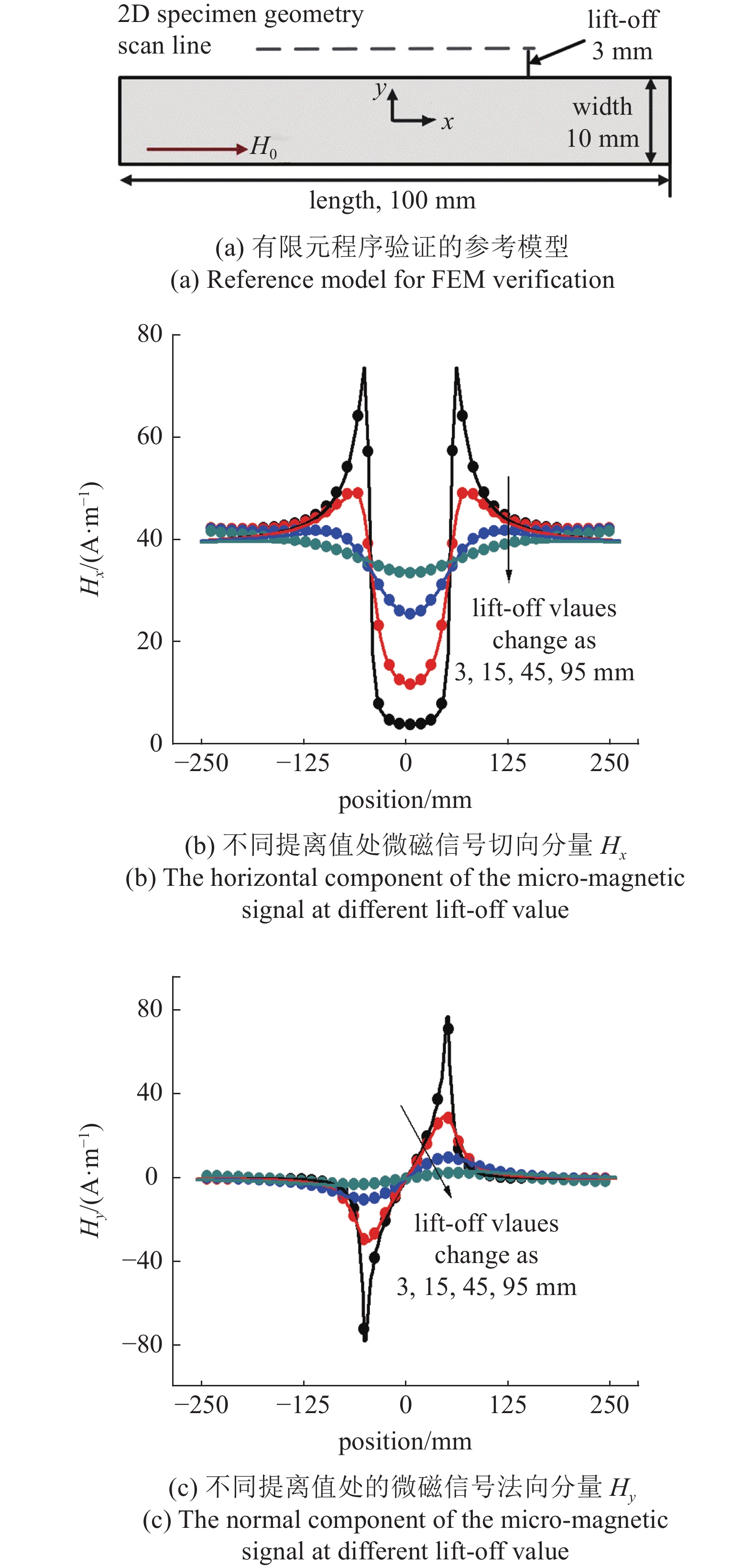
在理论分析前, 通过和已有文献的计算结果进行对比[23,31], 以证实本文有限元分析程序的正确性, 计算采用的参数与文献[31]所采用的参数保持一致. 如图2所示, 文献中对地磁场环境下不含损伤的二维光滑铁磁材料表面的微磁信号进行了理论分析, 图2(a)为铁磁材料的几何形状; 图2(b)为微磁信号切向分量Hx; 图2(c)为微磁信号法向分量Hy; 其中点为已有文献的计算结果[31], 实线为利用有限元方法重现的结果. 二维有限元计算中所采用相关参数为, 试件磁化率为517, 矩形试件长为100 mm, 宽为10 mm, 分别选取磁信号对应的提离值为3 mm, 15 mm, 45 mm和95 mm. 图2给出光滑试件不同提离值处的微磁信号切向分量Hx和法向分量Hy的对比图. 可以看出微磁信号在试件的左右两端存在一个明显的突变, 而远离试件位置处的切向磁场Hx为40 A/m, 法向磁场Hy为0 A/m, 和地磁场环境条件相一致. 本文静磁场有限元方法的计算结果与文献结果[31]吻合, 证实本文微磁信号分析中的有限元计算程序的正确性.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-2.jpg'"
class="figure_img
figure_type1 bbb " id="Figure2" />



图
2
磁信号分析的程序验证(点: 文献[31]结果, 线: 本文结果)



Figure
2.
Verification of magnetic signal analysis (points: result in Ref. [31], lines: present result)



下载:
全尺寸图片
幻灯片



2.3
微磁信号预测的定量验证


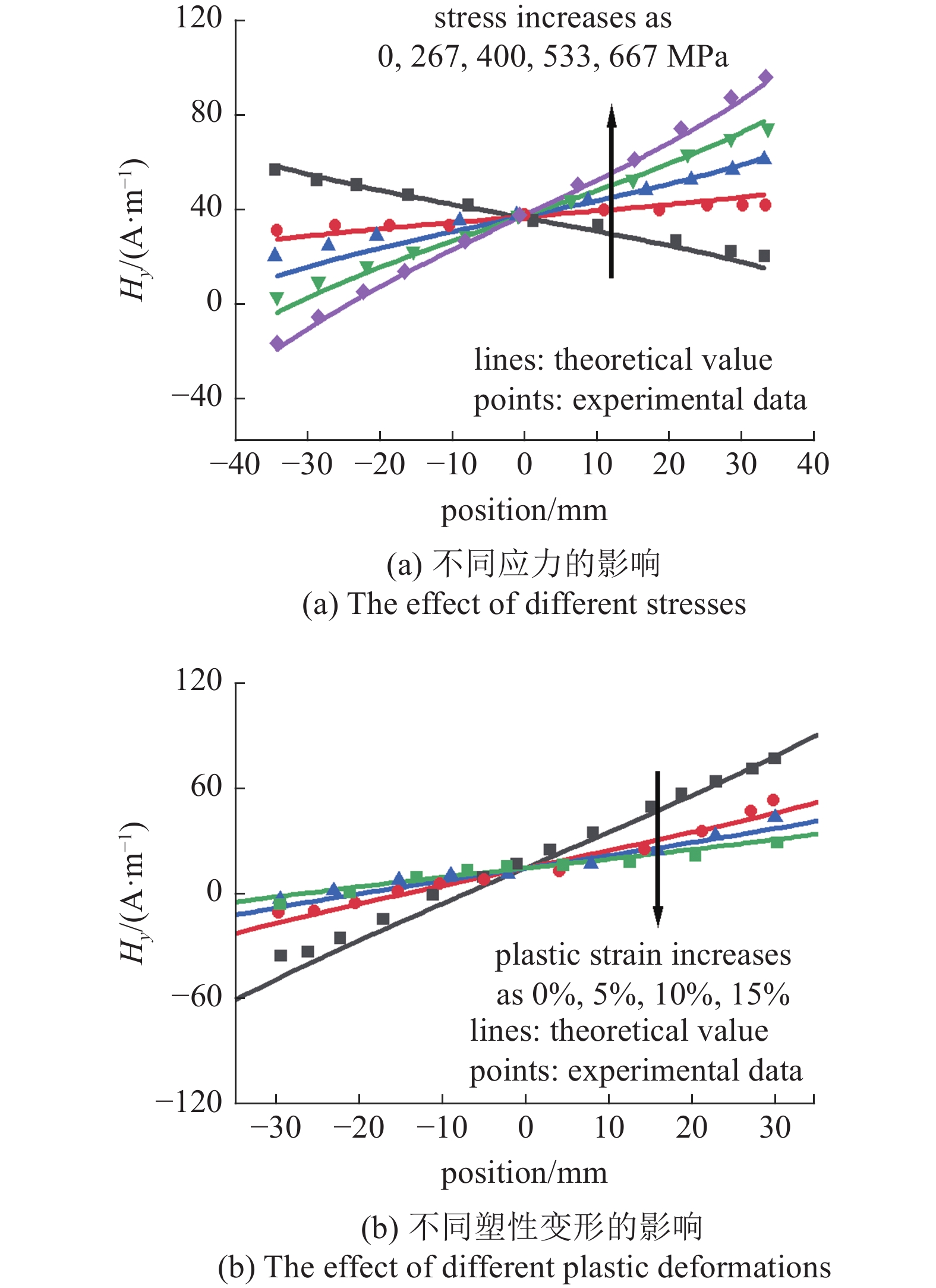
图3基于本文微磁信号正演分析的有限元求解, 分析讨论了铁磁材料在弹性载荷作用以及塑性变形条件下其表面的微磁信号分布. 基于微弱磁场作用下的应力磁化本构, 可以计算获得恒定环境磁场下磁化强度改变量随应力或塑性值的变化曲线, 进而就可以计算得到不同应力或塑性变形与磁化强度改变量间的对应关系, 拟合出不同应力或塑性变形与磁化强度改变量间的简化对应关系. 基于已公开的实验数据[32-33], 确立不同应力或塑性变形下磁化强度满足$ {boldsymbol{M}}{text{ = }}{{boldsymbol{M}}_0} + chi {boldsymbol{H}}{text{ + }}{k'_1}sigma /{sigma _s} - {k'_2}varepsilon _p^n $, 其中材料磁化率$ chi $取值200, 文献中采用的钢材屈服强度为$ {sigma _s} = $980 MPa, 磁化改变量关于应力的比率$ {k'_1} $=5.6 × 104 A/m, 磁化改变量关于塑性的比率$ {k'_2} $=8 × 104 A/m, $ {{n}} = $0.35. $ {{boldsymbol{M}}_0} $由材料无应力或塑性变形状态下的初始磁化决定. 针对长为150 mm的具有不同应力的18 CrNi4 A号钢试件, 图3(a)是本文有限元模拟的弹性载荷作用下材料表面的微磁信号与已有实验结果[32]的对比, 可以看出基于本文有限元分析程序能够描述弹性载荷与微磁信号之间的关系; 随着弹性载荷的增大, 材料表面的微磁信号绕测量中心逆时针旋转, 即微磁信号的斜率随着弹性载荷的增大逐渐增大. 针对长为210 mm的具有不同塑性变形的A3号钢试件, 图3(b)给出基于有限元分析程序模拟的不同塑性变形下材料表面微磁信号与已有实验结果[33]的对比, 可以看出本文模拟结果与实验数据吻合较好; 随着塑性变形增加, 材料表面的微磁信号绕测量中心顺时针旋转, 即微磁信号的斜率随着塑性变形的增加逐渐减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-3.jpg'"
class="figure_img
figure_type1 bbb " id="Figure3" />



图
3
不同弹性应力和塑性变形下试件表面微磁信号的理论预测与实验[32-33]结果的对比



Figure
3.
Comparison of theoretical predictions and experimental results[32-33] of micro-magnetic signals on the surface of specimens under different elastic stress loading and plastic deformation



下载:
全尺寸图片
幻灯片



3.
磁弹塑耦合模型的分析与讨论



3.1
磁弹塑性本构模型分析


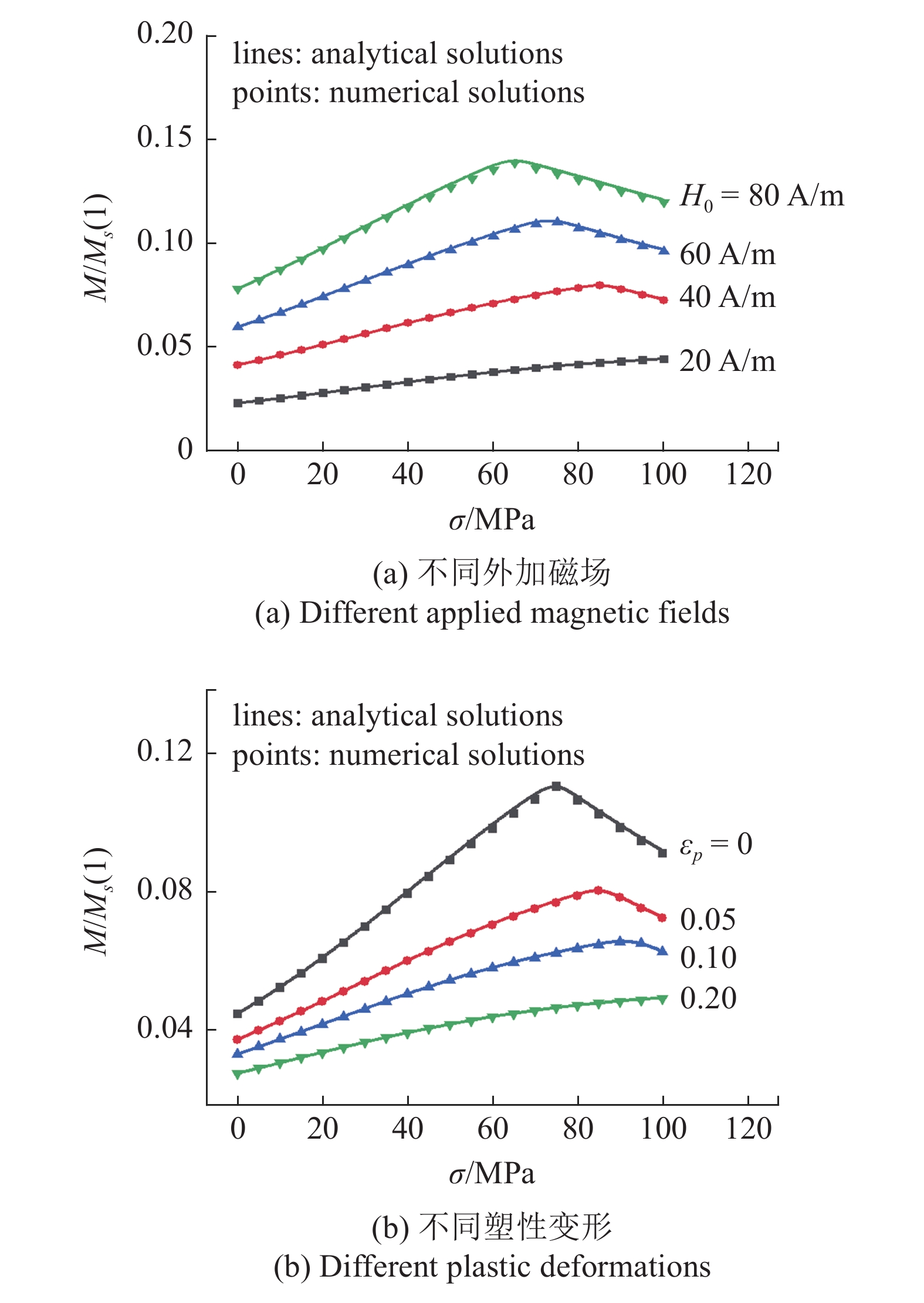
图4给出了基于本文公式(14)的理想磁化模型的解析解与数值求解结果的对比, 其中数值求解采用二分法或迭代求解等数值方法实现. 图4计算结果所采用的参数在表1中列出. 图4给出铁磁材料在应力和磁场作用下磁化强度的变化, 图4(a)是恒定磁场作用下材料的磁化强度随应力的变化; 图4(b)是恒定磁场、不同塑性变形条件下材料的磁化强度随应力的变化曲线. 通过对比可以发现本文理想磁化的解析解所反映的磁化强度与应力、外加磁场以及塑性变形之间的关系与数值解所揭示的规律完全一致. 恒定磁场下铁磁材料的磁化强度随着应力的增大先增大后减小, 同时也能反映磁化强度随着恒定磁场的增大而增大, 随着塑性变形的增大而减小. 本文提出的解析解可以方便对微磁无损检测中应力磁化效应的分析和理解.

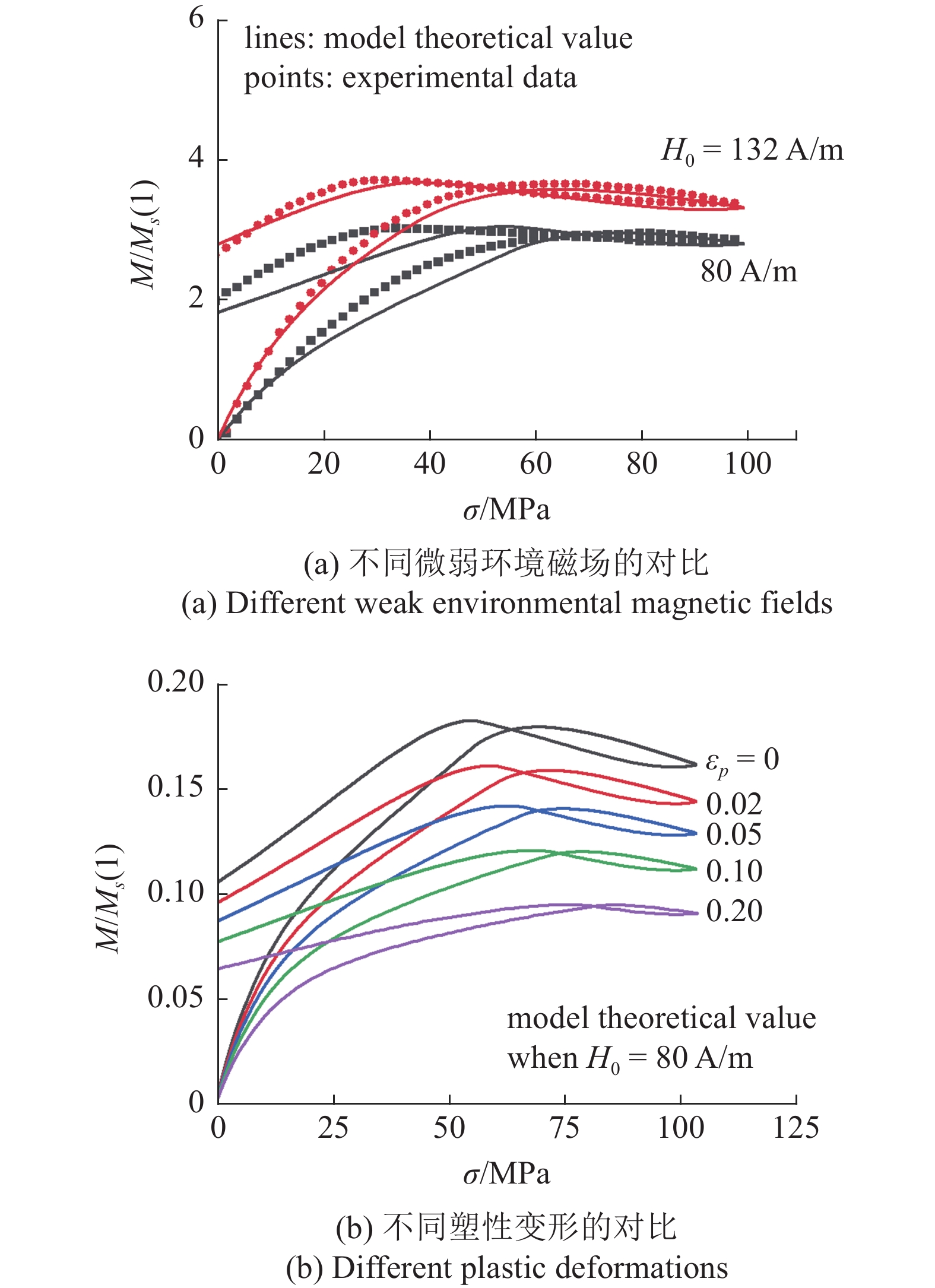
图5给出基于求解本文本构模型公式(16)预测的应力磁化曲线. 图5(a)是本文预测结果与实验数据[13]之间的对比, 模型预测中所采用的参数如表2所示, 未列出的参数取值与表1中的参数取值一致. 从图5(a)可以看出本文模型能够基本反映恒定磁场下应力加卸载对材料磁化行为的影响; 应力加载过程中, 随着应力的增大材料的磁化强度先增大后减小, 应力的卸载过程中, 磁化强度随着应力的减小同样呈现先增大后减小的变化趋势. 图5(b)讨论了材料的塑性变形程度对磁化行为的影响, 采用的模型参数与图4中采用的参数保持一致, 参数见表1. 从图5(b)可以看出塑性变形程度仅影响磁化强度的大小而对变化规律影响不大; 随着塑性变形程度的增加材料的磁化强度逐渐减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-4.jpg'"
class="figure_img
figure_type1 bbb " id="Figure4" />



图
4
理想磁化的解析解和数值解之间的比较



Figure
4.
Comparison between analytical and numerical solutions of ideal magnetization



下载:
全尺寸图片
幻灯片





表
1
理论模型参数值[14]



Table
1.
The parameter value of the theoretical model [14]



table_type2 ">
SymbolPhysical meaningValueSymbolPhysical meaningValue
$ E $/GPa elastic modulus 210 $ {M_s} $/(A·m-1) saturation magnetization 1.7 × 106
$ {sigma _s} $/MPa yield strength 250 $ {lambda _s} $/ppm saturation magnetostriction 4.17
$ beta $ change rate of magnetization with stress 3.7 $ {M_{{
m{ws}}}} $/(A·m-1)		 saturation wall-shift magnetization 9.5 × 105
$ a $/(A·m-1) magnetization parameter related to
initial permeability		 280 $ k $ dimensionless ratio about descending part
of magnetostrictive		 0.7
$ k' $ pinning coefficient 0.001 $ c $ flexibility coefficient of magnetic domain wall 0.08
$ {N_d} $ demagnetization factor 1.0 × 10?5 $ xi ' $ coefficient related to energy 1.0 × 106
$ eta $ correction of irreversible magnetization
with stress		 0.1 $ n $ exponential coefficient of pinning density and plastic deformation 0.8





下载:
导出CSV
|显示表格




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-5.jpg'"
class="figure_img
figure_type1 bbb " id="Figure5" />



图
5
不同环境磁场和塑性变形下的应力磁化



Figure
5.
Stress magnetization curve under different environmental magnetic fields and plastic deformation



下载:
全尺寸图片
幻灯片





表
2
应力磁化曲线预测中的参数取值[30]



Table
2.
Parameter value in stress magnetization curve prediction[30]



table_type1 ">
H/(A·m?1)βa/(A·m?1)$ eta $$ xi ' $(1)
803.52850.11.5 × 106
1324.43000.23 × 106





下载:
导出CSV
|显示表格



3.2
应力集中或塑性区尺寸对微磁信号的影响


这里对含矩形应力集中区或塑性区的铁磁材料表面微磁信号进行理论分析. 如图1(a)所示, 矩形应力集中区或塑性区位于铁磁材料的表面, 应力集中区或塑性区的长度和深度分别为l和d. 假定非应力集中区或塑性区的其余铁磁材料不受应力和塑性作用, 并且铁磁体受到水平于x轴强度为40 A/m的地磁场作用. 本节利用有限元模型对此问题进行理论分析.

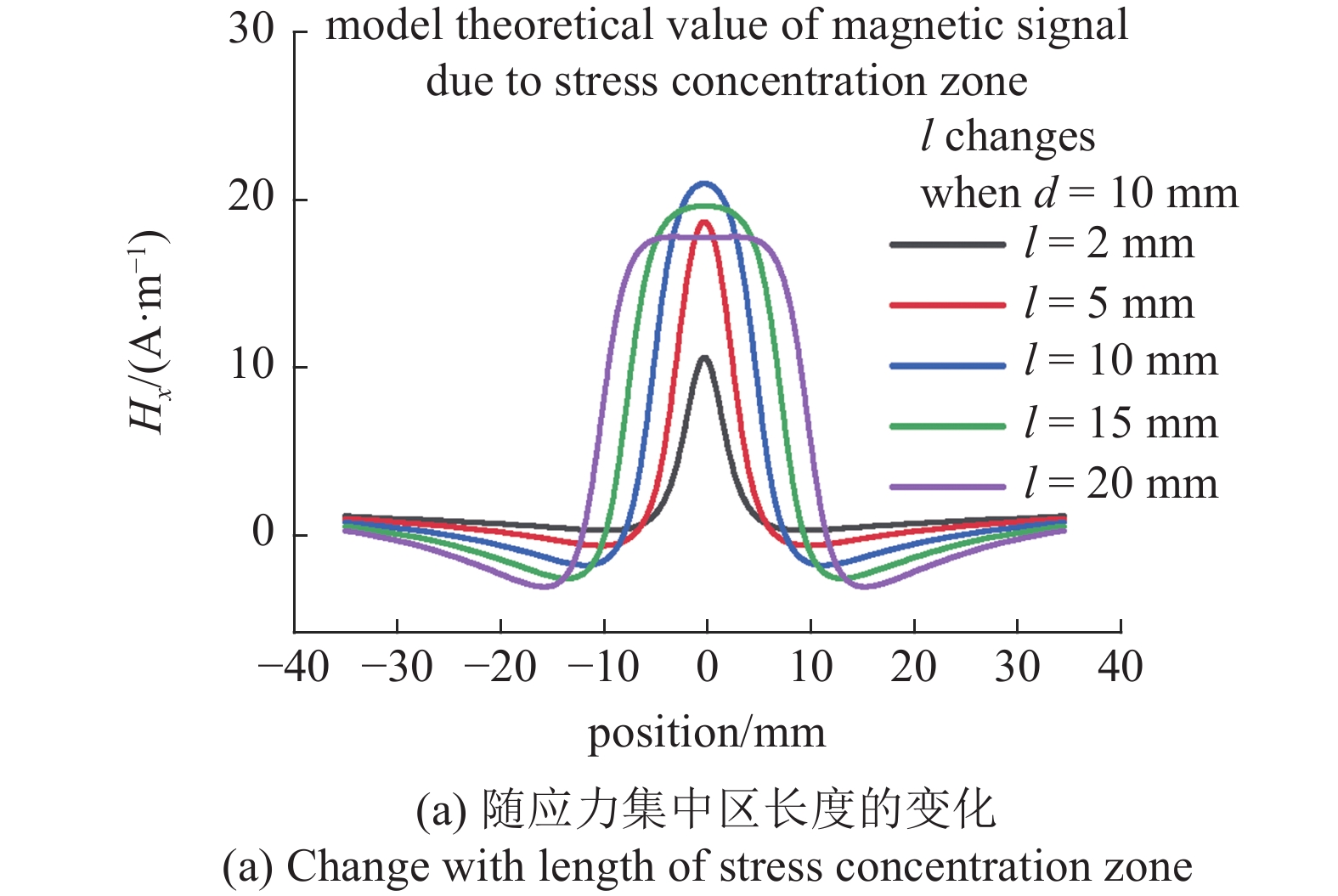
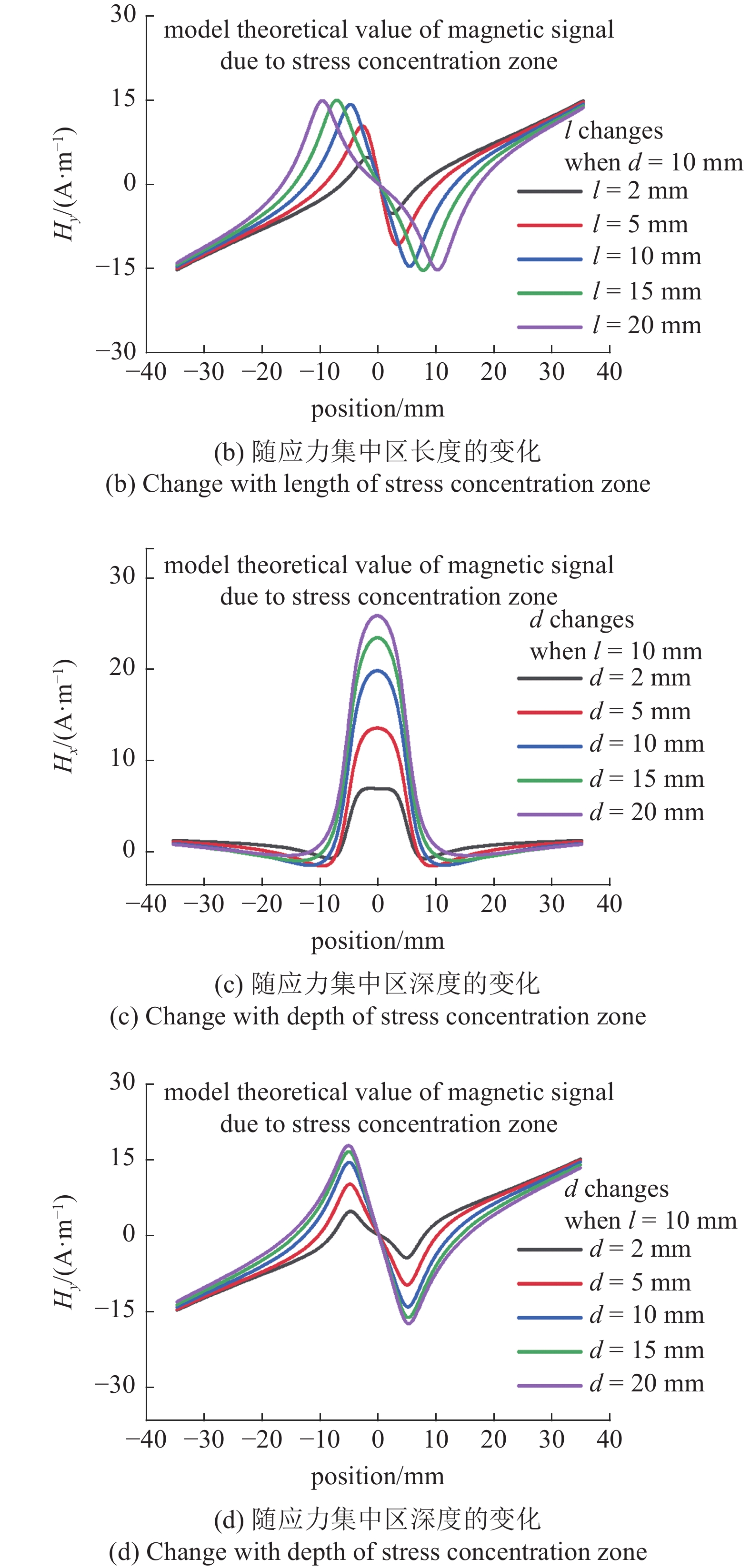
图6分析了应力集中区的尺寸对微磁信号的影响, 应力区存在150 MPa的恒定应力值. 模型计算所采用的参数与图3(a)所采用的参数保持一致. 图6(a)以及图6(b)是微磁信号随应力集中区长度的变化, 可以看出随着应力集中区长度的逐渐增大, 微磁信号的切向分量的峰值呈现先增大后减小的变化趋势且两个谷值之间的间距逐渐增大; 微磁信号的法向分量的峰值随着应力集中区长度的增大逐渐增大并趋于稳定且两个峰值之间的间距逐渐增大. 图6(c)以及图6(d)是微磁信号与应力集中区深度之间的联系, 可以看出随着应力集中区深度的逐渐增大, 微磁信号的切向分量的峰值逐渐增大; 微磁信号的法向分量的峰值随着应力集中区深度的增大逐渐增大.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-6-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6-1" />



6
应力集中区长度和深度对磁信号的影响



6.
The influence of the length and depth of the stress concentration zone on the magnetic signal



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-6.jpg'"
class="figure_img
figure_type1 bbb " id="Figure6" />



图
6
应力集中区长度和深度对磁信号的影响(续)



Figure
6.
The influence of the length and depth of the stress concentration zone on the magnetic signal (continued)



下载:
全尺寸图片
幻灯片


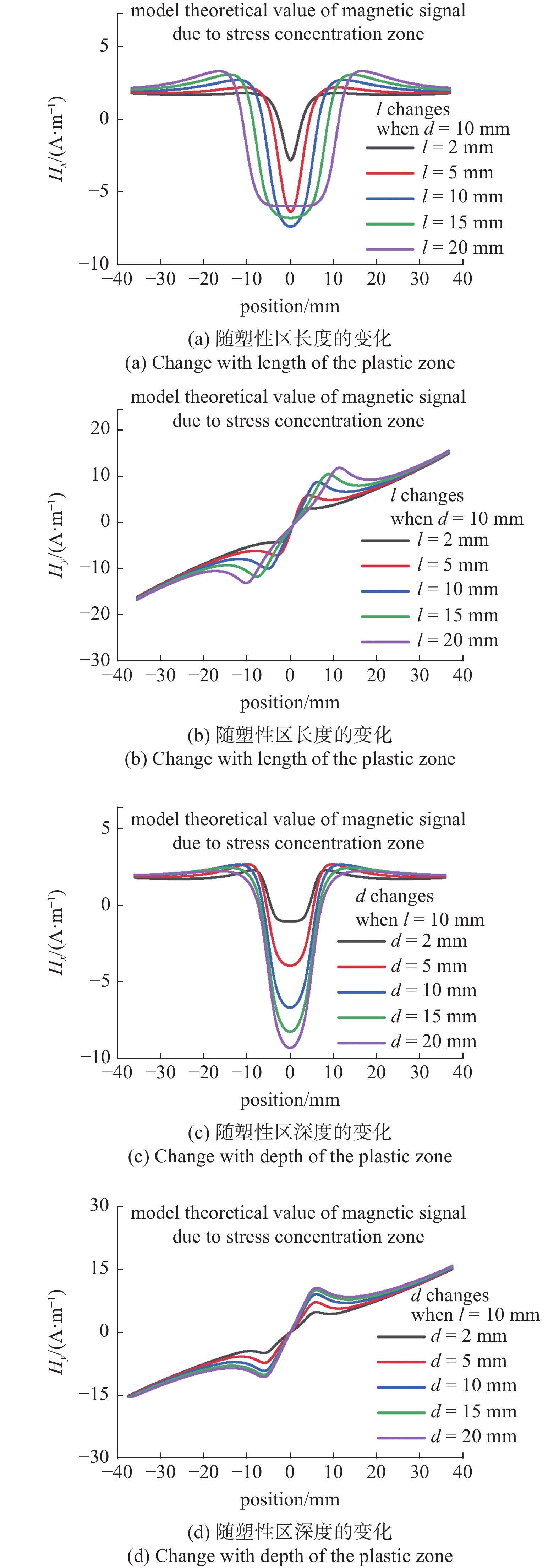
图7给出了塑性变形区的尺寸对微磁信号的影响, 塑性变形区存在20%的恒定塑性变形值. 计算所采用的参数与图3(b)采用的参数保持一致. 图7(a)以及图7(b)是微磁信号随塑性变形区长度的变化, 可以看出随着塑性变形区长度的逐渐增大, 微磁信号的切向分量的峰值的绝对值呈现先增大后减小的变化趋势且两个谷值之间的间距逐渐增大; 微磁信号的法向分量的峰值随着塑性变形区长度的增大逐渐增大且两个峰值之间的间距逐渐增大. 图7(c)以及图7(d)是微磁信号与塑性变形区深度之间的联系, 可以看出随着塑性变形区深度的逐渐增大, 微磁信号的切向分量的峰值逐渐增大; 而微磁信号的法向分量的峰值随着塑性变形区深度的增大逐渐增大. 从图6与图7的对比可以看出, 应力集中区与塑性变形区对微磁信号的影响规律基本是一致的, 相比较而言两者表面的微磁信号会出现正负号的翻转, 易通过信号峰谷值符号区分损伤类型是应力集中还是塑性变形.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-7.jpg'"
class="figure_img
figure_type1 bbb " id="Figure7" />



图
7
塑性区长度和深度对磁信号的影响



Figure
7.
The influence of the length and depth of the plastic zone on the magnetic signal



下载:
全尺寸图片
幻灯片



3.3
应力集中或塑性区尺寸对信号特征量的影响


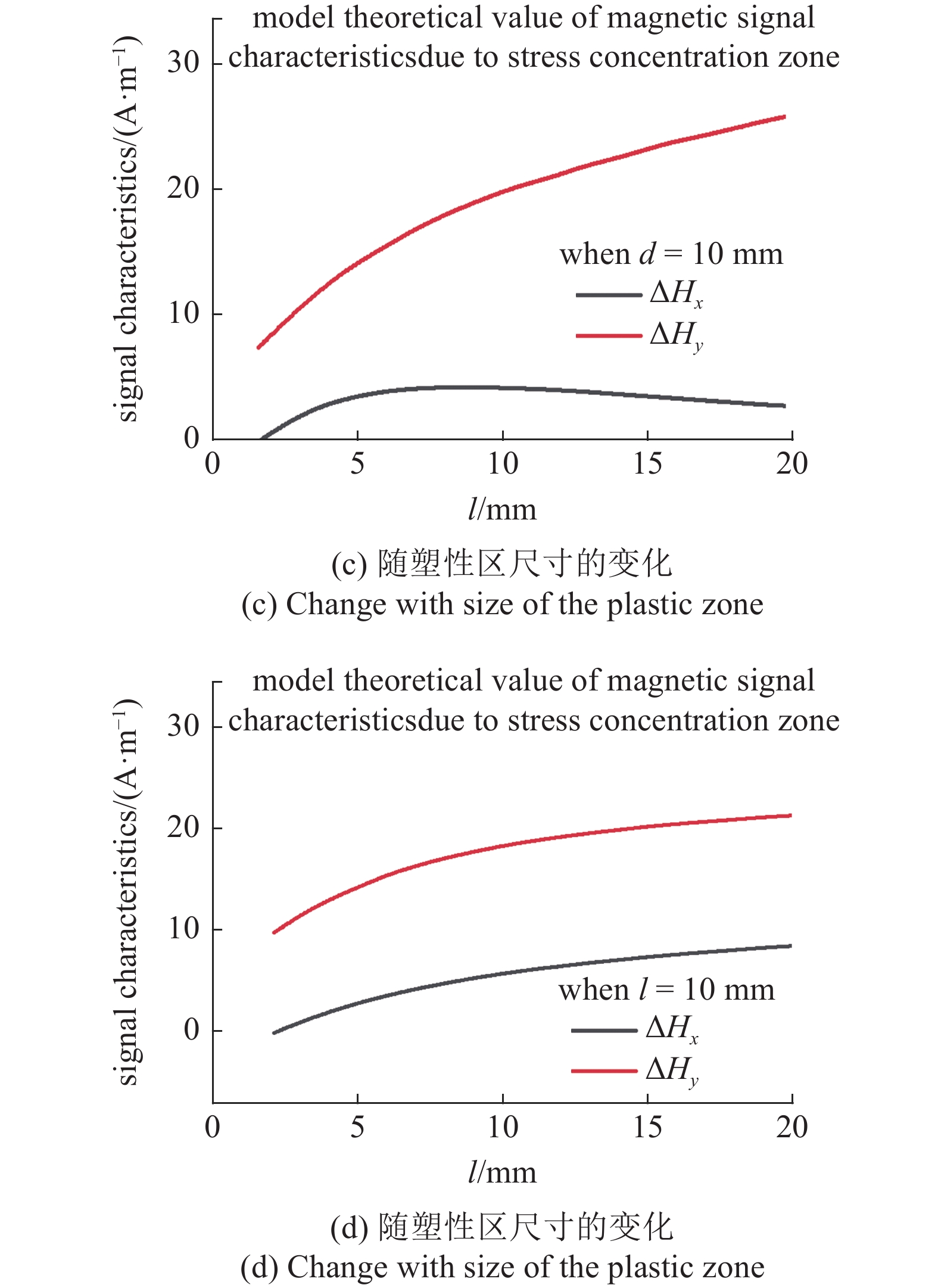
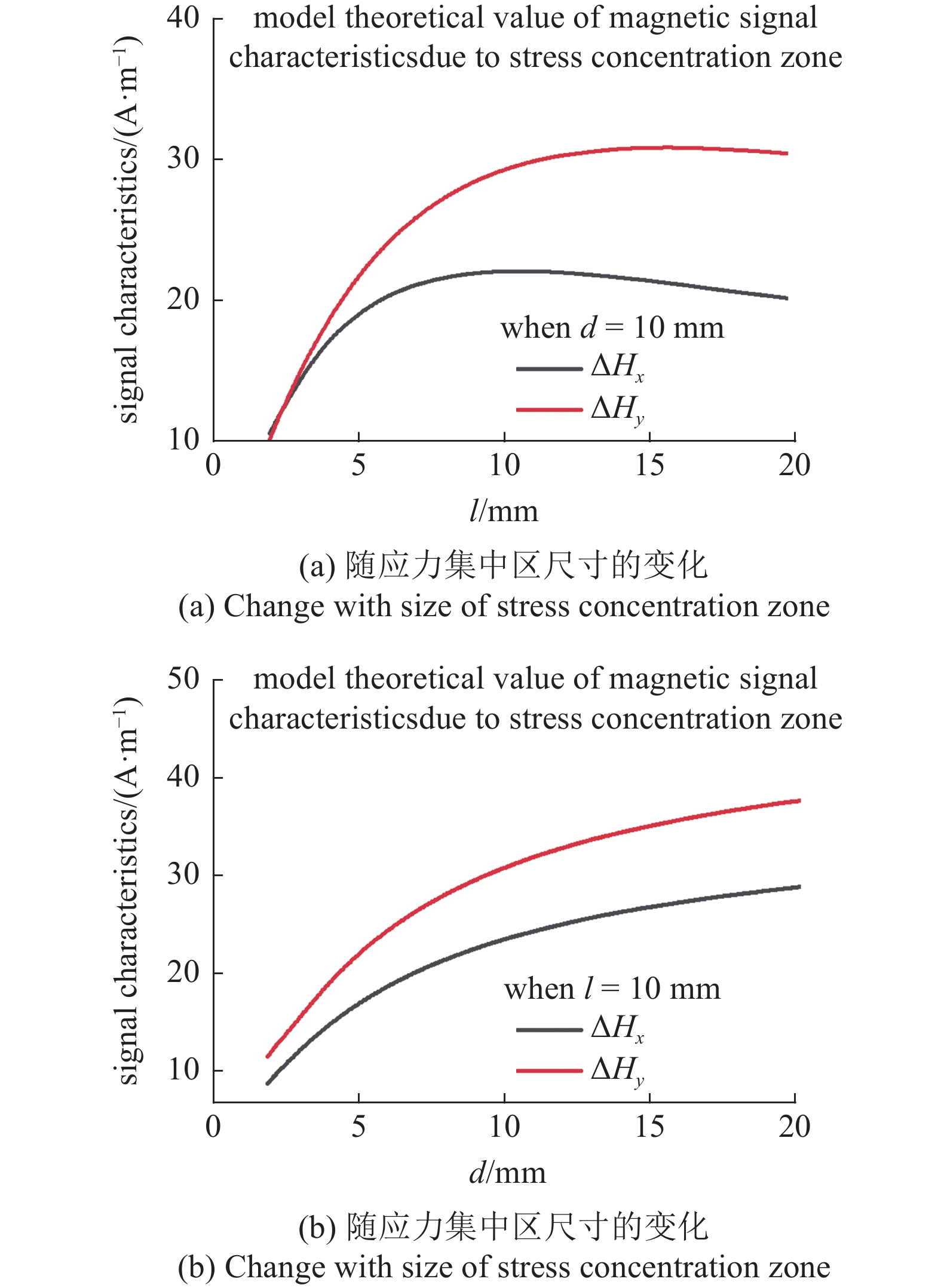
基于3.2节的理论结果计算微磁信号特征量, 图8讨论了不同应力集中区和塑性区长度和深度对微磁信号特征量的影响. 从图8(a)可以看出, 随着应力集中区长度的增加, 微磁信号切向分量特征值$ Delta {H_x} $先逐渐增大然后减小而法向分量特征值$ Delta {H_y} $呈现逐渐增大并趋于稳定; 从图8(b)可以看出, 随着应力集中区深度的增加, 微磁信号切向分量特征值$ Delta {H_x} $和法向分量特征值$ Delta {H_y} $均呈现逐渐增大的现象. 从图8(c)可以看出, 随着塑性变形区长度的增加, 微磁信号切向分量特征值$ Delta {H_x} $先逐渐增大然后缓慢减小而法向分量特征值$ Delta {H_y} $近线性增大; 从图8(d)可以看出, 随着塑性变形区深度的增加, 无论是微磁信号切向分量特征值$ Delta {H_x} $还是法向分量特征值$ Delta {H_y} $均呈现近线性增大的现象.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-8.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8" />



图
8
特征量的影响规律



Figure
8.
The influence law of characteristic quantity



下载:
全尺寸图片
幻灯片




onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-8-1.jpg'"
class="figure_img
figure_type1 bbb " id="Figure8-1" />




下载:
全尺寸图片
幻灯片



3.4
应力或塑性水平对检测信号的影响


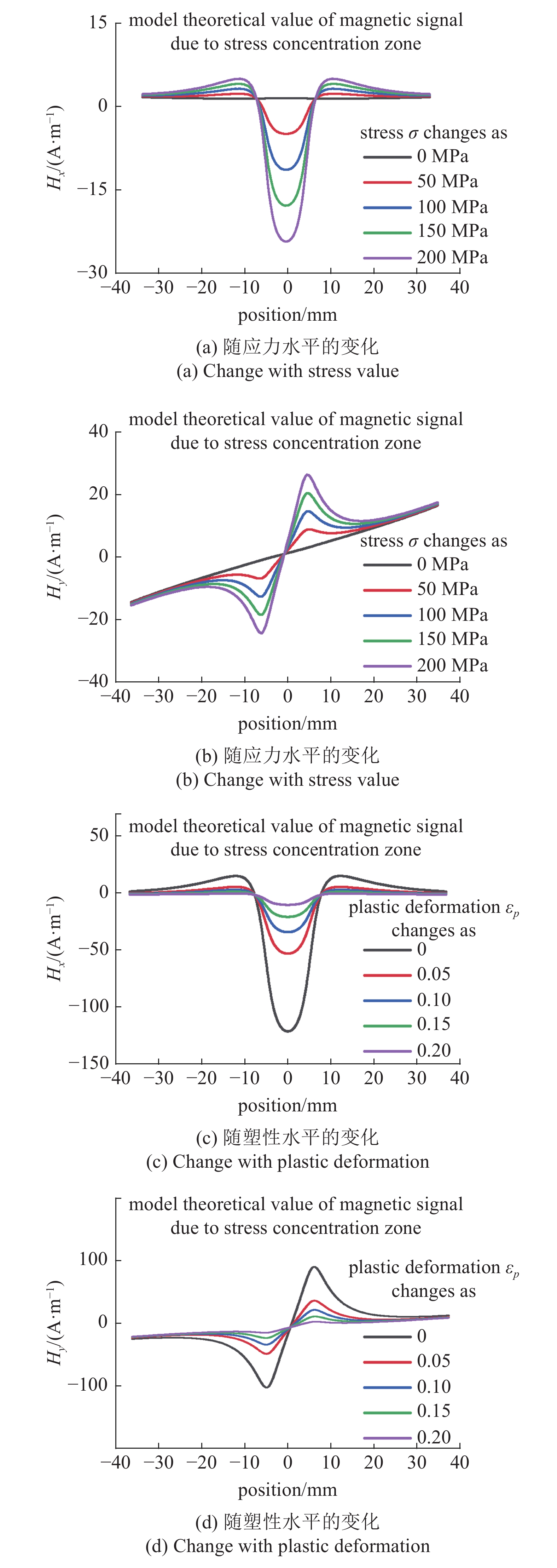
图9给出了应力大小和塑性水平对微磁信号的影响, 应力或塑性区尺寸为$ l = d = 10;{
m{mm}} $, 模型计算所采用的参数与图3所采用的参数保持一致. 当不考虑材料初始磁化时, 图9(a)与图9(b)给出应力集中区的应力值大小对材料表面微磁信号的影响, 在本文的分析讨论中我们假设应力集中区存在应力而材料的其余位置均是无应力状态. 图9(a)与图9(b)可以看出微磁信号随着应力的增大单调增大, 符合实验中观测到的微磁信号值随着应力值的增大而增强的现象. 图9(c)与图9(d)是塑性变形区的塑性程度对材料表面微磁信号的影响. 可以看出微磁信号值随着塑性变形程度的增大逐渐减小, 这是由于塑性变形会导致材料内部的钉扎点增多阻碍了磁畴的进一步转动进而使得材料的磁化强度逐渐减小.



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-9.jpg'"
class="figure_img
figure_type1 bbb " id="Figure9" />



图
9
不同应力或塑性水平对微磁信号的影响规律



Figure
9.
The influence law of different stress or plastic deformation value on micro-magnetic signal



下载:
全尺寸图片
幻灯片



3.5
应力或塑性影响规律的解释


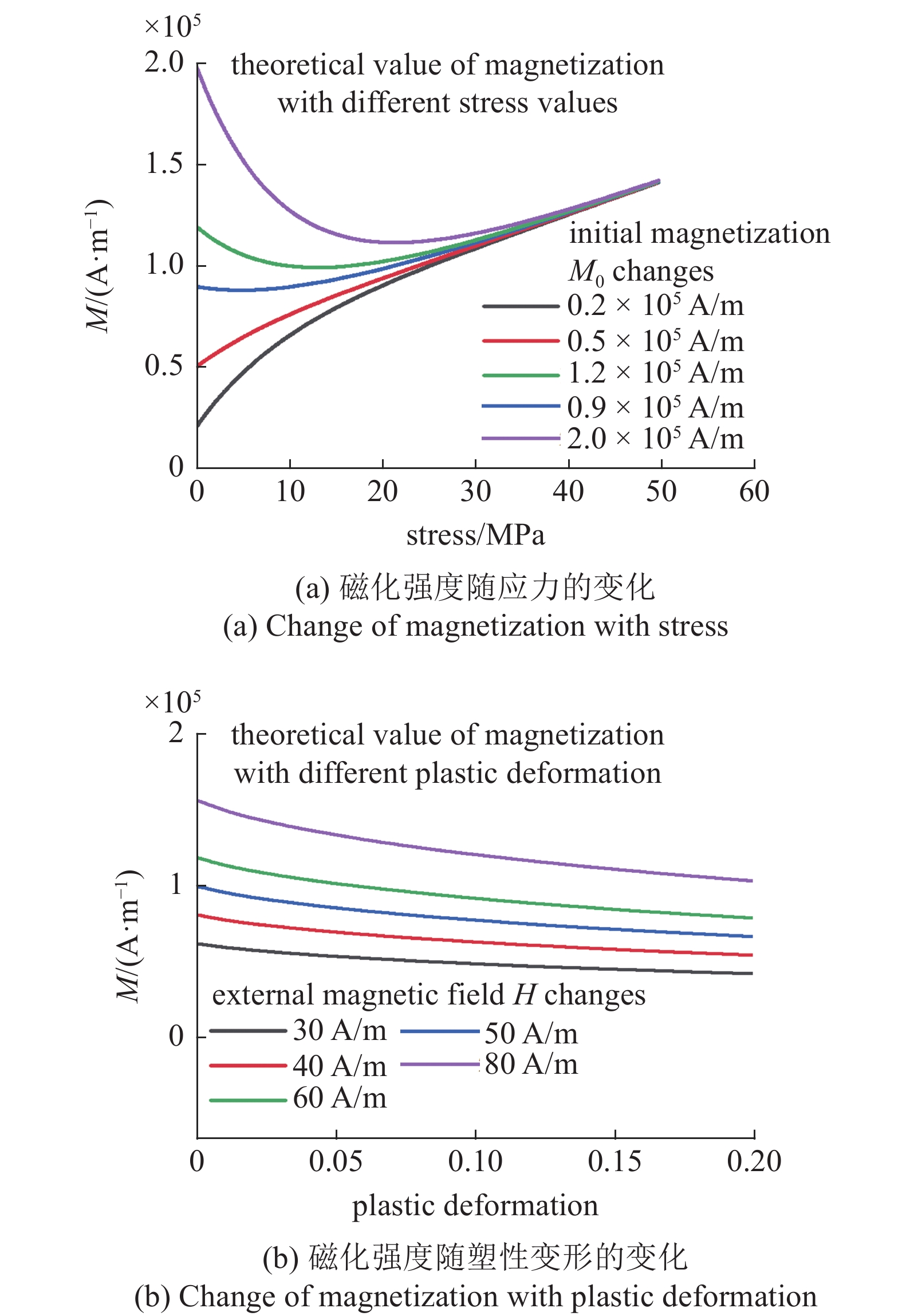
铁磁材料表面某区域存在应力集中或塑性变形时, 图9讨论了应力或塑性变形对微磁信号的影响. 分析模型没有考虑明显宏观损伤等的几何形貌影响, 并且理论研究中忽略微缺陷和微观组织的影响, 所以应力或塑性水平对微磁信号的影响主要源于该区域应力和塑性水平对材料磁化的直接影响. 图10进一步讨论应力和塑性水平对该区域磁化强度的影响. 不同****的微磁信号实验结果揭示的信号随应力的变化规律存在不一致, 即有实验中发现微磁信号强度随应力的增大而增大[34], 而有实验却发现微磁信号强度随应力的增大而减小[35]. 这可以利用不同初始磁化条件下磁化强度随应力的变化规律来解释. 从图10(a)可以看出应力磁化现象受初始磁化的影响. 当初始磁化较高, 应力加卸载过程将使得磁化降低, 导致微磁信号的减小; 反之, 应力加卸载过程将使得磁化单调升高, 导致微磁信号的增大. 图10(b)分析了不同外加磁场下, 材料磁化总是随着塑性增大而减小, 由于微磁信号与材料磁化存在正相关, 这意味着大塑性下钉扎效应的增强是导致微磁信号随塑性变形增大而减小的原因[33].



onerror="this.onerror=null;this.src='https://lxxb.cstam.org.cn/fileLXXB/journal/article/lxxb/2021/12//lxxb2021-325-10.jpg'"
class="figure_img
figure_type1 bbb " id="Figure10" />



图
10
不同应力或塑性水平对磁化强度的影响规律



Figure
10.
The influence of different stress value and plasticity deformation on magnetization



下载:
全尺寸图片
幻灯片



4.
结论


本文通过考虑塑性变形对铁磁材料磁化行为的影响, 基于有效场理论以及接近原理建立了铁磁材料的磁弹塑性耦合模型, 并结合磁场有限元理论分析讨论了应力集中区以及塑性变形区对材料表面微磁信号的影响. 通过与实验结果以及已有理论的对比发现, 本文建立的磁弹塑性耦合模型能够反映铁磁材料的应力磁化行为, 且微磁信号模拟与已有文献的结果十分吻合, 这证实了本文理论分析的正确性. 相比较已有力磁本构模型, 本文模型的主要优势是无磁滞理想磁化可以利用显式表达式直接求解, 这简化了力磁本构模型计算的复杂性, 方便对微磁无损检测中的力学耦合效应进行理论分析.

相关话题/塑性 信号 材料 环境 实验
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 低频振动隔离和能量采集双功能超材料
    引言超材料是一种具有人工周期性设计的复合材料,它具有天然材料所不具备超常物理特性[1-4].例如,由亚波长结构组成的声学超材料具有可以抑制声波或弹性波传播的带隙[5].超材料的应用主要包括机械波衰减[6-8]、低频隔振[9-11]和能量采集[12-13]等.实际的工程中,如一些特殊工况下(飞行器帆板 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度强化学习算法的颗粒材料应力?应变关系数据驱动模拟研究
    引言在研究泥沙、岩土、粉体等颗粒材料宏观力学行为时,通常在连续介质力学框架下建立其唯象本构模型,通过引入内变量来描述颗粒材料的路径相关、历史相关等特性[1-5].虽然基于连续假设的唯象本构模型在描述颗粒材料宏观力学特性时具备很好的工程适用能力,但是颗粒材料由于其自身的离散特性,具有摩擦性,剪胀性,压 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 亚毫米球体撞击液滴过程实验研究
    引言物体撞击液面广泛存在于自然界和工业过程,如昆虫水上行走、弹丸入水、湿法喷淋除尘、原料油催化裂化等[1-5].撞击过程包含液滴飞溅、空穴发展、毛细波传播、气体携带等复杂的流动现象[6-11].物体与气?液界面的相互作用对上述过程有重要影响,对物体撞击液面行为的研究能够为相关工业过程参数设计提供理论 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 均匀电场中气泡上升特性的实验研究
    引言强化传热技术在能源动力、石油工程、航空航天、化工等领域具有广泛的应用前景,而利用电场进行强化换热,能够有效减小换热器的体积和重量,提高能源利用效率[1-2].电场强化沸腾换热技术通过电场力控制气泡的生成、脱离、变形与运动[3-5],降低气泡脱离尺寸[6-7],加速气泡脱离频率[8],从而实现换热 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 水中开孔腔流激振荡控制实验研究
    引言空腔流激振荡是工程中常遇到的一类问题,它是指流体在流经开口结构时,边界层在开口前缘发生流动分离并形成不稳定的自由剪切层,在满足一定的流速和几何特征条件下,会引起剪切层发生稳定的自持振荡,产生很强的周期脉动压力,并通常引起高幅值纯音噪声辐射、附加阻力甚至是结构疲劳.以往对空腔流激振荡的研究主要集中 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 考虑混凝土塑性耗散的CDM-XFEM裂缝计算方法
    引言混凝土结构是建筑、交通、水利等领域的重要基础材料,其可塑性高、耐久性好是受广泛应用的主要原因.但混凝土抗拉强度远低于抗压强度[1],结构在服役期间受外界载荷的影响容易产生裂缝[2],裂缝的出现不仅会降低结构刚度,还为外部侵蚀介质的侵入提供了快捷通道,从而加速内部钢筋锈蚀[3-4]、降低结构承载力 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 倍频激励双转子振动同步机理与实验研究
    引言振动同步可以表征为运动系统根据内部子系统之间的耦合效应调整特征量的变化频率,并使子系统的位移、速度等变量具有一致性和统一性.近年来,由于同步在非线性耦合混沌系统[1-2]、复杂网络系统[3]、多轴控制系统[4-5]、振动筛系统[6-7]等工程技术中具有很高的应用价值和良好的应用前景,已成为国内外 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 颗粒材料计算力学专题序
    颗粒材料广泛地存在于自然环境、工业生产和日常生活等诸多领域,其受加载速率、约束条件等因素的影响具有复杂的力学行为.颗粒材料常与流体介质、工程结构物耦合作用并共同组成复杂的颗粒系统,并呈现出非连续性、非均质性的复杂力学特性.目前,离散元方法已成为解决不同工程领域颗粒材料问题的有力工具,然而其在真实颗粒 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 基于深度学习和细观力学的颗粒材料本构关系研究
    引言颗粒材料广泛存在于各类自然环境和工程活动中,人类几乎所有的基础设施都建造于岩土材料这类典型的颗粒材料上,理解和预测此类材料在外载作用下的力学响应具有重要的意义.岩土材料通常由粒径不一,形状各异的矿物颗粒以及颗粒之间的空隙组成.颗粒间的互相滑动会引起不可恢复的塑性变形,因而,颗粒材料在剪切作用下极 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01
  • 冲击载荷下颗粒材料临边界区域的波动行为及变形特征分析
    引言作为离散颗粒材料的土壤(或岩体),是日常生活中最常见的随机多孔介质,冲击载荷作用下材料的动力学响应对于工程实践和地质灾害防控有着重要的指导意义.注意到应力波的传播行为与介质性质密切相关,基于应力波的行为特征分析可提供一种非侵入式研究颗粒材料性质的途径.因此有非常多的****致力于研究冲击载荷作用 ...
    中科院力学研究所 本站小编 Free考研考试 2022-01-01

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.